Коэффициент перед логарифмом: Логарифм степени (коэффициент перед логарифмом): формула, примеры
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: alogab=b, a>0, a≠1, b>0. Также нужно помнить следующие свойства:
Определение 1- loga1=0 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaa=1logaa=1 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaap=p, при этом a>0, a≠1 и p может быть любым действительным числом.
- loga(x·y)=logax+logay, a>0, a≠1, x>0, y>0. В обобщенном виде это свойство можно представить как loga(x1·x2·…·xn)=logax1+logax2+…+logaxn, a>0, a≠1, x1>0, x2>0, …, xn>0
- ) logaxy=logax-logay.
- logaxy=logax-logay , при этом a>0, a≠1, x>0, y>0.
- logaxy=logax-logay , a>0, a≠1, x>0, y>0.
- logabp=p·logab, при этом a>0, a≠1, b>0, а p может быть любым действительным числом.
- это свойство является следствием предыдущего: logabn=1n·logab , a>0, a≠1, n может быть любым натуральным числом больше 1, b>0.
- logab=logcblogca , при этом a>0, a≠1, b>0, c>0, c≠1.
- свойство, также являющееся следствием: logab=1logba , где a>0, a≠1, b>0, b≠1.
- logaqbp=pq·logab , a>0, a≠1, b>0, p и q могут быть любыми действительными числами, q≠0
- logaqbp=pq , a>0, a≠1, p и q – любые действительные числа, q≠0.

- logaq ap=pq, blogac=clogab , при этом a>0, a≠1, b>0, c>0.
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что bn=b1n , если b≥0. Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
logaq bp=logabploga aq=p·logabq=pq·logab
То же относится и к последнему свойству из списка, выраженному формулой blogac=Clogac=clogab : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой alogab=b, a>0, a≠1, b>0.
Пример 1Условие: преобразуйте и вычислите значение следующих выражений: 1) 5log54 ; 2) 10lg(1+2·π), 3) 2+3log2+3 ln15 ; 4) 2log2(−7); 5) (-5)log-5 e3
Решение
В первом примере прослеживается формула alogab. У нас есть a=5, b=4, что соответствует необходимому условию a>0, a≠1, b>0. Используем нужное равенство alogab=b и получим 5log54=4.
Во втором случае a будет равно 10, b – 1+2·π. Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10lg(1+2·π) =1+2·π.
В третьем выражении у нас есть степень вида alogab, причем a=2+3 и b=ln15. Запишем: 2+3log2+3 ln15=ln15 . Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что -5log-5·e3=e3 , поскольку такое выражение смысла не имеет.
Ответ:1) 5log54=4; 2) 10lg(1+2·π)=1+2·π; 3) 2+3log2+3ln 15=ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1, имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма alogab=b, a>0, a≠1, b>0, но в перевернутом виде, т.е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
Далее возьмем примеры с другими свойствами логарифмов.
Пример 2Условие: вычислите, если возможно: 1) log−21, 2) log11,3) log01, 4) log71, 5) ln1, 6) lg 1,7) log3,751, 8) log5·π71.
Решение
В первых трех примерах мы видим не имеющие смысла выражения log−21, log11, log01. Основанием логарифма не может быть число меньше 1, в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7, e, 10, 3,75 и 5·π7, а под знаками логарифма везде 1. Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Ответ: 1, 2, 3 смысла не имеют; 4) log71=0, 5) ln1=0, 6) lg1=0, 7) log3,751=0, 8) log5·e71=0.
Пример 3Условие: вычислите значения: 1) log1313 , 2) ln e, 3) lg 10,4) log5·π3−2(5·π3−2), 5) log−3(−3), 6) log11.
Решение
Нам потребуется свойство логарифма, выраженное формулой logaa=1 при a>0, a≠1. Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1) log13=13=1, 2) ln e=1, 3) lg10=1, 4) log5·π3−2(5·π3−2)=1; 5,6 не имеют смысла.
Пример 4Условие: вычислите: 1) log3311, 2) log1+22(1+22)723 , 3) logπ5(π5)-2 , 4) log−10(−10)6.
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство logaap=p, где a>0, a≠1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log3311=11
- log1+22(1+2·2)723=723
- logπ5(π5)-2=-2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log−10(−10)6=6 не имеет смысла.

Ответ: 1) log3311=11, 2) log1+22(1+2·2)723=723 , 3) logπ5(π5)-2=-2 , 4) не имеет смысла.
Пример 5Условие: даны выражения log2,64·127, ln2+1π и lg((−5)·(−12)). Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: loga(x·y) = logax+logay, a>0, a≠1, x>0, y>0. В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:
log2,64·127=log2,6 4+log2,6127
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: logaxy=logax-logay, a>0, a≠1, x>0, y>0. Здесь в основании стоит положительное число e, также у нас есть положительный числитель 2+1 и знаменатель π, т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln2+1π=ln2+1-ln π .
Разберем третий пример. Начнем с того, что выражение lg((−5)·(−12)) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа -5 и -12 отрицательны. Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: lg((−5) ·(−12))=lg(5·12)=lg5+lg12.
Ответ: 1) log2,64·127=log2,64+log2,6127 , 2) ln2+1π=ln2+1-ln π , 3) lg((−5)·(−12))=lg5+lg12.
Пример 6Условие: упростите выражения log30,25+log316+log30,5 и ln23-ln13 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Ответ: 1) log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, 2) ln23-ln13=ln 2 .
Пример 7Условие: есть выражения log0,7511, log3-1(3-2+5·673)5+1 и log3(−5)6. Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида logabp. Берем свойство, которое выражается формулой вида
logabp=p·logab, где a>0, a≠1, b>0, p — любое действительное число. Поскольку условия a>0, a≠1, b>0 выполнены, то мы можем преобразовать logabpв произведение p·logab.
- в случае с первым выражением a равно 7, b – пяти и p– 11. Тогда log0,7511=11·log0,75.
- тут a=3-1, b=3-2+5·673, p=5+1 . Нужные условия выполнены, значит, мы можем записать, что:
log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) - у нас есть выражение той же структуры: logabp, a=3, b=−5, p=6, однако одно из условий не выполняется, а именно b у нас меньше 0. Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Ответ: 1) log0,7511=11·log0,75, 2) log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) 3) log3(−5)6=6·log35.
Применение формулы в обратном порядке в виде p·logab=logabp требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
Пример 8Условие: согласно таблице логарифмов, lg2≈0,3010 и lg5≈0,6990. Вычислите, сколько будет log25. Здесь же: запишите ln 11ln 3 в виде логарифма, основание которого равно 3.
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log25=lg 5lg 2
Вычисляем и находим ответ: lg 5lg 2≈0,69900,3010≈2,3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. logcblogca=logab .
Считаем: ln 11ln 3=log311
Ответ: 1) log25≈2,3223, 2) ln 11ln 3=log311 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Пример 9Условие: 1) дан логарифм ln1+π7 . Необходимо избавиться от корня под знаком логарифма; 2) выполните преобразование дроби 1log25 в логарифм с основанием 4; 3) преобразуйте логарифм loge2345 так, чтобы избавиться от степени в основании; 4) вычислите, сколько будет log2-13216 ; 5) осуществите замену 2,3log73 на степень с основанием 3.
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой logabn=1n·logab .В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
- во втором случае нам понадобится формула logab=1logba , примененная в обратном порядке. Получим 1log25=log52.
- здесь нам потребуется свойство logaqbp=pq·logab . Применяем его и получаем loge2345=452·ln 3=25·ln 3.
- в этом случае нам нужно будет следствие, выраженное формулой logaqap=pq: log(2)-13216=16-13=-12
- используем формулу свойства blogac=clogab и вычисляем ответ:
2,3log7·3=3log72,3
Ответ: 1) ln1+π7=17·ln(1+π) ; 2) 1log25=log52 ; 3) loge2345=25·ln 3; 4) log(2)-13216=-12 . 5) 2,3log7·3=3log72,3 .
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Условие: вычислите, сколько будет (log315−log35) ·7log75.
Решение
Мы можем заменить выражение в скобках логарифмом log3(15:5), используя свойство частного. Вычисляем его значение и получаем log3(15:5) =log33=1.
Согласно основному определению логарифма, значением 7log75 будет 5. Подставим в исходное выражение получившиеся результаты и найдем, что (log315−log35) ·7log75=1·5=5.
Вот все решение без комментариев:
(log315−log35)·7log75=log3 (15:5)·5==log33·5=1·5=5
Ответ: (log315−log35) ·7log75=5.
Пример 11Условие: вычислите, чему равен log3log223−1.
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Ответ: log3log223−1=0.
Пример 12Условие: выполните упрощение выражения 3ln 5ln 3log52 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5ln 3 как log35. У нас получилось 3log35log52 . Теперь применяем формулу основного определения логарифма 3log35=5 и получаем, что 3log35log52 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2.
Ответ: 3ln 5ln 3log52=2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log334, 52+log53, lg 0,01. Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
Определение 2- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln2532332 , log381.
- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2log223, 32·log35, 71+log74, 25(log35)-3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log15(0,2)7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число.
 Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log1981 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Пример 13Условие: вычислите или упростите выражения log6216, log3431243, log0,0000010,001.
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 63. Значит, log6216=log663=3.
- у нас есть числа 343 и 1243. Обратимся к таблице степеней и увидим, что их можно представить в виде 73 и 3−4. Выполняем дальнейшие преобразования и получаем:
log3431243=log733-4==-43·log73=-113·log73 - Поскольку 0,000001=10−6 и 0,001=10−3, тогда log0,0000010,001=log10−610−3= -3-6=12
Ответ: 1) log6216=3, 2) log3431243=-113·log73 ; 3) log0,0000010,001=12.
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Пример 14Условие: упростите выражение log3648·log23.
Решение
Выполняем разложение 648 на простые множители.
64832416281931222333
Значит, это число можно представить в виде 648=23·34. Следовательно, log3648·log23=log3(23·34)·log23
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log3(23·34)·log23=(log323+log334)·log23= =(3·log32+4)·log23.
Упрощаем выражение через раскрытие скобок:
(3·log32+4)·log23=3·log32·log23+4·log23.
В полученном выражении log32·log23 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3·log32·log23+4·log23=3·1+4·log23=3+4·log23.
Ответ: log3648·log23=3+4·log23.
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 323·3-2, 2·2273 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 15Условие: найдите значение выражений log52·5-0.5·5-153454 и log372919.
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 52·5−0,5·5−1=52−0,5−1=50,5. Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
53454=5344=534-4=5-314
Полученное выражение подставим в исходный логарифм, применив формулу logaqaq=pq, и получим ответ:
log52·5-0. 5·5-153454=log50.55-314=-3140.5==-13412=-132=-612
5·5-153454=log50.55-314=-3140.5==-13412=-132=-612
Во втором случае представим число 729 как 36 , а 19 как 3−2. Исходный логарифм приобретет вид log3363-2. Используя свойство корня из степени, преобразуем основание логарифма и получим:
336=333=31-3=3-2
Заканчиваем преобразование: log3363-2=log3-23-2=1 .
Ответ: 1) log52·5-0.5·5-153454=-612 ; 2) log372919=1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Пример 16Условие: вычислите значения log13-1132·3+1-5 и log2·cos1(1+cos2)3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
13-1=3+13-1·3+1=3+132-12=3+12
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
132·3+1-5=3+1532=3+1525=3+125
В результате преобразований у нас получился логарифм степени основания log3+123+135 . Значение данного выражения будет равно 5.
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos2a=1+cos2a2 :
log2·cos1(1+cos2)3=log2·cos1(2·cos21)3
Преобразуем второй логарифм, записав его как степень 2·cos2112 или же 2·cos123=2·cos16. Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1) log13-1132·3+1-5=5 ; 2) log2·cos1(1+cos2)3=6 .
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями ap·aq=ap+q. Чаще всего его применяют в обратном порядке, т. е. справа налево.
е. справа налево.
Условие: вычислите значения 3−2+log37 и 0,72−log0,70,1.
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3−2+log37=3−2·3log37. Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3−2·3log37= (19) ·7=79
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0,72−log0,70,1=0,72·0,7−log0,70,1. После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
0,72·0,7−log0,70,1=0,49·0,7log0,710=0,49·10=4,9
Ответ: 1) 3−2+log37=79; 2) 0,72−log0,70,1=4,9.
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой (ap)q=ap·q, например, если у нас есть выражение (eln2)3, то мы можем заключить, что значение части в скобках будет равно 2. Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
e3·ln2=eln2·3=(eln2)3 и (e3)ln2=e3·ln2=eln2·3=(eln2)3.
Посмотрим пример решения такой задачи.
Пример 18Условие: выполните упрощение выражений 2log223−3log23 и 5(log85) −1.
Решение
Отметим, что выражения 2log223и 2log223 не являются равными друг другу. Мы можем представить 2log223 как 2log23·log23. Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Вот запись всего решения:
2log223−3log23=2log23·log23−3log23==(2log23)log23−3log23=3log23−3log23=0
Перейдем ко второму примеру. Запись 25(log85)-1 не будет равна (25log85)−1. Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Так, 25(log85)-1=25log58. Поскольку 25 – это 52, имеем 5log58= (52)log58. То, что у нас получилось, представляем в виде (5log58). Нам осталось только вычислить значение: (5log58)2=82=64.
Ответ: 1) 2log223−3log23=0, 2) 25(log85)−1=64.
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
4−0,5+2·log43=4−0,5·42·log43==12·(4log43)2=12·32=12·9=4,5
Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log0,4253? Отметим, что 25 и 0,4 равны между собой 0,4=410=25, то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Пример 19Условие: вычислите значение выражения log0,46,25.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log0,46,25=log410625100=log25254
Теперь видно, что мы можем преобразовать 254 в виде (25)−2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log25254=log2525-2=-2
Ответ: -2.
Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log3-93-27 или log3((−2)·(−5)).
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log3((−2)·(−5)) к log3(−2)+log3(−5), применить свойство логарифма степени к log2(−2)6 или логарифма частного к log3-93-27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log3((−2)·(−5)). Структура выражения соответствует формуле loga(x·y), где a равно 3, x-3 и y-5. Поскольку условия a>0, a≠1, x>0, y>0 не выполнены, формулу loga(x·y)=logax+logay мы применить не можем, и равенство log3((−2)·(−5)) =log3(−2) +log3(−5) записать нельзя. Преобразования вида log3-93-27=log3-93-log3(-27) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0.
Вернемся опять к нашему примеру. Согласно правилам умножения, (−2)·(−5) =2·5, значит, log3((−2)·(−5))=log3(2·5). К выражению в таком виде мы уже можем применить формулу log3(2·5) =log32+log35. А вот для примера log2(−2)6 нужно будет выполнить следующие действия:
(−2)6= ((−1)·2)6=(−1)6·26=1·26=26
Значит, log2(−2)6=log226=6.
Пример 20Условие: найдите значение выражения log2-163-2-23.
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от -163-2-23 к -163-2-23 . Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
1632-23=2432-23=2432-23=243—23=22log2-163-2-23=log222=2
Ответ: log2-163-2-23=2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как loga(x·y)=loga|x|+loga|y|, где a>0, a≠1, x≠0, y≠0, то после преобразования мы получим log3((−2)·(−5)) =log3|−2|+log3|−5|=log32+log35.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log2(x+1)4. При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле logABp, где A равно 2, B – x+1, а p – четырем.
Мы видим, что заданное выражение соответствует виду logABp, где A=2, B=x+1 и p=4. Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу logabp=p·logab, но это допустимо лишь при условии a>0, a≠1, b>0, p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x+1>0, что аналогично x>−1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Почему надо учитывать область допустимых значений
Продолжая работу с выражением log2(x+1)4, проанализируем, как изменится область значений, когда мы выполним переход к виду 4·log2(x+1). Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Определение 3- когда мы переходим от логарифма произведения к сумме, например, ln(x·(x+3)) =lnx+ln(x+3) сузит нужную область.
- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log2xsin x на log2x−log2sinx .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени logabp=p·logab и формулу logabp=pq·logab . Примеры таких преобразований – logx3(x-8)2=23·logx(x-8) , ln(x+3)−4=−4·ln(x+3).

Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4·log2(x+1) к log2(x+1)4. В этом случае область расширяется от (−1, +∞) до (−∞, −1) ∪ (−1, +∞). Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Пример 21Условие: упростите 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от lg(x+2)7 к 7·lg(x+2) и от lg(x+2)4к 4·lg(x+2), нам нужно, чтобы x+2>0. Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
3·lg(x+2)7−lg(x+2)−5·lg(x+2)4==3·7·lg(x+2)−lg(x+2)−5·4·lg(x+2)==21·lg(x+2)−lg(x+2)−20·lg(x+2)==(21−1−20)·lg(x+2)=0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3·lg(x+2)7-lg(x+2)-5·lg(x+2)4==lg((x+2)7)3-lg(x+2)-lg((x+2)4)5==lg(x+2)21-lg(x+2)-lg(x+2)20==lg(x+2)21(x+2)·(x+2)20=lg1=0
Ответ: 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4=0.
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Пример 22Условие: выполнить упрощение выражения lg(x+2)4−lg(x+2)2.
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x>−2 и x<−2. Если x>−2, то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: lg(x+2)4−lg(x+2)2=4·lg(x+2) −2·lg(x+2) =2·lg(x+2). Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x+2 при x+2<0 как −|x+2|. В таком случае мы можем выполнить переход от lg(x+2)4−lg(x+2)2 к lg(−|x+2|)4−lg(−|x+2|)2, и далее к lg|x+2|4−lg|x+2|2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь |x+2|>0 при любом x.
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при |x+2|<0, имеем 2·lg|x+2|=2·lg(−(x+2)). Это и будет ответом на поставленный вопрос.
Ответ: lg(x+2)4-lg(x+2)2=2·lg(x+2), x+2>02·lg(-(x+2)), x+2<0 . Можно записать ответ компактнее, используя знаки модуля: lg(x+2)4-lg(x+2)2=2·lgx+2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Пример 23Условие: представьте выражение lnx-1·x-2x-3 как сумму и разность логарифмов линейных двучленов x−1, x−2 и x−3.
Решение
Вычисляем область допустимых значений данного выражения:
x-1·x-2x-2>0,(1, 2)∪3, +∞
Поскольку значения x−1, x−2 и x−3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
lnx-1·x-2x-3==ln(x-1)+ln(x-2)-ln(x-3)
А на интервале от одного до двух значение x−1 будет положительным, а x−2 и x−3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
lnx-1·x-2x-3=lnx-1·-x-2-x-3==ln(x-1)·x-2x-3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x−1, |x−2| и |x−3| будут положительными. В итоге имеем:
lnx-1·x-2x-3=ln(x-1)+lnx-2-lnx-3==lnx-1+ln(-(x-2))-ln(-(x-3))
Теперь объединяем получившиеся результаты.
Ответ: lnx-1·x-2x-3=lnx-1+ln(-(x-2))-ln(-(x-3))
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Определение 4- сумма логарифмов loga|X|+loga|Y|, a>0, a≠1 может быть использована вместо логарифма произведения loga(X·Y).
- Разность логарифмов loga|X|−loga|Y|, где a>0, a≠1, X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p·loga|B|, где a>0, a≠1, p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p.
Условие: выполните упрощение выражения 13·log8((x+4)·(x-2))-log8x+413x-2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
(x+4)·(x-2)>0,(x+4)13x-2>0-∞, -4∪2, +∞
У нас получилось, что значения выражений x+4, x−2 и (x+4)13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13·log8((x+4)·(x-2))-log8(x+4)13x-2==13·log8x+4+13·log8x-2—log8x+413-log8x-2==13·log8x+4+13·log8x-2—log8(x+14)13+log8x-2==13·log8x+4-log8(x+4)13+14·log8x-2
Зная свойства модуля, перепишем x+413 в виде x+413 . Значит, что:
Значит, что:
13·log8x+4-log8(x+4)13+14·log8x-2==13·log8x+4-log8x+413+14·log8x-2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13·log8x+4-log8x+413+14·log8x-2==13·log8x+4-13·log8x+4+14·log8x-2==14·log8x-2
Возможны и другие преобразования, которые дают тот же результат:
13·log8((x+4)·(x-2))-log8x+413x-2==log8((x+4)·(x-2))13-log8x+413x-2==log8((x+4)13·(x-2))13-log8x+413x-2==log8(x+4)13·(x-2)13x+413x-2=log8(x-2)14
Поскольку на области допустимых значений x−2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log8(x-2)14=14·log8x-2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14·log8(x−2), который был бы верен при x∈ (2, +∞), однако ошибочен на всей остальной области допустимых значений.
Ответ: 13·log8((x+4)·(x-2))-log8x+413x-2=14·log8x-2 .
Логарифмы. Свойства логарифмов. Формулы с логарифмами. Десятичные, натуральные логарифмы, основное логарифмическое тождество
Определение логарифма
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что ac = b: logab=c⇔ac=b(a>0,a≠1,b>0)      
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Основное логарифмическое тождество alogab=b(a>0,a≠1) (2)
Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Два очевидных следствия определения логарифма logaa=1(a>0,a≠1) (3)
loga1=0(a>0,a≠1) (4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частного loga(bc)=logab+logac(a>0,a≠1,b>0,c>0) (5)
logabc=logab−logac(a>0,a≠1,b>0,c>0) (6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Действительно, выражение loga(f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму logaf(x)+logag(x), мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифма logabp=plogab(a>0,a≠1,b>0) (7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
loga(f(x)2=2logaf(x)Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Формула перехода к новому основанию logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1) (8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
logab=1logba(a>0,a≠1,b>0,b≠1) (9)Десятичные и натуральные логарифмыДесятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy(x>0,y>0).
Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:
logab=lgblga=lnblna(a>0,a≠1,b>0)
Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).
| alogab=b(a>0,a≠1) |
| logaa=1(a>0,a≠1) |
| loga1=0(a>0,a≠1) |
| loga(bc)=logab+logac(a>0,a≠1,b>0,c>0) |
| logabc=logab−logac(a>0,a≠1,b>0,c>0) |
| logabp=plogab(a>0,a≠1,b>0) |
| logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1) |
| logab=1logba(a>0,a≠1,b>0,b≠1) |
Возможно, вас заинтересуют также:
| 1 | Упростить | квадратный корень s квадратный корень s^7 | |
| 2 | Упростить | кубический корень 8x^7y^9z^3 | |
| 3 | Упростить | arccos(( квадратный корень 3)/2) | |
| 4 | Risolvere per ? | sin(x)=1/2 | |
| 5 | Упростить | квадратный корень s квадратный корень s^3 | |
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) 2+n-72)=1/(n+9) |
Как решать логарифмы егэ профиль. Решение логарифмичеких уравнений
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм .
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень. ..
..
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.

- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.
Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
- Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения , но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
log 2 x = 4
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений . Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c одержали, обязательно нужно привести к уравнению вида:
log a f (x ) = log a g (x )
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел , одно из которых вообще не является логарифмом.
- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения , к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
log a f (x ) + log a g (x ) = log a f (x ) · g (x )
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
Как это сделать? Опять вспоминаем замечательную формулу:
a = log b b a
Здесь нужно понимать: когда мы говорим «Любое основание b », то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения , а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
0
Давайте посмотрим, что происходит в нашем случае:
1 = log 2 2 1 = log 2 2
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания . Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
log a b n = n · log a b
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k .
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n
), окажется в числителе. А то, что было степенью у основания, a
k
, отправится в знаменатель.
При этом то, что стояло в аргументе (в нашем случае это коэффициент n
), окажется в числителе. А то, что было степенью у основания, a
k
, отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log 2 2(9x 2 + 5) = log 2 (8x 4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9x 2 + 5) = 8x 4 + 14
Давайте раскроем скобки слева. Получим:
18x 2 + 10 = 8x 4 + 14
Перенесем все из левой части в правую:
8x 4 + 14 − 18x 2 − 10 = 0
Приведем подобные и получим:
8x 4 − 18x 2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4x 4 − 9x 2 + 2 = 0
Перед нами обычное биквадратное уравнение , и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x , а x 2 , потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная . И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x 2 + 5 (эта функция всегда положительна), либо 8x 4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9
Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.
Рациональные корни
Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1.
 Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.
Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ. - Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат , чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81
Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b , именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Непер — Neper — qaz.wiki
Логарифмическая единица для соотношений измерений физических величин поля и мощности
Непер (символ: Np ) является логарифмическая единица для коэффициентов измерений физических полей и энергетических величин, таких как усиление и потери электронных сигналов. Название устройства происходит от имени Джона Напьера , изобретателя логарифмов. Как и в случае децибел и бел , непер — это единица измерения, определенная в международном стандарте ISO 80000 . Он не является частью Международной системы единиц (СИ), но принят для использования вместе с СИ.
Определение
Как и децибел , непер — это единица логарифмической шкалы . В то время как Бел использует декадно (базовые 10) логарифм для вычисления коэффициентов, то непер использует натуральный логарифм , основанный на ряде Эйлера ( е ≈ 2,71828 ). Величина отношения в неперах определяется выражением
- L N п знак равно пер Икс 1 Икс 2 знак равно пер Икс 1 — пер Икс 2 . {\ displaystyle L _ {\ rm {Np}} = \ ln {\ frac {x_ {1}} {x_ {2}}} = \ ln x_ {1} — \ ln x_ {2}.}
где и — интересующие значения (амплитуды), а ln — натуральный логарифм. Когда значения квадратичны по амплитуде (например, мощности), они сначала линеаризуются путем извлечения квадратного корня перед логарифмом, или, что то же самое, результат уменьшается вдвое. {2} & {\ text {dB}} \\ & = 20 \ log _ {10} {\ frac {x_ {1}} {x_ {2}}} & {\ text {dB}} \\ & = \ ln {\ frac {x_ {1}} {x_ { 2}}} & {\ text {Np}}. \\\ конец {выровнено}}}
{2} & {\ text {dB}} \\ & = 20 \ log _ {10} {\ frac {x_ {1}} {x_ {2}}} & {\ text {dB}} \\ & = \ ln {\ frac {x_ {1}} {x_ { 2}}} & {\ text {Np}}. \\\ конец {выровнено}}}
Как и децибел, непер — безразмерная единица. Международный союз электросвязи (МСЭ) признает оба устройства. Только непер является когерентным с СИ.
Приложения
Непер — это естественная линейная единица относительной разницы , означающая, что в неперах (логарифмических единицах) относительные разности складываются, а не умножаются. Это свойство используется совместно с логарифмическими единицами в других основаниях, например, в бел.
Особенно к непер, однако, является то , что полученный блок centineper является асимптотически равной разности процентного при очень малых разностей — так как производная натурального логарифма (при 1) = 1; это не используется совместно с другими логарифмическими единицами, которые вводят коэффициент масштабирования из-за того, что производная не равна единице. Таким образом, сентинепер можно использовать как линейную замену процентной разницы. Линейное приближение для небольших процентных различий,
- ( 1 + δ ) ( 1 + ϵ ) знак равно 1 + δ + ϵ + δ ϵ ≈ 1 + δ + ϵ , {\ displaystyle (1+ \ delta) (1+ \ epsilon) = 1 + \ delta + \ epsilon + \ delta \ epsilon \ приблизительно 1+ \ delta + \ epsilon,}
широко используется, особенно в финансах — см., например, уравнение Фишера . Однако это только приблизительное значение, с увеличением погрешности при больших процентных изменениях. Эти линейные аппроксимации, измеренные вместо этого в сантинеперах, могут быть заменены точными равенствами и применимы к любому изменению величины, определяя следующую величину сантинепера для любого изменения δ {\ displaystyle \ delta}
D δ знак равно 100 пер ( 1 + δ ) — 1 1 знак равно 100 пер δ {\ displaystyle D _ {\ delta} = 100 \ ln {\ frac {(1+ \ delta) -1} {1}} = 100 \ ln \ delta}
Смотрите также
Рекомендации
дальнейшее чтение
- Туффенцаммер, Карл (1956).
 «Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [Децилог, мост между логарифмами, децибелами, непер и предпочтительными числами]. VDI-Zeitschrift (на немецком языке). 98 : 267–274.
«Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [Децилог, мост между логарифмами, децибелами, непер и предпочтительными числами]. VDI-Zeitschrift (на немецком языке). 98 : 267–274. - Паулин, Евгений (01.09.2007). Logarithmen, Normzahlen, Dezibel, Neper, Phon — natürlich verwandt! [ Логарифмы, предпочтительные числа, децибел, непер, фон — естественно связаны! ] (PDF) (на немецком языке). Архивировано (PDF) из оригинала 18 декабря 2016 года . Проверено 18 декабря 2016 .
внешняя ссылка
<img src=»https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>Почему релятивизм не проявился в коэффициенте перед логарифмом в формуле?
Причина в том, что этот коэффициент, как видно из вывода формулы, определяется величиной переданного импульса pe = F t. В случае релятивистских скоростей максимальное значение силы F, действующей со стороны частицы на электрон, увеличивается на множитель .
(Как указано в Теории поля, Ланд., Лифшиц закон Кулона пишется в особой системе координат, «сжатой» вдоль оси координат, вдоль которой движется частица )
С другой стороны время взаимодействия t уменьшается на множитель γ. Произведение их остается неизменным.
Рис. 3 Зависимость средних удельных ионизационных потерь энергии тяжелых частиц в свинце от энергии. Вся сложная кривая рисунка разделена буквами А, В, С, D, E, F
на отдельные участки с характерным для них поведением этой зависимости.
Зависимость ионизационных потерь от параметров частицы
(важное уточнение: до остановки частицы еще далеко)
1. Удельные ионизационные потери энергии (или линейная тормозная способность вещества):
пропорциональны квадрату заряда
частицы:
.
Это означает, что при одинаковой скорости ядро железа (z=26) теряет на ионизацию вещества в 676 раз больше энергии, чем протон.
2. Удельные потери не зависят от массы частицы М. Это получается из-за того,
что происходит взаимодействие электрических зарядов частиц, а не их масс. Однако, если сопоставлять потери на ионизацию различных частиц с одинаковой кинетической энергией, тогда в коэффициент перед логарифмическим членом неизбежно
войдет масса частицы, так как V2~ E/M. Поскольку в нерелятивистском случае ионизационные потери обратно пропорциональны квадрату скорости частицы:
, то .
Следовательно, частицы с одинаковой кинетической энергией теряют ее на ионизацию тем больше, чем больше их масса. Например, на единице своего пути дейтрон теряет на ионизацию энергию в 2 раза большую, чем протон с такой же кинетической энергией, а мюон в ~ 9 раз меньшую.
Рис. 1. Зависимость удельной потери энергии в воздухе от энергии частицы для нескольких типов частиц
Другой вариант иллюстрации ионизационных потерь энергии частицами с различными массами в кремнии представлен на рис. 2. (Почему в кремнии?)
Здесь потери энергии приведены не на единицу длины пути (в см), а на толщу вещества мг/см2 – т.е. .
Массовая тормозная способность:
Рис.2. Ионизационные потери заряженных
частиц в кремнии .
3. Удельные потери энергии на единице пути являются довольно сложной функцией скорости (и, следовательно, кинетической энергии) частицы. Эта зависимость схематически изображена на рис.3 , где по оси абсцисс отложена кинетическая энергия в единицах своей собственной энергии массы покоя Mc2, а по оси ординат – средние удельные потери энергии этой частицей на ионизацию среды.
Рис. 3 Зависимость средних
удельных ионизационных потерь энергии
тяжелых частиц в свинце от энергии. Вся
сложная кривая рисунка разделена буквами
А, В, С, D, E, F
Вся
сложная кривая рисунка разделена буквами
А, В, С, D, E, F
на отдельные участки с характерным для них поведением этой зависимости.
(BC). Участок (ВС) соответствует случаю, когда с, одной стороны, частица нерелятивистская, т.е. E < Mc2 и < 1, другой стороны, она настолько быстрая, что все электроны атомов могут считатьсясвободными. Поведение кривой в этой области (ВС) определяется коэффициентом перед квадратными скобками в формуле Бете-Блоха:
т.е. .
Такая зависимость в нерелятивистской области получилась из-за того, что переданный электрону импульс pe = F t, зависит от времени взаимодействия t, которое, в свою очередь, обратно пропорционально скорости частицы t ~ 1/ V. Переданная же
электрону энергия, потерянная частицей ~ 1/ V2 , и , следовательно , ~ 1/E.
Зависимость имеет место вплоть до релятивистских скоростей. При V ≈ c коэффициент перед скобкой принимает минимальное значение.
(CD). На участке (СD) кривой (см. рис.4) удельные ионизационные потери начинают увеличиваться. Этот рост потерь обусловлен ростом величины логарифмического члена, так как при 1 .
Поскольку этот множитель стоит под знаком логарифма, то и рост потерь наблюдается медленный — «логарифмический». Логарифмическое возрастание с увеличением энергии обычно называют релятивистским подъемом ионизации. Он начинается после того, как достигнет минимальной величины при V 0.96с. Частично этот подъем
происходит за счет близких столкновений,
так как увеличивается максимальная
передаваемая энергия Emaх
, а частично за счет далеких столкновений
из-за релятивистского увеличения bmax.
Рост потерь, обусловленный вторым
фактором, происходит из-за релятивистского
сжатия кулоновского поля частицы в
продольном направлении (вдоль траектории
частицы) и возрастания поля в поперечном
направлении. Рис.5 иллюстрирует сказанное:
для нерелятивистских частиц
эквипотенциальная поверхность имеет
сферически симметричную форму (а), а
форма эквипотенциальной поверхности
поля релятивистских частиц другая (б):
расстояние в продольном направлении
уменьшается в раз, а в поперечном — увеличивается в
раз, получается эллипсоид, «блин»,
который с увеличением скорости частицы
все более сплющивается в продольном
направлении и увеличивается в поперечном. Это означает, что все большее число
электронов среды попадает в поле
воздействия летящей частицы. Растет
bmax и все большему числу электронов
частица передает свою энергию.
Следовательно, и потери энергии частицей
на единице ее пути растут.
Это означает, что все большее число
электронов среды попадает в поле
воздействия летящей частицы. Растет
bmax и все большему числу электронов
частица передает свою энергию.
Следовательно, и потери энергии частицей
на единице ее пути растут.
Рис. Форма эквипотенциальной поверхности кулоновского поля: (а) для нерелятивистской, (б) релятивисткой скорости частицы
4.3 — Свойства логарифмов
4.3 — Свойства логарифмовИзменение базовой формулы
Одна дилемма состоит в том, что в вашем калькуляторе есть логарифмы только для двух оснований. База 10 (журнал) и база e (ln). Что произойдет, если вы захотите узнать логарифм для какой-то другой базы? Вам не повезло?
№ Изменена базовая формула для преобразования между разными базами. К найти базу журнала a, где a предположительно некоторое число, отличное от 10 или e , в противном случае вы просто использовали бы калькулятор,
Возьмите журнал аргумента, разделенный на журнал основания.
журнал a x = (журнал b x) / (журнал b a)
Там нет необходимости использовать основание 10 или e , но поскольку это два у вас есть на калькуляторе, вероятно, это те два, которые вы собираетесь использовать больше всего. Я предпочитаю натуральный журнал (ln — всего 2 буквы, а log — 3, плюс есть дополнительная выгода, о которой я знаю из расчетов). База, которая вы используете не имеет значения, только то, что вы используете одну и ту же базу для числителя и знаменатель.
журнал a x = (журнал x) / (журнал a) = (ln x) / (ln a)
Пример: журнал 3 7 = (ln 7) / (ln 3)
Логарифмы — экспоненты
Помните, что логарифмы — это показатели степени, поэтому свойства показателей свойства логарифмов.
Умножение
Какое правило, когда вы умножаете два значения с одинаковым основанием вместе
(x 2 * x 3 )? Правило состоит в том, что вы сохраняете базу и добавляете
экспоненты. Что ж, помните, что логарифмы — это показатели, и когда вы умножаете,
вы собираетесь сложить логарифмы.
Что ж, помните, что логарифмы — это показатели, и когда вы умножаете,
вы собираетесь сложить логарифмы.
журнал продукта — это сумма журналов.
журнал a xy = журнал a x + журнал a y
Дивизион
Правило при делении двух значений с одинаковым основанием — вычесть экспоненты. Следовательно, правило деления — вычитание логарифмов.
логарифм частного — это разница журналов.
журнал a (x / y) = журнал a x — журнал a y
Возведение в степень
Когда вы возводите количество в степень, правило состоит в том, что вы умножаете показатели все вместе. В этом случае одним из показателей будет лог, а другим — экспонента будет степенью, до которой вы увеличиваете количество.
Показатель аргумента — это коэффициент журнала.
журнал a x r = r * журнал a x
Мелодическая математика
Некоторые из приведенных выше утверждений очень мелодичны.То есть звучат хорошо. Это может помочь вам запомнить мелодическую математику, а не формулы.
- Журнал продукта представляет собой сумму логов
- Сумма журналов — это журнал продуктов
- Логарифм частного — разность бревен
- Разница журналов — это журнал частного
- Показатель аргумента — это коэффициент журнала
- Коэффициент логарифма — это показатель степени при аргументе
Ладно, последние два не такие мелодичные.
Общие ошибки
Я почти не решаюсь помещать здесь этот раздел. Кажется, когда я пытаюсь указать ошибка, которую люди собираются совершить, что больше людей совершают ее.
- журнал суммы НЕ является суммой журналов. Сумма журналов — это журнал
продукт. Журнал суммы не может быть упрощен.
журнал a (x + y) ≠ журнал a x + журнал a y - журнал разницы НЕ является разницей журналов.
 Разница
журналы — это журнал частного. Журнал различий не может быть упрощен.
Разница
журналы — это журнал частного. Журнал различий не может быть упрощен.
журнал a (x — y) ≠ журнал a x — журнал a y - An
показатель степени в журнале НЕ является коэффициентом журнала. Только когда аргумент
возведен в степень, можно превратить показатель степени в коэффициент. Когда
весь логарифм возведен в степень, то его нельзя упростить.
(бревно a x) r ≠ r * журнал a x - журнал частного не является частным из журналов.Частное бревен
от изменения базовой формулы. Журнал частного — это разница
журналов.
журнал a (x / y) ≠ (журнал a x ) / (журнал a г)
Основные правила журнала и расширяющиеся выражения журнала
Purplemath
Вы изучили различные правила для манипулирования и упрощения выражений с показателями, например, правило, которое гласит, что x 3 × x 5 равно x 8 , потому что вы можете складывать экспоненты.Аналогичные правила для логарифмов.
Правила журнала:
1) журнал b ( mn ) = журнал b ( m ) + журнал b ( n )
2) бревно b ( м / n ) = бревно b ( м ) — бревно b ( n )
3) бревно b ( м n ) = n · лог b ( м )
MathHelp.
 com
comМенее формально правила журнала могут быть выражены как:
1) Умножение внутри журнала можно превратить в сложение вне журнала, и наоборот.
2) Деление внутри журнала можно превратить в вычитание вне журнала, и наоборот.
3) Показатель степени для всего, что находится внутри бревна, можно вынести вперед как множитель, и наоборот.
Предупреждение: как и в случае с экспонентами, приведенные выше правила работают только , если основания совпадают. Например, выражение «log d ( m ) + log b ( n )» нельзя упростить, потому что основания («d» и «b») не совпадают, просто как x 2 × y 3 нельзя упростить, потому что основания ( x и y ) не совпадают.
Расширяющиеся логарифмы
Правила журнала могут использоваться для упрощения (или, точнее, для «уплотнения») выражений, для «расширения» выражений или для поиска значений. Начнем с расширения.
Когда в инструкциях говорится «расширить», они означают, что они дали мне одно выражение журнала с большим количеством информации внутри него, и они хотят, чтобы я использовал правила журнала, чтобы разбить журнал на множество отдельных терминов журнала, каждый из которых имеет только одна вещь внутри своего конкретного журнала.То есть они дали мне , один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
В этом случае у меня внутри журнала есть «2 x ». Поскольку «2 x » — это умножение, я могу разделить это выражение в соответствии с первым из приведенных выше правил журнала и превратить его в сложение вне журнала:
журнал 3 (2 x ) = журнал 3 (2) + журнал 3 ( x )
Тогда ответ, который они ищут:
Примечание: не пытайтесь вычислить «журнал 3 (2)» в вашем калькуляторе.Хотя вы будете правы, если скажете, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить в своем калькуляторе), то что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Если вы дадите «ответ» в виде десятичного приближения, вы должны ожидать потерю баллов.
У меня внутри журнала деление.Согласно второму правилу журнала, приведенному выше, его можно разделить на части как вычитание вне журнала, так:
журнал 4 ( 16 / x ) = журнал 4 (16) — журнал 4 ( x )
Первый член в правой части приведенного выше уравнения можно упростить до точного значения, применив основное определение логарифма. В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
Затем исходное выражение полностью раскрывается как:
журнал 4 ( 16 / x ) = 2 — журнал 4 ( x )
Всегда не забывайте находить время, чтобы проверить, можно ли упростить какие-либо термины в вашем расширении (например, журнал 4 (16) выше).
Показатель внутри бревна можно вынести вперед как множитель:
log 5 ( x 3 ) = 3 · log 5 ( x ) = 3log 5 ( x )
Приведенные выше примеры представляют собой очень простое использование правил журнала применительно к раскрытию выражений журнала. На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
URL: https://www.purplemath.com/modules/logrules.htm
Логарифмический коэффициент
Коэффициент, который появляется в члене в логарифмической форме, называется логарифмическим коэффициентом.
Введение
Логарифмические члены обычно образуются путем вовлечения хотя бы одной величины в логарифмическую форму.Если величина в логарифмической форме умножается на другую величину, чтобы сформировать логарифмический член, то величина в логарифмической форме называется логарифмическим коэффициентом для оставшейся величины.
Примеры
Посмотрите следующие примеры, чтобы понять, как определять логарифмические коэффициенты в логарифмических единицах.
$ (1) \, \, \, \, \, \, $ \ log_ {5} {16} $
Логарифм от 16 $ до основания 5 $ — это логарифм. Кажется, что нет никаких других факторов, участвующих в формировании термина $ \ log_ {5} {16} $, но он записывается один раз.Следовательно, $ \ log_ {5} {16} $ означает однократный $ \ log_ {5} {16} $.
$ \ implies \ log_ {5} {16} \, = \, 1 \ times \ log_ {5} {16}
$$ \ log_ {5} {16} $ называется коэффициентом логарифма $ 1 $.
$ (2) \, \, \, \, \, \, $ $ — \ log_ {e} {9} $
Как и в предыдущем случае, отрицательный знак логарифма от $ 9 $ до основания $ e $ математически записывается следующим образом. 2}} $
2}} $
Логарифмический член также может быть записан в форме продукта с помощью правила базового журнала обмена.2} {a} $ называется логарифмическим коэффициентом $ -0,5 $.
11 правил естественного журнала, которые необходимо знать
Если вы изучаете математику в средней школе или колледже, вы, скорее всего, будете изучать натуральный логарифм. Но что такое натуральные бревна? Что такое ln? Почему продолжает появляться буква е?
Естественный журнал может показаться сложным, но как только вы поймете несколько ключевых правил естественного журнала, вы сможете легко решать даже очень сложные на вид проблемы. В этом руководстве мы объясним четыре наиболее важных правила натурального логарифма, обсудим другие свойства натурального логарифма, которые вам следует знать, рассмотрим несколько примеров различной сложности и объясним, чем натуральные логарифмы отличаются от других логарифмов.
Что такое ln?
Натуральный логарифм, или ln, является обратной величиной e . Буква « e » представляет математическую константу, также известную как естественный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e равно примерно 2,71828.
e встречается во многих случаях в математике, в том числе в сценариях, касающихся сложных процентов, уравнений роста и уравнений распада.ln ( x ) — это время, необходимое для увеличения до x , а e x — это величина роста, произошедшая по прошествии времени x .
Поскольку e так часто используется в математике и экономике, и людям в этих областях часто требуется логарифм с основанием e числа, чтобы решить уравнение или найти значение, натуральный логарифм был создан как Быстрый способ записи и расчета базы журнала e . Естественный журнал просто позволяет людям, читающим задачу, знать, что вы берете логарифм числа с основанием e . Таким образом, ln ( x ) = log e ( x ). Например, ln ( 5 ) = log e ( 5 ) = 1,609.
Таким образом, ln ( x ) = log e ( x ). Например, ln ( 5 ) = log e ( 5 ) = 1,609.
Четыре основных правила естественного журнала
Есть четыре основных правила, которые вам нужно знать при работе с естественным логарифмом, и вы будете встречать каждое из них снова и снова в своих математических задачах. Хорошо их знайте, потому что они могут сбить с толку, когда вы их впервые увидите, и вы хотите убедиться, что у вас есть такие базовые правила, прежде чем переходить к более сложным темам логарифмирования.
Правило продукта
- ln (x) (y) = ln (x) + ln (y)
- Натуральный логарифм умножения x и y — это сумма ln x и ln y.
- Пример: ln (8) (6) = ln (8) + ln (6)
Правило частного
- ln (x / y) = ln (x) — ln (y)
- Натуральный логарифм деления x и y — это разность ln x и ln y.
- Пример: ln (7/4) = ln (7) — ln (4)
Взаимное правило
- ln (1 / x) = −ln (x)
- Натуральный логарифм обратной величины x противоположен ln x.
- Пример: ln (⅓) = -ln (3)
Правило мощности
- ln ( x y ) = y * ln (x)
- Натуральный логарифм числа x в степени y равен y умноженному на ln числа x.
- Пример: ln (5 2 ) = 2 * ln (5)
Ключевые свойства натурального бревна
В дополнение к четырем правилам натурального логарифма, описанным выше, также есть несколько свойств ln, которые вам необходимо знать, если вы изучаете натуральные логарифмы. Запомните их, чтобы вы могли быстро перейти к следующему этапу решения, не тратя время на попытки запомнить общие свойства ln.
Сценарий | ln Имущество |
ln отрицательного числа | Длина отрицательного числа не определена |
пер 0 | ln (0) не определено |
пер 1 | ln (1) = 0 |
Линия Infinity | ln (∞) = ∞ |
пер е | ln (эл. |
ln e повышен до x мощности | лин ( e x ) = x |
e повышен до мощности | e ln (x) = x |
Как видно из последних трех строк, ln ( e ) = 1, и это верно, даже если одна возведена в степень другой.Это потому, что ln и e являются обратными функциями друг друга.
Задачи выборки натурального журнала
Теперь пришло время проверить свои навыки и убедиться, что вы понимаете правила ln, применяя их к примерам задач. Ниже приведены три примера проблем. Попытайтесь решить их самостоятельно, прежде чем читать объяснение.
Проблема 1
Оценить ln (7 2 /5)
Сначала мы используем правило частного, чтобы получить: ln (7 2 ) — ln (5).
Затем мы используем правило мощности, чтобы получить: 2ln (7) -ln (5).
Если у вас нет калькулятора, вы можете оставить уравнение в таком виде или вычислить значения натурального логарифма: 2 (1,946) — 1,609 = 3,891 — 1,609 = 2,283.
Проблема 2
Оценить ln ( e ) / 7
Для этой задачи нам нужно запомнить, что ln ( e ) = 1
Это означает, что задача упрощается до 1/7, что и является нашим ответом.
Проблема 3
Решить ln (5 x -6) = 2
Когда у вас есть несколько переменных в круглых скобках, вы хотите сделать e основанием, а все остальное — показателем степени e . Тогда вы получите ln и e рядом друг с другом и, как мы знаем из правил естественного журнала, e ln (x) = x.
Итак, уравнение принимает вид e ln (5x-6) = e 2
Начиная с e ln (x) = x , e ln (5x-6) = 5x-6
Следовательно 5 x -6 = e 2
Поскольку e является константой, вы можете вычислить значение e 2 , либо используя клавишу e на вашем калькуляторе, либо используя оценочное значение e, равное 2. 718.
718.
5 x -6 = 7,389
Теперь добавим 6 к обеим сторонам
5 x = 13,389
Наконец, мы разделим обе стороны на 5.
х = 2,678
Чем натуральные логарифмы отличаются от других логарифмов?
Напоминаем, что логарифм — это противоположность степени. Если вы возьмете журнал числа, вы отмените экспоненту. Ключевое различие между натуральным логарифмом и другими логарифмами заключается в используемом основании.В логарифмах обычно используется основание 10 (хотя это может быть другое значение, которое будет указано), тогда как в натуральных логарифмах всегда будет использоваться основание e .
Это означает, что ln (x) = log e ( x )
Если вам нужно преобразовать логарифм в натуральный логарифм, используйте следующие два уравнения:
- журнал 10 ( x ) = ln (x) / ln (10)
- ln (x) = log 10 ( x ) / log 10 ( e )
За исключением разницы в основании (которая является большой разницей) правила логарифмирования и правила натурального логарифма одинаковы:
Правила логарифмирования | Правила |
журнал (xy) = журнал (x) + журнал (y) | ln (x) (y) = ln (x) + ln (y) |
журнал (x / y) = журнал (x) −log (y) | ln (x / y) = ln (x) −ln (y) |
журнал (x a ) = a журнал ( x ) | лин (x a ) = a ln ( x ) |
журнал (10 x ) = x | лин ( e x ) = x |
10 журнал (x) = x | e ln (x) = x |
Резюме: Правила естественного журнала
Натуральный логарифм или ln — это величина, обратная e. Правила естественного журнала сначала могут показаться нелогичными, но как только вы их изучите, их довольно просто запомнить и применить к практическим задачам.
Правила естественного журнала сначала могут показаться нелогичными, но как только вы их изучите, их довольно просто запомнить и применить к практическим задачам.
Четыре основных правила ln:
- ln (x) (y) = ln (x) + ln (y)
- ln (x / y) = ln (x) — ln (y)
- лин (1 / x) = — ln (x)
- n ( x y ) = y * ln (x)
Ключевое различие между натуральным логарифмом и другими логарифмами заключается в используемом основании.
Что дальше?
Пишете исследовательскую работу для школы, но не знаете, о чем писать? В нашем справочнике по темам исследовательских работ более 100 тем в десяти категориях, так что вы можете быть уверены, что найдете идеальную тему для себя.
Хотите узнать о самых быстрых и простых способах конвертации между градусами Фаренгейта и Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градусы Фаренгейта (или наоборот).
Сдаете SAT или ACT? Студенты часто испытывают трудности с математическим разделом этих тестов, но ознакомьтесь с нашими подробными руководствами по SAT Math и ACT Math, где вы найдете все, что вам нужно знать, чтобы сдать эти вопросы по математике.
Работа с логарифмами | Безграничная алгебра
Логарифмы произведений
Полезное свойство логарифмов гласит, что логарифм произведения двух величин является суммой логарифмов двух множителей.В символах [латекс] \ log_b (xy) = \ log_b (x) + \ log_b (y). [/ Latex]
Цели обучения
Свяжите правило продукта для логарифмов с правилами работы с показателями степени и используйте это правило для перезаписи логарифмов продуктов
Основные выводы
Ключевые моменты
- Логарифм произведения — это сумма логарифмов факторов.
- Правило произведения не применяется, если основания двух логарифмов различаются.

Ключевые термины
- показатель степени : Степень возведения числа, символа или выражения.{\ log_b (z)} = z [/ латекс]
Правило произведения для логарифмов
Логарифмы были введены Джоном Нэпиром в начале 17 века как средство упрощения вычислений. Логарифмы были быстро приняты навигаторами, учеными, инженерами и другими, чтобы упростить вычисления с помощью правил скольжения и таблиц логарифмов. Утомительные шаги многозначного умножения можно заменить поиском в таблице и более простым сложением, поскольку логарифм произведения является суммой логарифмов факторов:
[латекс] \ displaystyle log_b (xy) = log_b (x) + log_b (y) [/ latex]
Мы можем видеть, что это правило верно, если записать логарифмы в виде экспонент.p) = p \ log_b (x). [/ latex]
Цели обучения
Свяжите правило степени для логарифмов с правилами работы с показателями степени и используйте это правило для перезаписи логарифмов степеней
Основные выводы
Ключевые моменты
- Логарифм произведения — это сумма логарифмов факторов.
- Показатель степени [latex] p [/ latex] означает, что число умножается само на себя [latex] p [/ latex] количество раз. Поскольку логарифм продукта является суммой логарифмов факторов, логарифм числа [латекс] x [/ латекс] до степени [латекс] p [/ латекс] совпадает с логарифмом of [latex] x [/ latex] сложено вместе [latex] p [/ latex] раз, так что оно равно [latex] p \ log_b (x).3) \\ x + 1 & = 3 \ log_2 (10) \\ x & = 3 \ log_2 (10) -1 \ end {align} [/ latex]
Следовательно, решением будет [латекс] x = 3 \ log_2 (10) -1. [/ латекс]
Логарифмы частных
Логарифм отношения двух величин — это разность логарифмов величин. В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex]
Цели обучения
Свяжите правило частного для логарифмов с правилами работы с показателями и используйте это правило для переписывания логарифмов частных
Основные выводы
Ключевые моменты
- Логарифм числа — это показатель степени, на который нужно возвести другое фиксированное значение, основание, чтобы получить это число.
 3 [/ латекс].
3 [/ латекс].
Мы уже видели, что логарифм произведения — это сумма логарифмов множителей:
[латекс] \ displaystyle \ log_b (xy) = \ log_bx + \ log_by [/ latex]
Аналогично, логарифм отношения двух величин есть разность логарифмов:
[латекс] \ displaystyle \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — log_by. [/ Latex]
Мы можем показать, что это правда, на следующем примере:
Пусть [латекс] u = \ log_b x [/ latex] и [латекс] v = \ log_b y [/ latex].{100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс]
Изменение логарифмического основания
Логарифм, записанный с одним основанием, может быть преобразован в равную величину, записанную с другим основанием.
Цели обучения
Используйте формулу изменения основания для преобразования логарифмов в разные основания
Основные выводы
Ключевые моменты
- Основание логарифма можно изменить, выразив его как частное двух логарифмов с общим основанием.
- Изменение основания логарифма на [латекс] 10 [/ латекс] значительно упрощает вычисление; это можно сделать на калькуляторе.
Ключевые термины
- логарифм : Логарифм числа — это показатель степени, на который необходимо увеличить другое фиксированное значение, основание, чтобы получить это число.
- основание : Число в степени экспоненты.
Большинство обычных научных калькуляторов имеют ключ для вычисления логарифмов с основанием [латекс] 10 [/ latex], но не имеют ключей для других оснований.2 [/ latex], но получить точное приближение сложно. К счастью, может помочь изменение базовой формулы.
Изменение базовой формулы
Изменение базовой формулы логарифмов:
[латекс] \ displaystyle \ log_a (x) = \ frac {\ log_b (x)} {\ log_b (a)} [/ latex]
Таким образом, например, мы могли бы вычислить, что [latex] \ log_4 (9) = \ frac {\ log_ {10} (9)} {\ log_ {10} (4)} [/ latex], которое может быть вычислено на практически любой карманный калькулятор. z = \ log_bx [/ latex]
Использование правила мощности дает:
[латекс] \ Displaystyle Z \ cdot \ log_ba = \ log_b x [/ латекс]
Разделив обе стороны на [latex] \ log_ba [/ latex], получим:
[латекс] \ displaystyle z = {\ log_b x \ over \ log_ba}.2 + 1 \ over \ log_ {10} 5}. [/ латекс]
Использование преобразования логарифма в регрессии и прогнозировании
Концепции данных
Принципы и риски прогнозирования (pdf)
Знаменитое предсказание котировки
Как перемещать данные вокруг
Познакомьтесь с вашими данными
Корректировка инфляции (дефляция)
Сезонная корректировка
Стационарность и дифференциация
Логарифм преобразованиеВ преобразование логарифма
Введение в логарифмы : Логарифмы — одни из самых важные математические инструменты в инструментарии статистического моделирования, поэтому вы необходимо хорошо знать их свойства и способы использования. А функция логарифма определяется по «основанию», которое является положительное число: , если b обозначает базовое число, то Логарифм X по основанию b — это, по определению, число Y такое, что b Y = Х . Например, база-2 логарифм 8 равен 3, потому что 2 3 = 8, а по основанию 10 логарифм 100 равен 2, потому что 10 2 = 100. Есть три вида логарифмов. в стандартном использовании: логарифм с основанием 2 (преимущественно используется в информатике и теория музыки), десятичный логарифм (в основном используется в инженерии), и натуральный логарифм (преимущественно используется в математике и физика и в экономике и бизнесе ).В функции натурального журнала основание число — это трансцендентное число « e» чье десятичное разложение составляет 2,718282…, поэтому функция натурального логарифма и экспоненциальная функция ( e x ) противоположны друг другу. В только различия между этими тремя функциями логарифмирования являются мультипликативными коэффициенты масштабирования, поэтому логически они эквивалентны для целей моделирования, но выбор базы важен из соображений удобства и условности, в соответствии с настройкой.
В стандартных математических обозначениях, а также в Excel и большинстве другое аналитическое программное обеспечение, выражение LN (X) представляет собой натуральный логарифм от X, и EXP (X) — экспоненциальная функция от X, поэтому EXP (LN (X)) = X и LN (EXP (X)) = X. Это означает, что функция EXP может использоваться для преобразования прогнозы с естественным каротажем (и их соответственно нижняя и верхняя достоверность) пределы) обратно в реальные единицы. Вы не можете использовать функцию EXP, чтобы напрямую удалить из журнала статистику ошибок модели, подходящей для данные естественного каротажа.Тебе надо сначала преобразовать прогнозы обратно в реальные единицы, а затем пересчитать ошибки и статистика ошибок в реальных единицах измерения, если важно, чтобы они были числа. Однако ошибка статистику модели, адаптированной к данным естественного каротажа, часто можно интерпретировать как приблизительные меры процентов ошибка, как объяснено ниже, и в ситуациях, когда ведение журнала уместно в во-первых, часто бывает интересно измерить и сравнить ошибки в процентное соотношение.
Как правило, выражение LOG b (.) используется для обозначения функции логарифма с основанием b, и LN используется для частного случая натурального журнала, в то время как LOG часто используется для частного случая журнала base-10. В частности, LOG означает вход в систему по основанию 10. Excel. В Statgraphics, увы, функция, которая называется LOG — это натуральный журнал , в то время как функция логарифма с основанием 10 — LOG10. В оставшейся части этого раздела (и в другом месте на сайте), и LOG, и LN будут использоваться для ссылки на естественную функцию журнала для совместимости с Обозначение Statgraphics. Также, символ «≈» означает примерно равно, с приближение является более точным в относительном выражении для меньших абсолютных значения, как показано в таблице ниже.
Изменение в натуральный логарифм ≈ изменение в процентах : Натуральный логарифм. логарифм и его базовое число e обладают некоторыми магическими свойствами, которые вы может вспомнить из расчетов (и вы, возможно, надеялись, что никогда не встретите очередной раз).Например, функция e X является собственной производной, а производная LN (X) равна 1 / X. Но для целей бизнес-анализа, его большим преимуществом является то, что небольших изменений в естественных log переменной напрямую интерпретируется как процентное изменение, с очень близким приближением . Причина в том, что график Y = LN (X) проходит через точку (1, 0) и имеет там наклон 1, поэтому он касается прямая линия, уравнение которой имеет вид Y = X-1 (пунктирная линия на графике ниже):
Это свойство функции натурального журнала означает, что
LN (1 + r) ≈ r
когда r намного меньше единицы по величине. Почему это важно? Предположим, что X увеличивается на небольшой процент, например 5%. Это означает что он меняется с X на X (1 + r), где r = 0,05. Теперь обратите внимание:
LN (Х (1 + г)) = LN (X) + LN (1 + r) ≈ LN (X) + р
Таким образом, когда X увеличивается на 5%, т. е. умножается на коэффициент 1,05, естественное log X изменяется с LN (X) на LN (X) + 0.05, очень близко приближение. Увеличение X на 5% поэтому (почти) эквивалентно добавлению 0,05 к LN (X).
От теперь я буду называть изменения натуральных логарифмов как «Журналы различий». (В Statgraphics, преобразование X в diff-log буквально DIFF (LOG (X)). В следующей таблице показано точное соответствие для процентов в диапазоне от -50% до + 100%:
Как видите, процентные изменения и diff-logs почти точно такие же в диапазоне +/- 5%, и они остаются очень близко до +/- 20%.Для больших При процентном изменении они начинают асимметрично расходиться. Обратите внимание, что журнал изменений, соответствующий до 50% -ного уменьшения составляет -0,693, в то время как дифференциал для 100% -ного увеличения составляет +0,693, ровно противоположное число. Это отражает тот факт, что снижение на 50% с последующим увеличением на 100%. (или наоборот) вернет вас в то же место.
процентное изменение Y в период t определяется как (Y т -Y т-1 ) / Y т-1 , что всего на примерно на равно LN (Y t ) — LN (Y t-1 ), но приближение почти точное , если процентное изменение небольшое, как показано в таблице выше.В Статистические термины, это означает, что DIFF (Y) / LAG (Y, 1) практически идентичен ДИФФ (ЖУРНАЛ (Y)). Если ты не веришь мне, вот график процентного изменения продаж автомобилей по сравнению с первым разность его логарифма, увеличивая масштаб за последние 5 лет. Синий и красные линии практически неразличимы, за исключением самого высокого и самого низкого точки. (Опять же, LOG означает LN в Statgraphics.)
Если ситуация тот, в котором процентные изменения потенциально достаточно велики для этого аппроксимация будет неточной, лучше использовать логарифмические единицы, а не процентных единиц, поскольку при этом учитывается сложное Таким образом, он симметричен с точки зрения последовательностей прибылей и убытков . Дифференциальный журнал -0,5 с последующим значением +0,5 вернет вас к ваша исходная позиция, тогда как 50% убыток, за которым следует 50% прирост (или наоборот наоборот) оставляет вас в худшем положении.
(Вернуться к началу страницы.)
Линеаризация экспоненциального роста и инфляции: T логарифм продукта равен сумма логарифмов, то есть LOG (XY) = LOG (X) + LOG (Y), независимо от основание логарифма. Таким образом, регистрация преобразует мультипликативных отношений . в аддитивных отношений , и по тому же признаку он преобразует экспоненциальных (совокупный рост) трендов до линейных трендов.Логарифмируя переменные, которые связаны мультипликативно и / или экспоненциально растут со временем, мы можем часто объясняют их поведение линейными моделями. Например, вот график ЛОГА (АВТОПРОДАЖА). Обратите внимание, что преобразование журнала преобразует экспоненциальной модели роста до линейной , и одновременно преобразует мультипликативный (пропорционально-дисперсионный) сезонный образец в аддитивный (постоянная дисперсия) сезонный шаблон. (Сравните это с исходным графиком АВТОПРОДАЖИ.) Эти преобразования делают преобразованные данные более подходящими для соответствия линейные / аддитивные модели.
Регистрация серии часто имеет эффект, очень похожий на выкачивание: она выравнивается. модели экспоненциального роста и снижает гетероскедастичность (т. е. стабилизирует дисперсия). Таким образом, размер журнала составляет дюймов. мужской дефлятор «, который не требует никаких внешних данных (или каких-либо ломать голову над тем, какой индекс цен использовать).Лог не точно то же, что и дефляция — не устраняет восходящий тренд в данные, но это может исправить тенденцию, чтобы ее можно было лучше согласовать с линейная модель. Дефляция сама по себе не выпрямит экспоненциальную кривую роста, если рост частично реальные и лишь частично из-за инфляции.Если вы собирается записывать данные, а затем соответствовать модели, которая неявно или явно использует разность (е.g., случайное блуждание, экспоненциальное сглаживание или модель ARIMA), то это обычно избыточно для дефлятирования индексом цен, если уровень инфляции изменяется очень медленно: процентное изменение, измеренное в номинальных долларах, будет почти так же, как процентное изменение в постоянных долларах. В Statgraphics обозначение, это означает, что DIFF (LOG (Y / CPI)) почти идентичен DIFF (LOG (Y)): единственная разница между ними — очень слабый шум из-за колебаний в уровне инфляции.Чтобы продемонстрировать это, вот график первого разница зарегистрированных продаж автомобилей с дефляцией и без:
Путем регистрации вместо , вы избегаете необходимости включать явный прогноз будущей инфляции в модели: вы просто объединяете инфляцию в одну кучу с любыми другими источниками устойчивого роста соединения в исходных данных. логирование данные перед подгонкой модели случайного блуждания дают так называемое геометрическое случайное блуждание — i.е., случайное блуждание с геометрическим, а не линейным ростом. Геометрическое случайное блуждание — это модель прогнозирования по умолчанию, которая обычно используется для данных о ценах на акции. (Вернуться к началу страницы.)
Тренд измеряется в единицах натурального логарифма ≈ рост в процентах: Потому что изменения натурального логарифма (почти) равны до процентов изменений в исходной серии, отсюда следует, что наклон линии тренда, подогнанной к зарегистрированным данным, равно среднему значению % рост в оригинальной серии.Например, на графике ЖУРНАЛА (АВТОПРОДАЖА), показанном выше, если вы «на глаз» линии тренда, вы увидите, что объем зарегистрированных продаж автомобилей увеличивается на около 2,5 (с 1,5 до 4,0) за 25 лет, что в среднем составляет около 0,1 в год, т.е. 10% в год. Намного проще оцените эту тенденцию по зарегистрированному графику, а не по исходному незарегистрированному один! Полученная здесь цифра 10% составляет номинального роста , включая инфляция. Если бы мы вместо этого взглянули на линию тренда на графике зарегистрированного спущенного продажи, т.е., LOG (AUTOSALE / CPI), его наклон будет в среднем реальных процента рост.
Обычно тренд оценивается более точно путем подбора статистической модели который явно включает параметр локального или глобального тренда, например линейный модель тренда, случайного блуждания с дрейфом или линейного экспоненциального сглаживания. Когда модель такого типа сочетается с преобразованием бревна, его трендовый параметр можно интерпретировать как процентную скорость роста.
(Вернуться к началу страница.)
Ошибки измеряется в единицах натурального логарифма ≈ ошибки в процентах: Еще одно интересное свойство логарифма заключается в том, что ошибки в прогнозировании записанных рядов можно интерпретировать как приблизительные процентные ошибки в прогнозировании исходной серии, хотя процентные значения относительно прогнозных значений, а не фактических значений. (Обычно один интерпретирует «процентную ошибку» как ошибку, выраженную как процент от фактического значения, а не от прогнозируемого значения, хотя статистические свойства процентных ошибок обычно очень похожи независимо от того, от того, рассчитываются ли проценты относительно фактических значений или прогнозы.)
Таким образом, если вы используете оценку наименьших квадратов, чтобы подогнать модель линейного прогнозирования к зарегистрированным , вы неявно минимизируете среднеквадратичную ошибку в процентах, вместо среднеквадратичной ошибки в исходных единицах измерения, что, вероятно, является хорошим вещь, если преобразование журнала было подходящим в первую очередь. И если вы посмотрите статистику ошибок в зарегистрированных единицах, вы можете интерпретировать их как проценты, если они не слишком велики — скажем, если их стандартное отклонение равно 0.1 или менее. В этом диапазоне стандартное отклонение ошибок при прогнозировании зарегистрированного ряда составляет приблизительно стандартное отклонение процентных ошибок при прогнозировании исходного серии, а средняя абсолютная ошибка (MAE) при прогнозировании зарегистрированной серии равна приблизительно средняя абсолютная процентная ошибка (MAPE) при прогнозировании оригинальная серия. (Я использую эталон 0,1 здесь, потому что в этот момент изменение стандартного отклонения 2, критическое значение для 95% доверительного интервала будет равно 0.2, а соответствие между diff-логами и процентами начинает изрядно отваливаться быстро после этого, как показано в таблице выше. Если стандартное отклонение ошибки в зарегистрированных единиц больше 0,1, вам следует рассчитать доверительные интервалы в зарегистрированные единицы, а затем разнесите их нижнее и верхнее значения отдельно, используя функция EXP.)
(Вернуться к началу страница.)
Коэффициенты в логарифмической регрессии ≈ пропорциональные процентные изменения : Во многих экономических ситуациях (особенно соотношение цена-спрос), предельное влияние одной переменной на ожидаемая стоимость другого является линейной с точки зрения процентных изменений , а не абсолютных изменения.В таких случаях применяя преобразование натурального логарифма или разностного логарифма как в зависимые, так и в независимые переменные могут быть подходящими. Этот этот вопрос будет обсуждаться более подробно в главе о регрессии этих заметки. В частности, часть 3 продаж пива пример регрессии иллюстрирует применение преобразования журнала в моделирование влияния цены на спрос, в том числе как использовать EXP (экспоненциальная) функция для «снятия журнала» прогнозов и доверительных интервалов чтобы преобразовать их обратно в единицы исходных данных.
Калькулятор сжатых логарифмовДобро пожаловать в калькулятор сжатых логарифмов компании Omni , где мы увидим, как записать логарифмы или, скорее, логарифмические выражения в виде единого логарифма. Чтобы быть точным, мы попробуем упростить журналы, применив три простых формулы . Фактически, мы будем использовать те же самые, которые работают для расширяющих логарифмов ; мы просто сделаем все наоборот. Таким образом, мы узнаем, как вычесть и как добавить журналы (заметьте, с той же базой).
Что такое логарифм?
В связи с бушующей пандемией COVID-19 было довольно много разговоров о , скорости, с которой число случаев увеличивается с течением времени . С математической точки зрения такая вещь называется экспоненциальным ростом.
Как вы могли заметить, название предполагает, что это как-то связано с экспонентами . Действительно, если мы предположим, что каждый инфицированный человек передает болезнь, скажем,
4другим, то нулевой пациент заболел4человек.В свою очередь, они заразили4² = 4 * 4 = 16человек, которые позже заразились4³ = 4 * 4 * 4 = 64человек. В общем, мы описываем количество больных наn-м шаге показателем4ⁿ.Логарифм — это функция, обратная экспоненциальной. Чтобы все было точнее, давайте посмотрим следующее определение журнала.
💡 logₐ (b)дает вам мощность, до которой вам нужно поднятьa, чтобы получитьb.Однако обратите внимание, что в общем случае это может быть дробная экспонента.В приведенном выше примере эпидемии логарифм (с основанием
4) возвращает , на этом шаге мы получаем фиксированное количество зараженных . Например:log₄64 = 3Обратите внимание, что получение корня также считается обратной операцией по отношению к получению степени. Однако, в отличие от логарифмов, корни возвращают основание экспоненты , а не сам показатель (в приведенном выше языке: они возвращают, сколько людей заразилось от одного человека).Например:
³√64 = 4Прежде чем мы научимся перезаписывать журналы, давайте упомянем несколько важных фактов , касающихся их.
- Существует два очень частных случая логарифма , которые имеют уникальную запись: натуральный логарифм и логарифм с основанием
10. Обозначим ихln (x)иlog (x)(второй просто без малого10), а их основаниями являются, соответственно, число Эйлераeи (сюрприз, сюрприз!) номер10.Существует также двоичный логарифм, т.е. логарифм с основанием2, но он не так распространен, как первые два. - Функция логарифма определена только для положительных чисел. Другими словами, всякий раз, когда мы пишем
logₐ (b), нам требуется, чтобыbбыло положительным. - Независимо от основания, логарифм
1равен0. В конце концов, что бы мы ни возводили в степень0, мы получаем1. - Логарифмы чрезвычайно важны. А мы имеем в виду ЧРЕЗВЫЧАЙНО важный. Вне математики они используются в статистике , (например, логнормальное распределение), экономике, (например, индекс ВВП), медицине, (например, индексе QUICKI) и химии (например, период полураспада). Кроме того, довольно несколько физических единиц основаны на логарифмах, например шкала Рихтера, шкала pH и шкала дБ.
Хорошо, на данный момент описания хватит. Пора вернуться к математике и попробовать , упрощая журналы с помощью конкретных формул . Мы рассмотрим несколько ужасных выражений, связанных с журналами, и научимся, как записывать выражения в виде одного логарифма .
Как переписать логарифмы?
Как мы упоминали в первом разделе, логарифмы — это , операция, обратная степени . Поэтому неудивительно, что свойства этих двух факторов весьма связаны: в частности, для умножения и деления показателей степени.
Давайте начнем с упоминания одного свойства журнала, которое наш калькулятор сжатых логарифмов не использует — изменение базовой формулы . Это позволяет нам переключаться с одной основы журнала на другую, но по цене — мы получаем отношение двух выражений к одному. Если вы хотите узнать подробности, обязательно ознакомьтесь с специальным калькулятором изменения базы Omni.
Однако мы будем использовать здесь три другие формулы . Мы часто используем их для расширения логарифмов, но нет ничего плохого в том, чтобы работать с ними наоборот: для сжимаемых бревен вместо .Тем не менее, давайте посмотрим на них в первозданном виде.
- Логарифм произведения — это сумма логарифмов.
- Логарифм частного — это разность логарифмов.
- Логарифм показателя степени кратен логарифму.
Как видите, все они берут единый логарифм (произведения, частного или экспоненты), а расширяют его до более длинного выражения . Однако, если мы посмотрим на них назад, они запишут выражение в виде одного логарифма.Таким образом, мы получаем формулы для сложения журналов, вычитания журналов и умножения журналов на число . Все три вместе — это и есть калькулятор сжатых логарифмов.
Как сжать логарифмы?
Теперь мы рассмотрим теорию того, как переписывать логарифмы, и творит чудеса для наших нужд . Имейте в виду, что пока мы будем придерживаться формул, и как только мы получим их во всей красе, мы перейдем к примерам сжатия журналов в последнем разделе.
Прежде всего, возьмем простейшую из расширяющих формул: для логарифм степени .Давайте перевернем его, исправим обозначение, чтобы оно соответствовало тому, которое использовалось в калькуляторе сжатых логарифмов, и поместим его здесь для будущего использования:
Теперь мы будем использовать его (вместе со свойством product), чтобы узнать, как добавлять журналы. И мы имеем в виду не просто любую сумму — мы имеем в виду , добавляющие бревна с кратными .
x * logₙ (a) + y * logₙ (b) =?Мы начинаем с применения формулы первого уплотняющего журнала к обоим слагаемым, т.е. берем
xиyи перетаскиваем их внутрь:x * logₙ (a) + y * logₙ (b) = logₙ (aˣ) + logₙ (bʸ).Теперь, без кратных перед выражениями, мы можем перейти от добавления журналов к журналу продукта :
Что ж, мы видели, как добавлять журналы, поэтому не должно быть слишком сложно перейти оттуда к вычитанию журналов, верно?
x * logₙ (a) - y * logₙ (b) =?В самом деле, это не так. Начинаем так же: перетаскивая внутрь
xиy,x * logₙ (a) - y * logₙ (b) = logₙ (aˣ) - logₙ (bʸ),, и мы завершаем переводом журналов вычитания в журнал частного .
Вуаля! Это все три формулы, которые нам понадобятся для упрощения журналов. Итак, давайте теперь переключимся с символов на числа и получим пример, работающий с калькулятором сжатых логарифмов под рукой.
Пример: использование калькулятора конденсированных логарифмов
Со всеми объяснениями, которые мы видели до сих пор, нет необходимости в введении — , давайте просто разберемся с примером . Хотя технически мы только что познакомились, не так ли? Какая досада…
Мы покажем, как сжать логарифмы до:
3 * журнал₆4 + журнал₆9Прежде чем мы сами напишем выражение в виде единственного логарифма, давайте посмотрим, как переписать журналы с помощью калькулятора кратких логарифмов .
В верхней части нашего инструмента мы выбираем тип операции, с которой имеем дело . В нашем случае у нас есть сумма, поэтому мы выбираем «, добавление журналов » под « Использовать формулу для ». Это показывает нам символическое выражение с обозначением, используемым ниже:
x * logₙ (a) + y * logₙ (b).Сравнивая его с нашим, мы видим, что нам нужно ввести:x = 3,a = 4,b = 9иn = 6.Однако остается
y. Напомним, что по соглашению отсутствие числа перед функцией (в данном случае логарифм, но это то же самое, скажем, для тригонометрических функций) означает, что число фактически равно1. - Логарифм числа — это показатель степени, на который нужно возвести другое фиксированное значение, основание, чтобы получить это число.



 Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.

 Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.
Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ. «Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [Децилог, мост между логарифмами, децибелами, непер и предпочтительными числами]. VDI-Zeitschrift (на немецком языке). 98 : 267–274.
«Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [Децилог, мост между логарифмами, децибелами, непер и предпочтительными числами]. VDI-Zeitschrift (на немецком языке). 98 : 267–274.  Разница
журналы — это журнал частного. Журнал различий не может быть упрощен.
Разница
журналы — это журнал частного. Журнал различий не может быть упрощен.  ) = 1
) = 1
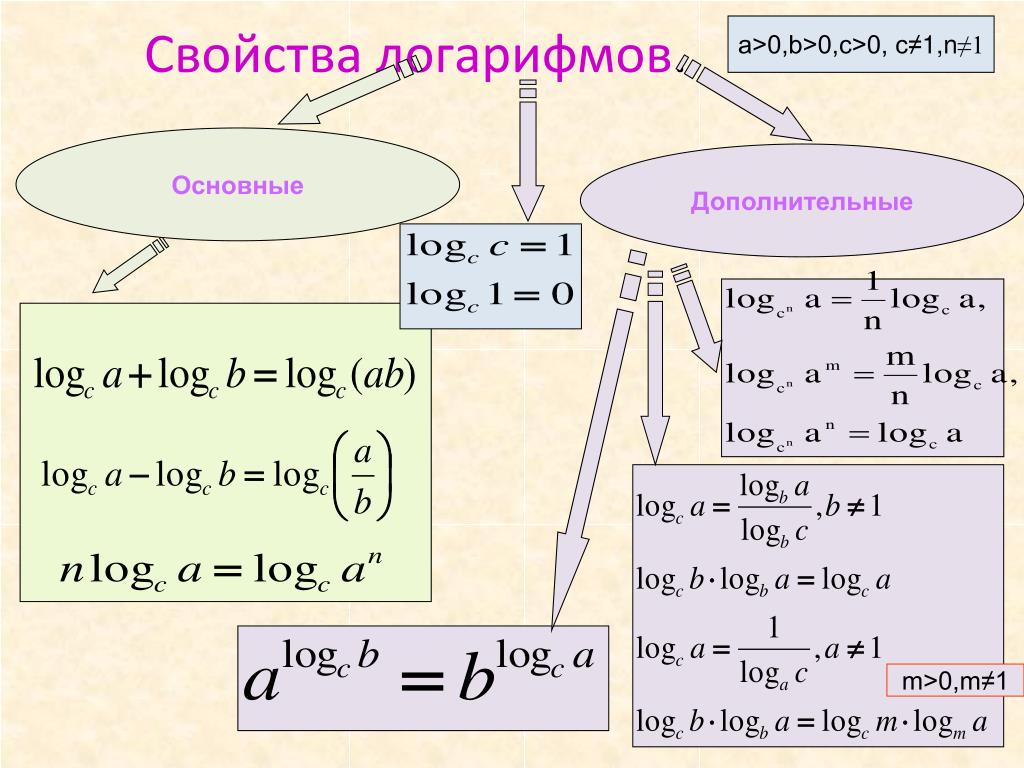 3 [/ латекс].
3 [/ латекс].