Кесте тригонометрия: синус, косинус, тангенс, котангенс, свойства функций. Формулы. Курсы по математике.
Таблица синусов, таблица значений синусов, в помощь студентам таблица синусов.
Содержание:
Таблица синусов — это посчитанные значения синусов от 0° до 360°. Когда нет рядом калькулятора таблица синусов просто незаменима. Для того, чтобы узнать чему равен синус от нужного Вам угла достаточно найти его в таблице и все. Таблица синусов — это основно материал тригонометрии, который необходимо знать или, как минимум, понимать. Пользуйтесь на здоровье таблицей значений синусов. Если Вы изучаете тригонометрические функции Вам может понадобиться перечень тригонометрических формулы.
Таблица синусов 0° — 180°
|
|
|
|
Таблица синусов 180° — 360°
|
|
|
|
На нашем сайте представлено много теоретического материала по тригонометрии. Здесь Вы можете найти таблицы тригонометрических функций: таблицу синусов, таблицу косинусов, таблицу тангенсов и таблицу котангенсов. Также специально для улучшения понимания материала по тригонометрии мы добавили тригонометрические формулы, чтобы решение тригонометрических задач по математике вызывало меньше затруднений. Пользуйтесь нашим сайтом и таблицей синусов на здоровье.
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Таблица Брадиса
Таблица БрадисаЧетырехзная математическая таблица Брадиса синусы, косинусы в градусах и минутах с точностью до одной минуты. Как пользоваться таблицей Брадиса sin cos пример. Значения синусов и косинусов для углов от 0 до 90 градусов.
Как пользоваться таблицей Брадиса sin cos пример. Значения синусов и косинусов для углов от 0 до 90 градусов.
Четырехзначная таблица Брадиса тангенсы, котангенсы от 0 до 90 градусов с точностью до одной минуты. Значения tg ctg таблица. Как пользоваться таблицей брадиса примеры. Таблица разбита на две части. В первой части таблицы Брадиса тангенсы от 0 до 75 и котангенсы от 15 до 90 градусов находятся при помощи дополнительных столбцов для 1, 2 и 3 минут. Во второй части тангенсы от 75 до 90 градусов и котангенсы от 0 до 15 градусов записаны прямо в таблицу с точностью до 1 минуты угла.
Математическая четырехзначная таблица синусов, косинусов, тангенсов в радианах. Значения sin, cos, tg от 0 до 3,14 радиан с точностью до 0,01 радиана.
Значения sin, cos, tg от 0 до 3,14 радиан с точностью до 0,01 радиана.
Смотрите так же:
Таблица значений тригонометрических функций — синусы, косинусы, тангенсы и котангенсы значения с дробями и корнями, тригонометрический круг картинка и знаки тригонометрических функций.
Тригонометрическая таблица и тригонометрический круг — интерактивная карта, угол вращаете курсором и смотрите значания функций для этого угла.
Таблица синусов от 0 до 360 градусов.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
07 февраля 2012 года — 22 сентября 2019 года.
© 2006 — 2021 Николай Хижняк. Все права защищены.
Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15)
Как найти значения тригонометрических функций для угла 15 градусов
Найдем значения синуса, косинуса и тангенса для угла 15 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 15 градусов — задача сложная. Однако, это не совсем так.
Нам на помощь придут формулы преобразования двойного угла тригонометрических функций.
Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).
Тогда, отталкиваясь от тождества:
cos 2α = 1 — 2sin2α
Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 — 2sin215
sin215 = ( 1 — cos 30 ) / 2
Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin215 = ( 1 — √3/2 ) / 2
sin 15 = √ (( 1 — √3/2 ) / 2 )
верхнюю часть дроби под корнем приведем к общему знаменателю (2)
sin 15 = √ (( (2 — √3) /2 ) / 2 ) = √( (2 — √3) / 4 )
теперь у нас одна дробь под знаком корня. Умножим числитель и знаменатель на два
sin 15 = √( (2 — √3) / 4 ) = √( (4 — 2√3) / 8 )
самый интересный момент, мы можем представить 4 — 2√3 как (√3-1)2
тогда
sin 15 = √( (√3-1)2 / 8 ) = (√3-1)/ √8 = (√3-1)/ (2√2)
путем несложных агебраических преобразований получаем:
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 15 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 15 градусов в виде десятичной дроби с четырьмя знаками после запятой.
|
π/12 |
синус 15 sin 15 |
косинус 15 cos 15 |
тангенс 15 tg 15 |
котангенс 15 ctg 15 |
|
Значение |
0.2588190451 |
0.96592582628 |
0. |
3.73205080757 |
Таблица Брадиса sin cos tg ctg
Калькулятор поможет рассчитать точные значения тригонометрических функций sin, cos, tg и ctg для различных значений углов в градусах или радианах.
На данной странице таблица Брадиса, которая дает значение sin, cos, tg, ctg любого острого угла, содержащего целое число градусов и десятых долей градуса. Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30′ = 0.9426.
Найти точное значениеТаблица Брадиса sin, cos
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 0 | 90° | ||||||||||||||
| 0° | 0,0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0872 | 85° | 3 | 6 | 9 |
| 5° | 0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 1736 | 80° | 3 | 6 | 9 |
| 10° | 1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 2588 | 75° | 3 | 6 | 8 |
| 15° | 2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 3420 | 70° | 3 | 5 | 8 |
| 20° | 3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 4226 | 65° | 3 | 5 | 8 |
| 25° | 4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 5000 | 60° | 3 | 5 | 8 |
| 30° | 5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 5736 | 55° | 2 | 5 | 7 |
| 35° | 5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 6428 | 50° | 2 | 4 | 7 |
| 40° | 6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 6909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 7071 | 45° | 2 | 4 | 6 |
| 45° | 7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 7660 | 40° | 2 | 4 | 6 |
| 50° | 7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 8192 | 35° | 2 | 3 | 5 |
| 55° | 8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 8660 | 30° | 1 | 3 | 4 |
| 60° | 8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 9063 | 25° | 1 | 3 | 4 |
| 65° | 9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9265 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9385 | 9391 | 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 9848 | 10° | 1 | 1 | 2 |
| 80° | 9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.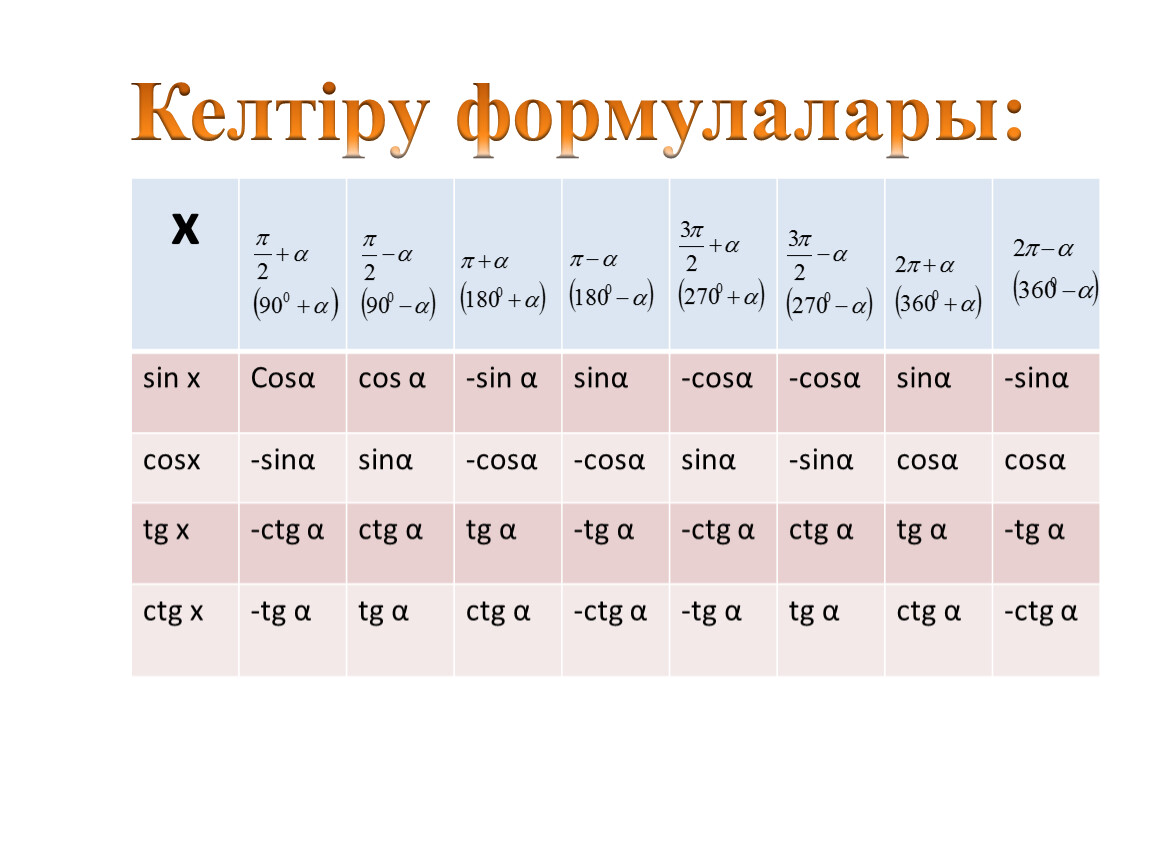 0 0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0° | 0 | 0 | 0 |
| 90° | 1 | ||||||||||||||
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos |
Таблица Брадиса tg, ctg
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
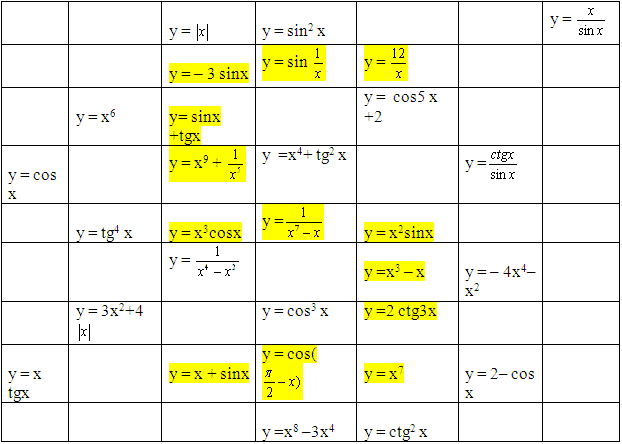
Тригонометрия – мәндер кестесі.
 Тригонометриялық функциялар
Тригонометриялық функцияларНазар аударыңыз!
Қосымша бар
555 арнайы бөлімдегі материалдар.
Өте «өте емес …» адамдар үшін
Ал «өте біркелкі …» дегендер үшін)
Ең алдымен, «Синус және косинус дегеніміз не? Тангенс және котангенс деген не?» сабағынан қарапайым, бірақ өте пайдалы қорытындыны еске сала кетейін.
Міне, нәтиже:
Синус, косинус, тангенс және котангенс олардың бұрыштарымен тығыз байланысты. Біз бір нәрсені білеміз — бұл басқа нәрсені білеміз дегенді білдіреді.
Басқаша айтқанда, әрбір бұрыштың өзінің тұрақты синусы мен косинусы болады. Әркімнің дерлік өз тангенсі мен котангенсі болады. Неліктен дерлік?Бұл туралы төменде толығырақ.
Бұл білім оқуға көп көмектеседі! Синустардан бұрыштарға және керісінше өту керек көптеген тапсырмалар бар. Бұл үшін бар синус кестесі.Сол сияқты, косинус бар тапсырмалар үшін — косинус кестесі.Ал, сіз ойладыңыз, бар жанама кестесіжәне котангенттер кестесі. )
)
Әртүрлі кестелер бар. Ұзын, онда не тең екенін көруге болады, айталық, sin37 ° 6 ‘. Біз Bradis кестелерін ашамыз, алты минут бойы отыз жеті градус бұрышты іздейміз және біз 0,6032 мәнін көреміз. Бұл санды (және мыңдаған басқа кесте мәндерін) жаттау мүлдем қажет емес екені анық.
Шын мәнінде, біздің уақытта котангенстердің тангенстерінің синусының косинустарының ұзын кестелері ерекше қажет емес. Бір жақсы калькулятор оларды толығымен ауыстырады. Бірақ мұндай кестелердің бар екенін білу зиян тигізбейді. Жалпы эрудиция үшін.)
Ал неге бұл сабақ?! — сен сұрадың.
Міне, себебі. Бұрыштардың шексіз санының арасында бар арнайы,ол туралы білу керек барлық… Барлық мектеп геометриясы мен тригонометриясы осы бұрыштарға салынған. Бұл тригонометрияның «көбейту кестесінің» бір түрі. Егер сіз, мысалы, sin50 ° тең екенін білмесеңіз, сізді ешкім айыптамайды.) Бірақ егер сіз sin30 ° не екенін білмесеңіз, лайықты екі алуға дайын болыңыз …
Осындайлардан арнайыбұрыштары да лайықты терілген.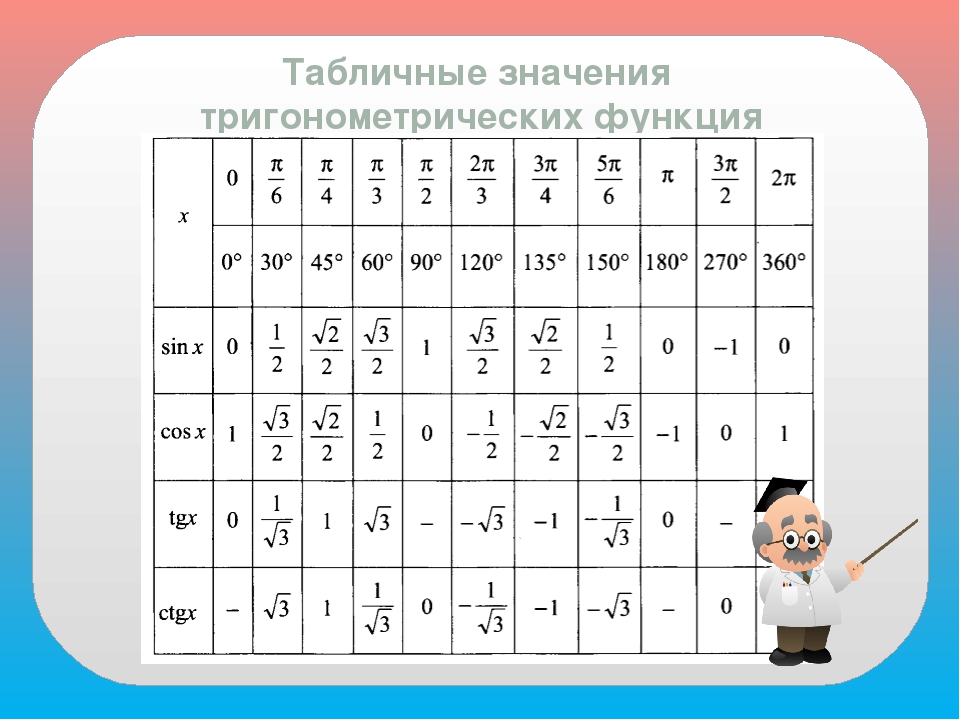 Мектеп оқулықтары әдетте жаттау үшін мейірімділікпен ұсынылады синустар кестесі және косинустар кестесіон жеті бұрышқа арналған. Және, әрине, тангенс кестесі және котангенс кестесісол он жеті бұрыш үшін … 68 мәнді есте сақтау ұсынылады. Айтпақшы, бір-біріне өте ұқсас, кейде қайталаңыз және белгілерді өзгертіңіз. Мінсіз визуалды жады жоқ адам үшін бұл әлі де міндет …)
Мектеп оқулықтары әдетте жаттау үшін мейірімділікпен ұсынылады синустар кестесі және косинустар кестесіон жеті бұрышқа арналған. Және, әрине, тангенс кестесі және котангенс кестесісол он жеті бұрыш үшін … 68 мәнді есте сақтау ұсынылады. Айтпақшы, бір-біріне өте ұқсас, кейде қайталаңыз және белгілерді өзгертіңіз. Мінсіз визуалды жады жоқ адам үшін бұл әлі де міндет …)
Біз басқа жолмен жүреміз. Есте сақтауды логика мен тапқырлыққа ауыстырайық. Содан кейін синустар және косинустар кестесі үшін 3 (үш!) мәнді есте сақтау керек. Және тангенс кестесі мен котангенс кестесі үшін 3 (үш!) мән. Болды. 68-ге қарағанда алты мағынаны есте сақтау оңай, менің ойымша …)
Біз осы алтыдан басқа барлық қажетті мәндерді күшті заңды парағының көмегімен аламыз. — тригонометриялық шеңбер. Егер сіз бұл тақырыпты зерттемеген болсаңыз, сілтемеге өтіңіз, жалқау болмаңыз. Бұл шеңбер тек осы сабаққа қажет емес. Ол таптырмас барлық тригонометрия үшін бірден. .. Мұндай құралды қолданбау — күнә! Сен қаламайсын? Бұл сіздің шаруаңыз. Есте сақтау синус кестесі. Косинус кестесі. Тангенстердің кестесі. Котангенттер кестесі.Әр түрлі бұрыштар үшін барлық 68 мән.)
.. Мұндай құралды қолданбау — күнә! Сен қаламайсын? Бұл сіздің шаруаңыз. Есте сақтау синус кестесі. Косинус кестесі. Тангенстердің кестесі. Котангенттер кестесі.Әр түрлі бұрыштар үшін барлық 68 мән.)
Сонымен, бастайық. Алдымен осы ерекше бұрыштардың барлығын үш топқа бөлейік.
Бұрыштардың бірінші тобы.
Бірінші топты қарастырайық он жеті бұрыштары арнайы… Бұл 5 бұрыш: 0 °, 90 °, 180 °, 270 °, 360 °.
Осы бұрыштар үшін котангенстердің тангенстерінің косинустарының синусы кестесі келесідей болады:
Бұрыш x(градуспен) | 0 | 90 | 180 | 270 | 360 |
Бұрыш x(радианмен) | 0 | ||||
күнә x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
tg x | 0 | зат есім емес | 0 | зат есім емес | 0 |
ctg x | зат есім емес | 0 | зат есім емес | 0 | зат есім емес |
Есте сақтағысы келетіндер — есте сақта.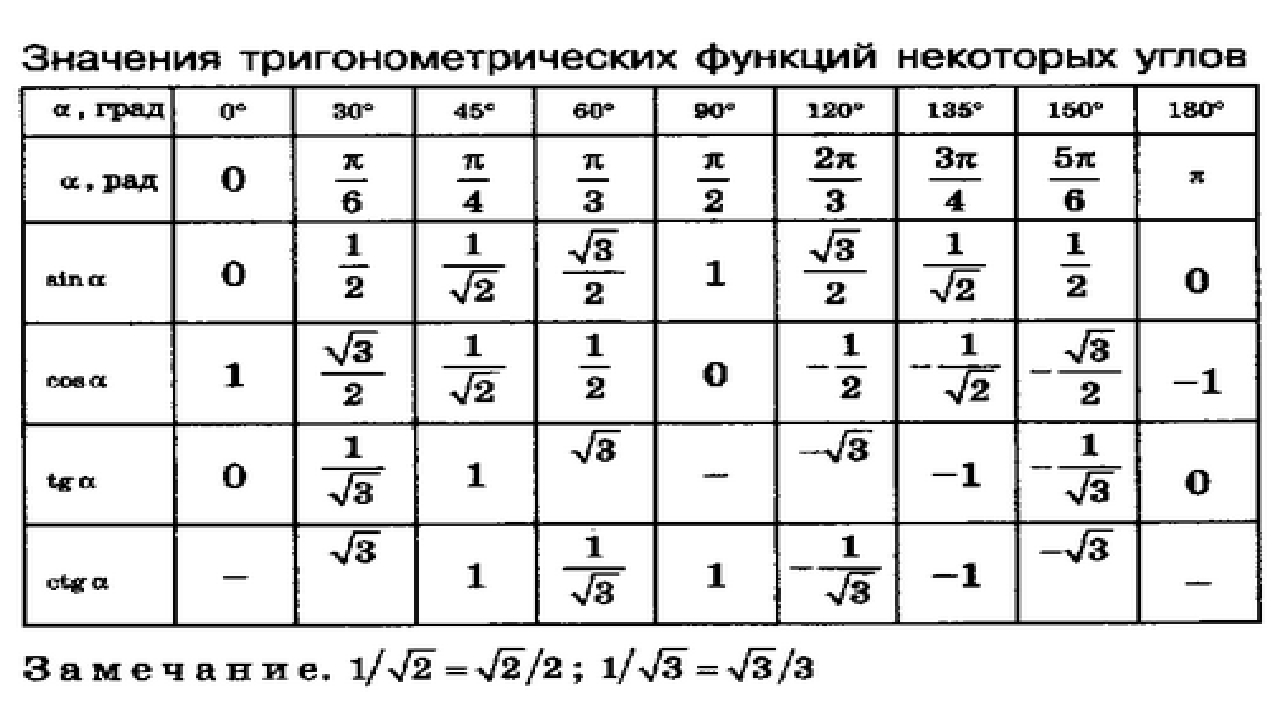 Бірақ мен бірден айта кету керек, бұл барлық және нөлдер бастың ішінде өте шатастырылады. Сіз қалағаныңыздан әлдеқайда күшті.) Сондықтан біз логиканы және тригонометриялық шеңберді қосамыз.
Бірақ мен бірден айта кету керек, бұл барлық және нөлдер бастың ішінде өте шатастырылады. Сіз қалағаныңыздан әлдеқайда күшті.) Сондықтан біз логиканы және тригонометриялық шеңберді қосамыз.
Шеңбер сызыңыз және оған бірдей бұрыштарды белгілеңіз: 0 °, 90 °, 180 °, 270 °, 360 °. Мен бұл бұрыштарды қызыл нүктелермен белгіледім:
Бұл бұрыштардың ерекшелігі неде екені бірден түсінікті. Иә! Бұл құлайтын бұрыштар дәл координат осінде!Негізінде, халықтың абдырап қалуы да содан… Бірақ біз шатастырмаймыз. Көп жаттаусыз осы бұрыштардың тригонометриялық функцияларын қалай табуға болатынын анықтап көрейік.
Айтпақшы, бұрыштың орналасуы 0 градус толығымен сәйкес келеді 360 градус бұрышпен. Бұл осы бұрыштардағы синустар, косинустар, тангенстердің дәл бірдей екенін білдіреді. Мен шеңберді жабу үшін 360 градус бұрышты белгіледім.
Емтиханның қиын стресстік жағдайында сіз қандай да бір түрде күмәндана бастадыңыз делік … 0 градустың синусы дегеніміз не? Нөлге ұқсайды.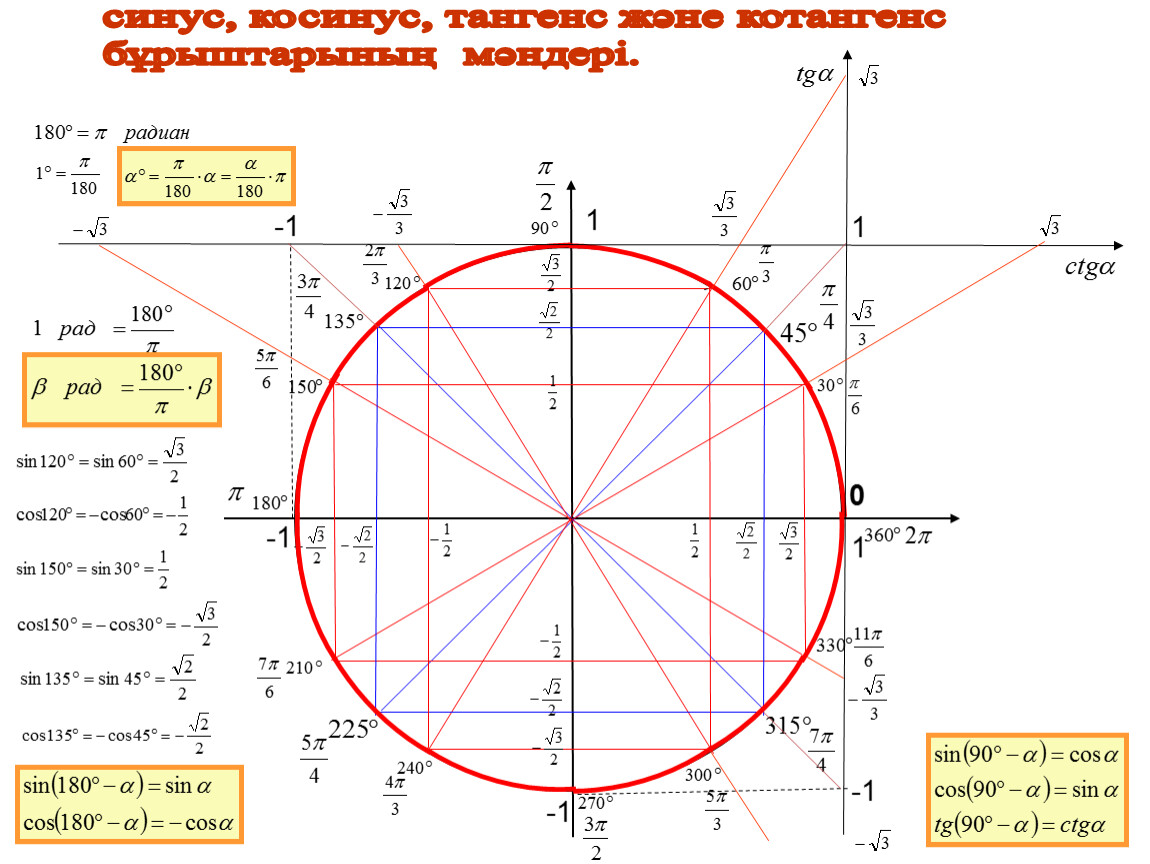 .. Біреу болса ше?! Механикалық жаттау — осындай нәрсе. Қатаң жағдайда күмәндер кеми бастайды …)
.. Біреу болса ше?! Механикалық жаттау — осындай нәрсе. Қатаң жағдайда күмәндер кеми бастайды …)
Сабырлы, тек сабырлы болыңыз!) Мен сізге 100% дұрыс жауап беретін және барлық күмәнді толығымен алып тастайтын практикалық техниканы айтамын.
Мысал ретінде, мысалы, 0 градустық синусын анық және сенімді түрде қалай анықтау керектігін анықтайық. Сонымен қатар, және косинус 0. Дәл осы мәндерде, біртүрлі, адамдар жиі шатастырады.
Ол үшін шеңберге сурет салу керек еріктіинъекция Н.С… Бірінші тоқсанда ол 0 градустан алыс болмады. Осы бұрыштың синусы мен косинусын осьтерге белгілеңіз NS,бәрі шынар. Бұл сияқты:
Ал енді — назар аударыңыз! Бұрышты азайтыңыз Н.С, қозғалатын жағын оське жақындатыңыз OH. Курсорды суреттің үстіне апарыңыз (немесе планшеттегі суретті түртіңіз) және сіз бәрін көресіз.
Енді қарапайым логиканы қосайық!Біз қарап, ойлаймыз: Синкс х бұрышының азаюымен қалай әрекет етеді? Бұрыш нөлге жақындағанда?Ол азайып барады! Және cosx өсіп келеді!Бұрыш толығымен құлаған кезде синустың не болатынын анықтау керек пе? Бұрыштың қозғалмалы жағы (А нүктесі) OX осіне орналасып, бұрыш нөлге айналғанда? Бұрыштың синусы да нөлге түсетіні анық. Ал косинус …-ке дейін өседі. Бұрыштың қозғалмалы жағының ұзындығы (тригонометриялық шеңбердің радиусы) неге тең? Бір!
Ал косинус …-ке дейін өседі. Бұрыштың қозғалмалы жағының ұзындығы (тригонометриялық шеңбердің радиусы) неге тең? Бір!
Міне, жауап. 0 градустың синусы 0. 0 градустың косинусы 1. Абсолютті темір және күмәнсіз!) Әйтпесе болуы мүмкін емес.
Дәл осылай, мысалы, 270 градус синусын білуге (немесе нақтылауға) болады. Немесе косинус 180. Шеңбер сызыңыз, еріктіБізді қызықтыратын координат осінің жанындағы төрттен бір бұрыш, бұрыштың жағын ойша жылжытыңыз және бұрыштың бүйір жағы оське түскенде синусы мен косинусының қандай болатынын ұстаңыз. Осымен болды.
Көріп отырғаныңыздай, бұл бұрыштар тобы үшін ештеңені жаттап алудың қажеті жоқ. Мұнда қажет емес синус кестесі…Иә және косинус кестесі— сондай-ақ.) Айтпақшы, тригонометриялық шеңберді бірнеше рет қолданғаннан кейін бұл мәндердің барлығы өздігінен есте қалады. Ал ұмытып қалса, мен 5 секундта шеңбер сызып, нақтыладым. Сертификат алу қаупі бар досыңызды дәретханадан шақырғаннан әлдеқайда оңай, солай ма?)
Тангенс пен котангенске келетін болсақ — бәрі бірдей.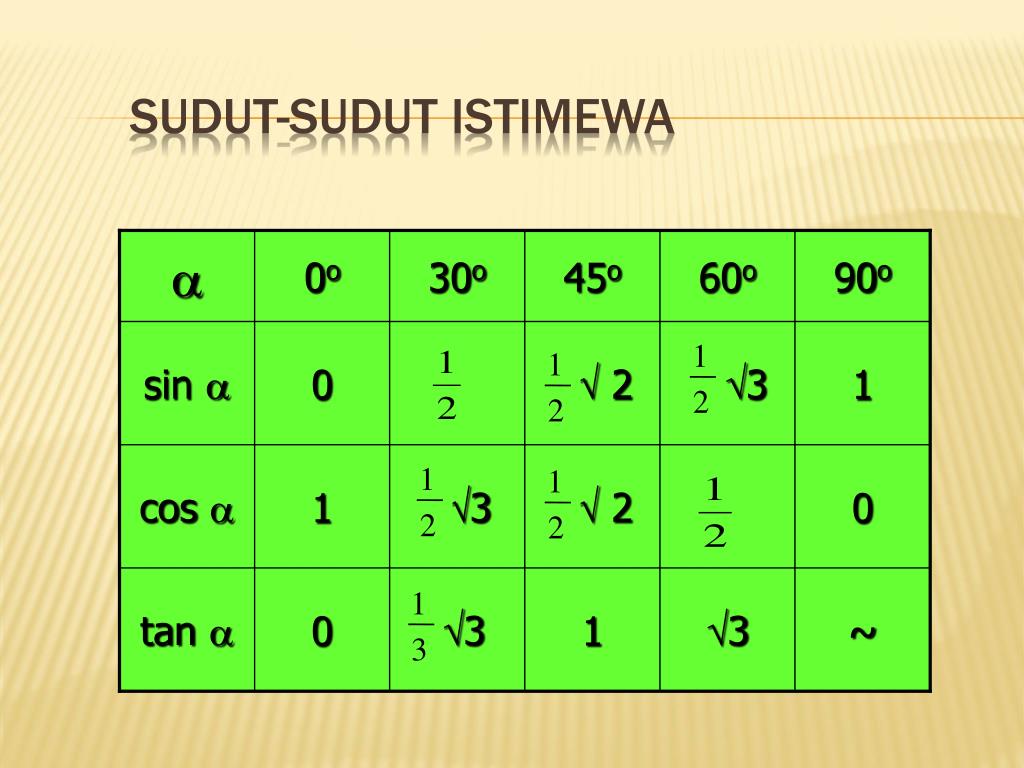 Шеңберге жанама (котангенс) сызығын саламыз — және бәрі бірден көрінеді. Олар нөлге тең және олар жоқ жерде. Сіз жанама және котангенс түзулерін білмейсіз бе? Бұл қайғылы, бірақ түзетілетін.) Тригонометриялық шеңбердегі тангенс және котангенс 555 бөліміне бардым — проблема жоқ!
Шеңберге жанама (котангенс) сызығын саламыз — және бәрі бірден көрінеді. Олар нөлге тең және олар жоқ жерде. Сіз жанама және котангенс түзулерін білмейсіз бе? Бұл қайғылы, бірақ түзетілетін.) Тригонометриялық шеңбердегі тангенс және котангенс 555 бөліміне бардым — проблема жоқ!
Егер сіз осы бес бұрыш үшін синусты, косинусты, тангенсті және котангентті қалай нақты анықтау керектігін түсінсеңіз — құттықтаймыз! Мүмкін болса, функцияларды енді анықтай алатыныңызды хабарлауға рұқсат етіңіз оське түсетін кез келген бұрыштар.Және бұл 450 °, және 540 °, және 1800 ° және шексіз сан …) Мен санадым (оң жақ!) Шеңбердегі бұрыш — және функциялармен ешқандай проблемалар жоқ.
Бірақ, жай ғана, бұрыштарды санау кезінде есептер мен қателер орын алады … Оларды қалай болдырмау керек, сабақта былай деп жазылған: Тригонометриялық шеңберге кез келген бұрышты градуспен салу (санау). Бастауыш, бірақ қателермен күресуде өте пайдалы.)
Міне, сабақ: Тригонометриялық шеңбердегі кез келген бұрышты радианмен қалай салуға (сануға) болады — бұл кенеттен болады. Мүмкіндіктер тұрғысынан. Айталық, бұрыш төрт жарты осьтің қайсысына түсетінін анықтаңыз
Мүмкіндіктер тұрғысынан. Айталық, бұрыш төрт жарты осьтің қайсысына түсетінін анықтаңыз
сіз мұны бірнеше секундта жасай аласыз. Мен қалжыңдап тұрған жоқпын! Бір-екі секундта. Әрине, тек 345 «pi» ғана емес …) Және 121, және 16 және -1345. Кез келген фактор бірден жауап беру үшін жақсы.
Ал егер бұрыш болса
Ойлан! Дұрыс жауап 10 секундта алынады.Бөлгішінде екі бар радиандардың кез келген бөлшек мәні үшін.
Шындығында, тригонометриялық шеңбер бұл үшін жақсы. жұмыс істей білу фактісі кейбірбұрыштарда автоматты түрде кеңейеді шексіз жиынбұрыштар.
Сонымен, он жетіден бес бұрышпен — есептелді.
Бұрыштардың екінші тобы.
Бұрыштардың келесі тобы 30 °, 45 ° және 60 °. Неліктен дәл осылар, мысалы, 20, 50 және 80 емес? Иә, әйтеуір солай болды… Тарихи.) Әрі қарай бұл бұрыштардың қаншалықты жақсы екені көрінетін болады.
Осы бұрыштар үшін котангенстердің тангенстерінің косинустарының синусының кестесі келесідей:
Бұрыш x(градуспен) | 0 | 30 | 45 | 60 | 90 |
Бұрыш x(радианмен) | 0 | ||||
күнә x | 0 | 1 | |||
cos x | 1 | 0 | |||
tg x | 0 | 1 | зат есім емес | ||
ctg x | зат есім емес | 1 | 0 |
Мен суретті аяқтау үшін алдыңғы кестеден 0 ° және 90 ° мәндерін қалдырдым.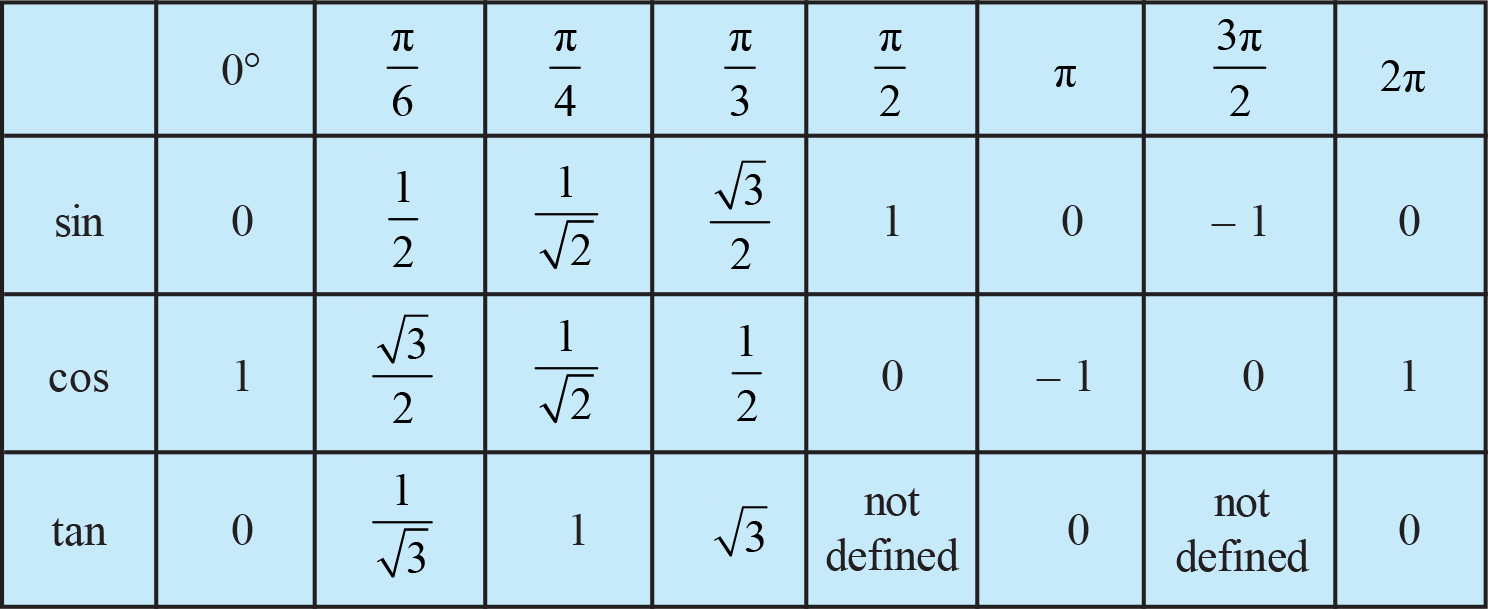 ) Бұл бұрыштардың бірінші тоқсанда жатқанын және өсетінін көру үшін. 0-ден 90-ға дейін. Бұл бізге одан әрі пайдалы болады.
) Бұл бұрыштардың бірінші тоқсанда жатқанын және өсетінін көру үшін. 0-ден 90-ға дейін. Бұл бізге одан әрі пайдалы болады.
30 °, 45 ° және 60 ° бұрыштары үшін кесте мәндерін есте сақтау керек. Қаласаңыз, ұсыныңыз. Бірақ бұл жерде де өмірді өзіңізге жеңілдетуге мүмкіндік бар.) Назар аударыңыз синус кесте мәндерібұл бұрыштар. Және салыстырыңыз косинус кестесінің мәндері …
Иә! Олар бірдей!Тек кері тәртіпте орналасқан. Бұрыштар артады (0, 30, 45, 60, 90) — және синус мәндері арттыру 0-ден 1-ге дейін. Калькулятор арқылы тексеруге болады. Ал косинус мәндері төмендеуі 1-ден нөлге дейін. Оның үстіне, өздерін бағалайды бірдей. 20, 50, 80 бұрыштары үшін бұл жұмыс істемейді …
Сондықтан пайдалы қорытынды. Үйрену жеткілікті үш 30, 45, 60 градус бұрыштары үшін мәндер. Және олардың синустың көбейетінін және косинустың төмендейтінін есте сақтаңыз. Синусқа қарай.) Жартылай (45°) олар кездеседі, яғни 45 градустық синусы 45 градустық косинусқа тең.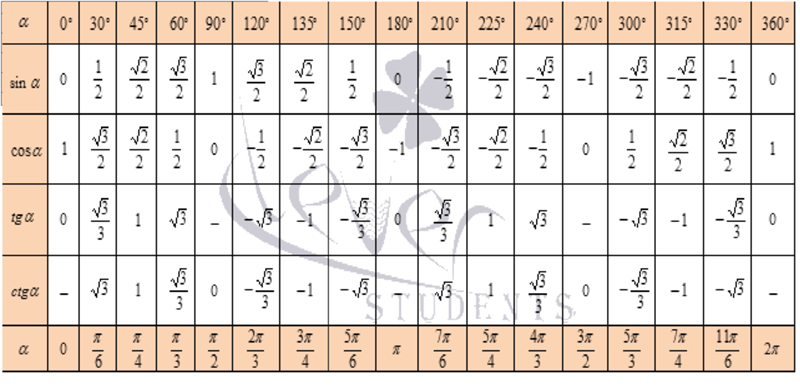 Содан кейін олар қайтадан алшақтайды … Үш мағынаны білуге болады, солай ма?
Содан кейін олар қайтадан алшақтайды … Үш мағынаны білуге болады, солай ма?
Тангенстермен — котангенстермен сурет тек бірдей. Бірге бір. Тек мағыналары әртүрлі. Бұл құндылықтар (тағы үшеу!) Сондай-ақ үйрену керек.
Жарайды, жаттаудың барлығы дерлік аяқталды. Сіз оське түсетін бес бұрыштың мәндерін қалай анықтау керектігін түсіндіңіз (үміттенемін) және 30, 45, 60 градус бұрыштарының мәндерін білдіңіз. Тек 8.
9 бұрыштан тұратын соңғы топпен күресу қалды.
Бұл бұрыштар:
120 °; 135 °; 150 °; 210 °; 225 °; 240 °; 300 °; 315 °; 330 °. Бұл бұрыштар үшін синустар кестесін, косинустар кестесін және т.б.
Қорқыныш, солай ма?)
Егер біз мұнда бұрыштарды қоссақ, мысалы: 405 °, 600 ° немесе 3000 ° және көптеген, көптеген бірдей әдемі?)
Немесе радиандағы бұрыштар? Мысалы, бұрыштар туралы:
және басқа да көптеген нәрселерді білуіңіз керек барлық.
Ең қызығы — мұны білу барлық — негізінде мүмкін емес. Механикалық жадты пайдалансаңыз.
Механикалық жадты пайдалансаңыз.
Және өте оңай, шын мәнінде, қарапайым — егер сіз тригонометриялық шеңберді қолдансаңыз. Тригонометриялық шеңбермен жұмысты үйренгеннен кейін, градустағы осы қорқынышты бұрыштардың барлығы оңай және әдемі түрде ескіге дейін қайнатылады:
Айтпақшы, менде тағы бірнеше қызықты сайттар бар.)
Мысалдар шешуге жаттығып, өз деңгейіңізді білуге болады. Лезде валидация сынағы. Оқу — қызығушылықпен!)
функциялармен және туындылармен танысуға болады.
Тангенс (tg x) және котангенс (ctg x) үшін анықтамалық деректер. Геометриялық анықтама, қасиеттер, графиктер, формулалар. Жанама және котангенс, туындылар, интегралдар, қатарларды кеңейту кестесі. Күрделі айнымалылар түріндегі өрнектер. Гиперболалық функциялармен байланыс.
Геометриялық анықтама
|БД | — центрі А нүктесінде орналасқан шеңбер доғасының ұзындығы.
α – радианмен өрнектелетін бұрыш.
Тангенс ( тг α) тікбұрышты үшбұрыштың гипотенузасы мен катеті арасындағы α бұрышына тәуелді тригонометриялық функция, қарама-қарсы катет ұзындығының қатынасына тең |ВС | іргелес аяқтың ұзындығына |АВ | .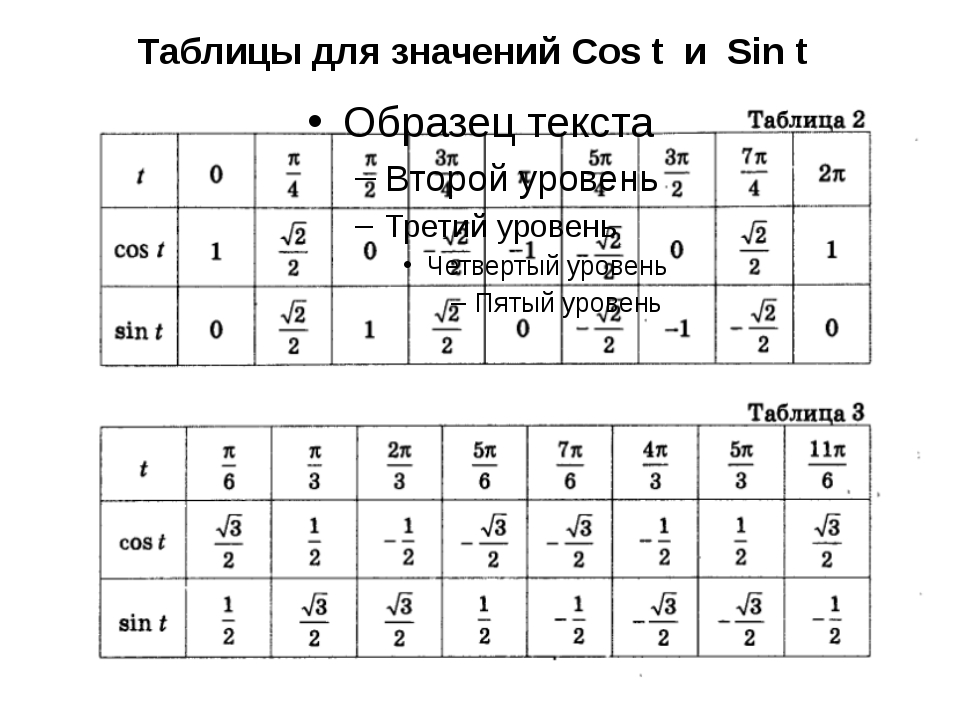 ..
..
котангенс ( ctg α) тікбұрышты үшбұрыштың гипотенузасы мен катеті арасындағы α бұрышына тәуелді тригонометриялық функция, көршілес катет ұзындығының қатынасына тең |АВ | қарсы аяқтың ұзындығына |б.з.б …
Тангенс
Қайда n— тұтас.
Батыс әдебиетінде тангенс келесідей белгіленеді:
.
;
;
.
Тангенс функциясының графигі, y = tg x
Котангенс
Қайда n— тұтас.
Батыс әдебиетінде котангенс былай белгіленеді:
.
Сондай-ақ келесі белгілер қабылданған:
;
;
.
Котангенс функциясының графигі, y = ctg x
Тангенс және котангенс қасиеттері
Мерзімділік
Функциялар y = tg xжәне y = ctg xπ периоды бар мерзімді.
Паритет
Тангенс және котангенс функциялары тақ.
Домендер мен мәндер, өсу, кему
Тангенс және котангенс функциялары анықталу облысында үздіксіз болады (үздіксіздіктің дәлелін қараңыз). Тангенс пен котангенстің негізгі қасиеттері кестеде келтірілген ( n— тұтас).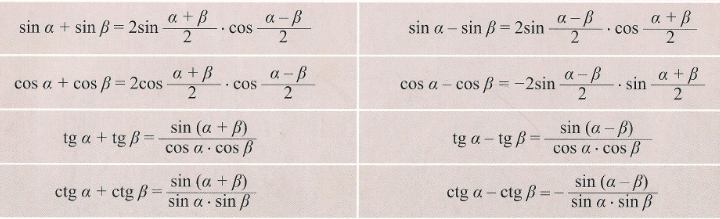
| y = tg x | y = ctg x | |
| Анықтау және үздіксіздік аймағы | ||
| Мәндер ауқымы | -∞ | -∞ |
| Көтерілу | — | |
| Төмендеу | — | |
| Төтенше жағдайлар | — | — |
| Нөлдер, у = 0 | ||
| у осімен қиылысу нүктелері, x = 0 | y = 0 | — |
Формулалар
Синус және косинус бойынша өрнектер
;
;
;
;
;
Қосынды мен айырманың тангенсі мен котангенсінің формулалары
Қалған формулаларды, мысалы, алу оңай
Жанамалардың туындысы
Тангенстердің қосындысы мен айырмасының формуласы
Бұл кестеде аргументтің кейбір мәндері үшін тангенс пен котангенс мәндері көрсетілген.
Күрделі сандармен берілген өрнектер
Гиперболалық функциялар бойынша өрнектер
;
;
Туындылар
;
.
.
Функцияның х айнымалысына қатысты n-ші ретті туынды:
.
Тангенстің формулаларын шығару>>>>; котангенс үшін>>>>
Интегралдар
Серияларды кеңейту
Х дәрежелеріндегі тангенстің кеңеюін алу үшін функциялар үшін дәрежелік қатардағы кеңейтудің бірнеше шарттарын қабылдау керек. күнә xжәне cos xжәне осы көпмүшелерді бір-біріне бөлу,. Бұл келесі формулаларды береді.
Сағат.
кезінде.
қайда B n- Бернулли сандары. Олар не қайталану қатынасы бойынша анықталады:
;
;
қайда.
Немесе Лаплас формуласы бойынша:
Кері функциялар
Тангенс пен котангенстің кері функциялары сәйкесінше доға жанама және доға котангенсі болып табылады.
Арктангенс, арктг
, қайда n— тұтас.
Арккотангенс, аркктг
, қайда n— тұтас.
Қолданылған әдебиет:
И.Н. Бронштейн, К.А. Семендяев, Техникалық оқу орындарының инженерлері мен студенттеріне арналған математика анықтамалығы, «Лан», 2009 ж.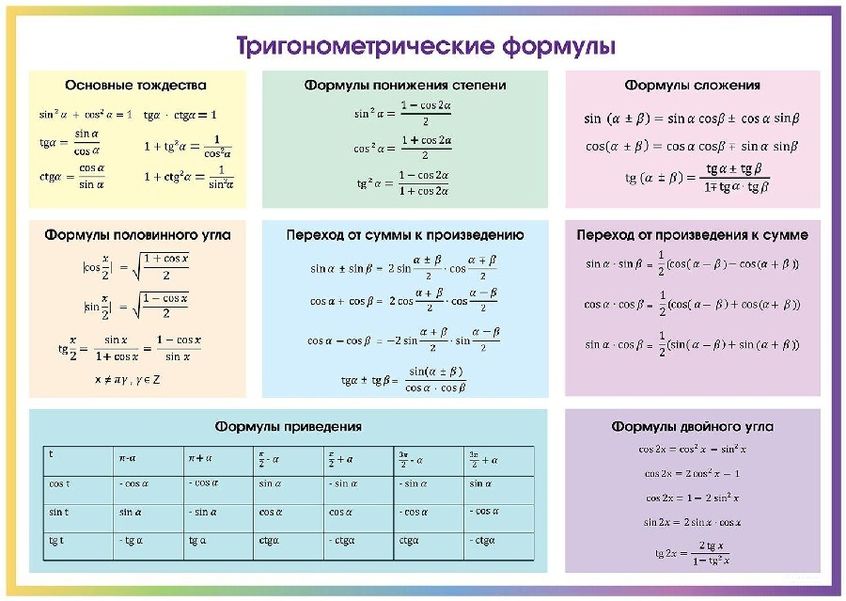
Г.Корн, Ғалымдар мен инженерлерге арналған математика анықтамалығы, 2012 ж.
Тригонометрия ғылым ретінде Ежелгі Шығыста пайда болған. Алғашқы тригонометриялық қатынастарды астрономдар дәл күнтізбе мен жұлдыз бағдарын жасау үшін шығарды. Бұл есептеулер сфералық тригонометриямен байланысты болды, ал мектеп курсында жазық үшбұрыштың жақтары мен бұрыштарының қатынасы зерттеледі.
Тригонометрия – тригонометриялық функциялардың қасиеттерін және үшбұрыштардың қабырғалары мен бұрыштарының арасындағы байланысты қарастыратын математиканың бөлімі.
1 мыңжылдықтағы мәдениет пен ғылымның гүлденген кезеңінде білім Ежелгі Шығыстан Грекияға тарады. Бірақ тригонометрияның негізгі жаңалықтары — араб халифаты ерлерінің сіңірген еңбегі. Атап айтқанда, түркімен ғалымы әл-Маразви тангенс және котангенс сияқты функцияларды енгізді, синус, тангенс және котангенс үшін алғашқы мәндер кестелерін құрастырды. Синус және косинус ұғымын үнді ғалымдары енгізді. Евклид, Архимед, Эратосфен сияқты ежелгі дәуірдің ұлы тұлғаларының еңбектерінде тригонометрияға көп көңіл бөлінеді.
Тригонометрияның негізгі шамалары
Сандық аргументтің негізгі тригонометриялық функциялары синус, косинус, тангенс және котангенс болып табылады. Олардың әрқайсысының өз графигі бар: синусоид, косинус, тангенс және котангенс.
Бұл шамалардың мәндерін есептеу формулалары Пифагор теоремасына негізделген. Оны мектеп оқушылары жақсырақ: «Пифагор шалбары, барлық бағытта бірдей» деген сөзбен жақсы біледі, өйткені дәлелдеу тең қабырғалы тік бұрышты үшбұрыш мысалында келтірілген.
Синус, косинус және басқа да тәуелділіктер кез келген тікбұрышты үшбұрыштың сүйір бұрыштары мен қабырғалары арасындағы қатынасты орнатады. А бұрышы үшін осы мәндерді есептеу формулаларын берейік және тригонометриялық функциялардың байланысын қадағалап көрейік:
Көріп отырғаныңыздай, tg және ctg кері функциялар. Егер a катетін sin A мен гипотенузаның c көбейтіндісі ретінде, ал b катетін cos A * c деп көрсетсек, онда тангенс пен котангенстің келесі формулаларын аламыз:
Тригонометриялық шеңбер
Графикалық түрде бұл шамалардың қатынасын келесідей көрсетуге болады:
Бұл жағдайда шеңбер α бұрышының барлық мүмкін мәндерін білдіреді — 0 ° -дан 360 ° дейін. Суреттен көріп отырғанымыздай, әрбір функция бұрыштың мәніне байланысты теріс немесе оң мән қабылдайды. Мысалы, α шеңбердің І және ІІ ширектеріне жататын болса, яғни 0°-тан 180°-қа дейінгі аралықта болса, sin α «+» белгісімен болады. α 180°-тан 360°-қа дейін болғанда (III және IV ширектер), sin α тек теріс болуы мүмкін.
Суреттен көріп отырғанымыздай, әрбір функция бұрыштың мәніне байланысты теріс немесе оң мән қабылдайды. Мысалы, α шеңбердің І және ІІ ширектеріне жататын болса, яғни 0°-тан 180°-қа дейінгі аралықта болса, sin α «+» белгісімен болады. α 180°-тан 360°-қа дейін болғанда (III және IV ширектер), sin α тек теріс болуы мүмкін.
Нақты бұрыштар үшін тригонометриялық кестелер құруға және шамалардың мәнін білуге тырысайық.
30°, 45°, 60°, 90°, 180° және т.б. тең α мәндері ерекше жағдайлар деп аталады. Олар үшін тригонометриялық функциялардың мәндері есептеліп, арнайы кестелер түрінде берілген.
Бұл бұрыштар кездейсоқ таңдалмаған. Кестелердегі π белгісі радиандарды білдіреді. Rad – дөңгелек доғаның ұзындығы оның радиусына сәйкес келетін бұрыш. Бұл мән әмбебап тәуелділікті орнату үшін енгізілген; радианмен есептеу кезінде радиустың см-дегі нақты ұзындығы маңызды емес.
Тригонометриялық функциялар кестелеріндегі бұрыштар радиандардың мәндеріне сәйкес келеді:
Сонымен, 2π толық шеңбер немесе 360 ° екенін болжау қиын емес.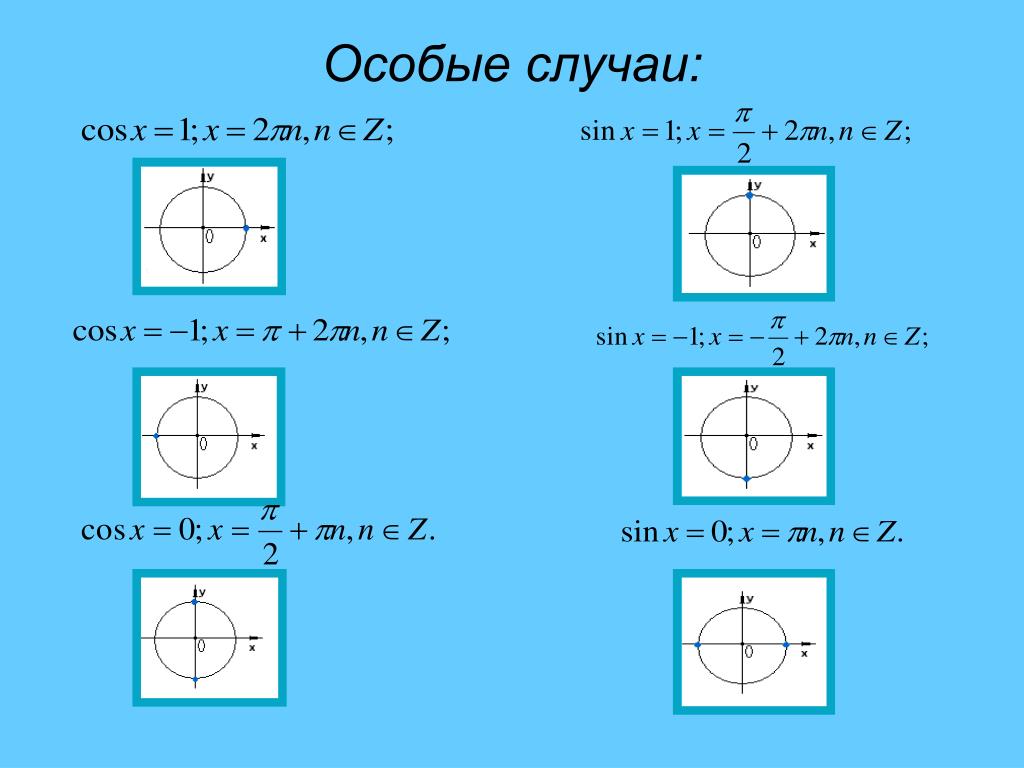
Тригонометриялық функциялардың қасиеттері: синус және косинус
Синус пен косинустың, тангенс пен котангенстің негізгі қасиеттерін қарастыру және салыстыру үшін олардың функцияларын салу қажет. Мұны екі өлшемді координаттар жүйесінде орналасқан қисық түрінде жасауға болады.
Синусиус толқыны мен косинус толқыны қасиеттерінің салыстырмалы кестесін қарастырайық:
| Синусоид | Косинус |
|---|---|
| y = sin x | y = cos x |
| ODZ [-1; 1] | ODZ [-1; 1] |
| sin x = 0, x = πk үшін, мұндағы k ϵ Z | cos x = 0, x = π / 2 + πk үшін, мұндағы k ϵ Z |
| sin x = 1, x = π / 2 + 2πk үшін, мұндағы k ϵ Z | cos x = 1, x = 2πk үшін, мұндағы k ϵ Z |
| sin x = — 1, x = 3π / 2 + 2πk үшін, мұндағы k ϵ Z | cos x = — 1, x = π + 2πk үшін, мұндағы k ϵ Z |
| sin (-x) = — sin x, яғни функция тақ | cos (-x) = cos x, яғни функция жұп |
| функциясы периодты, ең кіші периоды 2π | |
| sin x ›0, I және II кварталдарға жататын x үшін немесе 0 ° -дан 180 ° (2πk, π + 2πk) | cos x ›0, I және IV кварталдарға жататын х үшін немесе 270°-тан 90°-қа дейін (- π / 2 + 2πk, π / 2 + 2πk) |
| sin x ‹0, III және IV кварталдарға жататын x үшін немесе 180 ° -дан 360 ° дейін (π + 2πk, 2π + 2πk) | cos x ‹0, x II және III кварталдарға жатады немесе 90 ° -дан 270 ° дейін (π / 2 + 2πk, 3π / 2 + 2πk) |
[- π / 2 + 2πk, π / 2 + 2πk] аралықта артады. | [-π + 2πk, 2πk] аралықта артады |
| [π / 2 + 2πk, 3π / 2 + 2πk] аралықтарында азаяды. | аралықта азаяды |
| туынды (sin x) ’= cos x | туынды (cos x) ’= — sin x |
Функцияның жұп немесе жұп еместігін анықтау өте қарапайым. Тригонометриялық шамалардың белгілері бар тригонометриялық шеңберді елестетіп, ОК осіне қатысты графикті ойша «бүктеу» жеткілікті. Егер белгілер сәйкес келсе, функция жұп, әйтпесе тақ болады.
Радиандарды енгізу және синусоид пен косинустың негізгі қасиеттерін санау келесі заңдылықты беруге мүмкіндік береді:
Формуланың дұрыстығын тексеру өте оңай. Мысалы, x = π / 2 үшін синус косинус x = 0 сияқты 1-ге тең. Тексеруді кестелерге сілтеме жасау немесе берілген мәндер үшін функциялардың қисық сызықтарын қадағалау арқылы жүргізуге болады.
Тангентоидтық және котангентоидтық қасиеттер
Тангенс және котангенс функцияларының графиктері синус пен косинустан айтарлықтай ерекшеленеді. tg және ctg мәндері бір-біріне кері.
tg және ctg мәндері бір-біріне кері.
- Y = tg x.
- Тангентоид x = π / 2 + πk кезінде у-мәндерге ұмтылады, бірақ оларға ешқашан жетпейді.
- Тангентоидтың ең кіші оң периоды π.
- Tg (- x) = — tg x, яғни функция тақ.
- Tg x = 0, x = πk үшін.
- Функция артып келеді.
- Tg x ›0, x ϵ үшін (πk, π / 2 + πk).
- Tg x ‹0, x ϵ үшін (- π / 2 + πk, πk).
- Туынды (tg x) ’= 1 / cos 2 x.
Төмендегі мәтіндегі котангентоидтың графикалық көрінісін қарастырыңыз.
Котангенсоидтың негізгі қасиеттері:
- Y = ctg x.
- Синус және косинус функцияларынан айырмашылығы, тангентоидта Y барлық нақты сандар жиынының мәндерін қабылдай алады.
- Котангенсоид x = πk кезінде у мәндеріне ұмтылады, бірақ оларға ешқашан жетпейді.
- Котангенсоидтың ең кіші оң периоды π.
- Ctg (- x) = — ctg x, яғни функция тақ.
- Ctg x = 0, x = π / 2 + πk үшін.
- Функция азаяды.
- Ctg x ›0, x ϵ үшін (πk, π / 2 + πk).

- Ctg x ‹0, x ϵ үшін (π / 2 + πk, πk).
- Туынды (ctg x) ’= — 1 / sin 2 x Дұрыс
Ахиллес тасбақадан он есе жылдам жүгіріп, одан мың қадам артта қалды делік. Осы қашықтықты жүгіру үшін Ахиллес қажет уақыт ішінде тасбақа бір бағытта жүз қадам жорғалайды. Ахиллес жүз қадам жүгіргенде, тасбақа тағы он қадам жорғалайды және т.б. Процесс шексіз жалғасады, Ахиллес тасбақаны ешқашан қуып жете алмайды.
Бұл пайымдау барлық кейінгі ұрпақтар үшін логикалық соққы болды. Аристотель, Диоген, Кант, Гегель, Гильберт… Бұлардың бәрі бір жағынан Зенонның апорияларын қарастырды. Соққы соншалықты күшті болды « … қазіргі уақытта талқылаулар жалғасуда, ғылыми қоғамдастық әлі парадокстардың мәні туралы ортақ пікірге келе алмады … мәселені зерттеуге математикалық талдау, жиындар теориясы, жаңа физикалық және философиялық тәсілдер тартылды. ; олардың ешқайсысы сұрақтың жалпы қабылданған шешіміне айналды …«[Википедия,» Зенонның апориясы «]. Әркім олардың алданып жатқанын түсінеді, бірақ алдаудың не екенін ешкім түсінбейді.
; олардың ешқайсысы сұрақтың жалпы қабылданған шешіміне айналды …«[Википедия,» Зенонның апориясы «]. Әркім олардың алданып жатқанын түсінеді, бірақ алдаудың не екенін ешкім түсінбейді.
Математика тұрғысынан Зенон өзінің апориясында шамадан шамаға өтуді анық көрсетті. Бұл ауысу тұрақтылардың орнына қолдануды білдіреді. Менің түсінуімше, айнымалы өлшем бірліктерін қолданудың математикалық аппараты не әлі жасалмаған, не Зенонның апориясына қолданылмаған. Әдеттегі логикамызды қолдану бізді тұзаққа түсіреді. Біз ойлау инерциясы арқылы өзара уақыттың тұрақты өлшем бірліктерін қолданамыз. Физикалық тұрғыдан алғанда, бұл Ахиллес тасбақамен бір деңгейде болған кезде толығымен тоқтағанша уақыттың кеңеюі сияқты көрінеді. Уақыт тоқтап қалса, Ахиллес тасбақаны басып озып кете алмайды.
Біз үйренген логиканы аударсақ, бәрі өз орнына келеді. Ахиллес тұрақты жылдамдықпен жүгіреді. Оның жолының әрбір келесі сегменті алдыңғысынан он есе қысқа. Тиісінше, оны еңсеруге кететін уақыт бұрынғыға қарағанда он есе аз.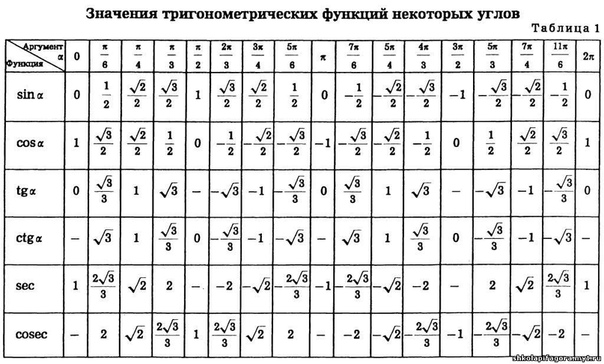 Бұл жағдайда «шексіздік» ұғымын қолданатын болсақ, онда «Ахиллес тасбақаны шексіз тез қуып жетеді» деу дұрыс болар еді.
Бұл жағдайда «шексіздік» ұғымын қолданатын болсақ, онда «Ахиллес тасбақаны шексіз тез қуып жетеді» деу дұрыс болар еді.
Бұл логикалық тұзақтан қалай құтылуға болады? Тұрақты уақыт бірлікте болыңыз және артқа кетпеңіз. Зенон тілінде ол былай көрінеді:
Ахиллес мың қадам жүгіретін уақыт ішінде тасбақа бір бағытта жүз қадам жорғалайды. Келесі уақыт аралығында, біріншіге тең, Ахиллес тағы мың қадам жүгіреді, ал тасбақа жүз қадам жорғалайды. Енді Ахиллес тасбақадан сегіз жүз қадам алда.
Бұл тәсіл ешқандай логикалық парадокссыз шындықты адекватты түрде сипаттайды. Бірақ бұл мәселенің толық шешімі емес. Эйнштейннің жарық жылдамдығының еңсерілмейтіндігі туралы мәлімдемесі «Ахиллес және тасбақа» Зенондық апорияға өте ұқсас. Бұл мәселені әлі де зерттеп, қайта ойластырып, шешуіміз керек. Ал шешімді шексіз көп сандардан емес, өлшем бірліктерінен іздеу керек.
Тағы бір қызықты апория Зенон ұшатын жебе туралы айтады:
Ұшатын жебе қозғалыссыз, өйткені ол уақыттың әр сәтінде тыныштықта болады, ал әр сәтте тыныштықта болғандықтан, ол әрқашан тыныштықта болады.
Бұл апорияда логикалық парадокс өте оңай еңсеріледі — уақыттың әр сәтінде ұшатын жебе кеңістіктің әртүрлі нүктелеріне тірелетінін нақтылау жеткілікті, бұл шын мәнінде қозғалыс. Осы жерде тағы бір жайтты атап өткен жөн. Жолдағы көліктің бір фотосуретінен оның қозғалу фактісін де, оған дейінгі қашықтықты да анықтау мүмкін емес. Автокөліктің қозғалыс фактісін анықтау үшін бір нүктеден әртүрлі уақыт нүктелерінде түсірілген екі фотосурет қажет, бірақ олардан қашықтықты анықтау мүмкін емес. Автокөлікке дейінгі қашықтықты анықтау үшін сізге бір уақытта ғарыштың әртүрлі нүктелерінен түсірілген екі фотосурет қажет, бірақ олар қозғалыс фактісін анықтай алмайды (әрине, есептеулер үшін қосымша деректер әлі де қажет, тригонометрия сізге көмектеседі). Менің ерекше назар аударғым келетіні, екі уақыт нүктесі мен кеңістіктегі екі нүкте әртүрлі нәрселер, оларды шатастырмау керек, өйткені олар зерттеуге әртүрлі мүмкіндіктер береді.
Сәрсенбі, 4 шілде 2018 жыл
Жиын және көп жиын арасындағы айырмашылық Уикипедияда өте жақсы құжатталған. Қараймыз.
Қараймыз.
Көріп отырғаныңыздай, «жиынның екі бірдей элементі болуы мүмкін емес», бірақ жиында бірдей элементтер болса, мұндай жиын «көп жиын» деп аталады. Мұндай абсурдтық логиканы парасатты тіршілік иелері ешқашан түсіне алмайды. Бұл «толық» деген сөзден ақыл-парасат жетіспейтін сөйлейтін тотықұстар мен үйретілген маймылдардың деңгейі. Математиктер бізге өздерінің сандырақ идеяларын уағыздап, қарапайым жаттықтырушы ретінде әрекет етеді.
Бірде көпірді салған инженерлер көпірді сынау кезінде көпірдің астында қайықта болған. Көпір опырылып қалса, біліксіз инженер өзі жасаған үйінділердің астында өледі. Көпір жүкке шыдаса, талантты инженер басқа көпірлерді салар еді.
Математиктер «чур, мен үйдемін», дәлірек айтсақ, «математика абстрактілі ұғымдарды зерттейді» деген сөздің астарына қалай тығылса да, оларды шындықпен тығыз байланыстыратын бір кіндік бар. Бұл кіндік ақша. Математикалық жиындар теориясын математиктердің өздеріне қолданайық.
Біз математиканы өте жақсы оқыдық, қазір кассада отырамыз, жалақымызды беріп жатырмыз. Міне, бізге математик өз ақшасына келеді. Біз оған барлық соманы есептеп, оны үстелге әртүрлі қадаларға саламыз, оларға бірдей номиналдағы вексельдерді саламыз. Содан кейін біз әрбір үйіндіден бір шотты алып, математикке оның «жалақысының математикалық жинағын» береміз. Математиканы түсіндіріп көрейік, ол бірдей элементтері жоқ жиын элементтері бірдей жиынға тең емес екенін дәлелдегенде ғана қалған шоттарды алады. Қызық осы жерден басталады.
Міне, бізге математик өз ақшасына келеді. Біз оған барлық соманы есептеп, оны үстелге әртүрлі қадаларға саламыз, оларға бірдей номиналдағы вексельдерді саламыз. Содан кейін біз әрбір үйіндіден бір шотты алып, математикке оның «жалақысының математикалық жинағын» береміз. Математиканы түсіндіріп көрейік, ол бірдей элементтері жоқ жиын элементтері бірдей жиынға тең емес екенін дәлелдегенде ғана қалған шоттарды алады. Қызық осы жерден басталады.
Біріншіден, депутаттардың «Өзгеге қолдана аласың, маған қолдана алмайсың!» деген логикасы жұмыс істейді. Әрі қарай, біз бір номиналдағы вексельдерде әртүрлі банкнот нөмірлері бар екеніне сендіреміз, яғни оларды бірдей элементтер деп санауға болмайды. Жарайды, жалақыны тиындармен есептейік — тиындарда сандар жоқ. Бұл жерде математик физиканы қатты еске түсіре бастайды: әртүрлі монеталарда кірдің әртүрлі мөлшері бар, кристалдық құрылымы мен әрбір монетадағы атомдардың орналасуы бірегей …
Ал енді менде ең қызықты сұрақ бар: мультижиын элементтері жиынның элементтеріне айналатын және керісінше болатын сызық қайда? Ондай сызық жоқ – бәрін бақсылар шешеді, ғылым бұл жерде еш жерде жатпаған.
Мына жерге қара. Біз алаңы бірдей футбол стадиондарын таңдаймыз. Өрістердің ауданы бірдей, яғни бізде мультисет бар. Бірақ бір стадиондардың атын алып қарасақ, көп нәрсе аламыз, себебі атаулары әртүрлі. Көріп отырғаныңыздай, элементтердің бірдей жиыны бір уақытта жиын және көп жиын болып табылады. Қалай дұрыс? Міне, математик-шаман-шуллер жеңінен тайраңдап, не жиынтық туралы, не мультисет туралы айта бастайды. Қалай болғанда да, ол бізді өзінің дұрыс екеніне сендіреді.
Заманауи бақсылардың жиын теориясымен қалай әрекет ететінін түсіну үшін оны шындыққа байланыстыру үшін бір сұраққа жауап беру жеткілікті: бір жиынның элементтері басқа жиынның элементтерінен қалай ерекшеленеді? Мен сізге «бір бүтін емес деп ойлайтын» немесе «тұтас ретінде ойланбайтын» болмай көрсетемін.
Жексенбі, 18 наурыз 2018 жыл
Санның цифрларының қосындысы – математикаға қатысы жоқ бақсылардың домбырамен билеуі. Иә, математика сабағында санның цифрларының қосындысын тауып, оны қолдануды үйретеді, бірақ сол себепті олар өз ұрпағына өнерін, даналығын үйрету үшін бақсы болып шығады, әйтпесе бақсылар өліп қалады.
Дәлелдеу керек пе? Википедияны ашып, сан бетінің цифрларының қосындысын табуға тырысыңыз. Ол жоқ. Математикада кез келген санның цифрларының қосындысын табуға болатын формула жоқ. Өйткені, сандар біз сандарды жазатын графикалық белгілер және математика тілінде тапсырма былай естіледі: «Кез келген санды білдіретін графикалық белгілердің қосындысын табыңыз». Математиктер бұл мәселені шеше алмайды, бірақ бақсылар — бұл қарапайым.
Берілген санның цифрларының қосындысын табу үшін не және қалай істейтінімізді көрейік. Сонымен, 12345 саны болсын. Осы санның цифрларының қосындысын табу үшін не істеу керек? Барлық қадамдарды ретімен орындап көрейік.
1. Санды қағазға жазамыз. Біз не істедік? Санды санның графикалық символына айналдырдық. Бұл математикалық операция емес.
2. Алынған бір суретті бөлек сандары бар бірнеше суретке кесеміз. Суретті кесу математикалық операция емес.
3. Жеке графикалық белгілерді сандарға түрлендіру. Бұл математикалық операция емес.
4. Алынған сандарды қос. Енді бұл математика.
12345 санының қосындысы 15. Бұл математиктер қолданатын бақсылардан алынған «қию және тігу курстары». Бірақ бұл бәрі емес.
Математика тұрғысынан санды қай санау жүйесінде жазғанымыз маңызды емес. Сонымен, әртүрлі санау жүйелерінде бір санның цифрларының қосындысы әртүрлі болады. Математикада санау жүйесі санның оң жағындағы төменгі таңба ретінде көрсетілген. 12345 саны көп, мен басымды алғым келмейді, туралы мақаладағы 26 санын қарастырыңыз. Бұл санды екілік, сегіздік, ондық және он алтылық санау жүйелерінде жазайық. Біз әрбір қадамды микроскоппен қарастырмаймыз, біз мұны әлдеқашан жасадық. Нәтижесін көрейік.
Көріп отырғаныңыздай, әртүрлі санау жүйелерінде бір санның цифрларының қосындысы әртүрлі болады. Бұл нәтиженің математикаға еш қатысы жоқ. Бұл тіктөртбұрыштың ауданын метр және сантиметрмен анықтау кезінде мүлдем басқа нәтижелерге қол жеткізетін сияқты.
Барлық санау жүйелеріндегі нөл бірдей көрінеді және цифрлардың қосындысы болмайды. Бұл фактінің тағы бір дәлелі. Математиктерге сұрақ: математикада сан емес нәрсе қалай белгіленеді? Математиктер үшін сандардан басқа ештеңе жоқ па? Бақсылар үшін мен бұған рұқсат бере аламын, ал ғалымдар үшін — жоқ. Шындық тек сандардан тұрмайды.
Бұл фактінің тағы бір дәлелі. Математиктерге сұрақ: математикада сан емес нәрсе қалай белгіленеді? Математиктер үшін сандардан басқа ештеңе жоқ па? Бақсылар үшін мен бұған рұқсат бере аламын, ал ғалымдар үшін — жоқ. Шындық тек сандардан тұрмайды.
Алынған нәтиже санау жүйелерінің сандар үшін өлшем бірліктері екенін дәлелдеу ретінде қарастырылуы керек. Өйткені, біз әртүрлі өлшем бірліктері бар сандарды салыстыра алмаймыз. Егер бірдей шаманың әртүрлі өлшем бірліктерімен бірдей әрекеттер оларды салыстырғаннан кейін әртүрлі нәтижелерге әкелетін болса, онда мұның математикаға еш қатысы жоқ.
Нағыз математика дегеніміз не? Бұл математикалық әрекеттің нәтижесі санның шамасына, қолданылатын өлшем бірлігіне және бұл әрекетті кім орындайтынына байланысты болмаған кезде.
Ой! Бұл әйелдердің әжетханасы емес пе?
— Жас әйел! Бұл – көкке көтерілу кезіндегі жандардың киелілігін айырусыз зерттейтін зертхана! Жоғарғы жағында гало және жоғары бағытталған көрсеткі.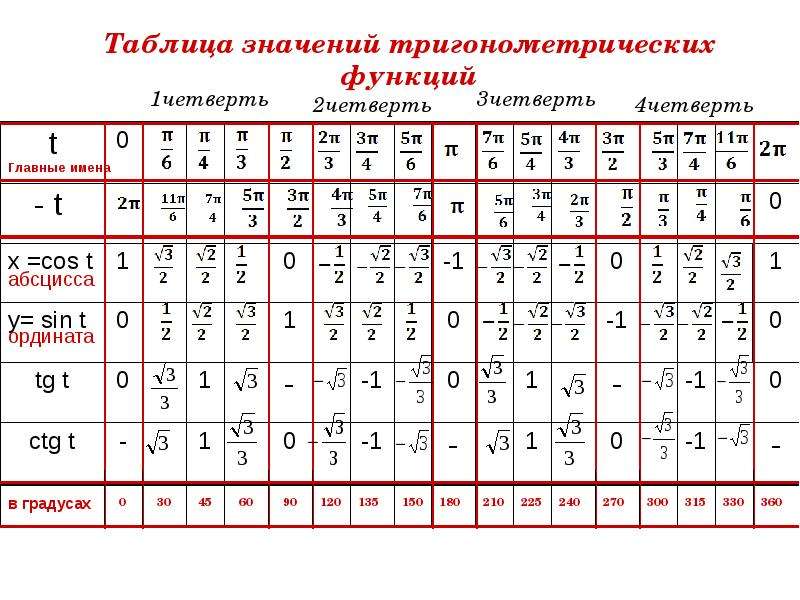 Тағы қандай дәретхана?
Тағы қандай дәретхана?
Әйел … Жоғарыдағы нимбус және төмен көрсеткі — еркек.
Егер мұндай дизайн өнерінің бір бөлігі күніне бірнеше рет көз алдымызда жыпылықтаса,
Содан кейін сіз кенеттен көлігіңізде біртүрлі белгішені табуыңыз таңқаларлық емес:
Өз басым, нәжіс шығаратын адамда (бір сурет) минус төрт градусты (бірнеше суреттен тұратын композиция: минус белгісі, төрт сан, градус белгісі) көре алатындай етіп өзіме күш саламын. Менің ойымша, бұл қыз физиканы білмейтін ақымақ емес. Оның графикалық бейнелерді қабылдау стереотипі бар. Ал математиктер мұны бізге үнемі үйретеді. Міне, мысал.
1А «минус төрт градус» немесе «бір а» емес. Бұл он алтылық санау жүйесіндегі «нәжіс» немесе «жиырма алты» саны. Осы санау жүйесінде үнемі жұмыс істейтін адамдар автоматты түрде сан мен әріпті бір графикалық таңба ретінде қабылдайды.
SIN 0. SINUS (SINUS (SIN X) және Косинус (Cos x)
Назар аударыңыз!
Бұл тақырып қосымша
555 арнайы бөлімдегі материалдар.
«Өте емес» қатты адамдар үшін
Және «өте …») үшін
Біріншіден, мен «Синус және косинс деген не?» Дегеннен қарапайым, бірақ өте пайдалы қорытынды еске саламын. Тангент және котангенес не?
Бұл тұжырым:
Синус, Косинус, тангенс және Котангенес олардың бұрыштарымен тығыз байланысты. Біз бір нәрсені білеміз — бұл, біз екіншісін білеміз.
Басқаша айтқанда, әр бұрышта өзінің тұрақты синтезі мен косинасы бар. Және барлығының дерлік өзіндік тангені және котангері бар. Неге дерлік? Төменде көрсетілген туралы.
Бұл білім өте жақсы көмектеседі! Синустардан бұрыштарға және керісінше көшу керек көптеген тапсырмалар бар. Бұл үшін бар синус кестесі. Сол сияқты, косинустары бар тапсырмалар үшін — косинус кестесі. Ал сіз ойлағандай, бар Үстелдер және катанценттер кестесі.)
Кестелер басқаша. Сізге не тең, айтуға, SIN37 ° 6 ‘деп отыра аласыз. Брэди үстелдерін ашыңыз, отыз жеті градус алты минутты іздеңіз және 0,6032 мәнін қараңыз. Бұл санды есте сақтау керек (және мыңдаған басқа кестелік мәндер) мүлдем қажет емес.
Бұл санды есте сақтау керек (және мыңдаған басқа кестелік мәндер) мүлдем қажет емес.
Негізінде, біздің заманымызда косиндік косандықтардың косиндік синустары өте қажет емес. Бір жақсы калькулятор оларды толығымен алмастырады. Бірақ бұл мұндай кестелердің болуына кедергі келтірмейді. Жалпы білім алу үшін.)
Неліктен бұл сабақ?! — сен сұрадың.
Бірақ неге. Шексіз бұрыштардың арасында бар арнайы, сіз білуіңіз керек бүкіл. Бұл бұрыштарда барлық мектеп геометрия және тригонометрия салынды. Бұл «Көңіл көтеру кестесі» тригонометриясы. Егер сіз ненің немесе не екенін білмесеңіз, мысалы, SIN50 °, ешкім сені айыптамайды.) Бірақ егер сіз күнәға тең екенін білмесеңіз, лайықты екі адамға дайын болыңыз …
Сондай арнайы Бұрыштар да қабылданады. Мектеп оқулықтары әдетте есте сақтауды ұсынады синус кестесі және косинус кестесі Он жеті бұрышқа. Әрине, taTlendens кестесі және катангендер кестесі Сол он жеті бұрышқа … И.Э. 68 мәнді есте сақтау ұсынылады. Айтпақшы, айтпақшы, бір-біріне өте ұқсас, содан кейін ол қайталанады және өзгереді. Керемет көрнекі жадсыз адам үшін — тағы бір міндет …)
Айтпақшы, айтпақшы, бір-біріне өте ұқсас, содан кейін ол қайталанады және өзгереді. Керемет көрнекі жадсыз адам үшін — тағы бір міндет …)
Біз басқа жолмен барамыз. Біз логикалық және балқытудың механикалық жақтауларын алмастырамыз. Содан кейін біз Sinus кестесі мен косинус кестесіне 3 (үш!) »(Үш (үш!)» Мәнін алуымыз керек. Және 3 (үш!) Тангенс кестелері мен ковангендер кестелері үшін мәндер. Болды. Алты мән 68-ден оңай есте сақтаңыз, маған ұқсайды …)
Барлық басқа маңыздылықтар біз осы алтыдан күшті заңды крибтің көмегімен аламыз — Тригонометриялық шеңбер. Егер сіз осы тақырыпты зерттемесеңіз, сілтеме бойынша жүріңіз, жалқау болмаңыз. Бұл шеңбер тек осы сабаққа ғана қажет емес. Ол алмастырылмайды тригонометрия үшін бірден. Мұндай құралды тек күнә жасамаңыз! Сен қаламайсын? Бұл сіздің шаруаңыз. Зерттеу синус кестесі. Косининг кестесі. TaTlendens кестесі. Катанценттер кестесі. Барлық бұрыштар үшін барлық 68 мән.)
Сонымен, бастайық. Бастау үшін біз осы арнайы бұрыштардың барлығын үш топқа бөлеміз.
Бұрыштардың бірінші тобы.
Бірінші топты қарастырайық он жетіден бұрыштар арнайы. Бұл 5 бұрыш, 0 °, 90 °, 180 °, 270 °, 360 °.
Бұл бұрыштарға арналған Cotanens Catanens Anganss-тің синус кестесі келесідей:
H бұрышы.(дәрежеде) | 0 | 90 | 180 | 270 | 360 |
H бұрышы.(Радиандарда) | 0 | ||||
күнә X. | 0 | 1 | 0 | -1 | 0 |
cos x. | 1 | 0 | -1 | 0 | 1 |
tg x. | 0 | мәні жоқ. | 0 | мәні жоқ. | 0 |
cTG X. | мәні жоқ. | 0 | мәні жоқ. | 0 | мәні жоқ. |
Есте сақтағысы келетіндер — есте сақтаңыз. Бірақ мен осы қондырғылар мен Zealics барлық қондырғылар мен Zealics-тің басында шатасқанын айтамын. Бұл мен қалағаннан әлдеқайда күшті.) Сондықтан, біз логикалық және тригонометриялық шеңберді қосамыз.
Біз шеңбер саламыз және осы бұрыштарды дәл осы бұрыштарды тойлаймыз: 0 °, 90 °, 180 °, 270 °, 360 °. Мен бұл бұрыштарды қызыл нүктелермен атап өттім:
Бірден осы бұрыштардың ерекшелігін көре аласыз. Иә! Бұлар түсетін бұрыштар дәл координаттар осіне! Сондықтан, адамдар шатастырады … Бірақ бізді шатастырмайды. Бұл бұрыштардың тригонометриялық функцияларын көп жаттауға қалай табуға болатынын қарастырайық.
Айтпақшы, 0 градус бұрышының орналасуы толығымен сәйкес келеді 360 градус бұрышы бар. Бұл дегеніміз, күнәкарлар, косайыптар, танггенттер бұл бұрыштардың толығымен бірдей екенін білдіреді. Мен шеңберді жабу үшін 360 градус бұрышын атап өттім.
Емтиханның күрделі күйзеліс жағдайында сіз қандай да бір жолмен жүрдім … Sine 0 градус дегеніміз не? Бұл нөлге тең сияқты … егер біреу болса, не?! Механикалық жақтаулар Мұндай нәрсе. Қиын жағдайда, күмәндану …)
Сабыр, тек тыныш!) Мен сізге жүз пайыздық дұрыс жауап беретін практикалық қабылдауды айтамын, бұл күмән тудырады, әрине, күмән тудырады.
Мысал ретінде, біз қалайша нақты және сенімді түрде анықтауға, айтуды, Sinus 0 градусқа қалай және сенімді түрде анықтауға болатынын және сенімді түрде анықтауға болатынын сипаттаймыз. Сонымен бірге, және косинус 0. Бұл бұл құндылықтарда, таңқаларлық, көбінесе адамдар шатастырады.
Мұны істеу үшін шеңбер сызыңыз еркін бұрыш сағ.. Бірінші тоқсанда, 0 градусқа дейін. Синус осьтерінде және осы бұрыштың косинусын ескеріңіз x, Бәрі — Чин-Чинар. Бұл сияқты:
Және қазір — назар! Бұрышты азайтыңыз сағ., қозғалмалы жағын оське апарыңыз О. Меңзерді суреттің үстіне жылжытыңыз (немесе планшеттегі суреттер түрінде) және бәрін қараңыз.
Енді қарапайым логиканы қосыңыз! Біз қарап, ойланамыз: sinx қалай жүреді x бұрышының төмендеуі бар? Бұрышқа нөлге жақындағанда? Бұл азаяды! Және cosx — артады! Бұрыш бәрі бар болған кезде синуспен не болатынын анықтау қалады? Бұрыштың жылжымалы жағы (A нүктесі A) осьте жұмсалған кезде, ал бұрышы нөлге тең болады? Синус бұрышы нөлге кететіні анық. Косуин … дейін … Бұрғылау жақтарының ұзындығы қандай (тригонометриялық шеңбердің радиусы)? Құрылғы!
Косуин … дейін … Бұрғылау жақтарының ұзындығы қандай (тригонометриялық шеңбердің радиусы)? Құрылғы!
Бұл жауап. Sinus 0 градус, 0 градус, 0 градус, 0 градусқа тең, 1-ге тең. Толығымен темір және ешқандай күмәнсіз!) Әйтпесе олай бола алмайды.
Мысалы, 270 градусқа синус білуге \u200b\u200bболады (немесе нақтылау). Немесе косинус 180. шеңбер сызыңыз, еркін Сізді қызықтыратын координаттардың бұрышы сізді қызықтырады, бұрыштың бүйірін едәуір жылжытыңыз және бұрыштың бүйір жағында тұрған кезде синус пен косинустың не болатынын біліңіз. Осымен болды.
Көріп отырғаныңыздай, бұрыштар үшін кез-келген нәрсені жаттап алудың қажеті жоқ. Мұнда қажет емес синус кестесі … Ия мен. косайров кестесі — Сонымен, тригонометриялық шеңбердің бірнеше өтінімдерінен кейін осы құндылықтардың бәрі өздері есте қалады. Егер олар ұмытып кетсе — мен шеңберді 5 секундқа салып, нақтыладым. Дәретханадан досыңыздан сертификат алу қаупі бар, дұрыс па?)
Тангенс пен Котаннезге келетін болсақ, бәрі бірдей. Біз таспен айналысамыз (Коттансенс) — және бәрі бірден көрінеді. Олар нөлге тең, қайда, қайда — жоқ. Танданған және котненстің сызығы туралы не білмеймін? Бұл қайғылы, бірақ бекітілген.) Біз Тригонометриялық шеңбердегі 555 тангенс және Котангенес секциясына бардық, және ешқандай проблемалар жоқ!
Біз таспен айналысамыз (Коттансенс) — және бәрі бірден көрінеді. Олар нөлге тең, қайда, қайда — жоқ. Танданған және котненстің сызығы туралы не білмеймін? Бұл қайғылы, бірақ бекітілген.) Біз Тригонометриялық шеңбердегі 555 тангенс және Котангенес секциясына бардық, және ешқандай проблемалар жоқ!
Егер сіз осы бес бұрышқа синус, косин, тангенс және катангенесті қалай нақты анықтауға болатынын түсінсеңіз — мен сіздерді құттықтаймын! Мен сізге хабарлаймын, енді сізге хабарласқым келеді оське түсіп қалған кез-келген бұрыштар. Бұл 450 °, және 540 °, ал 1800 °, ал 1800 °, тіпті шексіз сан …) Шеңбердегі бұрыш (дұрыс!) Бұрыштағы — және функцияларда ешқандай проблемалар жоқ.
Бірақ, тек кинастағыштармен және проблемалар бар, иә, қателіктер бар … Олардан қалай аулақ болуға болады … Олардан қалай аулақ болуға болады? Бұл қарапайым, бірақ ол қателіктерге қарсы күреске көмектеседі.)
Бірақ сабақ: радиандардағы тригонометриялық шеңбердегі кез-келген бұрышты қалай сурет салу керек (санау) — кенеттен пайда болады.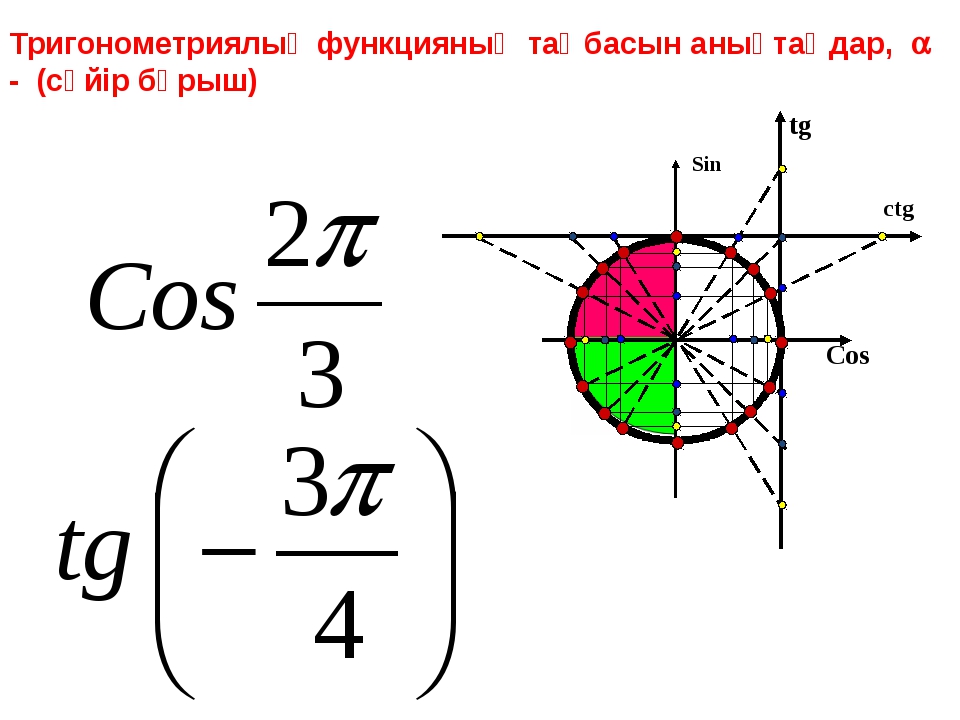 Мүмкіндіктер мағынасында. Айталық, төрт жартылай осьтің қайсысын анықтайық
Мүмкіндіктер мағынасында. Айталық, төрт жартылай осьтің қайсысын анықтайық
сіз бірнеше секундта аласыз. Мен қалжыңдап тұрған жоқпын! Бұл бірнеше секундта. Әрине, әрине, 345 «Пи» …) және 121 және 16 және -1345. Кез-келген барлық коэффициент лезде жауап алуға жарамды.
Және егер бұрыш болса
Ойлау! Дұрыс жауап 10 секунд ішінде алынады. Радиациялық радиацияның бөлшектері үшін, бөлшектердің бөлшектері үшін.
Шын мәнінде, бұл жақсы тригонометриялық шеңбер. Жұмыс қабілеттілігі кей-бір ол автоматты түрде бұрыштарды кеңейтеді шексіз жиынтық Бұрыштары.
Сонымен, он жеті бұрышы он жеті бұрышпен.
Бұрыштардың екінші тобы.
Келесі бұрыштар тобы — 30 °, 45 ° және 60 ° бұрыштар. Неліктен бұл, мысалы, 20, 50 және 80-де емес? Ия, қандай да бір жолмен болды … тарихи тұрғыдан болды.) Содан кейін бұл бұрыштардың жақсы екенін көреді.
Осы бұрыштарға арналған цехандықтардың жансұнғыштарының синус кестесі келесідей:
H бұрышы.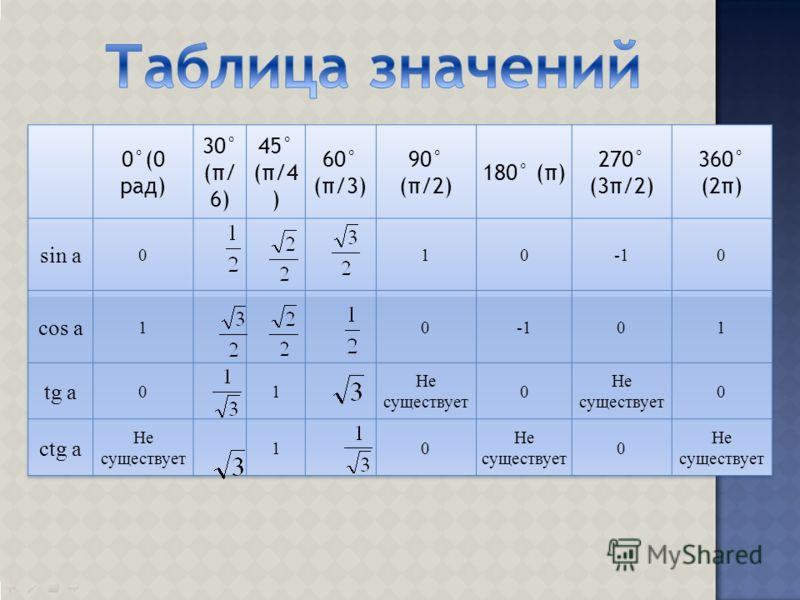 (дәрежеде) | 0 | 30 | 45 | 60 | 90 |
H бұрышы.(Радиандарда) | 0 | ||||
күнә X. | 0 | 1 | |||
cos x. | 1 | 0 | |||
tg x. | 0 | 1 | мәні жоқ. | ||
cTG X. | мәні жоқ. | 1 | 0 |
Мен мәндерді алдыңғы кестенің суретін аяқтау үшін 0 ° және 90 ° -тан 90 ° қалдырдым.) Бұл бұрыштар бірінші тоқсанда жыпылықтап, көбейіп жатқанын көруге болады. 0-ден 90-ға дейін. Ол ыңғайлы болады.
30 °, 45 ° және 60 ° бұрыштар үшін кесте мәндері. Қаласаңыз, бөліңіз. Бірақ мұнда менің өмірімді жеңілдетуге болады.) Назар аударыңыз синус кестесінің мәні Бұл бұрыштар. Және s салыстыру косинесс кестесінің құндылықтары …
Иә! Олар бірдей! Кері тәртіпте орналастырылған. Бұрыштар көбейеді (0, 30, 45, 60, 60, 90) — және синус құндылықтары өсу 0-ден 1-ге дейін сіз калькуляторға көз жеткізе аласыз. Және косинус құндылықтары — кему 1-ден нөлге дейін. Және құндылықтар сол. 20, 50, 80 бұрыштар үшін жұмыс істемейді …
Және косинус құндылықтары — кему 1-ден нөлге дейін. Және құндылықтар сол. 20, 50, 80 бұрыштар үшін жұмыс істемейді …
Демек, пайдалы қорытынды. Үйренуге жеткілікті үш Бұрыштардың мәні 30, 45, 60 градус. Есіңізде болсын, синус күшейіп, Косинус азайып келеді. Синуспен кездесу.) Жартылай (45 °) олар кездеседі, олар кездеседі, И.Э. \u200b\u200b45 градус 45 градусқа тең. Содан кейін тағы да келіседі … Үш мәнді үйренуге болады, дұрыс па?
Тангенттермен — котанценттермен сурет тек бірдей. Бірге бір. Тек мәндер басқаша. Бұл мәндер (тағы үш!) Бізге де үйрену керек.
Жақсы, есте сақтау және аяқталды. Сіз түсіндіңіздер (мен сенесіз), осьтің бес бұрышының мәндерін қалай анықтауға болады және осьтің бес бұрышының мәндерін қалай анықтауға болады және 30, 45, 60 градус бұрыштардың мәндерін білді. Барлығы 8.
Ол 9 бұрыштың соңғы тобымен күресуі керек.
Бұл бұл бұрыштар:
120 °; 135 °; 150 °; 210 °; 225 °; 240 °; 300 °; 315 °; 330 °. Бұл бұрыштар үшін синус кестесін, косинус үстелін және т.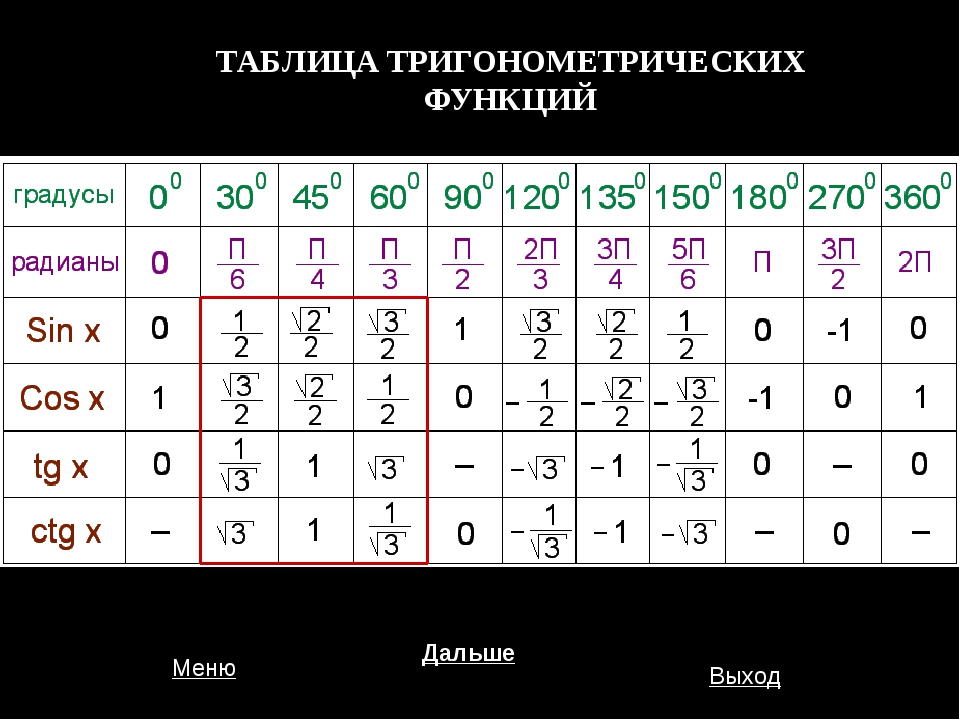 б. білу керек.
б. білу керек.
Түнгі таң, дұрыс па?)
Егер сіз мұнда бұрандыңызды қоссаңыз, мысалы: 405 °, 600 ° немесе 3000 ° және көптеген, көптеген, бірдей әдемі?)
Немесе радиандағы бұрыштар? Мысалы, бұрыштар туралы:
және басқалар, сіз білуіңіз керек бүкіл.
Білуге \u200b\u200bболатын күлкілі нәрсе бүкіл — бұл мүмкін емес. Механикалық жадты қолдансаңыз.
Және өте оңай, іс жүзінде қарапайым — егер сіз тригонометриялық шеңберді қолдансаңыз. Егер сізді трригонометриялық шеңбермен практикалық жұмыс жүргізсеңіз, барлық осы қорқынышты бұрыштар градусқа оңай және талғампаз болады:
Айтпақшы, менде тағы бір қызықты сайттар бар.)
Оған мысалдарды шешуге және сіздің деңгейіңізді білуге \u200b\u200bболады. Жедел тексеру арқылы тестілеу. Оқу — қызығушылықпен!)
Сіз мүмкіндіктермен және туындылармен таныса аласыз.
Тригонометриялық синус функциялары (SIN X) және косинус (COS X) үшін анықтамалық мәліметтер. Геометриялық анықтама, қасиеттері, графиктер, формулалар. Синустар мен косайыптар кестесі, туынды құралдар, интегралдар, рөлдер, сессиялар, моссендер. Күрделі айнымалылар арқылы өрнектер. Гиперболалық функциялармен байланыс.
Геометриялық анықтама, қасиеттері, графиктер, формулалар. Синустар мен косайыптар кестесі, туынды құралдар, интегралдар, рөлдер, сессиялар, моссендер. Күрделі айнымалылар арқылы өрнектер. Гиперболалық функциялармен байланыс.
Синус пен косинустың геометриялық анықтамасы
| BD | — доғалы шеңбердің ұзындығы орталықпен ортасында А..
α — Радиандарда көрсетілген бұрыш.
Анықтама
Синус (SIN α) — бұл гипотеза мен қатаң үшбұрыш коэффициентіне байланысты тригонометриялық функция және КАТЕТ КАТЕТ КАТЕТІ БАРЛЫҚ КОНФЕРЕНЦИЯЛЫҚ КАТЕГИЯЛЫҚ КАТЕГИЯЛЫҚ КАМПАНИЯЛАРДЫҢ ӨЗГЕРТУІ | BC арақатынасымен тең Гипотенузанстың ұзындығына | AC |.
Косинус (cos α) — бұл тригонометриялық функция, ICHOSTENOMA арасындағы α бұрышына және тікбұрышты үшбұрыштың катетіне, іргелес үшбұрыштың ұзындығына теңестірілген | AB | Гипотенузанстың ұзындығына | AC |.
Қабылданған белгілер
;
;
.
;
;
.
Sinus функциясы графигі, y \u003d sin x
Косинус функциясының кестесі, y \u003d cos x
Синус пен косинустың қасиеттері
Мерзімділік
Функциялар y \u003d. күнә X. және y \u003d. cos x. Кезеңмен периодтық 2 π..
күнә X. және y \u003d. cos x. Кезеңмен периодтық 2 π..
Тең титрі
Sinus функциясы тақ. Косинус функциясы де.
Анықтама және құндылықтар, шектен шығу, көбейту, азаю
Sine және Cosine функциялары олардың анықтамасы бойынша үздіксіз, яғни барлық х үшін (сабақтастықтың дәлелі). Олардың негізгі қасиеттері кестеде келтірілген (N — тұтас).
| y \u003d. күнә X. | y \u003d. cos x. | |
| Анықтама және үздіксіздік аймағы | — ∞ | — ∞ |
| Құндылықтар аймағы | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Өсу | ||
| Қарусыздану | ||
| Максима, y \u003d 1 | ||
| Minima, y \u200b\u200b\u003d — 1 | ||
| Зерос, y \u003d 0 | ||
| Орнату осіндегі қиылысу нүктесі, x \u003d 0 | y \u003d. 0 0 | y \u003d. 1 |
Негізгі формулалар
Синус және косиндік квадраттар
Синус пен косинустың формулалары және мөлшері мен айырмашылығы
;
;
Формулалар синустар мен косинустың туындылары
Соманың формулалары және айырмашылық
Косинус арқылы синус өрнегі
;
;
;
.
Синус арқылы косинус өрнегі
;
;
;
.
Тангенс арқылы өрнек
; .
Бізде болған кезде:
;
.
Көмегімен:
;
.
Синус және косинус үстелі, тангендер және коттергерлер
Бұл кестеде дәлелдердің кейбір мәндеріндегі синустар мен косайыптардың мәні көрсетілген.
Күрделі айнымалылар арқылы өрнектер
;
Формула Эйлер
{ -∞
Шон, Косахандар
Кері функциялар
Синус пен косинустың кері функциялары — арксинус және аркуозин.
Арксин, Арксин.
ArkkoSinus, Arccos.
Қолданылған әдебиет:
И. н. Бронштейн, К.А. Семендияев, режиссерлер менеджерлер мен студенттердің студенттері үшін анықтамалық «LAN», 2009 ж.
н. Бронштейн, К.А. Семендияев, режиссерлер менеджерлер мен студенттердің студенттері үшін анықтамалық «LAN», 2009 ж.
Ескерту. Бұл кестеде тригонометриялық функциялардың мәндері квадрат түбірді белгілеу үшін √ белгісін пайдаланады. Фракцияны белгілеу үшін — «/» белгісі.
Сондай-ақ қараңыз Пайдалы материалдар:
Үшін тригонометриялық функцияның анықтамалары, Оны тригонометриялық функцияны көрсететін өткелден табыңыз. Мысалы, 30 градус, біз 30 градусқа синус іздейміз — біз күннің тақырыбы бар бағанды \u200b\u200bіздейміз және біз осы кесте бағанының «30 градус» жолымен, сіз олардың қиылысында пайда болғанын оқыдыңыз — бір секунд. Сол сияқты косинус 60. дәрежелер синус 60. градус (қайтадан, күнә бағанасының қиылысында) және 60 градусқа дейін, біз SIR 60 \u003d √3 / 2 (√3 / 2) және т.б. Сол сияқты, басқа «танымал» бұрыштардың синустары, косинині және тангенстері бар.
Sinus pi, косиндік PI, тангенс Пи және радианның басқа бұрыштары
Төмендегі косинус кестесі, синус және тангенс, сонымен қатар, тригонометриялық функциялардың құндылығын табуға жарамды радиандарда орнатылған.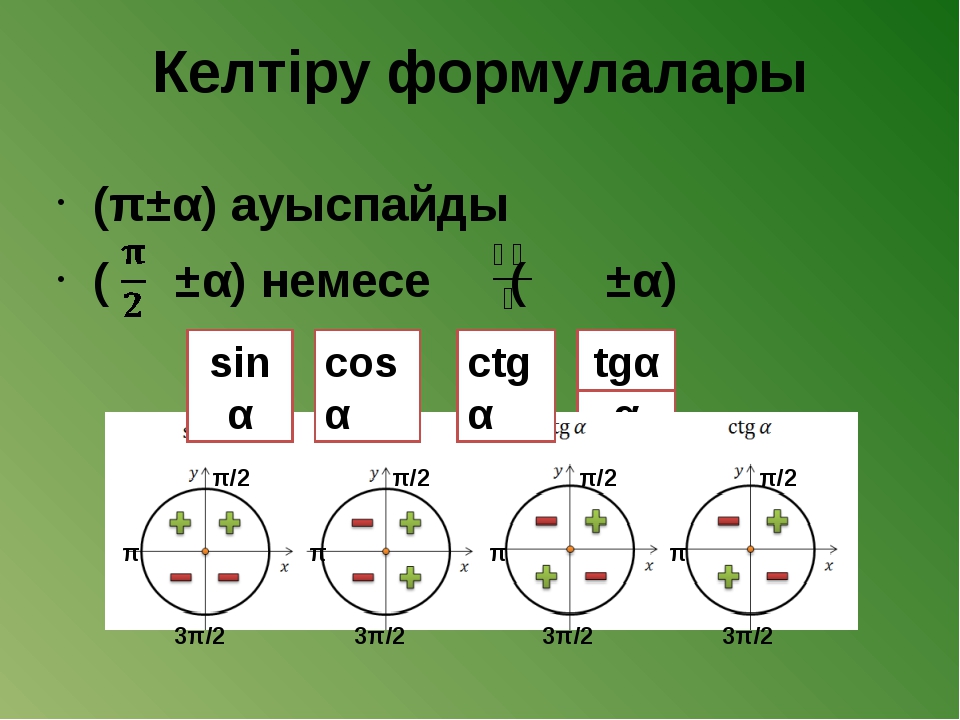 Мұны істеу үшін, бұрыштық мәндерінің екінші бағанын қолданыңыз. Осыған байланысты сіз танымал бұрыштардың құндылығын градустан радианға аудара аласыз. Мысалы, біз бірінші қатарда 60 градус бұрышын табамыз және оның астындағы радиандардағы құнын оқып аламыз. 60 градус π / 3 радианға тең.
Мұны істеу үшін, бұрыштық мәндерінің екінші бағанын қолданыңыз. Осыған байланысты сіз танымал бұрыштардың құндылығын градустан радианға аудара аласыз. Мысалы, біз бірінші қатарда 60 градус бұрышын табамыз және оның астындағы радиандардағы құнын оқып аламыз. 60 градус π / 3 радианға тең.
PI саны айналдыра ұзындығының бұрыштың дәрежесінен тәуелділігін біркелкі білдіреді. Осылайша, PI радиандары 180 градус.
PI (радиандар) арқылы көрсетілген кез-келген нөмірді оңай градусқа дейін, санын (π) 180-ге дейін ауыстыруға болады.
Мысалдар:
1. Синус б..
Sin π \u003d Sin 180 \u003d 0
Осылайша, Sinus Pi синус 180 градусқа тең, ал ол нөлге тең.
2. Косин..
Cos π \u003d cos 180 \u003d -1
Осылайша, косиндік PI 180 градус косинуспен бірдей және ол минусқа тең.
3. Тангенс П.
Tg π \u003d tg 180 \u003d 0
Осылайша, Тангент Пи таныс 180 градуспен бірдей және ол нөлге тең.
Синус құндылықтарының кестесі, косинет, бүйірлерге арналған тангенс 0 — 360 градус (жиі мәндер)
бұрыштың мәні α. (дәрежелер) | бұрыштың мәні α. (PI саны арқылы) | күнә. (синус) | cos. (косинус) | тг. (Тангент) | cTG. (Котангент) | сек. (сек) | cosec. (косекант) |
| 0 | 0 | 0 | 1 | 0 | — | 1 | — |
| 15 | π / 12. | 2 — √3 | 2 + √3 | ||||
| 30 | π / 6. | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π / 4. | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π / 3.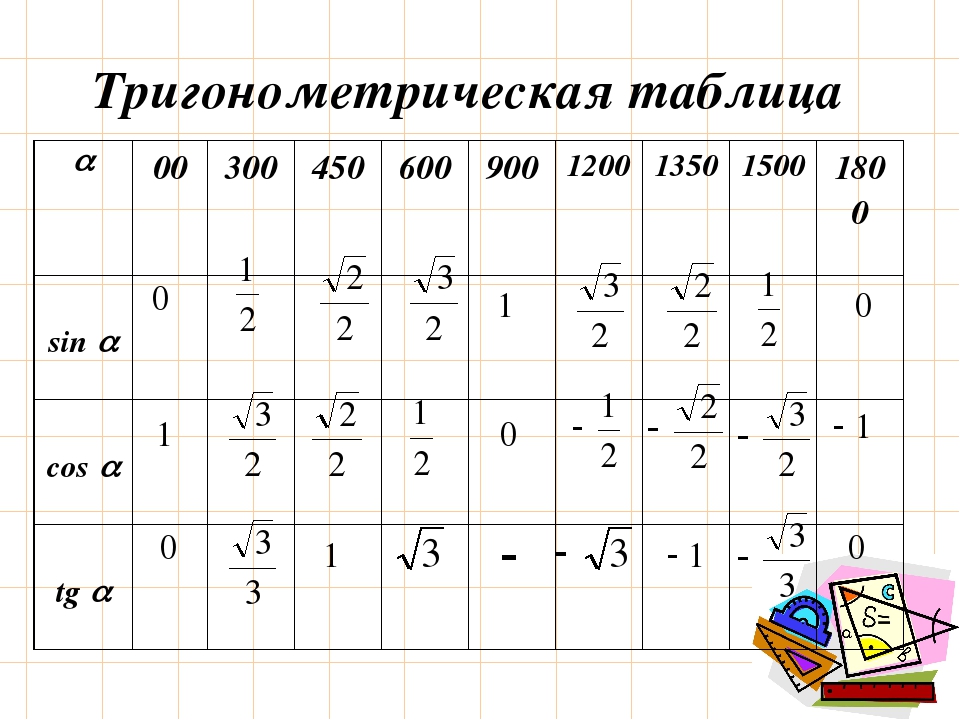 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12. | 2 + √3 | 2 — √3 | ||||
| 90 | π / 2. | 1 | 0 | — | 0 | — | 1 |
| 105 | 7π / 12. | — | — 2 — √3 | √3 — 2 | |||
| 120 | 2π / 3. | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4. | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π / 6. | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | — | -1 | — |
| 210 | 7π / 6. | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π / 3. | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/28. | -1 | 0 | — | 0 | — | -1 |
| 360 | 2π. | 0 | 1 | 0 | — | 1 | — |
Егер тригонометриялық функциялар кестесі функцияның мәнінің орнына мән болса, түтік көрсетілген (тангенс (TG) 90 градус, котангент (CTG) 180 градус), бұл функцияның ағымдық деңгейі бар дегенді білдіреді белгілі бір мән жоқ. Егер манекан болмаса — ұяшық бос, содан кейін біз әлі де қажетті мәнді жасаған жоқпыз. Бізді пайдаланушылардың бізге қалай келуге және кассаны жаңа құндылықтармен толықтырады, сонымен қатар косиндік құндылықтар, синустар мен танымалдылар туралы қазіргі мәліметтердің ең көп таралған құндылықтары туралы, көптеген тапсырмаларды шешу үшін жеткілікті.
Бізді пайдаланушылардың бізге қалай келуге және кассаны жаңа құндылықтармен толықтырады, сонымен қатар косиндік құндылықтар, синустар мен танымалдылар туралы қазіргі мәліметтердің ең көп таралған құндылықтары туралы, көптеген тапсырмаларды шешу үшін жеткілікті.
Ең танымал бұрыштар үшін SIR, COS, TG тригонометриялық функцияларының мәндер кестесі
0, 15, 30, 45, 60, 90 … 360 градус
(Сандық құндылықтар »Брэди кестелеріндегідей«)
| Бұрыштың мәні α (градус) | Радиандардағы α бұрышының мәні | Күнә (синус) | Cos (косинус) | TG (тангенс) | CTG (COTANGENT) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 | 0,2588 | 0,9659 | 0,2679 | ||
| 30 | 0,5000 | 0,5774 | |||
| 45 | 0,7071 | ||||
0,7660 | |||||
| 60 | 0,8660 | 0,5000 | 1,7321 | ||
7π / 18. |
Птолемейдің теоремасы дегеніміз не? » — Ғылым
Мазмұны
Птоломей теоремасы ‘кез келген циклдік төртбұрыш үшін оның диагональдарының көбейтіндісі қарама-қарсы жақтардың әрбір жұбының көбейтіндісінің қосындысына тең болады’ дейді. Теореманы әрі қарай кеңейтуге болады, бұл бесбұрыштың қабырғалары мен оның диагоналіне алтын қатынасын дәлелдеу үшін және Пифагор теоремасы, басқалармен қатар.
Микеланджелоның не екенін біліп көрдіңіз бе Қасиетті отбасы, Генрих Агриппа пентаграммада жазылған адам және Соңғы кешкі ас Сальвадор Далидің ұқсастығы бар ма?
Мұның бәрі мәңгілік көркемдік кереметтерінен басқа, жалпы дизайн философиясын / элементін ұстанады. Әрқайсысы бесбұрыштың пішінін қамтиды, ал кез-келген тұрақты бесбұрыштың диагоналіне қатынасы ‘Алтын қатынасты’ береді (1.618033…). Құрылыстағы алтын арақатынасты ұстанатын қолдан жасалған конструкциялар мен табиғи заттар әлемдегі ең эстетикалық жағымды заттар болып саналады.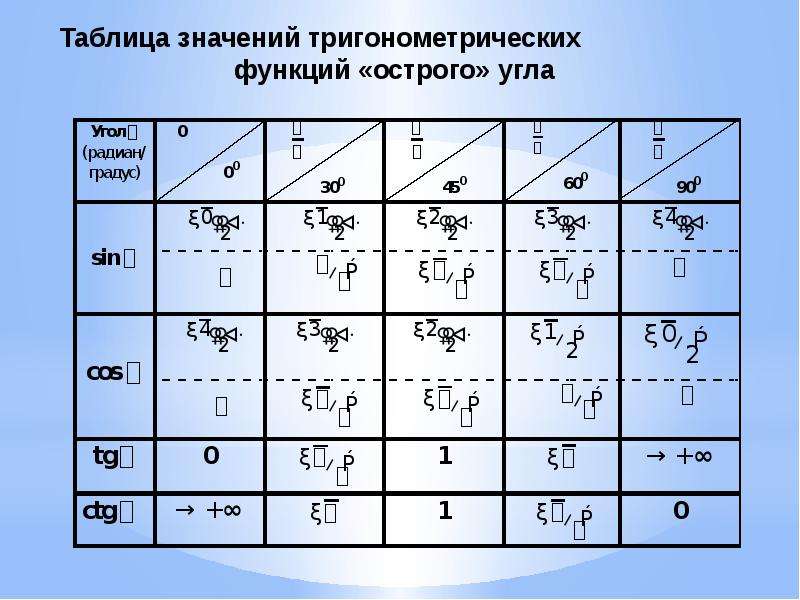
Бесбұрыштың диагональдары мен қабырғалары арасындағы бұл эстетикалық байланысты циклдік төртбұрыштар Плотемиясының теоремасын кеңейту арқылы дәлелдеуге болады. Сонымен қатар, Птолемей теоремасын Пифагор теоремасын дәлелдеу үшін де қолдануға болады, бірақ біз бұған жетпес бұрын Птолемей теоремасы дегеніміз не?
Птоломей теоремасы
Клавдий Птоломей көптеген салаларда тәжірибесі бар грек аңызы болды; ол астрономиядағы жұмыстарымен (Птолемейлік жүйе) ең танымал болғанымен, ол сондай-ақ терең математика шебері болды және қазір ‘Птоломей теоремасы’ деп аталатын теореманы ашты. Теорема Птоломейдің 1-кітабының 10-тарауында айтылды Алмагест және циклдік төртбұрыштың төрт жағы (төрт шыңы бір шеңберге орналасқан төртбұрыш) оның диагональдарымен байланысты.
Птоломей теоремасында ‘шеңберге салынған төртбұрыш үшін қарама-қарсы жақтардың әр жұбының көбейтінділерінің қосындысы оның екі диагоналының көбейтіндісіне тең’ делінген.
ABCD төртбұрышын барлық төбелерімен, яғни A, B, C, D шеңберде жатқанын қарастырайық, осылайша циклдік төртбұрышты құрайық.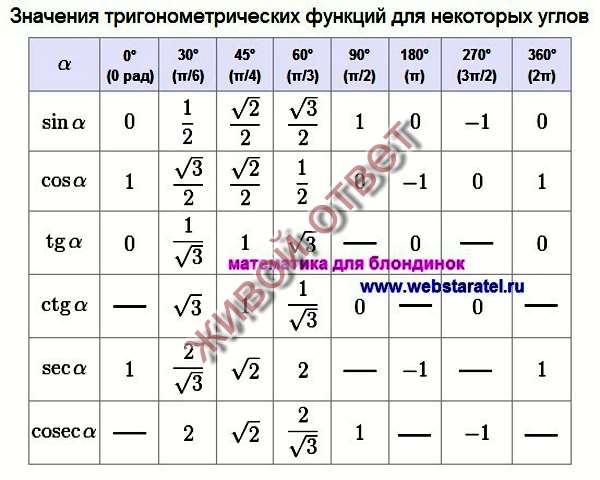 Мұнда AC және BD төртбұрыштың диагональдары, ал қалған барлық сызық сегменттері (AB, BC, CD, AD) оның бүйірлері болып табылады. Енді Птолемей теоремасы бойынша қарама-қарсы жақтардың көбейтіндісінің қосындысы (AB × CD + BC × AD) диагональдардың көбейтіндісіне тең болады (AC × BD).
Мұнда AC және BD төртбұрыштың диагональдары, ал қалған барлық сызық сегменттері (AB, BC, CD, AD) оның бүйірлері болып табылады. Енді Птолемей теоремасы бойынша қарама-қарсы жақтардың көбейтіндісінің қосындысы (AB × CD + BC × AD) диагональдардың көбейтіндісіне тең болады (AC × BD).
Математикалық,
AC × BD = (AB × CD) + (BC × AD)
Жоғарыда аталған қатынас және осылайша теорема бірнеше жылдар бойы дәлелденген бірнеше әдістер бар. Кейбір математиктер қатынасты дәлелдеу үшін тригонометриялық сәйкестікті пайдаланады, ал басқалары күрделі сандарды немесе инверсивті геометрияны қолданады. Дегенмен, барлық дәлелдеулердің ең қарапайымы (бізге сәйкес) ұқсас үшбұрыштарды және олардың қасиеттерін қолдану арқылы қамтамасыз етіледі.
Барлық дерлік математикалық дәлелдеулер сияқты, біз бір нәрсені болжаудан бастаймыз.
Жоғарыдағы циклдік төртбұрыш үшін AC диагональында ∠ABK = ∠CBD болатын К нүктесі бар.
Жоғарыда келтірілген диаграммада көрсетілгендей, BC доғасы ∠BAC & ∠BDC қосады және іштегі бұрыштық теоремаға сәйкес ∠BAC = ∠BDC.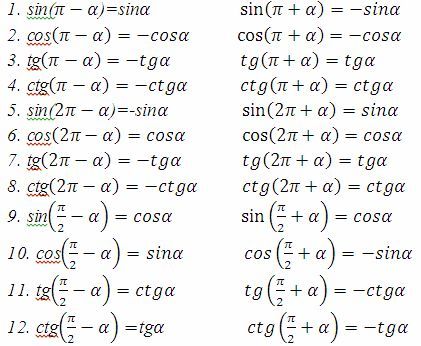 Сол сияқты АВ доғасы ∠ADB және ∠ACB бағындырады, сондықтан екі бұрыш тең болады (∠ADB = ∠ACB). Ұқсас үшбұрыштардың (AA) теоремасы бойынша △ ABK △ DBC-ге, ал △ KBC △ ABD-ге ұқсас.
Сол сияқты АВ доғасы ∠ADB және ∠ACB бағындырады, сондықтан екі бұрыш тең болады (∠ADB = ∠ACB). Ұқсас үшбұрыштардың (AA) теоремасы бойынша △ ABK △ DBC-ге, ал △ KBC △ ABD-ге ұқсас.
Ұқсас үшбұрыштар үшін △ ABK және △ DBC:
Сондықтан,
Сол сияқты, △ KBC және △ ABD үшбұрыштары үшін:
Сондықтан,
Жоғарыда келтірілген теңдеулерді қосқанда:
AK.DB + KC.BD = AB.DC + BC.AD
Мұнда DB және BD бірдей және ортақ еселік ретінде орындалуы мүмкін,
(AK + KC) .BD = AB.DC + BC.AD
Диаграммадан AK + KC = AC.
Сондықтан,
AC.BD = AB.DC + BC.AD
Мінекей. ABCD циклді төртбұрышының диагональдарының көбейтіндісі оның қарама-қарсы жақтарының көбейтіндісінің қосындысына тең, дәл осылай Птоломей теоремасы бізге айтады!
Қолданбалар
Бұрын айтылғандай, Птолемей теоремасын циклды бесбұрыштарға дейін кеңейтуге және оның қабырғалары мен диагональдары арасындағы алтын арақатынасын дәлелдеу үшін қолдануға болады.
ABCDE тұрақты циклды бесбұрыш үшін қабырғалары ‘а’, ал диагональдары ‘d’ ұзындығына тең.
ABCD төртбұрышына шоғырланып, Птоломей теоремасын қолдана отырып, біз мынаны аламыз:
AC.BD = BC.AD + AB.DC
Тиісті ұзындық мәндерін ауыстырып,
d.d = a.d + a.a
d2 = a.d + a2
Жоғарыдағы теңдеуді a2-ге бөлу
d2 / a2 = d / a + 1
Енді ‘d / a’ қатынасы ‘r’ арқылы ұсынылсын
Демек, r2 = r + 1
Қайта реттеу, r2 — r — 1 = 0
R үшін шешу,
r = (1 ± √1 — 4 (1) (- 1)) / 2
r = (1 ± √5) / 2
r = 1.618033…
Демек, тұрақты бесбұрыш қабырғаларының оның диагональдарына қатынасы (r = d / a = 1.618033) — алтын қатынас.
Птолемей теоремасын пайдаланып, Пифагор теоремасын дәлелдеу үшін шеңбер ішіне жазылған ABCD тікбұрышты елестетіңіз.
Птолемей теоремасын ABCD төртбұрышына қолдана отырып, бізде бар
AD⋅BC = AB⋅DC + AC⋅DB
Кез келген берілген төртбұрыш үшін екі диагональ сияқты қарама-қарсы жақтар тең болады. Демек, AB = CD, AC = BD және AD = BC.
BC2 = AB2 + AC2
Жоғарыда келтірілген теңдеу АВС тік бұрышты үшбұрышқа қолданылатын Пифагор теоремасынан басқа ештеңе емес.
Қорытынды сөз
Жоғарыда түсіндірілген екі қорытындыдан басқа, Птоломей аккордтар кестесін құру үшін циклдік төртбұрыштар теоремасын қолданды (синус функциясының кестесіне ұқсас тригонометриялық кесте, біз бүгінге дейін қолданамыз). Птоломейдің аккордтар кестесі мұндай бірінші болып табылмаса да, тригонометриялық функциялардың мәнін 30 incre өсімімен қамтамасыз етті, ал Гиппарх жасаған бірінші тригонометрия кестесі 7 ° 30 incre өсіммен мән берді.
Бұл интерполяциялардың дәлдеуіне алып келді және әртүрлі планеталардың, күннің, айдың, жұлдыздардың көтерілуі мен батуын, ай мен күннің тұтылу күндерін және т.с.с. есептеуге көмектесті.
Птоломейдің астрономиялық жұмысының бірігуі он үш кітап түрінде көрініс тапты, олар жиынтық ретінде « Алмагест, ол астрономия саласындағы ең ықпалды жұмыстардың бірі болып саналады. Оның жұмысы бұрынғы астрономиялық жұмыстардың бәрін ауыстырып, бірнеше жыл бойы жоғары билік жүргізді, сондықтан ежелгі заманның ең үлкен астрономиялық шығармасы ретінде бағаланды.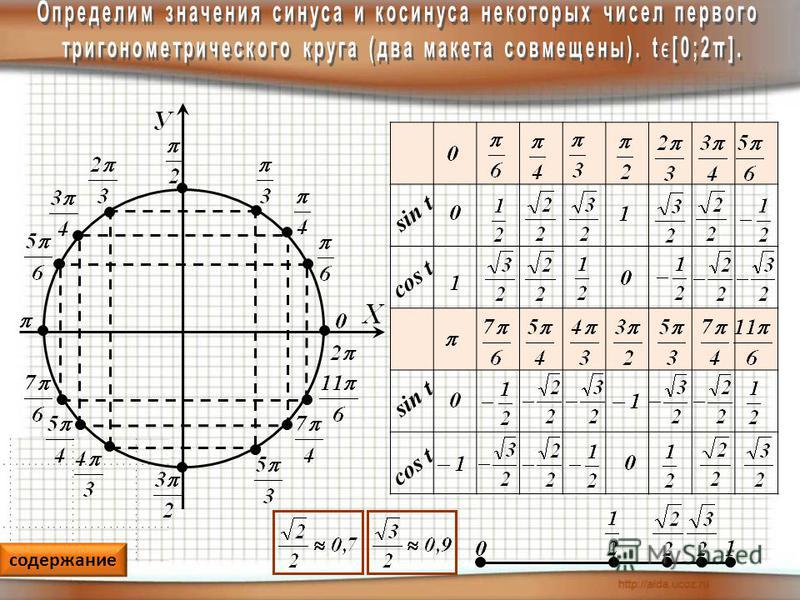
Птоломейдің көптеген астрономиялық жетістіктері аккордтар кестесін пайдаланбай мүмкін болмас еді, егер Птоломейдің циклды төртбұрыштары туралы теоремасы болмаса, салынбайтын еді!
(PDF) Большая сосиска из крошек
68 Электронные коммуникации в вероятности
набор положительной емкости. Верно ли, что носитель V
1
(A) неограничен, т. е. P[V
1
(A) >x] > 0 для всех x? Это легко сделать, если A имеет
сечение положительной (d − 1)-мерной меры Лебега, но я не могу доказать это в общем случае. Есть ли у вас какие-либо идеи?
Мы были заинтригованы этим вопросом, потому что он привел нас к размышлению об источнике
объема венской колбасы, когда А — это «маленькое» множество (т.г., неполярное множество нулевой
хаусдорфовой размерности на плоскости). Является ли это следствием макроскопического движения В (в случае
, в котором случай V
1
(А)) не был бы ограниченным, или микроскопических флуктуаций (в котором
случай В
1
(А) мог бы быть ограниченным, как квадратичная вариация)?
Наше доказательство следующей теоремы показывает, что хотя микроскопические флуктуации
B необходимы для положительности V
1
(A), макроскопическое поведение B, безусловно,
влияет на величину V
1
(А).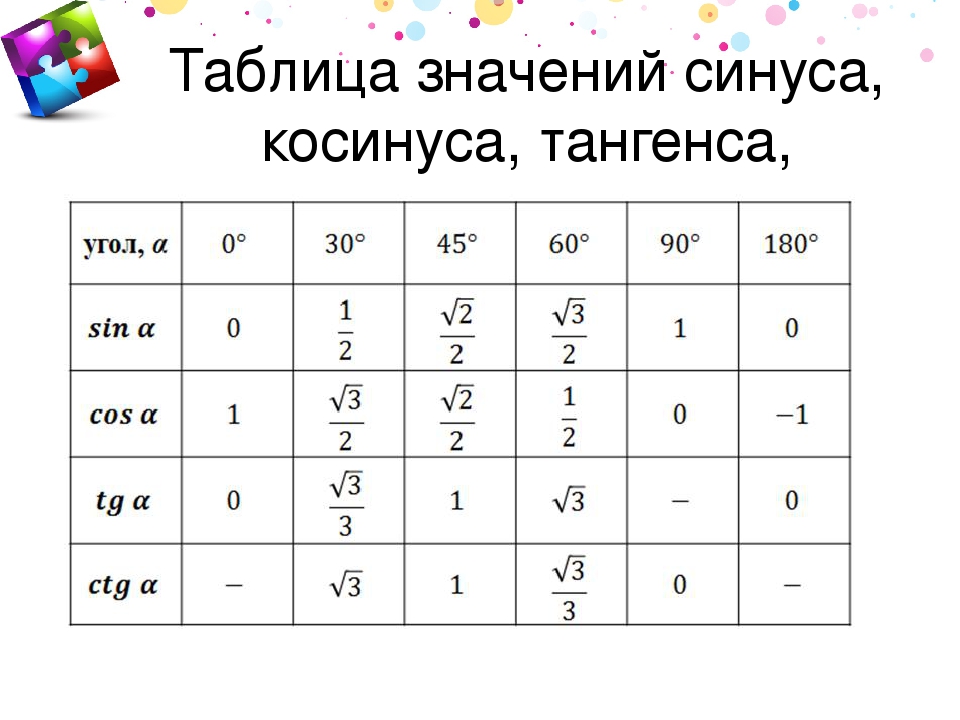
Теорема 1. Если емкость C(A) множества A ⊂
d
положительна, то V
1
(A) не ограничено.
Соответствующая мощность может быть определена для A ⊂
d
с d
с d ≥ 3, на
C (A) = SUP
μ
μ (A)
2
E (μ)
где E(µ)=
ZZ
c
d
dµ(x) dµ(y)
|x − y|
d−2
,
, а верхняя грань лежит по мерам, поддерживаемым на A.(константа c
d
не имеет значения
для наших целей). Аналогичная формула верна для d = 2 с логарифмическим ядром; в
этот случай C(A) часто называют константой Робина, и будет удобно ограничить
внимание множествами A диаметра меньше 1.
Обозначим через τ
A
время попадания A через Броуновское движение. Теоремом Фубини
E [V
1
(A)] =
Z
D
P
x
[τ
A
≤ 1] DX.
Из связи между теорией потенциала и броуновским движением следует, что
E[V
1
(A)] отлично от нуля тогда и только тогда, когда A имеет положительную емкость; см., например, [3], [2] или [4].
2. Рецепт
Для любого ядра K(x, y) соответствующая емкость определяется C
K
(A)=sup
µ
µ(A)
3
2
2
K
(µ)
где E
K
(µ)=
RR
K(x, y) dµ(x) dµ(y) и супремум над мерами на A.Мы
предполагаем, что K(x, x)=∞ для всех x и что для 0< |x − y| K , ядро K непрерывно и K(x, y) > 0. Для всех таких ядер справедлива следующая лемма. Лемма 1. Если множество A ⊂ d имеет C K (A) > 0, то для любого L<∞ существует >0 и подмножества A (A) > 0 2 , …, м
м
из такого, что
P
M
I = 1
C
K
(A
I
) ≥ l , а расстояние между
A
i
и A
j
не менее для всех i 6= j.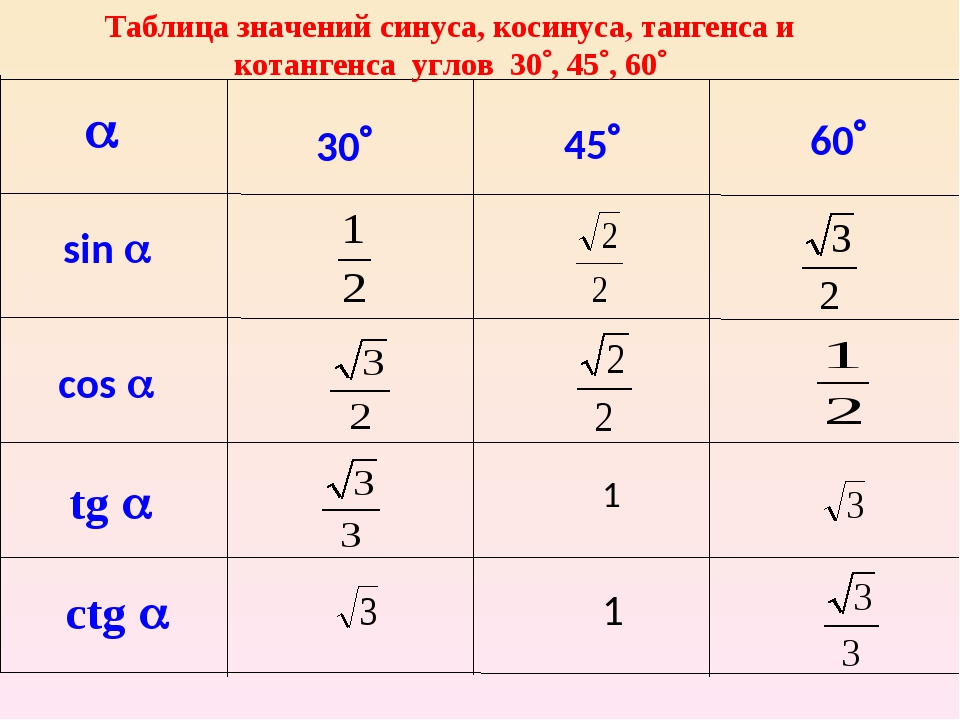 (m и зависят от A и L).
(m и зависят от A и L).
Доказательство. Можно предположить, что diam(A) K , иначе мы можем заменить A подмножеством положительной емкости и диаметра меньше R K . Пусть µ мера с носителем на A такая, что µ(A)=1 и E K (µ) < ∞. 1 2 1 2 А 8 4 1 2 1 2 1 2 1 2 S 2 2 1 5 6 7 8 1 2 1 4 2 + 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 BCDE Поскольку датчик потребляет около 60 мВт, было бы благоразумно отключить его питание, когда оно не требуется. Резисторы серии 5Vanalog 110nF размещать вблизи Осталось выяснить, как 1 R279 162K 1% удаленных источников. Конденсаторы 0-2,5 В, диапазон -5 В, целесообразно подключить 2-контактный разъем U26 U68 рядом с АЦП.Заземляющий провод R338. Альтернативой 3,3 В R3 100K 1% 1 10 может быть P-FET BAROMETER Ain0 SC_nCS5 4 1 2 R13 150K 1% 5Vanalog 2 SDA Out 3 BAROMETER R5 10K 1% Ain1 3 9 в Vcc, включенный с помощью Gnd SC_SCLK 150K 1 % R6 10K 1% N-FET. Imon+5V 4 Ain2 SCL R4 R7 10K 1% 5 Ain3 Imon+3,3V R339 100K 1% R8 10K 1% Ain4 Imon+2,5V 6 R104 10K 1% MPXA4115A 100K 1% R9 10K 1% Imon+1,8V 7 Ain5 R10 10K 1% Imon-5V 8 Ain6 DISC-OneSPE R11 10K 1% 16 Ain7 12 Q7 R12 10K 1% Ain8 Vdd 3. Из теоремы Пифагора, в 2 = а 2 + b 2 = 3 2 + 4 2 = (3 × 3) + (4 × 4) = 9 + 16 = 25 Если c 2 = 25, c = 5 . Это знаменитый треугольник 3 : 4 : 5 , используемый при съемке и измерении. Таких треугольников много (например, 5 : 12 : 13 ). Вы можете проверить, что 5 : 12 : 13 является прямоугольным треугольником, выполнив приведенные выше вычисления. Конечно, числа не обязательно должны быть целыми числами. Из теоремы Пифагора, а 2 = в 2 — б 2 = 15,3 2 — 4,7 2 = (15,3 х 15,3) — (4,7 х 4,7) = 234,09 — 22,09 = 212 Если а 2 = 212, а = 14,56 . Площадь указана по номеру А = ab/2 = 4,3 × 6,4 / 2 = 13,76 Существуют три основные тригонометрические функции.Они называются Синус , Косинус и Тангенс . Это записывается как Это записывается как Это записывается как Используя определения тригонометрических функций Sin φ / Cos φ
= (a / c) / (b / c) = (a / c) × (c / b) = a / b = Tan φ Используя определения тригонометрических функций Sin 2 φ + Cos 2 φ
= (a / c) 2 + (b / c) 2 = (a 2 / c 2 ) + (c 2 / b 2 ) = (a 2 2 ) 2 ) / с 2 . Но a 2 + b 2 = c 2 (из теоремы Пифагора) Следовательно, (а 2 + b 2 ) / с 2 = с 2 / с 2 = 1 . Значения тригонометрических функций для определенного угла можно найти в таблицах или на калькуляторе, как и в случае с логарифмами. Мы будем использовать их сейчас в некоторых примерах. Используя определение касательных и перестановку, мы имеем a = b × Tan φ = 12,6 × Tan 51 o = 12,6 × 1,235 С помощью калькулятора или таблиц находим, что Тан 51 o = 1,235 (с точностью до трех знаков после запятой). 12,6 × 1,235 = 15,56 м . Значение c можно найти с помощью теоремы Пифагора. Здесь мы будем использовать определение косинусов и переставлять. с = b / Cos φ = 12,6 / Cos 51 o = 12,6 / 0,629 = 20,03м. Используя определение касательных Tan φ = a / b = 9,6 / 7,4 = 1,297. Используя таблицы или калькулятор, φ = 52,37 o . Сумма трех углов всегда равна 180 o . = б × ч / 2 б 2 = а 2 + с 2 — (2 × а × с × Cos B) c 2 = a 2 + b 2 — (2 × a × b × Cos C) В первой версии правила косинусов, если угол A прямой, Cos 90 o = 0 .Тогда уравнение сводится к теореме Пифагора. a 2 = b 2 + c 2 — (2 × b × c × Cos 90 o ) = b 2 + c 2 — 0 = b 2 2 Отношение между сторонами и углами общего треугольника определяется Правилом синусов . По правилу косинусов, a 2 = b 2 + c 2 — (2 × b × c × Cos A) а 2 = 6,3 2 + 4,6 2 — (2 × 6,3 × 4,6 × Cos 32 o ) а 2 = 39,69 + 21,16 — (2 × 6,3 × 4,6 × 0,848) а 2 = 60,85 — 49,15 = 11,7 а = 3,42 м а / Sin A = c / Sin C Это можно изменить на Sin C = (c × Sin A) / a Подставляя различные значения, мы получаем Sin C = (c × Sin A) / a = (4.6 × Sin 32 или ) / 3,42
= (4,6 × 0,530) / 3,42 = 0,713 Поэтому С = 45,5 о Окончательный угол можно найти из А + В + С = 180 или Перестановка, В = 180 — А — С = 180 — 32 — 45,5 В = 102,5 о Используя уравнения, описанные в этом эссе, можно узнать все о треугольнике, используя всего несколько заданных битов информации. Это записывается как Это записывается как Это записывается как Система градусов , используемая для обычных угловых измерений, восходит к вавилонским временам.Полный круг равен 360 o ; половина круга 180 o ; а прямой угол равен 90 o . При математическом рассмотрении тригонометрических функций нам требуется более фундаментальная единица измерения угла. Это Радиан . 1 o = 0,0175 радиан Преобразование угла в радианы: 45 o = π/4 радиана поэтому Грех 45 o = Грех π/4 =
π/4 — ((π/4) 3 )/3! +
((π/4) 5 )/5! — …. = 0,785 — 0,081 + 0,002 — … = 0,706 Правильное значение, конечно, 0,707. Отношения: Эти уравнения можно объединить и записать в альтернативном формате, который называется Формула Эйлера : Используя формулу Эйлера и помня, что Sin π = 0 и Cos π = -1 (см. таблицу выше): e iπ = Cos π + (i × Sin π) = -1 + (i × 0) = -1 Эти числа обсуждаются далее в эссе «Введение в числа». 509 Превышен предел пропускной способности
509 Превышен предел пропускной способности
Сервер временно не может обслуживать ваши
запрос из-за того, что владелец сайта достиг своего
ограничение пропускной способности. Пожалуйста, повторите попытку позже.
Пожалуйста, повторите попытку позже. Схема — Ледник — Национальная лаборатория Лоуренса в Беркли
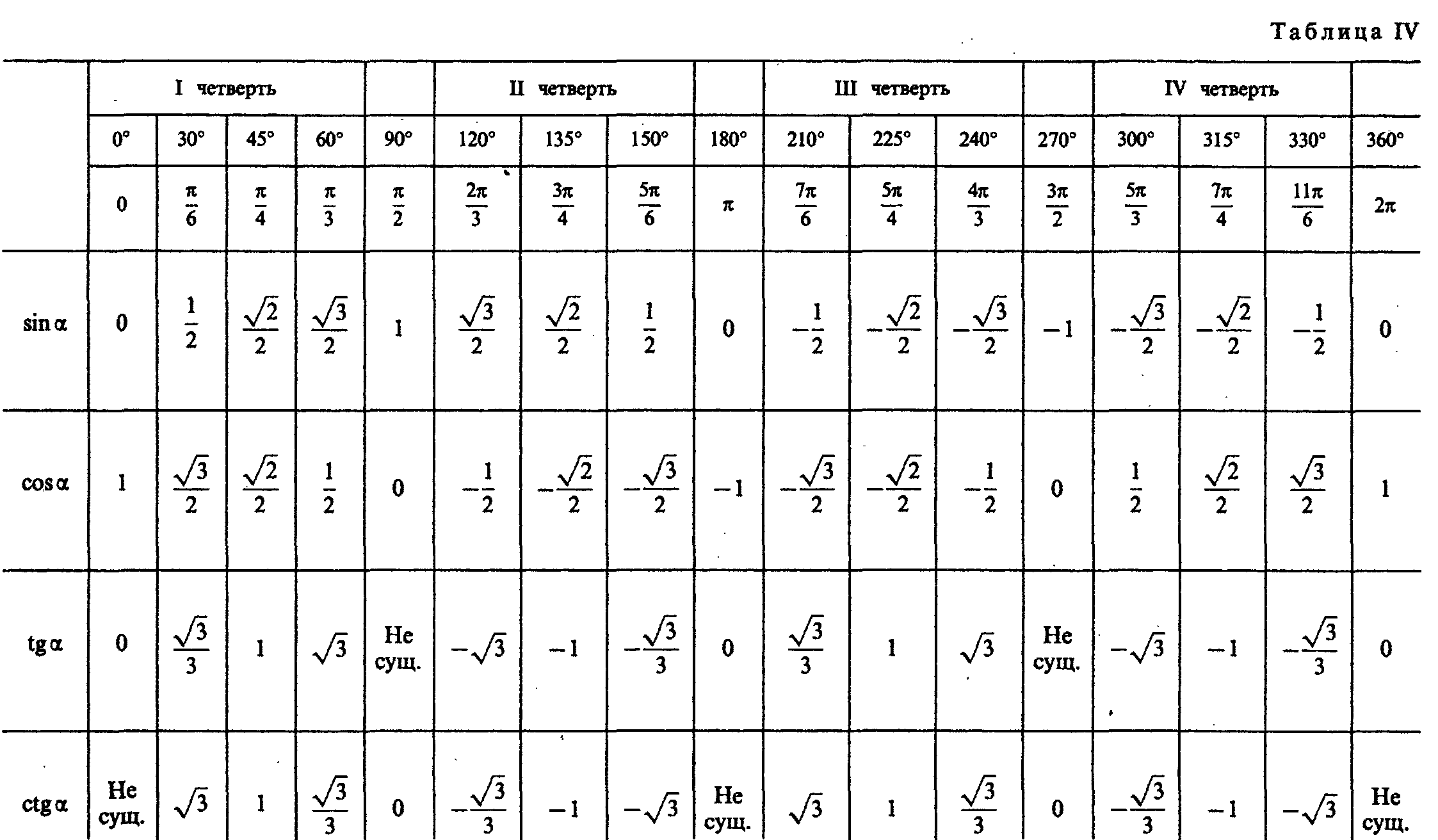 3V 4 1.8V 15 4 2N7002 2.5V R142 10K 1% 14 Ain9 R367 20 -(-5/2.5)-(+3,3+2,5+1,8)/4 =Vout R233 100K 1% 13 Ain10 11 3,3V Vout=Vs(0,009*P-0,09 5)+/-Error Ain11-RefGnd BAROMETER_ENA G 2 — 0,825 — 0,625 — 0,4 50) = 0,100 В C14 P = 10,55555556+(111,111 1111*Vout/Vs) Давайте просто предположим, что если +5 равно R1 MAX1139EEE C9 2,2 мкФ 6,3 В Tan 5 В и Baro масштабируются теми же 100 нФ R407, были мертвы. ЦП 5V 100K 1% фактор, так что в тех же единицах. 10K 1% вход контрольной микросхемы вызовет Переключатель FET, Q7, может привести к перезагрузке ниже примерно 4,750 В. (2.500/4096) x count TI утверждает, что имеет меньшую силовую часть, небольшое смещение из-за того, что она на C10 C3 C5 C7 C373 C435, но с точностью только до 2 градусов C (вероятно, сопротивление около 5 Ом.100nf 100nf 100nf 100nf 100nf 100nf внутри диапазона -25c и abov e) … C2 C4 C6 C8 C434 C1 100nf 100nf 100nf 100nf 100nf 100nf sc_sclk U55 2 7 6 5 SCL A0 A1 A2 VDD VDD GND SDA Tout DS1631U 1 3 D R51 10K 1% 3.3V vs NC NC NC NC NC SC_nCS7 1 2 Значения деталей, оканчивающиеся на «*», не должны монтироваться.
3V 4 1.8V 15 4 2N7002 2.5V R142 10K 1% 14 Ain9 R367 20 -(-5/2.5)-(+3,3+2,5+1,8)/4 =Vout R233 100K 1% 13 Ain10 11 3,3V Vout=Vs(0,009*P-0,09 5)+/-Error Ain11-RefGnd BAROMETER_ENA G 2 — 0,825 — 0,625 — 0,4 50) = 0,100 В C14 P = 10,55555556+(111,111 1111*Vout/Vs) Давайте просто предположим, что если +5 равно R1 MAX1139EEE C9 2,2 мкФ 6,3 В Tan 5 В и Baro масштабируются теми же 100 нФ R407, были мертвы. ЦП 5V 100K 1% фактор, так что в тех же единицах. 10K 1% вход контрольной микросхемы вызовет Переключатель FET, Q7, может привести к перезагрузке ниже примерно 4,750 В. (2.500/4096) x count TI утверждает, что имеет меньшую силовую часть, небольшое смещение из-за того, что она на C10 C3 C5 C7 C373 C435, но с точностью только до 2 градусов C (вероятно, сопротивление около 5 Ом.100nf 100nf 100nf 100nf 100nf 100nf внутри диапазона -25c и abov e) … C2 C4 C6 C8 C434 C1 100nf 100nf 100nf 100nf 100nf 100nf sc_sclk U55 2 7 6 5 SCL A0 A1 A2 VDD VDD GND SDA Tout DS1631U 1 3 D R51 10K 1% 3.3V vs NC NC NC NC NC SC_nCS7 1 2 Значения деталей, оканчивающиеся на «*», не должны монтироваться. Эти части предназначены для диагностики или реализации альтернативных методологий. 4,25 мВт x 4 + 7,5 мВт = 24,5 мВт плюс 3,3 мВт при преобразовании температуры + 6 мВт x 10 В/усл_эфф f = 67 мВт Последовательно размещайте резисторы рядом с удаленными источниками.C конденсаторы возле АЦП. R819 10k 1% Disc-MultiSCE 1 10 FADC_0_REF SC_NCS6 R820 10K 1% 2 AIN0 SDA R821 150K 1% SISTLELED-BRAILNES-CTL 3 AIN1 9 R822 10K 1% AIN2 SCL SC_SCLK DAC0_A 4 DAC0_B R823 150K 1% 5 AIN3 R824 10K 1% R825 10K 1% DAC0_C 6 Ain4 R826 150K 1% Ain5 Analog_Ref 7 R105 10K 1% DAC1_A R827 10K 1% 8 Ain6 3 R828 150K 1% 3 DAC2_B 16 Ain7 12 3.3V R810 10K 1 Rddin 9 VAdd 18 Ain3_C 18 Подставка 14 R829 20 FE_TEST_PULSE_AMPL R832 150K 1% 13 Ain10 11 Ain11-RefGnd C437 MAX1139EEE C436 2.2 мкФ 6,3 В Tan Нам нужно будет назначить разъемы 100 нФ на странице ATWD для входных сигналов DACx_y. % C438 C440 C442 C444 C446 C448 100NF 100NF 100NF 100NF 100NF 100NF C439 C441 C443 C445 C447 C449 100NF 100NF 100NF 100NF 100NF 100NF U97 0-2.
Эти части предназначены для диагностики или реализации альтернативных методологий. 4,25 мВт x 4 + 7,5 мВт = 24,5 мВт плюс 3,3 мВт при преобразовании температуры + 6 мВт x 10 В/усл_эфф f = 67 мВт Последовательно размещайте резисторы рядом с удаленными источниками.C конденсаторы возле АЦП. R819 10k 1% Disc-MultiSCE 1 10 FADC_0_REF SC_NCS6 R820 10K 1% 2 AIN0 SDA R821 150K 1% SISTLELED-BRAILNES-CTL 3 AIN1 9 R822 10K 1% AIN2 SCL SC_SCLK DAC0_A 4 DAC0_B R823 150K 1% 5 AIN3 R824 10K 1% R825 10K 1% DAC0_C 6 Ain4 R826 150K 1% Ain5 Analog_Ref 7 R105 10K 1% DAC1_A R827 10K 1% 8 Ain6 3 R828 150K 1% 3 DAC2_B 16 Ain7 12 3.3V R810 10K 1 Rddin 9 VAdd 18 Ain3_C 18 Подставка 14 R829 20 FE_TEST_PULSE_AMPL R832 150K 1% 13 Ain10 11 Ain11-RefGnd C437 MAX1139EEE C436 2.2 мкФ 6,3 В Tan Нам нужно будет назначить разъемы 100 нФ на странице ATWD для входных сигналов DACx_y. % C438 C440 C442 C444 C446 C448 100NF 100NF 100NF 100NF 100NF 100NF C439 C441 C443 C445 C447 C449 100NF 100NF 100NF 100NF 100NF 100NF U97 0-2. 5V SPAN FADC_0_REF R36 100 1 2 C385 10UF 6.8V TAN C386 100NF 1 2 R39 20 Обратите внимание, что это FADC — дифференциальный вход. Каскады усилителя и формирователя связаны по постоянному току. «Нижняя часть» пролета зависит от настройки опорного напряжения ATWD.То есть пьедестал для FADC = пьедестал для ATWD. V+ in должен быть установлен на ( Vpedestal — (span/2)) вольт или на несколько мВ ниже. 100 мВт U30 R132 9 17 R436 100 1 2 FLASH_AD_D0 20 VIN + D0 18 R437 100 1 2 FLASH_AD_D1 FADC_IN 10 D1 19 R438 100 1 2 VIN- D2 FLASH_AD_D2 20 R439 100 1 2 U23 (дифференциальный вход) 4 0 MHZ ADC Non D3 Flash_ad_d3 21 R440 100 1 2 FLASH_AD_D4 SC_nCS2 8 3 DISC-MultiSPE инвертирующий вход, используемый в качестве центральной шкалы D4 22 R441 100 1 2 FLASH_AD_D5 C121 SC_SCLK 10 CS OUTA 2 D5 ссылка.25 R442 100 1 2 100 нФ FLASH_AD_D6 SC_MOSI 9 SCLK FBA R14 10K 1% D6 26 R443 100 TP1 DAC-DO0 DIN 1 2 D7 FLASH_AD_D7 1 2 3,3 В 12 4 DAC-UP0 DISC-OneSPE 27 R444 _ 3 ADB 8 OUT 1 DAC-UP0 FLASH 1 5 2 28 R445 100 1 2 1 D9 FLASH_AD_D9 14 UPO FBB R15 10K 1 % 2 C26 U12 PDL FADC_0_Ref SC_CL 7 17 10 мкФ 6,8 В Tan 1 OTR FLASH_NCO 7 CLKx2 TP* VCL OUTC 16 13 2 FBC CL 1 % 5 CLK R16 10 выход 8 18 100 нФ C124 nCLKx2 OUTD FE_TEST_PULSE_AMPL 14 C126 FLASH_AD_STBY VR2.
5V SPAN FADC_0_REF R36 100 1 2 C385 10UF 6.8V TAN C386 100NF 1 2 R39 20 Обратите внимание, что это FADC — дифференциальный вход. Каскады усилителя и формирователя связаны по постоянному току. «Нижняя часть» пролета зависит от настройки опорного напряжения ATWD.То есть пьедестал для FADC = пьедестал для ATWD. V+ in должен быть установлен на ( Vpedestal — (span/2)) вольт или на несколько мВ ниже. 100 мВт U30 R132 9 17 R436 100 1 2 FLASH_AD_D0 20 VIN + D0 18 R437 100 1 2 FLASH_AD_D1 FADC_IN 10 D1 19 R438 100 1 2 VIN- D2 FLASH_AD_D2 20 R439 100 1 2 U23 (дифференциальный вход) 4 0 MHZ ADC Non D3 Flash_ad_d3 21 R440 100 1 2 FLASH_AD_D4 SC_nCS2 8 3 DISC-MultiSPE инвертирующий вход, используемый в качестве центральной шкалы D4 22 R441 100 1 2 FLASH_AD_D5 C121 SC_SCLK 10 CS OUTA 2 D5 ссылка.25 R442 100 1 2 100 нФ FLASH_AD_D6 SC_MOSI 9 SCLK FBA R14 10K 1% D6 26 R443 100 TP1 DAC-DO0 DIN 1 2 D7 FLASH_AD_D7 1 2 3,3 В 12 4 DAC-UP0 DISC-OneSPE 27 R444 _ 3 ADB 8 OUT 1 DAC-UP0 FLASH 1 5 2 28 R445 100 1 2 1 D9 FLASH_AD_D9 14 UPO FBB R15 10K 1 % 2 C26 U12 PDL FADC_0_Ref SC_CL 7 17 10 мкФ 6,8 В Tan 1 OTR FLASH_NCO 7 CLKx2 TP* VCL OUTC 16 13 2 FBC CL 1 % 5 CLK R16 10 выход 8 18 100 нФ C124 nCLKx2 OUTD FE_TEST_PULSE_AMPL 14 C126 FLASH_AD_STBY VR2. 5 15 19 100 нФ 6 PDWN 2 R262 39K FIN1018K8X REFCD FBD 6 R17 10K 1% REFT MODE 2 R405 REFAB 5V.5V 11 100nF JU28 DGND 7 1 20 Open Ckt 4 AVdd 12 B18 C13 AGND VDD C294 VREF AVdd 3.3V 1 2 3 23 100nF ADC-REF 1 2 SENSE DGnd 8 LI0805D121R C270 MAX5250BEAP 10uF 6.3V 2 AGnd C15 Open Ckt JU27 C29 C127 100 нФ AD9215BRU-65 Перемычка 100 нФ 100 нФ OSCON_6SC6R8M Компоненты, значение C295 которых заканчивается на «*» 100 нФ, не подлежат монтажу. NC NC 15 16 R46 Перемотайте SENSE на Gnd для диапазона 2 В. Разомкните Ckt Ra* SENSE SENSE на VREF для диапазона 1 В. U28 Подсоедините SENSE к делителю напряжения для диапазона =1,0(1+Ra/Rb).SC_nCS3 8 3 CS OUTA SingleLED-BRIGHTNESS-CTL SC_SCLK 10 2 SC_MOSI 9 SCLK FBA R22 10K 0,1% TP2 DAC-DO1 12 DIN 4 DAC-UP1 DOUT OUTB Зажим 13 5 1 14 UPO FBB R23 10K 0,1% TP* SC_CL 7 PDL 17 CL OUTC FL_REF U24 16 FBC R24 10k 0,1% 5VANALOG 3 18 VCC OFT DAC_OUT_1 1 15 19 C12 OUT REFCD FBD 6 R25 10K 0,1% Refab + C16 100NF * 100NF 11 5Vanalog 1 DGND 1 20 1 AGND VDD GND TLE2425ID C451 OSCON_6SC6R8M MAX5250BEAP 10 бит ЦАП C17 100 нФ R26 10K 1% R18 10K 1% R19 10K 1% R20 10K 1% R21 10K 1% R27 10K 0,1%* R28 10K 0.
5 15 19 100 нФ 6 PDWN 2 R262 39K FIN1018K8X REFCD FBD 6 R17 10K 1% REFT MODE 2 R405 REFAB 5V.5V 11 100nF JU28 DGND 7 1 20 Open Ckt 4 AVdd 12 B18 C13 AGND VDD C294 VREF AVdd 3.3V 1 2 3 23 100nF ADC-REF 1 2 SENSE DGnd 8 LI0805D121R C270 MAX5250BEAP 10uF 6.3V 2 AGnd C15 Open Ckt JU27 C29 C127 100 нФ AD9215BRU-65 Перемычка 100 нФ 100 нФ OSCON_6SC6R8M Компоненты, значение C295 которых заканчивается на «*» 100 нФ, не подлежат монтажу. NC NC 15 16 R46 Перемотайте SENSE на Gnd для диапазона 2 В. Разомкните Ckt Ra* SENSE SENSE на VREF для диапазона 1 В. U28 Подсоедините SENSE к делителю напряжения для диапазона =1,0(1+Ra/Rb).SC_nCS3 8 3 CS OUTA SingleLED-BRIGHTNESS-CTL SC_SCLK 10 2 SC_MOSI 9 SCLK FBA R22 10K 0,1% TP2 DAC-DO1 12 DIN 4 DAC-UP1 DOUT OUTB Зажим 13 5 1 14 UPO FBB R23 10K 0,1% TP* SC_CL 7 PDL 17 CL OUTC FL_REF U24 16 FBC R24 10k 0,1% 5VANALOG 3 18 VCC OFT DAC_OUT_1 1 15 19 C12 OUT REFCD FBD 6 R25 10K 0,1% Refab + C16 100NF * 100NF 11 5Vanalog 1 DGND 1 20 1 AGND VDD GND TLE2425ID C451 OSCON_6SC6R8M MAX5250BEAP 10 бит ЦАП C17 100 нФ R26 10K 1% R18 10K 1% R19 10K 1% R20 10K 1% R21 10K 1% R27 10K 0,1%* R28 10K 0. 1%* R29 10K 0,1%* Название Цифровой оптический модуль AD/DA Размер Номер документа Ред. C 1.1 A B C D Пятница, 16 мая 2003 г. Дата: Лист из 4 15 E
1%* R29 10K 0,1%* Название Цифровой оптический модуль AD/DA Размер Номер документа Ред. C 1.1 A B C D Пятница, 16 мая 2003 г. Дата: Лист из 4 15 E KryssTal: Тригонометрия
KryssTal: Тригонометрия
Рассмотрим прямоугольный треугольник, изображенный на схеме. a , b и c — боковые стороны; φ угол. Это греческая буква, которая произносится как фи .Угол между сторонами a и b равен 90 o , а прямой угол . Сторона c , лежащая против прямого угла, называется гипотенузой (от греческого слова, означающего , вытянуть ). Пифагор (ок. 582 г. до н. э. — ок. 497 г. до н. э.) доказал то, что сейчас называется Теорема Пифагора , хотя она веками использовалась в древнем мире для строительства и измерения.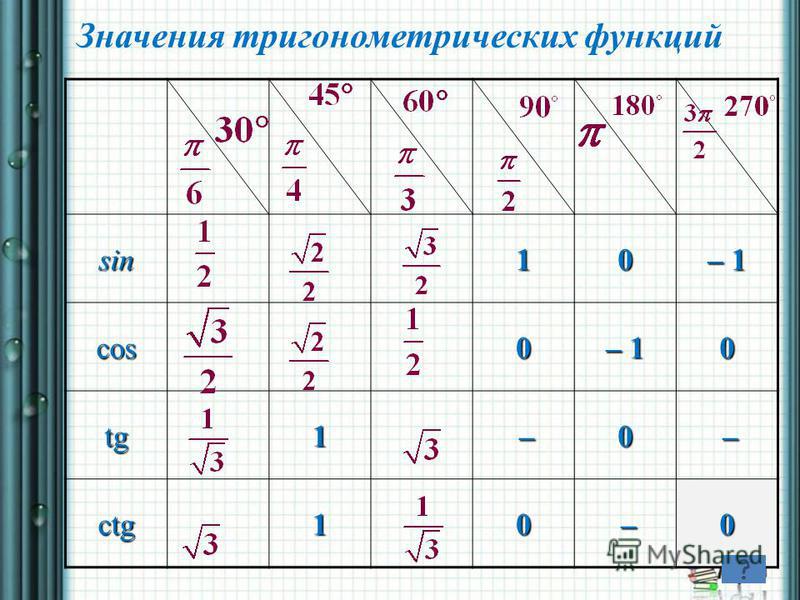 Теорема может быть описана следующим образом: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Математически это записывается как a 2 + b 2 = c 2 . Пример 1: Если прямоугольный треугольник имеет меньшие стороны длины 3 и 4. Какова длина гипотенузы?
Теорема может быть описана следующим образом: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Математически это записывается как a 2 + b 2 = c 2 . Пример 1: Если прямоугольный треугольник имеет меньшие стороны длины 3 и 4. Какова длина гипотенузы? 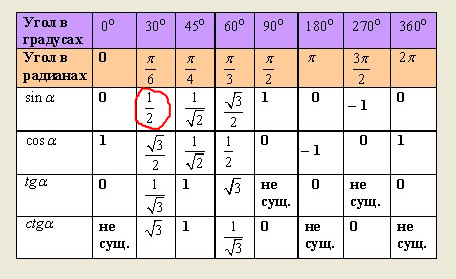
Площадь ( A ) прямоугольного треугольника находится по формуле A = ab/2 Пример 3: Найдите площадь прямоугольного треугольника с более короткими сторонами длины 4.3 и 6.4 соответственно.
Вернемся к схеме прямоугольного треугольника. Между сторонами a , b , c и углом φ имеется ряд соотношений. Они называются Тригонометрическими функциями .
Они называются Тригонометрическими функциями .
Обратите внимание на следующее: Sin 0 o = Cos 90 o = 0 Sin 30 o = Cos 60 o = 0.500 SIN 45 O = COS 45 o = 0,707 = 1 / (√2) SIN 60 O = COS 30 O = 0,866 = (√3) / 2 SIN 90 о = Cos 0 о = 1 Между 0 o и 90 o : Увеличение синусов от 0 до 1, Уголок Грех Кос Желто-коричневый 0 или 0,000 1.  000
000 0,000 30 или 0,500 0.866 0,577 45 или 0,707 0,707 1.000 60 или 0,866 0,500 1.732 90 или 1.000 0,000 Бесконечный
Косинусы уменьшаются от 1 до 0,
Тангенсы увеличиваются от 0 до бесконечности.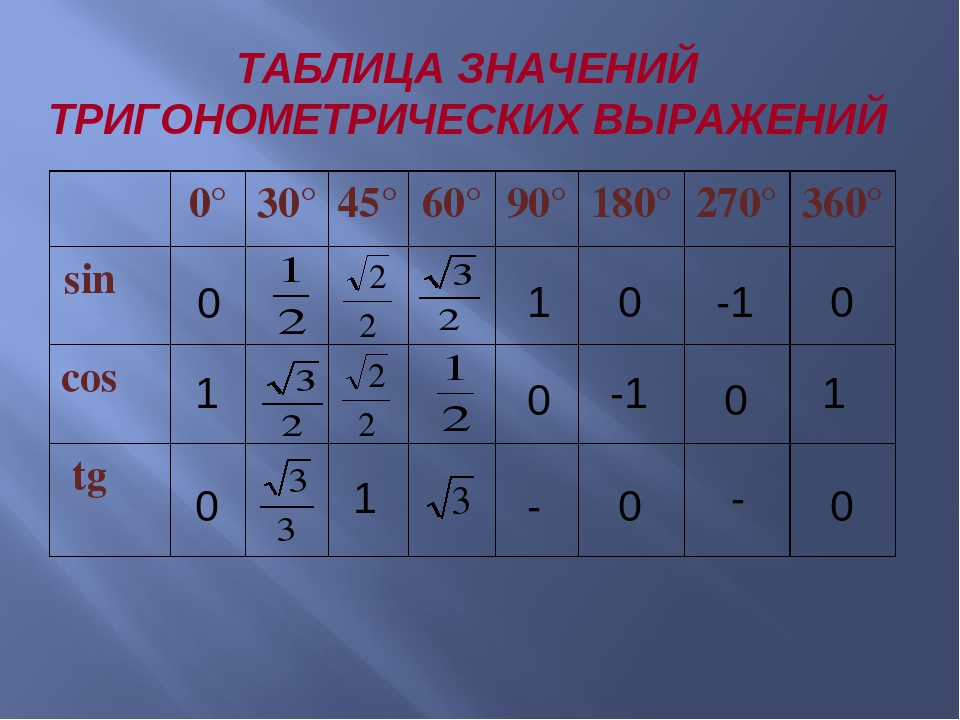 Ну наконец то, Кос(90 — Х) = Син(Х)
Ну наконец то, Кос(90 — Х) = Син(Х)
Грех(90 — Х) = Кос(Х) Значения тригонометрических функций (за исключением 0 o , 30 o , 45 o , 60 o , 90 o ) не являются целыми числами, дробями или сурдами.Они трансцендентны.
Три тригонометрические функции взаимосвязаны. Sin φ / Cos φ
= Tan φ Sin 2 φ + Cos 2 φ = 1 Примечание. Квадрат синуса угла, скажем, (Sin φ) 2 чаще записывается как Sin 2 φ. Эта форма применима ко всем тригонометрическим функциям.
Пример 4. Докажите, что Sin φ / Cos φ = Tan φ 
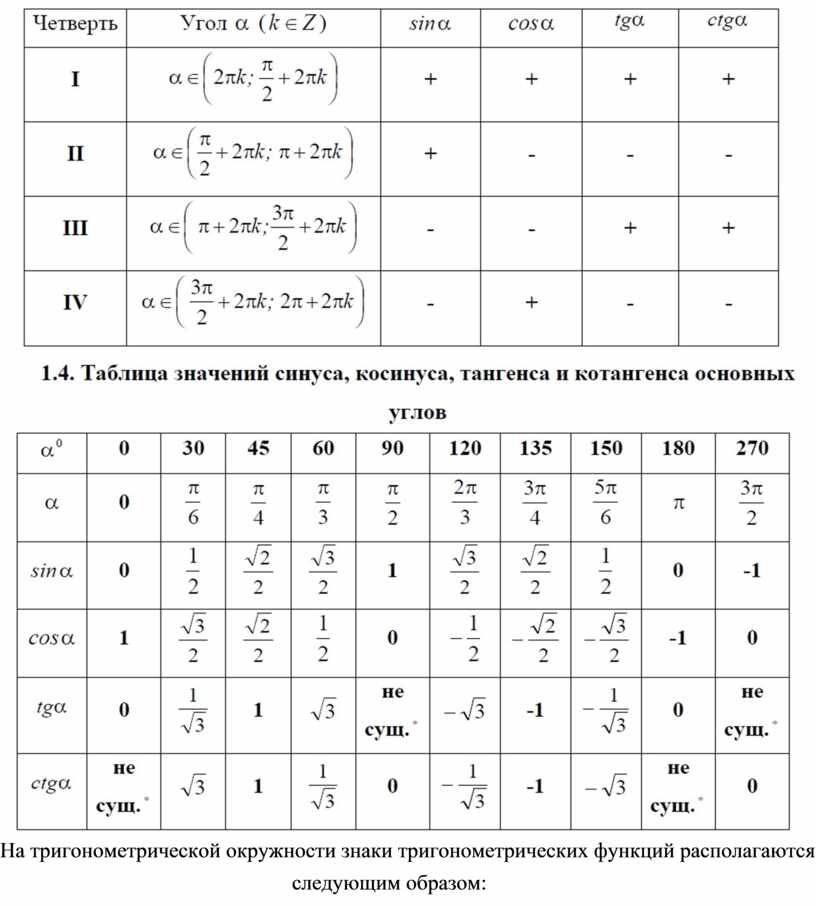 Это дает
Это дает
До сих пор мы рассматривали прямоугольные треугольники.В общем, треугольники могут иметь любые углы. Рассмотрим треугольник ниже. Треугольник имеет три стороны: a , b и c . Есть три угла: A , B , C (где угол A противоположен стороне a и т. д.). Высота треугольника х . Существует три формы этого правила. Все эквивалентны. a 2 = b 2 + c 2 — (2 × b × c × Cos A)
Существует три формы этого правила. Все эквивалентны. a 2 = b 2 + c 2 — (2 × b × c × Cos A)
 В приведенном выше примере мы вычислили, что a = 3,42 м, B = 102,5 o ,
С = 45,5 o .
В приведенном выше примере мы вычислили, что a = 3,42 м, B = 102,5 o ,
С = 45,5 o .
Помимо трех уже определенных тригонометрических функций, есть еще три, которые являются их обратными. Секанс угла φ определяется как величина, обратная косинусу.
Прежде чем мы рассмотрим ряды для тригонометрических функций, я хочу поговорить об углах. Эти числа были использованы, потому что они содержат много факторов и просты в использовании. Градусы — это искусственные единицы.
Эти числа были использованы, потому что они содержат много факторов и просты в использовании. Градусы — это искусственные единицы.
Полуокружность равна π радианам, а прямой угол равен π/2 радианам. 1 Радиан = 57,3 o Радиан градусов Грех Кос Желтовато-коричневый 0 0 0 1 0 π/2 90 1 0 Бесконечный π 180 0 -1 0 3π/2 270 -1 0 Бесконечный 2π 360 0 1 0
Существует ряд для оценки как синуса, так и косинуса. Эти ряды работают, только если угол φ выражен в радианах. Обе серии действительны для всех значений φ . Пример 10: Используйте ряд, чтобы найти значение Sin 45 o .
Эти ряды работают, только если угол φ выражен в радианах. Обе серии действительны для всех значений φ . Пример 10: Используйте ряд, чтобы найти значение Sin 45 o .
Посмотрите еще раз на две предыдущие серии. Теперь сравните их с экспоненциальной серией ниже. Приложив немного математики (не здесь!), можно показать, что тригонометрические функции связаны с числом e ( 2,71828183… ), основанием натуральных логарифмов) и мнимым числом . я .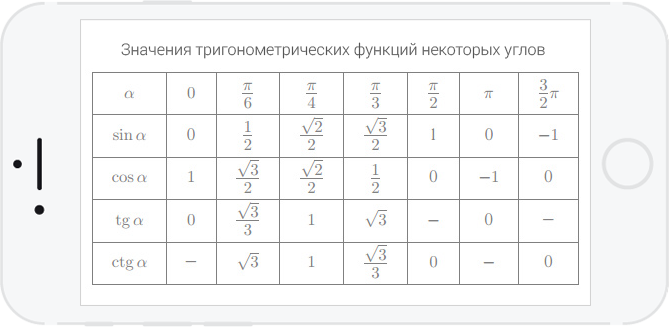 Разве математика не забавна? Пример 11: Каково значение e iπ ?
Разве математика не забавна? Пример 11: Каково значение e iπ ?
Знакомство с различными типами чисел: действительными, мнимыми, рациональными, иррациональными, трансцендентными.
Введение в алгебру и как решать простые, одновременные и квадратные уравнения.
Серия, разработанная Исааком Ньютоном, которая используется для расчетов. Подробнее об индексах: корни и степени. Факториалы. Комбинации.
Индекс и база. Определены логарифмы.Основание 10 и основание e. Использование логарифмов в вычислениях. Ряд для логарифмов.
Как решать уравнения, содержащие синусы, косинусы и тангенсы.
Сферическая тригонометрия — это тригонометрия треугольников, нарисованных на сфере.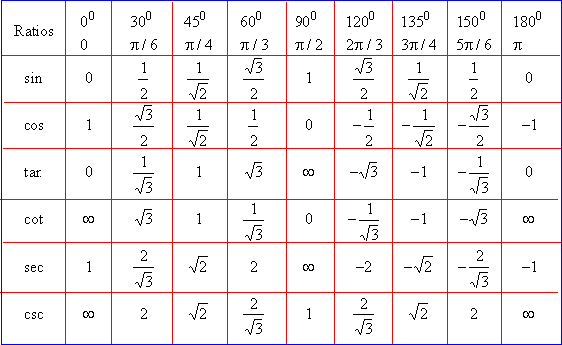

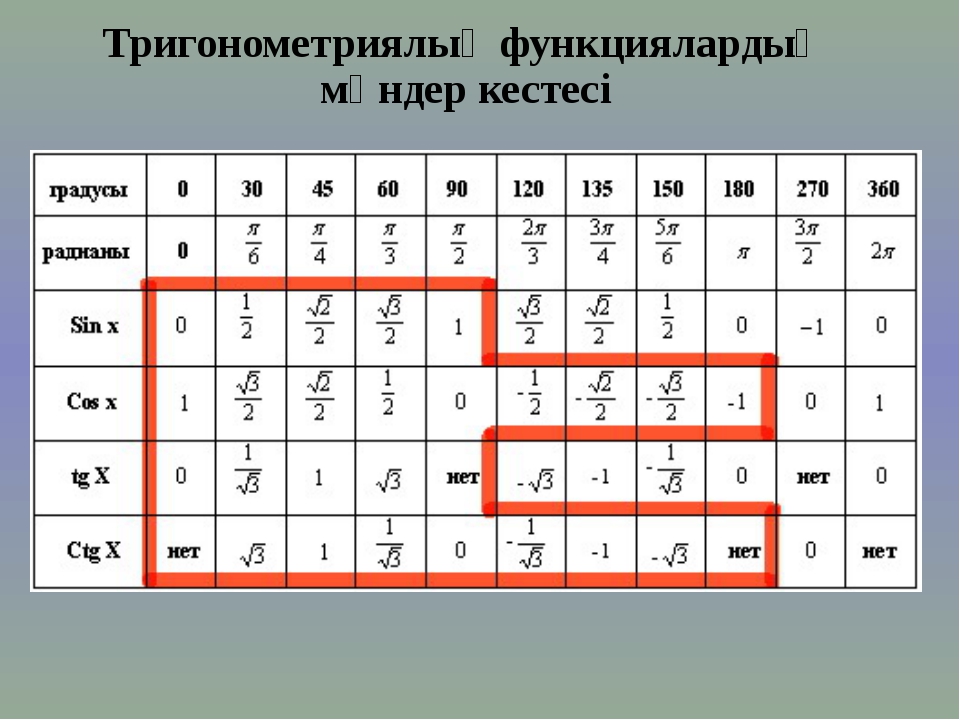
 5299
5299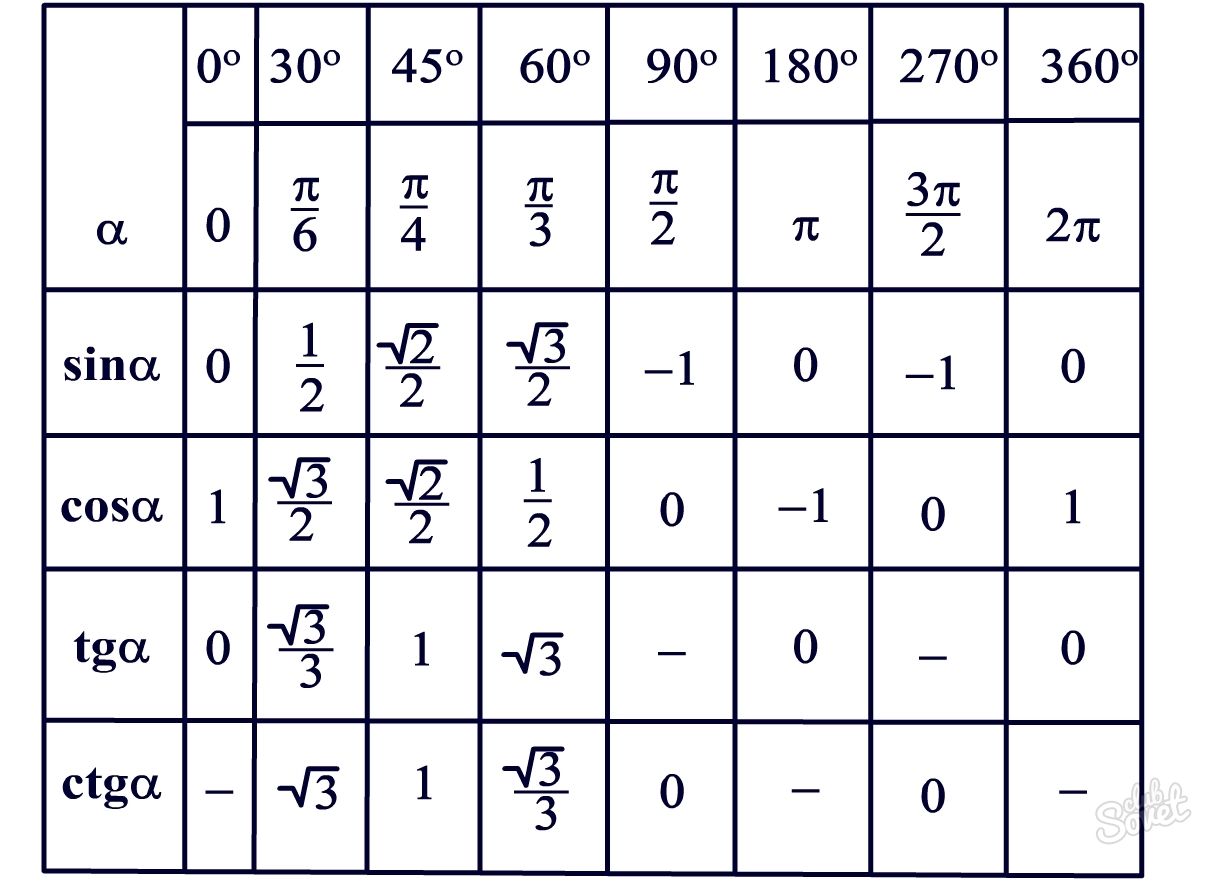
 9816
9816 9781
9781 8192
8192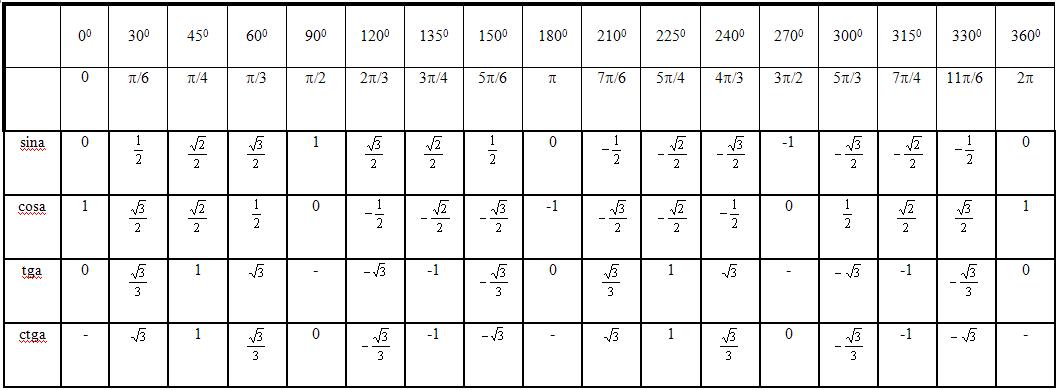 5299
5299 1564
1564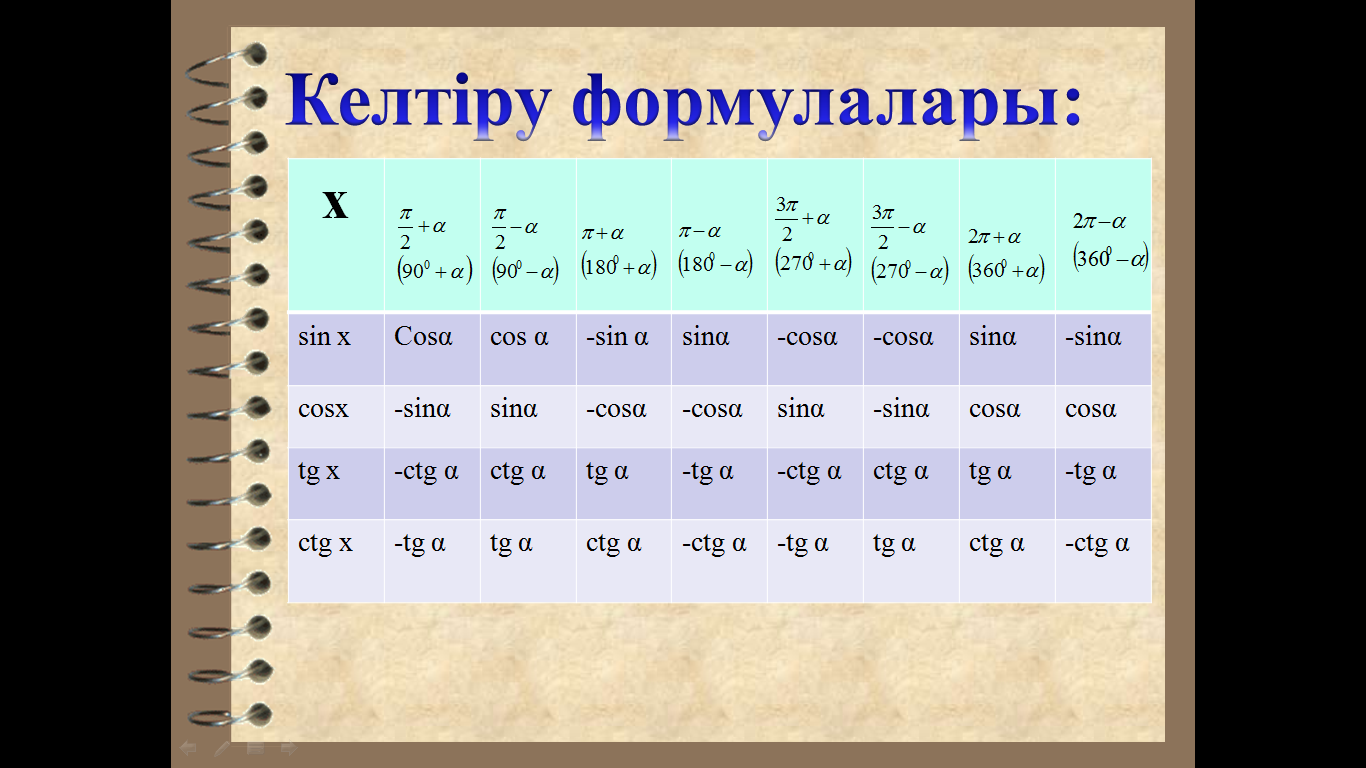 2079
2079 5736
5736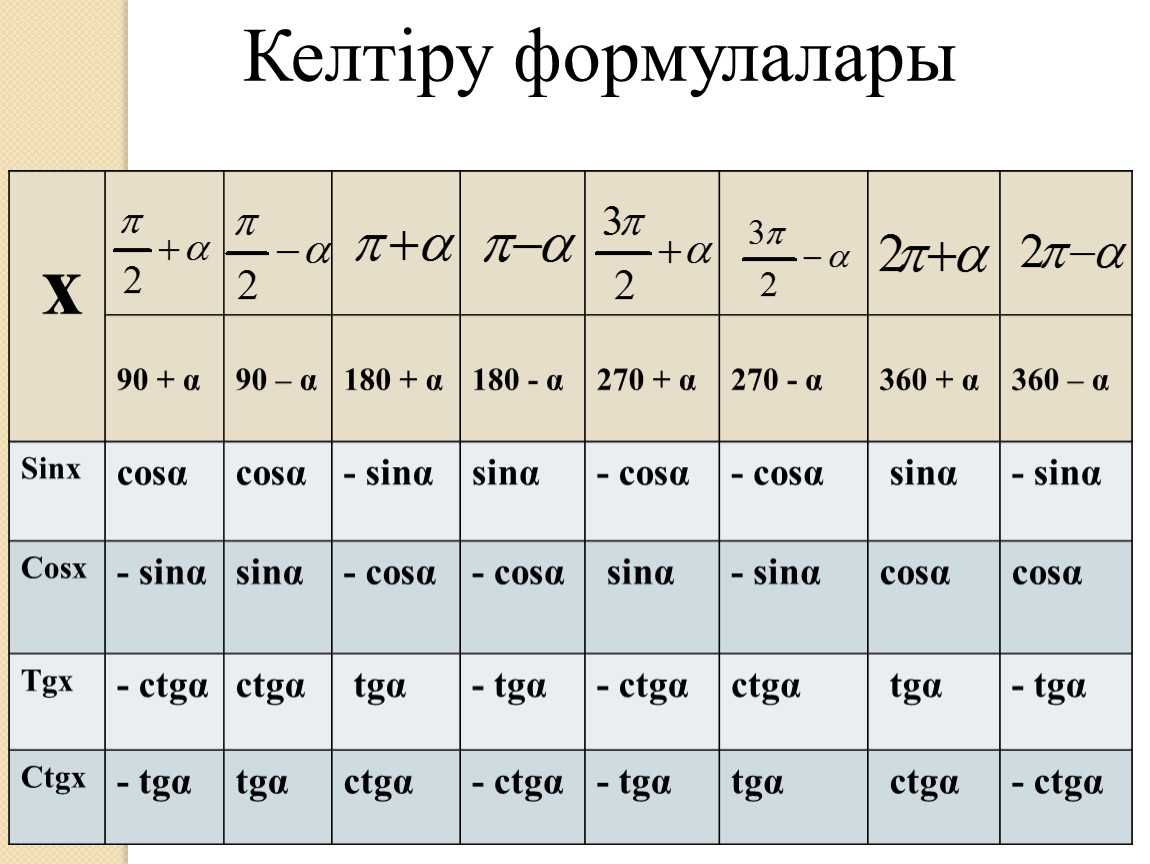 8387
8387 9848
9848 9781
9781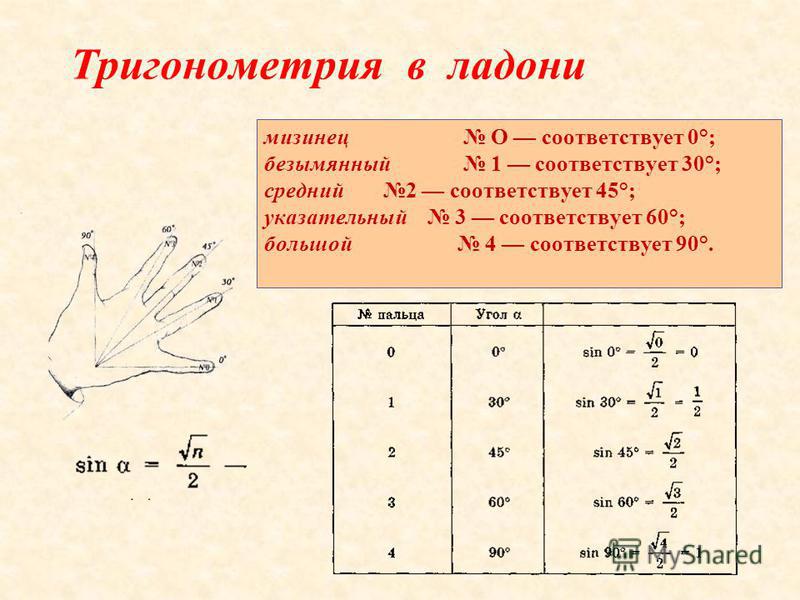 8192
8192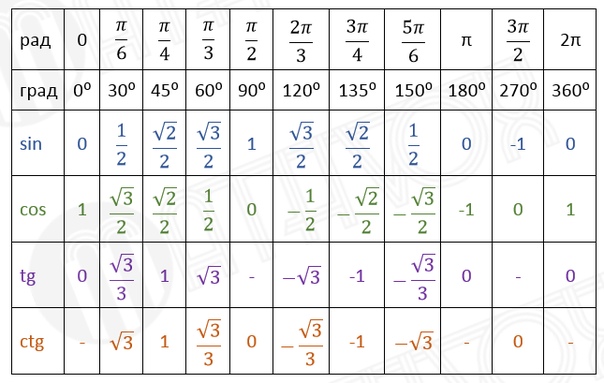 5446
5446 1736
1736 26794919243
26794919243