Калькулятор корень н степени: Калькулятор извлечения корня n-ой степени онлайн
Калькулятор извлечения корня n-ой степени онлайн
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из теоремы Пифагора и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
Арифметический корень из числа. Корень n-ой степени: определения, обозначение, примеры
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.
Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т. д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители.
Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169
.
Решение.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n
-ой степени какого-либо числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. ..»
..»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Среди множества знаний, которые являются признаком грамотности, на первом месте стоит азбука. Следующим, таким же «знаковым» элементом, являются навыки сложения-умножения и, примыкающие к ним, но обратные по смыслу, арифметические операции вычитания-деления. Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем. А, скажите, часто ли вам приходилось по жизни, извлекать корни, кроме, как на даче? Например, такая занимательная задачка, типа, корень квадратный из числа 12345… Есть еще порох в пороховницах? Осилим? Да нет ничего проще! Где тут мой калькулятор… А без него, врукопашную, слабо?
Следующим, таким же «знаковым» элементом, являются навыки сложения-умножения и, примыкающие к ним, но обратные по смыслу, арифметические операции вычитания-деления. Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем. А, скажите, часто ли вам приходилось по жизни, извлекать корни, кроме, как на даче? Например, такая занимательная задачка, типа, корень квадратный из числа 12345… Есть еще порох в пороховницах? Осилим? Да нет ничего проще! Где тут мой калькулятор… А без него, врукопашную, слабо?
Сначала уточним, что же это такое — квадратный корень числа. Вообще говоря, «извлечь корень из числа» означает выполнить арифметическое действие противоположное возведению в степень — вот вам и единство противоположностей в жизненном приложении. допустим, квадрат, это умножение числа на самое себя, т.е., как учили в школе, Х * Х = А или в другой записи Х2 = А, а словами — «Х в квадрате равняется А». Тогда обратная задача звучит так: квадратный корень числа А, представляет собой число Х, которое будучи возведено в квадрат равно А.
Тогда обратная задача звучит так: квадратный корень числа А, представляет собой число Х, которое будучи возведено в квадрат равно А.
Извлекаем квадратный корень
Из школьного курса арифметики известны способы вычислений «в столбик», которые помогают выполнить любые подсчеты с применением первых четырех арифметических действий. Увы… Для квадратных, и не только квадратных, корней таких алгоритмов не существует. А в таком случае, как извлечь квадратный корень без калькулятора? Исходя из определения квадратного корня вывод один — необходимо подбирать значение результата последовательным перебором чисел, квадрат которых приближается к значению подкоренного выражения. Только и всего! Не успеет пройти час-другой, как можно посчитать, используя хорошо известный прием умножения в «столбик», любой квадратный корень. При наличии навыков для этого достаточно пары минут. Даже не совсем продвинутый пользователь калькулятора или ПК делает это одним махом — прогресс.
А если серьезно, то вычисление квадратного корня часто выполняют, используя прием «артиллерийской вилки»: сначала берут число, квадрат которого, примерно, соответствует подкоренному выражению. Лучше, если «наш квадрат» чуть меньше этого выражения. Затем корректируют число по собственному умению-разумению, например, умножают на два, и… вновь возводят в квадрат. Если результат больше числа под корнем, последовательно корректируя исходное число, постепенно приближаются к его «коллеге» под корнем. Как видите — никакого калькулятора, только умение считать «в столбик». Конечно же, есть множество научно-аргументированных и оптимизированных алгоритмов вычислений квадратного корня, но для «домашнего применения» указанный выше прием дает 100% уверенность в результате.
Лучше, если «наш квадрат» чуть меньше этого выражения. Затем корректируют число по собственному умению-разумению, например, умножают на два, и… вновь возводят в квадрат. Если результат больше числа под корнем, последовательно корректируя исходное число, постепенно приближаются к его «коллеге» под корнем. Как видите — никакого калькулятора, только умение считать «в столбик». Конечно же, есть множество научно-аргументированных и оптимизированных алгоритмов вычислений квадратного корня, но для «домашнего применения» указанный выше прием дает 100% уверенность в результате.
Да, чуть не забыл, чтобы подтвердить свою возросшую грамотность, вычислим квадратный корень ранее указанного числа 12345. Делаем пошагово:
1. Возьмем, чисто интуитивно, Х=100. Подсчитаем: Х * Х = 10000. Интуиция на высоте — результат меньше 12345.
2. Попробуем, тоже чисто интуитивно, Х = 120. Тогда: Х * Х = 14400.И опять с интуицией порядок — результат больше 12345.
3. Выше получена «вилка» 100 и 120. Выберем новые числа — 110 и 115. Получаем, соответственно, 12100 и 13225 — вилка сужается.
Выберем новые числа — 110 и 115. Получаем, соответственно, 12100 и 13225 — вилка сужается.
4. Пробуем на «авось» Х=111. Получаем Х * Х = 12321. Это число уже достаточно близко к 12345. В соответствии с требуемой точностью «подгонку» можно продолжить или остановиться на полученном результате. Вот и все. Как и было обещано — все очень просто и без калькулятора.
Совсем немного истории…
Додумались до использования квадратных корней еще пифагорейцы, ученики школы и последователи Пифагора, за 800 лет до н.э. и тут же, «нарвались» на новые открытия в области чисел. И откуда что взялось?
1. Решение задачи с извлечением корня, дает результат в виде чисел нового класса. Их назвали иррациональными, иначе говоря, «неразумными», т.к. они не записываются законченным числом. Самый классический пример такого рода — квадратный корень из 2. Этот случай соответствует вычислению диагонали квадрата со стороной равной 1 — вот оно, влияние школы Пифагора. Оказалось, что у треугольника с вполне конкретным единичным размером сторон, гипотенуза имеет размер, который выражается числом, у которого «нет конца». Так в математике появились
Так в математике появились
2. Известно, что Оказалось, что эта математическая операция содержит еще один подвох — извлекая корень, мы не знаем, квадратом какого числа, положительного или отрицательного, является подкоренное выражение. Эта неопределенность, двойной результат от одной операции, так и записывается.
Изучение связанных с этим явлением проблем стало направлением в математике под названием теория комплексной переменной, имеющим большое практическое значение в математической физике.
Любопытно, что обозначение корня — радикал — применил в своей «Универсальной арифметике» все тот же вездесущий И. Ньютон, а в точности современный вид записи корня известен с 1690 года из книги француза Ролля «Руководство алгебры».
Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х дециметрам. Тогда площадь участка равна х ² квадратным дециметрам. Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Заметим, что один из квадратных корней х = 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а .
Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.
Арифметический квадратный корень из числа а обозначается так: √а.
Знак называется знаком арифметического квадратного корня; а — называется подкоренным выражением. Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.
Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.
Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа. Например, нельзя извлечь квадратный корень из числа — 4. Если бы такой корень существовал, то, обозначив его буквой х , мы получили бы неверное равенство х² = — 4, так как слева стоит неотрицательное число, а справа отрицательное.
Выражение √а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко записать так: √а ≥ 0, (√а )² = а . Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Квадратный корень из дроби
Вычислим . Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .
Так как и , то равенство верно. Итак, .
Теорема: Если а ≥ 0 и b > 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя. Требуется доказать, что: и .
Так как √а ≥0 и √b > 0, то .
По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.
Вычислить , по доказанной теореме .
Второй пример: Доказать, что , если а ≤ 0, b .
Еще примерчик: Вычислить .
.
Преобразование квадратных корней
Вынесение множителя из-под знака корня. Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:
Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;
Вычислить при х = 2. Непосредственная подстановка х = 2 в подкоренное выражение приводит к сложным вычислениям. Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.
Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а
если же а
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней .
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.

Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа .
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы. x |
Тригонометрические функции |
|
| Синус от x |
|
| Косинус от x |
|
| Тангенс от x . Можно вводить tg(x ) или tan(x ) |
|
| Котангенс от x . Можно вводить ctg(x ) или cot(x ) |
|
| Секанс от x , определяется как 1/cos(x ) |
|
| Косеканс от x , определяется как 1/sin(x ) |
|
| Арксинус от x . Можно вводить arcsin(x ) или asin(x ) |
|
| Арккосинус от x . Можно вводить arccos(x ) или acos(x ) |
|
| Арктангенс от x . Можно вводить arctg(x ) или atan(x ) |
|
| Арккотангенс от x . Можно вводить arcctg( Можно вводить arcctg(x ) или acot(x ) |
|
| Арксеканс от x |
|
| Арккосеканс от x |
|
Некоторые константы |
|
| Число Эйлера e = 2.718281828459045… |
|
| Число π = 3.141592653589793… |
|
Калькулятор корней онлайн — особенности извлечения корней с подробным объяснением
Калькулятор
Заполните поля для вычисления корня из числа
Онлайн-калькулятор – удобный ресурс, помогающий решать задачи, примеры, в котроых встречаются квадратные или степенные корни. Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Таблица корней от 0 до 99
Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.
При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Свойства арифметического квадратного корня
Пользоваться онлайн-калькулятором будет проще, если сначала упростить выражение, привести в удобный для вычисления вид. Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Умножение корней
Если произведение подкоренного выражения можно представить в виде двух множителей, достаточно перемножить корни, извлеченные из этих множителей: допустим, под корнем стоит число 576. Преобразуем его в два множителя: 64 и 9. Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Формулой свойство изображается так:
Раскладывая подкоренное значение на множители, можно значительно упростить процесс вычисления квадратных корней.
Деление корней
Следующее свойство удобно для извлечения корней из дробных чисел. Когда подкоренное выражение представлено в виде дроби, следует воспользоваться правилом деления. Проще запомнить это свойство по формуле:
Обратная формула трактуется следующим образом: корень из частного равен частному корней.
Допустим, нужно извлечь квадратный корень из дроби 25/144. Для этого необходимо извлечь корень из 25, это 5. Затем подобную манипуляцию произвести с делителем дроби: корень 144 равен двенадцати. После извлечения корня из 25/144 получаем дробь 5/8. Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Возведение в степень
Последнее свойство корней – это возведение его в степень. Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
При возведении подкоренного числа в квадрат с последующим извлечением квадратного корня получаем первоначальное подкоренное выражение. На слух выражение воспринимается сложно. Проще усвоить формулу:
Из формулы видно, что этим свойством удобно пользоваться при возведении квадратного корня в четную степень, ее можно сразу делить на два и убирать знак корня. Как всегда, пример: чтобы возвести в шестую степень квадратный корень числа 3, необходимо возвести число 3 в куб, степенной показатель 6 поделить пополам.
Внесение под знак корня
При решении задач и примеров возникает необходимость вносить под корень множитель. Например, чтобы вычислить 4 корня из 4, можно представить выражение в виде двух корней: первым подкоренным выражением будет 42, второе останется неизменным. Финальное выражение нетрудно произвести, воспользовавшись формулами:
Формулу запомнить легко, она может пригодиться на экзамене.
Сравнение корней
Для графического решения уравнений нередко приходится сравнивать корни. Как это сделать быстро при сравнении квадратных корней? Воспользоваться еще одним правилом: чем больше подкоренное выражение, тем больше значение корня. Допустим, нужно сравнить
2√3 и 3√2. Вносим числа в подкоренные выражения. Получаем под знаками корней два выражения: 22х3 и 32х2. Осталось сравнить числа 12 и 18. Второе больше.
Свойства квадратных корней распространяются на другие коренные значения: четные или нечетные. Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
На этом экскурс по свойствам, сравнению корней можно считать исчерпывающим. Зная эти правила обращения с корнями, можно упростить сложное выражение. Пользоваться нашим онлайн-калькулятором с подсказками очень просто. 2 + 3x = 0 $
2 + 3x = 0 $
Обратите внимание, что в нашем уравнении теперь только два члена, поэтому теперь мы можем использовать , разлагая на множители.2 = \ гидроразрыв {3} {2} \\ x_1x_2 = \ pm \ sqrt {\ frac {3} {2}} \end{выровнено} $$
Equation Solver: Wolfram|Alpha
О решении уравнений
Значение называется корнем многочлена, если .
Наибольший показатель появления в называется степенью . Если имеет степень , то хорошо известно, что есть корни, если принять во внимание кратность. Чтобы понять, что подразумевается под множественностью, возьмем, например, . Считается, что этот многочлен имеет два корня, оба равны 3.
О «теореме о факторах» узнают обычно на втором курсе алгебры, как о способе нахождения всех корней, являющихся рациональными числами. Также учатся находить корни всех квадратных многочленов, используя при необходимости квадратные корни (вытекающие из дискриминанта). Существуют более сложные формулы для выражения корней многочленов кубической и четвертой степени, а также ряд численных методов аппроксимации корней произвольных многочленов. В них используются методы комплексного анализа, а также сложные численные алгоритмы, и действительно, это область постоянных исследований и разработок.
В них используются методы комплексного анализа, а также сложные численные алгоритмы, и действительно, это область постоянных исследований и разработок.
Системы линейных уравнений часто решаются методом исключения Гаусса или подобными методами. Это также обычно встречается в учебных программах по математике средних школ или колледжей. Необходимы более совершенные методы для нахождения корней одновременных систем нелинейных уравнений. Аналогичные замечания справедливы для работы с системами неравенств: линейный случай можно обрабатывать с помощью методов, описанных в курсах линейной алгебры, тогда как полиномиальные системы более высокой степени обычно требуют более сложных вычислительных инструментов.
Как Wolfram|Alpha решает уравнения
Для решения уравнений Wolfram|Alpha вызывает функции Solve and Reduce языка Wolfram Language, которые содержат широкий спектр методов для всех видов алгебры, от основных линейных и квадратных уравнений до многомерных нелинейных систем. В некоторых случаях используются методы линейной алгебры, такие как исключение Гаусса, с оптимизацией для повышения скорости и надежности. Другие операции основаны на теоремах и алгоритмах из теории чисел, абстрактной алгебры и других продвинутых областей для вычисления результатов.Эти методы тщательно разработаны и выбраны, чтобы позволить Wolfram|Alpha решать самые разнообразные задачи, а также минимизировать время вычислений.
В некоторых случаях используются методы линейной алгебры, такие как исключение Гаусса, с оптимизацией для повышения скорости и надежности. Другие операции основаны на теоремах и алгоритмах из теории чисел, абстрактной алгебры и других продвинутых областей для вычисления результатов.Эти методы тщательно разработаны и выбраны, чтобы позволить Wolfram|Alpha решать самые разнообразные задачи, а также минимизировать время вычислений.
Хотя такие методы полезны для прямых решений, для системы также важно понимать, как человек решит ту же проблему. В результате, Wolfram|Alpha также имеет отдельные алгоритмы для пошаговой демонстрации алгебраических операций с использованием классических методов, которые люди легко распознают и которым легко следовать. Это включает в себя исключение, замену, квадратичную формулу, правило Крамера и многое другое.
Калькулятор корней комплексного числа
Калькулятор найдет корни $$$n$$$-го заданного комплексного числа, используя формулу де Муавра с показанными шагами.
Ваш ввод
Найдите $$$\sqrt[4]{81 i}$$$.
Решение
Полярная форма $$$81 i$$$ равна $$$81 \left(\cos{\left(\frac{\pi}{2} \right)} + i \sin{\left (\frac{\pi}{2} \right)}\right)$$$ (шаги см. в калькуляторе полярных форм).{\ frac {1} {n}} \ left (\ cos {\ left (\ frac {\ theta + 2 \ pi k} {n} \ right)} + i \ sin {\ left (\ frac {\ theta + 2 \pi k}{n} \right)}\right)$$$, $$$k=\overline{0..n-1}$$$.
Имеем $$$r = 81$$$, $$$\theta = \frac{\pi}{2}$$$ и $$$n = 4$$$.
- $$$k = 0$$$: $$$\sqrt[4]{81} \left(\cos{\left(\frac{\frac{\pi}{2} + 2\cdot \ pi\cdot 0}{4} \right)} + i \sin{\left(\frac{\frac{\pi}{2} + 2\cdot \pi\cdot 0}{4} \right)}\ справа) = 3 \ влево (\ cos {\ влево (\ гидроразрыва {\ пи} {8} \ вправо)} + я \ грех {\ влево (\ гидроразрыва {\ пи} {8} \ вправо)} \ вправо) = 3 \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} + 3 i \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2} {4}}$$$
- $$$k = 1$$$: $$$\sqrt[4]{81} \left(\cos{\left(\frac{\frac{\pi}{ 2} + 2\cdot \pi\cdot 1}{4} \right)} + i \sin{\left(\frac{\frac{\pi}{2} + 2\cdot \pi\cdot 1}{ 4} \right)}\right) = 3 \left(\cos{\left(\frac{5 \pi}{8} \right)} + i \sin{\left(\frac{5 \pi}{ 8} \right)}\right) = — 3 \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} {4}} + 3 i \ sqrt {\ frac {\ sqrt {2} }}{4} + \frac{1}{2}}$$$
- $$$k = 2$$$: $$$\sqrt[4]{81} \left(\cos{\left( \ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 2} {4} \ right)} + i \ sin {\ left (\ frac {\ frac {\ pi} {2} + 2\cdot \pi\cdot 2}{4} \right)}\right) = 3 \left(\cos{\left(\frac{9 \pi}{8} \right)} + i \sin{\ левый(\ frac{9 \pi}{8} \right)}\right) = — 3 \sqrt{\frac{\sqrt{2}}{4} + \frac{1}{2}} — 3 i \sqrt{ \frac{1}{2} — \frac{\sqrt{2}}{4}}$$$
- $$$k = 3$$$: $$$\sqrt[4]{81} \left (\ cos {\ left (\ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 3} {4} \ right)} + i \ sin {\ left (\ frac {\ frac { \pi}{2} + 2\cdot \pi\cdot 3}{4} \right)}\right) = 3 \left(\cos{\left(\frac{13 \pi}{8} \right) } + я \ sin {\ left (\ frac {13 \ pi} {8} \ right)} \ right) = 3 \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} { 4}} — 3 i \sqrt{\frac{\sqrt{2}}{4} + \frac{1}{2}}$$$
Ответить
$$$\sqrt[4]{81 i} = 3 \sqrt{\frac{\sqrt{2}}{4} + \frac{1}{2}} + 3 i \sqrt{\frac{ 1}{2} — \frac{\sqrt{2}}{4}}\примерно 2. 77163859753386 + 1.148050297095269 i$$$A
77163859753386 + 1.148050297095269 i$$$A
$$$\sqrt[4]{81 i} = — 3 \sqrt{\frac{1}{2} — \frac{\sqrt{2}}{4 }} + 3 i \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} \ приблизительно -1,148050297095269 + 2,77163859753386 i$$$A
$$$\sqrt [4] {81 i} = — 3 \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} — 3 i \ sqrt {\ frac {1} {2} — \frac{\sqrt{2}}{4}}\приблизительно -2,77163859753386 — 1,148050297095269 i$$$A
$$$\sqrt[4]{81 i} = 3 \sqrt{\frac{1} {2} — \ frac {\ sqrt {2}} {4}} — 3 i \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} \ приблизительно 1.148050297095269 — 2.77163859753386 i$$$A
| ЛИЦЕНЗИОННОЕ СОГЛАШЕНИЕ НА ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИЛОЖЕНИЯ TEXAS INSTRUMENTS Загружая программное обеспечение и/или документацию, вы соглашаетесь соблюдать следующие положения.
|
Как вычислить КВАДРАТНЫЙ КОРЕНЬ в Excel [5 лучших методов] + Добавить символ
Excel похож на швейцарский армейский нож для вычислений. От математических до финансовых, это для каждой вещи, которую вам нужно рассчитать. Вы можете вычислять простые и самые сложные вещи в Excel.
Возьмем пример КВАДРАТНЫЙ КОРЕНЬ . Квадратный корень — это довольно распространенный расчет, который мы делаем в нашей повседневной работе, и в Excel вы можете легко его вычислить.
Знаете что?
Я обнаружил, что существует пять различных способов вычисления квадратного корня в Excel. Да, пять разных методов, которые можно использовать в разных ситуациях. И сегодня в этом посте я хотел бы поделиться с вами этими пятью простыми методами нахождения квадратного корня числа в Excel. Итак, давайте изучим это дело.
Итак, давайте изучим это дело.
Что такое КВАДРАТНЫЙ КОРЕНЬ?
Прежде чем мы научимся его вычислять, важно понять, что он на самом деле означает, как мы его обычно вычисляем.Вычисление квадратного корня является обратным вычислением для возврата к корню из квадрата. Итак, когда вы вычисляете квадрат 10, умножая его на себя, это (10 * 10 = 100). Тогда квадратный корень означает возвращение от 100 к 10.
Вы можете узнать больше об этом из Википедии. Но теперь давайте узнаем, как мы можем сделать это в Excel.
Как я уже сказал, мы можем использовать 5 различных способов вычисления квадратного корня в соответствии с необходимостью или личными предпочтениями. Не все методы одинаковы, но полезны.
1. Используйте функцию КОРЕНЬ, чтобы найти КВАДРАТНЫЙ корень числа
Если вам нужно использовать только один метод для вычисления квадратного корня, используйте функцию КОРЕНЬ. Для этого есть специальная функция.
Вам просто нужно обратиться к ячейке или указать номер.
Синтаксис SQRT:
Где число — это число или ссылка на ячейку, которая содержит число, для которого вы хотите найти квадратный корень.
Примеры:
В приведенном ниже примере у нас есть число 625 в ячейке A1. Итак, чтобы вычислить квадратный корень для этого, мы можем вставить приведенную ниже формулу (Панель формул) в B1.
Возвращаемое значение равно 25, что является квадратным корнем из 625.
Как видите, SQRT прост в использовании и применении.
Но есть кикер.
Если у вас есть отрицательное число, как показано ниже, оно вернет #ЧИСЛО!.
Таким образом, решение этой проблемы заключается в использовании функции ABS вместе с SQRT.Вот пример:
Когда мы используем ABS, он преобразует число в абсолютное число. Это означает, что a преобразует отрицательное число в положительное.
2. Вычислить КВАДРАТНЫЙ корень числа с помощью функции СТЕПЕНЬ
Другой способ вычисления квадратного корня — использование функции СТЕПЕНЬ.
Функция POWER имеет большую мощность, чем SQRT, поскольку она возвращает результат возведения числа N в заданную степень.
Синтаксис POWER:
Где число — это число или ссылка на ячейку, содержащую число, для которого вы хотите найти квадратный корень, а мощность — это показатель степени для увеличения мощности.
Допустим, нам нужно найти квадратный корень числа из ячейки A1 (это 625), тогда мы можем использовать 1/2 в качестве аргумента степени в этой функции.
И формула будет следующей:
Как видите, она возвращает 25 в результате, что является квадратным корнем из 625.
3. Примените формулу экспоненты, чтобы получить КВАДРАТНЫЙ корень числа чтобы вставить простую формулу (кроме двух указанных выше методов) для вычисления квадратного корня, мы можем использовать простую формулу с использованием оператора экспоненты.
Эта формула похожа на СИЛУ. Единственная разница в том, что вместо функции нам нужно использовать оператор экспоненты.
Единственная разница в том, что вместо функции нам нужно использовать оператор экспоненты.
В приведенной выше формуле A1 в ячейке, где у нас есть число, для которого нам нужно найти квадратный корень, а затем мы использовали оператор степени, а затем (1/2) для возведения в степень.
Наилучшим преимуществом этой формулы является ее применение. Помимо квадратного корня, мы можем использовать его для вычисления кубического корня или любого корня n-й степени.
4. Код VBA для отображения КВАДРАТНОГО корня числа
Позвольте мне рассказать вам о другом сценарии, в котором нам нужно проверить квадратный корень числа вместо его вычисления в ячейке.
Код-1
Ниже приведен код VBA, который возвращает квадратный корень, когда мы выбираем ячейку и запускаем этот код.
Sub getSquareRoot()
Dim rng As Range
Dim sqr As Long
If Application. (1 / 2)
(1 / 2)
MsgBox «Квадратный корень из » & rng & » равен » & sqr, vbOKOnly, «Значение квадратного корня»
Else
MsgBox «Выберите числовое значение», vbOKOnly, «Ошибка»
End If
End Sub
Как работает этот код
7 Когда мы запускаем этот код, 9 он проверяет значение в выбранной ячейке и, если это значение является числом, вычисляет квадратный корень этого числа и показывает его в окне сообщения.
Обратите внимание, что если вы выберете более одной ячейки, этот код не будет работать.
Код-2
Используя приведенный ниже код, мы можем проверить ввод квадратного корня из числа, не имея фактического числа в ячейке.
Sub getSquareRoot()
Dim sqr As Long
Dim sqr As Long
sq = InputBox(«Введите значение для вычисления квадратного корня», «Вычисление квадратного корня»)
If IsNumeric(sq) = True Then
sqr = sq ^ (1 / 2)
MsgBox «Квадратный корень из » & sq & » равен » & sqr, vbOKOnly, «Значение квадратного корня»
Else
MsgBox «Пожалуйста, введите число. «, vbOKOnly, «Error»
«, vbOKOnly, «Error»
End If
End Sub
Как работает этот код
Когда мы запускаем этот код, он показывает нам поле ввода, запрашивающее число, для которого нам нужно получить квадратный корень.
И когда мы вводим это число, он вычисляет квадратный корень из этого числа и показывает окно сообщения с квадратным корнем
Вы можете использовать любой из приведенных выше кодов, который идеально подходит для вас
#5.Использование Power Query для преобразования чисел в квадратные корни
Вот еще один способ, который мы можем использовать, если вам нужно преобразовать несколько чисел в их квадратные корни.
Это Power Query.
Ниже у нас есть таблица, в которой у нас есть несколько чисел, и здесь мы хотим получить квадратный корень из этих чисел за один раз.
Примечание: Использование запроса мощности для квадратного корня является динамическим методом, каждый раз, когда вы вводите новое значение в свою таблицу, он будет возвращать квадратный корень из этого числа.
Теперь выполните следующие простые шаги.
- Прежде всего, выберите любую ячейку в таблице и перейдите на вкладку «Данные» ➜ «Получить и преобразовать данные» и нажмите «Из таблицы/диапазона».
- Как только вы нажмете на нее, Excel откроет редактор запросов Power и добавит в него эту таблицу.
- Отсюда нам нужно создать новый столбец со значениями квадратного корня, для этого перейдите на вкладку «Добавить столбец» и нажмите «Пользовательский столбец».
- На данный момент у нас открыто окно «Пользовательский столбец», и в этом окне нам нужно добавить следующее:
- Прежде всего, введите имя столбца «Квадратный корень» в поле ввода имени столбца.
- После этого введите приведенную ниже формулу в поле ввода формулы пользовательского столбца и нажмите OK.
- Теперь у нас есть новый столбец с квадратными корнями из числа в первом столбце.
- Отсюда вам нужно удалить первый столбец исходных значений.
 Итак, щелкните правой кнопкой мыши по нему и нажмите «Удалить».
Итак, щелкните правой кнопкой мыши по нему и нажмите «Удалить».
- После этого перейдите на главную вкладку и нажмите закрыть и тоже загрузить.
- Здесь открывается окно для загрузки данных. Прежде всего, выберите существующий рабочий лист и добавьте диапазон B1.Во-вторых, отметьте «Добавить в модель данных».
Как я уже сказал, эта таблица динамическая.
Когда вы вводите новое значение в исходную таблицу данных, оно автоматически вычисляет его квадратный корень в вашей новой таблице при ее обновлении.
И здесь мы не используем никаких формул.
[Дополнительный совет] Как добавить символ квадратного корня в Excel
После того, как вы вычислите квадратный корень из числа, следующее, что вы можете сделать, это добавить символ квадратного корня.
И для этого у нас есть два разных способа, которые мы можем использовать.
#1. Использование сочетания клавиш
Простой способ добавить символ квадратного корня — это сочетание клавиш Alt + 251.
При вводе 251 на цифровой клавиатуре необходимо удерживать клавишу Alt. и как только вы отпустите клавишу Alt, появится символ.
#2. Добавление символа КВАДРАТНОГО корня путем применения пользовательского форматирования
Это наиболее эффективный способ добавления символа.
Все, что вам нужно сделать, это выбрать все ячейки, открыть параметр пользовательского форматирования и добавить форматирование в панель ввода форматирования.
#3. VBA для добавления квадратного символа
Вы также можете использовать приведенный ниже код VBA, чтобы применить пользовательское форматирование ко всем ячейкам в выделении.
Sub Radical()
Selection.NumberFormat = ChrW(8730) & «General»
End Sub
Примечание: Преимущество использования методов №2 и №3 заключается в том, что вам не нужно добавлять символ ко всем ячейкам одну за другой, и когда вы добавляете символ в ячейку, значение в ячейке становится текстом и не может использоваться в дальнейшем как число.
Образец файла
Загрузите этот образец файла отсюда
Заключение
Если вы просто хотите узнать квадратный корень числа, тогда лучше всего подойдет метод VBA, выберите ячейку и запустите код.
В противном случае формулы лучше всего подходят, если вам нужно использовать значение квадратного корня в дальнейших вычислениях, и у нас есть три разные формулы в этом списке.
Power Query — это динамический метод, и его необходимо попробовать.
Теперь скажи мне одну вещь.
Какой ваш любимый метод вычисления квадратного корня в Excel?
Поделитесь со мной своим мнением в разделе комментариев, я буду рад услышать от вас. И, не забудьте поделиться этим списком с друзьями, я уверен, что они оценят его.
Вы должны прочитать это Далее
- Вычислить коэффициент в Excel: когда дело доходит до Excel, у нас нет какой-либо конкретной функции, которая могла бы помочь нам вычислить коэффициент.
 Но вы можете рассчитать его, используя некоторые пользовательские формулы […]
Но вы можете рассчитать его, используя некоторые пользовательские формулы […] - Средневзвешенное значение в Excel: Но я обнаружил, что лучший способ — использовать формулу, комбинируя функции СУММПРОИЗВ и СУММ. Этот метод прост и удобен в применении […]
- Сложные проценты в Excel: Сложные проценты являются одним из наиболее важных финансовых расчетов, которые большинство из нас часто выполняет в своей работе. И необходимо научиться вычислять его в Excel […]
- Вставка/ввод символа градуса в Excel: Если вы используете ноутбук, как я, вы обнаружите, что нет клавиши для ввода символа градуса.Работая с некоторыми данными, я обнаружил, что в Excel их можно вводить пятью различными способами […]
- Умножение с помощью специальной вставки: Иногда в Excel необходимо выполнить несколько быстрых вычислений. И вы можете использовать специальную вставку для этих быстрых вычислений вместо формул […]
- Вычислить возраст в Excel: В Excel, используя дату рождения человека, вы можете вычислить его / ее возраст с помощью функции DATEDIF [.
 ..]
..] - Усреднение первых 5 значений в Excel: чтобы усреднить первые 5 значений из списка, вы можете использовать формулу, основанную на комбинации НАИБОЛЬШИЙ и СРЕДНИЙ […]
Пунит использует Excel со времен учебы в колледже. Он помог тысячам людей понять возможности электронных таблиц и изучить Microsoft Excel. Вы можете найти его в Интернете, в твиттере об Excel, на беговой дорожке, а иногда и в горах.
Квадраты и квадратные корни
Сначала узнайте о квадратах, затем получите квадратные корни.
Как возвести число в квадрат
Чтобы возвести число в квадрат: умножьте его само на себя .
Пример: Сколько будет 3 в квадрате?
| 3 Квадрат | = | = 3 × 3 = 9 |
«Квадрат» часто записывается как маленькая двойка, например:
.
Здесь написано «4 в квадрате равно 16»
(маленькая двойка говорит
число появляется дважды при умножении)
Квадраты От 0
2 до 6 2| 0 Квадрат | = | 0 2 | = | 0 × 0 | = | 0 |
| 1 Квадрат | = | 1 2 | = | 1 × 1 | = | 1 |
| 2 в квадрате | = | 2 2 | = | 2 × 2 | = | 4 |
| 3 В квадрате | = | 3 2 | = | 3 × 3 | = | 9 |
| 4 В квадрате | = | 4 2 | = | 4 × 4 | = | 16 |
| 5 В квадрате | = | 5 2 | = | 5 × 5 | = | 25 |
| 6 Квадрат | = | 6 2 | = | 6 × 6 | = | 36 |
Отрицательные числа
Мы также можем возвести в квадрат отрицательных чисел .
Было интересно!
Когда мы возводим в квадрат отрицательное число , мы получаем положительное число .
Точно так же, как возведение в квадрат положительного числа:
.(Подробнее читайте Квадраты и квадратные корни в алгебре)
Квадратные корни
квадратный корень из идет в другую сторону:
3 в квадрате равно 9, поэтому квадратный корень из из 9 это 3
Квадратный корень числа равен …
… значение, которое может быть , умноженным само на , чтобы получить исходное число.
Квадратный корень из 9 равен …
… 3 , потому что при умножении 3 на получается 9 .
Это все равно, что спросить:
Что мы можем умножить само на себя, чтобы получить это?
Чтобы помочь вам вспомнить , подумайте о корне дерева: «Я знаю дерево , но какой корень его создал? » В данном случае дерево «9», а корень «3». |
Вот еще несколько квадратов и квадратных корней:
| 4 | 16 | |
| 5 | 25 | |
6 | 36 | |
7 | 49 | |
Десятичные числа
Это также работает для десятичных чисел.
Попробуйте ползунки ниже (примечание: «…» означает, что десятичные дроби продолжаются бесконечно):
Использование ползунков:
- Чему равен квадратный корень из 8 ?
- Чему равен квадратный корень из 9 ?
- Чему равен квадратный корень из 10 ?
- Сколько будет 1 в квадрате?
- Что такое 1,1 в квадрате?
- Что такое 2,6 в квадрате?
Негативы
Ранее мы обнаружили, что можем возводить в квадрат отрицательные числа:
Пример: (−3) в квадрате
(−3) × (−3) = 9
И, конечно же, 3 × 3 = 9 тоже.
Таким образом, квадратный корень из 9 может быть −3 или +3
.Пример: Чему равен квадратный корень из 25?
(-5) × (-5) = 25
5 × 5 = 25
Таким образом, квадратные корни из 25 равны −5 и +5
.Символ квадратного корня
| Это специальный символ, означающий «квадратный корень». это вроде как галочка, и на самом деле началась сотни лет назад в виде точки с движением вверх. Он называется радикалом и всегда делает математику важной! |
Мы используем его так:
и мы говорим «квадратный корень из 9 равен 3»
Пример: Что такое √25?
25 = 5 × 5, другими словами, когда мы умножаем 5 отдельно (5×5) получаем 25
Итак, ответ:
√25 = 5
Но подождите! Разве квадратный корень из не может также равняться −5 ? Потому что (−5) × (−5) = 25 тоже.
- Ну, квадратный корень из 25 может быть -5 или +5.
- Но когда мы используем радикальный символ √ , мы даем только положительный (или нулевой) результат .
Пример: Что такое √36?
Ответ: 6 × 6 = 36, поэтому √36 = 6
Идеальные квадраты
Совершенные квадраты (также называемые «квадратными числами») — это квадраты целых чисел:
.| Совершенный Квадраты | |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
и т. д… д… |
Постарайтесь запомнить их до 12.
Вычисление квадратных корней
Легко извлечь квадратный корень из полного квадрата, но это действительно трудно для работы других квадратных корней.
Пример: что такое √10?
Итак, 3 × 3 = 9 и 4 × 4 = 16, поэтому мы можем предположить, что ответ находится между 3 и 4.
- Попробуем 3,5: 3,5 × 3,5 = 12,25
- Попробуем 3.2: 3,2 × 3,2 = 10,24
- Попробуем 3,1: 3,1 × 3,1 = 9,61
- …
Приближаемся к 10, но для получения хорошего ответа потребуется много времени!
В этот момент я достаю свой калькулятор, и он говорит: .3.1622776601683793319988935444327 Но цифры продолжаются и продолжаются без какой-либо закономерности. Так даже ответ калькулятора только приближение ! |
Примечание: подобные числа называются иррациональными числами, если вы хотите узнать больше.
Самый простой способ вычисления квадратного корня
| Используйте кнопку квадратного корня вашего калькулятора! |
А также используйте свой здравый смысл, чтобы убедиться, что у вас есть правильный ответ.
Увлекательный способ вычисления квадратного корня
Существует забавный метод вычисления квадратного корня, который с каждым разом становится все более и более точным:
| а) начните с предположения (допустим, 4 — это квадратный корень из 10) | |
| б) разделить на предположение (10/4 = 2.5) c) прибавьте это к предположению (4 + 2,5 = 6,5) d) затем разделите результат на 2, другими словами, уменьшите его пополам. (6,5/2 = 3,25) e) теперь установите это как новое предположение и снова начните с b) |
- Наша первая попытка увеличила число с 4 до 3,25
- Повторный переход (от b до e ) дает нам: 3,163
- Повторный переход (от b до e ) дает нам: 3,1623
Итак, после 3-х раз вокруг ответ 3. 1623, что очень хорошо, потому что:
1623, что очень хорошо, потому что:
3,1623 х 3,1623 = 10,00014
Теперь… почему бы вам не попробовать вычислить квадратный корень из 2 таким образом?
Как угадать
Что, если нам нужно угадать квадратный корень из такого сложного числа, как «82 163″… ?
В этом случае мы могли бы подумать, что «82 163» состоит из 5 цифр, поэтому квадратный корень может состоять из 3 цифр (100×100=10 000), а квадратный корень из 8 (первая цифра) равен примерно 3 (3×3=9), поэтому 300 хорошее начало.
День квадратного корня
4 апреля 2016 года — День квадратного корня, потому что дата выглядит так: 4/4/16
Следующим после этого будет 5 мая 2025 года (5/5/25)
309 310 315, 1082, 1083, 2040, 3156, 2041, 2042, 3154
5 основных способов использования научного калькулятора
Большинство из нас постоянно носит с собой простой калькулятор; иначе известный как наш смартфон. Но что, если вы посещаете уроки математики и естественных наук на продвинутом уровне? Или если вы работаете в отрасли, где регулярно используются сложные расчеты для проектирования или разработки передовых концепций, таких как проектирование, геодезия, медицина или химия?
Тогда вам нужно что-то более подходящее для решения ваших сложных проблем. Научный калькулятор будет отвечать всем требованиям. И если вы планируете в ближайшем будущем посещать занятия по математике более высокого уровня, ваш профессор может потребовать от вас использования научного калькулятора.
Научный калькулятор будет отвечать всем требованиям. И если вы планируете в ближайшем будущем посещать занятия по математике более высокого уровня, ваш профессор может потребовать от вас использования научного калькулятора.В конце этой статьи мы рассмотрим 3 научных калькулятора HP с разной ценой, но сначала давайте подробно рассмотрим, что это такое, и 5 вещей, для которых вы можете использовать свой научный калькулятор.
Что такое научный калькулятор?
Научные калькуляторы выполняют те же функции, что и их стандартные электронные аналоги, но они также имеют множество других доступных функций.Сегодня на рынке есть три основных категории калькуляторов: бизнес, базовые и научные.
Вполне вероятно, что вы уже использовали базовый калькулятор на уроках математики в старшей школе, и, возможно, вы даже использовали бизнес-калькулятор или графический калькулятор на курсе экономики или бизнес-статистики.
Научный калькулятор, однако, единственный, который может выполнять определенные функции в таких областях, как тригонометрия, физика, химия и инженерия.
Научный калькулятор имеет дополнительные функции, позволяющие работать с экспонентами и логарифмами, которые требуют больше памяти для выполнения функций для достижения наилучших результатов.
Хотя вы также можете выполнять базовые вычисления, такие как сложение, вычитание, умножение и деление, это лишь малая часть типов уравнений, с которыми может справиться этот калькулятор.
Что я должен искать в научном калькуляторе?
Если вы планируете посещать какие-либо курсы, посвященные геометрии, систематизации, тригонометрии, инженерному делу и физике, то, вероятно, в какой-то момент вам придется научиться пользоваться научным калькулятором.Стоимость
Не стоит ожидать, что вы потратите больше 200 долларов на научный калькулятор.На самом деле у HP есть 3 устройства до 60 долларов (2 из них до 15 долларов). Будьте готовы заплатить немного больше, чем вы заплатите за базовый или бизнес-калькулятор, из-за его функций.
Функции
В зависимости от производителя у вас могут быть разные метки для ваших функций. По большей части они должны быть в состоянии выполнять одни и те же задачи. Если у вас есть доступ к учебному плану, еще раз проверьте, покупаете ли вы рекомендуемый вариант.
По большей части они должны быть в состоянии выполнять одни и те же задачи. Если у вас есть доступ к учебному плану, еще раз проверьте, покупаете ли вы рекомендуемый вариант.
Бонусные функции
Вам не обязательно иметь самую крутую модель, чтобы сдать экзамен, но за последние несколько лет в научных калькуляторах произошли некоторые важные улучшения.К ним относятся Wi-Fi и возможность поделиться своей работой с одноклассниками или инструктором.
Вот пять основных способов использования научного калькулятора и то, как вы можете ожидать его использования на следующем занятии.
1. Основные функции и показатели
Вычисление основных функций, таких как сложение, вычитание, умножение и деление. Следует иметь в виду, что знак вычитания (-) отличается от отдельной отрицательной функции. Это может привести к некоторой путанице в отношении отрицательных и положительных чисел, когда вы впервые начнете использовать калькулятор, потому что знаки выглядят одинаково.
Экспоненты, неизвестные числа
Наряду с отрицанием, вы также можете возводить числа в другую степень и находить квадратный корень из числа или формулы.
Экспоненты используются почти в любом курсе математики после начальной школы, но только научный калькулятор может выполнять любую алгебраическую функцию.Помимо использования калькулятора для вычисления известного числа, вы можете использовать его для вычисления неизвестного числа. Это полезно для алгебры или любой другой более сложной математики, которую вы можете изучать.
Порядок операций
Базовые калькуляторы отлично подходят для решения простых уравнений с одной или двумя переменными, но научные калькуляторы позволяют вводить задачи, в которых есть порядок операций.Если ввести одно из этих уравнений в обычный калькулятор, он не сможет правильно определить, к каким числам следует обращаться в первую очередь.
Однако, как только вы введете уравнение в научный калькулятор, он должен дать вам правильный ответ. Это связано с тем, что круглые скобки включены в качестве опции, что позволяет решать более сложные задачи. Это говорит калькулятору сначала выполнить эту операцию, как если бы вы делали это на бумаге.
Это связано с тем, что круглые скобки включены в качестве опции, что позволяет решать более сложные задачи. Это говорит калькулятору сначала выполнить эту операцию, как если бы вы делали это на бумаге.
Квадратный корень
Также можно использовать научный калькулятор, чтобы найти квадратный корень числа, и это одна из самых простых операций, которые вы можете выполнить.Введите число, нажмите клавишу SQRT, и появится ваш ответ.
Быстро или правильно? Теперь вы можете делать и то, и другое
Часто для поиска ответов на уравнения достаточно использовать одну или две клавиши, что может ускорить и упростить решение сложных задач.
И хотя сейчас большинство преподавателей поощряют использование калькуляторов в своих классах, стоит сначала спросить, разрешены ли устройства такого типа. Почти каждый может извлечь выгоду из использования научного калькулятора.
2. Логарифмы
После того, как вы расширите свои знания и изучите новые понятия, связанные с исчислением и тригонометрией, вполне вероятно, что вам придется изучить логарифмы. Эти формулы помогут вам рассчитать скорость, площадь и многое другое.
Эти формулы помогут вам рассчитать скорость, площадь и многое другое.
В прошлом это делалось почти полностью вручную. Теперь требуется всего несколько минут, чтобы ввести правильную информацию и решить задачу с помощью калькулятора.
Медицина и инженерия стали проще
Логарифмы в основном используются теми, кто занимается медициной и инженерией, но в какой-то момент с ними могут столкнуться и другие профессии. Их может быть сложно решить вручную, но с помощью научного калькулятора процесс может быть намного проще.
Ваше устройство, вероятно, решит натуральный логарифм уравнения в большинстве классов. Некоторые учителя могут объяснять логарифмы только с помощью научного калькулятора, потому что все, что для этого требуется, — это знать, как вводить правильную формулу.
Память является ключом к решению логарифмов
Еще одна причина, по которой вы можете захотеть использовать научный калькулятор для вычисления логарифмов, заключается в том, что они имеют встроенную память, которая позволяет вам хранить определенные уравнения.
Если вы работаете над чем-то, что требует нескольких сеансов, вы можете указать своему калькулятору сохранять то, что вы уже ввели в устройство.Это позволяет легко вернуться, если вам нужно сделать перерыв или если вы хотите попробовать другую комбинацию.
3. Функции синуса, косинуса и тангенса
Для тех, кто изучает тригонометрию или математический анализ, функция синуса является данностью. Они также часто появляются, если ваша карьера связана с какой-либо инженерной или архитектурной областью.
Вычисление синуса
Функция синуса используется для нахождения измерения определенного угла, особенно когда неизвестны другие стороны или углы.Вы также можете встретить арксинус, который часто используется для нахождения гипотенузы треугольника.
Как и логарифмы, это вычисление когда-то занимало некоторое время, пока вы просматривали один лист бумаги за другим. С научными калькуляторами вы можете получить ответ почти сразу после того, как правильно введете функцию. Найдите кнопки sin, cos и tan на любом калькуляторе, чтобы убедиться, что он поддерживает эти функции.
Найдите кнопки sin, cos и tan на любом калькуляторе, чтобы убедиться, что он поддерживает эти функции.
Построение графика синуса
Другим родственным вычислением, которое вам, возможно, придется выполнить, является построение графика синуса.Это прямой способ показать свою работу, и теперь многие классы требуют, чтобы вы знали, как графически отображать различные функции.
Функции косинуса
Точно так же вы можете построить график и решить функции косинуса. Косинус угла — это мера длины треугольника, и его чаще всего используют в курсах тригонометрии. Скорее всего, вы будете использовать косинусы, чтобы найти длину гипотенузы треугольника, а научный калькулятор также работает в обратном порядке с арккосинусами.
Косинусы можно найти для любого угла, даже если он большой или отрицательный. Опять же, вам может потребоваться показать, что вы знаете, что такое косинусы, используя калькулятор для построения графика.
Тангенс в градусах или радианах
Тангенс — это еще одно понятие, которое вам придется изучать на уроках тригонометрии, и оно также включает поиск неизвестных величин. В геометрии вы, скорее всего, столкнетесь с касательными при вычислении перпендикулярных линий.
В геометрии вы, скорее всего, столкнетесь с касательными при вычислении перпендикулярных линий.
В тригонометрии вы будете использовать его, чтобы найти значение противоположной стороны заданных значений.Вы также можете выбрать получение ответа в градусах или радианах в зависимости от требований преподавателя.
Опять же, научный калькулятор — единственный тип калькулятора, который может найти ответ на эти типы уравнений, и вполне вероятно, что в какой-то момент он вам понадобится в школе. Это может быть особенно верно, если ваш преподаватель требует, чтобы вы продемонстрировали, как умеете строить графики определенных функций, что может быть частью вашей итоговой оценки.
Совет для профессионалов: Убедитесь, что ваш калькулятор не находится в радианном режиме, если вы хотите, чтобы ваши ответы были в градусах, потому что это может нарушить ваше уравнение и дать вам совершенно другой ответ, чем тот, который вы ищете.
4. Научное обозначение
Калькулятор для научных расчетов используется не только для решения более сложных математических задач. На самом деле, одним из его лучших применений может быть то, что он может вычислять экспоненциальное представление. Для чисел, которые не могут быть записаны в форме десятичной точки, потому что они слишком велики, обычный калькулятор не сможет их покрыть.
На самом деле, одним из его лучших применений может быть то, что он может вычислять экспоненциальное представление. Для чисел, которые не могут быть записаны в форме десятичной точки, потому что они слишком велики, обычный калькулятор не сможет их покрыть.
Вы, скорее всего, будете использовать экспоненциальную запись, если планируете работать в области, связанной с наукой, инженерией и математикой, и вам определенно понадобится более сложный калькулятор для выполнения домашних заданий.x на вашем устройстве
В отличие от обычных калькуляторов, которые могут обрабатывать только меньшие значения, научный калькулятор может обрабатывать числа в гораздо более широком масштабе, что может быть полезно, когда дело доходит до сбора данных или работы физиком или химиком. Он также может вычислять отрицательную экспоненциальную запись.
Для тех, кто хочет заняться инженерным делом, есть специальный режим, который поможет вам рассчитать уравнения, характерные для вашей области. Вы найдете его как режим отображения ENG на своем устройстве, и он разработан, чтобы помочь передавать числа устно и посредством чтения.
Вы найдете его как режим отображения ENG на своем устройстве, и он разработан, чтобы помочь передавать числа устно и посредством чтения.
5. Двоичные функции
Подобно тому, как вы вводите уравнения в свой калькулятор для вычисления обозначений или логарифмов, тангенсов и синусов, научный калькулятор может решать двоичные функции. Эти уравнения требуют двух входных данных.
Вы, скорее всего, столкнетесь с этим в алгебре или математическом анализе, когда будете находить неизвестное, но вы также можете обсудить его, изучая декартово произведение и подмножества.
Это еще один тип уравнения, который трудно отследить, не имея калькулятора с памятью, потому что, если вы можете сохранить результаты, которые дает вам калькулятор, вы можете продолжить работу, которую вы выполнили раньше, или сохранить свои усилия для другого время.
Научные калькуляторы HP
Вот лучшие научные калькуляторы, доступные от HP:
Научный калькулятор HP 35s
Получите профессиональную производительность с научным калькулятором HP 35s . Это совершенный научный программируемый калькулятор HP RPN, который идеально подходит для инженеров, геодезистов, студентов колледжей, ученых и медицинских работников.
Это совершенный научный программируемый калькулятор HP RPN, который идеально подходит для инженеров, геодезистов, студентов колледжей, ученых и медицинских работников.- Идеально подходит для инженеров, геодезистов, студентов колледжей, ученых и медицинских работников
- Большой 2-строчный дисплей
- 30 КБ памяти
- 42 встроенных физических константы
- 800 регистров памяти
- Более 100 встроенных функций
- 7
- 4
Научный калькулятор HP 300s
Вооружитесь сложным научным калькулятором HP 300s+ с расширенными арифметическими, алгебраическими и тригонометрическими функциями для решения самых сложных математических и естественных наук.- Одобрено для использования на большинстве вступительных экзаменов в колледж
- Питание от солнечной батареи с резервным аккумулятором
- 4-строчный ЖК-дисплей формата учебника
- 9 регистров памяти
- 315 встроенных функций
Научный калькулятор HP 10s
Научный калькулятор HP 10s+ с удобным дизайном, легко читаемым дисплеем и широким набором алгебраических, тригонометрических, вероятностных и статистических функций для занятий математикой и естественными науками.



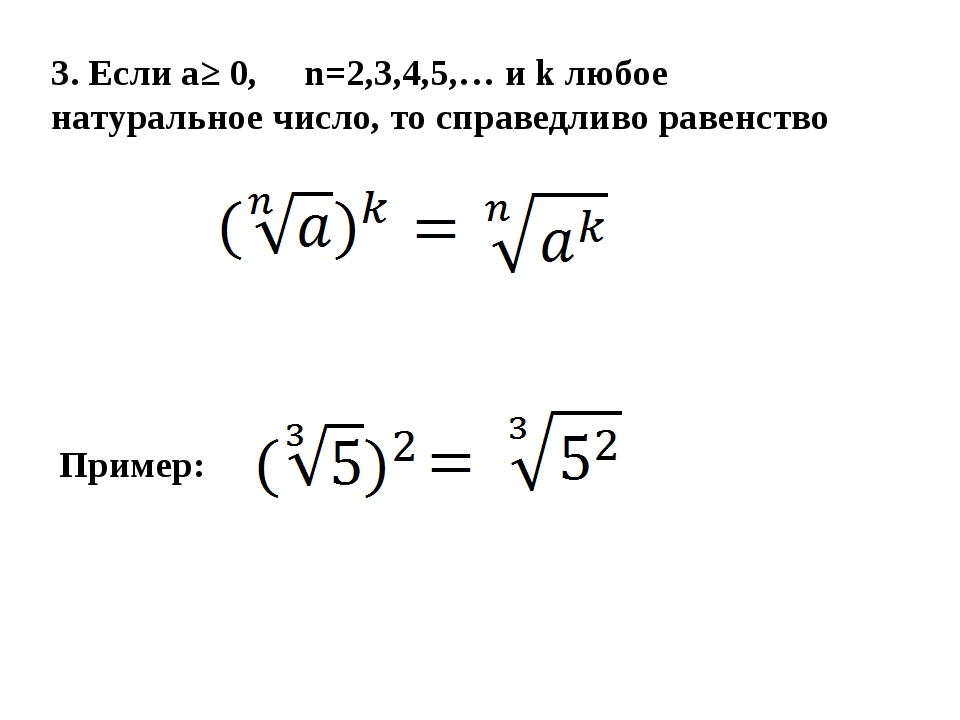
 При отсутствии такой документации поддержка предоставляется TI.
При отсутствии такой документации поддержка предоставляется TI.
 Вы соглашаетесь с тем, что вы не намереваетесь и не будете прямо или косвенно экспортировать, реэкспортировать или передавать Программу или технические данные в любую страну, в которую такой экспорт, реэкспорт или передача ограничены любым применимым законодательством США или закона, без надлежащего письменного согласия или лицензии, если требуется, Бюро экспортного управления Министерства торговли США или такого другого государственного органа, который может иметь юрисдикцию в отношении такого экспорта, реэкспорта или передачи.
Вы соглашаетесь с тем, что вы не намереваетесь и не будете прямо или косвенно экспортировать, реэкспортировать или передавать Программу или технические данные в любую страну, в которую такой экспорт, реэкспорт или передача ограничены любым применимым законодательством США или закона, без надлежащего письменного согласия или лицензии, если требуется, Бюро экспортного управления Министерства торговли США или такого другого государственного органа, который может иметь юрисдикцию в отношении такого экспорта, реэкспорта или передачи. 227-14 (июнь 1987 г.) или DFAR, 48 CFR. 252.227-7013 (октябрь 1988 г.), если применимо.
227-14 (июнь 1987 г.) или DFAR, 48 CFR. 252.227-7013 (октябрь 1988 г.), если применимо. Итак, щелкните правой кнопкой мыши по нему и нажмите «Удалить».
Итак, щелкните правой кнопкой мыши по нему и нажмите «Удалить». Но вы можете рассчитать его, используя некоторые пользовательские формулы […]
Но вы можете рассчитать его, используя некоторые пользовательские формулы […] ..]
..]