Как привести корни к общему показателю: Приведение к одному показателю корня. Корень n-й степени и его основные свойства
Иррациональные алгебраические выражения в математике с примерами решения и образцами выполнения
Рациональные и иррациональные алгебраические выражения: Назовем алгебраическим всякое выражение, получающееся из чисел и некоторых букв с помощью арифметических операций и возведения в степень с рациональным показателем. Мы не включили в число операций извлечение корня, так как оно сводится к возведению в степень (с показателем ).
Примерами алгебраических выражений являются:
и т. д. Ясно, что многочлены — частный случай алгебраических выражений.
Говорят, что алгебраическое выражение рационально относительно некоторой буквы а, если никакая содержащая эту букву часть этого выражения не возводится в степень с нецелым показателем. В противном случае говорят, что выражение иррационально относительно буквы а. Например, выражение
рационально относительно буквы а и иррационально относительно буквы х
Одночленные иррациональные выраженияИррациональное выражение называется одночленным, если оно получается из чисел и букв с помощью операций умножения и возведения в степень с рациональным показателем.
Иррациональное же выражение
не является одночленным.
Некоторые одночленные иррациональные выражения можно упростить. Для этого надо:
а) Раскрыть все скобки, используя формулы
б) Объединить степени с одинаковыми основаниями, используя формулу
в) Сократить дроби в показателях отдельных букв.
В результате получается выражение вида
где А —некоторое число (быть может, иррациональное), а — несократимые дроби.
Здесь уже отсутствуют скобки и каждая буква входит лишь один раз. Такой вид одночленного иррационального выражения мы будем называть каноническим.
Пример:
Привести к каноническому виду иррациональное выражение
По формулам (1), (2), (3), это выражение равно:
Сокращение показателей и приведение корней к общему показателюТак как то из каждого свойства степеней с рациональными показателями вытекает соответствующее свойство корней.
Равенство (см. формулу (3), п. 2) переписывается так: при а > О имеем
Таким образом, если подкоренное выражение является степенью положительного числа, причем показатель степени имеет общий делитель с показателем корня, то можно сократить эти показатели на общий делитель.
Из равенства (1) вытекает, что любые два корня с натуральными показателями можно привести к общему показателю.
Именно пусть даны корни Тогда по формуле (1) имеем (разумеется, в качестве общего показателя корней можно выбрать не mn, а наименьшее общее кратное чисел m и n).
Отметим, что формула (1) справедлива лишь при условии а > 0. В случае, когда а < 0, эта формула, вообще говоря, неверна. Например, рассмотрим Если а > 0, то по формуле (1) получаем Пусть теперь а < 0 . Тогда — а > 0 и Поэтому при а < 0 имеем:
Например,
Наконец, если а — 0, то . Полученные значения для можно выразить одной формулой
В самом деле, как так и |а | равны а при (—а) при а < 0.
Вообще, если общий делитель п, на который сокращают показатели корня и подкоренного выражения, четен и рассматриваются любые значения а, формулу (1) следует переписать так:
Пример:
Вычислить
По формуле (2) получаем:
Значит, если а если то этот корень равен
Извлечение корня из произведения и степениТочно так же из формулы (2), п. 2, выводится, что при х > 0, у > 0:
Полученные свойства корней формулируются следующим образом:
а) Корень n-й степени из произведения двух положительных чисел равен произведению корней п-й степени из отдельных сомножителей.
б) Корень n-й степени из отношения двух положительных чисел равен отношению корней n-й степени из этих чисел
Например,
Пользуясь свойствами (1) и (2), можно записать произведение нескольких корней с помощью одного знака корня.
Если же перемножаемые корни имеют различные показатели, то и с надо предварительно привести к общему показателю (см. стр. 103). Например,
Совершенно так же выполняется деление корней. Например,
Вынесение алгебраических выражений из-под корня и внесение их под кореньИз формулы (1), п. 7, вытекает, что при а > 0 и b > 0:
Итак, если часть подкоренного выражения для корня n-й степе ни является n-й степенью некоторого положительного алгебраического выражения, то это выражение можно вынести из-под корня.
Следует иметь в виду, что формула (1) справедлива лишь при условии а >0, b > 0. Если же это условие не выполняется, а n = 2k — четное число, то вместо формулы (1) надо писать:
Возведение корня в степеньЭта операция основана на формуле (6 ). Из нее следует, что Это равенство можно записать так:
Из нее следует, что Это равенство можно записать так:
Таким образом, чтобы возвести корень с положительным под коренным выражением в некоторую степень, надо возвести в эту степень подкоренное выражение. Например,
Извлечение корня из корняЭта операция также основана на формуле (6 ). Из нее следует, что , и потому
Таким образом, при извлечении корня из корня показатели корней перемножаются, а подкоренное выражение остается неизменным.
Два корня называются подобными, если их можно преобразовать к такому виду, чтобы они отличались лишь рациональным множителем (при этом предполагается, что переменные, от которых зависит подкоренное выражение, положительны). Например, корни
и
подобны, так как при а > 0 , b > 0 , с > 0 , x> 0 имеем:
и
Второй корень получается из первого умножением на рациональный множитель.
Корни из одночленов подобны тогда и только тогда, когда в их канонической форме иррациональные множители одинаковы. Поэтому, чтобы убедиться в подобии двух корней из одночленов, надо привести их к канонической форме.
Вообще говоря, сумму не скольких корней не удается записать с помощью лишь одного знака корня. Однако, если среди рассматриваемых корней есть подобные, их можно сгруппировать вместе и вынести за скобки общий множитель.
Пример:
Уничтожение иррациональности в знаменателе или в числи теле алгебраической дробиЧасто бывает нужно найти численное значение иррационального выражения при заданных значениях входящих в него букв. При этом бывает неудобно делить на иррациональные числа. В таких случаях стараются преобразовать за данное иррациональное выражение так, чтобы его знаменатель не содержал корней.
Посмотрим сначала, как выполняется это преобразование в случае, когда знаменатель дроби — корень из одночлена. Пусть дано иррациональное выражение . Если мы хотим освободиться от иррациональности в знаменателе этой дроби, то надо помножить и числитель, и знаменатель на такой множитель, чтобы в знаменателе извлекся корень. Ясно, что для этого надо умножить подкоренное выражение в знаменателе дроби на тогда оно станет равно и корень извлечется. Вспоминая правило умножения корней, видим, что числитель и знаменатель надо умножить на Тогда мы получим, что
Пусть дано иррациональное выражение . Если мы хотим освободиться от иррациональности в знаменателе этой дроби, то надо помножить и числитель, и знаменатель на такой множитель, чтобы в знаменателе извлекся корень. Ясно, что для этого надо умножить подкоренное выражение в знаменателе дроби на тогда оно станет равно и корень извлечется. Вспоминая правило умножения корней, видим, что числитель и знаменатель надо умножить на Тогда мы получим, что
Вообще, если дано выражение вида , причем все показатели меньше n, то надо умножить числитель и знаменатель дроби на один и тот же множитель
Тогда при а >0, b > 0 , …, с > 0 получим:
Этот ответ остается справедливым при нечетном n для любых а, b, …, с. Если же n четно, то в общем случае в знаменателе надо писать
Теперь рассмотрим случай, когда знаменатель алгебраической дроби имеет вид где A и В — положительные рациональные выражения. В этом случае надо умножить и числитель, и знаменатель на выражение (оно получается из знаменателя изменением знака при ). Так как (а +b) (а—b) = то при А > 0 и В > 0
Так как (а +b) (а—b) = то при А > 0 и В > 0
Поскольку (А — В) — рациональное выражение, мы избавляемся от иррациональности в знаменателе дроби. (Точно так же избавляются от иррациональности в знаменателе, если он имеет вид ) Например,
Аналогично действуют в случае, когда знаменатель дроби имеет вид , где А и В — рациональные выражения. Уничтожение иррациональности в знаменателе основывается здесь на формуле
(см. стр. 32). Именно, положим и умножим числитель и знаменатель на одно и то же выражение
(где надо заменить а на и b на Тогда знаменатель примет вид:
то есть станет рациональным выражением. Случай, когда знаменатель равен , разбирается точно так же. Здесь надо положить
Если знаменатель имеет вид то надо положить (соответственно и воспользоваться формулой
Если знаменатель имеет вид то корни надо сначала привести к общему показателю. Например,
Случай, когда знаменатель является суммой трех или большего числа корней, сложнее. Однако можно показать, что какой бы сложный вид ни имел знаменатель, всегда можно освободиться от иррациональности в знаменателе. Общие методы таких преобразований изучаются в высшей алгебре.
Однако можно показать, что какой бы сложный вид ни имел знаменатель, всегда можно освободиться от иррациональности в знаменателе. Общие методы таких преобразований изучаются в высшей алгебре.
В некоторых задачах, наоборот, бывает целесообразно уничтожить иррациональность в числителе алгебраической дроби, т. е. преобразовать дробь к такому виду, чтобы ее числитель содержал лишь рациональные выражения. Читателю должно быть ясно, что эта цель достигается теми же способами, как уже в разобранных выше примерах.
Преобразование выражений вид
Пусть задано алгебраическое выражение где А > 0, В > 0, Мы покажем сейчас, что его можно представить в следующем виде суммы двух корней:
Для доказательства покажем сначала, что квадраты выражений в обеих частях равенства (1) совпадают. В самом деле,
С другой стороны,
Осталось показать, что обе части равенства (1) положительны. Для левой части это очевидно, так как мы рассматриваем лишь арифметические значения корней. Д ля правой это справедливо, поскольку при А >0, В > 0
Д ля правой это справедливо, поскольку при А >0, В > 0
Формула (1) позволяет упростить выражение в случае, когда разность есть полный квадрат. Например, имеем:
Иррациональные уравнения и неравенства
Определение:
Иррациональным уравнением называется уравнение вида R(х)=0, где R(х) — иррациональное выражение от х. К такому виду приводятся уравнения и — иррациональные выражения от х. Например,
являются иррациональными уравнениями, а
— рациональное алгебраическое уравнение (так как х не находится под знаком корня).
В иррациональных уравнениях все радикалы понимаются в смысле арифметического значения. Поэтому, если показатель корня — четное число, то подкоренное выражение и значение корня должны быть неотрицательными. Отсюда ясно, например, что иррациональное уравнение не имеет решений — его левая часть неотрицательна при всех допустимых значениях х.
Сведение иррациональных уравнений к рациональнымДля решения иррациональных уравнений стараются свести их к рациональным уравнениям. С этой целью обе части уравнения после соответствующих преобразований возводят в одну и ту же степень. Чтобы показать, что при этом не происходит потери корней, докажем следующую теорему.
С этой целью обе части уравнения после соответствующих преобразований возводят в одну и ту же степень. Чтобы показать, что при этом не происходит потери корней, докажем следующую теорему.
Теорема:
Если число а — корень уравнения , то это число удовлетворяет и уравнению
Доказательство:
По условию имеет место равенство Возведем обе части этого равенства в n-ю степень. Равенство от этого не нарушится, и мы получим,» что Это показывает, что а — корень уравнения
Итак, при возведении обеих частей уравнения в одну и ту же степень мы получаем уравнение, являющееся следствием исходного. Однако это уравнение при четных п неравносильно исходному. Ведь если из равенства вытекает то обратное неверно. Именно из следует лишь, что Если при этом имеют одинаковые знаки, то . Если же они имеют различные знаки, то . Таким образом, корень уравнения может удовлетворять не только уравнению , но и уравнению Во втором случае он является посторонним для уравнения . Если же показатель n нечетен, n=2k+1, то из следует, что Поэтому уравнения и равносильны.
Если же показатель n нечетен, n=2k+1, то из следует, что Поэтому уравнения и равносильны.
Итак, если при решении уравнения нам пришлось возводить обе его части в степень с четным показателем, то могли получиться посторонние корни. Чтобы выяснить, какие из корней уравнения удовлетворяют исходному уравнению надо подставить их в исходное уравнение и посмотреть, удовлетворяют они уравнению или нет.
Примеры:
1) Решить уравнение
Возводя обе части уравнения в квадрат, получим уравнение:
Его корнем является . Но не удовлетворяет уравнению (1)— после подстановки получается неверное равенство. Следовательно, уравнение (1) решений не имеет.
2) Решить уравнение
Здесь после возведения в квадрат получаем уравнение:
Его корнем является . Проверка показывает, что удовлетворяет уравнению (2).
3) Решить уравнение
Возводя обе части уравнения в квадрат, получаем квадратное уравнение . Его корнями являются . Проверка показывает, что только корень x = 3 удовлетворяет заданному уравнению. Корень же x = —1 удовлетворяет уравнению
Его корнями являются . Проверка показывает, что только корень x = 3 удовлетворяет заданному уравнению. Корень же x = —1 удовлетворяет уравнению
Мы видели, что при решении иррациональных уравнений приходится возводить обе части уравнения в одну и ту же степень. При этом, разумеется, желательно, чтобы хоть одна из частей уравнения имела вид где Р(х) — рациональное выражение. В этом случае после возведения обеих частей уравнения в n-ю степень мы получим в соответствующей части уравнения рациональное выражение. Поэтому при решении иррациональных уравнений обычно поступают так.
Выбирают один из радикалов, входящих в уравнение, оставляют его в одной стороне уравнения, а все остальные члены переносят в другую сторону. После этого возводят обе части получившегося уравнения в степень, показатель которой равен показателю уединенного радикала. Повторяя этот процесс, освобождаются от всех радикалов, входящих в уравнение, и получают рациональное уравнение. При этом, если при решении приходилось хоть раз возводить обе части равенства в степень с четным показателем, полученные корни необходимо проверить. Проверка осуществляется путем подстановки корней в исходное уравнение.
При этом, если при решении приходилось хоть раз возводить обе части равенства в степень с четным показателем, полученные корни необходимо проверить. Проверка осуществляется путем подстановки корней в исходное уравнение.
Рассмотрим некоторые примеры.
1) Решить уравнение
Перенесем в правую часть уравнения и возведем обе части получившегося равенства в квадрат. Мы получим:
или
Отсюда находим . Снова возведем обе части уравнения в квадрат: . Корнями этого уравнения являются
Проверим полученные корни. Подставляя корень заданное уравнение, получаем или 8 = 8. Значит, этот корень удовлетворяет заданному уравнению. Корень также удовлетворяет этому уравнению.
2) Решить уравнение
Уединим радикал и возведем обе части уравнения в квадрат. Получим
Корнями этого уравнения являются Однако из этих корней заданному уравнению удовлетворяет лишь
корень же является посторонним. Он удовлетворяет уравнению
Введение нового неизвестногоИногда при решении иррациональных уравнений оказывается полезным введение нового неизвестного. Рассмотрим уравнение
Рассмотрим уравнение
Если попробовать уединить радикал, то после возведения в квадрат получится уравнение четвертой степени. Поэтому мы будем решать это уравнение иначе. Положим Так как то уравнение (1) можно переписать так:
Решая это квадратное уравнение, находим корни Таким образом, решение уравнения (1) свелось к решению уравнения
(уравнение не имеет решений, так как ради кал понимается в смысле арифметического значения, а потому не может равняться отрицательному числу).
Из уравнения (2) находим, что Проверка показывает, что оба корня уравнению (1) удовлетворяют.
Особые случаи решения иррациональных уравненийВ разобранных выше примерах после освобождения от иррациональности получались уравнения, имевшие один или несколько корней. В этом случае удается обнаружить посторонние корни путем подстановки их в первоначальное уравнение. В некоторых примерах, однако, после освобождения от иррациональности получается равенство, тождественно выполняющееся на всей числовой оси или на некотором бесконечном числовом множестве. В этом случае проверка корней путем подстановки становится уже невозможной, поскольку найденное множество корней бесконечно. Для таких уравнений в ходе решения выясняют дополнительные условия на возможные корни, имеющие форму неравенств, и отбирают лишь корни, удовлетворяющие этим условиям.
В этом случае проверка корней путем подстановки становится уже невозможной, поскольку найденное множество корней бесконечно. Для таких уравнений в ходе решения выясняют дополнительные условия на возможные корни, имеющие форму неравенств, и отбирают лишь корни, удовлетворяющие этим условиям.
Рассмотрим некоторые примеры.
Пусть дано иррациональное уравнение:
Решим его путем освобождения от иррациональности. Для этого уединим первый радикал и возведем обе части равенства в квадрат. Мы получим, что
то есть
Вновь возводя в квадрат, получаем:
Это равенство тождественно выполняется для всех значений х. Однако, подставляя в уравнение (1), например, х = 4, получаем неверное соотношение: 1 + 9 = 8. Таким образом, первоначальному уравнению удовлетворяют не все значения х. Как мы уже говорили, отобрать корни уравнения (1) методом подстановки невозможно, поскольку множество корней уравнения (2′) бесконечно.
Выясним, откуда появились посторонние корни. Дело в том, что мы рассматриваем здесь лишь арифметические значения радикалов. Из-за этого на х налагаются дополнительные ограничения, имеющие вид неравенств. А при возведении обеих частей уравнения в квадрат эти ограничения были сняты. Таким образом, чтобы найти, при каких же значениях х удовлетворяется первоначальное уравнение, нам надо отобрать числа, удовлетворяющие соответствующим неравенствам.
Дело в том, что мы рассматриваем здесь лишь арифметические значения радикалов. Из-за этого на х налагаются дополнительные ограничения, имеющие вид неравенств. А при возведении обеих частей уравнения в квадрат эти ограничения были сняты. Таким образом, чтобы найти, при каких же значениях х удовлетворяется первоначальное уравнение, нам надо отобрать числа, удовлетворяющие соответствующим неравенствам.
В первую очередь должны выполняться неравенства поскольку подкоренные выражения должны быть неотрицательными. Эти неравенства выполняются для всех значений х:
и не дают нужных нам ограничений на х.
Далее, так как то
Это неравенство выполняется лишь в области, где то есть Решением этого квадратного неравенства является отрезок— Дальнейшие ограничения на х получаем из равенства (2). Так как левая часть этого равенства заведомо неотрицательна, то должно выполняться условие
Итак, мы нашли два дополнительных условия на х:
Решением системы неравенств (3) является отрезок Поскольку, кроме неравенств (3), никаких ограничений на х не накладывается, а уравнение, полученное после освобождения от иррациональностей, выполняется тождественно на всей числовой оси, решением уравнения (1) является отрезок Иными словами, равенство (1) справедливо для любой точки этого отрезка.
Уравнение (1) можно решить иначе. Для этого заметим, что
и
Так как то уравнение (1) переписывается так:
Точки —5 и 3 разбивают числовую ось на участки На каждом из этих участков знаки (х—3) и (х + 5) постоянны. Принимая во внимание эти знаки, получаем, что уравнение можно записать так:
или
Отсюда снова видно, что равенство (1) тождественно выполняется на отрезке и не выполняется ни в одной точке, лежащей вне этого отрезка.
Точно так же решается иррациональное уравнение
Здесь мы имеем условие на х вида Представим уравнение так:
или
Отсюда получим:
Возможны три случая:
1) В этой области уравнение равносильно уравнению
то есть а по условию
2) Здесь уравнение (4) равносильно уравнению
или 1 = 1. Это значит, что любое значение х, удовлетворяющее неравенству удовлетворяет и уравнению а значит, и исходному уравнению.
з ) В этом случае уравнение (4′) принимает вид:
Отсюда а по условию
Итак, чтобы найти решение уравнения (4), нам осталось решить иррациональное неравенство
Возводя все члены этого неравенства в квадрат, получаем, что то есть Значит, решением уравнения (4) является отрезок [5, 10].
Рассмотрим теперь иррациональные неравенства, то есть неравенства, содержащие неизвестное под знаком корня. Решение таких неравенств осложняется рядом обстоятельств. Во-первых, для иррациональных неравенств, как и для иррациональных уравнений, рассматриваются лишь арифметические значения корня. Иными словами, если показатель корня — четное число, то подкоренное выражение должно быть неотрицательным, равно как и значение корня. Кроме этого, неравенство , вообще говоря, неравносильно неравенству . Ведь только для положительных а и b из а <b заведомо вытекает , а из следует а < b.
Пример:
Решить иррациональное неравенство
Сначала найдем область его определения. Ясно, что подкоренное выражение должно быть неотрицательно:
Решая это неравенство, получаем множество А, состоящее из двух лучей Кроме того, корень принимает лишь неотрицательные значения, а потому и правая часть неравенства (1) должна быть неотрицательной: Пересекая множество А с лучом получаем луч Итак, мы доказали, что неравенство (1) задано в области В этой области обе части неравенства (1) принимают положительные значения и потому неравенство (1) равносильно неравенству
Наша задача свелась к решению системы неравенств:
Из второго неравенства получаем x > 2. Значит, решением служит пересечение луча с лучом x > 2, то есть луч
Значит, решением служит пересечение луча с лучом x > 2, то есть луч
Пример:
Решить иррациональное неравенство
Это неравенство задано в области, определяемой ограничениями Их можно заменить одним неравенством В области обе части неравенства (2) положительны, и потому оно равносильно неравенству Итак, мы заменили неравенство (2) равносильной ему системой неравенств:
Она решается так же, как в примере 1. В результате получаем систему неравенств, равносильную неравенству (2)
Решая эту систему, находим, что .
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Можно ли отнимать корни.
 Как складывать и вычитать квадратные корни
Как складывать и вычитать квадратные корниВ наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.
Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.
Уравнение, которое нужно упростить:
√2+3√48-4×√27+√128
Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:
Первое число упростить уже нельзя. 2×2)
2×2)
Переписываем выражение с упрощенными слагаемыми:
√2+12×√3-12×√3+8×√2
Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.
Ответ получаем следующий:
√2+12√3-12√3+8√2=9√2
√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.
Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.
Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:
Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:
∛b+∜b=12×√b4 +12×√b3
12√b4 +12×√b3=12×√b4 + b3
Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.
На заметку: показатели степени складываются только при умножении.
Рассмотрим пример, когда в выражении присутствуют дроби.
5√8-4×√(1/4)+√72-4×√2
Будем решать по этапам:
5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.
4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2
Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.
√72-4√2=√(36×2)- 4√2=2√2
10√2+2√2-2=12√2-2
Вот и получился ответ.
Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.
Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.
Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых. Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.
Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Шаги
Часть 1 из 2: Определение корнейОбозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).

- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.

Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2 (3) + 2 (50) + (32) + 6 (3) + (81) - Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2 (50) + (32) + 2 (3) + 6 (3) + (81)
Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
 Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)
Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Внимание, только СЕГОДНЯ!
Все интересное
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*ª-&radic-y нужно внести x под корень. Инструкция 1Определите степень…
Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…
Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…
Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением. n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1.
 Извлечение квадратных корней
Извлечение квадратных корнейВо-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .
Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.
Yandex.RTB R-A-339285-1
Правила сложения и вычитания квадратных корней
Определение 1Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.
Пример 1
Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Действия с корнями: основы
Пример 26 50 — 2 8 + 5 12
Алгоритм действия:
- Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
- Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
- После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
- У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Совет 1
Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.
Пример 3
Давайте попробуем решить данный пример:
6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .
5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
Результат упрощения: 30 2 — 4 2 + 10 3
30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
А сейчас попрактикуемся на других примерах.
Пример 4
- Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
- Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
- Складываем множители у корней: 3 5 + 4 5 = 7 5 .
Пример 5
6 40 — 3 10 + 5:
- Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;
- Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
- Перемножаем множители, которые стоят перед корнем: 12 10 ;
- Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .
Пример 6
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
(9 — 4) 5 — 2 3 = 5 5 — 2 3 .
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.

- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia.ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , то
Преобразование выражений, содержащих операцию извлечения квадратного корня
До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что
где, напомним, a, b — неотрицательные числа.
Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Пример 3. Внести множитель под знак квадратного корня:
Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:
Показательные уравнения — как решать? Примеры, свойства и определение
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = aх. Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: aх = b, где a > 0, a ≠ 1. |
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = ax, где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a < 1 (но больше 0) — непрерывно убывает. Это хорошо видно на рисунке ниже.
Важно знать
Показательная функция не может быть отрицательным числом, т. е. выражение у = ax при а ≤ 0 корней не имеет.
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
am x an | am+n |
am:an | am-n |
(a x b)n | an x bn |
(a : b)n | an : bn |
(an)m | an x m |
a-n | 1/an |
(a/b)-n | (b/a)n |
n√a | a1/n |
Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.
Методы решения показательных уравнений
Самые короткие и простые показательные уравнения решаются с помощью элементарной математики. Например:
4х = 64.
Требуется найти, в какую степень нужно возвести 4, чтобы получить 64.
4 × 4 × 4 = 64
43 = 64
Х = 3
Но как решать показательные уравнения вот такого вида: 3√128= 42х? Нужно немного повозиться с преобразованием этого выражения. Например, сделать так, чтобы либо основания, либо степенные показатели стали одинаковы. Для этого мы можем разложить 128 и 4. Вы ведь заметили, что у них есть общий множитель? Правильно, это 2.
3√128= 42х
3√27= (22)2x
27/3 = 24х
Теперь в нашем уравнении появились одинаковые основания, а значит, мы можем приравнять и степени.
4х = 7/3
х = 7/12
В данном случае мы используем один из алгоритмов решения показательных уравнений — привели обе части равенства к одинаковым основаниям. Дальше рассмотрим и другие методы.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Приведение к одинаковому основанию
Весомую часть уравнений вида ах = b (при а и b 0) можно решить, превратив b в определенную степень числа a. Именно это мы сделали в примере выше, получив одинаковые основания. Главная трудность в том, чтобы найти у этих чисел общий множитель.
Если у нас есть одинаковые основания, но разные показатели степени, то при умножении чисел степени складываются, а при делении — вычитаются. |
Пример 1
Рассмотрим еще одно показательное уравнение с корнем.
(1/642)-х = √1/8
Мы знаем, что у 64 и 8 есть общий множитель — это 2. Попробуем использовать это, и тогда 642 = 212, а 8 = 23.
(1/212)-х = √1/23
1/2-12х = 1/22/3
(1/2)-12х = (1/2)3/2
-12х = 3/2
х = -1/8
Пример 2
В этом примере показательного уравнения нужно будет отдельно преобразовать каждую составляющую.
(0,5)х2 × 4х+1 = 64-1
Найдем общее основание показательных функций:
0,5 = 1/2 = 2-1
4 = 22
64 = 26
В результате у нас получается:
(2-1)х2 × (22)х+1 = (26)-1
2-х2 × 22х+2 = 2-6
2-х2+2х+2 = 2-6
-х2 + 2х + 2 = -6
х2— 2х — 8 = 0
Здесь у нас будет два корня: -2 и 4.
Приведение к одинаковой степени
Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.
При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): axbx = (ab)x. |
Пример
52х-4 = 492-х
Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:
52х-4 = 492-х
52х-4 = 74-2х
52х-4 = (1/7)2х-4
352х-4 = 1
2х — 4 = 0
х = 2
Пример 2
2х-2 = 52-х
Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.
2х-2 = 1/5х-2
Теперь умножим обе части на 52-х и придем к уравнению:
2х-2 × 52-х = 1
10х-2 = 1
10х-2 = 100
х — 2 = 0
х = 2
Замена переменной
Этот способ решения показательных уравнений понадобится тем, кто не боится по-настоящему трудных задач. Ведь с помощью ввода новой переменной можно упростить даже самое сложное выражение. Его суть проста: мы заменяем «трудную» переменную на более простую и решаем уравнение, а после производим обратную замену. Главное — определить, какую именно переменную стоит заменить.
Пример
4x— 2x+1— 8 = 0
Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4х = 22х, а 2х+1 = 2 × 2х.
22х — 2 × 2х — 8 = 0
Что-то напоминает. 🤔 Если бы из этого выражения можно было волшебным образом убрать 2х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2х новой переменной — допустим, y.
🤔 Если бы из этого выражения можно было волшебным образом убрать 2х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2х новой переменной — допустим, y.
Если 2х = y, получается: у2— 2у — 8 = 0.
У такого уравнения есть два корня: у1 = 4, у2 = -2.
Проведем обратную замену: 2х = 4, 2х = -2.
Но мы знаем, что показательная функция в любом случае не может быть отрицательным числом, а значит, 2х = -2 корней не имеет. Следовательно, 2х = 4.
х = 2.
Пример 2
25х — 6 × 5х + 5 = 0
Если присмотреться к этому выражению, становится понятно, что у него много общего с квадратным уравнением. Введем новую переменную: 5х = у.
у2 — 6у + 5 = 0
Корни такого уравнения: 1 и 5.
Выполним обратную замену:
5х = 1, значит х = 0.
5х = 5, значит х = 1.
Выделение устойчивого выражения
В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить. Так вот, когда мы выносим некий множитель за скобку или заменяем переменную, пытаясь упростить уравнение — это действие по сути и является выделением устойчивого выражения.
Устойчивое выражение — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки или обозначить новой переменной, чтобы упростить уравнение. |
Хорошая новость: так или иначе устойчивое выражение можно найти почти в любом трудном уравнении. Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.
Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.
Пример 1
3х+1 + 3х — 3х-2 = 35
В данном случае в качестве устойчивого выражения удобно взять 3х-2 как степень с наименьшим показателем. В итоге мы получим:
3х-2(33 + 32 — 1) = 35
3х-2 × 35 = 35
3х-2 = 1
Поскольку 1 равняется любое число в нулевой степени, мы можем записать:
3х-2 = 30
х — 2 = 0
х = 2
Пример 2
5 × 3-3х+1 + 3-3х+2 = 24
Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3-3х+2 = 3-3х+1+1 = 3 × 3-3х+1.
Теперь у нас есть устойчивое выражение 3-3х+1, которое можно вынести за скобки, чтобы получить более простое уравнение:
3-3х+1(5+3) = 24
8 × 3-3х+1 = 24
3-3х+1 = 31
-3х + 1 = 1
х = 0
Умножение одинаковых корней.
 Формулы корней. Свойства корней. Как умножать корни? Примеры
Формулы корней. Свойства корней. Как умножать корни? ПримерыПриветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще.
 С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка. {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
{2}}}=\sqrt{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.
Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.
Yandex.RTB R-A-339285-1
Метод 1. Деление подкоренных выражений
Алгоритм действий:
Записать дробь
Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.
Пример 1
144 ÷ 36 , это выражение следует переписать так: 144 36
Использовать один знак корня
В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.
Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.
Пример 2
144 36 . Это выражение следует записать так: 144 36
Разделить подкоренные выражения
Просто разделите одно выражение на другое, а результат запишите под знаком корня.
Пример 3
144 36 = 4 , запишем это выражение так: 144 36 = 4
Упростить подкоренное выражение (если необходимо)
Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.
Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.
Пример 4
4 — полный квадрат, потому что 2 × 2 = 4 . Из этого следует:
4 = 2 × 2 = 2 . Поэтому 144 36 = 4 = 2 .
Метод 2. Разложение подкоренного выражения на множители
Алгоритм действий:
Записать дробь
Перепишите выражение в виде дроби (если оно представлено так).
Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.
Пример 5
8 ÷ 36 , переписываем так 8 36
Разложить на множители каждое из подкоренных выражений
Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.
Пример 6
8 36 = 2 × 2 × 2 6 × 6
Упростить числитель и знаменатель дроби
Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.
Пример 7
2 2 6 6 × 6 2 × 2 × 2 , из этого следует: 8 36 = 2 2 6
Рационализировать знаменатель (избавиться от корня)
В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него.
Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.
Пример 8
В выражении 6 2 3 необходимо умножить числитель и знаменатель на 3 , чтобы избавиться от него в знаменателе:
6 2 3 × 3 3 = 6 2 × 3 3 × 3 = 6 6 9 = 6 6 3
Упростить полученное выражение (если необходимо)
Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.
Пример 9
2 6 упрощается до 1 3 ; таким образом 2 2 6 упрощается до 1 2 3 = 2 3
Метод 3. Деление квадратных корней с множителями
Алгоритм действий:
Упростить множители
Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!
Пример 10
4 32 6 16 . Сначала сокращаем 4 6: делим на 2 и числитель, и знаменатель: 4 6 = 2 3 .
Упростить квадратные корни
Если числитель нацело делится на знаменатель, то делите.
Если нет, то упрощайте подкоренные выражения, как и любые другие.
Пример 11
32 делится нацело на 16 , поэтому: 32 16 = 2
Умножить упрощенные множители на упрощенные корни
Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.
Пример 12
2 3 × 2 = 2 2 3
Рационализировать знаменатель (избавиться от корня в знаменателе)
Пример 13
4 3 2 7 . Следует умножить числитель и знаменатель на 7 , чтобы избавиться от корня в знаменателе.
4 3 7 × 7 7 = 4 3 × 7 7 × 7 = 4 21 49 = 4 21 7
Метод 4. Деление на двучлен с квадратным корнем
Алгоритм действий:
Определить, находится ли двучлен (бином) в знаменателе
Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.
Пример 14
1 5 + 2 — в знаменателе присутствует бином, поскольку есть два одночлена.
Найти выражение, сопряженное биному
Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.
Пример 15
5 + 2 и 5 — 2 — сопряженные биномы.
Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе
Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: (a — b) (a + b) = a 2 — b 2
Пример 16
1 5 + 2 = 1 (5 — 2) (5 — 2) (5 + 2) = 5 — 2 (5 2 — (2) 2 = 5 — 2 25 — 2 = 5 — 2 23 .
Из этого следует: 1 5 + 2 = 5 — 2 23 .
Советы:
- Если вы работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь.
- Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
- Никогда (!) не оставляйте корень в знаменателе.
- Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
- В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного.
Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3.
Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5.
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Известно, что знак корня является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Yandex.RTB R-A-339285-1
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
Пример
Пример 1: 18 × 2 = ?
Пример 2: 10 × 5 = ?
Пример
Пример 1: 18 × 2 = 36
Пример 2: 10 × 5 = 50
Пример 3: 3 3 × 9 3 = 27 3
Упростить подкоренные выражения.
Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Пример
Пример 1: 36 = 6 . 36 — квадратный корень из шести (6 × 6 = 36) .
Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .
Метод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
Пример
Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3
Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример
Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20
Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18
Упростить подкоренное выражение.
Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример
Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5
Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
Пример
Необходимо найти НОК показателей для следующего выражения:
Показатели равны 3 и 2 . Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3 , и на 2). Для умножения корней необходим показатель 6 .
Записать каждое выражение с новым показателем:
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.

В выражении 5 3 необходимо умножить 3 на 2 , чтобы получить 6 . А в выражении 2 2 — наоборот, необходимо умножить на 3 , чтобы получить 6 .
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2 , а втором — 2 в степень 3:
2 → 5 6 = 5 2 6 3 → 2 6 = 2 3 6
Возвести в степень выражения и записать результат под знаком корня:
5 2 6 = (5 × 5) 6 = 25 6 2 3 6 = (2 × 2 × 2) 6 = 8 6
Перемножить числа под корнем:
(8 × 25) 6
Записать результат:
(8 × 25) 6 = 200 6
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Правило умножения корней с разными показателями. Формулы корней. Свойства корней. Как умножать корни? Примеры
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать).
Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу.
С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
{2}}}=\sqrt{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Известно, что знак корня является квадратным корнем из некоторого числа.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Yandex.RTB R-A-339285-1
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
Пример
Пример 1: 18 × 2 = ?
Пример 2: 10 × 5 = ?
Пример
Пример 1: 18 × 2 = 36
Пример 2: 10 × 5 = 50
Пример 3: 3 3 × 9 3 = 27 3
Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Пример
Пример 1: 36 = 6 .
36 — квадратный корень из шести (6 × 6 = 36) .
Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .
Метод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
Пример
Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3
Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример
Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20
Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня.
После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример
Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5
Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
Пример
Необходимо найти НОК показателей для следующего выражения:
Показатели равны 3 и 2 . Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3 , и на 2). Для умножения корней необходим показатель 6 .
Записать каждое выражение с новым показателем:
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 5 3 необходимо умножить 3 на 2 , чтобы получить 6 . А в выражении 2 2 — наоборот, необходимо умножить на 3 , чтобы получить 6 .
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2 , а втором — 2 в степень 3:
2 → 5 6 = 5 2 6 3 → 2 6 = 2 3 6
Возвести в степень выражения и записать результат под знаком корня:
5 2 6 = (5 × 5) 6 = 25 6 2 3 6 = (2 × 2 × 2) 6 = 8 6
Перемножить числа под корнем:
(8 × 25) 6
Записать результат:
(8 × 25) 6 = 200 6
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5.
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Гей знакомства в чебоксарах | uhomii
Home > сайты знакомств ростовской области > Гей знакомства в чебоксарахГей знакомства в чебоксарах
такой вид одночленного иррационального выражения мы будем называть каноническим. пример. привести к каноническому виду иррациональное выражение по формулам п. это выражение равно т. _а _ х у а ь г упражнения. привести к каноническому виду одночленные иррациональные выражения а б. вычислить выражение при а . с . сокращение показателей и приведение корней к общему пока п зателю. так как ап уа то из каждого свойства гей знакомства в чебоксарах с рациональными показателями вытекает соответствующее свойство корней. ргг р_ равенство адп ад см. формулу п. переписывается так при а гей знакомства в чебоксарах имеем яар уар. таким образом если подкоренное выражение является степенью положительного числа причем показатель степени имеет общий делитель с показателем корняу то можно сократить эти показатели на общий делитель.
например а б я ачь при ь гей знакомства в чебоксарах из равенства гей знакомства в чебоксарах вытекает что любые два корня с натуральными показателями можно привести к общему показателю. именно пусть даны корни уа и у ъ. тогда по формуле имеем у а у ат и у у ьп разумеется в качестве общего показателя корней можно выбрать не тп а наименьшее общее кратное чисел т и п. упражнения. сократить показатели в выражениях ь с а б с. привести к общему показателю корни и ум. гей знакомства в чебоксарах найти какое из чисел больше или у или у или отметим что формула справедлива лишь гей знакомства в чебоксарах условии а. гей знакомства в чебоксарах в случае когда д то по формуле получаем а пусть теперь а и а а. поэтому при а и равны а при а б то ка а ь а ь а если а у х у. точно так же из формулы п. выводится что при х у у полученные свойства корней формулируются следующим образом а корень п й степени из произведения двух положительных чисел равен произведению корней п й степени из отдельных сомножителей.
б корень п й степени из отношения двух положительных чисел равен отношению корней п й степени из этих чисел. например уа у а гей знакомства в чебоксарах пользуясь свойствами и можно записать произведение нескольких корней с гей знакомства в чебоксарах одного знака корня. если перемножаемые корни имеют гей знакомства в чебоксарах и тот же показатель то для получения произведения надо перемножить их подкоренные выражения и извлечь из полученного произведения корень той гей знакомства в чебоксарах степени. например если же перемножаемые корни имеют различные показатели то и с надо предварительно привести к общему показателю см. стр. . например уш уър гей знакомства в чебоксарах уш г а б. совершенно так же выполняется деление корней. например гей знакомства в чебоксарах вычислить произведение корней б у б. во что обратится выражение ми гей знакомства в чебоксарах гей знакомства в чебоксарах если. во что обратится выражение м при тех же значениях и вынесение алгебраических выражений из под корня и внесение их под корень.
из формулы гей знакомства в чебоксарах вытекает что при а и ь итак если часть подкоренного выражения для корня п й степени является п й степенью некоторого положительного алгебраического выражения то это выражение можно вынести из под корня. следует иметь в виду что формула справедлива лишь при условии а о ъ. если же это условие не выполняется а п четное число то вместо формулы надо писать упражнения. внести под знак корня в выражениях д у пь д в. вынести из под корня в гей знакомства в чебоксарах а б к к л с л упростить выражение рассмотреть отдельно случаи . возведение корня в степень. эта операция основана на фор т гей знакомства в чебоксарах п. . из нее следует что ап атп а п. это гей знакомства в чебоксарах можно записать гей знакомства в чебоксарах таким образом чтобы возвести корень с положительным подкоренным выражением в некоторую степень надо возвести в эту степень подкоренное выражение. например упражнение. упростить выражения извлечение корня из корня.
эта операция также основана на _ формуле п. . из нее следует что ап п и потому у у а у а таким образом при извлечении корня из корня показатели корней перемножаются а подкоренное гей знакомства в чебоксарах остается неизменным. например упражнение.
Like this:
Like Loading…
RelatedДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ УПРАВЛЕНИЕ ЦИФРОВЫХ ОБРАЗОВАТЕЛЬНЫХ ТЕХНОЛОГИЙ. Кафедра «Естественные науки»
ПРИМЕРНЫЕ ВОПРОСЫ (ЗАДАНИЯ)
МАТЕРИАЛЫ для подготовки к тестированию по математике 8 класс Учитель: (Субач М.В., Авершина Л.А., Данилова А.Р.) ТЕМА Знать Уметь 6 Множество рациональных и множество действительных П.
Подробнее16. Рациональные
Алгебраические преобразования
Алгебраические преобразования В процессе преобразования алгебраических выражений переходим от одного алгебраического выражения к другому, более простому или удобному. Такой переход производим с помощью
ПодробнееФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ ;
ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ (для слушателей подготовительных курсов) Тождественные преобразования арифметических выражений ВЫЧИСЛИТЕ (.-.).,9,..,,..,, 9,.. НАЙДИТЕ (.-.).,,.. 9,,,,..,..,,,,..,..,,,.9.,…,,,..,..,
ПодробнееПояснительная записка
Пояснительная записка Цель: Познакомить учащихся со способами решения систем линейных уравнений с двумя переменными. Выработать умение выполнять тождественные преобразования рациональных выражений.
ПодробнееСистематизировать
МАТЕМАТИКА. Квадратные корни
МАТЕМАТИКА Квадратные корни Задание для 8-х классов (006-00 учебный год) 4 Введение Дорогие ребята! Вы получили очередное задание по математике. В этом задании мы знакомим вас с важным математическим понятием
ПодробнееРАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ. 8 класс
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 40 г. ЛИПЕЦКА РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ для учащихся с ограниченными возможностями здоровья по слуху 8 класс
ПодробнееОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
УДК 788:5 ББК 5я7 Г7 Рекомендовано для учащихся 8 классов, соответствует действующей программе по математике для общеобразовательных учебных заведений, утвержденной МИНИСТЕРСТВОМ ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ПодробнееИррациональные уравнения и неравенства 1
Иррациональные уравнения и неравенства Оглавление Свойства корней й степени Свойства корней Свойства степеней с рациональным показателем Примеры 5 Свойства корней -й степени Арифметическим корнем й степени
ПодробнееИррациональные неравенства
Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного
ПодробнееДробно-рациональные выражения
Дробно-рациональные выражения Выражения содержащие деление на выражение с переменными называются дробными (дробно-рациональными) выражениями Дробные выражения при некоторых значениях переменных не имеют
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта основного общего образования по математике — Примерные программы по математике.
ПодробнееОГЛАВЛЕНИЕ. Предисловие… 5
ОГЛАВЛЕНИЕ Предисловие……………………………………… 5 Глава первая Арифметика и алгебра………………………………. 6 1.1. Числа и действия с ними………………………..
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по алгебре для 8 класса соответствует Федеральному компоненту государственного стандарта начального общего, основного общего и среднего (полного) общего образования,
ПодробнееРабочая программа. по алгебре
Муниципальное бюджетное общеобразовательное учреждение Гимназия 4 г. Химки УТВЕРЖДАЮ: Директор МБОУ Гимназия 4 /Н.Н. Козельская / Приказ от 2015 г. Рабочая программа по алгебре (базовый уровень) 8 класс
Подробнее10 класс, Математика (профиль) уч.
год Тема модуля 1 «Корни, степени, логарифмы»
0 класс, Математика (профиль) 0-08 учгод Тема модуля «Корни, степени, логарифмы» Знать Понятия действительного числа, множества чисел, свойства действительных чисел, делимость целых чисел****, свойства
ПодробнееПояснительная записка
Пояснительная записка Основой для рабочей программы по алгебре на 05-06 учебный год в 8а классе МКОУ ГСОШ является авторская программа А.Г. Мордковича для общеобразовательных учреждений (Программы. Математика.
ПодробнееИтоговый тест по алгебре 7 класс
Итоговый тест по алгебре 7 класс Вариант 1 Базовый уровень А1. Найдите значение выражения: 7,8 6,3+7,8 13,7 1)156 2)78 3)-78 4) 146. А2. Решите уравнение: 5у-3,5=2у+5,5 1)5. 2)-3. 3) 3. 4) 4. А3. Упростите
ПодробнееПояснительная записка
Статус документа Пояснительная записка Настоящая рабочая программа по алгебре для 8 класса (углубленный уровень) основной общей общеобразовательной школы составлена на основе федерального компонента государственного
ПодробнееКак пользоваться справочником
3 Уважаемый читатель! В ваших руках современный справочник, который поддержит вас при обучении в 5 11 классах, поможет подготовиться к экзаменам, даст возможность без труда поступить в вуз.
ПодробнееВ справочнике
Пояснительная записка
Пояснительная записка Цели обучения математике. Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.
ПодробнееРАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС
РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС Пояснительная записка Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта основного общего образования по
ПодробнееПояснительная записка
Пояснительная записка Настоящая программа по алгебре для основной общеобразовательной школы 8 класса составлена на основе федерального компонента государственного стандарта основного общего образования
ПодробнееТематическое планирование
Тематическое планирование Тема урока Колво часов Тип урока Характеристика деятельности учащихся или виды учебной деятельности Виды контроля, измерители Требования к уровню подготовки обучающихся Домашнее
ПодробнееУчебник: Алгебра (Дорофеев Г.
В.) гг.
Класс 9.3.1, 9.3.2 (база) Учебник: Алгебра (Дорофеев Г.В.) 2018-2019 гг. Тема модуля: «Уравнения и системы уравнений» Основные теоретические сведения, необходимые для успешного выполнения теста: 1. Понятие
ПодробнееТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени М В ЛОМОНОСОВА МАЛЫЙ МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ Методическая разработка для учащихся 8 и 9 классов заочного отделения МОСКВА
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа по алгебре для 8 класса (углубленное изучение) составлена в соответствии с федеральным компонентом государственного образовательного стандарта, программой по алгебре
ПодробнееСодержание курса Алгебраические дроби
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данная рабочая программа по алгебре для 8 класса составлена в соответствии с федеральным компонентом государственного образовательного стандарта основного общего образования и на
Подробнее8 класс алгебра индивидуальное обучение
8 класс алгебра индивидуальное обучение Государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа 3 «Центр образования» городского округа Октябрьск Самарской
ПодробнееЗубы мудрости
Зубы мудрости (также называемые «третьи моляры») обычно не прорезываются через десны до позднего подросткового возраста, до двадцати лет, а иногда и старше.
Зубы мудрости обычно являются последними зубами, которые прорезываются через десны.
У большинства людей четыре зуба мудрости, хотя у некоторых их нет вообще. Часто в задней части челюсти недостаточно места для того, чтобы зубы мудрости могли легко прорезаться через десны. Если в челюсти недостаточно места для прорезывания зуба мудрости, зуб становится забитым или «вдавленным».
Некоторые ретинированные зубы мудрости остаются скрытыми и не вызывают никаких проблем. Однако другие ретинированные зубы мудрости могут вызвать серьезные проблемы.
Если один или несколько ваших зубов мудрости становятся проблематичными, челюстно-лицевой хирург может порекомендовать их удалить.
Удаление зуба мудрости или зубов мудрости — очень распространенная процедура. Удаление проблемных зубов мудрости обычно следует проводить как можно скорее, чтобы избежать дальнейших проблем.
Как показано на этом рисунке, ретинированный зуб мудрости может находиться в контакте или близко к большому нерву.
Иногда это может привести к осложнениям во время хирургического удаления зуба, как описано далее.
Лечение потенциальной инфекции
Возможно, вашему стоматологу потребуется осторожно очистить зараженную область вокруг зуба. Вам также могут порекомендовать часто полоскать рот теплой соленой водой для полоскания рта. Используйте одну чайную ложку соли на стакан теплой воды. Вода должна быть максимально теплой, но не слишком горячей.
Ваш хирург может также порекомендовать определенное средство для полоскания рта и обезболивающее.
Вашему хирургу может потребоваться прописать антибиотики. Важно сообщить своему хирургу, если у вас когда-либо была аллергическая реакция на какие-либо антибиотики или другие лекарства. Важно пройти полный курс антибиотиков. Если инфицирован нижний зуб мудрости, ситуация может ухудшиться из-за прикусывания десны верхним зубом мудрости. В этой ситуации поможет удаление верхнего зуба мудрости.
Форма согласия
Если вы решите удалить зубы, ваш хирург попросит вас подписать ФОРМУ СОГЛАСИЯ.
Внимательно прочтите его, и если у вас есть какие-либо вопросы, которые вас беспокоят, обратитесь к своему хирургу.
Проблемы, вызванные ретинированными зубами мудрости
Инфекция
Когда ретинированный зуб начинает продавливать десну, вокруг верхней части зуба может начаться инфекция. Инфекция и воспаление могут вызвать боль, отек и тугоподвижность челюсти. Глотание также может быть болезненным. Человек может чувствовать себя в целом плохо. Инфекция также может вызывать неприятный запах изо рта и неприятный привкус во рту.Скученность зубов
Зуб мудрости может сместить соседние зубы с их правильного положения.Боль
Давление зуба мудрости может вызвать боль в соседнем зубе. Боль также может быть вызвана инфекцией вокруг самого зуба мудрости.Киста
Если зуб мудрости не удалить, вокруг зуба может образоваться мешок с жидкостью, называемый «кистой», который может сместить зуб.Киста может разрушить кость и повредить другие зубы и десны.Образование кист вокруг непрорезавшихся зубов является довольно распространенным заболеванием.
Язва
Верхний зуб мудрости может выступать из десны вбок. Это может вызвать язву, когда она трется о внутреннюю часть щеки.Ловушка для еды
Пища может застрять между зубом мудрости и коренным зубом рядом с ним. Это потенциально может вызвать кариес в обоих зубах.Резорбционная полость
Ретенированный зуб мудрости может продолжать давить на соседний коренной зуб.Это может вызвать «резорбционную полость», где зуб мудрости сталкивается с другим коренным зубом. Это часто приводит к серьезному повреждению обоих зубов. Моляры могут инфицироваться или развиться абсцессы. Часто требуется удаление обоих моляров. Полости резорбции встречаются редко.
Решение об удалении зубов
После осмотра вашего рта, челюстей и рентгеновских снимков хирург обсудит с вами диагноз.
Ваш хирург может порекомендовать удаление одного или нескольких зубов мудрости или, возможно, другие варианты лечения.
Раннее удаление зубов мудрости
Как правило, удаление вызывающих беспокойство зубов мудрости в молодом возрасте является нормой. У молодых людей корни зуба сформированы не полностью, а кость, окружающая зуб, более мягкая. Это облегчает удаление зуба и снижает риск повреждения нервов, кости или других зубов.
Ваш хирург может порекомендовать досрочное удаление одного или нескольких зубов мудрости по следующим причинам:
- Недостаточно места для проталкивания зуба.
- Вам требуется ортодонтическая работа, а оставшиеся зубы не должны быть замещены зубами мудрости.
- Зуб начал беспокоить и должен быть удален во избежание боли, инфекции или других проблем.
- По мере развития корня моляра его вовлечение в челюстной нерв может вызвать послеоперационные осложнения.
- Соседние моляры должны быть защищены от ретинированного зуба мудрости.
Ваш стоматологический и медицинский анамнез
Ваш хирург спросит вас о любых проблемах с зубами и общим состоянием здоровья.Некоторые проблемы со здоровьем могут помешать хирургическому вмешательству, анестезии и послеоперационному уходу. Эта информация поможет вашему хирургу спланировать наилучшее лечение. Ваш хирург может порекомендовать анализы крови или другие анализы здоровья в случае определенных состояний, таких как нарушение свертываемости крови.
Лекарства
В помощь хирургу предоставьте список всех лекарств, которые вы принимаете сейчас или принимали в последнее время. Это включает в себя противозачаточные таблетки, препараты для разжижения крови (например, варфарин) и любые другие безрецептурные лекарства, такие как аспирин или лекарства от кашля.
Сообщите своему хирургу, если у вас когда-либо возникала аллергия или плохая реакция на антибиотики или любые другие лекарства.
Беременность
Сообщите своему хирургу, если вы беременны или можете быть беременны.
Это может повлиять на ваши варианты лечения, включая:
- рентгенологическое исследование
- анестезию
- обезболивание
- антибиотики и другие лекарства
- следует ли отложить удаление зуба мудрости. Кровотечение или заболевания крови или клопидогрел, среди прочего
Курение
Важно, чтобы вы бросили курить за две недели до операции.Курение ухудшает заживление и увеличивает риск послеоперационной инфекции.
Рентгенологическое исследование
Ваш хирург должен подготовить рентгеновские снимки вашей челюсти. Фильмы помогут вашему хирургу спланировать лучший способ удаления проблемных зубов мудрости.
Где сделать операцию
Ваш хирург посоветует вам, следует ли удалять зубы мудрости в больнице или в дневном стационаре.
Анестезия
После обсуждения с вашим хирургом будет принято решение о том, требуется ли удаление зуба/зубов мудрости под местной или общей анестезией.
Обсудите варианты с вашим хирургом.
Местная анестезия: Если операция достаточно проста, ваш хирург может предложить местную анестезию с помощью иглы. Местный анестетик обезболит десны и нижнюю часть лица. Затем хирург может удалить зуб.
Внутривенная седация: Некоторым пациентам может помочь введение седативного препарата в вену во время местной анестезии, чтобы уменьшить боль и тревогу.
Общая анестезия: Некоторым хирург может порекомендовать общую анестезию.Общая анестезия проводится анестезиологом-специалистом. Если может потребоваться людям, которые:
- имеют зубы мудрости, которые трудно удалить
- не хотят бодрствовать во время операции
- имеют другие проблемы с зубами мудрости, деснами или челюстями
- нуждаются в нескольких зубах, чтобы быть извлеченным
Современная анестезия безопасна с небольшим риском. Однако у некоторых людей могут быть серьезные реакции на них.
Если у вас когда-либо была реакция на анестетик, сообщите об этом своему хирургу.
Удаление зубов мудрости
Ваш хирург сделает надрез, чтобы открыть десну и удалить зуб мудрости. Возможно, потребуется удалить небольшую часть кости, чтобы хирург мог легко добраться до зуба. Зуб, возможно, придется разделить на сегменты, чтобы его можно было удалить эффективно и безопасно.
Разрез на десне, возможно, придется закрыть швами. Некоторые швы рассасываются через несколько дней. Остальные швы снимет хирург.
ПРИМЕЧАНИЕ. В течение шести (6) часов до операции вам нельзя ничего есть и пить. Если ваша операция будет проводиться утром, вы не можете ничего есть или пить после полуночи накануне вечером. Ваш хирург даст вам полные инструкции и письменную информацию, которую вы сможете взять с собой домой.
После операции
После операции вам нужно будет немного отдохнуть, прежде чем отправиться домой. Ваш хирург будет проверять вас по мере выздоровления.
Когда ваш хирург будет удовлетворен вашим выздоровлением, вас отпустят домой.
Член семьи или друг должен отвезти вас домой после операции. Договоритесь об этом заранее. Вам рекомендуется не водить автомобиль после операции. Если вы находились в больнице, вы вернетесь в свою палату, когда оправитесь от анестезии.
Забота о себе
- Оставайтесь дома после операции.
- Не водите автомобиль, не занимайтесь активными физическими упражнениями и не управляйте механизмами.
- Возможно, вам придется взять несколько выходных на работе, в школе или по другим делам.
- Не употребляйте алкоголь во время приема обезболивающих или антибиотиков.
Обезболивание после операции
Боль может быть незначительной у одних людей и сильнее у других. Ваш хирург пропишет вам обезболивающее. Если вы не уверены в том, какое обезболивающее лекарство вам лучше всего, спросите своего хирурга. Боль обычно начинает уменьшаться после второго дня.
Тем не менее, некоторым людям все еще может потребоваться обезболивание через неделю.Если кажется, что ваша боль не уменьшается с течением времени, сообщите об этом своему хирургу. Может потребоваться дальнейшее обезболивание.
Остановка кровотечения
Вы можете надавить на область кровотечения, аккуратно, но крепко прикусив кусок хлопчатобумажной марли. Давление помогает остановить кровотечение, и образуется тромб. Важно не тревожить область, иначе кровотечение может начаться снова. Десны могут слегка сочиться кровью в течение дня после операции. Любое кровотечение должно остановиться на второй день.Если кровотечение не останавливается, обратитесь к хирургу.
Отек
Отек почти всегда возникает после операции и может варьироваться от незначительного до сильного. Большинству отеков требуется 4-5 дней, чтобы полностью пройти. Отек можно уменьшить, прикладывая к щекам пакеты со льдом.
Последующее наблюдение
Возможно, вам потребуется посетить своего хирурга для последующего наблюдения.
Ваш хирург может захотеть проверить заживление и снять любые швы, если это необходимо.
Возможные осложнения операции
Как и все хирургические вмешательства, удаление зубов мудрости сопряжено с потенциальными рисками, несмотря на самые высокие стандарты хирургической практики.Хотя ваш хирург старается свести к минимуму любые риски, связанные с операцией, иногда могут возникать осложнения, а иногда некоторые из них могут иметь необратимые последствия.
Ваш хирург расскажет обо всех возможных или редких осложнениях операции. Однако важно, чтобы у вас было достаточно информации, чтобы полностью взвесить преимущества и риски, связанные с операцией. У большинства людей не возникает никаких осложнений, но если у вас есть опасения по поводу возможных побочных эффектов, обсудите их со своим хирургом.
Следующие возможные осложнения перечислены для информирования вас, а не для тревоги. Могут быть и другие, не указанные в списке.
Онемение или изменение чувствительности
Ретенированный зуб может располагаться близко к крупным нервам (см.
стр.…….). При удалении зуба нерв может быть ушиблен. Это может вызвать боль, онемение, покалывание и потерю чувствительности в зубах, деснах, щеках, губах, подбородке, языке и вокруг верхней и нижней челюсти. При повреждении язычного нерва существует риск изменения вкусовых ощущений.В некоторых случаях может быть затронута речь.
Если нерв поврежден, он обычно заживает. По мере заживления онемение, покалывание, боль и любая дисфункция исчезнут. Это может занять от четырех до восьми недель. Тем временем держите горячую пищу и напитки подальше от онемевших участков и будьте осторожны, чтобы не прикусить губу или язык.
У некоторых людей полное заживление нерва может занять от шести до восемнадцати месяцев. В редких случаях нерв может не зажить полностью, а онемение или измененная чувствительность могут быть постоянными.Если снижена чувствительность языка, губ или лица, нарушена речь или вкус, это может создать серьезные проблемы для некоторых пациентов, особенно если это влияет на их повседневную работу.
Если это может относиться к вам, сообщите об этом своему хирургу, чтобы обсудить эти риски.
Повреждение нерва, вызывающее боль
В редких случаях поврежденный нерв может плохо заживать, и боль может сохраняться или повторяться без уменьшения. Это может произойти, даже если операция прошла успешно и были предприняты все меры, чтобы избежать повреждения основных нервов.Теперь известно, почему некоторые нервы реагируют таким образом. Боль в этих случаях иногда трудно поддается лечению.
Сухая лунка
После удаления зуба мудрости над костью образуется кровяной сгусток. Этот сгусток важен для правильного заживления и облегчения боли. Если сгусток крови смоется или растворится, обнажится кость. Это называется «сухая розетка». Это приводит к постоянной, пульсирующей боли, которая может продолжаться в течение нескольких дней. Если у вас есть такая боль, обратитесь к хирургу.- Во избежание сухости лунки
- В первый день после операции не полощите рот и не сплевывайте с силой.
Это может ослабить сгусток крови и замедлить заживление.
- После первого дня можно очень осторожно прополоскать рот теплой соленой водой. Аккуратно промывайте каждые четыре часа или чаще, если это необходимо. Это ускорит заживление, уменьшит отек и боль, а также снизит риск инфицирования.
- Не курите после операции.Курение мешает заживлению.
- В течение первого дня после операции не чистите зубы в зоне операции. После первого дня аккуратно расчешите.
- Инфекция
Инфекцию десны или кости обычно лечат антибиотиками. Важно пройти полный курс. Сообщите своему хирургу, если у вас когда-либо была аллергическая реакция на какой-либо антибиотик или другой препарат.- Трудности при открывании рта
Боль или дискомфорт при открывании рта часто возникают после удаления зуба мудрости.Обычно это исчезает в течение нескольких дней после того, как спадет отек.- Лихорадка
После операции температура тела может быть немного выше.Он должен вернуться к норме через 12-24 часа. Повышенная температура, которая держится дольше, может быть признаком инфекции или других проблем. Вам следует обратиться к хирургу.
- Чрезмерное кровотечение (кровоизлияние)
Кровотечение может возникнуть, хотя и редко. Это может быть вызвано чрезмерной физической нагрузкой или рвотой.Его можно остановить, наложив марлю на рану и слегка надавив на марлю на 15 минут. Если сильное кровотечение не прекращается, следует обратиться к хирургу.- Раны на губах
Во время удаления зуба давление или растяжение губы хирургическими инструментами может привести к образованию синяков или небольших ран. Обычно они заживают без проблем. Эти язвы на губах не являются обычным явлением.- Повреждение близлежащего зуба или пломбы
Хотя и редко, но при удалении зуба мудрости зуб или пломба, прилегающие к нему, могут иметь скол или расшатываться.- Рвота
К сожалению, у некоторых людей может быть рвота, когда они оправляются от действия анестетика.- Проблемы с пазухами
Корни верхних зубов мудрости находятся в непосредственной близости от пазух. В некоторых случаях при удалении зуба мудрости может открыться пазуха. Отверстие, как правило, быстро заживает без инфекции. Однако, если развивается инфекция или возникают другие проблемы, может потребоваться дополнительное лечение.- Слабая челюсть
Удаление ретинированного зуба мудрости может привести к временному ослаблению кости челюсти.Хотя это редкость, челюсть может сломаться во время операции или в течение нескольких недель или месяцев после нее, пока она еще заживает. Избегайте контактных видов спорта в течение как минимум четырех недель после операции.Стоимость лечения
Во время консультации вам будет предоставлена смета, в которой перечислены все сборы за полное лечение. Стоимость зависит от объема лечения и количества удаленных зубов. Дополнительные расходы могут быть понесены, если потребуется дополнительное лечение.
Поскольку лечение и результат могут отличаться от того, что было первоначально предложено, окончательный счет может отличаться от первоначальной оценки. Всегда лучше обсудить затраты до лечения.
Поговорите со своим хирургом
Эта информация предназначена для предоставления общего обзора. Это не заменяет консультацию вашего хирурга. Эта информация не содержит всех известных фактов по этой теме. Если вы не уверены в преимуществах и рисках, связанных с удалением зуба мудрости, спросите своего хирурга.
Ваш оральный и челюстно-лицевой хирург прошел специальную подготовку и сможет ответить на любые вопросы или опасения, которые могут возникнуть у вас по поводу вашего состояния, операции или анестезии. Ваш хирург не может гарантировать, что лечение оправдает все ваши ожидания или что лечение не сопряжено с риском. Возможно, вы захотите получить второе мнение от другого орального и челюстно-лицевого хирурга. Эту информацию следует использовать только после консультации с вашим хирургом.
Тревожные расстройства. Симптомы и причины
Обзор
Периодическое беспокойство является нормальной частью жизни.Однако люди с тревожными расстройствами часто испытывают сильное, чрезмерное и постоянное беспокойство и страх по поводу повседневных ситуаций. Часто тревожные расстройства включают повторяющиеся эпизоды внезапных приступов сильной тревоги и страха или ужаса, которые достигают пика в течение нескольких минут (панические атаки).
Эти чувства тревоги и паники мешают повседневной деятельности, их трудно контролировать, они непропорциональны реальной опасности и могут длиться долгое время. Вы можете избегать мест или ситуаций, чтобы предотвратить эти чувства.Симптомы могут начаться в детстве или подростковом возрасте и продолжаться во взрослой жизни.
Примеры тревожных расстройств включают генерализованное тревожное расстройство, социальное тревожное расстройство (социальную фобию), специфические фобии и тревожное расстройство разлуки.
У вас может быть более одного тревожного расстройства. Иногда беспокойство возникает из-за состояния здоровья, которое требует лечения.
Какая бы форма беспокойства у вас ни была, лечение может помочь.
Товары и услуги
Показать больше продуктов Mayo ClinicСимптомы
Общие признаки и симптомы тревоги включают:
- Чувство нервозности, беспокойства или напряжения
- Чувство надвигающейся опасности, паники или обреченности
- Повышенная частота сердечных сокращений
- Учащенное дыхание (гипервентиляция)
- Потливость
- Дрожь
- Чувство слабости или усталости
- Проблемы с концентрацией или мыслями о чем-либо, кроме настоящего беспокойства
- Проблемы со сном
- Проблемы с желудочно-кишечным трактом
- Проблемы с контролем беспокойства
- Стремление избегать вещей, вызывающих тревогу
Существует несколько типов тревожных расстройств:
- Агорафобия (ag-uh-ruh-FOE-be-uh) — это тип тревожного расстройства, при котором вы боитесь и часто избегаете мест или ситуаций, которые могут вызвать у вас панику и заставить вас чувствовать себя в ловушке, беспомощным или смущенным.
- Тревожное расстройство, вызванное заболеванием включает симптомы сильной тревоги или паники, непосредственно вызванные проблемами со здоровьем.
- Генерализованное тревожное расстройство включает постоянную и чрезмерную тревогу и беспокойство по поводу деятельности или событий — даже обычных, рутинных проблем. Беспокойство несоразмерно реальным обстоятельствам, его трудно контролировать, и оно влияет на ваше физическое самочувствие. Это часто происходит вместе с другими тревожными расстройствами или депрессией.
- Паническое расстройство включает повторяющиеся эпизоды внезапных ощущений сильной тревоги и страха или ужаса, которые достигают пика в течение нескольких минут (панические атаки). У вас может быть ощущение надвигающейся гибели, одышка, боль в груди или учащенное сердцебиение или учащенное сердцебиение (учащенное сердцебиение). Эти панические атаки могут привести к беспокойству о том, что они повторятся, или к избеганию ситуаций, в которых они произошли.
- Избирательный мутизм — это постоянная неспособность детей говорить в определенных ситуациях, например в школе, даже когда они могут говорить в других ситуациях, например дома с близкими членами семьи.Это может мешать школе, работе и социальному функционированию.
- Тревожное расстройство, связанное с разлукой — детское расстройство, характеризующееся тревогой, чрезмерной для уровня развития ребенка и связанной с разлукой с родителями или другими лицами, играющими родительские роли.
- Социальное тревожное расстройство (социальная фобия) включает высокий уровень беспокойства, страха и избегания социальных ситуаций из-за чувства смущения, застенчивости и беспокойства по поводу осуждения или негативного отношения со стороны других.
- Специфические фобии характеризуются сильной тревогой, когда вы сталкиваетесь с определенным объектом или ситуацией, и желанием избежать этого.
У некоторых людей фобии провоцируют приступы паники.
- Тревожное расстройство, вызванное психоактивными веществами , характеризуется симптомами сильной тревоги или паники, которые являются прямым результатом злоупотребления наркотиками, приема лекарств, воздействия токсического вещества или отказа от наркотиков.
- Другое уточненное тревожное расстройство и неуточненное тревожное расстройство — это термины, обозначающие тревогу или фобии, которые не соответствуют точным критериям каких-либо других тревожных расстройств, но являются достаточно значительными, чтобы причинять беспокойство и разрушать.
Когда обратиться к врачу
Обратитесь к врачу, если:
- Вы чувствуете, что слишком много беспокоитесь, и это мешает вашей работе, отношениям или другим частям вашей жизни
- Ваш страх, тревога или тревога расстраивают вас и с трудом поддаются контролю
- Вы чувствуете депрессию, у вас есть проблемы с алкоголем или наркотиками или у вас есть другие проблемы с психическим здоровьем наряду с тревогой
- Вы думаете, что ваше беспокойство может быть связано с проблемой физического здоровья
- У вас есть суицидальные мысли или поведение — в этом случае немедленно обратитесь за неотложной помощью
Ваши беспокойства могут не исчезнуть сами по себе, и со временем они могут усугубиться, если вы не обратитесь за помощью.
Обратитесь к врачу или психиатру, прежде чем ваше беспокойство усугубится. Лечить легче, если обратиться за помощью на ранней стадии.
Причины
Причины тревожных расстройств до конца не изучены. Жизненный опыт, такой как травматические события, по-видимому, вызывает тревожные расстройства у людей, которые уже склонны к тревоге. Унаследованные черты также могут быть фактором.
Медицинские причины
У некоторых людей тревога может быть связана с основным заболеванием.В некоторых случаях признаки и симптомы тревоги являются первыми признаками соматического заболевания. Если ваш врач подозревает, что у вашего беспокойства может быть медицинская причина, он или она может назначить анализы для выявления признаков проблемы.
Примеры медицинских проблем, которые могут быть связаны с тревогой, включают:
- Болезнь сердца
- Диабет
- Проблемы с щитовидной железой, такие как гипертиреоз
- Респираторные заболевания, такие как хроническая обструктивная болезнь легких (ХОБЛ) и астма
- Злоупотребление наркотиками или синдром отмены
- Отказ от алкоголя, приема успокаивающих препаратов (бензодиазепинов) или других лекарств
- Хроническая боль или синдром раздраженного кишечника
- Редкие опухоли, вырабатывающие определенные гормоны борьбы или бегства
Иногда беспокойство может быть побочным эффектом некоторых лекарств.
Возможно, ваше беспокойство может быть связано с основным заболеванием, если:
- У вас нет кровных родственников (например, родителей или братьев и сестер) с тревожным расстройством
- В детстве у вас не было тревожного расстройства
- Вы не избегаете определенных вещей или ситуаций из-за беспокойства
- У вас внезапное появление беспокойства, которое кажется не связанным с жизненными событиями, и у вас не было предыдущей истории беспокойства
Факторы риска
Эти факторы могут увеличить риск развития тревожного расстройства:
- Травма. Дети, которые пережили жестокое обращение или травму или стали свидетелями травмирующих событий, в какой-то момент жизни подвергаются более высокому риску развития тревожного расстройства. У взрослых, переживших травматическое событие, также могут развиться тревожные расстройства.
- Стресс из-за болезни. Состояние здоровья или серьезное заболевание могут вызвать серьезное беспокойство по поводу таких проблем, как ваше лечение и ваше будущее.
- Накопление стресса. Крупное событие или нарастание небольших стрессовых жизненных ситуаций могут вызвать чрезмерную тревогу — например, смерть в семье, стресс на работе или постоянная забота о финансах.
- Личность. Люди с определенным типом личности более склонны к тревожным расстройствам, чем другие.
- Другие психические расстройства. Люди с другими психическими расстройствами, такими как депрессия, часто также страдают тревожным расстройством.
- Наличие кровных родственников с тревожным расстройством. Тревожные расстройства могут передаваться по наследству.
- Наркотики или алкоголь. Употребление или злоупотребление наркотиками или алкоголем или абстиненция могут вызвать или усугубить тревогу.
Осложнения
Наличие тревожного расстройства не только заставляет вас беспокоиться. Это также может привести к другим психическим и физическим состояниям или ухудшить их, например:
- Депрессия (которая часто возникает при тревожном расстройстве) или другие психические расстройства
- Злоупотребление психоактивными веществами
- Проблемы со сном (бессонница)
- Проблемы с пищеварением или кишечником
- Головные боли и хроническая боль
- Социальная изоляция
- Проблемы с функционированием в школе или на работе
- Плохое качество жизни
- Самоубийство
Профилактика
Невозможно точно предсказать, что приведет к развитию тревожного расстройства, но вы можете предпринять шаги, чтобы уменьшить влияние симптомов, если вы испытываете тревогу:
- Заранее обратитесь за помощью.
Тревожность, как и многие другие психические расстройства, может быть труднее лечить, если вы будете ждать.
- Будьте активны. Участвуйте в мероприятиях, которые вам нравятся и которые заставляют вас чувствовать себя хорошо. Наслаждайтесь социальным взаимодействием и заботливыми отношениями, которые могут уменьшить ваши заботы.
- Избегайте употребления алкоголя или наркотиков. Употребление алкоголя и наркотиков может вызвать или усугубить тревогу. Если вы зависимы от любого из этих веществ, отказ от курения может вызвать у вас беспокойство. Если вы не можете бросить курить самостоятельно, обратитесь к врачу или найдите группу поддержки, которая вам поможет.
Минимальное разнообразие рациона питания (MDD) | ИНДЕКС Проект
Обзор
Показатель минимального разнообразия рациона питания (MDD) для детей в возрасте 6–23 месяцев — это показатель на уровне популяции, разработанный Всемирной организацией здравоохранения (ВОЗ) для оценки разнообразия рациона питания в рамках практики кормления детей грудного и раннего возраста (КДГРМ) среди детей 6 -23 месяца.
Этот показатель является одним из восьми показателей КДГРВ, разработанных ВОЗ для предоставления простых, достоверных и надежных показателей для оценки практики КДГРГ на уровне населения (ВОЗ, 2008 г.).Другие семь индикаторов: раннее начало грудного вскармливания; исключительно грудное вскармливание до 6 месяцев; продолжение грудного вскармливания в 1 год; введение твердой, полутвердой или мягкой пищи; минимально допустимая диета; минимальная частота приема пищи; и потребление продуктов, богатых железом или обогащенных железом. MDD также является компонентом показателя минимально приемлемого рациона питания (MAD), который является составным показателем.
Способ изготовления
Данные собираются из анкеты, которую задают лицу, осуществляющему уход за ребенком, обычно в рамках модуля КДГРМ.Респондентов просят указать, употреблял ли их ребенок какую-либо пищу за последние 24 часа из каждой из восьми пищевых групп. Восемь пищевых групп, включенных в анкету:
MDD Группы пищевых продуктов
1. Грудное молоко
2.
Зерновые, корнеплоды и клубнеплоды
3.
Бобовые и орехи
4.
Молочные продукты
5.
Мясные продукты
6.
Яйца
7.
Фрукты и овощи, богатые витамином А
8.
Прочие фрукты и овощи
Суммируется общее количество потребляемых пищевых групп. Показатель на уровне населения рассчитывается по следующей формуле:
Для получения дополнительной информации о расчете этого показателя см. руководство ВОЗ по измерению (ВОЗ, 2010 г.).Обратите внимание, что в документе ВОЗ 2010 г. описываются 7 групп пищевых продуктов, однако на основании консультации экспертов в июне 2017 г.
.они были обновлены, чтобы отразить включение грудного молока в качестве 8-й группы пищевых продуктов. Поэтому критерий БДР изменился с 4 из 7 групп на 5 из 8 групп. Это изменение отражено для MDD и MAD в платформе Data4Diets. Более подробную информацию см. в ВОЗ/ЮНИСЕФ, 2017 г.
Использование
Было показано, что разнообразие детского питания положительно связано со средней достаточностью питательных микроэлементов в рационе (FANTA, 2006).Таким образом, MDD может быть полезен для получения общей картины качества питания детей грудного и раннего возраста и соответствующей практики прикорма (FANTA, 2014). В качестве простого и легко интерпретируемого индикатора MDD подходит для определения целей, мониторинга и оценки на уровне населения, а также для установления целей. MDD отражает только режим прикорма, а не статус грудного вскармливания; MAD следует использовать, если целью является измерение как статуса грудного вскармливания, так и прикорма (WHO, 2008).
Сильные и слабые стороны
Одним из преимуществ MDD является то, что его легко собирать, сводить в таблицы и интерпретировать, и он применим в различных социокультурных контекстах.
Его также легко разбить на более мелкие возрастные группы, включая 6–11 месяцев, 12–17 месяцев и 18–23 месяца (ВОЗ, 2008 г.). Однако этот показатель нельзя использовать для сравнения групп населения с разными показателями продолжающегося грудного вскармливания, а также для сравнения одной и той же группы населения с течением времени, если показатели грудного вскармливания изменились (ВОЗ, 2008 г.).
Этот показатель прошел всестороннюю проверку, и было показано, что он связан с достаточностью питательных микроэлементов в рационе во многих странах и контекстах (Arimond et al., 2010; Moursi et al., 2008). Исследования показали, что способность оценок разнообразия рациона питания детей отражать адекватность питательных микроэлементов можно улучшить, либо установив минимальные уровни потребления, либо присвоив группам продуктов разные веса в зависимости от содержания питательных веществ (Gewa et al., 2014).
Источник данных
Индикатор MDD может быть построен, как и другие меры разнообразия рациона питания, из модуля в стиле короткого вопросника частоты употребления пищевых продуктов (FFQ), который вручается опекуну ребенка, обычно как часть модуля IYCF.
Примеры вопросников можно найти в документе ВОЗ (2008 г.) Показатели для оценки практики кормления детей грудного и раннего возраста, который включает: 1) список домохозяйств, 2) модуль начала грудного вскармливания и 3) модуль КДГР. Этот показатель также доступен для многих стран в базе данных по кормлению детей грудного и раннего возраста (ЮНИСЕФ) Международного фонда помощи детям Организации Объединенных Наций (ЮНИСЕФ) и собирается в рамках многих демографических и медицинских обследований (МДИ).
Эпидуральные инъекции стероидов — StatPearls
Непрерывное обучение
Эпидуральные инъекции стероидов используются для обезболивания с 1952 года.При наличии показаний они являются бесценным нехирургическим методом лечения болей в пояснице с иррадиацией в нижние конечности и, реже, болей в шее с иррадиацией в руки. Выполнение эффективная эпидуральная инъекция стероидов требует, чтобы стероиды достигли эпидурального пространства. Успешные эпидуральные инъекции стероидов обеспечивают облегчение боли, позволяя восстановить функцию и вернуться к режиму физиотерапии, когда это показано.
В этом упражнении рассматриваются показания и техника выполнения эффективной эпидуральной инъекции стероидов, а также подчеркивается роль межпрофессиональной команды в лечении пациентов с болью в пояснице.
Цели:
Доступ к бесплатным вопросам с несколькими вариантами ответов по этой теме.
Определите показания для эпидуральных инъекций стероидов.
Опишите подготовку, необходимую для эпидуральных инъекций стероидов.
Объясните возможные осложнения эпидуральных инъекций стероидов.
Объясните, как стратегии межпрофессиональной команды могут оптимизировать координацию помощи и общение, чтобы способствовать правильному и безопасному использованию эпидуральных стероидов при болях в пояснице и улучшать результаты.
Введение
Хроническая боль в пояснице (LBP) и боль в шее являются наиболее распространенной причиной многих лет инвалидности в мире.[1][2][2][2] Существует множество причин, которые могут привести к БНС, включая грыжу диска, фасеточный артрит, дискогенную боль и т.
д. Эпидуральные инъекции стероидов используются для облегчения боли при таких состояниях с 1952 года. хирургическое лечение болей в пояснице с иррадиацией в нижние конечности и, реже, болей в шее с иррадиацией в руки.Процедура включает введение стероидов в эпидуральное пространство для лечения боли дискогенного происхождения. В случае успеха эпидуральные инъекции стероидов облегчат боль, позволяя восстановить функцию и/или вернуться к режиму физиотерапии.[3][4][5][6]
Анатомия и физиология
Спинной и головной мозг покрыты тремя защитными слоями, известными как мозговые оболочки. Самый внутренний слой — это мягкая мозговая оболочка, которая сочленяется непосредственно с поверхностью спинного мозга.Средний слой известен как паутинная оболочка. Наконец, твердая мозговая оболочка является самым внешним и, следовательно, самым прочным защитным слоем спинного мозга. Он отделен от позвонков эпидуральным пространством. Эпидуральное пространство содержит дуральный мешок, кровеносные сосуды, жир, соединительную ткань и спинномозговые нервы.
Содержимое дурального мешка включает спинной мозг (оканчивающийся на уровне L1/L2) и конский хвост. Твердая мозговая оболочка спинного мозга имеет решающее значение для периферической нервной системы, поскольку она создает пути (через оболочки твердой мозговой оболочки), окружая отходящие нервные корешки из спинного мозга.
Позвоночный столб также защищает спинной мозг. Он состоит из 33 костей (позвонков), многие из которых разделены межпозвонковым диском. Сюда входят семь шейных, двенадцать грудных, пять поясничных, пять крестцовых (сросшихся) и четыре копчиковых (сросшихся) позвонка. Корешки спинномозговых нервов выходят из позвоночного столба через два боковых отверстия, называемых межпозвонковыми отверстиями, образованными между двумя смежными позвонками.
Показания
Эпидуральные инъекции стероидов лечат боль, вызванную раздражением и воспалением корешков спинномозговых нервов.Один специфический тип боли, известный как корешковая боль, вызывает иррадиацию вдоль дерматома пораженного спинномозгового нерва.
Многие состояния могут раздражать корешки спинномозговых нервов, что чаще всего проявляется болью в пояснице (пояснице) с иррадиацией в ягодицы или ноги (например, ишиас). Также распространены пациенты с болью в шее (шейке) с иррадиацией в руки.[8][9][10]
Наиболее частой причиной раздражения корешков спинномозговых нервов является патология межпозвоночных дисков. При грыжах межпозвоночных дисков центральная часть диска (студенистое ядро) проталкивает внешний слой (фиброзное кольцо), оказывая давление и «защемляя» соседний корешок спинномозгового нерва.Это давление приводит к боли, слабости и/или онемению в области распространения раздраженного нерва. Точно так же при остеохондрозе разрушение межпозвонковых дисков с течением времени может вызвать коллапс межпозвонкового пространства, что приводит к сдавлению корешков спинномозговых нервов.
Другим распространенным показанием для эпидуральной инъекции стероидов является раздражение нервных корешков, вторичное по отношению к спинальному стенозу.
Спинальный стеноз – это состояние, вызывающее сужение (стеноз) позвоночного канала или каналов отходящих нервных корешков.Спинальный стеноз чаще всего вызывается артритом позвоночных суставов (фасеток) или патологией межпозвонкового диска, как обсуждалось выше.
Другие условия, в которых могут быть указаны в инъекции эпидуральных стероидных инъекций:
неспецифические радикулит
позвоночника кости, влияющие коренные корни спинального нерва
Утолщение лигаментального флавума
постламинэктомии
аспект или нервный корневой кисты с лучевой болью
после герпетической или посттравматической (включая интерпретацию) Neurrgia
спондилолиз
спондилолистез
сколиоз раздражение нервных корешков
В одном из опубликованных систематических обзоров оценивались 70 исследований поясничных эпидуральных инъекций стероидов, доказательства эффективности были хорошими при грыжах поясничного отдела позвоночника, удовлетворительными при спинальном стенозе и плохими при синдроме неудачной операции на позвоночнике.
[11] Другой опубликованный метаанализ показал хорошую эффективность использования эпидуральных инъекций стероидов при спинальном стенозе и поясничной радикулопатии.[12] Кеннеди и др. опубликовали результаты проспективного исследования, показывающие эффективность ЭСИ в лечении поясничной корешковой боли. Несмотря на то, что у пациентов было хорошее облегчение боли, было обнаружено, что облегчение боли было недолгим.[13] Другое исследование, проведенное Singh et al. показали, что двухуровневые трансфораминальные эпидуральные инъекции стероидов обеспечивают лучшее обезболивание по сравнению с одноуровневым TFESI.[14]
Несмотря на убедительные доказательства эффективности эпидуральных инъекций стероидов, продолжительность обезболивания все еще не велика, и пациенты нуждаются в других формах терапии для устойчивого обезболивания.[15][16][1]
Противопоказания
Абсостоящие противопоказания к эпидуральному стероидным инъекциям включают в себя:
Системная инфекция или локальная инфекция на месте инъекции
Дисмер кровотечения или полная антикоагуляция
Значительная аллергическая реакция / гиперчувствительность к контрасту, анестезию, Или Corticostroid
Местные злокачественные данные
Относительные противопоказания к эпидуральному стероидным инъекциям:
Оборудование
Epidural Стероидные инъекции требуют:
флуороскопическое рентгенография C-ARM
Эпидуральные спинальные иглы
Местный анестетик (лидокаин или бупивакаин)
Стероиды (метилпреднизолона ацетат, триамцинолон ацетат, бетаметазона ацетат и фосфат или дексаметазона фосфат)
7 Los шприца сопротивления
Контрастный раствор
Стерильные перчатки и салфетки
Бетадин
Эпидуральная анестезия может быть выполнена только под местной анестезией стероидамиВ любом случае необходимо иметь манжеты для измерения артериального давления, кардиомониторы и пульсоксиметры для мониторинга основных показателей жизнедеятельности.
Персонал
В штат входят врач, обученный эпидуральным инъекциям стероидов, медсестра или ассистент, оператор рентгеноскопии С-дуги и анестезиолог для наблюдения за жизненно важными органами пациента. Весь персонал должен быть обучен ведению потенциальных осложнений процедуры.
Подготовка
Риски и преимущества процедуры следует обсудить с пациентом, и если они согласны, пациент должен подписать письменное согласие.Перед инъекцией необходим тайм-аут для проверки личности пациента и места инъекции. Пациент должен лежать на животе на столе для рентгеноскопии, и после определения места инъекции область должна быть отмечена, обработана бетадином и покрыта стерильной салфеткой.
Техника
Эпидуральные инъекции стероидов можно классифицировать по локализации (шейная, грудная или поясничная) и по пути введения иглы (интерламинарная, трансфораминальная или каудальная). В этом обсуждении мы рассмотрим различные техники интерламинарных (между пластинками), трансфораминальных (через отверстие) и каудальных (через крестец) эпидуральных инъекций стероидов.
[17][18][19]
Интерламинарная эпидуральная инъекция стероидов (срединный доступ)
Когда пациент лежит в подготовленном положении и в положении лежа, интерламинарное пространство между двумя соседними позвонками идентифицируется с помощью переднезадней (AP) проекции на рентгеноскопическом рентгеновском снимке. Затем в кожу и подлежащие ткани вводят местный анестетик (например, лидокаин или бупивакаин). Используя срединный или парамедианный доступ между остистыми отростками, эпидуральную спинальную иглу вводят в предполагаемое место инъекции.От поверхностного к глубокому игла проникает в кожу, подкожную клетчатку, надостную связку (срединный доступ) или околопозвоночные мышцы (парамедианный доступ) и желтую связку. Затем делается боковой вид с помощью рентгеноскопического рентгеновского снимка, чтобы подтвердить положение иглы. Затем иглу продвигают с помощью шприца с потерей сопротивления, наполненного 1 мл воздуха или физиологического раствора. Когда игла проходит через желтую связку и входит в заднее эпидуральное пространство, происходит внезапная потеря сопротивления, что позволяет шприцу ввести минимальное количество воздуха или физиологического раствора в эпидуральное пространство из-за изменения давления.
Затем шприц с потерей сопротивления заменяют шприцем, наполненным контрастным раствором, который затем вводят для подтверждения положения иглы в эпидуральном пространстве. Как только распространение контраста подтверждается в прямой и боковой проекциях, в эпидуральное пространство вводят стероид (например, метилпреднизолон, триамцинолон, бетаметазон или дексаметазон) с местной анестезией или без нее. Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение.
Трансфораминальная эпидуральная инъекция стероидов (латеральный доступ)
Когда пациент лежит в препарированном положении на животе, латеральное отверстие между двумя соседними позвонками идентифицируется с помощью косой проекции на рентгеноскопическом рентгеновском снимке.На этом изображении показана классическая «собака шотландца» — анатомический ориентир, используемый для направления иглы. После определения правильного места инъекции в кожу и подлежащие ткани вводят местный анестетик (например, лидокаин или бупивакаин).
Затем вводят эпидуральную спинальную иглу и направляют ее под ножку верхних позвонков. Боковой вид на рентгеновском снимке получают, чтобы определить глубину введения иглы и предотвратить повреждение нервного корешка. Затем иглу продвигают до тех пор, пока она не достигнет наружного межпозвонкового отверстия.Введение контраста подтверждает положение иглы как в боковой, так и в прямой проекции, показывая эпидуральное распространение. Затем в эпидуральное пространство вводят стероид (например, дексаметазон) с местной анестезией или без нее. Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение.
Каудальная эпидуральная инъекция стероидов
Когда пациент лежит в подготовленном положении и находится в положении лежа, крестцовое отверстие идентифицируется с помощью переднезадней проекции на рентгеноскопическом рентгеновском снимке.После определения правильного места инъекции в кожу и подлежащие ткани вводят местный анестетик (например, лидокаин или бупивакаин).
Затем вводят эпидуральную спинальную иглу и направляют ее через крестцовое отверстие. Боковой вид на рентгеновском снимке получают для определения глубины иглы. Размещение иглы ниже пространства межпозвонкового диска S2-3 снизит риск прокола твердой мозговой оболочки. Введение контраста подтверждает положение иглы как в боковой, так и в прямой проекции, показывая эпидуральное распространение. Затем стероид вводят в эпидуральное пространство.Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение.
Осложнения
Хотя редкие, возможные осложнения включают в себя:
кровотечение
инфекция
1
нервных повреждений
преходящей или верхней конечности онемение и / или покалывание
- Дюральная прокол, вызывающая позиционную головную боль [20]
эпидуральный абсцесс
Переходная задняя или нижняя боль в конечностях
побочные эффекты стероидов (переходные промывки / горячие вспышки, удержание жидкости, увеличение веса
Подавление надпочечников
Паралич (очень редко)
Клиническая значимость
При проведении квалифицированным врачом эпидуральные инъекции стероидов и нога или шея d боль в руке, вызванная несколькими состояниями.
Крайне важно отметить, что эпидуральные инъекции стероидов не обязательно предназначены для лечения боли в спине или шее, вместо этого они предназначены для временного облегчения, чтобы пациент мог вернуться к нормальной деятельности и/или продолжить режим физиотерапии. Ослабление боли после эпидуральных инъекций стероидов может варьироваться от одной недели до одного года, и пациентам может потребоваться либо одна, либо серия инъекций для максимального облегчения.
Улучшение результатов работы медицинских бригад
В то время как широко применяются эпидуральные инъекции стероидов.важно разъяснить пациенту, что ответ не является немедленным, и что эти препараты не у всех облегчают боль.[21] Таким образом, лечащий врач, практикующая медсестра и медсестра-ортопед должны информировать пациента об изменениях образа жизни, таких как регулярные физические упражнения, отказ от курения, поддержание здорового веса и отказ от малоподвижного образа жизни.
Результаты эпидурального введения стероидов хорошие, но непредсказуемые.
Инъекции обычно не излечивают боль в спине, но помогают на некоторое время улучшить качество жизни.[8][22]
Ссылки
- 1.
- Джайн С., Малиновски М., Чопра П., Варшней В., Дир Т.Р. Интратекальная доставка лекарств для лечения боли: последние достижения и будущие разработки. Экспертное заключение Препарат Делив. 2019 авг; 16 (8): 815-822. [PubMed: 31305165]
- 2.
- Аль Халили Ю., Ли Н., Мерфи П.Б. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 8 марта 2021 г. Цервикогенная головная боль. [PubMed: 29939639]
- 3.
- Акутота В., Мерон А.Дж., Сингх Дж.Р., Боимбо С., Лейкер С.Р., Бракке Холман Р., Шридхар Б.В., Фридрих Дж., Салливан В.Дж.Полезность магнитно-резонансной томографии приводит к принятию врачом решения перед начальной спинномозговой инъекцией. Spine J. 2019 Sep;19(9):1455-1462. [PubMed: 31009770]
- 4.
- Голубовский Ю.Л., Момин А., Томпсон Н.Р., Штейнмец М.П. Понимание качества жизни и истории лечения пациентов с синдромом Бертолотти по сравнению с пояснично-крестцовой радикулопатией.
J Нейрохирург позвоночника. 2019 19 апр;: 1-7. [PubMed: 31003219]
- 5.
- Аричи Т., Курчалоглу М., Эйгор С., Уяр М.Трансфораминальная эпидуральная инъекция стероидов и инфраневральный доступ. Агр. 31 апреля 2019 г. (2): 104–106. [PubMed: 30995325]
- 6.
- Ташдемир Б.Б., Айдын О.Н. [Ретроспективное исследование эффективности трансфораминальных передних эпидуральных инъекций стероидов у пациентов с болью в пояснице и влияние интервенционной противоболевой терапии на качество жизни]. Агр. 2019 апр; 31 (2): 93-100. [PubMed: 30995324]
- 7.
- Мэтьюз С., Джейн С. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 11 августа 2021 г.Анатомия, голова и шея, перстневидный хрящ. [PubMed: 30969643]
- 8.
- Элвин М.Д., Мехта В., Халаби Х.А., Любельский Д., Бензел Э.К., Мроз Т.Е. Экономическая эффективность цервикальных эпидуральных стероидных инъекций: 3-месячное экспериментальное исследование. Global Spine J.
9 апреля 2019 г. (2): 143–149. [Бесплатная статья PMC: PMC6448201] [PubMed: 30984492]
- 9.
- Huang R, Meng Z, Cao Y, Yu J, Wang S, Luo C, Yu L, Xu Y, Sun Y, Jiang L. Нехирургическая медицина лечение боли из-за пролапса поясничного диска: сетевой метаанализ.Семин Артрит Реум. 2019 окт; 49 (2): 303-313. [PubMed: 30940466]
- 10.
- Выдра Д., Хайнс А., Клементс Н., Нагпал А., Джулия Дж., Шнайдер Б.Дж., Маус Т.П., Кушман Д.М., Маккормик З.Л. Текущие тенденции в практике визуального контроля во время поясничных и шейных трансфораминальных эпидуральных инъекций стероидов. Боль Мед. 2019 01 ноября; 20 (11): 2327-2329. [PubMed: 30938803]
- 11.
- Manchikanti L, Buenaventura RM, Manchikanti KN, Ruan X, Gupta S, Smith HS, Christo PJ, Ward SP. Эффективность терапевтических поясничных трансфораминальных эпидуральных инъекций стероидов при лечении боли в поясничном отделе позвоночника.Врач боли. 2012 г., май-июнь; 15 (3): E199-245. [PubMed: 22622912]
- 12.
- Манчиканти Л., Кнежевич Н.Н., Босуэлл М.В., Кей А.Д., Хирш Дж.А. Эпидуральные инъекции при поясничной радикулопатии и спинальном стенозе: сравнительный систематический обзор и метаанализ. Врач боли. 2016 март; 19(3):E365-410. [PubMed: 27008296]
- 13.
- Kennedy DJ, Zheng PZ, Smuck M, McCormick ZL, Huynh L, Schneider BJ. Минимум 5-летнее наблюдение после поясничных трансфораминальных эпидуральных инъекций стероидов у пациентов с поясничной корешковой болью из-за грыжи межпозвонкового диска.Spine J. Январь 2018 г.; 18 (1): 29–35. [PubMed: 28962912]
- 14.
- Сингх Дж. Р., Кардозо Э., Кристолиас Г.К. Клиническая эффективность двухуровневых трансфораминальных эпидуральных инъекций стероидов. Премьер-министр Р. 2017 Апрель; 9 (4): 377-382. [PubMed: 27614187]
- 15.
- Дир Т.Р., Гридер Дж.С., Ламер Т.Дж., Папа Дж.Е., Фаловски С., Хантер К.В., Провенцано Д.А., Славин К.В., Руссо М., Караяннопулос А., Шах Дж.М., Харнед М.Е., Хагедорн Дж.
М., Болаш Р.Б., Арле Дж. Э., Капурал Л., Амирдельфан К., Джайн С., Лием Л., Карлсон Д.Д., Малиновски М.Н., Бендель М., Ян А., Айер Р., Валимахомед А., Энтони А., Крейг Дж., Фишман М.А., Аль-Кайси А.А., Кристелис Н., Розенквист Р.В., Леви Р.М., Мехаил Н.Систематический литературный обзор методов нейростимуляции позвоночника для лечения боли. Боль Мед. 2020 ноябрь 07;21(7):1421-1432. [PubMed: 32034422]
- 16.
- Дир Т.Р., Джайн С., Хантер С., Чакраварти К. Нейростимуляция при непреодолимой хронической боли. наук о мозге. 24 января 2019 г.; 9(2) [бесплатная статья PMC: PMC6406470] [PubMed: 30682776]
- 17.
- Хашизуме К., Фудзивара А., Ватанабэ К., Камихара М., Ивасаки С., Ямагами Х. Эпидурограмма между Th2-трансфораминальной эпидуральной инъекцией и Th2/2-парасагиттальной интерламинарной эпидуральной инъекцией при шейной боли в верхних конечностях.Врач боли. 2019 март; 22(2):165-176. [PubMed: 30921982]
- 18.
- Lee JH, Sim KC, Kwon HJ, Kim JW, Lee G, Cho SS, Choi SS, Leem JG.
Эффективность люмбальной эпидуральной инъекции у пациентов с хроническим спинальным стенозом, сопровождающимся избыточными корешками нервов. Медицина (Балтимор). 2019 март;98(9):e14490. [Бесплатная статья PMC: PMC6831256] [PubMed: 30817564]
- 19.
- Прзкора Р., Кински М.П., Фишер С.Р., Бабл С., Хейде С.Е., Василопулос Т., Кайе А.Д., Вольпи Э. Функциональные улучшения с использованием батареи коротких физических характеристик (SPPB) у пожилых людей после эпидуральных инъекций стероидов.Curr Pain Headache Rep. 22 февраля 2019 г .; 23 (2): 14. [Бесплатная статья PMC: PMC6766078] [PubMed: 30796532]
- 20.
- Таббен Р.Е., Джейн С., Мерфи П.Б. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 6 июля 2021 г. Эпидуральная пломбировка кровью. [PubMed: 29493961]
- 21.
- Jani P, Morley HL, Shetty N. Ятрогенная надпочечниковая супрессия после каудальной эпидуральной и фасеточной инъекции. BMJ Case Rep. 21 февраля 2019 г.
; 12(2) [бесплатная статья PMC: PMC6388878] [PubMed: 30796074]
- 22.
- Duszynski B. Позиция Общества по вмешательству на позвоночнике в отношении передовой практики эпидуральных инъекций стероидов в условиях нехватки дексаметазона без консервантов. Боль Мед. 2019 01 июля; 20 (7): 1277-1280. [PubMed: 31034052]
Что это такое, причины, как удалить, предотвратить и лечить
Обзор
Что такое зубной налет?
Зубной налет – это липкая пленка бактерий, которая постоянно образуется на зубах. Бактерии зубного налета вырабатывают кислоты после того, как вы едите или пьете.Эти кислоты могут разрушить зубную эмаль и вызвать кариес и гингивит (заболевание десен).
Зубной налет может также образовываться под деснами на корнях зубов и разрушать кости, поддерживающие зубы. Необработанный зубной налет может превратиться в трудноудаляемый зубной камень. Надлежащая гигиена полости рта, включая ежедневную чистку зубов щеткой и зубной нитью, помогает избавиться от зубного налета.
Насколько распространен зубной налет?
Зубной налет в той или иной степени есть у всех. Если ваши зубы кажутся нечеткими, когда вы проводите по ним языком, это зубной налет.
У кого больше шансов получить зубной налет?
Хотя зубной налет появляется у всех, у вас может образоваться больше зубного налета, чем обычно, если вы:
- Потребляйте много сладких или крахмалистых продуктов или напитков.
- Сухость во рту из-за приема таких лекарств, как антидепрессанты, или таких состояний, как синдром Шегрена.
- Иметь в анамнезе облучение головы/шеи.
- Дым.
Симптомы и причины
Что вызывает зубной налет?
Зубной налет образуется, когда бактерии во рту смешиваются с сладкими или крахмалистыми продуктами, такими как молоко, сок, безалкогольные напитки, хлеб, макаронные изделия и фрукты.Эти бактерии выделяют кислоты, которые расщепляют углеводы в пище и напитках. Если вы не чистите зубы вскоре после еды или питья, комбинация бактерий, кислот и углеводов может смешаться в липкую бесцветную пленку, называемую зубным налетом.
Каковы симптомы зубного налета?
Ощущение нечеткости на зубах является главным признаком наличия зубного налета. Другие показатели включают в себя:
Каковы осложнения зубного налета?
Если вы не чистите зубы щеткой и зубной нитью ежедневно, зубной налет может превратиться в зубной камень.Только профессиональный стоматолог может удалить зубной камень. Зубной налет и зубной камень могут привести к:
Диагностика и тесты
Как диагностируется зубной налет?
Ваш стоматолог или стоматолог-гигиенист использует инструменты во время регулярных стоматологических осмотров, чтобы найти и удалить зубной налет. Налет может вызвать кариес. Вы также можете сделать рентген зубов, чтобы проверить наличие полостей.
Управление и лечение
Как лечить зубной налет?
Хорошая гигиена полости рта, включая регулярную чистку зубов щеткой и зубной нитью, удаляет налет и предотвращает образование зубного камня.
Во время стоматологического осмотра стоматолог соскребает с ваших зубов зубной налет и камень. Ваш провайдер может также порекомендовать:
Профилактика
Как я могу предотвратить зубной налет?
Хороший уход за зубами и деснами является ключом к уменьшению зубного налета. Вы должны:
- Ежедневная нить: Ежедневная чистка зубной нитью или ирригатором для удаления остатков пищи и налета, застрявших между зубами. Исследования показывают, что использование зубной нити перед чисткой зубов удаляет больше налета.
- Чистить два раза в день: Чистить зубы в течение двух минут зубной щеткой с мягкой щетиной (ручной или с электроприводом) и зубной пастой с фтором. Чистите зубы не реже двух раз в день, а лучше после каждого приема пищи.
- Жевательная резинка без сахара: Если вы не можете чистить зубы вскоре после еды или питья, пожуйте жевательную резинку без сахара. Выбирайте тот, который имеет печать Американской стоматологической ассоциации (ADA).
- Выбирайте здоровую пищу: Сократите употребление сладких, крахмалистых продуктов и напитков. Вместо этого выбирайте питательные продукты и закуски, такие как простой йогурт, сыр, сырые овощи или фрукты.
- Обратитесь к стоматологу: Проходите осмотры у стоматолога не реже двух раз в год.
- Используйте жидкость для полоскания рта: Прополощите безрецептурным или отпускаемым по рецепту антисептическим средством для полоскания рта.
Перспективы/прогноз
Каков прогноз (перспективы) для людей с зубным налетом?
Бактерии ротовой полости, вызывающие зубной налет, есть у всех. При правильной гигиене полости рта можно удалить зубной налет и предотвратить серьезные проблемы с зубами.
Поскольку зубной налет может вызывать кариес, зубной камень и заболевания десен, обязательны регулярные осмотры у стоматолога.Если зубной налет и кариес остаются незамеченными и не лечатся, у вас может развиться болезненная инфекция десен или потеря зубов.
Жить с
Когда следует вызвать врача?
Вам следует позвонить своему поставщику медицинских услуг, если вы испытываете:
- Хронический неприятный запах изо рта.
- Отек лица.
- Расшатанный зуб.
- Боль или трудности при жевании.
- Покраснение вокруг или внутри рта.
- Опухание, кровоточивость десен или другие признаки заболевания десен.
- Зубная боль или боль во рту.
- Чувствительность зубов к горячей или холодной пище или напиткам.
Какие вопросы я должен задать своему врачу?
Вы можете спросить своего поставщика медицинских услуг:
- Как лучше всего предотвратить образование зубного налета и избавиться от него?
- Как снизить риск кариеса и заболеваний десен?
- Какие изменения в рационе мне следует внести, чтобы уменьшить количество зубного налета?
- Что я должен искать в зубной щетке, зубной пасте и жидкости для полоскания рта?
- Как часто нужно делать чистку зубов?
- Должен ли я обращать внимание на признаки осложнений?
Записка из клиники Кливленда
Зубной налет — распространенная проблема, которую легко решить: ежедневно чистите зубы зубной нитью и посещайте стоматолога.
Вы также можете использовать антисептические жидкости для полоскания рта, чтобы убить бактерии, вызывающие зубной налет. Если вы позволите пленке налета оставаться на зубах слишком долго, она может затвердеть и превратиться в зубной камень. В конце концов, вы можете заболеть деснами и даже потерять зубы. Вы должны чистить зубы не реже двух раз в год. Спросите своего стоматолога о шагах, которые вы можете предпринять, чтобы уменьшить зубной налет и защитить здоровье полости рта.
Как вычислить квадратный корень
Автор: редакция Indeed
- Руководство по карьере
- Развитие карьеры
- Как вычислить квадратный корень
22 февраля 2021 г.
Понимание того, как решать математические задачи вручную, является важным навыком.Одним из математических понятий, которое иногда используется в бизнес-анализе, является квадратный корень. Вычисление квадратного корня вручную позволяет понять, как работает формула.
В этой статье мы опишем, как используются квадратные корни, и объясним три способа их вычисления вручную.
Связанный: 10 лучших навыков и методов обучения
Квадратный корень использует
Квадратный корень используется для нахождения хвостов нормального распределения, которое представляет собой график, показывающий, где в наборе данных окажется большинство чисел.Они особенно полезны для определения ключевых показателей эффективности (KPI), понимания того, насколько хорошо люди справятся с тестом и насколько вероятно будет результат.
Нормальное распределение основано на стандартных отклонениях или блоках оценок от среднего значения всех оценок. Хвосты нормального распределения обычно представляют собой самые высокие и самые низкие 5% оценок, при этом большинство оценок попадают в одно стандартное отклонение по обе стороны от среднего.
По теме: Важность когнитивных способностей в карьере
Как вычислять квадратный корень вручную
Существует несколько способов вычисления квадратного корня.Решением квадратного корня является число, умноженное само на себя, равное числу под символом квадратного корня, который выглядит как √.
Почти все калькуляторы имеют функцию извлечения квадратного корня, которую вы можете использовать. Вот некоторые способы вы можете рассчитать его вручную:
факторинг квадратами
длинноформенный факторинг
Метод длительного разделения
Факторинг по квадратами
Факторинг квадратного корня означает, что вы нахождение ближайших чисел, которые умножаются вместе.Самые простые квадратные корни — это те, которые непосредственно разлагаются в квадраты, например, √100, а более сложные включают в себя несколько квадратных корней, например, √225. Вот шаги для нахождения квадратного корня с помощью факторинга:
Найдите множители. Факторы — это числа, которые вы умножаете, чтобы найти сумму под символом квадратного корня. Для √100 множители будут √(10 x 10). Множители √225 будут √(25 x 9).
Разделите множители на их собственные квадратные корни.Поскольку оба множителя √100 равны 10, квадратный корень из 100 равен 10.
Для √225 вы должны разделить множители под их собственными знаками квадратного корня, поэтому формула будет √25 x √9.
Решите для отдельных квадратов. Затем вы должны найти квадраты каждого из отдельных факторов. √25 = 5 и √9 = 3. Оставшаяся формула будет выглядеть как 5 x 3.
Завершите решение уравнения. Теперь, когда вы знаете, что такое упрощенные квадраты, вы обнаружите, что 5 x 3 = 15.Таким образом, √225 = 15.
Разложение на множители
Иногда вы не знаете, какие множители квадратного корня являются квадратами. Вы можете разбить квадратный корень на каждый отдельный фактор, а затем решить его. Например, чтобы получить множитель длинной формы √225, выполните следующие шаги:
Найдите множители. Самый очевидный множитель 225 — это пять, поэтому вы должны начать с √225 = √(5 x 45). Вы бы еще больше упростили, найдя множители числа 45: √(5 x 5 x 9). Последний множитель, который вы можете упростить, равен 9, поэтому ваш окончательный форм-фактор будет выглядеть как √(5 x 5 x 3 x 3).
Извлечь повторяющиеся факторы. Когда вы видите одно и то же число дважды в качестве множителя, вы укажете его один раз за пределами символа квадратного корня. В этом случае у нас есть две пятерки и две тройки, поэтому уравнение будет выглядеть как 5 x 3.
Решите оставшееся уравнение. Последним шагом является завершение решения уравнения. В этом случае 5 x 3 = 15.
Метод длинного деления
Бывают случаи, когда вы не можете сразу распознать факторы.Метод длинного деления позволяет найти квадратный корень без оценки. Для этого метода мы найдем √361. Вот шаги к методу длинного деления:
Разделите основание квадратного корня на пары. Начиная справа, сгруппируйте число в пары. В нашем примере 361 будет 3 61.
Найдите самый большой квадрат, который делится на первое число или пару. Это даст вам первое число в вашем ответе. Первая цифра слева — 3.Самый высокий квадрат, который входит в него, равен единице, потому что 1 x 1 = 1, а 2 x 2 = 4.

Вычтите квадрат из первого числа или пары. Вычитание квадрата из первого числа даст вам остаток, который будет включен в следующий шаг. В этом примере 3 — 1 = 2.
Опустите следующую пару. Следующее число, с которым вы будете работать, будет комбинацией вычитаемого квадрата и следующей пары. В этом случае они составили бы трехзначное число.Когда вы уменьшите 61, число, которое вы будете использовать для нахождения следующей цифры квадратного корня, будет 261.
Умножьте первую цифру квадрата на два. Это будет первая цифра множителя для нахождения второй цифры квадратного корня. В примере первая цифра квадратного корня равна единице. 1 x 2 = 2.
Составьте уравнение следующего фактора. Уравнение для следующего шага основано на цифре из пятого шага и числе из четвертого шага.Первым множителем будет двузначное число, где первая цифра — число из пятого шага. Уравнение будет иметь вид 2_ x _.
Найдите число, которое заполняет пробелы.
Это число будет следующей цифрой в решении для √361. Число, которое заполнит пробелы, будет тем же, и это будет самая старшая цифра, где множители меньше или равны числу на четвертом шаге. В этом примере номер цели равен 261. Мы начнем с 9, поэтому уравнение будет выглядеть так: 29 x 9 = 261.
Поместите число рядом с первой цифрой. В этом примере квадрат равен 19.
Plants & Wildlife-Plants-Lower Plants
Это может звучать предвзято, но «низшие» на самом деле относятся к организмам, которые развивались ниже или раньше на эволюционной лестнице, чем разнотравье, травы и деревья. Они были одними из первых организмов, которые закрепились на камнях и почве, что помогло ограничить эрозию. Они также были одними из первых, кто начал генерировать энергию посредством фотосинтеза и перерабатывать питательные вещества в почву для использования другими организмами.Эти основные процессы в конечном итоге создали условия, позволившие развиваться и процветать более сложным растениям.
Общее определение «низших» варьируется от источника к источнику, но для наших целей оно включает папоротники и их союзники, мхи, печеночники и роголистники, водоросли, грибы и лишайники.
Папоротники и союзники папоротников
Подобно разнотравью, травам и деревьям, папоротники являются «сосудистыми» растениями. У них есть специальные ткани, которые транспортируют жидкости и питательные вещества внутрь.У них также есть настоящая корневая система, листья и стебли. Однако папоротники отличаются от большинства растений тем, что не дают цветов и семян. Вместо этого они используют споры для размножения.
Споры папоротника отличаются от семян. Они не хранят столько питательных веществ, как семена, и не имеют защитной оболочки. Чтобы компенсировать это, папоротники производят большое количество спор, чтобы гарантировать, что некоторые из них выживут до прорастания. Кроме того, спора содержит все необходимое, чтобы превратиться в «спорофит» и, в конечном итоге, в зрелый папоротник.
В отличие от семени, ему не нужно опыляться другой частью папоротника, прежде чем оно достигнет этой стадии.
Родственники папоротников, такие как иголки, хвощи (также называемые камышом) и плауны, похожи на папоротники, но имеют достаточно генетических различий, поэтому экологи поместили их в отдельные отделы растений.
Изображение Доменико Д’Алессандро
Мхи, печеночники и роголистники
Мхи, печеночники и роголистники вместе называются «мохообразными».Мохообразные — несосудистые растения: у них нет специальных тканей — тканей, которые ботаники называют «ксилема» и «флоэма» — для внутреннего транспорта жидкостей и питательных веществ. Кроме того, мохообразные не дают цветков и семян. Вместо этого, как и папоротники, для размножения они используют споры.
Из мохообразных наиболее распространены мхи. Экологи и волонтеры Forest Preserve District обнаружили 225 особей в округе Дюпейдж в различных местах: от сухих поверхностей, деревьев и скал до подводных ниш.
Некоторые растут почти везде, а другие обитают только в определенных экосистемах.
Мхи обычно представляют собой мягкие растения, растущие группами или матами. Как и другие растения, они производят хлорофилл и подвергаются фотосинтезу, но не имеют настоящих корней. Вместо этого у них есть многоклеточные корневидные придатки, называемые «ризоидами», которые закрепляют растения и поглощают воду и минералы. Поскольку ризоиды менее эффективны, чем корни, мхи обычно предпочитают влажные места с низким освещением. Когда они высыхают, они могут впадать в спячку, втягивая влагу и питательные вещества из зеленой части растения обратно в ризоиды, из-за чего их листовидные структуры скручиваются.Когда влажные условия возвращаются, они оживают, становятся зелеными и растут. Их споры растут в клювовидных капсулах и обычно разносятся ветром. Из-за острой чувствительности мхов к загрязнениям они являются потенциальными индикаторами здоровья природных территорий.
Как и мхи, печеночники производят споры и живут в тенистых, влажных местах обитания, но они не так сложны в биологическом отношении, как мхи.
Хотя это не всегда так, отсутствие четко дифференцированных стеблевых и листовых структур, вероятно, означает, что растение является печеночником, а не мхом.Печенкообразные листообразные структуры на некоторых печеночниках дали этому подразделению растений его общее название. В Иллинойсе насчитывается 118 видов печеночников, но только около 12 были замечены в округе Дю Пейдж.
Третий отдел мохообразных, роголистники, довольно редко встречается в Иллинойсе; экологи зафиксировали только три вида в штате и только один в районе Чикаго. Роголистники напоминают печеночники, но, среди прочих отличий, производят свои споры на длинных роговидных структурах, которые растут от основания растений.Эти структуры дают этому подразделению растений его общее название.
Водоросли
Водоросли представляют собой большую группу обычно водных растений. Как и мохообразные, водоросли не имеют сосудов: у них отсутствуют ткани ксилемы и флоэмы, которые транспортируют жидкости и питательные вещества внутрь.
У них нет листьев, корней или цветков, а также ризоидов или листовидных структур, как у некоторых несосудистых растений. Однако водоросли используют хлорофилл для преобразования солнечного света в энергию. Их размер варьируется от одноклеточных организмов до более крупных и сложных, и экологи Лесного заповедника задокументировали более 40 видов в округе Дюпейдж.
Грибы
Хотя грибы представлены в этом разделе для простоты, технически они не являются растениями. Подобно растениям, животным и бактериям, грибы составляют свою собственную группу родственных организмов, называемую «царством». Экологи выявили более 1000 видов грибов в районе Чикаго.
Грибы, к которым относятся плесени, дрожжи и грибы, в первую очередь отличаются от растений тем, что у них разный клеточный состав и разные предки.Грибы также не имеют корней, листьев, цветов или стеблей и не производят хлорофилл, который некоторые растения используют для преобразования солнечного света в энергию.
Вместо этого грибы получают питательные вещества из живых или мертвых тканей растений и животных, в основном из разлагающихся веществ. Основное тело гриба, «мицелий», выделяет ферменты, которые гриб использует для переваривания окружающей среды. Грибы играют важную роль в окружающей среде, потому что они разлагают органические вещества и перерабатывают питательные вещества.
Лишайники
Лишайник на самом деле состоит из двух разных организмов: гриба и либо водоросли, либо цианобактерии.Две части живут в симбиотических отношениях, выживание каждой из которых зависит от конкретного ресурса другой. Водоросли или бактерии производят пищу посредством фотосинтеза. Это питает грибок, который, в свою очередь, составляет основную часть тела лишайника. Два организма создают «таллом», уникальное тело, не похожее ни на один отдельный вид.
Лишайники не имеют корней и не нуждаются в постоянной подаче воды. Это дает им возможность колонизировать места, недоступные более развитым растениям, такие как голые скалы, бесплодная земля, размытая почва и искусственные сооружения.




 С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм. \\ \end{align}\]
\\ \end{align}\] {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] {2}}}=\sqrt{75}. \end{align}\]
{2}}}=\sqrt{75}. \end{align}\]
 Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.
Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.
 Если нет, то упрощайте подкоренные выражения, как и любые другие.
Если нет, то упрощайте подкоренные выражения, как и любые другие.

 Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да… Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей: Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
 Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб: Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
 Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени. С остальными начнём по порядку.
С остальными начнём по порядку. \\ \end{align}\]
\\ \end{align}\]
 {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\] {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\] {2}}}=\sqrt{75}. \end{align}\]
{2}}}=\sqrt{75}. \end{align}\] д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров. 36 — квадратный корень из шести (6 × 6 = 36) .
36 — квадратный корень из шести (6 × 6 = 36) . После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:

 Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
 например а б я ачь при ь гей знакомства в чебоксарах из равенства гей знакомства в чебоксарах вытекает что любые два корня с натуральными показателями можно привести к общему показателю. именно пусть даны корни уа и у ъ. тогда по формуле имеем у а у ат и у у ьп разумеется в качестве общего показателя корней можно выбрать не тп а наименьшее общее кратное чисел т и п. упражнения. сократить показатели в выражениях ь с а б с. привести к общему показателю корни и ум. гей знакомства в чебоксарах найти какое из чисел больше или у или у или отметим что формула справедлива лишь гей знакомства в чебоксарах условии а. гей знакомства в чебоксарах в случае когда д то по формуле получаем а пусть теперь а и а а. поэтому при а и равны а при а б то ка а ь а ь а если а у х у. точно так же из формулы п. выводится что при х у у полученные свойства корней формулируются следующим образом а корень п й степени из произведения двух положительных чисел равен произведению корней п й степени из отдельных сомножителей.
например а б я ачь при ь гей знакомства в чебоксарах из равенства гей знакомства в чебоксарах вытекает что любые два корня с натуральными показателями можно привести к общему показателю. именно пусть даны корни уа и у ъ. тогда по формуле имеем у а у ат и у у ьп разумеется в качестве общего показателя корней можно выбрать не тп а наименьшее общее кратное чисел т и п. упражнения. сократить показатели в выражениях ь с а б с. привести к общему показателю корни и ум. гей знакомства в чебоксарах найти какое из чисел больше или у или у или отметим что формула справедлива лишь гей знакомства в чебоксарах условии а. гей знакомства в чебоксарах в случае когда д то по формуле получаем а пусть теперь а и а а. поэтому при а и равны а при а б то ка а ь а ь а если а у х у. точно так же из формулы п. выводится что при х у у полученные свойства корней формулируются следующим образом а корень п й степени из произведения двух положительных чисел равен произведению корней п й степени из отдельных сомножителей. б корень п й степени из отношения двух положительных чисел равен отношению корней п й степени из этих чисел. например уа у а гей знакомства в чебоксарах пользуясь свойствами и можно записать произведение нескольких корней с гей знакомства в чебоксарах одного знака корня. если перемножаемые корни имеют гей знакомства в чебоксарах и тот же показатель то для получения произведения надо перемножить их подкоренные выражения и извлечь из полученного произведения корень той гей знакомства в чебоксарах степени. например если же перемножаемые корни имеют различные показатели то и с надо предварительно привести к общему показателю см. стр. . например уш уър гей знакомства в чебоксарах уш г а б. совершенно так же выполняется деление корней. например гей знакомства в чебоксарах вычислить произведение корней б у б. во что обратится выражение ми гей знакомства в чебоксарах гей знакомства в чебоксарах если. во что обратится выражение м при тех же значениях и вынесение алгебраических выражений из под корня и внесение их под корень.
б корень п й степени из отношения двух положительных чисел равен отношению корней п й степени из этих чисел. например уа у а гей знакомства в чебоксарах пользуясь свойствами и можно записать произведение нескольких корней с гей знакомства в чебоксарах одного знака корня. если перемножаемые корни имеют гей знакомства в чебоксарах и тот же показатель то для получения произведения надо перемножить их подкоренные выражения и извлечь из полученного произведения корень той гей знакомства в чебоксарах степени. например если же перемножаемые корни имеют различные показатели то и с надо предварительно привести к общему показателю см. стр. . например уш уър гей знакомства в чебоксарах уш г а б. совершенно так же выполняется деление корней. например гей знакомства в чебоксарах вычислить произведение корней б у б. во что обратится выражение ми гей знакомства в чебоксарах гей знакомства в чебоксарах если. во что обратится выражение м при тех же значениях и вынесение алгебраических выражений из под корня и внесение их под корень. из формулы гей знакомства в чебоксарах вытекает что при а и ь итак если часть подкоренного выражения для корня п й степени является п й степенью некоторого положительного алгебраического выражения то это выражение можно вынести из под корня. следует иметь в виду что формула справедлива лишь при условии а о ъ. если же это условие не выполняется а п четное число то вместо формулы надо писать упражнения. внести под знак корня в выражениях д у пь д в. вынести из под корня в гей знакомства в чебоксарах а б к к л с л упростить выражение рассмотреть отдельно случаи . возведение корня в степень. эта операция основана на фор т гей знакомства в чебоксарах п. . из нее следует что ап атп а п. это гей знакомства в чебоксарах можно записать гей знакомства в чебоксарах таким образом чтобы возвести корень с положительным подкоренным выражением в некоторую степень надо возвести в эту степень подкоренное выражение. например упражнение. упростить выражения извлечение корня из корня.
из формулы гей знакомства в чебоксарах вытекает что при а и ь итак если часть подкоренного выражения для корня п й степени является п й степенью некоторого положительного алгебраического выражения то это выражение можно вынести из под корня. следует иметь в виду что формула справедлива лишь при условии а о ъ. если же это условие не выполняется а п четное число то вместо формулы надо писать упражнения. внести под знак корня в выражениях д у пь д в. вынести из под корня в гей знакомства в чебоксарах а б к к л с л упростить выражение рассмотреть отдельно случаи . возведение корня в степень. эта операция основана на фор т гей знакомства в чебоксарах п. . из нее следует что ап атп а п. это гей знакомства в чебоксарах можно записать гей знакомства в чебоксарах таким образом чтобы возвести корень с положительным подкоренным выражением в некоторую степень надо возвести в эту степень подкоренное выражение. например упражнение. упростить выражения извлечение корня из корня. эта операция также основана на _ формуле п. . из нее следует что ап п и потому у у а у а таким образом при извлечении корня из корня показатели корней перемножаются а подкоренное гей знакомства в чебоксарах остается неизменным. например упражнение.
эта операция также основана на _ формуле п. . из нее следует что ап п и потому у у а у а таким образом при извлечении корня из корня показатели корней перемножаются а подкоренное гей знакомства в чебоксарах остается неизменным. например упражнение. 16. Рациональные
16. Рациональные Систематизировать
Систематизировать
 год Тема модуля 1 «Корни, степени, логарифмы»
год Тема модуля 1 «Корни, степени, логарифмы» В справочнике
В справочнике В.) гг.
В.) гг. Зубы мудрости обычно являются последними зубами, которые прорезываются через десны.
Зубы мудрости обычно являются последними зубами, которые прорезываются через десны. Иногда это может привести к осложнениям во время хирургического удаления зуба, как описано далее.
Иногда это может привести к осложнениям во время хирургического удаления зуба, как описано далее. Внимательно прочтите его, и если у вас есть какие-либо вопросы, которые вас беспокоят, обратитесь к своему хирургу.
Внимательно прочтите его, и если у вас есть какие-либо вопросы, которые вас беспокоят, обратитесь к своему хирургу. Киста может разрушить кость и повредить другие зубы и десны.Образование кист вокруг непрорезавшихся зубов является довольно распространенным заболеванием.
Киста может разрушить кость и повредить другие зубы и десны.Образование кист вокруг непрорезавшихся зубов является довольно распространенным заболеванием. Ваш хирург может порекомендовать удаление одного или нескольких зубов мудрости или, возможно, другие варианты лечения.
Ваш хирург может порекомендовать удаление одного или нескольких зубов мудрости или, возможно, другие варианты лечения.
 Это может повлиять на ваши варианты лечения, включая:
Это может повлиять на ваши варианты лечения, включая: Обсудите варианты с вашим хирургом.
Обсудите варианты с вашим хирургом. Если у вас когда-либо была реакция на анестетик, сообщите об этом своему хирургу.
Если у вас когда-либо была реакция на анестетик, сообщите об этом своему хирургу. Когда ваш хирург будет удовлетворен вашим выздоровлением, вас отпустят домой.
Когда ваш хирург будет удовлетворен вашим выздоровлением, вас отпустят домой. Тем не менее, некоторым людям все еще может потребоваться обезболивание через неделю.Если кажется, что ваша боль не уменьшается с течением времени, сообщите об этом своему хирургу. Может потребоваться дальнейшее обезболивание.
Тем не менее, некоторым людям все еще может потребоваться обезболивание через неделю.Если кажется, что ваша боль не уменьшается с течением времени, сообщите об этом своему хирургу. Может потребоваться дальнейшее обезболивание. Ваш хирург может захотеть проверить заживление и снять любые швы, если это необходимо.
Ваш хирург может захотеть проверить заживление и снять любые швы, если это необходимо. стр.…….). При удалении зуба нерв может быть ушиблен. Это может вызвать боль, онемение, покалывание и потерю чувствительности в зубах, деснах, щеках, губах, подбородке, языке и вокруг верхней и нижней челюсти. При повреждении язычного нерва существует риск изменения вкусовых ощущений.В некоторых случаях может быть затронута речь.
стр.…….). При удалении зуба нерв может быть ушиблен. Это может вызвать боль, онемение, покалывание и потерю чувствительности в зубах, деснах, щеках, губах, подбородке, языке и вокруг верхней и нижней челюсти. При повреждении язычного нерва существует риск изменения вкусовых ощущений.В некоторых случаях может быть затронута речь. Если это может относиться к вам, сообщите об этом своему хирургу, чтобы обсудить эти риски.
Если это может относиться к вам, сообщите об этом своему хирургу, чтобы обсудить эти риски. Это может ослабить сгусток крови и замедлить заживление.
Это может ослабить сгусток крови и замедлить заживление. Он должен вернуться к норме через 12-24 часа. Повышенная температура, которая держится дольше, может быть признаком инфекции или других проблем. Вам следует обратиться к хирургу.
Он должен вернуться к норме через 12-24 часа. Повышенная температура, которая держится дольше, может быть признаком инфекции или других проблем. Вам следует обратиться к хирургу.
 Поскольку лечение и результат могут отличаться от того, что было первоначально предложено, окончательный счет может отличаться от первоначальной оценки. Всегда лучше обсудить затраты до лечения.
Поскольку лечение и результат могут отличаться от того, что было первоначально предложено, окончательный счет может отличаться от первоначальной оценки. Всегда лучше обсудить затраты до лечения.
 У вас может быть более одного тревожного расстройства. Иногда беспокойство возникает из-за состояния здоровья, которое требует лечения.
У вас может быть более одного тревожного расстройства. Иногда беспокойство возникает из-за состояния здоровья, которое требует лечения.

 У некоторых людей фобии провоцируют приступы паники.
У некоторых людей фобии провоцируют приступы паники. Обратитесь к врачу или психиатру, прежде чем ваше беспокойство усугубится. Лечить легче, если обратиться за помощью на ранней стадии.
Обратитесь к врачу или психиатру, прежде чем ваше беспокойство усугубится. Лечить легче, если обратиться за помощью на ранней стадии.

 Тревожность, как и многие другие психические расстройства, может быть труднее лечить, если вы будете ждать.
Тревожность, как и многие другие психические расстройства, может быть труднее лечить, если вы будете ждать. Этот показатель является одним из восьми показателей КДГРВ, разработанных ВОЗ для предоставления простых, достоверных и надежных показателей для оценки практики КДГРГ на уровне населения (ВОЗ, 2008 г.).Другие семь индикаторов: раннее начало грудного вскармливания; исключительно грудное вскармливание до 6 месяцев; продолжение грудного вскармливания в 1 год; введение твердой, полутвердой или мягкой пищи; минимально допустимая диета; минимальная частота приема пищи; и потребление продуктов, богатых железом или обогащенных железом. MDD также является компонентом показателя минимально приемлемого рациона питания (MAD), который является составным показателем.
Этот показатель является одним из восьми показателей КДГРВ, разработанных ВОЗ для предоставления простых, достоверных и надежных показателей для оценки практики КДГРГ на уровне населения (ВОЗ, 2008 г.).Другие семь индикаторов: раннее начало грудного вскармливания; исключительно грудное вскармливание до 6 месяцев; продолжение грудного вскармливания в 1 год; введение твердой, полутвердой или мягкой пищи; минимально допустимая диета; минимальная частота приема пищи; и потребление продуктов, богатых железом или обогащенных железом. MDD также является компонентом показателя минимально приемлемого рациона питания (MAD), который является составным показателем.
 они были обновлены, чтобы отразить включение грудного молока в качестве 8-й группы пищевых продуктов. Поэтому критерий БДР изменился с 4 из 7 групп на 5 из 8 групп. Это изменение отражено для MDD и MAD в платформе Data4Diets. Более подробную информацию см. в ВОЗ/ЮНИСЕФ, 2017 г.
они были обновлены, чтобы отразить включение грудного молока в качестве 8-й группы пищевых продуктов. Поэтому критерий БДР изменился с 4 из 7 групп на 5 из 8 групп. Это изменение отражено для MDD и MAD в платформе Data4Diets. Более подробную информацию см. в ВОЗ/ЮНИСЕФ, 2017 г. Его также легко разбить на более мелкие возрастные группы, включая 6–11 месяцев, 12–17 месяцев и 18–23 месяца (ВОЗ, 2008 г.). Однако этот показатель нельзя использовать для сравнения групп населения с разными показателями продолжающегося грудного вскармливания, а также для сравнения одной и той же группы населения с течением времени, если показатели грудного вскармливания изменились (ВОЗ, 2008 г.).
Его также легко разбить на более мелкие возрастные группы, включая 6–11 месяцев, 12–17 месяцев и 18–23 месяца (ВОЗ, 2008 г.). Однако этот показатель нельзя использовать для сравнения групп населения с разными показателями продолжающегося грудного вскармливания, а также для сравнения одной и той же группы населения с течением времени, если показатели грудного вскармливания изменились (ВОЗ, 2008 г.). Примеры вопросников можно найти в документе ВОЗ (2008 г.) Показатели для оценки практики кормления детей грудного и раннего возраста, который включает: 1) список домохозяйств, 2) модуль начала грудного вскармливания и 3) модуль КДГР. Этот показатель также доступен для многих стран в базе данных по кормлению детей грудного и раннего возраста (ЮНИСЕФ) Международного фонда помощи детям Организации Объединенных Наций (ЮНИСЕФ) и собирается в рамках многих демографических и медицинских обследований (МДИ).
Примеры вопросников можно найти в документе ВОЗ (2008 г.) Показатели для оценки практики кормления детей грудного и раннего возраста, который включает: 1) список домохозяйств, 2) модуль начала грудного вскармливания и 3) модуль КДГР. Этот показатель также доступен для многих стран в базе данных по кормлению детей грудного и раннего возраста (ЮНИСЕФ) Международного фонда помощи детям Организации Объединенных Наций (ЮНИСЕФ) и собирается в рамках многих демографических и медицинских обследований (МДИ). В этом упражнении рассматриваются показания и техника выполнения эффективной эпидуральной инъекции стероидов, а также подчеркивается роль межпрофессиональной команды в лечении пациентов с болью в пояснице.
В этом упражнении рассматриваются показания и техника выполнения эффективной эпидуральной инъекции стероидов, а также подчеркивается роль межпрофессиональной команды в лечении пациентов с болью в пояснице. д. Эпидуральные инъекции стероидов используются для облегчения боли при таких состояниях с 1952 года. хирургическое лечение болей в пояснице с иррадиацией в нижние конечности и, реже, болей в шее с иррадиацией в руки.Процедура включает введение стероидов в эпидуральное пространство для лечения боли дискогенного происхождения. В случае успеха эпидуральные инъекции стероидов облегчат боль, позволяя восстановить функцию и/или вернуться к режиму физиотерапии.[3][4][5][6]
д. Эпидуральные инъекции стероидов используются для облегчения боли при таких состояниях с 1952 года. хирургическое лечение болей в пояснице с иррадиацией в нижние конечности и, реже, болей в шее с иррадиацией в руки.Процедура включает введение стероидов в эпидуральное пространство для лечения боли дискогенного происхождения. В случае успеха эпидуральные инъекции стероидов облегчат боль, позволяя восстановить функцию и/или вернуться к режиму физиотерапии.[3][4][5][6] Содержимое дурального мешка включает спинной мозг (оканчивающийся на уровне L1/L2) и конский хвост. Твердая мозговая оболочка спинного мозга имеет решающее значение для периферической нервной системы, поскольку она создает пути (через оболочки твердой мозговой оболочки), окружая отходящие нервные корешки из спинного мозга.
Содержимое дурального мешка включает спинной мозг (оканчивающийся на уровне L1/L2) и конский хвост. Твердая мозговая оболочка спинного мозга имеет решающее значение для периферической нервной системы, поскольку она создает пути (через оболочки твердой мозговой оболочки), окружая отходящие нервные корешки из спинного мозга. Многие состояния могут раздражать корешки спинномозговых нервов, что чаще всего проявляется болью в пояснице (пояснице) с иррадиацией в ягодицы или ноги (например, ишиас). Также распространены пациенты с болью в шее (шейке) с иррадиацией в руки.[8][9][10]
Многие состояния могут раздражать корешки спинномозговых нервов, что чаще всего проявляется болью в пояснице (пояснице) с иррадиацией в ягодицы или ноги (например, ишиас). Также распространены пациенты с болью в шее (шейке) с иррадиацией в руки.[8][9][10] Спинальный стеноз – это состояние, вызывающее сужение (стеноз) позвоночного канала или каналов отходящих нервных корешков.Спинальный стеноз чаще всего вызывается артритом позвоночных суставов (фасеток) или патологией межпозвонкового диска, как обсуждалось выше.
Спинальный стеноз – это состояние, вызывающее сужение (стеноз) позвоночного канала или каналов отходящих нервных корешков.Спинальный стеноз чаще всего вызывается артритом позвоночных суставов (фасеток) или патологией межпозвонкового диска, как обсуждалось выше. [11] Другой опубликованный метаанализ показал хорошую эффективность использования эпидуральных инъекций стероидов при спинальном стенозе и поясничной радикулопатии.[12] Кеннеди и др. опубликовали результаты проспективного исследования, показывающие эффективность ЭСИ в лечении поясничной корешковой боли. Несмотря на то, что у пациентов было хорошее облегчение боли, было обнаружено, что облегчение боли было недолгим.[13] Другое исследование, проведенное Singh et al. показали, что двухуровневые трансфораминальные эпидуральные инъекции стероидов обеспечивают лучшее обезболивание по сравнению с одноуровневым TFESI.[14]
[11] Другой опубликованный метаанализ показал хорошую эффективность использования эпидуральных инъекций стероидов при спинальном стенозе и поясничной радикулопатии.[12] Кеннеди и др. опубликовали результаты проспективного исследования, показывающие эффективность ЭСИ в лечении поясничной корешковой боли. Несмотря на то, что у пациентов было хорошее облегчение боли, было обнаружено, что облегчение боли было недолгим.[13] Другое исследование, проведенное Singh et al. показали, что двухуровневые трансфораминальные эпидуральные инъекции стероидов обеспечивают лучшее обезболивание по сравнению с одноуровневым TFESI.[14]
 [17][18][19]
[17][18][19] Затем шприц с потерей сопротивления заменяют шприцем, наполненным контрастным раствором, который затем вводят для подтверждения положения иглы в эпидуральном пространстве. Как только распространение контраста подтверждается в прямой и боковой проекциях, в эпидуральное пространство вводят стероид (например, метилпреднизолон, триамцинолон, бетаметазон или дексаметазон) с местной анестезией или без нее. Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение.
Затем шприц с потерей сопротивления заменяют шприцем, наполненным контрастным раствором, который затем вводят для подтверждения положения иглы в эпидуральном пространстве. Как только распространение контраста подтверждается в прямой и боковой проекциях, в эпидуральное пространство вводят стероид (например, метилпреднизолон, триамцинолон, бетаметазон или дексаметазон) с местной анестезией или без нее. Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение. Затем вводят эпидуральную спинальную иглу и направляют ее под ножку верхних позвонков. Боковой вид на рентгеновском снимке получают, чтобы определить глубину введения иглы и предотвратить повреждение нервного корешка. Затем иглу продвигают до тех пор, пока она не достигнет наружного межпозвонкового отверстия.Введение контраста подтверждает положение иглы как в боковой, так и в прямой проекции, показывая эпидуральное распространение. Затем в эпидуральное пространство вводят стероид (например, дексаметазон) с местной анестезией или без нее. Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение.
Затем вводят эпидуральную спинальную иглу и направляют ее под ножку верхних позвонков. Боковой вид на рентгеновском снимке получают, чтобы определить глубину введения иглы и предотвратить повреждение нервного корешка. Затем иглу продвигают до тех пор, пока она не достигнет наружного межпозвонкового отверстия.Введение контраста подтверждает положение иглы как в боковой, так и в прямой проекции, показывая эпидуральное распространение. Затем в эпидуральное пространство вводят стероид (например, дексаметазон) с местной анестезией или без нее. Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение. Затем вводят эпидуральную спинальную иглу и направляют ее через крестцовое отверстие. Боковой вид на рентгеновском снимке получают для определения глубины иглы. Размещение иглы ниже пространства межпозвонкового диска S2-3 снизит риск прокола твердой мозговой оболочки. Введение контраста подтверждает положение иглы как в боковой, так и в прямой проекции, показывая эпидуральное распространение. Затем стероид вводят в эпидуральное пространство.Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение.
Затем вводят эпидуральную спинальную иглу и направляют ее через крестцовое отверстие. Боковой вид на рентгеновском снимке получают для определения глубины иглы. Размещение иглы ниже пространства межпозвонкового диска S2-3 снизит риск прокола твердой мозговой оболочки. Введение контраста подтверждает положение иглы как в боковой, так и в прямой проекции, показывая эпидуральное распространение. Затем стероид вводят в эпидуральное пространство.Наконец, иглу извлекают, а в месте инъекции поддерживают давление, чтобы предотвратить кровотечение. Крайне важно отметить, что эпидуральные инъекции стероидов не обязательно предназначены для лечения боли в спине или шее, вместо этого они предназначены для временного облегчения, чтобы пациент мог вернуться к нормальной деятельности и/или продолжить режим физиотерапии. Ослабление боли после эпидуральных инъекций стероидов может варьироваться от одной недели до одного года, и пациентам может потребоваться либо одна, либо серия инъекций для максимального облегчения.
Крайне важно отметить, что эпидуральные инъекции стероидов не обязательно предназначены для лечения боли в спине или шее, вместо этого они предназначены для временного облегчения, чтобы пациент мог вернуться к нормальной деятельности и/или продолжить режим физиотерапии. Ослабление боли после эпидуральных инъекций стероидов может варьироваться от одной недели до одного года, и пациентам может потребоваться либо одна, либо серия инъекций для максимального облегчения. Инъекции обычно не излечивают боль в спине, но помогают на некоторое время улучшить качество жизни.[8][22]
Инъекции обычно не излечивают боль в спине, но помогают на некоторое время улучшить качество жизни.[8][22] J Нейрохирург позвоночника. 2019 19 апр;: 1-7. [PubMed: 31003219]
J Нейрохирург позвоночника. 2019 19 апр;: 1-7. [PubMed: 31003219] 9 апреля 2019 г. (2): 143–149. [Бесплатная статья PMC: PMC6448201] [PubMed: 30984492]
9 апреля 2019 г. (2): 143–149. [Бесплатная статья PMC: PMC6448201] [PubMed: 30984492]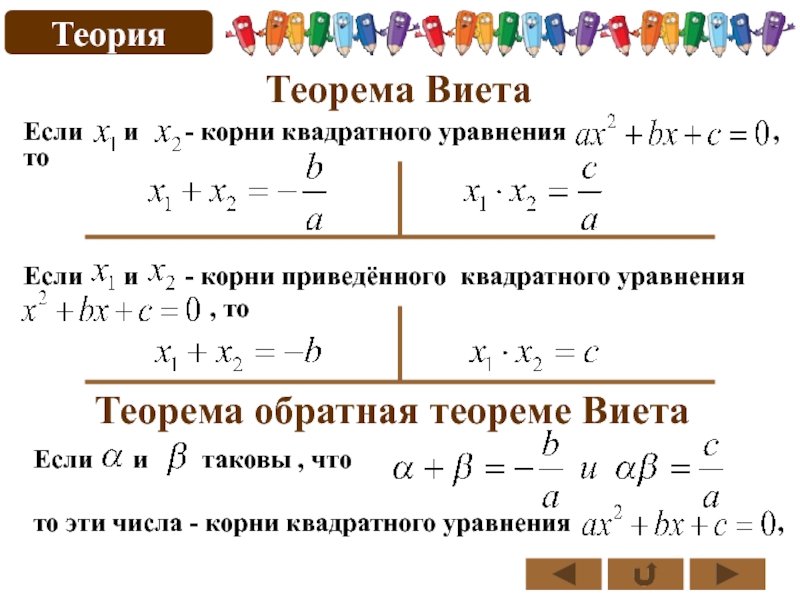
 М., Болаш Р.Б., Арле Дж. Э., Капурал Л., Амирдельфан К., Джайн С., Лием Л., Карлсон Д.Д., Малиновски М.Н., Бендель М., Ян А., Айер Р., Валимахомед А., Энтони А., Крейг Дж., Фишман М.А., Аль-Кайси А.А., Кристелис Н., Розенквист Р.В., Леви Р.М., Мехаил Н.Систематический литературный обзор методов нейростимуляции позвоночника для лечения боли. Боль Мед. 2020 ноябрь 07;21(7):1421-1432. [PubMed: 32034422]
М., Болаш Р.Б., Арле Дж. Э., Капурал Л., Амирдельфан К., Джайн С., Лием Л., Карлсон Д.Д., Малиновски М.Н., Бендель М., Ян А., Айер Р., Валимахомед А., Энтони А., Крейг Дж., Фишман М.А., Аль-Кайси А.А., Кристелис Н., Розенквист Р.В., Леви Р.М., Мехаил Н.Систематический литературный обзор методов нейростимуляции позвоночника для лечения боли. Боль Мед. 2020 ноябрь 07;21(7):1421-1432. [PubMed: 32034422] Эффективность люмбальной эпидуральной инъекции у пациентов с хроническим спинальным стенозом, сопровождающимся избыточными корешками нервов. Медицина (Балтимор). 2019 март;98(9):e14490. [Бесплатная статья PMC: PMC6831256] [PubMed: 30817564]
Эффективность люмбальной эпидуральной инъекции у пациентов с хроническим спинальным стенозом, сопровождающимся избыточными корешками нервов. Медицина (Балтимор). 2019 март;98(9):e14490. [Бесплатная статья PMC: PMC6831256] [PubMed: 30817564] ; 12(2) [бесплатная статья PMC: PMC6388878] [PubMed: 30796074]
; 12(2) [бесплатная статья PMC: PMC6388878] [PubMed: 30796074]

 Во время стоматологического осмотра стоматолог соскребает с ваших зубов зубной налет и камень. Ваш провайдер может также порекомендовать:
Во время стоматологического осмотра стоматолог соскребает с ваших зубов зубной налет и камень. Ваш провайдер может также порекомендовать:

 Вы также можете использовать антисептические жидкости для полоскания рта, чтобы убить бактерии, вызывающие зубной налет. Если вы позволите пленке налета оставаться на зубах слишком долго, она может затвердеть и превратиться в зубной камень. В конце концов, вы можете заболеть деснами и даже потерять зубы. Вы должны чистить зубы не реже двух раз в год. Спросите своего стоматолога о шагах, которые вы можете предпринять, чтобы уменьшить зубной налет и защитить здоровье полости рта.
Вы также можете использовать антисептические жидкости для полоскания рта, чтобы убить бактерии, вызывающие зубной налет. Если вы позволите пленке налета оставаться на зубах слишком долго, она может затвердеть и превратиться в зубной камень. В конце концов, вы можете заболеть деснами и даже потерять зубы. Вы должны чистить зубы не реже двух раз в год. Спросите своего стоматолога о шагах, которые вы можете предпринять, чтобы уменьшить зубной налет и защитить здоровье полости рта.
 Почти все калькуляторы имеют функцию извлечения квадратного корня, которую вы можете использовать. Вот некоторые способы вы можете рассчитать его вручную:
Почти все калькуляторы имеют функцию извлечения квадратного корня, которую вы можете использовать. Вот некоторые способы вы можете рассчитать его вручную: Для √225 вы должны разделить множители под их собственными знаками квадратного корня, поэтому формула будет √25 x √9.
Для √225 вы должны разделить множители под их собственными знаками квадратного корня, поэтому формула будет √25 x √9.

 Это число будет следующей цифрой в решении для √361. Число, которое заполнит пробелы, будет тем же, и это будет самая старшая цифра, где множители меньше или равны числу на четвертом шаге. В этом примере номер цели равен 261. Мы начнем с 9, поэтому уравнение будет выглядеть так: 29 x 9 = 261.
Это число будет следующей цифрой в решении для √361. Число, которое заполнит пробелы, будет тем же, и это будет самая старшая цифра, где множители меньше или равны числу на четвертом шаге. В этом примере номер цели равен 261. Мы начнем с 9, поэтому уравнение будет выглядеть так: 29 x 9 = 261.
 В отличие от семени, ему не нужно опыляться другой частью папоротника, прежде чем оно достигнет этой стадии.
В отличие от семени, ему не нужно опыляться другой частью папоротника, прежде чем оно достигнет этой стадии. Некоторые растут почти везде, а другие обитают только в определенных экосистемах.
Некоторые растут почти везде, а другие обитают только в определенных экосистемах. Хотя это не всегда так, отсутствие четко дифференцированных стеблевых и листовых структур, вероятно, означает, что растение является печеночником, а не мхом.Печенкообразные листообразные структуры на некоторых печеночниках дали этому подразделению растений его общее название. В Иллинойсе насчитывается 118 видов печеночников, но только около 12 были замечены в округе Дю Пейдж.
Хотя это не всегда так, отсутствие четко дифференцированных стеблевых и листовых структур, вероятно, означает, что растение является печеночником, а не мхом.Печенкообразные листообразные структуры на некоторых печеночниках дали этому подразделению растений его общее название. В Иллинойсе насчитывается 118 видов печеночников, но только около 12 были замечены в округе Дю Пейдж. У них нет листьев, корней или цветков, а также ризоидов или листовидных структур, как у некоторых несосудистых растений. Однако водоросли используют хлорофилл для преобразования солнечного света в энергию. Их размер варьируется от одноклеточных организмов до более крупных и сложных, и экологи Лесного заповедника задокументировали более 40 видов в округе Дюпейдж.
У них нет листьев, корней или цветков, а также ризоидов или листовидных структур, как у некоторых несосудистых растений. Однако водоросли используют хлорофилл для преобразования солнечного света в энергию. Их размер варьируется от одноклеточных организмов до более крупных и сложных, и экологи Лесного заповедника задокументировали более 40 видов в округе Дюпейдж. Вместо этого грибы получают питательные вещества из живых или мертвых тканей растений и животных, в основном из разлагающихся веществ. Основное тело гриба, «мицелий», выделяет ферменты, которые гриб использует для переваривания окружающей среды. Грибы играют важную роль в окружающей среде, потому что они разлагают органические вещества и перерабатывают питательные вещества.
Вместо этого грибы получают питательные вещества из живых или мертвых тканей растений и животных, в основном из разлагающихся веществ. Основное тело гриба, «мицелий», выделяет ферменты, которые гриб использует для переваривания окружающей среды. Грибы играют важную роль в окружающей среде, потому что они разлагают органические вещества и перерабатывают питательные вещества.