Как найти среднее значение: Как найти среднее арифметическое чисел?

Содержание

Как найти среднее арифметическое число в Excel

Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.

Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.

Как найти среднее арифметическое чисел?

Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.

Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:

Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:h2 и нажимаем ВВОД.
В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».

Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).

Теперь посмотрим, что еще умеет функция СРЗНАЧ.

Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:h2). Результат:

Среднее значение по условию

Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().

Найти среднее арифметическое чисел, которые больше или равны 10.

Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)

Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:

Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.

Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.

Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».

Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.

В результате вычисления функции получаем следующее значение:

Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.

Как посчитать средневзвешенную цену в Excel?

Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ.

Таблица для примера:

Как мы узнали средневзвешенную цену?

Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).

С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.

Среднее квадратическое отклонение: формула в Excel

Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.

Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.

Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:

среднеквадратическое отклонение / среднее арифметическое значение

Формула в Excel выглядит следующим образом:

СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).

Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.

Как найти среднее значение списка в Python

Среднее (среднее арифметическое) – математическая функция, которая вычисляется путем сложения числовых значений в списке и их деления на количество чисел в списке. Python предоставляет несколько встроенных математических функций; следовательно, он предоставляет различные способы вычисления среднего значения списка.

В этой статье будут обсуждаться различные подходы для получения среднего значения списков в Python в системе Linux. Вот список методов, упомянутых ниже:

Нахождение среднего значения списка с помощью функций sum() и len().
Нахождение среднего значения списка с помощью функции mean() путем импорта модуля статистики.
Нахождение среднего значения списка из функции mean() путем импорта модуля numpy.
Нахождение среднего значения списка из функции reduce() путем импорта функций functools и lambda().

Требования

Любая версия Python, которая будет установлена в вашей системе Linux, python3 предустановлен в последней версии Ubuntu.

Создание файла Python

Чтобы писать код на Python в Ubuntu, вы должны создать файл Python с расширением «.py», создать файл «python_file.py» с помощью указанной ниже команды:

$ nano python_file.py

Важная заметка:

# используется для написания комментариев (пояснительных операторов), они не выполняются во время выполнения программы.
Нажмите Ctrl + s, чтобы сохранить вновь созданный файл python, и Ctrl + x, чтобы выйти из файла.

Методы поиска среднего значения списка в Python

Общий синтаксис для поиска среднего по списку упомянут ниже:

среднее = [ сумма значений в списке ]/[ количество значений в списке ]

Следуйте любому из приведенных ниже методов, которые помогут вам найти среднее значение списка чисел в python:

Как найти среднее значение списка с помощью функций sum() и len()

Первый способ найти среднее – с помощью «функций sum() и len()».

Функция sum() вычисляет сумму всех значений в числовом списке, а функция len(), сокращенная до length, дает количество значений в списке. Ниже приведен синтаксис для вычисления среднего значения с использованием функций sum() и len():

average= sum(list)/len(list)

Список содержит числовые значения которых среднее должно быть вычислено. Напишите приведенный ниже код в «python_file.py», чтобы найти среднее значение по списку:

print("Поиск среднего с помощью функций sum() и len()")

list_values={1,3,5,7,9,11}

average=sum(list_values)/len(list_values)

print("Среднее значение list_values равно: ",average)

Чтобы получить желаемый результат, выполните код, написанный в «python_file.py», с помощью указанной ниже команды:

$ python3 python_file.py

Как найти среднее значение по функции mean() из модуля статистики

Другой способ вычислить среднее значение списка – использовать функцию mean(), импортировав модуль статистики. Функция mean принимает числовой список в качестве аргумента и выполняет функцию среднего значения в списке, но мы не можем использовать эту функцию без импорта модуля статистики, ниже указан его синтаксис:

 import statistics

average= mean(list)

где:

statistics: встроенный модуль в python, для выполнения средней функции импортировать этот модуль
list: содержит числовые значения, среднее значение которых должно быть вычислено.

Напишите приведенный ниже код в python_file.py для вычисления среднего значения списка с помощью функции mean:

import statistics

print ("Поиск среднего значения с помощью функции mean() в модуле статистики")

list_values={1,3,5,7,9,11}

average=statistics.mean(list_values)

print("Среднее значение list_values равно: ",average)

Чтобы получить желаемый результат, выполните код, написанный в python_file.

py, с помощью указанной ниже команды:

$ python3 python_file. ру

Как найти среднее значение с помощью функции среднего из модуля numpy

Мы можем вычислить среднее значение списка с помощью функции mean() из модуля «numpy». Модуль numpy – популярный выбор для работы с большими многомерными массивами. Он также имеет огромное количество математических функций, которые можно применять к массивам для выполнения множества задач. Одним из наиболее важных является метод mean(), который возвращает среднее значение для предоставленного списка, но этот список должен иметь тип массива.

Чтобы использовать модуль numpy для вычисления среднего значения, сначала вам необходимо установить его с помощью указанной ниже команды:

Ниже приводится синтаксис для вычисления среднего значения с использованием модуля «numpy»:

import numpy

average=numpy.mean(list)

где:

numpy: библиотека, которую нужно импортировать, чтобы использовать функцию среднего для вычисления среднего значения.
list: содержит числовые значения, среднее значение которых должно быть вычислено.

Напишите приведенный ниже код в «python_file.py», чтобы найти среднее значение списка, используя функцию mean из модуля numpy:

import numpy

print ( "Поиск среднего значения с помощью функции mean() в модуле numpy" )

list_values = [ 1 , 3 , 5 , 7 , 9 , 11 ]

average = numpy. mean ( list_values )

print ( "Среднее значение" list_values ":" , среднее )

Чтобы получить желаемый результат, выполните код, написанный в «python_file.py», с помощью указанной ниже команды:

$ python3 python_file.py

Как найти среднее с помощью функций сокращения и лямбда

Чтобы найти среднее значение списка с помощью reduce() и лямбда, вам необходимо импортировать модуль functools, чтобы использовать функцию reduce() в Python. Функция lambda() может использоваться для вычисления суммы, а функция reduce() может использоваться для итерации по списку.

import functools

average=functools.reduce(lambda i,j : i+j,list)/len(list)

где:

«i, j»: аргументы лямбды.
i + j: выражение для вычисления суммы списка с использованием аргументов лямбда.
len(): дает количество значений в списке.

Напишите приведенный ниже код в «python_file.py», чтобы найти среднее значение списка с помощью функций lambda() и reduce() из модуля «functools»:

import functools

print("Поиск среднего с помощью функций lambda() и reduce()")

def find_average(list_values):

average= functools.reduce(lambda i, j: i + j, list_values)/len(list_values)

return average

list_values={1,3,5,7,9,11}

average=find_average(list_values)

print("Среднее значение list_values равно:" , среднее)

Чтобы получить желаемый результат, выполните код, написанный в «python_file. py», с помощью указанной ниже команды:

$ python3 python_file.py

Заключение

Python предоставляет множество встроенных модулей для использования математических функций. Для расчета среднего значения списка используется метод. В статье 4 описаны методы с примерами для расчета среднего значения списка; используя функции sum() и len(), используя функцию mean() из статистического модуля, используя функцию mean() из модуля numpy и используя функции lambda() и reduce(). Прочитав эту статью, вы научитесь различным методам нахождения среднего значения на языке Python.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Среднее арифметическое

Определение. Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.

Примером среднего арифметического служат такие показатели, как урожайность, производительность, посещаемость, скорость движения на определенном участке. Вычисление среднего арифметического и его составляющих производится по следующему простом правилу.

Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Пример 1. У Васи было 2 яблока, у Кати — 10 яблок, а у Саши — 6. Среднее количество яблок:

Пример 2. Средняя посещаемость зала в столовой за неделю высчитывается из посещаемости в течение 7 дней: 145 человек в 1-й день; 152 человека во 2-й день; 158 человек в 3-й лень; 162 человека в 4-й день; 164 человека в 5-й день; 161 человек в 6-й день и 157 человек в 7-й день.

Найдем среднее арифметическое (посещаемость) за
неделю:

X_{среднее} = (145 + 152 + 158 + 162 + 164 + 161 + 157) : 7 = 157.

Можно определить среднюю посещаемость и как 1099 : 7 = 157 человек (1099 человек за 7 дней). Т. с. можно фиксировать общее количество посетителей за неделю без учета посещаемости по дням. Но тогда мы не будем знать, что наибольшее количество посетителей в день — 164 человека, а наименьшее — 145 человек, что в этом примере важно (кухня должна ориентироваться на максимальное посещение, от количества посетителей зависит выручка столовой н т. д.).

Во втором примере мы вели статистический учет, следовательно, среднее арифметическое — показатель и в статистике. Но вычисление среднего арифметического имеет смысл только в определенных пределах (небольших промежутках). Нам ничего не даст, например, среднее-мировое количество жителей в одной стране. Стран в мире более 200, а число жителей Индии и Китая совершенно несоизмеримо с количеством жителей Нидерландов или Люксембурга. Полученная средняя численность проживающих в одной стране не будет объективной характеристикой каждой из стран (из-за большого расхождения в числах).

Как рассчитать среднее время? —

Как найти среднее значение времени?

Чтобы найти среднее арифметическое чисел, надо: 1) сложить эти числа; 2) результат разделить на количество слагаемых: Примеры.

Что такое среднее время?

Среднее время по Гринвичу (англ. Greenwich Mean Time, GMT), или гринвичское время — среднее солнечное время меридиана, проходящего через прежнее место расположения Гринвичской королевской обсерватории около Лондона. Ранее, до 1972 года, гринвичское время, GMT, считалось точкой отсчёта времени в других часовых поясах.

Как рассчитать среднее значение?

Вычисление среднего арифметического

Определите набор чисел для вычисления среднего арифметического. Числа могут быть большими или маленькими, их может быть сколько угодно.
Сложите все эти числа, чтобы получить сумму.
Подсчитайте, сколько чисел входит в список.
Разделите сумму на количество чисел.

Как рассчитать среднее значение в Excel?

0:04

2:19

Рекомендуемый клип · 31 сек.

Excel Среднее значение группы чисел — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как найти среднее геометрическое чисел?

Среднее геометрическое Чтобы найти среднее геометрическое, нужно перемножить все числа и извлечь из них корень. Степень корня определяется количеством чисел.

Как найти процент от числа?

как найти процент от числа Разделить число на 100 и умножить на процент! Чтобы найти процент от данного числа, нужно данное число умножить на дробь, выражающую указанный процент.

В чем разница между UTC и GMT?

В повседневной жизни, когда дробная часть секунд не важна, среднее время по Гринвичу (GMT) может рассматриваться как эквивалент UTC или UT1. В противном случае, когда разница между UTC и UT1 существенна, использования термина среднее время по Гринвичу (GMT) избегают. GMT = UTC + 0, MSK = UTC+3 = GMT + 3.

Что такое GMT в часах?

GMT (UTC) и Мировое время GMT (Greenwich Mean Time) – среднее время по Гринвичу, связанное с суточным вращением Земли. В часах эта аббревиатура обозначает функцию одновременного отображения времени в двух часовых поясах.

Что такое Гринвич по географии?

Словарь синонимов Гринвич — (ГРИНУИЧ) пригород Лондона, где находилась основанная в 1657 астрономическая обсерватория. По международному соглашению меридиан, проходящий через Гринвичскую обсерваторию, в 1884 был принят за начальный в счете географических долгот и назван… … Морской словарь

Как получить среднее значение?

сложить все числа и поделить на их количество. Например возьмем твои числа (1,4,6,8). 1+4+6+8=19,так как у нас чисел 5 делим сумму на 5:19/5=3.8.Вывод 3.8 среднее арифметическое чисел 1,4,6,8.

Как рассчитать отклонение от среднего значения в Excel?

Метод 3 Вычисление стандартного отклонения

Поставьте курсор в ячейку ниже последнего введенного значения. Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel.
Введите знак равенства.
Наберите «СТАНДОТКЛОН».
Укажите диапазон данных.
Нажмите кнопку «Enter «.

19 окт. 2018 г.

Как найти среднее значение в ворде?

0:29

10:48

Рекомендуемый клип · 117 сек.

Вычисления в таблицах Word с помощью формул — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как округлить значение в Excel?

3:02

12:05

Рекомендуемый клип · 90 сек.

Округление чисел в Excel — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как рассчитать средний процент в Excel?

Рекомендуемый клип · 31 сек.

Вычисление среднего значения в Excel — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как посчитать сумму ячеек в Excel?

0:02

3:15

Рекомендуемый клип · 114 сек.

Excel:Как посчитать сумму чисел в столбце или строке — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Функция СРЗНАЧ (AVERAGE) — Справочник

Функция СРЗНАЧ чрезвычайно популярна в Excel, входит в группу «Автосумма» и возвращает среднее значение (среднее арифметическое) аргументов.

Описание функции СРЗНАЧ Возвращает среднее значение (среднее арифметическое) аргументов. Например, если диапазон A1:A20 содержит числа, формула
=СРЗНАЧ(A1:A20)
возвращает среднее значение этих чисел.
Дополнительный пример работы функции представлен на рисунке.
Пример вычисления среднего в Excel
Синтаксис
=СРЗНАЧ(число1; [число2]; …)
Аргументы
число1число2
Обязательный аргумент. Первое число, ссылка на ячейку или диапазон, для которого требуется вычислить среднее значение.
Необязательный аргумент. Дополнительные числа, ссылки на ячейки или диапазоны, для которых требуется вычислить среднее значение. Аргументов может быть не более 255.
Замечания
Аргументы могут быть числами, именами или ссылками на диапазоны или ячейки, содержащие числа.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является ссылкой на диапазон или ячейку, содержащую текст или логические значения, или ссылкой на пустую ячейку, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, являющиеся значениями ошибок или текстом, которые не могут быть преобразованы в числа, вызывают ошибки.
Если логические значения и текстовые представления чисел необходимо учитывать в расчетах, используйте функцию СРЗНАЧА.
Если требуется вычислить среднее значение только для тех значений, которые удовлетворяют определенным критериям, используйте функцию СРЗНАЧЕСЛИ или СРЗНАЧЕСЛИМН.
Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения, описанных ниже:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел эти величины оценки степени централизации равны. При ассиметричном распределении множества чисел они могут отличаться.
Пример
Видео работы функции
Работа с часто используемыми функциями (Автосумма)
<noscript><img src='/800/600/https/s0.slide-share.ru/s_slide/ec0f9531807aee24cfde2a40927fb049/abad3009-b48c-4b84-98a5-434a0a7198da.jpeg' /></noscript> youtube.com/embed/q1y7LCC07qI» frameborder=»0″ allowfullscreen=»»/>
Дополнительные материалы
Пятый вопрос четвертого занятия курса Excel от новичка до профессионала «Работа с часто используемыми функциями (Автосумма)»
Среднее арифметическое, размах, мода и медиана числового ряда
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a₁,a₁,..,a_n среднее арифметическое вычисляется по формуле:
\begin{align} & \overline{a}=\frac{a_1+a_2+…+a_n}{n}\\ \end{align}
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
\begin{align} & \overline{a}=\frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\\ \end{align}
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Формула взвешенного среднего | Калькулятор (шаблон Excel)

Формула взвешенного среднего (Содержание)
Средневзвешенная формула
Примеры формулы взвешенного среднего (с шаблоном Excel)
Калькулятор формулы взвешенного среднего
Средневзвешенная формула
Среднее — это точка в наборе данных, которая является средним значением всех точек данных, которые мы имеем в наборе. Он просто рассчитывается путем взятия суммы всех точек данных и деления на количество точек данных. Таким образом, когда мы вычислили простое среднее значение, всем точкам данных были даны одинаковые веса. Средневзвешенное значение — это среднее из набора данных, которое рассчитывается путем предоставления разным весам разных точек данных. Такое назначение различных весов дает нам гибкость в назначении большей мощности для более релевантной точки данных и меньшей мощности для менее релевантной точки данных. Но взвешенное среднее будет равно среднему арифметическому, если все веса равны.
Допустим, у нас есть набор данных X с n точками данных, который задается как X (X1, X2, X3 ……… ..Xn). Таким образом, формула для простого среднего значения просто определяется как:
Среднее арифметическое = (X1 + X2 + X3 ………. + Xn) / n
По-другому:
Среднее арифметическое = X1 / n + X2 / n + ………………… + Xn / n
Таким образом, все точки данных имеют одинаковый вес и задаются как 1 / n.
Но допустим, что веса различны и определяются как (w1, w2, w3 …………, wn). Таким образом, формула для средневзвешенного значения определяется как:
Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+ wn*Xn
Примеры формулы взвешенного среднего (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять формулу взвешенного среднего.
Вы можете скачать этот шаблон взвешенного среднего здесь — Шаблон взвешенного среднего
Формула взвешенного среднего — пример № 1
Допустим, у вас есть набор данных с 10 точками данных, и мы хотим рассчитать средневзвешенное значение для этого.
Набор данных: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
Вес: (20%, 15%, 10%, 10%, 5%, 3%, 2%, 7%, 5%, 13%)
Сначала мы рассчитываем произведение набора данных и весов.
Результат будет таким, как указано ниже.
Точно так же мы рассчитали для всех данных.
Средневзвешенное значение рассчитывается по формуле, приведенной ниже
Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn
Средневзвешенное значение = (4 * 25%) + (6 * 20%) + (8 * 10%) + (9 * 10%) + (22 * 5%) + (83 * 3%) + (98 * 2% ) + (45 * 7%) + (87 * 5%) + (10 * 13%)
Взвешенное среднее = 18, 25
Допустим, все веса равны, т.е. 10% для каждого набора данных.
Сначала мы рассчитываем произведение набора данных и весов.
Средневзвешенное значение рассчитывается по формуле, приведенной ниже
Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn
Средневзвешенное значение = (4 * 10%) + (6 * 10%) + (8 * 10%) + (9 * 10%) + (22 * 10%) + (83 * 10%) + (98 * 10% ) + (45 * 10%) + (87 * 10%) + (10 * 10%)
Взвешенное среднее = 37, 20
Среднее арифметическое рассчитывается по формуле, приведенной ниже
Среднее арифметическое = (сумма всех точек данных) / количество точек данных
Среднее арифметическое = (4 + 6 + 8 + 9 + 22 + 83 + 98 + 45 + 87 + 10) / 10
Среднее арифметическое = 37, 2
Поэтому, когда все веса равны, среднее арифметическое такое же, как среднее взвешенное
Формула взвешенного среднего — пример № 2
Допустим, у вас есть портфель, в котором у вас есть акции, облигации и товары. Таким образом, в основном у нас есть портфель, в который мы инвестировали в акции, облигации и товары. Ниже приведены веса / пропорции каждого инструмента в вашем портфеле:
Средневзвешенное значение рассчитывается по формуле, приведенной ниже
Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn
Средневзвешенное значение = 50% * 20% + 30% * 7% + 20% * 12%
Средневзвешенное значение = 14, 5%
Простая средняя доходность портфеля рассчитывается по формуле, приведенной ниже
Простая средняя доходность портфеля = сумма возвратов / количество товаров
Простая средняя доходность портфеля = (20% + 7% + 12%) / 3
Простая средняя доходность портфеля = 13%
Так что, если вы видите здесь, поскольку акции дали больший вес и принесли более высокую доходность, взвешенная доходность — это больше, чем простая доходность.
объяснение
Средневзвешенное значение — это, в основном, среднее значение точек данных, рассчитанное вместе с соответствующими весами. Нет необходимости в том, чтобы всегда все точки данных имели одинаковую релевантность, поэтому тогда недостаточно только простого вычисления. По этой причине взвешенное среднее имеет гораздо большее практическое значение, чем простое среднее. Например, мы знаем, что студенты должны сдавать разные типы экзаменов и должны сдавать разные задания. Все эти экзамены и задания имеют разный вес, данный им. Задание 1: 10%, Задание 2: 10%, Задание 3: 20%, Финальный экзамен: 60%. Поэтому, если ученик не выполнил хороших заданий во всех трех заданиях, он может хорошо подготовиться к тому, чтобы хорошо сдать итоговый экзамен, чтобы его средний балл повысился.
Простое среднее значение легко искажается крайними значениями / выбросами. Таким образом, взвешенное среднее — это правильный способ найти среднее для набора данных. Поэтому, если есть экстремальное значение, которое имеет очень меньшее значение, оно не окажет значительного влияния на среднее значение. Точно так же, если существует экстремальное значение и оно имеет большое значение, его влияние должно быть видно в среднем значении.
Актуальность и использование формулы взвешенного среднего
Середина очень проста, но все же один из важнейших элементов статистики. Это основная основа статистического анализа данных. Но в реальной и практической жизни среднее арифметическое — это просто теоретическая концепция, которая формирует основу для более актуального инструмента, то есть взвешенного среднего. Средневзвешенное значение имеет множество практических применений, таких как расчет средней доходности портфеля, вычисление средних оценок на экзаменах, определение стоимости капитала в капитальных проектах (WACC), определение стоимости запасов в конце периода, когда цены меняются, и т. Д. Таким образом, в основном взвешенное среднее преодолевает проблемы, которые имеют простое среднее значение и более актуальны Простой факт в том, что это имеет смысл. Использование одинаковых весов для всех элементов в наборе данных нецелесообразно. Например, запасы в компании приобретаются по разным ценам, поэтому простые средства не дадут точной стоимости запасов в конце периода. Или в капитальных проектах у компании может быть другой источник средств, такой как долг, капитал и т. Д., Так что просто принять среднее значение всех затрат — это неправильный путь. Взвешенное среднее более практично и актуально.
Калькулятор формулы взвешенного среднего
Вы можете использовать следующий калькулятор взвешенного среднего
ш ₁
X ₁
w ₂
X ₂
ш ₃
X ₃
ш ₄
X ₄
Средневзвешенная формула

Формула взвешенного среднего = ш ₁ * х ₁ + ш ₂ * х ₂ + ш ₃ * х ₃ + ш ₄ * х ₄
0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = 0
Рекомендуемые статьи
Это было руководство к формуле взвешенного среднего. Здесь мы обсудим, как рассчитать взвешенное среднее вместе с практическими примерами. Мы также предоставляем калькулятор взвешенного среднего с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
Руководство по гармонической средней формуле
Примеры ожидаемой формулы возврата
Как рассчитать численность населения?
Формула стоимости погашения
Как рассчитать среднее | Действительно. Чем больше вы понимаете, что такое среднее значение и как его рассчитать, тем лучше вы сможете реализовать его в бизнес-смысле и использовать в своих интересах. В этой статье мы определяем среднее значение, перечисляем шаги, которые необходимо предпринять для его расчета, и приводим пример для пояснения.
Связанный: Узнайте о том, как стать бизнес-аналитиком
Каков средний показатель?
Обычно известное как «среднее», среднее — это математический термин, который относится к сумме набора чисел, деленной на количество цифр в наборе данных. Другими словами, это центральное число, представляющее общий набор данных. Среднее значение также известно как «медиана» и «мода», хотя эти термины и расчеты используются реже, чем среднее значение. В целях сравнения «мода» относится к числу в наборе данных, которое встречается чаще всего, а «медиана» — это число в середине набора данных, когда набор данных приводится в порядок.Для наших целей мы сосредоточимся на среднем значении.
Зачем вычислять среднее значение?
Вычисление среднего значения — отличный способ разобраться в наборе чисел. Он также может сказать вам, как группа людей относится к определенному вопросу, вещи или продукту, если вы ведете бизнес. Вычисление среднего значения может быть полезным для вашего бизнеса или организации. Например, если вы определяете среднюю сумму продаж брюк нового фасона, это может помочь вам определить, сколько запасов нужно внести в будущем.Кроме того, это поможет вам узнать, стоит ли продолжать продавать эту конкретную одежду.
Связано: Узнайте, как стать менеджером по продажам
Как рассчитать среднее значение
Вот шаги, которые необходимо предпринять для расчета среднего значения:
Определите, что вы хотите усреднить.
Найдите сумму набора данных.
Определите количество чисел в вашем наборе данных.
Разделите сумму на количество чисел в вашем наборе данных.
Среднее равно сумме набора чисел, деленной на количество, которое является количеством добавляемых значений. Например, вы хотите получить среднее 13, 54, 88, 27 и 104. Найдите сумму чисел: 13 + 54 + 88+ 27 + 104 = 286. В нашем наборе данных пять чисел, поэтому разделите 286. на 5, чтобы получить 57,2. 57,2 это средний показатель.
1. Определите, что вы хотите усреднить
Чтобы рассчитать среднее значение, вам нужно определить, что именно вы хотите усреднить.Это может включать в себя что угодно, начиная от среднего количества продаж за определенный период, среднего количества заказанных вами запасов определенного товара, среднего количества сотрудников, которых вы наняли в прошлом году, или среднего размера заработной платы, которую вы ve дал вашим сотрудникам в данном году. Как только вы узнаете, какое среднее значение вы хотите, вы можете начать вычислять среднее значение.
2. Найдите сумму набора данных
Вторым шагом в вычислении среднего является определение суммы набора данных.Это можно сделать с помощью калькулятора, вручную, с помощью электронной таблицы или онлайн-калькулятора. Например, допустим, вы берете сумму следующих чисел: 2, 3, 4 и 5. Это означает, что вы будете складывать каждое из этих чисел вместе, чтобы получить сумму 14.
3. Определите сумму число чисел в вашем наборе данных
Следующий шаг включает определение количества чисел в вашем наборе данных. Для этого подсчитайте количество используемых вами значений. В приведенном выше примере есть четыре числа или значения.Если у вас есть два числа с одинаковым значением, вам нужно будет считать их, как если бы они были их собственными числами.
4. Разделите сумму на количество чисел в вашем наборе данных
Последний шаг включает в себя деление суммы, рассчитанной на втором шаге, на количество чисел в вашем наборе данных, которое было определено на третьем шаге. Это приведет к среднему или среднему значению.
Например, используя приведенный выше пример, вы должны разделить 14 на 4, чтобы получить 3,5. Следовательно, среднее значение этого набора данных равно 3.5.
Связанный материал: Путеводитель по карьере в сфере финансов
Когда использовать среднее значение
Среднее значение можно использовать во многих сценариях, как личных, так и профессиональных. Это отличный способ найти репрезентативное число для определенного набора данных. Среднее значение особенно полезно при попытке установить единственное значение для большого набора данных. В деловом смысле вы можете использовать среднее значение в следующих сценариях:
Среднее количество клиентов за данный период.
Среднее количество продаж за определенный период.
Среднее количество продаж определенного товара.
Среднее количество заработной платы, которую вы даете сотрудникам.
Среднесписочная численность работников за данный период.
Среднее количество ваших расходов.
Среднее количество месяцев, в течение которых вы получали прибыль.
Пример расчета среднего
При рассмотрении различных сценариев это может помочь понять конкретный термин или расчет.Вот пример того, как можно рассчитать среднее значение определенного набора данных.
Определение средней суммы продаж
Допустим, вы владеете обувным магазином и хотите определить среднюю сумму продаж новой пары кроссовок за один год. Для этого вы решаете использовать количество продаж каждый месяц, чтобы рассчитать среднее значение. Существа, что в году 12 месяцев, вы будете работать с 12 числами. Допустим, с января по декабрь вы продали следующие номера этих кроссовок: 50, 45, 39, 52, 40, 50, 48, 43, 38, 34, 37 и 48.Чтобы рассчитать среднее значение, вам нужно взять сумму этих чисел. Достигнув числа 524, вы разделите его на 12. Это количество чисел в этом наборе данных. Поскольку 524, разделенное на 12, равно примерно 43,67, вы определили, что среднее количество продаж, которое вы сделали в данном году на конкретной паре кроссовок, составляет 43,67.
Как рассчитать среднее значение
Среднее среднее чисел.
Легко посчитать: сложите всех чисел, затем разделите на количество чисел.
Другими словами, это сумма , деленная на количество .

Пример 1. Каково среднее значение этих чисел?
6, 11, 7
Сложите числа: 6 + 11 + 7 = 24
Разделите на сколько чисел (всего 3 числа): 24 / 3 = 8
Среднее значение равно 8
Почему это работает?
Это потому, что 6, 11 и 7, сложенные вместе, равно 3 лотам по 8:
Вы как будто «сглаживаете» числа
Пример 2: Посмотрите на эти номера:

3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
Сумма этих чисел равна 330
Есть пятнадцать номеров.
Среднее значение равно 330/15 = 22
Среднее из приведенных выше чисел равно 22
Отрицательные числа
Как вы обрабатываете отрицательные числа? Прибавление отрицательного числа равносильно вычитанию числа (без отрицательного числа). Например, 3 + (−2) = 3−2 = 1,
.
Зная это, давайте рассмотрим пример:
Пример 3: Найдите среднее значение этих чисел:
3, −7, 5, 13, −2
Сумма этих чисел равна 3 − 7 + 5 + 13 − 2 = 12
Есть 5 номеров.
Среднее равно 12 ÷ 5 = 2,4
Среднее из приведенных выше чисел равно 2,4
Вот как это сделать одной строкой:
Среднее = 3 − 7 + 5 + 13 − 2 5 = 12 5 = 2,4
Попробуйте сами!

Теперь взгляните на The Mean Machine.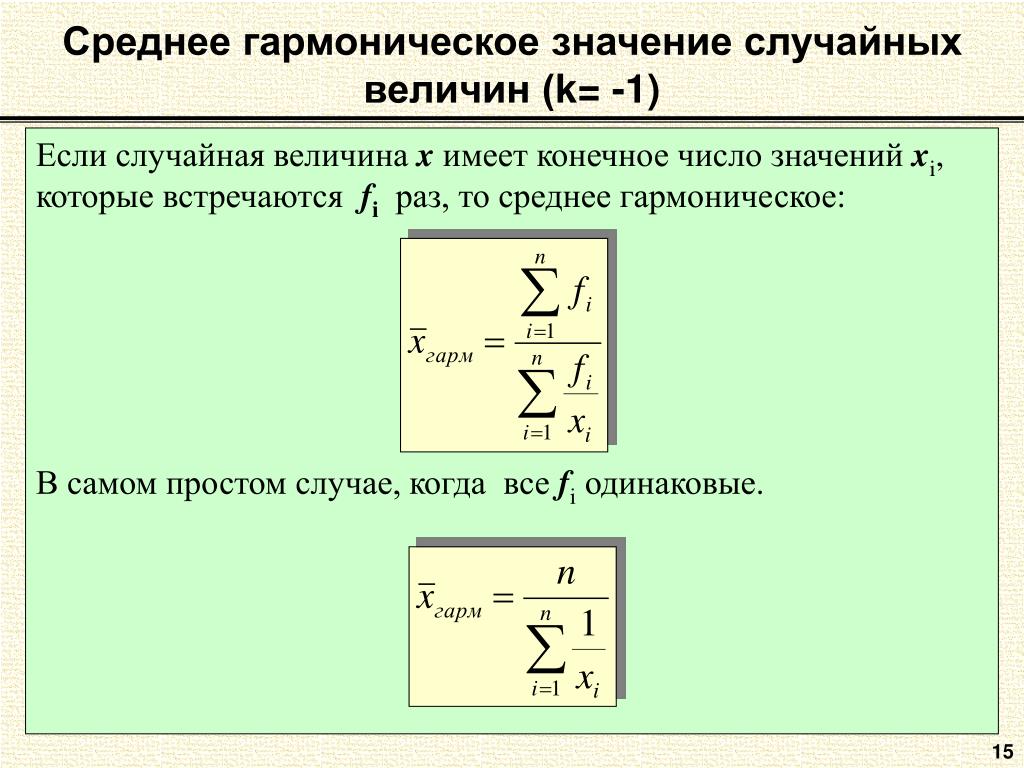

Дополнительная тема: среднее значение, которое мы только что рассмотрели, также называется средним арифметическим , потому что существуют и другие средние значения, такие как среднее геометрическое и среднее гармоническое.

691, 1453, 1454, 692, 1455, 1456, 2179, 2180, 3053, 3054
Среднее, медиана, режим: что это такое, как их найти
Содержание (Нажмите, чтобы перейти к этому разделу):
Все о…
Как найти среднее значение, медиану и моду вручную.
Найдите среднее значение, медиану и моду с помощью технологии:
Посмотрите видео, чтобы узнать, как найти среднее значение, медиану и моду:

Видео не видно? Кликните сюда.
Не знаете, как найти среднее значение, медиану и моду в статистике?
Среднее значение — это среднее значение набора данных.
Режим является наиболее распространенным числом в наборе данных.
Медиана — это середина набора чисел.
Из трех значений только среднее требует формулы. Мне нравится думать об этом в другом словарном смысле этого слова (например, это подло, а не хорошо!). Это потому, что по сравнению с двумя другими, с ним не так просто работать.
Советы, чтобы запомнить разницу
Не можете вспомнить разницу между средним значением, медианой и модой? Вот пара советов, которые могут помочь.
«A la mode» — французское слово, означающее модный ; Это также относится к популярному способу подачи мороженого. Итак, «Мода» — это самый популярный или модный член набора чисел. Слово MOde также похоже на MOst.
«Среднее» требует от вас арифметических действий (сложения всех чисел и деления), так что это и есть «среднее».
«Медиана» имеет то же количество букв, что и «Средний».
Среднее
Среднее по сравнению с медианой
Среднее по сравнению со средним
Конкретные «средние значения», обычно используемые в статистике
Другие типы
Оба являются показателями того, где находится центр набора данных (называемый в статистике «центральной тенденцией»), но обычно они представляют собой различных числа. Например, возьмем этот список чисел: 10, 10, 20, 40, 70.
Среднее значение (неофициально «среднее») находится путем сложения всех чисел и деления на количество предметов в наборе: 10 + 10 + 20 + 40 + 70 / 5 = 30.
Медиана находится путем упорядочивания множества от низшего к высшему и нахождения точной середины. Медиана — это просто среднее число: 20.
.
Иногда это два одинаковых номера. Например, набор данных 1, 2, 4, 6, 7 имеет среднее значение 1 + 2 + 4 + 6 + 7/5 = 4 и медиану (среднее значение) 4.
Когда вы только начинали заниматься математикой, вас, вероятно, учили, что среднее значение — это «средняя» величина для набора чисел. Вы сложили числа, разделили на количество предметов, которые вы можете и вуаля ! вы получаете среднее.Например, среднее 10, 6 и 20:
10 + 6 + 20 = 36 / 3 = 12.
Вы начали изучать статистику, и вдруг «среднее» стало называться средним. Что случилось? Ответ заключается в том, что они имеют одинаковое значение (это синонимы).
Тем не менее, технически , слово означает, что является сокращением от среднего арифметического. Мы используем разные слова в статистике, потому что есть несколько разных типов средств, и все они делают разные вещи.
Вероятно, вы встретите их на уроках статистики. У них очень узкие значения:
Ссылки
Кенни, Дж. Ф. и Кинг, Э. С. Математика статистики, Pt. 1, 3-е изд. Принстон, Нью-Джерси: Ван Ностранд, 1962.
.
Есть других типов средних, и вы будете использовать их в различных разделах математики. Большинство из них имеют очень узкое применение в таких областях, как финансы или физика; если вы занимаетесь элементарной статистикой, вы, вероятно, не будете с ними работать.
Это одни из самых распространенных типов, с которыми вы столкнетесь.
Средневзвешенное значение.
Среднее гармоническое.
Среднее геометрическое.
Среднее арифметико-геометрическое.
Среднеквадратичное среднее.
Среднее по Герону.
Графическое среднее
Они довольно распространены в статистике, особенно при изучении населения. Вместо того, чтобы каждая точка данных вносила одинаковый вклад в итоговое среднее значение, некоторые точки данных вносят больший вклад, чем другие.Если все веса равны, то это будет равно среднему арифметическому. Есть определенные обстоятельства, когда это может дать неверную информацию, как показано в парадоксе Симпсона.
Гармоническая формула.

Чтобы найти:
Сложите обратные числа в наборе. Чтобы найти обратную дробь, переверните дробь так, чтобы числитель стал знаменателем, а знаменатель стал числителем. Например, обратное число 6/1 равно 1/6.
Разделите ответ на количество предметов в наборе.
Возьмем обратное значение результата.
Среднее гармоническое довольно часто используется в физике. В некоторых случаях, связанных с коэффициентами и отношениями, он дает лучшее среднее значение, чем среднее арифметическое. Вы также найдете применение в геометрии, финансах и информатике.

Этот тип имеет очень узкое и специфическое применение в области финансов, социальных наук и технологий. Например, предположим, что вы владеете акциями, которые приносят 5% в первый год, 20% во второй год и 10% в третий год.Если вы хотите узнать среднюю норму прибыли, вы не можете использовать среднее арифметическое. Почему? Потому что, когда вы находите нормы прибыли, вы 90 204 умножаете 90 205, а не складываете. Например, первый год вы умножаете на 1,05.
Используется в основном в исчислении и машинных вычислениях (т.е. в качестве основы для многих компьютерных вычислений). Это связано с периметром эллипса. Когда он был впервые разработан Гауссом, он использовался для расчета планетарных орбит.Арифметико-геометрическая представляет собой (что неудивительно!) смесь среднего арифметического и геометрического. Математика довольно сложная, но вы можете найти относительно простое объяснение математики здесь.
Очень полезен в областях, изучающих синусоидальные волны, например, в электротехнике. Этот конкретный тип также называется квадратичным средним. См.: Среднеквадратичное значение / Среднеквадратичное значение.
Используется в геометрии для нахождения объема усеченной пирамиды. Пирамидальная усеченная пирамида — это, по сути, пирамида со срезанным концом.
Другое название наклона секущей: эквивалент средней скорости изменения между двумя точками.
2. Что такое режим?
Режим самый распространенный номер в наборе. Например, мода в этом наборе чисел 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33
3.
Что такое медиана?
Медиана — это среднее число в наборе данных.Чтобы найти медиану, перечислите точки данных в порядке возрастания, а затем найдите среднее число. Среднее число в этом наборе 28, так как под ним 4 числа и 4 числа выше:
23, 24, 26, 26, 28, 29, 30, 31, 33
Примечание : Если у вас есть четный набор чисел, усредните два средних, чтобы найти медиану. Например, медиана этого набора чисел равна 28,5 (28 + 29/2).
23, 24, 26, 26, 28, 29 , 30, 31, 33, 34
Как найти среднее значение, медиану и моду: РЕЖИМ
Шаг 1: Расположите числа так, чтобы вы могли четко видеть шаблоны .
Например, у нас есть 2, 19, 44, 44, 44, 51, 56, 78, 86, 99, 99. Режим — это число, которое встречается чаще всего. В данном случае: 44 , которое появляется три раза.
Как найти среднее значение, медиану и моду: MEAN
Шаг 2: Сложите числа, чтобы получить общее число .
Пример: 2 +19 + 44 + 44 +44 + 51 + 56 + 78 + 86 + 99 + 99 = 622 . Отложите этот номер на время.
Шаг 3: Подсчитайте количество чисел в ряду .
В нашем примере (2, 19, 44, 44, 44, 51, 56, 78, 86, 99, 99) у нас есть 11 чисел.
Шаг 4: Разделите число, которое вы нашли на шаге 2, на число, которое вы нашли на шаге 3.
В нашем примере: 622 / 11 = 56,5454545 . Это среднее , иногда называемое средним .
Разделите сумму на количество элементов, чтобы найти среднее значение.
Как найти среднее значение, медиану и моду: МЕДИАНА
Если на шаге 3 вы получили нечетное число, перейдите к шагу 5.Если у вас было четное число, перейдите к шагу 6.
Шаг 5: Найдите число в середине ряда.
Это медиана . 2, 19, 44, 44, 44, 51 ,56, 78, 86, 99, 99.
Шаг 6: Найдите два средних числа.
Например, 1, 2, 5, 6, 7, 8, 12, 15, 16, 17. Медиана — это число, которое находится в середине этих двух средних чисел (7 и 8), так что число будет 7.5 в данном случае. (Чтобы сделать это математически, сложите два числа вместе и разделите на 2).
Совет: У вас может быть несколько режимов. Например, режим 1, 1, 5, 5, 6, 6 равен 1, 5 и 6.
Нравится объяснение? Ознакомьтесь со Справочником по статистике практического мошенничества, в котором есть еще сотни пошаговых решений, таких как это!
Чтобы найти медиану среднего режима SPSS, вам потребуется использовать вкладку Частота .Это кажется немного нелогичным, но вкладка «Описательная статистика» не дает возможности найти моду или медиану.
SPSS имеет очень похожий интерфейс на Microsoft Excel. Поэтому, если вы раньше использовали Microsoft Excel, вы быстро адаптируетесь к SPSS.
SPSS Mean Mode Median: Шаги
Посмотрите видео по шагам:

Видео не видно? Кликните сюда.
Пример вопроса: Найдите медиану среднего режима SPSS для следующего набора данных: 20,23,35,66,55,66
Шаг 1: Откройте SPSS. В разделе «Чем бы вы хотели заняться?» диалоговом окне, щелкните переключатель «Введите данные», а затем нажмите «ОК». Откроется новый рабочий лист. Примечание. Если вы отказались от первого экрана справки, вы можете не увидеть эту опцию. В этом случае просто начните с шага 2.
Шаг 2: Введите данные в рабочий лист. Вы можете ввести данные в один столбец или несколько столбцов, если у вас несколько наборов данных. Для этого примера введите 20, 23, 35, 66, 55, 66 в столбец 1. Не оставляйте пробелов между данными (т.е. не оставляйте пустых строк).
Шаг 2: Нажмите «Анализ», наведите курсор на «Описательная статистика» и нажмите «Частоты».
Шаг 3: Нажмите «Статистика», а затем установите флажки «среднее», «мода» и «медиана». Дважды нажмите «Продолжить» (выберите «нет» в качестве типа диаграммы во втором окне).
Примечание . В некоторых версиях SPSS вам может потребоваться нажать «Продолжить» только один раз, и это может не дать вам выбора типа диаграммы.
Результаты частоты появятся в качестве выходных данных.В верхней части выходных данных будет отображаться среднее значение, мода и медиана.
Если вы прокрутите вниз, таблица частот также покажет вам режим. Мода определяется в статистике как число с наибольшей частотой (для этого выборочного набора данных чаще всего встречается число 66 с двумя результатами в столбце частоты).
Поиск среднего значения TI 83 или медианы TI 83 из списка данных можно выполнить двумя способами: путем ввода списка данных или с помощью начального экрана для ввода команд.Использование функции списка так же просто, как ввод данных на главный экран, и имеет дополнительное преимущество, заключающееся в том, что вы можете использовать данные для других целей после того, как вычислит среднее значение, моду и медиану (например, вы можете хотите создать гистограмму TI 83).
Шаги для среднего, медианы и моды на TI 83
Посмотреть видео о среднем значении и медиане на TI 83:

Не можете посмотреть видео? Кликните сюда.
Пример задачи : Найдите среднее значение и медиану высоты 20 самых высоких зданий в Нью-Йорке.высоты (в футах): 1250, 1200, 1046, 1046, 952, 927, 915, 861, 850, 814, 813, 809, 808, 806, 792, 778, 757, 755, 752 и 750.
Шаг 1: Введите приведенные выше данные в список. Нажмите кнопку STAT, а затем нажмите ENTER. Введите первое число (1250) и нажмите клавишу ВВОД. Продолжайте вводить цифры, нажимая кнопку ENTER после каждого ввода.
Шаг 2: Нажмите кнопку STAT.
Шаг 3: Нажмите кнопку со стрелкой вправо, чтобы выделить «Расч.
Шаг 4: Нажмите ENTER, чтобы выбрать «1-Var Stats», а затем введите имя списка. Например, чтобы ввести L1, нажмите [2nd] и [1].
Шаг 5: Нажмите ENTER еще раз. Калькулятор вернет среднее значение x̄. Для этого списка данных среднее значение TI 83 составляет 90 206 884,05 90 207 футов (округлено до 3 знаков после запятой).
Шаг 6: Перемещайте стрелку вниз, пока не увидите «Мед». Это медиана TI 83; для приведенных выше данных медиана составляет 90 206 813,05 90 207 футов.
Примечание: TI-83 plus не имеет встроенной функции режима, но как только вы войдете в свой список, довольно легко определить режим: это просто число, которое чаще всего встречается в наборе. Точно сказать не могу? Подробнее о режиме читайте здесь.
Вот оно!
Потеряли путеводитель? Загрузите новый здесь, на веб-сайте TI.
Посмотрите видео, чтобы узнать, как найти среднее значение в R:

Видео не видно? Кликните сюда.
Каталожные номера
Кенни, Дж.F. and Keeping, ES «Мода», «Отношение между средним, медианой и модой» и «Относительные достоинства среднего, медианы и моды». §4.7-4.9 в математике статистики, Pt. 1, 3-е изд. Принстон, Нью-Джерси: Ван Ностранд, стр. 50-54, 1962.
Цвиллингер, Д. (ред.). Стандартные математические таблицы и формулы CRC. Бока-Ратон, Флорида: CRC Press, с. 602, 1995.
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице Facebook .

Калькулятор средних значений — определение среднего числа чисел
Онлайн-калькулятор среднего значения используется для расчета среднего или среднего значения любого заданного набора данных. Помимо нахождения среднего или среднего числа, этот калькулятор среднего значения вычисляет и показывает график (распределение набора данных со средним значением), таблицу и некоторые другие параметры для данной группы чисел.
Внимательно прочтите это содержание, чтобы узнать, как найти среднее число, используя формулу среднего значения (пошаговый расчет), калькулятор среднего числа и многое другое! Но сначала давайте определим основное статистическое определение среднего.
Сколько в среднем:
Средний термин имеет разное количество значений. Можно сказать, что это одно число, которое используется для представления набора чисел. Когда дело доходит до математического контекста, среднее значение — это термин, который относится к среднему или среднему арифметическому.Простыми словами, это статистическая концепция, которая широко используется в нескольких областях. Попробуйте наш калькулятор средних чисел, чтобы найти среднюю сумму онлайн.
В частности, «средним» считается среднее арифметическое, в котором сумма чисел, деленная на количество чисел, усредняется. Согласно статистическим исследованиям, среднее значение, медиана и мода называются показателями центральной тенденции, а неформальное использование любого из этих показателей можно назвать средним значением.
Помните, что существует ряд различных средних значений, включая, помимо прочего, среднее значение, медиану, моду и диапазон.Вы можете попробовать этот бесплатный онлайн-калькулятор среднего среднего диапазона моды, чтобы найти меры центральной тенденции.
Что такое средняя формула:
Если вы хотите найти среднее значение набора чисел, просто сложив весь набор чисел и разделив их на количество чисел, которые у вас есть, для лучшего понимания давайте взглянем на приведенную формулу для среднего:
Среднее уравнение:
Среднее значение набора чисел = Сумма слагаемых / Количество слагаемых
Помните, что наш онлайн-калькулятор простых средних значений также использует ту же формулу при нахождении среднего значения для группы чисел.
Предположим, что имеется набор данных:
5, 6, 9, 11, 13, 12
Подставим значение в приведенную выше формулу, чтобы найти среднее значение заданных терминов:
Среднее значение набора чисел = 5 + 6 + 9 + 11 + 13 + 12 / 6
Среднее значение набора чисел = 56/6
Среднее значение набора чисел = 9,333

О калькуляторе средних значений:
Онлайн-калькулятор среднего значения позволяет рассчитать среднее/среднее/ожидаемое значение/центральное значение выборки или совокупности данных. Проще говоря, с помощью этого калькулятора становится легко найти среднее значение. Кроме того, этот искатель среднего используется для нахождения среднего геометрического, совокупности и стандартного отклонения, а также различных других значений, соответствующих заданному набору данных. Итак, как рассчитать среднее значение онлайн с помощью этого генератора средних значений, просто проведите пальцем вниз!
Как найти среднее число с помощью калькулятора среднего среднего:
Приведенный выше калькулятор усреднения на 100 % бесплатен и имеет простой и удобный интерфейс.Как только вы узнаете о среднем наборе данных, статистика данных станет простой. Итак, все, что вам нужно выполнить, чтобы найти среднее или среднее значение с помощью этого онлайн-калькулятора среднего числа:
Входы:
Прежде всего, вам просто нужно выбрать оператор, с помощью которого вы хотите разделить номера набора данных, это может быть как «пробел», «запятая», так и «определенный пользователем (означает определить себя)»
После выбора все, что вам нужно, чтобы добавить набор данных или группу чисел, разделив их с помощью разделителя выбора, и нажмите кнопку расчета этого калькулятора среднего числа
Вывод:
Этот калькулятор среднего числа вычисляет:
Среднее значение
Медиана (средний)
Режим (наиболее распространенный)
Диапазон (самый большой – самый маленький)
Расчет среднего значения
Среднее геометрическое
Порядок возрастания
По убыванию
Четные числа
Нечетные числа:
Общая сумма
Умножить на значения:
Стандартное отклонение населения
Стандартное отклонение выборки
Наибольшее значение
Самое низкое значение
Количество (общее количество)
Таблица распределения по заданному набору данных
Кроме того, этот калькулятор средних значений показывает график для «Распределения чисел со средними значениями»
Почему и как найти среднее значение набора данных?
Итак, что означает вычисление среднего или среднего значения заданных данных. Технически вы просто делите сумму терминов на количество (или количество) чисел в данном наборе данных. Но когда дело доходит до терминов реального мира, это больше похоже на равномерное распределение терминов всего набора данных между каждым из его чисел, а затем простое отступление назад, чтобы получить представление о том, какое значение получили все числа.
Тип среднего значения обычно принимается во внимание для понимания больших наборов данных или даже для оценки положения всей группы.Например, вас могут попросить найти средний балл в процентах в вашем классе, средний средний балл среди ваших друзей, среднее значение времени, которое требуется, чтобы дойти до автобусной остановки, среднюю сумму заработной платы для определенной работы и так далее! Для мгновенного расчета вы можете попробовать калькулятор среднего, который поможет вам вычислить среднее значение любой группы чисел.

Итак, как получить среднее, рассмотрим приведенные примеры:
Пример 1:
Есть 10 учеников, и на данный момент их совокупные оценки в процентах составляют: 78, 64, 87, 95, 88, 74, 82, 93, 79 и 82. Итак, найдите средний балл на уроке математики.
Начнем с суммирования всех баллов учеников:
78 + 64 + 87 + 95 + 88 + 74 + 82 + 93 + 79 + 82 = 822
Далее все, что вам нужно, разделить эту сумму на количество добавленных вами очков. (Просто посчитайте их, или даже вы можете просто отметить, что заявленная задача говорит вам, что их 10)
822 ÷ 10 = 82,2
Результат 82,2; это средний балл в вашем классе математики.
Вы можете проверить результат с помощью определителя среднего числа для дальнейшего подтверждения.Кроме того, вы можете попробовать этот инструмент на сайте calculate-online.net, чтобы превратить любое число или выражение в значащие цифры (сиг-фиг).
Пример 2:
Как получить среднее этих чисел 30, 30, 30, 30?
Итак, попробуем усреднить эти числа:
Среднее значение = 30 + 30 + 30 + 30 / 4
Среднее значение = 120/4
Среднее значение = 30
Имейте в виду, если набор чисел все одинаковый, то нет необходимости вычислять среднее значение, так как оно даст одно и то же число с числом в массиве. Например, у вас в массиве 60, 60, 60, 60, 60; он всегда будет давать 60. Если у вас есть 57, 57, 57, 57, 57, 57, то среднее значение этого массива равно 57. Для дальнейшего запроса используйте калькулятор усреднения, чтобы найти числа усреднения любого набора данных.
Зачем использовать онлайн-калькулятор среднего значения вместо ручного расчета:
Если в вашем массиве есть большие числа, вычисление может быть очень сложным. У вас могут быть десятки чисел вместо 3 или 4, и тогда вам следует использовать наш простой калькулятор среднего значения, потому что в нашем инструменте допуск равен 0.
Часто задаваемые вопросы (СРЕДНИЙ):
Как рассчитать среднее значение?
Помимо использования средства поиска среднего числа, вы можете легко вычислить среднее значение за 2 шага:
Прежде всего, вы должны сложить все термины
Далее следует разделить на количество добавленных терминов. Результат — ваше (среднее) среднее значение
.
Как рассчитать средний процент?
Для расчета среднего процента:
Все, что вам нужно для деления общего количества предметов, представленных в процентах, на общее количество предметов
Например:
Если из 500 карандашей убрали 200 книг.Просто надо разделить 200 на 500, что равно 0,40.
Каково среднее между двумя числами?
Среднее двух чисел вычисляется путем деления суммы двух чисел на два. Кроме того, вы можете использовать онлайн-калькулятор средних значений, чтобы найти среднее онлайн между любыми двумя или более числами по вашему выбору.
Что такое среднее 100 и 200?
Среднее значение для этих двух заданных чисел 100 и 200 равно 150.
Можете ли вы усреднить среднее значение?
Среднее из усредненных не называется средним. Эксперты показали, что мы не можем взять среднее из средних и надеяться, что оно будет соответствовать среднему.
Какие существуют типы средних значений?
С точки зрения математики, мы, люди, используем три разных типа среднего: среднее, моду и медиану, каждый из которых называется отдельным «нормальным значением».
«Средним» считается то, что вы получите, если будете делить все поровну
Говорят, что «режим» является наиболее распространенным значением
Говорят, что «медианой» является значение в середине набора данных
Почему мы рассчитываем среднее значение?
Несомненно, среднее — это термин, который часто используется в повседневной жизни для выражения количества, типичного для группы людей или вещей.
Средние значения очень полезны как:
Помогает обобщить большой объем данных в одно значение
Проще говоря, это указывает на некоторую изменчивость вокруг сингла в пределах исходных данных
Итак, используйте простой генератор средних значений, чтобы найти среднее число онлайн.
Как называется среднее от среднего?
Когда речь идет об усреднении средних, обычно существует рекомендуемый способ выполнения такой операции.Говорят, что это «средневзвешенные значения», и это отражает тот факт, что количество наблюдений может варьироваться среди разных групп.
Почему использование средних значений плохо?
Всякий раз, когда принимается во внимание среднее значение для работы с неопределенной величиной, помните, что оно в конечном итоге искажает результаты, причина этого только в том, что оно игнорирует влияние неизбежных вариаций. Средние значения обычно мешают инвестициям, бухгалтерскому учету, продажам, производственному планированию и даже прогнозированию погоды.
Среднее и среднее одно и то же?
Да, они оба одинаковые «среднее есть среднее» — «среднее» считается «средним», к которому вы привыкли, когда вы просто складываете все числа, а затем просто делите на количество чисел. . И, если вы не хотите делать это самостоятельно, то просто используйте онлайн-калькулятор среднего среднего, чтобы определить среднее или среднее значение для данной группы чисел.
Что такое средний калькулятор?
Калькулятор среднего значения — это онлайн-инструмент, который поможет вам узнать среднее значение любых данных.
Какое среднее значение между 80 и 100?
90 — это среднее значение между 80 и 100.
Почему средние значения вводят в заблуждение?
Средние значения могут вводить в заблуждение, если распределение набора данных сильно искажено с одной стороны, с небольшим количеством нерепрезентативных выбросов, которые сдвигают среднее значение в своем направлении.
Кроме того, выбросы могут снижать среднее значение, что даже заставляет социологов завышать риски конкретных событий.
Какое среднее значение между 60 и 80?
70 — это среднее 60 и 80.
Какое среднее значение между 85 и 100?
92,5 — это среднее значение 85 и 100.
Какое среднее значение между 70 и 100?
85 — среднее значение между 70 и 100.
Какое среднее значение между 50 и 100?
75 — среднее значение между 50 и 100.
Какое среднее значение между 60 и 100?
80 — это среднее значение между 60 и 100.
Какое среднее значение между 75 и 100?
87,5 — среднее значение между 75 и 100.
Включаете ли вы ноль в среднее значение?
Это будет полностью зависеть от того, являются ли эти значения действительно нулями или отсутствующими значениями. Если это «отсутствующие значения», то их нужно исключить, и счет падает. И если это действительно нули, то их необходимо включить в расчет среднего значения.
Как рассчитать средневзвешенное значение?
Для расчета средневзвешенного значения:
Прежде всего, нужно умножить каждое число на его вес
Далее нужно сложить все взвешенные числа
Затем вы должны разделить сумму на количество точек данных
Как рассчитать средний процент в Excel?
Чтобы рассчитать средний процент в Excel, выполните следующие действия:
Прежде всего, вы должны добавить нужные данные
Далее вы должны выделить все ячейки, затем щелкнуть правой кнопкой мыши и выбрать «Формат ячеек».
Теперь в поле «Формат ячеек» под номером вы должны выбрать проценты, а также указать желаемое количество знаков после запятой
Далее в другой ячейке нужно ввести = СРЗНАЧ(ячейка 1, ячейка 2,…)
Это все ваш средний процент в excel
Какое среднее значение лучше и почему?
Медиана (наряду с квартилями, децилями и процентилями) — лучший способ сегментировать данные на равные группы, независимо от конкретных терминов.Итак, медиана считается лучшей, если вы хотите разделить набор данных на две равные группы.
Среднее значение или медиана более точны?
Проще говоря, ответ зависит от формы базового распределения. Например, если данные являются гауссовскими, говорят, что среднее значение является более точным. Когда речь идет о двойном экспоненциальном распределении, медиана считается более точной.
Подведение итогов:
Независимо от того, сколько у вас чисел, наш калькулятор средних значений специально разработан для отображения точных результатов. Вот почему этот калькулятор средней суммы является идеальным вариантом для получения средних значений.
Каталожные номера:
Из Википедии, бесплатной энциклопедии – Расчет среднего – Формула среднего – Пифагорейские средние – Среднее арифметическое – Среднее геометрическое – Среднее гармоническое – Неравенство относительно AM, GM и HM – Статистическое положение – Мода – Медиана – Средний диапазон – Сводка типов – Разные типы — Средняя доходность в процентах и CAGR — Скользящее среднее
Из источника toppr – Количественные способности – Средние значения – Среднее значение данных – Наиболее распространенные способы определения меры центральной тенденции
Из научных источников – Математика – Вероятность и статистика – (СРЕДНЕЕ) Среднее/медиана/мода – Недавно обновлено Лизой Мэлони – Как и зачем вычислять среднее – Примеры формулы среднего
От источника пустышек — Образование — MathPre — Алгебра — Три типа среднего — Медиана, мода и среднее — Найти медиану — Найти моду — Вычислить среднее значение списка чисел

Сколько в среднем? | TheSchoolRun
Мы объясним, что означает термин «среднее» в математике, как найти среднее значение набора данных (и как детей учат делать это в начальной школе) и что такое среднее значение.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Каков средний показатель?
В математике средним значением в наборе чисел является среднее значение , вычисляемое путем деления суммы всех значений на количество значений.
Когда нам нужно найти среднее значение набора данных, мы складываем все значения, а затем делим эту сумму на количество значений .
Нахождение среднего значения: пошаговое описание процесса
Вот пример:
Это сумма, которую миссис Мэнселл потратила на покупку продуктов в прошлом месяце:
Неделя 1 67 фунтов стерлингов
Неделя 2 92
неделя 3 52
неделя 4 38
неделя 5 неделя 73
фунтов стерлингов неделя 6 86 фунтов стерлингов
Чтобы узнать среднюю сумму, которую миссис Мэнселл тратит на еду каждую неделю:
Сложите все значения: 92 + 52 + 38 + 73 + 86 = 408
Затем мы разделим 408 на количество значений (6) с помощью короткого деления. Это дало бы нам ответ 68. Таким образом, мы знаем, что средний расход миссис Мэнселл составлял 68 фунтов стерлингов.
Это также можно назвать нахождением «среднего среднего» набора данных и изучается детьми в 6 классе. В «старой» (до 2014 г.) национальной учебной программе детей также учили находить режим, диапазон и медиана ряда значений. С сентября 2015 года от детей 6-го класса требовалось знать только среднее значение.
Более простая задача, которую можно решить в уме, может быть такой:
Кейран записал баллы, которые он получил за тест по правописанию за первые шесть недель семестра:
Неделя 1 — 8
Неделя 2 — 6
Неделя 3 — 9
Неделя 4 — 8
Неделя 5 — 10
Неделя 6 — 7
Здесь общее количество равно 48, которое затем мысленно делится на 6, чтобы получить средний балл 8.
Детям важно понять, почему мы берем на себя труд найти среднее значение.
Нахождение среднего значения дает нам представление об общем поведении или тенденции – средние расходы миссис Мэнселл на покупки дают нам представление о том, тратит ли она обычно много или мало денег, а средний балл Кейран по правописанию дает нам представление как хорошо он обычно в правописании. Если бы нам дали только одно значение для оценки миссис Мэнселл или Кейрана, это могло бы не отражать их поведение в целом.

Формула среднего | Как рассчитать среднее? (Шаг за шагом)
Формула для расчета среднего
Среднее значение — это значение, которое используется для представления набора значений данных, так как среднее значение вычисляется из всех данных, и эта формула рассчитывается путем сложения всех значений заданного набора, обозначаемого суммированием X, и делением его на количество значений, указанных в наборе, обозначено N.
Среднее = (a ₁ + a ₂ + ….+ а _п ) / п
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторствоСтатья Ссылка будет гиперссылкой
Например:
Источник: Средняя формула (wallstreetmojo.com)
где a _i = i ^th наблюдение
n = количество наблюдений
Объяснение
Расчет среднего значения можно выполнить, выполнив следующие шаги:
Во-первых, определите наблюдения, и они обозначаются как ₁ , ₂ , …. ., a _n соответствует 1 ^st наблюдение, 2 ^nd наблюдение,…., n ^th наблюдение.

Далее определяется количество наблюдений, и оно обозначается n.

Наконец, вычисляется среднее значение путем сложения всех наблюдений и последующего деления результата на количество наблюдений, как показано ниже.

Среднее = (a ₁ + a ₂ + …. + a _n ) / n
Примеры
Пример №1
Возьмем в качестве примера Джона, который поступил в выпускную программу по науке об окружающей среде.Трехлетний курс обучения делится на шесть семестров, и окончательный средний процент рассчитывается на основе процентов, набранных во всех семестрах. Рассчитайте окончательный процент Джона на основе его следующего балла:
Ниже приведены данные для расчета среднего процента.
Дано,
a ₁ = 79%, a ₂ = 81%, a ₃ = 74%, a ₄ = 70%, a ₅ = 82%, a ₆ = n = 6
Используя приведенную выше информацию, расчет среднего значения будет следующим:
Среднее значение = (79% + 81% + 74% + 70% +82% + 85%) / 6
Среднее значение будет –
Таким образом, Дэвид набрал 78 процентов. 5% в выпускной программе.
Использует
Как следует из названия «усреднение», оно относится к центральной точке среди набора наблюдений. Когда он используется в математике, он представляет собой число, которое обычно является средним значением группы чисел. Этот термин часто используется для обозначения числа, которое представляет собой группу людей или вещей. Это очень важно, потому что помогает суммировать большое количество данных в одно значение, а также указывает на некоторую несогласованность вокруг единственного значения в исходных данных, что составляет очень важную часть теории центральной тенденции.
Рекомендуемые статьи
Это руководство по средней формуле. Здесь мы обсудим, как рассчитать среднее значение, используя его формулу и примеры, а также загружаемый шаблон Excel. Вы можете узнать больше о финансировании из следующих статей —
Как найти среднее значение в Excel 2013
Microsoft Excel включает несколько различных способов вычисления итогов или значений на основе данных вашей ячейки. Но если вам нужно знать, как найти среднее значение в Excel 2013, возможно, вам будет сложно найти функцию среднего значения в Excel 2013.
Возможно, вы знаете, как рассчитать среднее значение вручную, и даже можете вычислить его, выполнив пару шагов в Excel. Но на самом деле существует специальная формула, которая позволяет очень быстро найти среднее значение в Excel 2013. Это может сэкономить время и устранить ошибки, которые могут возникнуть при ручном выполнении вычислений.
Недавно мы писали об использовании формулы вычитания в Excel 2013, и опыт работы с подобными базовыми математическими операциями в сочетании с такой настраиваемой формулой Excel может дать вам прочную основу для изучения некоторых из более продвинутых доступных методов. вам в рамках Excel.
Как найти среднее значение в Excel 2013
Откройте электронную таблицу.
Выберите ячейку для формулы.
Щелкните Главная .
Щелкните стрелку справа от AutoSum и выберите Average .
Выберите ячейки для усреднения.
Наша статья продолжается ниже дополнительной информацией о нахождении среднего значения в Excel 2013, включая изображения этих шагов.
Как использовать функцию усреднения в Excel 2013 (руководство с иллюстрациями)
Действия, описанные в этой статье, были выполнены в Microsoft Excel 2013, но они также будут работать в большинстве других версий Excel.
Шаг 1. Откройте электронную таблицу в Excel 2013.
Шаг 2: Щелкните внутри ячейки, где вы хотите отобразить среднее значение.
Шаг 3: Щелкните вкладку
Home в верхней части окна.
Шаг 4: Щелкните стрелку справа от
Автосумма в разделе Редактирование в правой части навигационной ленты, затем щелкните параметр Среднее .
Шаг 5: Выберите ячейки, содержащие значения, для которых вы хотите рассчитать среднее значение, затем нажмите
. Введите на клавиатуре, чтобы рассчитать и отобразить среднее значение.
Как вручную создать формулу среднего значения в Excel 2013
Обратите внимание, что вы также можете вручную создать формулу среднего значения. Формат: =СРЗНАЧ(AA:BB) , где AA — первая ячейка в диапазоне, а BB — последняя ячейка в диапазоне. Вы всегда можете увидеть структуру формулы в электронной таблице, щелкнув ячейку, а затем проверив Панель формул над электронной таблицей. Панель формул показана на изображении ниже.Вы заметите, что формула видна в этом месте, даже если результат формулы отображается в самой ячейке.
Если вам интересно узнать больше об Excel 2013, вы можете прочитать еще несколько статей, которые мы написали по этой теме.
Дополнительные источники
Мэтью Берли пишет технические руководства с 2008 года. Его тексты появились на десятках различных веб-сайтов и были прочитаны более 50 миллионов раз.

РубрикаРазное

ш ₁
X ₁
w ₂
X ₂
ш ₃
X ₃
ш ₄
X ₄
Средневзвешенная формула

Формула взвешенного среднего =	ш ₁ * х ₁ + ш ₂ * х ₂ + ш ₃ * х ₃ + ш ₄ * х ₄
	0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 =	0