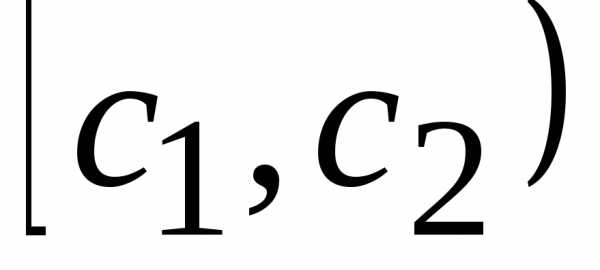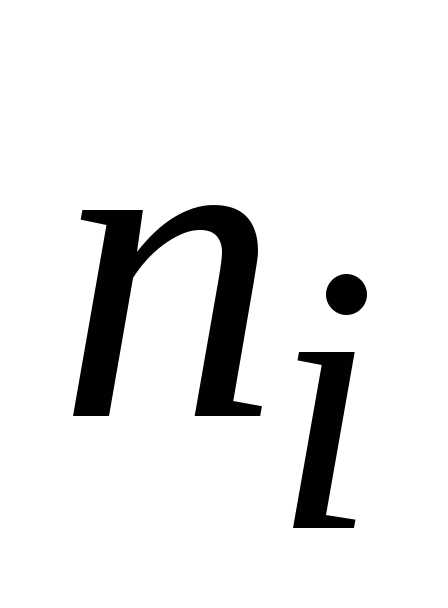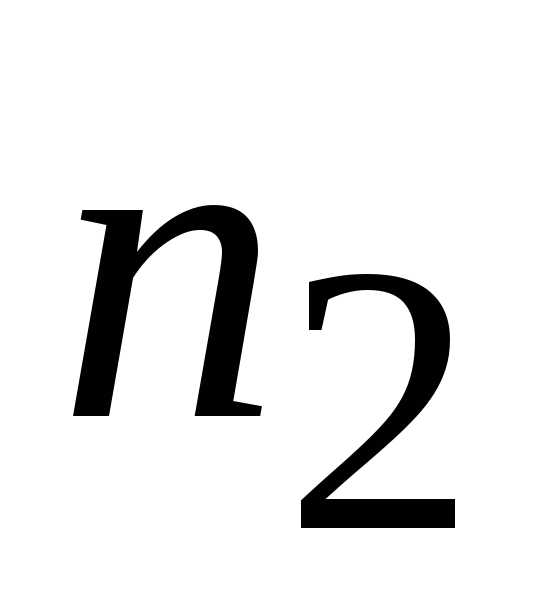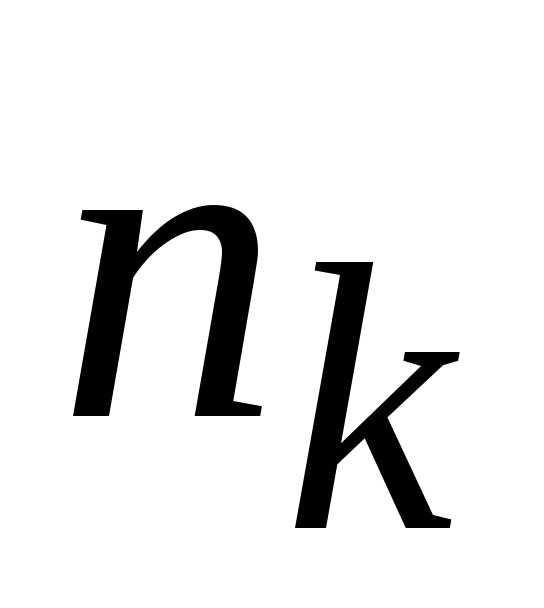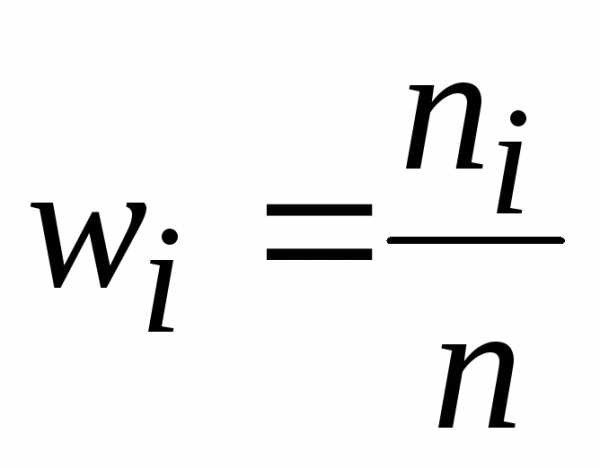Интервальный вариационный ряд построить онлайн – Построение дискретного вариационного ряда
Вариационный ряд — 23 Августа 2014 — Примеры решений задач
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
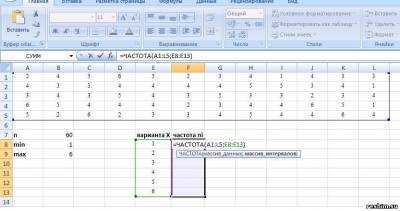
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.
Интервальный ряд | Примеры решений
Условие:
Имеются данные о возрастном составе рабочих (лет): 18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 25, 29, 29.
- Построить интервальный ряд распределения.
- Построить графическое изображение ряда.
- Графически определить моду и медиану.
Решение:
1) По формуле Стерджесса совокупность надо разделить на 1 + 3,322 lg 30 = 6 групп.
Максимальный возраст – 38, минимальный – 18.
Ширина интервала Так как концы интервалов должны быть целыми числами, разделим совокупность на 5 групп. Ширина интервала – 4.
Для облегчения подсчетов расположим данные в порядке возрастания: 18, 22, 22, 23, 24, 24, 25, 25, 26, 26, 27, 27, 28, 28, 28, 29, 29, 29, 29, 29, 30, 30, 31, 32, 32, 33, 34, 35, 38, 38.
Распределение возрастного состава рабочих
Графически ряд можно изобразить в виде гистограммы или полигона. Гистограмма – столбиковая диаграмма. Основание столбика – ширина интервала. Высота столбика равна частоте.
Полигон (или многоугольник распределения) – график частот. Чтобы его построить по гистограмме, соединяем середины верхних сторон прямоугольников. Многоугольник замыкаем на оси Ох на расстояниях, равных половине интервала от крайних значений х.
Мода (Мо) – это величина изучаемого признака, которая в данной совокупности встречается наиболее часто.
Чтобы определить моду по гистограмме, надо выбрать самый высокий прямоугольник, провести линию от правой вершины этого прямоугольника к правому верхнему углу предыдущего прямоугольника, и от левой вершины модального прямоугольника провести линию к левой вершине последующего прямоугольника. От точки пересечения этих линий провести перпендикуляр к оси х. Абсцисса и будет модой. Мо ≈ 27,5. Значит, наиболее часто встречаемый возраст в данной совокупности 27-28 лет.
Медиана (Mе) – это величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда.
Медиану находим по кумуляте. Кумулята – график накопленных частот. Абсциссы – варианты ряда. Ординаты – накопленные частоты.
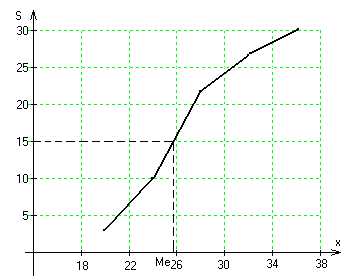
Для определения медианы по кумуляте находим по оси ординат точку, соответствующую 50% накопленных частот (в нашем случае 15), проводим через неё прямую, параллельно оси Ох, и от точки её пересечения с кумулятой проводим перпендикуляр к оси х. Абсцисса является медианой. Ме ≈ 25,9. Это означает, что половина рабочих в данной совокупности имеет возраст менее 26 лет.
3. Интервальный вариационный ряд
При большом
объеме выборки 
работа с
вариационными рядами представляет
определенные неудобства, и тогда
наблюдаемые данные группируют.
Группировка должна наиболее полно выявлять существенные свойства распределения. Существуют формулы для определения оптимального количества интервалов, но в психологии считается, что следует брать от 5 до 15 интервалов
Первый способ построения интервального ряда.
Если
у исследователя нет предварительной
информации о характере распределения
признака, то лучше задавать равные
интервалы,
при этом длина
интервала 
определяется по формул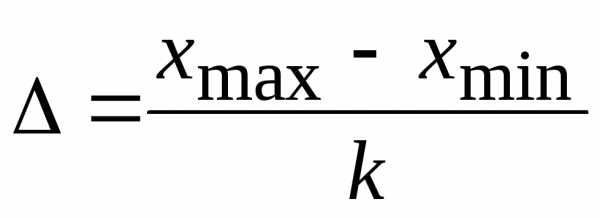е 
,
где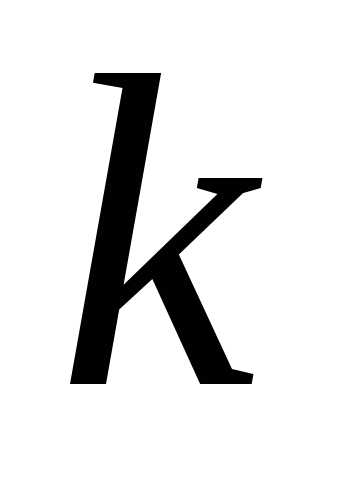
— количество выбранных интервалов (число
округляется до целого значения).
Начало
первого интервала равно
,
а конец(это будет одновременно и началом второго
интервала). Условимся все интервалы
считать соткрытым
правым концом: 
.
Построение интервалов заканчивается,
если в интервал попало наибольшее
значение признака
.
Далее
подсчитывают число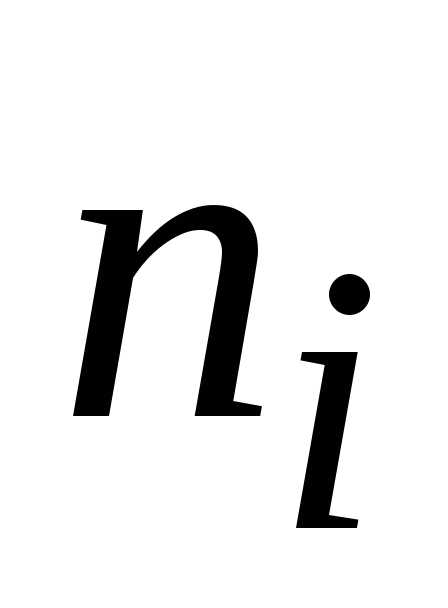 
значений признака, попавших в каждый
интервал (с учетом открытого правого
конца). Получается таблица, называемаяинтервальным
вариационным рядом
Интервалы
…
Сумма
Частоты,
…
Относительные частоты,
1
Второй способ построения интервального ряда.
Весь
диапазон значений признака от 
до
разбивается на равныеинтервалы,
называемые также классами.
Затем все варианты совокупности распределяются
по этим интервалам.
Порядок действий:
Пример построения интервального вариационного ряда.
Пусть измерен некоторый показатель для 30 испытуемых:
23, 29, 35, 7, 11, 18, 23, 30, 36, 18, 11, 8, 13, 20, 25,
27, 14, 30, 20, 20, 24, 19, 21, 26, 22, 16, 26, 25, 33, 27.
Это статистический ряд.
Расставим экспериментальные данные в возрастающем порядке, то есть построим вариационный ряд:
7, 8, 11, 11, 13, 14, 16, 18, 18, 19, 20, 20, 20, 21, 22,
23, 23, 24, 25, 25, 26, 26, 27, 27, 29, 30, 30, 33, 35, 36.
Число
классов (интервалов) для 
:
.
Минимальное
и максимальное значения: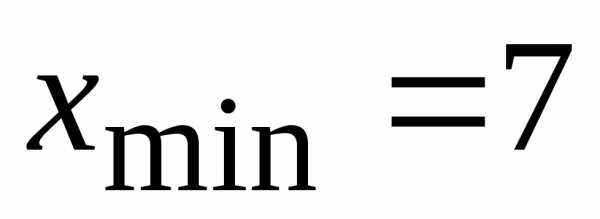 
,.
Вариационный размах: .
Величина интервала: .
Находим границы интервалов:
;
; ;
; ;
; .
Построим интервальный вариационный ряд.
Номера интервалов
Интервалы
Серединные значения интервалов
Частоты
1
4 – 10
7
2
2
10 – 16
13
4
3
16 – 22
19
8
4
22 – 28
25
10
5
28 – 34
31
4
6
34 – 40
37
2
5. Гистограмма
Вариационные ряды изображают графически с помощью полигона и гистограммы.
с1с2с3с4 с5с6с7с8с9
Гистограммой называется графическое изображение интервального вариационного ряда. На оси абсцисс откладываются отрезки, изображающие интервалы значений варьирующего признака, а затем на этих отрезках, как на основаниях, строятся прямоугольники, площади которых пропорциональны частотам (или относительным частотам).
Полигон
частот для
дискретного вариационного ряда — это
ломаная, отрезки которой соединяют
точки с координатами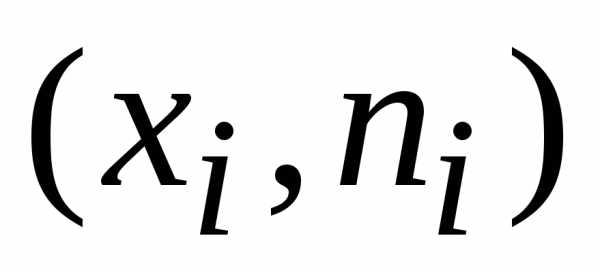 
.
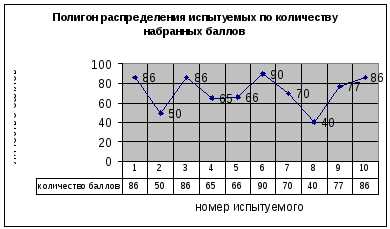
Полигон частот признака
studfiles.net
1.3.Построить дискретный вариационный ряд.
№ п/п | Значение варианты, х | Частота, f | № п/п | Значение варианты, х | Частота, f |
1 | 2 | 5 | 13 | 14 | 1 |
2 | 3 | 8 | 14 | 15 | 1 |
3 | 4 | 9 | 15 | 16 | 2 |
4 | 5 | 9 | 16 | 18 | 1 |
5 | 6 | 6 | 17 | 19 | 1 |
6 | 7 | 7 | 18 | 21 | 2 |
7 | 8 | 6 | 19 | 22 | 1 |
8 | 9 | 12 | 20 | 26 | 1 |
9 | 10 | 16 | 21 | 28 | 1 |
10 | 11 | 4 | 22 | 31 | 1 |
11 | 12 | 2 | 23 | Итого: | 100 |
12 | 13 | 4 |
|
1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.
Для начала определим число интервалов по формуле Стержеса.
n = 1 + 3,322∙lgN, где n – число интервалов, N – общее число единиц совокупности.
n = 1 + 3, 322∙2 = 7,644
Исходя из этого, будем рассматривать интервальный ряд с количеством интервалов 6, 7 и 8. Величину интервала определим по формуле:
Тогда величина интервала для интервального ряда с 5 интервалами равна 5,8, с 6 интервалами – 4,83, с 7 интервалами – 4,14, c 8 интервалами – 3,63.
№ п/п | Значение интервала | Частота, f | № п/п | Значение интервала | Частота, f | ||
1 | 2 — 7.8 | 44 | 1 | 2 – 6.83 | 37 | ||
2 | 7.8 — 13.6 | 44 | 2 | 6.83 – 11.66 | 44 | ||
3 | 13.6 — 19.4 | 6 | 3 | 11.66 – 16.49 | 10 | ||
4 | 19.4 — 25.2 | 3 | 4 | 16.49 – 21.32 | 4 | ||
5 | 25.2 — 31 | 3 | 5 | 21.32 – 26.15 | 2 | ||
Итого: | 100 | 6 | 26.15 – 31 | 2 | |||
| Итого: | 100 |
№ п/п | Значение интервала | Частота, f |
1 | 2 – 6,14 | 37 |
2 | 6,14 – 10.28 | 41 |
3 | 10.28 – 14.42 | 11 |
4 | 14.42 – 18.56 | 4 |
5 | 18.56 – 22.7 | 4 |
6 | 22.7 – 26.84 | 1 |
7 | 26.84 – 31 | 2 |
| Итого: | 100 |
№ п/п | Значение интервала | Частота, f |
1 | 2 – 5.63 | 31 |
2 | 5.63 – 9.26 | 31 |
3 | 9.26 – 12.89 | 22 |
4 | 12.89 – 16.52 | 8 |
5 | 16.52 – 20.15 | 2 |
6 | 20.15 – 23.78 | 3 |
7 | 23.78 – 27.41 | 1 |
8 | 27.41 – 31 | 2 |
| Итого: | 100 |
По полученным данным видно, что наиболее лучший вариант группировки – это интервальный вариационный ряд с 5 интервалами, так как прослеживается тенденция в уменьшении частот, а так же отсутствие интервалов с нулевыми частотами.
№ п/п | Значение интервала | Центр интервала | Частота, f | Накопленная частота |
1 | 2 – 7,8 | 4,9 | 44 | 44 |
2 | 7,8 – 13,6 | 10,7 | 44 | 88 |
3 | 13,6 – 19,4 | 16,5 | 6 | 94 |
4 | 19,4 – 25,4 | 22,4 | 3 | 97 |
5 | 25,4 – 31 | 28,1 | 3 | 100 |
1.5.Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).
Среднеарифметическая взвешенная.
Дискретный вариационный ряд.
,
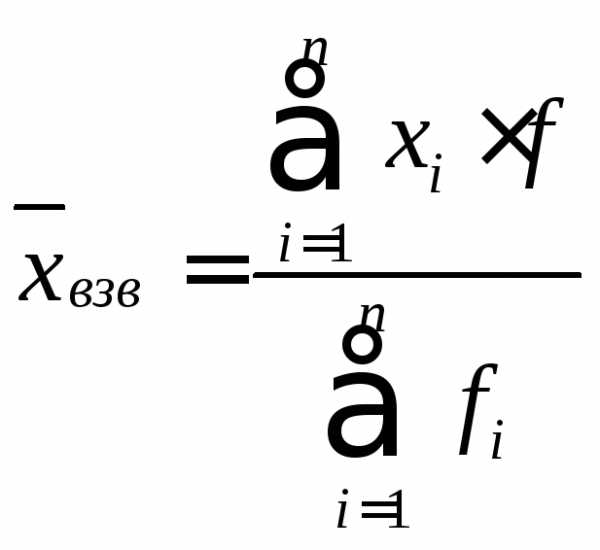где
Σxi∙fi – сумма произведений значений признака и их частот;
Σfi – сумма всех частот.
χ взв = 882/100=8,82
Интервальный вариационный ряд.
,
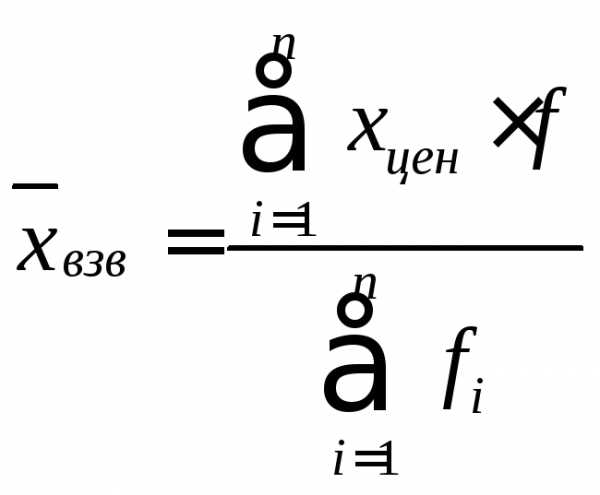где
Σxцен∙fi – сумма произведений центров интервалов и их частот;
Σfi – сумма всех частот.
χ взв = 963,52/100=9,64
Мода.
Дискретный вариационный ряд.
Это вариант имеющий наибольшую частоту f.
Интервальный вариационный ряд.
, где
х0 – нижняя граница модального интервала;
i0 – величина модального интервала;
f1, f2, f3 – частота интервала предшествующего, модального и следующего за модальным.
М0 = 2+5,8*((44-0)/(44-0)-(44-44))=7,8
Медиана.
Дискретный вариационный ряд.
Это вариант стоящий в центре ранжированного ряда.
Интервальный вариационный ряд.
,
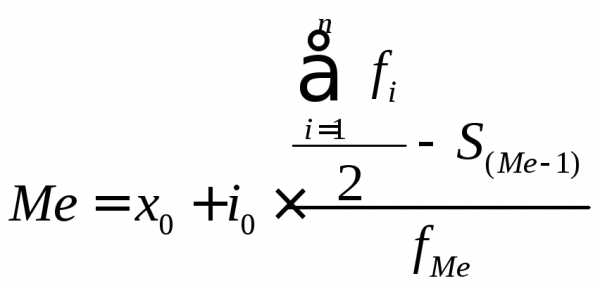где
х0 – нижняя граница медианного интервала;
i0 – величина медианного интервала;
Σfi – сумма всех частот;
S(Me – 1) – сумма накопленных частот интервалов, предшествующих медианному;
fMe – частота медианного интервала.
Размах вариации.
Дискретный вариационный ряд.
R=31 –2 = 29
Интервальный вариационный ряд.
R = 31 – 2 = 29
Среднее линейное отклонение.
Дискретный вариационный ряд.
l = (19,18+17,18+13,18+12,18+10,18+9,18+ 4,36+6,18+5,18+16,72+6,36+8,72+18,88+ 2,16+4,92+12,74+16,92+34,38+43,38+46,56+34,1)/100 = 374,82/100 = 3,75
Интервальный вариационный ряд.
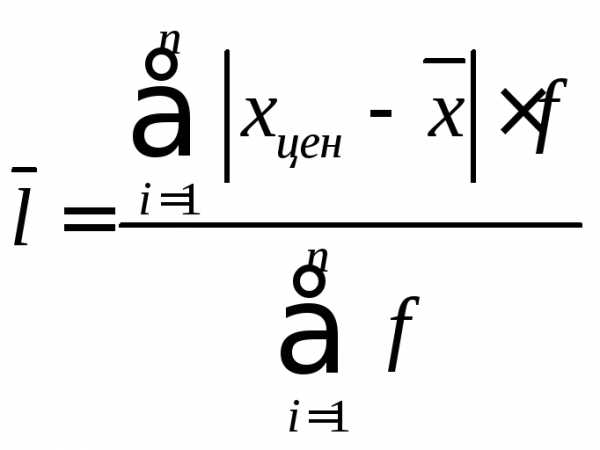
l = (172,48+82,72+46,08+40,74+57,84)/100 = 399,86/100 = 3,99
Дисперсия (средняя квадратов отклонений).
Дискретный вариационный ряд.
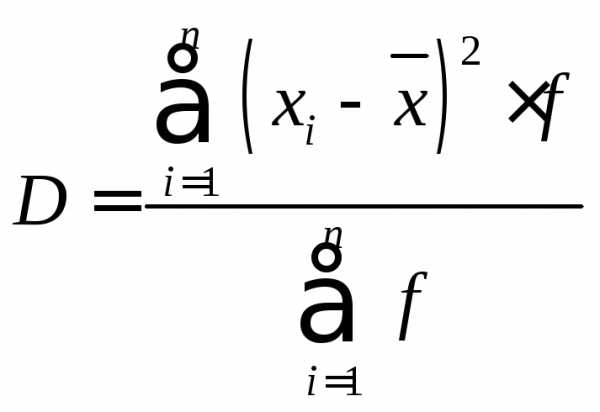
D = (232.56+270.98+209.09+131.33+47.7+
23.19+4.03+0.39+22.28+19+20.22+26.83+38.19+103.1+84.27+103.63+148.35+173.7+295.15+367.87+491.95)/100=2813.81/100=28.14
Интервальный вариационный ряд.
D = (672.12+155.5+353.89+553.25+1115.16)/
100=2853.92/100=28.54
Среднее квадратическое отклонение.
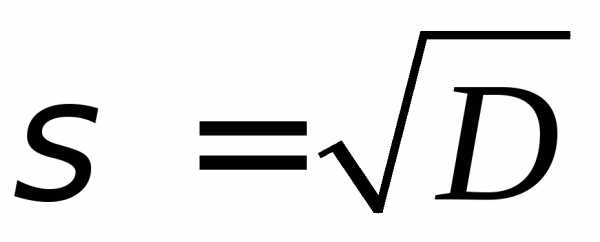
Дискретный вариационный ряд.
σ=√28.14=5.30
Интервальный вариационный ряд.
σ=√28.54=5.34
Коэффициент вариации.
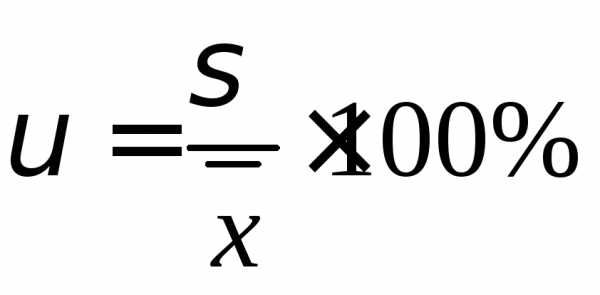
Дискретный вариационный ряд.
υ=(5.30/8.82)*100%=60.09%
Интервальный вариационный ряд.
υ=(5.34/8.82)*100%=60.54%
studfiles.net
Пример построения интервального вариационного ряда
Пусть измерен некоторый экономический показатель в 30 регионах:
23 29 35 7 11 18 23 30 36 18 11 8 13 20 25 27 14 30 20 20 24 19 21 26 22 16 26 25 33 27
Расставим экспериментальные данные в возрастающем порядке:
7 8 11 11 13 14 16 18 18 19 20 20 20 21 22 23 23 24 25 25 26 26 27 27 29 30 30 33 35 36
По таблице 1 определяем число классов
Таблица 1
Объем выборки n | Число классов K |
6-11 | 4 |
12-22 | 5 |
23-46 | 6 |
47-93 | 7 |
94-187 | 8 |
188-377 | 9 |
378-755 | 10 |
756-1515 | 11 |
Для n=30 число классов K=6. Найдем минимальное и максимальное значения вариант: хmin=7, хmax=36. Определим вариационный размах R= хmin-хmax=36-7=29.
Определим величину
классового интервала: =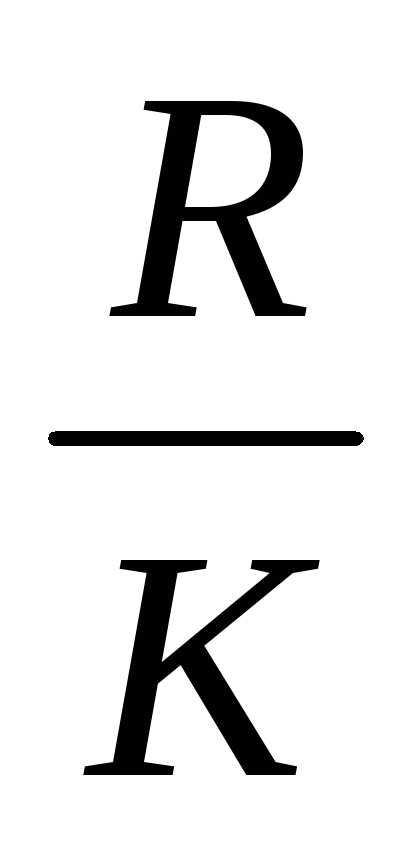
=
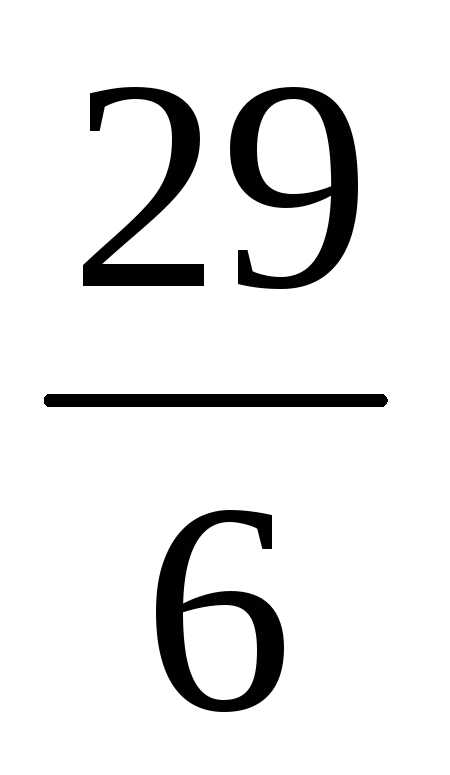=4,8.
Хн1= хmin=7; Хв1= хmin+=7+4,8=11,8
Обобщим полученные данные в таблице:
Таблица 2
Номера классов | Классовые интервалы | Серединные значения классов | Частоты | Накопленные частоты |
1 | 7-11,8 | 9,4 | 4 | 4 |
2 | 11,8-16,6 | 14,2 | 3 | 7 |
3 | 16,6-21,4 | 19 | 7 | 14 |
4 | 21,4-26,2 | 23,8 | 9 | 22 |
5 | 26,2-31 | 28,6 | 5 | 27 |
6 | 31-36 | 33,4 | 3 | 30 |
График, называемый гистограммой получается, если в прямоугольной системе координат отложить по оси абсцисс границы классов, а по оси ординат их частоты.
Если серединные точки вершин прямоугольников гистограммы соединить между собой, получится график дискретного варьирования, называемый полигоном распределения.
рис.1. Полигон распределения.
1.2. Мода распределения – это наиболее часто встречающееся значение ряда.
Среднее арифметическое распределения находится по формуле хср= (х1+х2+х3+ …+хn)/n
Дисперсия распределения находится по формуле:
D=
1.5. Стандартное
отклонение S=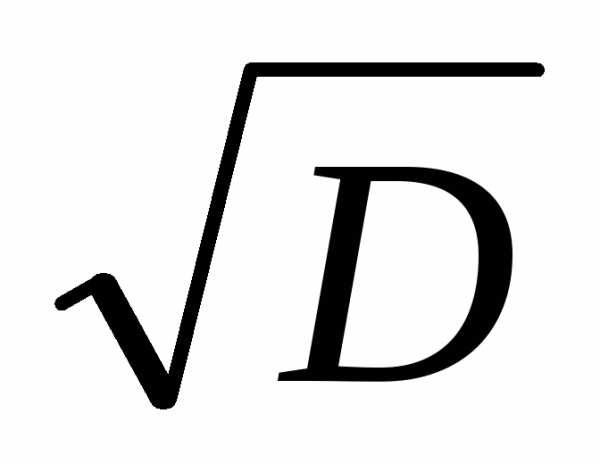
Пример расчета рангового коэффициента корреляции
Пусть при исследовании десяти человек получены следующие показатели Х и Y. Выясним, существует ли между ними связь. Для этого подсчитаем ранговый коэффициент корреляции и дадим его графическую интерпретацию.
Таблица 3
Х | Y |
175 | 2 |
176 | 3 |
179 | 8 |
180 | 9 |
181 | 6 |
184 | 7 |
185 | 13 |
186 | 11 |
191 | 10 |
192 | 12 |
Просуммируем их и подставим в формулу:
rs=1-
.
Таблица 4
№ | X | Y | Rx | Ry | |d| | d2 |
1 | 175 | 2 | 1 | 1 | 0 | 0 |
2 | 176 | 3 | 2 | 2 | 0 | 0 |
3 | 179 | 8 | 3 | 5 | 2 | 4 |
4 | 180 | 9 | 4 | 6 | 2 | 4 |
5 | 181 | 6 | 5 | 3 | 2 | 4 |
6 | 184 | 7 | 6 | 4 | 2 | 4 |
7 | 185 | 13 | 7 | 10 | 3 | 9 |
8 | 186 | 11 | 8 | 8 | 0 | 0 |
9 | 191 | 10 | 9 | 7 | 2 | 4 |
10 | 192 | 12 | 10 | 9 | 1 | 1 |
Сумма: | 30 | |||||
В нашем случае:
rs=1-
=0,81.
Оценим значимость коэффициента корреляции
tфакт.=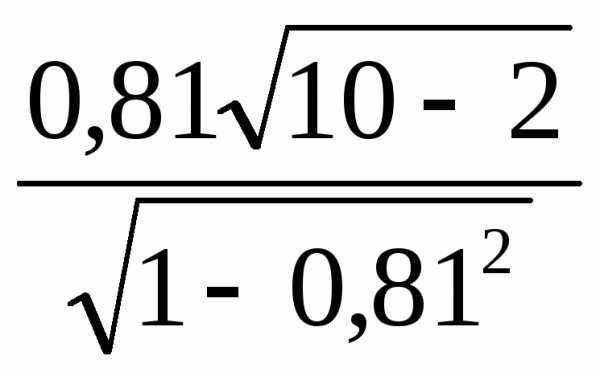
=3,92.
По таблице 5 Приложения 2 определяем, что для уровня значимости р=0,05 tкрит.=2,31. Следовательно, вычисленный коэффициент корреляции значимо отличается от нуля и между показателями х и у наблюдается линейная связь выше среднего.
Для графической интерпретации по оси х откладываются значения признака х, по оси у – значения признака у.
рис.2. Графическая интерпретация коэффициента корреляции.
По значению коэффициента корреляции и графической интерпретации можем сказать, что между признаками х и у есть средняя прямая связь.
studfiles.net
1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.
Для начала определим число интервалов по формуле Стержеса.
n = 1 + 3,322∙lgN, где n – число интервалов, N – общее число единиц совокупности.
n = 1 + 3, 322∙2 = 7,644
Исходя из этого, будем рассматривать интервальный ряд с количеством интервалов 5, 6, 7 и 8. Величину интервала определим по формуле:
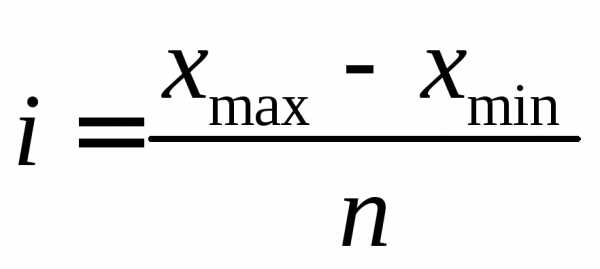
Тогда величина интервала для интервального ряда с 5 интервалами – 6,6, с 6 интервалами равна 5,5, с 7 интервалами – 4,72, с 8 интервалами – 4,125
n=6 n=7 n=8
№ п/п | Значение интервала | Интервальная частота, f | 5,5 | |
1 | 2 – 7,5 | 35 | n=6 | |
2 | 7,5 – 13 | 38 | ||
3 | 13 – 18,5 | 14 | ||
4 | 18,5 – 24 | 8 | ||
5 | 24 – 29,5 | 2 | ||
6 | 29,5 – 35 | 3 | ||
| Итого: | 100 | ||
n=5
№ п/п | Значение интервала | Интервальная частота, f | 4,72 | |
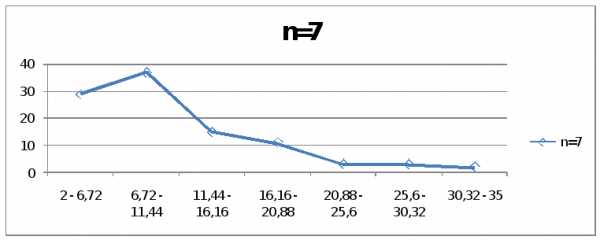
1 | 2 – 6,72 | 29 | n=7 | |
2 | 6,72 – 11,44 | 37 | ||
3 | 11,44 – 16,16 | 15 | ||
4 | 16,16 – 20,88 | 11 | ||
5 | 20,88 – 25,6 | 3 | ||
6 | 25,6 – 30,32 | 3 | ||
7 | 30,32 – 35 | 2 | ||
| Итого: | 100 | ||
№ п/п | Значение интервала | Интервальная частота, f | 4,125 | |
1 | 2 – 6,125 | 29 | n=8 | |
2 | 6,125 – 10,25 | 32 | ||
3 | 10,25 – 14,375 | 16 | ||
4 | 14,375 – 18,5 | 10 | ||
5 | 18,5 – 22,625 | 7 | ||
6 | 22,625 – 26,75 | 1 | ||
7 | 26,75 – 30,875 | 3 | ||
8 | 30,875 – 35 | 2 | ||
| Итого: | 100 | ||
№ п/п | Значение интервала | Интервальная частота, f | 6,6 |
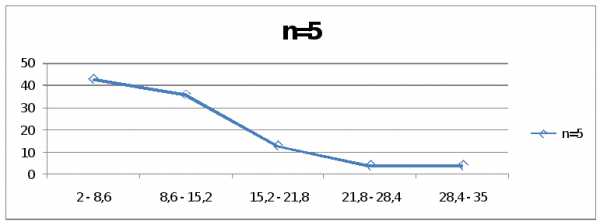
1 | 2 — 8,6 | 43 | n=5 |
2 | 8,6 — 15,2 | 36 | |
3 | 15,2 — 21,8 | 13 | |
4 | 21,8 — 28,4 | 4 | |
5 | 28,4 — 35 | 4 | |
| Итого | 100 |
По полученным данным видно, что наиболее лучший вариант группировки – это интервальный вариационный ряд с 5 интервалами, так как прослеживается тенденция в уменьшении частот, а так же отсутствие интервалов с нулевыми частотами.
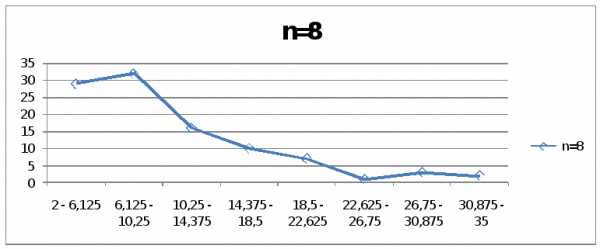
№ п/п | Значение интервала | Центр интервала, xц | Интервальная частота, f | Накопленная частота |
1 | 2 – 8,6 | 5,3 | 43 | 43 |
2 | 8,6 – 15,2 | 12,05 | 36 | 79 |
3 | 15,2 – 21,8 | 18,5 | 13 | 92 |
4 | 21,8 – 28,4 | 25,1 | 4 | 96 |
5 | 28,4 – 35 | 31,7 | 4 | 100 |
| Итого |
| 100 |
|
1.5.Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).
Среднеарифметическая взвешенная.
Дискретный вариационный ряд.
,
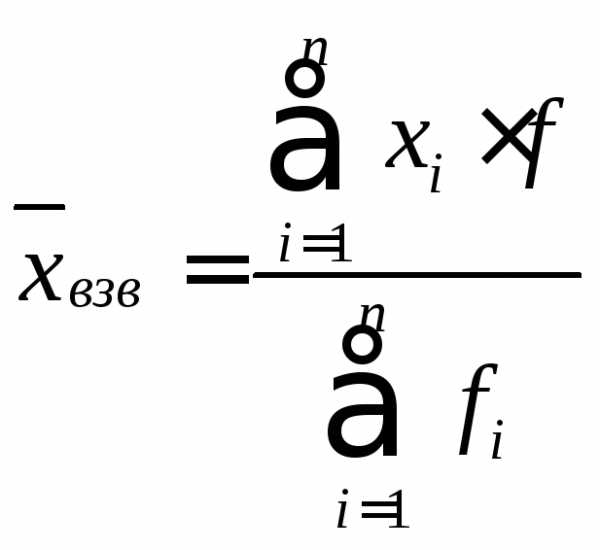где
Σxi∙fi – сумма произведений значений признака и их частот;
Σfi – сумма всех частот.
= 9,96
Интервальный вариационный ряд.
,
где
Σxцен∙fi – сумма произведений центров интервалов и их частот;
Σfi – сумма всех частот.
=
Мода.
Дискретный вариационный ряд.
Это вариант имеющий наибольшую частоту f.
Интервальный вариационный ряд.
, где
х0 – нижняя граница модального интервала;
i0 – величина модального интервала;
f1, f2, f3 – частота интервала предшествующего, модального и следующего за модальным.
=7,676
studfiles.net
вариационный ряд в Excel — Заказать учебники, решебники, методички — Банк готовых работ
Готовый шаблон построение вариационных рядов в Excel на файле.
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
— ЧАСТОТА(массив данных; массив интервалов) – для построение вариационного ряда. Аргументами являются диапазон массива выборочных данных и столбец интервалов. Если требуется построить дискретный ряд, то здесь указываются значения варианты, если интервальный – то верхние границы интервалов (их еще называют «карманами»). Поскольку результатом является столбец частот, введение функции следует завершить нажатием сочетания клавиш CTRL+SHIFT+ENTER. Заметим, что задавая массив интервалов при введении функции, последнее значение в нем можно и не указывать – в соответствующий «карман» будут помещены все значения, не попавшие в предыдущие «карманы». Иногда это помогает избежать ошибки, состоящей в том, что наибольшее выборочное значение не помещается автоматически в последний «карман»
Кроме того, для сложных группировок (по нескольким признакам) используют инструмент «сводные таблицы». Для построения атрибутивных и вариационных рядов их тоже можно использовать, но это излишне усложняет задачу. Также для построения вариационного ряда и гистограммы существует процедура «гистограмма» из надстройки «Пакет анализа» (чтобы использовать надстройки в Excel, их нужно сначала загрузить, по умолчанию они не устанавливаются)
www.reshim.su