Индивидуальные и общие индексы в статистике – 24) Понятие об индексах. Индивидуальные и общие индексы.
24) Понятие об индексах. Индивидуальные и общие индексы.
Индекс-это относительная величина сравнения сложных совокупностей и отдельных единиц. Он показывает во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Индексы – важнейший показатели статистики, которые используются для характеристики развития анализируемых показателей во времени, по территориям, для изучения структуры и взаимосвязей, выявления роли различных факторов в изменении сложных явлений.
Сложная совокупность — совокупность отдельных элементов которые непосредственно не подлежат суммированию. При сравнении отдельных единиц и сложных совокупностей различия условий сравнения могут проявляться:
-во времени (индексы времени)
-в пространстве(территориальные индексы)
-В выборе в качестве базы сравнения какого- либо условного уровня (планового показателя, уровня выполнения договорных обязательств)
Специфика индексов:
1.Индексы позволяют измерить изменения сложных явлений (например, индекс стоимости жизни)
2.Индексы позволяют проанализировать влияние отдельных факторов на изменение того или иного показателя (например, сумма выручки на транспорте)
3.Индексы являются показателями сравнения не только во времени, по территориям, но и другими показателями принятыми за базу сравнения.
Основным элементом индексного отношения является индексируемая величина. Основной элемент-это значение признака статистической совокупности, изменение которой является объектом изучения. (Например, при изучении цен, индексир. величина – цена единицы товара)
В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности
Индивид индекс характеризует изменение отдельных единиц стат совокупности. 1) Индивидуальный индекс цен:
-цена ед. товара в отчетном периоде — в базисном 2) Индивидуальный индекс физического объема продукции: 3) Индивидуальный индекс себестоимости продукции:
Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность 1) Общий индекс товарооборота: 2) Общий индекс суммарных издержек производства:
Важной особенностью общих индексов явл. то, что они обладают синтетическими и аналитическими с-вами.
Синтетич с-ва общих индексов состоит в том, что по средствам индексного метода производится соединение в целое разнородных величин стат. совокупности.
Аналитическое с-во состоит в том, что посредством индексного метода можно выявить влияние отдельных факторов на изменение изучаемого показателя.
( см. №25 агрегатная форма общего индекса)
25) Агрегатная форма общего индекса (индекс Пааше и Ласпейриса)
Основной формой общих индексов являются агрегатные индексы. Свое название они получили от лат. «aggrega» — присоединяю. В числители и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элемента изучаемой статистич. совокупности.
При этом в числителе и знаменателе общего индекса в агрегатной форме изменяется лишь значение индексируемой величины, а их соизмерители являются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода)
Соизмерители необходимы:
-для перехода от натуральных показателей разнородных единиц статистич. совокупности к однородным показателям для их сопоставления
-для выявления влияния факторов на изменения показателя совокупности
1)Общий индекс цен в агрегатной форме:
-Пааше: (соизмеритель )
(Индексируемая величина)
в
этой формуле в числителе
абсолютный прирост или убыль товарооборота за счет изменения цен:
-Ласпейрис: (соизмеритель)
В числителе – стоимость товара в базисном периоде по ценам текущего периода.
В знаменателе — стоимость товара в базисном периоде по ценам базисного периода
Прирост товарооборота при продажи товаров в базисном периоде по ценам текущего периода 2) Общий индекс в форме физического объема:
-Пааше
(соизмеритель)
— Ласпейриса:
2. Индивидуальные индексы. Теория статистики: конспект лекций
2. Индивидуальные индексы
Индивидуальные индексы характеризуют соотношение отдельных элементов совокупности.
Примером индивидуальных индексов может быть процент выполнения плана или динамика выпуска одного вида продукции, процент выполнения плана или динамика себестоимости одного вида продукции или соотношение выпуска одного вида продукции за один и тот же период в разных областях.
Индивидуальный индекс обозначается буквой Он определяется методом сопоставления двух величин, характеризующих уровень исследуемого статистического процесса или явления во времени или в пространстве, т. е. за два сравниваемых периода Период (уровень которого сравнивается) называется отчетным. или текущим, периодом и обозначается подстрочным знаком «I» а период, с уровнем которого проводится сравнение, называется базисным и обозначается подстрочным знаком «О» или «ря», если при внутрифирменном планировании сравнение проводится с планом. Если изменение явлений изучается за ряд периодов то каждый период обозначается соответственно подстрочным знаком «О», «1», «2», «3» и т. д.
В статистике количество обозначают буквой «q», цену – «р». себестоимость – «z», затраты времени на производство единицы продукции – «t».
Индивидуальные индексы выражаются следующим образом:
1) индекс физического объема продукции:
где q1 и q0 – количество произведенной продукции в отчетном и базисном периодах. Данный индекс характеризует изменение физического объема продукции во времени, в пространстве, если сравнивать производство одного и того же вида продукции за один и тот же период времени, но по разным объектам (заводам, территориям и т. д.), и плана, если фактический выпуск сравнивать с плановым заданием;
2) индекс цен:
где р1 и р0 – цена единицы продукции в отчетном и базисном периодах.
Индекс себестоимости:
где z1 и z0 – себестоимость единицы продукции в отчетном и базисном периодах. Индекс трудоемкости:
где t1 и t0 – затраты времени в отчетном и базисном периодах на производство единицы продукции.
Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:
Приведенные выше индексы: цен, физического объема и товарооборота взаимосвязаны между собой:
Эта взаимосвязь показывает, что изменение товарооборота складывается под воздействием динамики цены и изменения объема продажи данного товара.
Индивидуальные индексы по существу – это относительные величины динамики, выполнения плана или сравнения. Индекс как относительный показатель выражается в виде коэффициентов, когда база для сравнения принимается за единицу, и в процентах, когда база для сравнения принимается за 100.
Базисные и цепные индексы
Для определения статистических индексов нужно иметь данные за два периода или два сравниваемых уровня.
Если существуют данные за определенный ряд периодов или уровней, то в качестве базы для сравнения можно принять один и тот же начальный уровень или уровень предыдущего периода. В первом случае получим индексы с постоянной базой –
В экономическом анализе базисные и цепные индексы обладают определенными значениями.
Базисные экономические индексы характеризуют изменение статистических процессов за длительный период времени по отношению к одной отправной точке, но если возникнет необходимость следить за текущими изменениями статистического процесса, то применяются цепные индексы.
Если на основе базисных и цепных индексов исследуется один и тот же период, то это обозначает, что между ними есть взаимосвязь – это произведение цепных индексов, равное базисному Такая взаимосвязь принесет возможность вычислить базисные индексы по данным цепных индексов, и наоборот.
Общие индексы
Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве со–измерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д.
Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода.
Формула общего индекса товарооборота:
Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д.
Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических ин
дексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения.
Расчет агрегатного индекса цен по данной формуле был предложен немецким экономистом Г. Пааше, поэтому его принято называть индексом Пааше.
Поделитесь на страничкеСледующая глава >
econ.wikireading.ru
12.2. Индивидуальные и общие индексы
Индексы различаются по ряду признаков. В зависимости от объектов исследования различают индексы объемных (количественных) и индексы качественных показателей. К объемным относятся индексы, с помощью которых сравниваются количества, общие размеры совокупности того или иного явления. Это, например, индексы физического объема промышленной, сельскохозяйственной продукции, национального дохода и др. Во всех этих индексах количество обычно принято оценивать в неизменных (сопоставимых) ценах. В свою очередь к качественным относятся индексы цен, себестоимости производства продукции, производительности труда, урожайности и другие индексы. Все они исчисляются при сопоставимых фиксированных объемных показателях.
По степени охвата элементов совокупности различают индивидуальные, групповые и общие индексы. Индивидуальные индексы дают сравнительную характеристику отдельных элементов той или иной совокупности. Примером индивидуальных индексов может быть изменение объема производства какого-нибудь одного вида продукции, цен на один вид товара, урожайности одной культуры и т.д. Индивидуальные индексы количества какого-либо вида продукции рассчитываются по формуле:
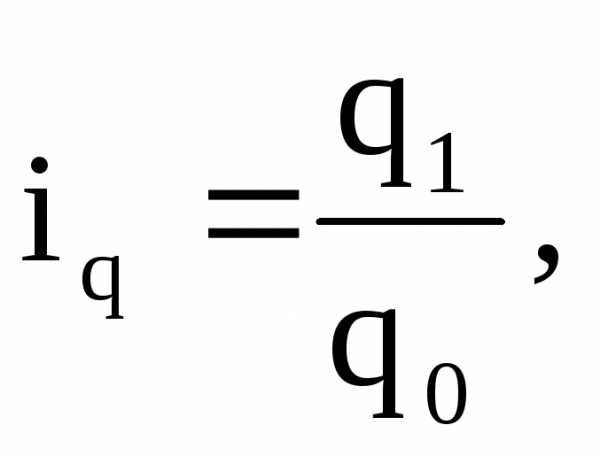(12.3)
где iq – индивидуальный индекс физического объема (количества) товара; q1, q2, физический объем (количество) товара соответственно в отчетном и базисном периодах.
Например, сельскохозяйственная организация продала следующее количество молока (поквартально): в I кв. –500 т, во 2-м – 600 т, в 3-м –700, в 4-м –450 т. Необходимо рассчитать индивидуальные индексы реализации молока за каждый последующий квартал по сравнению с первым кварталом:
За 2 квартал:
За 3 квартал:
За 4 квартал:
Следовательно, продажа молока в сельскохозяйственной организации во 2 и 3 кварталах шла с нарастанием, а в 4 квартале наблюдалось снижение.
Целесообразно отметить, что рассмотренные в 11 главе базисные и цепные коэффициенты роста могут считаться индивидуальными индексами.
Групповые индексы (субиндексы) характеризуют изменение отдельных, обычно однородных групп (частей) сложного явления. Так, например, индекс валовой продукции сельскохозяйственной организации в 2004 г. по сравнению с 2000 г. составил 150 %, а индексы продукции растениеводства – 138 %, продукции животноводства – 162 %. В этом примере индексы продукции растениеводства и животноводства выступают как групповые или субиндексы, входящие в общий индекс объема валовой продукции сельскохозяйственной организации. Групповые индексы имеют важное экономическое значение. Они помогают раскрыть закономерности в изменении структуры, в развитии отдельных частей изучаемого явления. Отметим, что групповые индексы по методике расчета аналогичны общим индексам.
Общие индексы характеризуют изменение всей совокупности в целом. Общий индекс может быть исчислен двумя способами: первый заключается в том, что сначала отыскивают общие соизмерители (веса) для индексируемых величин отчетного и базисного периодов, рассчитывают произведения, которые суммируют, и затем исчисляют отношение этих двух сумм. При втором способе сначала исчисляют индивидуальные индексы, характеризующие изменение отдельных элементов сложного явления, а затем – среднюю величину изменений всех сопоставимых элементов. Общие индексы, исчисленные первым способом, называются агрегатными, а вторым – средними. Агрегатные и средние индексы более подробно рассматриваются ниже.
В зависимости от базы сравнения различают базисные и цепные индексы. Необходимо обратить внимание на то, что базисные и цепные индексы, как индивидуальные, так и общие, могут быть рассчитаны только в том случае, если имеются данные не за 2, а за 3,4,5 и более периодов, или по 3,4,5 и более сравниваемым объектам.
Индексы, исчисляемые путем сравнения данных поочередно каждого последующего с данными одного периода, принятого за базу сравнения, называются базисными индексами. Например, общими базисными индексами физического объема товаров являются следующие:
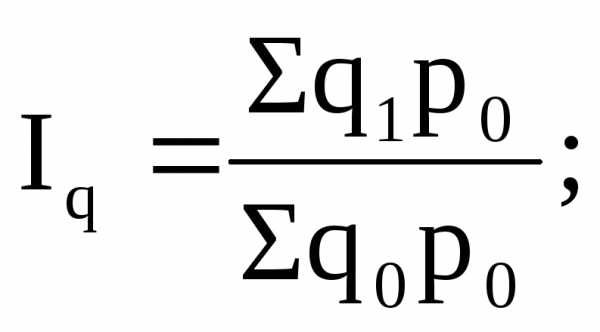
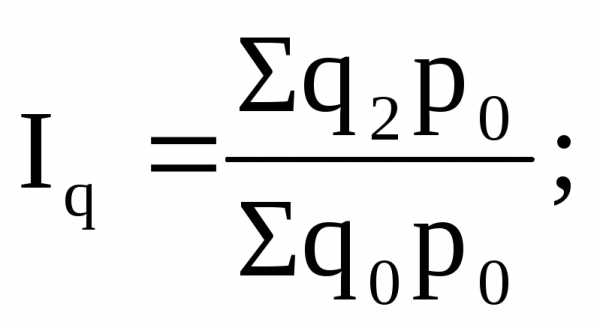
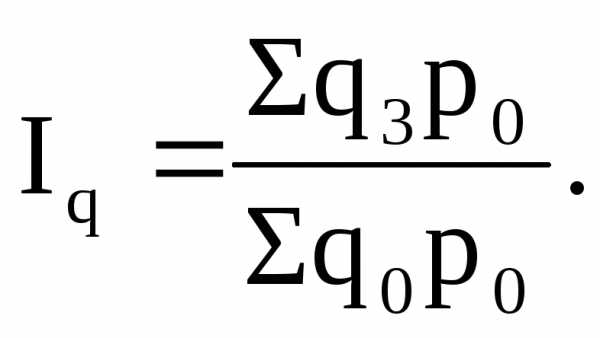
При этом отметим, что в знаменателе этих индексов общая (единая) база сравнения (Σ q0 p0).
Найдем общие базисные индексы физического объема по данным о реализации продукции молокоперерабатывающей организации за период 2001-2004 гг. Для этого прежде всего рассчитаем вспомогательные данные (табл. 12.1).
Полученные в табл. 12.1 итоговые суммы стоимости продукции за каждый год являются основой для расчета общих базисных индексов физического объема (количества):
за 2002 г. –
за 2003 г. –
за 2004 г. –
Таким образом, найденные индексы показывают, что общий объем реализованной продукции в молокоперерабатывающей организации в динамике неуклонно возрастает, причем базисные темпы роста повышаются из года в год. Это свидетельствует о динамичном, поступательном улучшении хозяйственной и экономической работы организации.
Индексы, исчисляемые путем сравнения данных каждого последующего периода с данными каждого предыдущего периода, принято называть цепными. Общие цепные индексы физического объема товаров за ряд периодов можно выразить следующим образом:
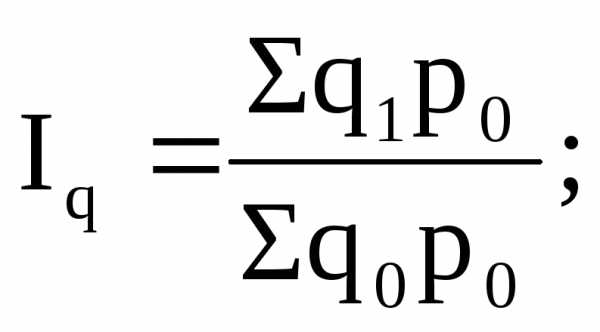
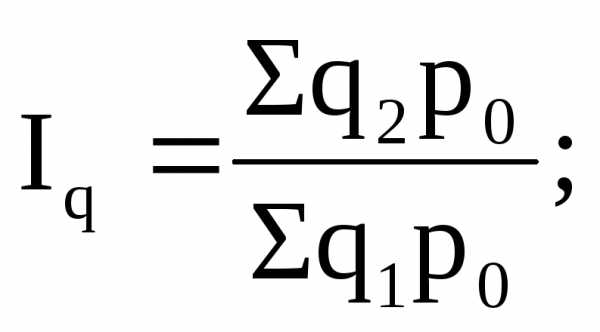
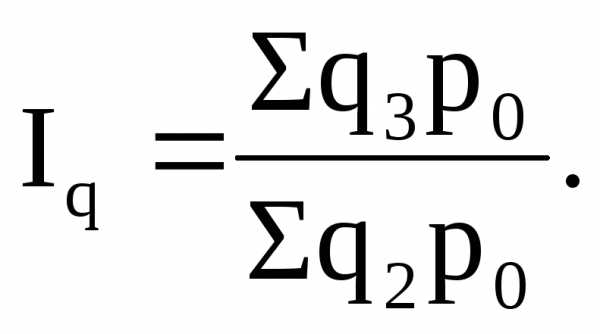
Необходимо отметить, что в знаменателе цепных индексов база сравнения систематически меняется.
Для расчета и оценки общих цепных индексов физического объема воспользуемся данными предыдущего примера, т.е. результатами реализации продукции молокоперерабатывающей организации за период 2001 –2004 гг. Все вспомогательные показатели приведены в табл. 12.1.
Итоговые суммы за каждый год, полученные в табл. 12.1, являются базой для расчета общих цепных индексов физического объема (количества):
за 2002 г. –
за 2003 г. –
за 2004 г. –
Результаты расчета цепных индексов показывают, что молокоперерабатывающая организация за изучаемый период (2001 – 2004 гг.) имела относительно стабильные (от 3 до 6 %) темпы прироста товарной продукции.
studfiles.net
СТАТИСТИЧЕСКИЕ ИНДЕКСЫ
Само слово «индекс» (index) означает показатель. Обычно этот термин используется для некоторой обобщающей характеристики изменений. Например, индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т.д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ.
В практике статистики индексы, наряду со средними величинами, являются наиболее распространенными статистическими показателями. Но индексы имеют три принципиальных отличия.
Во-первых, индексы позволяют измерить изменение сложных явлений (неоднородных статистических совокупностей). Например, нужно определить, как изменились за год расходы жителей г. Луганска на городской транспорт. Для ответа на этот вопрос необходимо знать численность пассажиров, перевезенных за год каждым видом транспорта, рассчитать среднемесячную численность пассажиров или взять точные данные из отчетов по месяцам, умножить численность на тариф перевозки (и число месяцев его действия – в случае использования среднемесячной численности) и полученные величины просуммировать. То же нужно сделать по данным за прошлый год. Затем сопоставить сумму расходов за последний год с суммой за прошлый год. То есть это не просто средние двух чисел, как при расчете, например, темпов динамики или приростов, а получение и сравнение некоторых агрегатированных величин.
Во-вторых, индексы позволяют проанализировать изменения – выявить роль отдельных факторов. Например, можно определить, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров, изменения тарифов, наконец, за счет соотношения в объеме перевозок разными видами транспорта.
В-третьих, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами. Например, интересно знать, не только как изменилось среднедушевое потребление мяса в Украине в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого потребления мяса в Украине и в развитых странах Запада, Востока. А также провести сравнение с нормативной величиной, отвечающей нормам рационального питания. Очевидно, что каждое направление сравнения вносит что-то новое.
Существует множество определений индекса.
Индекс – это показатель сравнений двух состояний одного и того же социально-экономического явления и представляет собой относительную величину, получаемую в результате сопоставления уровней сложных явлений во времени, в пространстве или с планом.
Индекс – это показатель, который сочетает в себе качества средних и относительных величин одновременно Обычно их применяют для характеристики сложных совокупностей единиц наблюдения, то есть состоящих из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости. Например, в магазине ассортимент товаров состоит из разновидностей, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, консервы – в банках, торты – в штуках, макароны – в пачках и т.д. Для определения общего объема реализации продуктов суммировать данные разнородные товары в натуральных единицах их учета, просто, нельзя, так как результат будет бессмысленным. Для получения обобщающих показателей в сложных статистических совокупностях необходимо применять индексный метод.
Индексный метод представляет собой совокупность приемов, которая исторически возникла для измерения динамики социально-экономических явлений. Это сравнительно молодой метод в статистике. В простейшей форме его стали применять более 100 лет тому назад, но по-настоящему этот метод начал развиваться значительно позднее, когда появились большие теоретические работы и практические исследования в этой области.
Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.
В зависимости от степени охвата и характера подвергнутых обобщению единиц изучаемой совокупности все индексы, употребляемые в статистике, делятся на два класса: индивидуальные (элементарные) и общие (сложные).
Индивидуальные индексы – это относительные числа, характеризующие изменения во времени показателей, относящихся к однородному объекту (к одной статистической совокупности), или изменения во времени показатели одновременно существующих однородных объектов (изменения уровней однотипных явлений). Индивидуальные индексы вычисляются просто. Если, например, требуется показать динамику цены или производительности труда, урожайности пшеницы или любой другой культуры с помощью индивидуальных индексов, то берут величину текущего периода и делят ее на величину сравниваемого периода.
Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц сложной статистической совокупности или изменение сложных общественных явлений во времени.
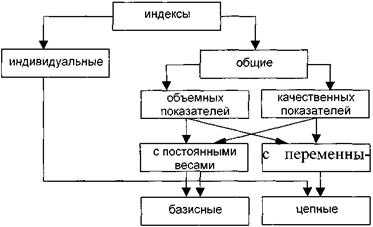
Рис. 13.1. Классификация статистических индексов
Общие индексы подразделяются на индексы объемных и качественных показателей.
К объемным показателям относятся:
— физический объем продукции (обозначается буквой ). Выражается в натуральных единицах объема: кг, литры, метры, мешки, банки, ящики;
— объем продукции или услуг (товарооборот), выраженный в стоимостной форме (обозначается буквами ). Выражается в денежной форме: грн., доллар.
К качественным показателям относятся:
— цена продукции или услуг (обозначается буквой ). Выражается в денежной форме: грн., доллар;
— себестоимость продукции или услуг (обозначается буквой ). Выражается в денежной форме: грн., доллар;
— затраты на производство продукции (обозначается буквами ). Выражается в денежной форме: грн., доллар.
При вычислении индексов различают сравниваемый уровень (отчетный период), и уровень, с которым производится сравнение, называемый базисным. Если показатель относится к сравниваемому (отчетному) уровню, то индексируемой величине присваивается символ «1» (например, – цена товара за отчетный период), а если показатель относится к базисному периоду, то индексируемой величине присваивается символ «0» (например, — объем продукции за базисный период).
Выбор базы сравнения определяется целью исследований. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком-либо периоде, предшествующем отношению. При этом возможны два способа расчета индексов – цепной и базисный.
Цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
Базисные индексы получают сопоставлением текущих уровней с уровнем периода, принятого за базу сравнения, т.е. база сравнения остается неизменной.
При использовании индексов как показателей выполнения плана, за базу сравнения принимаются плановые показатели.
В статистике индивидуальные индексы принято обозначать буквой «», а общие индексы – буквой «».
Рассмотрим порядок вычисления индивидуальных индексов. Как уже отмечалось, индивидуальные индексы определяются как отношение уровня исследуемого показателя за отчетный период к уровню того же показателя за базисный период. При этом основным элементом индексного отношения является индексируемая величина, под которой понимается значение показателя за отчетный период. Ее всегда записывают в числителе индексного отношения.
Индивидуальные индексы объема реализации или производства товаров определяют по формуле:
(13.1)
где – индивидуальный индекс объема продукции;
– объем продукции в текущем (отчетном) периоде;
– объем продукции в базисном периоде.
Индивидуальные индексы цены продукции или услуг определяются по формуле:
(13.2)
где – индивидуальный индекс цены продукции;
и – цена продукции в текущем (отчетном) и базисном периодах;
Индивидуальный индекс себестоимости продукции определяется по формуле:
(13.3)
где – индивидуальный индекс себестоимости продукции;
и – себестоимость продукции в текущем (отчетном) и базисном периодах;
Пример. Пусть предприятие во II квартале 2000 года изготовило 100 утюгов, которые реализовало по цене 60 грн. за 1 шт. При этом себестоимость изготовления утюгов равнялась 40 грн. за 1 шт. Во II квартале 2001 года это предприятие изготовило только 90 утюгов и реализовало их по цене 70 грн. за 1 шт. При этом себестоимость производства утюгов достигла 45 грн. за 1 шт.
Вычислим индивидуальные индексы объема, цены и себестоимости производства утюгов.
;;
На данном предприятии во II квартале 2001 г. по сравнению с тем же периодом 2000 г:
объем производства снизился на;
но при этом возросла цена продукции на ;
а себестоимость – возросла на .
Индивидуальные индексы для статистических исследований вычисляются крайне редко, так однородных совокупностей практически не бывает.
Основной формой общих индексов являются агрегатные индексы («aggrega» (лат.) – присоединять). В числители и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых сложных статистических совокупностей.
Для достижения сопоставимости разнородных единиц в сложных статистических совокупностях в индексные соотношения вводят специальные сомножители – так называемые, соизмерители. Они необходимы для перехода от натуральных измерений разнородных единиц к однородным показателям. При этом в числителе и знаменателе общего индекса изменяются лишь значения индексируемой величины, а их соизмерители остаются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода). Это необходимо для того, чтобы на величине индекса называлось лишь влияние фактора, который определяет изменения индексируемой величины.
Общий индекс цены.
(13.4)
Цена является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема () и обозначение его периода берем по числителю обозначения периода вычисления цены () (отношение цены в отчетном периоде к базисному ).
Общий индекс физического объема.
(13.5)
Физический объем является количественным показателем, поэтому соизмерителем берем качественный показатель цены () и его период берем по знаменателю обозначения периода вычисления физического объема () (отношение физического объема в отчетном периоде к базисному )
Общий индекс себестоимости..
(13.6)
Себестоимость является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема () и обозначение его периода берем по числителю обозначения периода вычисления себестоимости () (отношение себестоимости в отчетном периоде к базисному )
Общий индекс товарооборота.
(13.7)
Общий индекс затрат на производство.
(13.8)
Рассмотрим индексный метод изучения динамики сложных статистических совокупностей на примерах.
Пример. Пусть имеются сведения о ценах и реализации товаров за два периода. Эти данные приведены в табл. 13.1.
Как видно из табл. 13.1, совокупность товаров разнородная (единицы измерения). Определим агрегатный индекс цен.
,
т.е. цены возросли в целом на 13,9%. В данном примере цена – индексируемый показатель, а объем — вес, взятый за отчетный период.
Таблица 13.1
Реализация товаров
Товар | Единица измерения | I период (базисный) | II период (отчетный) | Индивидуальные индексы | |||
Цена за единицу товара, грн., () | Количество товара, () | Цена за единицу товара, грн., () | Количество товара, () | Цены, | Физического объема, | ||
А | т | 20 | 7500 | 25 | 9500 | 1,25 | 1,27 |
Б | м | 30 | 2000 | 30 | 2500 | 1,0 | 1,25 |
В | шт | 15 | 1000 | 10 | 1500 | 0,67 | 1,5 |
Можно в качестве весов взять объем и за базисный период. Тогда агрегатный индекс цен будет иметь вид:
,
т.е. цены возросли на 14,4 % (114,4-100 = 14,4%).
Используя два варианта расчета, получаем разное значение индекса цен. Какой из них ближе к реальному и принимать за действительный зависит от цели исследований.
Общее правило построения общих индексов.
— в исходные данные вводят необходимые буквенные обозначения;
— записывают формулу общего индекса;
— числитель и знаменатель формулы общего индекса расписывают в табличном виде;
— производят промежуточные расчеты;
— результаты вычислений подставляют в формулу общего индекса;
— вычисляют общий индекс и делают выводы.
Для того чтобы по двум известным индексам определить третий неизвестный, в статистике используется взаимосвязь между общими индексами. Индекс реализации продукции (товарооборота) равен произведению общего индекса физического объема на общий индекс цен, а индекс затрат на производство продукции равен произведению общего индекса себестоимости продукции на общий индекс физического объема.
(13.9)
(13.10)
При анализе хозяйственной деятельности предприятий и организаций использование общих индексов в ряде случаев затруднено из-за отсутствия отдельных отчетных данных, особенно при вычислении планируемых показателей. Поэтому на практике часто используют формулы расчета общих индексов как величин, средних из соответствующих индивидуальных индексов. В этом смысле общий индекс изучаемого явления рассматривается как результат изменения уровня данного явления у отдельных единиц совокупности. В процессе осреднения индивидуальных индексов веса подбираются такими, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме. И наоборот, агрегатная форма общего индекса позволяет выбрать взвешивающий показатель при расчете общего индекса в виде средней величины.
Средневзвешенный индекс – это средний из индивидуальных индексов, взвешенных на объемы, имеющие одинаковую размерность и зафиксировнные на неизменном уровне.
Средневзвешенный индекс физического объема получают, если преобразования делаются в числителе общего индекса, т.е. в среднеарифметической форме, через соответствующий индивидуальный индекс. При этом условный товарооборот , т.к. .
(13.11)
Средневзвешенный индекс цен получают, если преобразования делаются в знаменателе общего индекса, т.е. в среднегармонической форме.
(13.12)
При этом условный товарооборот вычисляется через индивидуальный индекс цен , откуда , а
При изучении коммерческой деятельности предприятий приходится осуществлять индексные сопоставления более чем за два периода. Поэтому индексные величины могут вычисляться как с постоянной, так и с переменной базами сравнения. При этом, если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляются базисные индексы. Но если требуется охарактеризовать последовательное изменение изучаемого явления из периода в период, то вычисляются цепные индексы.
В зависимости от задачи исследований и характера исходной информации, базисные и цепные индексы исчисляются как индивидуальные (однотоварные), так и общие. Способы расчета индивидуальных базисных и цепных индексов аналогичны расчету относительных величин динамики. Общие индексы, в зависимости от их вида (экономического содержания), вычисляются с переменными и постоянными весами – соизмерителями. Так, рассмотренная выше агрегатная форма общего индекса физического объема вычисляется как индекс с постоянными весами. Агрегатная форма общего индекса цен исчисляется как индекс с переменными весами.
Индивидуальные индексы физического объема.
Таким же образом можно записать индивидуальные индексы цены и себестоимости.
Общие индексы.
Общие индексы физического объема (цепные) в среднеарифметической форме:
; ;
Общие индексы цены (базисные) в среднегармонической форме:
; ;
Общие индексы цены (цепные) в среднегармонической форме:
; ;
Абсолютное изменение вычисляется как разность между числителем и знаменателем соответствующего индекса. Например, абсолютное изменение товарооборота в целом раскладывается на две составляющие:
за счет изменения цен
и за счет изменения физического объема товаров
Цепные и базисные индексы с постоянными весами находятся во взаимосвязи:
1. Произведение цепных индексов дает базисный индекс последнего периода:
2. Деление последующего базисного индекса на предыдущий базисный индекс дает цепной индекс последующего периода. В индексах с переменными весами такой зависимости нет.
Прогноз – это результат научной деятельности, направленной на выявление возможных состояний объектов в будущем, а также альтернативных путей и сроков достижения этого состояния. Прогнозирование – процесс разработки обоснованных прогнозов.
При стохастической связи причинная зависимость между факторными и результативными признаками проявляется не в каждом отдельном случае, а лишь при большом числе наблюдений, т.е. с изменением одной величины меняется распределение другой.
Индекс Доу-Джонса — средний показатель курсов акций группы крупнейших компаний США. Индекс публикуется фирмой «Dow Jones & Company» и представляет среднеарифметическое ежедневных котировок на момент закрытия биржи. Различают индексы Доу-Джонса для акций коммунальных, промышленных и транспортных компаний. Индекс Доу-Джонса служит показателем текущей хозяйственной конъюнктуры США и отражает реакцию американских деловых кругов на различные экономические и политические события.
www.ekonomstat.ru
Индексы и их значение в статистике. Индивидуальные индексы, их виды
В статистической практике индексный метод имеет такое же широкое распространение, как и метод средних величин.
Индексами называют сравнительные относительные величины, которые характеризуют изменение сложных социально-экономических показателей (показатели, состоящие из несуммируемых элементов) во времени, в пространстве, по сравнению с планом.
Индекс — это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.
Индексы формируют важнейшие экономические показатели национальной экономики и ее отдельных отраслей. Индексные показатели позволяют осуществить анализ результатов деятельности предприятий и организаций, выпускающих самую разнообразную продукцию или занимающихся различными видами деятельности. С помощью индексов можно проследить роль отдельных факторов при формировании важнейших экономических показателей, выявить основные резервы производства. Индексы широко используются в сопоставлении международных экономических показателей при определении уровня жизни, деловой активности, ценовой политики и т.д.
Существует два подхода в интерпретации возможностей индексных показателей: обобщающий (синтетический) и аналитический, которые в свою очередь определяются разными задачами.
Суть обобщающего подхода — в трактовке индекса как показателя среднего изменения уровня исследуемого явления. В этом случае основной задачей, решаемой с помощью индексных показателей, будет характеристика общего изменения многофакторного экономического показателя.
Аналитический подход рассматривает индекс как показатель изменения уровня результативной величины, на которую оказывает влияние величина, изучаемая с помощью индекса. Отсюда и иная задача, которая решается с помощью индексных показателей: выделить влияние одного из факторов в изменении многофакторного показателя.
От содержания изучаемых показателей, методологии расчета первичных показателей, целей и задач исследования зависят и способы построения индексов.
По степени охвата элементов явления индексы делят на индивидуальные и общие (сводные).
Индивидуальные индексы (i) — это индексы, которые характеризуют изменение только одного элемента совокупности.
Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. В зависимости от способа изучения общие индексы могут быть построены или как агрегатные (от лат. аggrega — присоединяю) индексы, или как средние взвешенные индексы (средние из индивидуальных).
В статистике имеют большое значение индексы переменного и фиксированного состава, которые используются при анализе динамики средних показателей.
Индексом переменного состава называют отношение двух средних уровней.
Индекс фиксированного состава есть средний из индивидуальных индексов. Он рассчитывается как отношение двух стандартизованных средних, где влияние изменения структурного фактора устранено, поэтому данный индекс называют еще индексом постоянного состава.
В зависимости от характера и содержания индексируемых величин различают индексы количественных (объемных) показателей и индексы качественных показателей.
К индексам количественных (объемных) показателей относятся такие индексы, как индексы физического объема производства продукции, затрат на выпуск продукции, стоимости продукции, а также индексы показателей, размеры которых определяются абсолютными величинами. Используются различные виды индексов количественных показателей.
Индекс физического объема продукции (ФОП) отражает изменение выпуска продукции.
Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида
где q1 и q0 — количество продукции данного вида в натуральном выражении в текущем и базисном периодах.
Аналогично рассчитывается индекс затрат на выпуск продукции (ЗВП), который отражает изменение затрат на производство и может быть как индивидуальным, так и агрегатным.
Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле
где z1 и z0 — себестоимость единицы продукции искомого вида в текущем и базисном периодах; q1 z1 и q0 z0 — суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах.
Рассмотрим построение индекса стоимости продукции (СП), который может определяться и как индивидуальный, и как агрегатный.
Индивидуальный индекс СП характеризует изменение стоимости продукции данного вида и имеет вид:
где p1 и p0 — цена единицы продукции данного вида в текущем и базисном периодах; q1 p1 и q0 p0 — стоимость продукции данного вида в текущем и базисном периодах.
Качественные показатели определяют уровень исследуемого итогового показателя и определяются путем соотношения итогового показателя и определенного количественного показателя (например, средняя заработная плата определяется путем соотношения фонда заработной платы и количества работников). К индексам качественных показателей относятся индексы цен, себестоимости, средней заработной платы, производительности труда.
Самым распространенным индексом в этой группе является индекс цен.
Индивидуальный индекс цен характеризует изменение цен по одному виду продукции
где p1 и p0 — цена за единицу продукции в текущем и базисном периодах.
Соответственно определяются индексы себестоимости и затрат рабочего времени по каждому виду продукции.
www.ekonomstat.ru
Индивидуальные индексы
16. Наиболее часто употребляемый метод измерения сезонных колебаний – это так называемый индекс сезонности. Порядок расчета индекса сезонности зависит от вида динамического ряда: стационарного или нестационарного. В стационарных (стабильных) рядах динамики, в которых нет ярко выраженной тенденции к росту или снижению, внутригодовые колебания происходят вокруг некоторого постоянного уровня. В этом случае формула расчета индекса сезонности следующая: где уi – фактические уровни ряда; – общий для всего динамического ряда средний уровень. Для того, чтобы получить устойчивую оценку размера сезонных колебаний, на которой не отражались бы особенности условий конкретного года, индекс сезонности рекомендуется рассчитывать за несколько лет, используя следующую формулу: , где Т – число лет.
В стационарных рядах динамики расчет индекса сезонности состоит в определении простой средней арифметической за одни и те же внутригодовые промежутки времени всего изучаемого периода, а затем в сопоставлении полученных средних с общей средней динамического ряда. Формула расчета: где – средний уровень по одноименным внутригодовым отрезкам времени (месяцам, кварталам). При наличии тренда, т. е. в нестационарных рядах динамики, порядок расчета индекса сезонности следующий: 1. По одноименным внутригодовым уровням ряда (месячным, квартальным) за ряд лет определяют расчетные уровни при помощи скользящей средней или методом аналитического выравнивания. 2. Определяется процентное отношение фактических уровней ряда уi и расчетных (выравненных) уровней. 3. Получение показателей сезонности усредняются за все годы. Упрощенная формула расчета индекса сезонности для нестационарных рядов динамики выглядит так: . Наглядное представление о характере колебаний позволяет получить график ‹‹сезонной волны››.
Интерполяцией называется расчет неизвестных уровней динамического ряда, исходя из имеющихся значений того же динамического ряда, либо по данным другого динамического ряда, связанного с характеризуемым. Метод экстраполяции основывается на предположении о неизменности факторов, определяющих развитие изучаемого объекта, и заключается в распространении закономерностей развития объекта в прошлом на его будущее.
Для прогнозирования в зависимости от характера исходной информации могут быть использованы различные группы методов экстраполяции: приемы, основанные на средних показателях динамики; методы, основанные на выявлении основной тенденции; адаптивные методы, учитывающие степень влияния предыдущих уровней. Особое место в прогнозировании занимают методы многофакторного моделирования. Временем упреждения при прогнозировании называется отрезок времени от момента, для которого имеются последние статистические данные, до момента, к которому относится прогноз. Рекомендуется руководствоваться следующим эмпирическим правилом: срок упреждения не должен превышать третьей части длины базы прогноза. Экстраполяция позволяет получить точечное значение прогноза. Однако точное совпадение прогнозных оценок с фактическими данными маловероятно. Следовательно, прогноз должен быть дан в виде интервала значений. Наиболее простым методом прогноза по данным изолированного ряда динамики является использование средних показателей ряда. При отсутствии тенденции можно предположить, что прогнозируемый уровень равен среднему значению уровней в прошлом. На основе нестационарных рядов динамики краткосрочные прогнозы могут быть получены в зависимости от типа развития с помощью среднего абсолютного прироста (если общая тенденция развития является линейной) и среднего темпа роста (в случае тенденции развития по геометрической прогрессии). Эти методы рассматриваются как предварительный прогноз и могут использоваться для оценки качества краткосрочных прогнозов, полученных иными методами, когда проводится сравнение ошибок прогноза. Распространенным методом является прогнозирование на основе экстраполяции тренда. Результаты прогноза зависят от принятого вида уравнения тренда. Долгосрочные прогнозы предполагают многофакторное моделирование динамики. Многофакторное моделирование осуществляется на основе анализа корреляции взаимосвязанных рядов динамики.
17. Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве.
Наиболее распространена сравнительная характеристика во времени. В этом случае индексы выступают какотносительные величины динамики. Индексный метод является также важнейшим аналитическим средством выявления связей между явлениями. При этом применяются уже не отдельные индексы, а их системы. В статистической практике индексы применяются при анализе развития всех отраслей экономики, на всех этапах экономической работы. В условиях рыночной экономики особенно возросла роль индексов цен, доходов населения, фондового рынка и территориальных индексов.
Статистика осуществляет классификацию индексов по следующим признакам:
1. В зависимости от объекта исследования:
индексы объемных (количественных) показателей (индексы физического объема: товарооборота, продукции, потребления)
индексы качественных показателей (индексы цен, себестоимости, заработной плата)
По степени охвата элементов совокупности:
индивидуальные индексы (дают сравнительную характеристику отдельных элементов явления)
общие индексы (характеризуют изменение совокупности элементов или всего явления в целом)
3. В зависимости от методологии исчисления общие индексы подразделяются на:
агрегатные (агрегатные индексы являются основной формой индексов и строятся как агрегаты путем взвешивания индексируемого показателя с помощью неизменной величины другого, взаимосвязанного с ним показателя).
средние (являются производными от агрегатных)
4. В зависимости от базы сравнения различают:
базисные (если при исчислении индексов за несколько периодов времени база сравнения остается постоянной)
цепные (если база сравнения постоянно меняется)
Способы построения индексов зависят от содержания изучаемого явления, методологии расчета исходных статистических показателей и целей исследования. В каждом индексе выделяют 3 элемента:
В каждом индексе выделяют 3 элемента:
индексируемый показатель — это показатель, соотношение уровней которого характеризует индекс
сравниваемый уровень — это тот уровень, который сравнивают с другим.
базисный уровень — это тот уровень, с которым производится сравнение.
Для расчета индекса необходимо найти отношение сравниваемого уровня к базисному и выразить его в виде коэффициента, если база сравнения приравнивается к единице, или в процентах, если база сравнения принимается за 100%. Обычно расчеты индексов производятся в форме коэффициентов с точностью до третьего знака после запятой, т. е. до 0,001, в форме процентов — до десятых долей процента, т.е. до 0,1%.
Для удобства построения индексов используется специальная символика:
i — символ индексируемого показателя — индекс, характеризующий изменение уровня элемента явления.
I — с подстрочным индексируемым показателем — для группы элементов или всей совокупности в целом.
q — количество проданных товаров или произведенной продукции в натуральном выражении
p — цена за единицу товара
z — себестоимость единицы продукции
w — производительность труда
T — отработанное время или численность работников
l — средняя заработная плата одного работника
Исходные данные | Расчетные данные | |||||||||||||
Товары | Базисный период | Отчетный период | Товарооборот млн.руб | Индивидуальные индексы | ||||||||||
Про-дано т.шт | Цена за 1 шт. т.руб | Про-дано т.шт | Цена за 1 шт. т.руб | Базисный период | Отчетный период | Отчетный период по ценам базисного периода | Физ. объема т-ооборота | Цен | Товаро-оборота | |||||
А | 1 | 2 | 3 | 4 | 5=1*2 | 6=3*4 | 7=3*2 | 8=3:1 | 9=4:2 | 10=6:5 | ||||
q0 | p0 | q1 | p1 | q0 * p0 | q1 * p1 | q1 * p0 | ||||||||
Телевизоры | 400 | 3 | 360 | 3,3 | 1200 | 1188 | 1080 | 0,9 | 1,1 | 0,99 | ||||
Видео-магнито-фоны | 200 | 2 | 250 | 1,8 | 400 | 450 | 500 | 1,250 | 0,9 | 1,125 | ||||
Итого | х | х | х | х | 1600 | 1638 | 1580 | 0,9875 | 1,037 | 1,024 | ||||
Индивидуальные индексы характеризуют изменение отдельного элемента явления.
Индивидуальный индекс физического объема товарооборота
Так, для изучения изменения количества проданных товаров (физического объема продаж) следует построить индивидуальный индекс физического объема товарооборота как отношение количества товара одного вида, проданного в отчетном периоде, к количеству того же товара, проданного в базисном периоде (iq = q1 / q0 ). Поскольку базисный уровень индексируемого показателя приравнивается к 1 или 100%, то разность между полученным индексом и 1 или 100% характерзиует относительную величину изменения количества проданного товара. По этому индексу можно определить и абсолютное изменение количества проданного товара в натуральном выражении как разность между числителем и знаменателем индекса .
Произведем расчет индивидуальных индексов физического объема товарооборота.
По телевизорам: или 90% и рассчитываем тыс.шт, то есть в отчетном периоде по сравнению с базисным было продано телевизоров на 40 тыс.штук, или на 10% меньше, чем в базисном году.
По видеомагнитофонам: , и рассчитываем тыс.шт, то есть количество проданных видеомагнитофонов возрасло на 50 тыс. штук или на 25%.
studfiles.net
27 Классификация индексов в статистике
Индексы в статистике классифицируются:
По содержанию изучаемых объектов.
По степени охвата элементов совокупности.
По методам расчета общих индексов.
Виды индексов по содержанию изучаемых величин:
По содержанию изучаемых величин индексы делятся на индексы качественных показателей и индексы количественных показателей. Деление индексов на такие виды важно для методологии их расчета.
Индексы качественных показателей в статистике
Индексы качественных показателей измеряют уровень явления или иную единицу совокупности и поэтому они являются расчетными, вторичными показателями интенсивности. Примерами таких индексов могут быть: индексы себестоимости продукции курса валют, производительности труда, и т. д. Индексируемые показатели таких индексов характеризуют уровень явления в расчете на единицу совокупности: цена за единицу продукции, заработная плата работника и т. д.
Качественные показатели измеряют не объем, а интенсивность, эффективность явления. Зачастую они являются либо средними, либо относительными величинами. Расчет этих индексов производится на базе одинаковых, неизменных количеств продукции.
Индексы количественных показателей в статистике
Индексы количественных показателей представляют индексы национального дохода, ВВП и т. д. Все индексируемые показатели этих индексов являются объемными, так как они характеризуют общий, суммарный размер определенного явления, а также выражаются абсолютными величинами.
Виды индексов по степени охвата элементов совокупности:
Индивидуальные индексы
Характеризуют отношение уровней только одного элемента совокупности, например рост (падение) цен на акции в ОАО. Индивидуальные индексы этообычные относительные величины, и индексами их можно назвать только в широком смысле. Одной из главных особенностей индивидуальных индексов является то, что если произведение двух или нескольких показателей образует новый экономически весомый показатель, то и произведение индексов этих показателей образует индекс нового показателя.
С аналитической точки зрения индивидуальные индексы характеризуют изменения индексируемой величины в текущем периоде по сравнению с базисным, т. е. во сколько раз она возросла или уменьшилась либо сколько процентов составляет ее рост или снижение. Они рассчитываются вычислением отношения двух индексируемых величин.
Общие индексы
Отражают изменение всех элементов сложного явления. Под сложным явлением понимается такая статистическая совокупность, отдельные элементы которой напрямую не подлежат суммированию. Это и есть индексы.
Название индекса оформляется подстрочным знаком — принятым обозначением индексируемого показателя. Одна из важных особенностей индексов состоит в том, что исследуемый показатель рассматривают не изолированно, а во взаимосвязи с другими показателями. Они имеют более сложную методику расчета. Для того чтобы рассчитать общие индексы, нужно соизмерить различные элементы совокупности, т. е. привести их к одному и тому же единству.
28 По методам расчета общих и групповых индексов выделяют индексы агрегатные и средние, вычисление которых составляет особый метод исследования, который называется индексным методом.
Агрегатный индекс представляет собой основную и наиболее распространенную форму индекса. Его составляющие: числитель и знаменатель представляют собой набор — «агрегат» (от лат. — складываемый, суммируемый) несоизмеримых и не суммируемых элементов — сумму произведения двух величин, одна из которых изменяется (индексируется), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы качественных показателей могут рассчитываться как индексы переменного состава и индексы постоянного состава.
В индексах переменного состава соотносятся показатели, рассчитанные на базе изменяющихся структур явлений, а индексы постоянного состава — на базе неизменной структуры явлений.
studfiles.net