График натурального логарифма: 2. Натуральные логарифмы. Функция у = lп х, её свойства, график, дифференцирование
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) ) |
|
| 17 | sec(30 град. ) | ||
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | ||
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.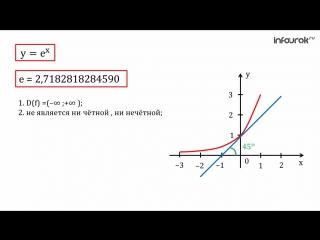 ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.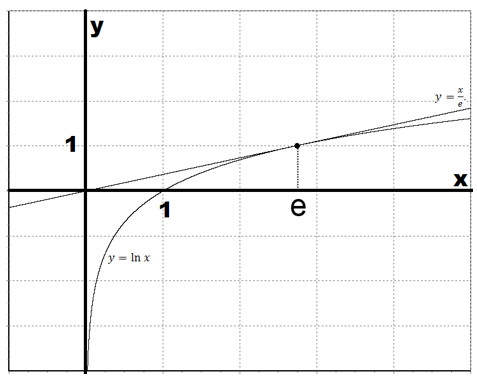 ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град.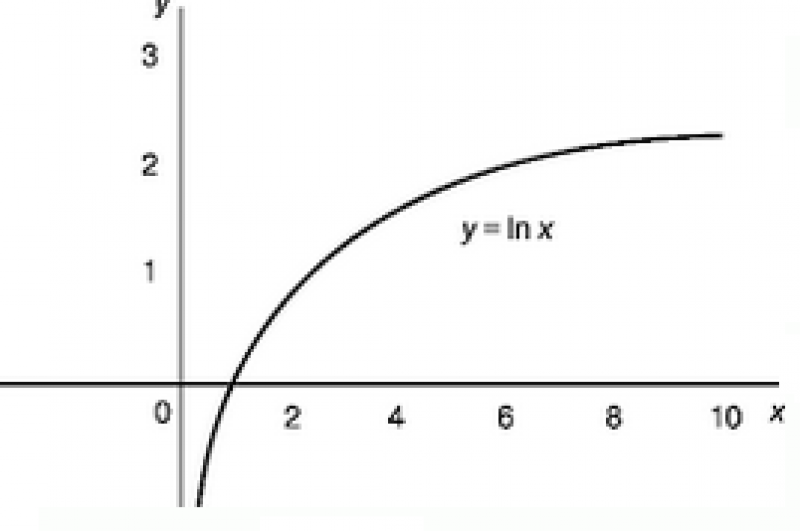 ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Натуральный логарифм, формулы и онлайн калькуляторы
Содержание:
Для различного рода теоретических и практических исследований наиболее удобным
основанием логарифма
является иррациональное число $e$.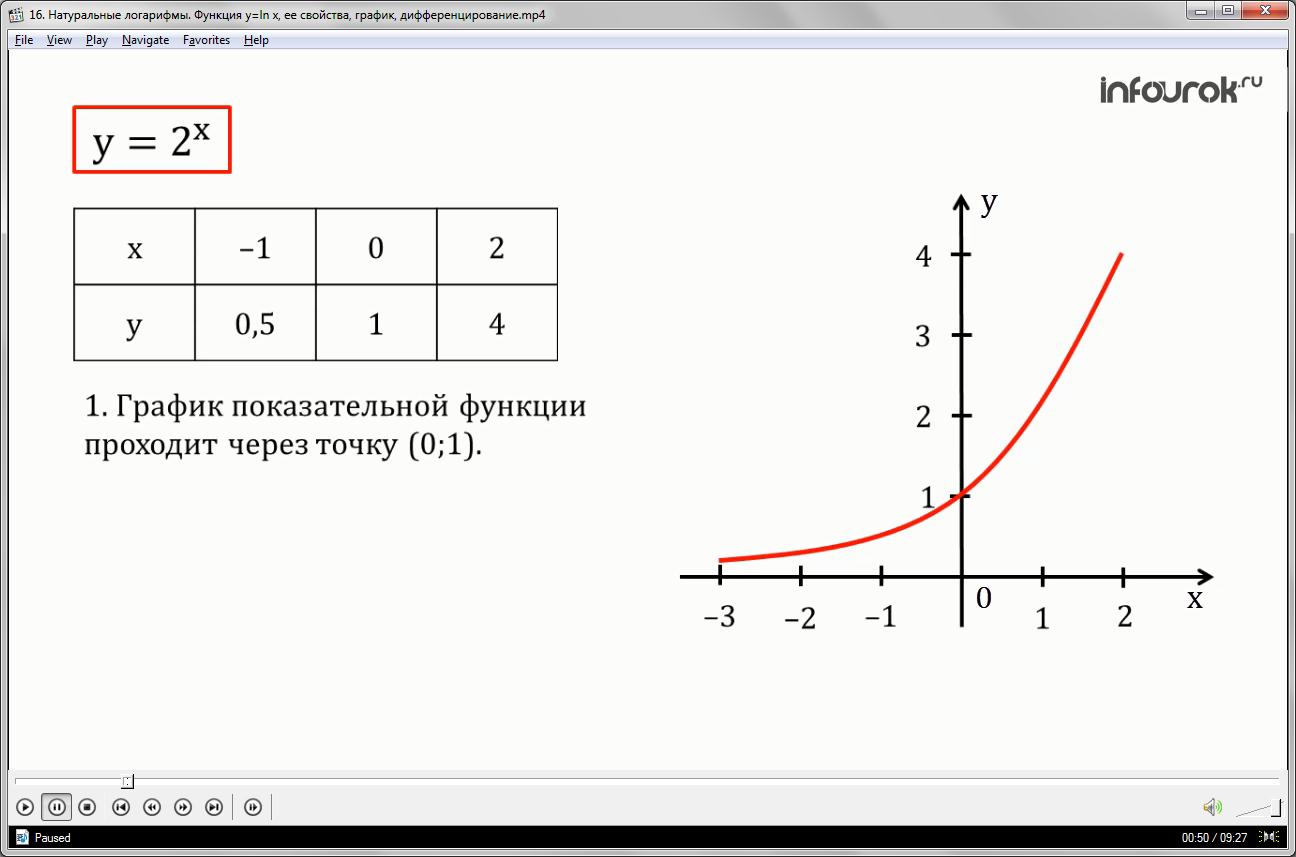 {2 n}}{n}+\ldots, |x| \lt 1$
{2 n}}{n}+\ldots, |x| \lt 1$
Читать дальше: десятичный логарифм.
Натуральный логарифм и его свойства
Определение и формулы натурального логарифма
Натуральный логарифм может быть определён для любого положительного действительного числа как площадь под гиперболой для .
Впервые натуральный логарифм встречается в работе «Logarithmotechnika» (1668) немецкого математика Николауса Меркатора (Николас (Николаус) Кауфман, около 1620-1687). Но еще в 1619 г. лондонский учитель математики Джон Спайделл, переиздавший таблицы логарифмов Непера (шотландский математик Джон Непер (1560-1617) и его сочинение «Описание удивительной таблицы логарифмов» 1614 года), составил таблицу натуральных логарифмов.
Первоначально натуральный логарифм называли гиперболическим, поскольку он соответствует площади под гиперболой; иногда называют логарифмом Непера. Термин «натуральный логарифм» («логарифмус натуралис») был предложен итальянским математиком Пьетро Менголи (1626-1686) в середине 16 века.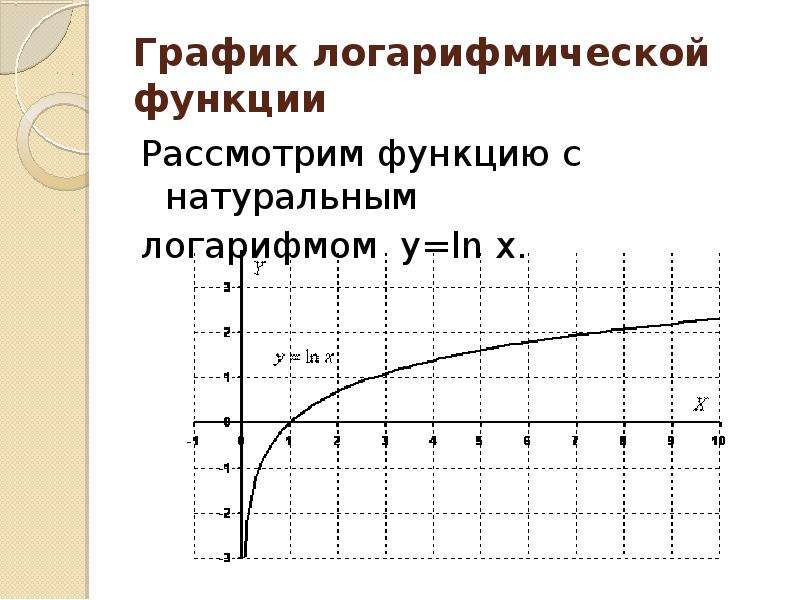
Свойства натурального логарифма
Натуральный логарифм обладает всеми свойствами, присущими логарифму по произвольному основанию:
1. Основное логарифмическое тождество:
2. .
3. .
4. .
5. .
6. .
7. Переход к новому основанию:
8. .
9. .
Функция натурального логарифма
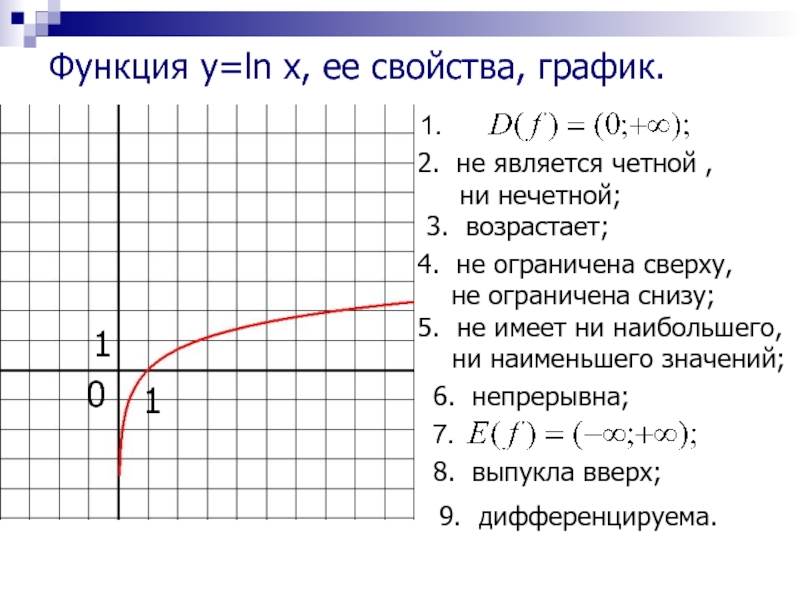
Функцией натурального логарифма есть функция , обладающая следующими свойствами:
1) Область определения: .
2) Множество значений: .
3) Функция общего вида.
4) Функция непериодическая.
5) График функции пересекается с осью абсцисс в точке .
6) Промежутки знакопостоянства: для и для .
7) Функция возрастает на всей области определения.
8) Точек минимума/максимума нет.
9) Вертикальная асимптота — прямая (ось ординат).
10) График:
Функция является обратной к экспоненциальной функции .
Производная логарифма натурального
Интеграл от натурального логарифма
Ряд Маклорена
Алгебра – 11 класс.
 x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:
x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:Свойства функции $y=\ln{x}$
1. $D(f)=(0;+∞)$.
2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.
В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции.
Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y’=(\ln{x})’=\frac{1}{x}$.
Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять. 2}$.
2}$.
график, основание, функции, предел, формулы и область определения. Натуральный логарифм, функция ln x
Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»
Что такое натуральный логарифм
Ребята, на прошлом уроке мы с вами узнали новое, особенное число – е. Сегодня мы продолжим работать с этим числом.Мы с вами изучили логарифмы и знаем, что в основании логарифма может стоять множество чисел, которые больше 0. Сегодня мы также рассмотрим логарифм, в основании которого стоит число е. Такой логарифм принято называть натуральным логарифмом.
 x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:
x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные: Свойства функции $y=\ln{x}$
1. $D(f)=(0;+∞)$.2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.
В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции .
Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.
Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять. 6=1$.
6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания:
Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $}
Натуральный логарифм е в квадрате. Логарифм. Определение двоичного логарифма, натурального логарифма, десятичного логарифма; экспоненциальной функции exp(x), числа e. Log, Ln. Формулы степеней и логарифмов. Использование логарифма, децибел
Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.
Если , то .
Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.
Вконтакте
Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:
Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.
Приведем некоторые тождества:
Приведем основные алгебраические выражения:
;
.
Внимание! может существовать только при x>0, x≠1, y>0.
Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.
Обозначения:
- lg x — десятичный;
- ln x — натуральный.
Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.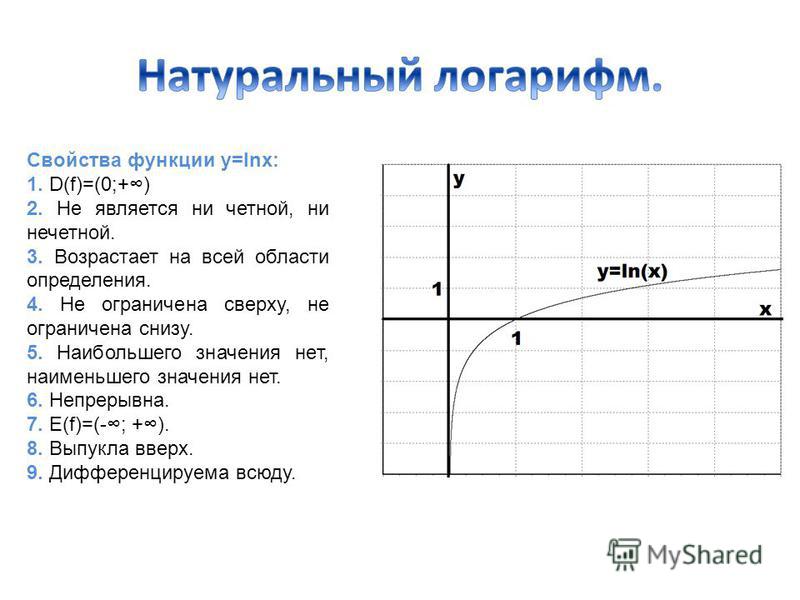
Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.
Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:
Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:
Для удобства мы можем взять пять опорных точек:
;
;
.
;
.
Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.
Построив по точкам график, получаем приблизительный график:
Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.
Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .
Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .
Предел натурального logИзучая график, возникает вопрос — как ведет себя функция при y
Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х
Предел натурального log можно записать таким образом:
Формула замены основания логарифмаИметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.
Начнем с логарифмического тождества:
Тогда любое число, либо переменную у можно представить в виде:
где х — любое число (положительное согласно свойствам логарифма).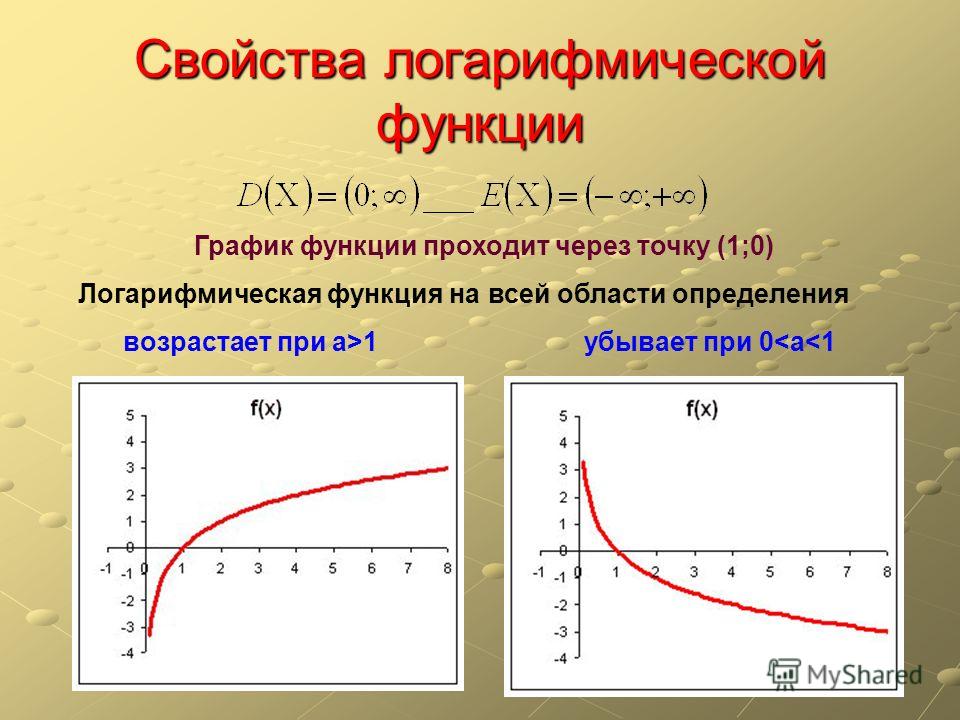
Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:
Воспользуемся свойством (только вместо «с» у нас выражение):
Отсюда получаем универсальную формулу:
.
В частности, если z=e, то тогда:
.
Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.
Решаем задачиДля того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.
Задача 1 . Необходимо решить уравнение ln x = 3.
Решение: Используя определение логарифма: если , то , получаем:
Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.
Решение: Используя определение логарифма: если , то , получаем:
.
Еще раз применим определение логарифма:
.
Таким образом:
.
Можно приближенно вычислить ответ, а можно оставить его и в таком виде.
Задача 3. Решите уравнение .
Решите уравнение .
Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:
.
Перед нами квадратное уравнение. Найдем его дискриминант:
Первый корень уравнения:
.
Второй корень уравнения:
.
Вспоминая о том, что мы производили подстановку t = ln x, получаем:
В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.
В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.
В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.
В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.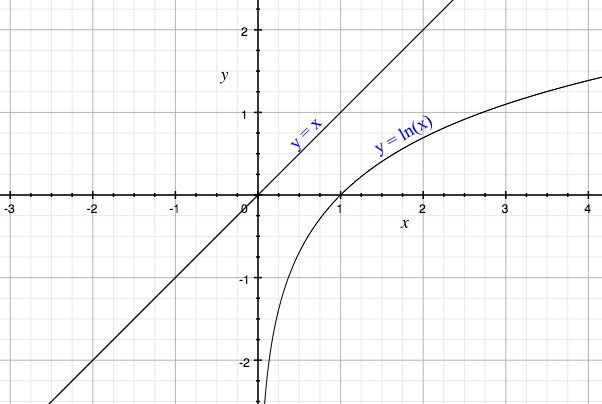
В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.
Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.
Натуральный логарифм Функция y=ln x ее свойства
Доказательство основного свойства натурального логарифма
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла.
 Нет такой степени!
Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b
будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача. Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Получили ответ: 3.

Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т. к. множитель всего один;
к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459…
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1 ; ln e 2 = 2 ; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.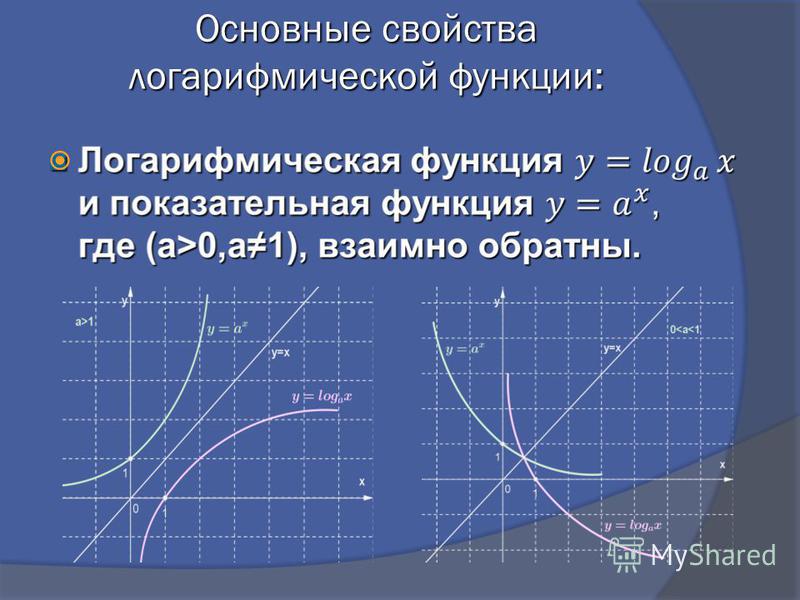
Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.
Число e означает рост
Число e означает непрерывный рост. Как мы видели в прошлом примере, e x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».
Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:
e x = e процент * время = e 1.0 * время = e время
Очевидно, что e x означает:
- насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
- например, через 3 промежутка времени я получу в e 3 = 20.08 раз больше «штуковин».
e x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.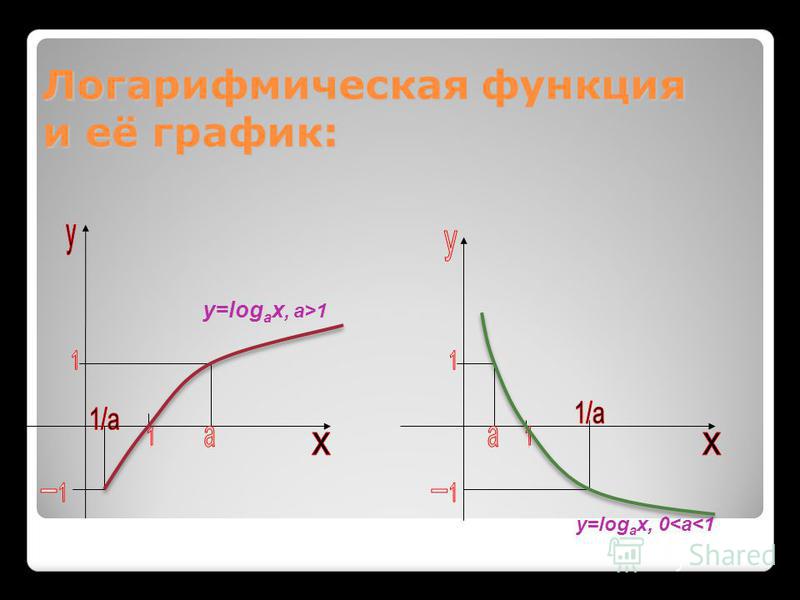
Натуральный логарифм означает время
Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali , отсюда и появилась аббревиатура ln.
И что эта инверсия или противоположность означает?
- e x позволяет нам подставить время и получить рост.
- ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.
Например:
- e 3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
- ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).
Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.
Этот нестандартный логарифмический счёт
Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.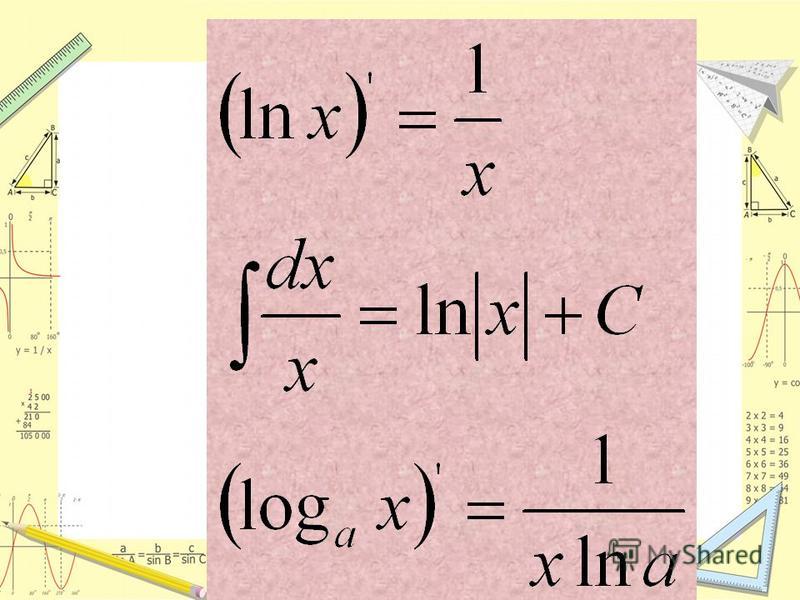
Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?
Ноль. Нуль. Нисколько. У вас уже это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.
- ln(1/2) = -ln(2) = -0.693
Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = -ln(3) = -1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.
Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до -3?
Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ. .. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
.. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
- ln(отрицательное число) = неопределено
«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.
Логарифмическое умножение — просто умора
Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.
Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):
- Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)
Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.
Это отношение сразу обретает смысл, если оперировать в терминах роста.
Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?
Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,
- ln(5/3) = ln(5) – ln(3)
Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается
- ln(a/b) = ln(a) – ln(b)
Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.
Не надо запоминать правила, попробуйте осознать их.
Использование натурального логарифма при произвольном росте
Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»
Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e x . Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.
Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:
Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:
- e x = e ставка*время
- e 100% * 3.4 года = 30
Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?
- ln(30) = 3.
 4
4 - ставка * время = 3.4
- 0.05 * время = 3.4
- время = 3.4 / 0.05 = 68 лет
Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».
- 100% за 3.4 года = 1.0 * 3.4 = 3.4
- 200% за 1.7 года = 2.0 * 1.7 = 3.4
- 50% за 6.8 года = 0.5 * 6.8 = 3.4
- 5% за 68 года = .05 * 68 = 3.4 .
Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.
Отпадный пример: Правило семидесяти двух
Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?
Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.
Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?
Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:
- ставка * время = 0.693
- время = 0.693 / ставка
Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.
Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:
10″:
- время на удвоение = 69.3 / ставка, где ставка выражена в процентах.
Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.
- время на удвоение = 72 / ставка
что и является правилом семидесяти двух. Всё шито-крыто.
Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить
- время на утроение = 110 / ставка
Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.
Что дальше?
Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.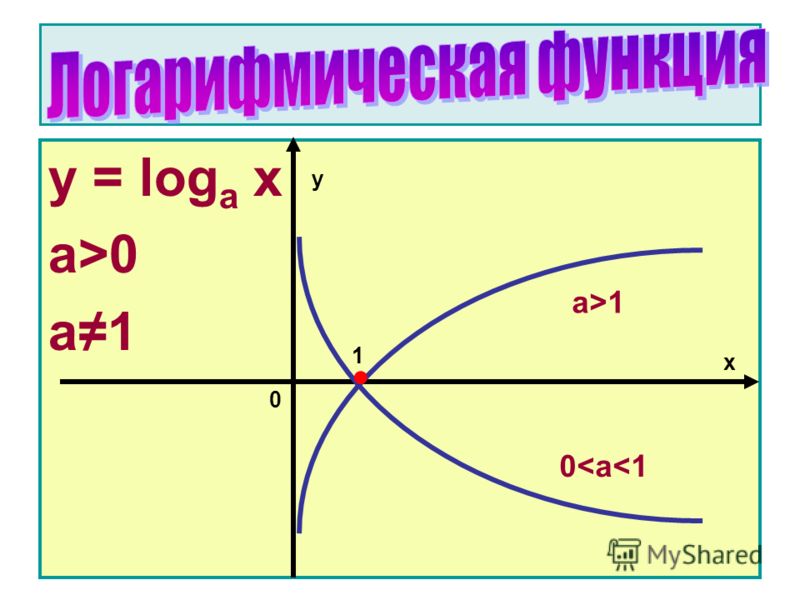
Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.
Дополнение: Натуральный логарифм от e
Быстрая викторина: сколько будет ln(e)?
- математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
- понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.
Мыслите ясно.
9 сентября 2013Это может быть, например, калькулятор из базового набора программ операционной системы Windows. Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
Переключите интерфейс калькулятора в расширенный режим, позволяющий осуществлять . По умолчанию он открывается в «обычном» виде, а вам нужен «инженерный» или « » (в зависимости от версии используемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.
Введите аргумент, натуральный которого нужно вычислить. Это можно сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.
Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет результат.
Воспользуйтесь каким-либо из -калькуляторов в качестве альтернативного вычисления значения натурального логарифма. Например, тем, который размещен по адресу http://calc.org.ua . Его интерфейс предельно прост — есть единственное поле ввода, куда вам надо впечатать значение числа, логарифм от которого надо вычислить. Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно. Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .
Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .
Термин «логарифм » произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».
Вам понадобится
- Доступ в интернет, Microsoft Office Excel или калькулятор.
Инструкция
Воспользуйтесь во множестве представленными в интернете -калькуляторами — это, пожалуй, и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифм а возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Видео по теме
Натуральный логарифм
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).
Натуральный логарифм — это логарифм по основанию , где e — иррациональная константа, равная приблизительно 2,718281 828 . Натуральный логарифм обычно обозначают как ln(x ), log e (x ) или иногда просто log(x ), если основание e подразумевается.
Натуральный логарифм числа x (записывается как ln(x) ) — это показатель степени , в которую нужно возвести число e , чтобы получить x .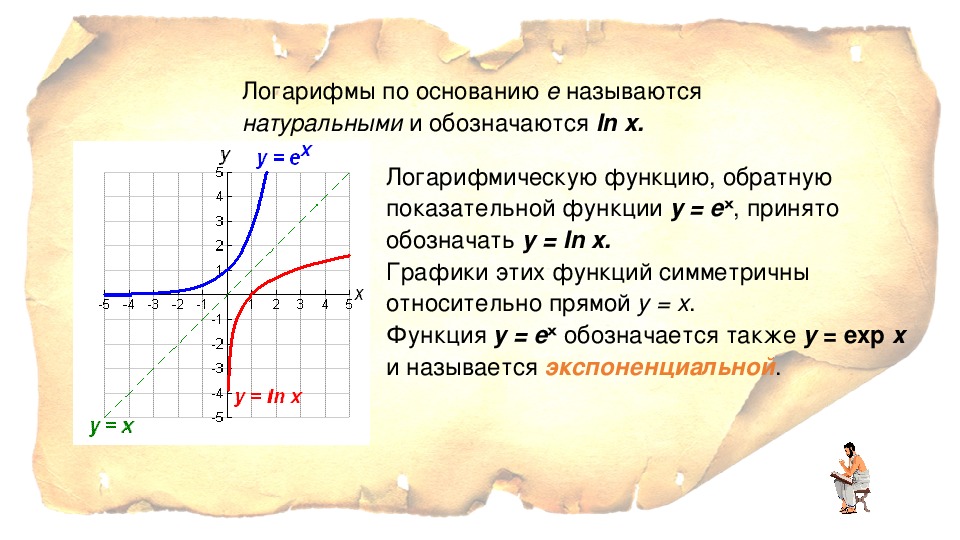 Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции :
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма.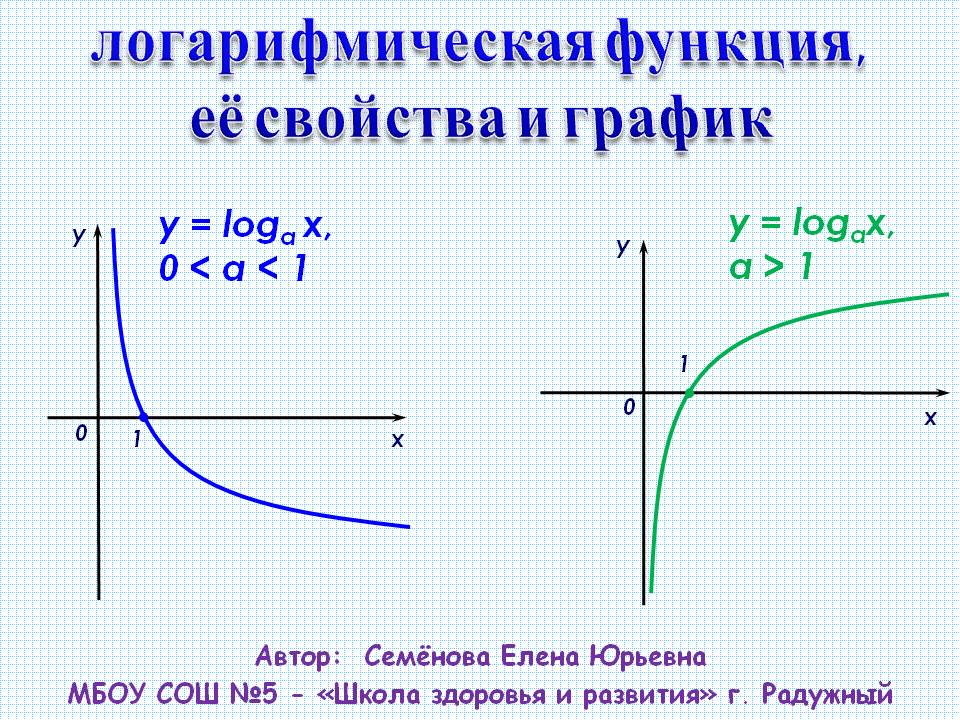 Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia , опубликованной в 1668 году , хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Натуральный логарифм принято обозначать через «ln(x )», логарифм по основанию 10 — через «lg(x )», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x )» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln 2 ln 3 4x 5 = [ ln( 3 )] 2 .
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 — «log 10 (x )».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x )» (или изредка «log e (x )»), когда они имеют в виду натуральный логарифм, а запись «log(x )» у них означает log 10 (x ).
log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:
Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.
Определение
Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т. е. как интеграл :
е. как интеграл :
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
при условии, что y = (x −1)/(x +1) и x > 0.Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная.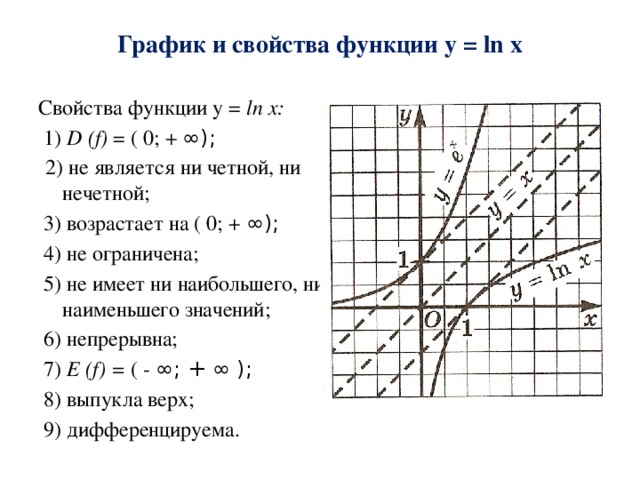 Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) — вычислительная сложность умножения двух n -значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e x для любого произвольного комплексного числа x , при этом используется бесконечный ряд с комплексным x . Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .
Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi . Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
См. также
- Джон Непер — изобретатель логарифмов
Примечания
- Mathematics for physical chemistry . — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5 , Extract of page 9
- J J O»Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
- Cajori Florian A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.
График логарифма и экспоненты. Основное свойство логарифмов и его следствия
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.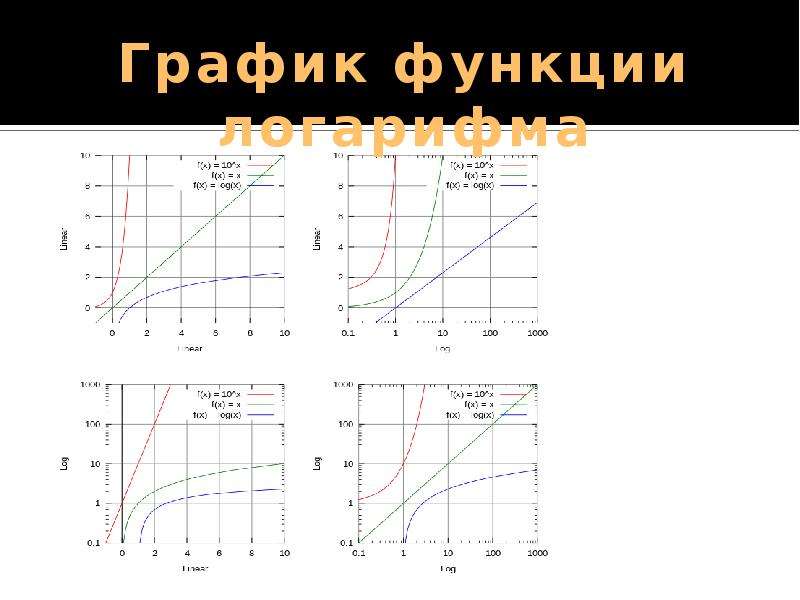
Определение
Натуральный логарифм — это функция y = ln x , обратная к экспоненте , x = e y , и являющаяся логарифмом по основанию числа е : ln x = log e x .
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/ x .
Исходя из определения , основанием натурального логарифма является число е :
е
≅ 2,718281828459045… ;
.
График функции y = ln x .
График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .
Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( — ∞ ).
При x → + ∞
пределом натурального логарифма является плюс бесконечность ( + ∞
). При больших x
логарифм возрастает довольно медленно.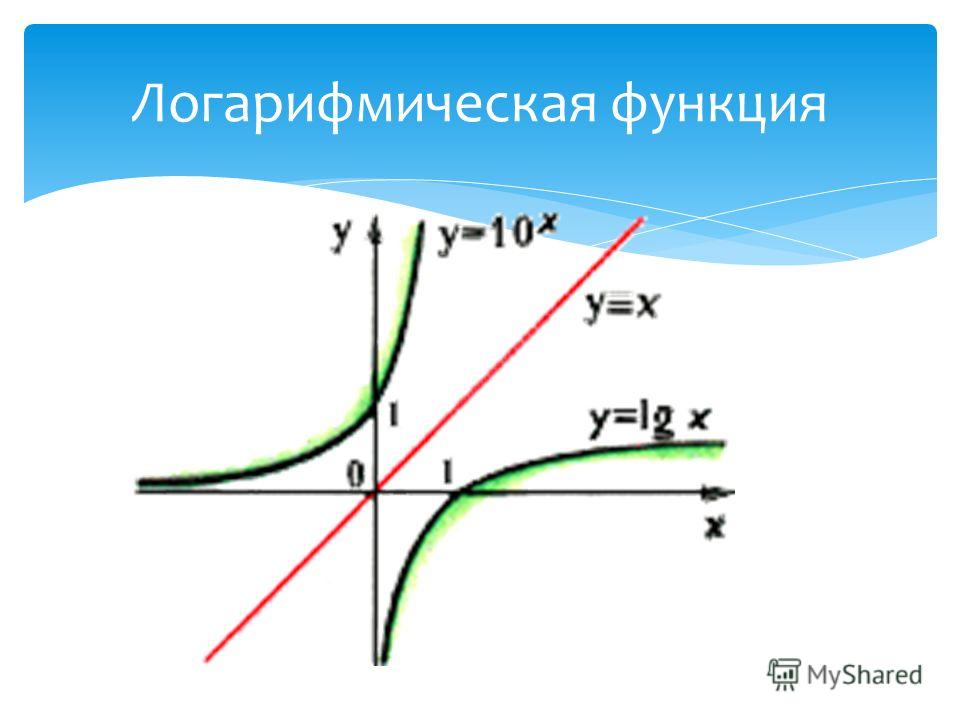 Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм» .
Обратная функция
Обратной для натурального логарифма является экспонента .
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям :
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z
:
.
Выразим комплексную переменную z через модуль r и аргумент φ :
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ
определен не однозначно. Если положить
,
где n — целое,
то будет одним и тем же числом при различных n
.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.
Число e означает рост
Число e означает непрерывный рост. Как мы видели в прошлом примере, e x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».
Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:
e x = e процент * время = e 1.0 * время = e время
Очевидно, что e x означает:
- насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
- например, через 3 промежутка времени я получу в e 3 = 20.08 раз больше «штуковин».
e x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.
Натуральный логарифм означает время
Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali
, отсюда и появилась аббревиатура ln.
Кстати, о причудах; по латыни он называется logarithmus naturali
, отсюда и появилась аббревиатура ln.
И что эта инверсия или противоположность означает?
- e x позволяет нам подставить время и получить рост.
- ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.
Например:
- e 3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
- ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).
Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.
Этот нестандартный логарифмический счёт
Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.
Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?
Ноль. Нуль. Нисколько. У вас уже
это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
Нуль. Нисколько. У вас уже
это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.
- ln(1/2) = -ln(2) = -0.693
Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = -ln(3) = -1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.
Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до -3?
Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ. .. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
.. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
- ln(отрицательное число) = неопределено
«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.
Логарифмическое умножение — просто умора
Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.
Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):
- Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)
Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.
Это отношение сразу обретает смысл, если оперировать в терминах роста.
Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?
Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,
- ln(5/3) = ln(5) – ln(3)
Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается
- ln(a/b) = ln(a) – ln(b)
Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.
Не надо запоминать правила, попробуйте осознать их.
Использование натурального логарифма при произвольном росте
Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»
Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e x . Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.
Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:
Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:
- e x = e ставка*время
- e 100% * 3.4 года = 30
Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?
- ln(30) = 3.
 4
4 - ставка * время = 3.4
- 0.05 * время = 3.4
- время = 3.4 / 0.05 = 68 лет
Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».
- 100% за 3.4 года = 1.0 * 3.4 = 3.4
- 200% за 1.7 года = 2.0 * 1.7 = 3.4
- 50% за 6.8 года = 0.5 * 6.8 = 3.4
- 5% за 68 года = .05 * 68 = 3.4 .
Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.
Отпадный пример: Правило семидесяти двух
Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?
Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.
Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?
Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:
- ставка * время = 0.693
- время = 0.693 / ставка
Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.
Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:
10″:
- время на удвоение = 69.3 / ставка, где ставка выражена в процентах.
Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.
- время на удвоение = 72 / ставка
что и является правилом семидесяти двух. Всё шито-крыто.
Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить
- время на утроение = 110 / ставка
Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.
Что дальше?
Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.
Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.
Дополнение: Натуральный логарифм от e
Быстрая викторина: сколько будет ln(e)?
- математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
- понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.
Мыслите ясно.
9 сентября 2013нередко берут цифру е = 2,718281828 . Логарифмы по данному основанию именуют натуральным . При проведении вычислений с натуральными логарифмами общепринято оперировать знаком l n , а не log ; при этом число 2,718281828 , определяющие основание, не указывают.
Другими словами формулировка будет иметь вид: натуральный логарифм числа х — это показатель степени , в которую нужно возвести число e , чтобы получить x .
Так, ln(7,389…) = 2, так как e 2 =7,389… . Натуральный логарифм самого числа e = 1, потому что e 1 =e , а натуральный логарифм единицы равен нулю, так как e 0 = 1.
Само число е определяет предел монотонной ограниченной последовательности
вычислено, что е = 2,7182818284… .
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма (функции y = ln x ) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a .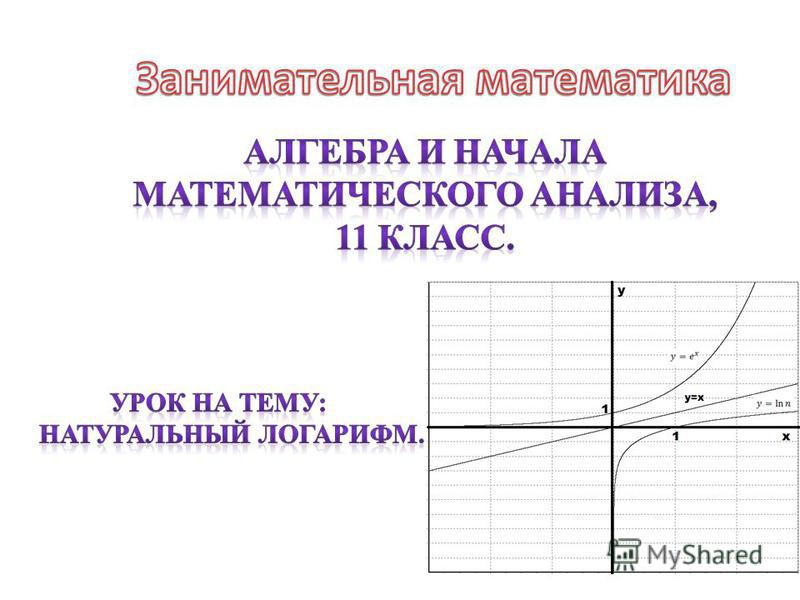
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм , как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
e ln(a) =a (a>0)
ln(e a) =a
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
ln (xy ) = ln (x ) + ln (y )
ln (х/у)= lnx — lny
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.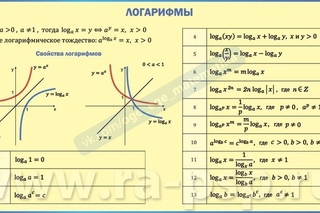
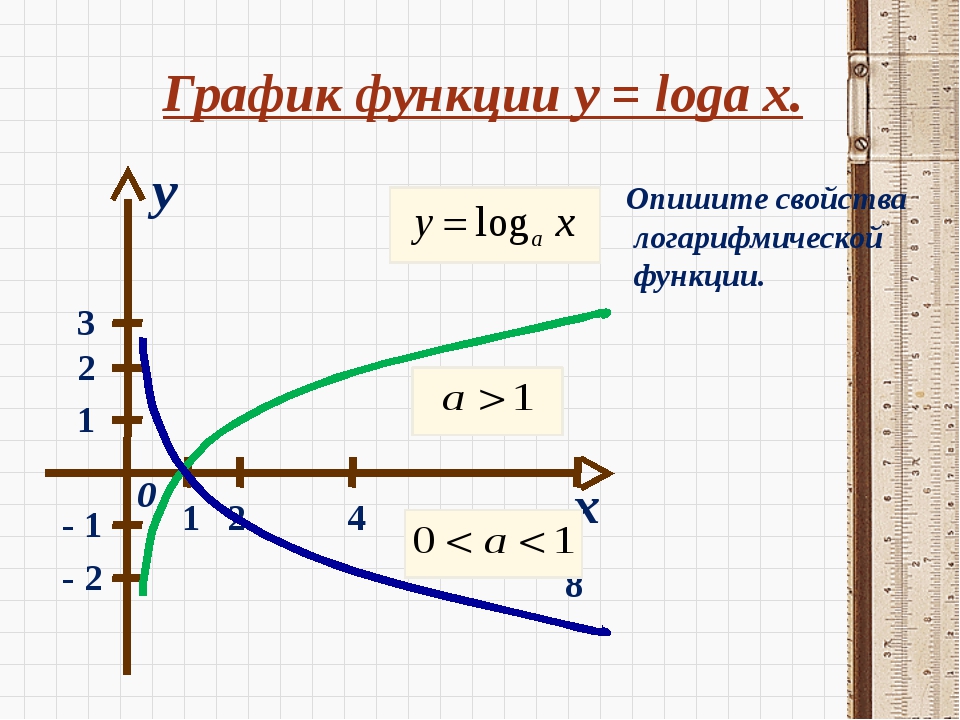
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма выступает минус бесконечность ( -∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).

- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма.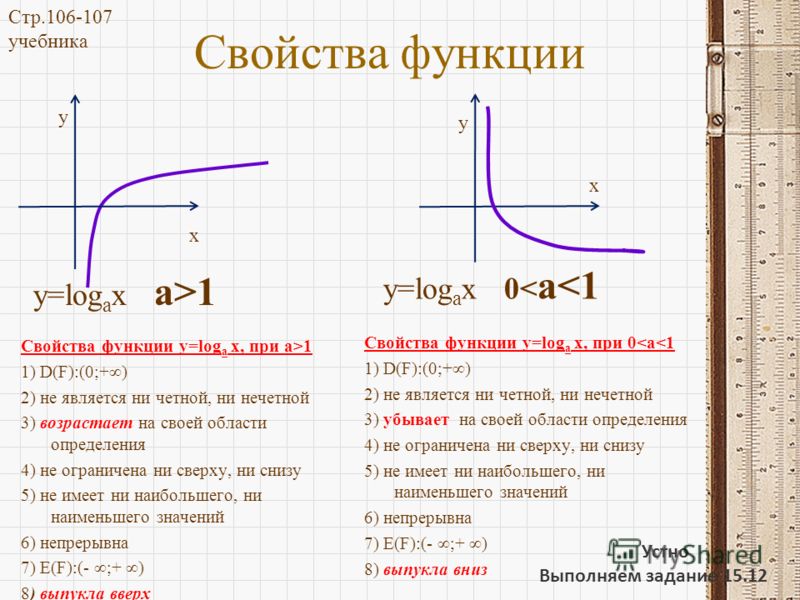 А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
- Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства.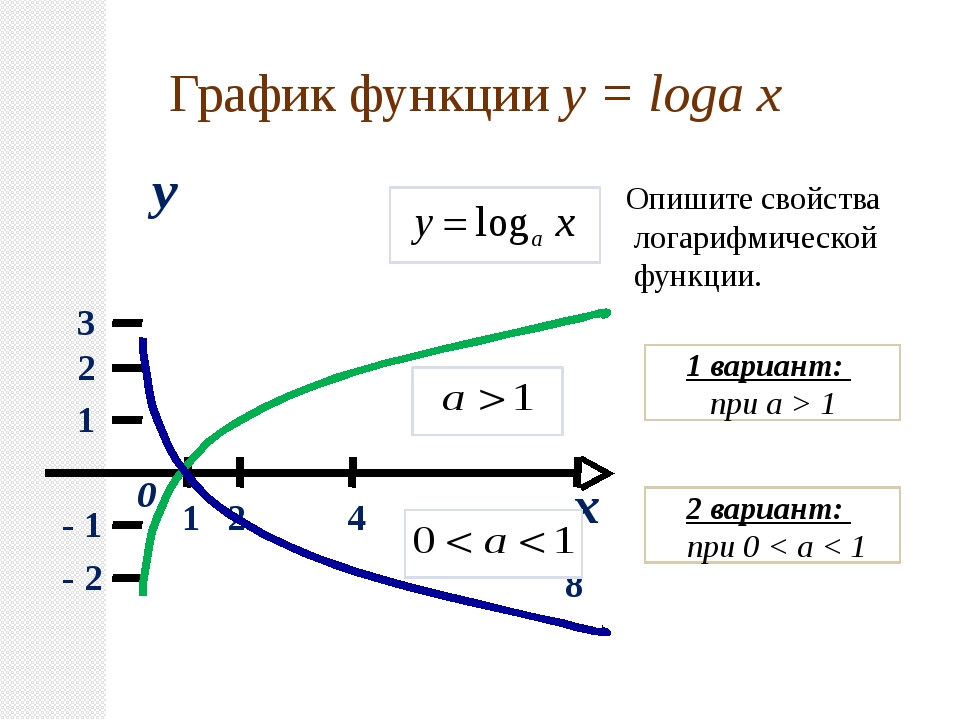 Давайте скорее с ними познакомимся.
Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
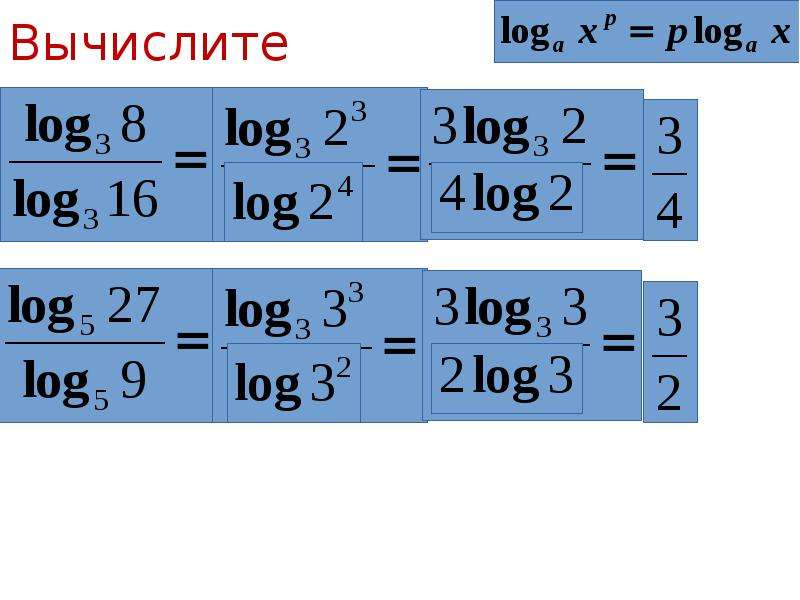
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение.
 Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Натуральный логарифм
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).
Натуральный логарифм — это логарифм по основанию , где e — иррациональная константа, равная приблизительно 2,718281 828 . Натуральный логарифм обычно обозначают как ln(x ), log e (x ) или иногда просто log(x ), если основание e подразумевается.
Натуральный логарифм числа x (записывается как ln(x) ) — это показатель степени , в которую нужно возвести число e , чтобы получить x . Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.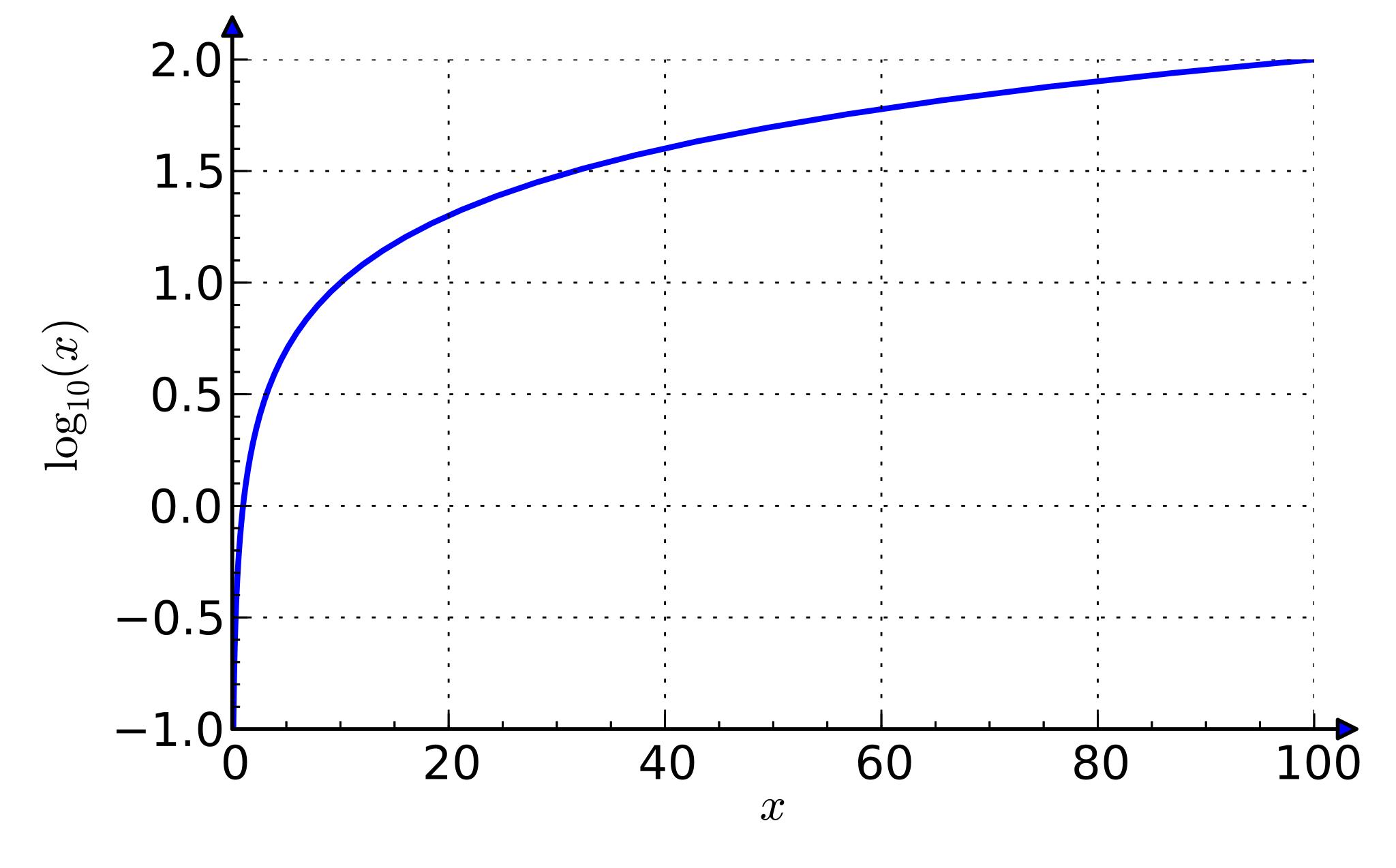
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции :
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма.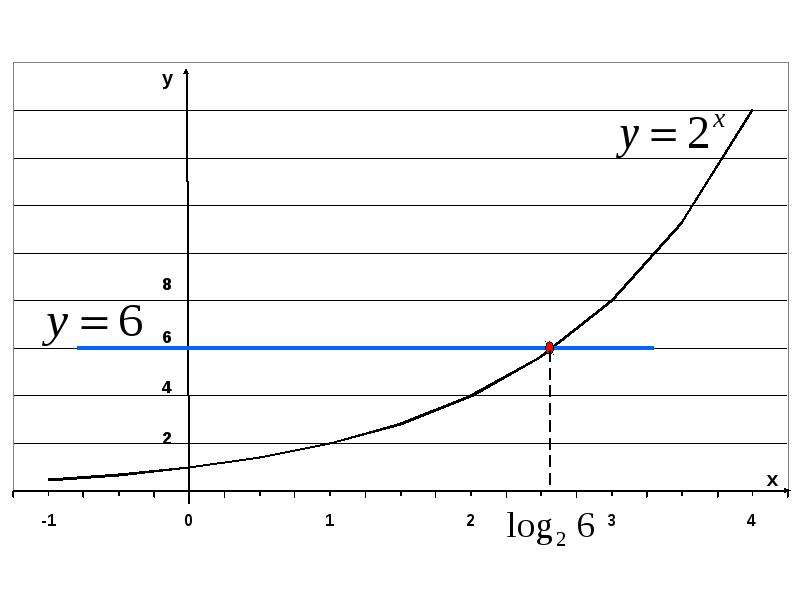 Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia , опубликованной в 1668 году , хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Натуральный логарифм принято обозначать через «ln(x )», логарифм по основанию 10 — через «lg(x )», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x )» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln 2 ln 3 4x 5 = [ ln( 3 )] 2 .
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 — «log 10 (x )».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x )» (или изредка «log e (x )»), когда они имеют в виду натуральный логарифм, а запись «log(x )» у них означает log 10 (x ).
log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:
Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.
Определение
Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т.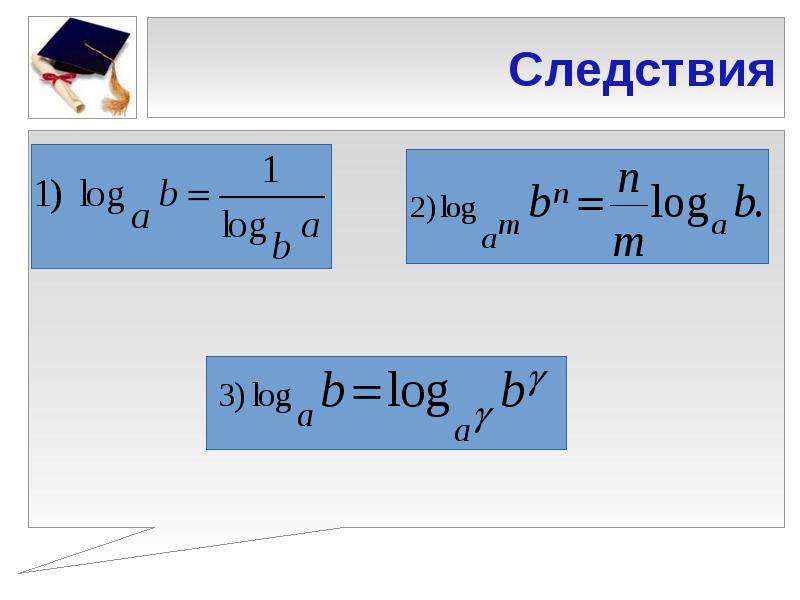 е. как интеграл :
е. как интеграл :
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
при условии, что y = (x −1)/(x +1) и x > 0.Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) — вычислительная сложность умножения двух n -значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e x для любого произвольного комплексного числа x , при этом используется бесконечный ряд с комплексным x . Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .
Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi . Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
См. также
- Джон Непер — изобретатель логарифмов
Примечания
- Mathematics for physical chemistry . — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5 , Extract of page 9
- J J O»Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
- Cajori Florian A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.
Как построить график ln (x) — видео и стенограмма урока
Шаги для решения ln (x)
Мы собираемся использовать свойства логарифмов для построения графика f ( x ) = ln ( x ). Логарифмическая функция имеет вид f ( x ) = log a ( x ), а log a ( x ) представляет собой число, которое мы возводим в a , чтобы получить x . Мы называем по основанию логарифмической функции.Функция f ( x ) = ln ( x ) является логарифмической функцией с основанием e , где e — иррациональное число со значением e = 2,71828 (округлено до 5 знаков после запятой). Вместо записи натурального логарифма в виде log e ( x ) мы используем запись ln ( x ).
Логарифмическая функция имеет вид f ( x ) = log a ( x ), а log a ( x ) представляет собой число, которое мы возводим в a , чтобы получить x . Мы называем по основанию логарифмической функции.Функция f ( x ) = ln ( x ) является логарифмической функцией с основанием e , где e — иррациональное число со значением e = 2,71828 (округлено до 5 знаков после запятой). Вместо записи натурального логарифма в виде log e ( x ) мы используем запись ln ( x ).
Мы собираемся использовать следующие свойства графика f ( x ) = log a ( x ) для построения графика f ( x ) = ln ( x ).
- Пересечение x или точка пересечения графика с осью x графика (1, 0).
- Ось y — это вертикальная асимптота графика. Другими словами, график приближается к оси y , но не касается ее.

- Область определения функции — все действительные числа, строго превышающие 0.
- Диапазон функции — все действительные числа.
- Если основание функции больше 1, то функция увеличивается или возрастает слева направо и принимает следующую общую форму.
Если основание функции больше 0 и меньше 1, то функция убывает или падает слева направо и принимает следующую общую форму.
Давайте рассмотрим эти свойства для f ( x ) = ln ( x ).Мы знаем, что основанием является e и e > 1. Следовательно, функция возрастает и принимает общую форму, показанную выше, когда основание больше 1. Кроме того, мы знаем, что график проходит через точку ( 1, 0) и приближается к оси y , но никогда не касается ее. Наконец, поскольку в домене все действительные числа строго больше 0, а в диапазоне — действительные числа, мы знаем, что весь график будет располагаться справа от оси y .Эти факты дают нам представление о том, как будет выглядеть график.
Наконец, поскольку в домене все действительные числа строго больше 0, а в диапазоне — действительные числа, мы знаем, что весь график будет располагаться справа от оси y .Эти факты дают нам представление о том, как будет выглядеть график.
Чтобы быть более точным, мы можем нанести несколько стратегических точек, поэтому мы знаем, что график точен. Чтобы найти точки, мы выбираем некоторые стратегические значения x , вставляем их в y = ln ( x ) и находим соответствующее значение y .
| x -значение | y = ln ( x ) |
|---|---|
| e = 2.7 | y = ln ( e ) = 1 |
| e 2 = 7,4 | y = ln ( e 2) = 2 |
| e 3 = 20,1 | y = ln ( e 3) = 3 |
Таким образом, мы имеем точки (2. 7, 1), (7.4, 2), (20.1, 3). Мы строим их вместе с другой нашей точкой (1, 0) и соединяем точки плавной кривой, которая принимает форму, описанную выше.
7, 1), (7.4, 2), (20.1, 3). Мы строим их вместе с другой нашей точкой (1, 0) и соединяем точки плавной кривой, которая принимает форму, описанную выше.
Вот решение проблемы:
Показан график f ( x ) = ln ( x ).
Справочник логарифмических функций
Это логарифмическая функция:
f (x) = журнал a (x)
— любое значение больше 0, кроме 1
Свойства зависят от значения «а»
- При a = 1 график не определен
- Кроме того, есть два случая, на которые стоит обратить внимание:
| a от 0 до 1 | a выше 1 | |
Пример: f (x) = log ½ (x) | Пример: f (x) = log 2 (x) | |
Для a от 0 до 1 | Для и и выше 1: |
Постройте график здесь (используйте ползунок «a»)
В общем, логарифмическая функция:
- всегда находится на положительной стороне (и никогда не пересекает) оси y
- всегда пересекает ось x при x = 1.
 .. то есть проходит через (1,0)
.. то есть проходит через (1,0) - равно 1 , когда x = a , другими словами, он проходит через (a, 1)
- — это инъективная (однозначная) функция
Его домен — положительные действительные числа: (0, + ∞)
Его диапазон — действительные числа:
Обратный
Таким образом, логарифмическая функция может быть «обращена» экспоненциальной функцией.
Функция натурального логарифма
Это «Натуральный» логарифм Функция:
f (x) = журнал e (x)
Где e — «Число Эйлера» = 2.718281828459 … и т. Д.
Но чаще пишут так:
f (x) = ln (x)
«ln» означает «бревно, натуральное»
Итак, когда вы видите ln (x), просто помните, что это логарифмическая функция с основанием e : log e (x).
График f (x) = ln (x)
В точке (e, 1) наклон линии составляет 1 / e , и прямая касается кривой.
Графики Логарифмические функции: примеры (стр. 3 из 3) Этот график будет аналогичным к графику log 2 ( x ), но он будет сдвинут боком. С «+»
3 «находится внутри
log, сдвиг графика не может быть ни вверх, ни вниз. Это означает, что
сдвиг должен быть влево или вправо. Но в какую сторону? Ты сможешь
отслеживать направление сдвига, глядя на базовую точку
(1, 0)
(«базовый», потому что он понятен и легко запоминается). Журнал будет
быть 0
когда аргумент, x + 3, равно 1.Когда это x + 3 равно 1?
Когда x = 2. Тогда основной
точка лог-графа (1,
0) будет сдвинут
на Поскольку в журнале не может быть
аргумент равен нулю или меньше, тогда у меня должно быть x + 3> 0, это
говорит мне, что для этого графика x всегда должно быть больше 3. График основной функция журнала y = журнал 2 ( x ) ползла по положительной стороне оси y для достижения оси x , с линией, никогда не идущей слева от ограничения, что x должно быть больше нуля. Чтобы напомнить себе об аналогичном ограничении этого журнала (где x всегда должно быть больше 3), Я вставлю пунктирную линию x = 3: Такая строка, которая
отмечает территорию, на которой график не должен идти, называется «вертикалью»
асимптота », или просто« асимптота ». После того, как я бросился в асимптоту, Рисую несколько точек: 2 0 = 1, поэтому журнал 2 (1)
= 0; х + 3 = 1 для x = 2: (2, 0) Затем, работая в другое направление: Авторское право Элизабет Стапель 2002-2011 Все права защищены 2 1 = 0. Обратите внимание, чтобы найти каждый
из этих точек я не начинал со значения x .
а затем загадать свой путь к значению y ;
это было бы слишком сложно, а я слишком ленив.Вместо этого я начал с
простой экспоненциальный оператор, переключил его на соответствующий
логарифмический оператор, а затем вычислили, для этого показателя (который
тоже моя y -значение),
какое значение x должно быть.
Если вы проверите это в своем
калькулятор, сначала не забудьте поставить « x + 3 «в скобках,
или калькулятор подумает, что вы имеете в виду « log 2 ( x )
+ 3 «, и вы
получить неправильный ответ; во-вторых, помните, что ваш калькулятор может только следовать
его программирование, которое он не может думать, поэтому график, который он отображает, скорее всего,
быть неверным, даже если вы правильно введете функцию.
Теперь вы хорошо знаете
что бревно не просто «заканчивается» там слева, бесполезно висит
в космосе.Почему калькулятор делает это неправильно? Потому что это просто машина,
и делает все возможное. Графики калькулятора аналогичны
как вы это делаете: он выбирает x -значений,
вычисляет y -значения,
отображает точки и соединяет точки. На рассмотрение: некоторые из них различные варианты одной и той же базовой логарифмической функции с соответствующий график под каждым уравнением.Обратите внимание, что даже если график перемещен влево или вправо, вверх или вниз, или перевернут вверх ногами, он все еще отображает ту же кривую:
|
Логарифмические функции и их графики
Логарифмические функции и их графики1 — Вычислить логарифмы
2 — Вычисление десятичных логарифмов
В таблице ниже показано, как значения x и y точек экспоненты кривую можно переключить, чтобы найти координаты точек на логарифмической изгиб.
| Пункт на экспоненциальная кривая | Соответствующий пункт на логарифмической кривой |
|---|---|
| (-3, 1/8) | (1/8, -3) |
| (-2, 1/4) | (1/4, -2) |
| (-1, 1/2) | (1/2, -1) |
| (0, 1) | (1, 0) |
| (1, 2) | (2, 1) |
| (2, 4) | (4, 2) |
| (3, 8) | (8, 3) |
Сравнение экспоненциальных и логарифмических функций
Давайте посмотрим на некоторые свойства
из двух функций.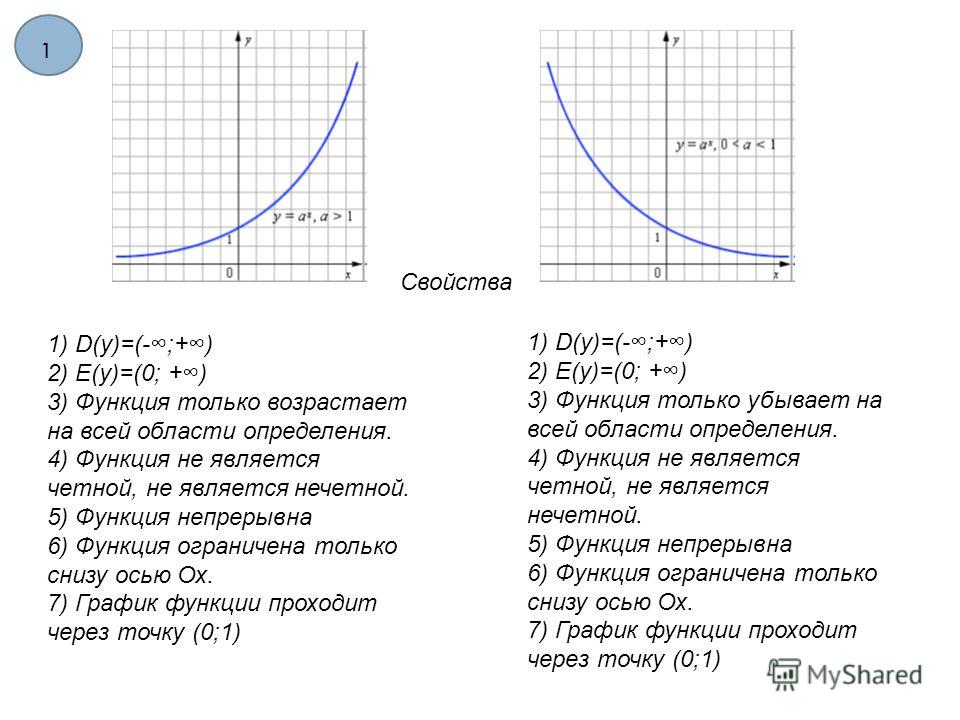
Стандартная форма логарифмической функции: y = log a x
Обратите внимание: если «a» в приведенном выше выражении не является нижним индексом (ниже, чем «журнал»), тогда вам нужно обновить веб-браузер.
Рабочее определение логарифма
В экспоненциальной функции x был показателем. Назначение обратной функции —
чтобы сообщить вам, какое значение x использовалось, когда вы уже знаете значение y. Итак, цель
логарифм должен сказать вам показатель степени.
Назначение обратной функции —
чтобы сообщить вам, какое значение x использовалось, когда вы уже знаете значение y. Итак, цель
логарифм должен сказать вам показатель степени.
Таким образом, наше простое определение логарифма состоит в том, что это показатель степени.
Другой способ взглянуть на выражение «log a x» — это «до какой степени (экспоненты) нужно возвести получить х? «
Эквивалентные формы
Логарифмическая форма уравнения y = log a x эквивалентна экспоненциальной форме x = a y .
Чтобы переписать одну форму в другую, оставьте основу такой же и поменяйте сторону с двумя другими ценности.
Свойства логарифмов
- журнал a 1 = 0, потому что 0 = 1
- Независимо от основания, если оно допустимо, логарифм 1 всегда равен 0. Это потому что логарифмические кривые всегда проходят через (1,0)
- журнал a a = 1, потому что a 1 = a
- Любое значение, возведенное в первую степень, означает, что
такое же значение.

- бревно a a x = x
- Логарифмическое основание x и степень x являются обратными функциями. Всякий раз, когда обратный функции применяются друг к другу, они инвертируются, и вы остаетесь с в аргумент, в данном случае x.
- log a x = log a y означает, что x = y
- Если два бревна с одинаковым основанием равны, то аргументы должны быть равны.
- log a x = log b x означает, что a = b
- Если два логарифма с одним и тем же аргументом равны, то основания должны быть равны.
3 — Вычислить натуральные логарифмы
Функции графического логарифма
В разделе об экспоненциальных функциях мы заявили, что
экспоненциальные функции взаимно однозначны. Один к одному
функции обладали тем особенным свойством, что они имели обратные
это тоже функции. И, как многие из вас говорили в классе,
и я так рад, что вы помните, функции «один-к-одному» могут
применяться к обеим сторонам уравнения. Они также проходят
горизонтальная линия тест.
Они также проходят
горизонтальная линия тест.
Этот раздел посвящен обратной экспоненциальной функция. Обратной к экспоненциальной функции является логарифмическая функция. Помните, что обратное функция получается переключением координат x и y. Это отражает график относительно прямой y = x. Как видно из графика справа, логарифмическая кривая является отражением экспоненциальной кривой.
В таблице ниже показано, как значения x и y точек экспоненты кривую можно переключить, чтобы найти координаты точек на логарифмической изгиб.
| Пункт на экспоненциальная кривая | Соответствующий пункт на логарифмической кривой |
|---|---|
| (-3, 1/8) | (1/8, -3) |
| (-2, 1/4) | (1/4, -2) |
| (-1, 1/2) | (1/2, -1) |
| (0, 1) | (1, 0) |
| (1, 2) | (2, 1) |
| (2, 4) | (4, 2) |
| (3, 8) | (8, 3) |
4 — Функция, обратная экспоненциальной
5 — Использование переводов для графических логарифмических функций
Содержание: Примечания по алгебре колледжа
Сайт Расс Фрит
Экспоненциальные и логарифмические функции Натуральный логарифм
Вы собираетесь изучить самую важную концепцию решения экспоненциальных и логарифмических уравнений.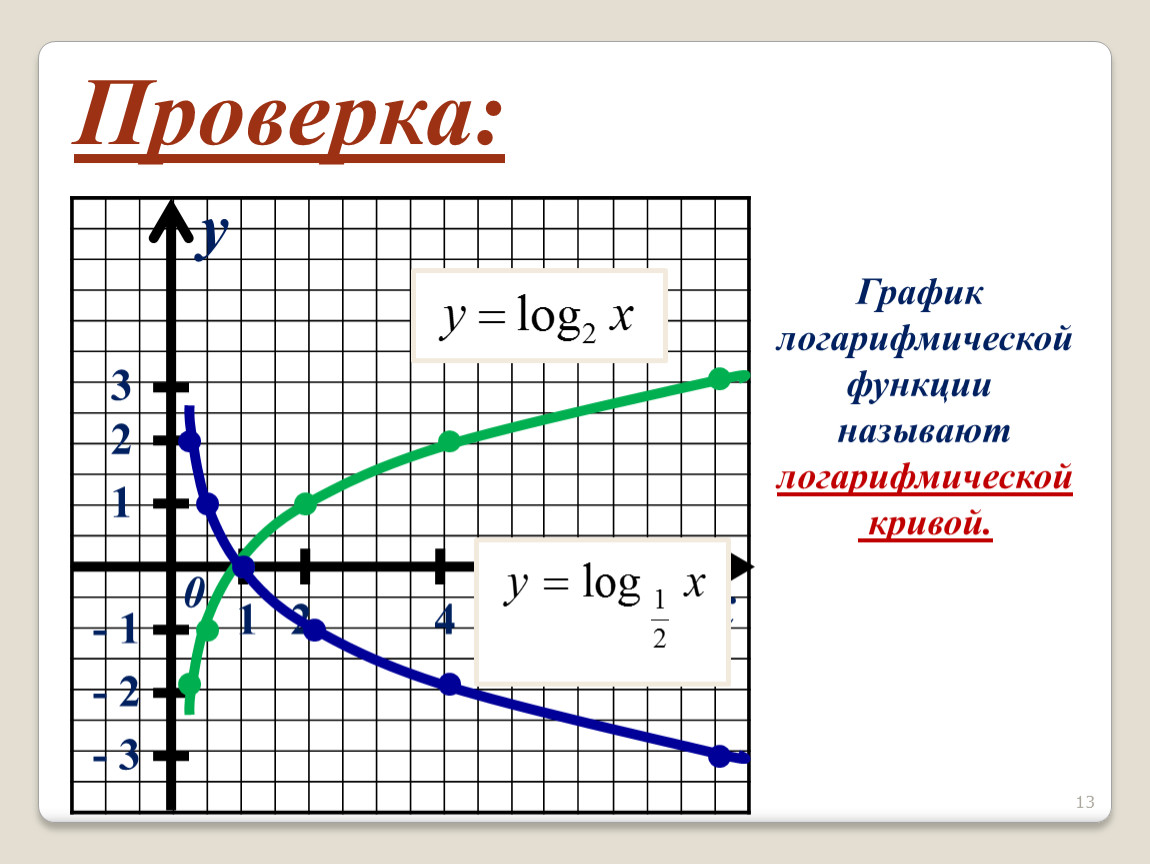 Натуральное бревно — очень удобный инструмент для использования в этой главе в качестве математического инструмента. Натуральный логарифм не только является обратной функцией функции e x , но и используется непосредственно в последующих разделах для решения как экспоненциальных, так и логарифмических уравнений.
Натуральное бревно — очень удобный инструмент для использования в этой главе в качестве математического инструмента. Натуральный логарифм не только является обратной функцией функции e x , но и используется непосредственно в последующих разделах для решения как экспоненциальных, так и логарифмических уравнений.
Вы изучите графики функции натурального логарифма, попрактикуетесь в использовании свойств, а также оцените функции натурального логарифма на своем калькуляторе. Не думайте слишком много шутить о натуральном бревне, мы уже знаем о них, но избавим вас от боли.
Натуральный логарифм, ln , является частным случаем, когда у вас есть f ( x ) = log e x . e — это база! Если бы мы записали это длинным путем, это выглядело бы так: f ( x ) = log 2.718281828 … x . В 1668 году какой-то умный парень по имени Николас Меркатор решил назвать это функцией натурального журнала. В 1600-х годах у нас не было блогеров, у нас были регистраторы, также известные как старомодные ботаники.
В 1600-х годах у нас не было блогеров, у нас были регистраторы, также известные как старомодные ботаники.
Это эквивалентные инструкции:
f ( x ) = log e x
f ( x ) = ln ( x ) как
Notice основание логарифма — e . Мы называем это естественным журналом, поэтому нам не нужно писать журнал e . Мы можем просто написать y = ln ( x ), и все поймут, что это означает.Наш маленький друг, e , хотел иметь свою собственную логарифмическую функцию. Что за парень!
Пример задачи
Постройте график функции натурального логарифма и ее обратного значения.
Синяя кривая — это функция y = e x , а функция натурального логарифма y = ln ( x ) — красная кривая. Поскольку они инвертированы, они, по сути, являются отражением над этой воображаемой диагональной линией y = x .
Пример задачи
Используя свойства логарифмов (из предыдущего раздела), перепишите эту функцию натурального логарифма как сумму или разность логарифмов:
Перепишите в суммах и разностях натуральных логарифмов.
Хорошо, давайте сделаем это поэтапно, сначала, поскольку это натуральный логарифм, он следует тем же свойствам логарифмов (которые мы узнали в предыдущем разделе).
Говоря об инверсиях, знаете ли вы, что мы можем применить инверсию натурального логарифма к экспоненциальной функции? Посмотрите на это волшебство:
e ln x = x
ln ( e x ) = x
Пример задачи
90650 Eval 9 .Поскольку теперь мы знаем, что функция, обратная функции e , равна ln , решение:
e ln 9 = 9.
Пример задачи
Evaluate ln ( e 1,9 ).
Легкие Шмеазы. Ответ — 1,9 благодаря нашему верному другу, обратному.
В последнем разделе «Графики логарифмических функций» мы упоминали, что вы можете преобразовать логарифм определенного основания в логарифм основания 10 с помощью простого трюка.
Запомните это …
y = log 2 x
… то же самое, что и это:
Точно так же мы можем сделать это с помощью натуральных журналов, которые нам помогут в следующем разделе решите уравнения. Если у нас есть y = log 3 x , мы можем преобразовать его в функцию естественного журнала, что некоторым людям нравится больше, чем работа с журналами.
Натуральные журналы менее громоздки, на вашем калькуляторе есть изящные маленькие кнопки для ln , и вам не нужно беспокоиться об изменении базы.Разбейте мюсли, мы будем натуральными!
Пример задачи
Преобразуйте журнал 6 100 в натуральные логарифмы и затем оцените (округлите до сотых).
Логарифм и экспоненциальные функции
Логарифм и экспоненциальные функцииФункция логарифма по основанию 10
Фон: Каждое положительное число, y , можно выразить как 10 с повышением до некоторого мощность, х .Эта связь описывается уравнениемy = 10 x ,и описывается этим графиком: Например, число 16 можно выразить как 10 1,2 . Это черная точка на графике. Мы определяем функцию, называемую логарифмом по основанию 10 , которая принимает число вроде 16 в качестве входных данных вычисляет, что его можно выразить как 10 1.2 , г. и возвращает показатель степени 1,2 в качестве выходного значения: Вот формальное определение функции логарифма по основанию 10.
| Определение: Логарифм по основанию 10 — это функция, которая принимает любое положительное число x в качестве входных данных и возвращает экспонента, до которой необходимо возвести основание 10, чтобы получить x .  Обозначается log ( x ). Обозначается log ( x ). |
Пример 1: Вычислить журнал (1000).
Аргумент функция логарифма (т.е. количество в скобках, 1000), легко выражается как 10 возводится в степень 3. Затем функция логарифмирования возвращает показатель степени.
журнал (1000) = журнал (10 3 ) = 3
Пример 2: Оценить журнал (10 5,7 ).
Аргумент уже выражен как 10 в степени, поэтому функция логарифмирования просто возвращает показатель степени.
журнал (10 5.7 ) = 5,7
Пример 3: Вычислить журнал (16).
По графику 16 = 10 1,2 . Функция логарифма возвращает показатель степени 1,2.
log (16) = log (10 1,2 ) = 1,2
График: Синяя кривая , показанная справа, представляет собой график функции логарифма по основанию 10, y = log ( х ). Обратите внимание, что для любого положительного значения x оно однозначно, а для любого отрицательного x оно не определено.Если сравнить этот график с графиком
из y = 10 x и выше
тогда вы видите, что одно можно получить от другого, поменяв местами
оси x и y .
Обратите внимание, что для любого положительного значения x оно однозначно, а для любого отрицательного x оно не определено.Если сравнить этот график с графиком
из y = 10 x и выше
тогда вы видите, что одно можно получить от другого, поменяв местами
оси x и y .
Для сравнения: красная кривая — это график функции натурального логарифма ( y = ln ( x ), рассмотренный в следующем разделе). График натурального логарифма имеет точно такую же форму как логарифм по основанию 10; это всего лишь 2.В 3 раза выше.
Важной особенностью функций логарифмирования (независимо от основания) является то, что они растут очень медленно. поскольку x становится очень большим. Они прекрасно описывают, как человек ухо воспринимает громкость и то, как человеческий глаз воспринимает яркость.
Домен и диапазон: Область определения функции логарифма по основанию 10 — это все положительные действительные числа, а диапазон —
все реальные числа.
Функция логарифма по основанию 10 может быть распространяется на комплексные числа, в этом случае домен — это все комплексные числа, кроме нуля.Логарифм нуля по основанию 10 всегда не определен.
Некоторые специальные значения функции логарифма по основанию 10
Решение уравнения 10 x = c для x с использованием функции логарифма по основанию 10
Предположим, что x неизвестно, но что 10 x равно известное значение c . Тогда нахождение x требует решения следующее уравнение для x .
10 x = cРешение
x = журнал ( c )Это потому, что найти журнал ( c ) означает выразить c как 10 до показателя степени, а затем возвращение этого показателя. Но в исходном уравнении этот показатель равен x .
 Обратите внимание, что если c отрицательно, то настоящего решения нет.
Однако есть комплексное решение.Более того, если c = 0, то решения вообще нет.
Обратите внимание, что если c отрицательно, то настоящего решения нет.
Однако есть комплексное решение.Более того, если c = 0, то решения вообще нет.log ( x ) и 10 x — обратные функции
Рассмотрим функцию 10 x , которая принимает x и возвращает 10 x , вот так:
Функция логарифма по основанию 10 должна делать прямо противоположное, а именно: Следовательно, это обратные функции.Обратите внимание на следующее:
- Поскольку функция 10 x является обратной функция логарифма по основанию 10 ее иногда называют функцией антилогарифма .
- Выше мы видели, что решение
10 x = y равно x = журнал ( y ). Мы должны посмотреть на эти два уравнения
как выражающие те же отношения между x и y , но
с разных точек зрения.
 Первое уравнение — это соотношение, решенное для y , а второй — отношение, разрешенное для x .
(Аналогия: « Том — брат Джейн »
эквивалентно утверждению, что « Джейн — сестра Тома ».)
Первое уравнение — это соотношение, решенное для y , а второй — отношение, разрешенное для x .
(Аналогия: « Том — брат Джейн »
эквивалентно утверждению, что « Джейн — сестра Тома ».) - В предыдущем пункте мы видели, что два уравнения,
10 x = y и x = журнал ( y ), сказано то же самое.Если мы заменим x в первом уравнении
используя x второго уравнения, мы получаем это тождество:
10 журнал ( y ) = y
и если во втором уравнении заменить на по и первого уравнения получаем это тождество:x = журнал (10 x )
Эти тождества полезны для демонстрации того, как логарифм и антилогарифм уравновешивают друг друга. - Если сравнить график
от до = журнал ( x ) до
график
из y = 10 x тогда вы видите, что одно можно получить от другого, поменяв местами
оси x и y .
 Это всегда происходит с обратными функциями.
Это всегда происходит с обратными функциями.
Как использовать функцию логарифма по основанию 10 в Algebra Coach
- Введите log (x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в квадратные скобки.
- Установите соответствующие параметры:
- Установите опцию точное / с плавающей запятой . В режиме с плавающей запятой вычисляется десятичный логарифм любого числа . В точном режиме логарифм по основанию 10 целого числа не вычисляется, потому что это приведет к приблизительному количеству.
- Включите комплексных чисел , если вы хотите иметь возможность оценивать логарифм по основанию 10 отрицательного или комплексного числа.
- Нажмите кнопку «Упростить».
Алгоритм для функции логарифма по основанию 10
Нажмите здесь
чтобы увидеть алгоритм, используемый компьютерами для вычисления функции логарифма по основанию 10.
Функция натурального логарифма
Предыстория: Возможно, вам будет полезно прочитать предыдущий раздел. перед чтением этого раздела используйте функцию логарифма по основанию 10.Две секции близко параллельны друг другу.Напомним, что функция логарифма по основанию 10 принимает такое число, как 16. в качестве входных данных вычисляет, что его можно записать как 10 1,2 , а затем возвращает показатель степени 1,2 в качестве выходного значения. Но зачем использовать основание 10? В конце концов, наверное единственная причина, по которой число 10 важно для людей, заключается в том, что у них есть 10 пальцев, которыми они впервые научились считать. Может быть, на какой-нибудь другой планете, населенной восьмипалыми существами, они используют базу 8!
На самом деле, наверное, самый важный номер в
вся математика (нажмите здесь, чтобы узнать почему)
это номер 2.71828…, которому мы даем имя e ,
в честь Леонарда Эйлера, который первым его открыл. Важно уметь взять любое положительное число, и , и выразить
это как e в некоторой степени, x .
Мы можем записать это соотношение в форме уравнения:
Важно уметь взять любое положительное число, и , и выразить
это как e в некоторой степени, x .
Мы можем записать это соотношение в форме уравнения:
y = e xНапример, 5 можно записать как e 1,6 (показатель степени приблизительный).Как мы узнаем, что это правильная мощность e ? Потому что мы получаем это из графика, показанного ниже.
Чтобы построить этот график, мы составили таблицу из нескольких очевидных значений y = e x , как показано ниже слева. Затем мы нанесли значения на график (это красные точки) и нарисовали плавный изгибаться через них. Затем мы заметили, что кривая проходит через y = 5 и x = 1,6 (черная точка). Это означает, что 5 = e 1.6 .
Если вы сравните этот график с графиком y = 10 x вы видите, что оба имеют одинаковую так называемую форму экспоненциального роста но этот график растет медленнее.
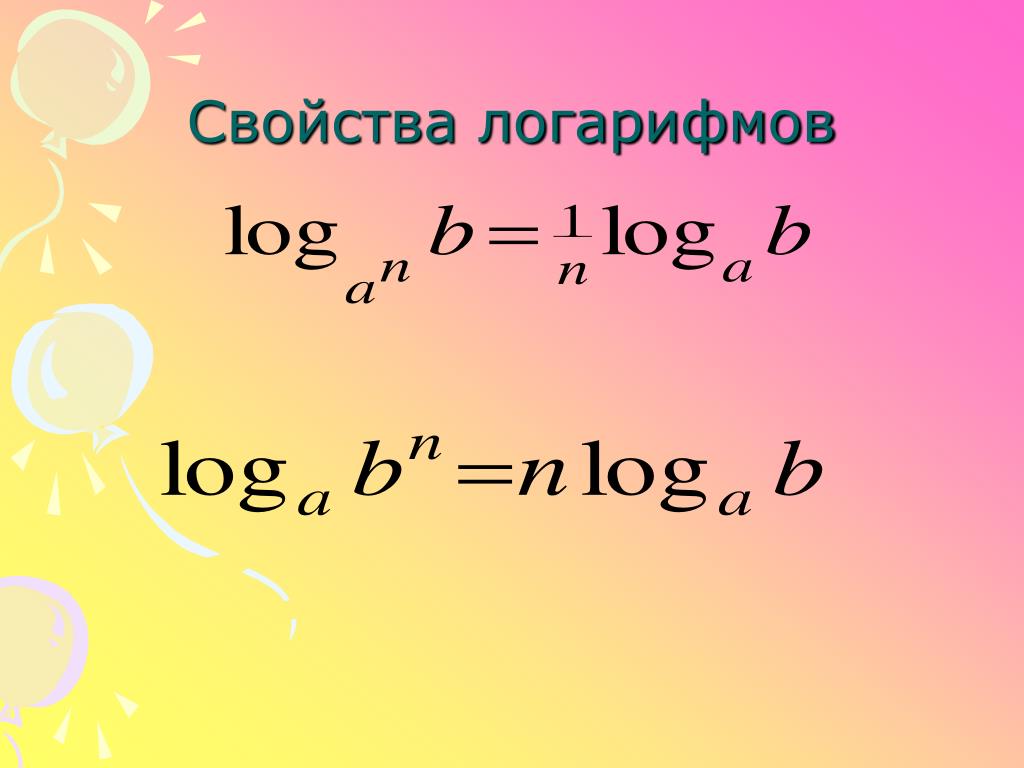
Затем мы определяем функцию, называемую натуральным логарифмом , которая принимает число вроде 5. в качестве входных данных вычисляет, что его можно записать как e 1.6 , г. и возвращает показатель степени 1,6 в качестве выходного значения. Вот формальное определение.
| Определение: Натуральный логарифм — это функция, которая принимает любое положительное число x в качестве входных данных и возвращает экспонента, до которой необходимо возвести основание e , чтобы получить x . Обозначается ln ( x ). ( e означает число 2,71828…) |
Обратите внимание, что во избежание путаницы функция натурального логарифма обозначается ln ( x ) и Логарифм по основанию 10 Функция обозначается как log ( x ).
Пример 1: Оценить ln ( e 4.7 ).
Аргумент функция натурального логарифма уже выражена так как e возведено в степень, поэтому функция натурального логарифма просто возвращает показатель степени.
ln ( e 4,7 ) = 4,7
Пример 2: Оцените ln (5).
По графику 5 = e 1,6 . Функция логарифма возвращает показатель степени 1.6.
ln (5) = 1,6
Пример 3: Оценить ln ( e ).
Выразите аргумент поскольку e возведен в степень 1 и вернет показатель степени.
ln ( e ) = ln ( e 1 ) = 1
Пример 4: Вычислить ln (1).
Выразите аргумент as e , возведенный в степень 0 и возвращающий показатель степени.
ln (1) = ln ( e 0 ) = 0
График: Красная кривая , показанная справа, представляет собой график функции натурального логарифма, y = ln ( х ).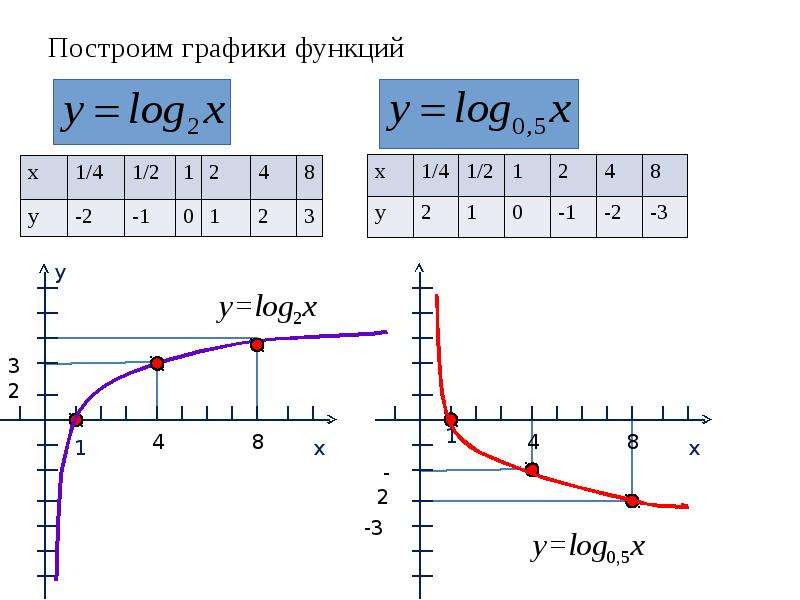 Обратите внимание, что для любого положительного значения x оно однозначно, а для любого отрицательного x оно не определено.
Если вы сравните этот график с
график y = e x тогда вы видите, что одно можно получить от другого, поменяв местами
оси x и y .
Обратите внимание, что для любого положительного значения x оно однозначно, а для любого отрицательного x оно не определено.
Если вы сравните этот график с
график y = e x тогда вы видите, что одно можно получить от другого, поменяв местами
оси x и y .
Для сравнения синяя кривая показывает функция логарифма по основанию 10, y = log ( x ). Он имеет точно такую же форму, но его высота составляет всего 43%.
Домен и диапазон: Область действия функции натурального логарифма — все положительные действительные числа, а диапазон —
все реальные числа.
Функция натурального логарифма может быть распространяется на комплексные числа, в этом случае домен — это все комплексные числа, кроме нуля.Натуральный логарифм нуля всегда не определен.
Решение уравнения e x = c для x с использованием функции натурального логарифма
Предположим, что x неизвестно, но что e x равно
известное значение c . Тогда для нахождения x необходимо решить это уравнение
для x :
Тогда для нахождения x необходимо решить это уравнение
для x :
e x = cРешение
x = ln ( c )потому что найти ln ( c ) означает выразить c как e , возведенное в степень, а затем возвращающее эту экспоненту.Но в исходном уравнении этот показатель равен x . Обратите внимание, что если c отрицательно, то настоящего решения нет. Однако есть комплексное решение. Более того, если c = 0, то решения вообще нет.
ln ( x ) и e x — обратные функции
Рассмотрим функцию e x , которая принимает x и возвращает e x , вот так:
Функция натурального логарифма должна делать прямо противоположное, а именно: Следовательно, это обратные функции.
Обратите внимание на следующее:
- Выше мы видели, что решение e x = y — это x = ln ( y ). Мы должны посмотреть на эти два уравнения как выражающие те же отношения между x и y , но с разных точек зрения. Первое уравнение — это соотношение, решенное для y , а второй — отношение, разрешенное для x .(Аналогия: « Том — брат Джейн » эквивалентно утверждению, что « Джейн — сестра Тома ».)
- В предыдущем пункте мы видели, что два уравнения, e x = y и x = ln ( y ), сказано то же самое.
Если мы заменим x в первом уравнении
используя x второго уравнения, мы получаем это тождество:
e ln ( y ) = y
и если во втором уравнении заменить на по и первого уравнения получаем это тождество:x = ln ( e x )
Эти тождества полезны для демонстрации того, как натуральный логарифм и e x функции отменяют друг друга.
- Если сравнить график от y = ln ( x ) до график из y = e x тогда вы видите, что одно можно получить от другого, поменяв местами оси x и y . Это всегда происходит с обратными функциями.
Как использовать функцию натурального логарифма в Algebra Coach
- Введите ln (x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в квадратные скобки.
- Установите соответствующие параметры:
- Установите опцию точное / с плавающей запятой . В режиме с плавающей запятой вычисляется натуральный логарифм любого числа . В точном режиме натуральный логарифм целого числа не вычисляется, потому что это приведет к приблизительному количеству.
- Установить e представляет / не представляет 2.718 … опция.
(Установите значение , это означает так что, например, ln (e 3 ) упрощается до 3.
 )
) - Включите комплексных чисел , если вы хотите иметь возможность оценивать натуральный логарифм отрицательного или комплексного числа.
- Нажмите кнопку «Упростить».
Алгоритм для функции натурального логарифма
Нажмите здесь чтобы увидеть алгоритм, используемый компьютерами для вычисления функции натурального логарифма.
Показательная функция (с основанием
e , функцией e x ) Предыстория: Возможно, вам будет полезно прочитать предыдущий раздел. о функции натурального логарифма перед чтением этого раздела. Там мы увидели, что можно использовать номер e . (что составляет примерно 2,71828…) в качестве основания и поднять его до любая степень, x , и произвольное положительное число y .Мы можем записать это соотношение в форме уравнения:y = e xВот график y = e x (синяя кривая).
 Для сравнения мы также приводим графики y = 2 x и y = 4 x .
Поскольку число e находится между 2 и 4
кривая y = e x лежит между кривыми y = 2 x и y = 4 x .
Для сравнения мы также приводим графики y = 2 x и y = 4 x .
Поскольку число e находится между 2 и 4
кривая y = e x лежит между кривыми y = 2 x и y = 4 x .Все три из этих кривых называются экспоненциальными функциями, потому что независимая переменная x находится в экспоненте. У всех троих есть собственность что чем выше по кривой вы поднимаетесь, тем круче они становятся. тем не мение y = e x имеет особое свойство, что на каждом В точке кривой наклон равен высоте . Это свойство уклонов делает его очень важной функцией в исчисление.
Примечание: В этом разделе, когда мы говорим «экспоненциальная функция», мы имеем в виду функцию с основанием e .
Вы можете рассматривать exp ( x ) как просто альтернативное (функциональное) обозначение для выражение e x .  Итак, конечно, функциональная форма exp ( x ) имеет все
свойства, которые имеет экспоненциальная форма e x .
У тренера по алгебре есть опция, позволяющая использовать ту или иную форму.
Вот таблица, в которой сравнивается «внешний вид» различных свойств в двух формах: Итак, конечно, функциональная форма exp ( x ) имеет все
свойства, которые имеет экспоненциальная форма e x .
У тренера по алгебре есть опция, позволяющая использовать ту или иную форму.
Вот таблица, в которой сравнивается «внешний вид» различных свойств в двух формах: |
График: Синяя кривая — график y = e x (я.е. экспоненты). Он обладает тем свойством, что его наклон везде равен высоте. Пунктирные красные линии показывают наклон кривой в различных точках вдоль Кривая. Обратите внимание, что наклон равен 5, когда высота равна 5, и так далее.
Если вы сравните этот график экспоненциальной функции с график функции натурального логарифма тогда вы видите, что одно можно получить от другого, поменяв местами оси x и y .
Домен и диапазон: Область экспоненциальной функции — все действительные числа, а диапазон —
все положительные действительные числа.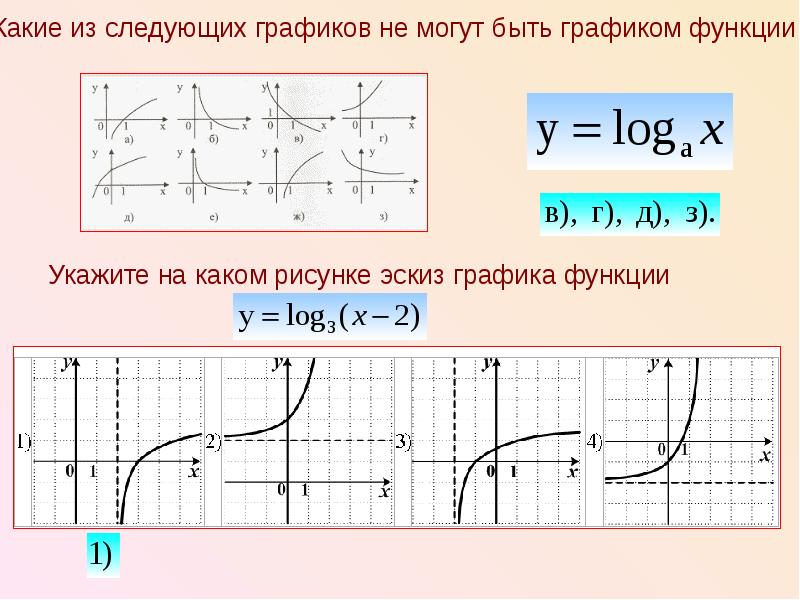
Показательная функция может быть распространяется на комплексные числа, в этом случае домен и диапазон — это комплексные числа.
Решение уравнения ln ( x ) = c для c с использованием экспоненциальной функции
Предположим, что x неизвестно, но что ln ( x ) равно известное значение c .Тогда для нахождения x необходимо решить это уравнение для x :
ln ( x ) = c .Решение такое:
x = e c , или x = exp ( c ).Это было объяснено в предыдущем разделе, посвященном функции натурального логарифма.
ln ( x ) и e x являются обратными функциями
Это было объяснено в предыдущем разделе, посвященном функции натурального логарифма.
Как использовать экспоненциальную функцию в Algebra Coach
- Введите exp (x) в текстовое поле, где x — аргумент.
 Аргумент должен быть заключен в квадратные скобки.
Аргумент должен быть заключен в квадратные скобки. - Установите соответствующие параметры:
- Задайте для параметра экспоненциальной функции следующее:
- Установите опцию с точной / с плавающей запятой . В режиме с плавающей запятой exp ( r ) для оценивается любое число r .В точном режиме exp ( i ) для любого целого числа i не оценивается, потому что это приведет к приблизительному количеству.
- Включите комплексных чисел , если хотите иметь возможность оценивать exp ( c ) для комплексного числа c .
- Нажмите кнопку «Упростить».

Алгоритм для e x или экспоненциальная функция
Нажмите здесь чтобы увидеть алгоритм, который компьютеры используют для оценки e x или exp ( x ).
Если вы нашли эту страницу в ходе веб-поиска, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
4.4: Графики логарифмических функций
Цели обучения
- Укажите область логарифмической функции.
- Граф логарифмических функций.
В предыдущем разделе было показано, как создание графического представления экспоненциальной модели дает некоторое представление о прогнозировании будущих событий.{y} \). Обычно при построении графика функции выбираются различные \ (x \) — значения, и каждое из них используется для вычисления соответствующего \ (y \) — значения. Напротив, для этого метода выбираются \ (y \) — значения, а затем вычисляются соответствующие \ (x \) — значения. {y}=x\)»>
{y}=x\)»>
Попробовать \ (\ PageIndex {1} \)
| (a) График: \ (y = \ log _ {3} (x) \). |
| (b) График: \ (y = \ log _ {5} (x) \).{-1} = ({\ color {Cerulean} {\ frac {1} {b}}}) \), что верно для любого \ (b \). В нашем следующем примере рассматривается график \ (y = log_ {b} (x) \) при \ (0 {y}=x\)»> |
Попробовать \ (\ PageIndex {2} \)
| (a) График: \ (y = \ log _ {\ frac {1} {2}} (x) \). |
| (b) График: \ (y = \ log _ {\ frac {1} {4}} (x) \). |
|
Следующие функции журнала \ (y = \ log _ {\ frac {1} {2}} (x), y = \ log _ {\ frac {1} {3}} (x) \) и \ (y = \ log _ {\ frac {1} {4}} (x) \) имеют похожие графики:
- Все графики имеют одинаковую базовую форму. Это потому, что все функции журнала имеют дробное основание \ (0
- Все графики содержат вертикальную асимптоту \ (x = 0 \) и ключевые точки \ ((1,0), \: (b, 1), \: \ left (\ frac {1} {b}, — 1 \ right) \), как и при \ (b> 1 \).

- Домен и диапазон также такие же, как при \ (b> 1 \). Область равна \ ((0, ∞) \), диапазон равен \ ((- ∞, ∞) \), а ось \ (y \) — вертикальная асимптота.
- Все графики содержат вертикальную асимптоту \ (x = 0 \) и ключевые точки \ ((1,0), \: (b, 1), \: \ left (\ frac {1} {b}, — 1 \ right) \), как и при \ (b> 1 \).
Мы суммируем эти свойства в таблице ниже.
ХАРАКТЕРИСТИКИ ГРАФИКА РОДИТЕЛЬСКОЙ ФУНКЦИИ, \ (f (x) = log_b (x) \)
Для любого действительного числа \ (x \) и константы \ (b> 0 \), \ (b ≠ 1 \) мы можем увидеть следующие характеристики на графике \ (f (x) = {\ log} _b (х) \):
- индивидуальная функция
- вертикальная асимптота: \ (x = 0 \)
- ключевых точек: \ (x \) — точка пересечения : \ ((1,0) \), \ ((b, 1) \) и \ (\ left (\ tfrac {1} {b}, — 1 \ справа) \)
- \ (y \) — перехват: нет Домен
- : \ ((0, \ infty) \)
- диапазон: \ ((- \ infty, \ infty) \)
- увеличивается, если \ (b> 1 \)
- уменьшается, если \ (0
Рисунок \ (\ PageIndex {3. 2} \) иллюстрирует графики трех логарифмических функций с разными основаниями, все больше 1. Он показывает, как изменение основания \ (b \) в \ (f (x) = {\ log} _b (x) \) может влияют на графики. Обратите внимание, что графики сжимаются по вертикали по мере увеличения значения базы. (Примечание: напомним, что функция \ (\ ln (x) \) имеет основание \ (e≈2.718 \).)
2} \) иллюстрирует графики трех логарифмических функций с разными основаниями, все больше 1. Он показывает, как изменение основания \ (b \) в \ (f (x) = {\ log} _b (x) \) может влияют на графики. Обратите внимание, что графики сжимаются по вертикали по мере увеличения значения базы. (Примечание: напомним, что функция \ (\ ln (x) \) имеет основание \ (e≈2.718 \).)
Семейство логарифмических функций включает родительскую функцию \ (y = {\ log} _b (x) \) вместе со всеми ее преобразованиями: сдвигами, растяжениями, сжатиями и отражениями.При построении графиков преобразований мы всегда начинаем с построения графика родительской функции \ (y = {\ log} _b (x) \). Ниже приведено краткое описание того, как построить график функций родительского журнала.
Практическое руководство: Постройте график родительской логарифмической функции \ (f (x) = {\ log} _b (x) \).
- Построить ориентиры логарифмической функции
- Нарисуйте и обозначьте вертикальную асимптоту \ (x = 0 \).
 y = x \).Выберите маленькие значения \ (y \) (например, 2, 3 и -1), вычислите соответствующее значение для \ (x \) и нанесите точку на график.
y = x \).Выберите маленькие значения \ (y \) (например, 2, 3 и -1), вычислите соответствующее значение для \ (x \) и нанесите точку на график. - Проведите плавную кривую через точки.
- Укажите область, \ ((0, \ infty) \), диапазон, \ ((- \ infty, \ infty) \), и вертикальную асимптоту, \ (x = 0 \).
- Нарисуйте и обозначьте вертикальную асимптоту \ (x = 0 \).
Попробовать \ (\ PageIndex {3} \)
График \ (f (x) = {\ log} _5 (x) \) и \ (f (x) = {\ log} _ {\ tfrac {1} {5}} (x) \). Укажите домен, диапазон и асимптоту.- Ответ
Ориентиры — это вертикальная асимптота \ (x = 0 \) и
ключевых точек \ ((1,0) \), \ ((5,1) \) и \ (\ left (\ tfrac {1} {5 }, — 1 \ right) \).Область — \ ((0, \ infty) \), диапазон — \ ((- \ infty, \ infty) \),
, а вертикальная асимптота — \ (x = 0 \).Ориентиры — это вертикальная асимптота \ (x = 0 \) и
ключевых точек \ ((1,0) \), \ (\ left (\ tfrac {1} {5}, — 1 \ right) \) и ( (5,1) \).
Область — \ ((0, \ infty) \), диапазон — \ ((- \ infty, \ infty) \),
, а вертикальная асимптота — \ (x = 0 \).
Графические преобразования логарифмических функций
Преобразования логарифмических графиков аналогичны преобразованиям других родительских функций. Мы можем сдвигать, растягивать, сжимать и отражать родительскую функцию \ (y = {\ log} _b (x) \) без потери основной формы. Общая схема процесса представлена ниже. Затем подробно описаны иллюстрации каждого типа трансформации. Наконец, в конце этого раздела приводится сводка шагов, связанных с построением графика функции с несколькими преобразованиями.
Практическое руководство: Постройте график логарифмической функции \ (f (x) \) с помощью преобразований.
- Определите родительскую функцию \ (f (x) \) и нанесите на график родительскую функцию \ (y = {\ log} _b (x) \) и ее асимптоту.

- Укажите преобразования на графике \ (y \), необходимые для получения графика \ (f (x) \).
- Используйте преобразования для графика \ (f (x) \) и его асимптоты.
График вертикального смещения
Когда константа \ (d \) добавляется к родительской функции \ (f (x) = {\ log} _b (x) \), результатом является вертикальный сдвиг \ (d \) единиц в направлении войдите в \ (d \).Чтобы визуализировать вертикальные сдвиги, мы можем наблюдать общий график родительской функции \ (f (x) = {\ log} _b (x) \) вместе со сдвигом вверх, \ (g (x) = {\ log} _b ( x) + d \) и сдвиг вниз, \ (h (x) = {\ log} _b (x) −d \).
Рисунок \ (\ PageIndex {4} \)ВЕРТИКАЛЬНЫЕ СДВИГИ ФУНКЦИИ РОДИТЕЛЯ \ (y = log_b (x) \)
Для любой константы \ (d \) функция \ (f (x) = {\ log} _b (x) + d \)
- сдвигает родительскую функцию \ (y = {\ log} _b (x) \) вверх на \ (d \) единицы, если \ (d> 0 \).
- сдвигает родительскую функцию на \ (y = {\ log} _b (x) \) вниз на \ (d \) единицы, если \ (d <0 \).

Новые координаты \ (y \) равны \ (y + d \).
Пример \ (\ PageIndex {4} \): построение графика вертикального сдвига родительской функции \ (y = log_b (x) \)
Нарисуйте график \ (f (x) = {\ log} _3 (x) −2 \) вместе с его родительской функцией. Включите ключевые точки и асимптоту на график. Укажите домен, диапазон и асимптоту.
Решение
Шаг 1. Постройте график родительской функции \ (y = {\ log} _3 (x) \). Ориентиры: вертикальная асимптота \ (x = 0 \) и ключевые точки: \ (x \) — пересечение , \ ((1,0) \), \ ((3,1) \) и \ ((\ tfrac {1} {3}, -1) \).y = x \) суть \ ((9,2) \) и \ ((27,3) \).
Шаг 2. Преобразование на графике \ (y \), необходимое для получения графика \ (f (x) \): сдвинуть вниз на 2 единицы.
Шаг 3. Сдвиг вниз на 2 единицы означает, что новые координаты \ (y \) находятся путем вычитания \ (2 \) из старых координат \ (y \). Следовательно,
- Вертикальная асимптота для переведенной функции \ (f \) по-прежнему равна \ (x = 0 \).

- Ключевые точки для переведенной функции \ (f \) — это \ ((1, −2) \), \ ((3, −1) \) и \ (\ left (\ frac {1} {3} , −3 \ справа) \).Дополнительные точки: \ (9, 0) \) и \ (27,1) \).
Область — \ ((0, \ infty) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 0 \).
Попробовать \ (\ PageIndex {4} \)
Нарисуйте график \ (f (x) = {\ log} _2 (x) +2 \) вместе с его родительской функцией. Включите ключевые точки и асимптоту на график. Укажите домен, диапазон и асимптоту.
- Ответ
- Рисунок \ (\ PageIndex {4b} \) График \ (f (x) = {\ log} _2 (x) +2 \)
Домен \ ((0, \ infty) \), диапазон \ ((- \ infty, \ infty) \), а вертикальная асимптота равна \ (x = 0 \).
График горизонтального смещения
Когда константа \ (c \) добавляется на вход родительской функции \ (f (x) = {\ log} _b (x) \), результатом является горизонтальный сдвиг \ (c \) единиц в напротив направления знака \ (c \). Чтобы визуализировать горизонтальные сдвиги, мы можем наблюдать общий график родительской функции \ (f (x) = {\ log} _b (x) \) и для \ (c> 0 \) рядом со сдвигом влево, \ (g ( x) = {\ log} _b (x + c) \), и сдвиг вправо, \ (h (x) = {\ log} _b (x − c) \). См. Рисунок \ (\ PageIndex {5} \).
Чтобы визуализировать горизонтальные сдвиги, мы можем наблюдать общий график родительской функции \ (f (x) = {\ log} _b (x) \) и для \ (c> 0 \) рядом со сдвигом влево, \ (g ( x) = {\ log} _b (x + c) \), и сдвиг вправо, \ (h (x) = {\ log} _b (x − c) \). См. Рисунок \ (\ PageIndex {5} \).
ГОРИЗОНТАЛЬНЫЕ СДВИГИ ФУНКЦИИ РОДИТЕЛЯ \ (y = log_b (x) \)
Для любой константы \ (c \) функция \ (f (x) = {\ log} _b (x + c) \)
- сдвигает родительскую функцию \ (y = {\ log} _b (x) \) влево на \ (c \) единицы, если \ (c> 0 \).
- сдвигает родительскую функцию \ (y = {\ log} _b (x) \) вправо на \ (c \) единицы, если \ (c <0 \).
Новые координаты \ (x \) равны \ (x — c \).
Пример \ (\ PageIndex {5} \): построение графика горизонтального смещения родительской функции \ (y = log_b (x) \)
Нарисуйте горизонтальный сдвиг \ (f (x) = {\ log} _3 (x − 2) \) рядом с его родительской функцией.Включите ключевые точки и асимптоты на график.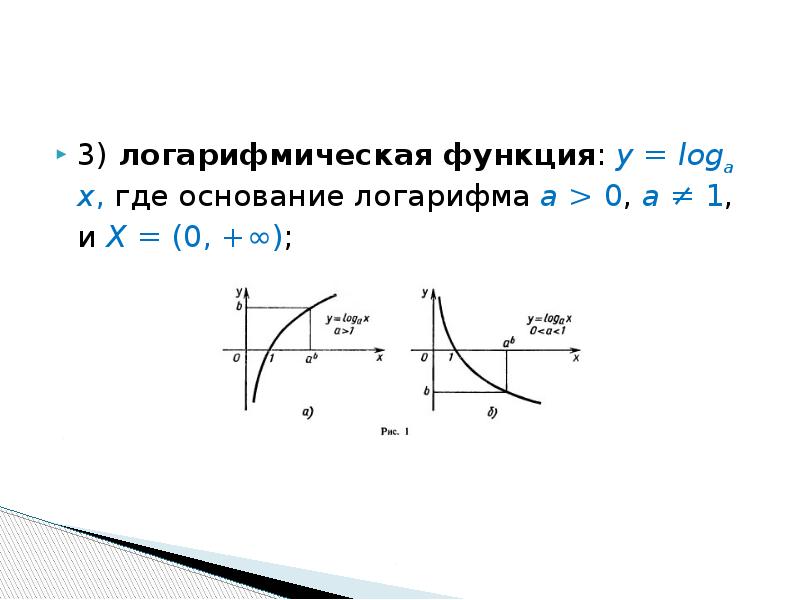 Укажите домен, диапазон и асимптоту.
Укажите домен, диапазон и асимптоту.
Решение
Шаг 1. Постройте график родительской функции \ (y = {\ log} _3 (x) \). Ориентиры: вертикальная асимптота \ (x = 0 \) и ключевые точки: x — пересечение , \ ((1,0) \), \ ((3,1) \) и \ ((\ tfrac {1} {3}, -1) \)
Шаг 2. Преобразование на графике \ (y \), необходимое для получения графика \ (f (x) \): сдвинуть вправо на 2 единицы.
Шаг 3. Сдвиг вправо на 2 единицы означает, что новые координаты \ (x \) находятся путем добавления \ (2 \) к старым координатам \ (x \).Следовательно,
- Вертикальная асимптота для преобразованной функции \ (f \) равна \ (x = 0 + 2) \) или \ (x = 2 \).
- Ключевые точки для переведенной функции \ (f \): \ ((3,0) \), \ ((5,1) \) и \ (\ left (\ frac {7} {3}, — 1 \ вправо) \).
Область — \ ((2, \ infty) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 2 \).
Попробовать \ (\ PageIndex {5} \)
Нарисуйте график \ (f (x) = {\ log} _3 (x + 4) \) вместе с его родительской функцией. Включите ключевые точки и асимптоты на график.Укажите домен, диапазон и асимптоту.
Включите ключевые точки и асимптоты на график.Укажите домен, диапазон и асимптоту.
- Ответ
- Рисунок \ (\ PageIndex {5b} \) График \ (f (x) = {\ log} _3 (x + 4) \)
Домен \ ((- 4, \ infty) \), диапазон \ ((- \ infty, \ infty) \) и асимптота \ (x = –4 \).
Графические отражения
Когда родительская функция \ (f (x) = {\ log} _b (x) \) умножается на \ (- 1 \), результатом является отражение относительно оси \ (x \) -. Когда вход умножается на \ (- 1 \), результатом является отражение относительно оси \ (y \) -.Чтобы визуализировать отражения, мы ограничиваем \ (b> 1 \) и наблюдаем за общим графиком родительской функции \ (f (x) = {\ log} _b (x) \) вместе с отражением о \ (x \) -ось, \ (g (x) = — {\ log} _b (x) \) и отражение относительно оси \ (y \) -, \ (h (x) = {\ log} _b (−x) \).
ОТРАЖЕНИЯ РОДИТЕЛЬСКОЙ ФУНКЦИИ \ (y = log_b (x) \)
\ (f (x) = — {\ log} _b (x) \; \; \; \) отражает родительскую функцию относительно оси \ (x \) -. Домен, диапазон и вертикальная асимптота не изменились.
Домен, диапазон и вертикальная асимптота не изменились.
\ (f (x) = {\ log} _b (−x) \; \; \; \) отражает родительскую функцию относительно оси \ (y \) -.Домен изменен.
Пример \ (\ PageIndex {8} \): построение графика отражения логарифмической функции
Нарисуйте график \ (f (x) = \ log (−x) \) вместе с его родительской функцией. Включите ключевые точки и асимптоту на график. Укажите домен, диапазон и асимптоту.
Решение
Шаг 1. Постройте график родительской функции \ (y = {\ log} (x) \). Ориентиры: вертикальная асимптота \ (x = 0 \) и ключевые точки: \ (\ left (\ frac {1} {10}, — 1 \ right) \), \ ((1,0) \) и \ ((10,1) \).
Шаг 2. Преобразование на графике \ (y \), необходимое для получения графика \ (f (x) \): отражение родительского графа относительно оси \ (y \) — .
Шаг 3. Отражение вокруг оси \ (y \) достигается умножением всех координат \ (x \) на -1. Следовательно,
- Вертикальная асимптота для переведенной функции \ (f \) остается \ (x = 0 \).

- Ключевые точки для переведенной функции \ (f \): \ (\ left (- \ frac {1} {10}, — 1 \ right) \), \ ((- 1,0) \) и \ ((-10,1) \).
Область — \ ((- \ infty, 0) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 0 \).
Попробовать \ (\ PageIndex {8} \)
График \ (f (x) = — \ log (−x) \). Укажите домен, диапазон и асимптоту.
- Ответ
- Рисунок \ (\ PageIndex {8b} \) График \ (f (x) = — \ log (−x) \).
Область — \ ((- \ infty, 0) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 0 \).
Графики растяжения и сжатия
Когда родительская функция \ (f (x) = {\ log} _b (x) \) умножается на константу \ (a> 0 \), результатом является вертикальное растяжение или сжатие исходного графика.Чтобы визуализировать растяжения и сжатия, мы устанавливаем \ (a> 1 \) и наблюдаем за общим графиком родительской функции \ (f (x) = {\ log} _b (x) \) рядом с вертикальным растяжением \ (g ( x) = a {\ log} _b (x) \) и вертикальное сжатие, \ (h (x) = \ dfrac {1} {a} {\ log} _b (x) \).
ВЕРТИКАЛЬНЫЕ РАСТЯЖЕНИЯ И СЖАТИЯ РОДИТЕЛЬСКОЙ ФУНКЦИИ \ (y = log_b (x) \)
Для любой константы \ (a \ ne 0 \) функция \ (f (x) = a {\ log} _b (x) \)
- растягивает родительскую функцию \ (y = {\ log} _b (x) \) по вертикали с коэффициентом \ (a \), если \ (| a |> 1 \).
- сжимает родительскую функцию \ (y = {\ log} _b (x) \) по вертикали с коэффициентом \ (a \), если \ (0 <| a | <1 \).
Новые координаты \ (y \) равны \ (ay \). (Это также будет включать вертикальное отражение, если оно есть).
Пример \ (\ PageIndex {6} \): построение графика растяжения или сжатия родительской функции \ (y = log_b (x) \)
Нарисуйте график \ (f (x) = 2 {\ log} _4 (x) \) вместе с его родительской функцией. Включите ключевые точки и асимптоту на график.Укажите домен, диапазон и асимптоту.
Решение
Шаг 1. Постройте график родительской функции \ (y = {\ log} _4 (x) \).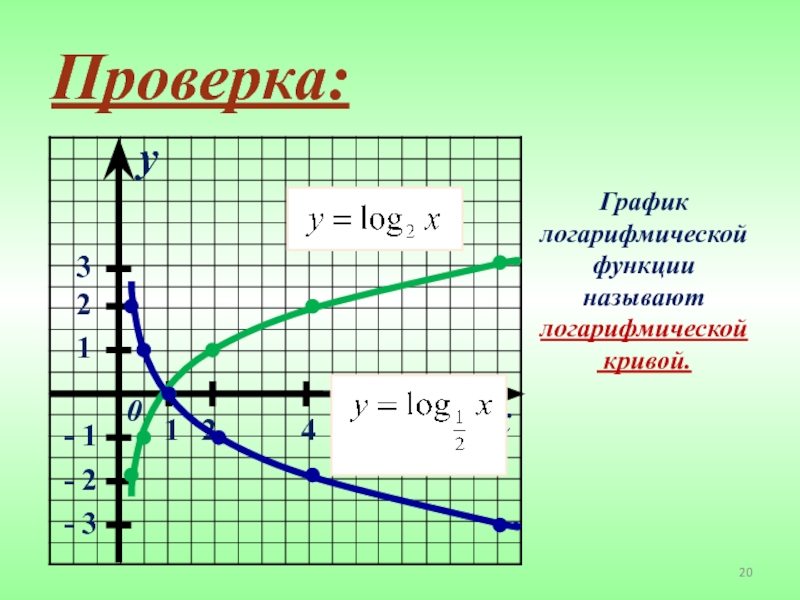 Ориентиры: вертикальная асимптота \ (x = 0 \) и ключевые точки: \ (\ left (\ frac {1} {4}, — 1 \ right) \), \ ((1,0) \) и \ ((4,1) \).
Ориентиры: вертикальная асимптота \ (x = 0 \) и ключевые точки: \ (\ left (\ frac {1} {4}, — 1 \ right) \), \ ((1,0) \) и \ ((4,1) \).
Шаг 2. Преобразование на графике \ (y \), необходимое для получения графика \ (f (x) \): растянуть функцию \ (f (x) = {\ log} _4 (x) \) в \ (2 \) раз.
Шаг 3. Вертикальное растяжение с коэффициентом \ (2 \) означает, что новые координаты \ (y \) находятся путем умножения координат \ (y \) на \ (2 \).Следовательно,
- Вертикальная асимптота для переведенной функции \ (f \) по-прежнему равна \ (x = 0 \).
- Ключевые точки для переведенной функции \ (f \): \ (\ left (\ frac {1} {4}, — 2 \ right) \), \ ((1,0) \) и \ (( 4,2) \).
Область — \ ((0, \ infty) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 0 \).
Попробовать \ (\ PageIndex {6} \)
Нарисуйте график \ (f (x) = \ dfrac {1} {2} {\ log} _4 (x) \) вместе с его родительской функцией.Включите ключевые точки и асимптоту на график.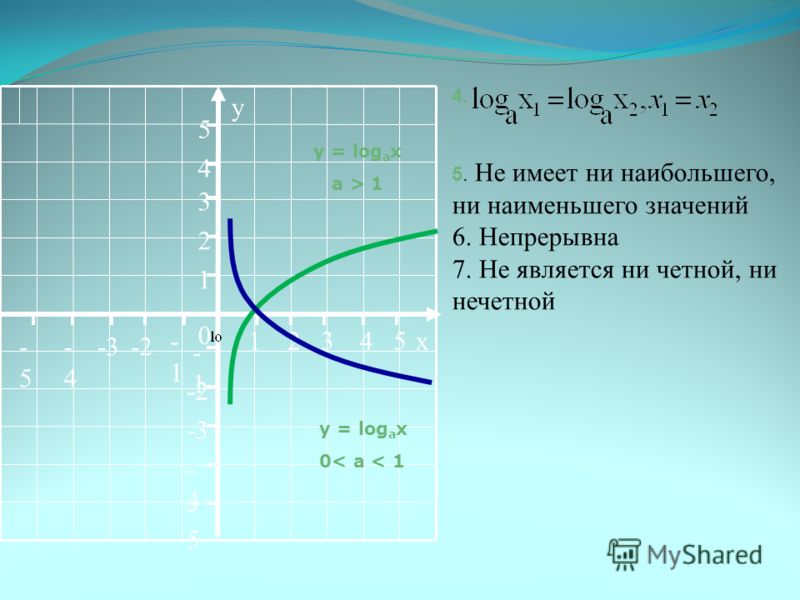 Укажите домен, диапазон и асимптоту.
Укажите домен, диапазон и асимптоту.
- Ответ
- Рисунок \ (\ PageIndex {6b} \) График \ (f (x) = \ dfrac {1} {2} {\ log} _4 (x) \)
Домен \ ((0, \ infty) \), диапазон равен \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 0 \).
Объедините горизонтальный сдвиг и вертикальное растяжение
Пример \ (\ PageIndex {7} \): объединение сдвига и растяжения
Нарисуйте график \ (f (x) = 5 {\ log} (x + 2) \).Укажите домен, диапазон и асимптоту.
Решение
Шаг 1. Изобразите родительскую функцию как \ (y = {\ log} (x) \). Ориентиры: вертикальная асимптота \ (x = 0 \) и ключевые точки: \ (\ left (\ frac {1} {10}, — 1 \ right) \), \ ((1,0) \) и \ ((10,1) \).
Шаг 2. Преобразования на графике \ (y \), необходимые для получения графика \ (f (x) \): перемещение влево \ (2 \) единиц (вычтите 2 из всех \ (x \) — координаты), затем растяните по вертикали в \ (5 \) раз (умножьте все \ (y \) — координаты на 5). (Поскольку эти два преобразования действуют перпендикулярно друг другу, порядок их выполнения не имеет значения, но рекомендуется выполнять все преобразования в заданном порядке, чтобы установить процедуру, которая всегда будет работать).
(Поскольку эти два преобразования действуют перпендикулярно друг другу, порядок их выполнения не имеет значения, но рекомендуется выполнять все преобразования в заданном порядке, чтобы установить процедуру, которая всегда будет работать).
Шаг 3. 1. \ (x \ longrightarrow x-2 \), 2. \ (y \ longrightarrow 5y \). Следовательно,
- Вертикальная асимптота для переведенной функции \ (f \) будет сдвинута на \ (x = −2 \).
- Ключевые точки для переведенной функции \ (f \): \ (\ left (-1 \ frac {9} {10}, — 5 \ right) \), \ ((- 1,0) \) и \ ((8,5) \).
Область — \ ((- 2, \ infty) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = −2 \).
Попробовать \ (\ PageIndex {7} \)
Нарисуйте график функции \ (f (x) = 3 {\ log} (x − 2) +1 \). Укажите домен, диапазон и асимптоту.
- Ответ
- Рисунок \ (\ PageIndex {7b} \) График функции \ (f (x) = 3 {\ log} (x − 2) +1 \).
Область значений — \ ((2, \ infty) \), диапазон — \ ((- \ infty, \ infty) \), а вертикальная асимптота — \ (x = 2 \).

Суммирование переводов логарифмической функции
Теперь, когда мы поработали с каждым типом преобразования для логарифмической функции, мы можем резюмировать, как построить график логарифмических функций, которые претерпели несколько преобразований своей родительской функции.
Построение логарифмической функции с использованием переводов
В этом разделе все переводы родительской логарифмической функции \ (y = {\ log} _b (x) \) имеют вид
\ (f (x) = a {\ log} _b (x + c) + d \) или \ (f (x) = a {\ log} _b (−x + c) + d \)
- Горизонтальные преобразования должны выполняться в определенном порядке
- Сначала сдвиньте по горизонтали влево на \ (c \) единицы, если \ (c> 0 \), или вправо, если \ (c <0 \).
- Затем, если коэффициент при \ (x \) отрицателен, график родительской функции отражается относительно оси y .
- Если \ (p \) — это \ (x \) — координата точки на родительском графе, то ее новое значение будет \ ((p − c) \) или, если присутствует отражение, \ (- (p −c) \)
- Вертикальные преобразования должны выполняться в определенном порядке
- Сначала выполняется растяжение или сжатие и отражение относительно оси \ (x \) —
- растянуто по вертикали с коэффициентом \ (| a | \), если \ (| a |> 0 \).

- сжимается по вертикали с коэффициентом \ (| a | \), если \ (0 <| a | <1 \).
- отражается относительно оси \ (x \) — , когда \ (a <0 \).
- растянуто по вертикали с коэффициентом \ (| a | \), если \ (| a |> 0 \).
- Наконец, сдвиньте вертикально вверх на \ (d \) единицы, если \ (d> 0 \), или вниз, если \ (d <0 \).
- Если \ (p \) — это \ (y \) — координата точки на родительском графе, то ее новое значение будет \ (ap + d \)
- Сначала выполняется растяжение или сжатие и отражение относительно оси \ (x \) —
- Диапазон всегда \ ((- \ infty, \ infty) \)
- Если коэффициент при \ (x \) был положительным, область значений равна \ ((- c, \ infty) \), а вертикальная асимптота равна \ (x = −c \).
- Если коэффициент при \ (x \) был отрицательным, область значений равна \ ((- \ infty, c) \), а вертикальная асимптота равна \ (x = c \).
Нахождение области определения и асимптоты логарифмической функции
Ранее область определения и вертикальная асимптота определялись путем построения графика логарифмической функции.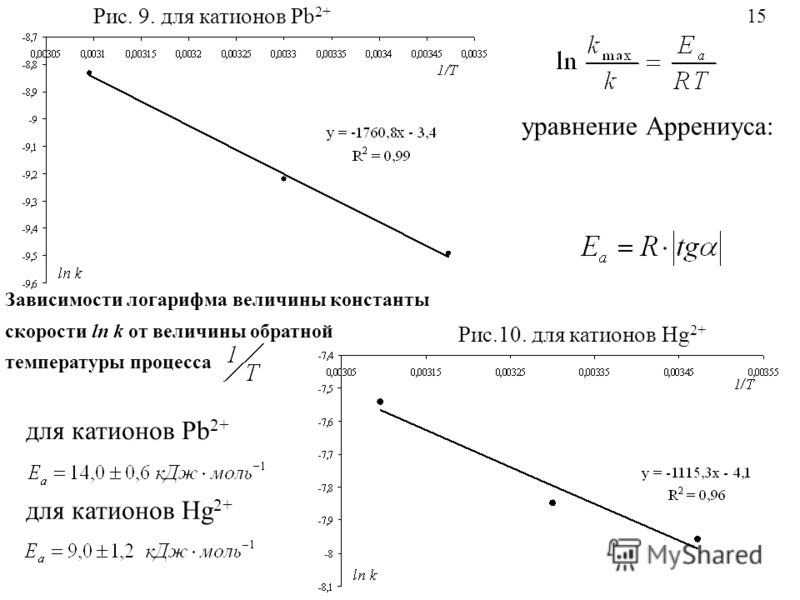 Также возможно определить область определения и вертикальную асимптоту любой логарифмической функции алгебраически. Здесь мы рассмотрим область (набор входных значений), для которой определена логарифмическая функция, и ее вертикальная асимптота.Икс\). Аналогично, применение преобразований к родительской функции \ (y = {\ log} _b (x) \) может изменить домен . Поэтому при нахождении области определения логарифмической функции важно помнить, что область определения состоит только из положительных действительных чисел . То есть аргумент логарифмической функции должен быть больше нуля .
Также возможно определить область определения и вертикальную асимптоту любой логарифмической функции алгебраически. Здесь мы рассмотрим область (набор входных значений), для которой определена логарифмическая функция, и ее вертикальная асимптота.Икс\). Аналогично, применение преобразований к родительской функции \ (y = {\ log} _b (x) \) может изменить домен . Поэтому при нахождении области определения логарифмической функции важно помнить, что область определения состоит только из положительных действительных чисел . То есть аргумент логарифмической функции должен быть больше нуля .
Например, рассмотрим \ (f (x) = {\ log} _4 (2x − 3) \). Эта функция определена для любых значений \ (x \) таких, что аргумент, в данном случае \ (2x − 3 \), больше нуля.Чтобы найти область, мы устанавливаем неравенство и решаем для \ (x \):
\ [\ begin {align *} 2x-3 &> 0 && \ qquad \ text {Показать аргумент больше нуля} \\ 2x &> 3 && \ qquad \ text {Добавить 3} \\ x &> 1. 5 && \ qquad \ текст {Разделить на 2} \\ \ end {align *} \]
5 && \ qquad \ текст {Разделить на 2} \\ \ end {align *} \]
В интервальной записи область значений \ (f (x) = {\ log} _4 (2x − 3) \) равна \ ((1.5, \ infty) \).
Инструкции: Для заданной логарифмической функции определите домен
- Установите неравенство, показывающее, что аргумент больше нуля.
- Решите относительно \ (x \).
- Запишите домен в интервальной записи.
Пример \ (\ PageIndex {9a} \): определение области логарифмического сдвига
Какова область определения \ (f (x) = {\ log} _2 (x + 3) \)?
Решение
Логарифмическая функция определяется только при положительном входе, поэтому эта функция определяется, когда \ (x + 3> 0 \). Решая это неравенство,
\ [\ begin {align *} x + 3 &> 0 && \ qquad \ text {Ввод должен быть положительным} \\ x &> -3 && \ qquad \ text {Subtract 3} \ end {align *} \]
Областью определения \ (f (x) = {\ log} _2 (x + 3) \) является \ ((- 3, \ infty) \). Вертикальная асимптота равна \ (x = −3 \)
Вертикальная асимптота равна \ (x = −3 \)
Попробовать \ (\ PageIndex {9a} \)
Какова область определения \ (f (x) = {\ log} _5 (x − 2) +1 \)?
- Ответ
Домен \ ((2, \ infty) \). Вертикальная асимптота равна \ (x = 2 \).
Найдите вертикальную асимптоту логарифмического графа
Асимптота логарифмического уравнения всегда на границе области . Следовательно, вертикальную асимптоту логарифмической функции можно получить, установив ее аргумент равным нулю и решив относительно \ (x \).
Практическое руководство: Для заданной логарифмической функции найти вертикальную асимптоту алгебраически
- Задайте неравенство, показывающее, что аргумент логарифмической функции равен нулю.
- Решите относительно \ (x \).
- Результатом является уравнение для вертикальной асимптоты логарифмической функции.
Пример \ (\ PageIndex {10a} \): определение области логарифмического сдвига и отражения
Какова область определения \ (f (x) = \ log (5−2x) \)? Каково уравнение его вертикальной асимптоты?
Решение
Логарифмическая функция определяется только при положительном входе, поэтому эта функция определяется, когда \ (5–2x> 0 \). Решая это неравенство,
Решая это неравенство,
\ [\ begin {align *} 5-2x &> 0 && \ qquad \ text {Ввод должен быть положительным} \\ -2x &> -5 && \ qquad \ text {Вычесть 5} \\ x & <\ dfrac {5 } {2} && \ qquad \ text {Разделить на -2 и переключить неравенство} \ end {align *} \]
Область определения \ (f (x) = \ log (5−2x) \) — \ (\ left (- \ infty, \ dfrac {5} {2} \ right) \). Вертикальная асимптота равна \ (x = \ dfrac {5} {2} \).
Попробовать \ (\ PageIndex {10a} \)
Какова область определения \ (f (x) = \ log (x − 5) +2 \)? Каково уравнение его вертикальной асимптоты?
- Ответ
\ ((5, \ infty) \) Вертикальная асимптота равна \ (x = 5 \).
Пример \ (\ PageIndex {10b} \): поиск вертикальной асимптоты логарифмового графа
Какова вертикальная асимптота \ (f (x) = — 2 {\ log} _3 (x + 4) +5 \)?
Решение
Вертикальная асимптота находится в точке \ (x = −4 \).
Анализ
Коэффициент, основание и сдвиг вверх не влияют на асимптоту.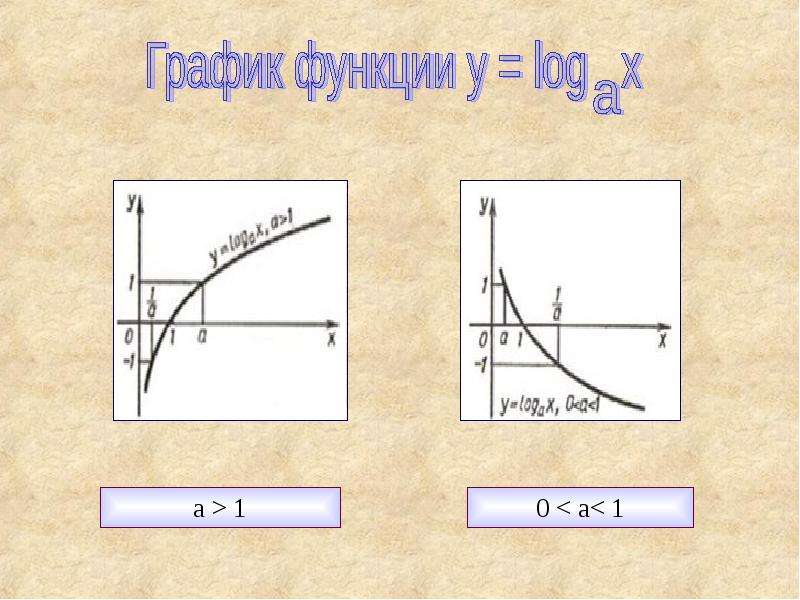 Сдвиг кривой на \ (4 \) единиц влево сдвигает вертикальную асимптоту к \ (x = −4 \).
Сдвиг кривой на \ (4 \) единиц влево сдвигает вертикальную асимптоту к \ (x = −4 \).
Попробовать \ (\ PageIndex {10b} \)
Какова вертикальная асимптота \ (f (x) = 3 + \ ln (x − 1) \)?
- Ответ
\ (х = 1 \)
Найдите уравнение логарифмической функции по ее графику
Пример \ (\ PageIndex {12} \): поиск уравнения из графика
Найдите возможное уравнение для десятичной логарифмической функции, изображенное ниже.
Решение
Этот график имеет вертикальную асимптоту в точке \ (x = –2 \) и был отражен вертикально.Мы еще не знаем вертикального сдвига или вертикального растяжения. Пока мы знаем, что уравнение будет иметь вид:
\ (е (х) = — а \ журнал (х + 2) + к \)
Оказывается, график проходит через точки \ ((- 1,1) \) и \ ((2, –1) \). Подставляя \ ((- 1,1) \),
\ [\ begin {align *} 1 & = -a \ log (-1 + 2) + k && \ qquad \ text {Substitute} (-1,1) \\ 1 & = -a \ log (1) + k && \ qquad \ text {Арифметика} \\ 1 & = k && \ qquad \ text {Потому что} \ log (1) = 0 \ end {align *} \]
Далее, подставляя в \ ((2, –1) \),
\ [\ begin {align *} -1 & = -a \ log (2 + 2) +1 && \ qquad \ text {Substitute} (2, -1) \\ -2 & = -a \ log (4) && \ qquad \ text {Арифметика} \\ a & = \ dfrac {2} {\ log (4)} && \ qquad \ text {Решить для a} \ end {align *} \]
Это дает нам уравнение \ (f (x) = — \ dfrac {2} {\ log (4)} \ log (x + 2) +1 \).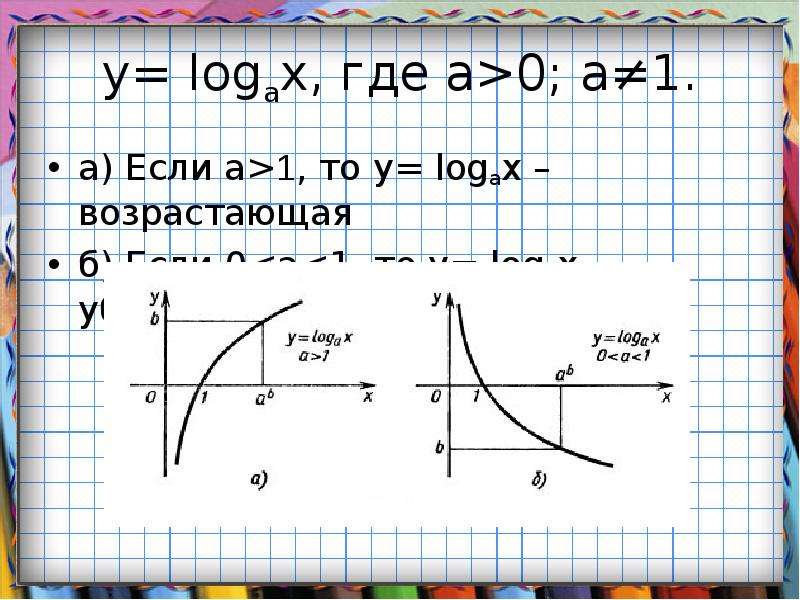 Это уравнение можно записать в несколько иной форме, используя формулу изменения базовой. В этой ситуации \ (\ dfrac {\ log (x + 2)} {\ log (4)} = {\ log} _4 (x + 2) \), поэтому уравнение можно записать как \ (f (x) = -2 {\ log} _4 (x + 2) +1 \).
Это уравнение можно записать в несколько иной форме, используя формулу изменения базовой. В этой ситуации \ (\ dfrac {\ log (x + 2)} {\ log (4)} = {\ log} _4 (x + 2) \), поэтому уравнение можно записать как \ (f (x) = -2 {\ log} _4 (x + 2) +1 \).
Анализ
Мы можем проверить этот ответ, вычислив различные значения нашего \ (f (x) \) и сравнив результат с соответствующими точками на графике.
| \ (х \) | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| \ (f (x) \) | 1 | 0 | −0.58 | -1 | -1,32 | -1,59 | -1,81 | –2 | -2,17 | -2,32 |
Попробовать \ (\ PageIndex {12} \)
Приведите уравнение натурального логарифма, изображенное ниже.
- Ответ
\ (е (х) = 2 \ ln (х + 3) -1 \)
Ключевые уравнения
Общая форма преобразования родительской логарифмической функции \ (f (x) = {\ log} _b (x) \) равно \ (f (x) = a {\ log} _b (x + c) + d \ )
Ключевые концепции
- Ориентирами на графике родительской функции \ (f (x) = {\ log} _b (x) \) являются: вертикальная асимптота \ (x = 0 \) и ключевые точки \ (x \) — пересечение , \ ((1,0) \), \ ((b, 1) \) и \ (\ left (\ tfrac {1} {b}, — 1 \ right) \).Домен \ ((0, \ infty) \) и диапазон \ ((- \ infty, \ infty) \),
- если \ (b> 1 \), функция возрастает.
- , если \ (0
- Уравнение \ (f (x) = {\ log} _b (x + c) \) сдвигает родительскую функцию \ (y = {\ log} _b (x) \) по горизонтали
- осталось \ (c \) единиц, если \ (c> 0 \).
- правых \ (c \) единиц, если \ (c <0 \)
- Уравнение \ (f (x) = {\ log} _b (x) + d \) сдвигает родительскую функцию \ (y = {\ log} _b (x) \) по вертикали
- вверх на \ (d \) единиц, если \ (d> 0 \).

- вниз на \ (d \) единицы, если \ (d <0 \)
- вверх на \ (d \) единиц, если \ (d> 0 \).
- Для любой константы \ (a> 0 \) уравнение \ (f (x) = a {\ log} _b (x) \)
- растягивает родительскую функцию \ (y = {\ log} _b (x) \) по вертикали с коэффициентом \ (a \), если \ (| a |> 1 \).
- сжимает родительскую функцию \ (y = {\ log} _b (x) \) по вертикали с коэффициентом \ (a \), если \ (| a | <\) 1
- Когда родительская функция \ (y = {\ log} _b (x) \) умножается на \ (- 1 \), результатом является отражение оси x .Когда ввод умножается на \ (- 1 \), результатом является отражение относительно оси y .
- Уравнение \ (f (x) = — {\ log} _b (x) \) представляет собой отражение родительской функции относительно оси x- .
- Уравнение \ (f (x) = {\ log} _b (−x) \) представляет собой отражение родительской функции относительно оси y- .
- Чтобы найти область определения логарифмической функции, установите неравенство, показывающее аргумент больше нуля, и решите относительно \ (x \).


 Нет такой степени!
Нет такой степени!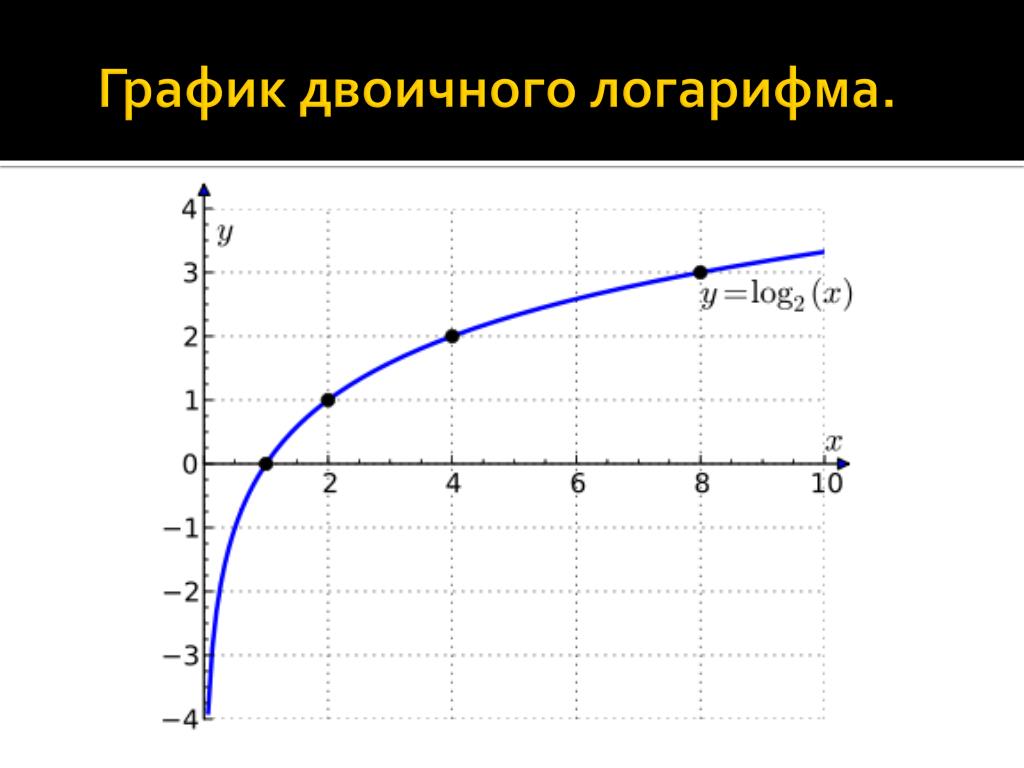

 4
4 4
4
 Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

 .. то есть проходит через (1,0)
.. то есть проходит через (1,0)  Если тебе не комфортно
с этой концепцией или этими манипуляциями, пожалуйста, просмотрите, как работать с
переводы
функций.
Если тебе не комфортно
с этой концепцией или этими манипуляциями, пожалуйста, просмотрите, как работать с
переводы
функций. Мне не нужно добавлять это к графику, но это может быть очень полезно, и
может убедить оценщика, что я знаю, что делаю.
Мне не нужно добавлять это к графику, но это может быть очень полезно, и
может убедить оценщика, что я знаю, что делаю. 5, поэтому журнал 2 (0,5)
= 1;
5, поэтому журнал 2 (0,5)
= 1;  На мой взгляд, этот метод намного проще в работе.
эти проблемы.
На мой взгляд, этот метод намного проще в работе.
эти проблемы.
 Но, хотя вы знаете, что
логарифмический график продолжается вниз вечно, бесконечно приближаясь к
ось y (или какой бы там ни была вертикальная асимптота), только калькулятор
знает, что пробовал одно значение x в его списке, получил «ОШИБКА» в качестве ответа, попробовал следующее значение x в его списке и получил действительное значение y .Поскольку на нем нет других точек перед первой, , и потому что он не может
подумайте , он начинает график с этой первой точки. Это еще один случай
«студент умный; калькулятор тупой». Не предполагайте, только потому, что
калькулятор отображает график определенным образом, это то, что на графике
на самом деле похоже. Используй голову!
Но, хотя вы знаете, что
логарифмический график продолжается вниз вечно, бесконечно приближаясь к
ось y (или какой бы там ни была вертикальная асимптота), только калькулятор
знает, что пробовал одно значение x в его списке, получил «ОШИБКА» в качестве ответа, попробовал следующее значение x в его списке и получил действительное значение y .Поскольку на нем нет других точек перед первой, , и потому что он не может
подумайте , он начинает график с этой первой точки. Это еще один случай
«студент умный; калькулятор тупой». Не предполагайте, только потому, что
калькулятор отображает график определенным образом, это то, что на графике
на самом деле похоже. Используй голову! «Графические логарифмические функции: примеры». Пурпурная Математика .
Доступно по номеру
«Графические логарифмические функции: примеры». Пурпурная Математика .
Доступно по номеру 
 Первое уравнение — это соотношение, решенное для y , а второй — отношение, разрешенное для x .
(Аналогия: « Том — брат Джейн »
эквивалентно утверждению, что « Джейн — сестра Тома ».)
Первое уравнение — это соотношение, решенное для y , а второй — отношение, разрешенное для x .
(Аналогия: « Том — брат Джейн »
эквивалентно утверждению, что « Джейн — сестра Тома ».) Это всегда происходит с обратными функциями.
Это всегда происходит с обратными функциями.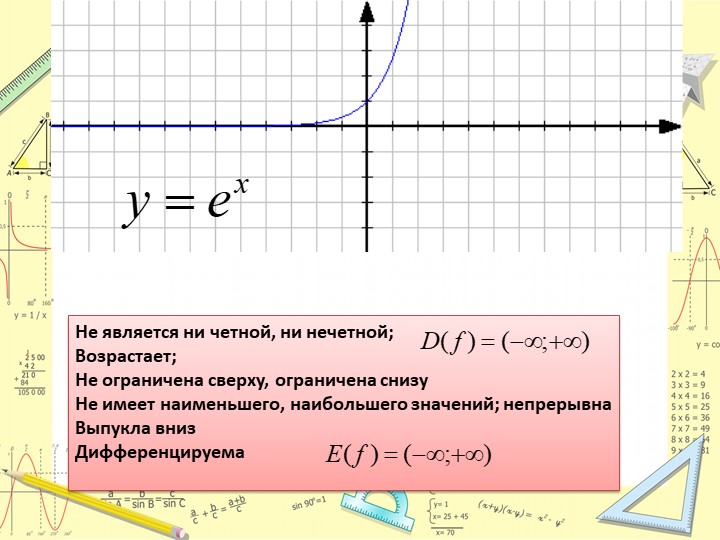
 )
) Аргумент должен быть заключен в квадратные скобки.
Аргумент должен быть заключен в квадратные скобки.
 y = x \).Выберите маленькие значения \ (y \) (например, 2, 3 и -1), вычислите соответствующее значение для \ (x \) и нанесите точку на график.
y = x \).Выберите маленькие значения \ (y \) (например, 2, 3 и -1), вычислите соответствующее значение для \ (x \) и нанесите точку на график.