Формулы сокращенного умножения для 4 степени: Формулы сокращенного умножения
Формулы сокращенного умножения
Формулы сокращенного умножения| Номер | Название формулы | Короткая запись | Раскрытие скобок/разложение на множители |
| (1) | Разность квадратов | a2-b2 | (a-b)(a+b) |
| (2) | Квадрат суммы/разности | (a±b)2 | a2±2ab+b2 |
| (3) | Квадрат суммы для n переменных | (a1+a2+…+an)2 | a12+a22+…+an2+2∑i,jaiaj |
| (4) | Сумма/разность кубов | a3±b3 | (a±b)(a2∓ab+b2) |
| (5) | Куб суммы/разности | (a±b)3 | a3±3a2b+3ab2±b3 |
| (6) | Куб суммы для n переменных | (a1+a2+…+an)3 | a13+a23+…+an3+3∑i,jai2aj+6∑i,j,kaiajak |
| (7) | Разность четвертых степеней | a4-b4 | (a-b)(a+b)(a2+b2) |
| (8) | Четвертая степень суммы/разности | (a±b)4 | a4±4a3b+6a2b2±4ab |
| (9) | Сумма/разность nх степеней | an-bn | (a±b)(an-1+an-2b+an-3b2+… +bn-3a2+bn-2a+bn-1) +bn-3a2+bn-2a+bn-1) |
| (10) | Сумма (2n+1)х степеней | a2n+1+b2n+1 | (a+b)(a2n-a2n-1b+a2n-2b2+…+b2n-2a2-b2n-1a+b2n) |
| (11) | Nая | (a±b)n | an±(n1)an-1b+(n2)an-2b2±..+(nn-2)a2bn-2±(nn-1)abn-1+bn |
— версия для печати
- Определение
- Nая степень числа — результат умножения числа на себя n раз. Также квадратом числа называется результат возведения числа в степень n (в nую степень).
- Пример:
- (4a—3b)3 = 64a
- Пояснение
- Под (nk) подразумевается биномиальный коэффициент, равный
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Формулы сокращенного умножения
Формулы сокращенного умножения
 А например с помощью Бинома Ньютона выполняется разложение на отдельные слагаемые степени двух переменных.
А например с помощью Бинома Ньютона выполняется разложение на отдельные слагаемые степени двух переменных.Формулы упрощения применяются для раскрытия скобок степеней, понижения степени суммы или разности, а так же для других математических упрощений. В приведенных ниже формулах, вместо символов «a» и «b»
Внизу страницы можно скачать формулы в виде картинок для последующей печати и использования в качестве справочного материала при решении задач.
1. Квадрат суммы
… … подготовка формул … …2. Квадрат разности
3. Сумма и разность квадратов
4. Сумма в третьей степени (куб суммы)
5. Разность в третьей степени (куб разности)
6. Сумма и разность кубов
7. Формулы сокращенного умножения для четвертой степени
8. Формулы сокращенного умножения для пятой степени
9. Формулы сокращенного умножения для шестой степени
10. Формулы сокращенного умножения для степени n, где
n — любое натуральное число11. Формулы сокращенного умножения для степени n, где
n — четное положительное число12. Формулы сокращенного умножения для степени n, где
n13. Некоторые свойства формул
Скачать формулы в виде изображения в виде картинок
Скачать формулы в виде изображения:
Формулы сокращенного умножения.
 7.
7.Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты
Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад
Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7).
Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.
Формулы сокращенного умножения
Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.
Квадрат суммы двух выражений
Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.
Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
Получили умножение многочлена на многочлен. Выполним его:
(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy
То есть выражение (2x + 3y)2 равно 4x2 + 12xy + 9y2
(2x + 3y)2 = 4x2 + 12xy + 9y2
Решим аналогичный пример, который попроще:
(a + b)2
Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)
(a + b)2 = (a + b)(a + b)
Выполним это умножение:
(a + b)2 = (a + b)(a + b) = a
То есть выражение (a + b)2 равно a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)
Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)
a = 2x
b = 3y
И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:
(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y2
Как и в прошлый раз получили многочлен 4x2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
(2x + 3y)2 = 4x2 + 12xy + 9y2
Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.
Первый способ:
(2 + 3)2 = 52 = 25
Второй способ:
(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25
Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.
Преобразовать выражение (5a + 3)2 в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9
Значит, (5a + 3)2 = 25a2 + 30a + 9.
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b
В результате получается следующая сумма площадей:
a2 + ab + ab + b2
Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Квадрат разности двух выражений
Формула квадрата разности двух выражений выглядит следующим образом:
(a − b)2 = a2 − 2ab + b2
Эту формулу можно прочитать так:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)
(a − b)2 = (a − b)(a − b)
Если выполнить это умножение, то получится многочлен a2 − 2ab + b2
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.
Воспользуемся формулой квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25
Значит, (7x − 5)2 = 49x2 − 70x + 25.
Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.
Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b
a2 − ab − (a − b)b
Раскроем скобки в выражении (a − b)b
a2 − ab − ab + b2
Приведем подобные слагаемые:
a2 − 2ab + b2
В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.
Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.
Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.
(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2
Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:
(5x − 2y)2 = (5x + (−2y))2
и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:
(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2
Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2
Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:
Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:
(x + y)2 = x2 + 2xy + y2
Куб суммы и куб разности
Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Формулу куба суммы двух выражений можно прочитать так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
А формулу куба разности двух выражений можно прочитать так:
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.
Выведем формулу куба суммы самостоятельно:
(a + b)3
Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)
(a + b)3 = (a + b)(a + b)(a + b)
Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2
(a + b)3 = (a + b)(a + b)2
При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.
Этот квадрат суммы равен выражению a2 + 2ab + b2.
Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).
(a + b)3 = (a + b)(a2 + 2ab + b2)
А это есть умножение многочлена на многочлен. Выполним его:
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Аналогично можно вывести формулу куба разности двух выражений:
(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1
Пример 2. Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(6a2 + 3b3)3= (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9
Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Пример 4. Преобразовать выражение (2x2 − x3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
Например:
(a − b)(a + b)
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
То есть выражение (a − b)(a + b) равно a2 − b2
(a − b)(a + b) = a2 − b2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:
(2x − 5)(2x + 5) = (2x)2 − 52
Вычислим правую часть, получим 4x2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25
Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4x2 − 25
(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.
Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.
Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49
Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)
Выполнить умножение (x2 − y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.
Далее вычисляем выражение в скобках:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9y2)
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2
Умножение разности двух выражений на неполный квадрат их суммы
Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:
Выглядит это произведение следующим образом:
(a − b)(a2 + ab + b2)
Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.
Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.
Действительно, первый член выражения 4x2 + 6xy + 9y2, а именно 4x2 является квадратом выражения 2x, поскольку (2x)2 = 4x2. Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3
(a − b)(a2 + ab + b2) = a3 − b3
Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы.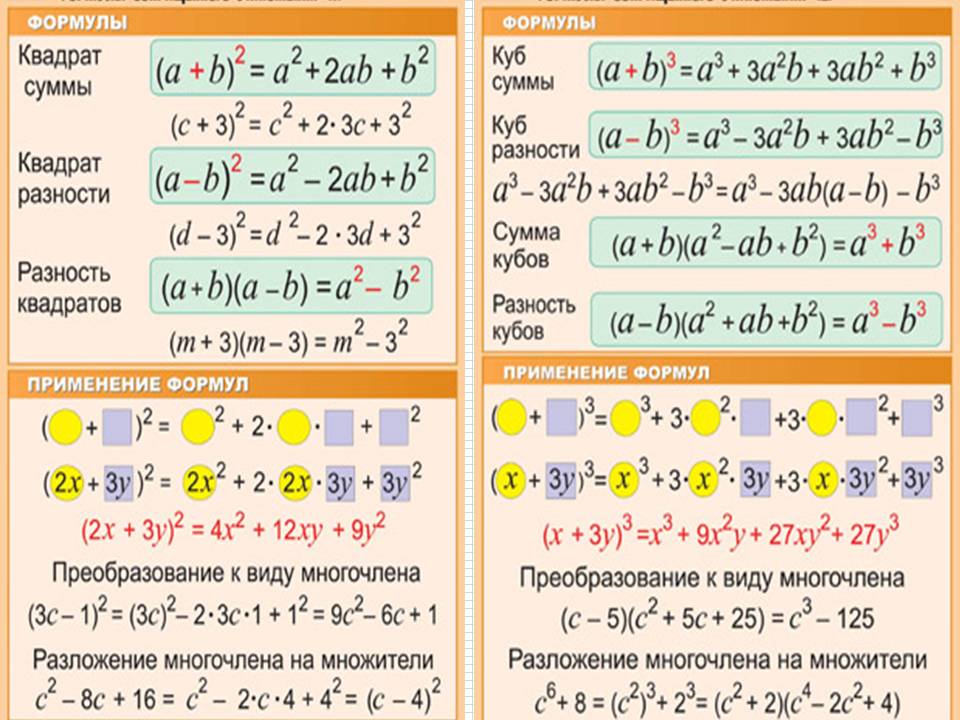 Эту формулу можно прочитать так:
Эту формулу можно прочитать так:
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
Пример 1. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y
(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3
Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3
Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)
Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3
Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3
(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3
Умножение суммы двух выражений на неполный квадрат их разности
Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:
(a + b)(a2 − ab + b2)
Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.
Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 − 6xy + 9y2 является неполным квадратом разности выражений 2x и 3y.
(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2
Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3
(a + b)(a2 − ab + b2) = a3 + b3
Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:
Эту формулу можно прочитать так:
Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.
Пример 1. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)
Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y
(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3
Пример 2. Выполнить умножение (2x + y)(4x2 − 2xy + y2)
Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x2 − 2xy + y2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3
Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3
(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) =
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3
Задания для самостоятельного решения
Задание 1. Преобразуйте выражение (m + n)2 в многочлен.
Решение:
(m + n)2 = m2 + 2mn + n2
Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.
Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64
Задание 3. Преобразуйте выражение (2x2 + 3x3)2 в многочлен.
Решение:
(2x2 + 3x3)2 = (2x2)2 + 2 × 2x2 × 3x3 + (3x3)2 = 4x4 + 12x5 + 9x6
Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.
Преобразуйте выражение (5a + 5)2 в многочлен.
Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25
Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.
Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2
Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.
Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625
Задание 7. Преобразуйте выражение (3x2 − y3)2 в многочлен.
Решение:
(3x2 − y3)2 = (3x2)2 − 2 × 3x2 × y3 + ( y3)2 = 9x4 − 6x2y3 + y6
Задание 8. Выполните умножение (x − y)(x + y)
Решение:
(x − y)(x + y) = x2 − y2
Задание 9. Выполните умножение (2x − y)(2x + y)
Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4x2 − y2
Задание 10. Выполните умножение (7 + 3y)(3y − 7)
Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49
Задание 11. Выполните умножение (x2 − 5)(x2 + 5)
Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25
Задание 12. Выполните умножение (a3 − b2)(a3 + b2)
Выполните умножение (a3 − b2)(a3 + b2)
Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4
Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)
Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6
Задание 14. Выполните умножение (9x − y2)(y2 + 9x)
Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81x2 − y4
Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)
Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3
Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)
Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19
Задание 17. Выполните умножение (4x + 1)(16x2 − 4x + 1)
Решение:
(4x + 1)(16x2 − 4x + 1) = (4x)3 + 13 = 64x3 + 1
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Формулы сокращенного умножения (ЕГЭ — 2021)
Подведем небольшой итог и запишем формулы квадрата суммы и разности в одну строку:
\( {{\left( a\pm b \right)}^{2}}={{a}^{2}}\pm 2ab+{{b}^{2}}\)
Теперь потренируемся «собирать» формулу из разложенного вида \( {{a}^{2}}\pm 2ab+{{b}^{2}}\) в вид \( {{\left( a\pm b \right)}^{2}}\). {2}}\)
{2}}\)
Потренируйся – преобразуй следующие выражения:
Справился? Закрепим тему. Выбери из приведенных ниже выражений те, которые можно представить в виде квадрата суммы или разности.
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс. / / Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.
| |||||||||||||||||||||
| Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||
«ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ»
Тема консультации: «ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ.
РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ»
Дидактическая основа
Дидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивают личностные и метапредметные результаты образования, соответствующие ФГОС.Содержание консультации
В соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 7 класса в феврале продолжается работа с четвертой главой «Введение в теорию многочленов». Изучаются три пункта второго параграфа:4.3.2. Разность квадратов;
4.3.3. Куб суммы и разности;
4.
 3.4. Сумма и разность кубов.
3.4. Сумма и разность кубов. После чего начинается работа с четвертым параграфом «Разложение многочленов на множители», из которого изучаются пункты:
4.4.1. Вынесение общего множителя за скобки;
4.4.2. Способ группировки;
4.4.3. Формулы сокращенного умножения и разложение многочленов.
Основные содержательные цели
- сформировать умение представлять разность квадратов, сумму и разность кубов в виде произведения и наоборот преобразовывать произведения многочленов определенного вида в разность квадратов, сумму и разность кубов с помощью соответствующих формул сокращенного умножения;
- сформировать умение представлять куб суммы и разности в виде многочлена стандартного вида и наоборот преобразовывать многочлен определенного вида в куб суммы или разности с помощью соответствующей формулы сокращенного умножения;
- сформировать умение применять формулы сокращенного умножения для алгебраических преобразований, связанных с умножением, и рационализации вычислений;
- сформировать умение раскладывать многочлены на множители следующими способами: вынесением за скобки общего множителя, способом группировки, с помощью формул сокращенного умножения;
- сформировать умение применять при разложении многочленов на множители различные вспомогательные приемы, такие как, перестановка слагаемых; представление члена многочлена в виде суммы или разности подобных ему членов; прибавление и вычитание одного и того же слагаемого, выделение полного квадрата;
- сформировать умение применять разложение на множители для алгебраических преобразований, решений уравнений и рационализации вычислений.
Тематическое планирование В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по данному учебнику возможно в условиях различных учебных планов образовательных учреждений.
 Поэтому тематическое планирование по изучению данного курса разработано в двух вариантах на 102 ч и на 136 ч. Вариант планирования, разработанный для 3 часов в неделю, обеспечивает выполнение государственного стандарта знаний, усвоение учебного содержания курса (по темам, обязательным для рассмотрения) и продвижение учащихся в развитии мышления, речи, познавательных интересов. При 4 часах в неделю содержание курса существенно расширяется.
Поэтому тематическое планирование по изучению данного курса разработано в двух вариантах на 102 ч и на 136 ч. Вариант планирования, разработанный для 3 часов в неделю, обеспечивает выполнение государственного стандарта знаний, усвоение учебного содержания курса (по темам, обязательным для рассмотрения) и продвижение учащихся в развитии мышления, речи, познавательных интересов. При 4 часах в неделю содержание курса существенно расширяется.Мы предлагаем Вам скачать тематическое планирование на 3 четверть (3 ч в неделю).
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Центр системно – деятельностной педагогики «Школа 2000…» рекомендует для работы по учебнику математики для 7 класса средней школы Л.Г. Петерсон, Д.Л. Абрарова, Е.В. Чутковой использовать по возможности 4 часа в неделю.
Мы предлагаем Вам скачать тематическое планирование на 3 четверть (4 ч в неделю).
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Методические рекомендации к организации учебного процесса
Глава 4. Введение в теорию многочленов
§ 3. Формулы сокращенного умножения
П. 2. Разность квадратов
1) В данном пункте учащиеся знакомятся с двумя формулами сокращенного умножения – формулой произведения суммы и разности двух выражений и формулой разности квадратов, которые, по сути, являются одинаковыми равенствами, в которых поменяли местами правую и левую части. Традиционно эта формула рассматривалась как одна – формула разности квадратов, что приводило к трудностям, возникающим у учащихся при умножении разности двух выражений на их сумму. Поэтому, чаще всего учителю приходилось регулярно использовать на уроках такой прием, как чтение данной формулы «в обратную сторону». Чтобы раз и навсегда показать учащимся, что любая из формул сокращенного умножения «работает» как справа налево, так и слева направо можно использовать материал данного пункта и специально обратить внимание учащихся на это. Можно пояснить учащимся, что для других «обратных» формул не используют отдельного названия, т.к. звучат их названия менее благозвучно, чем у формулы произведения разности и суммы двух выражений.
Чтобы раз и навсегда показать учащимся, что любая из формул сокращенного умножения «работает» как справа налево, так и слева направо можно использовать материал данного пункта и специально обратить внимание учащихся на это. Можно пояснить учащимся, что для других «обратных» формул не используют отдельного названия, т.к. звучат их названия менее благозвучно, чем у формулы произведения разности и суммы двух выражений. 2) В качестве мотивации к выводу новых формул можно предложить учащимся вычислить
за 30 секунд. После того как они не справятся с этим заданием за указанное время, пояснить, что с помощью формулы сокращенного умножения, открытой сегодня им это легко удастся.
3) Для открытия данных формул учащимся предлагается записать произведение суммы и разности а и b как многочлен стандартного вида. После этого учащимся предлагается обобщить полученное равенство для всех произведений подобного вида и сформулировать правило умножения суммы двух выражений на их разность. Опираясь на полученную формулу, учащиеся формулируют, как можно найти разность квадратов двух выражений (№ 318). Эту работу они могут выполнять самостоятельно в группах или в парах.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 2, а также понятия «сумма» и «разность». Для этого можно использовать задания №№ 316–317.
5) Чтобы показать геометрический смысл данной формулы можно использовать предметные геометрические модели прямоугольника и квадрата, предложенные в учебнике. Необходимо вырезать, прикладывать и перемещать предметные модели либо использовать возможности анимации современной техники. Это поможет учащимся с образным мышлением запомнить данные формулы.
6) Важно показать учащимся применение формул для рационализации вычислений (№№ 322, 337).
7) При 4-часовом планировании рекомендуется отвести больше времени на выполнение заданий более высокого уровня сложности (№№ 340–347).

8) Учащиеся применяют новые формулы для сокращения алгебраических дробей (№ 333), решения уравнений (№ 327, № 336), доказательства утверждений и тождеств (№№ 329, 334, 335). Для формирования умения применять формулы сокращенного умножения в учебнике и другие задания, которые предполагают решение задач с помощью уравнения (№ 339), сравнение значений выражений (№№ 342 – 343) и пр. Учитель выбирает из этих заданий те, которые считает целесообразным выполнить с учащимися.
9) При выполнении заданий на нахождение наибольшего и наименьшего значения выражений (№№ 345 – 346) следует вспомнить с учащимися необходимые свойства. Рекомендуется, после применения формулы произведения суммы выражений на их разность актуализировать, как изменяется разность при изменении ее компонентов. Свойство разности «Если значение уменьшаемого увеличить, то значение разности увеличится» и подобные ему свойства известны учащимся с начальной школы. Кроме того, рекомендуется спросить, какое наименьшее значение может принимать квадрат любого выражения (нуля).
П. 3. Куб суммы и разности
1) В данном пункте учащиеся знакомятся с двумя формулами сокращенного умножения – формулой куба суммы и куба разности.2) Для проблематизации можно предложить учащимся записать выражение
как многочлен стандартного вида, не используя правило умножения многочленов
3) Для открытия формулы куба суммы (разности) учащимся предлагается использовать задание № 377, в котором проедложены шаги по построению новой формулы. Рекомендуется сначала дать возможность учащимся составить план открытия нового знания самостоятельно. Имея опыт, построения формулы квадрата суммы и разности данная задача является для семиклассников посильной задачей.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 3, а также понятия «куб суммы» и «куб разности». Для этого можно использовать задания №№ 374–376.
5) Важно показать учащимся применение формул для рационализации вычислений (№№ 381 – 382).
6) Для формирования умения применять формулы куба суммы и разности в учебнике предлагается целый перечень заданий, которые предполагают доказательство тождеств, нахождение значений выражений, составление и решение уравнений. Учитель выбирает из них те задания, которые считает целесообразным выполнить со своими учениками.
7) После знакомства с формулами куба суммы и куба разности с учащимися следует обобщить, что теперь им известно как возводить двучлен во 2-ю и 3-ю степени и сообщить, что существуют формулы, позволяющие возводить двучлен в более высокую степень. Можно попросить одного из «сильных» учащихся сформулировать идею вывода подобных формул. При 4-часовом планировании (либо в более подготовленных классах) рекомендуется познакомить учащихся с алгоритмом возведения двучлена в n–ю степень (№№ 399 – 400).
П.4. Сумма и разность кубов
1) В данном пункте учащиеся знакомятся с формулами суммы и разности кубов.2) Для проблематизации можно предложить учащимся записать многочлены:
в виде произведения двух многочленов.
3) В связи с особенностями этих формул учащимся вряд ли удастся самостоятельно составить план открытия нового знания, поэтому учащимся предлагается использовать задание № 434, в котором даны шаги по построению новых формул.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 3, а также понятия «сумма кубов» и «разность кубов». Для этого можно использовать задания №№ 432–433.
5) Важно показать учащимся применение формул для рационализации вычислений (№№ 439).
6) Для формирования умения применять формулы суммы и разности кубов в учебнике также как и в других пунктах третьего параграфа предлагается перечень заданий, которые предполагают доказательство тождеств, нахождение значений выражений, составление и решение уравнений с использованием данных формул. Учитель выбирает из них те задания, которые считает целесообразным выполнить со своими учениками.
7) При 4-часовом планировании рекомендуется уделить больше времени на выполнение заданий более высокого уровня сложности (№№ 453–460).
8) При выполнении задания № 459 рекомендуется сначала проанализировать данные равенства, задать, например, следующие вопросы:
- Что записано в левой части равенства? (Произведение многочленов.)
- Что записано в правой части равенства? (Многочлены.)
- Как перейти от произведения многочленов к многочлену? (Перемножить данные многочлены.)
- Как можно рационализировать умножение алгебраических выражений? (Формулы сокращенного умножения помогают при таких преобразованиях.)
- Какие формулы вы здесь сразу видите, подчеркните соответствующие выражения.
Полезным будет показать рациональные способы выполнения данных преобразований, для этого можно воспользоваться заранее заготовленными образцами. Если по какой-либо причине подготовить образцы не удастся можно вызывать к доске не одного, а нескольких учащихся, которые бы параллельно доказывали тождество. После выполнения задания разобрать другие способы, которыми пользовались ученики. Кроме того, можно после того как основная часть класса закончит доказательство, следует поинтересоваться, кто нашел другой, более рациональный способ доказательства. Эти способы демонстрируются с помощью специального технического оборудования либо идея преобразования проговаривается вслух.
Целесообразно на примере а) сравнить два способа доказательства тождеств:
1) приведение левой части к правой, при котором придется применить формулу произведения суммы выражений на их разность и в полученном произведении «увидеть» формулу разности кубов;
2) приведение правой части к левой, при котором в разности шестых степеней можно «увидеть» разность кубов и разложить эту разность на произведение двучлена на трехчлен, а полученный двучлен разложить на сумму и разность по формуле разности квадратов.
Второй способ рекомендуется показать после применения первого. На данном этапе он рассматривается с целью опережающей подготовки учащихся к изучению темы «Разложение на множители с помощью формул сокращенного умножения».
§ 4. Разложение многочлена на множители
П.1 Вынесение общего множителя за скобки
1) В данном пункте учащиеся учатся выносить общий множитель за скобки, они уже имеют опыт простейших преобразований такого рода. Так, для первичного формирования умения приводить подобные слагаемые учащиеся выносили общий множитель за скобки на основании распределительного закона умножения.2) В данном пункте у учащихся формируется понятие разложения многочлена на множители. Нужно отметить, что под разложением на множители понимается разложение на буквенные множители. Так, вынесение за скобки числового множителя не является операцией разложения на множители. Например, представление многочлена 2a + 2ac в виде произведения 2(а + ас) не является разложением на множители, а в виде 2а (1 + с) является. Этот «нюанс» можно обговорить с учащимися при выполнении № 489.
3) Здесь же формируется умение раскладывать на множители путем вынесения общего множителя за скобки. Теперь учащиеся выполняют это преобразование на основании четко сформулированного правила: чтобы вынести за скобки общий множитель с можно в скобках записать многочлен, каждый член которого получен в результате его деления на с. Можно использовать предложенный в учебнике алгоритм вынесения за скобки общего множителя (в более подготовленном классе учащиеся могут построить его самостоятельно – № 493).
4) В связи с тем, что учащиеся уже знакомы с вынесением за скобки общего множителя, для проблематизации можно предложить учащимся сформулировать, что такое «разложение многочлена на буквенные множители».
5) Для построения логики открытия при подготовке к уроку учитель может воспользоваться заданием № 488.
6) Чтобы подготовить учащихся к открытию следует актуализировать с ними распределительное свойство умножения, использование этого свойства для рационализации вычислений. Для этой целей рекомендуется использовать задания №№ 485 – 488.
7) Задание № 497 готовит учащихся к следующему пункту. Часто у учащихся возникает сложность с вынесением за скобки общего множителя, который является многочленом. Чтобы преодолеть это возможное затруднение рекомендуется выполнить это задание с подчеркиванием общего множителя.
8) Задание № 498 показывает применение нового преобразования для решения уравнений. Особо следует подчеркнуть, что без разложения на множители уравнения данного вида учащиеся пока решить не могут.
9) Важно показать учащимся применение правила вынесения общего множителя для рационализации вычислений (№№ 496, 502).
П.2 Способ группировки
1) В данном пункте учащиеся учатся применять еще один способ разложения на множители – способ группировки.2) Для проблематизации можно предложить учащимся разложить на множители многочлен:
Причиной возникшего затруднения будет то, что данные одночлены не имеют общего множителя. Чтобы преодолеть свое затруднения учащиеся должны будут открыть новый способ разложения на множители.
3) Чтобы подготовить учащихся к открытию рекомендуется выполнить задание № 533, в котором учащимся придется переставлять слагаемые местами и группировать произведения, имеющие одинаковые множители, а также № 535. Позже эти идеи помогут семиклассникам построить новый способ самостоятельно.
4) Алгоритм способа группировки, построенный учащимися, может иметь вид:
1) Объединить члены многочлена в группы таким образом, чтобы в каждой группе были общие множители.
2) Найти общий множитель в каждой группе и вынести его.
3) Найти общий множитель в новом многочлене и вынести его.
5) Подготовка, проведенная в предыдущем пункте, дает возможность наряду с простейшими ситуациями использования способа группировки рассмотреть и случаи, которые требуют специальных приемов:
- перестановка слагаемых;
- представление члена многочлена в виде суммы или разности подобных ему членов;
- прибавление и вычитание одного и того же слагаемого.
6) Для проблематизации можно предложить учащимся разложить на множители с использованием способа группировки многочлены:
7) Для организации открытия можно воспользоваться учебником. Учащиеся самостоятельно отбирают и рассматривают примеры 2, 3 и 4 из текста. После работы с текстом учащимся предлагается выполнить задания на пробное действие.
8) Задания №№ 546, 554 показывают применение нового преобразования для решения уравнений. Причем, если раньше указание разложить на множители давалось в задании, то теперь такого указания в тексте задания нет. Анализируя вид уравнения, учащиеся должны понимать, что нужно преобразовать левую часть уравнения в произведение многочленов. Особо следует подчеркнуть, что без разложения на множители уравнения данного вида учащиеся пока решить не могут.
П.3 Формулы сокращенного умножения и разложение многочленов на множители
1) В данном пункте учащиеся учатся раскладывать на множители многочлены с использованием формул сокращенного умножения. Умение использовать формулы, в которых та или иная формула представлена в явном виде, должно быть уже сформировано в предыдущем параграфе. Теперь с учащимися разбираются случаи, когда для применения формулы сокращенного умножения необходимо выполнить предварительное преобразование исходного многочлена.2) Учащиеся учатся видеть в степенях «квадраты» и «кубы», группировать слагаемые для получения нужной формулы, пользуются уже известными приемами: перестановка слагаемых и прибавление и вычитание одного и того же слагаемого.
3) Для этапа актуализации рекомендуется использовать задания №№ 583 – 585, при выполнении которых учащиеся повторят те понятия и способы действий, которые понадобятся им на уроке.
4) № 586 можно использовать для проблематизации. Затруднение, возникшее при выполнении этого задания, потребует новых приемов для применения разложения на множители (либо отбора уже известных приемов для применения в новой ситуации).
5) При изучении данного пункта учащиеся знакомятся с таким приемом, как выделение полного квадрата, который дает возможность применить формулы сокращенного умножения (№ 588 (л–н), № 595(д), № 600 готовят учащихся к этому способу, № 601 требует применения способа). Естественно требовать от каждого ученика умения применять данный способ нельзя. Однако более способные учащиеся должны получить возможность познакомиться с приемом выделения полного квадрата. В восьмом классе этот прием даст возможность вывести формулу для решения квадратных уравнений.
Эталоны
В результате изучения данных пунктов учащиеся знают следующие формулы сокращенного умножения: формулу произведения суммы двух выражений на их разность, формулу разности квадратов; формулы куба суммы и куба разности; формулы суммы и разности кубов и умеют их применять. Учащиеся имеют возможность познакомиться с треугольником Паскаля и соответствующим алгоритмом для возведения двучлена в n–ю степень. Учащиеся знают, что значит разложить многочлен на множители и следующие способы разложения на множители: вынесением за скобки общего множителя, способом группировки, с помощью формул сокращенного умножения и умеют их применять. Учащиеся имеют возможность познакомиться с различными вспомогательными приемами, которые помогают применять вышеперечисленные способы разложения на множители.Методические рекомендации по планированию уроков
При организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствии с зоной ближайшего развития более подготовленных учащихся. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000…». В отличие от уроков, опубликованных нами в предыдущих консультациях, этот урок является примером урока рефлексивного типа. Подробнее с методикой подготовки и проведения уроков такого типа в 7-9 классах основной школы вы можете познакомиться в разделе Модификация технологии деятельности метода обучения на уроках разной целевой направленности в 7–9 классах основной школы нашей вводной консультации.
Урок 60
Тип урока: РТема урока: «Формулы сокращённого умножения»
Автор: Л.А Грушевская
Основные содержательные цели:
1) организовать самоконтроль умения применять формулы сокращённого умножения при выполнении заданий различного характера;
2) тренировать умение решать задачи на движение.
Мы предлагаем Вам cкачать сценарий урока
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Уважаемые коллеги! Предлагаем вам скачать решение некоторых задач на смекалку, которые входят в данные параграфы.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.
Полиномиальные тождества
Когда у нас есть сумма (разность) двух или трех чисел в степени 2 или 3 и нам нужно снять скобки, мы используем полиномиальные тождества(короткие формулы умножения) :
(x + y) 2 = x 2 + 2xy + y 2
(x — y) 2 = x 2 — 2xy + y 2
Пример 1: Если x = 10, y = 5a
(10 + 5a) 2 = 10 2 + 2 · 10 · 5a + (5a) 2 = 100 + 100a + 25a 2
Пример 2: если x = 10 и y равно 4
(10-4) 2 = 10 2 -2 · 10 · 4 + 4 2 = 100-80 + 16 = 36
Верно и обратное:
25 + 20a + 4a 2 = 5 2 + 2 · 2 · 5 + (2a) 2 = (5 + 2a) 2
Последствия вышеуказанных формул:
(-x + y) 2 = (y — x) 2 = y 2 — 2xy + x 2
(-x — y) 2 = (- (x + y)) 2 = (x + y) 2 = x 2 + 2xy + y 2
Формулы 3 степени:
(x + y) 3 = x 3 + 3x 2 y + 3xy 2 + y 3
(x — y) 3 = x 3 — 3x 2 y + 3xy 2 — y 3
Пример: (1 + 2 ) 3 = 1 3 + 3. 2 + 20 $
3) Решите уравнение: x 2 -25 = 0
Решение: x 2 -25 = (x — 5) (x + 5)
=> мы должны решить следующие 2 уравнения:
x — 5 = 0 или x + 5 = 0
, поэтому уравнение имеет два решения: x = 5 и x = -5.
Связанные ресурсы:
Викторина о полиномиальных тождествах
Упрощение полиномиальных выражений — проблемы с решениями
Факторинговые полиномы — проблемы с решениями
Полиномиальные тождества на форуме
Формулы сокращенного умножения | Кубенс
Формулы сокращенного умножения формулы умножения многочленов используются для разложения этих многочленов на множители, упрощения выражений и построения многочленов в стандартном виде.Формулы приведенного умножения нужно доказать непосредственно, открыв скобки и построив эти члены.
Формула квадратов
| квадрат суммы | |
| разность в квадрате | |
| разность квадратов | |
Formula куб.м.
| куб суммы | |
| куб разности | |
| сумма кубиков | |
| разность кубиков |
Формулы приведенного умножения в четвертой степени
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
Квадрат суммы
Разница между квадратами двух чисел равна произведению суммы этих чисел на их разность.
Разница квадратов
Куб представляет собой сумму двух чисел, равную потере первого дня плюс утроение квадрата произведения первого числа на второе, утроенное плюс произведение первого числа на квадрат второго плюс куб второго числа.
Куб суммы
Куб разницы равен котлу первого числа минус утроенное произведение квадрата первого числа на второе, утроенное плюс произведение первого числа на квадрат второго минус куб второй номер.
Куб разности
Сумма кубиков двух чисел равна произведению суммы этих чисел на неполный квадрат разности этих чисел.
Сумма кубиков
Разница между кубиками двух чисел равна произведению разности чисел на неполном квадрате суммы этих чисел.
Разница кубиков
сокращенных формул умножения. Решение двумя способами
Математические выражения (формулы) сокращенное умножение (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) чрезвычайно незаменимы во многих областях точных наук.Эти 7 символических обозначений незаменимы для упрощения выражений, решения уравнений, умножения многочленов, сокращения дробей, решения интегралов и многого другого. Это означает, что будет очень полезно понять, как они получены, для чего они нужны и, самое главное, как их запомнить, а затем применять. Затем, применив на практике сокращенную формулу умножения , сложнее всего будет увидеть, что такое x , а что есть. Очевидно, что никаких ограничений для a и b нет, что означает, что это могут быть любые числовые или буквальные выражения.
И вот они:
Первый x 2 — at 2 = (x — y) (x + y) . Для вычисления разности квадратов два выражения необходимо умножить на разности этих выражений на их суммы.
Второй (x + y) 2 = x 2 + 2xy + y 2 … Чтобы найти сумму в квадрате двух выражений, нужно сложить двойное произведение первого выражения ко второму плюс квадрат второго выражения к квадрату первого выражения.
Третий (x — y) 2 = x 2 — 2xy + y 2 … Чтобы вычислить квадрат разницы двух выражений, нужно вычесть двойное произведение первого выражения на второй плюс квадрат второго выражения из квадрата первого выражения.
Четвертый (x + y) 3 = x 3 + 3x 2 y + 3x 2 + y 3. Для вычисления суммы куба двух выражений нужно сложить куб первого выражение: тройное произведение квадрата первого выражения на второе плюс тройное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятый (x — y) 3 = x 3 — 3x 2 y + 3x 2 — at 3 … Для вычисления куба разности двух выражений необходимо вычесть из куб первого выражения: тройное произведение квадрата первого выражения на второе плюс тройное произведение первого выражения на квадрат второго минус куб второго выражения.
Шестой x 3 + at 3 = (x + y) (x 2 — xy + y 2) Чтобы вычислить сумму кубов двух выражений, нужно умножить суммы первого а вторые выражения — неполным квадратом разности этих выражений.
Седьмой x 3 — at 3 = (x — y) (x 2 + xy + y 2) Для выполнения вычисления кубов разности двух выражений, разницы между первым и вторым выражениями необходимо умножить на неполный квадрат суммы этих выражений.
Нетрудно вспомнить, что все формулы применяются для выполнения вычислений в обратном направлении (справа налево).
Существование этих закономерностей было обнаружено около 4 тысяч лет назад.Их широко использовали жители древнего Вавилона и Египта. Но в те времена они выражались словесно или геометрически и в расчетах не использовали буквы.
Давайте проанализируем доказательство квадрата суммы (a + b) 2 = a 2 + 2ab + b 2.
Первым эту математическую закономерность доказал древнегреческий ученый Евклид, работавший в Александрии в III веке до нашей эры, он применил для этого геометрический метод доказательства формулы, так как ученые Древней Греции не использовали буквы для обозначения чисел. .Обычно они использовали не «2», а «квадрат на отрезке а», не «ab», а «прямоугольник, заключенный между отрезками a и b».
На предыдущем уроке мы разобрались с факторингом. Мы освоили два способа: изъятие общего множителя за скобки и группирование. В этом руководстве следующий эффективный способ: сокращенных формул умножения … Короче — FSU.
Сокращенные формулы умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) необходимы во всех разделах математики.Они используются для упрощения выражений, решения уравнений, умножения многочленов, сокращения дробей, решения интегралов и т. Д. И т. Д. Короче говоря, есть все основания иметь дело с ними. Понять, откуда они берутся, зачем они нужны, как их запомнить и как применять.
Понимание?)
Откуда берутся сокращенные формулы умножения?
Равенства 6 и 7 написаны не очень привычным образом. Как бы наоборот. Это сделано специально.) Любое равенство работает как слева направо, так и справа налево. Эта запись проясняет происхождение FSO.
Они происходят от умножения.) Например:
(a + b) 2 = (a + b) (a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2
Вот и все, никаких научных уловок. Просто умножаем скобки и даем похожие. Получается всех сокращенных формул умножения. Сокращенное умножение связано с тем, что в самих формулах отсутствует умножение скобок и приведение похожих.Сокращенно.) Результат выдается сразу.
ФСО нужно знать наизусть. Без первых трех нельзя мечтать о тройке, без остальных — о четверке и А.)
Зачем нужны сокращенные формулы умножения?
Есть две причины учиться, даже запоминать эти формулы. Во-первых, готовый ответ на машине резко снижает количество ошибок. Но это не главная причина. А вот второй …
Если вам нравится этот сайт…Кстати, у меня для вас есть еще парочка интересных сайтов.)
Вы можете попрактиковаться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
вы можете ознакомиться с функциями и производными.
Сокращенные формулы выражений очень часто используются на практике, поэтому желательно выучить их все наизусть. До этого момента он будет служить нам верой и правдой, который мы рекомендуем распечатать и постоянно держать перед глазами:
Первые четыре формулы из составленной таблицы сокращенных формул умножения позволяют возвести в квадрат и куб сумму или разность двух выражений.Пятый — для краткого умножения разницы на сумму двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называется выражение в форме a 2 −ab + b 2) и разность двух выражений a и b на неполный квадрат их суммы (a 2 + ab + b 2) соответственно.
Стоит отдельно отметить, что каждое равенство в таблице является тождеством. Это объясняет, почему сокращенные формулы умножения также называют сокращенными тождествами умножения.
При решении примеров, особенно в которых есть факторизация многочлена, FSO часто используется в форме с переставленными левой и правой сторонами:
Последние три идентификатора в таблице имеют собственные имена. Формула a 2 — b 2 = (a — b) (a + b) называется формулой разности квадратов , a 3 + b 3 = (a + b) (a 2 −ab + b 2 ) — формула суммы кубиков , а a 3 −b 3 = (a — b) (a 2 + ab + b 2) — разница между кубиками … Обратите внимание, что мы не назвали FSU для соответствующих формул с переставленными частями из предыдущей таблицы.
Дополнительные формулы
Не помешает добавить еще несколько тождеств в таблицу формул сокращенного умножения.
Сферы применения формул приведенного умножения (FSU) и примеры
Основное назначение сокращенных формул умножения (fsu) объясняется их названием, то есть состоит в кратком умножении выражений.Однако сфера применения FSU намного шире и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное применение сокращенной формулы умножения было найдено в реализации идентичных преобразований выражений. Чаще всего эти формулы используются в процессе упрощения выражения .
Пример.
Упростим выражение 9 y− (1 + 3 y) 2.
Решение.
В этом выражении возведение в квадрат можно коротко выполнить, имеем 9 y− (1 + 3 y) 2 = 9 y− (1 2 + 2 1 3 y + (3 y) 2)… Осталось только раскрыть скобки и вывести аналогичные слагаемые: 9 y− (1 2 + 2 1 3 y + (3 y) 2) = 9 y — 1−6 y — 9 y 2 = 3 y — 1−9 л 2.
В числителе выражение — это разность кубиков двух выражений 2 · x и z 2, а в знаменателе — разность квадратов этих выражений. После применения соответствующих формул исходная дробь примет вид … Теперь вы можете отменить те же множители в числителе и знаменателе :.
Кратко подведем итоги всего решения:
Ответ:
.
Сокращенные формулы умножения иногда позволяют рационально оценивать значения выражений. В качестве примера покажем, как возвести число 79 в квадрат по формуле разности квадратов: 79 2 = (80−1) 2 = 80 2 −2 80 1 + 1 2 = 6400-160 + 1 = 6 241. Такой подход позволяет производить такие расчеты даже устно.
В заключение скажем еще об одном важном преобразовании — выделение квадрата бинома , в основе которого лежит формула приведенного умножения на квадрат суммы.Например, 4 x 2 + 4 x — 3 можно преобразовать в (2 x) 2 + 2 2 x 1 + 1 2 −4, а первые три члена заменяются с использованием квадрата формулы суммы. Таким образом, выражение принимает вид (2 x + 1) 2 −4. Такие преобразования широко используются, например, для.
Список использованной литературы.
- Алгебра: учеб. за 7 кл. общее образование. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; изд. С. А. Теляковский. — 17-е изд. — М .: Просвещение, 2008.- 240 с. : больной. — ISBN 978-5-09-019315-3.
- А.Г. Мордкович Алгебра. 7-й класс. В 14.00 Часть 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. — 13 изд., Перераб. — М .: Мнемосина, 2009. — 160 с .: Илл. ISBN 978-5-346-01198-9.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы): Учебное пособие. руководство по эксплуатации. — М .; Выше. шк., 1984.-351 с., ил.
Плюс в кубической формуле. Возведение куба Сокращенные формулы умножения
Сокращенные формулы выражений очень часто используются на практике, поэтому желательно выучить их все наизусть.До этого момента он будет служить нам верой и правдой, который мы рекомендуем распечатать и постоянно держать перед глазами:
Первые четыре формулы из составленной таблицы сокращенных формул умножения позволяют возвести в квадрат и куб сумму или разность двух выражений. Пятый — для краткого умножения разницы на сумму двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называется выражение вида a 2 −ab + b 2) и разность двух выражений a и b на неполный квадрат их суммы (a 2 + ab + b 2) соответственно.
Стоит отдельно отметить, что каждое равенство в таблице является тождеством. Это объясняет, почему сокращенные формулы умножения также называют сокращенными тождествами умножения.
При решении примеров, особенно в которых имеет место факторизация многочлена, FSO часто используется в форме с переставленными левой и правой сторонами:
Последние три идентификатора в таблице имеют собственные имена. Формула a 2 — b 2 = (a — b) (a + b) называется формулой разности квадратов , a 3 + b 3 = (a + b) (a 2 −ab + b 2 ) — формула суммы кубиков , а a 3 −b 3 = (a — b) (a 2 + ab + b 2) — разница между кубиками … Обратите внимание, что мы не назвали FSU для соответствующих формул с переставленными частями из предыдущей таблицы.
Дополнительные формулы
Не помешает добавить еще несколько тождеств в таблицу формул сокращенного умножения.
Сферы применения формул приведенного умножения (FSU) и примеры
Основное назначение сокращенных формул умножения (fsu) объясняется их названием, то есть состоит в кратком умножении выражений.Однако сфера применения FSU намного шире и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное применение сокращенной формулы умножения было найдено в реализации идентичных преобразований выражений. Чаще всего эти формулы используются в процессе упрощения выражения .
Пример.
Упростим выражение 9 y− (1 + 3 y) 2.
Решение.
В этом выражении возведение в квадрат можно коротко выполнить, имеем 9 y− (1 + 3 y) 2 = 9 y− (1 2 + 2 1 3 y + (3 y) 2)… Осталось только раскрыть скобки и вывести аналогичные слагаемые: 9 y− (1 2 + 2 1 3 y + (3 y) 2) = 9 y — 1−6 y — 9 y 2 = 3 y — 1−9 л 2.
На предыдущем уроке мы разобрались с факторингом. Мы освоили два метода: выведение общего множителя за скобки и группирование. В этом руководстве следующий эффективный способ: сокращенных формул умножения … Короче — FSU.
Сокращенные формулы умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) необходимы во всех разделах математики.Они используются для упрощения выражений, решения уравнений, умножения многочленов, сокращения дробей, решения интегралов и т. Д. И т. Д. Короче говоря, есть все основания иметь дело с ними. Понять, откуда они берутся, зачем они нужны, как их запомнить и как применять.
Понимание?)
Откуда берутся сокращенные формулы умножения?
Равенства 6 и 7 написаны не очень привычным образом. Как бы наоборот. Это сделано специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи яснее, откуда взялось ФСО.
Они происходят от умножения.) Например:
(a + b) 2 = (a + b) (a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2
Вот и все, никаких научных уловок. Просто умножаем скобки и даем похожие. Получается всех сокращенных формул умножения. Сокращенное умножение связано с тем, что в самих формулах отсутствует умножение скобок и приведение похожих.Сокращенно.) Результат выдается сразу.
ФСО нужно знать наизусть. Без первых трех нельзя мечтать о тройке, без остальных — о четверке с буквой А.)
Зачем нужны сокращенные формулы умножения?
Есть две причины учиться, даже запоминать эти формулы. Во-первых, готовый ответ на машине резко снижает количество ошибок. Но это не главная причина. А вот второй …
Если вам нравится этот сайт…Кстати, у меня для вас есть еще парочка интересных сайтов.)
Вы можете попрактиковаться в решении примеров и узнать свой уровень. Мгновенное проверочное тестирование. Учимся — с интересом!)
вы можете ознакомиться с функциями и производными.
Возведение в степень — это операция, тесно связанная с умножением; эта операция является результатом умножения числа на себя. Представим формулой: a1 * a2 *… * an = an.3 = 8.
Вообще возведение в степень часто используется в различных формулах математики и физики. Эта функция более научна, чем четыре основных: сложение, вычитание, умножение, деление.
Возведение числа в степень
Возведение числа в степень — несложная операция. Это связано с умножением, как отношения между умножением и сложением. Обозначение an — это краткое обозначение n-го числа чисел «a», умноженных друг на друга.3 = 9 * 9 * 9 = 81 * 9 = 729 … Девять в кубе равняются семистам двадцати девяти.
Формулы возведения в степень
Чтобы правильно возвести в степень, вам необходимо запомнить и знать формулы, перечисленные ниже. 3 = 8.Ответ: 8.
Итак, знаменатель дробной степени может быть 3 или 4 и до бесконечности любое число, и это число определяет степень квадратного корня, извлеченного из данного числа. Конечно, знаменатель не может быть нулевым.
Возведение корня в степень
Если корень возведен в степень, равную мощности самого корня, то ответом будет радикальное выражение. Например, (√x) 2 = x. И так в любом случае равенство степени корня и степени поднятия корня.2. Чтобы проверить решение, давайте переведем выражение в выражение с дробной степенью. Так как корень квадратный, знаменатель равен 2. А если корень возвести в четвертую степень, то в числителе 4. Получаем 4/2 = 2. Ответ: x = 2.
В любом случае лучше всего. просто преобразуйте выражение в выражение с дробной степенью. Если дробь не отменяется, то такой ответ будет при условии, что корень данного числа не выбран.
Возведение в степень комплексного числа
Что такое комплексное число? Комплексное число — выражение, имеющее формулу a + b * i; а, б — действительные числа.-9 = -5 + 12i.
Запишитесь на курс «Ускорение устного счета, НЕ мысленной арифметики», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить в квадрат числа и даже корень. За 30 дней вы научитесь использовать простые приемы для упрощения арифметических операций. В каждом уроке есть новые приемы, наглядные примеры и полезные задания.
Возведение в степень в Интернете
С помощью нашего калькулятора вы можете рассчитать возведение в степень числа:
Степень возведения в степень 7
Возведение в степень начинается только в седьмом классе.3 = 8.
Примеры решения:
Возведение в степень
Презентация о повышении до степени для семиклассников. Презентация может прояснить некоторые непонятные моменты, но, вероятно, не благодаря нашей статье.
Результат
Мы только что рассмотрели верхушку айсберга, чтобы лучше понимать математику — запишитесь на наш курс: Ускорение вербального счета — НЕ ментальной арифметики.
Из курса вы не только выучите десятки приемов упрощенного и быстрого умножения, сложения, умножения, деления, вычисления процентов, но и отработаете их в специальных задачах и обучающих играх! Вербальный счет также требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Сокращенные формулы умножения.
Изучение сокращенных формул умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; сумма и разность кубов двух выражений.
Применение сокращенных формул умножения при решении примеров.
Для упрощения выражений, факторизации многочленов и приведения многочленов к стандартной форме используются сокращенные формулы умножения. Сокращенные формулы умножения нужно знать наизусть .
Пусть a, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.
a 2 — b 2 = (a -b) (a + b)
4. Сумма куба двух выражений равна кубу первого выражения плюс троекратный квадрат первого выражения и второй плюс трижды первое выражение и квадрат второго плюс куб второго выражения.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Куб разности двух выражений равен кубу первого выражения минус троекратный квадрат первого выражения и второй плюс троекратный произведение первого выражения и квадрата второго минус куб второе выражение.
(а — б) 3 = а 3 — 3а 2 б + 3аб 2 — б 3
6. Сумма кубиков двух выражений равна произведению суммы первого и второго выражений на неполный квадрат разности этих выражений.
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражений на неполный квадрат суммы этих выражений.
a 3 — b 3 = (a — b) (a 2 + ab + b 2)
Применение сокращенных формул умножения при решении примеров.
Пример 1.
Рассчитать
а) Используя формулу квадрата суммы двух выражений, получаем
(40 + 1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получаем
98 2 = (100-2) 2 = 100 2-2 100 2 + 2 2 = 10000-400 + 4 = 9604
Пример 2.
Рассчитать
Используя формулу разности квадратов двух выражений, получаем
Пример 3.
Упростить выражение
(х — у) 2 + (х + у) 2
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(x — y) 2 + (x + y) 2 = x 2 — 2xy + y 2 + x 2 + 2xy + y 2 = 2x 2 + 2y 2
Сокращенные формулы умножения в одной таблице:
(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a + b )
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 \ u003d (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)
Комплексные числа: умножение
Комплексные числа: умножениеУмножение производится алгебраически.
Сложное умножение — это более сложная операция для понимания с алгебраической или геометрической точки зрения. Давайте сначала сделаем это алгебраически, а для умножения возьмем определенные комплексные числа, например 3 + 2 i и 1 + 4 i. В каждом есть два члена, поэтому, когда мы их умножим, мы получим четыре члена: (3 + 2 i ) (1 + 4 i ) = 3 + 12 i + 2 i + 8 i 2 .Теперь 12 i + 2 i упрощается до 14 i, конечно же, .А как насчет 8 i 2 ? Помните, что мы ввели i как сокращение для √ – 1, квадратного корня из –1. Другими словами, i — это то, что имеет квадрат –1. Таким образом, 8 i 2 равно –8. Следовательно, произведение (3 + 2 i ) (1 + 4 i ) равно –5 + 14 i.
Если вы обобщите этот пример, вы получите общее правило умножения
Помните, что ( xu — yv ), действительная часть продукта, является произведением реальных частей минус произведение мнимых частей, но ( xv + yu ) мнимая часть продукт, представляет собой сумму двух произведений одной действительной части и другой мнимой части.
Давайте посмотрим на некоторые частные случаи умножения.
Умножение комплексного числа на действительное
В приведенной выше формуле умножения, если v равно нулю, вы получите формулу для умножения комплексного числа x + yi и действительного числа u вместе: ( x + yi ) u = xu + yu i .Другими словами, вы просто умножаете обе части комплексного числа на действительное число.Например, 2 умножить на 3 + i будет просто 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваиваете расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Умножение на 2 можно рассматривать как преобразование, которое растягивает комплексную плоскость C на коэффициент 2 от 0; и умножение на 1/2 как преобразование, которое сжимает C в сторону 0.
Умножение и абсолютное значение.
Несмотря на то, что мы сделали только один случай для умножения, достаточно предположить, что абсолютное значение zw (то есть расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение . ш. Это было тогда, когда w было действительным числом u чуть выше. На самом деле это так в целом:Проверка этого тождества — это упражнение по алгебре.Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не придется иметь дело с квадратными корнями. Мы покажем | zw | 2 = | z | 2 | w | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда, согласно формуле умножения, zw равно ( xu — yv ) + ( xv + yu ) i. Вспомните из раздела об абсолютных величинах, что
| z | 2 = x 2 + y 2Аналогично имеем
| w | 2 = и 2 + v 2и, поскольку zw = ( xu — yv ) + ( xv + yu ) i,
| wz | 2 = ( xu — yv ) 2 + ( xv + yu ) 2Итак, чтобы показать | zw | 2 = | z | 2 | w | 2 , все, что вам нужно сделать, это показать, что
( xu — yv ) 2 + ( xv + yu ) 2 = ( x 2 + y 2 ) ( u 9458 u v 2 )и это простое упражнение по алгебре.
Полномочия
i. В следующем частном случае умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i 2 = –1. А как насчет i 3 ? Это всего лишь i 2 умноженное на i , то есть -1 умноженное на i. Следовательно, i 3 = — i. Это интересно: куб i — это собственное отрицание.Затем рассмотрим i 4 . Это квадрат i 2 , то есть квадрат –1. Таким образом, i 4 = 1. Другими словами, i — это корень четвертой степени из 1. Вы можете показать, что — i — это еще один корень четвертой степени из 1. И поскольку и –1, и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно, 1, i, –1 и — i. Это наблюдение связано с фундаментальной теоремой алгебры, поскольку уравнение z 4 = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня.Более высокие степени i теперь легко найти, когда мы знаем i 4 = 1. Например, i 5 равно i умножить на i 4 , и это всего лишь i. . Вы можете уменьшить мощность i на 4 и не изменить результат. Другой пример: i 11 = i 7 = i 3 = — i.
Как насчет отрицательной степени и ? Что является обратным для i, то есть i –1 ? По той же причине, что вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i –1 = i 3 = — i. Таким образом, i обратное — i. Представьте себе — число, обратное значение которого есть собственное отрицание! Конечно, легко проверить, что i раз — i равно 1, поэтому, конечно, i и — i являются обратными.
Корни единства.
Различные корни из 1 называются корнями из единицы. В общем, по фундаментальной теореме алгебры количество корней n -й степени из единицы равно n, , поскольку существует n корней у уравнения n -й степени z u — 1 = 0.Квадратные корни из единицы равны 1 и –1. Корни четвертой степени равны ± 1, ± i, , как отмечалось ранее в разделе, посвященном абсолютным значениям. Кроме того, в этом разделе упоминалось, что ± √2 / 2 ± i √2 / 2 были квадратными корнями из i и — i, и теперь с формулой умножения, которую легко проверить. Следовательно, восемь корней восьми из единицы равны ± 1, ± i, и ± √2 / 2 ± i √2 / 2. Обратите внимание, как эти восемь корней единицы равномерно расположены по единичной окружности. Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте их немного подождем.
Умножение комплексного числа на
i. В нашей цели по поиску геометрической интерпретации комплексного умножения, давайте теперь рассмотрим умножение произвольного комплексного числа z = x + yi на i. z i = ( x + yi ) i = — y + xi .Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на x единиц справа от мнимой оси и на y единиц выше действительной оси. Точка z i расположена на y единиц слева и x единиц сверху. Произошло то, что умножение на i повернулось в точку z на 90 ° против часовой стрелки вокруг начала координат до точки z i. Короче говоря, умножение на i дает поворот на 90 ° против часовой стрелки на 0.
Вы можете проанализировать, что происходит при умножении на — i таким же образом. Вы обнаружите, что умножение на — i дает поворот на 90 ° по часовой стрелке примерно на 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, которое подразумевается против часовой стрелки. Тогда мы можем сказать, что умножение на — i дает поворот на –90 ° вокруг 0 или, если хотите, поворот на 270 ° вокруг 0.
Геометрическая интерпретация умножения.
Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока посмотрим на результаты без обоснования. Мы видели два особых случая умножения: один на действительные числа, что приводит к масштабированию, другой на и , что приводит к вращению. Общий случай — это комбинация масштабирования и вращения.Пусть z и w будут точками на комплексной плоскости C .Проведите линии от 0 до z и от 0 до w . Длины этих строк — абсолютные значения | z | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | zw | что равно | z | | w |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Чего мы не знаем, так это направления линии от 0 до zw.
Ответ: «углы складываются». Мы определим направление линии от 0 до z по определенному углу, называемому аргументом из z , иногда обозначаемым arg ( z ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — прямая от 0 до z. Другая точка w имеет угол arg ( w ).Тогда произведение zw будет иметь угол, который является суммой углов arg ( z ) + arg ( w ). (На диаграмме arg ( z ) составляет около 20 °, а arg ( w ) составляет около 45 °, поэтому arg ( zw ) должно быть около 65 °.)
Таким образом, у нас есть два уравнения, которые определяют, где находится zw в C :
полиномов
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
Предполагаемые знания
Мотивация
Полиномы представляют следующий уровень алгебраической сложности после квадратичных.В самом деле, квадратичный — это многочлен степени 2. Мы можем факторизовать квадратичные выражения, решать квадратные уравнения и графы квадратичных функций, возникает очевидный вопрос,
как это можно сделать с алгебраическими выражениями более высокой степени.
Квадратичный x2 — 5x + 6 множится как (x — 2) (x — 3). Следовательно, уравнение x2 — 5x + 6 = 0
имеет решения x = 2 и x = 3.
Точно так же мы можем разложить на множители кубику x3 — 6×2 + 11x — 6 как (x — 1) (x — 2) (x — 3), что позволяет нам показать, что решения x3 — 6×2 + 11x — 6 = 0 являются х = 1, х = 2 или х = 3.В этом модуле мы увидим, как прийти к этой факторизации.
Полиномы во многих отношениях ведут себя как целые или целые числа. Мы можем складывать, вычитать и умножать два или более многочлена вместе, чтобы получить еще один многочлен. Так же, как мы можем разделить одно целое число на другое, получая частное и остаток, мы можем разделить один многочлен на другой и получить частное и остаток, которые также являются многочленами.
Квадратичное уравнение вида ax2 + bx + c имеет 0, 1 или 2 решения, в зависимости от того, какой дискриминант отрицательный, нулевой или положительный.Количество решений этого уравнения помогло нам построить график квадратичной функции y = ax2 + bx + c. Точно так же информация о корнях полиномиального уравнения позволяет нам дать грубый набросок соответствующей полиномиальной функции.
Помимо того, что полиномы являются интересными по своей сути объектами, они имеют важные приложения в реальном мире. Одно из таких приложений для кодов исправления ошибок обсуждается в Приложении к этому модулю.
Содержимое
Терминология
Многочлен — это такое выражение, как x5 — 2×3 + 8x + 3 или x4 — x2 + 1.Может быть любое количество терминов, но каждый член должен быть кратным целому числу в степени x. Таким образом, 2×3 — x не является многочленом.
Член с наибольшей степенью называется старшим членом, а его коэффициент — старшим коэффициентом. Если старший коэффициент равен 1, то многочлен называется моническим. Индекс главного члена называется степенью многочлена. Термин, не зависящий от, называется постоянным членом.
Таким образом, x5 — 2×3 + 8x + 3 является моническим многочленом степени 5 с постоянным членом 3, а
x4 — x2 + 1 является немоническим многочленом степени 4 со старшим коэффициентом и постоянным членом 1.
В первом полиноме все коэффициенты являются целыми числами, в то время как второй полином имеет иррациональный коэффициент. По большей части мы будем рассматривать только многочлены первого типа, но многое из того, что следует ниже, одинаково хорошо применимо и ко второму.
Для именования полиномов мы будем использовать обозначение функций, например p (x) или q (x). Таким образом, мы можем записать p (x) = x5 — 2×3 + 8x + 3 или q (x) = x4 — x2 + 1. Это позволяет нам удобно подставлять значения x, когда это необходимо.
Общий многочлен имеет вид
p (x) = тревога — an — 1xn — 1 + … + a1x + a0,
, где 0, а n — целое число. Коэффициенты, как правило, являются действительными числами.
УПРАЖНЕНИЕ 1
Запишите главный член, старший коэффициент, степень и постоянный член приведенного выше общего полинома.
Для полиномов малой степени мы используем следующие имена.
- полином степени 1 называется линейным
- полином степени 2 называется квадратичным
- полином степени 3 называется кубикой
- полином степени 4 называется квартикой
- полином степени 5 называется квинтикой
Многочлен, состоящий только из ненулевой константы, называется постоянным многочленом и имеет степень 0. Многочлен p (x) = 0 называется нулевым многочленом.В нем нет терминов, и поэтому нет ведущего термина. Лучше не определять степень нулевого многочлена. В некоторых книгах его степень обозначается как −1 или −∞.
Сложение, вычитание и умножение многочленов
Чтобы сложить или вычесть два многочлена, мы собираем похожие члены.
Обратите внимание, что мы обычно пишем члены многочлена от наибольшей к наименьшей степени. Иногда это называют стандартной формой многочлена.
Чтобы умножить два полинома, мы умножаем каждый член в первом полиноме на второй полином и собираем похожие члены.
ПРИМЕР
Многочлены P (x), Q (x) и R (x) задаются формулами P (x) = x3 — 2×2 + x — 1, Q (x) = 3×3 — 2×2 и R (x) = −x4 + 2×3 — 3×2. Находят:
а P (x) Q (x) b Q (x) R (x)
Решение
| P (x) Q (x) | = (x3 — x2 + x — 1) (3×3 — 2×2) | ||
| = x3 (3×2 — 2×2) — x2 (3×3 — 2×2) + x (3×3 — 2×2) — (3×3 — 2×2) | |||
| = 3×6 — 2×5 — 3×5 + 2×4 + 3×4 — 2×3 — 3×3 + 2×2 | |||
| = 3×6 — 5×5 + 5×4 — 5×3 + 2×2 | |||
| б | Q (x) R (x) | = (3×3 — 2×2) (- x4 + 2×3 — 3×2) | |
| = 3×3 (−x4 + 2×3 — 3×2) — 2×2 (−x4 + 2×3 — 3×2) | |||
| = −3×7 + 6×6 — 9×5 + 2×6 — 4×5 + 6×4 | |||
| = −3×7 + 8×6 — 13×5 + 6×4 |
Делящие многочлены
При делении одного целого числа на другое образуется частное и остаток.Таким образом дает 7 остаток 2. Есть разные способы записать этот результат.
- 37 ÷ 5 равно 7 остаток 2
- 37 ÷ 5 = 7
- 37 = 7 × 5 + 2
В выписке 37 ÷ 5 равно 7, остаток 2
- число 5, на которое мы делим, называется делителем
- число 37, на которое мы делим, называется делимым
- число 7 называется частным
- число 2 называется остатком
Ключевым моментом в отношении остатка является то, что он неотрицателен, но строго меньше делителя.Таким образом, используя третье представление, когда мы разделим два целых числа p и d> 0, мы можем написать
p = dq + r, где 0 ≤ r ≤ d.
Если остаток равен нулю, то мы говорим, что d является множителем p.
Эти основные утверждения, касающиеся арифметики, имеют аналоги, когда мы начинаем делить один многочлен на другой. Мы будем использовать ту же терминологию при обсуждении полиномиального деления. Это делается по образцу деления в столбик.
Деление многочлена p (x) на многочлен d (x) также дает частное q (x) и остаток r (x), поэтому мы можем записать
п (х) = d (х) q (х) + г (х).
Ключевой идеей при выполнении деления является продолжение работы с ведущими терминами, как показано в следующем примере.
ПРИМЕР
Мы разделим многочлен p (x) = 5×4 −7×3 + 2x — 4 на многочлен d (x) = x — 2, а затем выразим деление в виде p (x) = d (x) q (x ) + г (х).
Решение
| 5×3 | + | 3×2 | + | 6x | + | 14 | |||||
| х — 2 | 5×4 | – | 7×3 | + | 2x | – | 4 | (Разделите x на 5×4, получив 5×3.) | |||
| 5×4 | – | 10×3 | (Умножьте x — 2 на 5×3, а затем вычтите.) | ||||||||
| 3×3 | + | 2x | – | 4 | (Разделите x на 3×3, получив 3×2.) | ||||||
| 3×3 | – | 6×2 | (Умножьте x — 2 на 3×2 и затем вычтите.) | ||||||||
| 6×2 | + | 2x | – | 4 | (Разделите x на 6×2, получив 6x.) | ||||||
| 6×2 | – | 12x | (Умножьте x — 2 на 6x, а затем вычтите.) | ||||||||
| 14x | – | 4 | (Разделите x на 14x, получим 14.) | ||||||||
| 14x | – | 28 | (Умножьте x — 2 на 14 и затем вычтите.) | ||||||||
| 24 | (Это последний остаток.) |
Отсюда 5×4 — 7×3 + 2x — 4 = (x — 2) (5×3 + 3×2 + 6x + 14) + 24. (1)
В этом примере мы видим, что частное q (x) = 5×3 + 3×3 + 6x — 14, а остаток равен r (x) = 24.
Мы можем выполнить частичную проверку, подставив x = 2 в последнюю строку.
Из приведенного выше примера видно, что степень остатка меньше степени делителя, так как в противном случае мы могли бы продолжить деление.Таким образом, в случае линейного множителя остаток будет константой, и мы можем записать его как.
В общем, теперь мы можем написать p (x) = d (x) q (x) + r (x), где r (x) = 0, или, 0 ≤ степень (r (x)) <степень (d (Икс)).
УПРАЖНЕНИЕ 3
Разделите p (x) = 5×4 — 7×3 + 2x — 4 на d (x) = x2 — 2. Выразите результат в виде
p (x) = d (x) q (x) + r (x) где степень r (x) меньше степени d (x).
Обратите внимание, что в этом случае, поскольку делитель имеет степень 2, остаток будет либо равен 0, либо иметь степень не выше 1.
Теорема об остатке
Деление многочленов в длину — громоздкий процесс, и в некоторых случаях нас интересует только остаток. Это не появляется до конца вычислений. Когда мы делим многочлен p (x) на линейный множитель (x — a), мы можем довольно легко найти остаток.
Поскольку делитель линейный, p (x) = (x — a) q (x) + r, где r — постоянная. Подставляя x = a в обе части, получаем r = p (a).
Таким образом, остаток равен полиному, вычисленному при x = a.
Этот удивительный результат называется теоремой об остатке. Мы должны иметь в виду, что он вообще ничего не говорит о частном q (x) и работает только тогда, когда мы делим на линейный множитель (x — a).
УПРАЖНЕНИЕ 4
Полином p (x) = x5 — 7×3 + ax + 1 имеет остаток 13 после деления на x — 1. Найдите значение коэффициента a.
Теорема о факторах
Квадратичное разложение на множители — важный метод, который мы использовали для решения квадратных уравнений.Подобным образом мы хотели бы разработать некоторые методы факторизации многочленов.
Если линейный многочлен (x — a) является множителем многочлена p (x), то мы можем записать
p (x) = q (x) (x — a) и, таким образом, остаток от деления p (x) by (x — a) равно 0.
Используя теорему об остатке, мы доказали:
Теорема
.(x — a) является множителем многочлена p (x), если p (a) = 0. Если p (a) ≠ 0, то
(x — a) не является множителем p (x).
Число a, которое дает p (a) = 0, называется нулем многочлена.
Обратите внимание, что, поскольку (x — 2) и (x — 1) являются факторами p (x), то и их произведение равно
(x — 2) (x — 1) = x2 — 3 x + 2. Таким образом, мы могли найти третий множитель путем деления в столбик.
Деление p (x) на x2 — 3x + 2 дает (x — 3) в качестве третьего множителя, и поэтому мы получаем
после факторизации,
p (x) = x3 — 6×2 + 11x — 6 = (x — 1) (x — 2) (x — 3).
Альтернативный метод
Поскольку p (2) = 0 и p (1) = 0, а p (x) имеет степень 3, мы можем записать p (x) = (x — 2) (x — 1) (x — a)
Где a — число, которое предстоит определить.Поскольку p (0) = −6, имеем −2a = −6, поэтому a = 3.
УПРАЖНЕНИЕ 5
Многочлен p (x) = 3×6 — 5×3 + ax2 + bx + 10 делится на x + 1 и x — 2. Найдите значения коэффициентов a и b.
Факторинговые полиномы
Наша цель — взять многочлен с целыми коэффициентами и записать его как произведение многочленов меньшей степени, которые также имеют целые коэффициенты. Этот процесс называется факторингом по целым числам.
Теорема о факторах позволяет нам проверить, имеет ли многочлен p (x) линейный фактор (x — a). Если это так, то мы можем использовать длинное деление, чтобы найти многочлен q (x) такой, что p (x) = (x — a) q (x) и q (x) имеет степень на единицу меньше, чем степень p (x ). Таким образом, мы сможем повторять процесс над q (x) и так далее как можно чаще, чтобы получить полную факторизацию p (x).
Например,
Начнем с полинома p (x) = x3 + 4×2 — 7x — 10.
- Мы систематически ищем один линейный фактор, проверяя числа a = 1, — 1, 2, −2,…, пока не найдем целое значение a такое, что p (a) = 0.
p (1) = −12 ≠ 0, p (−1) = 0, поэтому (x + 1) является множителем.
- Затем мы используем длинное деление, чтобы разделить p (x) на (x + 1), чтобы получить p (x) = (x + 1) (x2 + 3x — 10).
Теперь квадратичная величина q (x) = x2 + 3x — 10 может быть разложена на множители, используя наши знания о квадратиках, как (x + 5) (x — 2), и поэтому полная факторизация p (x) равна
п (х) = (х + 1) (х + 5) (х — 2).
Чтобы помочь нам найти целое число ноль многочлена, мы используем следующий результат.
Теорема
.Если многочлен
p (x) = тревога + an − 1xn − 1 +… + a1x + a0
имеет целое число ноль a, тогда a является множителем постоянного члена a0.
Таким образом, в приведенном выше примере единственными возможными целыми нулями являются ± 1, ± 2, ± 5 или ± 10.
УПРАЖНЕНИЕ 6
Объясните, почему приведенная выше теорема верна.
ПРИМЕР
Разложите многочлен p (x) = x4 — 2×3 — 8x + 16 на множители.
Решение
- Нам нужно проверить только положительный и отрицательный множители 16.
P (1) = 1-2-8 + 16 ≠ 0, поэтому x — 1 не является множителем p (x).
P (−1) = 1 + 2 + 8 + 16 ≠ 0, поэтому x + 1 не является множителем p (x).
P (2) = 16-16-16 + 16 = 0, поэтому x — 2 является множителем.
После деления p (x) на x — 2, p (x) = (x — 2) (x3 — 8) - Пусть Q (x) = x3 — 8.
x — 1 и x + 1 не являются факторами Q (x), поскольку P (x) = (x — 2) Q (x), и они не являются факторами P (Икс).
Однако Q (2) = 8-8 = 0, поэтому x — 2 также является множителем Q (x).
После деления Q (x) на x — 2, Q (x) = (x — 2) (x2 + 2x + 4). - Квадратичный x2 + 2x + 4 не может быть разложен на множители, см. Ниже.
Следовательно, P (x) = (x — 2) 2 (x2 + 2x + 4) — полная факторизация P (x).
Обратите внимание, что квадратичный x2 + 2x + 4 = (x + 1) 2 + 3 всегда больше или равен 3, следовательно, квадратичный не имеет множителей.
УПРАЖНЕНИЕ 7
Сначала удалите очевидный общий множитель, разложите на множители многочлен
p (x) = 2×5 — 22×4 + 78×3 — 90×2.
Полиномиальные уравнения
Одним из основных методов решения квадратных уравнений был метод факторизации. Точно так же одно из основных приложений факторизации многочленов — решение полиномиальных уравнений.
ПРИМЕР
Решить x3 + 4 x2 — 7x — 10 = 0
Решение
В предыдущем примере мы разложили многочлен
p (x) = x3 + 4 x2 — 7x — 10 = 0 как (x + 1) (x + 5) (x — 2).
Таким образом, уравнение x3 + 4 x2 — 7x — 10 = 0 принимает вид (x + 1) (x + 5) (x — 2) = 0
Поскольку произведение трех факторов равно нулю, мы можем приравнять каждый фактор к нулю, чтобы найти решения. Таким образом, x + 1 = 0 или x — 2 = 0, или x + 5 = 0, что дает x = −1, x = 2 или x = −5.
Примечание: полином p (x) = (x — 1) (x — 2) 2 (x — 4) 3 имеет степень 6, но полиномиальное уравнение (x — 1) (x — 2) 2 (x — 4) 3 = 0 имеет только 3 (различных) решения x = 1 или x = 2 или x = 4.Таким образом, количество (различных) решений может быть меньше степени, но никогда не может превышать степень.
УПРАЖНЕНИЕ 8
Воспользуйтесь факторизацией p (x) = 2×5 — 22×4 + 78×3 −90×2 из приведенного выше упражнения, чтобы решить уравнение 2×5 — 22×4 + 78×3 — 90×2 = 0.
В некоторых ситуациях факторизация приводит к квадратному уравнению без реальных решений или без иррациональных решений. В этом случае нам может потребоваться завершить задачу, используя формулу корней квадратного уравнения.
ПРИМЕР
Решить x4 + 7×3 — 2×2 — 7x + 1 = 0
Решение
Многочлен x4 + 7×3 — 2×2 — 7x + 1 имеет факторизацию (x — 1) (x + 1) (x2 + 7x — 1).
Следовательно, уравнение принимает вид (x — 1) (x + 1) (x2 + 7x — 1) = 0.
Таким образом, решения x = 1, x = −1 и решения x2 + 7x — 1 = 0.
Используя формулу корней квадратного уравнения, b2 — 4ac = 49 + 4 = 53, поэтому квадратичная формула имеет решения
x = и x =.
Следовательно, квартика имеет четыре решения x = 1, −1 и x =.
Обратите внимание, что существуют полиномиальные уравнения с иррациональными корнями, которые нельзя решить с помощью описанной выше процедуры. Например, многочлен p (x) = x5 — 3×3 — 2×2 + 6 множится как
(x2 — 3) (x3 — 2), и поэтому уравнение x5 — 3×3 — 2×2 + 6 = 0 имеет решения, x =, x = — и x =.
В общем, разложение многочленов на целые числа является сложной задачей. Например, многочлен
x3 — 2 не может быть разложен на целые числа, но у него есть одно действительное решение, x =.
Построение полиномиальных функций
Полиномиальная функция — это функция вида y = p (x), где p (x) — полином.
В модуле Квадратичные функции мы увидели, как нарисовать график квадратичного
, указав
- перехватчики
- нахождение вершины.
Вершина — это пример точки поворота.
Для многочленов степени больше 2 поиск точек поворота не является элементарной процедурой и обычно требует использования исчисления:
- Чтобы найти точку пересечения оси y, положим x = 0.
- Чтобы найти точки пересечения по оси x, мы полагаем y = 0 и решаем соответствующее полиномиальное уравнение, если это возможно.
Возьмем многочлен y = x3 + x2 — 6x = x (x — 2) (x — 3).
Перехват по оси Y равен 0, а пересечение по оси x происходит, когда x (x — 2) (x — 3) = 0, то есть когда x = 0, 2 и 3.
Чтобы получить представление об общей форме кривой, мы можем подставить несколько контрольных точек.
Мы можем представить знак y с помощью диаграммы знаков:
С этой информацией мы можем начать набросок графика y = x (x — 2) (x + 3).
Знаковая диаграмма говорит нам, что график пересекает ось x в точках x = −3, 0 и 2, а также находится ли график выше или ниже оси a с каждой стороны этих точек. Он не сообщает нам максимальное и минимальное значения y между нулями.
Обратите внимание, что если x — большое положительное число, то p (x) также большое и положительное число. Например, если x = 10, то y = 1040. Если x — большое отрицательное число, то p (x) также является большим отрицательным числом. Например, если x = −10, то y = −840.
УПРАЖНЕНИЕ 9
Нарисуйте график y = (x + 2) (x + 1) (x — 1) (x — 2).
Графики многочленов с повторяющимися множителями
Полиномиальные функции, такие как p (x) = 3 (x — 1) 2 (x + 3) 5 (x — 4), которые содержат повторяющиеся множители, требуют особой осторожности.
Если мы рассмотрим, например, размер x4 для различных значений x, мы заметим
- x4 положительно как для положительных, так и для отрицательных значений x
- для значений x от -1 до 1, размер x4 меньше, чем значение x.
Графически это говорит нам, что график y = x4 имеет минимум при x = 0 и что около x = 0 график довольно плоский, но начинает резко увеличиваться при x> 1 и x <−1.
Графики y = x2 и y = x4 показаны для сравнения.
Оба этих графа имеют минимум при x = 0. В случае параболы мы называем это вершиной, но обычно мы не используем это слово для многочленов более высокой степени. Вместо этого мы говорим о поворотной точке и далее классифицируем ее как максимум или минимум.
Каждый из графиков y = −x2 и y = −x4 имеет максимум при x = 0.
Четные степени
То же самое происходит для всех положительных четных степеней x и для четных степеней (x — a). Следовательно, около нуля многочлена, который возникает из множителя с четной степенью, график имеет минимум или максимум и является «плоским» около этого нуля.
Нечетные степени
График y = (x — 2) пересекает ось x в точке x = 2, но не имеет там максимума или минимума.Так как это прямая линия, график в этой точке не плоский, он действительно имеет градиент 45 °. С другой стороны, график y = (x — 2) 3 ведет себя немного иначе при
x = 2. В Далее мы будем считать нечетные степени равными или равными 3.
Поскольку нечетная степень отрицательного числа отрицательна, знаковая диаграмма показывает, что
значения y графика y = x3 меняются от отрицательного к положительному, когда значения x перемещаются от -1 к 1. Как и выше, график квартира возле начала координат.
Отсюда график y = x3 выглядит так:
В начале у нас нет ни максимума, ни минимума. Точка x = 0 называется точкой заражения кривой.
ПРИМЕР
Постройте график y = 2×3 (x — 2) 2.
Решение
График проходит через начало координат и срезает ось x в точках x = 0 и x = 2. При x = 0 график имеет точку перегиба, а при x = 2 — минимум.Знаковая схема есть.
График:
УПРАЖНЕНИЕ 10
Нарисуйте график полиномиальной функции p (x) = (x + 3) 3 (x — 1) 3. (Вы должны обнаружить, что график симметричен относительно x = −1, вы понимаете, почему?)
Ссылки вперед
Основная теорема алгебры
Нули полинома также называют корнями соответствующего полиномиального уравнения.
Полиномиальное уравнение x2− 4 = 0 имеет два целых корня, x = 2, x = −2, а уравнение x2-2 = 0 имеет два действительных корня, x =, x = -. С другой стороны, уравнение x2 + 2 = 0 не имеет действительных корней. Кроме того, уравнение x3 — 1 = 0, которое множится как (x — 1) (x2 + x + 1 = 0), имеет только один действительный корень, поскольку квадратное уравнение x2 + x + 1 = 0 не имеет решений.
Чтобы правильно понять, сколько решений может иметь полиномиальное уравнение, нам нужно ввести комплексные числа.Комплексное число — это число в форме a + ib, где a, b — действительные числа и i2 = — 1. Комплексное число i часто называют мнимым числом. Обратите внимание, что если мы положим b = 0, мы получим действительное число, поэтому комплексные числа содержат набор всех действительных чисел.
Таким образом, хотя уравнение x2 + 1 = 0 не имеет вещественных решений, у него есть два комплексных решения, x = i и x = −i, и многочлен x2 + 1 может быть разложен на множители как (x — i) (x + i).
Великий математик Гаусс (1777–1855) дал первое доказательство следующего удивительного результата, который стал известен как Фундаментальная теорема алгебры.
Теорема
.Каждое полиномиальное уравнение степени больше 0 имеет хотя бы одно комплексное решение.
Учитывая этот результат, нетрудно показать, что:
Следствие
Каждое полиномиальное уравнение степени n больше 0 имеет ровно n решений с учетом кратности над комплексными числами.
УПРАЖНЕНИЕ 11
Объясните, как следствие можно вывести из теоремы.
Следовательно, каждый многочлен степени n больше 0 можно разложить на n линейных множителей, используя комплексные числа.
Обратите внимание, что выражение, учитывающее кратность, означает, что при заданном полиномиальном уравнении (x — 2) 3 (x + 1) 2 = 0, например, мы говорим, что корни равны x = 2, 2, 2, −1, −1 . Таким образом, мы говорим, что x = 2 — корень кратности 3, а x = −1 — корень кратности 2. Однако уравнение имеет только два (различных) корня.
точек поворота
Вершина параболы — пример точки поворота.Координата x точки поворота параболы y = ax2 + bx + c задается как x = -. Координаты x точек поворота многочлена не так просто найти и требуют использования дифференциального исчисления, которое изучается в высшей математике.
Корни многочлена
Предположим, что мы можем разложить на множители моническую квадратичную x2 + bx + c как (x — α) (x — β). Раскрывая их, мы видим, что сумма корней α + β равна −b, а произведение корней ab равно c.
Аналогичное упражнение можно выполнить на монических кубиках. То есть, если корни кубики
x3 + bx2 + cx + d равны α, β, γ, то можно показать, что
α + β + γ = −b, αβ + αγ + βγ = c и αβγ = −d,
Эти тождества определяют отношения между корнями многочлена и его коэффициентами.
УПРАЖНЕНИЕ 12
Выведите приведенные выше формулы.
История
Изучение уравнений степени больше двух восходит к арабской математике.Омар Хайям (1048–1141) большую часть своей жизни провел, пытаясь решить различные случаи кубического уравнения. Только в эпоху Возрождения было получено общее решение кубики. Точные детали отрывочны, но итальянский математик Кардано (1501–1576) сумел раскрыть секрет решения кубической формы своего соотечественника Тартальи и включил его в свою работу Ars Magna (Великое искусство), опубликованную в 1545 году.
Кубический
Кардано показал, как привести любое кубическое уравнение к виду x3 + px + c = 0, а затем, сделав замену x = u — v, свести задачу к решению квадратичной.На практике проще положить x = u + v.
УПРАЖНЕНИЕ 13
Положите x = y — в уравнение x3 + ax2 + bx + c = 0, чтобы показать, что полученное уравнение не содержит членов степени 2.
ПРИМЕР
Решите x3 + 3x — 1 = 0, используя замену x = u + v.
Решение
Переставляя уравнение и подставляя, получаем
(u + v) 3 = −3 (u + v) + 1.
Теперь мы расширяем левую часть и множим 3uv из двух членов, чтобы получить
u3 + v3 + 3uv (u + v) = 1 −3 (u + v).
Приравнивая коэффициенты при (u + v) с обеих сторон и приравнивая оставшиеся члены,
получаем
u3 + v3 = 1, 3uv = −3.
Кубирование второго уравнения дает
u3 + v3 = 1, u3v3 = -1,
На этом этапе у нас есть два числа u3, v3, сумма и произведение которых нам известны.Следовательно,
они будут удовлетворять квадратному уравнению z2 — z — 1 = 0, которое имеет решения z = или
z =. Эти решения представляют числа u3 + v3 в любом порядке, поэтому, взяв кубические корни, мы получим следующее решение исходного уравнения
х = и + v = +.
Это единственное реальное решение уравнения.
УПРАЖНЕНИЕ 14
Воспользуйтесь калькулятором, чтобы выразить это в десятичной форме, и убедитесь, что оно удовлетворяет исходному уравнению
.
Квартик
Решение общего уравнения четвертой степени было вскоре найдено учеником Кардано и его протеже Феррари. Он открыл метод, позволяющий свести задачу решения
квартики к задаче решения кубики.
В обоих случаях можно выразить решение данного уравнения, используя квадратные и более высокие корни, а также обычные арифметические операции (сложение, вычитание, умножение и деление). Такой раствор часто называют раствором с использованием радикалов.Решениями квадратного уравнения ax2 + bx + c = 0 являются x = и x = -, поэтому квадратное уравнение также может быть решено с использованием радикалов.
Потребовалось несколько сотен лет, прежде чем Абель (1802-1829) и Галуа (1811-1832) осознали, что невозможно найти решение общего уравнения пятой степени или общего уравнения более высокой степени с использованием радикалов. . Очевидно, что некоторые уравнения более высокой степени могут быть решены с использованием радикалов, например x5 — 32 = 0, но в общем случае это невозможно.
Корни многочленов
Хотя работа Кардано была большим прорывом, по-прежнему оставалось много безответных вопросов, касающихся полиномов. В 17 веке Декарт нашел тест, известный как правило знаков Декарта, для определения числа положительных действительных корней многочлена, в то время как Ньютон открыл так называемые тождества Ньютона, которые находят и связывают формулы для суммы k-х степеней корней многочлена. В XVIII и XIX веках великие математики Эйлер, Лагранж, Эйзенштейн и Гаусс еще больше расширили наше понимание полиномов и полиномиальных уравнений.Это привело к развитию того, что сегодня называется современной алгеброй, которая занимается изучением алгебраических структур.
Факторинговые полиномы
Выше мы видели, что когда мы изучаем многочлен, нам нужно указать, какие решения / факторы мы ищем. В частности, предположим, что p (x) — многочлен со степенью больше 0 и действительными коэффициентами
- над комплексными числами p (x) делится на линейные множители
- над действительными числами p (x) имеет все свои множители либо линейные, либо квадратичные
- над рациональными числами, можно найти полиномы сколь угодно большой
степени, которые являются неприводимыми, то есть они не могут быть выражены как произведение
двух полиномов с рациональными коэффициентами, каждый меньшей степени.
Основная теорема алгебры используется для доказательства первого из этих утверждений. Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые комплексные корни будут встречаться парами, известными как сопряженные пары. То есть, если a + ib — корень, то a — ib тоже. Этот факт можно использовать для доказательства второго утверждения.
УПРАЖНЕНИЕ 15
(Для этого нужно немного знать комплексные числа.)
Предположим, что все коэффициенты многочлена p (x) = dancingn — an — 1xn — 1 + … + a1x + a0 действительны.
- a
- Если α = a + ib является решением полиномиального уравнения, p (x) = dancingn — an — 1xn — 1 + … + a1x + a0 = 0, покажите, что = a — ib также является решением.
- б
- Покажите, что если x — α является множителем p (x), где α = a + ib — комплексное число, то квадратичный (x — α) (x -) также является множителем p (x) и что (x — α) (x -) имеет действительные коэффициенты.
- в
- Выведите, что каждый многочлен с действительными коэффициентами теоретически может быть разложен на множители как произведение линейных и / или квадратичных множителей с действительными коэффициентами. (Обратите внимание, что на практике это может быть очень сложной задачей.)
Эйзенштейн (ок. 1850 г.) предложил следующий остроумный тест на несводимость многочленов над рациональными числами.
Рассмотрим многочлен p (x) = travelling — an — 1xn — 1 + … + a1x + a0, где все коэффициенты являются целыми числами.Предположим, что мы можем найти простое число p, которое не делит старший коэффициент an, но которое делит все остальные коэффициенты. Тест говорит, что если квадрат того же простого числа не делит константный член, то есть p2 + a0, то p (x) неприводимо по рациональным числам.
ПРИМЕР
Многочлен p (x) = 5×7 + 6×6 — 15x 4 + 12x — 21 удовлетворяет критерию Эйзенштейна с простым p = 3, и поэтому p (x) не может быть выражено как произведение двух многочленов меньшей степени с целыми коэффициентами.То есть p (x) неприводимо.
УПРАЖНЕНИЕ 16
Объясните, как построить многочлен сколь угодно большой степени, который нельзя разложить на рациональные числа.
Маклорен серии
В 17-м и 18-м веках математики сделали замечательное открытие, что такие функции, как y = sin x и y = cos x, могут быть выражены с помощью «бесконечных многочленов», то есть многочленов, степени x которых продолжаются бесконечно.Это называется степенным рядом. Так, например,
sin x = x — + — +…,
, где очевидная закономерность продолжается вечно. Обозначение n! (читается как факториал n) — это сокращение от n (n — 1) (n — 2)… 3.2.1. Таким образом 5! = 5 × 4 × 3 × 2 × 1 = 120. Эти бесконечные ряды часто называют рядами Маклорена и имеют очень широкое применение как в математике, так и в физике.
На сегодняшний день остаются нерешенными проблемы, связанные с многочленами. В приложении ниже в общих чертах обсуждается замечательное применение полиномов в современных телекоммуникациях.
Приложение
Применение полиномов к кодам, исправляющим ошибки
Оцифровка информации
Информация обычно оцифровывается путем преобразования ее в последовательность нулей и единиц. Например, код ASCII для цифры 1 и буквы A — «1» 1000110 и «A» 1000001. Здесь мы будем предполагать, что все рассматриваемые сообщения представляют собой конечные последовательности нулей и единиц.
Когда ваш мобильный телефон отправляет или принимает сообщения или данные отправляются со спутников в глубоком космосе, информация может быть потеряна или повреждена по пути к месту назначения.
Поскольку информация отправляется как последовательности из 0 и 1, «поврежденный» 0 становится 1 и наоборот.
Простая проверка на наличие ошибок — это добавить контрольную цифру, чтобы в строке было четное число единиц и, следовательно, сумма цифр была четной.
Таким образом, мы кодируем 1 как 10001101 и A как 10000010.
Теперь, если байт передан и один из битов поврежден, то количество единиц становится нечетным, и поэтому получатель может запросить повторную передачу.
Этот код может обнаружить одну ошибку, но не может ее исправить.
Многочлены по модулю 2
Полином по модулю 2 — это полином, коэффициенты которого равны 0 или 1. Затем арифметические операции выполняются по модулю 2, так что 0 + 1 = 1 + 0 = 1 и 1 + 1 = 2 = 0.
Производим сложение по модулю 2.
ПРИМЕР
Если p (t) = t3 + 1 + 1, q (t) = t4 + t3 + t2 + 1
Тогда p (t) + q (t) = t4 + 2t3 + t2 + 2t + 2 = t4 + t2.
Умножение производится аналогично.
Решение
p (t) = t3 + 1 + 1, q (t) = t + 1, тогда
p (t) × q (t) = (t3 + t + 1) (t + 1) = t4 + t3 + t2 + 2t + 1 = t4 + t3 + t2 + 1
Кодирование
Теперь зафиксируем многочлен m1 (t) = t3 + t + 1.
Этот многочлен не может быть разложен на множители по модулю 2, поскольку единственные возможные корни — это 0 и 1, и ни один из них не работает.
Предположим теперь, что многочлен m1 (t) имеет корень a. То есть, a обладает тем свойством, что
α3 + α + 1 = 0 или α3 = α + 1 (напомним, что по модулю 2, −1 = 1)
Это число α очень интересно, и, используя приведенное выше уравнение, мы можем составить таблицу его степеней.
Мощность | Упрощенная форма
| α | | α | |
| α2 | | α2 | |
| α3 | | α + 1 | |
| α4 | | α2 + α | |
| α5 | | α2 + α + 1 | |
| α6 | | α2 + 1 | |
| α7 | | 1 |
Например, чтобы получить α5, мы умножаем α4 = α2 + α на α5 = α3 + α2 и заменяем α3 на α + 1, чтобы получить α5 = α + 1 + α2.
Таким образом, мы можем записать все степени α как комбинации 1, α и α2 (!!)
Теперь о кодах.
Мы начинаем с сообщения (a, b, c, d) в двоичном формате длиной 4, добавляем 3 контрольных цифры, чтобы получить
(a, b, c, d, x, y, z). Мы используем их как коэффициенты многочлена
p (t) = at6 + bt5 + ct4 + dt3 + xt2 + yt + z.
Цифры x, y, z выбраны так, чтобы p (t) делилось на многочлен m1 (t) = t3 + t + 1
Поскольку a является корнем m1 (t), он также является корнем p (t), и поэтому p (a) = 0.
ПРИМЕР
Возьмите сообщение (1, 0, 0, 1) и закодируйте его как (1, 0, 0, 1, x, y, z). Преобразуя в полином, получаем
| п (т) | знак равно t6 + t3 + xt2 + yt + z. | |
| Подставляя t = a и используя таблицу для упрощения, получаем | ||
| п (а) | = a6 + a3 + xa2 + ya + z. | |
| = (a2 + 1) + (a + 1) + xa2 + ya + z | ||
| = а2 (х + 1) + а (у + 1) + z. | ||
Теперь, если мы возьмем x = 1, y = 1, z = 0, тогда p (a) будет равно нулю.Следовательно, мы кодируем сообщение
(1, 0, 0, 1) как (1, 0, 0, 1, 1, 1, 0). Мы будем называть многочлен, соответствующий отправленному сообщению, C (t), поэтому C (a) = 0.
Исправление ошибок
Предположим, что одна ошибка возникает в пятом числе слева, поэтому мы получаем сообщение (1, 0, 1, 1, 1, 1, 0).
Таким образом, коэффициент t4 неверен и полином для полученного сообщения равен
R (t) = C (t) + t4
Подставляя t = α, получаем
R (α) = C (α) + α4 = α4
и поэтому мы знаем, где ошибка.
В общем, если бы была ровно одна ошибка в -ой цифре, мы получили бы
R (t) = C (t) + ti.
Тогда R (α) = C (α) + αi = αi, и поэтому вычисление R (a) дает позицию неправильной цифры.
Если R (α) = 0, то ошибок не было. Этот процесс, конечно, предполагает, что произошло не более 1
ошибки.
ПРИМЕР
Предполагая, что не более одной ошибки, исправьте и расшифруйте сообщение (1, 0, 0, 1, 0, 0, 1).
Решение
Преобразуя в полиномы, получаем
R (t) = t6 + t3 + 1
и т. Д.
R (α) = α6 + α3 + 1 = α2 + 1 + α + 1 + 1 = α2 + α + 1 = α5
Итак, исправленное сообщение было (1, 1, 0, 1, 0, 0, 1), которое декодируется как (1, 1, 0, 1).
Исправление более одной ошибки
Процедура кодирования и исправления, описанная выше, работает только в том случае, если при передаче возникла не более одной ошибки.
Полиномиальный метод может быть расширен для обнаружения и исправления более чем одной ошибки.
Детали этих кодов немного сложнее, но в них используются те же идеи, которые были развиты выше.
Коды, используемые для исправления множественных ошибок, называются кодами BCH и были открыты (независимо) Бозом и Чаудхури (в 1960 г.) и Хоккенгемом (в 1959 г.) — отсюда и название BCH.
В то время как арифметика теперь становится очень сложной, она легко выполняется компьютером, и можно создавать коды, которые могут обнаруживать и исправлять произвольное количество ошибок.
Современные коды исправления ошибок, используемые в технологии мобильных телефонов, снова более сложны, но в основном используют те виды оборудования, которые я описал выше.
В последнее время коды Рида-Соломона, которые представляют собой тип кода BCH, использовались в таких приложениях, как спутниковая связь, проигрыватели компакт-дисков, DVD-диски и дисководы.
ОТВЕТОВ НА УПРАЖНЕНИЯ
УПРАЖНЕНИЕ 1
Ведущий термин: тревога
Ведущий коэффициент:
Степень: n
Постоянный член: a0
УПРАЖНЕНИЕ 2
а 4×6 — 4×4 + 4×3 + x2 — 2x + 1
b i….сумма степеней полиномов
ii… произведение констант
УПРАЖНЕНИЕ 3
5×4 — 7×3 + 2x — 4 = (x2 — 2) (5×2 — 7x + 10) + (−12x + 16)
УПРАЖНЕНИЕ 4
а = 18
УПРАЖНЕНИЕ 5
a = -33 и b = -15
УПРАЖНЕНИЕ 6
Если P (a) = 0, то a0 = — anan — an − 1an − 1…. − A1a. Следовательно, a делит a0.
УПРАЖНЕНИЕ 7
2×2 (х — 3) 2 (х — 5)
УПРАЖНЕНИЕ 8
x = 0 или x = 3 или x = 5
УПРАЖНЕНИЕ 9
УПРАЖНЕНИЕ 10
УПРАЖНЕНИЕ 11
Для полиномиального уравнения P (x) = 0 существует решение x = a по теореме.Следовательно, x — a является фактором P (x) и P (x) = (x — a) Q (x). Уравнение Q (x) = 0 также имеет решение, поэтому с помощью теоремы можно найти новый линейный множитель.
УПРАЖНЕНИЕ 12
(x — α) (x — β) (x — γ) = x3 — (α + β + γ) x2 + (αβ + αγ + βγ) x + αβγ = x3 + bx2 + cx + d
Следовательно, результат b = — (α + β + γ), c = (αβ + αγ + βγ) и d = αβγ
УПРАЖНЕНИЕ 13
y3 — + — + d
УПРАЖНЕНИЕ 14
- a
- Возьмите конъюгаты с обеих сторон.Сопряжение с действительным — это то же самое, что и реальное.
- б
- Непосредственное следствие a и теоремы о факторах, а также того факта, что сумма и произведение комплексного числа и его сопряженного действительны.
- в
- Основная теорема и b дает результат
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений австралийского правительства.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Непортированная лицензия.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Почему учителям математики пора убирать BODMAS
Что означает BODMAS?
Акроним BODMAS означает скобки, порядки, деление, умножение, сложение, вычитание.
Иногда его называют BIDMAS (с «индексами» вместо «заказов») или правилом PEMDAS в Америке (с «круглыми скобками» и «экспонентами»).
Правило BODMAS
Это математическое правило диктует правильный порядок операций, которым нужно следовать, когда вы отвечаете на вопрос с математическим числовым предложением с различными операциями.
Первый шаг — сделать что-нибудь в скобках, затем заказать следующие (например, извлекать квадратный корень или индексы). Деление и умножение находятся на одном уровне, что означает, что им дается равный приоритет, и они должны выполняться слева направо, а не все деление, а затем все умножение. Точно так же сложение и вычитание находятся на одном уровне и должны выполняться слева направо.
Я начал свою педагогическую карьеру в средней школе. Молодой, нетренированный и еще не лысеющий, я попал на самый крутой этап обучения в моей жизни.
Еженедельные встречи с моим руководителем отдела были жизненно важны для обсуждения педагогики, и я строго придерживался его инструкций: «Никогда не сокращайте совокупную частоту», «Мы всегда подбрасываем монеты и получаем решку, мы никогда не подбрасываем монеты и не получаем орла», и что очень важно. , «Мы никогда, никогда не используем БОДМЫ».
Отказаться от использования BODMAS оказалось труднее, чем вы думаете.Приехали студенты, хорошо разбирающиеся в его применении.
Нам пришлось учить и . Нам приходилось убеждать комнаты, заполненные подростками, в том, что они должны изменить основные принципы своей арифметической системы убеждений. Это было сложно, потому что подростки ненавидят перемены и ненавидят прозелитизм взрослых.
Так зачем нам вообще беспокоиться? Что убедило весь отдел в том, что нужно приложить столько усилий для решения такого, казалось бы, тривиального вопроса?
BODMAS ошибочен.Это то что.
Неправильный ответ
Буквы обозначают скобки, порядок (что означает степень), деление, умножение, сложение, вычитание. Таким образом, предполагается, что в этой последовательности происходит упрощение любого данного математического выражения.
Например, чтобы оценить 3 + (3 + 3) 3 ÷ 3 — 3 x 3 , мы действуем в указанном выше порядке:
Это был бы действительно полезный алгоритм, если бы он работал в любой ситуации, но рассмотрим гораздо более простое выражение 1-2 + 4 .Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и выполнять сложение с последующим вычитанием:
Это ошибочно. Правильное значение — 3. BODMAS подвел нас. Позор БОДМАМ!
Математические задачи
У нас не может быть волшебной мнемоники, которая не работает все время; Предположим, он решил не работать в важный момент. Представьте, что вы пытаетесь объяснить своему ученику, что причина, по которой он потерял оценку на экзамене, заключалась в том, что то, что вы сказали ему, всегда работает, на самом деле не срабатывает во всех случаях, и, фактически, один из таких случаев произошел в тот документ GCSE.
Это не новая проблема. Я не первый, кто об этом пишет. Даже Википедия решает эту проблему и предлагает некоторые альтернативы. Студенты любят Википедию! Так почему же BODMAS все еще актуален?
В Хайгейте вокруг него было такое клеймо, что некоторые партии высмеивали меня более десяти лет после того, как мой коллега пережил обмен в классе, который проходил примерно так:
Учитель: Как нам упростить это выражение?
Ученик: БОДМАС, сэр.
Учитель: Мы здесь не используем БОДМЫ.
Студент: Но вот чему мистер Элтон научил нас в прошлом году, сэр.
После этого мне несправедливо присвоили прозвище «БОДМАС», которое преследовало меня повсюду. У меня не было защиты; Заявление подал платный студент, так что оно должно быть правдой. По крайней мере, один человек (он знает, кто он) все еще называет меня БОДМАСом чаще, чем он использует мое настоящее имя.
Несмотря на то, что я абсолютно не виновен в том, что запятнал умы невинных студентов, я чувствую себя обязанным исправить положение, поэтому я использую эту платформу именно так.Считайте это общественными работами.
Правильный ответ
Однако нет смысла бить БОДМАС, не предлагая альтернативы. Проиллюстрированная выше ошибка вызвана тем фактом, что сложение и вычитание не обязательно должны происходить в таком порядке. Если у нас есть строка из этих двух операций, она называется суммой, и мы должны работать слева направо:
Точно так же деление не более важно, чем умножение. Если у нас есть строка из этих двух операций, она называется продуктом, и мы снова будем работать слева направо:
У нас теперь такой порядок: скобки, порядок, продукты, суммы.
Это дает нам BOPS, который на целый слог короче, чем BODMAS, и имеет значительное преимущество в том, что он надежен.
Я уверен, что если бы кто-то предложил BOPS раньше BODMAS, то последний был бы предан безвестности. Даже сейчас еще не поздно избавиться от двусложных арифметических сокращений.
Я призываю своих коллег по всему миру запретить BIDMAS и очистить PEMDAS. Не оставляйте от них никаких следов. Позвольте BOPS нанести победный удар молодым математикам во всем мире.
Оуэн Элтон — учитель математики, автор / исполнитель глупых песен и автор математических минут. Вы можете следить за ним в Твиттере по адресу @owenelton.
.
 Целая положительная степень n суммы. (a + b)n=
Целая положительная степень n суммы. (a + b)n=