Формулы разности и суммы кубов и квадратов: Урок 30. сумма кубов. разность кубов — Алгебра — 7 класс

Урок 30. сумма кубов. разность кубов — Алгебра — 7 класс

Алгебра

7 класс

Урок № 30

Сумма кубов. Разность кубов

Перечень вопросов, рассматриваемых в теме:

• Формулы сокращённого умножения.
• Сумма кубов, разность кубов.
• Разложение многочлена на множители.
• Тождественные преобразования.
• Вычисление значения числовых выражений.

Тезаурус:

Формулы сокращённого умножения.

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

(a + b)(a – b) = a² – b²

a³ + b³= (a + b)(a ²– ab + b²)

a³ – b³= (a – b)(a² + ab + b²)

Применение:

• упрощение умножения многочленов;
• разложение многочлена на множители;
• вычисление значения числового выражения;
• тождественные преобразования.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Формула суммы кубов.

Рассмотрим произведение;

(a + b)(a² – ab + b²).

Применив правило умножения многочленов, и приведя подобные члены, получим:

(a + b)(a² – ab + b²) = a³ – a²b + ab² + ba² – ab² +b³ = a³ + b³

a³ + b³ = (a + b)(a² – ab + b²)

Равенство называют формулой суммы кубов.

Читается так: «сумма кубов двух чисел равна произведению суммы этих чисел и неполного квадрата их разности».

Формула разности кубов.

Аналогично докажем формулу разности кубов.

(a – b)(a² + ab + b²) = a³ + a²b + ab² – ba² – ab² – b³= a³ – b³

Читается так: «разность кубов двух чисел равна произведению разности этих чисел и неполного квадрата их суммы».

a³– b³= (a

– b)(a²+ ab + b²)

Выражения (a²+ ab + b²) и (a²– ab + b²) называют неполным квадратом суммы или разности.

Формула задаёт разложение многочленов:

a³ + b³ и a³ – b³ на два множителя:

(a + b)(a² – a b+ b²) и (a – b)(a²+ ab + b²).

Формулы суммы и разности кубов используют для упрощения вычислений.

Разбор решения заданий тренировочного модуля.

Задача 1.

Выполните умножение многочленов:

1. ( x + 3)(x² –3x +9) = x³ + 3³ = x³ + 27.
2. (2x – 3y)(4x² +6xy + 9y²) = (2x)³ – (3y)³ = 8x³ –27y³.

Задача 2.

Разложите многочлен на множители:

1. x³ – 8 y³ = x³ – (2y)³ = (x – 2y) (x² +2xy + 4y² )
2. 64 a³ – 27c³ = (4a)³ – (3c)³ = (4a – 3c)(16a² +12 ac + 9c²).

Задача 3.

Упростите выражение:

(x +2)(x² – 2x +4) – x(x–3)(x+3).

Решение:

x³ + 2³ – x(x² – 9) = x³ + 8 – x³ + 9x = 8 + 9x. 2\right)\]

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2) = a 3 − b 3

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а 3 » — это «(3а) 3 », значит, для формулы разности кубов вместо «a » мы используем «3a ».

Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».

Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов

«a 3 − b 3 = (a − b)(a 2 + ab + b 2) », то можно понять, что на месте «a » из первой скобки стоит «y 2 , а на месте «b » стоит «1 ».

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Быстро найти нужную формулу для расчета онлайн.

Геометрия. Алгебра.

---

Квадрат суммы

 

Квадрат разности

 

Разность квадратов

 

 

Куб суммы

 

Куб разности

 

Сумма кубов

 

Разность кубов

 

Разность n степеней

 

.

 

 

---

Разность кубов двух переменных равна произведению разности переменных на неполный квадрат суммы этих переменных.

Данное выражение справедливо для любых действительных чисел.

 

Сумма кубов двух переменных равна произведению суммы первой и второй переменной на неполный квадрат разности этих переменных.

Данное выражение справедливо для любых действительных чисел.

 

 

---

Куб разности двух переменных равен — куб первой переменной минус куб второй переменной, минус утроенное произведение квадрата первой переменной и второй переменной, плюс утроенное произведение первой переменной и квадрата второй переменной.

Данное выражение справедливо для любых действительных чисел.

 

---

Куб суммы двух переменных равен куб первой переменной плюс куб второй переменной, плюс утроенное произведение квадрата первой переменной и второй переменной, плюс утроенное произведение первой переменной и квадрата второй переменной.

Данное выражение справедливо для любых действительных чисел.

 

---

Разность квадратов двух переменных равна произведению разности и суммы этих переменных.

Данное выражение справедливо для любых действительных чисел.

 

---

Квадрат разности двух переменных равен сумме квадратов первой и второй переменных, минус их удвоенное произведение.

Данное выражение справедливо для любых действительных чисел.

 

---

Квадрат суммы двух переменных равен сумме квадратов первой и второй переменных плюс их удвоенное произведение.

Данное выражение справедливо для любых действительных чисел.

 

 

---

правила применения формул сокращенного умножения

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.

Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.

Разбираемся?)

Откуда берутся формулы сокращённого умножения?

Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.

Они берутся из умножения.) Например:

(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2

Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.

ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.)

Зачем нужны формулы сокращённого умножения?

Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.

И так вот они:

Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.

Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Третья (х — у) 2 = х 2 — 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Пятая (х — у) 3 = х 3 — 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.

Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.

Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).

О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.

Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .

Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

правила применения формул сокращенного умножения

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Yandex.RTB R-A-339285-1

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: a 2 — b 2 = a — b a + b
6. формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n

Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a — b 2 = a 2 — 2 a b + b 2 .

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a — b 2 = a — b a — b .

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9 y — (1 + 3 y) 2 .

Применим формулу суммы квадратов и получим:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСУ

Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения . Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).

Первая формула сокращенного умножения называется разность квадратов . Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.

а 2 — b 2 = (а — b)(a + b)

Разберем для наглядности:

22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)

Вторая формула о сумме квадратов . Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.

(а + b) 2 = a 2 +2ab + b 2

Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.

Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула это квадрат разности . Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.

(а +b) 2 = а 2 — 2аb + b 2

где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2

Четвертая формула сокращенного умножения называется куб суммы . Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.

(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3

Пятая, как вы уже поняли называется куб разности . Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.

(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3

Шестая называется — сумма кубов . Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.

а 3 + b 3 = (а+b)(а 2 -аb+b 2)

По другому можно сказать сумму кубов можно назвать произведение в двух скобках.

Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.

а 3 — b 3 = (а-b)(а 2 +аb+b 2)

И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.

Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!

Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм . Там все очень подробно написано и показано. Будет интересно!

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.

И так вот они:

Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.

Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Третья (х — у) 2 = х 2 — 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Пятая (х — у) 3 = х 3 — 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.

Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.

Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).

О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.

Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .

Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.

правила применения формул сокращенного умножения Формулы сокращенного умножения сумма и разность кубов

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2) = a 3 − b 3

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а 3 » — это «(3а) 3 », значит, для формулы разности кубов вместо «a » мы используем «3a ».

Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».

Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов
«a 3 − b 3 = (a − b)(a 2 + ab + b 2) », то можно понять, что на месте «a » из первой скобки стоит «y 2 , а на месте «b » стоит «1 ».

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: a 2 — b 2 = a — b a + b
6. формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n

Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a — b 2 = a 2 — 2 a b + b 2 .

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a — b 2 = a — b a — b .

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9 y — (1 + 3 y) 2 .

Применим формулу суммы квадратов и получим:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСУ

Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Веб-урок — Суммы и разности кубов

 

Цели

• Знать и (возможно) запомнить формулы суммы кубов и разности кубов
• Практика использования формул для простых случаев сумм и разностей кубов суммы и разности, которые имеют одну или несколько переменных

Описание урока

Подобно уже известной нам формуле разности квадратов, формула суммы и разности кубов обеспечивает успешный факторный подход к выражениям формы $a^3 \pm b^ 3$. 2 = (a+b)(a-b)$$Разность квадратов названа так, потому что то, что мы пытаемся учесть в этом случае, является буквально разностью двух квадратов. В этом уроке мы изучим формулу разложения суммы или разности кубов, а не квадратов. Хорошо это или плохо, это означает, что нам просто нужно запомнить формулу, но, как обычно, мы не будем готовы получить пятерку, если не потренируемся в ее использовании, чтобы мы могли увидеть все возможные способы ее использования. .

Формула(ы) суммы/разности кубов

Формула для разложения на множители суммы двух кубов почти идентична формулам для разложения на множители разности двух кубов.2\right)$$

Вы можете очень быстро доказать эти формулы, просто умножив правую часть и проверив, что в итоге вы получите сумму или разность в левой части формулы. На самом деле, если вы испугались теста и беспокоитесь, что перепутали знаки «плюс» и «минус», это хороший способ перепроверить, правильно ли вы записали формулу. формула со знаками $\pm$ и $\mp$. Я искренне считаю, что студенты более склонны все испортить, когда запоминают их по отдельности.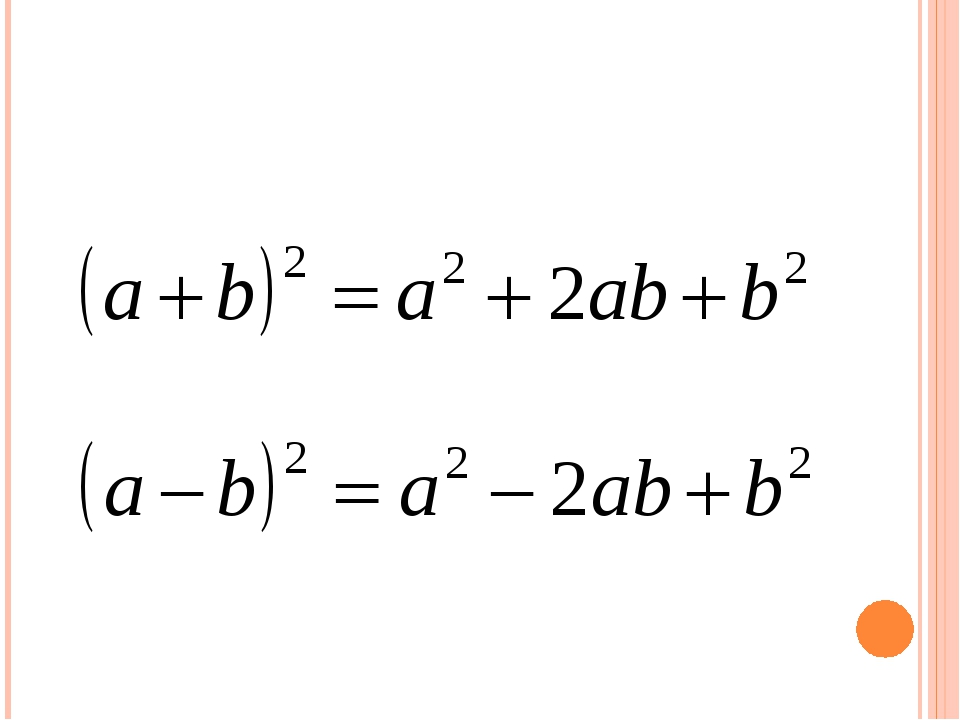 Знание одной формулы означает, что вы в равной степени подготовлены к любому случаю — и хотя вы не будете сталкиваться с этим почти так же часто, как с квадратичным факторингом, вы обязательно будете сталкиваться с ним время от времени, и от вас ожидается, что вы будете знать, что делать. Кроме того, стоит быстро упомянуть, что единственная причина, по которой у нас не было двух формул для использования, когда мы изучали метод факторинга разности квадратов, заключается в том, что «сумма квадратов» не может быть факторизована с действительными числами. Причина того, что сумму кубов можно разложить на множители, а сумму квадратов нельзя, заключается в том, что вы можете извлечь кубический корень из отрицательного числа, но не можете извлечь квадратный корень из отрицательного числа.2 + 2x + 4\right)$$Когда вы факторизуете сумму или разность кубов выражения с одной переменной, вы получаете линейный множитель и квадратичный множитель. Этот квадратичный множитель гарантированно будет простым или неприводимым. Другими словами, не тратьте время на дальнейшие попытки учесть это — у вас ничего не получится.

Мистер Математика делает это значащим

Безусловно, чаще всего этот метод факторизации используется для кубических выражений с одной переменной, используемых в случаях, когда мы также факторизуем квадратные числа или другие полиномиальные функции и уравнения.Тем не менее, есть два примечательных способа, с помощью которых учителя могут изменить эту концепцию, чтобы попытаться снизить вашу оценку. трудность. Прежде всего, если вы следовали моим урокам со времен славы, когда вы впервые познакомились с факторингом, вы знаете, что нужно всегда искать GCF в каждой факторинговой проблеме, каждый раз. Если вы не последуете моему неизменно правильному совету по факторингу, вы все равно привыкнете искать GCF в сумме или разности задач кубического факторинга, точно так же, как вы, вероятно, делали это в задачах, требующих факторизации разности квадратов.2 + 15x + 25\big)$$Еще раз, нам даже не нужно тыкать и тыкать в оставшиеся квадратные числа — квадратичный член в сумме / разности кубов, разложенных на множители, никогда больше не будет факторизуем. Множественные переменные Как мы видели в уроке по расширенной разнице квадратов »разложение ситуаций, связанных с мономами с несколькими переменными, не сильно отличается, хотя нужно проявлять больше осторожности, чтобы найти правильный квадратный корень или, в данном случае, кубический корень. Давайте посмотрим, как работает формула суммы/разности кубов, на примере.4\right)$$Стоит отметить, что более сложные задачи на сумму или разность кубов могут иметь оба этих качества (требование GCF и несколько переменных) одновременно. Мы увидим примеры этого в задачах в конце урока, а также в рабочем листе урока.

Испытайте это

Увидев несколько примеров, мы готовы закончить освоение этого метода факторинга. В отличие от многих других формул, которые мы изучаем в алгебре, вам никогда не придется использовать эту формулу в обратном порядке, поэтому достаточно небольшой практики, чтобы понять, как решить любую задачу, требующую факторизации с использованием этой техники.{12}}{2} — 32$$

Показать решение

$\blacktriangleright$ Это необычная задача, но хорошее упражнение для нестандартного мышления. Общего множителя нет, но ни один из членов не является в точности идеальным кубом. Однако, если мы умножим выражение на $2$, каждый член действительно будет идеальным кубом. Поскольку мы не можем просто взять выражение и умножить его на $2$ (поскольку это изменит выражение, что нам не разрешено делать), мы должны каким-то образом манипулировать им. Есть два взгляда на этот процесс: 1) Умножение на $2/2$ Умножение на $2/2$ принципиально не меняет выражение, поскольку мы, по сути, умножаем на $1$.6$

Распознавайте факторинговые возможности GCF и проверяйте их каждый раз, когда факторизуете

Будьте знакомы с факторингом суммы и разности фигур куба для многомерных сумм и разностей

формула для возможного дальнейшего разложения на множители (например, примеры 11 и 12)

Объяснение урока: Сумма и разность двух кубов

В этом объяснении мы узнаем, как разложить на множители сумму и разность двух кубов.

Чтобы понять сумму и разность двух кубов, давайте сначала вспомним очень похожее понятие: разность двух квадратов.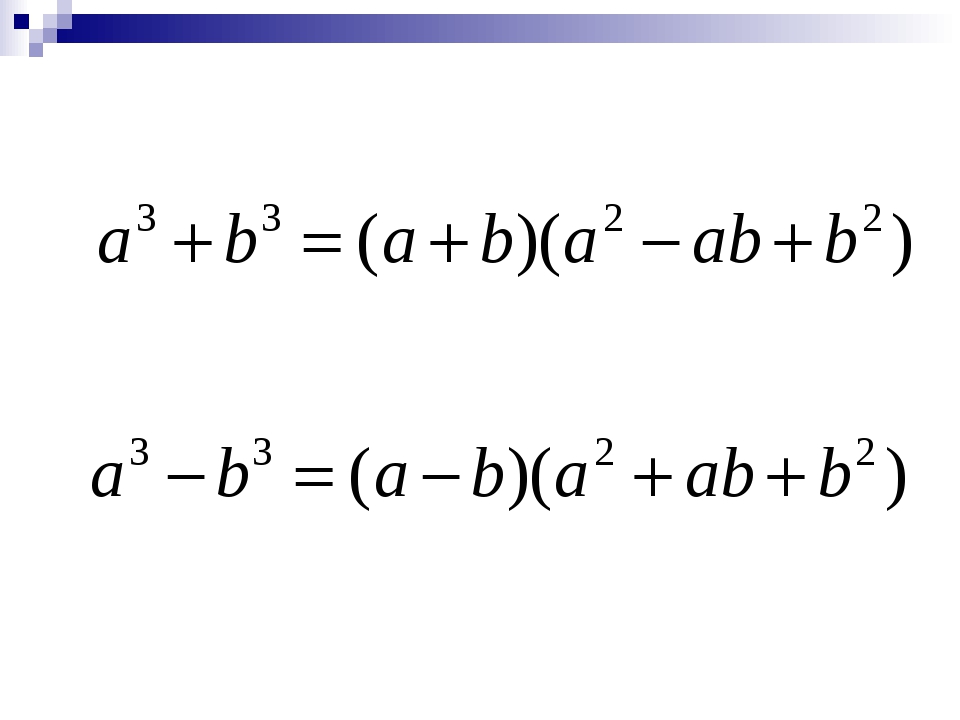 За два действительных числа 𝑎 и 𝑏, мы имеем 𝑎−𝑏=(𝑎−𝑏)(𝑎+𝑏).

Это разложение на множители разности двух квадратов можно проверить, раскрыв скобки в правой части уравнения. Мы находим, что (𝑎−𝑏)(𝑎+𝑏)=𝑎×𝑎+𝑎×𝑏−𝑏×𝑎−𝑏×𝑏=𝑎+𝑎𝑏−𝑎𝑏−𝑏=𝑎−𝑏.

Как и мы эта формула работает, потому что, хотя два биномиальных выражения обычно умножаются вместе, чтобы получить четыре члена, Члены 𝑎𝑏 и −𝑎𝑏 в середине сокращаются.Это тождество полезно, поскольку оно позволяет нам легко разложить на множители квадратные выражения, если они имеют вид 𝑎−𝑏. Мы могли бы задаться вопросом, есть ли подобное такая техника существует для кубических выражений. Другими словами, существует ли формула, которая позволяет нам разложить 𝑎−𝑏?

Давайте посмотрим, как может выглядеть факторизация 𝑎−𝑏. Можно предположить, что одним из факторов является 𝑎−𝑏, так как это также фактор 𝑎−𝑏. Предположим, что это так, тогда мы можем найдите другой множитель, используя деление в длину:

Поскольку остаток после деления равен нулю, это показывает, что 𝑎−𝑏 действительно является множителем и что правильный факторинг 𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏. 

Можно задаться вопросом, можно ли далее разложить на множители выражение 𝑎+𝑎𝑏+𝑏, поскольку оно является квадратичным выражение, однако на самом деле это самая упрощенная форма, которую оно может принимать (хотя мы не будем доказывать это в этом объяснении). Отметим, что, поскольку 𝑎 и 𝑏 могут быть любыми двумя числами, эта формула применима к любому выражению. это разница в два куба. В частности, мы имеем следующее определение.

Определение: разность двух кубов

Для двух действительных чисел 𝑎 и 𝑏 выражение 𝑎−𝑏 называется разность двух кубов .Его можно рассчитать следующим образом: 𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏.

Мы можем дополнительно проверить этот результат так же, как мы это сделали для разности двух квадратов. Если мы раскроем скобки в правой части уравнения находим (𝑎-𝑏) 𝑎 + 𝑎𝑏 + 𝑏 = 𝑎 × 𝑎 + 𝑎 × 𝑎𝑏 + 𝑎 × 𝑏-𝑏 × 𝑎-𝑏 × 𝑎𝑏-𝑏 × 𝑏 = 𝑎 + 𝑎𝑏 + 𝑎𝑏-𝑎𝑏-𝑎𝑏 — 𝑏 = 𝑎 = 𝑎 −𝑏.

Подобно тому, как средние члены сокращаются в разности двух квадратов, мы можем видеть, что то же самое происходит для разности кубики.

Этот результат невероятно полезен, поскольку он дает нам простой способ факторизовать определенные типы кубических уравнений, которые в противном случае были бы сложно учесть. Давайте посмотрим на пример того, как разность двух кубов может быть факторизована с использованием приведенного выше тождества.

Пример 1. Нахождение неизвестного путем факторизации разности двух кубов 𝑘.

Ответить

Этот вопрос можно решить двумя способами.Один из способов — раскрыть скобки в правой части уравнения и найти какое значение 𝑘 удовлетворяет обе стороны. Альтернативный способ состоит в том, чтобы признать, что выражение слева является разность двух кубов, так как 512=8. Это позволяет использовать формулу факторизации разности кубов.

Напомним, что у нас есть 𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏.

Поскольку данное уравнение имеет вид 𝑥−512=(𝑥−8)𝑥+𝑘+64, мы можем видеть что если мы возьмем 𝑎=𝑥 и 𝑏=8, оно искомого вида. Это означает, что 𝑘 должен быть равно 𝑎𝑏=8𝑥.

Чтобы показать, как получается этот ответ, давайте рассмотрим, что обычно происходит, если мы пытаемся раскрыть скобки. Мы бы хотели иметь (𝑥−8)𝑥+𝑘+64=𝑥×𝑥+𝑥×𝑘+𝑥×64−8×𝑥−8×𝑘−8×64=𝑥+𝑘𝑥−8𝑥+64𝑥−8𝑘−512=𝑥 +𝑥(𝑘−8𝑥)−8(𝑘−8𝑥)−512.

Чтобы это выражение было равно 𝑥−512, члены в середине должны сократиться. Эти термины имеют факторизуется таким образом, что выбор 𝑘=8𝑥 приводит к тому, что оба члена равны нулю.Если мы сделаем это, то обе части уравнения будут одинаковыми.

Следовательно, мы можем подтвердить, что 𝑘=8𝑥 удовлетворяет уравнению.

В предыдущем примере мы продемонстрировали, как кубическое уравнение, являющееся разностью двух кубов, можно разложить на множители по формуле с относительной легкостью. Заметим, однако, что кубическое уравнение не обязательно должно быть именно в такой форме, чтобы его можно было факторизовать. Предположим, для Например, мы взяли 𝑏=−𝑐 в формуле факторизации разности двух кубов. Тогда у нас было бы 𝑎−(−𝑐)=(𝑎−(−𝑐))𝑎+𝑎(−𝑐)+(−𝑐).

Используя тот факт, что (−𝑐)=𝑐 и ( −𝑐)=−𝑐, мы можем упростить это, чтобы получить 𝑎+𝑐=(𝑎+𝑐)𝑎−𝑎𝑐+𝑐.

Отметим также, что 𝑎−𝑎𝑐+𝑐 находится в самом упрощенном виде (т. е. не может быть далее факторизовано). Этот приводит к следующему определению, аналогичному предыдущему.

Определение: сумма двух кубов

Для двух действительных чисел 𝑎 и 𝑏 выражение 𝑎+𝑏 называется сумма двух кубов .Его можно рассчитать следующим образом: 𝑎+𝑏=(𝑎+𝑏)𝑎−𝑎𝑏+𝑏.

Проверим еще раз корректность этой формулы, раскрыв скобки в правой части. У нас есть (𝑎 + 𝑏) 𝑎-𝑎𝑏 + 𝑏 = 𝑎 × 𝑎-𝑎 × 𝑎𝑏 + 𝑎 × 𝑏 + 𝑏 × 𝑎-𝑏 × 𝑎𝑏 + 𝑏 × 𝑏 = 𝑎-𝑎𝑏 + 𝑎𝑏 + 𝑎𝑏-𝑎𝑏 + 𝑏 = 𝑎 + 𝑎 + 𝑎 = 𝑎 = 𝑎 = 𝑎 +𝑏.

Как и в предыдущих формулах, средние члены сокращают друг друга, что приводит к выражению, состоящему всего из двух членов.

Покажем, как можно использовать эту формулу на следующем примере.

Пример 2. Разложение суммы двух кубов на множители

Разложить на множители полностью 𝑥+8𝑦.

Ответ

Обратите внимание, хотя это может быть не сразу очевидно, данное уравнение является суммой двух кубов. Чтобы убедиться в этом, давайте посмотрим на срок 8𝑦. Мы видим, что это произведение 8, которое является совершенным кубом, и 𝑦, которое равно кубическая степень 𝑦. Следовательно, если мы возьмем кубический корень, мы найдем √8𝑦=√8√𝑦=2𝑦.

Итак, 8𝑦 — куб 2𝑦. Теперь вспомним, что сумму кубов можно записать в виде 𝑎+𝑏=(𝑎+𝑏)𝑎−𝑎𝑏+𝑏.

Подставляя 𝑎=𝑥 и 𝑏=2𝑦 в приведенную выше формулу, получаем 𝑥+8𝑦=(𝑥+2𝑦)𝑥−𝑥×2𝑦+(2𝑦)=(𝑥+2𝑦)𝑥−2𝑥𝑦+4𝑦.

Как было продемонстрировано в предыдущем примере, мы всегда должны помнить, что может быть не сразу очевидно, когда кубическое выражение сумма или разность кубов. Иногда может быть необходимо определить общие факторы в выражении, чтобы результат стал сумма или разность двух кубов. Рассмотрим пример, где это так.

Пример 3. Разложение на множители разности двух кубов

Полностью факторизовать 54𝑥−16𝑦.

Ответ

Прежде чем пытаться полностью разложить данное выражение на множители, отметим, что между членами есть общий множитель, равный 2.Следовательно, его можно рассчитать следующим образом: 54𝑥−16𝑦=227𝑥−8𝑦.

Отсюда видно, что выражение в скобках представляет собой разность кубов. Это потому, что каждый из 27𝑥 и 8𝑦 — произведение числа в совершенном кубе (т. е. 3=27 и 2=8) и переменная в кубе (𝑥 и 𝑦). Другими словами, мы имеем (3𝑥)−(2𝑦)=27𝑥−8𝑦.

Напомним, что разность двух кубов можно записать в виде 𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏.

Таким образом, полный факторинг 54𝑥−16𝑦=227𝑥−8𝑦=2(3𝑥−2𝑦)(3𝑥)+(3𝑥)(2𝑦)+(2𝑦)=2(3𝑥−2𝑦)9𝑥+6𝑥𝑦+4𝑦

Продолжим исследование выражений, не являющихся явно суммой или разностью кубов, рассматривая многочлен выражение с членами шестого порядка и увидеть, как мы можем комбинировать различные формулы, чтобы получить решение.

Пример 4. Факторизация разности квадратов, которая дает произведение суммы и разности кубов

Разложите на множители выражение 𝑥−𝑦.

Ответ

Хотя данное выражение содержит члены шестого порядка и у нас нет формулы для явного обращения с ними, мы обратите внимание, что мы можем применить законы показателей, чтобы помочь нам.В частности, выражение можно записать как разность двух квадраты следующим образом: 𝑥−𝑦=𝑥−𝑦.

Обратите внимание, что это также можно записать как разность кубов, но полученное выражение сложнее упростить. Напомним, что разность двух квадратов можно записать как 𝑎−𝑏=(𝑎+𝑏)(𝑎−𝑏).

Положив здесь 𝑎=𝑥 и 𝑏=𝑦, это дает нам 𝑥−𝑦=𝑥+𝑦𝑥−𝑦.

Теперь у нас есть произведение разности двух кубов и суммы двух кубов.Таким образом, мы можем применить следующую сумму и разность формулы: 𝑎+𝑏=(𝑎+𝑏)𝑎−𝑎𝑏+𝑏,𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏. Таким образом, 𝑥 и 𝑏=𝑦 и мы получаем полную факторизацию выражения: 𝑥−𝑦=𝑥+𝑦𝑥−𝑦=(𝑥+𝑦)𝑥−𝑥𝑦+𝑦(𝑥−𝑦)𝑥+𝑥𝑦+𝑦. 

В качестве последнего примера мы рассмотрим, как можно использовать формулу суммы кубов для решения алгебраической задачи.

Пример 5: вычисление выражения для суммы двух кубов

Если 𝑥𝑦=4 и 𝑥+5𝑦=−3, каково значение 𝑥+125𝑦?

Ответ

Начнем с того, что заметим, что 𝑥+125𝑦 — это сумма двух кубов.Это потому, что 125𝑦 125 раз 𝑦, оба из которых являются кубами. Итак, если мы возьмем его кубический корень, мы найдем √125𝑦=√125√𝑦=5𝑦.

Напомним, что у нас есть следующая формула для разложения суммы двух кубов на множители: 𝑎+𝑏=(𝑎+𝑏)𝑎−𝑎𝑏+𝑏.

Здесь, если положить 𝑎=𝑥 и 𝑏=5𝑦, 𝑥+125𝑦=(𝑥+5𝑦)𝑥−(𝑥)(5𝑦)+(5𝑦)=(𝑥+5𝑦)𝑥−5𝑥𝑦+25𝑦.

учитывая значение 𝑥+5𝑦, но не 𝑥−5𝑥𝑦+25𝑦. Однако это можно выразить этот множитель в терминах приведенных нами выражений.Предположим, мы умножаем 𝑥+5𝑦 с собой: (𝑥+5𝑦)(𝑥+5𝑦)=𝑥+10𝑥𝑦+25𝑦.

Это почти то же самое, что и второй множитель, но с добавлением 15𝑥𝑦. Другими словами, вычитая 15𝑥𝑦 с обеих сторон, имеем (𝑥+5𝑦)−15𝑥𝑦=𝑥−5𝑥𝑦+25𝑦.

Поскольку нам дано значение 𝑥𝑦, левая часть этого уравнения теперь выражается чисто в терминах выражения, значение которых нам известно. Следовательно, мы можем переписать 𝑥+125𝑦 следующим образом: 𝑥+125𝑦=(𝑥+5𝑦)𝑥−5𝑥𝑦+25𝑦=(𝑥+5𝑦)(𝑥+5𝑦)−15𝑥𝑦=(−3)(−3)−15×4=153.

Давайте подытожим ключевые моменты, которые мы узнали из этого объяснения.

Ключевые точки

• Разность двух кубов можно записать как 𝑎−𝑏=(𝑎−𝑏)𝑎+𝑎𝑏+𝑏.
• Аналогично, сумма двух кубов может быть записана как 𝑎+𝑏=(𝑎+𝑏)𝑎−𝑎𝑏+𝑏.
• Используя замены (например, 𝑎=2𝑥 или 𝑏=3𝑦), мы можем использовать приведенные выше формулы факторизовать различные кубические выражения.
• Определив общие множители в кубических выражениях, мы можем в некоторых случаях свести их к суммам или разностям кубов.
• Мы можем объединить формулу суммы или разности кубов с формулой разности квадратов, чтобы упростить выражения более высокого порядка.

diffcube

diffcube

Факторинг

Разность кубиков

---

Назад в Факторинг

---

Бином можно разложить на множители, только если он представляет собой одну из трех вещей: разность квадратов, разность кубов или сумму кубов.Бином является разностью кубов, если оба члена являются совершенными кубами. Вспомним, что нам, возможно, придется сначала выделить общий множитель.

Если мы определяем, что двучлен является разностью кубов, мы делим его на двучлен и трехчлен. Бином представляет собой кубический корень из первого члена минус кубический корень из второго члена. Трехчлен происходит от двучлена. Возводим в квадрат первый член бинома, меняем знак на сложение, умножаем два члена вместе и возводим в квадрат второй член бинома, как в следующей формуле
 

А 3 — В 3 = (А — В)(А 2 + АВ + В 2 )

---

Фактор каждого из следующих.

1. x ³ — 27: раствор

2. 8x ⁶ — 125: раствор

3. 250x ⁴ — 128x: решение
 

Вернуться к началу

---

№1 раствор

1. x ³ — 27

Сначала мы проверяем, что у нас есть разность кубов
, поскольку x ³ и 27 являются совершенными кубами, мы делаем
кубический корень из x равен x, а кубический корень из 27 равен 3
, поэтому наш бином равен (x-3)
, чтобы получить первый член трехчлена, мы возводим x в квадрат, получаем x ²
, чтобы получить второй член трехчлена, мы меняем знак на + и умножаем x на 3, получая +3x
, чтобы получить третий член трехчлена, мы возводим в квадрат 3, получая 9
, поэтому наш трехчлен равен (x ² + 3x + 9)
, а ответ равен (x-3)(x ² + 3x + 9). )

 
 

Назад к проблемам

---

Решение №2

2.8x ⁶ — 125

Сначала проверим, что у нас есть сумма кубов.
, так как 8x ⁶ и 125 являются совершенными кубами, у нас есть сумма кубов.
кубический корень из 8x ⁶ равен 2x ² , а кубический корень из 15 равен 5
поэтому наш бином равен (2x ² — 5)
теперь мы используем бином для создания трехчлена
мы возводим в квадрат первый член 2x ² , чтобы получить 4x ⁴ в качестве нашего первого члена
мы меняем знак с — на + и умножаем 2x ² и 5, чтобы получить +10x ² в качестве нашего среднего члена
мы возводим второй член в квадрат 5, чтобы получить 25 в качестве нашего третьего члена
, поэтому трехчлен равен (4x ⁴ + 10x ² + 25)
, поэтому наш ответ (2x — 5)(4x ² + 10x ² + 25)

Назад к проблемам

---

№3 раствор

3.250x ⁴ — 128x

Проверяя, есть ли у нас сумма кубов, мы не видим, что ни 250x ⁴ , ни 128x не являются совершенными кубами
125x ³ — 64)
Теперь оба 125x ³ и 64 являются совершенными кубами
кубический корень из 125x ³ равен 5x , а кубический корень из 64 равен 4
поэтому наш бином равен (5x — 4) Теперь, чтобы получить трехчлен, мы возводим в квадрат 5x, чтобы получить 25x ² в качестве нашего первого члена
, мы меняем знак на + и умножаем 5x и 4, чтобы получить +20x в качестве среднего члена
, мы возводим в квадрат 4, чтобы получить 16 в качестве нашего третьего члена
поэтому трехчлен равен (25x ² + 20x + 16)
, а ответ равен 2x(5x — 4)(25x ² + 20x + 16)

.

Назад к проблемам

---

4.Сумма и разность кубов

С этими выражениями мы встречались ранее (в разделе Специальные товары с кубами):

x ³ + Y ³ = ( x + x + x x

x ³ — Y ³ = ( x — y ) ( x x

Откуда они? Если вы умножите правую часть каждого, вы получите левую часть уравнения.

Примечание: Мы не можем далее факторизовать правые части.

Мы используем приведенные выше формулы для факторизации выражений, включающих кубы, как в следующем примере.

Пример

Коэффициент 64 x ³ + 125

Ответ:

Мы используем приведенную выше формулу суммы 2 кубов.

64 x ³ + 125

= (4 х ) ³ + (5) ³

= (4 x + 5)[(4 x ) ² — (4 x )(5) + (5) ² ]

= (4 х + 5)(16 х ² — 20 х + 25)

Как упоминалось выше, мы не можем далее разлагать выражение во второй скобке. Похоже, что это можно разложить на множители, чтобы получить (4 x -5) ² , однако, когда мы расширяем это, получается:

(4 x − 5) ² = 16 x ² − 40 x + 25

Этот «полный квадратный трехчлен» не совпадает с выражением, которое мы получили, разложив на множители сумму двух кубов.

Упражнения

Коэффициент:

(1) x ³ + 27

Ответить

Используя формулу суммы 2-х кубов, получаем:

x ³ + 27

= ( х ) ³ + (3) ³

= ( х + 3)[( х ) ² — ( х )(3) + (3) ² ]

= ( х + 3)( х ² — 3 х + 9)

(2) 3 м ³ − 81

Ответить

Используя формулу Разности 2 Кубов, получаем:

3 м ³ − 81

= 3( м ³ — 27)

= 3( м ³ — (3) ³ )

= 3( м — 3)[( м ) ² + ( м )(3) + (3) ² ]

= 3( м — 3)( м ² + 3 м + 9)

Разница двух кубиков

Существует особый случай при умножении многочленов, который дает следующее:

Многочлены

Многочлен выглядит так:

пример многочлена

Разность двух кубиков

Разность двух кубов является частным случаем умножения многочленов:

(a−b)(a ² +ab+b ² ) = a ³ − b ³

Иногда всплывает при решении задач, так что стоит запомнить.

И вот почему получается так просто (нажмите play):

Пример из геометрии:

Возьмите два куба длины x и y:

Большой куб «x» можно разделить на четыре меньших блока (кубоида), причем блок A представляет собой куб размера «y» :

Объемы этих ящиков:

• А = у ³
• В = х ² (х — у)
• С = ху(х — у)
• D = у ² (х — у)

Но вместе A, B, C и D составляют больший куб, объем которого x ³ :

x 3	=	у 3 + х 2 (х — у) + ху(х — у) + у 2 (х — у)
x 3 − у 3	=	x 2 (x — y) + xy(x — y) + y 2 (x — y)
x 3 − у 3	=	(х — у)(х 2 + ху + у 2 )

Эй! Мы пришли к той же формуле! Слава Богу.

Сумма двух кубов

Есть еще «Сумма двух кубов»

Меняя знак b в каждом случае, получаем:

(a+b)(a ² −ab+b ² ) = a ³ + b ³

(обратите внимание на минус перед «ab»)

 

Формула разности кубов – определение, объяснение и часто задаваемые вопросы

В алгебре куб числа n равен его третьей степени, т.е.е., результат трехкратного умножения «n». Куб числа выражается верхним индексом 3, например.

23 = 8 или (х + 1)³.

Или куб можно представить как число, умноженное на его квадрат:

n³ = n × n² = n × n × n.

Функция куба — это функция x ↦ x³ (часто обозначаемая как y = x³), которая отображает число в его куб. Это нечетная функция, так как

(- n)³ = — (n³).

Формула разности кубов

Формула разности кубов в алгебре используется для вычисления значения алгебраического выражения (a³ — b³). Проще говоря, он применяется для приравнивания разницы двух значений куба. Поэтому формула разности кубов в алгебре задается следующим образом:

a³ — b³ = (a — b) (a² + ab + b²)

Формула разности двух кубов

Выражение, которое встречается в разности двух кубов обычно очень трудно заметить. Разница между двумя кубами равна разнице их кубических корней, которая содержит квадраты кубических корней и противоположное произведение кубических корней.

Чтобы увидеть, к какому распределению приводит разность формул двух кубов, мы пытаемся увидеть, имеет ли распределение биномиальное значение,

(a — b),

, которое представляет собой разницу между двумя членами

(a² + ab + b²)

, у которого есть противоположность их произведению и квадратам двух терминов. Следовательно, формула разности двух кубов такова: —

a³ — b³  = (a — b) (a² + ab + b²)

Формула факторизации кубов

Мы всегда обсуждаем сумму двух кубов и разность двух кубов. бок о бок.Идея состоит в том, что они связаны с формированием. Единственное решение — запомнить закономерности, используемые в формулах.

Допустим —

Разложение на множители x³ — 8,

Это эквивалентно x³ — 2³. Поскольку знак — находится посередине, он превращается в разность кубов. Чтобы сделать факторинг, подставьте x и 2 в формулу разности кубов. Таким образом, получаем:

x³ — 8 = x³ — 2³

= (x — 2)(x² + 2x + 2²)

= (x — 2)(x² + 2x + 4)

Заключение 

Самыми популярными совершенными кубами являются те, у которых корни не десятичные, а целые числа.Чтобы факторизовать две разности совершенных кубов, помните, что разность двух совершенных кубов равна дисперсии их кубических корней, вычисленной как произведение их кубических корней и суммы их квадратов.

Сумма и разность кубов

Хороший способ представить факторинг как противоположность распределению. Например, если у вас было ( x + 3)( x – 3), и вы распределили, это будет выглядеть так:

( х + 3)( х – 3)

х ( х – 3) + 3 ( х – 3)

x ² – 3 x + 3 x – 9

x ² – 9

Итак, если вас попросили разложить x ² – 9, вас спросят, какие полиномы перемножаются, чтобы получить x ² – 9? Ответ, конечно же, ( x + 3)( x – 3).

Этот пример был выбран намеренно, потому что это пример разности квадратов . Первый и последний члены являются полными квадратами, и они вычитаются. Существует схема факторизации, которая довольно прямолинейна. Давайте формализуем этот шаблон, так как он свяжет что-то знакомое с тем, что здесь нового.

В нашем первом примере x ² – 9, a = 1 x и b = 3. Давайте посмотрим, что это значит.

Для этой разницы квадратов  Учет разницы квадратов дает (5 x ² – 7 y )(5 x ² + 7 y ). Давайте посмотрим, что в столбце.

В этом разделе мы научимся вычислять сумму и разность кубов.

Сумма кубов

Для нашего приложения бином может быть суммой кубов, если:

• Каждый член представляет собой число в кубе
• Каждый член положительный
• Операция в биноме есть сложение

Другими словами, сумма кубов представляет собой полином, где a и b положительны, в виде:

Прежде чем мы изучим шаблон для факторинга, давайте убедимся, что мы можем идентифицировать его части.Если части легко идентифицируются, факторинг представляет собой не что иное, как подстановку значений в формулу. Готовый?

В примере 1 a = x и b = 1.  

Вот как работает формула:

Давайте выполним умножение в правой части приведенного выше уравнения, чтобы убедиться, что это правильная факторизация.

Теперь попробуем пример.

Разность кубиков

Сумма кубов отличается от разности кубов только в операции. Сумма кубов складывает два числа в кубе. Разность кубов вычитает два числа в кубе. Вот несколько примеров.

Формула разности кубов выглядит следующим образом.

Для факторизации разницы кубов: 

1. Идентифицировать a и b
2. Подставить a и b в формулу

Давайте попробуем решить самую сложную задачу из приведенных выше:  64 – 27 x ⁶ .Вот A = 4, потому что 4 ³ = 64, а b = 3 x ² , потому что (3 x ² ) ³ = 27 x x ⁶ .