Формулы квадратов и кубов: Формулы сокращенного умножения 💣
Формулы сокращенного умножения 💣
Знакомство с сокращенным умножением начинается впервые в седьмом классе. Тема непростая: нужно выучить наизусть много формул. Но зато вы сможете быстрее решать задачки без ошибок. Проверим?
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.
Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2.
Докажем, что a2 — b2 = (a — b) * (a + b).
Поехали:
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a2 — b2 = a
- Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
- Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)
- Вынесем общие множители за скобки:
(a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)
- Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
- Результат доказательства: a2 — b2 = (a — b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.
a * (a — b) + b * (a — b) = (a — b) * (a + b)Остальные ФСУ можно доказать аналогичным методом.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+ 2 * an-1 * an
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
an − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10)2.
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с3 – 8.
Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Шпаргалки по математике родителей
Все формулы по математике под рукой
Формулы сокращенного умножения. Разность квадратов, квадрат суммы, разность кубов, бином Ньютона.
Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или квадрата суммы просто невозможно.
Итак, семь формул «школьной» алгебры, которые должны знать все:
| Название | Формула |
| Квадрат суммы | (A + B)2 = A2 + 2AB + B2 |
| Квадрат разности | (A — B)2 = A2 — 2AB + B2 |
| Разность квадратов | (A — B)(A + B) = A2 — B2 |
| Куб суммы | (A + B)3 = A3 + 3A2B + 3AB2+ B3 |
| Куб разности | (A — B)3 = A3 — 3A2B + 3AB2 — B3 |
| Сумма кубов | A3 + B3 = (A + B)(A2 — AB + B2) |
| Разность кубов | A3 — B3 = (A — B)(A2 + AB + B2) |
Версия для печати в формате png
Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.
Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).
Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.
Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?
Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона.
Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
(A + B)n = An + Cn1An-1B + Cn2An-2B2 + … + CnkAn-kBk + … + Bn.
Здесь Cnk = n!/(k! • (n-k)!).
Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!
А что можно сказать по поводу разности квадратов, разности кубов и т.
п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?
Да, можно. Вот эта формула:
An — Bn = (A — В)(An-1 + An-2B + An-3B2 + … + Bn-1).
Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:
An + Bn = (A + В)(An-1 — An-2B + An-3B2 — … + Bn-1).
Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.
Возможно, вам будут интересны другие материалы:
- Тест по математике для 7 класса
- Тест по математике для 8 класса
- Проценты. Задачи «на проценты». Часть I
- Четность. Задачи: от элементарных до «олимпиадных»
- ОГЭ по математике — пробный тест № 1
- Подготовка к ОГЭ-2021 по математике
Решение уравнений с квадратами и кубами — Понятие
Многие формулы для расчета объемов (формулы объема призмы, объема цилиндров, объема конусов и объема пирамид) требуют решения уравнений с квадратными корнями или кубическими корнями.
Чтобы решить эти уравнения, мы используем многие из тех же принципов, которые мы изучили при решении уравнений с квадратными корнями в алгебре, таких как выделение неизвестной переменной и упрощение.
квадратный корень кубический корень
В геометрии вы будете решать задачи с квадратными и кубическими корнями. Итак, мы рассмотрим здесь 3 быстрые задачи.
Первое уравнение с одной переменной r и r возводится в квадрат. Так что вам придется сделать пару шагов здесь. Первый шаг: вы собираетесь исключить то, что умножает r в квадрате, а это 4 пи. Итак, я собираюсь разделить обе стороны на 4 пи. Так что это должно выглядеть знакомо, это то, что вы делали в прошлом году по алгебре. 4 пи, деленное на 4 пи, равно 1. Все, что делится само на себя, равно 1. В правой части остается только r в квадрате. С левой стороны у нас есть пи, деленное на пи, что равно 1, и у нас есть 80, деленное на 4, что равно 20. Итак, чтобы решить это для r, мне нужно отменить возведение в квадрат, которое является возведением в квадрат квадратного корня.
Таким образом, квадратный корень из 20 я люблю упрощать, представляя его как два квадратных корня, умноженных вместе. И я могу сказать, что 20 — это 10, умноженное на 2, но я не знаю ни одного из этих квадратных корней как целого числа, но я могу записать его как квадратный корень из 4, умноженный на квадратный корень из 5. Квадратный корень из 4 равен 2. Итак, мы собираемся сказать, что r равно удвоенному квадратному корню из 5.
Давайте посмотрим еще два. Вот следующий. х в кубе равно 27. Что ж, чтобы отменить кубирование чего-либо, я возьму не квадратный, а кубический корень. Таким образом, кубический корень из x в кубе будет равен x. Я должен проделать ту же операцию с другой стороны, и кубический корень из 27 будет равен 3. Теперь, если мы вернемся к нашей первой задаче, мы заметим кое-что, что я мог бы сказать, что это было положительно или минус 2, умноженный на квадратный корень из 5. Поскольку мы занимаемся геометрией и почти всегда говорим о расстояниях, мы почти всегда будем извлекать положительный корень.
Потому что 2 умножить на квадратный корень из 5, умноженный на 20, и если я возьму отрицательное значение, умноженное само на себя, мы также получим 20. Так что тут может быть два ответа. Однако, если мы вернемся к этому кубическому корню, если я сказал, что х может быть -3, давайте просто кратко взглянем на это. -3 куб. -3 раза -3 равно 9. Итак, у меня будет 9 раз -3, что равно -27. Так что обратите внимание, что с кубическим корнем вы получите только один ответ. Отрицательный не будет одним из ваших ответов.
Последнее, что мы собираемся рассмотреть, это то, что вы будете решать, когда будете говорить об объеме сферы. Чтобы изолировать здесь r, сначала возьмем обратную величину четырех третей. Итак, я собираюсь умножить обе части на три четверти. Значит, три четверти умножить на 823. Я введу это в свой калькулятор. Три четверти умножить на 823 — это 617,25. Итак, что мы сделали, так это выделили число пи, умноженное на r в кубе. Я пока не умею извлекать кубический корень, поэтому я собираюсь разделить обе части на число Пи.
Итак, теперь я собираюсь получить еще одну десятичную дробь, я собираюсь разделить ее на число пи и получить 19.6.5 округлим. 196,5 равно r в кубе.
Теперь, когда у нас есть только r в кубе, мы можем взять кубический корень и выделить r. Итак, мы возьмем кубический корень из обеих сторон, и я скажу, что кубический корень из нашего куба равен r, и в моем калькуляторе я напечатаю, если ваш учитель еще не показал вам способ вы вводите это, вы собираетесь ввести 196,5, а затем сказать, чтобы он увеличил его до дроби. Потому что дробный корень или, простите, дробное выражение на самом деле берет корень. Итак, здесь вы собираетесь возвести его в третью степень. Так что в моем калькуляторе я собираюсь ввести 196,5, и мы поднимем его до, теперь не забудьте поставить эти скобки здесь, иначе ваш калькулятор просто поднимет его до первого, а затем разделит все на 3. Итак, я собираюсь сказать одну треть, и я получаю 5,8. Так что я собираюсь написать, что немного здесь. r = 5,8, и мы не знаем, каковы наши единицы измерения, поэтому просто оставим это как есть.
Итак, помните, что когда вы пытаетесь решить задачи с площадью поверхности, каждый раз, когда что-то возводится в квадрат или когда что-то возводится в куб, вы будете брать квадратный или кубический корень, чтобы изолировать свои переменные.
Специальный факторинг: суммы и разности кубов и совершенные квадраты
Дифф. of SquaresPerfect-Square Tri’sRecognizing Patterns
Purplemath
Две другие специальные формулы факторинга, которые вам нужно запомнить, очень похожи друг на друга; это формулы для факторизации сумм и разностей кубов. Вот две формулы:
Факторизация суммы кубов:
a 3 + b 3 = ( a + b )( a 2 − ab + b 2 )
Factoring a Difference of Cubes:
a 3 − b 3 = ( a − b )( a 2 + ab + b 2 ) Вы узнаете больше об этих формулах
90 А пока просто запомните их.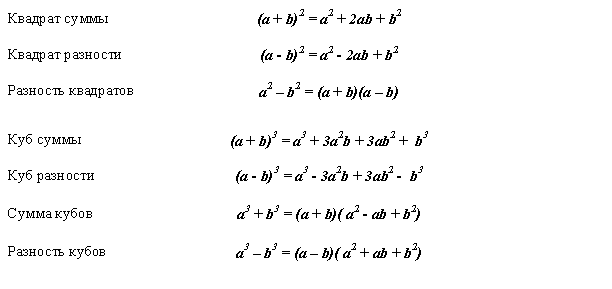
Содержимое продолжается ниже
MathHelp.com
Чтобы облегчить запоминание, сначала обратите внимание, что члены в каждой из двух формул факторизации абсолютно одинаковы. Затем обратите внимание, что каждая формула имеет только один знак «минус». Различие между двумя формулами заключается в расположении этого одного знака «минус»:
Для разности кубов знак «минус» идет в линейном множителе, a − b ; для суммы кубов знак «минус» стоит перед квадратичным множителем, а 2 − аб + б 2 .
Некоторые люди используют мнемонику « SOAP «, чтобы отслеживать знаки; буквы обозначают линейный множитель, имеющий «тот же» знак, что и знак в середине исходного выражения, затем квадратичный множитель, начинающийся со знаком «противоположный» тому, что был в исходном выражении, и, наконец, второй знак внутри исходного выражения. квадратичный множитель «всегда положителен».
и 3 ± B 3 = ( A [ То же самое ] B ) ( A 2 [ Выступая 40004 AB [ 40004444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444. b 2 )
Какой бы метод ни помог вам сохранить эти формулы в чистоте, используйте его, потому что вы не должны предполагать, что вам дадут эти формулы на тесте. Вы должны ожидать, что должны знать их.
Примечание. Квадратичная часть каждой формулы куба не размножает , поэтому не тратьте время на его разложение. Да, A 2 — 2 AB + B 2 и A 2 + 2 AB + B 2 Фактор, но так это было из -за того, что 2 -ы условия. Квадратичные члены этих формул суммы и разности кубов не имеют , что «2», и, следовательно, не может быть множителем .
Когда вам дали пару кубиков для разложения, тщательно применяйте соответствующее правило. Под «осторожно» я подразумеваю «использование круглых скобок, чтобы отслеживать все, особенно отрицательные знаки». Вот некоторые типичные проблемы:
Коэффициент
x 3 − 8
Это эквивалентно x 3 − 2 3 . Со знаком «минус» посередине это разность кубов. Для факторинга я подставлю x и 2 в формулу разности кубов. Таким образом, я получаю:
х 3 — 8 = х 3 — 2 3
= ( x — 2) ( x 2 + 2 x + 2 2 )
= ( x — 2) ( x 2930330 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 .
х + 4)
Коэффициент 27
x 3 + 1
Первый член содержит куб 3 и куб x . Но как насчет второго срока?
Прежде чем запаниковать из-за отсутствия видимого куба, я вспомнил, что 1 можно рассматривать как возведённую в любую степень, которую я захочу, поскольку 1 в любой степени остаётся всего лишь 1. В этом случае мне нужна степень 3, так как это даст мне сумму кубов. Это означает, что выражение, которое они мне дали, может быть выражено как:
(3 x ) 3 + 1 3
Таким образом, чтобы учесть, я подставлю 3 x и 1 в формула суммы кубов. Это дает мне:
27 x 3 + 1 = (3 x ) 3 + 1 3
= (3 x + 1) (3 x ) 2 — (3) х )(1) + 1 2 )
= (3 х + 1)(9 х 2 − 3 х + 1) 6 17
5
Коэффициент
x 3 у 6 − 64 Во-первых, я отмечаю, что они дали мне бином (многочлен с двумя членами) и что степень x в первом члене равна 3, поэтому, даже если бы я не работал в «суммах и различия кубов» моего учебника, я бы обратил внимание, что, возможно, мне следует думать в терминах этих формул.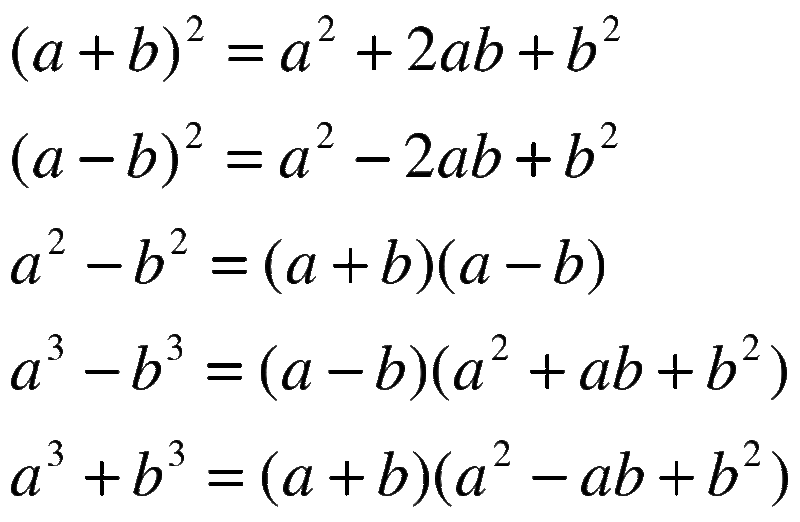
Глядя на другую переменную, я замечаю, что степень числа 6 является кубом степени числа 2, поэтому другая переменная в первом члене также может быть выражена в терминах куба; а именно, как куб квадрата и .
Второе слагаемое равно 64, которое, как я помню, является кубом числа 4. (Если бы я не помнил или не был уверен, я бы схватил свой калькулятор и попытался вычислить что-то в кубе, пока не получил правильное значение, иначе я бы взял кубический корень из 64.)
Итак, теперь я знаю, что с «минусом» посередине это разница в два куба; а именно:
( xy 2 ) 3 − 4 3
Подставляя в соответствующую формулу, я получаю:
x 3 y 6 − 64 = ( xy 2 ) 3 − 4 3
= ( xy 2 − 4)(( xy 2 ) 2 + ( XY 2 ) (4) + 4 2 )
= ( XY 2 — 4) ( x 2 77778 7778 7778 778 778 7 7 7 7 7 7 7 7 7 7 7 7 7 7.
7 7 7 — 4). 4 + 4 xy 2 + 16)
Эм… Я знаю, что 16 равно не куб чего угодно; на самом деле он равен 2 4 . Как дела?
Дело в том, что они ожидают, что я использую то, что я узнал о простом факторинге, чтобы сначала преобразовать это в разность кубов. Да, 16 = 2 4 , но 8 = 2 3 , куб. Я могу получить 8 из 16, разделив на 2. Что произойдет, если я разделю 250 на 2? Я получаю 125, что является кубом 5. То, что они мне дали, можно переформулировать как:
2(2 3 x 3 -5 3 )
Я могу применить формулу разницы в кубиках к тому, что находится внутри скобков:
2 3 x 3 -5 3 = (2 x ) 9003 3 — (5) 3
= (2 х — 5)((2 х ) 2 + (2 х )(5) + (5) 0 0 5 909 39 0 2 = (2 x − 5)(4 x 2 + 10 x + 25)
Собрав все вместе, я получаю окончательную факторизованную форму:
2(2 x − 5)(4 x 2 + 10 x + 25)
Коэффициент −
x 3 − 125.
Моей первой реакцией могло бы быть прямое применение формулы разности кубов, поскольку 125 = 5 3 . А что насчет того знака «минус» впереди?
Поскольку ни одна из формул факторинга, которые они мне дали, не включает «минус» впереди, может быть, я могу вынести «минус» из множителя…?
— х 3 — 125 = -1 х 3 — 125
= -1( х 3 0065 9 Ага) Теперь в скобках сумма кубов, которую я могу разложить на множители. У меня есть сумма куба x и куба 5, поэтому:
x 3 + 5 3 = ( x + 5)(( x 9) 2 — ( х )(5) + (5) 2 ) = ( х + 5)( х 2 − 5 х + 25) Собрав все вместе, я получаю: −1( х + − 5)( − 5)( − 5)( х 9029 0) 5 x + 25) Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в факторизации суммы кубов.