Формулы крамера для решения систем: определение, теорема и примеры решения задач
Теорема Крамера
Системы линейных алгебраических уравнений При решении систем линейных уравнений обсуждаются 3 вопроса: а) существует ли решение системы уравнений, б) сколько разных решений имеет система уравнений, в) алгоритм решения. Ниже излагаются основные результаты в этой области математики, позволяющие исчерпывающим образом ответить на эти вопросы.Теорема Крамера
Система двух уравнений, два неизвестных
Рассмотрим систему линейных алгебраических уравнений \[ a_{11}x_1+a_{12}x_2=b_1, \quad \quad(17) \] \[ a_{21}x_1+a_{22}x_2=b_2, \quad \quad(18) \]числа \(a_{ik}, b_i\), \(i,k=1,2\) считаются заданными, требуется найти неизвестные \(x_1,x_2\) . Эту систему можно решить исключением неизвестных. Например, умножим первое уравнение на \(a_{22}\) и вычтем второе, умноженное на \(a_{12}\), получим:
\[ (a_{11}a_{22}-a_{21}a_{12})x_1=b_1a_{22}-b_2a_{12}, \]
так что если \(a_{11}a_{22}-a_{21}a_{12} \neq 0, \)
\[
x_1=\frac{b_1a_{22}-b_2a_{12}}{a_{11}a_{22}-a_{21}a_{12}}.
Если второе уравнение умножить на \(a_{11}\) и вычесть из него первое уравнение, умноженное на \(a_{21}\), получим: \[ x_2=\frac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{21}a_{12}}. \quad \quad(20) \]
Введем следующие обозначения. Матрицей коэффициентов системы уравнений (17)-(18) назовем матрицу \[ A=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right), \] столбец правых частей системы \[ B=\left (\begin{array}{c} b_1 \\b_2 \end{array} \right). \]
Тогда формулы (19), (20) можно переписать следующим образом:
\[
x_1=\frac{detC_1}{detA}, x_2=\frac{detC_2}{detA}, \quad \quad(21)
\]
где матрица \(C_k\), \(k=1,2\), получается из матрицы \(A\) заменой ее \(k\)-того столбца на столбец \(B\). Формулы (21) называются формулами Крамера для системы из 2 уравнений с двумя неизвестными. Они описывают единственное решение системы уравнений в данном случае.
Они описывают единственное решение системы уравнений в данном случае.
Система \(n\) уравнений, \(n\) неизвестных
Рассмотрим систему \(n\) линейных алгебраических уравнений с \(n\) неизвестными, \[ a_{11}x_1+a_{12}x_2+ ….+a_{1n}x_n=b_1, \quad \quad(22) \] \[ a_{21}x_1+a_{22}x_2+…+a_{1n}x_n=b_2, \quad \quad(23) \] \[ ………………………………………………….. \] \[ a_{n1}x_1+a_{n2}x_2+…+a_{nn}x_n=b_n. \quad \quad(24) \]
Матрицей коэффициентов системы уравнений назовем матрицу
\[
A=\left(
\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} &\ldots & a_{1n} \\
a_{21} & a_{22} & a_{23} &\ldots & a_{2n} \\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{n1} &a_{n2} & a_{n3} & \ldots & a_{nn}
\end{array}
\right) ,
\]
образуем столбец правых частей системы
\[
B=\left (\begin{array}{cccc} b_1 & b_2 & \ldots &b_n \end{array} \right)^T.
В целом решение систем методом Крамера и методом обратной матрицы требует выполнения 2 условий: матрица коэффициентов системы должна быть квадратной ( т.е. число уравнений должно совпадать с числом неизвестных) и эта матрица должна быть невырожденной. К тому же практическая реализация этих методов связана с весьма громоздкими вычислениями, так что они имеют лишь теоретическое значение. На практике используют существенно более простой в реализации метод Гаусса, который к тому же позволяет решать и более общие системы уравнений. Этот метод описан ниже.
Решить системы методом Крамера и методом обратной матрицы.
а) \[ x_1+x_2+2x_3=-1, \] \[ 2x_1-x_2+2x_3=-4, \] \[ 4x_1+x_2+4x_3=-2. \]
б) \[ 3x_1+2x_2+x_3=5, \] \[ 2x_1+3x_2+x_3=1, \] \[ 2x_1+x_2+3x_3=11. \]
в)
\[
2x_1+x_2-x_3=2,
\]
\[
3x_1+x_2-2x_3=3,
\]
\[
x_1+x_3=3. \]
\]
Условия применения метода крамера. Линейные уравнения
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
Навигация по странице.
Метод Крамера — вывод формул.
Пусть нам требуется решить систему линейных уравнений вида
Где x 1 , x 2 , …, x n – неизвестные переменные, a i j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b 1 , b 2 , …, b n — свободные члены. Решением СЛАУ называется такой набор значений x 1 , x 2 , …, x n при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B
, где — основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, — матрица – столбец свободных членов, а — матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x 1 , x 2 , …, x n
, матрица становится решением системы уравнений и равенство A ⋅ X = B
обращается в тождество .
После нахождения неизвестных переменных x 1 , x 2 , …, x n
, матрица становится решением системы уравнений и равенство A ⋅ X = B
обращается в тождество .
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).
Метод Крамера основывается на двух свойствах определителя матрицы:
Итак, приступим к нахождению неизвестной переменной x 1
. Для этого умножим обе части первого уравнения системы на А 1 1
, обе части второго уравнения – на А 2 1
, и так далее, обе части n-ого
уравнения – на А n 1
(то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А
):
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x 1 , x 2 , …, x n
, и приравняем эту сумму к сумме всех правых частей уравнений:
Если обратиться к озвученным ранее свойствам определителя, то имеем
и предыдущее равенство примет вид
откуда
Аналогично находим x 2
. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А
:
Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А
:
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x 1 , x 2 , …, x n и применяем свойства определителя:
Откуда
.
Аналогично находятся оставшиеся неизвестные переменные.
Если обозначить
То получаем формулы для нахождения неизвестных переменных по методу Крамера .
Замечание.
Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера .
Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .
Решение.
Основная матрица системы имеет вид . Вычислим ее определитель по формуле :
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .
Вычисляем эти определители:
Находим неизвестные переменные x 1
и x 2
по формулам :
Выполним проверку. Подставим полученные значения x 1
и x 2
в исходную систему уравнений:
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера .
Решение.
Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле
Имеем
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :
Таким образом,
Ответ:
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x 1 , x 2 , …, x n . Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x , y и z вместо x 1 , x 2 и x 3 ). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:
Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:
Осталось найти неизвестные переменные по формулам :
Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите раздел ):
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3
.
Пример.
Решите методом Крамера систему линейных уравнений , где a и b – некоторые действительные числа.
Решение.
Ответ:
Пример.
Найдите решение системы уравнений методом Крамера, — некоторое действительное число.
Решение.
Вычислим определитель основной матрицы системы: . выражения есть интервал , поэтому при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем и :
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ — определитель матрицы системы ,
Δ i — определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.

- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т. е. имеет вид
е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A — 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A — 1 , мы получим решение системы:
14) слева на A — 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).
18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
…………………………………………………………………. . . | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
…………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = — 3 + 2t
x 2 = — 1 — 3t
x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).
Метод Крамера . Применение для систем линейных уравнений
Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами — числа
Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй — при котором из неизвестным он находится.
Если определитель матрицы не равен нулю
то система линейных алгебраических уравнений имеет единственное решение.
Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.
Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной
Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой.
Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.
Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Эквивалентные преобразования СЛАУ
1) перестановка местами уравнений;
2) умножение (или деление) уравнений на отличное от нуля число;
3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.
Решение СЛАУ можно найти разными способами.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:
— определители, образованные с заменой -го столбца, столбцом из свободных членов.
Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
—————————————————————
Задача 1.
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера
Решение.
Найдем определитель матрицы коэффициентов при неизвестных
Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:
По формулам Крамера находим неизвестные
Итак единственное решение системы.
Задача 2.
Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.
Решение.
Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.
Найдем составляющие определителя:
Подставим найденные значения в определитель
Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:
Вычислим определители по формулам Крамера:
Разложим каждый из определителей по столбцу в котором есть больше нулей.
По формулам Крамера находим
Решение системы
Данный пример можно решить математическим калькулятором YukhymCALC . Фрагмент программы и результаты вычислений наведены ниже.
——————————
МЕТОД К Р А М Е Р А
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Посмотреть материалы:
{jcomments on}
Решение методом Крамера системы линейных уравнений 3-4-го порядка
Решать системы линейных алгебраических уравнений второго, третьего, изредка четвертого порядка методом Крамера достаточно часто придется студентам младших курсов учебы при изучении основ линейной алгебры. Для большинства студентов стационарной формы учебы такие задания не являются сложными, однако кто выбрал заочную учебу или дистанционную, или пропустил по определенным причинам практические занятия, вычисления выглядят непонятными и тяжелыми. Чтобы исправить такую ситуацию в данной статье будут приведены наиболее распространены примеры данной темы и схема их решения. Если Вы хорошо поймете принцип их решения, то на практике у Вас не будет трудностей с подобными заданиями.
Для большинства студентов стационарной формы учебы такие задания не являются сложными, однако кто выбрал заочную учебу или дистанционную, или пропустил по определенным причинам практические занятия, вычисления выглядят непонятными и тяжелыми. Чтобы исправить такую ситуацию в данной статье будут приведены наиболее распространены примеры данной темы и схема их решения. Если Вы хорошо поймете принцип их решения, то на практике у Вас не будет трудностей с подобными заданиями.
Для начала выберем задание из сборника задач Дубовика В.П., Юрика І.І. «Высшая математика».
————————————
Примеры
Решить систему линейных алгебраических уравнений.
1) (1. 153)
2) (4. 165)
3) (4. 174)
Решение.
1) В случае двух уравнений решение можно получить более простым способом. Выражаемый из второго уравнения
и подставим в первое
Раскрыв скобки, сгруппируем подобные слагаемые
Отсюда получим решение
Переменнуюнайдем подстановкой в любое из уравнений
Таким образом решением системы двух уравнений будут следующие значения
Поскольку цель статьи научить студентов решать по методике Крамера то решим данный пример и етим методом.
Для этого выпишем систему линейных уравнений в виде
Найдем детерминант основной части
Для вычисления вспомогательных определителей ставим столбец свободных членов на место первой строки для и на место второй для . В результате получим
Подставим найденные значения в формулы Крамера
и найдем неизвестные
Из рассмотренного примера видим что вычисление при двух уравнениях с двумя неизвестными достаточно простые.
2) Запишем систему трех алгебраических уравнений в удобном для решения виде
Найдем детерминант системы по правилу треугольников
Для вычисления дополнительных определителей подставляем столбец свободных членов на место первого, второго и третьего столбцов. В результате получим
Вычисляем неизвестные за формулами Крамера
Для данного примера нахождения решения также не слишком сложно, хотя по сравнению с системой двух уравнений вычислений заметно прибавилось.
3) Записываем систему уравнений четвертого порядка в виде
Находим главный определитель системы. При вычислении детерминантов четвертого порядка их необходимо раскладывать за строками или столбцами у каторых больше всего нулей. Поскольку в данном случае нулей главный определитель не имеет то разложим его за первой строкой
и найдем соответствующие детермиінанты третьего порядка
Подставим найденные значения в определитель
По такой же схеме вычисляем вспомогательные определители, напомню лишь, что они образуются заменой столбца в главном определителе на столбец свободных членов (обозначен черным цветом). Я не буду приводить детальных излаганий, однако Вы можете проверить, что детерминанты примут значение
Подставив в формулы Крамера, после вычислений будем иметь
На этом пример решено.
Системы четырех линейных уравнений наиболее трудоемкие в вычислениях, для вычисления их решения нужно решать 5*4 определители третьего порядка, в то время как системы трех уравнений лиш 4. Будьте внимательные при вычислениях ведь самая малая ошибка может иметь следствием неверный результат.
Будьте внимательные при вычислениях ведь самая малая ошибка может иметь следствием неверный результат.
———————————————-
Посмотреть материалы:
Метод крамера для произвольных систем линейных уравнений. Метод крамера решения систем линейных уравнений
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :
Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:
относительно переменных х и у .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
—
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя.
 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. - При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
- Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $\Delta\neq 0$.
- Для каждой переменной $x_i$($i=\overline{1,n}$) необходимо составить определитель $\Delta_{x_i}$, полученный из определителя $\Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
- Найти значения неизвестных по формуле $x_i=\frac{\Delta_{x_{i}}}{\Delta}$ ($i=\overline{1,n}$).
Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.
Пример №1
Решить СЛАУ $\left\{\begin{aligned}
& 3x_1+2x_2=-11;\\
& -x_1+5x_2=15.
\end{aligned}\right. $ методом Крамера.
$ методом Крамера.
Решение
Матрица системы такова: $ A=\left( \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array} \right)$. Определитель этой матрицы:
$$\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|=3\cdot 5-2\cdot(-1)=17.$$Как вычисляется определитель второго порядка можете глянуть здесь.
Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $\Delta_{x_1}$ и $\Delta_{x_2}$. Определитель $\Delta_{x_1}$ получаем из определителя $\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $\left(\begin{array} {c} -11\\ 15\end{array}\right)$:
$$ \Delta_{x_1}=\left|\begin{array}{cc}-11&2\\15&5\end{array}\right|=-55-30=-85. $$Аналогично, заменяя второй столбец в $\Delta=\left|\begin{array}{cc}3&2\\-1&5\end{array}\right|$ столбцом свободных членов, получим:
$$ \Delta_{x_2}=\left|\begin{array} {cc} 3 & -11\\ -1 & 15\end{array}\right|=45-11=34. $$
$$
Теперь можно найти значения неизвестных $x_1$ и $x_2$.
$$x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{-85}{17}=-5;\;x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{34}{17}=2.$$В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:
$$\left\{\begin{aligned} & 3x_1+2x_2=3\cdot(-5)+2\cdot{2}=-11;\\ & -x_1+5x_2=-(-5)+5\cdot{2}=15. \end{aligned}\right.$$Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.
Ответ: $x_1=-5$, $x_2=2$.
Пример №2
Решить СЛАУ $ \left\{\begin{aligned} & 2x_1+x_2-x_3=3;\\ & 3x_1+2x_2+2x_3=-7;\\ & x_1+x_3=-2. \end{aligned} \right.$, используя метод Крамера.
Решение
Определитель системы:
$$\Delta=\left| \begin{array} {ccc} 2 & 1 & -1\\ 3 & 2 & 2 \\ 1 & 0 & 1 \end{array}\right|=4+2+2-3=5. $$
$$
Как вычисляется определитель третьего порядка можете глянуть здесь.
Заменяя первый столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_1}$:
$$ \Delta_{x_1}=\left| \begin{array} {ccc} 3 & 1 & -1\\ -7 & 2 & 2 \\ -2 & 0 & 1 \end{array}\right|=6-4-4+7=5. $$Заменяя второй столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_2}$:
$$ \Delta_{x_2}=\left| \begin{array} {ccc} 2 & 3 & -1\\ 3 & -7 & 2 \\ 1 & -2 & 1 \end{array}\right|=-14+6+6-7-9+8=-10. $$Заменяя третий столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_3}$:
$$ \Delta_{x_3}=\left| \begin{array} {ccc} 2 & 1 & 3\\ 3 & 2 & -7 \\ 1 & 0 & -2 \end{array}\right|=-8-7-6+6=-15. $$Учитывая все вышеизложенное, имеем:
$$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{5}{5}=1;\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-10}{5}=-2; \; x_3=\frac{\Delta_{x_3}}{\Delta}=\frac{-15}{5}=-3. $$
$$Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:
$$\left\{\begin{aligned} & 2x_1+x_2-x_3=2\cdot{1}+(-2)-(-3)=3;\\ & 3x_1+2x_2+2x_3=3\cdot{1}+2\cdot(-2)+2\cdot(-3)=-7;\\ & x_1+x_3=1+(-3)=-2. \end{aligned} \right.$$Проверка пройдена, решение системы уравнений методом Крамера найдено верно.
Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & 2x_1+3x_2-x_3=15;\\ & -9x_1-2x_2+5x_3=-7. \end{aligned}\right.$ используя метод Крамера.
Решение
Матрица системы $ \left( \begin{array} {ccc} 2 & 3 & -1\\ -9 & -2 & 5 \end{array} \right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:
$$ \left \{ \begin{aligned} & 2x_1+3x_2=x_3+15;\\ & -9x_1-2x_2=-5x_3-7. \end{aligned} \right.
$$
\end{aligned} \right.
$$
Теперь матрица системы $ \left( \begin{array} {cc} 2 & 3 \\ -9 & -2 \end{array} \right) $ стала квадратной, и определитель её $\Delta=\left| \begin{array} {cc} 2 & 3\\ -9 & -2 \end{array}\right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:
$$ \begin{aligned} & \Delta_{x_1} =\left| \begin{array} {cc} x_3+15 & 3\\ -5x_3-7 & -2 \end{array}\right| =-2x_3-30-\left(-15x_3-21\right) =13x_3-9;\\ \\ & \Delta_{x_2} =\left| \begin{array} {cc} 2 & x_3+15\\ -9 & -5x_3-7 \end{array}\right| =-10x_3-14-\left(-9x_3-135\right) =-x_3+121. \end{aligned} $$ $$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{13x_3-9}{23};\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-x_3+121}{23}. $$
Ответ можно записать в таком виде: $\left\{\begin{aligned}
& x_1=\frac{13x_3-9}{23};\\
& x_2=\frac{-x_3+121}{23};\\
& x_3\in R. \end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
\end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
Примечание
В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ
$\left\{\begin{aligned}
& 2x_1-5x_2+10x_3=14;\\
& -4x_1+10x_2-7x_3=5.
\end{aligned}\right.$. Если перенести в правые части уравнений $x_3$, получим: $
\left\{\begin{aligned}
&2x_1-5x_2=-10x_3+14;\\
&-4x_1+10x_2=7x_3+5.
\end{aligned}\right.$. Определитель данной системы $\Delta=\left| \begin{array} {cc} 2 & -5\\ -4 & 10 \end{array}\right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $
\left\{\begin{aligned}
&2x_1+10x_3=5x_2+14;\\
&-4x_1-7x_3=-10x_2+5. \end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.
\end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.
Пример №4
Решить СЛАУ
$$\left\{\begin{aligned} &x_1-5x_2-x_3-2x_4+3x_5=0;\\ &2x_1-6x_2+x_3-4x_4-2x_5=0; \\ &-x_1+4x_2+5x_3-3x_4=0. \end{aligned}\right.$$методом Крамера.
Решение
Матрица системы $\left(\begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \\ 2 & -6 & 1 & -4 & -2 \\ -1 & 4 & 5 & -3 & 0 \end{array}\right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:
$$ \left\{\begin{aligned} & x_1-5x_2-x_3=2x_4-3x_5;\\ & 2x_1-6x_2+x_3=4x_4+2x_5; \\ & -x_1+4x_2+5x_3=3x_4. \end{aligned}\right. $$
$$
\begin{aligned}
& \Delta
=\left| \begin{array} {ccc} 1 & -5 & -1\\ 2 & -6 & 1\\-1 & 4 & 5 \end{array}\right|
=19;\\
\\
& \Delta_{x_1}
=\left| \begin{array} {ccc} 2x_4-3x_5 & -5 & -1\\ 4x_4+2x_5 & -6 & 1\\3x_4 & 4 & 5 \end{array}\right|
=-17x_4+144x_5;\\
\\
& \Delta_{x_2}
=\left| \begin{array} {ccc} 1 & 2x_4-3x_5 & -1\\ 2 & 4x_4+2x_5 & 1\\-1 & 3x_4 & 5 \end{array}\right|
=-15x_4+41x_5;\\
\\
& \Delta_{x_3}
=\left| \begin{array} {ccc} 1 & -5 & 2x_4-3x_5\\ 2 & -6 & 4x_4+2x_5\\-1 & 4 & 3x_4 \end{array}\right|
=20x_4-4x_5.
\end{aligned}
$$
$$
$$
\begin{aligned}
& \Delta
=\left| \begin{array} {ccc} 1 & -5 & -1\\ 2 & -6 & 1\\-1 & 4 & 5 \end{array}\right|
=19;\\
\\
& \Delta_{x_1}
=\left| \begin{array} {ccc} 2x_4-3x_5 & -5 & -1\\ 4x_4+2x_5 & -6 & 1\\3x_4 & 4 & 5 \end{array}\right|
=-17x_4+144x_5;\\
\\
& \Delta_{x_2}
=\left| \begin{array} {ccc} 1 & 2x_4-3x_5 & -1\\ 2 & 4x_4+2x_5 & 1\\-1 & 3x_4 & 5 \end{array}\right|
=-15x_4+41x_5;\\
\\
& \Delta_{x_3}
=\left| \begin{array} {ccc} 1 & -5 & 2x_4-3x_5\\ 2 & -6 & 4x_4+2x_5\\-1 & 4 & 3x_4 \end{array}\right|
=20x_4-4x_5.
\end{aligned}
$$
Ответ таков: $\left\{\begin{aligned}
& x_1=\frac{-17x_4+144x_5}{19};\\
& x_2=\frac{-15x_4+41x_5}{19};\\
& x_3=\frac{20x_4-4x_5}{19}; \\
& x_4\in R; \; x_5\in R.
\end{aligned}\right. $ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.
Метод Крамера для решения системы двух линейных уравнений: алгоритм следования, примеры.
Квадратная матрица 2-го порядка и её определитель
Квадратной матрицей 2-го порядка A называется таблица из 4-х чисел вида: $$ A = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} $$
В квадратной матрице 2-го порядка две строки и два столбца.
Например: $ |A| = \begin{vmatrix} 1 & -4 \\ 2,5 & 3 \\ \end{vmatrix} $
Определителем матрицы 2-го порядка называется число:
$$ A = \begin{vmatrix} a & b \\ c & d \\ \end{vmatrix} = ad-bc $$
Например: $\begin{vmatrix} 1 & -4 \\ 2,5 & 3 \\ \end{vmatrix} = 1\cdot3-2,5\cdot(-4) = 3+10 = 13$
Метод Крамера для решения системы 2-х линейных уравнений
Дана система 2-х линейных уравнений:
$$ {\left\{ \begin{array}{c} a_1 x+b_1 y=c_1 \\ a_2 x+b_2 y=c_2 \end{array} \right.} $$
Определим главный определитель системы:
$$ \Delta = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \end{vmatrix} = a_1 b_2-a_2 b_1 $$
и вспомогательные определители:
$$ \Delta_x = \begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \\ \end{vmatrix} = c_1 b_2-c_2 b_1, \Delta_y = \begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \\ \end{vmatrix} = a_1 c_2-a_2 c_1 $$
Тогда решение системы:
$$ {\left\{ \begin{array}{c} x = \frac{\Delta_x}{\Delta} \\ y = \frac{\Delta_y}{\Delta} \end{array} \right. } $$
} $$
Соотношение коэффициентов уравнений, значений определителей, расположения прямых и количества решений:
$ \frac{a_1}{a_2} \neq \frac{b_1}{b_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $
$ \Delta \neq 0 $
$ \Delta = 0, \Delta _x \neq 0, \Delta_y \neq 0 $
$ \Delta = \Delta_x = \Delta_y = 0$
Прямые пересекаются
Прямые параллельны
Прямые совпадают
Бесконечное множество решений
Внимание!
Метод Крамера используется в линейной алгебре для решения систем линейных уравнений произвольного порядка $N \ge 2$.
Главный определитель, вспомогательные определители и решения таких систем находятся аналогично.
Поэтому для метода Крамера несложно составить алгоритм и запрограммировать для решения прикладных задач.
Метод Крамера для N=3 (три уравнения, три переменных) рассмотрен в §49 данного справочника.
Примеры
Пример 1. Решите систему уравнений методом Крамера:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 5 & -4 \\ 2 & -3 \\ \end{vmatrix} = 5\cdot(-3)-2\cdot(-4) = -15+8 =-7 $$
$$ \Delta_x = \begin{vmatrix} 3 & -4 \\ 4 & -3 \\ \end{vmatrix} = 3\cdot(-3)-4\cdot(-4) = -9+16 = 7 $$
$$ \Delta_y = \begin{vmatrix} 5 & 3 \\ 2 & 4 \\ \end{vmatrix} = 5\cdot4-2\cdot3 = 20-6 = 14 $$
$$ x = \frac{\Delta_x}{\Delta} = \frac{7}{-7} = -1, y = \frac{\Delta_y}{\Delta} = \frac{14}{-7} = -2 $$
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 4 & -3 \\ 3 & -4 \\ \end{vmatrix} = 4\cdot(-4)-3\cdot(-3) = -16+9 = -7 $$
$$ \Delta_x = \begin{vmatrix} 7 & -3 \\ 0 & -4 \\ \end{vmatrix} = 7\cdot(-4)-0\cdot(-3) = -28 $$
$$ \Delta_y = \begin{vmatrix} 4 & 7 \\ 3 & 0 \\ \end{vmatrix} = 4\cdot0-3\cdot7 = -21 $$
$$ x = \frac{\Delta_x}{\Delta} = \frac{-28}{-7} = 4, y = \frac{\Delta_y}{\Delta} = \frac{-21}{-7} = 3 $$
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right. } $
} $
$$ \Delta = \begin{vmatrix} 5 & -4 \\ 2 & 3 \\ \end{vmatrix} = 5\cdot3-2\cdot(-4) = 15+8 = 23 $$
$$ \Delta_a = \begin{vmatrix} 9 & -4 \\ -1 & -3 \\ \end{vmatrix} = 9\cdot3-(-1)\cdot(-4) = 27-4 = 23 $$
$$ \Delta_b = \begin{vmatrix} 5 & 9 \\ 2 & -1 \\ \end{vmatrix} = 5\cdot(-1)-2\cdot9 = -5-18 = -23 $$
$$ a = \frac{\Delta_a}{\Delta} = \frac{23}{23} = 1, b = \frac{\Delta_b}{\Delta} = \frac{-23}{23} = -1 $$
Ответ: (1;-1)
$ r) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 7 & 4 \\ 3 & 2 \\ \end{vmatrix} = 7\cdot2-3\cdot4 = 14-12 = 2 $$
$$ \Delta_a = \begin{vmatrix} 5 & 4 \\ 1 & 2 \\ \end{vmatrix} = 5\cdot2-1\cdot4 = 10-4 = 6 $$
$$ \Delta_b = \begin{vmatrix} 7 & 5 \\ 3 & 1 \\ \end{vmatrix} = 7\cdot1-3\cdot5 = 7-15 = -8 $$
$$ a = \frac{\Delta_a}{\Delta} = \frac{6}{2} = 3, b = \frac{\Delta_b}{\Delta} = \frac{-8}{2} = -4 $$
Ответ: (3;-4)
Пример 2*. 2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
Ответ: 1) $a \neq \pm5$; 2) a = 5; 3) a = -5
9.8: Решение систем с помощью правила Крамера
Цели обучения
- Оценить 2 × 2 определителя.
- Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
- Оценить 3 × 3 определителя.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
- Знать свойства определителей.
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика.Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2 × 2
Определитель — это действительное число, которое может быть очень полезным в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
НАЙТИ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2 × 2
Определитель матрицы 2 × 2 при заданном
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
определяется как
Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, в том числе \(\det(A)\) и замена скобок в матрице прямыми, \(| A |\).
Пример \(\PageIndex{1}\): нахождение определителя матрицы \(2 × 2\)
Найдите определитель данной матрицы.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Раствор
\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ & = 27 \конец{выравнивание*}\]
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в году. Курб алгебры . Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Мы исключаем одну переменную, используя операции со строками, и находим другую.Скажем, что мы хотим найти \(x\). Если уравнение \ref{eq2} умножается на коэффициент, противоположный коэффициенту \(y\) в уравнении \ref{eq1}, уравнение \ref{eq1} умножается на коэффициент \(y\) в уравнении \ref {eq2}, и мы добавим два уравнения, переменная \(y\) будет исключена.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Умножить}R_1 \text{ на }b_2 \\ -&\underline{b_1a_2x-b_1b_2y=-b_1c_2} & \text{Умножить}R_2 \text { по }-b_1 \\ & b_2a_1x-b_1a_2x=b_2c_1-b_1c_2 \end{align*}\]
Теперь найдите \(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac {\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Аналогично, чтобы найти \(y\), мы исключим \(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply}R_1 \text{ на }a_2 \\ -& \underline{a_1a_2x-a_1b_2y=-a_1c_2} & \text{Multiply}R_2 \ text{ by }-a_1 \\ & a_2b_1y-a_1b_2y =a_2c_1-a_1c_2 \end{align*}\]
Решение для \(y\) дает
\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac {a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align* }\]
Обратите внимание, что знаменатель для \(x\) и \(y\) является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения \(x\) и \(y\), но правило Крамера также вводит новое обозначение:
- \(D\): определитель матрицы коэффициентов
- \(D_x\): определитель числителя в решении \(x\)
\[х=\dfrac{D_x}{D}\]
- \(D_y\): определитель числителя в решении \(y\)
\[y=\dfrac{D_y}{D}\]
Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Тогда мы можем выразить \(x\) и \(y\) как частное двух определителей.
Тогда мы можем выразить \(x\) и \(y\) как частное двух определителей.
ПРАВИЛО КРАМЕРА ДЛЯ \(2×2\) СИСТЕМ
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
Решение с использованием правила Крамера дано как
\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{ бматрица}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix }}\; , D\neq 0 \end{align}\]
Если мы находим \(x\), столбец \(x\) заменяется столбцом констант.Если мы ищем \(y\), столбец \(y\) заменяется постоянным столбцом.
Пример \(\PageIndex{2}\): использование правила Крамера для решения системы \(2 × 2\)
Решите следующую систему \(2 × 2\), используя правило Крамера.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Раствор
Найдите \(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3 \\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end {выравнивание*}\]
Найдите \(у\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\ 2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align* }\]
Решение: \((2,−3)\).
Упражнение \(\PageIndex{1}\)
Используйте правило Крамера, чтобы решить систему \(2 × 2\) уравнений.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Ответить
\((3,−7)\)
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Найдите определитель матрицы 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- Дополнить \(A\) первыми двумя столбцами.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
- Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали.
 Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Алгебра выглядит следующим образом:
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Пример \(\PageIndex{3}\): нахождение определителя матрицы 3 × 3
Найдите определитель матрицы \(3 × 3\) по данному
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Раствор
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
\[\begin{align*} | А | &= \влево| \begin{массив}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{массив}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3) (2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Упражнение \(\PageIndex{2}\)
Найдите определитель матрицы 3 × 3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Ответить
\(−10\)
Q&A: Можно ли использовать тот же метод для нахождения определителя большей матрицы?
Нет, этот метод работает только для матриц 2 × 2 и 3 × 3. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы \(3 × 3\), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц \(2 × 2\). Однако по мере увеличения порядка матрицы до \(3 × 3\) требуется гораздо больше вычислений.
Когда мы вычисляем определитель равным нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.
Рассмотрим систему уравнений \(3 × 3\).
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue} d_3 \\ \end{выравнивание}\]
\(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\), \(z=\dfrac{D_z}{D}\), \(D≠ 0\)
где
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Если мы записываем определитель \(D_x\), мы заменяем столбец \(x\) столбцом констант. Если мы записываем определитель \(D_y\), мы заменяем их столбец y на постоянный столбец. Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.
Если мы записываем определитель \(D_y\), мы заменяем их столбец y на постоянный столбец. Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.
Пример \(\PageIndex{4}\): решение системы \(3 × 3\) с использованием правила Крамера
Найдите решение данной системы \(3 × 3\), используя правило Крамера.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Раствор
Используйте правило Крамера.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\), \(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\ \14&3&−2\end{vmatrix}\), \(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\), \(D_z=\begin{vmatrix }1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)
Затем,
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac {-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
Решение: \((1,3,−2)\).
Упражнение \(\PageIndex{3}\)
Используйте правило Крамера, чтобы решить матрицу \(3 × 3\).
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Ответить
\(\влево(−2,\dfrac{3}{5},\dfrac{12}{5}\вправо)\)
Пример \(\PageIndex{5A}\): использование правила Крамера для решения несогласованной системы
Решите систему уравнений по правилу Крамера.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Раствор
Начнем с нахождения определителей \(D\), \(D_x\) и \(D_y\).
\(D=\begin{vmatrix}3&-2\\6&-4\end{vmatrix}=3(-4)−6(-2)=0\)
Мы знаем, что определитель, равный нулю, означает, что либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.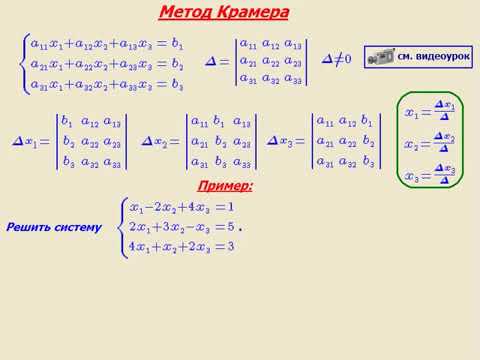
- Умножить уравнение \ref{eq3} на \(−2\).
- Добавьте результат к уравнению \ref{eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\ ;\;\;\;\; 0=−8 \end{align*}\]
Получаем уравнение \(0=−8\), которое неверно. Следовательно, система не имеет решений. График системы показывает две параллельные линии. См. рисунок \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\)Пример \(\PageIndex{5B}\): использование правила Крамера для решения зависимой системы
Решите систему с бесконечным числом решений.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end {выравнивание}\]
Раствор
Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{массив}\right|\)
Затем,
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1 )−6(3)(−2)=0\)
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Мы должны выполнить исключение, чтобы узнать.
Мы должны выполнить исключение, чтобы узнать.
1. Умножьте уравнение \ref{eq5} на \(−2\) и добавьте результат к уравнению \ref{eq7}:
\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\ ;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]
2. Получение ответа \(0=0\), утверждение, которое всегда истинно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой.См. рисунок \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\)Понимание свойств определителей
Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.{−1}\) — величина, обратная определителю матрицы \(A\).

- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример \(\PageIndex{6}\): Иллюстрация свойств определителей
Проиллюстрируйте каждое из свойств определителей.
Раствор
Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)
Дополнить \(A\) первыми двумя столбцами.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&-1&0&0\end{массив}\right]\)
Затем
\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0 (1)(1)+1(0)(2)\\ &= -2 \end{align*}\]
Свойство 2 указывает, что при перестановке строк меняется знак.Учитывая
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)( 5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(- 3)\\ &= 20-3\\ &= 17 \end{align*}\]
Свойство 3 гласит, что если две строки или два столбца идентичны, определитель равен нулю.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{массив}\right]\\ \det(A)& =1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\ \ &=4-4+8+4-4-8\\ &=0 \end{align*}\]
Свойство 4 гласит, что если строка или столбец равны нулю, определитель равен нулю.{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \ конец{выравнивание*}\]
Свойство 6 гласит, что если любую строку или столбец матрицы умножить на константу, определитель умножается на тот же коэффициент. Таким образом,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \ конец{выравнивание*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4) \\ &=-4 \end{выравнивание*}\]
Пример \(\PageIndex{7}\): использование правила Крамера и свойств определителя для решения системы
Найдите решение данной системы \(3 × 3\).
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\ конец{выравнивание}\]
Раствор
Используя правило Крамера, мы имеем
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество.Мы должны выполнить исключение, чтобы узнать.
1. Умножьте уравнение \ref{eq10} на \(–2\) и добавьте результат к уравнению \ref{eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
Получение утверждения, являющегося противоречием, означает, что система не имеет решения.
СМИ
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.
Ключевые понятия
- Определитель для \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) равен \(ad-bc\).См. пример \(\PageIndex{1}\).
- Правило Крамера заменяет столбец переменной столбцом константы. Решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\). См. пример \(\PageIndex{2}\).
- Чтобы найти определитель матрицы \(3×3\), увеличьте первые два столбца. Сложите три диагональных элемента (слева вверху справа внизу) и вычтите три элемента по диагонали (слева внизу справа вверху). См. пример \(\PageIndex{3}\).
- Чтобы решить систему из трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого требуемого решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{ D_y}{D}\), \(z=\dfrac{D_z}{D}\).См. пример \(\PageIndex{4}\).
- Правило Крамера также полезно для нахождения решения системы уравнений без решения или с бесконечным числом решений. См. Пример \(\PageIndex{5}\) и Пример \(\PageIndex{6}\).
- Некоторые свойства определителей полезны при решении задач. Например:
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.{−1}\) — величина, обратная определителю матрицы \(A\).
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. Пример \(\PageIndex{7}\) и Пример \(\PageIndex{8}\).
Авторы и авторство
Правило Крамера
Магазин Крамера Правило
Дана система линейных уравнения, правило Крамера — удобный способ решить только одну из переменных без решения всей системы уравнений.Обычно они не преподавать правило Крамера таким образом, но это должно быть точкой Правило: вместо решения всей системы уравнений можно использовать Крамера, чтобы решить только для одной единственной переменной.
Давайте использовать следующее система уравнений:
У нас левая сторона системы с переменными («матрица коэффициентов») а правая часть со значениями ответов.Позволять Д – определитель матрицы коэффициентов вышеуказанной системы, и пусть D x быть определителем, образованным заменой x -столбца значения со значениями столбца ответов:
система
из | коэффициент | ответ | D x :
определитель коэффициента |
2 х + 1 г + 1 из = 3 |
Аналогично, D и и D Z тогда будет: Авторское право Элизабет Стапель 2004-2011 Все права защищены
Оценка каждого определителя (используя описанный здесь метод), получаем:
Правило Крамера гласит, что x = Д х Д , г = Д у Д , и з = D z D .То есть:
х = 3 / 3 = 1, y = 6 / 3 = 2 , и z = 9 / 3 = 3
Это все, что нужно Крамеру Правило.Чтобы найти любую переменную, которую вы хотите (назовите ее «» или «бета»), просто оцените определяющее частное D Д . (Пожалуйста не просите меня объяснить, почему это работает. Просто поверь мне, что детерминанты может творить многие виды магии.)
- Учитывая следующее системы уравнений, найдите значение z .
Решить только для z , Сначала я нахожу определитель коэффициента.
Потом формирую D z заменив третий столбец значений столбцом ответа:
Затем я составляю частное и упростить: |
|
Суть правила Крамера заключается в том, что вам не нужно решать всю систему, чтобы получить одно значение тебе нужно.Это сэкономило мне немало времени на некоторых тестах по физике. я забыть то, над чем мы работали (что-то с проводами и токами, я думаю), но правило Крамера было намного быстрее, чем любой другой метод решения (и Видит Бог, мне нужно было дополнительное время). Не позволяйте всем подпискам и прочему запутать вас; Правило действительно довольно простое. Вы просто выбираете переменную вы хотите решить, замените столбец значений этой переменной в определитель коэффициента со значениями столбца ответов, оцените, что определителя и разделить на определитель коэффициента.это все к этому.
Почти.
Что делать, если определитель коэффициента ноль? На ноль делить нельзя, так что это значит? я не могу пойти в технические подробности здесь, но » D = 0″ означает, что система уравнений не имеет единственного решения. Система может быть несовместимой (вообще нет решения) или зависимые (бесконечное решение, которое может быть выражается в виде параметрического решения, такого как «( a , и + 3, и 4)»).С точки зрения правила Крамера, « D = 0″ означает, что вам придется использовать какой-то другой метод (например, матричный операции со строками) для решить систему. Если Д = 0, вы не можете использовать Крамера Правило.
Топ | Вернуться к индексу
Процитировать эту статью как: | Стапель, Элизабет.«Правило Крамера». Пурпурная математика . Доступно с |
7.8 Решение систем с помощью правила Крамера — Колледжская алгебра
Цели обучения
В этом разделе вы:
- Оцените 2 × 2 определителей.
- Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
- Оценить 3 × 3 определителей.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
- Знать свойства определителей.
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях.В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2×2
Определитель — это действительное число, которое может быть очень полезным в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Найдите определитель матрицы 2 × 2
Определитель матрицы 2×22×2, заданный
определяется как
Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, включая det(A)det(A) и замену скобок в матрице прямыми линиями |A|.|A|.
Пример 1
Нахождение определителя матрицы 2 × 2
Найдите определитель данной матрицы.
Решение
det(A)=|52−63|=5(3)−(−6)(2)=27det(A)=|52−63|=5(3)−(−6)(2)=27Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во Введении к анализу линий алгебры. Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует.Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.
a1x+b1y=c1(1)a2x+b2y=c2(2)a1x+b1y=c1(1)a2x+b2y=c2(2)Мы исключаем одну переменную, используя операции со строками, и находим другую.Скажем, что мы хотим найти x.x. Если уравнение (2) умножить на коэффициент, противоположный коэффициенту yy в уравнении (1), уравнение (1) умножить на коэффициент yy в уравнении (2), и мы сложим два уравнения, переменная yy будет устранено.
b2a1x + b2b1y = b2c1Multiply R1by b2-b1a2x-b1b2y = -b1c2Multiply R2by-b1 ________________________________________________________ b2a1x-b1a2x = b2c1-b1c2b2a1x + b2b1y = b2c1Multiply R1by b2-b1a2x-b1b2y = -b1c2Multiply R2by-b1 ________________________________________________________ b2a1x-b1a2x = b2c1-b1c2Теперь, решить за х.Икс.
b2a1x-b1a2x = b2c1-b1c2x (b2a1-b1c2x (b2a1-b1a2) = b2c1-b1c2 x = b2c1-b1c2b2a1-b1a2 = | C1B1C2B2 || A1B1A2B2 | B2A1X-B1A2X = B2C1-B1C2X (B2A1-B1A2) = B2C1-B1C2 x = B2C1- b1c2b2a1−b1a2=|c1b1c2b2||a1b1a2b2|Аналогично, чтобы найти y,y, мы исключим x.x.
a2a1x + a2b1y = a2c1Multiply R1by а2-a1a2x-a1b2y = -a1c2Multiply R2by-a1 ________________________________________________________ a2b1y-a1b2y = a2c1-a1c2a2a1x + a2b1y = a2c1Multiply R1by а2-a1a2x-a1b2y = -a1c2Multiply R2by-a1 ________________________________________________________ a2b1y-a1b2y = a2c1-a1c2Решение для уу Дает
A2B1Y-A1B2Y = A2C1-A1C2Y (A2B1-A1B2) = A2C1-A1C2 y = A2C1-A1C2A2B1-A1B2 = A1C2-A2C1A1B2-A2B1 = | A1C1A2C2 || A1B1A2B2 | A2B1Y-A1B2Y = A2C1-A1C2Y (A2B1-A1B2) =a2c1−a1c2 y=a2c1−a1c2a2b1−a1b2=a1c2−a2c1a1b2−a2b1=|a1c1a2c2||a1b1a2b2|Обратите внимание, что знаменатель для xx и yy является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения xx и y, y, но правило Крамера также вводит новое обозначение:
- D:D: определитель матрицы коэффициентов
- Dx:Dx: определитель числителя в решении xx
- Dy:Dy: определитель числителя в решении yy
Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Тогда мы можем выразить xx и yy как частное двух определителей.
Правило Крамера для систем 2×2
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
a1x+b1y=c1a2x+b2y=c2a1x+b1y=c1a2x+b2y=c2Решение с использованием правила Крамера дано как
x=DxD=|c1b1c2b2||a1b1a2b2|,D≠0;y=DyD=|a1c1a2c2||a1b1a2b2|,D≠0.x=DxD=|c1b1c2b2||a1b1a2b2|,D≠0;y =DyD=|a1c1a2c2||a1b1a2b2|,D≠0.Если мы находим x,x, столбец xx заменяется столбцом констант. Если мы ищем y, y, столбец yy заменяется столбцом констант.
Пример 2
Использование правила Крамера для решения системы 2 × 2
Решите следующую систему 2×22×2, используя правило Крамера.
12x+3y=15 2x−3y=1312x+3y=15 2x−3y=13Решение
Решите для х.х.
x=DxD=|15313−3||1232−3|=−45−39−36−6=−84−42=2x=DxD=|15313−3||1232−3|=−45−39−36 −6=−84−42=2Найдите y.у.
y=DyD=|1215213||1232−3|=156−30−36−6=−12642=−3y=DyD=|1215213||1232−3|=156−30−36−6=−12642=− 3Решение (2,−3).(2,−3).
Попытайся #1
Используйте правило Крамера, чтобы решить систему уравнений 2 × 2.
х+2у=-11-2х+у=-13 х+2у=-11-2х+у=-13Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но определить определитель матрицы 3 × 3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5.Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху вниз справа) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Найдите определитель матрицы 3×3.
А=[a1b1c1a2b2c2a3b3c3]А=[a1b1c1a2b2c2a3b3c3]- Дополнить AA первыми двумя столбцами. det(A)=|a1b1c1a2b2c2a3b3c3|a1a2a3b1b2b3|det(A)=|a1b1c1a2b2c2a3b3c3|a1a2a3b1b2b3|
- От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали.Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
- Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Алгебра выглядит следующим образом:
|A|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1|A|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1Пример 3
Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 по данным
А=[0213-11401]А=[0213-11401]Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
|A|=|0213−11401|0342−10|=0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0( 1)(0)−1(3)(2)=0+8+0+4−0−6=6|A|=|0213−11401|0342−10|=0(−1)(1)+ 2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2)=0+8+0+4−0 −6=6Попытайся #2
Найдите определитель матрицы 3 × 3.
det(A)=|1−371111−23|det(A)=|1−371111−23|вопросы и ответы
Можно ли использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для матриц 2×22×2 и 3×33×3.Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.
Рассмотрим систему уравнений 3 × 3.
х=DxD,y=DyD,z=DzD,D≠0x=DxD,y=DyD,z=DzD,D≠0где
Если мы записываем определитель Dx,Dx, мы заменяем столбец xx столбцом констант. Если мы записываем определитель Dy,Dy, мы заменяем столбец yy столбцом констант.Если мы записываем определитель Dz,Dz, мы заменяем столбец zz столбцом констант. Всегда проверяйте ответ.
Пример 4
Решение системы 3 × 3 с помощью правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
x+y−z=63x−2y+z=−5x+3y−2z=14x+y−z=63x−2y+z=−5x+3y−2z=14Решение
Используйте правило Крамера.
D=|11−13−2113−2|,Dx=|61−1−5−21143−2|,Dy=|16−13−51114−2|,Dz=|1163−2−51314|D=| 11−13−2113−2|,Dx=|61−1−5−21143−2|,Dy=|16−13−51114−2|,Dz=|1163−2−51314|Затем,
x=DxD=-3-3=1y=DyD=-9-3=3z=DzD=6-3=-2x=DxD=-3-3=1y=DyD=-9-3=3z=DzD=6 −3=−2Решение (1,3,−2).(1,3,−2).
Попытайся #3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
x−3y+7z=13x+y+z=1x−2y+3z=4x−3y+7z=13x+y+z=1x−2y+3z=4Пример 5
Использование правила Крамера для решения несогласованной системы
Решите систему уравнений по правилу Крамера.
3x−2y=4 (1)6x−4y=0 (2)3x−2y=4 (1)6x−4y=0 (2)Решение
Начнем с нахождения определителей D,Dx и Dy.D,Dx и Dy.
D=|3−26−4|=3(−4)−6(−2)=0D=|3−26−4|=3(−4)−6(−2)=0Мы знаем, что определитель, равный нулю, означает, что либо система не имеет решений, либо имеет бесконечное число решений.Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножить уравнение (1) на −2,−2.
- Добавьте результат к уравнению (2).(2).
Получаем уравнение 0=−8,0=−8, которое неверно. Следовательно, система не имеет решений. График системы показывает две параллельные линии. См. рис. 1.
Фигура 1
Пример 6
Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным числом решений.
x−2y+3z=0(1)3x+y−2z=0(2)2x−4y+6z=0(3)x−2y+3z=0(1)3x+y−2z=0(2) 2x−4y+6z=0(3)Решение
Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.
|1−2331−22−46 | 1−2312−4||1−2331−22−46 | 1−2312−4|Затем,
1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1)−6 (3)(−2)=01(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)( −2)(1)−6(3)(−2)=0Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений.Мы должны выполнить исключение, чтобы узнать.
- Умножьте уравнение (1) на −2−2 и добавьте результат к уравнению (3): −2x+4y−6z=02x−4y+6z=00=0−2x+4y−6z=02x−4y+6z=00=0
- Получение ответа 0=0,0=0, утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. рис. 2.
Фигура 2
Понимание свойств определителей
Есть много свойств определителей.Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
Свойства определителей
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца совпадают, определитель равен нулю.
- Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
- Определитель обратной матрицы A−1A−1 является обратной величиной определителя матрицы A.A.
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример 7
Иллюстрация свойств определителей
Проиллюстрируйте каждое из свойств определителей.
Решение
Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
A=[12302100−1]A=[12302100−1]Дополнить AA первыми двумя столбцами.
А=[12302100−1|100220]А=[12302100−1|100220]Затем
det(A)=1(2)(-1)+2(1)(0)+3(0)(0)−0(2)(3)−0(1)(1)+1(0) (2)=−2det(A)=1(2)(−1)+2(1)(0)+3(0)(0)−0(2)(3)−0(1)(1) +1(0)(2)=−2Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая
A=[−154−3],det(A)=(−1)(−3)−(4)(5)=3−20=−17B=[4−3−15],det(B)= (4)(5)−(−1)(−3)=20−3=17A=[−154−3],det(A)=(−1)(−3)−(4)(5)= 3−20=−17B=[4−3−15],det(B)=(4)(5)−(−1)(−3)=20−3=17Свойство 3 утверждает, что если две строки или два столбца одинаковые, определитель равен нулю.
А=[122222−122 | 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2)=4−4+8+4−4−8=0A=[122222−122 | 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2)=4−4+8+4−4−8=0Свойство 4 гласит, что если строка или столбец равны нулю, определитель равен нулю. Таким образом,
A=[1200],det(A)=1(0)−2(0)=0A=[1200],det(A)=1(0)−2(0)=0Свойство 5 гласит, что определитель обратной матрицы A−1A−1 является обратной величиной определителя A.A. Таким образом,
A=[1234],det(A)=1(4)−3(2)=−2A−1=[−2132−12],det(A−1)=−2(−12)− (32)(1)=-12A=[1234],det(A)=1(4)−3(2)=-2A-1=[-2132-12],det(A-1)=-2 (−12)−(32)(1)=−12Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент.Таким образом,
A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)−3(4) =−4A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)−3( 4)=−4Пример 8
Использование правила Крамера и свойств определителя для решения системы
Найдите решение данной системы 3 × 3.
2x+4y+4z=2(1)3x+7y+7z=−5(2) x+2y+2z=4(3)2x+4y+4z=2(1)3x+7y+7z=−5 (2) х+2у+2г=4(3)Решение
Используя правило Крамера, мы имеем
Д=|244377122|Д=|244377122|Обратите внимание, что второй и третий столбцы идентичны.Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.
- Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1). −2x−4y−4x=−8 2x+4y+4z=20=−6−2x−4y−4x=−8 2x+4y+4z=20=−6
Получение утверждения, являющегося противоречием, означает, что система не имеет решения.
7.8 Секционные упражнения
Устный
1 .Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.
2 .Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу 2×22×2.
3 .Объясните, что в терминах обратной матрицы означает наличие определителя, равного 0.
4 .Определитель матрицы AA 2×22×2 равен 3. Если вы поменяете строки и умножите первую строку на 6, а вторую строку на 2, объясните, как найти определитель, и дайте ответ.
Алгебраический
Для следующих упражнений найдите определитель.
13 .|−2−33,14 000||−2−33,14 000|
14 .|−1.10.67.2−0,5||−1.10.67.2−0,5|
15 .|−10001000−3||−10001000−3|
16 .|−14002300−3||−14002300−3|
18 .|2-313-41-561||2-313-41-561|
19 .|−214−42−82−8−3||−214−42−82−8−3|
20 .|6-12-4-3519-1||6-12-4-3519-1|
21 .|51−12313−6−3||51−12313−6−3|
22 .|1,12−1−4004,1−0,42,5||1,12−1−4004.1−0,42,5|
23 .|2-1.63.11.13-8-9.302||2-1.63.11.13-8-9.302|
24 .|−12131415−16170018||−12131415−16170018|
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
25 .2x−3y=−14x+5y=92x−3y=−14x+5y=9
26 .5x−4y=2−4x+7y=65x−4y=2−4x+7y=6
27 .6x−3y=2−8x+9y=−16x−3y=2−8x+9y=−1
28 .2x+6y=125x−2y=132x+6y=125x−2y=13
29 .4x+3y=232x-y=-14x+3y=232x-y=-1
30 .10x−6y=2−5x+8y=−110x−6y=2−5x+8y=−1
31 .4x−3y=−32x+6y=−44x−3y=−32x+6y=−4
32 .4x−5y=7−3x+9y=04x−5y=7−3x+9y=0
33 .4x+10y=180-3x-5y=-1054x+10y=180-3x-5y=-105
34 .8x−2y=−3−4x+6y=48x−2y=−3−4x+6y=4
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
35 .x+2y-4z=-17x+3y+5z=26-2x-6y+7z=-6x+2y-4z=-17x+3y+5z=26-2x-6y+7z=-6
36 .-5x+2y-4z=-474x-3y-z=-943x-3y+2z=94-5x+2y-4z=-474x-3y-z=-943x-3y+2z=94
37 .4x+5y-z=-7-2x-9y+2z=85y+7z=214x+5y-z=-7-2x-9y+2z=85y+7z=21
38 .4x−3y+4z=105x−2z=−23x+2y−5z=−94x−3y+4z=105x−2z=−23x+2y−5z=−9
39 .4x−2y+3z=6−6x+y=−22x+7y+8z=244x−2y+3z=6−6x+y=−22x+7y+8z=24
40 .5x+2y-z=1-7x-8y+3z=1,56x-12y+z=75x+2y-z=1-7x-8y+3z=1,56x-12y+z=7
41 .13x-17y+16z=73-11x+15y+17z=6146x+10y-30z=-1813x-17y+16z=73-11x+15y+17z=6146x+10y-30z=-18
42 .−4x−3y−8z=−72x−9y+5z=0,55x−6y−5z=−2−4x−3y−8z=−72x−9y+5z=0.55x−6y−5z=−2
43 .4x-6y+8z=10-2x+3y-4z=-5x+y+z=14x-6y+8z=10-2x+3y-4z=-5x+y+z=1
44 .4x-6y+8z=10-2x+3y-4z=-512x+18y-24z=-304x-6y+8z=10-2x+3y-4z=-512x+18y-24z=-30
Технология
В следующих упражнениях используйте функцию определителя в графической утилите.
45 .|108
10300243||108
10300243|
46 . |10210-
-2-1011-2||10210-
-2-1011-2|
|1217401210050022,0000002||1217401210050022,0000002|
48 .|1000230045607890||1000230045607890|
Реальные приложения
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислите определитель. Будет ли уникальное решение? Если да, то найти единственное решение.
49 .Два числа в сумме дают 56. Одно число на 20 меньше другого.
50 .Два числа в сумме дают 104. Если сложить два раза первое число и два раза второе число, получится 208
. 51 .Три числа в сумме дают 106. Первое число на 3 меньше второго числа. Третье число на 4 больше первого числа.
52 .Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше первых двух вместе взятых.
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.
53 .Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых.В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет?
54 .Вы инвестируете 80 000 долларов на два счета, 22 000 долларов на один счет и 58 000 долларов на другой счет. В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов?
55 .Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов.Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл. США, а общая сумма выручки составила 12 756 долл. США, сколько было продано детских билетов и билетов для взрослых?
56 .Концертный зал продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов. Если общий доход составил 18 090 долларов США и был продан 321 билет, то сколько было продано одиночных билетов и сколько билетов для пар?
57 .Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски.Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого цвета стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
58 .Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен. Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов.Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?
59 .В вашем саду выращивают два вида помидоров, зеленый и красный. Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?
60 .На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука.Какую долю рынка занимает каждый овощ?
61 .На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. Для каждого фрукта найдите процент от общего количества проданных фруктов.
62 .Три группы выступили на концертной площадке. Первая группа взимала 15 долларов за билет, вторая группа взимала 45 долларов за билет, а последняя группа взимала 22 доллара за билет.Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу?
63 .Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов. Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
64 .Мужчины в возрасте 20–29, 30–39 и 40–49 лет составляли 78% заключенных в тюрьме в прошлом году. В этом году те же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет сократилась до 3434 человек по сравнению с их предыдущим населением. Первоначально в возрастной группе 30–39 лет заключенных было на 2% больше, чем в возрастной группе 20–29 лет. Определите процент заключенных для каждой возрастной группы в прошлом году.
65 .В женской тюрьме неподалеку общее количество заключенных в возрасте от 20 до 49 лет составляло 5525 человек.В этом году возрастная группа 20-29 лет увеличилась на 10%, возрастная группа 30-39 лет уменьшилась на 20%, а возрастная группа 40-49 лет удвоилась. Сейчас там 6040 заключенных. Первоначально в возрастной группе 30–39 лет было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.
Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает приготовить пищевую смесь из миндаля, сушеной клюквы и орехов кешью в шоколаде. Информация о пищевой ценности этих продуктов представлена в таблице 1.
| Жир (г) | Белок (г) | Углеводы (г) | |
|---|---|---|---|
| Миндаль (10) | 6 | 2 | 3 |
| Клюква (10) | 0,02 | 0 | 8 |
| Кешью (10) | 7 | 3,5 | 5.5 |
Стол 1
66 .Для специальной «низкоуглеводной» трейловой смеси имеется 1000 штук смеси. Общее количество углеводов 425 г, общее количество жиров 570,2 г. Если орехов кешью на 200 штук больше, чем клюквы, сколько штук каждого предмета будет в смеси?
67 .Для смеси «походной» в составе смеси 1000 шт., содержащих 390,8 г жира, 165 г белка. Если миндаля столько же, сколько орехов кешью, то сколько каждого элемента содержится в смеси?
68 .Для смеси «Энергия-бустер» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если количество миндаля и кешью в сумме равно количеству клюквы, сколько каждого элемента содержится в смеси?
Решение линейных систем с использованием правила Крамера
Решение линейных систем с использованием правила Крамера
Что такое правило Крамерса
Правило Крамерса — это метод решения систем линейных уравнений, в которых число неизвестных равно количеству уравнений в системе.Техника состоит из набора уравнений, включающих определители и отношения, чтобы получить уникальный набор решений для линейной системы.
На протяжении этого урока мы сосредоточимся на объяснении метода решения системы, которую мы будем называть правилом Крамерса 3×3 и правилом Крамерса 2×2, это означает, что мы сосредоточимся на случаях, когда у нас есть система уравнений с 3 уравнениями для 3 неизвестных ( n=3) или система с 2 уравнениями для 2 неизвестных (n=2). Причина этого в том, что правило Крамерса непрактично, когда система имеет более высокий порядок, чем 3, другие методы, такие как решение линейной системы с матрицами с использованием исключения Гаусса или простое решение систем линейных уравнений путем подстановки гораздо более эффективны с точки зрения вычислений. работать через линейную систему.Правило Стилла Крамерса является важной частью линейной алгебры, которую следует учитывать из-за ее математической строгости и глубокого понимания транскрипции линейных систем в матрицы и наоборот, когда такие системы имеют уникальные решения.
Как пользоваться правилом Крамерса
Но что такое правило Крамерса perse? Вместо того, чтобы повторять определение правила Крамерса, давайте немного лучше продемонстрируем технику, подробно рассмотрев ее шаги.
Действия при использовании линейной алгебры по правилу Крамерса:
1.\enspace Для линейной системы из трех уравнений и трех неизвестных и для линейной системы из двух уравнений и двух неизвестных, представленных ниже:ax+by+cz=m ax+ by + cz = m \quad \quad \quad \quad \quad \quad \quad ax+by+cz=m dx+ey+fz=nax+by=mdx+ey+fz=n \quad \quad ax+by=m dx+ey+fz=nax+by=m gz+hy+iz=ocx+dy=ngz+hy+iz=o \quad \quad cx+dy=n gz+hy+iz=ocx+dy=n Уравнение 1: Системы линейных уравнений. 3 уравнения для 3 неизвестных слева, 2 уравнения для 2 неизвестных справа 2.\enspace Система линейных уравнений должна быть преобразована в матрицу дополнений.
- В расширенной матрице элементы в левой части вертикальной линии, представляющей знак равенства, соответствуют квадратной матрице коэффициентов. Эта квадратная матрица коэффициентов будет использоваться для получения ряда определителей на нашем следующем шаге.
- В расширенной матрице элементы вектора-столбца справа от знака равенства будут использоваться в качестве замены некоторых элементов при получении набора определителей на следующем шаге.
- Расширенные матрицы для системы с тремя уравнениями и тремя неизвестными и системы двух уравнений с двумя неизвестными, представленной в уравнении 1, выглядят следующим образом:
- Учтите, что правило Крамерса можно использовать с любой системой из n уравнений для n неизвестных (пока уравнений столько же, сколько неизвестных, количество не имеет значения). Мы выбрали для представления случаи, в которых n=3 \, n = 3\, n=3 и n=2 \, n = 2 \, n=2, поскольку они обычно используются, прежде чем мы решим продолжить наши вычисления. другой и более удобной техникой.
Уравнение 2: расширенные матрицы из систем линейных уравнений
- Другими словами, для случая, когда n=3 \, n=3 \, n=3, мы будем вычислять 4 определителя. Для случая, когда n=2 \, n = 2 \, n=2, вычислим 3 определителя.
- Все определители названы на основе переменных, содержащихся в рассматриваемой системе линейных уравнений. Например, для случая, когда в системе три неизвестных, у вас есть переменные xxx, yyy, zzz, следовательно, определители будут: DxD_xDx, DyD_yDy, DzD_zDz.Для случая, когда в системе два неизвестных, у вас есть переменные xxx, yyy, следовательно, определители будут: DxD_xDx, DyD_yDy. Кроме того, в каждом случае всегда есть дополнительный определитель, который мы просто называем DDD.
- Определитель DDD всегда является определителем матрицы квадратных коэффициентов (которую мы назвали CCC) из левой части расширенной матрицы. Для систем, где n=3 \, n= 3 \, n=3 и n=2 \, n=2 \, n=2. Определитель DDD будет следующим:
- Определители DxD_xDx, DyD_yDy, Dz…D_z …Dz… получаются путем замены вектора-столбца b из уравнения 2 в соответствующий столбец матрицы квадратных коэффициентов.
Уравнение 3: Определитель D
Уравнение 4: Формулировка определителей D x , D y , D z 4. \enspace После того, как определители были вычислены, мы просто следуем следующим соотношениям, чтобы получить значения переменных из систем уравнений:
x=DxD \large x= \frac{D_x}{D} \quad \quad \quad \quad \quad x=DDx
y=DyDx=DxD \large y= \frac{D_y}{D} \quad \quad x= \frac{D_x}{D} y=DDyx=DDx
z=DzDy=DyD \large z= \frac{D_z}{D} \quad \quad y= \frac{D_y}{D} z=DDzy=DDy Уравнение 5: Нахождение решений переменных для систем линейных уравнений.3 уравнения для 3 неизвестных слева, 2 уравнения для 2 неизвестных справа
В общем, каждое уравнение для каждой переменной, как показано в уравнении 5, представляет собой то, что мы называем формулой правила Крамерса. Во многих книгах и опубликованных материалах это называется просто правилом Крамерса, тогда как на самом деле этот метод требует нескольких уравнений. По той же причине иногда вы можете увидеть этот метод, называемый матричным правилом Крамерса (обычно ссылаясь на расширенную матрицу из уравнения 2 или набор определителей из уравнений 3 и 4).
Как видите, решение систем уравнений с помощью правила Крамерса очень быстро становится очень утомительным, и именно поэтому этот метод обычно остается в стороне, и люди предпочитают использовать такие методы, как сокращение строк посредством исключения Гаусса. Если мы сравним такие два метода, мы ясно увидим, что по мере увеличения количества уравнений в системе и, следовательно, неизвестных, матрицы правил Крамерса становятся больше, а метод длиннее, поскольку для его решения требуется n + 1 количество определителей; Мало того, с увеличением n и определители становятся больше.
Поэтому в этом уроке мы сосредоточимся на решении систем линейных уравнений, содержащих до 3 уравнений с 3 неизвестными, более высокие значения n предлагается решать с помощью других методов решения систем линейных уравнений.
Правило Крамерса для решения системы уравнений
Объяснив этапы выполнения правила Крамерса, давайте научимся использовать его при решении систем линейных уравнений.
Мы разделим этот раздел на две части: одна посвящена решению системы из 2 уравнений с 2 неизвестными (n=2n=2n=2), а другая посвящена решению системы из 3 уравнений с 3 неизвестными.
Используйте правило Крамерса для решения системы двух линейных уравнений с двумя неизвестными, как показано ниже: х+2у=3х+2у=3 х+2у=3 2x+3y=12x+3y=1 2x+3y=1 Уравнение 6: Система 2 линейных уравнений для 2 неизвестных
Преобразуем систему в расширенную матрицу: Уравнение 7: Расширенная матрица для системы 2×2
Затем мы вычисляем 3 требуемых определителя (помните, что шаг 3 нашего метода диктует, что нам нужно вычислить n+1 \, n+1 \,n+1 определитель. Для этого случая у нас есть система из 2 неизвестных, таким образом n=2 \, n=2 \, n=2, поэтому n+1=2+1=3 \, n+1 = 2+1 =3\, n+1=2+1=3, и, следовательно, нужно решить 3 определителя).
Следуя уравнению 3, мы сначала решим определитель правила Крамерса D: Уравнение 8: Определитель правила Крамерса D
Обратите внимание, что этот определитель DDD является просто определителем матрицы квадратных коэффициентов из левой части расширенной матрицы в уравнении 7.
Теперь, чтобы решить определители, относящиеся к каждой из переменных в уравнениях из системы, нам нужно заменить столбец, относящийся к каждой переменной в матрице квадратных коэффициентов, на столбец из правой части расширенной матрицы.Таким образом, определители DxD_xDx, DyD_yDy равны:
Уравнение 9: Детерминанты правила Крамерса, относящиеся к каждой переменнойЧтобы наконец найти уникальное решение для каждой переменной в уравнениях, мы теперь решим уравнение по правилу Крамерса для каждого из них: x=DxD=7−1=−7 \large x = \frac{D_x}{D} = \frac{7}{-1} = -7 x=DDx=−17=−7
y=DyD=−5−1=5 \large y = \frac{D_y}{D} = \frac{-5}{-1} = 5 y=DDy=−1−5=5 Уравнение 10: Решение переменных x и y
Итак, система решена! Решения для переменных xxx и yyy таковы: x=−7,y=5x=-7, y=5x=−7,y=5.
Теперь давайте посмотрим на процесс выполнения правила Крамерса 3×3!
Используйте правило Крамерса, чтобы решить систему уравнений с тремя неизвестными, как показано ниже: х+4у+3г=1 х+4у+3г=1 х+4у+3г=1 х+2у+9г=1х+2у+9г=1 х+2у+9г=1 х+6у+6г=1х+6у+6г=1 х+6у+6г=1 Уравнение 11: Система 3 линейных уравнений для 3 неизвестных
Преобразуем систему в расширенную матрицу: Уравнение 12: Расширенная матрица для системы 3×3
А затем вычисляем 4 необходимых определителя. Начиная с определителя DDD: Уравнение 13: Определитель правила Крамерса D
Этот определитель DDD является просто определителем матрицы квадратных коэффициентов из левой части расширенной матрицы в уравнении 12.
Теперь, чтобы решить определители, связанные с каждой из переменных в уравнениях из системы, мы заменим столбец, относящийся к каждой переменной в квадратной матрице коэффициентов, столбцом, идущим из правой части расширенной матрицы. Итак, определители DxD_xDx, DyD_yDy, DzD_zDz равны: Уравнение 14: Детерминанты правила Крамерса, относящиеся к каждой переменной
Решение для переменных xxx, yyy и zzz: x=DxD=−18−18=1 \large x = \frac{D_x}{D} = \frac{-18}{-18} = 1 x=DDx=−18−18=1
y=DyD=0−18=0 \large y = \frac{D_y}{D} = \frac{0}{-18} = 0 y=DDy=−180=0
z=DzD=0−18=0 \large z = \frac{D_z}{D} = \frac{0}{-18} = 0 z=DDz=−180=0 Уравнение 15: Решение переменных x и y
Итак, система решена! х=1,у=0,г=0х=1, у=0, г=0х=1,у=0,г=0
Таким образом, для того, чтобы использовать правило Крамера для решения линейных уравнений, мы: перепишем систему в расширенную матрицу, используем левую часть этой матрицы как матрицу квадратных коэффициентов, а правую часть как подстановку для соответствующих решений для каждой переменной в матрице коэффициентов, установите n + 1 определителей для системы, оцените определители и примените уравнения правила Крамерса, чтобы найти уникальные решения для переменных.
Помните, что если вы не полностью удовлетворены этой техникой, вы всегда можете выполнить доказательство по правилу Крамерса, решив систему, используя любой из других методов, которые вы уже знаете для решения линейных систем уравнений.
Примеры правил Крамерса
В этом разделе мы добавим несколько других примеров упражнений, в которых мы используем правило Крамерса для решения систем уравнений. Мы начнем с нескольких примеров систем 2×2 и закончим проблемой 3×3. Пример 1 Решите следующую линейную систему, используя правило Крамерса: 5x+3y=1 5x+3y=15x+3y=1 х+у=2х+у=2х+у=2 Уравнение 16: Система 2 линейных уравнений для 2 неизвестных
Преобразуем систему в расширенную матрицу: Уравнение 17: Расширенная матрица для системы 2×2
А затем вычисляем 3 необходимых определителя: Уравнение 18: Детерминанты правила Крамерса
Теперь используйте DDD, DxD_xDx, DyD_yDy, чтобы окончательно найти уникальное решение для каждой переменной в уравнениях: х=DxD=-52=-2.5 \large x = \frac{D_x}{D} = \frac{-5}{2} = -2,5 x=DDx=2−5=−2,5
y=DyD=92=4,5 \large y = \frac{D_y}{D} = \frac{9}{2} = 4,5 y=DDy=29=4,5 Уравнение 19: Решение переменных x и y
Итак, решения для переменных xxx и yyy таковы: x=−2,5,y=4,5x=-2,5, y=4,5x=−2,5,y=4,5 Пример 2 Решите следующую линейную систему, используя правило Крамерса: у=3х+5 у=3х+5 у=3х+5 у=4х-2у=4х-2 у=4х-2 Уравнение 20: Система 2 линейных уравнений для 2 неизвестных
Мы преобразуем приведенную выше систему в стандартную запись, чтобы позже мы могли преобразовать ее в расширенную матрицу: y=3x+5 y=3x+5 \quad y=3x+5→−3x+y=5 \quad -3x+y=5−3x+y=5 y=4x−2y=4x-2 \quad y=4x−2→−4x+y=−2 \quad -4x+y=-2 −4x+y=−2 Уравнение 21: Система 2 линейных уравнений для 2 неизвестных
Преобразуем систему в расширенную матрицу: Уравнение 22: Расширенная матрица для системы 2×2
А затем вычисляем 3 необходимых определителя: Уравнение 23: Детерминанты правила Крамерса
Теперь используйте DDD, DxD_xDx, DyD_yDy, чтобы окончательно найти уникальное решение для каждой переменной в уравнениях: x=DxD=71=7 \large x = \frac{D_x}{D} = \frac{7}{1} = 7 x=DDx=17=7
y=DyD=261=26 \large y = \frac{D_y}{D} = \frac{26}{1} = 26 y=DDy=126=26 Уравнение 24: Решение переменных x и y
Итак, решения для переменных xxx и yyy таковы: x=7,y=26x=7, y=26x=7,y=26 Пример 3 Решите следующую линейную систему, используя правило Крамерса: 2x+4y=3 2x+4y=32x+4y=3 4x+8y=64x+8y=64x+8y=6 Уравнение 25: Система 2 линейных уравнений для 2 неизвестных
Преобразуем систему в матрицу правил Крамерса (расширенная матрица): Уравнение 26: Расширенная матрица для системы 2×2
А затем вычисляем 3 необходимых определителя: Уравнение 27: Детерминанты правила Крамерса
Теперь используйте DDD, DxD_xDx, DyD_yDy, чтобы окончательно найти уникальное решение для каждой переменной в уравнениях: x=DxD=00=0 \large x = \frac{D_x}{D} = \frac{0}{0} = 0 x=DDx=00=0
y=Dyy=00=0 \large y = \frac{D_y}{y} = \frac{0}{0} = 0 y=yDy=00=0 Уравнение 28: Решение переменных x и y
Итак, решения для переменных xxx и yyy таковы: x=0,y=0x=0, y=0x=0,y=0 Пример 4 Для последнего примера правила Крамерса мы будем решать систему из 3 уравнений для 3 неизвестных: х+3у+4г=4 х+3у+4г=4х+3у+4г=4 −x+3y+2z=2-x+3y+2z=2−x+3y+2z=2 3x+9y+6z=-63x+9y+6z=-63x+9y+6z=-6 Уравнение 29: Система 3 линейных уравнений для 3 неизвестных
Преобразуем систему в расширенную матрицу: Уравнение 30: Расширенная матрица для системы 3×3
А затем вычисляем 4 искомых определителя: Уравнение 31: Детерминанты правила Крамерса
Теперь используйте DDD, DxD_xDx, DyD_yDy, чтобы окончательно найти уникальное решение для каждой переменной в уравнениях: x=DxD=72−36=−2 \large x = \frac{D_x}{D} = \frac{72}{-36} = -2 x=DDx=-3672=-2
y=DyD=72−36=−2 \large y = \frac{D_y}{D} = \frac{72}{-36} = -2 y=DDy=−3672=−2
y=DzD=−108−36=3 \large y = \frac{D_z}{D} = \frac{-108}{-36} = 3 y=DDz=−36−108=3 Уравнение 32: Решение переменных x, y и z
И система решается! Решения для переменных xxx, yyy и zzz таковы: x=−2,y=−2,z=3x=-2, y=-2, z=3x=-2,y=-2,z=3
В этом последнем упражнении мы хотели бы поработать над доказательством правила Крамерса, решив систему из уравнения 24 другим методом и проверив результат.
Таким образом, мы используем подстановку для решения системы:
x + 3y + 4z=4−x + 3y + 2z=23x + 9y + 6z=−6 x \, + \, 3y \, + \, 4z=4 \quad \quad \quad -x \, + \ , 3y \, + \, 2z=2 \quad \quad \quad 3x \, + \, 9y \, + \, 6z=-6x+3y+4z=4−x+3y+2z=23x+9y+6z =−6
решить forx x x в 1-м уравнении и подставить его в 3-м:
х=4−3y−4zx =4-3y-4z х=4−3y−4z
3(4−3y−4z) + 9y + 6z=−6 3(4-3y-4z) \, + \, 9y \, + \, 6z=-6 \; 3(4−3y−4z)+9y+6z=−6→ −6z + 12=−6 \; -6z \, + \, 12=-6 −6z+12=-6
-6z=-18 -6z=-18 \; −6z=−18→ z=3 \; г=3 г=3 Уравнение 33: Решение системы 3×3 подстановкой (часть 1)
Теперь продолжим технику подстановки, подставив найденное значение переменной zzz в первое и второе уравнения и получим новую упрощенную систему из 2-х уравнений для 2-х неизвестных: х + 3y + 4z=4 x \, + \, 3y \, + \, 4z = 4 \; x+3y+4z=4→ x + 3y + 4(3)=4 \; х \, + \, 3у \, + \, 4(3) = 4 \; х+3у+4(3)=4→ х + 3у=−8 \; х \, + \, 3y=-8x+3y=-8
−x + 3y + 2z=2 -x \, + \, 3y \, + \, 2z = 2 \; −x+3y+2z=2→ −x + 3y + 2(3)=2 \;-x \, + \, 3y \, + \, 2(3)= 2 \; −x+3y+2(3)=2→ −x + 3y=−4 \; — х \, + \, 3у=-4-х+3у=-4
Новые уравнения:
x + 3y=−8−x + 3y=−4x \, + \, 3y=-8 \quad \quad \quad -x \, + \, 3y=-4x+3y=-8−x+3y= −4 Уравнение 34: Решение системы 3×3 подстановкой (часть 2)
Используя эти новые выражения из уравнения 29, найдите x во втором уравнении и подставьте его в первое уравнение, чтобы найти yyy: 3y + 4=x 3y \, + \, 4=x \; 3y+4=x→ (3y + 4) + 3y=−8 \; (3y \, + \, 4) \, + \, 3y=-8(3y+4)+3y=-8 6y + 4=−8 6y \, + \, 4 = -8 \; 6y+4=−8→ 6y=−12 \; 6у=-126у=-12 у=-2у=-2у=-2 Уравнение 35: Решение системы 3×3 подстановкой (часть 3)
И завершаем это, подставляя найденное значение y во второе выражение из уравнения 29: −x + 3y=−4 -x \, + \, 3y=-4 \; −x+3y=−4→ −x + 3(−2)=−4 \; -х \, + \, 3(-2)=-4-х+3(-2)=-4 −x−6=−4 -x-6=-4 \; −x−6=−4→ −x=2 \; -х=2-х=2 х=-2х=-2х=-2 Уравнение 36: Решение системы 3×3 подстановкой (часть 4)
Окончательные найденные значения переменных xxx,yyy и zzz: x=−2,y=−2,z=3x=-2, y=-2, z=3x=-2,y=-2,z =3
Таким образом, уникальные решения для переменных в линейной системе уравнений совпадают с ответами, полученными с помощью правила Крамерса для матриц! И вы можете ясно видеть, что оба подхода хороши для нас, чтобы использовать их при решении систем.
В завершение нашего сегодняшнего урока, как всегда, у нас есть несколько рекомендаций для ваших дальнейших занятий. Во-первых, это подробная статья, в которой вы можете найти пример использования правила Крамерса для решения двух уравнений с двумя неизвестными. И затем эта ссылка на обратную матрицу и правило Крамерса, где вы можете найти пример системы 3×3 внизу.
На этом урок окончен, увидимся на следующем!
3.5 Детерминанты и правило Крамера – Колледжская алгебра для управленческих наук
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика.Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2×2
Определитель — это действительное число, которое может быть очень полезным в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений.Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные можно расшифровать только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Определитель матрицы 2 2, заданный
определяется как:
от
Обратите внимание, что для определителей мы используем прямые вертикальные линии.Другими словами, дет.
Выглядит знакомо? Должно. Помните, что это был знаменатель в скаляре, который мы умножаем на матрицу 2 2 с переключенными диагоналями и противоположными диагоналями, чтобы создать обратную. Таким образом, обратная матрица 2 2, как показано выше, будет:
.
Найдите определитель данной матрицы
от
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году. системы с любым числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать определитель .Несогласованные решения имеют по крайней мере один определитель числителя, отличный от нуля. Зависимые решения имеют ноль в качестве определителя в обоих числителях. Для нахождения общего решения необходимо использовать другой метод.
Чтобы понять, как и почему работает правило Крамера, мы направим вас к исходному материалу в OpenStax College Algebra.
Короче говоря, правило Крамера начинается с системы уравнений, например:
и мы можем показать, что
Обратите внимание, что знаменатель для обоих и является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения, но правило Крамера также вводит новое обозначение:
Обратите внимание, что ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Затем мы можем выразить и как:
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
Решение с использованием правила Крамера задается как:
Для
Если мы ищем , столбец заменяется столбцом констант. Если мы ищем для , столбец заменяется постоянным столбцом.
Решите следующую систему, используя правило Крамера
Найти
Найти
Найти
Решение (2,-3).
Используйте правило Крамера, чтобы решить систему уравнений.
Вычисление определителя матрицы
Найти определитель матрицы несложно, но найти определитель матрицы сложнее. Один из методов состоит в том, чтобы дополнить матрицу повторением первых двух столбцов, получив матрицу. Затем мы вычисляем сумму произведений записей вниз по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей вверх по каждой из трех противоположных диагоналей (слева внизу справа вверху).Это легче понять с визуальным и пример.
Найдите определитель матрицы.
Шаг 1: Дополнить первыми двумя столбцами:
Шаг 2: От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали. , затем начните с и умножьте слева направо по диагонали, а затем . Добавьте эти три продукта.
Шаг 3: Теперь сверху справа: умножьте записи по обратной диагонали. , затем начните с и умножьте справа налево по диагонали, а затем .Добавьте эти три продукта и вычтите это значение из значения на шаге 2.
Алгебра выглядит следующим образом:
Найдите определитель матрицы :
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,
Детерминанты также можно найти с помощью технологий. После того, как матрица введена в ваш калькулятор. Переход к МАТРИЦА – МАТЕМАТИКА и det и вызов рассматриваемой матрицы предоставит определитель для матрицы.В Excel =mdeterm также найдет определитель матрицы. Методы, упомянутые в этом разделе, работают только для указанного размера. Для больших матриц рекомендуется использовать калькулятор, Excel или другую программу.
Найдите определитель матрицы .
от
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы, мы можем применить правило Крамера для решения системы из трех уравнений и трех неизвестных.Правило Крамера для систем следует той же схеме, что и для систем. Однако требуются дополнительные расчеты.
Рассмотрим систему:
где:
Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Всегда проверяйте ответ.
Решите следующую систему, используя правило Крамера.
Используйте правило Крамера.
Затем,
Решение (1,3,-2).
Используйте правило Крамера для решения системы:
а. Решите систему уравнений (если возможно), используя правило Крамера.
Начнем с нахождения определителей:
Теперь мы знаем, что оно либо зависимо, либо противоречиво.Давайте посмотрим на один из других определителей.
Поскольку -16 \neq 0, мы имеем противоречивое решение.
б. Решите следующую систему уравнений (если возможно, или дайте общее решение, если зависит).
Найдем D с помощью техники, калькулятора или Excel.
Мы знаем, что это зависимая или противоречивая система. Мы могли бы найти все три других определителя, чтобы увидеть, является ли он зависимым, и если да, то нам пришлось бы использовать rref в калькуляторе, чтобы найти общее решение.По этой причине сейчас быстрее просто использовать rref. Существует онлайн-версия от planetcalc.
Сокращенная ступенчатая форма строки матрицы:
В виде уравнений это:
Итак, если это действительное число, то:
Вот несколько свойств, которые могут упростить и ускорить поиск определителей.
- Если матрица имеет форму верхнего треугольника (в нижнем треугольнике под диагональю все нули), то определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю.
- Если матрица содержит строку или столбец из нулей, определитель равен 0.
- Определитель обратной матрицы равен обратной величине определителя матрицы .
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Применение определителя к системам: правило Крамера
Применение определителя к системам: правило КрамераМы видели, что определитель может быть полезен при нахождении обратной невырожденной матрицы.Мы можем использовать эти выводы при решении линейных систем, для которых матричный коэффициент невырожден (или обратим).
Рассмотрим линейную систему (в матричной форме)
А Х = В
где A — коэффициент матрицы, B — неоднородный член, а X — неизвестная матрица-столбец. У нас есть:
Теорема. Линейная система AX = B имеет единственное решение тогда и только тогда, когда A обратима.В этом случае решение дается так называемыми формулами Крамера :
Где x I — это неизвестные системы или записи x , а матрица A I получается от A , заменив I Th столбец за столбцом B . Другими словами, мы имеем
где b i — это записи B .
В частности, если линейная система AX = B однородна, то есть , тогда, если A обратимо, единственное решение будет тривиальным, то есть . Поэтому, если мы ищем ненулевое решение системы, матричный коэффициент A должен быть сингулярным или необратимым. Мы также знаем, что это произойдет тогда и только тогда, когда . Это важный результат.
Пример. Решите линейную систему
Ответ. Во-первых, обратите внимание, что
откуда следует, что матричный коэффициент обратим. Таким образом, мы можем использовать формулы Крамера. У нас есть
Мы оставляем детали читателю, чтобы найти
Заметим, что легко видеть, что z =0. Действительно, определитель, дающий z , имеет две одинаковые строки (первую и последнюю). Мы рекомендуем вам проверить, что значения, найденные для x , y и z , действительно являются решением данной системы.
Примечание. Помните, что формулы Крамера справедливы только для линейных систем с обратимым матричным коэффициентом.
[Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]S.O.S MATH: домашняя страница
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор : М.А. Хамси
Copyright 1999-2022 MathMedics, LLC. Все права защищены.Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователя онлайн за последний час
Решения с использованием определителей с тремя переменными
Линейные уравнения: решения с использованием определителей с тремя переменными
Определитель матрицы 2 × 2 определяется следующим образом:
Определитель матрицы 3 × 3 можно определить, как показано ниже.
Каждый младший определитель получается вычеркиванием первого столбца и одной строки.
Пример 1
Оцените следующий определитель.
Сначала найдите второстепенные определители.
Решение
Чтобы использовать определители для решения системы из трех уравнений с тремя переменными (правило Крамера), скажем, x , y и z , четыре определителя должны быть сформированы в соответствии с этой процедурой:
Запишите все уравнения в стандартной форме.
Создайте определитель знаменателя, D , используя коэффициенты x , y и z из уравнений и оцените его.
Создать
- 7 x
- 04 , d Z D Z D Z D Z D Y D , и Z -numerator, D Z заменив соответствующие коэффициенты x , y и z константами из уравнений в стандартной форме и вычислить каждый определитель.
- 7 x
Ответы для x , y и z следующие:
Пример 2
Решите эту систему уравнений, используя правило Крамера.
Найдите второстепенные определители.
Используйте константы для замены x ‐коэффициентов.
Используйте константы для замены y ‐коэффициентов.
Используйте константы для замены z ‐коэффициентов.
Следовательно,
Чек оставлен вам.

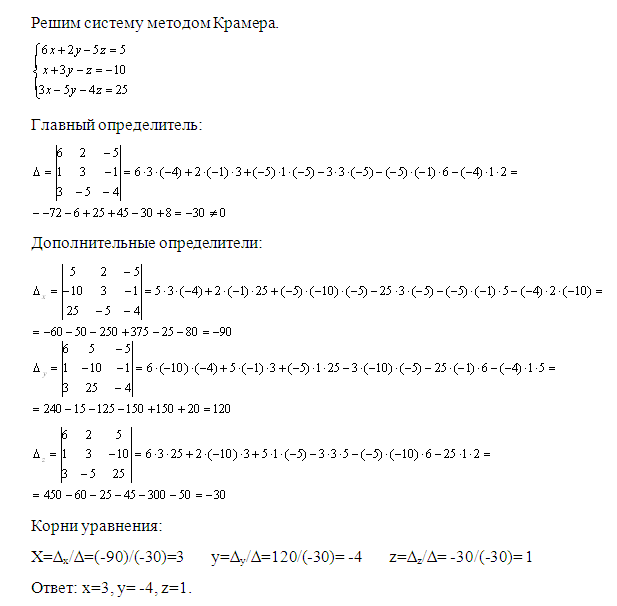


 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.