Формулы корней тригонометрических уравнений таблица: Формулы корней тригонометрических уравнений в таблице
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 2 Для синуса: Для косинуса: Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции: Методы решения тригонометрических уравнений Решение любого тригонометрического уравнения состоит из двух этапов:
Рассмотрим на примерах основные методы решения. Алгебраический метод. В этом методе делается замена переменной и ее подстановка в равенство. Пример. Решить уравнение: 2cos2(x+π6)−3sin(π3—x)+1=02cos2(x+π6)-3sin(π3—x)+1=0 Решение. Используя формулы приведения, имеем: 2cos2(x+π6)−3cos(x+π6)+1=02cos2(x+π6)-3cos(x+π6)+1=0, делаем замену: cos(x+π6)=ycos(x+π6)=y, тогда 2y2−3y+1=02y2-3y+1=0, находим корни: y1=1,y2=12y1=1,y2=12, откуда следуют два случая: 1. 2. cos(x+π6)=12cos(x+π6)=12, x+π6=±arccos12+2πnx+π6=±arccos12+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn. Ответ: x1=−π6+2πnx1=-π6+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn. Разложение на множители. Пример. Решить уравнение: sinx+cosx=1sinx+cosx=1. Решение. Перенесем влево все члены равенства: sinx+cosx−1=0sinx+cosx-1=0. Используя формулы двойного угла, преобразуем и разложим на множители левую часть: sinx—2sin2 x2=0sinx—2sin2 x2=0, 2sin x2cos x2−2sin2 x2=02sin x2cos x2-2sin2 x2=0, 2sin x2(cos x2−sin x2)=02sin x2(cos x2-sin x2)=0,
Ответ: x1=2πnx1=2πn, x2=π2+2πnx2=π2+2πn. Приведение к однородному уравнению Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов: asinx+bcosx=0asinx+bcosx=0 (однородное уравнение первой степени) или asin2x+bsinxcosx+ccos2x=0asin2x+bsinxcosx+ccos2x=0 (однородное уравнение второй степени). Потом разделить обе части на cosx≠0cosx≠0 — для первого случая, и на cos2x≠0cos2x≠0 — для второго. Получим уравнения относительно tg xtg x: a tg x+b=0a tg x+b=0 и a tg2x+b tg x+c=0a tg2x+b tg x+c=0, которые нужно решить известными способами. Пример. Решить уравнение: 2sin2x+sinxcosx—cos2x=12sin2x+sinxcosx—cos2x=1. Решение. Запишем правую часть, как 1=sin2x+cos2x1=sin2x+cos2x: 2sin2x+sinxcosx—cos2x=2sin2x+sinxcosx—cos2x= sin2x+cos2xsin2x+cos2x, 2sin2x+sinxcosx—cos2x−2sin2x+sinxcosx—cos2x- sin2x—cos2x=0sin2x—cos2x=0 sin2x+sinxcosx—2cos2x=0sin2x+sinxcosx—2cos2x=0. Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на cos2x≠0cos2x≠0, получим: sin2xcos2x+sinxcosxcos2x—2cos2xcos2x=0sin2xcos2x+sinxcosxcos2x—2cos2xcos2x=0 tg2x+tgx—2=0tg2x+tgx—2=0. Введем замену tgx=ttgx=t, в результате t2+t—2=0t2+t—2=0. Корни этого уравнения: t1=−2t1=-2 и t2=1t2=1. Тогда:
Ответ. x1=arctg(−2)+πnx1=arctg(-2)+πn, n∈Zn∈Z, x2=π4+πnx2=π4+πn, n∈Zn∈Z. Переход к половинному углу Пример. Решить уравнение: 11sinx—2cosx=1011sinx—2cosx=10. Решение. Применим формулы двойного угла, в результате: 22sin(x2)cos(x2)−22sin(x2)cos(x2)- 2cos2x2+2sin2x2=2cos2x2+2sin2x2= 10sin2x2+10cos2x210sin2x2+10cos2x2 4tg2x2—11tgx2+6=04tg2x2—11tgx2+6=0 Применив описанный выше алгебраический метод, получим:
Ответ. x1=2arctg2+2πn,n∈Zx1=2arctg2+2πn,n∈Z, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z. ⇐ Предыдущая12 Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 972; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Электронный справочник по математике для школьников тригонометрия решение простейших тригонометрических уравнений
| Справочник по математике | Тригонометрия |
Содержание
| Решение уравнения sin x = a |
| Решение уравнения cos x = a |
| Решение уравнения tg x = a |
| Решение уравнения ctg x = a |
Простейшими тригонометрическими уравнениями называют уравнения вида:
sin x = a , cos x = a ,
tg x = a , ctgx = a .
где a – произвольное число.
Решение уравнения sin
x = a| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1
Рис. 1
Частные случаи решения уравнений sin x = a
| Уравнение | Решение |
| sin x = – 1 | |
| sin x = 0 | |
| sin x = 1 |
Уравнение: sin x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: sin x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: sin x = 1 Решение: |
Решение уравнения cos
x = a| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2
Рис. 2
Частные случаи решения уравнений cos x = a
| Уравнение | Решение |
| cos x = – 1 | |
| cos x = 0 | |
| cos x = 1 |
Уравнение: cos x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 1 Решение: |
Решение уравнения tg
x = a| Обычная форма записи решения: | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Рис. 3
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
| tg x = – 1 | |
| tg x = 0 | |
| tg x = 1 | |
Уравнение: Решение: |
Уравнение: tg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 0 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 1 Решение: |
Уравнение: Решение: |
Решение уравнения ctg
x = a| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
Рис. 4
Частные случаи решения уравнений ctg x = a
| Уравнение | Решение |
| ctg x = – 1 | |
| ctg x = 0 | |
| ctg x = 1 | |
Уравнение: Решение: |
Уравнение: ctg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: ctg x = 0 Решение: |
Решение: |
Уравнение: ctg x = 1 Решение: |
Уравнение: Решение: |
Сводка тригонометрических формул
Сводка тригонометрических формул На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.
На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.Формулы для дуг и секторов окружностей
Вы можете легко найти длину дуги и площадь сектора для угла θ в круге радиусом r .
| Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах. Чтобы перевести градусы в радианы, умножьте количество градусов на | |
| Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах. |
Формулы для прямоугольных треугольников
Наиболее важными формулами тригонометрии являются формулы прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус теты — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, а тангенс — это отношение противоположная сторона соседней стороне.
Эти три формулы вместе известны мнемоникой SohCahToa. Кроме того, есть очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.
Зная, что два острых угла дополняют друг друга, то есть дают в сумме 90°, можно решить любой прямоугольный треугольник:
- Если известны две из трех сторон, то можно найти третью сторону и оба острых угла.
- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Формулы для косоугольных треугольников
Эти формулы работают для любого треугольника, острого, тупоугольного или прямоугольного. Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначены прописными буквами
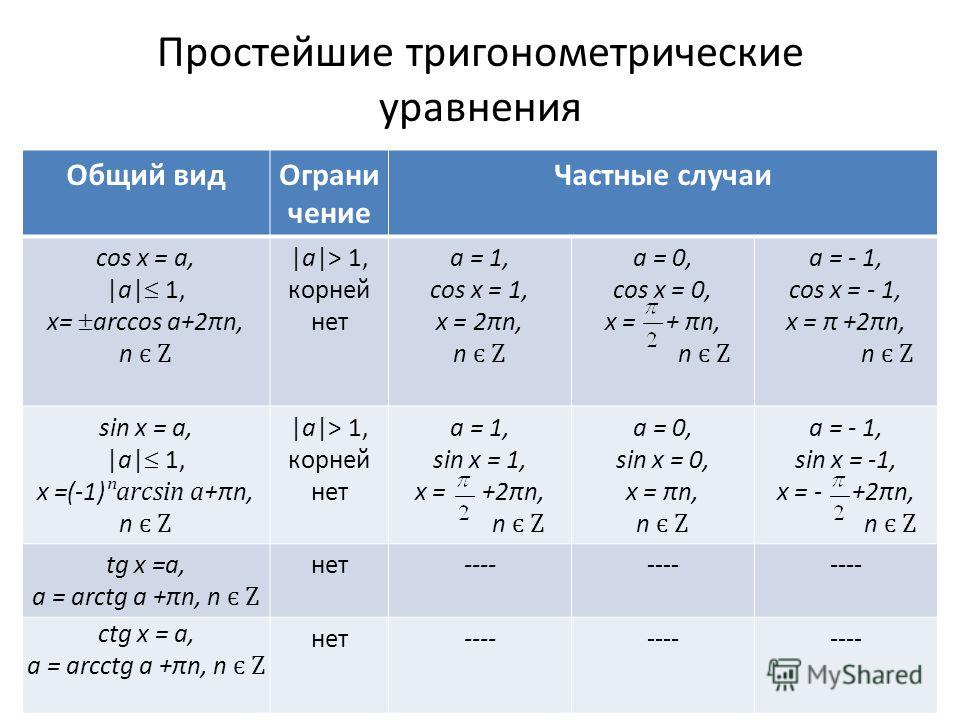
Есть две важные формулы для косых треугольников. Они называются законом косинусов и законом синусов.
Закон косинусов обобщает формулу Пифагора на все треугольники. Он говорит, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумма квадратов двух других сторон минус 2. ab cos  C , удвоенное произведение их на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.
С помощью этих двух формул вы можете решить любой треугольник:
- Если вам известны два угла и сторона, вы можете найти третий угол и две другие стороны.
- Если известны две стороны и угол между ними, можно найти третью сторону и оба других угла.

- Если вы знаете две стороны и угол, противолежащий одной из них, то существует два варианта угла, противолежащего другому (один острый и один тупой), и для обоих вариантов вы можете определить оставшийся угол и оставшуюся сторону.
Формулы площади треугольников
Существует три различных полезных формулы площади треугольника, и какую из них использовать, зависит от имеющейся у вас информации.
| Половина основания, умноженная на высоту. Это обычный способ использования, так как он самый простой, и у вас обычно есть эта информация. Выберите любую сторону для вызова базы b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh . | |
Формула Герона. Это полезно, когда вы знаете три стороны a , b и c треугольника, и все, что вы хотите знать, это площадь. Пусть s составляют половину их суммы, называемой полупериметром . Тогда площадь является квадратным корнем произведения s , s — a , s — b и s — c . Тогда площадь является квадратным корнем произведения s , s — a , s — b и s — c . | |
| Формула «бок-угол-бок». Используйте это, когда вы знаете две стороны, a и b , и прилежащий угол, C . Площадь равна половине произведения двух сторон на синус прилежащего угла. |
Тригонометрические формулы — Примеры | Список тригонометрических формул
Тригонометрические формулы представляют собой наборы различных формул, включающих тригонометрические тождества, используемые для решения задач, основанных на сторонах и углах прямоугольного треугольника. Эти формулы тригонометрии включают тригонометрические функции, такие как синус, косинус, тангенс, косеканс, секанс, котангенс для заданных углов. Давайте подробно изучим эти формулы, включающие тождества Пифагора, тождества произведения, тождества кофункций (углы сдвига), тождества суммы и разности, тождества двойного угла, тождества половинного угла и т. д., в следующих разделах.
д., в следующих разделах.
| 1. | Список формул тригонометрии |
| 2. | Основные формулы тригонометрии |
| 3. | Тригонометрические формулы, включающие взаимные тождества |
| 4. | Таблица тригонометрических соотношений |
| 5. | Тригонометрические формулы, включающие периодические тождества (в радианах) |
| 6. | Тригонометрические формулы, включающие тождества кофункций (в градусах) |
| 7. | Тригонометрические формулы, включающие тождества суммы и разности |
| 8. | Множественные и дольные углы |
| 9. | Сумма и произведение тождеств |
| 10. | Формулы обратной тригонометрии |
| 11. | Тригонометрические формулы, использующие законы синусов и косинусов |
12. | Часто задаваемые вопросы по формулам тригонометрии |
Список формул тригонометрии
Тригонометрические формулы можно разделить на различные категории в зависимости от задействованных тригонометрических тождеств. Давайте посмотрим на приведенные ниже наборы различных формул тригонометрии.
- Формулы основных тригонометрических соотношений: это формулы тригонометрии, относящиеся к основным тригонометрическим соотношениям sin, cos, tan и т. д.
- Взаимные тождества: сюда входят формулы тригонометрии, имеющие дело с обратными отношениями между отношениями триггеров.
- Таблица тригонометрических соотношений: Значения тригонометрии представлены для стандартных углов в таблице тригонометрии.
- Периодические тождества: они содержат формулы тригонометрии, которые помогают найти значения тригонометрических функций для сдвига углов на π/2, π, 2π и т. д.
- Тождества кофункций: Тригонометрические формулы для тождеств кофункций изображают взаимосвязи между тригонометрическими функциями.

- Тождества суммы и разности: Эти тригонометрические формулы используются для нахождения значения тригонометрической функции для суммы или разности углов.
- Половинные, двойные и тройные тождества: Эти тригонометрические формулы включают значения тригонометрических функций для половинных, двойных или тройных углов.
- Sum to Product Identities: Эти тригонометрические формулы используются для представления произведения тригонометрических функций в виде их суммы или наоборот.
- Формулы обратной тригонометрии: формулы обратной тригонометрии включают формулы, связанные с обратными тригонометрическими функциями, такими как обратный синус, обратный косинус и т. д.
- Закон синусов и закон косинусов
Некоторые основные формулы тригонометрии можно увидеть на изображении ниже. Рассмотрим их подробно в следующих разделах.
Основные формулы тригонометрии
Основные формулы тригонометрии используются для нахождения соотношения тригонометрических соотношений и отношения соответствующих сторон прямоугольного треугольника. В тригонометрии используются шесть основных тригонометрических отношений, также называемых тригонометрическими функциями: синус, косинус, секанс, косеканс, тангенс и котангенс, которые записываются как sin, cos, sec, csc, tan, cot. Тригонометрические функции и тождества выводятся с использованием прямоугольного треугольника в качестве эталона. Мы можем узнать значения синуса, косинуса, тангенса, секанса, косеканса и котангенса, учитывая размеры прямоугольного треугольника, используя формулы тригонометрии, как,
В тригонометрии используются шесть основных тригонометрических отношений, также называемых тригонометрическими функциями: синус, косинус, секанс, косеканс, тангенс и котангенс, которые записываются как sin, cos, sec, csc, tan, cot. Тригонометрические функции и тождества выводятся с использованием прямоугольного треугольника в качестве эталона. Мы можем узнать значения синуса, косинуса, тангенса, секанса, косеканса и котангенса, учитывая размеры прямоугольного треугольника, используя формулы тригонометрии, как,
Формулы тригонометрических соотношений
- sin θ = Перпендикуляр/Гипотенуза
- cos θ = основание/гипотенуза
- тангенс θ = Перпендикуляр/Основание
- с θ = гипотенуза/основание
- косек θ = гипотенуза/перпендикуляр
- кроватка θ = основание/перпендикуляр
Тригонометрические формулы, включающие взаимные тождества
Косеканс, секанс и котангенс являются обратными величинами основных тригонометрических отношений синуса, косинуса и тангенса. Все взаимные тождества также получены с использованием прямоугольного треугольника в качестве эталона. Эти взаимные тригонометрические тождества выводятся с использованием тригонометрических функций. Формулы тригонометрии на взаимных тождествах, приведенные ниже, часто используются для упрощения тригонометрических задач.
Все взаимные тождества также получены с использованием прямоугольного треугольника в качестве эталона. Эти взаимные тригонометрические тождества выводятся с использованием тригонометрических функций. Формулы тригонометрии на взаимных тождествах, приведенные ниже, часто используются для упрощения тригонометрических задач.
- cosec θ = 1/sin θ
- сек θ = 1/cos θ
- кроватка θ = 1/загар θ
- sin θ = 1/косек θ
- cos θ = 1/сек θ
- загар θ = 1/кот θ
Таблица тригонометрических соотношений
Вот таблица тригонометрических формул для углов, которые обычно используются для решения тригонометрических задач. Таблица тригонометрических соотношений помогает найти значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 9°.0°.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Углы (в радианах) | 0° | №/6 | №/4 | π/3 | π/2 | № | 3π/2 | 2π |
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| потому что | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| желтовато-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| сек | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Тригонометрические формулы, включающие периодические тождества (в радианах)
Тригонометрические формулы, включающие периодические тождества, используются для сдвига углов на π/2, π, 2π и т. д. Все тригонометрические тождества цикличны по своей природе, что означает, что они повторяются через точку. Этот период различен для разных формул тригонометрии периодических тождеств. Например, tan 30° = tan 210°, но это неверно для cos 30° и cos 210°. Вы можете обратиться к формулам тригонометрии, приведенным ниже, чтобы проверить периодичность функций синуса и косинуса.
д. Все тригонометрические тождества цикличны по своей природе, что означает, что они повторяются через точку. Этот период различен для разных формул тригонометрии периодических тождеств. Например, tan 30° = tan 210°, но это неверно для cos 30° и cos 210°. Вы можете обратиться к формулам тригонометрии, приведенным ниже, чтобы проверить периодичность функций синуса и косинуса.
Первый квадрант:
- sin (π/2 – θ) = cos θ
- cos (π/2 – θ) = sin θ
- sin (π/2 + θ) = cos θ
- cos (π/2 + θ) = – sin θ
Второй квадрант:
- sin (3π/2 – θ) = – cos θ
- cos (3π/2 – θ) = – sin θ
- sin (3π/2 + θ) = – cos θ
- cos (3π/2 + θ) = sin θ
Третий квадрант:
- sin (π – θ) = sin θ
- соз (π – θ) = – соз θ
- грех (π + θ) = – грех θ
- cos (π + θ) = – cos θ
Четвертый квадрант:
- sin (2π – θ) = – sin θ
- соз (2π — θ) = соз θ
- грех (2π + θ) = грех θ
- , потому что (2π + θ) = потому что θ
Тригонометрические формулы, включающие тождества кофункций (в градусах)
Тригонометрические формулы тождеств кофункций обеспечивают взаимосвязь между различными тригонометрическими функциями. Формулы тригонометрии кофункций представлены в градусах ниже:
Формулы тригонометрии кофункций представлены в градусах ниже:
- sin(90° − x) = cos x
- cos(90° — x) = sin x
- загар(90° — х) = раскладушка х
- кроватка(90° — х) = загар х
- сек(90° — х) = косек х
- косек(90° — х) = сек х
Тригонометрические формулы, включающие тождества суммы и разности
Тождества суммы и разности включают тригонометрические формулы sin(x + y), cos(x — y), cot(x + y) и т. д.
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) — sin(x)sin(y)
- tan(x + y) = (tan x + tan y)/(1 — tan x • tan y)
- sin(x – y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- тангенс(х — у) = (тангенс х — тангенс у)/(1 + тангенс х • тангенс у)
Тригонометрические формулы для кратных и дольных углов
Тригонометрические формулы для кратных и дольных углов могут быть использованы для расчета значения тригонометрических функций для половинного угла, двойного угла, тройного угла и т. д.
д.
Тригонометрические формулы, включающие тождества половин угла
Половина угла x представлена несколькими приведенными ниже тригонометрическими формулами.
sin (x/2) = ±√[(1 — cos x)/2]
cos (x/2) = ± √[(1 + cos x)/2]
tan (x/2) = ±√[(1 — cos x)/(1 + cos x)]
или, tan (x/2) = ±√[(1 — cos x)(1 — cos x)/(1 + cos x) )(1 — cos x)]
tan (x/2) = ±√[(1 — cos x) 2 /(1 — cos 2 x)]
⇒ tan (x/2) = (1 — cos x)/sin x
Тригонометрические формулы, включающие тождества двойного угла
Двойной угол x представлен несколькими приведенными ниже тригонометрическими формулами.
- sin (2x) = 2sin(x) • cos(x) = [2tan x/(1 + tan 2 x)]
- cos (2x) = cos 2 (x) — sin 2 (x) = [(1 — tan 2 x)/(1 + tan 2 x)]
- cos (2x) = 2cos 2 (x) — 1 = 1 — 2sin 2 (x)
- тангенс (2x) = [2tan(x)]/ [1 — тангенс 2 (х)]
- сек (2x) = сек 2 х/(2 — сек 2 х)
- косек (2x) = (сек х • косек х)/2
Тригонометрические формулы, включающие тождества тройного угла
Тройка угла x представлена в нескольких приведенных ниже тригонометрических формулах.
- sin 3x = 3sin x — 4sin 3 x
- cos 3x = 4 cos 3 x — 3cos x
- tan 3x = [3tanx — tan 3 x]/[1 — 3tan 2 х]
Формулы тригонометрии — тождества суммы и произведения
Тригонометрические формулы для суммы или произведения тождеств используются для представления суммы любых двух тригонометрических функций в форме их произведения или наоборот.
Тригонометрические формулы, включающие тождества продуктов
- sinx⋅cosy = [sin(x + y) + sin(x − y)]/2
- cosx⋅cosy = [cos(x + y) + cos(x − y)]/2
- sinx⋅siny = [cos(x − y) − cos(x + y)]/2
Тригонометрические формулы, включающие тождества суммы и произведения
Комбинацию двух острых углов A и B можно представить с помощью тригонометрических отношений в приведенных ниже тригонометрических формулах.
- sinx + siny = 2[sin((x + y)/2)cos((x − y)/2)]
- sinx − siny = 2[cos((x + y)/2) sin((x − y)/2)]
- cosx + cosy = 2[cos((x + y)/2)cos((x − y)/2)]
- cosx — уютный = -2 [sin ((x + y)/2) sin ((x — y)/2)]
Формулы обратной тригонометрии
Используя формулы обратной тригонометрии, тригонометрические соотношения инвертируются для создания обратных тригонометрических функций, таких как sin θ = x и θ = sin −1 x. Здесь x может иметь значения в целых числах, десятичных дробях, дробях и показателях степени.
Здесь x может иметь значения в целых числах, десятичных дробях, дробях и показателях степени.
- sin -1 (-x) = -sin -1 x
- cos -1 (-x) = π — cos -1 x
- рыжевато-коричневый -1 (-x) = -tan -1 x
- косек -1 (-x) = -косек -1 x
- сек -1 (-x) = π — сек -1 x
- детская кроватка -1 (-x) = π — детская кроватка -1 x
Тригонометрические формулы, использующие законы синусов и косинусов
Закон синуса: Закон синуса и закон косинуса определяют отношение между сторонами и углами треугольника. Закон синусов дает отношение сторон и угла, противолежащего стороне. В качестве примера берется отношение стороны «а» и противолежащего ей угла «А».
(sin A)/a = (sin B)/b = (sin C)/c
Закон косинуса: Закон косинуса помогает найти длину стороны для заданных длин двух других сторон и включенный угол. Например, длину «а» можно найти с помощью двух других сторон «b» и «с» и прилежащего к ним угла «А».
Например, длину «а» можно найти с помощью двух других сторон «b» и «с» и прилежащего к ним угла «А».
- a 2 = b 2 + c 2 — 2bc cosA
- b 2 = a 2 + c 2 — 2ac cosB
- с 2 = а 2 + b 2 — 2ab cosC
где, a, b, c — длины сторон треугольника, а A, B, C — углы треугольника.
Связанные темы
- Грех Кос Тан
- Тригонометрические тождества
- Функции косеканса, секанса и котангенса
- Тригонометрические соотношения
- Тригонометрические формулы для класса 10
- Тригонометрический калькулятор
Примеры использования формул тригонометрии
Пример 1: Рэйчел дано тригонометрическое соотношение тангенса θ = 5/12. Помогите Рэйчел найти тригонометрическое отношение cosec θ, используя формулы тригонометрии.

Решение:
tan θ = перпендикуляр/ основание = 5/12
Перпендикуляр = 5 и основание = 12
Гипотеназа 2 = перпендикуляр 2 + База 2
2 + База 2 2 + база 2 2 + база 2 3 2 + база 2 3 2 + база0002 Hypotenuse 2 = 5 2 + 12 2Гипотеназа 2 = 25 + 144
Гипотеновая
cosec θ = гипотенуза/перпендикуляр = 13/5
Ответ: Используя формулы тригонометрии, cosec θ = 13/5
Пример 2: В рамках задания Сэмюэль должен найти значение Sin 15º, используя формулы тригонометрии. Как мы можем помочь Самуэлю найти ценность?
Решение:sin 15°
= sin (45° — 30°)
= sin 45°cos 30° — cos 45°sin 30°
= [(1/√3) -2 (1/√3) √2) × (1/2)] = (√3 — 1)/2√2
Ответ: sin 15° = (√3 — 1)/2√2
Пример 3: Если sin θcos θ = 5, найдите значение (sin θ + cos θ) 2 , используя формулы тригонометрии.

Решение:
(sin θ + cos θ) 2
= sin 2 θ + cos 2 θ + 2sinθcosθ
= (1) + 2 (5) = 1 + 10 = 11
Ответ: (sin θ + cos θ) 2 3. = 11
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по тригонометрической формуле
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о тригонометрических формулах
Что такое тригонометрические формулы?
Тригонометрические формулы используются для решения задач, основанных на сторонах и углах прямоугольного треугольника, с использованием различных тригонометрических тождеств. Эти формулы можно использовать для вычисления тригонометрических отношений (также называемых тригонометрическими функциями), sin, cos, tan, csc, sec и cot.
Эти формулы можно использовать для вычисления тригонометрических отношений (также называемых тригонометрическими функциями), sin, cos, tan, csc, sec и cot.
Что такое Основная формула тригонометрии?
Основные формулы тригонометрии включают представление основных тригонометрических соотношений в терминах отношения соответствующих сторон прямоугольного треугольника. Они задаются следующим образом: sin θ = Противоположная сторона/Гипотенуза, cos θ = Прилегающая сторона/Гипотенуза, tan θ = Противоположная сторона/Прилегающая сторона.
Что такое формулы тригонометрических соотношений?
В тригонометрии используются три основные функции: синус, косинус и тангенс. Формулы тригонометрических соотношений имеют следующий вид:
- Функция синуса: sin(θ) = противоположность / гипотенуза
- Функция косинуса: cos(θ) = смежная / гипотенуза
- Функция касания: tan(θ) = Противоположный / Смежный
Что такое тригонометрические формулы для четных и нечетных тождеств?
Тригонометрические формулы, включающие четные и нечетные тождества, задаются следующим образом:
- sin(–x) = –sin x
- cos(-x) = cosx
- тангенс(–х) = –тангенс х
- csc (–x) = –csc x
- сек (–x) = сек х
- детская кроватка (-x) = -кроватка x
Какие формулы тригонометрии включают пифагорейские тождества?
Три фундаментальные формулы тригонометрии, включающие пифагорейские тождества, задаются следующим образом:
К какому треугольнику применимы тригонометрические формулы?
Формулы тригонометрии применимы к прямоугольным треугольникам.

 Все правила по сольфеджио
Все правила по сольфеджио
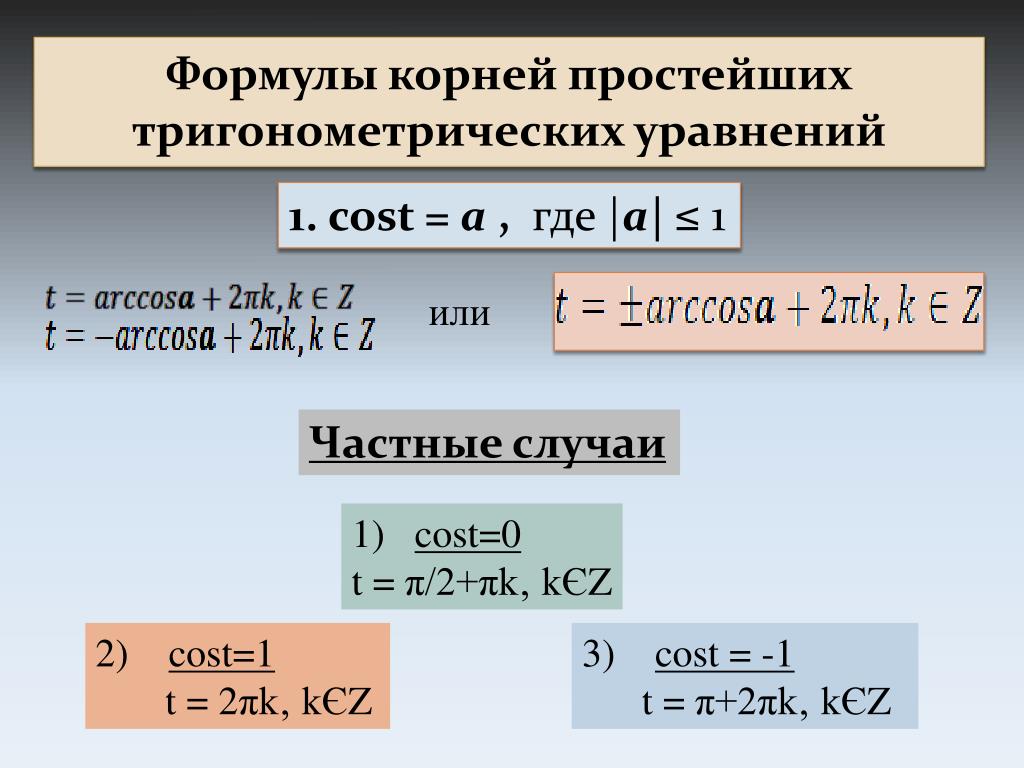 cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn.
cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn.

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.005 с.)


