Формулу разности квадратов: Формула разности квадратов — урок. Алгебра, 7 класс.
Урок 29. разность квадратов — Алгебра — 7 класс
Алгебра
7 класс
Урок № 29
Разность квадратов
Перечень вопросов, рассматриваемых в теме:
- Формулы сокращённого умножения.
- Разность квадратов.
- Разложение многочлена на множители.
- Тождественные преобразования.
- Вычисление значения числовых выражений.
Тезаурус:
Применение:
• упрощение умножения многочленов;
• разложение многочлена на множители;
• вычисление значения числового выражения;
• тождественные преобразования.
Основная литература:
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М.

- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Вы знаете формулы квадрата суммы и квадрата разности.
Сегодня мы рассмотрим ещё одну формулу и покажем её справедливость, применив это правило.
Рассмотрим произведение:
Формула разности квадратов.
Получено равенство, которое называют формулой разности квадратов.
Формулу разности квадратов используют:
• для упрощения умножения многочленов;
• для разложения многочлена на множители;
• для упрощения вычислений.
На рисунке выделена красным контуром, состоит из желтого и зеленого прямоугольников.
Площади составлены из одинаковых прямоугольников, значит, они равны.
Тождество.
Для преобразования выражений используют тождество:
Разбор решения заданий тренировочного модуля.
Задача 1.
Задача 2.
Примеры:
Задача 3.
Вычисление значений числовых выражений.
В первом случае вы, вероятно, находили квадрат числа умножением в столбик, во втором случае устно.
Ответ: 200.
Формула разности квадратов двух выражений.
Жамашева Г.А, учитель высшей категории математики и физики КГУ «СОШ № 1»
ЗКО, Жанибекский р-н, п. Жанибек
Алгебра 7в класс.
Тема: Формула разности квадратов двух выражений.
Цель урока: знать формулу разности квадратов двух выражений, уметь применять при вычислении.
Задачи:
— повторить правила умножения многочлена на многочлен.
— уметь применять теоретические знания при решении упражнений.
— развивать умение работать самостоятельно.
— объективно оценивать результат своего труда.
Тип урока: изучение нового материала.
Оборудование: презентация, карточки для устной и письменной работы.
Ход урока:
Организационный момент
Рефлексия настроения.
Приветствую всех вас! Мы начинаем урок алгебры. Я пришла к вам на урок с хорошим настроением.
Надеюсь, что хорошее настроение будет нас сопровождать весь урок и поможет нам добиться хороших результатов. Успехов Вам!
Садитесь. Открыли тетради. Приготовились к проверке домашнего задания.
Решите уравнение
6+(2-4х)+5=3(1-3х)
6+2-4х+5=3-9х
-4х+9х=3-13
5х=-10
х=-2 ответ: -2.
3х(2х-1)-6х(7+х)=90
6х2-3х-42х-6х2=90
х=-2 ответ: -2
5х2+3х=0
х(5х+3)=0
х=0 или 5х+3=0
5х=-3
х=-0,6 ответ: 0; -0,6
0,3х2-3х=0
0,3х(х-10)=0
0,3х=0 или х-10=0
х=10 ответ: 0; 10
Разложите на множители.
а) 4с4 — 6х2с2 +8с=2с(2с3 – 3х2с+4)
б) 10ха2 – 15а3 – 20а4х= 5а
в) 8а4в3 – 12а2в4+16а3в2= 4а2в2(2а2в – 3в2+4а)
(Заранее на доске написаны ответы по домашнему заданию)
— Есть ли вопросы по домашнему заданию?
— Эпиграфом к нашему уроку возьмем слова С. Ковалевской
Ковалевской
«У математиков существует свой язык — это формулы» (Слайд №2)
— Как вы думаете, что мы будем сегодня изучать?
— формулы
И приступаем мы к изучению одной из главных тем курса алгебры 7 класса
— Формулы сокращенного умножения
Почему формулам дали название «Формулы сокращенного умножения»?
(Ответы учащихся)
Судя по названию для чего нужны эти формулы?
— Чтобы облегчить процесс умножения – совершенно верно
Сегодня на уроке мы с вами рассмотрим первую формулу из этой группы.
Формула разности квадратов двух выражений (откройте тетради, запишите число и тему урока) (Слайд №3)
Желаю работать, желаю трудиться,
Желаю успехов сегодня добиться,
Ведь в будущем все это вам пригодиться,
И легче в дальнейшем вам будет учиться.
Ну, а чтоб все на уроке прошло без заминки – его мы начнем, ну конечно, с разминки.
Сейчас я предлагаю вам задание для работ в группах. У меня здесь перепутались карточки к вопросам. Помогите для вопроса найти ответ
Вопросы
Что называется числовыми множителями?
Что называется буквенными множителями?
Что такое одночлен?
Что называется коэффициентом одночлена?
Что такое подобные одночлены
Что такое степень одночлена?
Что такое многочлен?
Что называется двучленом?
Что такое трехчлен?
Что такое степень многочлена?
Как выполнить умножение одночлена на многочлен?
Как выполнить умножение многочлена на многочлен?
Как по -другому называется одночлен?
Как по -другому называется многочлен?
Как по -другому называется двучлен?
Ответы
Множители, записанные с помощью цифр
Множители, записанные буквами и их натуральными степенями
Произведение числовых и буквенных множителей и их степеней
Числовой множитель одночлена, записанного в стандартном виде
Одночлены, имеющие общую буквенную часть и отличающиеся друг от друга только коэффициентами
Сумму показателей степеней всех переменных
Алгебраическая сумма нескольких одночленов
Многочлен, состоящий из двух членов
Многочлен, состоящий из трех членов
Наибольшую из степеней одночленов, входящих в многочлен стандартного вида
Чтобы умножить многочлен на одночлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить
Моном
Полином
Бином
(Слайд №5)
(группы выполняют задания и по окончании работы сверяют свои ответы)
Следующее задание для работы в парах.
Задание «Домино» (5 мин)
(у учащихся на партах карточки, похожие на домино, на одной части карточки задание, на другой ответ. Учащимся необходимо собрать домино, т.е. расположить карточки так, чтобы задания находилось рядом с правильным ответом)
Затем осуществляется проверка (Слайд №6)
После выполнения задания учащимся выставляют в оценочный лист напротив задания «+» если задание выполнено, верно, «-» если неверно.
(Слайд №7) Найдите квадраты чисел
42; 52; 12; 82;
(2а)2; (3в)2; (6m)2;
(n)2 ; ()2; (3 ) 2
Ответы
16; 25; 1; 64;
4а2; 9в2; 36m2;
n2 ; 2 ; 2 у6
(Слайд № 8). Запишите числа в виде квадратов.
Запишите числа в виде квадратов.
Ответы
16а2; 25в2; 49м2; 100х2 (4а)2; (5в)2; (7m)2; (10х)2;
0,04у2; 0,64с2; 0,01а2; (0,2у)2; (0,8с)2; (0,1а)2;
2 ; 4 ; 6 у6 ()2 ; (2)2; ( 3у3)2
Изучение нового материала.
Я предлагаю вам решить следующие примеры на упрощение выражений.
(Слайд №9)
(а-в)*(а+в) а2 – в2
(m-n)*(m+n) m2 – n2
(х-у)*(х+у) х2 – у2
(с-d)*(c+d) c2 – d2
(p-q)*(p+q) p2 – q2
Какую закономерность вы заметили при решении этих заданий?
Что у них общего и в чем различие?
Какой вывод можно сделать?
Имеет ли смысл выполнять подробную запись решение подобных заданий.

( Слайд №10).
(а-в)*(а+в)= а2-ав+ав-в2= а2 –в2
( Слайд №11).
(а-в)*(а+в)= а2 –в2
а2 –в2=(а-в)*(а+в)
Любое равенство в математике употребляется как слева направо, так и справа налево. Этой формуле в математике дано специальное название – разность квадратов.
Ее читают: Произведение разности двух выражений и их сумма равно разности квадратов этих выражений.
Разность квадратов двух выражений равна произведению разности этих выражений и их сумма.
4.Закрепление полученных знаний.
(Слайд №12)
Выполните умножение (устно).
а) (7m-3)*(7m+3) 49m2 – 9
б) (6а-1)*(6а+1) 36а2 – 1
в) (1+4в)*(1 -4в) 1 – 16в2
г) (5а+2)*(5а — 2) 25а2 — 4
д) (10р3 -7q)*(10p3+7q) 100p6 – 49q2
е) (8d+в5c3)*(8d -5c3) 64d2 – 25c6
Слайд №13 Решение примеров
Вычислите значение произведения чисел по образцу.
79х81=(80-1)(80+1)=802 – 12= 6400-1=6399
По учебнику
Страница 89 №371 (2;4)
5.Самостоятельная работа.
(Слайд 14) Преобразуйте выражение по формуле.
Х2 – 36 (х-6)(х+6)
0,25 – с2 (0,5- с)(0,5+с)
144 – m2 (12-m)(12+m)
25у2 — 49 (5у — 7)(5у+7)
121в2 – с2 (11в – с) (11в + с)
16х2 – 81у2 (4х– 9у) (4х +9у)
c2d2 – a2 (cd — a)(cd + a)
a2b2 -9y2 (ab -3y)(ab+3у)
(7х-9)(7х+9) 49х2 – 81
(в – 4а)(в+4а) в2 – 16а2
Критерии оценивания
Правильно выполненные 10 заданий – «5»
8-9 – «4»
5-7 – «3»
0-4 – необходимы дополнительные занятия.
(Слайд №15)
Решите примеры.
(17,5 – 15,5) х23 = 16
(1,5*1,5 :0,45)2 = 25
(-3)2 + ()-1 = 12
1002 – ((2*10)3 + 32) = 1991
Числа 25,16, 12, 1991.
Как они связаны между собой?
16.12.1991 25-лет независимости нашей Республики
(Слайд 16) Казахстан. видеофильм (1мин)
(Слайд 17) Домашнее задание
§2 № 369 (н) №371 (н) стр.89
Какие слова мы сегодня взяли девизом нашего урока.
Как называется формула, которую мы изучили?
Кто запишет эту формулу на доске?
Как звучит формулировка этой формулы?
Итог урока. Рефлексия
«Байтерек»
«Байтерек» каменный цветок, распутив лепестки, представил миру огромный блистающий шар – символ жизни и добра, озаряющий окрестности яркими бликами отраженных лучей солнца. 2
2
Розкладіть на множники квадратний тричлен 1) а2-18а+172)-х2-4х+213) 9х2+30х+254) -18х2+5х+ 2помогите пожалуйста
Поможіть зробити контрольну з алгебри
Укажите соответствующий вывод для каждого неравенства. Обоснуйте свой ответ а) x2-3x + 5<0b) -5×2 + 3x + 2>0c) x2+ 6x + 9≤0d) x2 – 4≥01. Неравен … ство не имеет решений. 2. Решением неравенства является вся числовая прямая. 3. Решением неравенства является одна точка. 4. Решением неравенства является закрытый промежуток. 5. Решением неравенства является открытый промежуток. 6. Решением неравенства является объединение двух промежутков
Функция задана формулой y = –2x + 3. Определите:1) значение функции, если значение аргумента равно 3;2) значение аргумента, при ко то ром значение фун
… кции равно 5;3) проходит ли график функции через точку B (–1; 5).Постройте график функции y = 5x – 4. Пользуясь графиком, найдите:1) значение функции, если значение аргумента равно 1;2) значение аргумента, при ко то ром значение функции равно 6. Не выполняя построения, найдите координаты точек пересечения графика функции y = 0,2x – 10 с осями координат.При каком значении k график функции y = kx – 15 проходит через точку C (–2; –3)?Постройте график функции у ={ х/2, если х ≤ 4;{ 2, если х > 4.
Не выполняя построения, найдите координаты точек пересечения графика функции y = 0,2x – 10 с осями координат.При каком значении k график функции y = kx – 15 проходит через точку C (–2; –3)?Постройте график функции у ={ х/2, если х ≤ 4;{ 2, если х > 4.
Укажите соответствующий вывод для каждого неравенства. Обоснуйте свой ответ а) x2-3x + 50b) -5×2 + 3x + 20c) x2+ 6x + 90d) x2 – 401. Неравенство не им … еет решений. 2. Решением неравенства является вся числовая прямая. 3. Решением неравенства является одна точка. 4. Решением неравенства является закрытый промежуток. 5. Решением неравенства является открытый промежуток. 6. Решением неравенства является объединение двух промежутков
помогите пожалуйста, нужно решить уровнение
Розв’яжіть систему рівнянь(3x+2y = 6;4x-2y — 8способом додавання.
Чи є число 7 коренем рівняння: 1)х+4=10 2)3 х=21
алгебра кр даю 100 балов за. 5 заданія
Розв’яжіть систему рівняньx+2y = 11;2x-3y=1способом підстановки.
Формулы сокращенного умножения. Разность квадратов, квадрат суммы, разность кубов, бином Ньютона.
Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или квадрата суммы просто невозможно. Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,162 — 2 • 3,16 • 1,16 + 1,162. Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!
Итак, семь формул «школьной» алгебры, которые должны знать все:
| Название | Формула |
| Квадрат суммы | (A + B)2 = A2 + 2AB + B2 |
| Квадрат разности | (A — B)2 = A2 — 2AB + B2 |
| Разность квадратов | (A — B)(A + B) = A2 — B2 |
| Куб суммы | (A + B)3 = A3 + 3A2B + 3AB2+ B3 |
| Куб разности | (A — B)3 = A3 — 3A2B + 3AB2 — B3 |
| Сумма кубов | A3 + B3 = (A + B)(A2 — AB + B2) |
| Разность кубов | A3 — B3 = (A — B)(A2 + AB + B2) |
Версия для печати в формате png
Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.
Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).
Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.
Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?
Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона. Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
(A + B)n = An + Cn1An-1B + Cn2An-2B2 + … + CnkAn-kBk + … + Bn.
Здесь Cnk = n!/(k! • (n-k)!).
Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!
А что можно сказать по поводу разности квадратов, разности кубов и т. п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?
п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?
Да, можно. Вот эта формула:
An — Bn = (A — В)(An-1 + An-2B + An-3B2 + … + Bn-1).
Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:
An + Bn = (A + В)(An-1 — An-2B + An-3B2 — … + Bn-1).
Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.
Формула разности квадратов. 7-й класс
Цели урока:
Вывести формулу разности квадратов двух выражений и тренировать способности к её практическому применению
- образовательная: Обеспечить условия для усвоения формулы (а-в)(a+в)=a2—в2 сокращенного умножения многочленов и удобного вычисления значения выражения.
 Проверить
уровень усвоения изученной темы;
Проверить
уровень усвоения изученной темы;
- развивающая: показать необходимость и удобство формулы для нахождения значения выражения, формирование внутренних процессов интеллектуального, личностного, эмоционального развития;
- воспитательная: поддержание работоспособности на уроке, содействовать воспитанию интереса к математике, аккуратности.
Тип урока:
Урок изучения нового материала.Структура урока:
- Организационный момент.
- Устная работа(с закрытыми глазами).
- Актуализация опорных знаний. Постановка целей урока и мотивация изучения темы.
- Изучения нового материала.
- Закрепление изученного материала.
- Проверка усвоения материала.

- Домашнее задание.
- Рефлексия.
- Итог урока.
План урока
I. Организационный момент.
II. Устная работа
(с закрытыми глазами).С целью концентрации внимания. Учитель читает последовательно каждый пример, ребята решают его и готовность выполнять следующий показывают поднятием руки. В конце задания (через 5-6 примеров) ребята открывают глаза, сверяют ответы.
III. Актуализация опорных знаний
. “Презентация”(5m)2
(а4)3
57•63
Как вы считаете есть ли какой либо другой более удобный способ умножить эти числа?
IV. Постановка целей урока и мотивация изучения темы.
Тема: “Формула разности
квадратов”. (цели ставят дети)
(цели ставят дети)
Наша задача на сегодня – разобраться, как с помощью этой формулы удобнее и быстрее выполнять умножение двух многочленов и посмотреть, где ее можно применить.
V. Изучение нового материала.
Запишите произведение многочленов и упростите его.
(2а+в) (2а-в)=
(а-10)(а+10)=
(а-в)(а+в)=
Что у вас получилось?
Читается так: “Произведение разности двух выражений на их сумму равно разности квадратов этих выражений”.
Записать на доске !
“Формулы сокращенного умножения”(Почему?)
Рассмотрим пример: (4а+1)(4а-1) = (4а)2 – 12=16а2 – 1.
Как вы думаете, важен ли порядок множителей в произведении? Почему?
Поэтому, когда мы работаем с формулой важно обращать внимание на разность выражений.
VI. Закрепление.

№356
Как вы думаете, можно ли ещё как то использовать данную формулу.
Этой формулой можно пользоваться и справа налево, и слева направо.
Если мы будем на нее смотреть справа налево, то получим сокращенное (короткое) умножение многочленов, а если слово на право – представление разности квадратов в виде произведения (в дальнейшем это будем называть разложение на множители).
№351
№352
Физминутка.
VII. Проверка усвоения материала.
Немного отдохнули, а теперь напишем сам. работу. На выполнение работы вам дается не больше 10 минут. А потом мы вместе ее проверим. Успехов!
| Вариант 1. 1. Выполните умножение многочленов, используя формулу разности квадратов а) (х+2)•(х-2) б) (2х-3у)•(2х+3у) в) (а2-5)(5+а2) 2. 68 • 72 |
Вариант П. 1. Выполните умножение многочленов, используя формулу разности квадратов а) (у+3)•(у-3) б) (3а-5b)•(3a+5b) в) (b2+4)(4-b2) 2. Найдите значение числового выражения, используя формулу (а-b)•(a+b)=a2-b2 91 • 89 |
Возьмите в руки карандаши, проверьте свою работу с решением на экране. Если у вас задание выполнено правильно, поставьте “+”, если ошибка – разберитесь и поставьте “-”, а исправлять будете дома.
VIII. Домашнее задание.
$21 №357, №353,№351(2)
IX. Рефлексия.
Вернёмся к примеру
57•63 = (60-3)(60+3)=602-32=3600-9=3591
X.
 Итог урока.
Итог урока. Сегодня на уроке мы познакомились с формулой разности квадратов, научились ее применять и убедились, что потратили время не зря – ведь ее можно успешно применять. Мне с вами понравилось работать, спасибо. Оценки!
Приложение
Формулы сокращенного умножения — Образовательный сайт Казахстана
Главная » Математика» Алгебра » Формулы сокращенного умноженияСПРАВОЧНЫЙ МАТЕРИАЛ
1.
Если эту формулу записать справа налево, то получим , т. е. разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
Например,
2. Тождество (2) называют формулой квадрата суммы. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Например,
3. Тождество (3) называют формулой квадрата разности. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Например,
4. Если эту формулу записать справа налево, то, получим сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Примечание. Выражение напоминает нам трехчлен , который равен квадрату разности х и у. Однако в данном выражении вместо удвоенного произведения х и у стоит просто их произведение. Именно поэтому выражение называют неполным квадратом разности.
Например,
5. Если эту формулу записать справа налево, то получим , т. е. разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Например,
Выражение вида называют неполным квадратом суммы.
Приведем еще четыре формулы:
6. Тождество (6) называют кубом суммы.
7. Тождество (7) называют кубом разности.
8.
9. Тождества (8) и (9) называют квадратом трехчлена.
УПРАЖНЕНИЯ С РЕШЕНИЯМИ
1. Разложить на множители:
Разложить на множители:
Решение.
1) Выражение в явной форме ни одно из семи тождеств не представляет, но число 16 можно представить в виде степени с основанием 4, т. е. . Тогда выражение примет иной вид:
а это уже формула разности квадратов, и, применив эту формулу, получим:
2) Объединим в одну группу последние три члена, вынеся — 1 за скобки. Получим
так как можно разложить по формуле разности квадратов.
3) Это выражение в явной форме ни под одно тождество не подходит. Анализируя пример, видим, что в каждом слагаемом можно вынести общий множитель 6 за скобки. Получим:
Выражение в скобках представляет собой разложенный квадрат суммы двух выражений:
Теперь наше выражение примет вид:
4) Представим данный многочлен в виде разности кубов двух выражений и, применив формулу, получим:
Этот пример можно решить и вторым способом.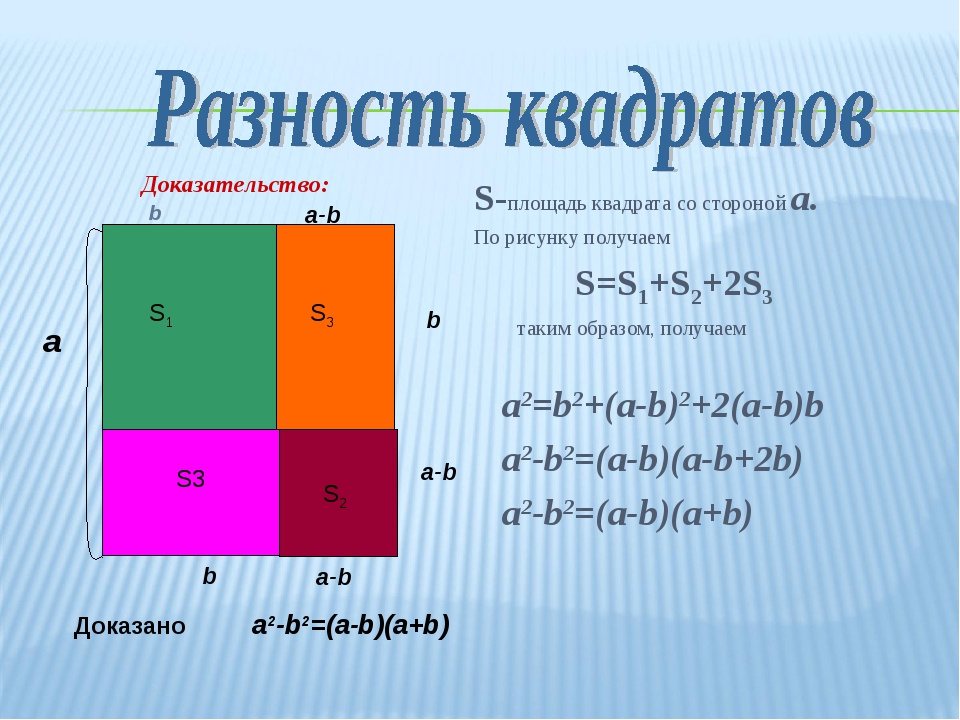 Для этого представим данный многочлен в виде разности квадратов двух выражений, получим:
Для этого представим данный многочлен в виде разности квадратов двух выражений, получим:
Теперь мы получили выражение, состоящее из двух сомножителей: разности кубов двух выражений и суммы кубов двух выражений. Первый из них разлагается на множители по формуле (5), а второй — по формуле (4):
5) Данный многочлен легко можно представить в виде суммы кубов двух выражений таким образом:
Применив формулу суммы кубов, получим:
2. Сравнить числа:
Решение.
Следовательно,
3. Найти значение выражения где .
Решение:
4. Доказать, что при любом натуральном k значение выражения делится на 12.
Решение. Воспользовавшись формулой , упростим данное выражение:
Полученное выражение 12k делится на 12 без остатка.
5. Доказать, что значение выражения не зависит от переменной х.
Решение. Выполним указанные действия:
После преобразования данного выражения получили число 144, а это и означает, что выражение не зависит от переменной х.
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Фактор разницы квадратов
Фактор разницы квадратов Вот шаги, необходимые для факторинга разницы квадратов:| Шаг 1 : | Определите, есть ли у этих четырех терминов что-нибудь общее, называемое наибольшим общим фактором или GCF. Если это так, вычтите GCF. Не забудьте включить GCF в свой окончательный ответ. |
| Шаг 2 : | Каждую задачу о разнице квадратов можно разложить на множители следующим образом: a 2 — b 2 = (a + b) (a — b) или (a — b) (a + b).Итак, все, что вам нужно сделать, чтобы учесть эти типы проблем, — это определить, какие квадраты чисел дадут желаемые результаты. |
| Шаг 3 : | Определите, можно ли еще раз разложить оставшиеся факторы. |
Пример 1 — Коэффициент:
| Шаг 1 : Решите, есть ли у четырех членов что-либо общее, называемое наибольшим общим множителем или GCF. Если это так, вычтите GCF.Не забудьте включить GCF в свой окончательный ответ. В этом случае у этих двух терминов есть только общая 1, что бесполезно. | |
| Шаг 2 : Чтобы разложить эту проблему на форму (a + b) (a — b), вам нужно определить, какие квадраты будут равны x 2 , а какой квадрат будет равен 36. В этом случае варианты выбора равны x и 6, потому что (x) (x) = x 2 и (6) (6) = 36. | |
| Шаг 3 : Определите, можно ли дополнительно разложить какие-либо из оставшихся факторов.В этом случае они не могут, поэтому окончательный ответ: |
Пример 2 — Коэффициент:
| Шаг 1 : Решите, есть ли у четырех членов что-либо общее, называемое наибольшим общим множителем или GCF. Если это так, вычтите GCF. Не забудьте включить GCF в свой окончательный ответ. В этом случае у этих двух терминов есть только общая 1, что бесполезно. | |
| Шаг 2 : Чтобы разложить эту проблему на форму (a + b) (a — b), вам нужно определить, какие квадраты будут равны 4x 2 , а какой квадрат будет равен 81.В этом случае возможны варианты 2x и 9, потому что (2x) (2x) = 4x 2 и (9) (9) = 81. | |
| Шаг 3 : Определите, можно ли дополнительно разложить какие-либо из оставшихся факторов. В этом случае они не могут, поэтому окончательный ответ: |
Нажмите здесь, чтобы узнать о практических задачах
Пример 3 — Коэффициент:
| Шаг 1 : Решите, есть ли у четырех членов что-либо общее, называемое наибольшим общим множителем или GCF.Если это так, вычтите GCF. Не забудьте включить GCF в свой окончательный ответ. В этом случае у этих двух терминов есть общее число 2, что дает: | |
| Шаг 2 : Чтобы разложить эту проблему на форму (a + b) (a — b), вам нужно определить, какие квадраты будут равны 9x 2 , а какой квадрат будет равен 49y 2 . В этом случае возможны варианты 3x и 7y, потому что (3x) (3x) = 9x 2 и (7y) (7y) = 49y 2 . | |
| Шаг 3 : Определите, можно ли дополнительно разложить какие-либо из оставшихся факторов. В этом случае они не могут, поэтому окончательный ответ: |
Нажмите здесь, чтобы узнать о практических задачах
Пример 4 — Коэффициент:
| Шаг 1 : Решите, есть ли у четырех членов что-либо общее, называемое наибольшим общим множителем или GCF. Если это так, вычтите GCF.Не забудьте включить GCF в свой окончательный ответ. В этом случае у этих двух терминов есть общее число 9x, в результате чего получается: | .|
| Шаг 2 : Чтобы разложить эту проблему на форму (a + b) (a — b), вам необходимо определить, какие квадраты будут равны x 2 , а какой квадрат будет равен 9. В этом случае варианты выбора равны x и 3, потому что (x) (x) = x 2 и (3) (3) = 9. | |
| Шаг 3 : Определите, можно ли дополнительно разложить какие-либо из оставшихся факторов.В этом случае они не могут, поэтому окончательный ответ: |
Нажмите здесь, чтобы узнать о практических задачах
Пример 5 — Коэффициент:
| Шаг 1 : Решите, есть ли у четырех членов что-либо общее, называемое наибольшим общим множителем или GCF. Если это так, вычтите GCF. Не забудьте включить GCF в свой окончательный ответ. В этом случае у этих двух терминов есть только общая 1, что бесполезно. | |
| Шаг 2 : Чтобы разложить эту проблему на форму (a + b) (a — b), вам нужно определить, какие квадраты будут равны 16×4, а какой квадрат будет равен 1. В этом случае варианты: 4x 2 и 1, потому что (4x 2 ) (4x 2 ) = 16x 4 и (1) (1) = 1. | |
| Шаг 3 : Определите, можно ли дополнительно разложить какие-либо из оставшихся факторов.В этом случае один из факторов представляет собой разность квадратов, а другой фактор представляет собой сумму квадратов, которая не учитывается. Чтобы множить разность квадратов, вам нужно определить, какие квадраты будут равны 4x 2 , а какой квадрат будет равен 1. В этом случае возможны варианты 2x и 1, потому что (2x) (2x) = 4x 2 и (1 ) (1) = 1. Итак, окончательный ответ: | |
| Шаг 4 : Определите, можно ли дополнительно разложить какие-либо из оставшихся факторов.В этом случае они не могут, поэтому окончательный ответ: |
Нажмите здесь, чтобы узнать о практических задачах
Разница квадратов — объяснение и примеры
Квадратное уравнение — это полином второй степени, обычно имеющий форму f (x) = ax 2 + bx + c, где a, b, c, ∈ R, и a ≠ 0. Термин «a» относится к как старший коэффициент, а ‘c’ — абсолютный член f (x). Каждое квадратное уравнение имеет два значения неизвестной переменной, обычно известных как корни уравнения (α, β).
В чем разница квадратов?
Разница двух квадратов — это теорема, которая говорит нам, можно ли записать квадратное уравнение как произведение двух биномов, в котором один показывает разность квадратных корней, а другой показывает сумму квадратных корней.
В этой теореме следует отметить то, что она не применяется к СУММУ квадратов.
Формула разности квадратов
Формула разности квадратов — это алгебраическая форма уравнения, используемого для выражения разницы между двумя значениями квадрата.Разница в квадрате выражается в виде:
a 2 — b 2 , где и первый, и последний член являются точными квадратами. Факторизация разницы двух квадратов дает:
a 2 — b 2 = (a + b) (a — b)
Это верно, потому что (a + b) (a — b) = a 2 — ab + ab — b 2 = a 2 — b 2
Как разность квадратов разложить на множители?
В этом разделе мы узнаем, как факторизовать алгебраические выражения, используя формулу разности квадратов.Чтобы разложить разность квадратов на множители, предпринимаются следующие шаги:
- Проверить, имеют ли члены наибольший общий множитель (GCF), и вынести его. Не забудьте включить GCF в свой окончательный ответ.
- Определите числа, которые дадут одинаковые результаты, и примените формулу: a 2 — b 2 = (a + b) (a — b) или (a — b) (a + b)
- Проверить можете ли вы дополнительно разложить оставшиеся термины.
Давайте решим несколько примеров, выполнив следующие действия.
Пример 1
Фактор 64 — x 2
Решение
Поскольку мы знаем, что квадрат 8 равен 64, мы можем переписать выражение как;
64 — x 2 = (8) 2 — x 2
Теперь примените формулу a 2 — b 2 = (a + b) (a — b), чтобы разложить выражение на множители;
= (8 + х) (8 — х).
Пример 2
Факторизовать
x 2 −16
Решение
Так как x 2 −16 = (x) 2 — (4) 2 , следовательно примените формулу разностного квадрата a 2 — b 2 = (a + b) (a — b), где a и b в данном случае равны x и 4 соответственно.
Следовательно, x 2 — 4 2 = (x + 4) (x — 4)
Пример 3
Фактор 3a 2 — 27b 2
Решение
Поскольку 3 — это GCF терминов, мы его вычитаем.
3a 2 — 27b 2 = 3 (a 2 — 9b 2 )
= 3 [(a) 2 — (3b) 2 ]
Теперь примените 2 — b 2 = (a + b) (a — b) получить;
= 3 (a + 3b) (a — 3b)
Пример 4
Фактор x 3 — 25x
Решение
Поскольку GCF = x, множите его;
x 3 — 25x = x (x 2 -25)
= x (x 2 -5 2 )
Примените формулу a 2 — b 2 = (a + b) (а — б) получить;
= х (х + 5) (х — 5).
Пример 5
Разложите выражение на множители (x — 2) 2 — (x — 3) 2
Решение
В этой задаче a = (x — 2) и b = (x — 3)
Теперь применим a 2 — b 2 = (a + b) (a — b)
= [(x — 2) + (x — 3)] [(x — 2) — (x — 3)]
= [x — 2 + x — 3] [x — 2 — x + 3]
Объедините похожие термины и упростите выражения;
[x — 2 + x — 3] [x — 2 — x + 3] => [2x — 5] [1]
= [2x — 5]
Пример 6
Фактор множителя выражение 25 (x + y) 2 — 36 (x — 2y) 2 .
Решение
Перепишите выражение в виде a 2 — b 2 .
25 (x + y) 2 — 36 (x — 2y) 2 => {5 (x + y)} 2 — {6 (x — 2y)} 2
Применить формулу a 2 — b 2 = (a + b) (a — b), чтобы получить,
= [5 (x + y) + 6 (x — 2y)] [5 (x + y) — 6 (x — 2y)]
= [5x + 5y + 6x — 12y] [5x + 5y — 6x + 12y]
Соберите похожие термины и упростите;
= (11x — 7y) (17y — x).
Пример 7
Фактор 2x 2 — 32.
Решение
Вынести за множитель GCF;
2x 2 -32 => 2 (x 2 -16)
= 2 (x 2 -4 2 )
Применяя формулу квадратов разности, получаем:
= 2 (x + 4) (x — 4)
Пример 8
Фактор 9x 6 — y 8
Решение
Сначала перепишите 9x 6 — y 8 в виде а 2 — б 2 .
9x 6 — y 8 => (3x 3 ) 2 — (y 4 ) 2
Применить a 2 — b 2 = (a + b) (а — б) получить;
= (3x 3 — y 4 ) (3x 3 + y 4 )
Пример 9
Разложите выражение на множители 81a 2 — (b — c) 2
Решение
Перепишите 81a 2 — (b — c) 2 как a 2 — b 2
= (9a) 2 — (b — c) 2
Применяя формулу a 2 — b 2 = (a + b) (a — b), получаем, что
= [9a + (b — c)] [9a — (b — c)]
= [9a + b — c] [9a — b + c]
Пример 10
Фактор 4x 2 — 25
Решение
= (2x) 2 — (5) 2
= (2x + 5) (2x — 5
Практические вопросы
Факторизуйте следующие алгебраические выражения:
- y 2 — 1
- x 2 -81
- 16x 4 — 1
- 9x 3 — 81x
- 18x 2 — 98y 2
- 4x 2 -81
- 25m 2 -9n 2
- 1 — 4z 2
- x 4 — y 4
- y 4 -144
diffsqrs
diffsqrs
Факторинг
Разница квадратов
Вернуться к факторингу
Бином может быть факторизован, только если это одна из трех вещей: разность квадратов, разность кубов или сумма кубов.Бином — это разница квадратов, если оба члена являются точными квадратами. Напомним, нам, возможно, сначала придется выделить общий фактор.
Если мы определяем, что бином представляет собой разность квадратов, мы разлагаем его на два бинома. Первый — это квадратный корень из первого члена минус квадратный корень из второго члена. Второй — квадратный корень из первого члена плюс квадратный корень из второго члена, как в следующей формуле:
Разложите на множители по каждому из следующих факторов.
1. x 2 — 25: решение
2. 16x 4 — 100: раствор
3. 50x 2 — 72: решение
К началу
Решение № 1
1. x 2 — 25
Сначала мы проверяем, что бином является разностью квадратов.
x 2 — это идеальный квадрат, как и 25, так что да, у нас есть разница квадратов.
квадратный корень из x 2 равен x, а квадратный корень из 25 равен 5
, поэтому наш ответ (x — 5) (x + 5)
Вернуться к проблемам
Решение №2
2.16x 4 -100
16x 4 — это идеальный квадрат, как и 100, поэтому у нас есть разница квадратов
Здесь мы должны сначала вычесть общий множитель, если мы этого не сделаем, наш ответ не будет полностью учтено.
Наш общий множитель равен 4, что дает нам 4 (4x 4 -25)
квадратный корень 4x 4 равен 2x 2 , квадратный корень 25 равен 5.
, поэтому наш ответ равен 4 (2x 2 -5) (2x 2 + 5)
Вернуться к проблемам
# 3 решение
3.50x 2 -72
Здесь ни 50x 2 , ни 72 не являются полными квадратами, но мы должны сначала вычесть общий множитель
, общий множитель равен 2, что дает нам 2 (25x 2 — 36)
Теперь оба 25x 2 и 36 — идеальные квадраты, поэтому у нас есть разница квадратов.
Квадратный корень из 25x 2 равен 5x, а квадратный корень из 36 равен 6.
, поэтому наш ответ: 2 (5x — 6) (5x + 6)
Назад к задачам
Факторинговая разность двух квадратов
В какой-то момент вашего изучения алгебры вас попросят разложить выражения на множители, распознавая некоторые особые шаблоны.Разница двух квадратов — одна из самых распространенных. Хорошая новость в том, что эту форму очень легко идентифицировать.
Всякий раз, когда у вас есть бином, в котором каждый член возведен в квадрат (с показателем 2), и у них есть вычитание в качестве среднего знака, вы гарантированно получите случай разности двух квадратов.
Приведенная ниже диаграмма должна обеспечить интуитивное понимание этой концепции.
Убедившись, что у вас есть разница в два квадрата, вы можете теперь разложить ее на множители как произведение двух биномов с чередующимися знаками , в середине, положительным и отрицательным.
Формула разности двух квадратов
Это других способов записать формулу разности двух квадратов с использованием переменных. Научитесь распознавать их по-разному, чтобы точно знать, как с ними обращаться.
Примеры того, как множить разность двух идеальных квадратов
Давайте рассмотрим несколько примеров!
Пример 1: Разложите приведенный ниже бином на множители, используя метод разницы двух квадратов.2}. Ясно, что у нас есть разница в два квадрата, потому что знак между двумя членами в квадрате — это вычитание.
В этом примере решение разбито на несколько шагов, чтобы выделить процедуру. Как только вы освоитесь с процессом, вы можете пропустить множество шагов. Фактически, вы можете сразу перейти от разницы двух квадратов к ее множителям.
Пример 2: Разложите на множители приведенный ниже бином.
Сначала кажется, что это не разница в два квадрата.2}? Это должно быть вдвое больше, чем
Для второго члена число при умножении само на себя дает 49 — это 7, потому что
Решение этой проблемы выглядит так:
Пример 3: Разложите на множители приведенный ниже бином.
Эта проблема немного отличается, потому что оба члена бинома содержат переменные. Если мы сможем показать, что это идеальные квадраты, тогда все будет в порядке!
- Первый член представляет собой полный квадрат, так как
- Более того, второй также является точным квадратом, потому что
Применяя формулу для разности двух квадратов, получаем:
Пример 4: Разложите на множители приведенный ниже бином.2} = \ left ({2y} \ right) \ left ({2y} \ right) и, очевидно, 9 = \ left (3 \ right) \ left (3 \ right).
Это означает, что вам нужно еще раз применить формулу для разности двух квадратов.
Вот полное решение этой проблемы.
Пример 5: Разложите на множители приведенный ниже бином.
Обратите внимание, что у бинома есть только один вид переменной — «x». Основная стратегия, когда вы видите что-то похожее, состоит в том, чтобы исключить наибольший общий фактор (GCF) среди переменных.4}. Если вычесть это, вы получите
Теперь мы можем разобраться с биномом в скобках. На самом деле это разница в два квадрата, потому что мы можем выразить каждый член бинома как выражение со степенью 2.
Затем применим формулу разности двух квадратов:
Мы закончили? Неа! Вторая скобка по-прежнему означает разность двух квадратов. У нас нет другого выбора, кроме как еще раз вычленить это.
Просмотрите биномы еще раз, чтобы увидеть, сохраняется ли разница в два квадрата.2}, а второй член равен 4. Поскольку оба члена возведены в квадрат и разделены вычитанием, это действительно случай разницы двух квадратов.
Вы можете оставить его в таком виде в качестве окончательного ответа. Но лучший ответ — комбинировать одинаковые термины, добавляя или вычитая константы. Это также упрощает ответ, избавляясь от внутренних скобок.
Возможно, вас заинтересует:
Факторинг разности двух квадратов практических задач
Факторинговая сумма и разность двух кубов
Факторинговая сумма и разность двух кубов практические задачи
разность квадратов | Блестящая вики по математике и науке
Примеры и задачи в этом разделе немного сложнее для улучшения навыков решения проблем.\ text {th} (n − 1) -й член равен 1, поэтому конечный результат равен n + 12n \ frac {n + 1} {2n} 2nn + 1. □ _ \ квадрат □
Упростим (5 + 6 + 7) (5 + 6−7) (5−6 + 7) (- 5 + 6 + 7). \ Left (\ sqrt5 + \ sqrt6 + \ sqrt7 \ right) \ left (\ sqrt5 + \ sqrt6 — \ sqrt7 \ right) \ left (\ sqrt5- \ sqrt6 + \ sqrt7 \ right) \ left (- \ sqrt5 + \ sqrt6 + \ sqrt7 \ right). (5 +6 +7) (5 +6 — 7) (5 −6 +7) (- 5 +6 +7).
Мы можем расширить его, но это требует много времени и очень подвержено ошибкам. Пусть личность решит эту проблему.2 \\ & = 5 + 6 + 2 \ sqrt {30} -7 \\ & = 4 + 2 \ sqrt {30}. \ End {align} (5 +6 +7) (5 +6 −7) = (5 +6) 2− (7) 2 = 5 + 6 + 230 −7 = 4 + 230.
Аналогичным образом произведение двух последних членов будет
.(5−6 + 7) (- 5 + 6 + 7) = (7+ (5−6)) (7− (5−6)) = — 4 + 230. \ begin {выровнено} \ big (\ sqrt5- \ sqrt6 + \ sqrt7 \ big) \ big (- \ sqrt5 + \ sqrt6 + \ sqrt7 \ big) & = \ left (\ sqrt7 + \ big (\ sqrt5- \ sqrt6 \ big) \ right) \ left ( \ sqrt7- \ big (\ sqrt5- \ sqrt6 \ big) \ right) \\ & = — 4 + 2 \ sqrt {30}. \ end {выровнен} (5 −6 +7) (- 5 +6 +7) = (7 + (5 −6)) (7 — (5 −6)) = — 4 +230.
Конечный результат: (4 + 230) (- 4 + 230) = 4 (30) −16 = 104. \ Left (4 + 2 \ sqrt {30} \ right) \ left (-4 + 2 \ sqrt { 30} \ right) = 4 (30) -16 = 104. (4 + 230) (- 4 + 230) = 4 (30) −16 = 104. □ _ \ квадрат □
Попробуйте решить следующие задачи самостоятельно. 210x = (10624 + 25) 2- (10624-25) 2
Какое значение xxx удовлетворяет приведенному выше уравнению?
Отправьте свой ответ
Вычислите следующее выражение:
1234567892- (123456788 × 123456790).{2} — (123456788 \ times 123456790) .1234567892– (123456788 × 123456790).
Если вы используете калькулятор, точность которого недостаточно высока, чтобы ответить на этот вопрос, тогда вы ответите на этот вопрос неверно.
Если
x = 4 (5 + 1) (54 + 1) (58 + 1) (516 + 1), x = \ frac {4} {\ big (\ sqrt {5} +1 \ big) \ big (\ sqrt [4] {5} +1 \ big) \ big (\ sqrt [8] {5} +1 \ big) \ big (\ sqrt [16] {5} +1 \ big)}, x = (5 +1) (45 +1) (85 +1) (165 +1) 4,
, тогда каково значение (1 + x) 48? (1 + x) ^ {48}? (1 + x) 48?
Отправьте свой ответ
Если бы у вас было , только , учитывая, что
4382716062 = 192082000625819236,438271606 ^ {2} = 192082000625819236,4382716062 = 192082000625819236,
можете ли вы найти сумму цифр точного значения 5617283952561728395 ^ {2} 5617283952?
Примечания: Да, не используйте Wolfram Alpha или калькулятор для решения этой проблемы (хотя вы можете использовать калькулятор для вычисления суммы цифр). {\ color {# 624F41} y} & = & \ large {\ frac 5 3} \\ \\ \\ \ large {\ color {# 624F41} x} — {\ color {# 624F41} y} & = & \ large \,? \ end {align} 2x − 2y4x − 4yx − y === 135?
Детали и предположения:
- xxx и yyy — действительные числа.
512 128 256 32 14 20 64 54
Принято, что x, y∈Z + x, y \ in \ Bbb {Z ^ +} x, y∈Z +, и они удовлетворяют уравнению, приведенному ниже:
∏k = 05 (52k + 62k) = 6x − 5y. 2 $ составляет $ 225 — 196 = 29 $
30: не работает
Вы можете выразить 22 из 30 чисел как разность двух полных квадратов.2 $.
Если бы $ 2 $ можно было записать как разность двух квадратов, тогда $ (a + b) = 2 $ и $ (a — b) = 1 $, поскольку $ 2 $ является простым числом, и очевидно, что $ a — b Таким образом, решая одновременные уравнения, $ b = 2 — a $, поэтому $ a — (2 — a) = 1 $, $ 2a = 3 $ и $ a = \ frac {3} {2} $. Таким образом, $ 2 $ нельзя представить как разность двух целых квадратов.
Этот метод можно обобщить для любого простого числа $ p $, решив $ (a + b) = p $ и $ (a — b) = 1 $
Сложение уравнений дает $ 2a = p + 1 $, поэтому $ a = \ frac {p + 1} {2} $.Поскольку $ a — b = 1 $, $ b = a-1 $, поэтому $ b = \ frac {p + 1} {2} — 1 = \ frac {p-1} {2} $. Таким образом, любое нечетное простое число можно записать как разность двух квадратов.
Любое квадратное число $ n $ можно также записать как разность двух квадратов, взяв $ a = \ sqrt {n} $ и $ b = 0 $.
Как правило, число может быть записано как разность двух квадратов, если у него есть два множителя одинаковой четности, поскольку, если $ a + b $ нечетно, а $ a — b $ четно, при сложении двух уравнений мы получит нечетные $ 2a $, поэтому решение не будет целым.2 $ можно переписать в виде $ (a + b) (a-b) $.
Предположим, что $ u $ и $ v $ — два делителя $ x $, такие что $ u = a + b $ и $ v = a — b $.
Вычитая два уравнения, получаем $ u — v = 2b $.
Это говорит нам о том, что разница между двумя факторами всегда будет, даже если число может быть записано в этой форме.
Теперь, чтобы получить четную разницу, нам нужно, чтобы либо $ u $, и $ v $ были нечетными, либо оба были четными. Следовательно, любое число с двумя четными или нечетными множителями может быть записано в этой форме.
Это оставляет числа, которые всегда будут иметь один нечетный и один четный множители.
Если $ v $ является нечетным множителем $ x $, оно должно иметь разложение на простые множители только нечетных чисел.
Предположим, что $ u $ является четным делителем $ x $ и содержит более одного $ 2 $ в своем разложении на простые множители.
Это означает, что $ u $ может быть разделено на два и все равно будет четным, и в то же время $ v $ может быть увеличено вдвое, чтобы оно также стало четным. Это означает, что $ x $ имеет пару факторов, которые оба являются четными, и поэтому могут быть записаны как разность двух квадратов.
Если оба множителя нечетные, будет получена и четная разница, поэтому, если при разложении на простые множители $ x $ нет двоек, то x можно записать как разность двух квадратов.
Это оставляет случай, когда в факторизации на простые множители приходится ровно одна $ 2 $. Это означает, что один фактор должен содержать $ 2 $, а не другой, и что факторами нельзя манипулировать описанным выше способом. Это всегда будет оставлять коэффициенты с нечетной разницей, предполагая, что $ x $ не может быть записано как разность двух квадратов.
Это также дает очень хороший алгоритм для поиска двух квадратов с разницей в $ x $:
1. Определите, сколько $ 2 $ s в разложении на простые множители $ x $. Если есть только один, x нельзя записать как разность двух квадратов.
2. Выберите пару факторов, которые являются как четными, так и нечетными, назовите их $ u $ и $ v $. Найдите их разность и разделите ее на 2, чтобы найти меньший квадрат. $ \ frac {u — v} {2} = b $ из предыдущего.
3. Возведите в квадрат $ b $ и прибавьте его к $ x $. Квадратный корень из суммы, и это $ a $.2 = 60 $
Факторизация трехчленных квадратов и разности квадратов
Обзор
Квадраты трехчлена также известны как трехчлены полного квадрата и представляют собой квадраты биномиальных выражений. Они множатся как (a + b) (a + b) или (a — b) (a — b), где a и b — действительные числа. Такие формы, как (a + b) (a -b), являются специальными произведениями, которые также называют разностью квадратов.
Трехчленные квадраты
Когда возведенный в квадрат бином, такой как (a + b) (a + b), умножается с использованием FOIL, значения a и b следуют определенному шаблону.Напомним, что первый член — это 2 , внешний и внутренний члены — это ab + ba, а последний член — это b 2 . Если многочлен имеет форму ax 2 + bx + c, a и c являются полными квадратами, а коэффициент b вдвое больше суммы ac, это полный квадрат трехчлена. Предположим, что многочлен равен 36x 2 + 60x + 25. 36x 2 — это полный квадрат 6x, а 25 — полный квадрат 5. Внутренние и внешние члены равны 30x + 30x или 60x. Этот полином равен (6x + 5) 2 .
Рис. 1: Трехчлен полного квадрата следует определенной схеме.
Отрицательные
Что, если возведенный в квадрат бином равен (a — b) (a — b)? Когда он умножается с использованием FOIL, a 2 является полным квадратом, как и b 2 . Знак 2ab отрицательный, потому что это сумма двух отрицательных произведений. Предположим, что многочлен равен 100x 2 — 80x + 16. Квадратный корень из 100x 2 равен 10x, а квадратный корень из 16 равен -4. Произведение 10 и -4 равно -40, а дважды -40 равно -80.Этот полином равен (10x — 4) 2 .
Рисунок 2: Пример, когда средний член отрицательный.
Другие образцы
Если трехчлен имеет форму –ax 2 + bx + c или ax 2 — bx — c или ax 2 + bx — c, он не соответствует квадрату трехчлена. Коэффициент квадрата члена не может быть отрицательным, даже если член представляет собой полный квадрат. Когда отрицательный результат умножается на другой отрицательный, получается положительный результат.Точно так же, если константа c не является полным квадратом, трехчлен не следует квадрату трехчлена.
Различия квадратов
Последний специальный шаблон, который следует рассмотреть, это (a + b) (a — b). Поскольку умножение коммутативно, оно совпадает с (a — b) (a + b). Это называется разностью квадратов. Когда (a + b) (a — b) умножается с использованием FOIL, первый член равен 2 , а последний член равен b 2 . Внешний член –ab, а внутренний член — ab, что в сумме равно нулю.Они нейтрализуют друг друга. Предположим, что полином равен 144x 2 + 81. Квадратный корень из 144x 2 равен 12x, а квадратный корень из 81 равен 9. По шаблону факторизация составляет (12x + 9) (12x — 9).
Рисунок 3: Пример формы (a + b) (a — b).
Заинтересованы в услугах репетитора по алгебре? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.
SchoolTutoring Academy — ведущая компания в сфере образовательных услуг для школьников и школьников.Мы предлагаем учебные программы для учащихся K-12, AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Spearfish, SD: посетите Tutoring in Spearfish, SD
.




 Найдите значение числового выражения,
используя формулу (а-b)•(a+b)=a2-b2
Найдите значение числового выражения,
используя формулу (а-b)•(a+b)=a2-b2