Формула сокращенного умножения примеры: Примеры решения задач с формулами сокращенного умножения

Содержание

Примеры решения задач с формулами сокращенного умножения

Содержание:

Формулы сокращенного умножения активно используются в решении задач, так как позволяют в некоторых случаях свести умножение одного выражения (многочлена, числа) на другое к компактному, легко запоминающемуся результату. То есть на практике можно сэкономить время, не умножая каждый раз одно выражение на другое, а воспользовавшись уже известным результатом.

Перед изучением примеров решения задач советуем изучить теоретический материал по формулам сокращенного умножения, прочитать все определения и свойства.


Квадрат суммы

Теоретический материал по теме — квадрат суммы.

Пример

Задание. Раскрыть скобки

Решение. Решение проведем в два этапа, первый — возведем в квадрат по определению, то есть умножим выражение на себя; второй — используем формулу сокращенного умножения «квадрат суммы».

1.

По определению:

2. Используя формулу сокращенного умножения:

Как видно, использование формулы сокращенного умножения привело к более быстрому решению.

Квадрат разности

Теоретический материал по теме — квадрат разности.

Слишком сложно?

Примеры решения задач с формулами сокращенного умножения не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Раскрыть скобки

Решение. Решение проведем в два этапа, первый — возведем в квадрат по определению, то есть умножим выражение на себя; второй — используем формулу сокращенного умножения «квадрат разности».

1. По определению:

2. Используя формулу сокращенного умножения:

Как видно, использование формулы сокращенного умножения привело к более быстрому решению. Использование такой формулы уменьшит вероятность ошибки.


Разность квадратов

Теоретический материал по теме — разность квадратов.

Пример

Задание. Раскрыть скобки

Решение. Решение проведем в два этапа, первый — умножим два двучлена по определению, то есть умножим выражение на ; второй — используем формулу сокращенного умножения «разность квадратов».

1. По определению:

2. Используя формулу сокращенного умножения:

Как видно, использование формулы сокращенного умножения привело к более быстрому решению.


Куб суммы

Теоретический материал по теме — куб суммы.

Пример

Задание. Раскрыть скобки

Решение. Решение проведем в два этапа, первый — возведем в куб по определению, то есть умножим выражение два раза на себя; второй — используем формулу сокращенного умножения «куб суммы».

1. По определению:

2. Используя формулу сокращенного умножения:

Как видно, использование формулы сокращенного умножения значительно упростило и ускорило решение.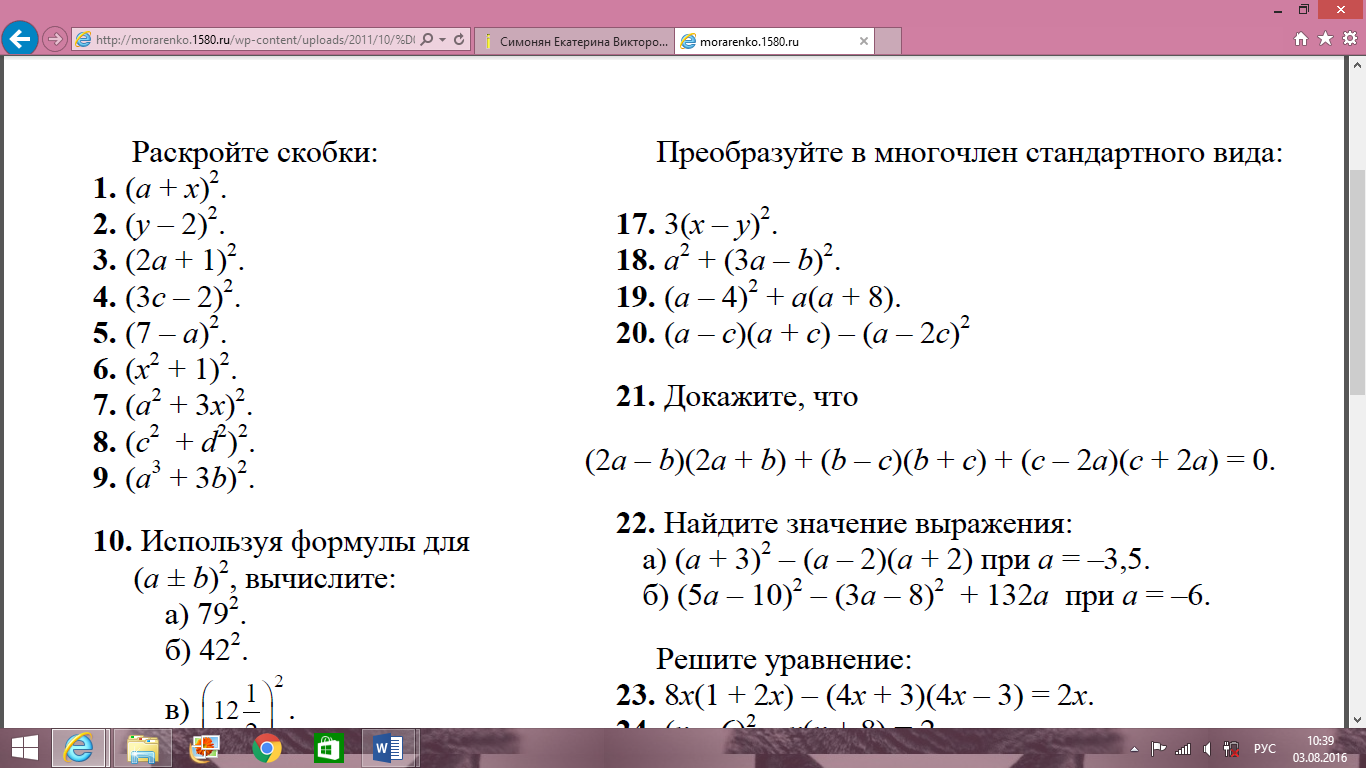

Куб разности

Теоретический материал по теме — куб разности.

Пример

Задание. Раскрыть скобки

Решение. Решение проведем в два этапа, первый — возведем в куб по определению, то есть умножим выражение два раза на себя; второй — используя формулу сокращенного умножения «куб разности».

1. По определению:

2. Используя формулу сокращенного умножения:

Как видно, использование формулы сокращенного умножения упростило решение на несколько шагов и скоратило вероятность ошибки.


Сумма кубов

Теоретический материал по теме — сумма кубов.

Пример

Задание. Разложить выражение на множители:

Решение.


Разность кубов

Теоретический материал по теме — разность кубов.

Пример

Задание. Разложить выражение на множители.

Решение.

Читать первую тему — квадрат суммы, раздела формулы сокращенного умножения.

Формулы сокращенного умножения. Примеры

Формулы сокращенного умножения применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.

Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.


Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.

Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.

Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях. 7.

Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7).

Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.

Формулы сокращенного умножения

Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.

Предварительные навыки

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.

Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)2 = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2

То есть выражение (2x + 3y)2 равно 4x2 + 12xy + 9y2

(2x + 3y)2 = 4x2 + 12xy + 9y2

Решим аналогичный пример, который попроще:

(a + b)2

Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (

a + b)

(a + b)2 = (a + b)(a + b)

Выполним это умножение:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2

То есть выражение (a + b)2 равно a2 + 2ab + b2

(a + b)2 = a2 + 2ab + b2

Оказывается, что случай (a + b)2 можно распространить для любых

a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (

a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y2

Как и в прошлый раз получили многочлен 4x2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y

)2 = 4x2 + 12xy + 9y2

Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)2 = 5

2 = 25

Второй способ:

(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9

Значит, (5a + 3)2 = 25a

2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

В результате получается следующая сумма площадей:

a2 + ab + ab + b2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b)2 = a2 − 2ab + b2

Эту формулу можно прочитать так:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)

(a − b)2 = (a − b)(a − b)

Если выполнить это умножение, то получится многочлен a2 − 2ab + b2

(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2

Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25

Значит, (7x − 5)2 = 49x2 − 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b

a2 − ab − (a − b)b

Раскроем скобки в выражении (a − b)b

a2 − ab − ab + b2

Приведем подобные слагаемые:

a2 − 2ab + b2

В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.

(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2

Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y)2 = (5x + (−2y))2

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2

Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)

(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2

Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y)2 = x2 + 2xy + y2

Куб суммы и куб разности

Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(a − b)3 = a3 − 3a2b + 3ab2 − b3

Формулу куба суммы двух выражений можно прочитать так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.  

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. 

При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.

Выведем формулу куба суммы самостоятельно:

(a + b)3

Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)

(a + b)3 = (a + b)(a + b)(a + b)

Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2

(a + b)3 = (a + b)(a + b)2

При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.

Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).

(a + b)3 = (a + b)(a2 + 2ab + b2)

А это есть умножение многочлена на многочлен. Выполним его:

(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3

Аналогично можно вывести формулу куба разности двух выражений:

(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3

Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1

Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:

(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1

Пример 2. Преобразовать выражение (6a2 + 3b3)3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(6a2 + 3b3)3= (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9

Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a3 − 3a2b + 3ab2 − b3

(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4  + 27n2 − 27

Пример 4. Преобразовать выражение (2x2 − x3)3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a3 − 3a2b + 3ab2 − b3

(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9

Умножение разности двух выражений на их сумму

Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

(a − b)(a + b)

В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:

(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2

То есть выражение (a − b)(a + b) равно a2 − b2

(a − b)(a + b) = a2 − b2

Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.

Пример 1. Выполнить умножение (2x − 5)(2x + 5)

В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:

(2x − 5)(2x + 5) = (2x)2 − 52

Вычислим правую часть, получим 4x2 − 25

(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25

Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4x2 − 25

(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25

Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2

Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2

В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.

Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.

Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.

Пример 3. Выполнить умножение (7 + 3x)(3x − 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49

Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)

(a − b)(a + b) = a2 − b2

(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6

Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)

В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)

Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.

Далее вычисляем выражение в скобках:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9y2)

Теперь умножим −1 на выражение в скобках и получим окончательный результат:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2

Умножение разности двух выражений на неполный квадрат их суммы

Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:

(a − b)(a2 + ab + b2)

Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.

Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.

Действительно, первый член выражения 4x2 + 6xy + 9y2, а именно 4x2 является квадратом выражения 2x, поскольку (2x)2 = 4x2. Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.

Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2

(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3

То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3

(a − b)(a2 + ab + b2) = a3 − b3

Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы.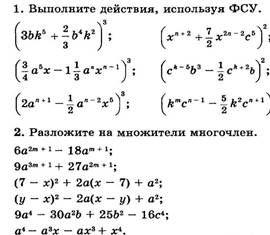 Эту формулу можно прочитать так:

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.

Пример 1. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)

Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y

(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3

Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3.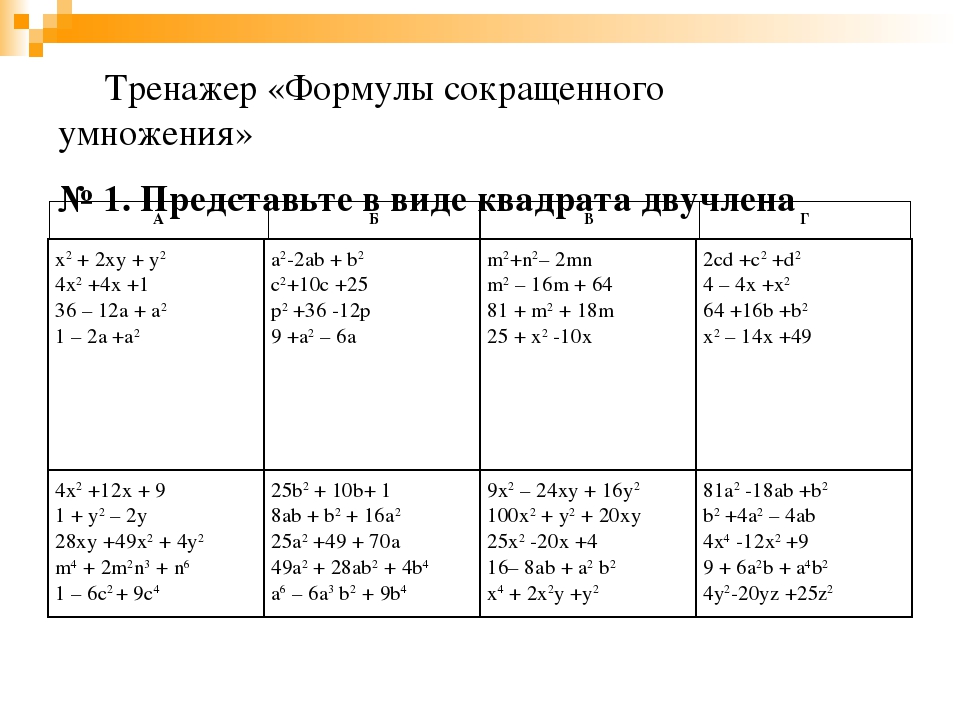 У нас получится тот же результат, но решение станет длиннее:

(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3

Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)

Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3

(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3

Умножение суммы двух выражений на неполный квадрат их разности

Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:

(a + b)(a2 − ab + b2)

Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.

Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x2 − 6xy + 9y2 является неполным квадратом разности выражений 2x и 3y. 

(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2

Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a2 − ab + b2

(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3

То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3

(a + b)(a2 − ab + b2) = a3 + b3

Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:

Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.

Пример 1. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)

Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y

(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:

(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3

Пример 2. Выполнить умножение (2x + y)(4x2 − 2xy + y2)

Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x2 − 2xy + y2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3

(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:

(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) = 
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3

Задания для самостоятельного решения

Задание 1. Преобразуйте выражение (m + n)2 в многочлен.

Решение:

(m + n)2 = m2 + 2mn + n2

Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.

Решение:

(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64

Задание 3. Преобразуйте выражение (2x2 + 3x3)2 в многочлен.

Решение:

(2x2 + 3x3)2 = (2x2)2 + 2 × 2x2 × 3x3 + (3x3)2 = 4x4 + 12x5 + 9x6

Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.

Решение:

(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25

Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.

Решение:

(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2

Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.

Решение:

(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625

Задание 7. Преобразуйте выражение (3x2 − y3)2 в многочлен.

Решение:

(3x2 − y3)2 = (3x2)2 − 2 × 3x2 × y3 + ( y3)2 = 9x4 − 6x2y3 + y6

Задание 8. Выполните умножение (x − y)(x + y)

Решение:

(x − y)(x + y) = x2 − y2

Задание 9. Выполните умножение (2x − y)(2x + y)

Решение:

(2x − y)(2x + y) = (2x)2 − y2 = 4x2 − y2

Задание 10. Выполните умножение (7 + 3y)(3y − 7)

Решение:

(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49

Задание 11. Выполните умножение (x2 − 5)(x2 + 5)

Решение:

(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25

Задание 12. Выполните умножение (a3 − b2)(a3 + b2)

Решение:

(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4

Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)

Решение:

(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6

Задание 14. Выполните умножение (9x − y2)(y2 + 9x)

Решение:

(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81x2 − y4

Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)

Решение:

(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3

Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)

Решение:

(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19

Задание 17. Выполните умножение (4x + 1)(16x2 − 4x + 1)

Решение:

(4x + 1)(16x2 − 4x + 1) = (4x)3 + 13 = 64x3 + 1

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Формулы сокращенного умножения

Формулы сокращенного умножения помогают существенно облегчить вычисления.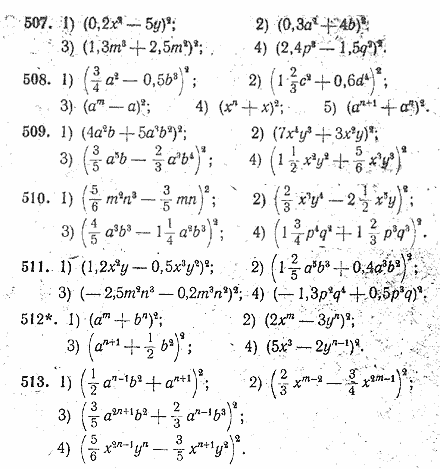 Суть их применения заключается в том, что вместо того, чтобы раз от разу совершать одни и те же алгебраические преобразования, можно сразу записывать их результат. Кроме того, разложение на множители по формулам сокращенного умножения часто помогает решить на первый взгляд сложные уравнения и неравенства.

Итак, вспомним формулы сокращенного умножения:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

8. Полезные тождества:

Примеры  использования формул сокращенного умножения:

1. Вычислить: 1992

1992=(200-1)2=2002-2х200+1=40000-400+1=39601

2. Вычислить:

3. Решить уравнение:  

Перенесем слагаемые в левую часть:

 

Разложим на множители по формуле разности квадратов:

Очевидно, что выражение во вторых скобках  не равно нулю ни при каких значениях х.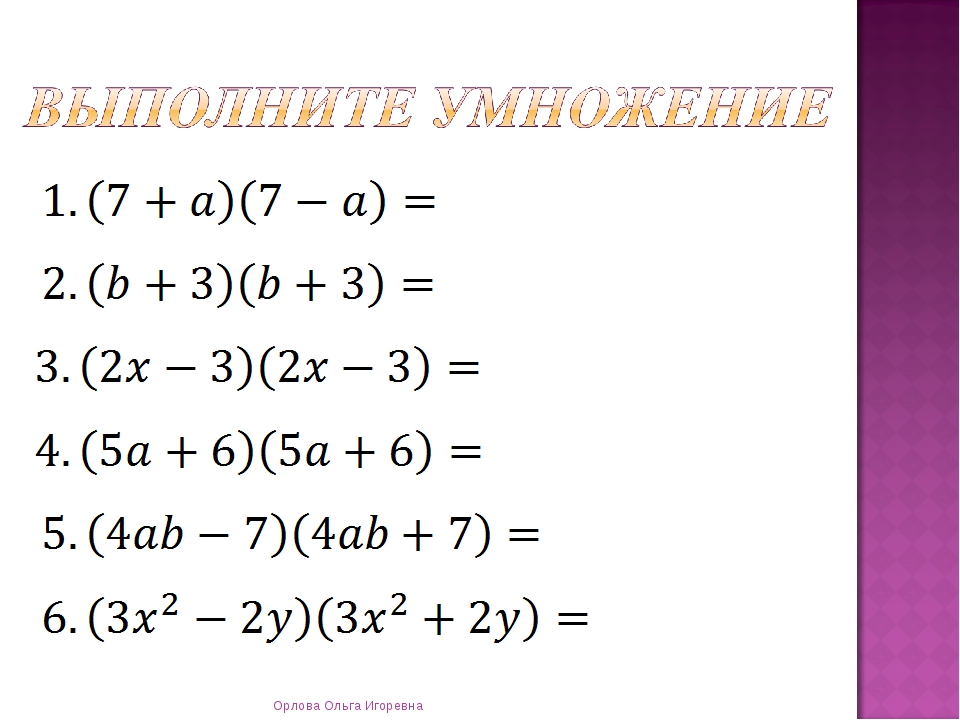 Приравняем к нулю выражение в первых скобках:

Снова разложим на множители по формуле разности квадратов:

 

 

x=1/3

Скачать таблицу формулы сокращенного умножения

Формулы сокращенного умножения с примерами решения

Содержание:

Формулы сокращенного умножения

Умножение разности двух выражений на их сумму

Умножим разность

Итак,

Полученное тождество позволяет умножать разность двух выражений на их сумму не по правилу умножения двух многочленов, а сокращенно: сразу записывать произведение в виде Поэтому доказанное тождество называют формулой сокращенного умножения. Формулируют се так:

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Умножим по этому правилу разность на сумму

Из переместительного свойства умножения следует, что произведение суммы двух выражений и их разности равно разности квадратов этих выражений:

Примеры выполнения заданий:

Пример №135

Выполнить умножение:

Решение:

Пример №136

Вычислить

Решение:

Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений

Возведем в квадрат сумму

Итак,

Полученное тождество называют формулой квадрата суммы. Оно является формулой сокращенного умножения, поскольку позволяет возводить в квадрат сумму любых двух выражений не по правилу умножения двух многочленов, а сокращенно: сразу записывать квадрат в виде трехчлена

Формулируют формулу квадрата суммы так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение этих выражений плюс квадрат второго выражения.

Возведем в квадрат сумму

При возведении суммы в квадрат промежуточные преобразования можно выполнять устно:

Квадрат разности двух выражений

Возведем в квадрат разность

Итак, получили такую формулу квадрата разности:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения.

Квадрат суммы и квадрат разности двух выражений еще называют квадратом двучлена.

Квадраты противоположных чисел равны: Поэтому при возведении в квадрат выражений и можно пользоваться формулами:

Для тех, кто хочет знать больше

Чтобы возвести сумму или разность двух выражений в куб, можно использовать формулы куба суммы или куба разности:

Докажем эти формулы.

Формулируют формулу куба суммы так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.

Формулу куба разности формулируют аналогично.

Примеры выполнения заданий:

Пример №137

Возвести в квадрат выражение:

Решение:

Разложение на множители разности квадратов двух выражений

В тождестве поменяем местами левую и правую части:

Полученное тождество называют формулой разности квадратов двух выражений.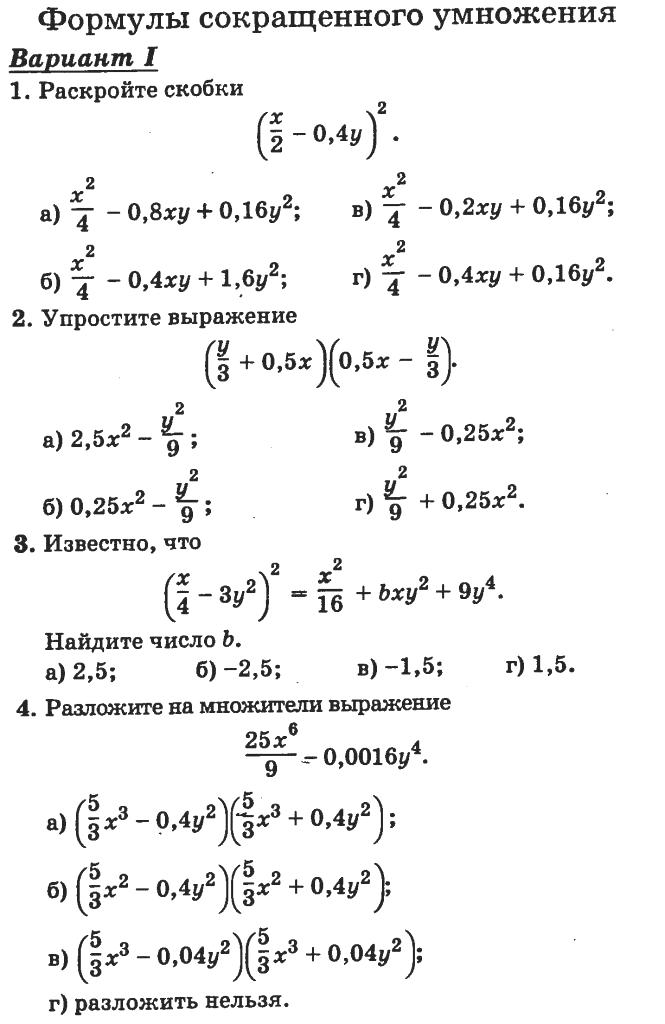 Формулируют ее так:

Разность квадратов двух выражении равна произведению разности этих выражений и их суммы.

Формула разности квадратов позволяет разложить на множители двучлена Ее можно использовать при разложении на множители разности квадратов любых двух выражений. Например:

Сравните

Примеры выполнения заданий:

Пример №138

Разложить на множители:

Решение:

Пример №139

Вычислить

Решение:

Пример №140

Решить уравнение

Решение:

Ответ. 9; -3.

Разложение многочленов на множители с использованием формул квадрата суммы и квадрата разности

Запишем формулы квадрата суммы и квадрата разности двух выражений (квадрата двучлена), поменяв в них левые и правые части:

Первая из этих формул дает разложение на множители трехчлена а вторая — трехчлена

Примеры выполнения заданий:

Пример №141

Разложить на множители трехчлен

Решение:

Пример №142

Найти значение выражения при

Решение:

Запишем сначала трехчлен в виде квадрата двучлена:

При получим:

При получим:

Разность и сумма кубов двух выражений

Разность квадратов двух выражений можно разложить на множители по формуле разности квадратов. При разложении на множители разности кубов двух выражений используют формулу разности кубов:

Докажем это тождество, перемножив выражения

В формуле разности кубов трехчлен называют неполным квадратом суммы выражений (он напоминает трехчлен который является «полным» квадратом суммы выражений ). Поэтому формулу разности кубов можно сформулировать так:

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

При разложении на множители суммы кубов двух выражений используют формулу суммы кубов:

Докажем это тождество:

Трехчлен называют неполным квадратом разности выражений . Следовательно,

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Примеры выполнения заданий:

Пример №143

Разложить на множители:

Решение:

Применение нескольких способов для разложения многочленов на множители

Часто при разложении многочлена на множители нужно использовать несколько способов. Если это возможно, то разложение уместно начинать с вынесения общего множителя за скобки.

Рассмотрим несколько примеров:

1. Разложим на множители многочлен

Сначала вынесли общий множитель за скобки, а потом применили формулу разности квадратов.

2. Разложим на множители многочлен

Все члены многочлена имеют общий множитель Вынесем eго за скобки:

Многочлен разложим на множители способом группировки:

Таким образом,

Примеры выполнения заданий:

Пример №144

Разложить на множители трехчлен:

Решение:

а) Если к выражению прибавить то есть 9, то получим выражение, которое является квадратом двучлена

Поэтому, выделив квадрат этого двучлена, получим:

Пример №145

Разложить на множители многочлен

Решение:

Пример №146

Решить уравнение

Решение:

Разложим левую часть уравнения на множители:

Получим уравнение

откуда:

Ответ:

Применение преобразований выражений

Нам уже встречались задачи, при решении которых нужно было преобразовывать то или иное выражение. Чаще всего мы использовали преобразования выражений при решении уравнений, доказательстве тождеств, нахождении значений выражении. Рассмотрим еще некоторые задачи, решение которых связано с преобразованием выражений.

Сравнение значений многочлена с нулем
Пример №147

Доказать, что многочлен принимает только положительные значения.

Решение:

Выделив из трехчлена квадрат двучлена, получим:

Мы представили многочлен в виде суммы двух слагаемых Слагаемое : при любых принимает только неотрицательные значения, слагаемое 2 — положительно. Поэтому выражение принимает только положительные значения. Поскольку то и выражение принимает только положительные значения.

Нахождение наибольшего и наименьшего значений выражений

Исходя из равенства полученного в примере 1, можно

указать наименьшее значение многочлена Оно равно причем это наименьшее значение многочлен принимает при

Пример №148

Найти наибольшее значение многочлена

Решение:

Преобразуем данный многочлен так:

Наибольшее значение многочлена равно 5.

Решение задач на делимость
Пример №149

Доказать, что значение выражения делится на 8 при любом целом значении

Решение:

Упростим данное выражение:

При любом целом значении произведение делится на 8, поэтому и значение выражения делится на 8.

Нахождение значений многочлена с помощью микрокалькулятора
Пример №150

С помощью микрокалькулятора найти значение многочлена

Решение:

Значение данного многочлена искать удобнее, если его предварительно преобразовать так:

При схема вычислений имеет вид:

Выполнив вычисления, найдем значение многочлена. Оно равно 109,264.

Интересно знать

Античные математики использовали формулы сокращенного умножения задолго до нашей эры. В те времена формулы представлялись не в привычном нам символическом виде, а формулировались словами.

Ученые Древней Греции алгебраические утверждения, формулы, выражающие определенные зависимости между величинами, трактовали геометрически. Так, произведение они рассматривали как площадь прямоугольника со сторонами

Приведем пример алгебраического утверждения, которое было известно древнегреческим ученым и в геометрической терминологии формулировалось так: площадь квадрата, построенного на сумме двух отрезков, равна сумме площади квадратов, построенных на каждом из этих отрезков, плюс удвоенная площадь прямоугольника, построенного на этих отрезках.

Нетрудно догадаться, что речь идет о формуле квадрата суммы, которую мы символически записываем так:

Дроби. Формулы сокращенного умножения

Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1, \ 2, \ 3, \ 4 \ \) и т.д.
\(\bullet\) Множество целых чисел \(\mathbb{Z}\) состоит из натуральных чисел, противоположных им (\(-1, \ -2, \ -3 \) и т. д.) и нуля \(0\).
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\).   Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).  

Факт 2.
\(\bullet\) Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex] &\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)   \(\bullet\) Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)   \(\bullet\) Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\)  

Факт 2.
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:   \(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot 2\llap{/}}{3\cdot 2\llap{/}}=\dfrac{49}3\\[2ex] &\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot 7\llap{/}}{7\llap{/}\cdot 5}=\dfrac 85\\[2ex] &\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot 3\cdot 2\llap{/}}=\dfrac{14}{15}\end{aligned}\)   \(\bullet\) Если \(\dfrac ab\) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель \(b\) делится только на числа \(2\) и \(5\). 2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex] &{\small{\text{и т.д.}}}\end{aligned}\]

Знакомые и незнакомые формулы сокращенного умножения и их применение при решении задач

Администрация города Магнитогорска

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа № 25

при Магнитогорской Государственной консерватории»

города Магнитогорска

Проект

Тип: исследовательский

Тема: «Знакомые и незнакомые формулы сокращенного умножения и
их применение при решении задач»

Автор работы: Миронов Ярослав

Класс: 7 Б

Руководитель проекта: Губа О.Н., учитель математики

Магнитогорск

2020

Содержание

Введение

Глава 1 Теоретическая часть

1.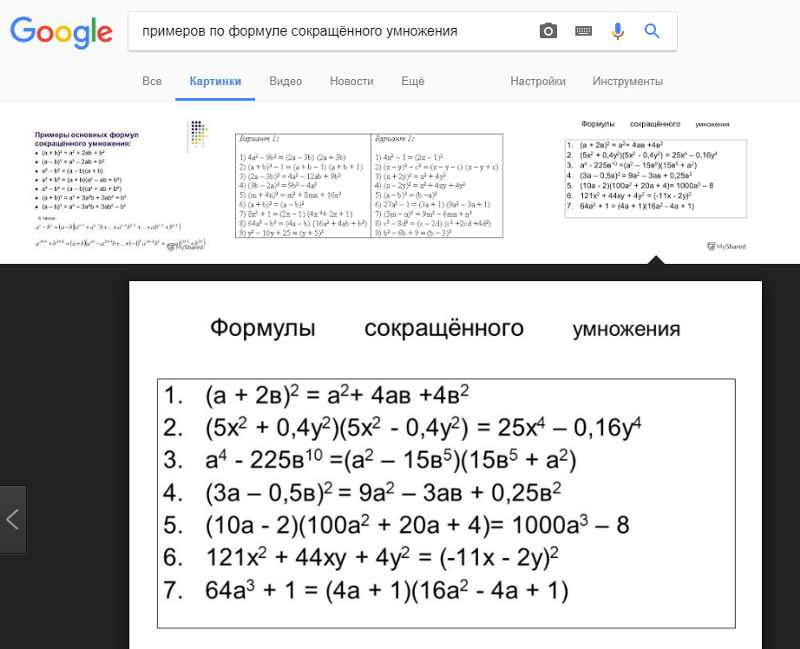 1. Исторические сведения.

1.2. Анализ школьных учебников.

1.3. Анкетирование учащихся и анализ полученных результатов.

Глава 2 Практическая часть

2.1. Возведение в квадрат суммы нескольких слагаемых.

2.2. Возведение многочлена в n – ую степень.

2.3. Треугольник Паскаля.

2.4. Применение формул сокращенного умножения для решения задач.

Заключение

Литература

Приложение

Введение

Актуальность

В курсе математики 7 класса изучаются формулы сокращенного умножения, но мне показалось, что это еще не все формулы, которые рассматриваются в школьном курсе, и я задался целью узнать о них больше, так как эти формулы помогают рационально выполнять некоторые задания.

В ходе работы мною были рассмотрены вопросы школьной и внешкольной программы, а также исторические сведения по теме. Часть работы посвящена формулам сокращенного умножения, которых нет в учебнике алгебры 7 класса. Эта тема значимая в курсе математики и применяется на протяжении всего периода обучения: при умножении многочленов, упрощении алгебраических выражений, сокращении дробей, разложении на множители, решении уравнений и других. Я хочу углубить свои знания по этой очень интересной теме.

Решение нестандартных задач, задач повышенного уровня, олимпиадных задач требует применение знакомых формул сокращенного умножения в незнакомой, нестандартной ситуации и применения новых неизвестных в школьном курсе формул сокращенного умножения.

Цель: изучение формул сокращённого умножения (далее ФСУ) и их применения  в решении задач и примеров.

Объект исследования: формулы сокращенного умножения.

Предмет исследования: применение формул сокращенного умножения.

Задачи

  1. Собрать сведения из истории математики о формулах сокращенного умножения.

  2. Провести опрос по данной теме среди школьников, проанализировать действующие учебники.

  3. Подобрать и прорешать задачи с применением формул сокращенного умножения.

  4. Составить справочную таблицу.

Гипотеза исследования:

Я думаю, что, после изучения данной темы, и применения ее на практике, я расширю и углублю свои знания, а это будет способствовать развитию логического и творческого мышления в процессе решения проблемных задач. Это поможет мне подготовиться к выпускному экзамену по математике в 9 классе, так как я смогу рационально выполнять некоторые упражнения.

Методы

В ходе выполнения данного проекта применялись методы сбора, анализа, опроса, классификации информации.

Глава 1 Теоретическая часть

    1. Исторические сведения

Некоторые правила сокращенного умножения были известны еще около 4 тыс. лет назад. Тогда было принято все алгебраические утверждения выражать в геометрической форме. Особенно широко алгебраическими тождествами пользовался в 3 в до н.э. древнегреческий геометр Евклид. У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а», а «квадрат на отрезке а», не «ав», а «прямоугольник, содержащийся между отрезками а и в». Например, тождество ( а + в )= а + 2ав + в во второй книге «Начал» Евклида формулировалось так: « Если прямая линия (имеется в виду отрезок) как- либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками». Доказательство опиралось на геометрические соображения. Некоторые термины подобного геометрического изложения алгебры сохранились до сих пор. Так, мы называем вторую степень числа квадратом, а третью степень — кубом числа.

Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям, был древнегреческий ученый-математик, живший в III веке до н. э. Диофант Александрийский. В своей книге «Арифметика» Диофант формулы квадрата суммы, квадрата разности и разности квадратов рассматривал уже с арифметической точки зрения. Ну а современную символику алгебраические тождества получили благодаря двум математикам, а именно Виету и Декарту(16 век).

На современном уровне развития математики данные формулы были обоснованы Исааком Ньютоном. При небольших значениях n коэффициенты можно найти из треугольника Паскаля. Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент для определения этих самых коэффициентов, который впоследствии назвали «треугольник Паскаля».

    1. Анализ школьных учебников

На уроке математики я познакомился с формулами сокращенного умножения, которые знаю наизусть. Мне стало интересно, а как эта тема дана в других учебниках, есть ли еще формулы?! Проанализировав учебную литературу по математике других авторов, я выделил семь основных ФСУ, которые есть в каждом учебнике. Все они доказываются раскрытием скобок через умножение многочленов и приведением подобных слагаемых.

Разность квадратов:

(a +b) (a – b) = a² — b² (1)

Квадрат суммы и квадрат разности:

(a + b)² = a² + 2ab +b² (2)

(a – b)² = a² — 2ab + b² (3)

Сумма и разность кубов:

(a + b) (a² — ab + b²) = a³ +b³ (4)

(a – b) (a² + ab + b²) = a³ — b³ (5)

Куб суммы и куб разности:

(a + b)³ = a³ + 3a²b + 3ab² + b³ (6)

(a –b)³ = a³ — 3a²b + 3ab² — b³ (7)

Эти семь формул – полный джентльменский набор. Две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот – справа налево. Это не просто так. Любая формула в математике работает в обоих направлениях – как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.

  Они берутся из… умножения. Вот ведь удивил, да? Что ж, смотрите сами. Берём, например, самую первую формулу по списку:

        (a+b)2 = (a+b)(a+b) = a2+ab+ba+b2 = a2+2ab+b2

Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения.  Сокращённое умножение – потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!

  Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) – о четвёрке и выше.

 Полезная вещь первая – самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок – меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.

  Дело в том, что вся математика строится на преобразованиях выражений. Вся! От школьной до высшей. Сообразил, что, где и как преобразовать и упростить – решил пример. Не сообразил – увы, не решил. Есть, допустим, выражение (a-b)(a+b). Как его можно преобразовать? Да просто тупо перемножить скобки и привести подобные. Не вопрос. А вот что делать с a2–b2? Чему это равняется? Попробуй, догадайся! Только знания и спасают.

     Сравним два равенства:

        (a-b)(a+b) = a2–b2

        и

        a2–b2 = (a-b)(a+b)

        Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами – не совсем. Возьмём первую запись, слева направо:

        (a-b)(a+b) = a2–b2

        Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:

        a2–b2 = (a-b)(a+b)

        А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, – это разложение на множители! А разложение на множители – процедура поважнее простого умножения.

        И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:

        (a+b)2 = (a+b)(a+b) =…

        (a-b)2 = (a-b)(a-b) = …

        (a-b)(a+b) = …

        (a+b)3 = (a+b)(a+b)(a+b) =…

        и т.д.

Формулы школьного курса следует знать наизусть, так как они применяются практически во всех разделах математики. Ниже приведенные формулы не нужно заучивать наизусть, но показывать их применение для нестандартных задач очень полезно, особенно при подготовке к олимпиадам.

Следствия из формул сокращенного умножения:

(а+b)2-2аb=а2+2аb+b2-2аb=а2+b2

(а-b)2+2аb=а2-2аb+b2+2аb=а2+b2

Квадрат суммы (разности) трех выражений:

(а+b+с)2=а2+b2+с2+2аb+2ас+2bс

(а-b+с)2=а2+b2+с2-2аb+2ас-2bс

(а+b-с)2=а2+b2+с2+2аb-2ас-2bс

(а-b-с)2=а2+b2+с2 -2аb-2ас+2bс

Биквадрат суммы, разности.

(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4

(a − b)4 = a4 − 4a3b + 6a2b2 − 4ab3 + b4

an − bn = (a − b)(an − 1 + an − 2b + an − 3b2 + … + a2bn − 3 + abn − 2 + bn − 1), где n ϵ N Рассмотрим таблицу формул, не входящих в школьную программу, которые полезны при решении задач повышенной сложности, с помощью которых решены многие трудные олимпиадные задачи.

Формулы, позволяющие сократить преобразования выражений и упростить решения сложных задач.

    1. Анкетирование учащихся и анализ полученных результатов

Для реализации данного проекта сначала я решил провести анкетирование.

Анкетирование прошли учащиеся двух классов: 9 «А» и 7 «А». Я составил вопросы, которые, на мой взгляд, помогут мне в исследовании моего проекта. Ниже представлена анкета:

Сколько формул сокращенного умножения вы знаете? Запишите их.


  1. Где вы применяете формулы сокращенного умножения?


  1. Знаете ли вы, кто придумал эти формулы?


После проведения анкетирования я обработал ответы учащихся, и получились следующие результаты:

Вопрос №1. Сколько формул сокращенного умножения вы знаете? Запишите их.

Знают все 7

Знают первые 3-5

Не знают

10

21

10

Вывод: как видно, что большинство учащихся не все знают формулы, а 10 человек не смогли их вообще написать, 10 человек написали все семь. Тем самым, я решил, что необходимо составить справочную таблицу с основными формулами, см. Приложение 1.

Вопрос №2. Где вы применяете формулы сокращенного умножения?

В математике

В других школьных предметах

Никак

35

4

2

Вывод: можно сделать вывод, что ФСУ применяются школьниками только на уроках математики, реже в физике и химии.

Вопрос №3. Знаете ли вы, кто придумал эти формулы?

Да

Нет

15

26

Вывод: опрос показал, что школьники не знают историю возникновения формул сокращенного умножения.

Глава 2 Практическая часть

2.1. Возведение в квадрат суммы нескольких слагаемых

Для чего сначала я рассмотрел три способа возведения в квадрат суммы трех слагаемых (a+b+c)2 .

Первый способ: геометрический.

Сначала разбил квадрат на фигуры, как показано на рисунке. После чего нашел площадь каждого полученного квадрата или прямоугольника.

Так как площадь целой фигуры равна сумме площадей его частей, то получил равенство для площади прямоугольника: S=a2+ab+ac+ab+b2+bc+ac+bc+c2. После упрощения: S=a2+ b2+c2+2ab+2ac+2bc.

Второй способ: выполнил алгебраическое умножение многочленов.

(a+b+c)*(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2=a2+ b2+c2+2ab+2ac+2bc.

Третий способ: представил данную сумму как сумму двух слагаемых и возвел ее в квадрат. ((a+b)+c)2=(a+b)2+2(a+b)c+c2=a2+ c2+b2+2ab +2ac+2bc.

Во всех трех случаях результат получил одинаковый:

(a+b+c)2=a2+ c2+b2+2ab +2ac+2bc=a2+ c2+b2+2(ab+ac+bc)

Аналогичными способами я вывел формулу для возведения в квадрат суммы четырех слагаемых.

Геометрический способ

(через вычисление площади квадрата). Таким образом, площадь квадрата равна сумме площадей его частей:

S=a2+ b2+ c2+d2+

+2ab+2ac+2ad+2bc+2bd

Умножение многочленов: (a+b+c+d)*(a+b+c+d)=a2+ab+ac+ad+ab+b2+bc+bd+ac+bc+c2+cd+ad+bd+cd+d2==a2+ b2+ c2+ d2+2ab+2ac+2ad+2bc+2bd

Преобразование в квадрат суммы двух слагаемых:

((a+b)+(c+d))2=(a+b)2+2(a+b)(c+d)+(c+d)2=a2+2ab+b2+2ac+2ad+2bc+2bd+c2+

+2cd+d2=a2+ b2+ c2+ d2+2ab+2ac+2ad+2bc+2bd

И опять я в каждом случае получил одинаковый результат, то есть

(a+b+c+d)2=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd=a2+b2+c2+d2+2(ab+ac+ad+bc+bd)

Вывод: После проведенной работы я предположил, что в квадрат можно возвести сумму нескольких слагаемых. Подтверждение этому я нашел в справочной литературе:

(a1 + a2 + …+ aп )² = a1² + a2² +…+ 2(a1 a2 + a1 a3 +…+ ai aj +…+ an-1 a.)

Итак, квадрат суммы n слагаемых равен сумме их квадратов плюс удвоенная сумма всевозможных попарных произведений этих слагаемых вида ai aj ,

где i < j.

2.2. Возведение многочлена в n – ую степень

Дальше меня заинтересовало: как возвести сумму двух слагаемых в более высокую степень, например в четвертую, пятую или шестую. И я решил поэкспериментировать.

Для начала я рассмотрел куб суммы двух слагаемых, для чего расписал его в виде произведения суммы двух слагаемых на квадрат тех же слагаемых: (a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3

Потом поработал с четвертой степенью двух слагаемых, представил ее как результат произведения квадратов двух слагаемых и получил:

(a+b)4=(a+b)2(a+b)2=(a2+2ab+b2)(a2+2ab+b2)=a4+4a3b+6a2b2+4ab3+b4

Аналогичным способом возвел в пятую степень сумму двух слагаемых:

(a+b)5=(a+b)2(a+b)3=(a2+2ab+b2)(a3+3a2b+3ab2+b3)=a5+5a4b+10a3b2+10a2b3+

+5ab4+b5

Попробовал расписать шестую степень как произведение квадрата и четвертой степени суммы двух слагаемых:

(a+b)6=(a+b)2(a+b)4=(a2+2ab+b2)(a4+4a3b+6a2b2+4ab3+b4)=a6+6a5b+15a4b2+

+20a3b3+15a2b4+6ab5+b6

Затем седьмую степень представил как произведение куба суммы и четвертой степени суммы:(a+b)7=(a+b)3(a+b)4=(a3+3a2b+3ab2+b3)*

*(a4+4a3b+6a2b2+4ab3+b4)=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7

Надо заметить, что данные преобразования можно было производить и другим способом. Например, сумму двух слагаемых возвести в шестую степень, как произведение кубов тех же самых слагаемых.

Особенно меня удивило то, что все коэффициенты (их я выделил жирным шрифтом), полученные в результате умножения, были симметрическими. Оказалось, что это неспроста, данная закономерность среди коэффициентов многочлена называется «Треугольник Паскаля» по имени его автора.

2.3. Треугольник Паскаля

Но кроме закономерности среди коэффициентов прослеживается так же замечательная закономерность и среди степеней получившегося многочлена. Оказывается степени входящих одночленов образуются следующим образом: степень первого слагаемого, начиная с большей, с каждым разом уменьшается на единицу, а степень второго слагаемого наоборот увеличивается от нулевой до наибольшей.

Строится «Треугольник Паскаля» следующим образом. В вершине треугольника пишем 1. Единица соответствует выражению (a+b), поскольку любое число, возведённое в нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень: (a+b)=a+b. Идём дальше. Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «квадрат суммы»: a+2ab+b.

Следующий ряд, как и предыдущий, начинается и заканчивается единицами, а между ними — суммы цифр, находящихся сверху: 1, 3, 3, 1. Мы получили коэффициенты разложения «куба суммы». Ряд коэффициентов двучлена четвёртой степени составят 1, 4, 6, 4, 1 и так далее.

Номер Строки

    1. 1

    2. 1 1

    3.   1 2 1

    4. 1 3 3 1

    5. 1 4 6 4 1

    6. 1 5 10 10 5 1

    7. 1 6 15 20 15 6 1

    8. 1 7 21 35 35 21 7 1

… ……

Сравнивая два способа решения, заключаю, что применяя для нахождения коэффициентов в разложении треугольник Паскаля, возведение в любую степень решается рациональнее. Поэтому, если мне придется возводить двучлен в п-ую степень, я буду применять второй способ.

Дальше я предлагаю рассмотреть примеры, которые прорешал самостоятельно и в которых применяются формулы сокращенного умножения (ФСУ). В некоторых из них я применил способ группировки, который изучается в курсе математики 7 класса.

2.4. Применение формул сокращенного умножения для решения задач

  1. Вычислить рациональным способом:

а) (652-322-97*11): (612-362)+(562-262): (662-162)

Решение: данное выражение не очень сложное. Сначала я преобразую его и запишу в виде дроби:

Далее буду вычислять по действиям:

В этом примере я примени формулы разности квадратов и квадрата суммы двух слагаемых.

Ответ: (652-322-97*11): (612-362)+(562-262): (662-162)=4,48

б)

Решение: в отличие от предыдущего это выражение насыщено различными

формулами. Начинаю выполнять его по действиям, не забывая применять

формулы сокращенного умножения:

Ответ:

При помощи ФСУ можно производить упрощение алгебраических выражений.

2. Упросить выражение:

а)

Решение:

В этом примере во втором действии я применил формулы разности квадратов и разности кубов двух слагаемых и выполнил сокращение дробей.

Ответ:

б)

Решение:

После применения сочетательного закона умножения сначала я использовал формулы разности и суммы кубов, а затем разность квадратов двух слагаемых.

Ответ:

3. Упростить и вычислить:

а)

Решение: применяю формулы разность квадратов и квадрат разности двух слагаемых.

, подставляю заданное значение в получившееся выражение и вычисляю:

Ответ: -11/3

б)

Решение: в данном случае произведу группировку четырех слагаемых, а в последнем действии распишу формулу разности квадратов:

, теперь вычисления будут более простыми:

Ответ: -25

В данных примерах я не только выполнил упрощение выражений с помощью формул сокращенного умножения, но и произвел вычисления для каждого случая.

Формулы сокращенного умножения также применяют и для решения алгебраических уравнений. Так как в курсе 7 класса уравнения, представленные ниже, не изучаются, то и решить их другим способом я не мог.

4. Решить уравнение: а)

Сначала я разложу второе слагаемое на сумму двух слагаемых, а далее применю способ группировки.

Ответ: х=1, х=3

б)

Правую часть уравнения разложу по формуле квадрата разности, а потом выполню действия как в предыдущем примере.

Ответ: х=1/3, х=-3

в)

Сначала применяю формулы разности кубов и квадратов, далее привожу подобные слагаемые и перехожу к решению элементарного уравнения.

Ответ: х=3

г)

Данное уравнение отличается от предыдущих тем, что в нем два неизвестных, поэтому в решении одна переменная будет выражена через другую.

Ответ: а=в, а=2в

Также с помощью ФСУ можно выполнять доказательство тождественно равных выражений.

5. Доказать тождество из «Арифметики» Диофанта:

Решение: свернул знаменатель первой и третьей дроби в квадрат разности двух слагаемых, привел выражение к общему знаменателю, далее перенес все в левую часть и привел подобные слагаемые. В результате получил, что левая часть тожественно равна правой.

Заключение

При изучении материала по этой теме, я узнал много нового и интересного. Оказалось, что формулы сокращенного умножения можно использовать для рационального вычисления выражений, при упрощении выражений, при решении уравнений, доказательстве тождеств и так далее.

В процессе работы я самостоятельно вывел различные формулы сокращенного умножения, причем некоторые из них доказал несколькими способами, познакомился с треугольником Паскаля.

Я решил множество интересных задач, которые не встречались на уроке математики. Мне очень нравится предмет математика, я считаю, что те знания, которые я приобрел, готовя эту работу, пригодятся мне в дальнейшей учебе и подготовке к выпускным экзаменам. Данная тема актуальна, так как математику нельзя представить без формул сокращенного умножения, потому что они применяются не только в школьном курсе, но и в курсе высшей математики. Созданная мною работа может использоваться другими учащимися и преподавателями математики на своих уроках. Мне понравилось заниматься исследовательской работой.

Литература

  1. https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2013/02/09/formuly-sokrashchennogo-umnozheniya

  2. http://groiro.by/informatizaciya/primeneniia_formul.pdf

  3. https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2013/02/09/formuly-sokrashchennogo-umnozheniya

  4. http://tepka. ru/algebra-7/54.html

Приложение

Справочная таблица с основными формулами сокращенного умножения

Формула сокращенного умножения

Наиболее важные сокращенные формулы умножения.

Формулы сокращенного умножения позволяют выполнять вычисления намного быстрее.
Наиболее часто используемые сокращенные формулы умножения:

(
a + b ) 2 = a 2 + 2 из + b 2
(
a — b ) 2 = a 2 — 2 из + b 2
(
a + b + c ) 2 = a 2 + b 2 + c 2 + 2 из + 2 ac + 2 bc
a 2 — b 2 = ( a + b ) ( a — b )
(
a + b ) 3 = a 3 + 3 a 2 b + 3 из 2 + b 3
(
a — b ) 3 = a 3 — 3 a 2 b + 3 из 2 — b 3
a 3 + b 3 = ( a + b ) ( a 2 — из + b 2 )
a 3 — b 3 = ( a — b ) ( a 2 + из + b 2 )

Сокращенные формулы умножения полезны для умножения или расширения алгебраических выражений. Они облегчают эффективный подсчет. Таких паттернов очень много. Ниже мы перечислим несколько наиболее часто используемых.

Квадрат суммы чисел

  • ( a + b ) 2 = a 2 + 2 из + b 2
    например: 31 2 = (30 + 1) 2 = 30 2 + 2 × 30 + 1 = 900 + 60 + 1 = 961

  • не встречается равенство: ( a + b ) 2 = a 2 + b 2
    e.г 25 = (3 + 2) 2 ≠ 3 2 + 2 2 = 13

  • обоснование формулы счетом:
    ( a + b ) 2 = ( a + b ) × ( a + b ) = aa + из + ba + bb = a 2 + 2 из + b 2

Квадрат разности чисел

Квадрат суммы трех чисел

  • ( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 из + 2 ac + 2 bc
    e. г: 111 2 = (100 + 10 + 1) 2 = 100 2 + 10 2 +1 + 2 × 100 × 10 + 2 × 100 + 2 × 10 = 10000 + 100 + 1 + 2000 + 200 + 20 = 12321

  • не встречается равенство: ( a + b + c ) 2 = a 2 + b 2 + c 2
    например 36 = (3+ 2 + 1) 2 ≠ 3 2 + 2 2 + 1 2 = 14

  • обоснование формулы:
    ( a + b + c ) 2 = ( a + b + c ) × ( a + b + c ) = aa + от + ac + ba + bb + bc + that + cb + cc = a 2 + b 2 + c 2 + 2 из + 2 ac + 2 до н.э.

Произведение суммы и разности чисел = Разность квадратов чисел

Куб суммы чисел

  • ( a + b ) 3 = a 3 + 3 a 2 b + 3 из 2 + b 3
    e. г: 101 3 = (100 + 1) 3 = 100 3 + 3 × 100 2 + 3 × 100 + 1 =
    = 1000000 + 30000 + 300 + 1 = 1030301

  • не встречается равенство: ( a + b ) 3 = a 3 + b 3
    например 125 = (3 + 2) 3 ≠ 3 3 + 2 3 = 35

  • обоснование формулы счетом:
    ( a + b ) 3 = ( a + b ) × ( a + b ) × ( a + b ) = ( aa + из + ba + bb ) × ( a + b ) = aaa + aab + aba + fig + baa + раздел + bba + bbb =
    = a 3 + 3 a 2 b + 3 из 2 + b 3

Куб разности чисел

  • ( a — b ) 3 = a 3 — 3 a 2 b + 3 из 2 — b 3
    е. г: 99 3 = (100-1) 3 = 100 3 — 3 × 100 2 + 3 × 100 — 1 =
    = 1000000 — 30000 + 300 — 1 = 970299

Сумма кубиков чисел

a 3 + b 3 = ( a + b ) × ( a 2 — от + b 2 )

обоснование формулы:

( a + b ) × ( a 2 — от + b 2 ) = aa 2 — aab + от 2 + ba 2 — Раздел + bb 2 = a 3 — a 2 b + из 2 + a 2 b — из 2 + b 3 =
= a 3 + b 3

Разность кубиков чисел

a 3 — b 3 = ( a — b ) × ( a 2 + из + b 2 )

обоснование формулы:

( a — b ) × ( a 2 + из + b 2 ) = aa 2 + aab + из 2 — ba 2 — Раздел — bb 2 = a 3 + a 2 b + из 2 — a 2 b — из 2 — b 3 =
= a 3 — b 3

Разность четвертых степеней чисел

a 4 — b 4 = ( a — b ) × ( a 3 + a 2 b + из 2 + b 3 ) = ( a + b ) × ( a 3 — a 2 b + из 2 — b 3 )

Sum n — эти степени чисел (для n нечетные !!!)

a n + b n = ( a + b ) ( a n -1 — a n -2 b + a n -3 b 2 -… + b n -1 )

Разница n — эти степени чисел (для n четные !!!)

a n — b n = ( a + b ) ( a n -1 — a n -2 b + a n -3 b 2 -… + b n -1 )

Разница n — эти степени чисел (для каждого n натуральные)

a n — b n = ( a — b ) ( a n -1 + a n -2 b + a n -3 b 2 +… + a 2 b n -3 + от n -2 + b н -1 )

Как раскрывается формула.

Сокращенные формулы умножения

Как раскрывается формула. Сокращенные формулы умножения — Гипермаркет Знаний

Сокращенные формулы умножения (FSF) необходимы для умножения и увеличения чисел, выражений, включая многочлены. То есть с помощью формул можно работать с числами намного быстрее и проще. Таким образом, вы можете составить обычное уравнение из сложного уравнения, что упростит задачу.

Таблица с формулами сокращенного умножения

Название Формула Как читать
Квадрат суммы Квадрат первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения.
Квадрат разницы Квадрат разницы между двумя выражениями равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Суммарный куб Куб разности двух выражений равен кубу первого выражения плюс троекратное произведение квадрата первого выражения на второе выражение, плюс троекратное произведение первого выражения и второго квадрата плюс второе выражение в кубе.
Куб разницы Куб разности двух величин равен первому выражению в кубе минус троекратное произведение первого выражения в квадрате на второе выражение плюс троекратное произведение первого выражения на второй квадрат минус второе выражение в кубе.
Разность квадратов Разница между квадратами первого и второго выражений равна произведению разницы между двумя выражениями на их сумму.
Сумма кубиков Произведение суммы двух величин на неполный квадрат разницы равно сумме их кубиков.
Разница кубиков Произведение разности двух выражений на неполный квадрат суммы равно разности их кубиков.

Обратите внимание на первые четыре формулы. Благодаря им вы можете возвести в квадрат или куб сумму (разность) двух выражений. Что касается пятой формулы, то ее нужно использовать для краткого умножения разности или суммы двух выражений.

Последние две формулы (6 и 7) используются для умножения сумм обоих выражений на их неполный квадрат разницы или суммы.

Приведенные выше формулы довольно часто нужны на практике. Поэтому их желательно знать наизусть.

Если вы встретите пример факторизации многочлена, то во многих случаях вам нужно переставить левую и правую части.

Например, возьмем ту же первую формулу:

и поместим левую часть вправо, а правую часть — влево:

Эту же процедуру можно проделать с остальными формулами.

Доказательство ФСО

Остановимся на доказательствах сокращенных формул умножения. Это не сложно. Вам просто нужно открыть скобки.Рассмотрим первую формулу — квадрат суммы :.

Шаг первый.

Возведем a + b во вторую степень. Для этого не будем трогать градус, а произведем банальное умножение: = x.

Шаг второй. Теперь достаем скобки: x + x.

Шаг третий … Раскройте скобки: x + x + x + x.

Шаг четвертый … Умножаем, не забывая о знаках: x + x +.

Шаг пятый … Упростим выражение :.

Таким же образом можно доказать абсолютно любую формулу сокращенного умножения.

Примеры и решения с использованием FSO

Обычно эти семь формул используются, когда вам нужно упростить выражение, чтобы решить уравнение или даже общий пример.

Пример 1

Задача

Упростите выражение:

Как видите, первая формула сокращенного умножения — Квадрат суммы — подходит для этого примера.

Решение

Исходя из первой формулы, пример необходимо факторизовать. Для этого смотрим на формулу и подставляем цифры вместо букв. В нашем случае «a» равно 3x, а «b» — 5:

Мы читаем правую часть и записываем результат. Получаем:

В примере нужно перемножить все, что умножается, и мы сразу получаем ответ:

Конечно, есть примеры и с дробями. Но, если вы научитесь решать простые примеры, то других типов вы не будете бояться.

Пример 2

Задача

Упростите выражение

Решение

= — xx + =

Удвоенное произведение этих выражений равно -, что совпадает со вторым членом трехчлена (с знак плюс), что означает

Итак, как видите, в примерах нет ничего сложного. Главное знать формулы, где их можно применить, а где можно без них.

Полезные источники

  1. Арефьева И.Г., Пирютко О. Н. Алгебра: учебное пособие для 7-х классов общеобразовательных учреждений: Минск «Народная Асвета», 2017 — 304 с.
  2. Никольский С.М., Потапов М.К. Алгебра 7 класс: М: 2015 — 287 с.
  3. Рубин А.Г., Чулков П.В. Алгебра. 7-й класс. Москва: 2015 — 224 с.

FSU — формулы сокращенного умножения по алгебре для 7 класса с примерами обновлено: 22 ноября 2019 г. Автор: Scientific Articles.Ru

Сокращенные формулы выражений очень часто используются на практике, поэтому желательно выучить их все наизусть.До этого момента он будет служить нам верой и правдой, который мы рекомендуем распечатать и постоянно держать перед глазами:

Первые четыре формулы из составленной таблицы сокращенных формул умножения позволяют возвести в квадрат и куб сумму или разность двух выражений. Пятый предназначен для краткого умножения разницы на сумму двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называется выражение в форме a 2 −ab + b 2) и разность двух выражений a и b на неполный квадрат их суммы (a 2 + ab + b 2) соответственно.

Следует отдельно отметить, что каждое равенство в таблице является тождеством. Это объясняет, почему сокращенные формулы умножения также называют сокращенными тождествами умножения.

При решении примеров, особенно в которых имеет место факторизация многочлена, FSO часто используется в форме с переставленными левой и правой сторонами:


Последние три идентификатора в таблице имеют собственные имена. Формула a 2 — b 2 = (a — b) (a + b) называется формулой разности квадратов , a 3 + b 3 = (a + b) (a 2 −ab + b 2) — формула суммы кубиков , но a 3 −b 3 = (a — b) (a 2 + ab + b 2) — формула разности кубиков … Обратите внимание, что мы не называли FSU для соответствующих формул с переставленными частями из предыдущей таблицы.

Дополнительные формулы

Не помешает добавить еще несколько тождеств в таблицу сокращенных формул умножения.

Сферы применения сокращенных формул умножения (ФСУ) и примеры

Основное назначение сокращенных формул умножения (fsu) объясняется их названием, то есть состоит в кратком умножении выражений.Однако область применения FSU намного шире и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное применение сокращенной формулы умножения было найдено в выполнении идентичных преобразований выражений. Чаще всего эти формулы используются в процессе упрощения выражения .

Пример.

Упростим выражение 9 y− (1 + 3 y) 2.

Решение.

В этом выражении возведение в квадрат можно выполнить сокращенно, мы имеем 9 y− (1 + 3 y) 2 = 9 y− (1 2 + 2 1 3 y + (3 y) 2)… Осталось только раскрыть скобки и привести аналогичные слагаемые: 9 y− (1 2 + 2 1 3 y + (3 y) 2) = 9 y — 1−6 y — 9 y 2 = 3 y — 1− 9 л 2.

В числителе выражение — это разность кубиков двух выражений 2 x и z 2, а в знаменателе — разность квадратов этих выражений. После применения соответствующих формул исходная дробь примет вид … Теперь вы можете отменить те же множители в числителе и знаменателе :.

Кратко подведем итоги всего решения:

Ответ:

.

Сокращенные формулы умножения иногда позволяют рационально оценивать значения выражений. В качестве примера покажем, как возвести число 79 в квадрат с помощью формулы возведения в квадрат разности: 79 2 = (80−1) 2 = 80 2 −2 80 1 + 1 2 = 6 400–160 + 1 = 6 241. Это подход позволяет проводить такие расчеты даже устно.

В заключение скажем еще об одном важном преобразовании — выделение квадрата двучлена , в основе которого лежит формула сокращенного умножения на квадрат суммы.Например, 4 x 2 + 4 x — 3 можно преобразовать в (2 x) 2 + 2 2 x 1 + 1 2 −4, а первые три члена заменяются с использованием квадрата формулы суммы. Таким образом, выражение принимает вид (2 x + 1) 2 −4. Такие преобразования широко используются, например, для.

Библиография.

  • Алгебра: уч. за 7 кл. общее образование. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; изд. С. А. Теляковский. — 17-е изд. — М .: Просвещение, 2008.- 240 с. : больной. — ISBN 978-5-09-019315-3.
  • А.Г. Мордкович Алгебра. 7-й класс. В 14.00 Часть 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. — 13 изд., Перераб. — М .: Мнемозина, 2009. — 160 с .: Илл. ISBN 978-5-346-01198-9.
  • Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы): Учебное пособие. руководство. — М .; Выше. шк., 1984.-351 с., ил.

Также будут задачи для самостоятельного решения, на которые вы сможете увидеть ответы.

Сокращенные формулы умножения позволяют выполнять идентичные преобразования выражений — полиномов. С их помощью можно факторизовать полиномы, а, применяя формулы в обратном порядке, произведения биномов, квадратов и кубов можно представить в виде полиномов. Рассмотрим все общепринятые формулы сокращенного умножения, их вывод, общие задачи для идентичных преобразований выражений с помощью этих формул, а также домашние задания (ответы на них можно найти по ссылкам).

Квадрат суммы

Формула квадрата суммы — равенство

(Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа).

Вместо a и b в эту формулу можно подставить любые числа.

Формула возведения в квадрат суммы часто используется для упрощения вычислений. Например,

Используя формулу квадрата суммы, можно факторизовать многочлен, а именно представить его как произведение двух одинаковых множителей.

Пример 1.

.

Пример 2. Запишите выражение в виде полинома

Решение. По формуле квадрата суммы получаем

Квадрат разницы

Формула квадрата разности — равенство

(Квадрат разницы между двумя числами равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа).

Формула квадрата разности часто используется для упрощения вычислений. Например,

Используя формулу квадрата разности, полином можно разложить на множители, а именно представить как произведение двух одинаковых множителей.

Формула следует из правила умножения многочлена на многочлен:

Пример 5. Запишите выражение в виде полинома

Решение. По формуле квадрата разности получаем

.

Самостоятельно примените сокращенную формулу умножения, а затем посмотрите решение

Выбор полного квадрата

Часто полином второй степени содержит квадрат суммы или разности, но он скрыт. Чтобы получить полный квадрат явно, вам нужно преобразовать многочлен. Для этого, как правило, один из членов полинома представляется в виде удвоенного произведения, а затем это же число добавляется и вычитается из полинома.

Пример 7.

Решение. Этот многочлен можно преобразовать следующим образом:

Здесь мы представили 5 x как удвоенное произведение 5/2 на x , добавили к многочлену и вычли из него то же число, а затем применили формулу для вычисления квадрата суммы двучлена.

Итак, мы доказали равенство

,

равняется полному квадрату плюс число.

Пример 8. Рассмотрим полином второй степени

Решение.Сделаем на нем следующие преобразования:

Здесь мы ввели 8 x в виде удвоенного произведения x на 4, добавили к многочлену и вычли из него то же число 4², применили формулу квадрата разницы для двучлена x — 4 .

Итак, мы доказали равенство

,

, показывающий, что многочлен второй степени

равно полному квадрату плюс число −16.

Самостоятельно примените сокращенную формулу умножения, а затем посмотрите решение

Суммарный куб

Формула куба суммы — равенство

(куб суммы двух чисел равен кубу первого числа плюс три раза квадрату первого числа и второго, плюс три раза произведение первого числа и квадрата второго, плюс куб второго числа).

Формула куба суммы отображается следующим образом:

Пример 10. Записать выражение в виде полинома

Решение. По формуле куба суммы получаем

Самостоятельно примените сокращенную формулу умножения, а затем посмотрите решение

Куб разницы

Формула куба разности — равенство

(куб разности двух чисел равен кубу первого числа минус тройное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго минус куб второго числа).

Используя формулу куба, можно факторизовать суммы полиномов, а именно представить их как произведение трех одинаковых множителей.

Формула для куба разности отображается следующим образом:

Пример 12. Запишите выражение в виде полинома

Решение. По формуле куба разности получаем

Самостоятельно примените сокращенную формулу умножения, а затем посмотрите решение

Разница квадратов

Формула разности квадратов — равенство

(разность квадратов двух чисел равна произведению суммы этих чисел на их разность).

Используя формулу куба, можно факторизовать суммы любого многочлена вида.

Доказательство формулы получено с использованием правила умножения многочленов:

Пример 14. Запишите произведение в виде многочлена

.

Решение. По формуле разности квадратов получаем

Пример 15. Фактор

Решение. Это выражение в явном виде ни под какую тождественность не укладывается.Но число 16 можно представить как степень с основанием 4: 16 = 4². Тогда исходное выражение примет другую форму:

,

и это уже формула разности квадратов, и, применив эту формулу, получаем

При вычислении алгебраических многочленов для упрощения вычислений используйте сокращенные формулы умножения … Всего таких формул семь. Вы должны знать их все наизусть.

Также следует помнить, что вместо «a» и «b» формулы могут содержать как числа, так и любые другие алгебраические многочлены.

Разница квадратов

Помните!

Разность квадратов двух чисел равна произведению разницы между этими числами и их суммы.

а 2 — б 2 = (а — б) (а + б)
  • 15 2 — 2 2 = (15 — 2) (15 + 2) = 13 17 = 221
  • 9a 2 — 4b 2 c 2 = (3a — 2bc) (3a + 2bc)

Квадрат суммы

Помните!

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.


(а + б) 2 = а 2 + 2ab + б 2

Обратите внимание, что с помощью этой сокращенной формулы умножения легко найти квадраты больших чисел без использования калькулятора или длинного умножения. Поясним на примере:

Найдите 112 2.

  • Разложим 112 на сумму чисел, квадраты которых мы хорошо помним.
    112 = 100 + 1
  • Давайте запишем сумму чисел в скобки и поставим квадрат над скобками.
    112 2 = (100 + 12) 2
  • Воспользуемся формулой квадрата суммы:
    112 2 = (100 + 12) 2 = 100 2 + 2100 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула возведения в квадрат суммы также верна для любого алгебраического полинома.

  • (8a + c) 2 = 64a 2 + 16ac + c 2

Внимание!

(a + b) 2 не равно (a 2 + b 2)

Квадрат разницы

Помните!

Квадрат разницы между двумя числами равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.


(а — б) 2 = а 2 — 2ab + б 2

Также стоит запомнить очень полезное преобразование:

(a — b) 2 = (b — a) 2

Формула выше доказывается простым раскрытием скобок:

(a — b) 2 = a 2 −2ab + b 2 = b 2 — 2ab + a 2 = (b — a) 2

Суммарный куб

Помните!

Куб суммы двух чисел равен кубу первого числа плюс три квадрата первого числа и второго плюс три квадрата второго плюс куб второго.


(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Как запомнить куб суммы

Запомнить эту «пугающую» формулу довольно просто.

  • Научитесь начинать с «тройки».
  • Два полинома в центре имеют коэффициенты 3.
  • Напомним, что любое число до нуля равно 1. (a 0 = 1, b 0 = 1). Легко видеть, что в формуле происходит уменьшение степени «а» и увеличение степени «б». Вы можете убедиться в этом:
    (a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Внимание!

(a + b) 3 не равно a 3 + b 3

Куб разницы

Помните!

Куб разности двух чисел равен кубу первого числа минус троекратный квадрат первого числа и второго плюс три умножения произведения первого числа и квадрата второго минус куб второй.


(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Эта формула запоминается так же, как и предыдущая, но только с учетом чередования знаков «+» и «-». Первому члену «а 3» предшествует «+» (мы не пишем его по правилам математики). Это означает, что следующему члену будет предшествовать «-», затем снова «+» и так далее.

(a — b) 3 = + a 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Сумма кубов

Не путать с кубом суммы!

Помните!

Сумма кубиков равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

Сумма кубиков — произведение двух скобок.

  • Первая скобка — это сумма двух чисел.
  • Вторая скобка представляет собой неполный квадрат разности чисел. Выражение называется неполным квадратом разности:
    (a 2 — ab + b 2)
    Этот квадрат неполный, так как в середине вместо удвоенного произведения стоит обычное произведение чисел.

Разница кубиков

Не путать с кубом разницы!

Помните!

Разность кубиков равна произведению разности двух чисел на неполный квадрат суммы.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Будьте осторожны при написании символов.

Применение сокращенных формул умножения

Следует помнить, что все приведенные выше формулы также используются справа налево.

Многие примеры в учебных пособиях предназначены для того, чтобы помочь вам снова собрать многочлены с помощью формул.

  • а 2 + 2а + 1 = (а + 1) 2
  • (ac — 4b) (ac + 4b) = a 2 c 2 — 16b 2

Таблицу со всеми формулами сокращенного умножения вы можете скачать в разделе «

При вычислении алгебраических многочленов для упрощения вычислений используйте сокращенные формулы умножения … Всего таких формул семь. Вы должны знать их все наизусть.

Также следует помнить, что вместо a и b формулы могут содержать как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Разница между квадратами двух чисел равна произведению разницы между этими числами и их суммы.

а 2 — б 2 = (а — б) (а + б)

Квадрат суммы

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b) 2 = a 2 + 2ab + b 2

Обратите внимание, что с помощью этой сокращенной формулы умножения легко найти квадраты больших чисел без использования калькулятора или длинного умножения. Поясним на примере:

Найдите 112 2.

Разложим 112 на сумму чисел, квадраты которых мы хорошо помним.
112 = 100 + 1

Напишем сумму чисел в скобках, а над скобками поставим квадрат.
112 2 = (100 + 12) 2

Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10,000 + 2 400 + 144 = 12 544

Помните, что формула квадрата суммы также верна для любого алгебраического многочлена.

(8a + c) 2 = 64a 2 + 16ac + c 2

Внимание !!!

(a + b) 2 не равно a 2 + b 2

Разница в квадрате

Квадрат разницы между двумя числами равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.

(а — б) 2 = а 2 — 2ab + б 2

Также стоит вспомнить очень полезную трансформацию:

(a — b) 2 = (b — a) 2
Формула выше доказывается простым раскрытием скобок:

(a — b) 2 = a 2 — 2ab + b 2 = b 2 — 2ab + a 2 = (b — a) 2

Суммарный куб

Куб суммы двух чисел равен кубу первого числа плюс троекратный квадрат первого числа и второй плюс троекратный квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Запомнить эту «пугающую» формулу довольно просто.

Научитесь начинать с 3.

Два полинома в центре имеют коэффициенты 3.

IN Напомним, что любое число в нулевой степени равно 1. (a 0 = 1, b 0 = 1). Легко видеть, что степень a в формуле уменьшается, а степень b увеличивается. Вы можете убедиться в этом:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Внимание !!!

(a + b) 3 не равно a 3 + b 3

Куб разницы

Куб разницы между двумя числами равен кубу первого числа минус три раза квадрат первого числа и второго плюс три раза произведение первого числа и квадрата второго минус куб секунда.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Эта формула запоминается так же, как и предыдущая, но только с учетом чередования знаков «+» и «-». Первому члену a 3 предшествует «+» (мы не пишем его по правилам математики). Это означает, что следующему члену будет предшествовать «-», затем снова «+» и так далее.

(а — б) 3 = + а 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Сумма кубиков ( Не путать с кубом суммы!)

Сумма кубиков равна произведению суммы двух чисел на неполный квадрат разницы.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

Сумма кубиков — произведение двух скобок.

Первая скобка представляет собой сумму двух чисел.

Вторая скобка представляет собой неполный квадрат разности чисел. Выражение называется неполным квадратом разности:

A 2 — ab + b 2
Этот квадрат неполный, так как в середине вместо удвоенного произведения стоит обычное произведение чисел.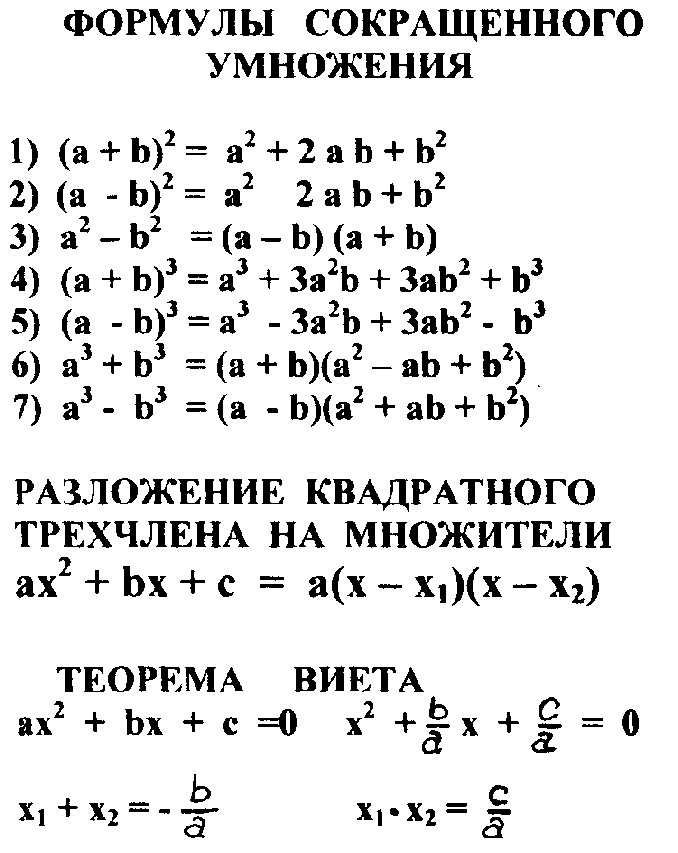

Кубы Различий (Не путать с Кубами Разностей !!!)

Разница между кубиками равна произведению разницы двух чисел на неполный квадрат суммы.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Будьте осторожны при написании символов. Следует помнить, что все приведенные выше формулы также используются справа налево.

Трудно запомнить сокращенные формулы умножения? Причине легко помочь. Просто нужно вспомнить, как изображена такая простая вещь, как треугольник Паскаля. Тогда вы всегда и везде будете помнить эти формулы, а точнее не вспоминать, а восстанавливать.

Что такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена формы в многочлен.

Развернем, например:

В этой записи легко запомнить, что в начале стоит куб первого числа, а в конце — куб второго числа. Но что посередине, вспомнить сложно. И даже то, что в каждом следующем члене степень одного фактора все время уменьшается, а второго увеличивается — это легко заметить и запомнить, сложнее обстоит дело с запоминанием коэффициентов и знаков (плюс или минус?).

Итак, шансы в первую очередь. Не запоминайте их! На полях тетради быстро нарисуйте треугольник Паскаля, и вот они — коэффициенты уже перед нами. Начинаем рисовать с трех единиц, одна сверху, две снизу, справа и слева — ага, уже треугольник получается:

Первая строка с единицей равна нулю. Затем идет первое, второе, третье и так далее. Чтобы получить вторую строку, вам нужно снова добавить единицы по краям, а в центре написать число, полученное сложением двух чисел над ним:

Записываем третью строку: снова по краям блока, и снова, чтобы в новой строке получилось следующее число, складываем числа над ним в предыдущей:


Как вы уже догадались, в каждой строке мы получаем коэффициенты разложения бинома в полином:


Ну, а знаки запомнить еще проще: первый такой же, как в расширяемом биноме (сумму раскрываем — значит плюс, разность означает минус), а потом знаки чередуются!

Вот такая вот полезная штука — треугольник Паскаля. 2 \ вправо) \]

Сокращенные формулы умножения (ACF) используются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют сделать расчеты более компактными и быстрыми.

В этой статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательства формул сокращенного умножения.

Впервые тема БСС рассматривается в рамках курса «Алгебра» для 7 класса.Ниже приведены 7 основных формул.

Сокращенные формулы умножения

  1. формула для вычисления квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
  2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
  3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
  4. формула разностного куба: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
  5. формула разности квадратов: a 2 — b 2 = a — b a + b
  6. формула суммы кубиков: a 3 + b 3 = a + b a 2 — a b + b 2
  7. формула разности кубиков: a 3 — b 3 = a — b a 2 + a b + b 2

Буквы a, b, c в этих выражениях могут быть любыми числами, переменными или выражениями. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и представим ниже, обведя рамкой.

Первые четыре формулы позволяют вычислить, соответственно, квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разницу квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы представляют собой, соответственно, умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Сокращенную формулу умножения иногда также называют сокращенной формулой умножения. Это неудивительно, поскольку всякое равенство — это тождество.

При решении практических примеров часто используют сокращенные формулы умножения с переставленными левой и правой частями. Это особенно полезно, когда имеет место факторизация многочлена.

Дополнительные сокращенные формулы умножения

Не будем ограничиваться курсом алгебры 7-го класса и добавим еще несколько формул в нашу таблицу БСС.

Сначала рассмотрим биномиальную формулу Ньютона.

a + b n знак равно C n 0 a n + C n 1 a n — 1 b + C n 2 a n — 2 b 2 +. … + C n n — 1 a b n — 1 + C n n b n

Здесь C n k — биномиальные коэффициенты, которые находятся в строке n треугольника Паскаля. Биномиальные коэффициенты рассчитываются по формуле:

С N К знак равно N! к! (N — k)! = п (п — 1) (п — 2). … (п — (к — 1)) к!

Как видите, FSE для квадрата и куба разности и суммы является частным случаем биномиальной формулы Ньютона для n = 2 и n = 3 соответственно.

А что, если в сумме, которую нужно возвести во власть, больше двух? Пригодится формула квадрата суммы трех, четырех и более членов.

а 1 + а 2 +. … + а п 2 знак равно а 1 2 + а 2 2 +. … + а п 2 + 2 а 1 а 2 + 2 а 1 а 3 +. … + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 +. … + 2 a 2 a n + 2 a n — 1 и n

Другая формула, которая может оказаться полезной, — это формула для разности n-х степеней двух членов.

a n — b n знак равно a — b a n — 1 + a n — 2 b + a n — 3 b 2 +. … + a 2 b n — 2 + b n — 1

Эту формулу обычно делят на две формулы — для четной и нечетной степеней соответственно.

Для четных индикаторов 2м:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 +. … + b 2 м — 2

Для нечетных показателей 2m + 1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 +. … + b 2 м

Формулы для разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы для n = 2 и n = 3 соответственно.Для разности кубиков b также заменяется на — b.

Как читать сокращенные формулы умножения?

Мы дадим соответствующие формулировки для каждой формулы, но сначала мы поймем принцип чтения формул. Удобнее всего это сделать на собственном примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2.

Они говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разницы между двумя выражениями a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

Прочтите формулу a + b 3 = a 3 + 3 a 2 b + 3 ab 2 + b 3. Куб суммы двух выражений a и b равен сумме кубиков этих выражений, в три раза превышающей квадрат первого выражения на второе и троекратный квадрат второго выражения на первое выражение.

Переходим к чтению формулы разности кубов a — b 3 = a 3 — 3 a 2 b + 3 ab 2 — b 3. Куб разности двух выражений a и b равен кубу первое выражение минус три раза квадрат первого выражения и второго плюс три раза квадрат второго выражения и первого выражения минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается следующим образом: разность квадратов двух выражений равна произведению разницы и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называются, соответственно, неполным квадратом суммы и неполным квадратом разности.

Имея это в виду, формулы для суммы и разности кубиков будут выглядеть следующим образом:

Сумма кубиков двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разница между кубиками двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Подтверждение FSO

Доказать ФСО довольно просто. Исходя из свойств умножения, умножаем части формул в скобки.

Например, рассмотрим формулу квадрата разницы.

a — b 2 = a 2 — 2 a b + b 2.

Чтобы возвести выражение во вторую степень, вам нужно умножить это выражение само на себя.

а — б 2 = а — б а — б.

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2.

Формула доказана. Остальные ФСО доказываются аналогично.

Примеры применения БСС

Целью использования сокращенных формул умножения является быстрое и краткое умножение и возведение в степень выражений. Однако это далеко не вся сфера деятельности ФСО. Они широко используются для сокращения выражений, сокращения дробей, разложения многочленов на множители. Вот несколько примеров.

Пример 1. FSO

Упростим выражение 9 y — (1 + 3 y) 2.

Применяем формулу суммы квадратов и получаем:

9 лет — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2 . FSO

Уменьшить дробь 8 x 3 — z 6 4 x 2 — z 4.

Обратите внимание, что выражение в числителе — это разница между кубиками, а знаменатель — это разница в квадратах.

8 x 3 — z 6 4 x 2 — z 4 знак равно 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z.

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

FSO также помогают вычислять значения выражений.Главное — уметь замечать, где применять формулу. Покажем это на примере.

Возведем в квадрат число 79. Вместо громоздких вычислений напишем:

79 = 80 — 1; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241.

Казалось бы, сложные вычисления выполняются быстро с использованием сокращенных формул умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена.Выражение 4 x 2 + 4 x — 3 можно преобразовать в 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4. Такие преобразования широко используются при интегрировании.

Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter

Формулы или сокращенные правила умножения используются в арифметике или, скорее, в алгебре для более быстрого процесса вычисления больших алгебраических выражений. Сами формулы являются производными от правил, существующих в алгебре для умножения нескольких многочленов.

Использование этих формул обеспечивает довольно быстрое решение различных математических задач, а также помогает упростить выражения. Правила алгебраического преобразования позволяют выполнять некоторые манипуляции с выражениями, следуя которым вы можете получить выражение в левой части равенства в правой части или преобразовать правую часть равенства (чтобы получить выражение в левой части после знак равенства).

Удобно знать формулы, используемые для сокращенного умножения по памяти, так как они часто используются при решении задач и уравнений.Ниже приведены основные формулы, включенные в этот список, и их названия.

Квадрат суммы

Чтобы вычислить квадрат суммы, вам нужно найти сумму, состоящую из квадрата первого члена, удвоенного произведения первого члена на второе и квадрата второго. В виде выражения это правило записывается следующим образом: (a + c) ² = a² + 2ac + c².

Квадрат разницы

Чтобы вычислить квадрат разницы, вам нужно вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятого с противоположным знаком), и квадрат второго числа.В виде выражения это правило выглядит так: (a — c) ² = a² — 2ac + c².

Разница квадратов

Формула для разницы между двумя числами в квадрате равна произведению суммы этих чисел на их разность. В виде выражения это правило выглядит следующим образом: a² — c² = (a + c) · (a — c).

Куб суммы

Для вычисления куба суммы двух членов необходимо вычислить сумму, состоящую из куба первого члена, тройного произведения квадрата первого члена и второго тройного члена. произведение первого члена и второго квадрата, а также куб второго члена.В форме выражения это правило выглядит следующим образом: (a + c) ³ = a³ + 3a²c + 3ac² + c³.

Сумма кубиков

Согласно формуле, она приравнивается к произведению суммы этих членов на их неполный квадрат разности. В форме выражения это правило выглядит следующим образом: a³ + c³ = (a + c) · (a² — ac + c²).

Пример. Необходимо рассчитать объем фигуры, которая получается сложением двух кубиков.Известны только размеры их сторон.

Если значения сторон малы, то вычисления просты.

Если длины сторон выражаются громоздкими числами, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности выглядит следующим образом: как сумма третьей степени первого члена, утроить отрицательное произведение квадрата первого члена на второе, утроить произведение первого члена на квадрат второго и отрицательный куб второго члена. В форме математического выражения куб разности выглядит так: (a — c) ³ = a³ — 3a²c + 3ac² — c³.

Разница кубиков

Формула разности кубов отличается от суммы кубов только одним знаком. Таким образом, разность кубиков представляет собой формулу, равную произведению разности этих чисел на их неполный квадрат суммы. По форме разница кубиков выглядит следующим образом: a 3 — c 3 = (a — c) (a 2 + ac + c 2).

Пример. Необходимо рассчитать объем фигуры, который останется после вычитания желтой объемной фигуры из объема синего куба, который также является кубом. Известен только размер стороны большого и малого куба.

Если боковые значения небольшие, то вычисления довольно просты. А если длины сторон выражены значащими числами, то стоит воспользоваться формулой под названием «Кубы разности» (или «Куб разности»), которая значительно упростит вычисления.

Комплексные числа: умножение

Комплексные числа: умножение

Умножение производится алгебраически.

Комплексное умножение сложнее понять с алгебраической или геометрической точки зрения. Давайте сначала сделаем это алгебраически, а для умножения возьмем определенные комплексные числа, например 3 + 2 i и 1 + 4 i. В каждом есть два члена, поэтому, когда мы их умножим, мы получим четыре члена: (3 + 2 и ) (1 + 4 и ) = 3 + 12 i + 2 i + 8 i 2 .

Теперь 12 i + 2 i упрощается до 14 i, конечно. А как насчет 8 i 2 ? Помните, что мы ввели i как сокращение для √ – 1, квадратного корня из –1. Другими словами, i — это то, чей квадрат равен –1. Таким образом, 8 i 2 равно –8. Следовательно, произведение (3 + 2 i ) (1 + 4 i ) равно –5 + 14 i.

Если вы обобщите этот пример, вы получите общее правило умножения

Помните, что ( xu — yv ), действительная часть продукта, является произведением реальных частей минус произведение мнимых частей, но ( xv + yu ) мнимая часть продукт, представляет собой сумму двух произведений одной действительной части и другой мнимой части.

Давайте посмотрим на некоторые частные случаи умножения.

Умножение комплексного числа на действительное

В приведенной выше формуле умножения, если v равно нулю, вы получите формулу для умножения комплексного числа x + yi и действительного числа u вместе: ( x + yi ) u = xu + yu i .

Другими словами, вы просто умножаете обе части комплексного числа на действительное число.Например, 2 умножить на 3 + i будет просто 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваиваете расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Умножение на 2 можно рассматривать как преобразование, которое растягивает комплексную плоскость C на коэффициент 2 от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.

Умножение и абсолютное значение.

Несмотря на то, что мы сделали только один случай для умножения, достаточно предположить, что абсолютное значение zw (то есть расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение ш. Это было тогда, когда w было действительным числом u чуть выше. На самом деле это так в целом:

Проверка этого тождества — это упражнение по алгебре.Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не придется иметь дело с квадратными корнями. Мы покажем | zw | 2 = | z | 2 | w | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда, согласно формуле умножения, zw равно ( xu — yv ) + ( xv + yu ) i. Вспомните из раздела об абсолютных величинах, что

| z | 2 = x 2 + y 2

Аналогично имеем

| w | 2 = u 2 + v 2

и, поскольку zw = ( xu — yv ) + ( xv + yu ) i,

| wz | 2 = ( xu — yv ) 2 + ( xv + yu ) 2

Итак, чтобы показать | zw | 2 = | z | 2 | w | 2 , все, что вам нужно сделать, это показать, что

( xu — yv ) 2 + ( xv + yu ) 2 = ( x 2 + y 2 ) ( u 2 + v 2 )

и это простое упражнение по алгебре.

Полномочия

i. В нашем следующем частном случае умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i 2 = –1. Что насчет i 3 ? Это просто i 2 умножить на i , и это будет -1 умножить на i. Следовательно, i 3 = — i. Что интересно: куб и — это собственное отрицание.Далее рассмотрим i 4 . Это квадрат i 2 , то есть квадрат –1. Итак, i 4 = 1. Другими словами, i — это корень четвертой степени из 1. Вы можете показать, что — i — это еще один корень четвертой степени из 1. И поскольку и –1, и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно, 1, i, –1 и — i. Это наблюдение связано с фундаментальной теоремой алгебры, поскольку уравнение z 4 = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня.

Более высокие степени i легко найти теперь, когда мы знаем i 4 = 1. Например, i 5 — это i , умноженное на i 4 , и это всего лишь i. . Можно уменьшить мощность i на 4 и не изменить результат. Другой пример: i 11 = i 7 = i 3 = — i.

Как насчет отрицательных степеней и ? Что является обратным для i, то есть i –1 ? По той же причине, что вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i –1 = i 3 = — i. Таким образом, i обратное значение — i. Представьте себе — число, обратной величиной которого является собственное отрицание! Конечно, легко проверить, что i раз — i равно 1, поэтому, конечно, i и — i являются обратными.

Корни единства.

Различные корни из 1 называются корнями из единицы. В общем, по Фундаментальной теореме алгебры количество n корней -й степени из единицы равно n, , так как существует n корней у уравнения n -й степени. z u — 1 = 0.Квадратные корни из единицы равны 1 и –1. Корни четвертой степени равны ± 1, ± i, , как отмечалось ранее в разделе, посвященном абсолютным значениям. Кроме того, в этом разделе упоминалось, что ± √2 / 2 ± i √2 / 2 были квадратными корнями из i и — i, и теперь с формулой умножения, которую легко проверить. Следовательно, восемь корней восемь из единицы равны ± 1, ± i, и ± √2 / 2 ± i √2 / 2. Обратите внимание на то, как эти восемь корней единицы равномерно распределены по единичной окружности.

Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте их немного подождем.

Умножение комплексного числа на

i. В нашей цели по поиску геометрической интерпретации комплексного умножения, давайте теперь рассмотрим умножение произвольного комплексного числа z = x + yi на i. z i = ( x + yi ) i = — y + xi .

Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на x единиц справа от мнимой оси и на y единиц выше действительной оси. Точка z i расположена на y единиц слева и x единиц выше. Произошло то, что умножение на i повернулось в точку z на 90 ° против часовой стрелки вокруг начала координат до точки z i. Короче говоря, умножение на i дает поворот на 90 ° против часовой стрелки на 0.

Вы можете проанализировать, что умножение на — i делает таким же образом. Вы обнаружите, что умножение на — i дает поворот на 90 ° по часовой стрелке примерно на 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, которое подразумевается против часовой стрелки. Тогда мы можем сказать, что умножение на — i дает поворот на –90 ° вокруг 0 ​​или, если хотите, поворот на 270 ° вокруг 0.

Геометрическая интерпретация умножения.

Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока посмотрим на результаты без обоснования. Мы видели два особых случая умножения: один на вещественные числа, что приводит к масштабированию, другой на и , что приводит к вращению. Общий случай — это комбинация масштабирования и вращения.

Пусть z и w будут точками на комплексной плоскости C .Проведите линии от 0 до z и от 0 до w . Длины этих строк — абсолютные значения | z | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | zw | что равно | z | | Вт |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Чего мы не знаем, так это направления линии от 0 до zw.

Ответ: «углы складываются». Мы определим направление линии от 0 до z по определенному углу, называемому аргументом z , иногда обозначаемым arg ( z ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — прямая от 0 до z. Другая точка w имеет угол arg ( w ).Тогда произведение zw будет иметь угол, который является суммой углов arg ( z ) + arg ( w ). (На диаграмме arg ( z ) составляет около 20 °, а arg ( w ) составляет около 45 °, поэтому arg ( zw ) должно быть около 65 °. )

Таким образом, у нас есть два уравнения, которые определяют, где находится zw в C :


Порядок действий: PEMDAS

Purplemath

Если вас просят упростить что-то вроде «4 + 2 × 3», естественно возникает вопрос: «Как мне это сделать? Потому что есть два варианта!» Я мог бы добавить первым:

4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18

…или я мог сначала умножить:

4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10

Какой ответ правильный?

MathHelp.

com

Кажется, ответ зависит от того, как вы смотрите на проблему.Но у нас не может быть такой гибкости в математике; математика не будет работать, если вы не можете быть уверены в ответе или если можно вычислить одно и то же выражение, чтобы вы могли прийти к двум или более различным ответам.

Чтобы устранить эту путаницу, у нас есть некоторые правила приоритета, установленные, по крайней мере, еще в 1500-х годах, которые называются «порядком операций». «Операциями» являются сложение, вычитание, умножение, деление, возведение в степень и группирование; «порядок» этих операций указывает, какие операции имеют приоритет (выполняются) перед другими операциями.

Распространенным методом запоминания порядка действий является аббревиатура (или, точнее, «акроним») «PEMDAS», которая превращается в мнемоническую фразу «Пожалуйста, извините, моя дорогая тетя Салли».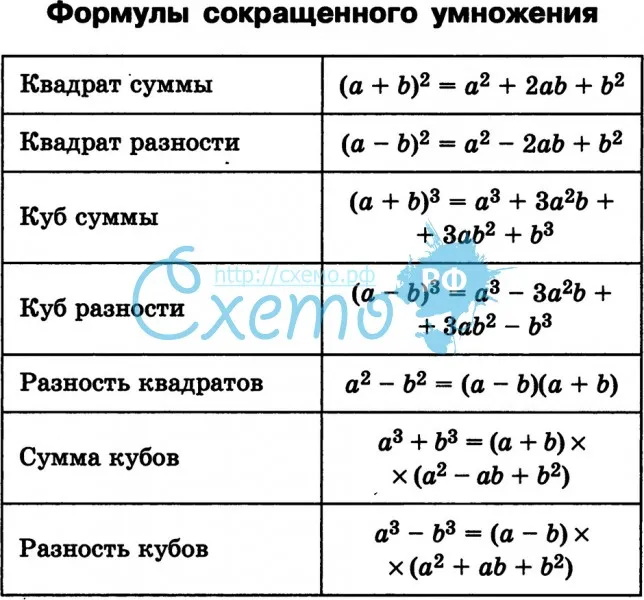 Эта фраза означает «круглые скобки, экспоненты, умножение и деление, сложение и вычитание» и помогает запомнить их порядок. В этом списке указаны ранги операций: скобки опережают показатели, которые превосходят умножение и деление (но умножение и деление находятся в одном ранге), а умножение и деление превосходят сложение и вычитание (которые вместе находятся в нижнем ранге).Другими словами, приоритет:

  1. Круглые скобки (внутри них упростить)
  2. Экспоненты
  3. Умножение и деление (слева направо)
  4. Сложение и вычитание (слева направо)

Когда у вас есть несколько операций одного ранга, вы просто действуете слева направо. Например, 15 ÷ 3 × 4 не 15 ÷ (3 × 4) = 15 ÷ 12, а скорее (15 ÷ 3) × 4 = 5 × 4, потому что, идя слева направо, вы попадаете в разделение подпишитесь первым.

Если вы не уверены в этом, проверьте это на своем калькуляторе, который был запрограммирован с иерархией порядка операций. Например, набрав указанное выше выражение в графическом калькуляторе, вы получите:

Используя приведенную выше иерархию, мы видим, что в вопросе «4 + 2 × 3» в начале этой статьи ответ 2 был правильным, потому что мы должны выполнить умножение, прежде чем выполнять сложение.

(Примечание: носители британского английского часто вместо этого используют аббревиатуру «BODMAS», а не «PEMDAS». BODMAS означает «скобки, порядки, деление и умножение, а также сложение и вычитание». и «порядки» совпадают с показателями, два акронима означают одно и то же. Кроме того, вы можете видеть, что буквы «M» и «D» перевернуты в британо-английской версии; это подтверждает, что умножение и деление того же «звания» или «уровня».Канадцы, говорящие по-английски, разделяют разницу, используя BEDMAS.)

Порядок операций был определен во избежание недопонимания, но PEMDAS может создать свою собственную путаницу; некоторые студенты иногда склонны применять иерархию, как будто все операции в задаче находятся на одном «уровне» (просто идут слева направо), но часто эти операции не «равны». Во многих случаях это помогает решать проблемы изнутри, а не слева направо, потому что часто некоторые части проблемы находятся «глубже», чем другие.Лучший способ объяснить это — привести несколько примеров:

Мне нужно упростить термин с показателем, прежде чем пытаться добавить 4:

Я должен упростить в круглых скобках, прежде чем я смогу прописать экспоненту. Только тогда я смогу добавить 4.

4 + (2 + 1) 2 = 4 + (3) 2 = 4 + 9 = 13

  • Упростить 4 + [–1 (–2 — 1)]
    2 .

Я не должен пытаться делать эти вложенные круглые скобки слева направо; этот метод слишком подвержен ошибкам. Вместо этого я постараюсь работать изнутри. Сначала я упрощу внутри фигурных скобок, затем упрощу внутри квадратных скобок и только потом займусь квадратом. После этого я наконец могу добавить 4:

4 + [–1 (–2 — 1)] 2

= 4 + [–1 (–3)] 2

= 4 + [3] 2

= 4 + 9

= 13

Использование квадратных скобок («[» и «]» выше) вместо скобок не имеет особого значения.Скобки и фигурные скобки (символы «{» и «}») используются, когда есть вложенные круглые скобки, как помощь для отслеживания того, какие круглые скобки к которым идут. Различные символы группировки используются только для удобства. Это похоже на то, что происходит в электронной таблице Excel, когда вы вводите формулу, используя круглые скобки: каждый набор скобок имеет цветовую кодировку, поэтому вы можете определить пары:

  • Упростить 4 (
    –2 / 3 + 4 / 3 ).

Сначала я упрощу внутри скобок:

Итак, мой упрощенный ответ

8 / 3

На следующей странице есть еще примеры отработанных примеров ….

URL: https: // www.purplemath.com/modules/orderops.htm

Правило

BODMAS — Что такое Правило BODMAS? Определение, Формула

Правило BODMAS — это аббревиатура, которая используется для запоминания порядка операций, которым необходимо следовать при решении математических выражений. Это означает B — скобки, O — порядок степеней или корней, D — деление, M — умножение, A — сложение и S — вычитание. Это означает, что выражения, содержащие несколько операторов, необходимо упрощать слева направо только в этом порядке.Сначала мы решаем скобки, затем степени или корни, затем деление или умножение (в зависимости от того, что идет первым из левой части выражения), и, наконец, вычитание или сложение, в зависимости от того, что идет слева.

В этом уроке мы узнаем о правиле BODMAS, которое помогает решать арифметические выражения, содержащие множество операций, таких как сложение (+), вычитание (-), умножение (×), деление (÷) и скобки () .

Что такое БОДМАС?

BODMAS, называемый порядком операций, представляет собой последовательность для выполнения операций в арифметическом выражении.Математика — это все о логике и некоторых стандартных правилах, которые упрощают наши вычисления. Итак, BODMAS — одно из тех стандартных правил упрощения выражений, которые имеют несколько операторов.

В арифметике выражение или уравнение состоит из двух компонентов:

Числа

Числа — это математические значения, используемые для подсчета и представления величин, а также для выполнения вычислений. В математике числа можно классифицировать как натуральные числа, целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, комплексные числа, мнимые числа.

Операторы или операторы

Оператор — это символ, который объединяет два числа и дает выражение или уравнение. В математике наиболее распространены операторы сложения (+), вычитания (-), умножения (×), деления (÷). Для математических выражений или уравнений, в которых задействован только один оператор, найти ответ довольно просто. В случае нескольких операторов найти решение становится немного сложнее! Давайте разберемся в этом на примере. Дженни и Рон отдельно решили математическое выражение 6 × 3 + 2.Ниже приведены два разных метода, с помощью которых Дженни и Рон решили выражение:

Метод Дженни: 6 × 3 + 2 = 6 × 5 = 30, Метод Рона: 6 × 3 + 2 = 18 + 2 = 20.

Как мы видим, Дженни и Рон получили разные ответы. В математике мы знаем, что на это выражение может быть только один правильный ответ. Как решить, кто прав? В таких случаях мы используем BODMAS , чтобы найти правильный ответ. Давайте посмотрим на приведенный ниже пример, чтобы понять, как работает BODMAS:

Значение и определение правила BODMAS

Правило BODMAS используется для оценки математических выражений и выполнения сложных вычислений гораздо более простым и стандартным способом.

BODMAS Определение

Согласно правилу BODMAS, чтобы решить любое арифметическое выражение, мы сначала решаем члены, записанные в скобках, а затем мы упрощаем экспоненциальные члены и переходим к операциям деления и умножения, а затем, в конце концов, работаем над сложением и вычитанием. . Соблюдение порядка операций в правиле BODMAS всегда приводит к правильному ответу. Упрощение терминов внутри скобок можно произвести напрямую. Это означает, что мы можем выполнять операции внутри скобок в порядке деления, умножения, сложения и вычитания.Если в выражении есть несколько скобок, все одинаковые типы скобок могут быть решены одновременно. Например, (14 + 19) ÷ (13-2) = 33 ÷ 11 = 3.

Для понимания терминов и операций, обозначенных аббревиатурой BODMAS, в правильном порядке, ознакомьтесь с таблицей, приведенной ниже.

Б [{()}] Кронштейны
O x² Орден Сил или Корней
D ÷ Отдел
М × Умножение
А + Дополнение
ю.– Вычитание

BODMAS против PEMDAS

BODMAS и PEMDAS — два акронима, которые используются для запоминания порядка операций.Правило BODMAS почти аналогично правилу PEMDAS . Существует различие в сокращении, потому что некоторые термины известны под разными названиями в разных странах. При использовании правила BODMAS или правила PEMDAS мы должны помнить, что, когда мы подходим к шагу деления и умножения, мы решаем операцию, которая идет первой из левой части выражения. То же правило применяется к сложению и вычитанию, то есть мы решаем операцию, которая идет первой слева.

Когда использовать БОДМЫ?

BODMAS используется, когда в математическом выражении содержится более одной операции. Существует последовательность определенных правил, которые необходимо соблюдать при использовании метода BODMAS. Это дает правильную структуру для получения уникального ответа для каждого математического выражения.

Следующие условия:

  • Если есть скобка, откройте скобку, затем добавьте или вычтите члены. а + (б + с) = а + б + с, а + (б — в) = а + б — с
  • Если есть отрицательный знак, просто откройте скобку, умножьте отрицательный знак на каждый член внутри скобки.а — (Ь + с) ⇒ а — Ь — с
  • Если есть какой-либо термин вне скобок, умножьте этот внешний член на каждый член внутри скобок. a (b + c) ⇒ ab + ac
    • .

Простые способы запомнить правило BODMAS

Простые правила запоминания правила BODMAS приведены ниже:

  • Сначала упростите скобки.
  • Решите все экспоненциальные члены.
  • Выполните деление или умножение (слева направо)
  • Выполните сложение или вычитание (слева направо)

Распространенные ошибки при использовании правила BODMAS

При применении правила BODMAS для упрощения выражений можно допустить несколько распространенных ошибок, и эти ошибки приведены ниже:

  • Наличие нескольких скобок может вызвать путаницу, и мы можем получить неправильный ответ.Таким образом, если в выражении есть несколько скобок, все одинаковые типы скобок могут быть решены одновременно.
  • Ошибка возникает в некоторых случаях из-за отсутствия правильного понимания сложения и вычитания целых чисел. Например, 1-3 + 4 = -2 + 4 = 2. Но иногда допускаются следующие ошибки, которые приводят к неправильному ответу, например, 1-3 + 4 = 1-7 = -6.
  • Ошибка при предположении, что деление имеет более высокий приоритет над умножением, а сложение имеет более высокий приоритет над вычитанием. Следование правилу слева направо при выборе этих операций помогает получить правильный ответ.
  • Умножение и деление являются операциями одного уровня и должны выполняться в последовательности слева направо (в зависимости от того, что идет первым в выражении), то же самое со сложением и вычитанием, которые являются операциями одного уровня, выполняемыми после умножения и деления. Если кто-то решает сначала деление перед умножением (что находится слева от операции деления), поскольку D стоит перед M в BODMAS, они могут в конечном итоге получить неправильный ответ.

Темы, связанные с BODMAS

Щелкните любую из тем из списка ниже, чтобы узнать больше о BODMAS или других связанных статьях.

Часто задаваемые вопросы по правилу BODMAS

Что такое правило Бодма в математике?

Правило BODMAS относится к правилу, которому следуют при решении математических выражений. BODMAS — это порядок операций для математических выражений, которые включают более одной операции. Акроним расшифровывается как B — скобки, O — порядок степеней, D — деление, M — умножение, A — сложение и S — вычитание.

Как работает правило BODMAS?

В любом арифметическом выражении, если используется несколько операций, нам нужно решить члены в порядке правила BODMAS. Сначала решаем часть, написанную в скобках. После решения скобок мы выполняем операции умножения и деления слева направо в зависимости от того, что идет первым в выражении. Тогда мы получим упрощенное выражение, состоящее только из операций сложения и вычитания. Решаем сложение и вычитание слева направо и получаем окончательный ответ.Так работает BODMAS.

Применяется ли BODMAS при отсутствии скобок?

Да, даже если скобок нет, правило BODMAS все равно используется. Нам нужно выполнить остальные операции в том же порядке. Следующий шаг после скобок (B) — это порядок степеней или корней, за которым следует деление, умножение, сложение и затем вычитание.

Что означает буква O в Бодмасе?

O в Bodmas означает «Порядок», что означает упрощение показателей степени или корней в выражении, если таковые имеются, перед арифметическими операциями. В некоторых странах «О» используется для обозначения «из», что снова означает умножение.

Как применить правило Бодмаса?

Правило BODMAS может применяться к выражениям, которые имеют более одного оператора. В этом случае мы сначала упрощаем скобки от самой внутренней скобки до самой внешней [{()}], затем мы оцениваем значения показателей или корней, затем упрощаем умножение и деление, а затем, наконец, выполняем операции сложения и вычитания. при движении слева направо.

Почему порядок действий важен в реальной жизни?

Порядок операций — это сокращенное правило, которое позволяет вам следовать правильному порядку при решении различных частей математического выражения. Это универсальное правило: решать все математические операции, чтобы получить правильный ответ.

Когда правило Бодмаса неприменимо?

Правило BODMAS не применимо к уравнениям. Это применимо к математическим выражениям, имеющим более одного оператора.

Кто изобрел правило Бодмаса? Когда это было представлено?

Правило BODMAS было введено математиком Ахиллесом Реселельтом в 1800-х годах.

Какова полная форма правила Бодмаса?

Полная форма BODMAS: скобки, порядок, деление, умножение, сложение, вычитание.

Используют ли калькуляторы BODMAS?

Калькуляторы

также используют правило BODMAS. Научные калькуляторы автоматически применяют операции в правильном порядке.

Значение умножения. Мысленный счет — полный курс арифметики

Так как истинно в арифметике, что мы можем умножать, разлагая множитель, правый распределительный закон алгебры может быть применен к арифметике.

Пример 7. Умножьте 16 × 5 мысленно, разложив 16 на десятки и единицы.

Ответ . Шестнадцать пятерок равны Десять пятерок + шесть пятерок:
50 + 30 = 80.

Пример 8. Вычислите мысленно 34 × 6, разложив 34.

Решение . 34 × 6 = 30 × 6 + 4 × 6 = 1 8 0 + 2 4 = 20 4.

«Тридцать четыре шестерки равны тридцатью шестеркам плюс четырем шестеркам».

Пример 9. Умножение на 11. 11 × 45.

Умножение на 11 особенно просто, потому что 11 равно 10 + 1.

11 × 45, следовательно, 10 × 45 + 1 × 45:

4 5 0 + 4 5 = 4 9 5.

Другими словами, чтобы умножить на 11, просто прибавьте к числу 10-кратное число.

Пример 10. 11 × 6 . 2 = 6 2 + 6 . 2 = 6 8 . 2

Для выполнения этой или любой из этих проблем в письменной форме —

— это не более чем письменный трюк для получения правильного ответа.

Пример 11.Сколько это 13 × 12?

Ответ . Если вы знаете, что

12 × 12 = 144,

, то 13 × 12 — это просто еще один 12:

13 × 12 = 144 + 12 = 156.

(Урок 5, Вопрос 3.)

Или мы могли бы посчитать 12 так:

Тринадцать 12, = Десять 12 + Три 12
= 120 + 36
= 156.

Как мысленно возвести число в квадрат

Квадратная фигура — это четырехгранная фигура, у которой все стороны равны

и все углы прямые.

«Возвести в квадрат» число означает умножить его само на себя.

«9 в квадрате» = 9 × 9 = 81.

Чтобы найти площадь квадратной фигуры, то есть пространство, ограниченное четырьмя прямыми линиями, возведите в квадрат длину стороны.(См. Урок 10.) Если бы каждая сторона была измерена, например, числом 6, то площадь была бы измерена как 6 × 6 = 36.

Теперь предположим, что мы хотим мысленно возвести в квадрат двузначное число, например 24. Следующая геометрическая арифметика показывает, как это сделать.

Посмотрите на эту квадратную фигуру, у которой каждая сторона равна 24.

Тогда площадь этого квадрата будет 24 × 24. Но мы можем разбить 24 на 20 + 4. Следовательно, весь квадрат будет состоять из следующего:

Квадрат 20, а это 400.

Два прямоугольника, каждый площадью 20 × 4 = 80.

И квадрат 4, что равно 16.

Другими словами, квадрат 20 + 4 равен

.

Квадрат 20, плюс

Дважды 20 × 4, плюс

Площадь 4.

400 + 160 + 16 = 576.

Это несложный мысленный расчет.

Пример 12.Площадь 52.

Решение . 52 = 50 + 2.

Квадрат 50 + 2 равен

Квадрат 50 плюс

Дважды 50 × 2, плюс

Площадь 2.

2500 + 200 + 4 = 2704.

Задача 1. Квадрат 35.

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!

Квадрат 30 + 5 равен:

Квадрат 30 + Дважды 30 × 5 + Квадрат 5.

900 + 300 + 25 = 1225.

Пример 13. Квадрат 48.

Решение . Вместо квадрата 40 + 8 проще возвести в квадрат 50-2.

Квадрат 50-2 равняется

Площадь 50, минус

Дважды 50 × 2, плюс

Площадь 2.

2500 — 200 + 4 = 2304.

Весь квадрат равен квадрату 50. Он составлен из квадрата 48 плюс два прямоугольника, 50 и умноженные на 2, которые мы должны вычесть. Но не стоит дважды вычитать квадрат 2. Поэтому мы добавляем его в конце.

Задача 2. Квадрат 39.

Квадрат 40-1 равен:

Квадрат 40 — Дважды 40 × 1 + Квадрат 1.

1600 — 80 + 1 = 1521.

На этом этапе, пожалуйста, «переверните» страницу и выполните несколько задач .

или

Перейти к разделу 2:

Распределительное свойство умножения

Введение | Главная | Содержание

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: teacher @ themathpage.com


.
РубрикаРазное

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *