Формула скороченого множення: Неприпустима назва — Вікіпедія
ᐉ Формули скороченого множення. Приклади
Формули скороченого множення. Приклади
Формули скороченого множення застосовують для спрощення обчислень, а також розкладання многочленів на прості множники, швидкого множення многочленів.
Більшість формул скороченого множення можна отримати з біному Ньютона, в цьому Ви скоро переконаєтеся.
Формули для квадратів застосовують в обчисленнях найчастіше.
Їх починають вивчати в шкільній програми починаючи з 7 класу і до кінця навчання формули для квадратів та кубів школярі повинні знати на зубок.
ЧИТАЙТЕ ТАКОЖ: Відсоток від числа
Формули для кубів теж не надто складні і їх потрібно знати при зведенні многочленів до стандартного вигляду, для спрощення піднесення суми чи різниці змінної і числа до кубу.
Формули позначені червоним отримують з попередніх групуванням доданків.
Розв’язок. Що таке біном Ньютона Ви мабуть вже знаєте. Якщо ні то нижче наведені біноміальні коефіцієнти
Вони утворюються наступним чином: по краю ідуть одиниці, коефіцієнти між ними в нижньому рядку утворюють сумуванням сусідніх верхніх. Якщо ми маємо різницю в якомусь степені, то знаки в розкладі чергуються від плюса до мінуса. Таким чином для сьомого порядку отримаємо такий розклад
Уважно також погляньте як змінюються показники – для першої змінної вони спадають на одиницю в кожному наступному доданку, відповідно для другої – на одиницю зростають. В сумі показники завжди повинні бути рівні степені розкладу (=7).
Чому дорівнює куб суми двох чисел. Формули скороченого множення
При розрахунку алгебраїчних многочленів для спрощення обчислень використовуються формули скороченого множення . Всього таких формул сім. Їх все необхідно знати напам’ять.
Слід також пам’ятати, що замість a і b в формулах можуть стояти як числа, так і будь-які інші алгебраїчні многочлени.
різниця квадратів
Різниця квадратів двох чисел дорівнює добутку різниці цих чисел і їх суми.
a 2 — b 2 = (a — b) (a + b)
квадрат суми
(a + B) 2 = a 2 + 2ab + b 2
Зверніть увагу, що за допомогою цієї формули скороченого множення легко знаходити квадрати великих чисел, Не використовуючи калькулятор або множення в стовпчик. Пояснимо на прикладі:
Знайти 112 2.
Розкладемо 112 на суму чисел, чиї квадрати ми добре помнім.2
112 = 100 + 1
Запишемо суму чисел в дужки і поставимо над дужками квадрат.
112 2 = (100 + 12) 2
Скористаємося формулою квадрата суми:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544
Пам’ятайте, що формула квадрат суми також справедлива для будь-яких алгебраїчних многочленів.
(8a + с) 2 = 64a 2 + 16ac + c 2
Застереження !!!
(A + b) 2 не дорівнює a 2 + b 2
квадрат різниці
Квадрат різниці двох чисел дорівнює квадрату першого числа мінус подвоєний добуток першого на друге плюс квадрат другого числа.
(a — b) 2 = a 2 — 2ab + b 2
Також варто запам’ятати дуже корисне перетворення:
(A — b) 2 = (b — a) 2
Формула вище доводиться простим розкриттям дужок:
(A — b) 2 = a 2 — 2ab + b 2 = b 2 — 2ab + a 2 = (b — a) 2
куб суми
Куб суми двох чисел дорівнює кубу першого числа плюс утроенное твір квадрата першого числа на друге плюс утроенное твір першого на квадрат другого плюс куб другого.
(A + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Запам’ятати цю «страшну» на вигляд формулу досить просто.
Вивчіть, що на початку йде a 3.
Два багаточлена посередині мають коефіцієнти 3.
ВЗгадайте, що будь-яке число в нульовому ступені є 1. (a 0 = 1, b 0 = 1). Легко помітити, що у формулі йде зниження ступеня a і збільшення ступеня b. У цьому можна переконатися:
(a 0 = 1, b 0 = 1). Легко помітити, що у формулі йде зниження ступеня a і збільшення ступеня b. У цьому можна переконатися:
Застереження !!!
(A + b) 3 не дорівнює a 3 + b 3
куб різниці
Куб різниці двох чисел дорівнює кубу першого числа мінус утроенное твір квадрата першого числа на друге плюс утроенное твір першого числа на квадрат другого мінус куб другого.
(A — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Запам’ятовується ця формула як і попередня, але тільки з урахуванням чергування знаків «+» і «-». Перед першим членом a 3 варто «+» (за правилами математики ми його не пишемо). Значить, перед наступним членом стоятиме «-», потім знову «+» і т.д.
(A — b) 3 = + a 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Сума кубів ( Не плутати з кубом суми!)
Сума кубів дорівнює добутку суми двох чисел на неповний квадрат різниці.
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
Сума кубів — це твір двох дужок.
Перша дужка — сума двох чисел.
Друга дужка — неповний квадрат різниці чисел. Неповним квадратом різниці називають вираз:
A 2 — ab + b 2
Даний квадрат неповний, тому що посередині замість подвоєного твори звичайне твір чисел.
Різниця кубів (Не плутати з кубом різниці !!!)
Різниця кубів дорівнює добутку різниці двох чисел на неповний квадрат суми.
a 3 — b 3 = (ab) (a 2 + ab + b 2)
Будьте уважні при записі знаків.Слід пам’ятати, що всі формули, приведені вище, використовується також і справа наліво.
Важко запам’ятовуються формули скороченого множення? Делу легко допомогти. Потрібно просто запам’ятати, як зображується така проста річ, як трикутник Паскаля. Тоді ви згадайте ці формули завжди і всюди, вірніше, не згадаєте, а відновите.
Що ж таке трикутник Паскаля? Цей трикутник складається з коефіцієнтів, які входять в розкладання будь-якого ступеня двочлена виду в многочлен.
Розкладемо, наприклад,:
У цьому записі легко запам’ятовується, що спочатку варто куб першого, а в кінці — куб другого числа. А ось що посередині — запам’ятовується складно. І навіть те, що в кожному наступному доданок ступінь одного множника весь час зменшується, а другого — збільшується — нескладно помітити і запам’ятати, важче справа йде з запам’ятовуванням коефіцієнтів і знаків (плюс там або мінус?).
Отже, спочатку коефіцієнти. Не треба їх запам’ятовувати! На полях зошита швиденько малюємо трикутник Паскаля, і ось вони — коефіцієнти, вже перед нами. Малювати починаємо з трьох одиничок, одна зверху, дві нижче, правіше і лівіше — ага, вже трикутник виходить:
Перший рядок, з одного одиничкою — нульова. Потім йде перша, друга, третя і так далі. Щоб отримати другий рядок, потрібно по краях знову приписати одинички, а в центрі записати число, отримане складанням двох чисел, що стоять над ним:
Записуємо третій рядок: знову по краях одиниці, і знову, щоб отримати наступне число в новому рядку, складемо числа, які стоять над ним у попередній:
Як ви вже здогадалися, ми отримуємо в кожному рядку коефіцієнти з розкладання двочлена в многочлен:
Ну а знаки запам’ятати ще простіше: перший — такий же, як в розкладати Двочленні (розкладаємо суму — значить, плюс, різниця — значить, мінус), а далі знаки чергуються!
 Користуйтеся!
Користуйтеся!Формули або правила скороченого множення використовуються в арифметиці, а точніше — в алгебрі, для більш швидкого процесу обчислення великих алгебраїчних виразів. Самі ж формули отримані з існуючих в алгебрі правил для множення декількох многочленів.
Використання даних формул забезпечує досить оперативне рішення різних математичних задач, а також допомагає здійснювати спрощення виразів. Правила алгебраїчних перетворень дозволяють виконувати деякі маніпуляції з виразами, дотримуючись яких можна отримати в лівій частині рівності вираз, що стоїть в правій частині, або перетворити праву частину рівності (щоб отримати вираз, що стоїть в лівій частині після знака рівності).
Зручно знати формули, що застосовуються для скороченого множення, на пам’ять, так як вони нерідко використовуються при вирішенні завдань і рівнянь. Нижче перераховані основні формули, що входять в даний список, і їх найменування.
квадрат суми
Щоб обчислити квадрат суми, необхідно знайти суму, що складається з квадрата першого доданка, подвоєного твори першого доданка на друге і квадрата другого. У вигляді вираження дане правило записується в такий спосіб: (а + с) ² = a² + 2ас + ².
У вигляді вираження дане правило записується в такий спосіб: (а + с) ² = a² + 2ас + ².
квадрат різниці
Щоб обчислити квадрат різниці, необхідно обчислити суму, що складається з квадрата першого числа, подвоєного твори першого числа на друге (узяте з протилежним знаком) і квадрата другого числа. У вигляді вираження дане правило виглядає наступним чином: (а — с) ² = а² — 2ас + ².
різниця квадратів
Формула різниці двох чисел, зведених в квадрат, дорівнює добутку суми цих чисел на їх різницю. У вигляді вираження дане правило виглядає наступним чином: a² — с? = (A + c) · (a — c).
куб суми
Щоб обчислити куб суми двох доданків, необхідно обчислити суму, що складається з куба першого доданка, потроєного твори квадрата першого доданка і другого, потроєного твори першого доданка і другого в квадраті, а також куба другого доданка. У вигляді вираження дане правило виглядає наступним чином: (а + с) ³ = а³ + 3а²с + 3ас² + с³.
сума кубів
Відповідно до формули, прирівнюється до добутку суми даних доданків на їх неповний квадрат різниці. У вигляді вираження дане правило виглядає наступним чином: а³ + с³ = (а + с) · (а² — ас + с?).
У вигляді вираження дане правило виглядає наступним чином: а³ + с³ = (а + с) · (а² — ас + с?).
Приклад.Необхідно обчислити об’єм фігури, яка утворена складанням двох кубів. Відомі лише величини їх сторін.
Якщо значення сторін невеликі, то виконати обчислення просто.
Якщо ж довжини сторін виражаються в громіздких числах, то в цьому випадку простіше застосувати формулу «Сума кубів», яка значно спростить обчислення.
куб різниці
Вираз для кубічної різниці звучить так: як сума третього ступеня першого члена, потроєного негативного твори квадрата першого члена на другий, потроєного твори першого члена на квадрат другого і негативного куба другого члена. У вигляді математичного виразу куб різниці виглядає наступним чином: (а — с) ³ = а³ — 3а²с + 3ас² — с³.
різниця кубів
Формула різниці кубів відрізняється від суми кубів лише одним знаком. Таким чином, різниця кубів — формула, яка дорівнює добутку різниці даних чисел на їх неповний квадрат суми. У вигляді математичного виразу різницю кубів виглядає наступним чином: а 3 — з 3 = (ас) (а 2 + ас + з 2).
У вигляді математичного виразу різницю кубів виглядає наступним чином: а 3 — з 3 = (ас) (а 2 + ас + з 2).
Приклад.Необхідно обчислити об’єм фігури, яка залишиться після вирахування з обсягу синього куба об’ємної фігури жовтого кольору, яка також є кубом. Відома лише величина боку маленького і великого куба.
Якщо значення сторін невеликі, то обчислення досить прості. А якщо довжини сторін виражаються в значних кількостях, то варто застосувати формулу, названу «Різниця кубів» (або «Куб різниці»), которае значно спростить обчислення.
Формули скороченого вираження дуже часто застосовуються на практиці, так що їх все бажано вивчити напам’ять. До цього моменту нам буде служити вірою і правдою, яку ми рекомендуємо роздрукувати і весь час тримати перед очима:
Перші чотири формули з складеної таблиці формул скороченого множення дозволяють зводити в квадрат і куб суму або різницю двох виразів. П’ята призначена для короткого множення різниці і суми двох виразів. А шоста і сьома формули використовуються для множення суми двох виразів a і b на їх неповний квадрат різниці (так називають вираз виду a 2 -a · b + b 2) і різниці двох виразів a і b на неповний квадрат їх суми (a 2 + a · b + b 2) відповідно.
А шоста і сьома формули використовуються для множення суми двох виразів a і b на їх неповний квадрат різниці (так називають вираз виду a 2 -a · b + b 2) і різниці двох виразів a і b на неповний квадрат їх суми (a 2 + a · b + b 2) відповідно.
Варто окремо зауважити, що кожне рівність в таблиці являє собою тотожність. Цим пояснюється, чому формули скороченого множення ще називають тотожністю скороченого множення.
При вирішенні прикладів, особливо в яких має місце розкладання многочлена на множники, ФСУ часто використовують у вигляді з переставленими місцями лівими і правими частинами:
Три останніх тотожності в таблиці мають свої назви. Формула a 2 -b 2 = (a-b) · (a + b) називається формулою різниці квадратів, a 3 + b 3 = (a + b) · (a 2 -a · b + b 2) — формулою суми кубів, а a 3 -b 3 = (a-b) · (a 2 + a · b + b 2) — формулою різниці кубів. Зверніть увагу, що відповідними формулами з переставленими частинами з попередньої таблиці ФСУ ми ніяк не назвали.
додаткові формули
У таблицю формул скороченого множення не завадить додати ще кілька тотожностей.
Сфери застосування формул скороченого множення (ФСУ) і приклади
Основне призначення формул скороченого множення (ФСУ) пояснюється їх назвою, тобто, воно складається в короткому множенні виразів. Однак сфера застосування ФСУ набагато ширше, і не обмежується коротким множенням. Перелічимо основні напрямки.
Безсумнівно, центральне додаток формули скороченого множення знайшли у виконанні тотожних перетворень виразів. Найбільш часто ці формули використовуються в процесі спрощення виразів.
Приклад.
Спростіть вираз 9 · y- (1 + 3 · y) 2.
Рішення.
В даному вираженні зведення в квадрат можна виконати скорочено, маємо 9 · y- (1 + 3 · y) 2 = 9 · y- (1 2 + 2 · 1 · 3 · y + (3 · y) 2). Залишається лише розкрити дужки і привести подібні члени: 9 · y- (1 2 + 2 · 1 · 3 · y + (3 · y) 2) = 9 · y-1-6 · y-9 · y 2 = 3 · y-1-9 · y 2.
Дотримання Вашої конфіденційності важливо для нас. З цієї причини, ми розробили Політику Конфіденційності, яка описує, як ми використовуємо і зберігаємо Вашу інформацію. Будь ласка, ознайомтеся з нашими правилами дотримання конфіденційності і повідомте нам, якщо у вас виникнуть будь-які питання.
З цієї причини, ми розробили Політику Конфіденційності, яка описує, як ми використовуємо і зберігаємо Вашу інформацію. Будь ласка, ознайомтеся з нашими правилами дотримання конфіденційності і повідомте нам, якщо у вас виникнуть будь-які питання.
Збір і використання персональної інформації
Під персональною інформацією розуміються дані, які можуть бути використані для ідентифікації певної особи або зв’язку з ним.
Від вас може бути запрошено надання вашої персональної інформації в будь-який момент, коли ви зв’язуєтеся з нами.
Нижче наведені деякі приклади типів персональної інформації, яку ми можемо збирати, і як ми можемо використовувати таку інформацію.
Яку персональну інформацію ми збираємо:
- Коли ви залишаєте заявку на сайті, ми можемо збирати різну інформацію, включаючи ваші ім’я, номер телефону, адреса електронної пошти тощо
Як ми використовуємо вашу персональну інформацію:
- Зібрана нами персональна інформація дозволяє нам зв’язуватися з вами і повідомляти про унікальні пропозиції, акції та інших заходах і найближчі події.

- Час від часу, ми можемо використовувати вашу персональну інформацію для відправки важливих повідомлень і повідомлень.
- Ми також можемо використовувати персональну інформацію для внутрішніх цілей, таких як проведення аудиту, аналізу даних і різних досліджень з метою поліпшення послуг, що надаються нами і надання Вам рекомендацій щодо наших послуг.
- Якщо ви берете участь в розіграші призів, конкурсі або подібному стимулюючому заході, ми можемо використовувати надану вами інформацію для управління такими програмами.
Розкриття інформації третім особам
Ми не розкриваємо отриману від Вас інформацію третім особам.
винятки:
- У разі якщо необхідно — відповідно до закону, у судовому порядку, в судовому розгляді, і / або на підставі публічних запитів або запитів від державних органів на території РФ — розкрити вашу персональну інформацію. Ми також можемо розкривати інформацію про вас якщо ми визначимо, що таке розкриття необхідно або доречно в цілях безпеки, підтримання правопорядку, чи інших суспільно важливих випадках.

- У разі реорганізації, злиття або продажу ми можемо передати зібрану нами персональну інформацію відповідній третій особі — правонаступнику.
Захист особистих даних
Ми вживаємо заходів обережності — включаючи адміністративні, технічні та фізичні — для захисту вашої персональної інформації від втрати, крадіжки, і недобросовісного використання, а також від несанкціонованого доступу, розкриття, зміни та знищення.
Дотримання вашої конфіденційності на рівні компанії
Для того щоб переконатися, що ваша персональна інформація знаходиться в безпеці, ми доводимо норми дотримання конфіденційності і безпеки до наших співробітників, і строго стежимо за виконанням заходів дотримання конфіденційності.
У попередньому уроці ми розібралися з розкладанням на множники. Освоїли два способи: винесення спільного множника за дужки і угруповання. У цьому уроці — наступний потужний спосіб: формули скороченого множення. У короткої записи — ФСУ.
Формули скороченого множення (квадрат суми і різниці, куб суми і різниці, різниця квадратів, сума і різниця кубів) вкрай необхідні у всіх розділах математики. Вони застосовуються у спрощенні виразів, вирішенні рівнянь, множенні многочленів, скорочення дробів, вирішенні інтегралів і т.д. і т.п. Коротше, є всі підстави розібратися з ними. Зрозуміти звідки вони беруться, навіщо вони потрібні, як їх запам’ятати і як застосовувати.
Вони застосовуються у спрощенні виразів, вирішенні рівнянь, множенні многочленів, скорочення дробів, вирішенні інтегралів і т.д. і т.п. Коротше, є всі підстави розібратися з ними. Зрозуміти звідки вони беруться, навіщо вони потрібні, як їх запам’ятати і як застосовувати.
Розбираємося?)
Звідки беруться формули скороченого множення?
Рівності 6 і 7 записані не дуже звично. Як би навпаки. Це спеціально.) Будь-яке рівність працює як зліва направо, так і справа наліво. У такого запису зрозуміліше, звідки беруться ФСУ.
Вони беруться з множення.) Наприклад:
(A + b) 2 = (a + b) (a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2
Ось і все, ніяких наукових хитрощів. Просто перемножуємо дужки і наводимо подібні. так виходять всі формули скороченого множення. скороченамноження — це тому, що в самих формулах немає перемноження дужок і приведення подібних. Скорочено.) Відразу дан результат.
ФСУ потрібно знати напам’ять. Без перших трьох годі й мріяти про трійку, без інших — про четвірці з п’ятіркою.)
Без перших трьох годі й мріяти про трійку, без інших — про четвірці з п’ятіркою.)
Навіщо потрібні формули скороченого множення?
Є дві причини, вивчити, навіть зазубрити ці формули. Перша — готову відповідь на автоматі різко зменшує кількість помилок. Але це не найголовніша причина. А ось друга …
Якщо Вам подобається цей сайт …До речі, у мене є ще парочка цікавих сайтів для Вас.)
Можна потренуватися у вирішенні прикладів і дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося — з інтересом!)
можна познайомитися з функціями і похідними.
Презентация к уроку алгебры «Подорож по країні формул скороченого множення»
Відкритий урок в 7 – Б класі з теми: «Подорож по країні формул скороченого множення»
Підготувала
Вчитель математики
Морозова Л. А.
А.
Подорож по країні формул скороченого множення
Мета:
- повторити і узагальнити вивчений матеріал;
- показати велич алгебри як науки серед наук
У математиків існує своя мова-це формули.
С. Ковалевська
Французький письменник 19 століття Анатоль Франс одного дня помітив: ”Навчатися можна лише весело, щоб переварити знання, треба поглинати їх з апетитом.” Сьогодні ми дотримаємося поради письменника, будемо весело з бажанням поглинати знання, які згодяться нам в майбутньому.
Згадаємо формули
- (a+b) 2 =
- (a-b) 2 =
- a 2 — b 2 =
- a 3 + b 3 =
- a 3 — b 3 =
a 2 + 2ab + b 2
a 2 — 2ab + b 2
(a + b)(a — b)
(a + b)(a 2 — ab +b 2 )
(a — b)(a 2 + ab +b 2 )
Вирушаємо в подорож !
Зупинка усних вправ
a 4 — b 2
1 — X 4
a 2 + 2am + m 2
16 — p 2
x 2 — 4x +4
25 — x 2
(7 — 3a) 2
(3 — y)(9 + 3y + y 2 )
8a 3 + b 3
Зупинка помилок
(3+2x) 2 =9+12x+4x 2 (7+с) 2 =49-14с+с 2
(m-2n)(2n+m)=m 2 -4n 2 (3x-1)(3x+1)=9x -1
(p-10) 2 =p 2 -20p+10 (2a+1) 2 =4a 2 +2a+1
Що таке многочлен?
Многочлен
Це сума одночленів
Що таке одночлен ?
Одночлен
Добуток числових і буквених множників
Дивовижні назви
Поліном
Моном
Біном
121х 4 — 81у²
Трином
4х² + 4ху + у²
Многочлен з однією змінною
x 4 — 2х²у + у²
(0,5x+2y)²
y 4 — 4xy ² + 4x ²
Рівняння
(11x²-9y)(11x²+9y)
0,25x² + 2xy +4y²
(2x + y)²
Многочлен
Одночлен
(y² — 2x)²
(x² — y)²
Тричлен
Двочлен
Закодований сигнал
- (х .
 .. у) 2 = х 2 – 2ху +…
.. у) 2 = х 2 – 2ху +…
- 8 +…= (…+ х)(4 – 2х+…)
- (… –…) 2 = 9х 2 … …+25у 2
- (… … …) 2 = … – 28ху … 49х 2
- (… – 11)(у +…) = y 2 – …
- (х – …) 2 =… … 20х … …
Зупинка тестування
? ? ? ? ?
Перетворіть добуток у многочлен
Е
А
(2х+1)(1-2х)
М
(2х-у)(2х+у)
(2х+3у)(3у-2х)
Т
С
(х 2 -2)(2+х 2 )
К
(7х-2)(7х+2)
О
(4+5у)(5у-4)
И
(8у+5х)(5х-8у)
І
(0,2+х)(0,2-Х)
(5-с 4 )(5+с 4 )
Перевір себе!
С Е М І О Т И К А
1.
49х 2 — 4
2.
1 — 4х 2
3.
9у 2 — 4х 2
4.
5.
25 — с 8
25х 2 — 64у 2
6.
х 4 — 4
7.
0,04-х 2
8.
25у 2 — 16
9.
4х 2 — у 2
Семіотика — наука, яка досліджує властивості знаків і знакових систем.
Зарядка для очей
Зупинка натхненної праці
Доведемо, що
а = b.
Відомо, що
а 2 – 2 а b + b 2 = b 2 – 2 а b + а 2 ,
тоді
(а – b) 2 = (b– а) 2 .
Звідси випливає рівність
а – b = b – а.
Перенесемо доданки
а + а = b + b.
Зведемо подібні
2а = 2 b.
З цього випливає
а = b!
Софізм – це твердження, що містить заздалегідь помилку, що приводить до невірного твердження.
Історичні відомості
Формули скороченого множення були відомі ще 4000 років тому. Учені Древньої Греції представляли величини не числами або буквами, а відрізками прямих. Замість “добуток ав” говорили “прямокутник, що міститься між а і в”, замість а² “квадрат на відрізку а”.
У книзі Евкліда “Начала” правило квадрата суми виражається так: “Якщо пряма лінія як-небудь розітнута точкою С, то квадрат на всій прямій дорівнює квадратам на відрізках разом з двічі узятим прямокутником, ув’язненим між відрізками”.
(а+в) 2 = а 2 +2ав+в 2
Квадрат суми, квадрат різниці і різниця квадратів
Виконали учениці 7-Б класу
ЗСОШ №143
Маслова Дар‘я, Мершавка Дар‘я
Квадрат суми. Формула №1
Формула №1
B
C
- S АВСD =AB x AD
- AB= a+b,
- AD=a+b
- S АВСD =(a+b) (a+b) = =(a+b) 2
- S АВСD =a 2 +ab+ab+b 2 =
- =a 2 +2ab+b 2 =(a+b) 2
(a+b) 2 =a 2 +2ab+b 2
в
a
D
A
a
в
Квадрат різниці. Формула №2
в
B
C
S фігури = (a – b) 2
S АВСD =а 2
S фігури =
= a 2 – b 2 –b(a–b) –b(a-b)=
= a 2 -b 2 -2b(a-b)=
= a 2 -b 2 -2ab+2b 2 =
= a 2 -2ab+b 2
a
D
A
a-в
( a-b) 2 =a 2 -2ab+b 2
А
Різниця квадратів. Формула №3
С
В
S AHFMND =
= S AHFK – S DNMK =
= a 2 – b 2
в
Н
F
S ABCD = S AHFMND
a
S ABCD = (a – b)(а + b)
N
M
a 2 -b 2 =(a-b)(a+b)
K
А
D
a-в
Дякуємо за увагу!
Підніми свою картку
багато чого не зрозуміло
є питання
все зрозуміло
Домашнє завдання
№ 818, 826, 827
№ 823, 824, 825
Подорож благополучно
завершилася.
До нових зустрічей
на математичній колії.
Формули скороченого множення » Народна Освіта
Формули скороченого множення призначені для скорочення обсягів обчислень, спрощення скорочення дробів у буквених виразах (многочлен можна перевести в добуток і навпаки — добуток у многочлен).
|
1. Формула квадрата суми двох виразів: |
Правило. Квадрат суми двох виразів дорівнює квадрату пер* шого виразу плюс подвоєний добуток першого виразу і другого, плюс квадрат другого виразу.
|
Приклади. |
У першому прикладі представлено тризначне число як сума двох розрядних одиниць, зручних для піднесення до квадрату.
У другому прикладі перший доданок є двочленом.
|
2. |
Правило. Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток першого і другого виразів плюс квадрат другого виразу.
|
Приклади. |
У першому прикладі число замінено на різницю розрядних одиниць, зручних для піднесення до квадрату.
У другому прикладі маєкіо різницю двочленів, квадрат кожного можна замінити многочленом за формулами скороченого множення, далі при обчисленні застосовується зведення подібних доданків. Результат обчислень (число без невідомого) показує, що квадрат заданої різниці не залежить від значення букви.
|
3. Формула різниці квадратів двох виразів: |
Правило. Різниця квадратів двох виразів дорівнює добутку суми і різниці цих виразів.
|
Приклади. |
У Другому прикладі коефіцієнти при квадратах двочлена треба розглядати як квадрати чисел, тобто як добуток алгебраїчних множників.
Отже, вирази у формулі — це одночлени 4с і 3у. Знак різниці квадратних двочленів визначається за множником з різницею, а не з сумою, оскільки в сумі доданки можна міняти місцями, а в різниці ні. Вираз 16с2 — 9у2 не дорівнює виразу 9у1— 16с2.
|
4. Формула куба суми двох виразів: |
Правило. Куб суми двох виразів дорівнює кубу першого ви* разу плюс потроєний добуток квадрата першого і другого виразів плюс потроєний добуток першого виразу і квадрата другого виразу плюс куб другого виразу.
|
Щоб одержати формулу куба суми двох виразів, можна перемножити квадрат суми і суму тих самих виразів: |
|
Приклад. |
|
5. Формула куба різниці двох виразів: |
Правило. Куб різниці двох виразів дорівнює кубу першого виразу мінус потроєний добуток квадрата першого і другого виразів плюс потроєний добуток першого і квадрата другого виразів мінус куб другого виразу.
|
Щоб одержати формулу куба різниці двох виразів, можна перемножити квадрат різниці і різницю тих самих виразів: |
|
6. Формула різниці кубів двох виразів: |
|
7. Формула суми кубів двох виразів: |
|
Правило. Сума кубів двох виразів дорівнює добутку суми цих виразів І неповного квадрата їх різниці. |
Правило. Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їх суми.
Архітектура. Побутова техніка. Каналізація. Сходи. Меблі. Вікна. Опалення. Ремонт. Будівництво
Звичайних дробів.
Додавання алгебраїчних дробів
Запам’ятайте!
Складати можна тільки дроби з однаковими знаменниками!
Не можна додавати дроби без перетворень
Можна додавати дроби
При додаванні алгебраїчних дробів з однаковими знаменниками:
- чисельник першого дробу складається з чисельником другого дробу;
- знаменник залишається колишнім.
Розглянемо приклад складання алгебраїчних дробів.
Так як знаменник у обох дробів «2а», значить, дробу можна скласти.
Складемо чисельник першого дробу з чисельником другого дробу, а знаменник залишимо тим самим. При додаванні дробів в отриманому чисельнику наведемо подібні.
Віднімання алгебраїчних дробів
При відніманні алгебраїчних дробів з однаковими знаменниками:
- з чисельника першого дробу віднімається чисельник другого дробу.

- знаменник залишається колишнім.
Важливо!
Обов’язково укладіть в дужки весь чисельник віднімається дробу.
Інакше ви зробите помилку в знаках при розкритті дужок віднімається дробу.
Розглянемо приклад віднімання алгебраїчних дробів.
Так як в обох алгебраїчних дробів знаменник «2с», значить, ці дроби можна вичитати.
Віднімемо від чисельника першого дробу «(a + d)» чисельник другого дробу «(a — b)». Не забудемо укласти чисельник віднімається дробу в дужки. При розкритті дужок використовуємо правило розкриття дужок.
Приведення алгебраїчних дробів до спільного знаменника
Розглянемо ще один приклад. Потрібно скласти алгебраїчні дроби.
У такому вигляді скласти дробу не можна, так як у них різні знаменники.
Перш ніж складати алгебраїчні дроби їх необхідно привести до спільного знаменника.
Правила приведення алгебраїчних дробів до спільного знаменника дуже схожі на правила приведення до спільного знаменника звичайних дробів. .
.
У підсумку ми повинні отримати многочлен, який без залишку розділиться на кожен колишній знаменник дробів.
щоб привести алгебраїчні дроби до спільного знаменника необхідно зробити наступне.
- Працюємо з числовими коефіцієнтами. Визначаємо НОК (найменше спільне кратне) для всіх числових коефіцієнтів.
- Працюємо з многочленами. Визначаємо все різні багаточлени в найбільших ступенях.
- Твір числового коефіцієнта і всіх різних многочленів в найбільших ступенях і буде спільним знаменником.
- Визначаємо, на що потрібно помножити кожну алгебраїчну дріб, щоб отримати загальний знаменник.
Повернемося до нашого прикладу.
Розглянемо знаменники «15a» і «3» обох дробів і знайдемо для них спільний знаменник.
- Працюємо з числовими коефіцієнтами. Знаходимо НОК (найменше спільне кратне — це число, яке без залишку ділиться на кожен числовий коефіцієнт). Для «15» і «3» — це «15».
- Працюємо з многочленами. Необхідно перерахувати всі многочлени в найбільших ступенях.
 У знаменниках «15a» і «5» є тільки
У знаменниках «15a» і «5» є тільки
один одночлен — «а». - Перемножимо НОК з п.1 «15» і одночлен «а» з п.2. У нас вийде «15a». Це і буде спільним знаменником.
- Для кожного дробу задамо собі питання: «На що потрібно помножити знаменник цього дробу, щоб отримати« 15a »?».
Розглянемо перший дріб. У цій дроби і так знаменник «15a», значить, її не потрібно ні на що множити.
Розглянемо другу дріб. Поставимо запитання: «На що потрібно помножити« 3 », щоб отримати« 15a »?» Відповідь — на «5a».
При приведенні до спільного знаменника дробу множимо на «5a» і чисельник, і знаменник.
Скорочену запис приведення алгебраїчної дроби до спільного знаменника можна записати через «будиночки».
Для цього тримаємо в думці спільний знаменник. Над кожною дробом зверху «в будиночку» пишемо, на що множимо кожну з дробів.
Тепер, коли у дробів однакові знаменники, дробу можна скласти.
Розглянемо приклад віднімання дробів з різними знаменниками.
Розглянемо знаменники «(x — y)» і «(x + y)» обох дробів і знайдемо для них спільний знаменник.
У нас є два різних многочлена в знаменниках «(x — y)» і «(x + y)». Їх твір буде спільним знаменником, тобто «(X — y) (x + y)» — спільний знаменник.
Додавання і віднімання алгебраїчних дробів за допомогою формул скороченого множення
У деяких прикладах, щоб привести алгебраїчні дроби до спільного знаменника, потрібно використовувати формули скороченого множення.
Розглянемо приклад складання алгебраїчних дробів, де нам буде потрібно використовувати формулу різниці квадратів.
У першій алгебраїчної дробу знаменник «(p 2 — 36)». Очевидно, що до нього можна застосувати формулу різниці квадратів.
Після розкладання многочлена «(p 2 — 36)» на твір многочленів
«(P + 6) (p — 6)» видно, що в дробах повторюється многочлен «(p + 6)». Значить, спільним знаменником дробів буде твір многочленів «(p + 6) (p — 6)».
У цій статті ми розглянемо основні дії з алгебраїчними дробами:
- скорочення дробів
- множення дробів
- ділення дробів
Почнемо з скорочення алгебраїчних дробів.
Здавалося б, алгоритм очевидний.
щоб скоротити алгебраїчні дроби, потрібно
1. Розкласти чисельник і знаменник дробу на множники.
2. Скоротити однакові множники.
Однак, школярі часто роблять помилку, «скорочуючи» не множники, а складові. Наприклад, є любителі, які в дроби «скорочують» на і отримують в результаті, що, зрозуміло, не так.
Розглянемо приклади:
1. Скоротити дріб:
1. Розкладемо на множники чисельник за формулою квадрата суми, а знаменник за формулою різниці квадратів
2. Розділимо чисельник і знаменник на
2. Скоротити дріб:
1. Розкладемо на множники чисельник. Так як чисельник містить чотири доданків, застосуємо угруповання.
2. Розкладемо на множники знаменник. Так само можна застосувати угруповання.
3. Запишемо дріб, яка у нас вийшла і скоротимо однакові множники:
Множення алгебраїчних дробів.
При множенні алгебраїчних дробів ми чисельник множимо на чисельник, а знаменник множимо на знаменник.
Важливо! Не потрібно поспішати виконувати множення в чисельнику і знаменнику дробу. Після того, як ми записали в чисельнику твір числителей дробів, а в знаменнику — твір знаменників, потрібно розкласти на множники кожен множник і скоротити дріб.
Розглянемо приклади:
3. Спростіть вираз:
1. Запишемо твір дробів: в чисельнику твір числителей, а в знаменнику твір знаменників:
2. Розкладемо кожну дужку на множники:
Тепер нам потрібно скоротити однакові множники. Зауважимо, що вирази і відрізняються тільки знаком: і в результаті поділу першого виразу на друге отримаємо -1.
Отже,
Ділення алгебраїчних дробів ми виконуємо за таким правилом:
Тобто щоб розділити на дріб, треба помножити на «перевернуту».
Ми бачимо, що ділення дробів зводиться до множення, а множення, в кінцевому підсумку, зводиться до скорочення дробів.
Розглянемо приклад:
4. Спростіть вираз:
Спростіть вираз:
Формули скороченого вираження дуже часто застосовуються на практиці, так що їх все бажано вивчити напам’ять. До цього моменту нам буде служити вірою і правдою, яку ми рекомендуємо роздрукувати і весь час тримати перед очима:
Перші чотири формули з складеної таблиці формул скороченого множення дозволяють зводити в квадрат і куб суму або різницю двох виразів. П’ята призначена для короткого множення різниці і суми двох виразів. А шоста і сьома формули використовуються для множення суми двох виразів a і b на їх неповний квадрат різниці (так називають вираз виду a 2 -a · b + b 2) і різниці двох виразів a і b на неповний квадрат їх суми (a 2 + a · b + b 2) відповідно.
Варто окремо зауважити, що кожне рівність в таблиці являє собою тотожність. Цим пояснюється, чому формули скороченого множення ще називають тотожністю скороченого множення.
При вирішенні прикладів, особливо в яких має місце розкладання многочлена на множники, ФСУ часто використовують у вигляді з переставленими місцями лівими і правими частинами:
Три останніх тотожності в таблиці мають свої назви. Формула a 2 -b 2 \u003d (a-b) · (a + b) називається формулою різниці квадратів, a 3 + b 3 \u003d (a + b) · (a 2 -a · b + b 2) — формулою суми кубів, а a 3 -b 3 \u003d (a-b) · (a 2 + a · b + b 2) — формулою різниці кубів. Зверніть увагу, що відповідними формулами з переставленими частинами з попередньої таблиці ФСУ ми ніяк не назвали.
Формула a 2 -b 2 \u003d (a-b) · (a + b) називається формулою різниці квадратів, a 3 + b 3 \u003d (a + b) · (a 2 -a · b + b 2) — формулою суми кубів, а a 3 -b 3 \u003d (a-b) · (a 2 + a · b + b 2) — формулою різниці кубів. Зверніть увагу, що відповідними формулами з переставленими частинами з попередньої таблиці ФСУ ми ніяк не назвали.
додаткові формули
У таблицю формул скороченого множення не завадить додати ще кілька тотожностей.
Сфери застосування формул скороченого множення (ФСУ) і приклади
Основне призначення формул скороченого множення (ФСУ) пояснюється їх назвою, тобто, воно складається в короткому множенні виразів. Однак сфера застосування ФСУ набагато ширше, і не обмежується коротким множенням. Перелічимо основні напрямки.
Безсумнівно, центральне додаток формули скороченого множення знайшли у виконанні тотожних перетворень виразів. Найбільш часто ці формули використовуються в процесі спрощення виразів.
Приклад.
Спростіть вираз 9 · y- (1 + 3 · y) 2.
Рішення.
В даному вираженні зведення в квадрат можна виконати скорочено, маємо 9 · y- (1 + 3 · y) 2 \u003d 9 · y- (1 2 + 2 · 1 · 3 · y + (3 · y) 2). Залишається лише розкрити дужки і привести подібні члени: 9 · y- (1 2 + 2 · 1 · 3 · y + (3 · y) 2) \u003d 9 · y-1-6 · y-9 · y 2 \u003d 3 · y-1-9 · y 2.
В даному уроці буде розглянуто додавання і віднімання алгебраїчних дробів з однаковими знаменниками. Ми вже знаємо, як додавати і віднімати звичайні дроби з однаковими знаменниками. Виявляється, що алгебраїчні дроби підкоряються тим же самим правилам. Уміння працювати з дробом з однаковими знаменниками є одним з наріжних каменів у вивченні правил роботи з алгебраїчними дробами. Зокрема, розуміння даної теми дозволить легко освоїти більш складну тему — додавання і віднімання дробів з різними знаменниками. В рамках уроку ми вивчимо правила додавання і віднімання алгебраїчних дробів з однаковими знаменниками, а також розберемо цілий ряд типових прикладів
Правило додавання і віднімання алгебраїчних дробів з однаковими знаменниками
Сфор-му-ли-ру-му пра-ви-ло сло-же-ня (ви-чи-та-ня) ал-Геб-ра-та-че-ських дро-бей з оди-на-ко-ви -ми зна-ме-на-ті-ля-ми (воно сов-па-да-ет з ана-ло-гич-ним пра-ви-лом для обик-но-вен-них дро-бей): тобто для сло-же-ня або ви-чи-та-ня ал-Геб-ра-та-че-ських дро-бей з оди-на-ко-ви-ми зна-ме-на-ті-ля-ми необ -хо-ді-мо со-ста-вить со-від-вет-ству-ю-щую ал-Геб-ра-та-че-ську суму чис-лі-ті-лей, а зна-ме-на-тель залишити без змін.
Це пра-ви-ло ми раз-бе-Рем і на при-ме-ре обик-но-вен-них дро-бей, і на при-ме-ре ал-Геб-ра-та-че-ських дро- бей.
Приклади застосування правила для звичайних дробів
При-мер 1. Сло-жити дробу:.
Рішення
Сло-жим чис-лі-ті-ли дро-бей, а зна-ме-на-тель осту-вим таким же. Після цього раз-ло-жим чис-лі-тель і зна-ме-на-тель на про-стие мно-жи-ті-ли і з-кра-тім. За-лу-чим: .
При-ме-ча-ня: стан-дарт-ва ошиб-ка, ко-то-рую до-пус-ка-ють при ре-ше-ванні по-доб-но-го роду при-ме-рів, за -клю-ча ет ся в сле-ду-ю-щем спо-со-бе ре-ше-ня: . Це гру-бей-Шая ошиб-ка, по-скільки-ку зна-ме-на-тель осту-ет-ся таким же, яким був в ис-хід-них дро-бях.
При-мер 2. Сло-жити дробу:.
Рішення
Дан-ва за-да-ча нічим не від-ли-ча ет ся від попе-ду-щей:.
Приклади застосування правила для алгебраїчних дробів
Від обик-но-вен-них дро-бей пе-рей-дём до ал-Геб-ра-та-че-ським.
При-мер 3. Сло-жити дробу:.
Ре-ху: як уже го-во-ри-лось вище, сло-же-ня ал-Геб-ра-та-че-ських дро-бей нічим не від-ли-ча ет ся від сло- ж-ня обик-но-вен-них дро-бей. Як і це-му метод ре-ше-ня такої ж:.
Як і це-му метод ре-ше-ня такої ж:.
При-мер 4. Ви-честь дробу:.
Рішення
Ви-чи-та-ня ал-Геб-ра-та-че-ських дро-бей від-ли-ча ет ся від сло-же-ня толь-ко тим, що в чис-лі-тель за- пі-си-ва-ет-ся раз-ність чис-лі-ті-лей ис-хід-них дро-бей. Як і це-му.
При-мер 5. Ви-честь дробу:.
Рішення: .
При-мер 6. спрощено-стить:.
Рішення: .
Приклади застосування правила з подальшим скороченням
У дробу, до то раю по-лу-ча ет ся в ре-зуль-та-ті сло-же-ня або ви-чи-та-ня, мож-ли-ни-кра-ще- ня. Крім того, не варто за-б-вать про ОДЗ ал-Геб-ра-та-че-ських дро-бей.
При-мер 7. спрощено-стить:.
Рішення: .
При цьому . По-про-ще, якщо ОДЗ ис-хід-них дро-бей сов-па-да-ет з ОДЗ ито-го-вої, то його можна не вка-зи-вать (адже дріб, по-лу-чен- ная в від-ве-ті, також не буде су-ще-ство-вать при со-від-вет-ству-ю-чих зна-че-ні-ях пе-ре-мен-них). А ось якщо ОДЗ ис-хід-них дро-бей і від-ве-та не сов-па-да-ет, то ОДЗ вка-зи-вать необ-хо-ді-мо.
При-мер 8. спрощено-стить:.
Рішення: . При цьому y (ОДЗ ис-хід-них дро-бей не сов-па-да-ет з ОДЗ ре-зуль-та-та).
Додавання і віднімання звичайних дробів з різними знаменниками
Щоб скла-ди-вать і ви-чи-тать ал-Геб-ра-та-че-ські дроби з раз-ни-ми зна-ме-на-ті-ля-ми, про-ве-дём ана-ло -гію з обик-но-вен-ни-ми дро-бе-ми і пе-ре-ні-се її на ал-Геб-ра-та-че-ські дробу.
Рас-смот-рим про-стей-ший при-заходів для обик-но-вен-них дро-бей.
При-мер 1.Сло-жити дробу:.
Рішення:
Вспом-ним пра-ви-ло сло-же-ня дро-бей. Для на-ча-ла дробу необ-хо-ді-мо при-ве-сти до про-ще-му зна-ме-на-ті-лю. У ролі об-ще-го зна-ме-на-ті-ля для обик-но-вен-них дро-бей ви сту-па-ет най-мен-шиї загальне крат-ве (НОК) ис-хід-них зна-ме-на-ті-лей.
Опрі-де-ле-ня
Най-мен-шиї на-ту-раль-ве число, ко-то-рої де-літ-ся од-но-ча-мен-но на числа і.
Для на-хо-де-ня НОК необ-хо-ді-мо раз-ло-жити зна-ме-на-ті-ли на про-стие мно-жи-ті-ли, а потім ви-брати все про- стие мно-жи-ті-ли, ко-то-які вхо-дять в раз-ло-же-ня обох зна-ме-на-ті-лей.
; . Тоді в НОК чисел долж-ни вхо-дить дві двой-ки і дві трой-ки:.
Після на-хо-де-ня про-ще-го зна-ме-на-ті-ля, необ-хо-ді-мо для каж-дой з дро-бей знайти до-пол-ні-тель-ний мно- жи-тель (фак-ти-че-скі, по-де-лити загальний зна-ме-на-тель на зна-ме-на-тель з-від-вет-ству-ю-щей дробу).
Потім каж-дая дріб розумно-жа-ет-ся на по-лу-чен-ний до-пол-ні-тель-ний мно-жи-тель. За-лу-ча-ють-ся дроби з оди-на-ко-ви-ми зна-ме-на-ті-ля-ми, скла-ди-вать і ви-чи-тать ко-то-які ми на -учі-лись на про-шлих уро-ках.
За-лу-ча-ем: .
відповідь:.
Рас-смот-рим ті-перь сло-же-ня ал-Геб-ра-та-че-ських дро-бей з раз-ни-ми зна-ме-на-ті-ля-ми. Сну-ча-ла рас-смот-рим дробу, зна-ме-на-ті-ли ко-то-яких яв-ля-ють-ся чис-ла-ми.
Додавання і віднімання алгебраїчних дробів з різними знаменниками
При-мер 2.Сло-жити дробу:.
Рішення:
Ал-го-ритм ре-ше-ня аб-со-лют-но ана ло гі-чен попе-ду-ще-му при-ме-ру. Легко по-до-брати загальний зна-ме-на-тель дан-них дро-бей: і до-пол-ні-тель-ні мно-жи-ті-ли для каж-дой з них.
.
відповідь:.
Отже, сфор-му-ли-ру-ем ал-го-ритм сло-же-ня і ви-чи-та-ня ал-Геб-ра-та-че-ських дро-бей з раз-ни-ми зна-ме-на-ті-ля-ми:
1. Знайти най-мен-ший загальний зна-ме-на-тель дро-бей.
2. Знайти до-пол-ні-тель-ні мно-жи-ті-ли для каж-дой з дро-бей (по-де-лів загальний зна-ме-на-тель на зна-ме-на-тель дан -ної дробу).
3. До-мно-жити чис-лі-ті-ли на со-від-вет-ству-ю-щие до-пол-ні-тель-ні мно-жи-ті-ли.
4. Сло-жити або ви-честь дробу, поль-зу-Ясь пра-ви-ла-ми сло-же-ня і ви-чи-та-ня дро-бей з оди-на-ко-ви-ми зна -ме-на-ті-ля-ми.
Рас-смот-рим ті-перь при-заходів з дро-бе-ми, в зна-ме-на-ті-ле ко-то-яких при-сут-ству-ють бук-вен-ні ви-ра-же -ня.
Відверто кажучи, ці формули повинен пам’ятати будь-який учень сьомого класу. Вивчати алгебру навіть на шкільному рівні і не знати формулу різниці квадратів або, скажімо, квадрата суми, просто неможливо. Вони постійно зустрічаються при спрощення алгебраїчних виразів, при скороченні дробів і навіть можуть допомогти в арифметичних обчисленнях. Ну, наприклад, вам потрібно обчислити в думці: 3,16 2 — 2 3,16 1,16 + 1,16 2. Якщо ви почнете вважати це «в лоб», вийде довго і нудно, а якщо скористаєтеся формулою квадрата різниці, відповідь отримаєте за 2 секунди!
Ну, наприклад, вам потрібно обчислити в думці: 3,16 2 — 2 3,16 1,16 + 1,16 2. Якщо ви почнете вважати це «в лоб», вийде довго і нудно, а якщо скористаєтеся формулою квадрата різниці, відповідь отримаєте за 2 секунди!
Отже, сім формул «шкільної» алгебри, які повинні знати всі:
| Назва | Формула |
| квадрат суми | (A + B) 2 \u003d A 2 + 2AB + B 2 |
| квадрат різниці | (A — B) 2 \u003d A 2 — 2AB + B 2 |
| різниця квадратів | (A — B) (A + B) \u003d A 2 — B 2 |
| куб суми | (A + B) 3 \u003d A 3 + 3A 2 B + 3AB 2 + B 3 |
| куб різниці | (A — B) 3 \u003d A 3 — 3A 2 B + 3AB 2 — B 3 |
| сума кубів | A 3 + B 3 \u003d (A + B) (A 2 — AB + B 2) |
| різниця кубів | A 3 — B 3 \u003d (AB) (A 2 + AB + B 2) |
Зверніть увагу: ніякої формули суми квадратів не існує! Не дозволяйте своїй фантазії заходити надто далеко.
Як найпростіше запам’ятати всі ці формули? Ну, скажімо, побачити певні аналогії. Наприклад, формула квадрата суми схожа на формулу квадрата різниці (відмінність лише в одному знакові), а формула куба суми — на формулу куба різниці. Далі, в складі формул різниці кубів і суми кубів ми бачимо щось схоже на квадрат суми і квадрат різниці (тільки коефіцієнта 2 не вистачає).
Але найкраще ці формули (як і будь-які інші!) Запам’ятовуються на практиці. Вирішуйте більше прикладів на спрощення алгебраїчних виразів, і все ф-ли запам’ятаються самі собою.
Цікавим школярам буде, ймовірно, цікаво узагальнити наведені факти. Ось, скажімо, існують формули квадрата і куба суми. А що, якщо розглянути висловлювання на кшталт (A + B) 4, (A + B) 5 і навіть (A + B) n, де n — довільне натуральне число? Чи можна побачити тут будь — яку закономірність?
Так, подібна закономірність існує. Вираз виду (A + B) n називається біном Ньютона. Я рекомендую допитливим школярам самим вивести формули для (A + B) 4 і (A + B) 5, а далі спробувати побачити загальний закон: порівняти, наприклад, ступінь відповідного бинома і ступінь кожного з доданків, які виходять при розкритті дужок; порівняти ступінь бінома з кількістю доданків; спробувати знайти закономірності в коефіцієнтах. Ми не будемо зараз заглиблюватися в цю тему (для цього потрібен окрема розмова!), А лише запишемо готовий результат:
Ми не будемо зараз заглиблюватися в цю тему (для цього потрібен окрема розмова!), А лише запишемо готовий результат:
(A + B) n \u003d A n + C n 1 A n-1 B + C n 2 A n-2 B 2 + … + C n k A n-k B k + … + B n.
Тут C n k \u003d n! / (K! (N-k)!).
Нагадую, що n! — це 1 2 … n — твір всіх натуральних чисел від 1 до n. Називається цей вислів факторіалом числа n. Наприклад, 4! \u003d 1 2 3 4 \u003d 24. Факторіал нуля вважається рівним одиниці!
А що можна сказати з приводу різниці квадратів, різниці кубів і т. П.? Чи існує тут якась закономірність? Чи можна привести загальну формулу для A n — B n?
Так можна. Ось ця формула:
A n — B n \u003d (A — В) (A n-1 + A n-2 B + A n-3 B 2 + … + B n-1).
Більш того, для непарних ступенів n існує аналогічна ф-ла і для суми:
A n + B n \u003d (A + В) (A n-1 — A n-2 B + A n-3 B 2 — … + B n-1).
Ми не будемо зараз виводити ці формули (до речі, це не дуже складно), але знати про їхнє існування, безумовно, корисно. 2 \ right) \]
2 \ right) \]
Формули скороченого множення (ФСУ) застосовуються для зведення в ступінь і множення чисел і виразів. Часто ці формули дозволяють зробити обчислення більш компактно і швидко.
У даній статті ми перерахуємо основні формули скороченого множення, згрупуємо їх в таблицю, розглянемо приклади використання цих формул, а також зупинимося на принципах доказів формул скороченого множення.
Вперше тема ФСУ розглядається в рамках курсу «Алгебра» за 7 клас. Наведемо нижче 7 основних формул.
Формули скороченого множення
- формула квадрата суми: a + b 2 = a 2 + 2 a b + b 2
- формула квадрата різниці: a — b 2 = a 2 — 2 a b + b 2
- формула куба суми: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
- формула куба різниці: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
- формула різниці квадратів: a 2 — b 2 = a — b a + b
- формула суми кубів: a 3 + b 3 = a + b a 2 — a b + b 2
- формула різниці кубів: a 3 — b 3 = a — b a 2 + a b + b 2
Літерами a, b, c в даних виразах можуть бути будь-які числа, змінні або вирази. Для зручності використання краще вивчити сім основних формул напам’ять. Зведемо їх в таблицю і наведемо нижче, обвівши рамкою.
Для зручності використання краще вивчити сім основних формул напам’ять. Зведемо їх в таблицю і наведемо нижче, обвівши рамкою.
Перші чотири формули дозволяють обчислювати відповідно квадрат або куб суми або різниці двох виразів.
П’ята формула обчислює різницю квадратів виразів шляхом твори їх суми та різниці.
Шоста і сьома формули — відповідно множення суми і різниці виразів на неповний квадрат різниці і неповний квадрат суми.
Формула скороченого множення іноді ще називають тотожністю скороченого множення. В цьому немає нічого дивного, так як кожне рівність являє собою тотожність.
при вирішенні практичних прикладівчасто використовують формули скороченого множення з переставленими місцями лівими і правими частинами. Це особливо зручно, коли має місце розкладання многочлена на множники.
Додаткові формули скороченого множення
Не будемо обмежуватися курсом 7 класу з алгебри і додамо в нашу таблицю ФСУ ще кілька формул.
По-перше, розглянемо формулу бінома Ньютона.
a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 +. . + C n n — 1 · a · b n — 1 + C n n · b n
Тут C n k — біноміальні коефіцієнти, які стоять в рядку під номером n в трикутнику Паскаля. Біноміальні коефіцієнти обчислюються за формулою:
C n k = n! k! · (N — k)! = N (n — 1) (n — 2). . (N — (k — 1)) k!
Як бачимо, ФСУ для квадрата і куба різниці і суми — це окремий випадок формули бінома Ньютона при n = 2 і n = 3соответственно.
Але що, якщо доданків в сумі, яку потрібно звести в ступінь, більше, ніж два? Корисною буде формула квадрата суми трьох, чотирьох і більше доданків.
a 1 + a 2 +. . + A n 2 = a 1 2 + a 2 2 +. . + A n 2 + 2 a 1 a 2 + 2 a 1 a 3 +. . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 +. . + 2 a 2 a n + 2 a n — 1 a n
Ще одна формула, яка може стати в нагоді — формула формула різниці n-их ступенів двох доданків.
a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 +. . + A 2 b n — 2 + b n — 1
Цю формулу звичайно поділяють на дві формули — відповідно для парних і непарних ступенів.
Для парних показників 2m:
a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 +. . + B 2 m — 2
Для непарних показників 2m + 1:
a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 +. . + B 2 m
Формули різниці квадратів і різниці кубів, як ви здогадалися, є окремими випадками цієї формули при n = 2 і n = 3 відповідно. Для різниці кубів b також замінюється на — b.
Як читати формули скороченого множення?
Дамо відповідні формулювання для кожної формули, але спочатку розберемося з принципом читання формул. Зручніше за все робити це на прикладі. Візьмемо найпершу формулу квадрата суми двох чисел.
a + b 2 = a 2 + 2 a b + b 2.
Кажуть: квадрат суми двох виразів a і b дорівнює суміквадрата першого виразу, подвоєного твори виразів і квадрата другого виразу.
Всі інші формули читаються аналогічно. Для квадрата різниці a — b 2 = a 2 — 2 a b + b 2 запишемо:
квадрат різниці двох виразів a і b дорівнює сумі квадратів цих виразів мінус подвоєний добуток першого і другого виразу.
Прочитаємо формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3. Куб суми двох виразів a і b дорівнює сумі кубів цих виразів, потроєного твори квадрата першого виразу на друге і потроєного твори квадрата другого виразу на перший вираз.
Переходимо до читання формули для різниці кубів a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3. Куб різниці двох виразів a і b дорівнює кубу першого виразу мінус утроенное твір квадрата першого виразу на друге, плюс утроенное твір квадрата другого виразу на перший вираз, мінус куб другого виразу.
П’ята формула a 2 — b 2 = a — b a + b (різниця квадратів) читається так: різниця квадратів двох виразів дорівнює добутку різниці і суми двох виразів.
Вирази типу a 2 + a b + b 2 і a 2 — a b + b 2 для зручності називають відповідно неповним квадратом суми і неповним квадратом різниці.
З огляду на це, формули суми і різниці кубів прочитав так:
Сума кубів двох виразів дорівнює добутку суми цих виразів на неповний квадрат їх різниці.
Різниця кубів двох виразів дорівнює добутку різниці цих виразів на неповний квадрат їх суми.
доказ ФСУ
Довести ФСУ досить просто. Грунтуючись на властивостях множення, проведемо множення частин формул в дужках.
Для прикладу розглянемо формулу квадрата різниці.
a — b 2 = a 2 — 2 a b + b 2.
Щоб звести вираз в другу ступінь потрібно цей вислів помножити само на себе.
a — b 2 = a — b a — b.
Розкриємо дужки:
a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2.
Формула доведена. Решта ФСУ доводяться аналогічно.
Приклади застосування ФСУ
Мета використання формул скороченого множення — швидке і коротке множення і зведення виразів в ступінь. Однак, це не вся сфера застосування ФСУ. Вони широко використовуються при скороченні виразів, скорочення дробів, розкладанні многочленів на множники. Наведемо приклади.
Приклад 1. ФСУ
Спростимо вираз 9 y — (1 + 3 y) 2.
Застосуємо формулу суми квадратів і отримаємо:
9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2
Приклад 2. ФСУ
ФСУ
Скоротимо дріб 8 x 3 — z 6 4 x 2 — z 4.
Помічаємо, що вираз в чисельнику — різниця кубів, а в знаменнику — різниця квадратів.
8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z.
Скорочуємо і отримуємо:
8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z
Також ФСУ допомагають обчислювати значення виразів. Головне — вміти помітити, де застосувати формулу. Покажемо це на прикладі.
Зведемо в квадрат число 79. Замість громіздких обчислень, запишемо:
79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .
Здавалося б, складне обчисленняпроведено швидко всього лише з використанням формул скороченого множення і таблиці множення.
Ще один важливий момент- виділення квадрата двочлена. Вираз 4 x 2 + 4 x — 3 можна перетворити на вигляд 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4. Такі перетворення широко використовуються в інтегруванні.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl + Enter
Формули або правила скороченого множення використовуються в арифметиці, а точніше — в алгебрі, для більш швидкого процесу обчислення великих алгебраїчних виразів. Самі ж формули отримані з існуючих в алгебрі правил для множення декількох многочленів.
Самі ж формули отримані з існуючих в алгебрі правил для множення декількох многочленів.
Використання даних формул забезпечує досить оперативне рішення різних математичних задач, а також допомагає здійснювати спрощення виразів. Правила алгебраїчних перетворень дозволяють виконувати деякі маніпуляції з виразами, дотримуючись яких можна отримати в лівій частині рівності вираз, що стоїть в правій частині, або перетворити праву частину рівності (щоб отримати вираз, що стоїть в лівій частині після знака рівності).
Зручно знати формули, що застосовуються для скороченого множення, на пам’ять, так як вони нерідко використовуються при вирішенні завдань і рівнянь. Нижче перераховані основні формули, що входять в даний список, і їх найменування.
квадрат суми
Щоб обчислити квадрат суми, необхідно знайти суму, що складається з квадрата першого доданка, подвоєного твори першого доданка на друге і квадрата другого. У вигляді вираження дане правило записується в такий спосіб: (а + с) ² = a² + 2ас + ².
квадрат різниці
Щоб обчислити квадрат різниці, необхідно обчислити суму, що складається з квадрата першого числа, подвоєного твори першого числа на друге (узяте з протилежним знаком) і квадрата другого числа. У вигляді вираження дане правило виглядає наступним чином: (а — с) ² = а² — 2ас + ².
різниця квадратів
Формула різниці двох чисел, зведених в квадрат, дорівнює добутку суми цих чисел на їх різницю. У вигляді вираження дане правило виглядає наступним чином: a² — с? = (A + c) · (a — c).
куб суми
Щоб обчислити куб суми двох доданків, необхідно обчислити суму, що складається з куба першого доданка, потроєного твори квадрата першого доданка і другого, потроєного твори першого доданка і другого в квадраті, а також куба другого доданка. У вигляді вираження дане правило виглядає наступним чином: (а + с) ³ = а³ + 3а²с + 3ас² + с³.
сума кубів
Відповідно до формули, прирівнюється до добутку суми даних доданків на їх неповний квадрат різниці. У вигляді вираження дане правило виглядає наступним чином: а³ + с³ = (а + с) · (а² — ас + с?).
У вигляді вираження дане правило виглядає наступним чином: а³ + с³ = (а + с) · (а² — ас + с?).
Приклад.Необхідно обчислити об’єм фігури, яка утворена складанням двох кубів. Відомі лише величини їх сторін.
Якщо значення сторін невеликі, то виконати обчислення просто.
Якщо ж довжини сторін виражаються в громіздких числах, то в цьому випадку простіше застосувати формулу «Сума кубів», яка значно спростить обчислення.
куб різниці
Вираз для кубічної різниці звучить так: як сума третього ступеня першого члена, потроєного негативного твори квадрата першого члена на другий, потроєного твори першого члена на квадрат другого і негативного куба другого члена. У вигляді математичного виразу куб різниці виглядає наступним чином: (а — с) ³ = а³ — 3а²с + 3ас² — с³.
різниця кубів
Формула різниці кубів відрізняється від суми кубів лише одним знаком. Таким чином, різниця кубів — формула, яка дорівнює добутку різниці даних чисел на їх неповний квадрат суми. У вигляді різниця кубів виглядає наступним чином: а 3 — з 3 = (ас) (а 2 + ас + з 2).
У вигляді різниця кубів виглядає наступним чином: а 3 — з 3 = (ас) (а 2 + ас + з 2).
Приклад.Необхідно обчислити об’єм фігури, яка залишиться після вирахування з обсягу синього куба об’ємної фігури жовтого кольору, яка також є кубом. Відома лише величина боку маленького і великого куба.
Якщо значення сторін невеликі, то обчислення досить прості. А якщо довжини сторін виражаються в значних кількостях, то варто застосувати формулу, названу «Різниця кубів» (або «Куб різниці»), которае значно спростить обчислення.
правила застосування формул скороченого множення
Формули або правила скороченого множення використовуються в арифметиці, а точніше — в алгебрі, для більш швидкого процесу обчислення великих алгебраїчних виразів. Самі ж формули отримані з існуючих в алгебрі правил для множення декількох многочленів.
Використання даних формул забезпечує досить оперативне рішення різних математичних задач, а також допомагає здійснювати спрощення виразів. Правила алгебраїчних перетворень дозволяють виконувати деякі маніпуляції з виразами, дотримуючись яких можна отримати в лівій частині рівності вираз, що стоїть в правій частині, або перетворити праву частину рівності (щоб отримати вираз, що стоїть в лівій частині після знака рівності).
Правила алгебраїчних перетворень дозволяють виконувати деякі маніпуляції з виразами, дотримуючись яких можна отримати в лівій частині рівності вираз, що стоїть в правій частині, або перетворити праву частину рівності (щоб отримати вираз, що стоїть в лівій частині після знака рівності).
Зручно знати формули, що застосовуються для скороченого множення, на пам’ять, так як вони нерідко використовуються при вирішенні завдань і рівнянь. Нижче перераховані основні формули, що входять в даний список, і їх найменування.
квадрат суми
Щоб обчислити квадрат суми, необхідно знайти суму, що складається з квадрата першого доданка, подвоєного твори першого доданка на друге і квадрата другого. У вигляді вираження дане правило записується в такий спосіб: (а + с) ² \u003d a² + 2ас + ².
квадрат різниці
Щоб обчислити квадрат різниці, необхідно обчислити суму, що складається з квадрата першого числа, подвоєного твори першого числа на друге (узяте з протилежним знаком) і квадрата другого числа. У вигляді вираження дане правило виглядає наступним чином: (а — с) ² \u003d а² — 2ас + ².
У вигляді вираження дане правило виглядає наступним чином: (а — с) ² \u003d а² — 2ас + ².
різниця квадратів
Формула різниці двох чисел, зведених в квадрат, дорівнює добутку суми цих чисел на їх різницю. У вигляді вираження дане правило виглядає наступним чином: a² — с? \u003d (A + c) · (a — c).
куб суми
Щоб обчислити куб суми двох доданків, необхідно обчислити суму, що складається з куба першого доданка, потроєного твори квадрата першого доданка і другого, потроєного твори першого доданка і другого в квадраті, а також куба другого доданка. У вигляді вираження дане правило виглядає наступним чином: (а + с) ³ \u003d а³ + 3а²с + 3ас² + с³.
сума кубів
Відповідно до формули, прирівнюється до добутку суми даних доданків на їх неповний квадрат різниці. У вигляді вираження дане правило виглядає наступним чином: а³ + с³ \u003d (а + с) · (а² — ас + с?).
Приклад. Необхідно обчислити об’єм фігури, яка утворена складанням двох кубів. Відомі лише величини їх сторін.
Відомі лише величини їх сторін.
Якщо значення сторін невеликі, то виконати обчислення просто.
Якщо ж довжини сторін виражаються в громіздких числах, то в цьому випадку простіше застосувати формулу «Сума кубів», яка значно спростить обчислення.
куб різниці
Вираз для кубічної різниці звучить так: як сума третього ступеня першого члена, потроєного негативного твори квадрата першого члена на другий, потроєного твори першого члена на квадрат другого і негативного куба другого члена. У вигляді математичного виразу куб різниці виглядає наступним чином: (а — с) ³ \u003d а³ — 3а²с + 3ас² — с³.
різниця кубів
Формула різниці кубів відрізняється від суми кубів лише одним знаком. Таким чином, різниця кубів — формула, яка дорівнює добутку різниці даних чисел на їх неповний квадрат суми. У вигляді різниця кубів виглядає наступним чином: а 3 — з 3 \u003d (ас) (а 2 + ас + з 2).
Приклад. Необхідно обчислити об’єм фігури, яка залишиться після вирахування з обсягу синього куба об’ємної фігури жовтого кольору, яка також є кубом. 2 \\ right) \\]
2 \\ right) \\]
У попередніх уроках ми розглянули два способи розкладання многочлена на множники: винесення спільного множника за дужки і спосіб угруповання.
У цьому уроці ми розглянемо ще один спосіб розкладання многочлена на множники із застосуванням формул скороченого множення.
Рекомендуємо кожну формулу прописати не менше 12 разів. Для кращого запам’ятовування випишіть все формули скороченого множення собі на невелику шпаргалку.
Згадаймо, як виглядає формула різниці кубів.
a 3 — b 3 \u003d (ab) (a 2 + ab + b 2)Формула різниці кубів не надто проста для запам’ятовування, тому рекомендуємо використовувати спеціальний спосіб для її запам’ятовування.
Важливо розуміти, що будь-яка формула скороченого множення діє і в зворотний бік .
(A — b) (a 2 + Ab + b 2) \u003d a 3 — b 3Розглянемо приклад. Необхідно розкласти на множники різниця кубів.
Звернемо увагу, що «27а 3» — це «(3а) 3», значить, для формули різниці кубів замість «a» ми використовуємо «3a».
Використовуємо формулу різниці кубів. На місці «a 3» у нас стоїть «27a 3», а на місці «b 3», як і у формулі, варто «b 3».
Застосування різниці кубів в зворотну сторону
Розглянемо ще один приклад. Ви бажаєте перевести твір многочленів в різниця кубів, використовуючи формулу скороченого множення.
Зверніть увагу, що твір многочленів «(x — 1) (x 2 + x + 1)» нагадує праву частину формули різниці кубів «», тільки замість «a» стоїть «x», а на місці «b» стоїть «1» .
Використовуємо для «(x — 1) (x 2 + x + 1)» формулу різниці кубів в зворотну сторону.
Розглянемо приклад складніше. Потрібно спростити твір многочленів.
Якщо порівняти «(y 2 — 1) (y 4 + y 2 + 1)» з правою частиною формули різниці кубів
« a 3 — b 3 \u003d (ab) (a 2 + ab + b 2)», То можна зрозуміти, що на місці« a »з першої дужки варто« y 2, а на місці «b» стоїть «1».
Формули скороченого множення.
Вивчення формул скороченого множення: квадрата суми і квадрата різниці двох виразів; різниці квадратів двох виразів; куба суми і куба різниці двох виразів; суми і різниці кубів двох виразів.
Застосування формул скороченого множення при вирішенні прикладів.
Для спрощення виразів, розкладання многочленів на множники, приведення многочленів до стандартному виду використовуються формули скороченого множення. Формули скороченого множення потрібно знати напам’ять.
Нехай а, b R. Тоді:
1. Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток першого виразу на друге плюс квадрат другого виразу.
(A + b) 2 \u003d a 2 + 2ab + b 2
2. Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток першого виразу на друге плюс квадрат другого виразу.
(A — b) 2 \u003d a 2 — 2ab + b 2
3. різниця квадратівдвох виразів дорівнює добутку різниці цих виразів і їх суми.
a 2 — b 2 \u003d (a -b) (a + b)
4. куб сумидвох виразів дорівнює кубу першого виразу плюс утроенное твір квадрата першого виразу на друге плюс утроенное твір першого виразу на квадрат другого плюс куб другого виразу.
(A + b) 3 \u003d a 3 + 3a 2 b + 3ab 2 + b 3
5. куб різницідвох виразів дорівнює кубу першого виразу мінус утроенное твір квадрата першого виразу на друге плюс утроенное твір першого виразу на квадрат другого мінус куб другого виразу.
(A — b) 3 \u003d a 3 — 3a 2 b + 3ab 2 — b 3
6. сума кубівдвох виразів дорівнює добутку суми першого та другого виразу на неповний квадрат різниці цих виразів.
a 3 + b 3 \u003d (a + b) (a 2 — ab + b 2)
7. різниця кубів двох виразів дорівнює добутку різниці першого і другого виразу на неповний квадрат суми цих виразів.
a 3 — b 3 \u003d (ab) (a 2 + ab + b 2)
Застосування формул скороченого множення при вирішенні прикладів.
Приклад 1.
обчислити
а) Використовуючи формулу квадрата суми двох виразів, маємо
(40 + 1) 2 \u003d 40 2 + 2 · 40 · 1 + 1 2 \u003d 1600 + 80 + 1 \u003d 1681
б) Використовуючи формулу квадрата різниці двох виразів, отримаємо
98 2 \u003d (100 — 2) 2 \u003d 100 2 — 2 · 100 · 2 + 2 2 \u003d 10000 — 400 + 4 \u003d 9604
Приклад 2.
обчислити
Використовуючи формулу різниці квадратів двох виразів, отримаємо
Приклад 3.
спростити вираз
(Х — у) 2 + (х + у) 2
Скористаємося формулами квадрата суми і квадрата різниці двох виразів
(Х — у) 2 + (х + у) 2 \u003d х 2 — 2ху + у 2 + х 2 + 2ху + у 2 \u003d 2х 2 + 2у 2
Формули скороченого множення в одній таблиці:
(A + b) 2 \u003d a 2 + 2ab + b 2
(A — b) 2 \u003d a 2 — 2ab + b 2
a 2 — b 2 \u003d (a — b) (a + b)
(A + b) 3 \u003d a 3 + 3a 2 b + 3ab 2 + b 3
(A — b) 3 \u003d a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 \u003d (a + b) (a 2 — ab + b 2)
a 3 — b 3 \u003d (ab) (a 2 + ab + b 2)
Формули скороченого множення (ФСУ) застосовуються для зведення в ступінь і множення чисел і виразів. Часто ці формули дозволяють зробити обчислення більш компактно і швидко.
У даній статті ми перерахуємо основні формули скороченого множення, згрупуємо їх в таблицю, розглянемо приклади використання цих формул, а також зупинимося на принципах доказів формул скороченого множення.
Вперше тема ФСУ розглядається в рамках курсу «Алгебра» за 7 клас. Наведемо нижче 7 основних формул.
Формули скороченого множення
- формула квадрата суми: a + b 2 \u003d a 2 + 2 a b + b 2
- формула квадрата різниці: a — b 2 \u003d a 2 — 2 a b + b 2
- формула куба суми: a + b 3 \u003d a 3 + 3 a 2 b + 3 a b 2 + b 3
- формула куба різниці: a — b 3 \u003d a 3 — 3 a 2 b + 3 a b 2 — b 3
- формула різниці квадратів: a 2 — b 2 \u003d a — b a + b
- формула суми кубів: a 3 + b 3 \u003d a + b a 2 — a b + b 2
- формула різниці кубів: a 3 — b 3 \u003d a — b a 2 + a b + b 2
Літерами a, b, c в даних виразах можуть бути будь-які числа, змінні або вирази. Для зручності використання краще вивчити сім основних формул напам’ять. Зведемо їх в таблицю і наведемо нижче, обвівши рамкою.
Перші чотири формули дозволяють обчислювати відповідно квадрат або куб суми або різниці двох виразів.
П’ята формула обчислює різницю квадратів виразів шляхом твори їх суми та різниці.
Шоста і сьома формули — відповідно множення суми і різниці виразів на неповний квадрат різниці і неповний квадрат суми.
Формула скороченого множення іноді ще називають тотожністю скороченого множення. В цьому немає нічого дивного, так як кожне рівність являє собою тотожність.
При вирішенні практичних прикладів часто використовують формули скороченого множення з переставленими місцями лівими і правими частинами. Це особливо зручно, коли має місце розкладання многочлена на множники.
Додаткові формули скороченого множення
Не будемо обмежуватися курсом 7 класу з алгебри і додамо в нашу таблицю ФСУ ще кілька формул.
По-перше, розглянемо формулу бінома Ньютона.
a + b n \u003d C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 +. . + C n n — 1 · a · b n — 1 + C n n · b n
Тут C n k — біноміальні коефіцієнти, які стоять в рядку під номером n в трикутнику Паскаля. Біноміальні коефіцієнти обчислюються за формулою:
C n k \u003d n! k! · (N — k)! \u003d N (n — 1) (n — 2). . (N — (k — 1)) k!
. (N — (k — 1)) k!
Як бачимо, ФСУ для квадрата і куба різниці і суми — це окремий випадок формули бінома Ньютона при n \u003d 2 і n \u003d 3соответственно.
Але що, якщо доданків в сумі, яку потрібно звести в ступінь, більше, ніж два? Корисною буде формула квадрата суми трьох, чотирьох і більше доданків.
a 1 + a 2 +. . + A n 2 \u003d a 1 2 + a 2 2 +. . + A n 2 + 2 a 1 a 2 + 2 a 1 a 3 +. . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 +. . + 2 a 2 a n + 2 a n — 1 a n
Ще одна формула, яка може стати в нагоді — формула формула різниці n-их ступенів двох доданків.
a n — b n \u003d a — b a n — 1 + a n — 2 b + a n — 3 b 2 +. . + A 2 b n — 2 + b n — 1
Цю формулу звичайно поділяють на дві формули — відповідно для парних і непарних ступенів.
Для парних показників 2m:
a 2 m — b 2 m \u003d a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 +. . + B 2 m — 2
Для непарних показників 2m + 1:
a 2 m + 1 — b 2 m + 1 \u003d a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 +. . + B 2 m
. + B 2 m
Формули різниці квадратів і різниці кубів, як ви здогадалися, є окремими випадками цієї формули при n \u003d 2 і n \u003d 3 відповідно. Для різниці кубів b також замінюється на — b.
Як читати формули скороченого множення?
Дамо відповідні формулювання для кожної формули, але спочатку розберемося з принципом читання формул. Зручніше за все робити це на прикладі. Візьмемо найпершу формулу квадрата суми двох чисел.
a + b 2 \u003d a 2 + 2 a b + b 2.
Кажуть: квадрат суми двох виразів a і b дорівнює сумі квадрата першого виразу, подвоєного твори виразів і квадрата другого виразу.
Всі інші формули читаються аналогічно. Для квадрата різниці a — b 2 \u003d a 2 — 2 a b + b 2 запишемо:
квадрат різниці двох виразів a і b дорівнює сумі квадратів цих виразів мінус подвоєний добуток першого і другого виразу.
Прочитаємо формулу a + b 3 \u003d a 3 + 3 a 2 b + 3 a b 2 + b 3. Куб суми двох виразів a і b дорівнює сумі кубів цих виразів, потроєного твори квадрата першого виразу на друге і потроєного твори квадрата другого виразу на перший вираз.
Переходимо до читання формули для різниці кубів a — b 3 \u003d a 3 — 3 a 2 b + 3 a b 2 — b 3. Куб різниці двох виразів a і b дорівнює кубу першого виразу мінус утроенное твір квадрата першого виразу на друге, плюс утроенное твір квадрата другого виразу на перший вираз, мінус куб другого виразу.
П’ята формула a 2 — b 2 \u003d a — b a + b (різниця квадратів) читається так: різниця квадратів двох виразів дорівнює добутку різниці і суми двох виразів.
Вирази типу a 2 + a b + b 2 і a 2 — a b + b 2 для зручності називають відповідно неповним квадратом суми і неповним квадратом різниці.
З огляду на це, формули суми і різниці кубів прочитав так:
Сума кубів двох виразів дорівнює добутку суми цих виразів на неповний квадрат їх різниці.
Різниця кубів двох виразів дорівнює добутку різниці цих виразів на неповний квадрат їх суми.
доказ ФСУ
Довести ФСУ досить просто. Грунтуючись на властивостях множення, проведемо множення частин формул в дужках.
Для прикладу розглянемо формулу квадрата різниці.
a — b 2 \u003d a 2 — 2 a b + b 2.
Щоб звести вираз в другу ступінь потрібно цей вислів помножити само на себе.
a — b 2 \u003d a — b a — b.
Розкриємо дужки:
a — b a — b \u003d a 2 — a b — b a + b 2 \u003d a 2 — 2 a b + b 2.
Формула доведена. Решта ФСУ доводяться аналогічно.
Приклади застосування ФСУ
Мета використання формул скороченого множення — швидке і коротке множення і зведення виразів в ступінь. Однак, це не вся сфера застосування ФСУ. Вони широко використовуються при скороченні виразів, скорочення дробів, розкладанні многочленів на множники. Наведемо приклади.
Приклад 1. ФСУ
Спростимо вираз 9 y — (1 + 3 y) 2.
Застосуємо формулу суми квадратів і отримаємо:
9 y — (1 + 3 y) 2 \u003d 9 y — (1 + 6 y + 9 y 2) \u003d 9 y — 1 — 6 y — 9 y 2 \u003d 3 y — 1 — 9 y 2
Приклад 2. ФСУ
Скоротимо дріб 8 x 3 — z 6 4 x 2 — z 4.
Помічаємо, що вираз в чисельнику — різниця кубів, а в знаменнику — різниця квадратів.
8 x 3 — z 6 4 x 2 — z 4 \u003d 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z.
Скорочуємо і отримуємо:
8 x 3 — z 6 4 x 2 — z 4 \u003d (4 x 2 + 2 x z + z 4) 2 x + z
Також ФСУ допомагають обчислювати значення виразів. Головне — вміти помітити, де застосувати формулу. Покажемо це на прикладі.
Зведемо в квадрат число 79. Замість громіздких обчислень, запишемо:
79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .
Здавалося б, складне обчислення проведено швидко всього лише з використанням формул скороченого множення і таблиці множення.
Ще один важливий момент — виділення квадрата двочлена. Вираз 4 x 2 + 4 x — 3 можна перетворити на вигляд 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 \u003d 2 x + 1 2 — 4. Такі перетворення широко використовуються в інтегруванні.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl + Enter
1.7: Рисование органических структур — Химия LibreTexts
Необходимо рисовать структурные формулы для органических соединений, потому что в большинстве случаев молекулярная формула не представляет однозначно отдельное соединение. Различные соединения, имеющие одинаковую молекулярную формулу, называются изомерами , а преобладание органических изомеров отражает необычайную гибкость углерода в образовании прочных связей с самим собой и с другими элементами. Когда группа атомов, составляющих молекулы различных изомеров, связана друг с другом принципиально разными способами, мы называем такие соединения структурными изомерами .Существует семь структурных изомеров C 4 H 10 O, и структурные формулы для них приведены в следующей таблице. Эти формулы представляют все известные и возможные соединения C 4 H 10 O и демонстрируют общую структурную особенность. Ни в одной из этих структур нет ни двойных, ни тройных связей, ни колец.
Различные соединения, имеющие одинаковую молекулярную формулу, называются изомерами , а преобладание органических изомеров отражает необычайную гибкость углерода в образовании прочных связей с самим собой и с другими элементами. Когда группа атомов, составляющих молекулы различных изомеров, связана друг с другом принципиально разными способами, мы называем такие соединения структурными изомерами .Существует семь структурных изомеров C 4 H 10 O, и структурные формулы для них приведены в следующей таблице. Эти формулы представляют все известные и возможные соединения C 4 H 10 O и демонстрируют общую структурную особенность. Ни в одной из этих структур нет ни двойных, ни тройных связей, ни колец.
Структурных формул C 4 Н 10 O изомеры
| Кекулы формула | Сгущенных формулы | Стенографии Формула |
Упрощение структурных формул может быть достигнуто без потери информации, которую они передают. В сокращенных структурных формулах связи с каждым углеродом опущены, но каждая отдельная структурная единица (группа) записывается с цифрами в нижнем индексе, обозначающими несколько заместителей, включая атомы водорода. Сокращенные (линейные) формулы полностью опускают символы для углерода и водорода. Каждый отрезок прямой линии представляет собой связь, концы и точки пересечения линий представляют собой атомы углерода, а правильное количество атомов водорода рассчитывается исходя из четырехвалентности углерода. Несвязывающие электроны валентной оболочки в этих формулах не учитываются.
В сокращенных структурных формулах связи с каждым углеродом опущены, но каждая отдельная структурная единица (группа) записывается с цифрами в нижнем индексе, обозначающими несколько заместителей, включая атомы водорода. Сокращенные (линейные) формулы полностью опускают символы для углерода и водорода. Каждый отрезок прямой линии представляет собой связь, концы и точки пересечения линий представляют собой атомы углерода, а правильное количество атомов водорода рассчитывается исходя из четырехвалентности углерода. Несвязывающие электроны валентной оболочки в этих формулах не учитываются.
Развитие способности визуализировать трехмерную структуру по двумерным формулам требует практики и в большинстве случаев помощи молекулярных моделей. Как отмечалось ранее, студентам и профессиональным химикам доступны многие виды наборов моделей, и начинающим студентам рекомендуется приобрести один из них.
Формула Кекуле
Структурная формула отображает атомы молекулы в том порядке, в котором они связаны. Он также изображает, как атомы связаны друг с другом, например, одинарная, двойная и тройная ковалентная связь.Ковалентные связи показаны линиями. Число черточек указывает, является ли связь одинарной, двойной или тройной ковалентной связью. Структурные формулы полезны, потому что они объясняют свойства и структуру соединения, которые не всегда могут быть представлены эмпирическими и молекулярными формулами.
Он также изображает, как атомы связаны друг с другом, например, одинарная, двойная и тройная ковалентная связь.Ковалентные связи показаны линиями. Число черточек указывает, является ли связь одинарной, двойной или тройной ковалентной связью. Структурные формулы полезны, потому что они объясняют свойства и структуру соединения, которые не всегда могут быть представлены эмпирическими и молекулярными формулами.
Пример. Формула Кекуле для этанола:
Сокращенная формула
Сокращенные структурные формулы показывают порядок атомов, как и структурные формулы, но записываются в одну строку, чтобы сэкономить место и сделать запись более удобной и быстрой.Сокращенные структурные формулы также помогают показать, что группа атомов связана с одним атомом в соединении. Когда это происходит, вокруг группы атомов используются круглые скобки, чтобы показать, что они вместе.
Пример. Краткая структурная формула этанола: CH 3 CH 2 OH (молекулярная формула этанола C 2 H 6 O).
Сокращенная формула
Поскольку органические соединения иногда могут быть сложными, формулы линейного угла используются для более эффективного описания атомов углерода и водорода путем замены букв линиями.Атом углерода присутствует везде, где линия пересекает другую линию. Затем предполагается, что атомы водорода завершают каждую из четырех связей углерода. Все остальные атомы, которые связаны с атомами углерода, выписываются. Формулы линейного угла помогают показать структуру и порядок атомов в соединении, делая преимущества и недостатки аналогичными структурным формулам.
Пример. Сокращенная формула для этанола:
Авторы
- Джин Ким (UCD), Кристина Боннетт (UCD)
Что означают скобки?
Вспомните, что существует как минимум 4 основных способа представления молекул, с которыми вы познакомились в первую неделю охема.
- Наивысший уровень детализации представляет собой точечная структура Льюиса , которая точками показывает расположение всех электронов.

- Второй уровень детализации — это структурная формула , в которой точки заменены линиями.
- Третий уровень детализации — линейная диаграмма , где углерод-углеродные связи представлены линиями, а атомы водорода полностью опущены.
Несколько промежуточное место в этих формулах занимает то, что мы называем « сокращенная формула ».Это способ полностью изобразить молекулы в текстовой форме. До того, как текстовые процессоры и графические программы позволяли легко включать изображения, сокращенные формулы были методом выбора, когда вы хотели передать структуру чего-либо без необходимости рисовать это.
Это легко для простых углеводородов, таких как пропан: CH 3 CH 2 CH 3 . Практически невозможно составить полезную сокращенную формулу для чего-то вроде морфина.
Между этими двумя крайностями есть несколько хитростей, за которыми нужно следить. Кронштейны являются одним из них.
Кронштейны являются одним из них.
Скобки помогают в двух отношениях. Они могут 1) уменьшить объем работы и 2) устранить двусмысленность структуры.
1) Экономия времени 1) Экономия Например, рассмотреть разницу между записью CH 3 CH 2 CH 2 CH 2 CH 2 CH 2 CH 2 CH 3 и CH 3 (CH 2 ) 6 CH 3 . Гораздо меньше работы, верно? Химики тяготеют к решениям, которые предполагают выполнение меньшего объема работы. Использование скобок — не проблема. 2) Уменьшение неоднозначности Второе использование квадратных скобок для уменьшения неоднозначности . Вспомните математику: есть разница между 4 + 2 * 3 и (4+2)*3. Точно так же мы используем скобки в органической химии. Рассмотрим случай, когда у вас есть четыре группы CH 3 , присоединенные к углероду.Вы бы не написали это CH 3 CH 3 CH 3 CH 3 C ; такое написание подразумевает цепочку, и каждая из этих групп CH 3 может быть прикреплена только к одной вещи. C CH 3 4 немного лучше, но расположение этих чисел рядом друг с другом сбивает с толку (это выглядит как CCH 34 ). Поэтому поместите группы CH 3 в скобки и напишите C(CH 3 ) 4 . Здесь нет двусмысленности . Эквивалентным (но менее эффективным) способом записи структуры будет CH 3 C(CH 3 ) 3 . 3) Карбонилы Карбонильные атомы кислорода (это C=O) также можно указать, заключив их в скобки. Таким образом, CH 3 C(O)CH 3 подразумевает, что второй углерод имеет двойную связь с кислородом. 4) Ветвление Скобки также могут использоваться для обозначения ветвления. Например, CH 3 CH(CH 3 )CH 2 CH 3 изображает 4-углеродную цепь, где CH 3 в скобках непосредственно присоединен к углероду перед ним.Это помогает выделить полезное эмпирическое правило: посмотрите слева от скобки t , чтобы увидеть, к какому атому он присоединен. Есть некоторые дополнительные хитрости со структурными формулами, которые не включают скобки, но их все равно важно знать. Альдегиды представлены CHO Карбоновые кислоты представлены CO 2 H (или COOH) Сложные эфиры представлены CO 2 R (или COOR)

Вот некоторые репрезентативные примеры
репрезентативные примеры.Как появится больше, я их добавлю. Дайте мне знать, если я пропустил что-то важное!
переход — CSS: каскадные таблицы стилей
Это свойство является сокращением для следующих свойств CSS:
переход: край-справа 4s;
переход: край-справа 4с 1с;
переход: поле-вправо 4s облегчение входа-выхода;
переход: поле-вправо 4 с, облегчение входа-выхода 1 с;
переход: поле-справа 4s, цвет 1s;
переход: все 0,5 сек. переход: наследовать;
переход: начальный;
переход: возврат;
переход: не установлен;
переход: наследовать;
переход: начальный;
переход: возврат;
переход: не установлен;
Свойство перехода указано как один или несколько переходов с одним свойством, разделенных запятыми.
Каждый переход одного свойства описывает переход, который должен быть применен к одному свойству (или специальные значения все и нет ). Включает в себя:
- ноль или одно значение, представляющее свойство, к которому должен применяться переход. Это может быть любой из:
- ключевое слово
нет - ключевое слово
все - a
- ключевое слово
- ноль или один
- ноль, один или два
<время>значений.Первое значение, которое может быть проанализировано как время, назначаетсяtransition-duration, а второе значение, которое может анализироваться как время, назначаетсяtransition-delay.
Посмотрите, что происходит, когда списки значений свойств имеют разную длину. Короче говоря, дополнительные описания переходов сверх числа фактически анимируемых свойств игнорируются.
Простой пример
В этом примере выполняется четырехсекундный переход размера шрифта с задержкой в одну секунду, когда пользователь наводит курсор на элемент.
HTML
Наведите курсор на меня
УСБ
.цель {
размер шрифта: 14px;
переход: размер шрифта 4s 1s;
}
.цель:наведите {
размер шрифта: 36px;
}
Есть еще несколько примеров переходов CSS, включенных в статью Использование переходов CSS.
Таблицы BCD загружаются только в браузере
Аббревиатуры, обычно используемые в детской
Эдвард Ф. Белл, доктор медицины
Статус экспертной оценки: Внутреннее экспертное рассмотрение 13.02.12
A/B – приступ апноэ/брадикардии (эпизод апноэ и/или брадикардии)
A/B/D – приступ апноэ/брадикардии/десатурации кислорода (эпизод апноэ и/или брадикардии и/или снижения насыщения кислородом)
AGA – соответствует гестационному возрасту
ARNP – зарегистрированная практикующая медсестра (PNP или NNP)
ASD – дефект межпредсердной перегородки
BBT – группа крови ребенка
BM – дефекация
BPD – бронхолегочная дисплазия
CBG – газы капиллярной крови
CHD – врожденный порок сердца или врожденный порок сердца
CHF – застойная сердечная недостаточность
CMV – цитомегаловирус
CNM – сертифицированная медсестра-акушерка
CNS – центральная нервная система
CPAP – постоянное положительное давление в дыхательных путях
C/S – кесарево сечение
CPT – физиотерапия органов грудной клетки
CSF – спинномозговая жидкость
ЦВН – центральное венозное питание
Рентгенография – рентген грудной клетки
ДВС-синдром – диссеминированное внутрисосудистое свертывание крови
ДР – родильный зал
ЭКМО – экстракорпоральная мембранная оксигенация n
ELBW – экстремально низкая масса тела при рождении
ETC – центр неотложной помощи
ETT – эндотрахеальная трубка
FOC – лобно-затылочная окружность
FTP – отсутствие прогресса
G-P- — gravida ____para____ (беременности; беременности, приведшие к рождению хотя бы одного ребенка)
GBS – стрептококк группы B
HB, HGB, Hb или Hgb – гемоглобин
HC – окружность головы
HCT – гематокрит
HFJV – высокочастотная струйная вентиляция
HFV – высокочастотная частотная вентиляция
HFOV – высокочастотная осциллирующая вентиляция
HM – грудное молоко
HMD – болезнь гиалиновых мембран
HMF – обогатитель грудного молока (делает грудное молоко 0. 8 ккал/куб.см)
8 ккал/куб.см)
ГУС – УЗИ головы
ВАК или ВАБ – искусственный аборт
ИДМ – ребенок матери с сахарным диабетом
ИВЛ – перемежающаяся принудительная вентиляция легких
ИНО – ингаляция оксида азота
ВМУ – внутриутробная гибель плода
ЗВУР – задержка внутриутробного развития
ЭКО – экстракорпоральное оплодотворение
IVH – внутрижелудочковое кровоизлияние
L+D – роды и роды
LGA – большие для гестационного возраста
LLSB – нижняя левая граница грудины
LMD – местный врач (использование поставщика первичной медико-санитарной помощи – предпочтительно PCP)
LSB – левый край грудины
MAP – среднее давление в дыхательных путях
MAS – синдром аспирации мекония
MBT – группа крови матери
MCL – среднеключичная линия
MGF – дедушка по материнской линии
MGM – бабушка по материнской линии
NAD – отсутствие явного дистресса
NAVA – нейрокорректированная вспомогательная вентиляция легких
NC – назальная канюля
NEC – некротизирующий энтероколит
NICU – отделение интенсивной терапии новорожденных
NNP – неонатальная медсестра titioner
NNS – неонатальный скрининг (метаболический скрининг новорожденных)
NO – оксид азота
NPCPAP – постоянное положительное давление в носоглотке
NPO – ничего через рот
NSIMV – назофарингеальная синхронизированная прерывистая принудительная вентиляция легких
NTD – дефект нервной трубки
NVN – венозное питание новорожденных (местный термин, не рекомендуется для внешних коммуникаций)
PC – контроль давления
PCO2 – парциальное давление углекислого газа
PCP – поставщик первичной медико-санитарной помощи
PDA – открытый артериальный проток
PEEP – пиковое давление и давление на выдохе
PF – смесь для недоношенных детей
PFC – стойкое кровообращение плода
PFO – открытое овальное окно
PGE1 – простагландин E1
PGF – дедушка по отцу
PGM – бабушка по отцу
PICC – чрескожно введенный центральный катетер
PIE – интерстициальная эмфизема легких
PIH – гипертензия, вызванная беременностью
PIP – пиковое давление вдоха
PIV – периферический внутривенный катетер
ФКУ – фенилкетонурия, заболевание, выявляемое на ННС
ПМИ – точка максимального импульса
ПНП – врач-педиатр
РО2 – парциальное давление кислорода
ПРК – персистирующая легочная гипертензия
ПЛГН – персистирующая легочная гипертензия новорожденных преждевременное излитие плодных оболочек
ППС – периферический стеноз легочной артерии
ПБЦ – эритроцитарная масса (концентрированная суспензия эритроцитов для переливания)
ПРОП – преждевременное излитие плодных оболочек (до начала родов) или пролонгированное излитие плодных оболочек
ПС – поддержка давлением
ПТЛ – преждевременные роды
PVL – перивентрикулярная лейкомаляция
PVN – парентеральное или периферическое венозное питание
RA – комнатный воздух (21% кислорода)
RCM – край правой реберной дуги
RDS – респираторный дистресс-синдром
ROM – разрыв плодных оболочек ИЛИ объем движений
РН – ретинопатия недоношенных
РСВ – респираторно-синцитиальный вирус
SAB или SAb – s самопроизвольный аборт
SF – исходная смесь или стандартная смесь (обогащенная железом смесь для искусственного вскармливания)
SGA – малая для гестационного возраста
SIMV – синхронизированная перемежающаяся принудительная вентиляция легких
SO2 – насыщение кислородом
TCM – чрескожный монитор (для PO2, PCO2)
TG – истинная глюкоза (правильнее называть глюкозой крови, «ложной» глюкозы не бывает)
ТПП – полное парентеральное питание
ТТН – транзиторное тахипноэ новорожденных
ОАК – катетер пупочной артерии
УВК – катетер пупочной вены
ОНМТ – очень низкая рождаемость вес ребенка
ДМЖП – дефект межжелудочковой перегородки
ВС – показатели жизнедеятельности
10.
 1 Сокращенная структура и линейная структура – CHEM 1114 – Введение в химию
1 Сокращенная структура и линейная структура – CHEM 1114 – Введение в химиюЦели обучения
К концу этого раздела вы сможете:
- Интерпретация конденсированных и линейных структур.
- Нарисуйте сжатую структуру данной структуры Льюиса или линейной структуры.
- Нарисуйте линейную структуру данной структуры Льюиса или конденсируйте структуру.
Если вы посмотрите в этой главе и других источниках на то, как изображаются органические соединения, вы увидите, что рисунки несколько отличаются от структур Льюиса, которые вы привыкли видеть в своем учебнике по общей химии.В некоторых источниках вы увидите конденсированных структуры для более мелких молекул вместо полных структур Льюиса:
Рисунок 1. Сравнение структур Льюиса и конденсированных структур.
Пример 1
Определите структуру Льюиса следующей конденсированной структуры олеиновой кислоты, жирной кислоты, которая естественным образом содержится в различных животных и растительных жирах и маслах.
CH 3 (CH 2 ) 7 CH=CH(CH 2 ) 7 COOH
Раствор
Начните с рисования CH 3 .(CH 2 ) 7 представляет собой повторяющуюся единицу, то есть вы должны нарисовать семь CH 2 один за другим, которые связаны с CH, который связан с CH, а затем еще семь CH 2 с. COOH представляет собой карбоновую кислоту, что означает, что у вас есть C = O, связанный с O-H. Всегда дважды проверяйте свою структуру, чтобы убедиться, что каждый углерод образует четыре связи. Когда вы это сделаете, вы увидите, что два CH должны быть связаны двойной связью.
Проверьте себя
Наиболее распространенные органические соединения, которые, вероятно, есть у вас дома: ацетон (CH 3 COCH 3 ), содержащийся в жидкости для снятия лака, уксусная кислота (CH 3 COOH), обнаруженная в уксусе, и изопропанол ((CH 3 ) 2 CHOH), содержащийся в медицинском спирте. Определите структуру Льюиса для каждого из этих бытовых химикатов.
Определите структуру Льюиса для каждого из этих бытовых химикатов.
Ответить
Чаще всего химики-органики и биологические химики используют сокращенное обозначение чертежей, называемое линейными структурами , также известными как скелетные структуры или линейные структуры связи . Соглашение довольно простое и упрощает рисование молекул, но к линейным структурам нужно немного привыкнуть.Атомы углерода изображаются не заглавной С, а «углом» между двумя связями или свободным концом связи. Молекулы с открытой цепью обычно вытянуты в форме «зигзага». Водороды, присоединенные к углероду, обычно не показаны: скорее, как и неподеленные пары, они просто подразумеваются (если не показан положительный формальный заряд, предполагается, что все атомы углерода имеют полный октет валентных электронов). Водороды, связанные с азотом, кислородом, серой или чем-либо, кроме углерода , показаны , но обычно нарисованы без показа связи. Следующие примеры иллюстрируют соглашение.
Следующие примеры иллюстрируют соглашение.
Как вы можете видеть, «урезанная» линейная структура позволяет намного легче увидеть основную структуру молекулы и места, где есть что-то еще, кроме одинарных связей C-C и C-H. Для более крупных и сложных биологических молекул становится непрактичным использовать полные структуры Льюиса. И наоборот, очень маленькие молекулы, такие как этан, должны изображаться с их полными льюисовскими или конденсированными структурами.
Иногда один или несколько атомов углерода в линейной структуре изображаются с заглавной буквы C, если это облегчает понимание объяснения. Если вы пометите углерод буквой C, вы также должны нарисовать атомы водорода для этого углерода .
Пример 2
Нарисуйте линейные структуры для этих двух молекул:
Решение
Каждый атом углерода превращается в конец линии или место пересечения линий. Все атомы водорода, присоединенные к атомам углерода, исключены из структуры (хотя нам все равно нужно признать, что они там есть):
Все атомы водорода, присоединенные к атомам углерода, исключены из структуры (хотя нам все равно нужно признать, что они там есть):
Проверьте себя
Нарисуйте линейные структуры для этих двух молекул:
Ответы
Пример 3
Определите химическую формулу молекулы, представленной здесь:
Решение
Есть восемь мест, где линии пересекаются или заканчиваются, что означает, что в молекуле восемь атомов углерода.Поскольку мы знаем, что атомы углерода имеют тенденцию образовывать четыре связи, каждый атом углерода будет иметь количество атомов водорода, необходимое для четырех связей. Это соединение содержит 16 атомов водорода для молекулярной формулы C 8 H 16 .
Расположение атомов водорода:
Проверь себя
Определите химическую формулу молекулы, представленной здесь:
Ответить
С 9 Н 20
Пример 4
Определите структуру Льюиса следующей линейной структуры L-аскорбиновой кислоты (витамин С):
Раствор
В каждом углу или на пересечении линий или в конце линии добавьте C:
Каждый C образует четыре связи. Если некоторые из них не видны, добавьте связь к H для каждой отсутствующей связи . Также покажите связь между буквами О и Н.
Если некоторые из них не видны, добавьте связь к H для каждой отсутствующей связи . Также покажите связь между буквами О и Н.
Проверьте себя
Определите структуру Льюиса следующей линейной структуры ацетаминофена, лекарства от боли и лихорадки, содержащегося в тайленоле.
Ответить
Ключевые понятия и резюме
Конденсированные структуры и линейные структуры позволяют очень кратко представить органические структуры.
Упражнения
1. Нарисуйте линейную структуру связи для следующих соединений:
a) (HO) 3 C(CH 2 ) 2 N(CH 2 CHO)CH(CH 2 CH 3 ) 2 б) CH 3 (CH 2 ) 3 CH(CH 3 )(CH 2 ) 2 OCH 2 0 CH 3 2 OCH 2 0 CH 3 c) HOOCCH 2 O(CH 2 ) 2 N(CH 2 CH 3 ) 2 d) HOCCH 2 CH(CH 3 )CH 2 CH(CH 3 )(CH 2 ) 2 COOCH 3 e) H 2 NCH 2 [CH(CH 3 )] 2 (CH) 4 CO(CH 2 ) f) ClCH 2 CH(CH 3 )COCH 2 OCH 2 CO(CH 2 ) 2 CH 3 2. Ответы 1. 2. а) С 13 Н 26 О; CH 3 (CH 2 ) 3 C (CH 3 ) 2 C (CH 3 ) 2 CH 2 Coch 3 б) С 8 Н 14 О 2 ; CHOCH 2 CO(CH 2 ) 4 CH 3 в) С 5 Н 7 О 4 Н; COOH(CH 2 ) 2 (CO) 2 NH 2 г) С 12 Н 25 О 2 Н; CH 3 OCO (CH 2 ) 2 C (CH 3 ) 2 C (CH 3 ) 2 CH (CH 3 ) NH 2 д) C 12 H 25 ВКЛ; CH 3 (CH 2 ) 4 CON(CH 2 CH 2 CH 3 ) 2 f) C 8 H 16 O 3 ; CH 3 CH 2 CH(OCH 3 )(CH 2 ) 3 COOH Этот контент также можно загрузить в формате интерактивного PDF. Этот текст опубликован в соответствии с лицензией Creative Commons, для ссылки и адаптации, пожалуйста, нажмите здесь. Перец Хабанеро (фото: https://www. Жаркий августовский вечер в парке посреди Северного Гудзона, штат Висконсин, в деревне с населением чуть менее 4000 человек на реке Санта-Крус на западной окраине штата. Линия людей сидит за столами, установленными внутри брезентовой палатки.На глазах у ликующей толпы друзей, семьи и соседей эти смельчаки собираются вступить в бой. . .с фруктовой тарелкой. К несчастью для участников, речь идет о хабанеро, одном из самых острых сортов перца чили, обычно встречающемся на рынках Северной Америки. В этом конкретном случае команды из пяти человек будут соревноваться, чтобы первыми съесть целый фунт перца. Когда начинается еда, сначала все кажется хорошо. Однако в течение тридцати секунд то, что начинает происходить, совершенно предсказуемо и понятно любому, кто когда-либо по ошибке наливал на обеденную тарелку слишком много острого соуса. Лица краснеют, начинают течь пот и слезы, проглатывается обильное количество холодной воды. Хотя технически участники соревнуются друг с другом, настоящим противником в этом соревновании — причиной всей боли и страданий — является химическое соединение капсаицин, источник остроты острого перца чили. Состоящий из четырех элементов углерода, водорода, кислорода и азота, капсаицин вырабатывается растением перца с целью защиты от голодных млекопитающих.Молекула связывается и активирует рецепторный белок млекопитающих под названием TrpV1, который в нормальных условиях выполняет функцию обнаружения высоких температур и отправки сигнала в мозг — «жарко, держись подальше!» Эта стратегия работает достаточно хорошо на всех видах млекопитающих, кроме Первый: мы, люди (по крайней мере, некоторые из нас), кажется, единственные в своей склонности на самом деле искать жжение острого перца в нашей еде. Интересно, что у птиц также есть белок теплового рецептора, который очень похож на рецептор TrpV1 у млекопитающих, но птицы совершенно не чувствительны к капсаицину.В этом есть эволюционная логика: перцу выгодно быть съеденным птицей, а не млекопитающим, потому что птица может распространить семена перца на гораздо большую территорию. Область рецептора, отвечающая за чувствительность к капсаицину, оказывается весьма специфичной. Вернувшись на перечный фестиваль North Hudson Pepperfest, те, у кого немного больше здравого смысла, отказываются от болезненных последствий перегрузки капсаицином и вместо этого предаются более приятным химическим явлениям. Маленькая девочка, наслаждающаяся рожком мороженого, отчасти реагирует на химическое действие другого органического соединения, называемого ванилином. Что такого особенного в капсаицине и ванилине, из-за чего эти два соединения оказывают столь разительно различное воздействие на наше сенсорное восприятие? Оба производятся растениями, и оба состоят из элементов углерода, водорода, кислорода и (в случае капсаицина) азота.С момента зарождения химии как науки химики были очарованы — и на протяжении большей части своей истории — озадачены бесчисленными свойствами соединений, происходящих из живых существ. Сегодня, как вы, вероятно, уже знаете, термин «органический» — применительно к химии — относится не только к молекулам живых существ, но и ко всем соединениям, содержащим элемент углерода, независимо от происхождения. Начиная с начала 19 века, когда химики путем тщательных экспериментов узнали о составе и свойствах «органических» соединений, таких как жирные кислоты, уксусная кислота и мочевина, и даже выяснили, как синтезировать некоторые из них, начиная с исключительно «неорганических» компонентов. , они начали понимать, что концепция «жизненной силы» неверна и что свойства как органических, так и неорганических молекул на самом деле можно понять, используя одни и те же фундаментальные химические принципы. Они также начали более полно ценить уникальные свойства элемента углерода, которые делают его столь важным в химии живых существ, в той мере, в какой он требует отдельной области химии. Углерод образует четыре стабильные связи либо с другими атомами углерода, либо с водородом, кислородом, азотом, серой, фосфором или галогеном. Характерные способы связывания углерода позволяют ему служить скелетом или каркасом для построения больших сложных молекул, включающих цепи, разветвления и кольцевые структуры. Хотя «органическая химия» больше не означает исключительно изучение соединений живых существ, тем не менее, желание понять и повлиять на химию жизни является движущей силой большей части работы химиков-органиков, независимо от того, является ли их целью изучение чего-то принципиально нового. о реактивности углерод-кислородной связи, открыть новый лабораторный метод, который можно использовать для синтеза лекарства, спасающего жизнь, или лучше понять сложный химический танец, происходящий в активном центре фермента или рецепторного белка. В этой главе вы познакомитесь с некоторыми из наиболее фундаментальных принципов органической химии. С понятиями, которые мы изучаем, мы можем начать понимать, как углерод и очень небольшое количество других элементов в периодической таблице могут комбинироваться предсказуемым образом, создавая практически безграничный химический репертуар. По мере прочтения вы обнаружите, что эта глава содержит много обзоров тем, которые вы, вероятно, уже изучили на вводном курсе химии, но, вероятно, также будет несколько новых для вас понятий, а также некоторые темы. которые вам уже знакомы, но рассматриваются более подробно и с большим акцентом на биологически значимых органических соединениях. Мы начнем с напоминания о том, как химики изображают связи в органических молекулах с помощью условного рисунка «структура Льюиса», сосредоточив внимание на концепции «формального заряда».Мы рассмотрим общие схемы связывания шести элементов, необходимых для всех форм жизни на Земле: углерода, водорода, азота, кислорода, серы и фосфора, а также галогенов (фтора, хлора, брома и йода). Затем мы продолжим с некоторыми из основных навыков, связанных с рисованием и обсуждением органических молекул: понимание соглашения о рисовании «линейной структуры» и других полезных способов сокращения и упрощения структурных рисунков, изучение функциональных групп и изомеров, а также изучение как систематически называть простые органические молекулы. ( Вернуться к началу ) Как видно из приведенных выше молекул капсаицина и ванилина, наиболее распространенными атомами в органических соединениях являются углерод и водород.Другие атомы, которые обычно образуют ковалентные связи в органических структурах, также включают кислород, азот, серу и фосфор. Реже галогены, такие как хлор, бром и йод, также могут быть включены в органические молекулы. Вспомним из главы 4, что правило октета помогло нам определить, что углерод обычно образует четыре ковалентные связи, азот и фосфор образуют по три, кислород и сера образуют по две, а галогены образуют только одну связь. Таблица 5.1. Модели ковалентных связей атомов, обычно встречающихся в органических молекулах *Примечание: водород на самом деле не следует правилу октета, так как его валентная оболочка заполнена 2 e – По мере нашего продвижения в изучении органических молекул мы обнаруживаем, что они становятся намного сложнее, чем простые ионные и ковалентные соединения, обсуждавшиеся в главе 3. Что, если кислород связан вот так? Как бы вы рассчитали официальное обвинение? Это не предпочтительная конфигурация для кислорода, но поскольку кислород настолько электроотрицательен, он может легче нести отрицательный формальный заряд, чем атомы с меньшей электроотрицательностью. Теперь рассмотрим структуру аниона фосфата (PO 4 3- ). Это самая распространенная форма фосфора, встречающаяся во всех живых организмах на планете, включая человека. Он обычно входит в состав органических молекул, таких как ДНК, белки и АТФ (аденозинтрифосфат), хранилище энергии клетки (рис. 5.1). Рисунок 5.1 Структуры аденозинтрифосфата (АТФ) и дезоксирибонуклеиновой кислоты (ДНК). Ион фосфата является важным компонентом как (A.) структура АТФ и (Б.) структура ДНК. Диаграмма модели ДНК предоставлена: Zephyris — собственная работа, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=15027555 Как нам нарисовать структуру Льюиса для иона фосфата? (1) Определите наименее электроотрицательный(е) элемент(ы) в молекуле. Это будет центральный атом (атомы), вокруг которого связаны другие, более электроотрицательные атомы. (Обратите внимание, что водород никогда не может быть центральным атомом, поскольку он может образовывать только одну ковалентную связь). Для PO 4 3- перечислите все атомы, в центре которых находится фосфор. Кроме того, перечислите любые дополнительные электроны из-за отрицательного заряда всей молекулы и ваши ожидания относительно связывающей способности каждого атома для достижения октета. Обратите внимание, что у нас есть четыре атома кислорода, которые должны быть связаны с фосфором. Таким образом, мы ожидаем, что P будет находиться в состоянии связи 5 для этой молекулы (т.е. 3 будет недостаточно). Обратите внимание, что неподеленная пара электронов в P расщеплена, и каждый электрон используется для расширенной орбитальной связи с другими атомами. (2) Подсчитайте общее количество валентных электронов, присутствующих в молекуле. Для этого сложите все валентные электроны для каждого присутствующего атома. (3) Постройте оболочку для связанных атомов с центральным атомом (атомами) и рассчитайте формальный заряд (заряды). Установите связи между внешними атомами и центральным атомом Добавьте все оставшиеся электроны, чтобы завершить правило октета/дуэта (или, при необходимости, расширенные орбитали) для оставшихся атомов Если у вас закончились электроны до того, как все атомы заполнили валентные оболочки, начинают образовывать двойные связи там, где это необходимо Рассчитайте формальный заряд каждого атома в молекуле, а затем используйте сумму для расчета формального заряда всей молекулы. Посмотрите приведенный выше видеоурок, который поможет вам нарисовать структуру фосфата по Льюису. Вы увидите, что начинать нужно с центрального фосфора. Обратите внимание, что нужно использовать правило расширенной орбиты вместо октета, чтобы иметь возможность связываться со всеми атомами кислорода. Что касается фосфора, мы знаем, что он образует 5 связей в расширенном орбитальном формате (таблица 5.1) и требует в общей сложности 10 электронов вместо обычных 8, которые мы привыкли видеть с помощью правила октетов.Итак, начните с рисования этих 5 связей. Вы заметите, что вам нужно создать одну двойную связь с одним из атомов кислорода, чтобы завершить 5 связей. После этого заполните неподеленную пару электронами для всех атомов, пока не получите в общей сложности 32 электрона. (убедитесь, что каждый кислород достигает состояния октета. Далее рассчитайте формальные заряды на каждом атоме. Как показано выше, кислород, который имеет 2 связанные пары электронов и две заимствованные пары, имеет формальный заряд ноль, в то время как кислород, который имеет одну связанную пару пара электронов и три неподеленные пары имеют формальный заряд 1 –. (4) При необходимости нарисуйте резонансные структуры. Для нашей фосфатной (PO 4 3-) структуры выше, если мы рассмотрим каждый из атомов кислорода внутри молекулы, они по своей сути не отличаются друг от друга. Таким образом, каждый кислород, окружающий фосфор, должен иметь равные возможности для образования положения двойной связи. Мы показали, что двойная связь образуется в нижнем положении, но она имеет равновероятную вероятность образования с любым из трех других атомов кислорода. На самом деле ни одна из резонансных структур не представляет собой истинную структуру.Истинная структура находится где-то посередине между всеми возможными резонансными конформациями. Однако рисование резонансных структур дает ученым возможность обсудить истинную конформацию структуры и дает возможность предсказать химическую реактивность молекулы. (наверх) Органические молекулы, по сравнению с простыми солями и ковалентными соединениями, показанными в главах 3 и 4, могут быть довольно большими и разветвленными структурами с множеством ответвлений.Таким образом, важно понимать, как рисовать органические молекулы, чтобы понимать трехмерную форму молекулы. Молекулярная формула — это самый простой способ представить соединение путем подсчета всех различных типов атомов и перечисления их по порядку. C 5 H 12 +8O 2 →5CO 2 +6H 2 O В подобных случаях порядок связывания в органической молекуле не важен. Две указанные выше структуры представляют действительные структуры с молекулярной формулой C 5 H 12 .Однако каждая из этих структур представляет собой другую молекулу с немного отличающимися химическими свойствами. Когда соединения имеют одинаковую молекулярную формулу, но имеют разный порядок связывания атомов, они известны как структурные изомеры . (вы также можете увидеть термин конституциональных изомеров ). Перечислили ли мы все возможные структурные изомеры для формулы C 5 H 12 ? Нет! Используйте приведенный ниже пример, чтобы увидеть, можете ли вы создать третий структурный изомер. (наверх) Структурная формула показывает, как связаны различные атомы, и может быть более полезной, чем просто написание молекулярной формулы соединения. Существуют различные способы рисования структурных формул, и вам необходимо ознакомиться со всеми из них. Они включают отображаемую формулу, сокращенные формулы и линейные структуры. Формула , отображаемая , показывает все связи в молекуле в виде отдельных строк, где каждый атом написан в конце каждой строки с использованием аббревиатуры элемента из периодической таблицы.Все структуры C 6 H 12 выше записаны в отображаемых формулах . Вы должны помнить, что каждая линия представляет собой пару общих электронов. Например, на рисунке 5.2 ниже показана отображаемая формула метана рядом с трехмерными представлениями. Рисунок 5.2: Три различных представления CH 4 Слева — модель мяча и стержня, в центре — отображаемая формула, а справа — заполняющая пространство модель. Обратите внимание, что отображаемая формула метана не представляет трехмерную форму молекулы, показанную на диаграмме заполнения пространства справа. Метан не плоский с валентными углами 90°. Это несоответствие между тем, что вы рисуете, и тем, как на самом деле выглядит молекула, может привести к проблемам, если вы не будете осторожны. Таким образом, для органической химии важно начать думать о структурах в их трехмерной форме. Чем больше вы практикуетесь, тем больше вы сможете визуализировать и вращать молекулу в своей голове.Например, рассмотрим простую молекулу с молекулярной формулой CH 2 Cl 2 . Вы могли бы подумать, что есть два разных способа расположения этих атомов, если бы вы нарисовали отображаемую формулу. Но эти две структуры на самом деле абсолютно одинаковы. Одна структура на самом деле является простым вращением другой. Рассмотрим немного более сложную молекулу C 2 H 5 Cl. Отображаемая формула может быть записана в следующем виде: Но, опять же, это одно и то же. Посмотрите на модели ниже. По мере того, как вы продолжаете практиковаться в построении структурных формул, вы научитесь лучше распознавать и различать изомеры, которые действительно отличаются друг от друга, и версии одной и той же молекулы, написанные с разных трехмерных точек зрения. Для чего-либо, кроме самых простых молекул, рисование полностью отображаемой формулы может быть громоздким и занимать слишком много места, особенно для всех углерод-водородных связей. Обратите внимание, что частично конденсированная структура по-прежнему дает очень четкое представление о том, где каждый из атомов связан в пространстве. Однако с полностью уплотненной структурой может быть сложно точно увидеть схемы склеивания. Полностью конденсированная форма содержит больше информации о порядке связывания, чем молекулярная формула, так что атомы, которые непосредственно связаны с соседним атомом, располагаются рядом с этим атомом в конденсированной форме, а не простой подсчет всего атомного вида как в молекулярной формуле. Работая в обратном направлении, мы можем использовать конденсированную структуру этановой кислоты в качестве примера, чтобы воссоздать частично конденсированную структуру. Обратите внимание, что это удовлетворяет правилу октета для первого атома углерода (четыре связи с другими атомами). Три атома водорода также заполнены своими одинарными связями с первым углеродом. Второму углероду теперь назначена одна связь с первым углеродом.Нам нужно присвоить оставшиеся три связи. Из сокращенной формулы видно, что первый кислород присоединен ко второму углероду, однако после этого мы становимся неуверенными в положении второго кислорода. Мы можем ясно сделать вывод, что последний атом водорода связан со вторым атомом кислорода, поскольку он находится в этом положении. Однако, поскольку кислород может образовывать две связи, мы не можем быть уверены, основываясь только на конденсированной структуре, что второй кислород связан со вторым углеродом или с первым кислородом. Если вы не уверены, какой атом с каким связан, лучше всего нарисовать потенциальные структуры и оценить их потенциальную правильность. Из приведенного выше анализа возможных структур становится ясно, что ни одна из структур не удовлетворяет правилу октета для одного или нескольких атомов внутри молекулы, как это написано в настоящее время. Однако нижняя структура менее удовлетворительна, чем верхняя структура, поскольку у второго атома углерода отсутствуют 2 ковалентные связи, в то время как все остальные атомы удовлетворяют требованиям октета к связыванию.На верхней диаграмме и у второго атома углерода, и у первого атома кислорода отсутствует одна связь. Эта структура легко удовлетворяет правилу октета, помещая двойную связь между углеродом 2 и кислородом 1 внутри молекулы. Принимая во внимание, что решение проблемы отсутствия двух углеродных связей для второго атома углерода в нижней структуре исправить нелегко. Таким образом, верхняя структура является более вероятной, чем нижняя структура с добавлением двойной связи между углеродом и кислородом. Хотя сгущенные структуры легче записывать, чем отображаемые или частично сгущенные структуры, они могут оказаться немного более сложными для определения трехмерного рисунка связи атомов. В строке или формуле скелета все атомы водорода не показаны и все атомы углерода не помечены, а указаны в конце или изгибе в каждой строке, оставляя только углеродный скелет с присоединенными к нему функциональными группами. . Любые гетероатомы (любой другой атом, кроме углерода или водорода) и атомы водорода, присоединенные к гетероатомам, показаны в сжатой форме.Например, отображаемая структура, частично конденсированная структура и линейная формула для 2-бутанола (C 4 H 10 O) выглядят так: В линейной или скелетной диаграмме могут быть сделаны следующие предположения: на стыке каждой линии и на конце каждой линии есть атом углерода. к каждому углероду присоединено столько атомов водорода, что общее число связей на этом углероде равно 4. все гетероатомы (и атомы водорода, присоединенные к гетероатомам) показаны в сжатом виде на скелетной структуре. В рамках органической химии и биохимии ученые обычно используют комбинацию этих различных форматов для представления химических структур. Важно ознакомиться с рисованием и интерпретацией всех возможных представлений. Бывают случаи, когда важно иметь возможность показать точное трехмерное расположение частей некоторых молекул при использовании структурного представления.Для этого облигации показаны условными обозначениями: Например, вы можете захотеть показать трехмерное расположение групп вокруг атома углерода, имеющего группу -ОН в 2-бутаноле. (наверх) Часто при рисовании органических структур химики считают удобным использовать букву «R» для обозначения части молекулы за пределами интересующей области. Группа R — это удобный способ сокращения структур больших биологических молекул, особенно когда нас интересует что-то, что происходит конкретно в одном месте молекулы. Например, в главе 15, когда мы рассматриваем биохимические окислительно-восстановительные реакции с участием молекулы флавина, мы будем сокращать большую часть структуры флавина (т.R = FAD), который вообще не изменяется в интересующих реакциях: В качестве альтернативы мы можем использовать символ «разрыв», чтобы указать, что мы смотрим на небольшой кусочек или часть более крупной молекулы. Это обычно используется в контексте рисования групп на больших полимерах, таких как белки или ДНК. Наконец, группы R можно использовать для краткой иллюстрации ряда родственных соединений, таких как семейство антибиотиков на основе пенициллина. Правильное использование аббревиатур — очень важный навык, который необходимо развивать при изучении органической химии в биологическом контексте, потому что, хотя многие биомолекулы очень большие и сложные (и рисовать их можно целую вечность!), обычно мы сосредотачиваемся только на одной небольшой части молекулы. где происходит изменение. Как правило, вы никогда не должны сокращать любой атом, участвующий в разрыве или образовании связи , который иллюстрируется: сокращайте только ту часть молекулы, которая не участвует в интересующей реакции. Например, углерод № 2 в приведенном ниже реагенте/продукте определенно участвует в изменении связи, и поэтому его не следует включать в группу «R». Если вы не уверены, следует ли рисовать часть структуры или сокращать ее, безопаснее всего будет нарисовать ее. (наверх) Как видно из раздела 5. Помните, что структурных изомеров имеют одинаковые атомы, но порядок, в котором атомы связаны друг с другом, различен, что приводит к различным физическим и химическим свойствам. Например, этанол является жидкостью при комнатной температуре, тогда как диэтиловый эфир представляет собой газ. Если атомы соединенного соединения имеют один и тот же порядок, но их трехмерное расположение в пространстве различается, они считаются изомерами особого типа, называемыми стереоизомерами . Существует особый вид стереоизомеров, называемых энантиомерами , которые являются зеркальными отражениями друг друга, но не накладываются друг на друга. Это означает, что как бы вы ни поворачивали их в пространстве, вы никогда не сможете поставить их друг на друга и получить одно и то же соединение. Одним из примеров является 2-бутанол , который можно изобразить в виде пары энантиомеров (рис.5.3). Рисунок 5.3: Энантиомеры 2-бутанола. Энантиомеры показаны в трехмерной структурной формуле на верхней диаграмме и в модели шара и стержня на нижней диаграмме. (наверх) энантиомеры обладают свойством c гиральности . Хиральность — это термин, который дается объектам, которые являются зеркальными отражениями, но не накладываются друг на друга. Рисунок 5.4: Природа хиральности. Углерод становится хиральным, когда с ним связаны четыре разных заместителя. Как бы вы ни вращали молекулу слева, вы не можете наложить ее на молекулу справа. Источник: Хиральность руками.jpg: Неизвестная производная работа: — πϵρ ήλιο ℗ — Хиральность руками. Стереоизомеры, не являющиеся энантиомерами, такие как глюкоза и галактоза, показанные выше, до , имеют хиральные центры и не накладываются друг на друга, но они не являются зеркальным отображением друг друга.Только стереоизомеры, которые также являются зеркальными отражениями и не накладываются друг на друга, называются энантиомерами. Энантиомеры очень трудно отделить друг от друга. Они почти идентичны по своим физическим и химическим свойствам. У них одинаковая молекулярная масса, одинаковая полярность, одинаковые температуры плавления и кипения и т. д. На самом деле энантиомеры настолько похожи, что даже имеют одно и то же название! На рис. 5.3 показаны два энантиомера 2-бутанола. Обе молекулы представляют собой 2-бутанол. Но они 90 513, а не 90 524 – точно такая же молекула, точно так же, как ваш левый ботинок не 90 513 в точности 90 524 такой же, как ваш правый.Они являются несовместимыми зеркальными отображениями друг друга. Как мы сообщаем об этой разнице? Одно небольшое различие между энантиомерами заключается в направлении, в котором поляризованный свет будет вращаться, когда попадает на молекулу. Таким образом, для описания абсолютной конфигурации требуется другая система. Система приоритетов Кана-Ингольда-Прелога (CIP) была разработана для определения абсолютной стереоконфигурации энантиомеров как зловещей (S) или прямой (R). В этой системе группам, присоединенным к хиральному углероду, отдается приоритет в зависимости от их атомного номера ( Z ).Атомы с более высоким атомным номером (больше протонов) имеют более высокий приоритет (т. е. S > P > O > N > C > H). Для определения стереохимии поместите группу с самым низким приоритетом от себя так, чтобы остальные три группы были обращены к вам. Назначить приоритет остальным группам. Правила этой системы стереохимической номенклатуры на первый взгляд довольно просты. В качестве первого примера мы будем использовать простой трехуглеродный сахарный глицериновый альдегид.Попробуйте сделать модель стереоизомера глицеральдегида, показанную ниже. Если у вас нет набора для химического моделирования, простой альтернативой являются зубочистки и леденцы. Убедитесь, что вы делаете правильный энантиомер! Первое, что мы должны сделать, это присвоить приоритет каждому из четырех заместителей, связанных с хиральным углеродом . В этой номенклатурной системе приоритеты основаны на атомном номере, причем более высокие атомные номера имеют более высокий приоритет.Сначала рассмотрим атомы, непосредственно связанные с хиральным углеродом: это H, O (в гидроксиле), C (в альдегиде) и C (в группе CH 2 OH). Два приоритета просты: водород с атомным номером 1 является самым низким (№4) приоритетом, а гидроксильный кислород с атомным номером 8 имеет приоритет №1. Затем мы обводим круг, определяемый группами приоритетов №1, №2 и №3, в порядке возрастания. В нашем примере с глицеральдегидом этот круг расположен по часовой стрелке, что говорит нам о том, что этот углерод имеет конфигурацию «R» и что эта молекула представляет собой (R)-глицеральдегид.Для (S)-глицеральдегида круг, описанный приоритетными группами № 1, № 2 и № 3, направлен против часовой стрелки (но сначала мы должны перевернуть молекулу так, чтобы буква Н указывала в плоскость страницы) . В случае 2-бутанола (рис. 5.5) легко определить первый и четвертый приоритеты. -OH имеет первый приоритет, а -H — четвертый приоритет. Как вы назначаете 2-й и 3-й приоритет, поскольку оба этих атома являются углеродом? Если приоритет для прикрепленного атома одинаков, вам нужно посмотреть на следующий уровень и оценить приоритет там.Для 2-бутанола одна группа – это -CH 3 , а другая – это -CH 2 CH 3 . В первой ситуации, если мы посмотрим на следующий уровень, этот углерод связан с тремя другими атомами водорода (все они имеют очень низкий приоритет). Во второй ситуации углерод связан с двумя атомами водорода и одним углеродом. Поскольку C имеет более высокий приоритет, чем H, группа -CH 2 CH 3 будет иметь более высокий приоритет, чем группа -CH 3 . Когда всем группам будет присвоен приоритет, вы сможете определить, в каком направлении он будет двигаться.Если это в направлении по часовой стрелке, молекуле дается обозначение «R». Рисунок 5.5: Стереохимия 2-бутанола. Систему приоритетов CIP можно использовать для определения абсолютной стереоконформации энантиомеров (наверх) Интересно, что энантиомеры имеют одинаковые физические свойства и точно такие же химические свойства, , за исключением , когда они реагируют с другими хиральными молекулами.Таким образом, хиральные молекулы имеют потенциально радикальные различия в физиологии и медицине. Например, в 1960-х годах в Западной Европе для облегчения утреннего недомогания у беременных женщин широко прописывался препарат под названием талидомид. Талидомид ранее использовался в других странах в качестве антидепрессанта и считался безопасным и эффективным. Однако вскоре врачи поняли, что что-то пошло не так: многие дети, рожденные женщинами, принимавшими талидомид во время беременности, страдали тяжелыми врожденными дефектами. B a by родился от матери, принимавшей талидомид во время беременности. Позднее исследователи поняли, что проблема заключалась в том, что талидомид поставлялся в виде смеси двух различных изомерных форм, называемой рацемической смесью . Один из изомеров является эффективным лекарством, а другой вызывает побочные эффекты. Обе изомерные формы имеют одинаковую молекулярную формулу и одинаковую связь между атомами, поэтому они не являются просто структурными изомерами.Они отличаются расположением в трехмерном пространстве около одного тетраэдрического хирального углерода. Таким образом, эти две формы талидомида представляют собой энантиомеров . Обратите внимание, что рассматриваемый углерод имеет четыре разных заместителя (два из них просто связаны кольцевой структурой). Тетраэдрические атомы углерода с четырьмя различными группами заместителей называются стереоцентрами . Глядя на структуру того, что мы называем двумя изомерами талидомида, вы можете быть не совсем уверены, что на самом деле это две разные молекулы.Чтобы убедиться, что они действительно разные, давайте создадим обобщенную картину тетраэдрического углеродного стереоцентра с четырьмя заместителями, обозначенными R 1 -R 4 . Два стереоизомера нашей упрощенной модели выглядят так: Если вы внимательно посмотрите на рисунок выше, то заметите, что молекула А и молекула В являются зеркальными отражениями друг друга (линия, обозначенная буквой «σ», представляет собой зеркальную плоскость). Более того, они не накладываются друг на друга : если мы возьмем молекулу А, перевернем ее и поместим рядом с молекулой В, мы увидим, что две структуры не могут быть наложены друг на друга. Если вы сделаете модели двух стереоизомеров талидомида и проделаете то же самое, вы увидите, что они тоже являются зеркальными отображениями и не могут быть наложены друг на друга (это поможет взглянуть на цветную версию рисунка ниже). Талидомид представляет собой хиральную молекулу . Вот еще несколько примеров хиральных молекул, которые существуют в виде пар энантиомеров. В каждом из этих примеров имеется единственный стереоцентр, указанный стрелкой.(Многие молекулы имеют более одного стереоцентра, но до этого мы доберемся чуть позже!) Вот несколько примеров молекул, которые ахиральны (не хиральны). Обратите внимание, что ни у одной из этих молекул нет стереоцентра (атома, связанного с четырьмя разными заместителями). При оценке молекулы на хиральность важно понимать, что использование штрихового/сплошного клина не обязательно означает, что молекула является хиральной. Другие элементы помимо углерода могут быть стереоцентрами. Фосфорный центр иона фосфата и органических эфиров фосфорной кислоты, например, имеет тетраэдрическую форму и, таким образом, потенциально является стереоцентром. Проблемы с визуализацией хиральности и энантиомеров? Может быть полезно посмотреть это видеоурок (наверх) Талидомид, который использовался в 1960-х годах для лечения депрессии и утренней тошноты, продавался в виде смеси 50:50 энантиомеров R и S – это называется рацемической смесью . Проблема с рацемическим талидомидом, как мы узнали выше, заключается в том, что только энантиомер R является эффективным лекарством, тогда как энантиомер S вызывает мутации у развивающегося плода. Каким образом такая, казалось бы, тривиальная структурная вариация приводит к таким драматическим (и в данном случае трагическим) различиям в биологической активности? Практически все лекарства работают, так или иначе взаимодействуя с важными белками в наших клетках: они могут связываться с белками болевых рецепторов, чтобы, например, блокировать передачу болевых сигналов, или закупоривать активный центр фермента, который участвует в синтезе боли. холестерин.Белки представляют собой хиральные молекулы и очень чувствительны к стереохимии: так же, как правая перчатка не налезет на левую руку, белок, способный прочно связываться с ( R )-талидомидом, может вообще плохо связываться. Вместо этого кажется, что ( S )-талидомид каким-то образом взаимодействует с белком, участвующим в развитии растущего плода, в конечном итоге вызывая наблюдаемые врожденные дефекты. Рисунок 5.5. Сайты связывания лекарств на белках стереоспецифичны. Источник: www.kshitij-iitjee.com/Study/Chemistry/Part2/Chapter3/109.jpg Болеутоляющее средство ибупрофен, отпускаемое без рецепта, в настоящее время продается в виде рацемической смеси, но эффективен только энантиомер S . К счастью, энантиомер R не вызывает каких-либо опасных побочных эффектов, хотя его присутствие, по-видимому, увеличивает время, необходимое для того, чтобы ( S )-ибупрофен начал действовать. С помощью вашего инструктора вы можете лично убедиться в биологической важности стереоизомерии. Два энантиомера по-разному взаимодействуют с белками обонятельных рецепторов в вашем носу, генерируя передачу различных химических сигналов в обонятельный центр вашего мозга. (наверх) Количество известных органических соединений довольно велико. На самом деле органических соединений известно во много раз больше, чем всех других (неорганических) соединений, открытых до сих пор, всего около 7 миллионов органических соединений. К счастью, органические химические вещества состоят из относительно небольшого числа одинаковых частей, объединенных по-разному, что позволяет нам предсказать, как может реагировать соединение, которое мы никогда раньше не видели, путем сравнения того, как другие молекулы, содержащие те же самые типы частей, реагируют. Эти части органических молекул называются функциональными группами и состоят из определенных моделей связи с атомами, наиболее часто встречающимися в органических молекулах (C, H, O, N, S и P). Идентификация функциональных групп и способность прогнозировать реакционную способность на основе свойств функциональных групп является одним из краеугольных камней органической химии. Функциональные группы представляют собой определенные атомы, ионы или группы атомов, обладающие постоянными свойствами.Функциональная группа составляет часть большей молекулы. Например, -ОН, гидроксильная группа, характерная для спиртов, представляет собой кислород с присоединенным водородом. Его можно найти на любом количестве различных молекул. Точно так же, как элементы обладают отличительными свойствами, функциональные группы имеют характерный химический состав. Функциональная группа -ОН на одной молекуле будет иметь тенденцию реагировать аналогично, хотя, возможно, и не идентично, с -ОН на другой молекуле. Органические реакции обычно происходят в функциональной группе, поэтому изучение реакционной способности функциональных групп подготовит вас к пониманию многих других аспектов органической химии. Функциональные группы — это структурные единицы в органических соединениях, которые определяются определенными связями между определенными атомами. Структура капсаицина, соединения, обсуждавшегося в начале этой главы, включает в себя несколько функциональных групп, обозначенных на рисунке ниже и поясняемых в этом разделе. По мере нашего продвижения в изучении органической химии будет чрезвычайно важно уметь быстро распознавать наиболее распространенные функциональные группы, поскольку они являются ключевыми структурными элементами, определяющими реакцию органических молекул .На данный момент мы будем беспокоиться только о рисовании и распознавании каждой функциональной группы, как показано Льюисом и линейными структурами. (наверх) «По умолчанию» в органической химии (по сути, отсутствие каких-либо функциональных групп) дается термин алкан , характеризующийся одинарными связями между углеродом и углеродом, или между углеродом и водородом.Метан, CH 4 , — это природный газ, который вы можете сжигать в своей печи. Октан, C 8 H 18 , является компонентом бензина. Алкены (иногда называемые олефинами) имеют двойные углерод-углеродные связи, а алкины имеют тройные углерод-углеродные связи. В главе 6 мы изучим природу связи алкенов и алкинов и узнаем, что связь в алкенах является тригонально-плоской, а в алкинах — линейной. Кроме того, многие алкены могут принимать две геометрические формы: цис или транс . цис и транс формы данного алкена представляют собой разные изомеры с разными физическими свойствами, потому что, как мы узнаем в главе 6, существует очень высокий энергетический барьер для вращения вокруг двойной связи. В приведенном ниже примере очевидна разница между цис- и транс- алкенами. Алканы, алкены и алкины классифицируются как углеводороды , поскольку они состоят исключительно из атомов углерода и водорода.Алканы называются насыщенными углеводородами , потому что углероды связаны с максимально возможным числом атомов водорода — другими словами, они насыщены атомами водорода. Углерод с двойной и тройной связью в алкенах и алкинах имеет меньше атомов водорода, связанных с ними, поэтому они называются ненасыщенными углеводородами . Как мы увидим в следующей главе, водород может присоединяться к двойным и тройным связям в ходе реакции, называемой «гидрированием». (наверх) Примерами ароматической группы являются бензол (который раньше был широко используемым растворителем в органической лаборатории, но который оказался канцерогенным) и нафталин, соединение с характерным запахом «нафталина». Когда углерод алкана связан с одним или несколькими атомами галогена, группа обозначается как алкилгалогенид или галогеналкан .Хлороформ — полезный растворитель в лаборатории и один из первых анестетиков, использовавшихся в хирургии. Хлордифторметан использовался в качестве хладагента и в аэрозольных распылителях до конца двадцатого века, но его использование было прекращено после того, как было обнаружено, что он оказывает вредное воздействие на озоновый слой. Бромэтан представляет собой простой алкилгалогенид, часто используемый в органическом синтезе. Алкилгалогенидные группы довольно редко встречаются в биомолекулах. В функциональной группе спирта углерод связан одинарной связью с группой ОН (группа ОН, когда она является частью более крупной молекулы, называется гидроксильной группой ). Обратите внимание, что определение фенола гласит, что гидроксильный кислород должен быть непосредственно присоединен к одному из атомов углерода ароматического кольца. Таким образом, указанное ниже соединение представляет собой , а не фенол — это первичный спирт. Различие важно, потому что, как мы увидим позже, существует значительная разница в реакционной способности спиртов и фенолов (наверх) В функциональной группе простого эфира кислород связан с двумя атомами углерода. (наверх) Амины характеризуются атомами азота с одинарными связями с водородом и углеродом.Так же, как существуют первичные, вторичные и третичные спирты, существуют первичные, вторичные и третичные амины. Аммиак — это особый случай, в котором нет атомов углерода. Одним из наиболее важных свойств аминов является то, что они являются основными и легко протонируются с образованием катионов аммония. В случае, когда азот имеет четыре связи с углеродом (что несколько необычно для биомолекул), его называют ионом четвертичного аммония. Примечание. Не смущайтесь тем, как термины «первичный», «вторичный» и «третичный» применяются к спиртам и аминам — определения разные.В спиртах важно, со сколькими другими атомами углерода связан углерод спирта , а в аминах важно, со сколькими атомами углерода связан азот . (наверх) Фосфат и его производные функциональные группы широко распространены в биомолекулах. Фосфат, связанный с одной органической группой, называется фосфатным эфиром ; когда он имеет две связи с органическими группами, он называется фосфатным диэфиром.Связь между двумя фосфатами создает ангидрид фосфата. Существует ряд функциональных групп, содержащих двойную углерод-кислородную связь, которую обычно называют карбонилом . (наверх) Когда карбонильный углерод связан с одной стороны с углеродом (или водородом), а с другой стороны с кислородом, азотом или серой, функциональная группа считается одним из «производных карбоновой кислоты», обозначение, которое описывает набор связанных функциональных групп.Основным членом этого семейства является функциональная группа карбоновой кислоты , в которой карбонил связан с гидроксильной группой. Наконец, нитрил группа характеризуется тройной связью углерод-азот, как показано в структуре ацетонитрила. Одно соединение часто содержит несколько функциональных групп, особенно в биологической органической химии. Молекулы сахара с шестью атомами углерода, глюкоза и фруктоза, например, содержат альдегидные и кетоновые группы соответственно, и обе содержат пять спиртовых групп. Гормон тестостерон, аминокислота фенилаланин и метаболит гликолиза дигидроксиацетонфосфат содержат несколько функциональных групп, как указано ниже. Хотя это и не полный список, этот раздел охватывает большинство важных функциональных групп, с которыми мы столкнемся в биохимии.В Таблице 5.2 представлены сводные данные обо всех группах, перечисленных в этом разделе. Определите функциональные группы (кроме алканов) в следующих органических соединениях. Укажите, являются ли спирты и амины первичными, вторичными или третичными. Нарисуйте по одному примеру каждого соединения, соответствующего описанию ниже, используя линейные структуры. а) соединение с молекулярной формулой C 6 H 11 NO, которое включает функциональные группы алкена, вторичного амина и первичного спирта b) ион с молекулярной формулой C 3 H 5 O 6 P 2-, который включает альдегидные, вторичные спиртовые и фосфатные функциональные группы. c) Соединение с молекулярной формулой C 6 H 9 NO, имеющее амидную функциональную группу, но не имеющее , а не , алкеновую группу. (наверх) Международный союз теоретической и прикладной химии (IUPAC, обычно произносится как глаз -you-pack ) разработал систему для обозначения органических соединений. Название органического соединения обычно начинается с определения того, что называется «исходной цепью» , которая представляет собой самую длинную прямую цепь атомов углерода.Мы начнем с простейших структур алканов с прямой цепью. CH 4 называется метан , а C 2 H 6 этан . В приведенной ниже таблице продолжаются названия более длинных алканов с прямой цепью: обязательно запомните их, поскольку они являются основой для остальной части номенклатурной системы ИЮПАК (а также широко используются для обозначения биомолекул). 1 углерод: метан 2 атома углерода: этан 3 атома углерода: пропан 4 атома углерода: бутан 5 атомов углерода: пентан 6 атомов углерода: гексан 7 атомов углерода: гептан 8 атомов углерода: октан 9 атомов углерода: нонан 10 атомов углерода: декан Заместители, ответвляющиеся от основной исходной цепи, расположены по числу атомов углерода, при этом используются наименьшие возможные числа (например, обратите внимание ниже, что соединение слева называется 1-хлорбутан, , а не , 4-хлорбутан). Другие распространенные названия углеводородных заместителей включают изопропил, трет--бутил и фенил . Обратите внимание, что в приведенном ниже примере «этильная группа» (синяя) не рассматривается как заместитель, а включается как часть исходной цепи, а метильная группа рассматривается как заместитель.Название ИЮПАК для углеводородов с прямой цепью всегда основано на максимально длинной исходной цепи , которая в данном случае состоит из четырех атомов углерода, а не из трех. Циклические алканы называются циклопропан, циклобутан, циклопентан, циклогексан и т. д.: В случае нескольких заместителей используются префиксы ди , три и тетра . Функциональные группы имеют характерные суффиксы.Спирты, например, имеют « ол », добавленное к названию исходной цепи вместе с номером, обозначающим расположение гидроксильной группы. Кетоны обозначаются как « один ». Алкены обозначаются окончанием «ен» и, при необходимости, указываются расположение и геометрия двойной связи. Соединения с несколькими двойными связями называются диенами, триенами и т. д. Некоторые группы могут присутствовать только на концевом атоме углерода, поэтому порядковый номер не требуется: альдегиды оканчиваются на «al», карбоновые кислоты — на «oic acid», а карбоксилаты — на «oate». Эфиры и сульфиды обозначаются двумя группами по обе стороны от кислорода или серы. Если амид имеет незамещенную группу –NH 2 , суффикс будет просто «амид». Для сложных эфиров используется суффикс «оат». Группа, присоединенная к кислороду, названа первой. Все примеры, которые мы видели до сих пор, были простыми в том смысле, что в каждой молекуле присутствовала только одна функциональная группа. Конечно, в системе ИЮПАК гораздо больше правил, и, как вы можете себе представить, именование ИЮПАК больших молекул с несколькими функциональными группами, кольцевыми структурами и заместителями может очень быстро стать очень громоздким.Незаконный наркотик кокаин, например, имеет название IUPAC «метил (1 R , 2 R , 3 S , 5 S )-3-(бензоилокси)-8-метил-8-азабицикло[ 3.2. Вы можете понять, почему система ИЮПАК мало используется в биохимии — молекулы слишком большие и сложные. Еще одна сложность заключается в том, что даже вне биологического контекста многие простые органические молекулы почти повсеместно известны под их «общим названием», а не под названием ИЮПАК.Соединения уксусная кислота, хлороформ и ацетон являются лишь несколькими примерами. В биохимии обычно используются несистематические названия (такие как «кокаин», «капсаицин», «пируват» или «аскорбиновая кислота»), и когда используется систематическая номенклатура, она часто специфична для класса рассматриваемой молекулы: разные системы имеют эволюционировали, например, для жиров и для углеводов. В этом тексте мы не будем слишком подробно сосредотачиваться на номенклатуре ИЮПАК или какой-либо другой системе номенклатуры, но если вы предпримете более углубленное изучение органической или биологической химии, от вас могут ожидать более подробного изучения одной или нескольких систем наименования. Материалы главы 5 были адаптированы и изменены из следующих ресурсов Creative Commons, если не указано иное: 1. Викиучебники. (2015) Органическая химия. Доступно по ссылке: https://en.wikibooks.org/wiki/Organic_Chemistry. 2. Кларк Дж. (2014) Как рисовать органические молекулы. Доступно по адресу: http://chem.libretexts.org/Core/Organic_Chemistry/Fundamentals/How_to_Draw_Organic_Molecules 3.Содерберг, Т. (2016). Органическая химия с биологическим акцентом. Опубликовано Creative Commons by-nc-sa 3.0. 4. Анонимно. (2012) Введение в химию: общая, органическая и биологическая (V1.0). Опубликовано Creative Commons by-nc-sa 3.0. Доступно по адресу: http://2012books.lardbucket.org/books/introduction-to-chemistry-general-organic-and-biological/index.html Область микроэлектроники играет огромную роль в нашей жизни.Он отвечает за крошечные мозги — микрочипы — которые питают большинство электронных устройств в наши дни: знакомые технологии, такие как смартфоны и телевизоры, важное медицинское оборудование, от слуховых аппаратов до МРТ, и даже бытовые приборы, такие как микроволновые печи и термостаты. Наша зависимость от микрочипов теперь подчеркивается дефицитом, останавливающим производство автомобилей и сотовых телефонов. Из соображений снабжения и безопасности растет интерес к производству большего количества полупроводников и микрочипов в США.S. Благодаря своим передовым объектам, стратегическим партнерствам, образовательным программам и исследовательским возможностям Университет штата Аризона позиционирует Аризону как идеальный центр для этой растущей отрасли. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ: Как ASU и отраслевые партнеры развивают полупроводниковый бизнес в Аризоне. В основном полупроводники используются для изготовления микрочипов, микрочипы — это физические устройства, которые можно держать на ладони, а микроэлектроника относится к области или отрасли в целом. Полупроводники — это материал, обладающий свойствами как проводников, таких как алюминий, так и изоляторов, таких как стекло. Полупроводники, такие как кремний, позволили нам сделать электронные устройства меньше, быстрее и надежнее. Обычно они поступают на фабрики в виде тонких плоских вафель, похожих на обеденную тарелку. «Когда у вас есть много разных слоев полупроводников в различных структурах, вы получаете такие устройства, как транзисторы, а устройства, соединенные вместе, становятся микрочипами», — говорит Закари Холман, доцент Школы электротехники, вычислительной техники и энергетики. В настоящее время люди часто используют термин «полупроводники» как сокращение для микросхем и других устройств, изготовленных из полупроводниковых материалов. Закари Холман отражается на кремниевой пластине в здании завода макротехнологий АГУ в Исследовательском парке АГУ. «Микро» означает микрометр, что составляет одну миллионную часть метра. (В среднем человеческий волос имеет толщину около 60 микрометров.) Микрочипы сами по себе не такие крошечные, но если вы поместите один из них под микроскоп, он будет иметь особенности и области в микрометровом масштабе.Сегодня некоторые чипы имеют характеристики даже в нанометровом масштабе. Нанометр — это одна миллиардная часть метра. В 2021 году индустрия высоких технологий приветствовала увеличение производительности суперкомпьютерного чипа размером с iPad, а также создание самой маленькой в мире однокристальной системы размером с пылевого клеща. Несмотря на огромную разницу в размерах, оба являются микроэлектронными устройствами, потому что оба имеют характеристики микрометрового масштаба. Микрочипы, используемые в повседневных компьютерах и смартфонах, имеют размер от ногтя до почтовой марки. Производственный процесс стал намного сложнее с тех пор, как в 1959 году был представлен первый микрочип . Все начинается с проектирования: инженеры используют программное обеспечение для проектирования структуры микрочипа, подобно архитектору, создающему план дома. Проект отправляется на производственный завод — часто называемый для краткости фабрикой, а иногда и литейным цехом, — который берет базовую полупроводниковую пластину и покрывает ее различными материалами, такими как металлы, оксиды и другие полупроводники. «Они также выполняют этапы формирования паттерна, которые аналогичны процессам экспонирования пленки старой камеры. После нанесения слоя пластина попадает в химическую ванну или в газовую среду, которая удаляет материал из выбранных областей, в то время как другие области остаются защищенными», — говорит Холман. Эти этапы формирования рисунка вытравливают многослойную пластину, чтобы она соответствовала исходному дизайну. В одной вафле много чипсов, поэтому, когда все ее слои готовы, фабрика «нарезает» ее кубиками, отделяя отдельные чипсы, как ломтики листового пирога.Последний шаг — упаковать чипы, прикрепив их к печатным платам, тем зеленым пластиковым панелям, которые вы найдете внутри электроники. Фабрика отправляет окончательные творения другим производителям, которые используют их для производства таких продуктов, как автомобили, телевизоры и мобильные телефоны. Графика Ширин Дулинг Производители из технологических, автомобильных и других отраслей промышленности ожидали, что их продажи снизятся во время пандемии COVID-19, поэтому они заказали меньше чипов у фабрик.Однако оптимизм по поводу пандемии и доступность вакцины летом 2021 года привели к увеличению потребительских расходов. Теперь фабрики наводнены дополнительными запросами, так как многие отрасли пытаются заказать больше микросхем одновременно. «Быстро увеличить поставки сложно, потому что процесс изготовления чипа занимает месяцы, — говорит Холман. «Сами фабрики очень сложные и дорогие. От начала строительства до запуска фабрики обычно проходит три с лишним года. Согласно отчету Ассоциации полупроводниковой промышленности за 2020 год, в настоящее время большая часть производства полупроводников и микросхем осуществляется за границей, при этом на США приходится чуть более 12% мирового производства. Строительство дополнительных заводов в США помогло бы уменьшить аналогичную глобальную нехватку микросхем в будущем, увеличив общие производственные мощности в мире. Если американские фабрики будут отдавать приоритет заказам от американских потребителей, это также может помочь защитить нашу внутреннюю цепочку поставок. «Подумайте о U.Компьютерные системы Министерства обороны США, системы связи, транспортные системы — все они полагаются на микроэлектронные устройства для правильной работы», — говорит Надя Блисс, исполнительный директор Глобальной инициативы безопасности ASU. Эти устройства являются неотъемлемой частью не только военных операций, но и критически важных секторов, таких как здравоохранение и экономика. По словам Блисса, если какой-либо из них будет скомпрометирован, последствия также повлияют на национальную безопасность. В недавнем отчете Комиссия национальной безопасности по искусственному интеллекту отметила необходимость разработки устойчивой цепочки поставок микрочипов и полупроводников в США.S., чтобы оставаться впереди на арене геополитических технологий. «Увеличение разработки и производства этих технологий в США устранит серьезную уязвимость национальной безопасности — враждебная страна может вмешаться в технологию в какой-то момент в цепочке поставок», — говорит Блисс. Центр передовой электроники и фотоники предоставляет компаниям доступ к экспертам и оборудованию ASU, чтобы они могли разрабатывать новые материалы, методы и конструкции для микроэлектроники в промышленных масштабах.Фото Andy DeLisle Образованная рабочая сила является ключом к тому, чтобы Аризона стала домом для производства микроэлектроники. В то время как ASU готовит первоклассных выпускников инженерных специальностей в течение 65 лет, инженерные школы Айры А. Фултона в настоящее время инвестируют в кадровый резерв специально для микроэлектроники, создавая свою новую Школу производственных систем и сетей. «С появлением новых производственных мощностей в Долине от Intel и Taiwan Semiconductor Manufacturing Corp., мы ожидаем более 10 000 новых рабочих мест», — говорит Кевин Рейнхарт, директор по управлению исследовательскими проектами в Knowledge Enterprise ASU. Эти и многие другие компании могут воспользоваться исследовательским опытом и специализированным оборудованием ASU на объектах ASU, таких как Центр передовой электроники и фотоники, ASU NanoFab и Центр материалов Айринга. «На объекте MacroTechnology Works ASU у нас есть 50 000 квадратных футов чистых помещений, — говорит Рейнхарт.«С точки зрения университета, мы очень уникальны в этом аспекте». Эти помещения также дают возможность студентам ASU получить важный практический опыт, который нужен работодателям. (Узнайте, как ваша компания может стать партнером ASU.) Кроме того, ASU будет использовать средства Инициативы новой экономики Аризоны для создания пяти научно-технических центров, два из которых будут способствовать микроэлектронной промышленности штата — Energy Materials and Devices. Центр и Центр передового производства. Университет стремится увеличить финансирование микроэлектроники в Аризоне. ASU сыграла ведущую роль в добавлении поддержки отечественной микроэлектронной промышленности — так называемого Закона о чипах для Америки — в Закон о разрешении на национальную оборону 2021 года. Вода является важной частью процесса производства чипов.Между добавлением каждого тонкого слоя вафли фабрика должна смывать все остатки, чтобы никакие бактерии или частицы не препятствовали микроскопическим путям чипсов. Но чтобы смыть каждую крупинку мусора, сама вода должна быть очень чистой — без минералов, без органических веществ. Фабрики создают для этой цели так называемую сверхчистую воду, и она настолько чиста, что ее пить людям на самом деле небезопасно. При производстве сверхчистой воды и мытье вафель образуется много остаточных сточных вод.Так зачем строить больше фабрик в пустыне Аризоны, где мало воды? «Важным вопросом является не «Достаточно ли у нас воды?» но «Как мы инвестируем нашу ограниченную воду?», — говорит Дэйв Уайт, директор Глобального института устойчивого развития и инноваций и профессор Школы общественных ресурсов и развития. Производство приносит государству множество преимуществ, включая квалифицированные, высокооплачиваемые рабочие места и поставку продукции, пользующейся высоким спросом. Но государство также получает выгоду от производственных предприятий — в Аризоне есть высокообразованная рабочая сила и низкий риск экологических опасностей, таких как землетрясения или ураганы. Фабрики в Аризоне должны быть инновационными и эффективными при использовании и повторном использовании воды, но это также верно для хлопковых полей и домов, говорит Уайт. Партнерство Intel с городом Чендлер — яркий пример того, как фабрики могут добиться этого.Там они берут сточные воды с заводов Intel и закачивают их обратно в землю. По мере того, как она фильтруется через землю, вода естественным образом очищается, а также подпитывает водоносный горизонт. Аспирант Дэвид Киспе работает в здании MacroTechnology Works в Исследовательском парке ASU. Говорите о будущем микрочипов, и вы обязательно столкнетесь с законом Мура.Это скорее идея, чем проверенная научная теория. По сути, в нем говорится, что вычислительная мощность микрочипов удваивается (а их размер уменьшается вдвое) примерно каждые два года. Это означает, что микрочипы достигнут предела, после которого их уже нельзя будет улучшить. Холман сравнивает закон Мура со сценой из «Spinal Tap», где рок-музыкант демонстрирует свой усилитель, повышающий мощность до 11 вместо обычных 10. меньше в двух измерениях, и эта ручка уже повернута до 11.Вот почему в будущем технические инновации в микроэлектронике будут строиться в трех измерениях», — говорит он. Объединение различных функций, которые обычно существуют на отдельных чипах, таких как звук, дисплей, вычисления и память, для создания универсального чипа — это еще одно новое направление для микроэлектронных технологий, добавляет он. Кроме того, микроэлектроника будет играть решающую роль в переходе на возобновляемые источники энергии. По данным Управления энергетической информации США, только 12.В 2020 году 6% нашего национального потребления энергии приходилось на возобновляемые источники. «Как нам приблизиться к ста процентам? Что ж, вам нужно гораздо больше контролировать, где электричество вырабатывается, где оно потребляется и хранится, а также когда», — говорит Холман. Электроника, которая может обмениваться информацией и распределять энергию по сети, позволит нам получать энергию из многих возобновляемых источников и знать, сколько энергии доступно из источника в любой момент времени. Ежегодно около 300 солнечных дней в году, в сочетании с возможностями исследований, разработок и производства в области микроэлектроники, Аризона является идеальным местом для поиска технологических решений, необходимых для устойчивого и передового будущего. Специалист по коммуникациям, ASU Knowledge Enterprise 480-727-5616
mkass@asu.8
7 1 8 90 9
CH 7
8
 Для следующих соединений укажите химическую формулу и сокращенную структуру:
Для следующих соединений укажите химическую формулу и сокращенную структуру: Глава 5 – Введение в органическую химию – Химия
Глава 5 – Введение в органическую химию  Для интерактивного PDF требуется Adobe Reader для полной функциональности.
Для интерактивного PDF требуется Adobe Reader для полной функциональности. 5 Важность хиральности во взаимодействиях белков 5.6 Распознавание общих органических функциональных групп Алканы Алкены и алкины Ароматические соединения Алкилгалогениды Спирты, фенолы и тиолы Эфиры и сульфиды Амины Органические фосфаты Альдегиды и кетоны Карбоновые кислоты и их производные Нитрилы Практика распознавания функциональных групп в молекулах 5.7 Краткий обзор органической номенклатуры 5.8 Каталожные номера
5 Важность хиральности во взаимодействиях белков 5.6 Распознавание общих органических функциональных групп Алканы Алкены и алкины Ароматические соединения Алкилгалогениды Спирты, фенолы и тиолы Эфиры и сульфиды Амины Органические фосфаты Альдегиды и кетоны Карбоновые кислоты и их производные Нитрилы Практика распознавания функциональных групп в молекулах 5.7 Краткий обзор органической номенклатуры 5.8 Каталожные номера
5.1 Боль, удовольствие и органическая химия  flickr.com/photos/jeffreyww/)
flickr.com/photos/jeffreyww/)
 В 2002 году ученым удалось вставить небольшой сегмент (чувствительного к капсаицину) гена крысиного рецептора TrpV1 в нечувствительную куриную версию гена, и полученный химерный (смешанного вида) рецептор был чувствителен к капсаицину ( Cell ). 2002 , 108 , 421).
В 2002 году ученым удалось вставить небольшой сегмент (чувствительного к капсаицину) гена крысиного рецептора TrpV1 в нечувствительную куриную версию гена, и полученный химерный (смешанного вида) рецептор был чувствителен к капсаицину ( Cell ). 2002 , 108 , 421). Термин «органический» от греческого organikos применялся к этим соединениям, и считалось, что они содержат некую «жизненную силу», которая отличает их от «неорганических» соединений, таких как минералы, соли и металлы. , и что позволило им работать на совершенно другом наборе химических принципов.Как иначе, кроме как под действием «жизненной силы», такая небольшая подгруппа элементов могла объединиться в соединения с таким множеством различных свойств?
Термин «органический» от греческого organikos применялся к этим соединениям, и считалось, что они содержат некую «жизненную силу», которая отличает их от «неорганических» соединений, таких как минералы, соли и металлы. , и что позволило им работать на совершенно другом наборе химических принципов.Как иначе, кроме как под действием «жизненной силы», такая небольшая подгруппа элементов могла объединиться в соединения с таким множеством различных свойств?
 Хотя люди веками ели острый перец и продукты со вкусом ванили, мы только сейчас, в последние несколько десятилетий, начинаем понимать, как и почему один вызывает жгучую боль, а другой — чистое вкусовое удовольствие. Мы понимаем, что точное геометрическое расположение четырех элементов в капсаицине позволяет ему поместиться внутри связывающего кармана теплового рецептора TrpVI, но на сегодняшний день у нас еще нет подробного трехмерного изображения белка TrpVI, связанного с капсаицином.Мы также знаем, что различное расположение атомов углерода, водорода и кислорода в ванилине позволяет ему связываться со специфическими обонятельными рецепторами, но опять же, многое еще предстоит выяснить о том, как именно это происходит.
Хотя люди веками ели острый перец и продукты со вкусом ванили, мы только сейчас, в последние несколько десятилетий, начинаем понимать, как и почему один вызывает жгучую боль, а другой — чистое вкусовое удовольствие. Мы понимаем, что точное геометрическое расположение четырех элементов в капсаицине позволяет ему поместиться внутри связывающего кармана теплового рецептора TrpVI, но на сегодняшний день у нас еще нет подробного трехмерного изображения белка TrpVI, связанного с капсаицином.Мы также знаем, что различное расположение атомов углерода, водорода и кислорода в ванилине позволяет ему связываться со специфическими обонятельными рецепторами, но опять же, многое еще предстоит выяснить о том, как именно это происходит.
 Наконец, мы объединим все это с обзором структур наиболее важных классов биологических молекул — липидов, углеводов, белков и нуклеиновых кислот, — на которые мы будем постоянно ссылаться в оставшейся части книги.
Наконец, мы объединим все это с обзором структур наиболее важных классов биологических молекул — липидов, углеводов, белков и нуклеиновых кислот, — на которые мы будем постоянно ссылаться в оставшейся части книги.
5.2 Рисование органических молекул  Водород является исключением из правила октета, так как это самый маленький элемент, а его валентная оболочка заполнена двумя электронами.Таким образом, водород может образовывать одну связь с другим атомом. Сера и фосфор также могут иметь образцы связывания, которые являются исключениями из правила октета. Они оба имеют расширенную орбитальную связь с фосфором, который также обычно образует пять ковалентных связей, а сера способна образовывать четыре или шесть ковалентных связей. В таблице 5.1 представлено графическое представление этих шаблонов. Когда вы рисуете органические молекулы, важно обращать внимание на правила связывания, чтобы все атомы достигли предпочтительных состояний связывания.
Водород является исключением из правила октета, так как это самый маленький элемент, а его валентная оболочка заполнена двумя электронами.Таким образом, водород может образовывать одну связь с другим атомом. Сера и фосфор также могут иметь образцы связывания, которые являются исключениями из правила октета. Они оба имеют расширенную орбитальную связь с фосфором, который также обычно образует пять ковалентных связей, а сера способна образовывать четыре или шесть ковалентных связей. В таблице 5.1 представлено графическое представление этих шаблонов. Когда вы рисуете органические молекулы, важно обращать внимание на правила связывания, чтобы все атомы достигли предпочтительных состояний связывания. Из-за этой сложности органические соединения часто имеют более одного определенного структурного состояния, в котором они могут существовать, и нередко молекула может переходить из одного состояния в другое. Когда электроны в молекуле могут перемещаться из одной области молекулы в другую, создавая эти альтернативные структуры. Это определяется как резонанс, и состояния, возникающие в результате этих сдвигов, как резонансных структур . Обратите внимание, что резонансные структуры дают химикам более конкретное представление о молекулах.Однако настоящие молекулы не существуют в том или ином структурном состоянии. Вместо этого они существуют в более аморфном переходном состоянии, которое находится где-то посередине между всеми возможными комбинациями. Некоторые формы резонанса могут быть более стабильными, чем другие, и будут оказывать большее влияние на общую структуру молекулы, чем другие формы резонанса. Таким образом, нам нужен способ точно предсказать, какие резонансные структуры могут возникнуть внутри молекулы и какие состояния будут наиболее стабильными.
Из-за этой сложности органические соединения часто имеют более одного определенного структурного состояния, в котором они могут существовать, и нередко молекула может переходить из одного состояния в другое. Когда электроны в молекуле могут перемещаться из одной области молекулы в другую, создавая эти альтернативные структуры. Это определяется как резонанс, и состояния, возникающие в результате этих сдвигов, как резонансных структур . Обратите внимание, что резонансные структуры дают химикам более конкретное представление о молекулах.Однако настоящие молекулы не существуют в том или ином структурном состоянии. Вместо этого они существуют в более аморфном переходном состоянии, которое находится где-то посередине между всеми возможными комбинациями. Некоторые формы резонанса могут быть более стабильными, чем другие, и будут оказывать большее влияние на общую структуру молекулы, чем другие формы резонанса. Таким образом, нам нужен способ точно предсказать, какие резонансные структуры могут возникнуть внутри молекулы и какие состояния будут наиболее стабильными. Это можно сделать, используя метод формального начисления рисования структур Льюиса. Формальный заряд атома рассчитывается как количество валентных электронов атома минус количество электронов, которыми атом «владеет». Количество электронов, принадлежащих атому, можно рассчитать, добавив количество неподеленных электронов + половину количества общих электронов. Помните, что 2 e – являются общими для каждой линии, проведенной между двумя атомами (одна линия = 2 e – ).Например, если кислород связан с двумя другими атомами, мы могли бы рассчитать формальный заряд кислорода, вычитая количество электронов, «принадлежащих» кислороду, из числа электронов на его валентной оболочке:
Это можно сделать, используя метод формального начисления рисования структур Льюиса. Формальный заряд атома рассчитывается как количество валентных электронов атома минус количество электронов, которыми атом «владеет». Количество электронов, принадлежащих атому, можно рассчитать, добавив количество неподеленных электронов + половину количества общих электронов. Помните, что 2 e – являются общими для каждой линии, проведенной между двумя атомами (одна линия = 2 e – ).Например, если кислород связан с двумя другими атомами, мы могли бы рассчитать формальный заряд кислорода, вычитая количество электронов, «принадлежащих» кислороду, из числа электронов на его валентной оболочке:



 Если мы вычислим формальный заряд фосфора, мы увидим, что P имеет 5 валентностей e- за вычетом электронов неподеленной пары и половины электронов связанной пары. P не имеет неподеленных пар и имеет 10 электронов связанных пар. Таким образом, половина от 10 = 5, 5 – 5 = 0. Таким образом, P имеет формальный заряд, равный нулю. Поскольку три атома кислорода имеют заряд 1 – , а два других атома равны нулю, общий заряд молекулы равен 3 – . Завершенная структура Льюиса для фосфата должна выглядеть так:
Если мы вычислим формальный заряд фосфора, мы увидим, что P имеет 5 валентностей e- за вычетом электронов неподеленной пары и половины электронов связанной пары. P не имеет неподеленных пар и имеет 10 электронов связанных пар. Таким образом, половина от 10 = 5, 5 – 5 = 0. Таким образом, P имеет формальный заряд, равный нулю. Поскольку три атома кислорода имеют заряд 1 – , а два других атома равны нулю, общий заряд молекулы равен 3 – . Завершенная структура Льюиса для фосфата должна выглядеть так: Таким образом, мы можем показать структуру с положением двойной связи во всех других возможных конформациях:
Таким образом, мы можем показать структуру с положением двойной связи во всех других возможных конформациях:
5.3 Различные представления органических молекул Молекулярные формулы  Например, сахар глюкоза содержит 6 атомов углерода, 12 атомов водорода и 6 атомов кислорода. Тогда молекулярная формула будет записана как C 6 H 12 O 6 . По соглашению углерод указывается первым, водород вторым, за ним следуют кислород, азот, сера, фосфор и, наконец, любые галогены.Однако для органической химии молекулярные формулы не дают много информации. Они просто предоставляют количество атомов каждого типа, присутствующих в молекуле, но ничего не говорят вам о том, как атомы соединяются вместе в пространстве. Таким образом, молекулярные формулы очень редко используются в органической химии, поскольку они не дают полезной информации о связи в молекуле. Одно из немногих мест, где вы можете их встретить, это уравнения горения простых углеводородов, например:
Например, сахар глюкоза содержит 6 атомов углерода, 12 атомов водорода и 6 атомов кислорода. Тогда молекулярная формула будет записана как C 6 H 12 O 6 . По соглашению углерод указывается первым, водород вторым, за ним следуют кислород, азот, сера, фосфор и, наконец, любые галогены.Однако для органической химии молекулярные формулы не дают много информации. Они просто предоставляют количество атомов каждого типа, присутствующих в молекуле, но ничего не говорят вам о том, как атомы соединяются вместе в пространстве. Таким образом, молекулярные формулы очень редко используются в органической химии, поскольку они не дают полезной информации о связи в молекуле. Одно из немногих мест, где вы можете их встретить, это уравнения горения простых углеводородов, например: Однако для большинства биологически важных реакций форма молекулы обычно имеет решающее значение для функции молекулы, очень похожей на ключ, вставляемый в замок. Таким образом, порядок соединения становится очень важным. Например, C 5 H 12 , показанные в уравнении выше, могут быть связаны друг с другом более чем одним способом:
Однако для большинства биологически важных реакций форма молекулы обычно имеет решающее значение для функции молекулы, очень похожей на ключ, вставляемый в замок. Таким образом, порядок соединения становится очень важным. Например, C 5 H 12 , показанные в уравнении выше, могут быть связаны друг с другом более чем одним способом:
Структурные формулы и трехмерные модели 
 Наше моделирование VSEPR из главы 4 показало, что углерод принимает тетраэдрическое подтверждение, где каждый валентный угол равен 109 o . Молекула не плоская, в плоскости бумаги.Воспроизведите видео ниже, чтобы увидеть, как они выглядят как вращающиеся модели мяча и клюшки.
Наше моделирование VSEPR из главы 4 показало, что углерод принимает тетраэдрическое подтверждение, где каждый валентный угол равен 109 o . Молекула не плоская, в плоскости бумаги.Воспроизведите видео ниже, чтобы увидеть, как они выглядят как вращающиеся модели мяча и клюшки. Вы можете упростить — или сократить — формулу, написав, например, CH 3 или CH 2 вместо того, чтобы показывать все связи C-H. Например, этановая кислота (C 2 H 4 O 2 ) может отображаться в полностью выведенной форме, частично конденсированной форме и полностью конденсированной форме.
Вы можете упростить — или сократить — формулу, написав, например, CH 3 или CH 2 вместо того, чтобы показывать все связи C-H. Например, этановая кислота (C 2 H 4 O 2 ) может отображаться в полностью выведенной форме, частично конденсированной форме и полностью конденсированной форме. Глядя на положение первого атома углерода, видно, что три атома водорода и один атом углерода связаны с первым атомом углерода:
Глядя на положение первого атома углерода, видно, что три атома водорода и один атом углерода связаны с первым атомом углерода:


Чертежи сокращенных органических структур  Если мы просто хотим в целом сослаться на функциональную группу, не рисуя конкретную молекулу, например, мы можем использовать «группы R», чтобы сосредоточить внимание на интересующей группе:
Если мы просто хотим в целом сослаться на функциональную группу, не рисуя конкретную молекулу, например, мы можем использовать «группы R», чтобы сосредоточить внимание на интересующей группе:
5.4 Стереоизомеры, энантиомеры и хиральность  3, органическая химия включает в себя бесконечно разнообразные структуры, возникающие из-за того, как атомы собраны в 3-мерном пространстве. Предоставления только молекулярной формулы соединения часто недостаточно для определения соединения, поскольку многие молекулярные формулы имеют множество структурных изомеров. Например, молекулярная формула C 2 H 6 O, молекула всего из 9 атомов, может относиться к диметиловому эфиру или этанолу, в зависимости от того, находится ли кислород в середине или на конце углеродной цепи.
3, органическая химия включает в себя бесконечно разнообразные структуры, возникающие из-за того, как атомы собраны в 3-мерном пространстве. Предоставления только молекулярной формулы соединения часто недостаточно для определения соединения, поскольку многие молекулярные формулы имеют множество структурных изомеров. Например, молекулярная формула C 2 H 6 O, молекула всего из 9 атомов, может относиться к диметиловому эфиру или этанолу, в зависимости от того, находится ли кислород в середине или на конце углеродной цепи. Молекулы сахара глюкоза и галактоза являются стереоизомерами. Они отличаются положением одной группы -ОН, как показано на диаграмме ниже:
Молекулы сахара глюкоза и галактоза являются стереоизомерами. Они отличаются положением одной группы -ОН, как показано на диаграмме ниже:
Хиральность Говорят, что Термин «хиральный» происходит от греческого слова «ручность», т.е. праворукость или леворукость. Ваши руки хиральны: ваша правая рука является зеркальным отражением вашей левой руки, но если вы положите одну руку поверх другой, обеими ладонями вниз, вы увидите, что они не накладываются друг на друга. (рис. 5.4). Таким образом, хиральные объекты являются зеркальными отображениями друг друга, но не могут быть наложены друг на друга. Углерод становится хиральным, когда к нему присоединены четыре различных заместителя. В приведенном выше примере вы заметите, что к центральному углероду присоединены четыре различные группы: группа -OH, группа -H, группа -CH 3 и группа -CH 2 CH 3 .
Термин «хиральный» происходит от греческого слова «ручность», т.е. праворукость или леворукость. Ваши руки хиральны: ваша правая рука является зеркальным отражением вашей левой руки, но если вы положите одну руку поверх другой, обеими ладонями вниз, вы увидите, что они не накладываются друг на друга. (рис. 5.4). Таким образом, хиральные объекты являются зеркальными отображениями друг друга, но не могут быть наложены друг на друга. Углерод становится хиральным, когда к нему присоединены четыре различных заместителя. В приведенном выше примере вы заметите, что к центральному углероду присоединены четыре различные группы: группа -OH, группа -H, группа -CH 3 и группа -CH 2 CH 3 . jpg
jpg Один энантиомер будет вращать свет по часовой стрелке, а другой — против часовой стрелки. Версия по часовой стрелке обозначается буквой «D» для правовращающего (или правостороннего), а версия против часовой стрелки обозначается буквой «L» для левовращающего (или левостороннего).Однако вращение света нельзя использовать для предсказания абсолютной стереоконфигурации молекулы (т. е. вы не можете сказать, какой энантиомер будет вращать свет вправо или влево, пока вы не проведете эксперимент).
Один энантиомер будет вращать свет по часовой стрелке, а другой — против часовой стрелки. Версия по часовой стрелке обозначается буквой «D» для правовращающего (или правостороннего), а версия против часовой стрелки обозначается буквой «L» для левовращающего (или левостороннего).Однако вращение света нельзя использовать для предсказания абсолютной стереоконфигурации молекулы (т. е. вы не можете сказать, какой энантиомер будет вращать свет вправо или влево, пока вы не проведете эксперимент).
 Углерод имеет атомный номер 6. Какая из двух групп «С» имеет приоритет №2, альдегидная или CH 2 OH? Чтобы определить это, отодвинем от стереоцентра еще одну связь: для альдегида мы имеем двойную связь с кислородом, а в группе СН 2 ОН мы имеем одинарную связь с кислородом.Если атом один и тот же, двойные связи имеют более высокий приоритет, чем одинарные связи. Следовательно, альдегидной группе назначается приоритет №2, а группе CH 2 OH — приоритет №3. Распределив наши приоритеты, мы следим за тем, чтобы приоритетная группа № 4 (водород) была направлена от нас, в плоскость страницы (это уже так).
Углерод имеет атомный номер 6. Какая из двух групп «С» имеет приоритет №2, альдегидная или CH 2 OH? Чтобы определить это, отодвинем от стереоцентра еще одну связь: для альдегида мы имеем двойную связь с кислородом, а в группе СН 2 ОН мы имеем одинарную связь с кислородом.Если атом один и тот же, двойные связи имеют более высокий приоритет, чем одинарные связи. Следовательно, альдегидной группе назначается приоритет №2, а группе CH 2 OH — приоритет №3. Распределив наши приоритеты, мы следим за тем, чтобы приоритетная группа № 4 (водород) была направлена от нас, в плоскость страницы (это уже так).
 Приоритетное движение против часовой стрелки обозначается буквой «S». В нашем примере 2-бутанол слева показывает приоритет движения против часовой стрелки, что дает S-энантиомер. Молекула справа показывает R-энантиомер с приоритетом движения по часовой стрелке.
Приоритетное движение против часовой стрелки обозначается буквой «S». В нашем примере 2-бутанол слева показывает приоритет движения против часовой стрелки, что дает S-энантиомер. Молекула справа показывает R-энантиомер с приоритетом движения по часовой стрелке.
Талидомид – история непредвиденных последствий 

 Это две разные молекулы!
Это две разные молекулы! Хиральные молекулы иногда рисуют без использования клиньев. И наоборот, клинья можно использовать для атомов углерода, не являющихся стереоцентрами — посмотрите, например, на рисунки глицина и цитрата на рисунке выше. Просто потому, что вы видите пунктирные и сплошные клинья в структуре, не следует автоматически предполагать, что вы смотрите на стереоцентр.
Хиральные молекулы иногда рисуют без использования клиньев. И наоборот, клинья можно использовать для атомов углерода, не являющихся стереоцентрами — посмотрите, например, на рисунки глицина и цитрата на рисунке выше. Просто потому, что вы видите пунктирные и сплошные клинья в структуре, не следует автоматически предполагать, что вы смотрите на стереоцентр.
5.5 Важность хиральности во взаимодействиях белков 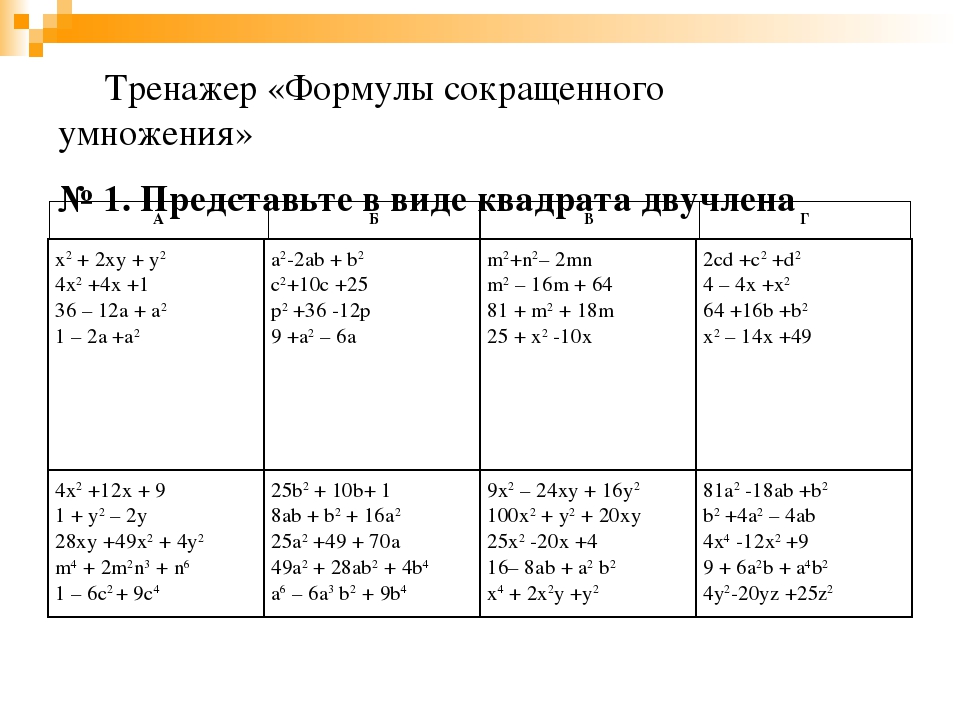 «Волнистая» связь в химической структуре указывает на рацемическую смесь — таким образом, рацемический ( R/S ) талидомид будет выглядеть как:
«Волнистая» связь в химической структуре указывает на рацемическую смесь — таким образом, рацемический ( R/S ) талидомид будет выглядеть как: к ( S )-талидомид (это поможет просмотреть цветную версию рисунка ниже).
к ( S )-талидомид (это поможет просмотреть цветную версию рисунка ниже). Карвон представляет собой хиральную молекулу растительного происхождения, которая пахнет мятой колосовой в форме R и тмином (пряностью) в форме S .
Карвон представляет собой хиральную молекулу растительного происхождения, которая пахнет мятой колосовой в форме R и тмином (пряностью) в форме S .
5.6 Распознавание общих органических функциональных групп 

 Большая часть оставшейся части вашего изучения органической химии будет посвящена изучению того, как различные функциональные группы ведут себя в органических реакциях. Ниже приводится краткое введение в основные органические функциональные группы.
Большая часть оставшейся части вашего изучения органической химии будет посвящена изучению того, как различные функциональные группы ведут себя в органических реакциях. Ниже приводится краткое введение в основные органические функциональные группы.
Алканы
Алкены и алкины  Этен, простейший пример алкена, представляет собой газ, который служит клеточным сигналом во фруктах, чтобы стимулировать созревание.(Если вы хотите, чтобы бананы созрели быстро, положите их в бумажный пакет вместе с яблоком — яблоко выделяет газ этен (также называемый этиленом), запуская процесс созревания в бананах). Этин, обычно называемый ацетиленом, используется в качестве топлива в сварочных горелках.
Этен, простейший пример алкена, представляет собой газ, который служит клеточным сигналом во фруктах, чтобы стимулировать созревание.(Если вы хотите, чтобы бананы созрели быстро, положите их в бумажный пакет вместе с яблоком — яблоко выделяет газ этен (также называемый этиленом), запуская процесс созревания в бананах). Этин, обычно называемый ацетиленом, используется в качестве топлива в сварочных горелках.
Ароматические соединения  Ароматические группы представляют собой плоские (плоские) кольцевые структуры и широко распространены в природе.
Ароматические группы представляют собой плоские (плоские) кольцевые структуры и широко распространены в природе.
Спирты, фенолы и тиолы  За исключением метанола, все спирты можно разделить на первичные, вторичные и третичные. В первичном спирте углерод, связанный с группой ОН, также связан только с одним другим углеродом. Во вторичном спирте и третичном спирте углерод связан с двумя или тремя другими атомами углерода соответственно. Когда гидроксильная группа непосредственно присоединена к ароматическому кольцу, полученная группа называется фенолом. Сернистый аналог спирта называется тиолом (от греческого thio — сера).
За исключением метанола, все спирты можно разделить на первичные, вторичные и третичные. В первичном спирте углерод, связанный с группой ОН, также связан только с одним другим углеродом. Во вторичном спирте и третичном спирте углерод связан с двумя или тремя другими атомами углерода соответственно. Когда гидроксильная группа непосредственно присоединена к ароматическому кольцу, полученная группа называется фенолом. Сернистый аналог спирта называется тиолом (от греческого thio — сера).
Простые эфиры и сульфиды  Ниже представлена структура диэтилового эфира, распространенного лабораторного растворителя, а также одного из первых соединений, которые стали использовать в качестве анестетика во время операций. Сернистый аналог эфира называется тиоэфиром или сульфидом .
Ниже представлена структура диэтилового эфира, распространенного лабораторного растворителя, а также одного из первых соединений, которые стали использовать в качестве анестетика во время операций. Сернистый аналог эфира называется тиоэфиром или сульфидом .
Амины 
Органические фосфаты  Кетоны и альдегиды представляют собой две близкородственные функциональные группы на основе карбонила, которые реагируют очень похожим образом. В кетон атом углерода карбонила связан с двумя другими атомами углерода.В альдегиде , карбонильный углерод связан с одной стороны с водородом, а с другой стороны с углеродом. Исключением из этого определения является формальдегид, в котором карбонильный углерод связан с двумя атомами водорода.
Кетоны и альдегиды представляют собой две близкородственные функциональные группы на основе карбонила, которые реагируют очень похожим образом. В кетон атом углерода карбонила связан с двумя другими атомами углерода.В альдегиде , карбонильный углерод связан с одной стороны с водородом, а с другой стороны с углеродом. Исключением из этого определения является формальдегид, в котором карбонильный углерод связан с двумя атомами водорода. Форма карбоксилат-иона пожертвовала H + раствору. Другими производными являются сложные эфиры карбоновых кислот (обычно называемые просто сложными эфирами), тиоэфиры, амиды, ацилфосфаты, хлорангидриды и ангидриды кислот . За исключением хлорангидридов и ангидридов кислот, производные карбоновых кислот очень распространены в биологических молекулах и/или метаболических путях, и их структура и реакционная способность будут более подробно обсуждаться в следующих главах.
Форма карбоксилат-иона пожертвовала H + раствору. Другими производными являются сложные эфиры карбоновых кислот (обычно называемые просто сложными эфирами), тиоэфиры, амиды, ацилфосфаты, хлорангидриды и ангидриды кислот . За исключением хлорангидридов и ангидридов кислот, производные карбоновых кислот очень распространены в биологических молекулах и/или метаболических путях, и их структура и реакционная способность будут более подробно обсуждаться в следующих главах. Соединение с несколькими спиртовыми группами часто называют полиолом .
Соединение с несколькими спиртовыми группами часто называют полиолом . Обязательно укажите местонахождение всех ненулевых формальных сборов. Все атомы должны иметь полные октеты (фосфор может превышать правило октетов). Для них существует множество возможных правильных ответов, поэтому обязательно уточните свои структуры у своего инструктора или репетитора.
Обязательно укажите местонахождение всех ненулевых формальных сборов. Все атомы должны иметь полные октеты (фосфор может превышать правило октетов). Для них существует множество возможных правильных ответов, поэтому обязательно уточните свои структуры у своего инструктора или репетитора.
5.7 Краткий обзор органической номенклатуры  Хотя система ИЮПАК удобна для обозначения относительно небольших простых органических соединений, она обычно не используется для обозначения биомолекул, которые имеют тенденцию быть довольно большими и сложными. Однако неплохо (даже для биологов) ознакомиться с базовой структурой системы IUPAC и уметь рисовать простые структуры на основе их названий IUPAC.
Хотя система ИЮПАК удобна для обозначения относительно небольших простых органических соединений, она обычно не используется для обозначения биомолекул, которые имеют тенденцию быть довольно большими и сложными. Однако неплохо (даже для биологов) ознакомиться с базовой структурой системы IUPAC и уметь рисовать простые структуры на основе их названий IUPAC. Когда заместителями являются малые алкильные группы, используются термины метил , этил и пропил .
Когда заместителями являются малые алкильные группы, используются термины метил , этил и пропил .
 В случае замещенного амида группа, присоединенная к азоту амида, называется первой вместе с буквой « N », чтобы уточнить, где находится эта группа. Обратите внимание, что приведенные ниже структуры основаны на трехуглеродной (пропановой) исходной цепи.
В случае замещенного амида группа, присоединенная к азоту амида, называется первой вместе с буквой « N », чтобы уточнить, где находится эта группа. Обратите внимание, что приведенные ниже структуры основаны на трехуглеродной (пропановой) исходной цепи. 1] октан-2-карбоксилат (это название включает обозначения для стереохимии).
1] октан-2-карбоксилат (это название включает обозначения для стереохимии).
Каталожные номера: ASU крупный игрок в области микроэлектроники
20 января 2022 г.
Университетские эксперты делятся своими мыслями об этом микроскопическом мире

В чем разница между микроэлектроникой, полупроводниками и микросхемами?

Насколько малы микроэлектронные устройства?

Как делают микрочипы?
 «Этот процесс повторяется до сотни раз, чтобы сформировать все элементы дизайна этого чипа».
«Этот процесс повторяется до сотни раз, чтобы сформировать все элементы дизайна этого чипа». Почему сейчас не хватает микрочипов? Являются ли больше фабрик решением?
 Спрос на микрочипы у производителей внезапно превысил предложение.
Спрос на микрочипы у производителей внезапно превысил предложение.
Какие вопросы национальной безопасности следует учитывать при использовании микроэлектроники?
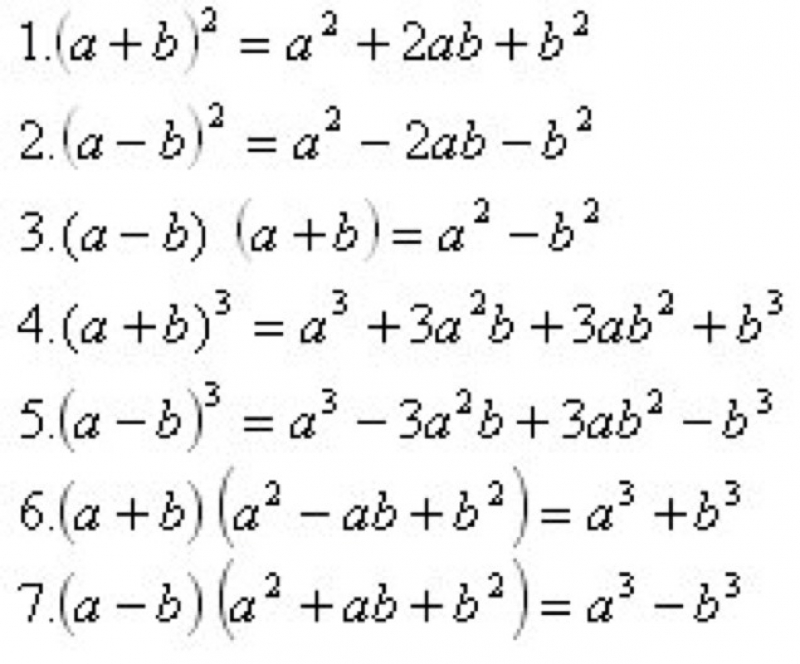
Как ASU помогает Аризоне лидировать в микроэлектронной промышленности США?
 Там они могут разрабатывать новые материалы, методы и конструкции для микроэлектроники в промышленных масштабах.
Там они могут разрабатывать новые материалы, методы и конструкции для микроэлектроники в промышленных масштабах. Если закон о финансировании будет принят, ASU предложит Национальную сеть микроэлектроники с базовым предприятием, поддерживаемым университетом, в Аризоне.
Если закон о финансировании будет принят, ASU предложит Национальную сеть микроэлектроники с базовым предприятием, поддерживаемым университетом, в Аризоне. Заводы по производству используют тонны воды, так почему же мы строим их в пустыне?
 «Нам нужно искать наиболее эффективные способы использования воды, которые принесут наибольшую социальную, экономическую и экологическую отдачу. Я бы назвал производство полупроводников в нашем регионе бережливой к воде отраслью.”
«Нам нужно искать наиболее эффективные способы использования воды, которые принесут наибольшую социальную, экономическую и экологическую отдачу. Я бы назвал производство полупроводников в нашем регионе бережливой к воде отраслью.” Уровень грунтовых вод относительно низок по всему штату, поэтому партнерство Intel и Chandler — это решение сразу двух насущных проблем.
Уровень грунтовых вод относительно низок по всему штату, поэтому партнерство Intel и Chandler — это решение сразу двух насущных проблем. Что ждет микроэлектронику дальше?

Микала Касс




 .. у) 2 = х 2 – 2ху +…
.. у) 2 = х 2 – 2ху +… Формула квадрата різниці двох виразів:
Формула квадрата різниці двох виразів:


 У знаменниках «15a» і «5» є тільки
У знаменниках «15a» і «5» є тільки 
 переход: наследовать;
переход: начальный;
переход: возврат;
переход: не установлен;
переход: наследовать;
переход: начальный;
переход: возврат;
переход: не установлен;
