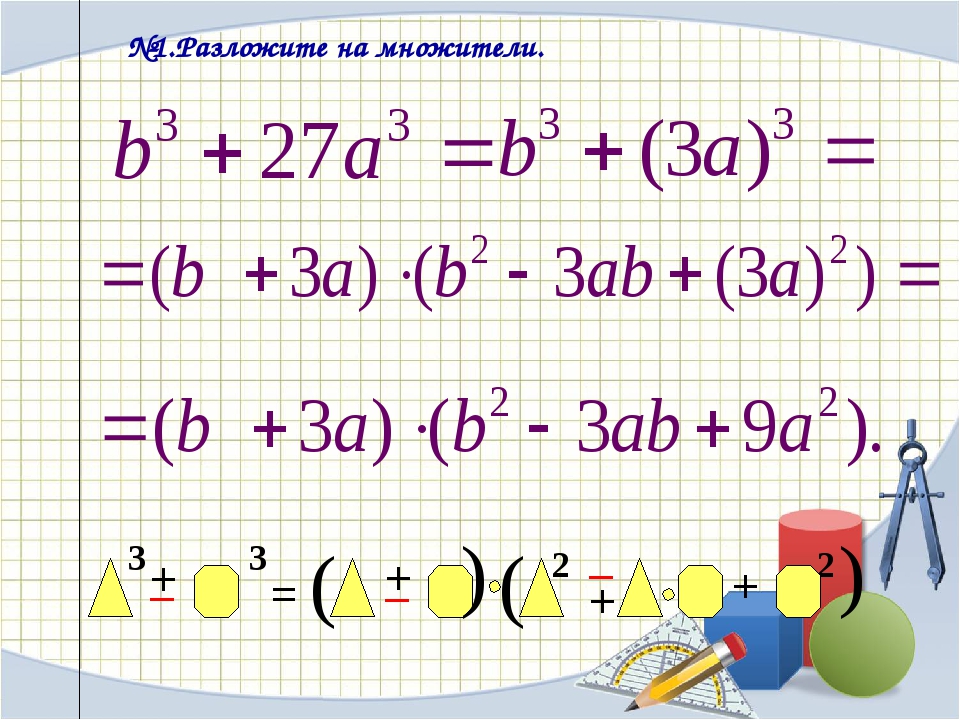Формула разложения суммы куба: Урок 30. сумма кубов. разность кубов — Алгебра — 7 класс

Урок 30. сумма кубов. разность кубов — Алгебра — 7 класс

Алгебра

7 класс

Урок № 30

Сумма кубов. Разность кубов

Перечень вопросов, рассматриваемых в теме:

• Формулы сокращённого умножения.
• Сумма кубов, разность кубов.
• Разложение многочлена на множители.
• Тождественные преобразования.
• Вычисление значения числовых выражений.

Тезаурус:

Формулы сокращённого умножения.

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

(a + b)(a – b) = a² – b²

a³ + b³= (a + b)(a ²– ab + b²)

a³ – b³= (a – b)(a² + ab + b²)

Применение:

• упрощение умножения многочленов;
• разложение многочлена на множители;
• вычисление значения числового выражения;
• тождественные преобразования.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Формула суммы кубов.

Рассмотрим произведение;

(a + b)(a² – ab + b²).

Применив правило умножения многочленов, и приведя подобные члены, получим:

(a + b)(a² – ab + b²) = a³ – a²b + ab² + ba² – ab² +b³ = a³ + b³

a³ + b³ = (a + b)(a² – ab + b²)

Равенство называют формулой суммы кубов.

Читается так: «сумма кубов двух чисел равна произведению суммы этих чисел и неполного квадрата их разности».

Формула разности кубов.

Аналогично докажем формулу разности кубов.

(a – b)(a² + ab + b²) = a³ + a²b + ab² – ba² – ab² – b³= a³ – b³

Читается так: «разность кубов двух чисел равна произведению разности этих чисел и неполного квадрата их суммы».

a³– b³= (a – b)(a²+ ab + b²)

Выражения

(a²+ ab + b²) и (a²– ab + b²) называют неполным квадратом суммы или разности.

Формула задаёт разложение многочленов:

a³ + b³ и a³ – b³ на два множителя:

(a + b)(a² – a b+ b²) и (a – b)(a²+ ab + b²).

Формулы суммы и разности кубов используют для упрощения вычислений.

Разбор решения заданий тренировочного модуля.

Задача 1.

Выполните умножение многочленов:

1. ( x + 3)(x² –3x +9) = x³ + 3³ = x³ + 27.
2. (2x – 3y)(4x² +6xy + 9y²) = (2x)³ – (3y)³ = 8x³ –27y³.

Задача 2.

Разложите многочлен на множители:

1. x³ – 8 y³ = x³ – (2y)³ = (x – 2y) (x² +2xy + 4y² )
2. 64 a³ – 27c³ = (4a)³ – (3c)³ = (4a – 3c)(16a² +12 ac + 9c²).

Задача 3.

Упростите выражение:

(x +2)(x² – 2x +4) – x(x–3)(x+3).

Решение:

x³ + 2³

– x(x² – 9) = x³ + 8 – x³ + 9x = 8 + 9x.

Ответ: 8 + 9x.

Задача 4.

Доказать, что выражение 123³ + 27³ кратно 50.

Используем формулу:

a³ + b³ = (a + b)(a² – ab + b²),

получим: (123 + 27)(123²–123 · 27 + 27²) =150 · (123²–123 · 27 + 27²).

Произведение делится на 50, так как первый множитель делится на 50: (150 : 50 = 3). Нет необходимости считать значение выражения в скобках. Утверждение доказано.

Формулы сокращенного умножения 💣

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

 

1. Разность квадратов двух выражений равна произведению их разности и их суммы.


2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.


3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.


4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.


5. Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.


6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.


7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a² — b² = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a² — b².

Важно знать, что разность квадратов не равна квадрату разности: a² — b² ≠ (a — b)².

Докажем, что a² — b² = (a — b) * (a + b).

Поехали:

1. Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
   + a * b — a * b = 0

   a² — b² = a² — b² + ab — ab

2. Сгруппируем иначе: a² — b² + a * b — a * b = a² — a * b + a * b — b²


3. Продолжим группировать: a² — a * b — b² +a * b = (a² — a * b) + (a * b — b²)


4. Вынесем общие множители за скобки:

   (a² — a * b) + (a * b — b²) = a *(a — b) + b *(a — b)

5. Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)


6. Результат доказательства: a² — b² = (a — b) * (a + b)


7. Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a² — b², нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a² — b².

Остальные ФСУ можно доказать аналогичным методом.

 

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два. 

(a₁+a₂+…+a_n)² = a₁² + a₂² + … + a_n-1² + a_n² + 2 * a₁ * a₂ + 2 * a₁ * a₃ + 2 * a₁ * a₄ + … +

+ 2 * a₁ * a_n-1 + 2 * a₁ * a_n + 2 * a₂ * a₃

+ 2 * a₂ * a₄ + … + 2 * a₂ * a_n-1 + 2 * a₂ * a_n +…+

+ 2 * a_n-1 * a_n

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

aⁿ − bⁿ = (a − b) * (a^n-1 + a^n-2 * b + a^n-3 * b² + … + a * b^n-2 + b^n-1).

Для четных показателей можно записать так:

a^2*m − b^2*m = (a² − b²) *(a^2*m−2 + a^2*m−4 * b² + a^2*m−6 * b⁴ + … + b^2*m−2).

Для нечетных показателей:

a^2*m+1 − b^2*·m+1 = (a − b) * (a^2*m + a^2*m−1 * b + a^2*m−2 * b² + … + b^2*m).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10)².

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)² = 55² + 2 * 55 * 10 + 10² = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с³ – 8.

Как решаем: применим разность кубов: 64 * с³ – 8 = (4 * с)³ – 2³ = (4 * с – 2)((4 * с)² + 4 * с * 2 + 2²) = (4 * с – 2)(16 * с² + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

1. Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y² + 7 * y * x — 7 * y * x — x² = 49 * y² — x².
2. Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)² — x² = 49 * y² — x².

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

---

---

Запишите вашего ребенка на увлекательные уроки математики в детскую школу Skysmart. 2 )$$

Мы получили формулу суммы кубов.

Формулы сокращённого умножения. Неполный квадрат суммы и разности

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

a² + b² = (a + b)² — 2ab  —  сумма квадратов;

a² — b² = (a + b)(a — b)  —  разность квадратов;

(a + b)² = a² + 2ab + b²  —  квадрат суммы;

(a — b)² = a² — 2ab + b²  —  квадрат разности;

a³ + b³ = (a + b)(a² — ab + b²)  —  сумма кубов;

a³ — b³ = (a — b)(a² + ab + b²)  —  разность кубов;

(a + b)³ = a³ + 3a²b + 3ab² + b³  —  куб суммы;

(a — b)³ = a³ — 3a²b + 3ab² — b³  —  куб разности.

Обратите внимание, что  a  и  b  в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

a² + b² = (a + b)² — 2ab.

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)² — 2ab = (a + b)(a + b) — 2ab = a² + ab + ab + b² — 2ab = a² + b².

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

a² — b² = (a + b)(a — b).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a — b) = a² — ab + ab — b² = a² — b².

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b)² = a² + 2ab + b².

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b².

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(a — b)² = a² — 2ab + b².

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)² = (a — b)(a — b) = a² — ab — ab + b² = a² — 2ab + b².

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

a³ + b³ = (a + b)(a² — ab + b²).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a² — ab + b²) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³.

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

a³ — b³ = (a — b)(a² + ab + b²).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a — b)(a² + ab + b²) = a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³.

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

(a + b)³ = a³ + 3a²b + 3ab² + b³.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)³ = (a + b)(a + b)² = (a + b)(a² + 2ab + b²) = a³ + 2a²b + ab² + a²b + 2ab² + b³ = a³ + 3a²b + 3ab² + b³.

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(a — b)³ = a³ — 3a²b + 3ab² — b³.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)³ = (a — b)(a — b)² = (a — b)(a² — 2ab + b²) = a³ — 2a²b + ab² — a²b + 2ab² — b³ = a³ — 3a²b + 3ab² — b³.

Неполный квадрат суммы

Выражение:

a² + 2ab + b²

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

a² + ab + b²,

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

Выражение:

a² — 2ab + b²

это квадрат разности, который также называется полным квадратом разности относительно выражения:

a² — ab + b²,

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

правила применения формул сокращенного умножения. Формулы сокращенного умножения Сумма и разность кубов двух выражений задания

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2) = a 3 − b 3

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а 3 » — это «(3а) 3 », значит, для формулы разности кубов вместо «a » мы используем «3a ».

Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».

Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов
«a 3 − b 3 = (a − b)(a 2 + ab + b 2) », то можно понять, что на месте «a » из первой скобки стоит «y 2 , а на месте «b » стоит «1 ».

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: a 2 — b 2 = a — b a + b
6. формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n

Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a — b 2 = a 2 — 2 a b + b 2 .

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a — b 2 = a — b a — b .

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9 y — (1 + 3 y) 2 .

Применим формулу суммы квадратов и получим:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСУ

Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Возведение в квадрат и куб суммы и разности двух выражений. Разложение на множители с помощью формул квадрата суммы и

88. Возведение в квадрат и куб суммы и разности двух выражений. Разложение на множители с помощью формул квадрата суммы и квадрата разности.

Мы уже знаем, как умножить многочлен на многочлен. Но для некоторых случаев есть формулы, которые помогут существенно ускорить расчеты. Это формулы сокращенного умножения. Сегодня мы познакомимся с четырьмя из них.

Возведем в квадрат сумму (a+b):

(a+b)² = (a+b)(a+b)

Применим правило умножения многочлена на многочлен:

(a+b)(a+b) = a*a+a*b+b*a+b*b = a²+ab+ab+b² = a²+2ab+b²

Мы получили формулу:

(a+b)² = a²+2ab+b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Аналогично выведем формулу для квадрата разности:

(a-b)² = (a-b)(a-b) = a*a-a*b-b*a+b*b = a²-ab-ab+b² = a²-2ab+b²

(a-b)² = a²-2ab+b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Теперь, используя эти формулы, выведем формулы для куба суммы и куба разности двух выражений:

(a+b)³ = (a+b)(a+b)² = (a+b)(a²+2ab+b²) = a*a²+a*2ab+a*b²+b*a²+b*2ab+b*b² = a³+2a²b+ab²+a²b+2ab²+b³ = a³+3a²b+3ab²+b³

(a+b)^{3= a3+3a2b+3ab2+b3}

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб третьего выражения.

Это правило не так-то легко запомнить? Достаточно выучить формулу! Правило – это всего лишь ее словесное описание.

Аналогично найдем формулу куба разности:

(a-b)³ = (a-b)(a-b)² = (a-b)(a²-2ab+b²) = a*a²-a*2ab+a*b²-b*a²+b*2ab-b*b² = a³-2a²b+ab²-a²b+2ab²-b³ = a³-3a²b+3ab²-b³

(a-b)³ = a³-3a²b+3ab²-b³

Если в формуле для куба суммы все одночлены соединены знаками «+», что понятно – минусу просто неоткуда взяться, то в формуле для куба разности знаки между одночленами чередуются: «-» «+» «-».

Формулы сокращенного умножения используются также при разложении на множители.

Пример 1. Разложим на множители многочлен 81a²-18ab+b².

Можно ли слагаемое 81а² представить в виде квадрата одночлена? 81 – это квадрат числа 9. Тогда 81а² = 9²а² = (9а)². Причем -18аb = -2*9a*b.

«Свернем» многочлен, используя формулу квадрата суммы:

81a²-18ab+b^{2= (9а)2-2*9a*b+b2= (9а-b)2= (9а-b)(9а-b).}

Чему равна разность кубов: формула, доказательство, примеры

В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, разложение разности кубов на множители. Также разберем примеры решения задач для закрепления представленного материала.

Формула разности кубов

Разность кубов чисел/выражений равняется произведению их разности на неполный квадрат их суммы.

a³ – b³ = (a – b)(a² + ab + b²)

Полный квадрат суммы выглядит следующим образом: (a + b)² = a² + 2ab + b². В нашем случае во второй скобке напротив второго слагаемого нет множителя 2, поэтому выражение является неполным.

Формула верна и в обратную сторону:

(a – b)(a² + ab + b²) = a³ – b³

Примечание: a³ – b³ ≠ (a – b)³

Доказательство формулы

Достаточно просто умножить скобку (a – b) на (a² + ab + b²), чтобы убедиться в том, что выражение верно, т.е. пойти от обратного:

(a – b)(a² + ab + b²) = a³ + a²b + ab² – a²b – ab² – b³ = a³ – b³.

Примеры задач

Задание 1
Представьте в виде произведения множителей выражение: (7x)³ – 5³.

Решение
(7x)³ – 5³ = (7x – 5)((7x)² + 7x ⋅ 5 + 5²) = (7x – 5)(49x² + 35x + 25)

Задание 2
Представьте выражение 512x³ – 27y³ в виде разности кубов и разложите его на множители.

Решение
512x³ – 27y³ = ((8x)³ – (3y)³) = (8x – 3y)((8x)² + 8x ⋅ 3y + (3y)²) = (8x – 3y)(64x² + 24xy + 9y²)

Специальный факторинг: суммы и разности кубов и идеальные квадраты

Purplemath

Две другие специальные формулы факторизации, которые вам нужно запомнить, очень похожи друг на друга; это формулы для разложения сумм и разностей кубов. Вот две формулы:

Факторинг суммы кубов:

a ³ + b ³ = ( a + b ) ( a ² — ab + b ² )

Фактор разницы кубов:

a ³ — b ³ = ( a — b ) ( a ² + ab + b ² )

На более продвинутых курсах вы узнаете, как они пришли к этим формулам.А пока просто запомните их.

MathHelp.

com

Чтобы помочь с запоминанием, сначала обратите внимание, что членов в каждой из двух формул факторизации абсолютно одинаковы.Затем обратите внимание, что в каждой формуле есть только один знак «минус». Разница между двумя формулами заключается в расположении знака «минус»:

Для разницы кубов знак «минус» ставится в линейном множителе, a — b ; для суммы кубиков знак «минус» стоит в квадратичном множителе, a ² — ab + b ² .

Некоторые люди используют мнемонику « SOAP », чтобы отслеживать знаки; буквы обозначают линейный множитель, имеющий «тот же» знак, что и знак в середине исходного выражения, затем квадратичный множитель, начинающийся со «противоположного» знака того, что было в исходном выражении, и, наконец, второй знак внутри квадратичный множитель «всегда положителен».

a ³ ± b ³ = ( a [ Тот же знак ] b ) ( a ² [ напротив знака ] ab [ Всегда Положительный ] b ² )

Какой бы метод лучше всего ни помогал вам сохранять эти формулы прямо, используйте его, потому что вы не должны предполагать, что вам дадут эти формулы на тесте.Вы должны ожидать, что вам нужно будет их знать.

Примечание. Квадратичная часть каждой формулы куба не учитывает множитель , поэтому не тратьте время на попытки разложить его на множители. Да, a ² -2 ab + b ² и a ² + 2 ab + b ^{2 Коэффициент} , но это из-за двойки в середине термины. Квадратичные члены этих формул суммы и разности кубов не имеют , равного «2», и, таким образом, не может разложить на множители .

---

Когда вам дается пара кубиков для факторизации, внимательно примените соответствующее правило. Под «осторожно» я имею в виду «использование круглых скобок для отслеживания всего, особенно отрицательных знаков». Вот несколько типичных проблем:

Это эквивалентно x ³ -2 ³ . Со знаком «минус» посередине это разница кубиков. Чтобы провести факторинг, я подставлю x и 2 в формулу разности кубов.Так я получаю:

x ³ — 8 = x ³ — 2 ³

= ( x -2) ( x ² + 2 x + 2 ² )

= ( x -2) ( x ² + 2 x + 4)

---

Первый член содержит куб 3 и куб x .А как насчет второго срока?

Прежде чем паниковать по поводу отсутствия кажущегося куба, я помню, что 1 можно рассматривать как возведенную в любую степень, которая мне нравится, поскольку 1 для любой степени все еще равна 1. В этом случае мне нужна степень 3, так как это даст мне сумму кубиков. Это означает, что выражение, которое они мне дали, можно выразить как:

Итак, чтобы разложить множители, я подставлю 3 x и 1 в формулу суммы кубов.Это дает мне:

27 x ³ + 1 = (3 x ) ³ + 1 ³

= (3 x + 1) ((3 x ) ² — (3 x ) (1) + 1 ² )

= (3 x + 1) (9 x ² — 3 x + 1)

---

Во-первых, я отмечаю, что они дали мне бином (двухчленный многочлен) и что мощность x в первом члене равна 3, поэтому, даже если я не работал с «суммами и разностями» кубиков »в моем учебнике, я бы заметил, что, возможно, мне следует думать в терминах этих формул.

Глядя на другую переменную, я замечаю, что степень 6 является кубом степени 2, поэтому другая переменная в первом члене также может быть выражена в кубе; а именно, как куб квадрата у .

Второй член — 64, который, как я помню, является кубом 4. (Если бы я не вспомнил или не был уверен, я бы схватил свой калькулятор и попробовал вычислить кубики, пока не получил правильное значение. , иначе я бы взял кубический корень из 64.)

Итак, теперь я знаю, что с минусом в середине это разница в два куба; а именно это:

Подставляя подходящую формулу, я получаю:

x ³ y ⁶ — 64 = ( xy ² ) ³ — 4 ³

= ( xy ² -4) (( xy ² ) ² + ( xy ² ) (4) + 4 ² )

= ( xy ² -4) ( x ² y ⁴ + 4 xy ² + 16)

---

• Используя соответствующую формулу, множите 16

  x ³ — 250.

Гм … Я знаю, что 16 — это , а не куб чего-либо; на самом деле он равен 2 ⁴ . Как дела?

Что случилось, они ожидают, что я использую то, что я узнал о простом факторинге, чтобы сначала преобразовать это в разность кубов. Да, 16 = 2 ⁴ , но 8 = 2 ³ , куб. Я могу получить 8 из 16, разделив на 2.Что будет, если я разделю 250 на 2? Я получаю 125, что является кубом из 5. То, что они мне дали, можно переформулировать как:

Я могу применить формулу разности кубов к тому, что находится в круглых скобках:

2 ³ x ³ — 5 ³ = (2 x ) ³ — (5) ³

= (2 x -5) ((2 x ) ² + (2 x ) (5) + (5) ² )

= (2 x -5) (4 x ² + 10 x + 25)

Собирая все вместе, я получаю окончательную факторизованную форму:

2 (2 x -5) (4 x ² + 10 x + 25)

---

Моей первой реакцией могло бы стать применение формулы разности кубов, поскольку 125 = 5 ³ . Но как насчет того знака «минус» впереди?

Поскольку ни одна из приведенных мне формул факторинга не включает «минус» впереди, может быть, я смогу вычесть «минус» …?

— x ³ — 125 = –1 x ³ — 125

Ага! Теперь то, что внутри скобок, — это сумма кубов, которую я могу разложить на множители. У меня есть сумма куба x и куба 5, поэтому:

x ³ + 5 ³ = ( x + 5) (( x ) ² — ( x ) (5) + (5) ² )

= ( x + 5) ( x ² -5 x + 25)

Собирая все вместе, получаем:

–1 ( x + 5) ( x ² — 5 x + 25)

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении суммы кубов.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления .)

---

---

URL: https://www.purplemath.com/modules/specfact2.htm

Как найти сумму и разность кубов

Обновлено 23 ноября 2020 г.

Лиза Мэлони

Иногда единственный способ выполнить математические вычисления — это грубая сила. 3 — 125

и должны ее разложить на множители.2)

Опять же, если все, что вам нужно сделать, это множить разницу кубов, это ваш ответ.

Частные дроби Кубический знаменатель

Частные дроби Кубический знаменатель:

Здесь мы увидим несколько примеров разложения неполных дробей с кубическими знаменателями.

Кубический знаменатель дробных частей — примеры

Пример 1:

Разложите следующие рациональные выражения на частичные дроби.

x / (x-1) ³

Решение:

Разложив знаменатель, получим

x / (x-1) ³ = (A (x — 1) ² + B (x — 1) + C) / (x-1) ³

x = A (x — 1) ) ² + В (х — 1) + С

Если x = 1 1 = C C = 1

Если x = 0 0 = A (0-1) 2 + B (0-1) + C 0 = A — B + 1 A — B = -1 —- (1 )

Если x = 2 2 = A (2-1) 2 + B (2-1) + C 2 = A + B + 1 A + B = 1 —- (2)

(1) + (2)

A — B + A + B = -1 + 1

2A = 0

A = 0

Применяя значения A в первом уравнении, мы получаем

0 — B = -1

B = 1

Следовательно, решение

Пример 2:

Разложите следующие рациональные выражения на частичные дроби.

1 / (x ⁴ -1)

Решение:

Разложив знаменатель, получим

1 = A (x — 1) (x ² + 1) + B (x + 1) (x ² +1) + (Cx + D) (x + 1) (x-1)

Если x = 1 1 = B (2) (2) 4B = 1 B = 1/4

Если x = -1 1 = A (-2) (2) -4A = 1 A = -1/4

Если x = 0 1 = A + B — D 1 = (1/4) + (1/4) — D 1 = (2/4) — D D = (1/2 ) — 1 D = -1/2

Следовательно, решение —

Пример 3:

Разложите следующие рациональные выражения на частичные дроби.

(x — 1) ² / (x ³ + x)

Решение:

Разложив знаменатель, получим

(x — 1) ² = A (x ² + 1) + (Bx + C) x

Если x = 0 1 = A

Если x = 1 0 = 2A + B + C 0 = 2 + B + C B + C = -2 — (1)

Если x = -1 4 = 2A + (-B + C) (- 1) 4 = 2A + B — C 4 = 2 + B — C 2 = B — C — (2)

(1) + (2)

-2 + 2 = B + C + B — C

0 = 2B

B = 0

Применяя значение B в первом уравнении, мы получаем

C = -2

Следовательно, решение

Пройдя все, что было сказано выше, мы надеемся, что студенты поняли, как разложить рациональное выражение с кубическим знаменателем на частичные дроби.

Помимо того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямому и обратному изменению

Проблемы со словами по цене за единицу

Проблемы со словами по количеству слов

Задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование в метрические единицы в словесных задачах

Проблемы со словами по простому проценту

Проблемы со словами по сложным процентам

Проблемы со словами по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами для разметки

и

задачи

задачи с десятичными числами

задачи со словами на дроби

задачи со словами на смешанные фракции

задачи со словами с одношаговым уравнением

задачи со словами линейных неравенств

Задачи со словами

Проблемы со временем и рабочими словами

Проблемы со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами из теоремы Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами при сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращения в процентах

Сокращения в таблице времен

Сокращения времени, скорости и расстояния

Сокращения соотношения и пропорции

Домен и диапазон рациональных функций 9992 Домен и диапазон 9 рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

видение

Л.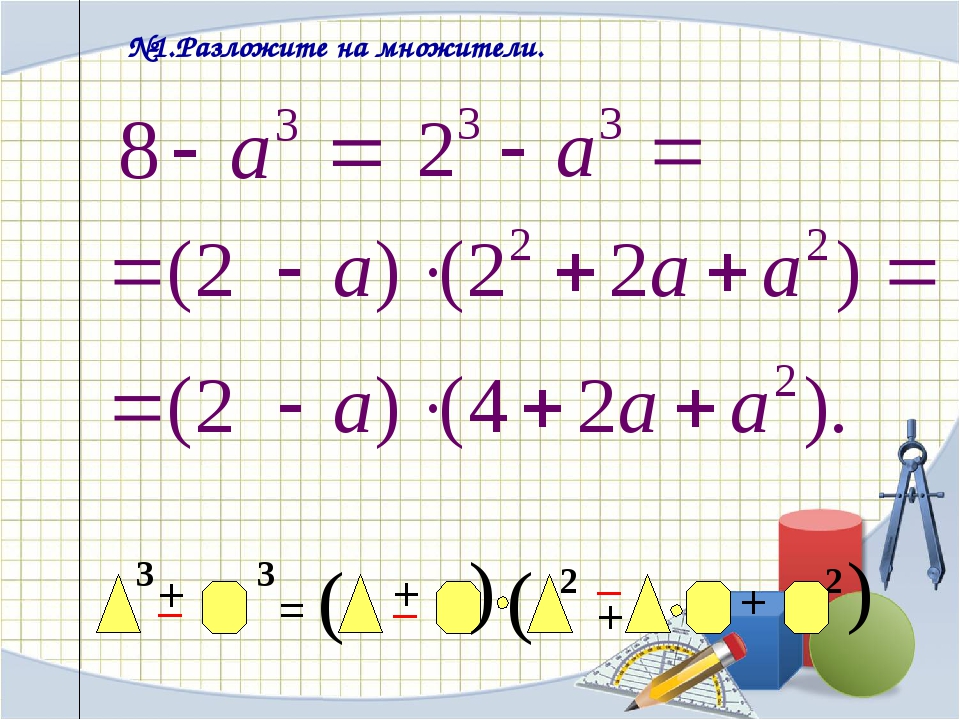 Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

(PDF) По сумме семи кубов

В сумме семи кубиков 1307

Если N больше 41, мы полагаем k = N − 41

333  и имеем NδN≥41 + 36k (так как

41 сумма из 7 кубов в [455,495] и k таких сумм в каждой из 36 арифметических

прогрессий между 496 и 454 + N).Таким образом, мы имеем NδN≥41 + 36 N − 41

333 −1≥

4

37.

V. О доказательстве теоремы 1

Чтобы доказать, что каждое целое число от 1 290 741 до 150003 = 3,375 1012 является суммой

5 кубов, мы сначала вычислили таблицы сумм 2, 3 и 4 неотрицательных

кубиков до 109:

суммы hcubes

1064454 107875 713364

10720546 1037872 8259118

10895090 10172774 713

10895090 10172774 713

10895090 10172774 713

x <(a + 1)

3для 108 ≤a≤15000, мы проверили

, что x можно записать как сумму пяти кубиков, сначала посмотрев на таблицу сумм

четырех кубов для x − a3, в случае отказа для x− (a − 1) 3 и т. д.Если таблица

из четырех кубиков была слишком маленькой, мы вычитали наибольший куб из

x− (a − k) 3 и просматривали таблицу сумм трех кубиков и так далее. Следовательно,

мы искали представление x = (a − k)

3 + C

4, где C

4 обозначает сумму

четырех кубов — с наименьшим k. Обозначим это значение k (x).

Программа, которая создает таблицы сумм кубов, программу проверки

грамма и гистограммы k (x) для 108 ≤a≤15000, может быть получена из

http: // www.loria.fr/~zimmerma/records/cubes.html. Следующая таблица

дает значение наибольшего x, найденного в интервале [1083,150003], такое, что

k (x) = m для каждого мин [6,18]. Максимальные и средние значения k (x) для каждого интервала

a3≤x <(a + 1)

3 показаны на рисунке 1. На рисунке 2 показано для каждого lin

[0 −6] процент xin [a3 , (a + 1)

3

] такое, что k (x) = l.

margest x≤3,375 1012 таких, что k (x) = m

6 a = 13637, x = a3 + 2018319 = 2536044484172

7 a = 7636, x = a3 + 94359676 = 445338035132

8 a = 6627, x = 6627, x а3 + 8276314 = 2

0

9 а = 4768, х = а3 + 822342 = 108395695174

10 а = 2765, х = а3 + 97142 = 2113

67

11 а = 2473, х = а3 + 784633 = 120005000 =

000 =

000 =

000 =

8 x = a3 + 7033521 = 7095986482

13 a = 1185, x = a3 + 1002929 = 1665009554

14 a = 963, x = a3 + 1516531 = 894572878

15 a = 810, x = a3 + 1120900 = 532561900 =

32561900 725, x = a3 + 718511 = 381796636

17 a = 645, x = a3 + 996097 = 269332222

18 a = 434, x = a3 + 225636 = 81972140

Из рисунка 2 видно, что для a≡2 [3], процентное соотношение xin [a3, (a + 1) 3−1]

такое, что k (x) = 2 (i.е. x − a3 и x− (a − 1) 3 не являются суммой четырех кубиков, но

x− (a − 2) 3is) намного меньше, чем для других значений a.

Частичное дробное разложение

Идея частичного разложения на фракции

Рациональная функция — это функция вида

\ [{f \ left (x \ right) = \ frac {{P \ left (x \ right)}} {{Q \ left (x \ right)}},} \]

, где \ (P \ left (x \ right) \) и \ (Q \ left (x \ right) \) — многочлены от \ (x \) с \ (Q \ left (x \ right) \ not \ Equiv 0. 2} + 5x + 4}}} = {\ frac {2} {{x + 1}} + \ frac {3} {{x + 4}}.} \]

Частичное дробное разложение используется для интегрирования рациональных функций.

Данный метод включает следующие основные этапы:

1. Убедитесь, что дробь является правильной рациональной функцией.
2. Разложите многочлен \ ({Q \ left (x \ right)} \) в знаменателе на линейные и / или квадратичные множители.
3. Разложите дробь на сумму частичных дробей.

Давайте подробно рассмотрим каждый шаг.

Шаг \ (1. \) Сокращение неправильной дроби

В правильном рациональном выражении \ (\ large {\ frac {{P \ left (x \ right)}} {{Q \ left (x \ right)}}} \ normalsize, \) степень числителя \ ( {P \ left (x \ right)} \) меньше степени знаменателя \ ({Q \ left (x \ right)}. \)

Если \ (\ large {\ frac {{P \ left (x \ right)}} {{Q \ left (x \ right)}}} \ normalsize \) неверно, мы делим числитель \ ({P \ left (x \ right)} \) на знаменатель \ ({Q \ left (x \ right)} \), чтобы получить

\ [{\ frac {{P \ left (x \ right)}} {{Q \ left (x \ right)}} = F \ left (x \ right) + \ frac {{R \ left (x \ справа)}} {{Q \ left (x \ right)}},} \]

, где \ (F \ left (x \ right) \) — многочлен, а \ (\ large {\ frac {{R \ left (x \ right)}}} {{Q \ left (x \ right)}}} \ normalsize \) — правильная дробь.

Шаг \ (2. \) Разложение знаменателя \ (Q \ left (x \ right) \) на линейные / квадратичные множители

Любой многочлен с действительными коэффициентами может быть разложен на произведение линейных и / или неприводимых квадратичных множителей.

Шаг \ (3. \) Разбиение рациональной функции на сумму частичных дробей

Разложение на частичные дроби рациональной функции \ (\ large {\ frac {{R \ left (x \ right)}} {{Q \ left (x \ right)}}} \ normalsize \) зависит от факторов знаменатель \ ({Q \ left (x \ right)}.\ mu}}}.} \]

После определения частичного разложения на дроби неизвестные коэффициенты могут быть найдены путем очистки дробей и приравнивания коэффициентов одинаковых степеней с двух сторон. В результате система всегда должна иметь уникальное решение.

---

Решенные проблемы

Щелкните или коснитесь проблемы, чтобы увидеть решение.

Пример 1

Разложите дробь \ (\ large {\ frac {6} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} \ normalsize.2} + 2x + 2} \ right)}}} \ normalsize \) с использованием дробных дробей.

Пример 1.

Разложите дробь \ (\ large {\ frac {6} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} \ normalsize. \)

Решение.

Множители знаменателя линейны. Следовательно, числители дробей будут постоянными. Разложение частичной фракции имеет вид

\ [{\ frac {6} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} = {\ frac {A} {{x + 2}} + \ frac {B} {{x — 4}}.} \]

Добавляем дробные дроби справа:

\ [{\ frac {A} {{x + 2}} + \ frac {B} {{x — 4}}} = {\ frac {{A \ left ({x — 4} \ right) + B \ left ({x + 2} \ right)}} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} = {\ frac {{Ax — 4A + Bx + 2B}} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} = {\ frac {{\ left ({A + B} \ right) x + \ left ({2B — 4A} \ right)}} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}.} \]

Это выражение равно исходной дроби, то есть

\ [{\ frac {6} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} = {\ frac {{\ left ({A + B} \ right) x + \ left ({2B — 4A} \ right)}} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}.} \]

Поскольку у этих дробей одинаковые знаменатели, мы можем приравнять их числители:

\ [6 = \ left ({A + B} \ right) x + \ left ({2B — 4A} \ right). \]

Отсюда

\ [{\ left \ {\ begin {array} {l} А + В = 0 \\ 2Б — 4А = 6 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = — В \\ 2B + 4B = 6 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = — В \\ 6B = 6 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = — 1 \\ B = 1 \ end {array} \ right. .} \]

Окончательный ответ дает

\ [{\ frac {6} {{\ left ({x + 2} \ right) \ left ({x — 4} \ right)}}} = {\ frac {1} {{x — 4}} — \ frac {1} {{x + 2}}.} \]

Пример 2.

Разложите дробь \ (\ large {\ frac {3x} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}} \ normalsize. \)

Решение.

Поскольку множители знаменателя линейны, разложение на частную дробь записывается в виде

\ [{\ frac {{3x}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}} = {\ frac {A} {{x + 1 }} + \ frac {B} {{x — 2}}.} \]

Упрощая правую часть, получаем

\ [{\ frac {A} {{x + 1}} + \ frac {B} {{x — 2}}} = {\ frac {{A \ left ({x — 2} \ right) + B \ left ({x + 1} \ right)}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}} = {\ frac {{Ax — 2A + Bx + B}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}} = {\ frac {{\ left ({A + B} \ right) x + \ left ({B — 2A} \ right)}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}.} \]

Это выражение равно исходной дроби:

\ [{\ frac {{3x}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}} = {\ frac {{\ left ({A + B} \ right) x + \ left ({B — 2A} \ right)}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right)}}.} \]

Дроби с обеих сторон имеют одинаковые знаменатели, поэтому приравняем их числители:

\ [3x = \ left ({A + B} \ right) x + \ left ({B — 2A} \ right). \]

Затем

\ [{\ left \ {\ begin {array} {l} А + В = 3 \\ В — 2А = 0 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А + 2А = 3 \\ В = 2А \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} 3А = 3 \\ В = 2А \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = 1 \\ В = 2 \ end {array} \ right.2} — 7x + 10}}} = {\ frac {A} {{x — 2}} + \ frac {B} {{x — 5}}.} \]

Определите неизвестные коэффициенты \ (A \) и \ (B: \)

\ [{\ frac {A} {{x — 2}} + \ frac {B} {{x — 5}}} = {\ frac {{A \ left ({x — 5} \ right) + B \ left ({x — 2} \ right)}} {{\ left ({x — 2} \ right) \ left ({x — 5} \ right)}}} = {\ frac {{Ax — 5A + Bx — 2B}} {{\ left ({x — 2} \ right) \ left ({x — 5} \ right)}}} = {\ frac {{\ left ({A + B} \ right) x — 5A — 2B}} {{\ left ({x — 2} \ right) \ left ({x — 5} \ right)}}. } \]

Тогда мы можем написать

\ [{\ frac {{x + 4}} {{\ left ({x — 2} \ right) \ left ({x — 5} \ right)}}} = {\ frac {{\ left ({ A + B} \ right) x — 5A — 2B}} {{\ left ({x — 2} \ right) \ left ({x — 5} \ right)}}.} \]

Приравняем числители:

\ [x + 4 = \ left ({A + B} \ right) x — 5A — 2B. \]

Отсюда

\ [{\ left \ {\ begin {array} {l} А + В = 1 \\ — 5А — 2Б = 4 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = 1 — В \\ — 5 \ влево ({1 — B} \ вправо) — 2B = 4 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = 1 — В \\ — 5 + 5B — 2B = 4 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = 1 — В \\ 3B = 9 \ end {array} \ right.,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = — 2 \\ В = 3 \ end {array} \ right.2} + 7x + 6}}} = {\ frac {{2x — 3}} {{\ left ({x + 1} \ right) \ left ({x + 6} \ right)}}.} \]

Знаменатель содержит линейные множители. Следовательно, частичное разложение на фракции равно

.

\ [{\ frac {{2x — 3}} {{\ left ({x + 1} \ right) \ left ({x + 6} \ right)}}} = {\ frac {A} {{x + 1}} + \ frac {B} {{x + 6}}.} \]

Упростите правую часть:

\ [{\ frac {A} {{x + 1}} + \ frac {B} {{x + 6}}} = {\ frac {{A \ left ({x + 6} \ right) + B \ left ({x + 1} \ right)}} {{\ left ({x + 6} \ right) \ left ({x + 1} \ right)}}} = {\ frac {{Ax + 6A + Bx + B}} {{\ left ({x + 6} \ right) \ left ({x + 1} \ right)}}} = {\ frac {{\ left ({A + B} \ right) x + \ left ({6A + B} \ right)}} {{\ left ({x + 6} \ right) \ left ({x + 1} \ right)}}.} \]

как

\ [{\ frac {{2x — 3}} {{\ left ({x + 1} \ right) \ left ({x + 6} \ right)}}} = {\ frac {{\ left ({ A + B} \ right) x + \ left ({6A + B} \ right)}} {{\ left ({x + 6} \ right) \ left ({x + 1} \ right)}},} \]

мы можем написать

\ [{2x — 3} = {\ left ({A + B} \ right) x + \ left ({6A + B} \ right).} \]

Это дает:

\ [{\ left \ {\ begin {array} {l} А + В = 2 \\ 6А + В = — 3 \ end {array} \ right. ,} \; \; \ Rightarrow {\ left \ {\ begin {array} {l} А = 2 — В \\ 6 \ влево ({2 — B} \ вправо) + B = — 3 \ end {array} \ right.2}}}.} \]

Пример 7.

Определите разложение на частичную дробь для функции \ (\ large {\ frac {{30x}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right) \ left ({x + 3} \ right)}}} \ normalsize. \)

Решение.

Разложение на частичную дробь имеет вид

\ [{\ frac {{30x}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right) \ left ({x + 3} \ right)}}} = {\ frac {A} {{x + 1}} + \ frac {B} {{x — 2}} + \ frac {C} {{x + 3}}.} \]

Мы объединяем частичные дроби с правой стороны в единую дробь, а затем приравниваем числители с обеих сторон.2}} + {\ left ({A + 4B — C} \ right) x} + {\ left ({- 6A + 3B — 2C} \ right).} \]

Отсюда получаем следующую систему уравнений:

\ [\ left \ {\ begin {array} {l} A + B + C = 0 \\ A + 4B — C = 30 \\ — 6A + 3B — 2C = 0 \ end {array} \ right .. \]

Решив ее, находим неизвестные коэффициенты:

\ [A = 5, \; B = 4, \; C = — 9. \]

Частичное разложение на фракции равно

\ [{\ frac {{30x}} {{\ left ({x + 1} \ right) \ left ({x — 2} \ right) \ left ({x + 3} \ right)}}} = {\ frac {5} {{x + 1}} + \ frac {4} {{x — 2}} — \ frac {9} {{x + 3}}.2}} + {\ left ({\ color {red} A — \ color {red} {2B} + \ color {red} C + \ color {red} D} \ right) \ color {red} x} + {\ color {blue} B — \ color {blue} {2C} + \ color {blue} {2D}.} \]

Приравнивая коэффициенты при одинаковых степенях с обеих сторон, получаем

\ [{\ left \ {\ begin {align} \ color {magenta} A + \ color {magenta} C & = \ color {magenta} 0 \\ — \ color {darkgreen} {2A} + \ color {darkgreen} B + \ color {darkgreen} D & = \ color {darkgreen} 0 \\ \ color {red} A — \ color {red} {2B} + \ color {red} {C} + \ color {red} D & = \ color {red} 0 \\ \ color {blue} B — \ color {blue} {2C} + \ color {blue} {2D} & = \ color {blue} {16} \ end {align} \ right.2} + 2x + 2}} — \ frac {1} {{x — 1}}. } \]

Эндрю Букер решает задачу суммы трех кубов для 33

Математики долго задавались вопросом, можно ли выразить число 33 как сумму трех кубов, то есть имеет ли уравнение 33 = x ³ + y ³ + z ³. Они знали, что 29 может быть записано, например, как 3³ + 1³ + 1³, тогда как 32 не может быть выражено как сумма трех целых чисел, каждое из которых возведено в третью степень. Но дело 33-х оставалось нераскрытым 64 года.

Итак, Эндрю Букер, математик из Бристольского университета, наконец расколол его: он обнаружил, что (8,866,128,975,287,528) ³ + (–8,778,405,442,862,239) ³ + (–2,736,111,468,807,040) ³ = 33.

Букер нашел это 16-значные целые числа, разработав новый алгоритм поиска, чтобы выделить их из квадриллионов возможных. Алгоритм работал на университетском суперкомпьютере три недели подряд. (Он говорит, что думал, что это займет шесть месяцев, но решение «появилось раньше, чем я ожидал».Когда в начале этого месяца в Интернете появилась новость о его решении, коллеги-теоретики чисел и энтузиасты математики были в лихорадке от волнения. Согласно видео Numberphile об открытии, Букер буквально прыгнул от радости в своем офисе, когда узнал об этом.

«Он нашел действительно более эффективный способ поиска решений».

Почему такой восторг? Отчасти это просто сложность поиска такого решения. С 1955 года математики использовали самые мощные компьютеры, которые только могли найти, для поиска в числовой строке тройки целых чисел, удовлетворяющих уравнению «суммы трех кубов» k = x ³ + y ³ + z ³, где k — целое число.Иногда решения просты, например, k = 29; в других случаях известно, что решения не существует, как в случае со всеми целыми числами, которые оставляют после деления остаток 4 или 5 при делении на 9, например, число 32.

Но обычно решения «нетривиальны». В этих случаях трио кубических целых чисел, например (114 844 365) ³ + (110 902 301) ³ + (–142 254 840) ³, что равно 26, больше похоже на лотерейный билет, чем на что-либо с предсказуемой структурой. На данный момент для теоретиков чисел единственный способ найти такие решения — это снова и снова играть в математическую «лотерею», используя грубую силу компьютерного поиска, чтобы пробовать различные комбинации целых чисел в кубе, и надеяться на «победу».»

Но даже при более мощных компьютеров и более эффективных алгоритмов выброшенных на проблему, некоторые целые числа упрямо отказывались давать какие-либо выигрышные билеты. И 33 был особенно упорным случаем: пока Букер не нашел своего решения, это было одно из двух целых чисел, оставшихся ниже 100 (за исключением тех, для которых решения определенно не существует), которое все еще не могло быть выражено в виде суммы трех кубов. . С 33 в стороне, остается только 42.

math master В этом видео Брэди Харан берет интервью у теоретика чисел Эндрю Букера о своем новом решении задачи суммы трех кубов для данного случая. из 33.Numberphile

Причина, по которой на поиск решения для 33 потребовалось так много времени, заключается в том, что поиск достаточно далеко вверх по числовой строке — вплоть до 10 ¹⁶ , или 10 квадриллионов, и так же далеко вниз до отрицательных целых чисел — для правого Численное трио было непрактичным с точки зрения вычислений, пока Букер не разработал свой алгоритм. «Он не просто запустил эту штуку на более крупном компьютере по сравнению с компьютерами 10 лет назад — он нашел действительно более эффективный способ поиска решений», — сказал Тим Браунинг, теоретик чисел из Института науки и технологий Австрии.

Предыдущие алгоритмы «не знали, что они искали», — пояснил Букер; они могли эффективно искать в заданном диапазоне целых чисел решения для k = x ³ + y ³ + z ³ для любого целого числа k , но они не могли найти конкретное число, например, k = 33. Алгоритм Букера мог бы, и поэтому он работает, «может быть, в 20 раз быстрее, с практической точки зрения», — сказал он, — чем алгоритмы, использующие нецелевой подход.

Имея на руках выигрышный билет 33, Букер в следующий раз планирует поискать решение для 42 (он уже определил, что ни один из них не существует в диапазоне 10 квадриллионов; ему придется смотреть дальше в числовой строке, чтобы минимум 10 ¹⁷ .) Но даже когда он или другой теоретик чисел определил решения по сумме трех кубов для каждого подходящего целого числа до 100, тогда они столкнутся с еще 11 «упрямыми» целыми числами без суммы трех -кубики решений от 101 до 1000, и бесконечное их количество.Более того, по словам Букера и других экспертов, каждое новое решение, найденное для одного из этих противников, не проливает теоретического света на то, где и как найти следующее. «Я не думаю, что это достаточно интересные исследовательские цели сами по себе, чтобы оправдать большие суммы денег, чтобы произвольно использовать суперкомпьютер», — сказал Букер.

Так зачем вообще заморачиваться с 33 или 42?

Также по математике

Выберите статистику, которой хотите быть

Дженис Каплан и Барнаби Марш

Однажды в 1954 году женщина по имени Энн Ходжес была в своем доме в Силакоге, штат Алабама, и дремала на диване под большим одеялом, когда кусок черного камня пробил потолок и ударил ее по бедру…. ПОДРОБНЕЕ

Что «достаточно интересно», — объяснил Букер, — это то, что каждое новое решение является «инструментом, помогающим вам решить, что является правдой» в самой задаче суммы трех кубов. Эта проблема, сформулированная как k = x ³ + y ³ + z ³, является тем, что теоретики чисел называют диофантовым уравнением — разновидностью алгебраической структуры, свойства которой очаровывали математиков на протяжении тысячелетий. «Они достаточно богаты, чтобы закодировать [другие математические] утверждения, не имеющие ничего общего с диофантовыми уравнениями», — сказал Браунинг.«Они достаточно богаты, чтобы моделировать компьютеры».

Диофантовы уравнения — это полиномиальные уравнения, неизвестные переменные которых должны принимать целые значения. Их основные свойства могут сбить с толку теоретиков чисел. Например, не существует математического метода, который мог бы надежно сказать, имеет ли какое-либо данное диофантово уравнение решения. По словам Букера, проблема суммы трех кубов «одна из простейших» из этих сложных диофантовых уравнений. «Это прямо на границе того, с чем мы можем справиться», — добавил Браунинг.

По этой причине теоретики чисел стремятся понять все, что они могут, о суммах трех кубиков. Основным результатом было бы доказательство гипотезы о том, что k = x ³ + y ³ + z ³ имеет бесконечно много решений для каждого целого числа k , за исключением тех k , которые имеют остаток от 4 или 5 после деления на 9. Инструменты, разработанные для такого доказательства, могут вскрыть логику проблемы или применить к другим диофантовым уравнениям.Такие результаты, как оценка Букера для 33, подтверждают эту гипотезу, вселяя у теоретиков чисел больше уверенности в том, что это доказательство заслуживает дальнейшего изучения. Действительно, каждый раз теоретики чисел просматривали числовую строку с помощью своих алгоритмов поиска — например, расширяя число до 10 ¹⁴ в 2009 году, до 10 ¹⁵ в 2016 году и теперь до 10 ¹⁶ в 2019 году — новые решения для ранее упрямых целых чисел были надежно найдены, выбивая возможные контрпримеры к гипотезе.

«Все это своего рода накопление данных», — сказал Браунинг. Он отметил, что новое решение Букера для 33 «не изменит ход математических исследований в этой области. Но приятно видеть, что дела идут так, как должны «.

Джон Павлус — писатель и режиссер, чьи работы публиковались в сериях Scientific American, Bloomberg Businessweek, и The Best American Science and Nature Writing . Он живет в Портленде, штат Орегон.

Автор: Люси Ридинг-Икканда / Журнал Quanta

Перепечатано с разрешения блога Quanta Magazine Abstractions.

Сумма и разница кубиков

Сумма или разница двух кубиков может быть разложена на произведение биномиальный умножить на трехчлен.

Это, Икс 3 + y 3 знак равно ( Икс + y ) ( Икс 2 — Икс y + y 2 ) а также Икс 3 — y 3 знак равно ( Икс — y ) ( Икс 2 + Икс y + y 2 ) .

Мнемоника знаков факторизации — слово «SOAP», буквы означают «Тот же знак», что и в середине исходного выражения, «Противоположный знак» и «Всегда положительный».

Это, Икс 3 ± y 3 знак равно ( Икс [ Одно и тоже знак ] y ) ( Икс 2 [ Противоположный знак ] Икс y [ Всегда Положительный ] y 2 )

Пример 1:

Фактор 27 п 3 + q 3 .

Попробуйте записать каждый из терминов в виде куба выражения.

27 п 3 + q 3 знак равно ( 3 п ) 3 + ( q ) 3

Для перезаписи используйте факторизацию суммы кубов.

27 п 3 + q 3 знак равно ( 3 п ) 3 + ( q ) 3 знак равно ( 3 п + q ) ( ( 3 п ) 2 — 3 п q + q 2 ) знак равно ( 3 п + q ) ( 9 п 2 — 3 п q + q 2 )

Пример 2:

Фактор 40 ты 3 — 625 v 3 .

Вынести за скобки GCF из двух условий.

40 ты 3 — 625 v 3 знак равно 5 ( 8 ты 3 — 125 v 3 )

Попробуйте записать каждый член бинома в виде куба выражения.

8 ты 3 — 125 v 3 знак равно ( 2 ты ) 3 — ( 5 v ) 3

Для перезаписи используйте факторизацию разности кубов.

5 ( 8 ты 3 — 125 v 3 ) знак равно 5 ( ( 2 ты ) 3 — ( 5 v ) 3 ) знак равно 5 [ ( 2 ты — 5 v ) ( ( 2 ты ) 2 + 10 ты v + ( 5 v ) 2 ) ] знак равно 5 ( 2 ты — 5 v ) ( 4 ты 2 + 10 ты v + 25 v 2 )

.