Формула произведения логарифмов: Логарифм произведения, сумма логарифмов, формулы и онлайн калькуляторы
| 1. | Логарифм произведения | 1 вид — рецептивный | лёгкое | 2 Б. | Применение логарифма произведения. |
| 2. | Логарифм частного | 1 вид — рецептивный | лёгкое |
2 Б.
|
Применение логарифма частного. |
| 3. | Формула перехода от одного основания логарифма к другому основанию | лёгкое | 2 Б. | Применение формулы перехода от одного основания логарифма к другому основанию. | |
4.
|
2 вид — интерпретация | лёгкое | 3 Б. | Применение свойств логарифмов (логарифм степени и произведения). | |
| 5. | Основное логарифмическое тождество (логарифм степени) | 2 вид — интерпретация | среднее |
4 Б.
|
Применение основного логарифмического тождества с логарифмом степени и определением логарифма. |
| 6. | Свойства логарифмов (степени и произведения) | 2 вид — интерпретация | среднее | 4 Б. | Применение свойств логарифмов (логарифм степени и произведения). |
7.
|
Свойства логарифмов (степени и частного) | 2 вид — интерпретация | среднее | 4 Б. | |
| 8. | Логарифм степени (произведение) | 2 вид — интерпретация | среднее |
3 Б. |
Вычисление произведения логарифмов с использованием логарифма степени. |
| 9. | Логарифм степени (частное) | 2 вид — интерпретация | среднее | 5 Б. | Вычисление частного логарифмов с использованием логарифма степени. |
10.
|
Свойства логарифмов (степень основания, основное логарифмическое тождество) | среднее | 7 Б. | Применение свойств логарифма (степень основания, основное логарифмическое тождество). | |
| 11. | Свойства логарифмов | сложное |
7 Б.
|
Применение свойств логарифма (сложение логарифмов, логарифм степени). | |
| 12. | Свойства логарифмической функции | 2 вид — интерпретация | среднее | 2 Б. | Применение свойств логарифмической функции (возрастание и убывание). Сумма логарифмов. |
13. |
Формула перехода к новому основанию (метод подстановки) | 3 вид — анализ | сложное | 7 Б. | Применение формулы перехода к новому основанию, метод введения новой переменной. |
| 14. | Логарифм произведения (тригонометрическое выражение) | 3 вид — анализ | сложное |
7 Б.
|
Преобразование выражения, стоящего под знаком логарифма в формулу двойного аргумента. |
| 15. | Логарифм произведения | 3 вид — анализ | сложное | 5 Б. | Применение свойств: логарифм произведения и логарифм степени. |
определение и формулы для умножения частного, примеры решения задач
Что такое логарифм произведения
ОпределениеЛогарифм числа по основанию определяется как показатель степени, в которую надо возвести основание, чтобы получить число.
Число а обычно называют основанием, а число b — аргументом логарифма.
Логарифм имеет следующий вид \(\log_a\left(b\right)\) и читается как «логарифм b по основанию a».
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Существуют логарифмы со специальными обозначениями. К ним относятся:
- Десятичный логарифм, который обозначается как lg и всегда имеет основание равное 10: \(\log_{10}=lg.\)
- Натуральный логарифм, который обозначается как ln и всегда имеет основание равное е = 2,718281… (это число иррационально, его невозможно вычислить точно), \(\log_e=ln.\)
Логарифм также имеет основные свойства, которые необходимо помнить для решения примеров:
ТеоремаЛогарифм произведения двух чисел \(x\) и \(y\) равен сумме логарифмов этих чисел, если \(x\), \(y\), \(a\) — положительные числа, где \(a\) — основание и \(a\neq1\). {k+l}\) следует, что \(k+l=\log_a\left(x\times y\right).\)
{k+l}\) следует, что \(k+l=\log_a\left(x\times y\right).\)
Если \(k=\log_a\left(x\right)\) и \(l=\log_a\left(y\right)\), то \(\log_a\left(x\times y\right)=\log_a\left(x\right)+\log_a\left(y\right).\)
Логарифм произведения трех положительных чисел
Формула логарифма произведения применяется также и для нескольких положительных множителей. Возьмем для примера три числа и запишем формулу логарифма произведения в преобразованном виде.
\(\log_a\left(x_1\times x_2\times x_3\right)=\log_a\left(x_1\right)+\log_a\left(x_2\right)+\log_a\left(x_3\right)\)
где \(a\) — логарифмическое основание и \(a, x_1,\;x_2,\;x_3 > 0, a\neq0.\)
Логарифм произведения степени, частного
Помимо логарифма произведения, рассмотрим такие понятия как логарифм степени и частного. Они являются не менее важными для решения задач.
ОпределениеЛогарифм степени с положительным основанием — это показатель степени, умноженный на логарифм ее основания. m\right)=m\times\log_a\left(x\right)\)
m\right)=m\times\log_a\left(x\right)\)
Логарифм частного двух положительных чисел — это разность между логарифмом делимого и логарифмом делителя.
\(\log_a\left(\frac xy\right)=\log_a\left(x\right)-\log_a\left(y\right)\)
Примеры решения задач на логарифмы
Задача 1
Вычислить \(\log_{11}\left(21\right).\)
Решение
Разложим аргумент логарифма на более простые числа и применим формулу логарифма произведения. Получим:
\(\log_{11}\left(21\right)=\log_{11}\left(3\times7\right)=\log_{11}\left(3\right)+\log_{11}\left(7\right)\)
Задача 2
Вычислить \(\log_{1,8}\left(1,8\times\sqrt{11}\right).\)
Решение
Применим формулу логарифма произведения для нескольких множителей. Получим:
\(\log_{1,8}\left(1,8\times\sqrt{11}\right)=\log_{1,8}\left(1,8\right)+\log_{1,8}\left(\sqrt{11}\right)=1+\log_{1,8}\left(\sqrt{11}\right)\)
Задача 3
Вычислить \(\log_{12}\left(\frac8{13}\right). 2\right)=2\times\log_4\left(5\right)\)
2\right)=2\times\log_4\left(5\right)\)
Формулы логарифмов
Логарифмом числа b по основанию a называется показатель степени в которую нужно возвести a , чтобы получить b:
c = log a b ⇔ ac = b , причем b > 0, a > 0, a ≠ 1
Свойства логарифма:
a log a b = b
log a 1 = 0
Логарифм произведения:
log a (u ∙ v) = log a u + log a v
Логарифм отношения:
logauvlogaulogav
Логарифм степени и корня:
log a u n = n ∙ log a u
Формула перехода к новому основанию:
logablogcblogac
Формулы, следующие из свойств логарифма:
lognblognalogmblogmalogablog n a ∙ log m b = log m a ∙ log n b
a log n b = b log n a
Сравнение логарифмов:
Что такое логарифмы: свойства и формулы
- Что такое логарифм?
- Для чего нужны логарифмы?
- Свойства и формулы логарифмов
- Онлайн-калькулятор логарифмов
Логарифмы традиционно считаются сложной темой в математике, однако созданы они были именно для того, чтобы облегчать расчеты. Если раньше ученики старших классов могли просто проигнорировать эту тему, то с введением обязательного ВНО по математике, логарифмы необходимо понимать и уметь использовать.
Если раньше ученики старших классов могли просто проигнорировать эту тему, то с введением обязательного ВНО по математике, логарифмы необходимо понимать и уметь использовать.
Рассказываем, что это такое и почему это не так сложно, как кажется.
Что такое логарифм?
Логарифм – это функция двух переменных, то есть степень, в которую надо возвести основание, чтобы получить аргумент.
Звучит сложно, но дальше будет проще. Расшифруем определение в классической формуле логарифма:
a – основа
x – аргумент
b – значение логарифма
Попробуем подставить простые значения, которые помогут понять принцип работы логарифма:
В какую степень надо возвести 2, чтобы получить 64? В 6.
Поэтому ответ будет:
Еще один пример для тренировки:
Это значит, что 1000 можно получить, если возвести 10 в 4 степень, то есть 4 раза умножить на себя.
Для чего нужны логарифмы?
Логарифмы используются для упрощения подсчетов, когда речь идет об умножении больших цифр, а под рукой нет калькулятора. В давние времена, до повсеместного распространения компьютеров, логарифмы использовались для проведения расчетов в области строительства и черчения, в проектировании техники. А логарифмичные линейки и таблицы были неотъемлемыми инструментами архитекторов, математиков и инженеров.
Если у вас возникают сложности с пониманием логарифмов, хорошим решением станут занятия с репетитором по алгебре. Вместе вы сможете в вашем индивидуальном ритме усвоить каждое свойство логарифмов и проработать полученные знания на практике. Репетитора по любому предмету вы всегда можете найти на сайте Буки.
Попробуем более сложный пример, на котором будет более понятно истинное предназначение логарифмов. Умножим 42,5 на 378 с помощью логарифмической схемы. Для этого необходимо каждый из множителей представить в виде 10 в некоторой степени. Итак:
Умножим 42,5 на 378 с помощью логарифмической схемы. Для этого необходимо каждый из множителей представить в виде 10 в некоторой степени. Итак:
А значит, что:
Попробуем записать пример с помощью логарифма, где 10 будет основой, а 4,2059 – логарифмом.
Если умножим 42,5 на 378 на калькуляторе или вручную и без использования логарифмов, получим то же значение – 16065.
Этот пример мы не могли бы решить логарифмично без знания определенных свойств логарифма, а именно – свойств десятичного логарифма и правила умножения логарифмов. Рассмотрим подробнее некоторые из главных свойств.
Читайте также: Как помочь ребенку подготовиться к ЗНО?Свойства и формулы логарифмов
Логарифмы является удобным и легким способом проводить вычисления, если вы знаете свойства и формулы логарифмов. Все свойства являются действительными в случае, если a>0, a≠1, b>0, c>0
Логарифм единицы из любой основой равен нулю.

Так как в степени ноль равен единице
Логарифм произведения равен сумме логарифмов.
Логарифм суммы равна логарифму произведения.
Логарифм деления равен разнице логарифмов.
Логарифм вычитания равен частному логарифмов.
Логарифм степени равен произведению показателя степени, умноженного на логарифм основания.
Онлайн-калькуляторы логарифмов
Вычислить логарифмы онлайн можно и с помощью стандартного калькулятора от Google. Однако есть и ряд специальных ресурсов, которые помогут и проводить логарифмические вычисления и решать другие математические задачи.
Однако есть и ряд специальных ресурсов, которые помогут и проводить логарифмические вычисления и решать другие математические задачи.
Например, на сайте Symbolab.com можно вычислять логарифмы с пошаговым решением конкретных примеров. Этот онлайн-калькулятор удивительно удобен, если вы хотите отработать свои навыки или на примерах любой сложности понять, как функционируют логарифмы. Кроме того, множество других типичных математических вычислений вместе с пояснениями доступны на сайте бесплатно.
На мультифункциональном сайте RapidTables вы также сможете найти бесплатный и удобный, хотя и более упрощенный, чем в предыдущем калькуляторе, инструмент для вычисления логарифмов.
Не только онлайн-калькулятор логарифмов, но и перечень стандартных логарифмических свойств вы можете найти на сайте Calculator.net в разделе Log calculator.
Читайте также: Рейтинг университетов Украины по специальностям
Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln). Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||
Свойства логарифмов
здравствуйте уважаемые ученики 11-х классов всем привет ребята сегодня мы поговорим про свойство логарифмов я нашел учебники некое количество свойств логарифма давайте обсудим эти свойства и там есть такая логарифм по основанию а о а в степени у равно как это вообще понимать что это значит давайте подумаем об этом примере ну например логарифм по основанию 2 от два в третьей степени что это такое основание 2 а показать на логарифм а это степени два в третьей степени но два в третьей степени это 8 получается в логарифм по основанию 2 по 8 потому что 2 в степени 3 до 8 логарифм по основанию 2 от 8 равен трем почему потому что 2 в третьей степени даст восемь теперь давайте сразу пропустим эту часть как в какую степень нужно возвести 2 чтобы получилось два в три и степень в третью степень нужно возвести и все это очень легко просто фирму логарифм по основанию 5 и 5 в седьмой степени равно попробуйте пожалуйста самостоятельно догадаться какой будет ответ в какую степень нужно возвести 5 чтобы получилось 5 в седьмой степени ну так в седьмую она возвести мне кажется что эта формула очень простая здесь даже как бы показывает ничего нужно наглядно с этой формулы закончили какие еще есть формулы какие еще есть формулы свойств логарифмов есть допустим вот такая формула а в степени логарифм по основанию а от b равно b и так у нас есть степень основание степени это а показатель степени это логарифм что такое логарифм в логарифм путая дверь который показав показатели степени логарифм это такое число что если мы основании возведем в эту степень в это число то получится вот это число то есть сам по себе логарифм вот этот который написан это такая степень чтобы если мы в эту степень возведем вот это число то получится вот это число так мы как раз вот это число и возводим в эту степень и получается вот это число давайте пример какого-нибудь 7 в степени логарифм по основанию 7 вот например 49 давать работу подальше оставим равно логарифму по основанию всей от 49 это два правильно потому что 7 нужно возвести во вторую степень чтобы получить 49 правильно 7 нужно возвести во вторую всеми чтобы получить 49 поэтому эта степень равна двум это этот логарифм равен 2 получается 7 в степени 2 этого получается 49 то есть семь нужно возвести во второй в стиме что получит 49 получается что этот логарифм равен 2 тогда 7 во второй степени равно 49 и как мы видим получается вот здесь то же самое число что здесь если они часто совпадают потому что этот логарифм это такая степень в которую нужно возвести основание чтобы получить показания так мы именно семёрку и возводим вот в такой стиль поэтому 49 и получаем это вот эти формулы они больше основаны на на определение логарифма то есть они все убегают из определения логарифму есть еще формула которую мы с вами раньше не проходили тыс если эти две формулы мы уже как-то разбирали то следующая формула у нас встречается с вами впервые логарифм по основанию а от произведения b умножить на c равно логарифм по основанию а от b плюс логарифм по основанию а вот с давайте какой нибудь наглядный пример разберешь например у нас есть логарифм по основанию 2 от 35 логарифм основали 2-го 35 логарифм по основанию 2 35 это 7 умножить на 5 35 можно представить в виде произведения 7 и может и тогда такие логарифму такой логарифм мы можем представить в виде суммы логарифмов логарифм по основанию 2 от 7 плюс логарифм по основанию 2 от 5 это я просто записал пример как этой формулой пользоваться то есть если мы показатели можем представить в виде произведения то дальше мы можем представить это в виде суммы двух логарифмов но соответственно и наоборот если у нас есть сумма двух логарифмов я основание у этих двух логарифмов одинаковые то в принципе мы можем их сложить когда мы их складываем если основание одинаковые то показатели у них перемножаются можно какую-то сторону можно и в обратном что давайте попробуем такой пример так у нас получилось верное утверждение например 4 это логарифм по основанию 2 от 2 в четвертой степени то сколько будет двора 2444 16 что ли да получается 2 в четвертой степени это 16 поэтому 4 это логарифм по основанию 2 от 16 правильно 2 умножаем на 24 еще умножаем на 28 еще умножаем на 216 поэтому логарифм по основанию 2 от 16 равен 4 хорошо забыли про это логарифм по основанию 2 16 это 4 умножить на 4 до 16 до 4 умножить на 4 получается что это логарифм по основанию 2 4 плюс логарифм по основанию 2 от 4 логарифм по основанию 2 4 равен 2 получается два плюс два давайте даже другое число возьмем например ради интереса пускай будет 5 тогда здесь будет 16 1632 году тогда если здесь 532 тогда здесь 8 умножить на 4 до 32 это 8 умножить на 4 тогда здесь 8 а здесь 4 логарифм основали 2 от 8 это 3 равно 3 плюс 2 итак 5 это логарифм по словам 2 32 потому что 2 степени 532 дальше рассказывать произведение 32 это 8 умножить на 4 тогда это логарифм по основанию 2 от 8 и логарифм основали 2 of 4 но здесь мы ставим знак плюс логарифм по основанию 2 от 8 до 3 логарифм по основанию 2 4 это 2 я конечно данную формулу не доказал использование данной формулы я я не доказал но на конкретном примере мы увидим что она действительно работает если умножить тогда здесь него ставить знак плюс и в принципе получается 5 и 3 + 2 это одно и то же но я думаю что у нас будет какое-то видео на данную формулу мыши по потренируемся какие еще есть формулы есть наоборот частное здесь у нас было произведение а есть частные то есть логарифм по основанию b делить на c как вы думаете чему это будет равно там здесь б а здесь c если было умножение мы вставили знак + если деление то ставим знак минус давайте как один пример попробуем решить например логарифм по основанию 3 под 80 1 делить на 9 равно ну например и поэтому примерных продукта логарифм от 8 по основанию 3 от 81 минус логарифм по основанию 3 от 9 вот смотрите было 8 ст 1 делить на 9 поэтому здесь 81 здесь 9 и ставить знак минус логарифм по основанию 3 от 81 gta 4 потому что 3 в четвертой степени то снова всем ст-1 а3 даст 9 во второй степени между ними знак минус получается 2 получается 24 минус 2 получается по с другой стороны другой стороны 81 разделить на 9 будет 9 поэтому это логарифм по основанию 3 по 9 81 делим на 9 гудели а логарифм по основанию 3 от 9 как раз равен двум осмотрите все правильно получается можете взять какие-то свои числа другие не 81 и 9 а другие и попробуют проведения формула все равно будет работать какие у нас еще есть формулы что-то сегодня плохо стирается почему-то то закрыл страничку вот так произведения разобрали частное разобрали кстати говоря есть ряд нюансов о которых я ничего не сказал вот я использовал формула да какие то нужно конечно а говорится во первых основание логарифма то что а да у нас во всех формулах основание логарифма это буква а так вот а с одной стороны это положительное число или с другой стороны они равна одному это ограничение действует всегда и везде не важно какую именно формулы мы берем всегда основание логарифма должно быть больше 0 и не равно единице всегда показатель логарифм должен быть положительным числом то есть мой формулах использовали буквы a и b и c в основание было а показатель она горит мы использовали буквы bbc эти буквы они тоже должны быть строго положительными нельзя чтобы они были отрицательными это действует это правило действует для всех формул то есть показатель догорит мы всегда должен быть положительным основании тоже должно быть положительным и не равно 1 таки еще формулы и вести а есть еще вот такая форма есть еще такая логарифм по основанию а вот b в степени m равно r умножить на логарифм а по основанию х от б это формула немножко похоже на самую первую формулу которое у нас было но она чуть-чуть другая то есть если у нас вот здесь есть степень мы можем ее вынести эту степень вперед со знаком умножить со знаком давайте понимать пример покажу например логарифм по основанию 2 по основанию 3 например вот 7 в квадрате основание 3 показатели 7 в квадрате мы не можем никак ты это посчитать потому что 7 в квадрате это 49 и чтобы трое из тройки получить 49 мы ни в какую степень не можем известить поэтому все что мы можем сделать это вот эту двойку вынести вперед со знаком умножения и у вас получается 2 умножить на логарифм по основанию 3 got7 вот такой такое вот применение иногда это применяют для того чтобы даже не знаю например у нас есть один логарифм такой и один выберешь такой у них основании одинаковые показатели разные если вот от степени избавиться торгу показатель например одинаковые иногда в редких случаях это этой формулы пользуются для решения этих ему пример очках что еще все форму есть кстати говоря такая же форма на основании но и щас я его не вижу так значит здесь опять же а у нас должно быть и бы положительные числа они равно одному вот р любое число ну на этом наверно формулу закончились основные да есть еще некая царева здесь что значит если у нас есть два локализма с одинаковым основанием я нам лучше чуток 6 расскажу здесь например б а здесь например с если есть два логарифмов с одинаковыми словами то если эти логарифмы равны между собой тогда овны и показатели этих логарифмов если логарифмы равны то равны и показатели этих логарифм если например у нас один логарифмом больше другого здесь опять же об этом не написали давать я расскажу все равно да если например один логарифм больше другого то это значит что этот показатель больше этого показателя но только в тех случаях когда у нас больше одного если основание больше и ниц и то сравнивая два логарифм а если мы видим что один логарифму больше другого основания одинаковые с даже показатели больше показателя если вдруг основание у нас лежит в интервале от нуля до единицы то знаки нужно обязательно менять когда мы переходим от самих логарифмов их показателям то знаки обязательно меняются если основание было меньше единицы ноги основание должно быть нынешний то есть например мы решали задачи мы говорим что у нас есть логарифм по основанию 2 от x это больше чем логарифм по основанию 2 от 10 основании одинаковые можем перейти к показателям x больше десяти потому что основание у нас больше 1 2 раза больше чем один а если у нас будет например логарифм по основанию 0,5 x больше либо равно чем логарифм по основанию целых пять десятых от 7 обмен тогда x меньше либо равно 7 почему знак меняем потому что основание меньше 1 ну еще пример и логарифм по основанию 0,5 от x больше либо равно логарифм по основанию 0,6 от 10 тогда x10 какое поставим знак больше или меньше никакой не можем поставить знак потому что здесь одно основание а здесь другое основание если основание разные здесь одно а здесь другое ничего делать не можем не можем их сравнивать то есть сравнивать можно только логарифму с одинаковым основанием это были все свойства логарифмов которые хотел вам рассказать на этом все ребят всем пока
Определение логарифма, логарифм произведения, степени, частного.
 Решение показательных и логарифмических уравнений и неравенств
Решение показательных и логарифмических уравнений и неравенствОПРЕДЕЛЕНИЕ ЛОГАРИФМА. ЛОГАРИФМ ПРОИЗВЕДЕНИЯ, СТЕПЕНИ, ЧАСТНОГО.
Определение. Логарифмом положительного числа по основанию () называется показатель степени, в которую надо возвести , чтобы получить .
В записи число является основанием степени, — показателем, — степенью. Число - это показатель степени, в которую надо возвести основание , чтобы получить число . Следовательно, - это логарифм числа по основанию :
.
Можно сказать, что формулы и равносильны, выражают одну и ту же связь между числами , и (при > 0, ¹ 1, > 0). Число - произвольно, никаких ограничений на показатель степени не накладывается.
Равенство
называется основным логарифмическим тождеством.
Представляя в равенстве выражение в виде степени, получим ещё одно тождество
.
Теорема. Для чисел > 0, > 0, > 0, ¹ 1 верны следующие тождества, выражающие свойства логарифмов:
1) , т. е. логарифм произведения равен сумме логарифмов множителей;
2) , т. е. логарифм дроби равен разности логарифмов числителя и знаменателя;
3) , т. е. логарифм степени равен показателю степени, умноженному на логарифм основания.
Доказательство. 1) Пусть , . По основному логарифмическому тождеству , . Перемножим эти равенства: . По свойству степеней , т. е. . По определению логарифма
, т. е.
, что и требовалось доказать.
2) Пусть , . По основному логарифмическому тождеству: , . Тогда
.
По свойству степеней
, т. е.
.
По определению логарифма
, т. е.
, что и требовалось доказать.
3) Пусть . По основному логарифмическому тождеству . Тогда
.
По определению логарифма
, т. е. . Теорема доказана.
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ. ФОРМУЛА ПЕРЕХОДА ОТ ОДНОГО ОСНОВАНИЯ К ДРУГОМУ.
Если в равенстве основание равно 10, то логарифм называется десятичным и обозначается . Если же в равенстве основание равно , где - бесконечная непериодическая десятичная дробь, то логарифм называется натуральным и обозначается . Свойства десятичных и натуральных логарифмов аналогичны свойствам обыкновенных логарифмов и они отличаются лишь формой записи.
Рассмотрим некоторые свойства логарифмов:
- Логарифм единицы по любому основанию равен нулю, т. е. .
- Если логарифм некоторого числа равен нулю, то это число равно единице, т. е. когда , то .
- Если число и основание
логарифма равны между собой, то логарифм равен единице, т.
 е. . В частности ,
.
е. . В частности ,
. - Если логарифм некоторого числа равен единице, то это число равно основанию логарифма, т. е. если , то .
- Если два числа имеют один и тот же логарифм при данном основании, то эти числа равны между собой, т. е. из равенства следует .
- Если число и основание логарифма одновременно больше или меньше единицы, то логарифм положителен, т. е. если (или ) то .
- Если число и основание логарифма расположены по разные стороны от единицы, то логарифм отрицателен, т. е. если а или а , то .
- . В частности , .
- Если основание логарифма больше единицы, то большему из двух положительных чисел соответствует больший логарифм, т. е. если и , то .
- Если основание логарифма
меньше единицы, то большему из двух положительных чисел соответствует
меньший логарифм, т.
 е. если и , то .
е. если и , то .
Между логарифмами некоторого положительного числа с двумя разными основаниями и существует зависимость, которую можно выразить формулой
.
Эту формулу называют формулой перехода от одного основания к другому. В частности из неё следует, что или , кроме того , .
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ ЛОГАРИФМЫ.
Используя свойства логарифмов, можно представить логарифм некоторого выражения, составленного из положительных чисел с помощью операций умножения, деления и возведения в степень, в виде суммы логарифмов входящих в него чисел.
Такое преобразование называют логарифмированием.
Пример 1. Прологарифмировать выражение по основанию ().
.
Решение. Применяя свойства логарифмов, получим
.
Во многих случаях
приходится решать обратную задачу, т. е. находить выражение, логарифм которого
представлен через логарифмы некоторых чисел. Такое преобразование называют потенцированием.
е. находить выражение, логарифм которого
представлен через логарифмы некоторых чисел. Такое преобразование называют потенцированием.
Пример 2. Найти , если
.
Решение. Используя свойства логарифмов, получаем:
. Таким образом . Отсюда .
РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ И ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ.
Доказательство правила произведения логарифмов
Формула
$\log_{b}{(m \times n)}$ $\,=\,$ $\log_{b}{m}+\log_{b}{n}$
Правило произведения является наиболее часто используемым логарифмическим тождеством в логарифмах. Он утверждает, что логарифм произведения величин равен сумме их логов. Это может быть доказано математически в алгебраической форме с помощью соотношения между логарифмами и показателями и правилом произведения показателей.
Запись количества в экспоненциальной форме
$m$ и $n$ — две величины, обе величины выражаются в форме продукта на основе другой величины $b$. {\ Displaystyle с} $
{\ Displaystyle с} $
Теперь представим уравнение в логарифмической форме.
$\ подразумевает \log_{b}{p} = s$
Заменить фактические значения величин $s$ и $p$.
$\ подразумевает \log_{b}{(m.n)} = x+y$
Получить логарифмическое свойство
Логарифм произведения двух величин $m$ и $n$ по основанию $b$ равен сумме величин $x$ и $y$.
На самом деле, $x \,=\, \log_{b}{m}$ и $y \,=\, \log_{b}{n}$. Замените их, чтобы получить свойство правила произведения логарифмов.
$\,\,\, \поэтому \,\,\,\,\,\, \log_{b}{(mn)}$ $\,=\,$ $\log_{b}{m}+ \log_{b}{n}$
Доказано, что логарифм произведения двух величин по основанию равен сумме их логов по одному основанию. Этот фундаментальный принцип не ограничивается двумя величинами и может применяться более чем к двум величинам. Поэтому это логарифмическое тождество используется в качестве формулы в математике.
$\log_{\displaystyle b}{(mno \cdots)}$ $=$ $\log_{b} m$ $+$ $\log_{b} n$ $+$ $\log_{b} o$ $\большой + \cdots$
Примеры правила произведения логарифмов
Основное правило произведения логарифмов представляет собой математическое соотношение между логарифмом произведения двух или более чисел и суммой их логарифмов.
Использовать
Свойство закона произведения логарифмов в основном используется в математике в двух случаях.
- Для сокращения суммы логарифмов двух или более величин как логарифма произведения величин.
- Разложить логарифм количества как сумму логарифмов двух или более величин, произведение которых равно количеству.
Примеры
Обратите внимание на каждый случай использования правила произведения в качестве формулы из следующих примеров.
Преобразование суммы в форму произведения
Если сумма двух или более логарифмических членов, основания которых совпадают и соединены знаком плюс, то сумма логарифмов величин может быть упрощенно записана как логарифм произведения величин по правилу произведения логарифмов.
$(1) \,\,\,\,\,\,$ $\log{3} + \log{4}$
$\ подразумевает \log{3}+\log{4} \,=\, \log{(3 \times 4)}$
$\ подразумевает \log{3}+\log{4} \,=\, \log{12}$
$(2) \,\,\,\,\,\,$ $\log_{2}{5}$ $+$ $\log_{2}{6}$ $+$ $\log_{2} {7}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{2}{(5 \times 6 \times 7)}$ $\,=\,$ $\log_{2}{210}$
$(3) \,\,\,\,\,\,$ $\log_{e}{8} + \log_{e}{9} + \log_{e}{10} + \log_{e {11}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{e}{(8 \times 9 \times 10 \times 11)}$ $\,=\,$ $\log_{e}{7920}$
$(4) \,\,\,\,\,\,$ $\log_{27}{\Bigg(\dfrac{2}{3}\Bigg)}$ $+$ $\log_{27} {\Bigg(\dfrac{4}{5}\Bigg)}$ $+$ $\log_{27}{\Bigg(\dfrac{6}{7}\Bigg)}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{27}{\Bigg(\dfrac {2}{3} \times \dfrac{4}{5} \times \dfrac{6}{7}\Bigg)}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{27}{\Bigg(\dfrac {2 \times 4 \times 6}{3 \times 5 \times 7}\Bigg)}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\require{cancel} \log_{27}{ \Bigg(\dfrac{2 \times 4 \times \cancel{6}}{\cancel{3} \times 5 \times 7}\Bigg)}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{27}{\Bigg(\dfrac {2 \times 4 \times 3}{1 \times 5 \times 7}\Bigg)}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{27}{\Bigg(\dfrac {24}{35}\Bigg)}$
$(5) \,\,\,\,\,\,$ $\log_{x}{a} + \log_{x}{b} + \log_{x}{c}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{x}{(a \times b \раз в)}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\,\,$ $\log_{x}{abc}$
Преобразование произведения в сумму
Правило произведения логарифмов также используется для преобразования логарифма количества в сумму логарифмов количества путем преобразования количества в произведение двух или более количеств.
$(1) \,\,\,\,\,\,$ $\log_{3}{10}$
$\implies \log_{3}{10}$ $\,=\,$ $\log_{3}{(2 \times 5)}$
$\implies \log_{3}{10}$ $\,=\,$ $\log_{3}{2} + \log_{3}{5}$
$(2) \,\,\,\,\,\,$ $\log{105}$
$\ подразумевает \log{105} \,=\, \log{(3 \times 5 \times 7)}$
$\ подразумевает \log{105} \,=\, \log{3} + \log{5} + \log{7}$
$(3) \,\,\,\,\,\,$ $\log_{17}{1430}$
$\имплициты \log_{17}{1430} \,=\, \log_{17}{(2 \times 5 \times 11 \times 13)}$
$\имплициты \log_{17}{1430}$ $\,=\,$ $\log_{17}{2}$ $+$ $\log_{17}{5}$ $+$ $\log_{ 17}{11}$ $+$ $\log_{17}{13}$
$(4) \,\,\,\,\,\,$ $\log_{a}{xy}$
$\ подразумевает \log_{a}{xy} = \log_{a}{(x \times y)}$
$\ подразумевает \log_{a}{xy} = \log_{a}{x} + \log_{a}{y}$
$(5) \,\,\,\,\,\,$ $\log_{e}{\Bigg(\dfrac{15}{7}\Bigg)}$
$\ подразумевает \log_{e}{\Bigg(\dfrac{15}{7}\Bigg)} \,=\, \log_{e}{\Bigg(\dfrac{3 \times 5}{7} \Бигг)}$
$\ подразумевает \log_{e}{\Bigg(\dfrac{15}{7}\Bigg)} \,=\, \log_{e} 3 + \log_{e}{\Bigg(\dfrac {5 {7}\Bigg)}$
Правила логарифмирования – объяснение и примеры
Что такое логарифм? Зачем мы их изучаем? И каковы их правила и законы?
Начнем с того, что логарифм числа «b» можно определить как степень или степень, в которую нужно возвести другое число «a», чтобы получить результат, равный числу b.
Мы можем представить это утверждение символически как;
log a b = n.
Точно так же мы можем определить логарифм числа как обратную его степень. Например, log a b = n можно экспоненциально представить как; а н = б.
Таким образом, мы можем сделать вывод, что;
a n = b ⇔ log a b = n.
Хотя логарифмы изучают в школах для упрощения вычислений с большими числами, они по-прежнему играют важную роль в нашей повседневной жизни.
Давайте рассмотрим некоторые из этих применений логарифмов:
- Мы используем логарифмы для измерения кислотности и щелочности химических растворов.
- Измерение интенсивности землетрясений производится по шкале Рихтера с использованием логарифмов.
- Уровень шума измеряется в дБ (децибелах) по логарифмической шкале.
- Экспоненциальные процессы, такие как распад отношения активных изотопов, рост бактерий, распространение эпидемии в популяции и охлаждение трупа, анализируются с использованием логарифмов.

- Для расчета периода выплаты кредита используется логарифм.
- В исчислении логарифм используется для различения сложных задач и определения площади под кривыми.
Как и у показателей степени, у логарифмов есть правила и законы, которые работают так же, как правила показателей степени. Важно отметить, что законы и правила логарифмов применимы к логарифмам любого основания. Однако во всех вычислениях должна использоваться одна и та же база.
Мы можем использовать законы и правила логарифмирования для выполнения следующих операций:
- Приведение логарифмических функций к экспоненциальной форме.
- Сложение
- Вычитание
- Умножение
- Деление
- Расширение и сжатие
- Решение логарифмических уравнений.
Законы логарифмов
Логарифмические выражения могут быть записаны по-разному, но в соответствии с определенными законами, называемыми законами логарифмов. Эти законы могут быть применены к любому основанию, но при расчете используется одно и то же основание.
Четыре основных закона логарифмов включают:
Закон правила произведения
Первый закон логарифмов утверждает, что сумма двух логарифмов равна произведению логарифмов.Первый закон представлен как;
⟹ Журнал + log b = log ab
Пример:
- log 2 5 + log 2 4 = log 2 (5 × 4) = log 2 20
- log 10 6 + log 10 3 = log 10 (6 x 3) = log 10 18
- log x + log y = log (x * y) = log xy 4 9093
- log 10 6 – log 10 3 = log 10 (6/3) 8 0 3
- log 2 4x — log 2 x = log 2 (4x / x) = log 2 4
- log 10 5 3
5 3 = 3 log 10 5
- 2 10190
- 5 ln x 2 = ln x (2 * 5 ) = ln x 10
- лог 4 16 = (лог 16) / (лог 4).

- Учитывая, что a n = b ⇔ log a b = n, логарифм числа b определен только для положительных действительных чисел.
- Логарифм положительного действительного числа может быть отрицательным, нулевым или положительным.
- 3 2 = 9 ⇔ Log = 9 ⇔ Log 3 9 = 2
- 5 4 = 625 ⇔ log 5 625 = 4
- 7 0 = 1 ⇔ log 7 1 = 0
- 2 -3 = 1 / 8 ⇔ log 2 ( 1 / 8 ) = -3
- 10 -20 = 0,01 ⇔ log 10 01 = -2
- 2 6 = 64 ⇔ log 2 64 = 6
- 3 — 4 = 1/3 4 = 1/81 ⇔ log 3 1/81 = -4
- 10 -2 = 1/100 = 0.
 01 ⇔ log 10 01 = -2
01 ⇔ log 10 01 = -2 - Логарифмические значения данного числа различны для разных оснований.
- 9 81 ≠ LOG 3 81
- LOG 2 16 ≠ LOG 4 16
- Logarithms до базы 10 называются общими логарифми. Когда логарифм записывается без основания нижнего индекса, мы предполагаем, что основание равно 10.
- log 21 = log 10
- log 0.05 = log 10 05
- Логарифм по основанию «е» называется натуральным логарифмом. Константа e приблизительно равна 2,7183. Натуральные логарифмы выражаются как ln x, что равно log e
- Логарифмическое значение отрицательного числа является мнимым.
- Логарифм 1 по любому конечному ненулевому основанию равен нулю.
A 0 = 1 ⟹ Log A 1 = 0. - Логарифм любого положительного числа к тому же основанию равно 1.

- log 10 10 = 1
- log 2 2 = 1
- Учитывая, что x = log A M, то 10189 Журнал M = A
9
log x = log (4x * x) = log 4x.
⟹ журнал A − журнал B = журнал (A/B)
Пример:
Закон правила мощности
⟹ Журнал A N = N Журнал A
Пример:
Изменение закона базового правила
⟹ log B x = (log A x) / (log A b)
Пример 4:
Правила логарифмов
Логарифмы — очень дисциплинированная область математики. Они всегда применяются в соответствии с определенными правилами и положениями.
При игре с логарифмами необходимо помнить следующие правила:
⟹ a > 0 (a ≠ 1), a n > 0.
Примеры
примеры
Примеры
Пример:
7 0 = 1 ⇔ LOG 7 1 = 0
а 1 = а ⟹ log а а = 1.
примеров
Пример 1 Оцените следующее выражение. log 2 8 + log 2 4 Решение Применяя закон правила произведения, получаем; log 2 8 + log 2 4 = log 2 (8 x 4) = log 2 32 Перепишите 32 в экспоненциальной форме, чтобы получить показатель степени. 32 = 2 5 Следовательно, 5 — это правильный ответ Пример 2 оценить журнал 3 162 — LOG 3 2 Решение Это выражение вычитания; поэтому мы применяем закон частного правила. log 3 162 — log 3 2 = log 3 (162/2) = log 3 81 Написать аргумент в экспоненциальной форме 81 = 3 4 Следовательно, ответ 4. Пример 3 Разверните приведенное ниже логарифмическое выражение. Log 3 (27x 2 Y 5 ) Решение Log (27x 2 y 5 ) = log 3 27 + log 3 x 2 + log 3 y 5 y 5 = log 3 (9) + log 3 (3) + 2Log 3 x + 5Log 3 Y , но журнал 3 9 = 3 Подставить, чтобы получить. = 3 + log 3 (3) + 2log 3 x + 5Log 3 Y Пример 4 Рассчитать значение log √2 64. Решение ⟹ log √2 64 = log √2 (2) 6 ⟹ log √2 64 = 6Log √2 (2) ⟹ log √2 64 = 6Log √2 (√2) 2 ⟹ log √2 64 = 6 * 2LOG √2 (√2) ⟹ LOG √2 64 = 12 * 2 (1) ⟹ log √2 64 = 12 Пример 5 Найдите x, если log 0.1 (0,0001) = x Решение ⟹ log 0,1 (0,0001) = log 0,1 (0,1) 4 ⟹ log 0,1 (0,0001) = 4Log 0,1 0,1 ⟹ log 0.1 (0,0001) = 4 (1) ⟹ log 0,1 (0,0001) = 4 Следовательно, x = 4. Пример 6 Найти значение x , 2log x = 4log3 Решение 2logx = 4log3 Разделите каждую сторону на 2. ⟹ log x = (4log3) / 2 ⟹ log x = 2Log3 ⟹ log x = log3 2 ⟹ log x = log9 x = 9 Пример 7 Вычислить log 2 (5x + 6) = 5 Решение Переписать уравнение в экспоненциальной форме 2 5 = 5x + 6 Упростить. 32 = 5x + 6 32 = 5x + 6 Вычтете обе стороны уравнения на 6 32 — 6 = 5x + 6 — 6 26 = 5x x = 26/5 Пример 8 Решите log x + log (x−1) = log (3x + 12) Решение ⇒ log [x (x — 1)] = log (3x + 12) Чтобы получить, отбросьте логарифмы; ⇒ [x (x − 1)] = (3x + 12) Применить распределительное свойство, чтобы убрать скобки. ⇒ x 2 — x = 3x + 12 ⇒ x 2 — x — 3x — 12 = 0 ⇒ x 2 — 4x — 12 = 0 ⇒ (x — 6) ( x+2) = 0 ⇒x = − 2, x= 6 Поскольку аргумент логарифма не может быть отрицательным, то правильный ответ: x = 6. Пример 9 – ln (2x) = ln 4x Solution ln [32/(2x)] = ln 4x Отбросьте натуральные бревна. [32/ (2x)] = 4x 32/ (2x) = 4x. Крест умножить. 32 = (2x)4x 32 = 8x 2 Разделите обе стороны на 8, чтобы получить; x 2 = 4 x = – 2, 2 Поскольку мы не можем иметь логарифм отрицательного числа, то х = 2 остается правильным ответом. Это история об интересном полете фантазии с математикой. Я нашел это интригующим, и надеюсь, что вы тоже. Вот факт, который всплывает в средней школе по математике: вы можете понизить умножение до сложения, используя логарифмы. То есть: То есть вы можете вычислить журнал продукта, учитывая только журналы факторов. Сегодняшним студентам это может показаться просто еще одним алгебраическим тождеством.Но в эпоху, когда еще не было калькуляторов, это была главная причина, по которой типичный старшеклассник вообще интересовался логарифмами! Умножение сложнее, чем сложение, поэтому, если у вас есть способ представления чисел, превращающий умножение в сложение, это поможет. Это весь принцип, лежащий в основе выполнения умножения, например, с помощью логарифмической линейки: нужно просто преобразовать в логарифмы, сложить полученные расстояния, а затем преобразовать обратно. Точно так же можно использовать логарифмы, чтобы перевести степени в умножение: Но если мы представляем себе мир, в котором мы работаем исключительно с логарифмами, не совсем справедливо просто умножать на y , поэтому я собираюсь переписать это (условимся, что все логарифмы натуральные) как: Там есть дополнительная экспоненциальная функция, но если мы примем ее как данность, мы теперь можем вычислить логарифм степени, используя только умножение, экспоненциальную функцию и логарифмы входы. Интересный вопрос: как насчет сложения? Следующее работает , а не , хотя учителя математики признают это очень распространенной ошибкой! Итак, мы можем завершить это уравнение? На первый взгляд, рассматривая логарифм как преобразование операций на один порядок вниз (умножение в сложение и показатели степени в умножение), кажется, что требуется операция на порядок ниже , чем сложение. Что может поместиться в таком месте? Мы можем начать отвечать на этот вопрос, используя простую алгебру и наши существующие тождества.Давайте предположим, что x не равно нулю (так как тогда у него все равно не было бы логарифма!), и тогда мы можем разложить: Таким образом, применяя логарифмическое правило для умножения, мы получаем изящную маленькую формулу: Обратите внимание, что хотя презентация здесь не выглядит симметричной, это действительно так. Опять же, если представить, что у нас есть только логарифмы, а не фактические значения, эта дробь в конце — это своего рода мошенничество.Как и в случае с формулой умножения, я введу явную экспоненту, и это здорово упростит. Чтобы это было более понятно, я назову новую функцию h и определю в терминах этого: Правда, избавиться от сложения не удалось, но это куда-то ведет. интересный. Но что это за загадочная функция h ? Мы можем начать исследовать h , взглянув на график. На первый взгляд кажется, что h ( x ) приблизительно равно нулю для любых входных данных, меньших -2, и приблизительно x для любых входных данных, превышающих 2. Действительно, мы можем изобразить две функции на одних и тех же осях и увидеть, что они совпадают, кроме нуля. (Вы также можете проверить это, рассуждая о формуле. Для входных данных, намного меньших нуля, экспоненциальный член становится незначительным, а для входных данных, намного больших нуля, постоянный член становится незначительным.Это основа не слишком строгого доказательства того, что это асимптоты.) Таким образом, мы можем рассматривать h как мягкую выпрямленную линейную функцию; то, что вы получаете, просто округляя выпрямленную линейную функцию вокруг ее острого угла. (Эта выпрямленная линейная функция, кстати, была популяризирована в машинном обучении, где по причинам, которые зависят от того, кого вы спросите, она оказалась чрезвычайно успешной в качестве функции активации для искусственных нейронных сетей. Итак, если ч так похоже на выпрямленную линейную функцию , что происходит, когда вы (неточно) используете саму выпрямленную линейную функцию в приведенной выше формуле суммы. Примечательно, что вы получаете это: Другими словами, с точки зрения логарифмов, сложение чисел приблизительно равносильно взятию максимума! По крайней мере, когда разница между числами велика.На самом деле в этом есть смысл. Если вы прибавите очень большое число к очень маленькому числу, результат действительно будет примерно таким же, как и большое число. (Помните, что, поскольку мы думаем только о числах с логарифмами, оба входа должны быть положительными. Мы можем извлечь из этого шаблона что-то вроде «мягкая» максимальная функция, которая равна почти , как если бы она просто задавала больший из двух своих аргументов, но если аргументы близки, то она округляет кривую.К сожалению, фраза softmax уже означает что-то другое и несколько более сложное для упомянутого выше сообщества машинного обучения, поэтому, возможно, вместо этого мы должны называть это как-то вроде smoothmax . Тогда у нас есть ответ: На самом деле, его нелегко вычислить в том смысле, в каком вычисляются произведения и мощности, но это все же дает некоторую интуицию для функции, согласно которой выполняет вычисление логарифма суммы, учитывая логарифмы слагаемые.Во всяком случае, я достаточно удовлетворен этим ответом. Это говорит нам о том, что данная функция smoothmax может играть роль сложения в математических выражениях. Это означает, что все алгебраические свойства сложения должны выполняться и для smoothmax . Это интересно! Например, smoothmax должны быть коммутативными. То есть: Действительно, это правда. Я сделал это наблюдение выше, когда впервые вводил формулу.Можно также ожидать, что smoothmax является ассоциативным. То есть: И действительно, хотя алгебра немного сложнее, это тоже оказывается правдой. На самом деле нам не нужно показывать каждое из них с помощью сложной алгебры. Мы уже показали, что smoothmax — это сложение , просто используя логарифмы для представления чисел. Я думаю, что все становится еще интереснее, когда мы рассматриваем свойство дистрибутива . Однако есть вещи, которые не работают. Вы также можете надеяться на что-то вроде свойства идентичности, поскольку для сложения у нас есть x + 0 = x. Это не так хорошо получается, потому что мы не умеем логарифмировать ноль! В конечном итоге мы хотим написать что-то вроде: Это имело бы смысл, учитывая асимптотическое поведение функции smoothmax , но мы играем здесь как бы быстро и свободно с бесконечностями, поэтому я бы не назвал это истинным тождеством. .Чтобы правильно сказать, нужны ограничения. Вы также должны быть осторожны, ожидая, что smoothmax будет действовать как максимум! Например: Это странно… но не в том случае, если вы помните, что smoothmax наименее точен, когда два его входа расположены близко друг к другу, поэтому оба входа одинаковы — это наихудший сценарий. На самом деле, говоря о плавном максимизации числа с самим собой: , что напоминает своего рода определение сложения логарифмических натуральных чисел как «повторение smoothmax числа с самим собой», во многом в том же смысле, что и умножение на Натуральные числа можно определить как многократное сложение числа с самим собой, укрепляя представление о том, что эта операция как бы на один порядок ниже, чем сложение. Вот и все.Это насколько далеко простирается мой полет фантазии. Я нашел это достаточно интересным, чтобы поделиться. Логарифм
является показателем. г
= б х экспоненциальная форма х
= log b y логарифмический
форма x — логарифм y по основанию b log b y — это степень, в которую мы должны возвести b, чтобы получить y Мы выражаем x через y Примеры х = бревно б у Логарифм 1 всегда равен 0. Любое число может служить основанием b. Логарифмы
по основанию 10 широко используются. Таким образом, обычно опускают индекс.Если основание не отображается, подразумевается, что основание равно 10. журнал 10 у = log у Рассмотрим следующие таблицы и соответствующие графики: x f(x) = e x x f(x)= ln x 0 1 1 0 1 2. 2,7 1 2 7,39 7,39 2 3 20 20 3 [Индекс] Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится
на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату. Чтобы подать уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. Отправьте жалобу нашему назначенному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: К концу этого раздела вы сможете: Будьте готовы 10. Прежде чем начать, пройдите этот тест на готовность. Оценка: ⓐ a0a0 ⓑ a1.a1. Будьте готовы 10.11 Запишите с рациональным показателем: x2y3.x2y3. Будьте готовы 10.12 Округлить до трех знаков после запятой: 2,5646415. Теперь, когда мы узнали об экспоненциальных и логарифмических функциях, мы можем ввести некоторые свойства логарифмов.Это будет очень полезно, поскольку мы продолжаем решать как экспоненциальные, так и логарифмические уравнения. Первые два свойства вытекают из определения логарифмов. Поскольку a0=1,a0=1, мы можем преобразовать это в логарифмическую форму и получить loga1=0.loga1=0. Кроме того, поскольку a1=a,a1=a, мы получаем logaa=1. В следующем примере мы могли бы вычислить логарифм путем преобразования в экспоненциальную форму, как мы делали ранее, но распознавание и последующее применение свойств экономит время. Вычислить, используя свойства логарифмов: ⓐ log81log81 и ⓑ log66.log66. ⓐ ⓑ Попробуйте 10,55 Оцените, используя свойства логарифмов: ⓐ log131log131 ⓑ log99.журнал99. Попробуйте 10,56 Вычислить, используя свойства логарифмов: ⓐ log51log51 ⓑ log77. Следующие два свойства также можно проверить, преобразовав их из экспоненциальной формы в логарифмическую или наоборот. Экспоненциальное уравнение alogax=xalogax=x преобразуется в логарифмическое уравнение logax=logax,logax=logax, которое верно только для положительных значений для x . Логарифмическое уравнение logaax=xlogaax=x преобразуется в показательное уравнение ax=ax,ax=ax, что также является верным утверждением. Эти два свойства называются обратными свойствами, потому что, когда мы имеем одно и то же основание, возведение в степень «отменяет» бревно, а взятие бревна «отменяет» возведение в степень. Эти два свойства показывают композицию функций. Оба получили функцию тождества, которая снова показывает, что экспоненциальная и логарифмическая функции являются обратными функциями. Для a>0,a>0,x>0x>0 и a≠1,a≠1, В следующем примере применяются обратные свойства логарифмов. Оцените, используя свойства логарифмов: ⓐ 4log494log49 и ⓑ log335.log335. ⓐ ⓑ Попробуйте 10,57 Вычислить, используя свойства логарифмов: ⓐ 5log5155log515 ⓑ log774.log774. Попробуйте 10,58 Вычислить, используя свойства логарифмов: ⓐ 2log282log28 ⓑ log2215.log2215. Есть еще три свойства логарифмов, которые будут полезны в нашей работе. В свойстве произведения показателей, am·an=am+n,am·an=am+n, мы видим, что для умножения одного и того же основания мы складываем показатели степени. Свойство продукта логарифмов, logaM·N=logaM+logaNlogaM·N=logaM+logaN говорит нам взять журнал произведения, мы добавляем журнал факторов. Если M>0,N>0,a>0M>0,N>0,a>0 и a≠1,a≠1, то Логарифм произведения равен сумме логарифмов. Мы используем это свойство, чтобы записать журнал продукта в виде суммы журналов каждого фактора. Используйте свойство продукта логарифмов, чтобы записать каждый логарифм как сумму логарифмов. Если возможно, упростите: ⓐ log37xlog37x и ⓑ log464xy. ⓐ ⓑ Попробуйте 10.59 Используйте свойство продукта логарифмов, чтобы записать каждый логарифм как сумму логарифмов. ⓐ log33xlog33x ⓑ log28xylog28xy Попробуйте 10,60 Используйте свойство продукта логарифмов, чтобы записать каждый логарифм как сумму логарифмов. Упростите, если можно. ⓐ log99xlog99x ⓑ log327xylog327xy Точно так же в Частном Свойстве Экспонент, aman=am-n,aman=am-n, мы видим, что для деления одного и того же основания мы вычитаем экспоненты.Факторное свойство логарифмов, logaMN=logaM-logaNlogaMN=logaM-logaN говорит нам взять логарифм частного, мы вычитаем логарифм числителя и знаменателя. Если M>0,N>0,a>0M>0,N>0,a>0 и a≠1,a≠1, то Логарифм частного есть разность логарифмов. Обратите внимание, что logaM-logaN≠loga(M-N).logaM-logaN≠loga(M-N). Мы используем это свойство, чтобы записать логарифм частного как разницу логарифмов каждого фактора. Используйте частное свойство логарифмов, чтобы записать каждый логарифм как разность логарифмов. ⓐ ⓑ Попробуйте 10.61 Используйте частное свойство логарифмов, чтобы записать каждый логарифм как разность логарифмов. ⓐ log434log434 ⓑ logx1000logx1000 Попробуйте 10,62 Используйте частное свойство логарифмов, чтобы записать каждый логарифм как разность логарифмов.Упростите, если можно. ⓐ log254log254 ⓑ log10ylog10y Третье свойство логарифмов связано со степенным свойством показателей степени, (am)n=am·n, (am)n=am·n, мы видим, что для возведения степени в степень мы умножаем показатели степени. Свойство мощности логарифмов, logaMp=plogaMlogaMp=plogaM, говорит нам взять логарифм числа, возведенного в степень, мы умножаем степень на логарифм числа. Если M>0,a>0,a≠1M>0,a>0,a≠1 и pp — любое действительное число, то Логарифм числа, возведенного в степень как произведение степени, умноженной на логарифм числа. Мы используем это свойство для записи логарифма числа, возведенного в степень, как произведение степени, умноженной на логарифм числа. Используйте мощное свойство логарифмов, чтобы записать каждый логарифм как произведение логарифмов. Упростите, если можно. ⓐ ⓑ Попробуйте 10,63 Используйте мощное свойство логарифмов, чтобы записать каждый логарифм как произведение логарифмов. ⓐ log754log754 ⓑ logx100logx100 Попробуйте 10,64 Используйте мощное свойство логарифмов, чтобы записать каждый логарифм как произведение логарифмов. Упростите, если можно. ⓐ log237log237 ⓑ logx20logx20 Мы суммируем здесь свойства логарифмов для удобства. Хотя натуральные логарифмы являются частным случаем этих свойств, часто бывает полезно также показать версию каждого свойства в виде натурального логарифма. Если M>0,N>0,a>0,a≠1M>0,N>0,a>0,a≠1 и pp — любое действительное число, то Теперь, когда у нас есть свойства, мы можем использовать их для «расширения» логарифмического выражения. Обычно мы применяем свойства произведения и частного перед применением свойства мощности. Используйте свойства логарифмов, чтобы расширить логарифм log4(2x3y2)log4(2x3y2). Упростите, если можно. Попробуйте 10,65 Используйте свойства логарифмов, чтобы расширить логарифм log2(5x4y2)log2(5x4y2). Попробуйте 10,66 Используйте свойства логарифмов, чтобы расширить логарифм log3(7x5y3)log3(7x5y3). Упростите, если можно. Когда у нас есть радикал в логарифмическом выражении, полезно сначала записать его радикал как рациональный показатель степени. Используйте свойства логарифмов, чтобы расширить логарифм log2x33y2z4log2x33y2z4. Упростите, если можно. Попробуйте 10,67 Используйте свойства логарифмов, чтобы расширить логарифм log4x42y3z25log4x42y3z25. Упростите, если можно. Попробуйте 10,68 Используйте свойства логарифмов, чтобы расширить логарифм log3x25yz3log3x25yz3. Упростите, если можно. Противоположностью расширению логарифма является сжатие суммы или разности логарифмов, имеющих одинаковое основание, в единый логарифм. Мы снова используем свойства логарифмов, чтобы помочь нам, но в обратном порядке. Чтобы сжать логарифмические выражения с одним и тем же основанием в один логарифм, мы начинаем с использования свойства Power, чтобы получить коэффициенты логарифмических терминов равными единице, а затем, при необходимости, свойств продукта и частного. Используйте свойства логарифмов, чтобы сжать логарифм log43+log4x-log4ylog43+log4x-log4y. Упростите, если можно. Попробуйте 10,69 Используйте свойства логарифмов, чтобы сократить логарифм log25+log2x-log2ylog25+log2x-log2y. Попробуйте 10,70 Используйте свойства логарифмов, чтобы сжать логарифм log36-log3x-log3ylog36-log3x-log3y. Упростите, если можно. Используйте свойства логарифмов, чтобы сократить логарифм 2log3x+4log3(x+1)2log3x+4log3(x+1). Упростите, если можно. Попробуйте 10. Используйте свойства логарифмов, чтобы сократить логарифм 3log2x+2log2(x−1)3log2x+2log2(x−1). Упростите, если можно. Попробуйте 10,72 Используйте свойства логарифмов, чтобы сократить логарифм 2logx+2log(x+1)2logx+2log(x+1). Упростите, если можно. Чтобы вычислить логарифм с любым другим основанием, мы можем использовать Формулу смены основания.Мы покажем, как это получается. Формула смены базы вводит новую базу b.b. Это может быть любое основание b , которое мы захотим, где b>0,b≠1.b>0,b≠1. Поскольку в наших калькуляторах есть ключи для логарифмов по основанию 10 и основанию e , мы перепишем формулу изменения основания с новым основанием как 10 или e . Для любых логарифмических оснований a,ba,b и M>0,M>0, Когда мы используем калькулятор для вычисления значения логарифма, мы обычно округляем до трех знаков после запятой. Округление до трех знаков после запятой, приблизительное значение log435.log435. Попробуйте 10,73 Округление до трех знаков после запятой, приблизительное значение log342.log342. Попробуйте 10,74 Округление до трех знаков после запятой, приблизительное значение log546.log546. Использование свойств логарифмов В следующих упражнениях используйте свойства логарифмов для оценки. ⓐ log41log41 ⓑ log88log88 ⓐ log121log121 ⓑ lnelne ⓐ 3log363log36 ⓑ log227log227 ⓐ 5log5105log510 ⓑ log4410log4410 ⓐ 8log878log87 ⓑ log66-2log66-2 ⓐ 6log6156log615 ⓑ log88-4log88-4 ⓐ 10log510log5 ⓑ log10-2log10-2 ⓐ 10log310log3 ⓑ log10-1log10-1 ⓐ eln4eln4 ⓑ lne2lne2 ⓐ eln3eln3 ⓑ lne7lne7 В следующих упражнениях используйте свойство произведения логарифмов, чтобы записать каждый логарифм как сумму логарифмов.Упростите, если возможно. В следующих упражнениях используйте частное свойство логарифмов, чтобы представить каждый логарифм как сумму логарифмов. Упростите, если возможно. В следующих упражнениях используйте свойство мощности логарифмов, чтобы раскрыть каждое из них. Упростите, если возможно. В следующих упражнениях используйте свойства логарифмов, чтобы расширить логарифм. Упростите, если возможно. log33x+2y25z2log33x+2y25z2 log25x32y2z44log25x32y2z44 В следующих упражнениях используйте свойства логарифмов, чтобы сжать логарифм. Упростите, если возможно. log280-log25log280-log25 log336-log34log336-log34 log34+log3(x+1)log34+log3(x+1) log25-log2(x-1)log25-log2(x-1) log73+log7x-log7ylog73+log7x-log7y log52-log5x-log5ylog52-log5x-log5y 4log2x+6log2y4log2x+6log2y 6log3x+9log3y6log3x+9log3y log3(x2-1)-2log3(x-1)log3(x2-1)-2log3(x-1) log(x2+2x+1)−2log(x+1)log(x2+2x+1)−2log(x+1) 4logx-2logy-3logz4logx-2logy-3logz 3lnx+4lny-2lnz3lnx+4lny-2lnz 13logx-3log(x+1)13logx-3log(x+1) 2log(2x+3)+12log(x+1)2log(2x+3)+12log(x+1) Использовать формулу смены базы В следующих упражнениях используйте формулу изменения основания, округляя до трех знаков после запятой, чтобы аппроксимировать каждый логарифм. Напишите свойство продукта своими словами. Применимо ли это к каждому из следующих? loga5x,loga5x,loga(5+x).loga(5+x). Почему или почему нет? Напишите свойство мощности своими словами. Применимо ли это к каждому из следующих? logaxp,logaxp,(logax)r.(logax)r. Почему или почему нет? Используйте пример, чтобы показать, что Объясните, как найти значение log715log715 с помощью калькулятора. ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела. ⓑ По шкале от 1 до 10, от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?



logarithm Сумма.Это история интересного… | Крис Смит

Вопрос

Частичный ответ
 Замена значений x и y не меняет результат.
Замена значений x и y не меняет результат. h: Мягкая выпрямленная линейная функция
 Это звучит как так называемая «выпрямленная линейная ” function:
Это звучит как так называемая «выпрямленная линейная ” function: Частично причина этого успеха в том, что он настолько прост, что его можно вычислить быстро. Но этого недостаточно, чтобы объяснить весь его успех! Я подозреваю, что другая часть причины заключается в том, что она тесно связана с суммами именно в смысле того самого исследования, которое мы сейчас проводим.)
Частично причина этого успеха в том, что он настолько прост, что его можно вычислить быстро. Но этого недостаточно, чтобы объяснить весь его успех! Я подозреваю, что другая часть причины заключается в том, что она тесно связана с суммами именно в смысле того самого исследования, которое мы сейчас проводим.) Вернемся к сумме
 Нам не нужно беспокоиться о случае, когда оба числа большие, но с противоположными знаками.)
Нам не нужно беспокоиться о случае, когда оба числа большие, но с противоположными знаками.)
А как насчет алгебры?
 Помните, что когда мы работаем с бревнами, умножение заменяется сложением, поэтому мы имеем следующее: максимум два числа, а затем добавить x , это то же самое, что добавить x к каждому, а затем взять максимум! Это интуитивно проверяется.
Помните, что когда мы работаем с бревнами, умножение заменяется сложением, поэтому мы имеем следующее: максимум два числа, а затем добавить x , это то же самое, что добавить x к каждому, а затем взять максимум! Это интуитивно проверяется. Действительно, именно здесь истинная функция max имеет недифференцируемый острый угол, который необходимо сгладить. И действительно, точное поведение задается сложением , а не максимумами, и сложение не идемпотентно (т.т. е. добавление числа к самому себе не возвращает того же числа).
Действительно, именно здесь истинная функция max имеет недифференцируемый острый угол, который необходимо сгладить. И действительно, точное поведение задается сложением , а не максимумами, и сложение не идемпотентно (т.т. е. добавление числа к самому себе не возвращает того же числа). Логарифмы
Логарифмы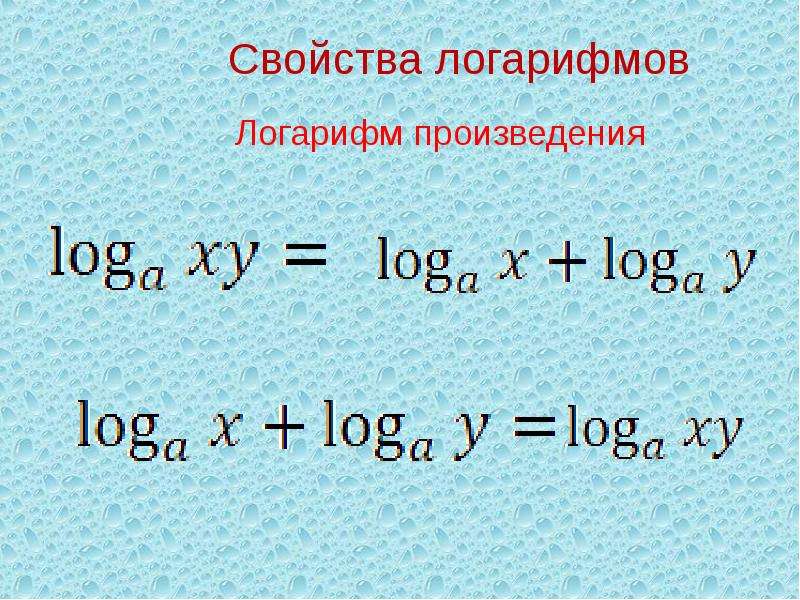 Логарифм – показатель степени, указывающий, в какой степени
основание должно быть поднято, чтобы произвести данное число.
Логарифм – показатель степени, указывающий, в какой степени
основание должно быть поднято, чтобы произвести данное число. х = журнал 2 8 Это означает логарифм 8 по основанию 2.Это
показатель степени, до которого нужно возвести 2, чтобы получить 8. . Мы знаем, что 2(2)(2)
= 8. Следовательно, x = 3,
Мы знаем, что 2(2)(2)
= 8. Следовательно, x = 3, х = журнал 6 36 Это означает логарифм 36 по основанию 6. Это
показатель, в который нужно возвести 6, чтобы получить 36. Мы знаем, что 6(6)
= 36. Следовательно, x = 2, . х = log 10 10 000 Это означает логарифм 10 000 по основанию 10.Это
это показатель степени, в которую нужно возвести 10, чтобы получить 10 000. Мы знаем
что 10(10)(10)(10) = 10 000. Следовательно, х = 4, журнал б б = 1 Логарифм любого числа по тому же основанию равен 1. х = журнал 11 11 Это означает логарифм 11 по основанию 11.  Это показатель степени
до которого нужно возвести 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, х = 1,
Это показатель степени
до которого нужно возвести 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, х = 1, журнал б 1 = 0 Натуральный
(Наперовы) логарифмы Основание равно e.
логарифм e x = ln x ln x — показатель степени, в которую нужно возвести e, чтобы получить x. 
Почему мы хотим использовать логарифмы? Для упрощения расчетов во многих случаях.
Правила логарифмирования Правило продукта Правило частных Силовое правило Это правило полезно, поскольку позволяет решать уравнения
где переменная является показателем степени.
Экспоненциальные и логарифмические функции являются обратными функциями 7
7 Умножение и деление логарифмов — Математика средней школы

 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105 10.4 Использование свойств логарифмов — Алгебра среднего уровня 2e
Цели обучения
 10
10
Если вы пропустили эту проблему, просмотрите пример 5.14.
Если вы пропустили эту проблему, просмотрите пример 8.27.
Если вы пропустили эту проблему, просмотрите пример 1.34. Использование свойств логарифмов
 logaa=1.
logaa=1. Свойства логарифмов
loga1=0logaa=1loga1=0logaa=1 Пример 10.28
Решение
log81log81 Используйте свойство loga1=0loga1=0. 0log81=00log81=0
log66Использовать свойство,logaa=1.1log66=1log66Использовать свойство,logaa=1.1log66=1 log77.
log77. Обратные свойства логарифмов

Пример 10.29
Решение
4log494log49 Используйте свойство alogax=xalogax=x. 94log49=994log49=9 log335log335 Используйте свойство alogax=xalogax=x. 5log335=55log335=5  Мы знаем, что экспоненциальные функции и логарифмическая функция очень взаимосвязаны. Наше определение логарифма показывает нам, что логарифм является показателем эквивалентной экспоненты.Свойства показателей имеют родственные свойства показателей.
Мы знаем, что экспоненциальные функции и логарифмическая функция очень взаимосвязаны. Наше определение логарифма показывает нам, что логарифм является показателем эквивалентной экспоненты.Свойства показателей имеют родственные свойства показателей. Свойство произведения логарифмов
Пример 10.30
 log464xy.
log464xy. Решение
log37xlog37x Использовать свойство продукта, loga(M·N)=logaM+logaNloga(M·N)=logaM+logaN. log37+log3xlog37+log3x log37x=log37+log3xlog37x=log37+log3x log464xylog464xy Использовать свойство продукта, loga(M·N)=logaM+logaNloga(M·N)=logaM+logaN. log464+log4x+log4ylog464+log4x+log4y Упростите, оценив log464log464. 3+log4x+log4y3+log4x+log4y log464xy=3+log4x+log4ylog464xy=3+log4x+log4y  Упростите, если можно.
Упростите, если можно. Частное свойство логарифмов
Пример 10.31
 Упростите, если можно.
Упростите, если можно.
ⓐ log557log557 и ⓑ logx100logx100 Решение
лог557лог557 Используйте свойство «частное», logaMN=logaM-logaNlogaMN=logaM-logaN. log55-log57log55-log57 Упрощение. 1-log571-log57 log557=1-log57log557=1-log57 logx100logx100 Используйте свойство «частное», logaMN=logaM-logaNlogaMN=logaM-logaN. logx-log100logx-log100 Упрощение. logx-2logx-2 logx100=logx-2logx100=logx-2  Упростите, если можно.
Упростите, если можно. Свойство степени логарифмов
 По сути, мы берем показатель степени и бросаем его перед логарифмом.
По сути, мы берем показатель степени и бросаем его перед логарифмом. Пример 10.32
ⓐ log543log543 и ⓑ logx10logx10 Решение
лог543лог543 Используйте свойство Power, logaMp=plogaMlogaMp=plogaM. 3log543log54 log543=3log54log543=3log54 logx10logx10 Используйте свойство Power, logaMp=plogaMlogaMp=plogaM. 10logx10logx logx10=10logxlogx10=10logx  Упростите, если можно.
Упростите, если можно. Свойства логарифмов
Свойство База аа База ee лога1=0лога1=0 In1=0In1=0 логаа=1логаа=1 лнэ=1лнэ=1 Обратные свойства alogax=xlogaax=xalogax=xlogaax=x elnx=xlnex=xelnx=xlnex=x Свойство произведения логарифмов loga(M·N)=logaM+logaNloga(M·N)=logaM+logaN ln(M·N)=lnM+lnNln(M·N)=lnM+lnN Частное свойство логарифмов logaMN=logaM-logaNlogaMN=logaM-logaN lnMN=lnM−lnNlnMN=lnM−lnN Степенное свойство логарифмов логаМп=плогаМлогаМп=плогам lnMp=plnMlnMp=plnM  Это означает писать логарифм как сумму или разность и без каких-либо степеней.
Это означает писать логарифм как сумму или разность и без каких-либо степеней. Пример 10.33
Решение
log4(2x3y2)log4(2x3y2) Использовать свойство продукта, logaM·N=logaM+logaNlogaM·N=logaM+logaN. log42+log4x3+log4y2log42+log4x3+log4y2 Используйте свойство Power, logaMp=plogaMlogaMp=plogaM, в двух последних терминах. log42+3log4x+2log4ylog42+3log4x+2log4y Упрощение. 12+3log4x+2log4y12+3log4x+2log4y log4(2x3y2)=12+3log4x+2log4ylog4(2x3y2)=12+3log4x+2log4y  Упростите, если можно.
Упростите, если можно. Пример 10.34
Решение
log2x33y2z4log2x33y2z4 Перепишите радикал с рациональным показателем. log2(x33y2z)14log2(x33y2z)14 Используйте свойство Power, logaMp=plogaMlogaMp=plogaM. 14log2(x33y2z)14log2(x33y2z) Используйте свойство «частное», logaM·N=logaM-logaNlogaM·N=logaM-logaN. 14(log2(x3)−log2(3y2z))14(log2(x3)−log2(3y2z)) Использовать свойство продукта, logaM·N=logaM+logaNlogaM·N=logaM+logaN, во втором члене. 
14(log2(x3)-(log23+log2y2+log2z))14(log2(x3)-(log23+log2y2+log2z)) Используйте свойство Power, logaMp=plogaMlogaMp=plogaM, в скобках. 14(3log2x-(log23+2log2y+log2z))14(3log2x-(log23+2log2y+log2z)) Упростите путем распространения. 14(3log2x-log23-2log2y-log2z)14(3log2x-log23-2log2y-log2z) log2x33y2z4=14(3log2x-log23-2log2y-log2z)log2x33y2z4=14(3log2x-log23-2log2y-log2z) 
Пример 10.35
Решение
Все выражения журнала имеют одно и то же основание, 4. log43+log4x-log4ylog43+log4x-log4y Первые два термина добавлены, поэтому мы используем свойство продукта, logaM+logaN=logaM·NlogaM+logaN=logaM·N. log43x-log4ylog43x-log4y Поскольку журналы вычитаются, мы используем свойство Quotient, logaM-logaN=logaMNlogaM-logaN=logaMN. log43xylog43xy log43+log4x-log4y=log43xylog43+log4x-log4y=log43xy  Упростите, если можно.
Упростите, если можно. Пример 10.36
Решение
Логарифмические выражения имеют одно и то же основание, 3. 2log3x+4log3(x+1)2log3x+4log3(x+1) Используйте свойство Power, logaM+logaN=logaM·NlogaM+logaN=logaM·N. log3x2+log3(x+1)4log3x2+log3(x+1)4 Термины добавлены, поэтому мы используем свойство продукта, logaM+logaN=logaM·NlogaM+logaN=logaM·N. log3x2(x+1)4log3x2(x+1)4 2log3x+4log3(x+1)=log3x2(x+1)42log3x+4log3(x+1)=log3x2(x+1)4  71
71 Используйте формулу смены основания
Предположим, мы хотим оценить logaMlogaM. логаМлогаМ Пусть y=logaMy=logaM. у=logaMy=logaM Перепишите выражение в экспоненциальной форме. ай=май=М Возьмите logblogb с каждой стороны. logbay=logbMlogbay=logbM Используйте свойство Power. 
ylogba=logbMylogba=logbM Решите для yy. y=logbMlogbay=logbMlogba Замените y=logaMy=logaM. logaM=logbMlogbalogaM=logbMlogba Сменная базовая формула
 Это дает нам приблизительное значение, поэтому мы используем символ приблизительного равенства (≈)(≈).
Это дает нам приблизительное значение, поэтому мы используем символ приблизительного равенства (≈)(≈). Пример 10.37
Решение
Используйте формулу смены основания. Определите a и M . Выберите 10 для b . Введите выражение log35log4log35log4 в калькулятор
, используя кнопку журнала для десятичной системы счисления.Округлить до трех знаков после запятой.
Раздел 10.4 Упражнения
Практика ведет к совершенству


Письменные упражнения
284.
log(a+b)≠loga+logb.log(a+b)≠loga+logb. Самопроверка



 Десятичные (lg) и натуральные логарифмы (ln).
Десятичные (lg) и натуральные логарифмы (ln). Но ряд:
Но ряд: е. . В частности ,
.
е. . В частности ,
. е. если и , то .
е. если и , то .

 01 ⇔ log 10 01 = -2
01 ⇔ log 10 01 = -2