Формула полной вероятности доказательство – Формулы полной вероятности и Байеса (с доказательством). Примеры.
Формулы полной вероятности и Байеса (с доказательством). Примеры.
Формула полной вероятности. Теорема.
Теорема. Если событие F может произойти только при условии появления одного из событий (гипотез) A1,А2,…,Аn образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события F: |
□ По условию гипотезы А1,А2,…,Аn образуют полную группу, следовательно, они единственно возможные и несовместные. Т.к гипотезы А1,А2,…,Аn — единственно возможные, а событие F может произойти только вместе с 1 из гипотез, то
В силу того что гипотезы А1,А2,…,Аn несовместны, можно применить теорему сложения вероятностей:
По теореме умножения вероятностей .■
Следствием теоремы умножения и формулы полной вероятности является формула Байеса.
Она применяется,
когда событие F, которое может появиться
только с одной из гипотез А1,А2,…,Аn образующих полную группу событий,
произошло и необходимо произвести
количественную переоценку априорных вероятностей
этих гипотез P(A1),
Р(А2),…,
Р(Аn),
известных о испытания, Т.е. надо найти апостериорные (получаемые после проведения испытания)
условные вероятности гипотез
P
□ Для получения искомой формулы запишем теорему умножения вероятностей событий F и Аi в двух формах:
, откуда
или с учетом формулы
полной вероятности: 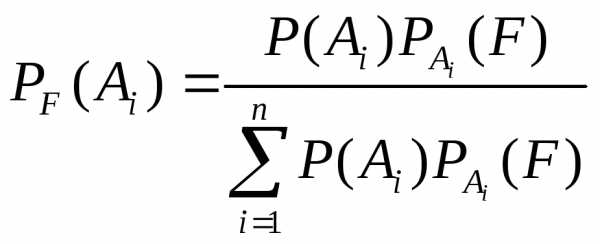 .
■
.
■
Значение формулы Байеса состоит в том, что при наступлении события Р, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в эк-ке, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.
Пример: Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго — 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит: а) l-му стрелку; б) 2-му стрелку?
Решение. Обозначим события:
А1 — оба стрелка не попали в мишень; А2
Найдем вероятности гипотез и условные вероятности события F для этих гипотез:
Р(A1) = 0,2 · 0,6 = 0,12, РА1(F) = 0;
Р(А2) = 0,8 · 0,4 = 0,32, РА2(F) = 0;
Р(А3) = 0,8 · 0,6 = 0,48, РА3(F) = l;
Р(А4) = 0,2 · 0,4 = 0,08, РА4(F) = l.
Теперь по формуле Байеса:
, ,
Т.е. вероятность того, что попал в цель l-й стрелок при наличии одной пробоины, в 6 раз выше, чем для второго стрелка.
Повторные независимые испытания. Формула Бернулли (с выводом). Примеры.
Если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же. Эта последовательность независимых испытаний получила название схемы Бернулли.
Формула Бернулли
Где  .
.
□ Пусть  и
и — соответственно появление и непоявление
событияА в i-ом
испытании (i = 1,2,…,n), а
— соответственно появление и непоявление
событияА в i-ом
испытании (i = 1,2,…,n), а 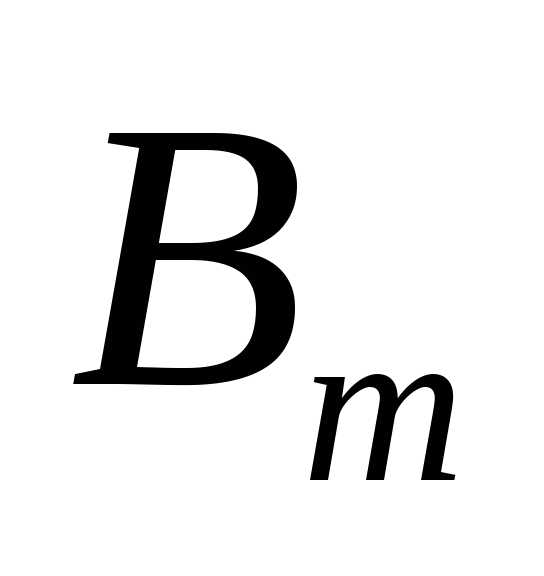
Представим событие 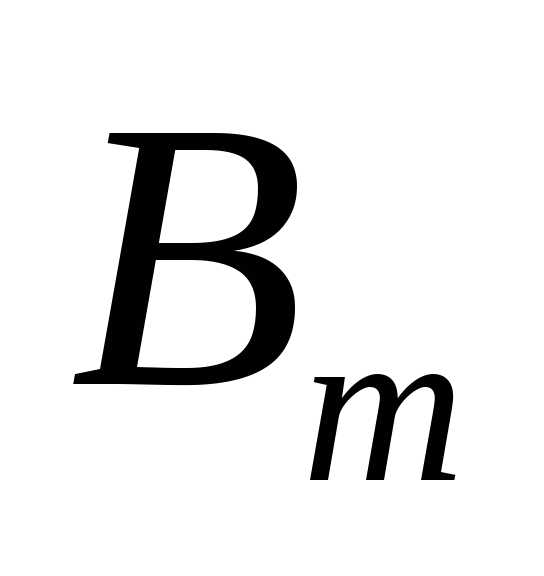 через элементарные события
через элементарные события .
.
Например, при n = 3, m = 2 событие ,
т.е. событие А произойдет 2 раза в 3 испытаниях, если оно произойдет в l-м и 2-м испытаниях (и не произойдет в 3-м), или в l-м и 3-м (и не произойдет во 2-м), или произойдет во 2-м и 3-м (и не произойдет в l-м).
,
Т.е. каждый вариант
появления события Вm
(каждый член суммы) состоит из m
появлений события А и n-m
непоявлений, т.е. из m
событий А и из n-m
событий  с различными индексами.
с различными индексами.
Число всех комбинаций
(слагаемых суммы) равно числу способов
выбора из n
испытаний m,
в которых событие А произошло, т.е. числу
сочетаний  .
Вероятность каждой такой комбинации
(каждого варианта появления события
Вm)
по теореме умножения для независимых
событий равна
.
Вероятность каждой такой комбинации
(каждого варианта появления события
Вm)
по теореме умножения для независимых
событий равна 
 ,
а
,
а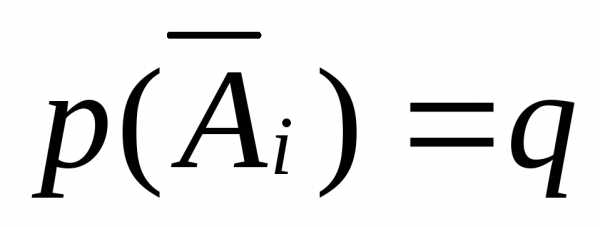 ,i
= 1,2,…,n.
В связи с тем, что комбинации между собой
несовместны, по теореме сложения
вероятностей получим
,i
= 1,2,…,n.
В связи с тем, что комбинации между собой
несовместны, по теореме сложения
вероятностей получим.■
studfiles.net
Тема 5. Формула полной вероятности, вероятности гипотез,
и среднее число «успехов»
Важным следствием совместного применения теоремы сложения и умножения вероятностей являются выводы формулы полной вероятности и теоремы Байеса. Напомним, что события образуют полную группу событий, если выполняются условия
.
Систему таких событий называют также разбиением. Сформулируем основное утверждение, относительно полной вероятности любого события.
1. Формула полной вероятности (фпв)
Теорема 1. Пусть образуют полную группу событий. Вероятность появления событияА, которое может наступить лишь при условии появления одного из несовместных событий равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события
(1)  .
.
Доказательство.Посколькуто на основании свойств операций над событиями получим. Из того, что, следует, что, т.е. событиятакже несовместны. Тогда по теореме сложения вероятностей получим
.
На основании теоремы умножения вероятностей были доказаны равенства , для всех. Следовательно, формула (1) доказана.
Формулу (1) называют
Пример 1.В первой урне 3 белых и 5 красных шара, во второй 6 белых и 4 красных. Из второй урны в первую наудачу перекладывают 2 шара. Найти вероятность того, что шар, наудачу извлеченный из первой урны, будет белым.
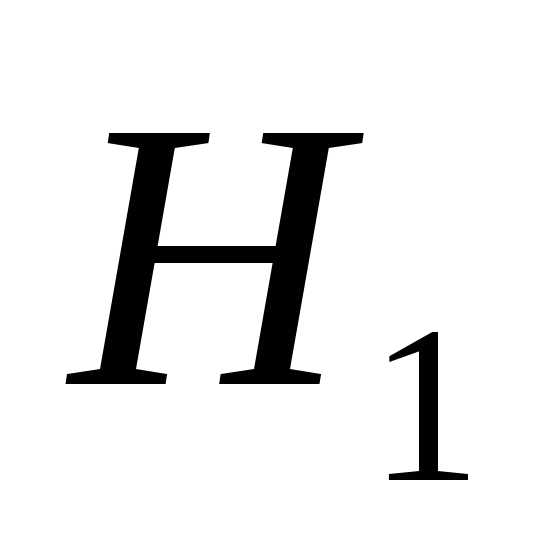 – событие, что оба шара белые;
– событие, что оба шара белые;
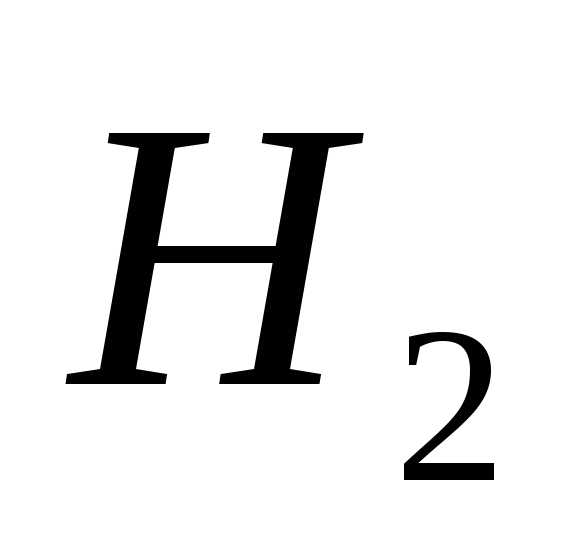 –
событие, что оба шара красные;
–
событие, что оба шара красные;
 –
событие, что один шар белый и один
красный.
–
событие, что один шар белый и один
красный.
Других вариантов гипотез быть не может,
а одно из этих событий обязательно
наступит, поэтому  ,
,  ,
,  –
составляют полную группу событий. Тогда
применима формула полной вероятности.
Найдем вероятности гипотез
–
составляют полную группу событий. Тогда
применима формула полной вероятности.
Найдем вероятности гипотез
,
где В– событие, что первый шар белый, С – событие, что второй шар белый.
, )
)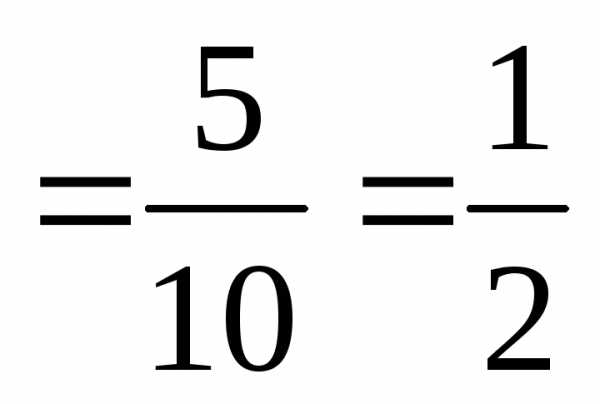 ;
;

,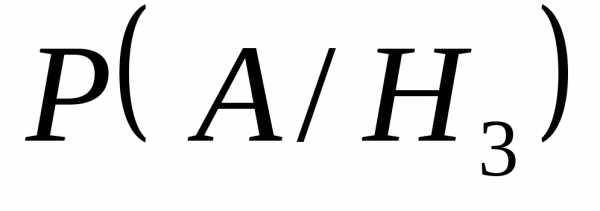
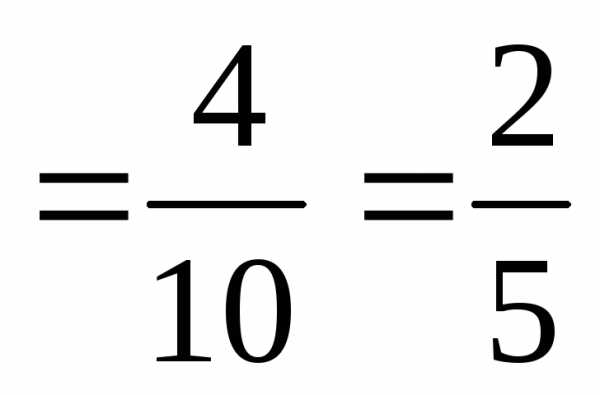 .
.
Подставляя в формулу, получим
.
2. Вероятность гипотез (формулы Байеса).
Одним из важным следствием формулы (1) является формулы Байеса.
Пусть событие Аможет наступить при
условии появления одного из несовместных
событийобразующих
полную группу событий гипотез. Вероятность
появления событияАопределяется
по формуле полной вероятности. Допустим,
что произведено испытание, в результате
которого наступило событиеА. Ставим
задачу: определить, как изменились (в
связи с тем, что событие уже
наступило) вероятности гипотез. Другими
словами, будем искать условные вероятностипосле наступления события
уже
наступило) вероятности гипотез. Другими
словами, будем искать условные вероятностипосле наступления события  в данном эксперименте. Имеет место,
следующее утверждение.
в данном эксперименте. Имеет место,
следующее утверждение.
Теорема 2.Справедливы формулы вероятностей гипотез
(2)
Эти формулы называются формулами Байеса (или формулами гипотез) — по имени английского математика, который их вывел и опубликовал в 1764г.
Доказательство. Равенства (2) непосредственно выводятся на основании формулы умножения
и.
Так как левые части этих формул равны, приравнивая правые части, получим равенство (2).
Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известен результат испытания, вследствие, которого наступило событие А.
Такой анализ имеет большое практическое значение с точки зрения «эффективности проведённого опыта». Таким образом, можно непосредственно увидеть какая гипотеза (или какие гипотезы) больше способствовали наступлению событияА, а это в свою очередь прямо указывает наглавные факторы (гипотезы), из-за которых достигается тот или иной практический результат.
Пример 2. Мимо заправки проезжают в 4 раза больше легковых машин, чем грузовых. При этом заправляются каждая вторая грузовая машина и каждая пятая легковая. Найти вероятности того, что заправившаяся машина – легковая.
Решение: Составим гипотезу:Н1– событие, что заправилась легковая машина,Н2– событие, что заправилась грузовая. А – событие, что машина заправилась. Тогда по формуле полной вероятности
.
найдем эти вероятности 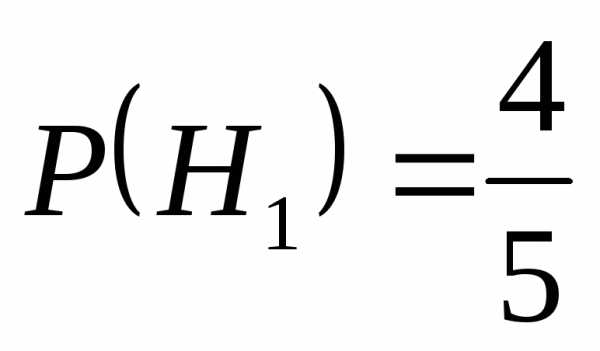 и
и ,
так как по условию легковых в 4 раза
больше грузовых
,
так как по условию легковых в 4 раза
больше грузовых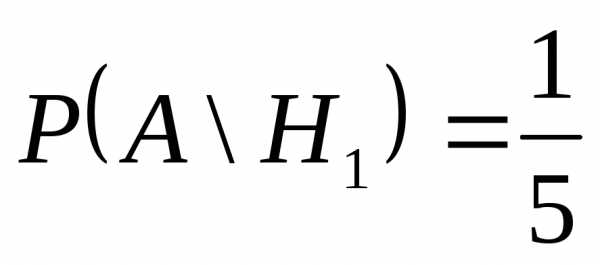 и
и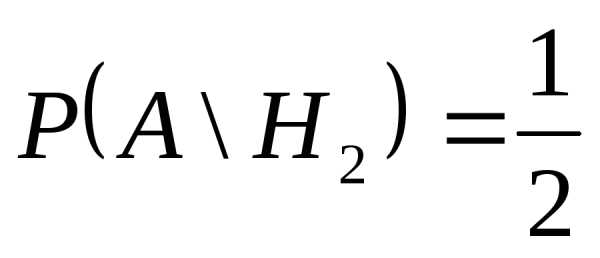 ,
так как по условию задачи из легковых
машин заправляется каждая пятая, а из
грузовых – каждая вторая. Тогда.
Теперь по формуле Байеса найдем
,
так как по условию задачи из легковых
машин заправляется каждая пятая, а из
грузовых – каждая вторая. Тогда.
Теперь по формуле Байеса найдем
,.
Пример 3. В отборочный цех завода поступает 40 % деталей из 1 цеха и 60 % процентов из второго цеха. В первом цехе производится 90 % стандартных деталей, а во втором 95 % стандартных деталей. Найти вероятность того, что наудачу взятая сборщиком деталь окажется
1. Стандартной.
2. Найти вероятность того, что эта стандартная деталь изготовлена вторым цехом
Решение. Выбор детали можно разбить
на два этапа. Первый – это выбор цеха.
Имеется две гипотезы: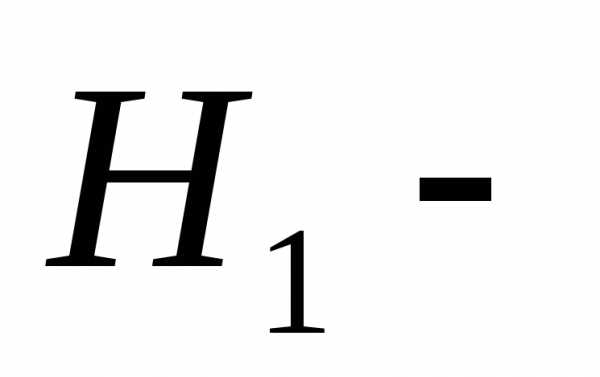 деталь изготовлена первым цехом,
деталь изготовлена первым цехом,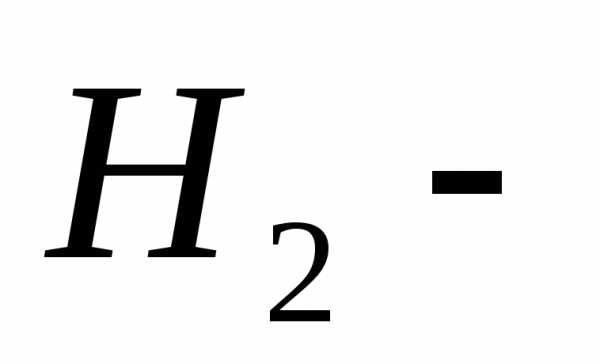 деталь изготовлена первым цехом. Второй
этап выбор детали. Событие
деталь изготовлена первым цехом. Второй
этап выбор детали. Событие —
извлечённая на удачу деталь оказалась
стандартной. Понятно, что события
—
извлечённая на удачу деталь оказалась
стандартной. Понятно, что события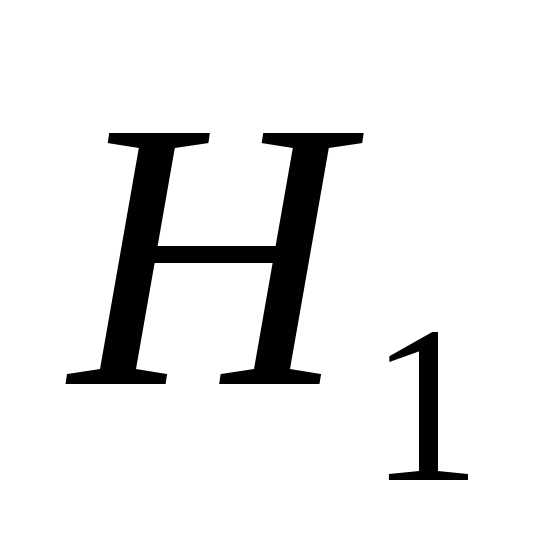 и
и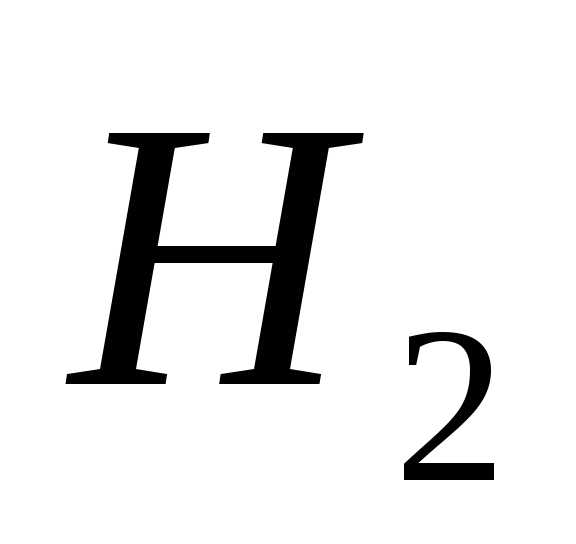 образуют полную группу,.
Числа 0, 90 и 0, 95 являются условными
вероятностями события
образуют полную группу,.
Числа 0, 90 и 0, 95 являются условными
вероятностями события при условии гипотез
при условии гипотез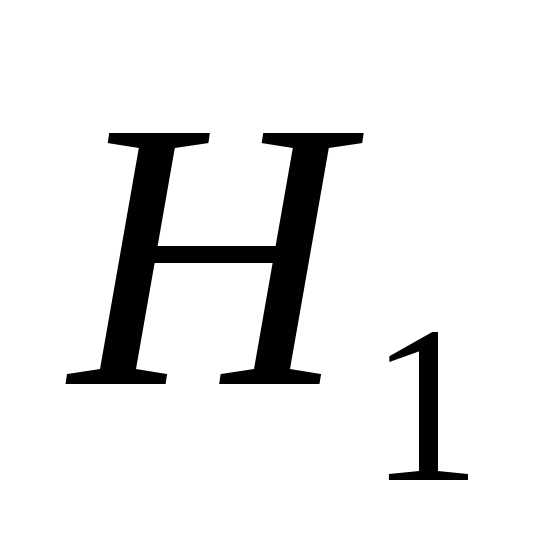 и
и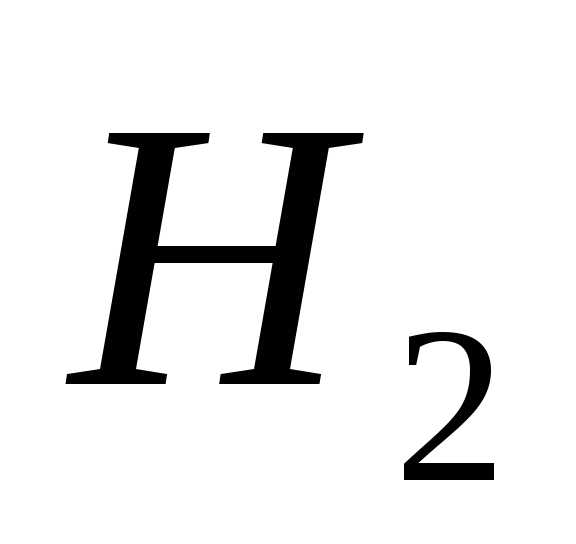 соответственно,
т.е.По формуле полной вероятности (1) вычисляем
соответственно,
т.е.По формуле полной вероятности (1) вычисляем
.
Следовательно, наудачу взятая сборщиком деталь с вероятностью 0,93 будет стандартной.
Теперь найдём вероятности того, что эта стандартная деталь изготовлена вторым цехом.
Определим вероятность гипотезы 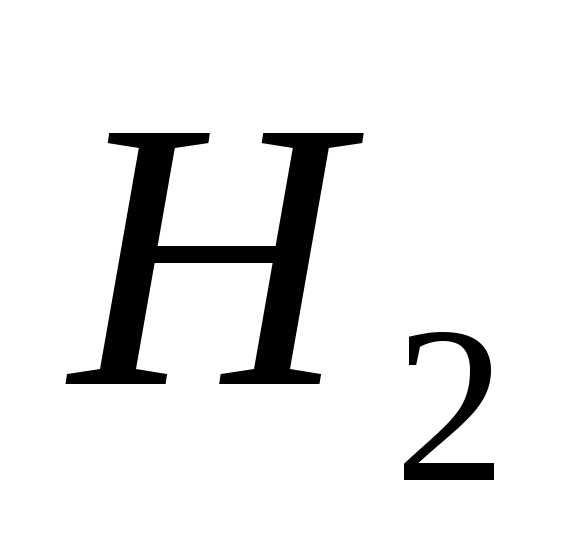 ,
способствующего данному результату
(т.е. событиеА уже произошло).
Применим формулы (2), получим
,
способствующего данному результату
(т.е. событиеА уже произошло).
Применим формулы (2), получим
.
Задания 1. Найдите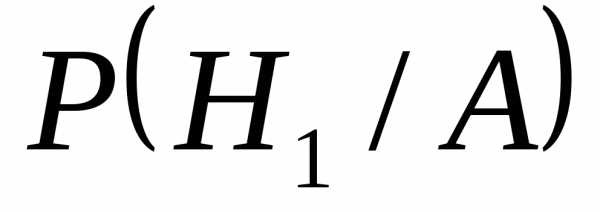 ,
и сравните полученные результаты.
,
и сравните полученные результаты.
2. Покажите, что если ,
то
,
то ,
,
т.е. система событий образует полную группу событий.
Среди гипотез
гипотезу с номером
с номером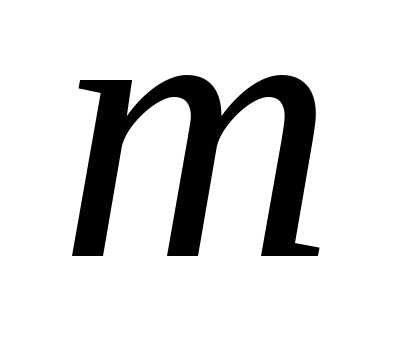 — будем называть наиболее подходящей
гипотезой для наступления события А,
если.
— будем называть наиболее подходящей
гипотезой для наступления события А,
если.
Легко заметить, что здесь возможны
равенства:при всех номерах,
при этом, если ,
то систему гипотез будем называтьунимодальнойи если
же
,
то систему гипотез будем называтьунимодальнойи если
же ,
то систему гипотез будем
называтьполимодальнойсистемой.
,
то систему гипотез будем
называтьполимодальнойсистемой.
Указанные свойства системы гипотез особенно важны для исследования так называемых «чёрных ящиков».
studfiles.net
8.Формула полной вероятности.
Определение 3.1. Пусть событиеАможет произойти только совместно с одним из событийН1,Н2,…,Нп, образующих полную группу несовместных событий. Тогда событияН1,Н2,…,Нп называютсягипотезами.
Теорема 3.1.Вероятность событияА, наступающего совместно с гипотезамиН1,Н2,…,Нп, равна:
(3.1)
где p(Hi) – вероятностьi— й гипотезы, а p(A/Hi) – вероятность событияАпри условии реализации этой гипотезы. Формула (3.1) носит названиеформулы полной вероятности.
Доказательство.
Можно считать событие Асуммой попарно несовместных событийАН1,АН2,…,АНп. Тогда из теорем сложения и умножения следует, что
что и требовалось доказать.
9. Формула Бейеса.
Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Например, в предыдущем примере извлечение из урны белого шара говорит о том, что этой урной не могла быть третья, в которой нет белых шаров, то естьр(Н3/А) = 0. Для переоценки вероятностей гипотез при известном результате опыта используетсяформула Байеса:
(3.2)
Действительно, из (2.7) получим, что откуда следует справедливость формулы (3.2).
10. Формула (схема) Бернулли.
Рассмотрим
серию из писпытаний, в каждом из
которых событиеАпоявляется с одной
и той же вероятностьюр, причем
результат каждого испытания не зависит
от результатов остальных. Подобная
постановка задачи называетсясхемой
повторения испытаний. Найдем вероятность
того, что в такой серии событиеАпроизойдет ровнокраз (неважно, в
какой последовательности). Интересующее
нас событие представляет собой сумму
равно-вероятных несовместных событий,
заключающихся в том, чтоАпроизошло
в некоторыхкиспытаниях и не
произошло в остальныхп – киспытаниях. Число таких событий равно
числу сочетаний изппок, то
есть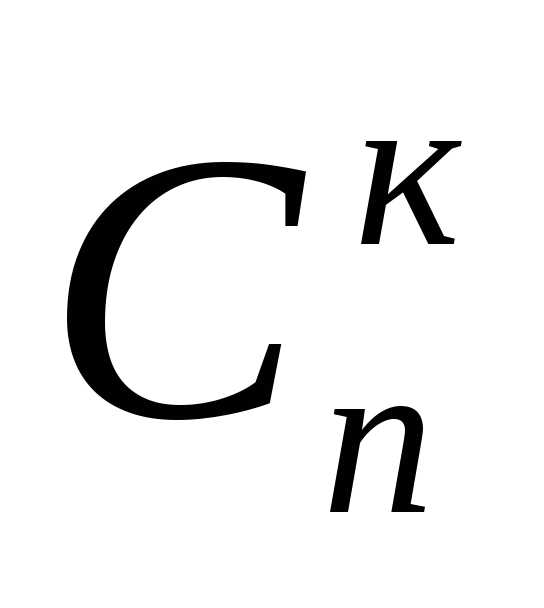 ,
а вероятность каждого из них:pkqn—k,
гдеq = 1 –p – вероятность того, что в данном опытеАне произошло. Применяя теорему
сложения для несовместных событий,
получимформулу Бернулли:
,
а вероятность каждого из них:pkqn—k,
гдеq = 1 –p – вероятность того, что в данном опытеАне произошло. Применяя теорему
сложения для несовместных событий,
получимформулу Бернулли:
. (3.3)
11. Предельные теоремы в схеме Бернулли. Формула Пуассона и условия её применимости.
Формула Бернулли требует громоздких расчетов при большом количестве испытаний. Можно получить более удобную для расчетов приближенную формулу, если при большом числе испытаний вероятность появления Ав одном опыте мала, а произведениепр = λсохраняет постоянное значение для разных серий опытов ( то есть среднее число появле-ний событияАв разных сериях испытаний остается неизменным). Применим формулу Бернулли:
Найдем предел полученного выражения при
Таким образом, формула Пуассона
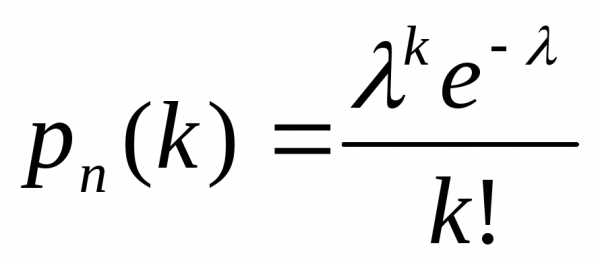 (3.4)
(3.4)
позволяет найти вероятность кпоявлений событияАдля массовых (пвелико) и редких (рмало) событий.
Предельные теоремы
Предельные теоремы для схем Бернулли
Так как число успехов в последовательности из независимых испытаний Бернулли, можно представить в виде:
(1)
где — независимые одинаково распределенные бернуллиевские случайные величины. Мы знаем в явном виде распределение , а именно:
,
где — вероятность успеха в единичном испытании.
Вместе с тем, во многих задачах приходится находить вероятности при больших значениях .
Это может вызвать значительные вычислительные трудности ввиду громоздкости биномиальных коэффициентов и необходимости возводить числа и в высокие степени. Ниже мы рассмотрим две важные предельные ситуации, когда биномиальное распределение может быть приближено другими распределениями.
studfiles.net
Формула полной вероятности. Формула Байеса
Условие задачи 1
На фабрике станки 1,2 и 3 производят соответственно 20%, 35% и 45% всех деталей. В их продукции брак составляет соответственно 6%, 4%, 2%. Какова вероятность того, что случайно выбранное изделие оказалось дефектным? Какова вероятность того, что оно было произведено: а) станком 1; б) станком 2; в) станком 3?
Решение задачи 1
Гипотезы и условные вероятности
Обозначим через событие, состоящее в том, что стандартное изделие оказалось дефектным.
Событие может произойти только при условии наступления одного из трех событий:
-изделие произведено на станке 1;
— изделие произведено на станке 2;
— изделие произведено на станке 3;
Запишем условные вероятности:
Формула полной вероятности
Если событие может произойти только при выполнении одного из событий , которые образуютполную группу несовместных событий, то вероятность события вычисляется по формуле
По формуле полной вероятности находим вероятность события :
Формула Байеса
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.
Вероятность того, что дефектное изделие изготовлено на станке 1:
Вероятность того, что дефектное изделие изготовлено на станке 2:
Вероятность того, что дефектное изделие изготовлено на станке 3:
Условие задачи 2
Группа состоит из 1 отличника, 5 хорошо успевающих студентов и 14 студентов, успевающих посредственно. Отличник отвечает на 5 и 4 с равной вероятностью, хорошист отвечает на 5, 4 и 3 с равной вероятностью, и посредственно успевающий студент отвечает на 4,3 и 2 с равной вероятностью. Случайно выбранный студент ответил на 4. Какова вероятность того, что был вызван посредственно успевающий студент?
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
Решение задачи 2
Гипотезы и условные вероятности
Возможны следующие гипотезы:
-отвечал отличник;
-отвечал хорошист;
–отвечал посредственно занимающийся студент;
Пусть событие -студент получит 4.
Условные вероятности:
Формула полной вероятности
По формуле полной вероятности, вероятность события :
Формула Байеса
По формуле Байеса найдем вероятность того, что был вызван посредственно успевающий студент:
Ответ:
К оглавлению решебника по теории вероятностей и математической статистике 〉
100task.ru
Лекция 1.5. Формула полной вероятности. Формула Байеса
Тема 1.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ, ФОРМУЛА БАЙЕСА
План лекции:
Независимость событий.
Формула полной вероятности.
Формула Байеса.
Список литературы:
Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.
Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. — М.: Высшая школа, 2007. — 480 с.
Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст] / Н.Ш. Кремер — М: ЮНИТИ, 2002. – 543 с.
п.1. Независимость событий
Если при наступлении события вероятность события не меняется, то события и называются независимыми.
Теорема: Вероятность совместного появления двух независимых событий и (произведения и ) равна произведению вероятностей этих событий.
Доказательство: События и независимы, следовательно . В этом случае формула произведения событий и можно записать как .
События называются попарно независимыми, если независимы любые два из них.
События называются независимыми в совокупности, если каждое из этих событий и событие равное произведению любого числа остальных событий, независимы.
Теорема: Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.
.
Простейшие свойства вероятностей:
;
;
;
;
;
Свойства условных вероятностей
;
;
;
если , то ;
;
;
;
.
п.2. Формула полной вероятности
Теорема 1 (формула полной вероятности). Пусть события образуют полную группу несовместных событий. Будем эти события называть гипотезами. Тогда вероятность любого события того же поля событий равна:
Доказательство. Так как события образуют полную группу событий, то событие можно представить в виде: (это означает, что событие может произойти А только вместе с одним из событий ). Так как события несовместны то:
Пример 1. Детали поступают на конвейер с трех станков. Первый станок производит 25% всех деталей, второй 35% и третий 40% деталей. Первый станок выпускает 1% бракованных деталей, второй 3% , третий 5%. Определить вероятность того, что случайно выбранная с конвейера деталь окажется бракованной.
Решение. Введем обозначения событий: — деталь окажется бракованной; события — деталь изготовлена соответственно первым, вторым или третьим производителем. По условию задачи:
, , ;
, , .
По формуле полной вероятности находим:
п.3. Формула Байеса
Теорема 2 (формула Байеса). Пусть событие , которое могло произойти вместе с одним из событий , образующих полную группу несовместных событий, наступило. Тогда условная вероятность того, что осуществилась гипотеза равна:
Поскольку данная формула позволяет вычислить апостериорные вероятности по априорным, то ее также называют формулой переоценки гипотез.
Доказательство. По определению условной вероятности:
.
Пример 3. В условиях примера 1 определить вероятность того, что взятая деталь была изготовлена на первом станке, если она оказалась бракованной.
Решение. Требуется переоценить вероятность гипотезы . По формуле Байеса имеем:
.
Вероятность стала меньше, поскольку если деталь оказалась бракованной, то более вероятно, что она произведена вторым, либо третьим станком.
Пример 4. В корзине находится один шар — с равной вероятностью белый или черный. В корзину опускается белый шар, и после перемешивания извлекается один шар. Он оказался белым. Какова вероятность, что в корзине остался белый шар.
Решение. Пусть гипотеза — в корзине исходно находится белый шар, гипотеза — в корзине находится черный шар. Так как с равной вероятностью в корзине может находиться как белый, так и черный шар, то: . После того, как в корзину был опущен белый шар, вероятность вынуть белый шар (событие ) в предположении гипотезы есть: . Аналогично, вероятность вынуть белый шар в предположении гипотезы : . Следовательно по формуле полной вероятности:
.
Тогда вероятность, что в корзине остался белый шар (то есть верна гипотеза ):
.
Пример 5. Два стрелка стреляют по мишени, делая по одному выстрелу. Вероятность попадания для первого стрелка 0,8, для второго – 0,4. После стрельбы в мишени обнаружена только одна пробоина. Найти вероятность того, что попал первый стрелок.
Решение. Некоторая сложность в данной задаче состоит в том, что мы уже решали аналогичную прямую задачу, не привлекая при этом формулу полной вероятности.
Введем обозначения: — попал в цель только один стрелок, первый стрелок попал в цель, -второй стрелок попал в цель. Тогда: . То есть, можно считать, что событие может наступить в результате осуществления двух гипотез: — попал в цель только первый стрелок, — попал в цель только второй стрелок. Имеем: , , , .
..
studfiles.net
4. Формула полной вероятности.
Определение. Если событие  может происходить только с одним из
событий
может происходить только с одним из
событий
, которые образуют полную группу событий, то события называются гипотезами.
Поскольку события образуют полную группу событий, то сумма их вероятностей равна единице
,
Согласно следствию 3 из теоремы сложения. Это равенство следует применять при проверке правильности составления системы гипотез.
Теорема
(формула полной вероятности). Если событие  может произойти только с одной из гипотез ,
то вероятность события
может произойти только с одной из гипотез ,
то вероятность события  равна сумме произведений вероятностей
гипотез на условные вероятности события
равна сумме произведений вероятностей
гипотез на условные вероятности события ,
вычисленные при условии, что соответствующая
гипотеза имела место
,
вычисленные при условии, что соответствующая
гипотеза имела место
.
Доказательство.
Пример. В трех одинаковых урнах находятся шары. В первой урне находятся только белые шары, во второй только черные, а в третьей урне два черных и три белых шара.
Найти вероятность того, что наудачу выбранный шар из случайно выбранной урны является белым.
Запишем, прежде всего, условие задачи, вводя соответствующие обозначения.
Дано: событие  состоит в том, что будет выбран белый
шар.
состоит в том, что будет выбран белый
шар.
Гипотеза  состоит в том, что выбрана первая урна
(состав урны: все белые шары).
состоит в том, что выбрана первая урна
(состав урны: все белые шары).
Гипотеза 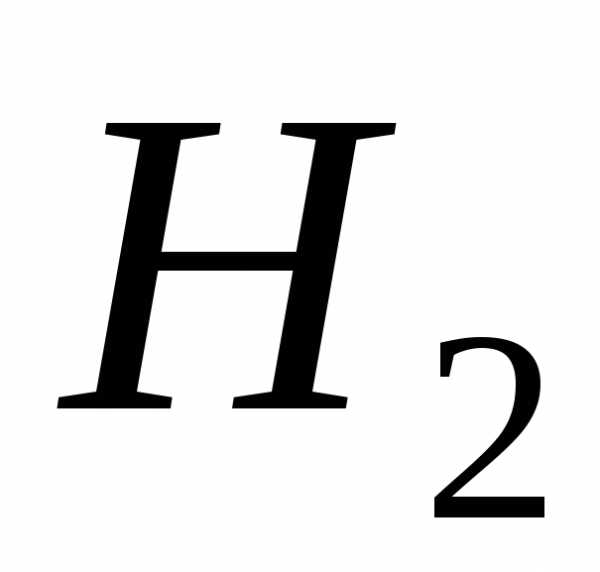 состоит в том, что выбрана вторая урна
(состав урны: все черные шары).
состоит в том, что выбрана вторая урна
(состав урны: все черные шары).
Гипотеза  состоит в том, что выбрана третья урна
(состав урны: 2 черных и 3 белых шара).
состоит в том, что выбрана третья урна
(состав урны: 2 черных и 3 белых шара).
Найти: 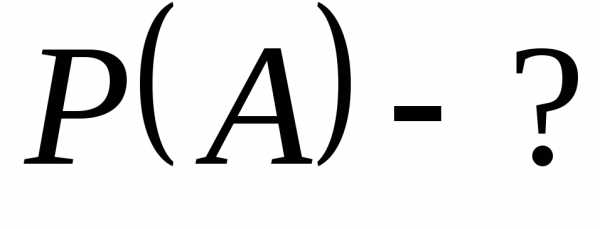
Решение.
Дерево вероятностей
Для решения задач, в которых решения принимаются в условиях стохастической неопределенности, удобно использовать так называемое «дерево вероятностей».
Определение. Деревом вероятностей называется графический метод, который показывает последовательность стратегических решений и предполагаемые последовательности действий при каждом возможном блоке случайных обстоятельств.
Построение дерева решения начинается с первого решения и продвигается вперед через ряд последовательных событий и решений, при этом вероятностные события обозначаются кружками, а принимаемые решения квадратиками. Ответвления из квадратиков представляют стратегии, а ответвления из кружков — внешние условия. При каждом решении или событии у дерева вероятностей появляются ответвления, которые показывают соответственно возможное направление действий до тех пор, пока, наконец, все логические последовательности решений и вытекающие из них события не будут вычерчены. Отметим, что ответвления из кружков имеют вероятности, причем сумма вероятностей для всех ответвлений, вытекающих из любого кружка, должна равняться единице.
Из
формулы полной вероятности следует,
что для вычисления вероятности события  необходимо
осуществить перебор всех путей, ведущих
к результирующему
событию
необходимо
осуществить перебор всех путей, ведущих
к результирующему
событию  ; вычислить
и расставить на соответствующих путях
вероятности
; вычислить
и расставить на соответствующих путях
вероятности 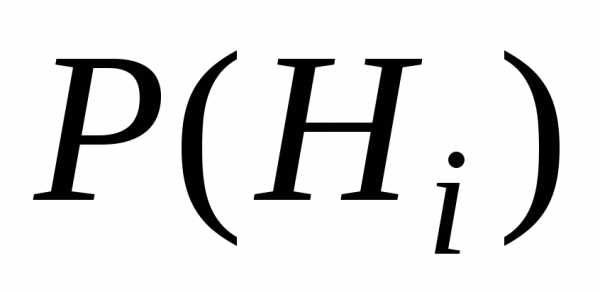 того, что движение будет происходить
поданному
пути, и вероятности
того, что движение будет происходить
поданному
пути, и вероятности 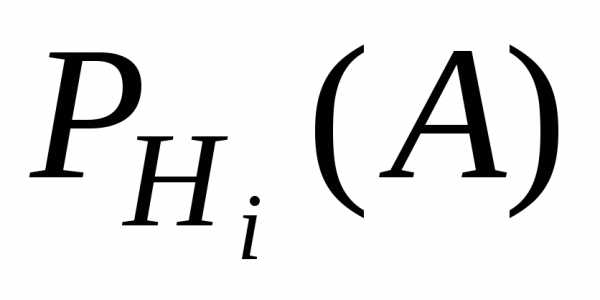 того,
что на данном пути будет
достигнуто конечное событие
того,
что на данном пути будет
достигнуто конечное событие  . Затем вероятности,
стоящие на
одном пути, перемножаются, а результаты,
полученные для различных
путей, складываются.
. Затем вероятности,
стоящие на
одном пути, перемножаются, а результаты,
полученные для различных
путей, складываются.
Каждое из условий может, в свою очередь, делиться на несколько дополнительных условий или гипотез, т.е. на каждом этапе оно допускает неограниченное число ветвлений схемы, поэтому при решении задач более удобно пользоваться не самой формулой полной вероятности, а графической схемой полной вероятности или соответствующим деревом вероятностей.
Пример. Трое
преподавателей принимают экзамен в
группе из
30 человек, причем первый опрашивает 6
студентов, второй — 3,
а третий — 21 студента (выбор студентов
производится случайным
образом из списка). Отношение трех
экзаменаторов к слабо подготовившимся
различное: шансы таких студентов сдать
экзамен
у первого преподавателя равны 40 %, у
второго — только 10
%, зато у третьего — 70 %. Найти вероятность
того, что слабо подготовившийся
студент сдаст экзамен. Решение. Обозначим
через  ,
,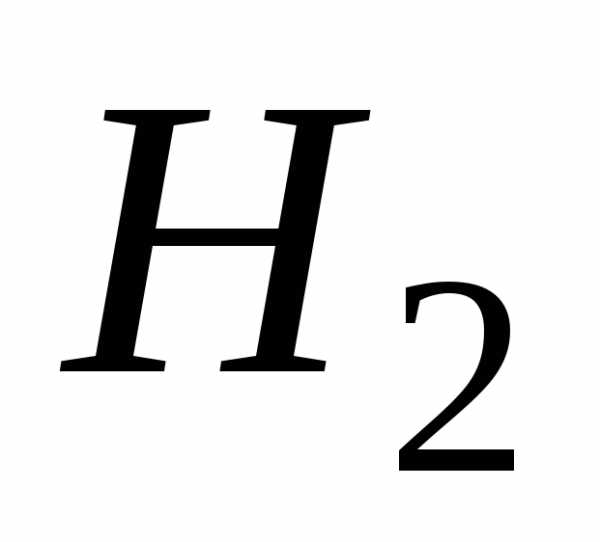
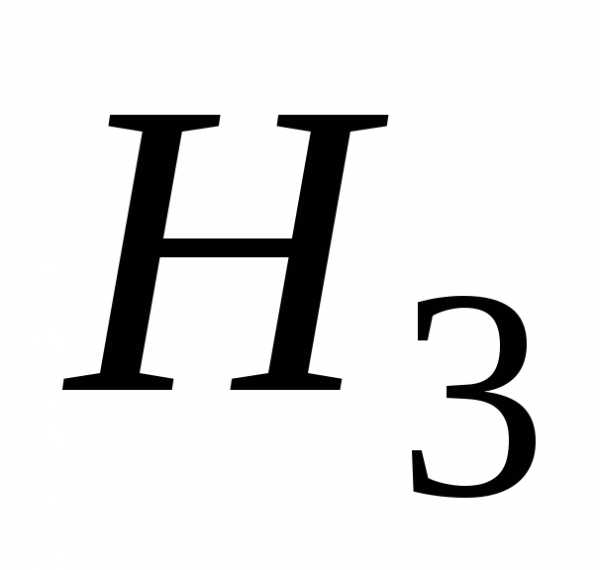 —
гипотезы, состоящие в том, что
слабо подготовившийся студент отвечал
первому, второму и
третьему экзаменатору соответственно.
По условию задачи
—
гипотезы, состоящие в том, что
слабо подготовившийся студент отвечал
первому, второму и
третьему экзаменатору соответственно.
По условию задачи
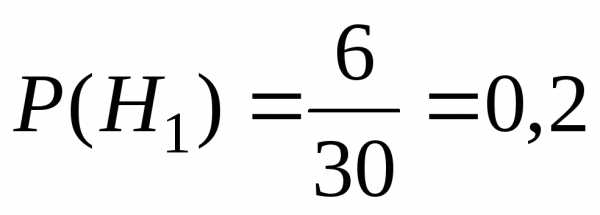
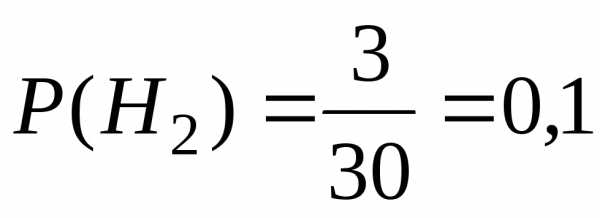
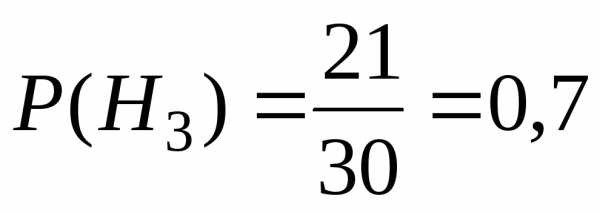
Пусть
событие  состоит в том, что слабо подготовившийся
студент сдал экзамен.
Тогда по условию задачи
состоит в том, что слабо подготовившийся
студент сдал экзамен.
Тогда по условию задачи
.
По формуле полной вероятности получаем
.
Построим для рассматриваемой задачи дерево решений
studfiles.net
8.Формула полной вероятности. Формула Бейеса
Если событие А может произойти только при выполнении одного из событи, которые образуютполную группу несовместных событий, то вероятность события А вычисляется по формуле.Эта формула называетсяформулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий , вероятности появления которых. СобытиеА может произойти только вместе с каким-либо из событий , которые будем называтьгипотезами. Тогда по формуле полной вероятности
Если событие А произошло, то это может изменить вероятности гипотез .
По теореме умножения вероятностей
,откуда.Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез называютсяапостериорными вероятностями, тогда как —априорными вероятностями.
9. Формула Бернулли. Примеры использования.
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события АА в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события АА в единичном испытании буквой рр, т.е. p=P(A)p=P(A), а вероятность противоположного события (событие АА не наступило) — буквой q=P(A¯¯¯¯)=1−pq=P(A¯)=1−p.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли
Pn(k)=Ckn⋅pk⋅qn−k,q=1−p.Pn(k)=Cnk⋅pk⋅qn−k,q=1−p.
Распределение числа успехов (появлений события) носит название биномиального распределения.
10.Дискретные и непрерывные случайные величины и их характеристики.
Одним из основных в теории вероятностей является понятие случайной величины. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от многих случайных причин, которые заранее не могут быть учтены. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение. Характеристикой среднего значения случайной величины служит математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:Дисперсию удобно вычислять по формуле:
.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно. Помимо функции распределения для непрерывных случайных величин, существует еще один удобный способ задания закона распределения — плотность вероятности. Пусть функция распределения F(x) данной НСВ Х непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек. Тогда производная f(x) ее функции распределения называется плотностью распределения непрерывной СВ Х (или «плотностью вероятности», или просто «плотностью»): Числовые характеристики НСВ:Математическое ожидание непрерывной случайной величины Х с плотностью вероятности f(x) находится по формуле: При этом математическое ожидание существует, если интеграл в правой части формулы абсолютно сходится: это значит, что сходится интеграл Дисперсия непрерывной случайной величины Х с плотностью вероятности f(x) находится по формуле
или
Средним квадратическим отклонением случайной величины Х называется число ,определяемое равенством.Величинанеотрицательна и имеет ту же размерность, что и СВ Х.
11.Законы распределения случайных величин Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно. Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать. Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы. Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, …, хn с соответствующими им вероятностями р1, р2, …, рn:
38. Оценка точности – это центральный вопрос в любых вычислениях. СКП искомых параметров ( j mx ) вычисляется по формуле: mx Qjj j = μ (10) где μ — ошибка единицы веса. [ ] n k pv − = 2 μ Сумма [ ] 2 pv в данном случае вычисляется на последнем этапе решения задачи, при вычислении i v по найденным X j |
studfiles.net
