Формула квадратичная – Квадратичная функция одной переменной — Википедия

• Уравнение вида

называется квадратным уравнением. Число D = b² — 4ac — дискриминант этого уравнения.
Если

Квадратные уравнения и неравенства. Алгоритмы решения квадратного уравнения и неравенства. Формулы дискриминанта и корней квадратного уравнения. Теорема Виета. Примерно 7 класс (13 лет)

dpva.ru

Квадратичная функция

Квадратичная функция — функция вида:

f(x)=ax²+bx+c

или

y(x)=ax²+bx+c

Где  a≠0.

В уравнении квадратичной функции:

a –старший коэффициент

b – второй коэффициент

с  свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции

y(x)=x²

или

f(x)=x²

.

Имеет вид и строится по «базовым точкам»:

a>0

Парабола состоит из 2 частей: одна находится в I четверти, где значения X и Y положительные, а вторая часть – во II четверти, где значения X отрицательные, а значения Y  положительные.

y(x)>0, при x∈(-∞;0)∪(0;+∞)

Если двигаться по одной ветви параболы от -∞ к 0, то мы замечаем, что функция убывает, если двигаться по другой ветви гиперболы от 0 до +∞, то мы замечаем, что функция возрастает.

Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как y(x)=x² при любых значениях остальных коэффициентов.

График функции

y(x)=-x² 

Имеет вид и строится по «базовым точкам»:

Парабола состоит из 2 частей: одна находится в III четверти, где значения X и Y  отрицательные, а вторая часть – в IV четверти, где значения X  положительные, а значения Y отрицательные.

y(x)<0, при x∈(-∞;0)∪(0;+∞)

Если двигаться по одной ветви параболы от  -∞ к 0, то мы замечаем, что функция возрастает, если двигаться по другой ветви гиперболы от 0 до  +∞, то мы замечаем, что функция убывает.

Свойства функции y(x)=x²:

1)    Область определения функции:

D(f)=(-∞;0)∪(0;+∞). 

2)Область значения функции:

Если a<0

E(f)=(-∞;0].

Если a>0

E(f)=[0;+∞).

3)Наибольшее и наименьшее значение функции:

Если a<0, то Y_наиб=0,Y_наим нет.

Если a>0, тоY_наим=0, Y_наиб нет.

4)Y(x)=x²— четная функция(т.к.f(-x)=x²=(-x)²=f(x) ).

График симметричен относительно оси oY  .

5) Ограниченность функции:

Если a>0, функция ограничена снизу.

Если a<0, функция ограничена сверху.

6) Функция пересекает оси oX и oY в точке (0;0)

Перемещение параболы y(x)=x²

Если добавить константу d (где d любое число), в качестве слагаемого к X, то произойдет перемещение параболыпо оси  (вместе с вертикальной асимптотой).

В таком случае уравнением функции станет:

y(x)=(x±d)²

Если d>0 (y(x)=(x+d)²), то график функции передвигается по оси oX  влево.

Для примера возьмем уравнение y=(x+2)²

Если d<0 (y(x)=(x-d)²), то график функции передвигается по оси oX  вправо.

Для примера возьмем уравнение y=(x-2)²

Если добавить константу c(где cлюбое число) к X² в качестве слагаемого, то произойдет перемещение параболы по оси oY (вместе с горизонтальной асимптотой)

В таком случае уравнением функции станет:

 y(x)=(x)²±c

 Если  c>0 (y(x)=(x)²+c), то график функции передвигается по оси oY вверх.

Для примера возьмем уравнение y=(x)²+2

Если  c<0 (y(x)=(x)²-c), то график функции передвигается по оси oY вниз.

Для примера возьмем уравнение y=(x)²-3

Дискриминант и нахождение корней

y=ax²+bx+c

ax²+bx+c=0

D=(b)²-4ac

1) 1) Если D>0 то уравнение ax²+bx+c=0 имеет 2 решения,  уравнение y=ax²+bx+c имеет 2 точки пересечения с осью oX:

Если a>0, график функции будет иметь примерный вид:

2) Если D=0, то уравнение ax²+bx+c=0 имеет 1 решение,=> уравнениеy=ax²+bx+c имеет 1 точку пересечения с осью oX.

Если a>0, график функции будет иметь примерный вид:

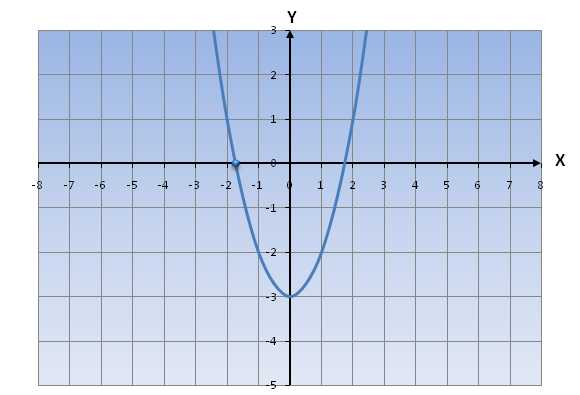
3) Если  D<0, то уравнение ax²+bx+c=0 не имеет решения, => уравнениеy=ax²+bx+c не имеет общих точек пересечения с осью oX.

Если a>0, график функции будет иметь примерный вид:

Координаты вершины параболы

Координаты вершины параболы находятся через данные формулы:

Прямая, проходящая через вершину параболы является осью симметрии параболы.

   Точка пересечения с осью oY

Так как абсцисса любой точки, лежащей на оси oY равна нулю, чтобы найти точку пересечения параболы y=ax²+bx+c с осью oY, нужно в уравнение параболы вместо Xподставить 0, тогда y(0)=c. 

Алгоритм построения квадратичной параболы

1) Направление ветвей.

2) Координаты вершины параболы.

3) Корни дискриминанта.

4) Дополнительные точки.

5) Построение графика.

Разложениеквадратного трехчлена

Пример №1

Построим функцию y=x²-6x+15

В квадратичном трехчлене x²-6x+15, чтобы выразить квадрат разности, используем формулу сокращенного умножения.

Базовая формула: (a±b)²=x²±2ab+b²,

Выразим квадрат разности: x²-6x+15=(x²-6x+9)+6,

Соберем формулу: (x²-6x+9)+6=(x-3)²+6,

У нас получилась функция y=(x-3)²+6,

Мы замечаем, что график функции смещен на 3 по оси oX вправо и на 6 по оси oY вверх.

Следовательно, график функции y=(x-3)²+6 будет выглядеть таким образом:

Пример №2

Построим функцию y=x²+8x+17

В квадратичном трехчлене x²+8x+17,чтобы выразить квадрат разности, используем формулу сокращенного умножения.

Базовая формула: (a±b)²=x²±2ab+b²,

Выразим квадрат разности: x²+8x+17=(x²+8x+16)+1,

Соберем формулу: (x²+8x+16)+1=(x+4)²+1,

У нас получилась функция y=(x+4)²+1,

Мы замечаем, что график функции смещен на 4 oX влево и на 1 по оси oY вверх.

Следовательно, график функции y=(x+4)²+1 будет выглядеть таким образом:

Итог:

Чтобы разложить квадратный трехчлен, использую такой алгоритм:

1) Выразим квадрат разности из данного трехчлена, с помощью формул сокращенного умножения;

2) Соберем, получившуюся формулу;

3) «Прочитаем» график, на смещение, относительно осей координат;

4) Построим график.

Автор статьи: Мажаров Данила Михайлович

Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна

www.teslalab.ru

Квадратичная формула — Большая Энциклопедия Нефти и Газа, статья, страница 1

Квадратичная формула

Cтраница 1

Квадратичные формулы никогда не приводят к физически неприемлемым соотношениям еЭМ, что возможно при использовании линейных формул и особенно неудобно П ри решении тех задач, в которых величина параметра е находится только в конце расчета.  [1]

Однако квадратичные формулы Шези и Дарси-Вейсбаха очень удобны для практических целей и целесообразны с точки зрения единообразия расчета и обычно применяются как для турбулентного, так и для ламинарного режимов. Отклонения же от квадратичного закона учитываются тем, что коэффициенты Я, и С ставятся в косвенную зависимость от скорости. Таким образом, эти формулы устанавливают только общую форму закона сопротивлений. Для определения же численного значения потери напора необходимо в каждом отдельном случае учесть, кроме того, еще и влияние всех указанных выше факторов.  [2]

Точность квадратичных формул значительно выше, чем линейных, и является практически достаточной при любых значениях исходных величин.  [3]

Это уравнение легко решается по квадратичной формуле ( см. раздел III.  [4]

Действительные значения параметров рассчитываются с помощью линейных и квадратичных формул.  [5]

Это значение 2 точнее, чем полученное с применением квадратичной формулы.  [6]

Для этой цели, вообще говоря, могут быть использованы как линейные, так и квадратичные формулы.  [7]

Уравнение ( 2) дает общее решение уравнения второй степени с одним неизвестным; его часто называют квадратичной формулой. Однако только одно из них имеет физический смысл, поскольку все отрицательные и невещественные решения должны быть отброшены. И даже когда оба корня положительны, один из них обычно приводит к отрицательному значению других неизвестных в системе уравнений, которые привели в результате преобразований к квадратному уравнению.  [8]

Re; потери напора при движении осадков и однородных жидкостей практически одинаковы, и коэффициент /, может быть определен по любой квадратичной формуле, используемой при расчете канализационной сети.  [9]

При турбулентном режиме коэффициент Я, практически не зависит от Re; потери напора при движении осадков и однородных жидкостей практически одинаковы, и коэффициент К может быть определен по любой квадратичной формуле, используемой при расчете канализационной сети.  [10]

Применение квадратичных формул ни в коей мере не оправдывается точностью существующих в настоящее время данных и может даже увеличить ошибку в экстраполированном значении величины а благодаря усилению влияния экспериментальных ошибок.  [11]

Уравнение второй степени может быть решено алгебраически. Однако необдуманное использование квадратичной формулы иногда приводит к невразумительным и неточным результатам; поэтому данный способ решения не всегда наилучший.  [12]

Придавая определенные значения величинам [ Н ] и С, решим квадратное уравнение относительно [ Fe3 ] для каждой точки. Это можно было бы сделать по квадратичной формуле, но поскольку обычно известно приближенное значение величины [ Fe3 ], то легче использовать его для оценки последнего члена. Тогда новое значение величины [ Fe3 ], полученное из уравнения ( 10), можно подставить еще раз — для получения лучшего приближения. Такое вычисление легко поддается программированию для решения на ЭВМ.  [14]

Этим завершается вольное описание желаемого исполнения алгоритма для решения квадратных уравнений. Вернемся теперь к рассмотрению некоторых типичных уравнений, чтобы посмотреть, как работают для них квадратичные формулы.  [15]

Страницы:      1    2

www.ngpedia.ru

График квадратичной функции | Формулы с примерами

Графики квадратичной функции 9 класс

Примеры, свойства, правила

   I способ — выделение полного квадрата:

y = 2x² — 4x + 3 = 2(x² — 2x) + 3 =

= 2(x² — 2 • x • 1 + 1²) — 2 • 1² + 3 = 2(x — 1)² + 1;

   II способ — по формулам:

x₀ =    -4   2 • 2 = 1,    y₀ = y(1) = 2 • 1² — 4 • 1 + 3 = 1, значит y = 2(x — 1)² + 1.

2)  y = 2 — 3x² + x = 2 — 3(x² — 13x) =

= 2 — 3(x² — 2 • 16 • x + (16)² + 3 • (16)²) = -3 (x — 16)² + 2 1 12.

График квадратичной функции, рисунок

1)  вдоль оси OX на X₀ вправо, если x₀ > 0,
или на |x₀| влево, если x₀

2)  вдоль оси OY на y₀ вверх, если y₀ > 0,
или на |y₀| вниз, если y₀

Порядок выполнения сдвигов — любой.

Ось симметрии — прямая x = x₀.

Область значений — интервал [y₀, +?), если a > 0, или (-?, y₀], если a

Формулы по алфавиту:

formula-xyz.ru

2.2 Первая основная квадратичная форма поверхности.

_{В произвольной точке Р поверхности (u,v) зададим направление, выбрав u=u(t), v=v(t). Отношение дифференциалов}

_{определяет направление на поверхности , имеем}

.

_{Производная от (u,v) по направлению du: dv имеет вид:}

.

_{Малое смещение} ds по кривой _{(u(t),v(t)) на поверхности вычисляется на основании равенств .}

_{Отсюда получаем ,вычисляя скалярный квадрат}

_=,

_ds2=.

_{Введем обозначения}

_{, .}

_{Значения этих скалярных произведений зависят от выбора точки Р поверхности . Выражение:}

_{называется первой квадратичной формой поверхности (u,v).}

Вычисление первой квадратичной формы в произвольной и выбранной точке.

Вычислим первую квадратичную форму в выбранной точке.

Найдем

Теперь, когда найдены значения E,F и G, напишем формулу первой квадратичной формы в произвольной точке:

Нами получена формула первой квадратичной формы в произвольной точке.

Теперь, подставив наши значения в формулу первой квадратичной формы, найдем ее значение в выбранной точке:

Первая квадратичная форма в выбранной точке найдена.

2.3Вторая квадратичная форма поверхности.

На поверхности (u,v) рассмотрим линию u=u(s), v=v(s) в естественной параметризации : .

Кривизна кривой : (s) =,

где k₁ кривизна кривой, — единичный вектор главной нормали кривой. Обозначим- единичный вектор нормали поверхности

(u,v) , это вектор .

Умножим скалярно и:

,

если — угол междуи. Величина

Называется нормальной кривизной (s) на поверхности (u,v) или нормальной кривизной поверхности

.

Вычислим k_n в окрестности точки Р=(x₀,y₀,z₀) . Находим

,

,

,

здесь и, так как. Обозначим

, ,.

На основании формул:

и имеем

Коэффициенты L,M,N вычислены в точке Р поверхности .Выражение для нормальной кривизны линии на поверхности таково:

.

Отсюда получаем

.

Воспользуемся значением ds² из первой квадратичной формы поверхности

.

Квадратичная форма

Называется второй квадратичной формой поверхности.

Вычисление второй квадратичной формы поверхности в произвольной и выбранной точке.

Найдем вторую квадратичную форму в произвольной точке:

Вычислим, для начала чему равен , подставив ранее полученные значенияE, G и F для первой квадратичной формы:

Найдем векторное произведение и:

=

Затем вычислим ,и:

Найдем коэффициенты второй квадратичной формы, подставив в формулы

наши значения:

L=

M=

N=0

Теперь напишем формулу второй квадратичной формы поверхности в произвольной точке

Вторая квадратичная форма в произвольной точке найдена.

Подставив значения в нашу формулу, получим уравнение второй квадратичной формы в выбранной точке:

Уравнение второй квадратичной формы в выбранной точке найдено.

2.4 Полная и средняя кривизны поверхности.

Рассмотрим регулярную (u,v) в окрестности точки Р.

.

Отсюда получаем

.

Дифференцируем это неравенство по x и по y

.

Главные направления в касательной плоскости определяются этой системой уравнений, если она имеет ненулевые решения, т.е. в случае ∆=0

Значение определителя

.

Главные кривизны есть корни выписанного уравнения. Воспользуемся теоремой Виета

,

где К- полная кривизна поверхности (Гауссова кривизна),

Н- средняя кривизна поверхности.

Вычисление полной и средней кривизны поверхности

Мы вычислили полную и среднюю кривизну поверхности.

studfiles.net