Это ассоциативно: Недопустимое название — Викисловарь
Как развить креативность с помощью метода ассоциаций
Ветас Разносторонний
Основатель творческого инкубатора Creative Happens. Преподаёт креативность в НИУ ВШЭ, ведёт блог «101 метод развития креативности» и Telegram-канал «Креативность 101».Почему важно развивать креативность?
Сегодня весь мир говорит о навыке, ценность которого за последние пять лет выросла в несколько раз. Этот навык — креативность.
На пороге четвёртой индустриальной революции в мире, который, кажется, медленно сходит с ума, люди должны заново придумать свою роль, чтобы остаться нужными и полезными. Иначе что нам останется после неизбежной автоматизации и роботизации всех отраслей и большинства рядовых профессий?
Даже если предыдущий абзац сложно читается и вы не хотите в это верить, перечитайте его ещё раз. Креативность в этом понимании — это не просто умение найти красивую картинку или подобрать рифму к слову «жуй», а возможность продолжать осмысленную жизнь, возможность жить и радоваться, возможность творить и быть полезным.
Я расскажу вам о нескольких инструментах, которые можно брать и применять для поиска новых идей сразу, не имея академического образования в креативности. Сегодня будет первый пост креативной серии про базовый инструмент творческого человека.
Что такое ассоциации?
Ассоциациями в психологии называют связи, возникающие между отдельными событиями, фактами, предметами или явлениями, которые находятся в сознании человека и закреплены в его памяти.
Как они работают?
При наличии ассоциативной связи между явлениями A и B возникновение в сознании A влечёт появление в сознании явления B. Процесс ассоциативного мышления протекает в два этапа: сначала анализ, затем синтез. У вас не получится придумать что-то, что ранее не существовало, так как ассоциативное мышление производит новые комбинации встречавшегося ранее.
Для чего мне это?
С помощью ассоциативного мышления можно улучшить качество жизни. Мы используем ассоциации ежедневно. С их помощью, сознательно или подсознательно, мы находим связи между разными категориями и явлениями, решаем сложные задачи, создаём новые коммерческие продукты и предметы искусства, пишем отличные истории, снимаем кино и искромётно шутим.
Применять ассоциативное мышление для повышения качества жизни можно:
- для рутины и ежедневных дел;
- в семейных отношениях;
- в творчестве, юморе, искусстве;
- в рекламе и маркетинге;
- в продажах;
- при решении технических проблем;
- в изобретательстве;
- для развития бизнеса.
А какие ассоциации есть?
- По сходству. Явления схожи по некоторым признакам: телевизор — ящик, облако — вата.
- По контрасту. Явления противоположны по некоторым признакам: чёрное — белое, смех — грусть.
- По расположению в пространстве или во времени. Явления близки друг к другу: гром — молния, картина — стена.
- Причинно-следственные. Явления связаны как причина и следствие: нарушение — штраф, сарказм — драка.
Как использовать метод ассоциаций для решения творческих задач?
Правильно поставленная задача — половина успеха. И неважно, кто это сказал. Вам понадобится:
И неважно, кто это сказал. Вам понадобится:
- Сформулировать первый вариант задачи.
- Разобрать задачу на составляющие.
- Для каждого элемента задачи написать 15–20 ассоциаций.
- Переформулировать задачу, используя созданные ассоциации, написать не менее 10 новых формулировок.
- Выбрать самую подходящую формулировку.
- Реализовать.
Как составить цепь ассоциаций?
Вам потребуется всего шесть минут. За три минуты нужно записать на листе цепь ассоциаций к слову «творчество». Каждое следующее слово должно быть ассоциацией к предыдущему.
Начало цепи: творчество — картина — краска — ворс — буйвол — луг — … Чем закончится такая цепь через три минуты, сложно предположить. Допустим, у меня получилось слово «колония».
Теперь у вас есть два слова: «творчество» и ваше последнее слово в цепи. Засеките ещё три минуты и попытайтесь создать и описать продукт, сервис или услугу, которые объединяют первое и последнее слово. Вариантов может быть несколько.
Вариантов может быть несколько.
Мои примеры («творчество» + «колония»):
- специальная реабилитационная территория, в которую приезжают на постой перегоревшие офисные менеджеры;
- тематическая выставка современного искусства, посвящённая колонизации человеком других планет;
- аукцион предметов, созданных заключёнными.
Как тренировать ассоциативное мышление?
Ассоциативное мышление, как часть мышления творческого человека, можно и нужно развивать. Самые простые способы — играть в настольные игры с друзьями и каждый день практиковать ассоциативную цепь.
Результат такой работы над собой — более гибкое мышление, интересные идеи для работы и жизни. Вы можете получить результат через 20–60 дней. Примерно столько формируется устойчивая привычка.
Есть ли какие-то приложения и сервисы, которые мне помогут?
- Приложение This That для iOS. Предлагает два слова, ваша задача — связать их в один продукт.
appbox fallback https://apps. apple.com/ru/app/931487639
apple.com/ru/app/931487639
- Набор кубиков для рассказывания историй Story Cubes. Есть и мобильное приложение. Классно играть в большой компании.
АССОЦИАТИВНЫЕ ПЛАНЫ ВЫРАЖЕНИЯ КОГНИТИВНОГО ЛИНГВОСОЦИАЛЬНОГО КОНСТРУКТА «ВЕРА» В РУССКОМ ЯЗЫКОВОМ СОЗНАНИИ
1
УДК 811.161.1’37
АССОЦИАТИВНЫЕ ПЛАНЫ ВЫРАЖЕНИЯ КО-
ГНИТИВНОГО ЛИНГВОСОЦИАЛЬНОГО КОН-
СТРУКТА «ВЕРА» В РУССКОМ
ЯЗЫКОВОМ СОЗНАНИИ
М. И. Казакова, студентка
e-mail: [email protected]
ФГАОУ ВО «Балтийский федеральный университет
имени Иммануила Канта»
Т. Ф. Кузенная, канд. пед. наук, доц.
e-mail: [email protected]
ФГАОУ ВО «Балтийский федеральный университет
имени Иммануила Канта»
В последние два десятилетия XX века складывается такое направление в языкознании,
как когнитивная лингвистика. В нем мы видим новый виток в изучении отношений языка и
мышления. Благодаря данному направлению в науке, широкое распространение получил ас-
социативный эксперимент, выявляющий специфику человеческого восприятия ключевых
понятий языка. В работе рассматривается смысловой объем когнитивного конструкта «вера»,
В работе рассматривается смысловой объем когнитивного конструкта «вера»,
объединяющего психический, концептуальный, религиозный и чувственно-эмоциональный
уровни. Систематизируются значения входящих в понятие «вера» лексем, анализируются и
классифицируются данные, полученные в ходе проведения ассоциативного эксперимента.
Выделяются тематические планы употребления ассоциатов-синонимов, составляющих се-
мантическое поле «вера» для выявления особенности восприятия данной когнитивной линг-
восоциальной единицы. Все это позволяет выявить лингвокультурную специфику данного
понятия в разных дискурсах.
Ключевые слова: ассоциативные планы, эксперимент, вера, понятие, ассоциат-
синоним
ВВЕДЕНИЕ
«Сколько людей, столько и мнений», – гласит известная пословица, но к ней можно
добавить: «столько же непохожих жизненных опытов, взглядов и ориентиров, которые люди
определяют для себя на том или ином этапе жизни». Но есть то, что является ключевым для
Но есть то, что является ключевым для
каждого, та база, которая настолько укоренилась в человеческом сознании, что стала есте-
ственной и неотъемлемой частью существования.
ОБЪЕКТ ИССЛЕДОВАНИЯ
Объектом исследования является объем понятия «вера», который заключает в себе
широкий семантический и культурологический ассоциативный спектр: идея надежды, идея
верности, разочарование, сфера знания, истинности, сфера взаимоотношения людей. Все эти
элементы представляют особый интерес в современной когнитивной лингвистике.
ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ
Целью работы является верификация культурной уникальности понятия «вера» в рус-
ской языковом сознании на основе его содержания и объема. Для этого необходимо было
выявить способы лексической репрезентации конструкта «вера», проанализировать его связь
с такими близкими понятиями, как «достоверность», «уверенность» и «доверие».
Статья на тему «Ассоциативный (ассоциативно-деятельностный) подход.
 Специфика организации и методическое обеспечение образовательного процесса»
Специфика организации и методическое обеспечение образовательного процесса»Статья на тему
«Ассоциативный (ассоциативно-деятельностный) подход. Специфика организации и методическое обеспечение образовательного процесса»
За последние годы изменилось отношение педагогов школы к применению современных образовательных технологий: от сомнения до внедрения. В чем же основное отличие традиционных методов преподавания от новых? Деятельность учителя носит объяснительно-иллюстративный характер, а сам учитель становится транслятором этих знаний. Учащиеся воспринимают сообщаемое, осмысливают, запоминают, заучивают, воспроизводят, тренируются и т.п. Их деятельность носит репродуктивный характер. Хорошо это или плохо? Не то и не другое – репродуктивная деятельность неизбежна при любом характере обучения. Следовательно, основное отличие новых технологий – это идея диалога, где ученик рассматривается как субъект обучения.
Одним из компонентов инновационных технологий обучения является ассоциативный метод.
Идеи о взаимосвязи предметов в воображении развились ещё в античной философии (Аристотель, Платон), но сам термин «ассоциация», был введён в 1698 году Джоном Локком для обозначения взаимосвязи между представлениями, вызванными случайным стечением обстоятельств. Окончательное оформление ассоциативная теория обучения получила в классно-урочной системе Я.А.Коменского.
Ассоциация (в психологии) — это связь психических процессов (ощущений, представлений, мыслей, чувств, движений и т.п.), при которой протекание одного из них вызывает появление другого.
Анализ основных законов образования ассоциаций (ассоциации по сходству, по смежности, причинно-следственные ассоциации) и вторичных законов их образования (длительность первоначальных впечатлений, их оживленность, частота, отсроченность по времени), привели исследователей к выводу, что эти законы являются ничем иным, как условиями наилучшего запоминания.
В качестве основного закона мышления выступает закон упрочения.
Силы ассоциаций зависят от частоты их повторения. В итоге основным результатом обучения выступает репродуктивное мышление. Это является причиной того, что у многих выпускников формируются опыт творческой деятельности, умение самостоятельно добывать знания, готовность свободно включаться в реальную деятельность.
Ассоциативный подход — усвоение знаний рассматривается как процесс установления ассоциативных связей между представлениями и понятиями, имевшимися в прежнем опыте и вновь усваиваемыми посредством установления сходства и различия между ними.
В качестве психологических предпосылок выступают следующие положения:
• механизмом любого акта учения является ассоциация;
• всякое обучение своим основанием имеет наглядность, т е. опирается на чувственное познание, поэтому обогащение сознания обучаемых образами и представлениями — основная задача процесса обучения;
• наглядные образы важны не сами по себе, а постольку, поскольку обеспечивают продвижение сознания к обобщениям на основе сравнения;
• основной метод ассоциативного обучения — упражнение.
Одним из важнейших условий применения метода является эмоциональность учителя:
Ассоциативный метод реализуется через ассоциативные образы. Существуют определённые требования к образам:
Ассоциативный образ обязательно должен быть связан каким-то общим признаком.
— цвету;
— месту расположения;
— форме;
— звучанию;
— действию;
— вкусу;
— материалу;
— назначению;
— количеству.
Не следует навязывать ребенку своей ассоциации!
Ценность идеи – наличие у каждого своего ассоциативного образа при данных требованиях: связь и общая заданная тема.
Применение ассоциативного метода реализуется через систему упражнений.
Для учащихся начальной школы часто бывает трудным запоминание математических терминов и компонентов действий: сложение, вычитание, умножение и деление.
Ассоциативные цепочки помогают учащимся ориентироваться в названиях компонентов и быстрее их запоминать. Так на уроках математики можно использовать
Ассоциативные цепочки можно использовать и на уроках окружающего мира при изучении специальной терминологии, природных зон, при работе с картой, при изучении животного мира и т.д.
Кроме ассоциативной цепочки в работе начальной школы используется
 д.
д.При помощи знаков и символов учащимся предлагается изобразить герб героя, герб числа, герб математического действия. При помощи символов и знаков, придуманных самими же детьми, учебный материал или отдельные элементы урока формируются в смысловые группы. Так, например, на уроках окружающего мира каждый ребенок придумывает свой символ живой и неживой природы. Таким образом, что по его элементам другие дети могут назвать составляющие живой и неживой природы. Так же говоря об ассоциативном восприятии, на различных этапах урока детям предлагается из музыкальных произведений выбрать то, которое у них ассоциируется с художественным произведением, с характером героя, с настроением.
Для более успешного запоминания словарных слов используется прием ассоциативного запоминания.
Орфограмма представлена в виде яркого образа, связанного с личным опытом ребенка. Так же используются короткие сказки или рассказы о слове с использованием ассоциативной пантомимики. Например: изучая словарное слово “помидор”, дети показывают пальцем круглую, или овальную форму помидора и это движение ассоциируется у них с буквой “о” в написании этого слова. Работая над словом “народ”, мы говорим, что на параде от радости люди кричат “Ура!”. Акцент делается на букву “а”. Это ассоциируется с написанием этой буквы в слове “народ”. Так же дети легко запоминают правильное написание словарных слов, когда опираются на личные ощущения, связанные с этим словом. Например: произнося слово “лимон”, у детей возникает ассоциация с чем – то кислым и их губы растягиваются. Волей неволей они произносят звук “и” в слове “лимон”.
Например: изучая словарное слово “помидор”, дети показывают пальцем круглую, или овальную форму помидора и это движение ассоциируется у них с буквой “о” в написании этого слова. Работая над словом “народ”, мы говорим, что на параде от радости люди кричат “Ура!”. Акцент делается на букву “а”. Это ассоциируется с написанием этой буквы в слове “народ”. Так же дети легко запоминают правильное написание словарных слов, когда опираются на личные ощущения, связанные с этим словом. Например: произнося слово “лимон”, у детей возникает ассоциация с чем – то кислым и их губы растягиваются. Волей неволей они произносят звук “и” в слове “лимон”.
В начальной школе используются наглядные опорные карты со словарными словами, где орфограмма является ярким образом и способствует лучшему запоминанию словарных слов. На первом этапе детям предлагаются готовые опорные карты, а затем они уже сами предлагают свои варианты таких карт. При чем ассоциации у каждого ребенка могут быть различные.
Результатами работы данного метода являются:
Творческая активность детей;
Раскрепощение личности каждого ребёнка;
Создание ситуации успеха;
Обогащение словарного запаса;
Развитие логического мышления;
Улучшение памяти учащихся;
Приобретение опыта работы в группах, в парах, самостоятельно;
Усиление мотивации в обучении.

Таким образом, поиск путей совершенствования обучения, в основе которого лежат ассоциативные теории, направлен на выявление путей и условий развития познавательной самостоятельности, активности и творческого мышления учащихся. В этом отношении показателен опыт педагогов-новаторов:
укрупнение дидактических единиц усвоения (П.М.Эрдниев, Б.П. Эрдниев),
интенсификация обучения на основе принципа наглядности (В.Ф.Шаталов, С.Д. Шевченко и др.),
опережающее обучение и комментирование (С.Н.Лысенкова), повышение воспитывающего потенциала урока (Е.Н.Ильин, Т.И.Гончарова и др.),
совершенствование форм организации обучения и взаимодействия педагогов и учащихся на уроке (И.М.Чередов, С.Ю.Курганов, В.К.Дьяченко, А.Б.Резник, Н.П.Гузик и др.),
индивидуализация обучения (И.П.Волков и др.).
Ассоциативным теориям обучения, которые изначально не ориентированы на развитие творческого потенциала учащихся, противостоят теории, опирающиеся на деятельностный подход. К ним относятся теория проблемного обучения (А.М.Матюшкин, М.И.Махмутов и др.), теория поэтапного формирования умственных действий (П.Я.Гальперин. Н.Ф.Талызина и др.), теория учебной деятельности (В.ВДавыдов, Д.Б.Эльконин и др.).
К ним относятся теория проблемного обучения (А.М.Матюшкин, М.И.Махмутов и др.), теория поэтапного формирования умственных действий (П.Я.Гальперин. Н.Ф.Талызина и др.), теория учебной деятельности (В.ВДавыдов, Д.Б.Эльконин и др.).
что это? Отвечаем на вопрос. Значение и объяснение
Есть слова, значения которых нам не слишком часто пригождаются в повседневной жизни, но их необходимо понимать, потому что жизнь состоит не только из быта. Как кажется, именно из таких сегодняшний наш гость – ассоциативность. Это (характер слова) выяснится в процессе разбора.
Значение
Сложность в том, что существительное «ассоциативность» в принципе встречается нечасто. Если нам надо изумиться случайным связям, которые возникают в голове человека, то мы выберем скорее словосочетание «ассоциативный ряд», чем существительное. То есть преимущество у прилагательного, и это неспроста. Толковый словарь, например, тоже не признает самостоятельного значения слова «ассоциативность» и отсылает нас к прилагательному. Что ж, давайте последуем по предложенному адресу: «Устанавливаемый по ассоциации (второе значение)». Не откладывая дела в долгий ящик, посмотрим это самое второе значение слова «ассоциация»: «Связь между отдельными представлениями, при которой одно из представлений вызывает другое».
Что ж, давайте последуем по предложенному адресу: «Устанавливаемый по ассоциации (второе значение)». Не откладывая дела в долгий ящик, посмотрим это самое второе значение слова «ассоциация»: «Связь между отдельными представлениями, при которой одно из представлений вызывает другое».
Причем ассоциации не всегда бывают предсказуемыми. Например, у человека, думающего о рассказе «Маска» Чехова, может возникать в воображении кадр из фильма «Маска» (1994) с Джимом Керри. На первый взгляд, никакой связи нет. Но если вдуматься, то она есть, потому что поведение столь разных главных героев одинаково провокационно. И даже источник один и тот же – желание развлечься. Однако большинству людей такая ассоциативность (и это понятно) покажется странной.
Ассоциация как способ исцеления
Пусть читатель не пугается, в наши планы не входит глубокое погружение в историю психоанализа, да это и не нужно. Иногда самые странные и безумные ассоциации могут служить дорогой к подсознанию. Как известно, автором метода свободных ассоциаций является З. Фрейд. Представьте: человек лежит на кушетке, а З. Фрейд сидит в изголовье. Клиент не видит психоаналитика и начинает называть слова и словосочетания, которые ему просто приходят на ум. Пока поток льется без препятствий, психолог не вступает в игру: он не нужен. Как только возникает пауза, психоаналитик спрашивает клиента, в чем причина. Таким образом, специалист разматывает тугой клубок проблемы и добирается до ее корней. Другими словами, иногда ассоциативность – это прекрасный профессиональный инструмент, как скальпель хирурга.
Фрейд. Представьте: человек лежит на кушетке, а З. Фрейд сидит в изголовье. Клиент не видит психоаналитика и начинает называть слова и словосочетания, которые ему просто приходят на ум. Пока поток льется без препятствий, психолог не вступает в игру: он не нужен. Как только возникает пауза, психоаналитик спрашивает клиента, в чем причина. Таким образом, специалист разматывает тугой клубок проблемы и добирается до ее корней. Другими словами, иногда ассоциативность – это прекрасный профессиональный инструмент, как скальпель хирурга.
Стереотип – это ведь тоже ассоциация
Да, забыли сказать: мы насыщаем материал фактическими примерами, потому что (и это очень важно) у объекта исследования нет синонимов. А так как свято место пусто не бывает и тема интересная, то можно поговорить о не менее существенных вещах, связанных с ассоциативным рядом в принципе.
Давайте воспроизведем три основных стереотипа, взятых случайным образом:
- Блондинки – глупые.
- Мужчины плохо готовят.

- Все женщины умеют готовить.
Плюс стереотипа в том, что не надо особенно думать, потому что есть шаблон, схема, готовый образ. А минус в том, что он мешает воспринимать жизнь так, как она есть, а не так, как нам кажется. Большинство стереотипов могут не соответствовать реальности в каждом конкретном случае, но правы в общем. В противном случае они бы исчезли.
И поэтому, когда мы видим блондинку, мы сразу думаем, что она необразованная и нашпигована различными штампами. Но такая ассоциативность – это тоже своего рода клише. Отличный пример разрыва этого шаблона представлен в фильме «Блондинка в законе» (2001). В кинокартине умело эксплуатируются расхожие истины о белокурых дамах, а затем опровергаются поведением главной героини.
Остальные два стереотипа тоже не всегда правы. Но все равно большинство людей, смотря на мужчину, думает, что он со сковородками на «вы», а с женщиной обратная история. Нужно ли говорить, что значение ассоциативности в данном случае немногого стоит?
Мышление ассоциативное — Энциклопедия по экономике
Оно отлично умеет получать, запоминать и при необходимости вызывать из архива любые нужные сведения этот механизм называется памятью, и устроен он таким чудесным образом, что обращение к одной мысли автоматически ведет за собой переход к другим, тематически связанным. Это называется ассоциативным мышлением.
[c.260]
Это называется ассоциативным мышлением.
[c.260]Экспертные оценки с обратной связью 3.2 Ассоциативность человеческого мышления [c.257]
Обычно в принятии любого решения присутствуют в различной степени три момента интуиция, суждение и рациональность. При принятии чисто интуитивного решения люди основываются на собственном ощущении того, что их выбор правилен. Правильность УР достигается благодаря возможности человека проникнуть в суть решаемой проблемы и понять ее. Часто такое проникновение приходит неожиданно, когда человек занимается другими делами, или даже во сне. Развитое ассоциативное мышление помогает человеку решать совершенно разноплановые проблемы. Здесь присутствует шестое чувство , своего рода озарение. [c.46]
К изобретательству наиболее склонны люди с хорошо развитым ассоциативным мышлением. Поиск возможных технических решений весьма увлекательный и в то же время напряженный процесс. Многим конструкторам он доставляет интеллектуальное наслаждение, подобное тому, какое испытывает любитель шахматной игры. Мозг такого человека находится в состоянии творческого поиска даже в те моменты, когда сам человек занят совершенно другим делом. Конструктор знает, что то или иное техническое решение может возникнуть в его сознании совершенно неожиданно. Часто это бывает в транспорте, нередко в кино или театре, бывали случаи — и во сне. Разгадка механизма творчества — неотъемлемое условие создания искусственного интеллекта. На заре технического творчества поиск конструктивного решения всецело относился к области искусства. В настоящее время этот процесс все ближе примыкает к науке. Использование систематизированных и обобщенных знаний в поиске технических решений — характерная черта современного проектирования. Знания нужны не для того, чтобы освободить человека от творчества, а для того, чтобы сделать его более целенаправленным. Стремление к сокращению сроков проектирования не позволяет надеяться на спонтанное озарение, его нужно стимулировать. Нередки случаи, когда наиболее удачный вариант технического решения возникал в конце разработки и уже не мог быть использован.
Мозг такого человека находится в состоянии творческого поиска даже в те моменты, когда сам человек занят совершенно другим делом. Конструктор знает, что то или иное техническое решение может возникнуть в его сознании совершенно неожиданно. Часто это бывает в транспорте, нередко в кино или театре, бывали случаи — и во сне. Разгадка механизма творчества — неотъемлемое условие создания искусственного интеллекта. На заре технического творчества поиск конструктивного решения всецело относился к области искусства. В настоящее время этот процесс все ближе примыкает к науке. Использование систематизированных и обобщенных знаний в поиске технических решений — характерная черта современного проектирования. Знания нужны не для того, чтобы освободить человека от творчества, а для того, чтобы сделать его более целенаправленным. Стремление к сокращению сроков проектирования не позволяет надеяться на спонтанное озарение, его нужно стимулировать. Нередки случаи, когда наиболее удачный вариант технического решения возникал в конце разработки и уже не мог быть использован. [c.118]
[c.118]
Середина описания — какой он, наш объект. Нужно описать отдельные части или детали предмета, а если это живой объект — те свойства, которые делают объект интересным. Среди них важно выделить самую характерную деталь или свойство. Это позволит создать впечатляющий образ предмета. Помочь в этом может сравнение. Вот почему оратору так необходимы воображение, фантазия, ассоциативное мышление [c.98]
Ассоциативное мышление респондента может быть включено с помощью вопросов типа Какие мысли у вас возникают в связи с данным обстоятельством О чем вы думаете, когда видите то или это и подобные. Вопросы такого рода должны задаваться наряду с традиционными и казаться респондентам обычными, не несущими в себе никакого скрытого подтекста. Однако эти вопросы (выведывающие сокровенное) должны быть органично вплетены в общую канву беседы. Такие приемы побуждают некоторых из респондентов говорить то, что им приходит в голову в данный момент, в соответствии с ассоциациями, появляющимися в процессе умело направляемой интервьюером беседы. Тогда опрашиваемые (хотя и не все) могут раскрыться и высказать то, что вряд ли сочли бы возможным для оглашения в открытой беседе. Например, о приемлемых для них размерах чаевых, об интимных деталях туалета и т.п.
[c.210]
Тогда опрашиваемые (хотя и не все) могут раскрыться и высказать то, что вряд ли сочли бы возможным для оглашения в открытой беседе. Например, о приемлемых для них размерах чаевых, об интимных деталях туалета и т.п.
[c.210]
По способу воздействия PR-кампании подразделяются на рациональные и эмоциональные. Стратегии рациональной PR-кампании ориентируются на то, чтобы информировать, обращаться к потенциальной аудитории с призывом принимать решения, чтобы убедить аудиторию, приводить убедительные аргументы. В таких стратегиях часто используются чертежи или графики для того, чтобы усилить и подкрепить впечатление от сказанного. Стратегии эмоциональной (ассоциативной) PR-кампании обращаются к чувствам, эмоциям, подсознательным импульсам. Они воздействуют через ассоциативное мышление. Излюбленное средство, применяемое в таких стратегиях, — рисунок, символ, большое значение придается цветовой гамме, часто используется звук. [c.245]
Третьей особенностью рекламного стиля мышления является, на наш взгляд, его высокая ассоциативность — умение улавливать и устанавливать связи с другими, смежными областями знания, культуры, деятельности. Иначе говоря — широта мышления, богатство знаний.
[c.12]
Иначе говоря — широта мышления, богатство знаний.
[c.12]
Образный ОРТ апеллирует к эмоциям потребителя, к его ассоциативно-образному мышлению. В образном ОРТ активно используются все средства языковой выразительности речевые фигуры, тропы, особые синтаксические конструкции, призванные усилить производимое [c.133]
Акцентный монтаж строится на нарушении принципов комфортного монтажа. Именно на нарушении, а не на незнании. Это особый тип монтажного мышления, где все решают вкус и чувство меры режиссера, его способность парадоксально мыслить, расставлять акценты и умение вязать ассоциативные цепочки. [c.535]
Информационная модель воздействия, как правило, строится с учетом особенностей восприятия представителями различных культур, религий, образа жизни в расчете на два типа памяти (логическую и ассоциативную), а также на целый ряд других основополагающих принципов и механизмов мышления и восприятия. [c.243]
Использование метафор активизирует ассоциативное и образное мышление. В силу этого метафора — прекрасный материал для личностных проекций. Порождая метафорический образ, человек вкладывает в него не только то, что он осознает в отображаемой реальности, но и свои бессознательные ее видения, их эмоциональную окраску, ценностное отношение к этой реальности. Все это весьма важно при проведении диагностики.
[c.293]
В силу этого метафора — прекрасный материал для личностных проекций. Порождая метафорический образ, человек вкладывает в него не только то, что он осознает в отображаемой реальности, но и свои бессознательные ее видения, их эмоциональную окраску, ценностное отношение к этой реальности. Все это весьма важно при проведении диагностики.
[c.293]
Чтобы приспосабливаться, нужно выбрать путь непротивления учебе и переменам. Для этого нужна готовность выйти за рамки мышления, ограниченного понятиями, воспоминаниями и ассоциативными связями. Кроме того, нужна готовность овладеть наукой управлять энергией внутреннего мира тогда можно избавиться от отрицательных последствий болезненных воспоминаний. Научитесь менять знак болезненного воспоминания на обратный -и оно перестанет быть болезненным. Если отрицательно заряженное воспоминание разрядить (то есть лишить этой энергии), оно не [c.182]
Основой укрепления памяти является наблюдательность. После наблюдения наступает этап ассоциативного мышления. Существуют три естественных закона запоминания метод связок, система зацепок, тренировка наблюдательности.
[c.325]
Существуют три естественных закона запоминания метод связок, система зацепок, тренировка наблюдательности.
[c.325]
Приведенные выше примеры показывают, что имиджи строятся на ассоциациях. Мышление человека ассоциативно. Это — закон нашей психологии. Ассоциации — необходимое условие нашей психической деятельности. Физиологическую основу возникновения ассоциаций составляет открытый великим русским ученым Иваном Павловым механизм образования временной нервной связи между различными участками коры головного мозга, замыкание этих участков. [c.73]
На самом же деле произойдет противоположное каждый раз, когда потребитель будет слышать эту рекламу, она будет ассоциироваться у него с популярным исполнителем. Но вот обратного процесса не произойдет. Знакомая мелодия привлечет внимание к рекламе, знакомая персона усилит интерес, а ассоциативное мышление поможет привнести в эту рекламу свойства и признаки узнаваемого фрагмента реальности. [c.60]
Или вот еще вариант. Попробуйте сколотить команду единомышленников (можно привлечь коллег по работе или членов семьи) и с помощью несложных игровых тренингов начните развивать свое ассоциативное мышление, память и воображение, что, в конечном счете, поможет вам сделать речь более гладкой, яркой и образной.
[c.35]
Попробуйте сколотить команду единомышленников (можно привлечь коллег по работе или членов семьи) и с помощью несложных игровых тренингов начните развивать свое ассоциативное мышление, память и воображение, что, в конечном счете, поможет вам сделать речь более гладкой, яркой и образной.
[c.35]
МакКлелланд определяет мотив как эффективно окрашенную ассоциативную сеть , то есть модель мышления с приложенными позитивными чувствами. Чтобы инструктировать кого-либо по мотивации достижения, преподаватель должен четко рассказать учащемуся, что такое мысли о достижении — и проассоциировать обдумывание 11 элементов мотивированной на достижение мысли с приятными результатами. Обдумывание этих 11-ти мыслей по определению повышает у человека мотивацию достижения. [c.291]
Другой способ выявления своего творческого потенциала заключается в развитии навыков ассоциативного мышления. Вы сами можете научиться свободным ассоциациям. Оглядитесь вокруг себя и выберите какой-нибудь объект, расслабьтесь и посмотрите, какие мысли придут вам в голову. Чем чаще вы будете это проделывать, тем легче вам будет даваться сам процесс. Вы обнаружите, что количество и разнообразие ассоциаций растет. Стремитесь думать о самых смешных, глупых, сумасшедших ассоциациях — так вы разовьете способность находить оригинальные ассоциации.
[c.416]
Чем чаще вы будете это проделывать, тем легче вам будет даваться сам процесс. Вы обнаружите, что количество и разнообразие ассоциаций растет. Стремитесь думать о самых смешных, глупых, сумасшедших ассоциациях — так вы разовьете способность находить оригинальные ассоциации.
[c.416]
Чарли начал со своей центральной темы настоящий и долгосрочный успех приходит к тем людям, которые прилагают усилия, направленные сначала на построение решетки интеллектуальных моделей, а затем на то, чтобы научиться мыслить ассоциативно, многодисциплинарным образом. Чарли предупредил, что это потребует определенного труда, особенно в том случае, если полученное вами образование принудило вас к узкой специализации. Но как только эти модели прочно займут место в вашем уме, вы окажетесь интеллектуально оснащенными, для того чтобы решать множество самых разнообразных задач. Вы сможете потянуться и взять ту модель, которая дает самое лучшее решение стоящей перед вами проблемы. Все, что вам надо сделать, — это знать и развивать правильные алгоритмы мышления . Несомненно, Бенджамин Франклин согласился бы g этой мыслью.
[c.29]
Несомненно, Бенджамин Франклин согласился бы g этой мыслью.
[c.29]
На обложке выделяются один — два элемента, концентрирующие на себе внимание. Именно они в первую очередь влияют на ассоциативное мышление читателей и принятие решения о том, чтобы взять книгу в руки. Это может быть все, что угодно, в зависимости от того, чем именно издатель намерен привлечь читателей. Наиболее часто используются следующие элементы имя автора, если автор популярен имя автора плюс элемент картинки автор плюс название (для классики) название или название плюс элемент картинки, если автор не известен. [c.73]
Анализ научно-технической информации Иерархическая декомпозиция Матричный анализ Сетевой анализ Прямые экспертные оценки Экспертные оценки с обратной связью 2.4 2.5 2.6 2.7 3.1 3.2 Свойство научно-технической информации опережать реализацию научно-технических достижений в общественной практике Расчленяемость сложных объектов (проблем, целей, задач и т.п.) на более простые элементы с образованием непересекающихся иерархически соподчиненных подмножеств Соотносимость (качественная или количественная) между множеством целей и средств их реализации Взаимообусловленность элементов сложной работы, ограничивающая снизу предельно короткий срок ее выполнения при заданной продолжительности элементарных операций Приближение обобщенных независимых оценок к истинным Ассоциативность человеческого мышления
[c. 143]
143]
В основе брейнсторминга лежит принцип ассоциативной психологии мышления в групповой ситуации взаимного стимулирования. Исследования в этой области показали, что новые и самые неожиданные идеи возникают обычно по ассоциации с какой-либо другой, но привычной и знакомой идеей, в ситуациях непринужденного разговора и группового общения. Непременным условием возникновения таких ассоциаций является отсутствие или ослабление стереотипов и шаблонов привычного группового мышления, ориентированного на принятые и одобренные образцы. [c.126]
Метафору можно назвать скрытым сравнением. Удачные метафоры позволяют лучше понять суть явлений, сделать их зримыми, вызывают эмоции, надолго остаются в памяти. Оратор постоянно ищет образы тех явлений, о которых он собирается рассказать слушателям. Образы рождаются, когда мы наблюдаем жизнь, размышляем, сопереживаем. Они возникают как синтез нашего эмоционального отклика на какое-то событие и ассоциативной способности мышления. Примеры метафор Душа настоящего человека есть самый сложный, и самый неясный, и самый певучий музыкальный инструмент (начало речи А. Блока Памяти В.А. Комиссаржевской ) Закон об обеспечении государственного бюджета был костылем, который помог преодолеть трудности только одного года (из выступления бывшего федеративного канцлера ФРГ К. Киссингера).
[c.79]
Блока Памяти В.А. Комиссаржевской ) Закон об обеспечении государственного бюджета был костылем, который помог преодолеть трудности только одного года (из выступления бывшего федеративного канцлера ФРГ К. Киссингера).
[c.79]
Иногда ассоциативное мышление интервьюеры могут попытаться включить посредством предоставления респонденту возможности произнести первое, что придет ему на ум в ответ на произнесенное интервьюером слово, показанную картинку или видеосюжет и т.п. Таким образом пытаются выяснить возникающие у людей ассоциации в ответ на рекламные сообщения, как в виде текста, так и в виде рекламных роликов или рекламных телевизионных программ. Говорят, что телевизионная передача Последний герой , которая шла по телевидению (программа ОРТ) зимой и весной 2002 г. и была посвящена девственной, почти первозданной, жизни современных людей на острове, расположенном в экваториальных широтах,— голубое море, желтый песок, зеленые пальмы — предназначалась для рекламы напитка J-7 . Она вызывала у зрителей ассоциации, связанные с райским наслаждением , образно представляемым рекламой конфет Баунти ,— тоже море, песок, пальмы, — что, очевидно, наряду с увеличени-4 ем продаж J-7 способствовало и росту продаж конфет. Таким образом, эти конфеты получили дополнительную и бесплатную рекламу. Ассоциативное мышление — важная категория, определяющая поведение людей при совершении покупок, изучать его можно и нужно посредством соответствующих проекционных методов.
[c.210]
Таким образом, эти конфеты получили дополнительную и бесплатную рекламу. Ассоциативное мышление — важная категория, определяющая поведение людей при совершении покупок, изучать его можно и нужно посредством соответствующих проекционных методов.
[c.210]
Здесь на помощь приходят разнообразные методики творческого мышления. Несмотря на все их многообразие, профессиональные креаторы всегда самостоятельно вырабатывают собственный алгоритм действий, который чаще всего сочетает модификации различных креативных приемов (например, весьма эффективно комбинирование мозгового штурма и ассоциативного метода) и актов медитации. [c.63]
Остановимся еще на одном тоже важном для построения систем классификации свойстве человеческого мышления. Известно, что при образовании понятий значительную роль играют ассоциации, возникающие у всех нас при работе с языковыми и внеязыковыми текстами. Упомянем о результатах, относящихся к семантическому пространству Ч. Осгуда, Идея, которую много лет развивал этот ученый и его многочисленные ученики и последователи, заключалась в том, что все понятия, которыми оперирует человек, занимают определенное местоположение в специальном субъективном семантическом пространстве, метрика которого отражает ассоциативную близость тех или иных понятий. Само это пространство строится следующим образом. Для естественного языка берутся антонимичные пары типа большой — маленький, острый — тупой, быстрый — медленный, добрый — злой и т. п. Для каждой такой пары (обычно в языке их 300—400) строится шкала, в которой сами эти слова занимают концевые позиции, а середину шкалы—нейтральное выражение (например, не большой, не маленький и т. п.). Кроме того на шкале имеется еще некоторое число делений, которые могут и не обозначаться
[c.165]
Само это пространство строится следующим образом. Для естественного языка берутся антонимичные пары типа большой — маленький, острый — тупой, быстрый — медленный, добрый — злой и т. п. Для каждой такой пары (обычно в языке их 300—400) строится шкала, в которой сами эти слова занимают концевые позиции, а середину шкалы—нейтральное выражение (например, не большой, не маленький и т. п.). Кроме того на шкале имеется еще некоторое число делений, которые могут и не обозначаться
[c.165]
Для обсуждения вынесенного в заголовок вопроса предположим, что мышление является дихотомичным. В таком случае в ассоциативном эксперименте набор и частота ассоциаций на антонимы должна быть равна как минимум между самими антонимами. В противном случае предложение симметричной шкалы между антонимами в шкале семантического дифференциала является внесением исследовательского артефакта в мышление человека. [c.108]
Таким образом, гипотеза о дихотомичности мышления результатами ассоциативного исследования не подтвердилась можно сделать вывод об отсутствии в повседневном мышлении синонимов и антонимов, а их использование в массовой коммуникации будет приводить к смещению восприятия рекламируемого объекта вплоть до нарушения идентификации. [c.109]
[c.109]
Основой укрепления памяти является наблюдательность. Мы можем запомнить ничего, что ускользнуло бы от нашего на-одепия. А после наблюдения наступает второй этап — ассо-тивное мышление путем разглядывания или на слух запоми-ше возможно, только если объект ассоциируется в нашем со-.нии с чем-либо, что мы уже знаем или помним. Большинство запоминаемого ассоциируется с уже известным ассоциативных связей — забывается. [c.305]
Чрезвычайно важно отметить, что ассоциативное мышление каннибалистично сильная ассоциация без сожаления пожирает все другие возможные ассоциативные связи. Данный феномен очень хорошо знаком актерам кино, которые становятся заложниками сыгранных ими ролей. [c.60]
Такое мышление не является линейным, логичным, лево-полушарным возможно, что это своего рода свободно-ассоциативное обдумывание, характерное для право-полушарного функционирования. Стремление овладеть способностью быстрого схватывания сути вещей, казаться компетентным или соперничать со старшими, либо с супервизором, влияет на это мыслительное пространство. Супервизор должен работать так, чтобы понимать аналитическую суть происходящего и противодействовать потенциальным помехам в мыслительном процессе.
[c.7]
Супервизор должен работать так, чтобы понимать аналитическую суть происходящего и противодействовать потенциальным помехам в мыслительном процессе.
[c.7]
Представление на рисунках человеческих фигур в виде символов, подсознательно понятных каждому зрителю, давно и широко применяется как в рекламе, так и в нерекламных изображениях. Однако художник, создававший предложенный выше баннер, не учел один важный аспект символ — это объект, апеллирующий непосредственно к интуитивному восприятию человека, включающий механизм ассоциативного мышления. Он незамедлительно вызывает в сознании аудитории взаимосвязанные цепочки образов широкая галка — чайка — море круг с расходящимися лучами — солнце — лето и т. д. Немного подправив приведенную выше картинку, мы получим изображение, которое в большинстве случаев обязательно возникнет в подсознании зрителя при взгляде на этот баннер (рис. 7.17). [c.147]
Ассоциативный вид — Энциклопедия по машиностроению XXL
Все указанные изображения связаны с моделью изменения в модели приводят к изменению изображения в ассоциативном виде. [c.22]
[c.22]Создать новый чертеж из модели позволяет создать чертеж с ассоциативным видом текущей трехмерной модели [c.219]
Создание ассоциативных видов 281 [c.281]
Создание ассоциативных видов [c.281]
Ассоциативный вид — это вид чертежа, ассоциативно связанный с определенной ЗВ-моделью. При изменении формы или размеров модели изменяется изображение на всех связанных с ней ассоциативных видах. В свою очередь, проекционные виды чертежа, созданные с помощью команды Стандартные виды, находятся в проекционной связи со своим главным видом. По содержанию ГОСТ 2.305—68 устанавливает следующее название основных видов, получаемых на основных плоскостях проекций [c.281]
Создание ассоциативных видов 283 [c.283]
Создание ассоциативных видов 285 [c.285]
Создание ассоциативных видов 287
[c. 287]
287]
Создание ассоциативных видов 289 [c.289]
Создание ассоциативных видов 291 [c.291]
Проекционная связь управляет проекционной связью между ассоциативными видами [c.291]
Создание ассоциативных видов 293 [c.293]
Создание ассоциативных видов 295 [c.295]
Создание ассоциативных видов 297 [c.297]
Создание ассоциативных видов 299 [c.299]
Создание ассоциативных видов 301 [c.301]
Ассоциативный вид — вид чертежа, ассоциативно связанный с существующей моделью (деталью или сборкой). При изменении формы, размеров и топологии модели изменяется и изображение во всех связанных с ней видах. [c.313]
Опорный вид — ассоциативный вид чертежа, использующийся при создании другого вида. Так, для проекционных видов базовым является главный вид, для разреза/ сечения — вид, в котором располагается обозначение секущей плоскости и т. п.
[c.313]
п.
[c.313]
Ассоциативные виды, а затем на панели инструментов по кнопке [c.396]
Вкладки Формат, Вставка, Модели и Параметры присутствуют на Панель свойств Ввод текста при заполнении основной надписи чертежа, содержащего ассоциативные виды модели. Пример такого состояния системы показан на рис. 5.44. [c.445]
| Рис. 5.44. Состояние системы при заполнении основной надписи чертежа, содержащего ассоциативные виды модели |
При создании в чертежах ассоциативных видов моделей, содержащих поверхности, пользователь может управлять их отображением в видах. [c.680]
[c.680]
Панель Параметры нового вида на вкладке Параметры имеет два текстовых окна и кнопку для раскрытия возможных масштабов вида. В текстовых полях Масштаб введите масштаб, который будет по умолчанию использоваться при создании Произвольного и Стандартных ассоциативных видов, а также при созда- [c.910]
НИИ всех не ассоциативных видов. Масштаб может быть задан в виде отношения любых чисел. Можно также выбрать масштаб вида из стандартного ряда. Для этого щелкните по кнопке, расположенной между полями ввода масштаба. Из появившегося меню выберите нужный масштаб. Масштаб видов, установленный при настройке текущего листа, будет применяться только для вновь создаваемых видов масштаб видов, созданных до изменения настройки, останется прежним, [c.911]
В разделе Передаваемые объекты присутствует группа опций, позволяющая указать, изображения каких объектов требуется по умолчанию передавать из модели в чертеж при построении ассоциативных видов.
 В дальнейшем, при настройке параметров конкретного ассоциативного вида, набор параметров можно изменить на вкладке Объекты Панели свойств.
[c.911]
В дальнейшем, при настройке параметров конкретного ассоциативного вида, набор параметров можно изменить на вкладке Объекты Панели свойств.
[c.911]Панель Параметры нового вида на вкладке Линии позволяет производить отрисовку ассоциативных видов чертежа видимыми линиями, а также включать/ отключать различные стили отрисовки для невидимых линий, линий переходов или линий сгиба. Образец линии отображается на вкладке справа. [c.911]
Панель Синхронизация данных основной надписи и модели позволяет настроить параметры синхронизации данных модели и основной надписи чертежа, содержащего ассоциативные виды. . [c.911]
Создание в чертеже ассоциативных видов — видов, ассоциативно связанных с моделями. [c.62]
Здесь в соответствии с иерархической структурой осуществляется декомпозиция ЭМП на сборочные узлы и детали. Причем блоки иерархической структуры содержат лишь дешифраторы соответствующих кодов и указатели. Иными словами, иерархическая структура используется лишь для целей кодирования ЭМП и его компонентов и установления конструктивных связей между ними. Все числовые данные содержатся в блоках, ассоциативно связанных с соответствующими элементами иерархической структуры. Например, с блоком ЭМП на самом верхнем уровне связаны все блоки, содержащие интегральные данные относительно изделия в целом (блоки расчетных параметров и характеристик, числовых данных чертежей общего вида, технологической системы производства, технико-экономических показателей и т. п.). С блоком Провод на самом нижнем уровне связаны блоки, содержащие данные относительно материала и марки, количества проводов в пазу, длин отдельных проводов и суммарной длины, стоимости и т. п. Очевидно, что с понижением уровня иерархической структуры уменьшается ЧИСЛО ассоциативно связанных блоков.
[c.196]
Иными словами, иерархическая структура используется лишь для целей кодирования ЭМП и его компонентов и установления конструктивных связей между ними. Все числовые данные содержатся в блоках, ассоциативно связанных с соответствующими элементами иерархической структуры. Например, с блоком ЭМП на самом верхнем уровне связаны все блоки, содержащие интегральные данные относительно изделия в целом (блоки расчетных параметров и характеристик, числовых данных чертежей общего вида, технологической системы производства, технико-экономических показателей и т. п.). С блоком Провод на самом нижнем уровне связаны блоки, содержащие данные относительно материала и марки, количества проводов в пазу, длин отдельных проводов и суммарной длины, стоимости и т. п. Очевидно, что с понижением уровня иерархической структуры уменьшается ЧИСЛО ассоциативно связанных блоков.
[c.196]
Эта операция билинейна, коммутативна, дистрибутивна и ассоциативна. В результате ее применения каждой паре векторов ставится в соответствие тензор 8. Перечисленные свойства операции непосредственно следуют из вида коэффициентов Зрд.
[c.57]
Перечисленные свойства операции непосредственно следуют из вида коэффициентов Зрд.
[c.57]
Сгибы, имеющиеся в листовой детали, могут отображаться как в согнутом, так и в разогнзггом состоянии. Имеется возможность показа листовой детали в развернутом состоянии. Ассоциативные виды листовой детали в чертеже создаются так же, как и ассоциативные виды обычной детали. При этом, если в листовой детали настроены параметры развертки, то в чертеже возможно формирование изображения развертки этой детали. [c.22]
Этот процесс чрезвычайно трудно осуществить на уровне логики. Логика позволяет получать определенные следствия из начальных посылок, следуя строгому набору допустимых правил. Однако в ней отсутствует механизм контроля адекватности самих начальных посылок. Нахождение связей между явлениями, имеющими, с точки зрения привычных нам представлений, мало общего, не позволяет использовать аппарат логики. Наиболее перспективным здесь видится использование интуитивных способностей человека, С1Снованных на нежестких ассоциативных связях, то есть метода проведения аналогий между объектами и явлениями,
[c. 11]
11]
Произвольно возникающие повреждения характеризуются мень-щими видовыми составами грибов. Как правило, поражение вызвано одним из видов грибов. Природные штаммы грибов более активны, чем музейные, а поражаемость металлов избирательная. При инфицировании музейными культурами повренгдения не отличаются от произвольных, но возникают при ассоциативном действии несколько штаммов. Количество поражаемых материалов больше, а скорость роста выше. [c.33]
Департамент анализа данных и машинного обучения
В Департаменте анализа данных, принятия решений и финансовых технологий разработали решение для построения ассоциативного ряда хэштегов с помощью построения семантического пути в сети хэштегов. О полученных результатах исследователи рассказали на международной конференции по сетевому анализу NET 2019.
Сергей Вячеславович Макрушин, заместитель заведующего кафедрой Банковская автоматизация и информационные технологии, совместно со студентом факультета Прикладной математики и информационных технологий Никитой Блохиным создали алгоритм построения семантического пути в сети совместной встречаемости хэштегов и протестировали его для большого набора данных из соцсети Instagram. Они предложили оригинальную формулировку математической задачи построения семантического пути и вычислительно эффективный механизм его построения для очень больших сетей.
Они предложили оригинальную формулировку математической задачи построения семантического пути и вычислительно эффективный механизм его построения для очень больших сетей.
«Уметь построить семантический путь может быть интересно с практической точки зрения, например, с помощью этого алгоритма можно дать рекомендации тем пользователям соцсетей, которые активно используют хэштеги в рекламных и маркетинговых кампаниях для привлечения новых подписчиков», — отметил С.В. Макрушин, выступая с презентацией на конференции по сетевому анализу NET 2019, которая состоялась в «Яндексе».
Для исследования был собран корпус из 14,6 млн сообщений в Instagram, содержащих хэштеги, и построена сеть из 1,7 млн узлов-хэштегов, между которыми было установлено 64 млн связей, отражающих совместное использование хэштегов в сообщениях пользователей. Чтобы сократить вычислительную сложность построения семантического пути, были отброшены наименее важные связи. Фильтрация позволила уменьшить количество связей до десятков тысяч, что примерно в 10 раз меньше чем в исходной сети. Для задачи построения семантической сети была сформулирована оригинальная постановка задачи оптимизации, для которой были подобраны параметры и специализированная метрика семантической близости хэштегов. Это позволило построить вычислительно эффективные алгоритмы решения задачи.
Для задачи построения семантической сети была сформулирована оригинальная постановка задачи оптимизации, для которой были подобраны параметры и специализированная метрика семантической близости хэштегов. Это позволило построить вычислительно эффективные алгоритмы решения задачи.
Так, при построении ассоциативного ряда хэштегов между двумя конечными узлами #курсовыеработыназаказ и #лень были обнаружены сильные семантические связи с другими хэштегами, такими как #контрольныеназаказ, #советыпредпринимателя и #эконометрика.
В ходе исследования были использованы два способа построения ассоциативных семантических рядов — глобальный кратчайший путь и «жадный» локальный алгоритм. Сбор и предварительная обработка данных были реализованы на языке программирования Python, хранение сети в графовой базе данных ArangoDB.
Что такое ассоциативная собственность? — Определение, факты и примеры
Что такое ассоциативная собственность? Это свойство указывает, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается одинаковой независимо от группировки слагаемых (или множимых).
Группировка означает использование скобок или квадратных скобок для группировки номеров.
Ассоциативное свойство включает 3 или более чисел.
Числа, сгруппированные в скобках или квадратных скобках, становятся одним целым.
Ассоциативное свойство может использоваться только при сложении и умножении, но не при вычитании или делении.
Пример ассоциативного свойства для добавления
Примеры ассоциативного свойства для умножения:
Приведенные выше примеры показывают, что изменение группировки не приводит к изменению ответа.
Ассоциативное свойство полезно при сложении или умножении нескольких чисел. Группируя, мы можем создавать более мелкие компоненты для решения. Это делает вычисления сложения или умножения нескольких чисел проще и быстрее.
Пример Дополнение :
17 + 5 + 3 = (17 + 3) + 5
= 20 + 5
= 25
Здесь сложение 17 и 3 дает 20. Затем сложение 5 с 20 дает 25. Группировка помогла найти ответ легко и быстро.
Затем сложение 5 с 20 дает 25. Группировка помогла найти ответ легко и быстро.
Пример Умножение :
3 × 4 × 25 = (25 × 4) × 3
= 100 × 3
= 300
Здесь умножение 25 на 4 дает 100. Тогда 3 можно легко умножить на 100, чтобы получить 300.
Однако мы не можем применить свойство ассоциативности к вычитанию или делению. Когда мы меняем группировку чисел при вычитании или делении, это меняет ответ, и, следовательно, это свойство неприменимо.
Пример Вычитание :
10 – (5 – 2) = 10 – 3 = 7
(10 – 5) – 2 = 5 – 2 = 3
Итак, 10 – (5 – 2) ≠ (10 – 5) – 2
Пример Раздел :
(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3
24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12
Итак, (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2)
Интересные факты |
определение слова ассоциативный в The Free Dictionary
Если мы обнаружим в данном случае, что наш смутный образ, скажем, неописуемой собаки имеет те ассоциативные эффекты, которые имели бы все собаки, но не те, которые принадлежат какой-либо конкретной собаке или породе собак, мы можем сказать, что наш образ означает «собака» в целом. Выступая на открытии семинара, организованного 17-18 апреля в Тунисе по вопросам интеграции иностранных студентов в Тунисе по инициативе Главного управления по делам студентов в партнерстве с Фондом Конрада Аденауэра и несколькими партнерами из гражданского общества, Халбус указал на необходимость сотрудничества и координации между различными институциональными и ассоциативными субъектами для преодоления всех препятствий на пути к улучшению этой интеграции. leur pays d’accueil, en serve la locale a l’echelle des communes, des mairies et d’autres, представители учреждений.Будь то толстые блоки или тонкие строфы, ассоциативный стих мексиканского поэта Алехандро Тарраба падает подобно водопаду, усеянный краткими образами и эрудированными ссылками, которые придают этому двойному переводу вид интерпретируемой возможности. Конечный автомат (FSM): FSM контролирует чтение и запись. сигналы данных как для кэш-памяти, так и для основной памяти, они указывают, какой набор кэш-памяти имеет запрошенный адрес, отправляя сигналы для (GMux) и для (блока контроллера LRU), если набор ассоциативный был выбран из кэш-памяти при прямом сопоставлении.
Выступая на открытии семинара, организованного 17-18 апреля в Тунисе по вопросам интеграции иностранных студентов в Тунисе по инициативе Главного управления по делам студентов в партнерстве с Фондом Конрада Аденауэра и несколькими партнерами из гражданского общества, Халбус указал на необходимость сотрудничества и координации между различными институциональными и ассоциативными субъектами для преодоления всех препятствий на пути к улучшению этой интеграции. leur pays d’accueil, en serve la locale a l’echelle des communes, des mairies et d’autres, представители учреждений.Будь то толстые блоки или тонкие строфы, ассоциативный стих мексиканского поэта Алехандро Тарраба падает подобно водопаду, усеянный краткими образами и эрудированными ссылками, которые придают этому двойному переводу вид интерпретируемой возможности. Конечный автомат (FSM): FSM контролирует чтение и запись. сигналы данных как для кэш-памяти, так и для основной памяти, они указывают, какой набор кэш-памяти имеет запрошенный адрес, отправляя сигналы для (GMux) и для (блока контроллера LRU), если набор ассоциативный был выбран из кэш-памяти при прямом сопоставлении. В любом случае, для того, чтобы чтобы объяснить широкую изменчивость ложных воспоминаний, большинство исследований было сосредоточено на ассоциативной силе, которая связывала критические и изучаемые слова вместе.Показано, что при определенных свойствах формы кривизны криволинейные системы Рота-Бакстера (A, R, S, [omega]) индуцируют ассоциативные и (левые) предлиевские произведения на алгебре A. Этот процесс обучения называется ассоциативное обучение. Поэтому он утверждал, что общей чертой между ними является стремление определить «единицу обучения» и природу ассоциативной структуры, возникающей в результате воздействия на животных определенных процедур обусловливания. Андерсон (1983) и Коллинз и Лофтус (1975) предполагает, что знание слова в любой области (т.г., фонологический, семантический, визуальный), приобретенный в результате бесчисленных встреч, где присутствовали другие слова, составляет сети взаимосвязанных слов (т. е. ассоциативные сети).
В любом случае, для того, чтобы чтобы объяснить широкую изменчивость ложных воспоминаний, большинство исследований было сосредоточено на ассоциативной силе, которая связывала критические и изучаемые слова вместе.Показано, что при определенных свойствах формы кривизны криволинейные системы Рота-Бакстера (A, R, S, [omega]) индуцируют ассоциативные и (левые) предлиевские произведения на алгебре A. Этот процесс обучения называется ассоциативное обучение. Поэтому он утверждал, что общей чертой между ними является стремление определить «единицу обучения» и природу ассоциативной структуры, возникающей в результате воздействия на животных определенных процедур обусловливания. Андерсон (1983) и Коллинз и Лофтус (1975) предполагает, что знание слова в любой области (т.г., фонологический, семантический, визуальный), приобретенный в результате бесчисленных встреч, где присутствовали другие слова, составляет сети взаимосвязанных слов (т. е. ассоциативные сети).ассоциативный — Викисловарь
Английский[править]
Этимология
От ассоциированный + -ive .
Произношение[править]
- (США) IPA (ключ) : /əˈsoʊ.ʃi.ə.tɪv/, /əˈsoʊ.si.ə.tɪv/
Прилагательное[править]
ассоциативный ( сравнительный более ассоциативный , превосходный наиболее ассоциативный )
- Относящийся к, возникающий в результате или характеризующийся ассоциацией; способный к ассоциации; стремление к ассоциации или объединению.
- 1998 , Kazimierz Zieliński, Pairing, Continuity, Contingency — What’s the Difference , Anna Neugebauer (редактор), Macroмолекулярное взаимодействие в мозге Associative Механизмы: Proceedings of the International 63,
- В настоящее время обусловливание рассматривается как частный случай ассоциативного научения, которое дает животному (как и человеку) способность обнаруживать, запоминать, извлекать и использовать взаимосвязи между сигналами и подкрепляющими факторами, а также контролировать вознаграждения и аверсивные действия.
 Мероприятия.
Мероприятия.
- В настоящее время обусловливание рассматривается как частный случай ассоциативного научения, которое дает животному (как и человеку) способность обнаруживать, запоминать, извлекать и использовать взаимосвязи между сигналами и подкрепляющими факторами, а также контролировать вознаграждения и аверсивные действия.
- 1998 , Kazimierz Zieliński, Pairing, Continuity, Contingency — What’s the Difference , Anna Neugebauer (редактор), Macroмолекулярное взаимодействие в мозге Associative Механизмы: Proceedings of the International 63,
- (алгебра бинарного оператора * {\ displaystyle *}) Такое, что для любых операндов a, b {\ displaystyle a, b} и c {\ displaystyle c}, (a * b) * c = a * ( б * с) {\ Displaystyle (а * б) * с = а * (б * с)}; (кольца и т. д.), операция умножения которых ассоциативна.
- 2000 , Фредди Ван Ойстайен, Алгебраическая геометрия для Ассоциативная Алгебры , Марсель Деккер, стр. 235,
- Возможно, преимущество « ассоциативной алгебраической геометрии», которую мы пытались развить в предыдущих главах, состоит в том, что она не зависит от сплетений и дальнейших обобщений, потому что она остается в силе до тех пор, пока соответствующие «функциональные» кольца, построенные в эти теории являются ассоциативными алгебрами.
- 2006 , Ибрагим Асем, Дэниел Симсон, Анджей Сковронски, Элементы теории представлений ассоциативных алгебр, 1: методы теории представлений , Cambridge University Press, стр.
 vii,
vii,- В настоящее время общепризнано, что теория представлений ассоциативных алгебр восходит к гамильтоновскому описанию комплексных чисел парами действительных чисел.
- 2014 , Мигель Кабрера Гарсия, Анхель Родригес Паласиос, Не- Ассоциативные Нормированные алгебры, Том 1: Теоремы Видава-Палмера и Гельфанда-Наймарка , Cambridge University Press, стр. 1,
- В этом разделе мы развиваем основы теории нормированных алгебр, уделяя особое внимание случаю полных нормированных унитальных ассоциативных комплексных алгебр.
- 2000 , Фредди Ван Ойстайен, Алгебраическая геометрия для Ассоциативная Алгебры , Марсель Деккер, стр. 235,
- (вычисление) Адресуется ключом более сложным, чем целочисленный индекс.
- Ассоциативные массивы AWK могут быть проиндексированы строками.
Ассоциативным воспоминаниям когда-то уделялось значительное внимание.
Антонимы[править]
Гипонимы[править]
Производные термины[править]
Связанные термины[править]
Переводы[править]
алгебраическое свойство оператора
- Приведенные ниже переводы необходимо проверить и вставить выше в соответствующие таблицы переводов, удалив все номера.
 Числа не обязательно совпадают с числами в определениях. Инструкции см. в Викисловаре: Макет записи § Переводы.
Числа не обязательно совпадают с числами в определениях. Инструкции см. в Викисловаре: Макет записи § Переводы.
Переводы для проверки
Прилагательное[править]
ассоциативный
- средний род единственного числа от ассоциативный
Произношение[править]
Прилагательное[править]
ассоциативный
- женский род единственного числа от associatif
итальянский[править]
Прилагательное[править]
ассоциативный f pl
- женский род множественного числа от associativo
Анаграммы
Шведский[править]
Прилагательное[править]
ассоциативный
- абсолютно определенный натуральный мужской род единственного числа от ассоциативный .

Коммутативное, ассоциативное и дистрибутивное свойство? [Видео и практика]
Как вы, возможно, уже поняли за годы уроков математики и домашних заданий, математика по своей природе является последовательной, а это означает, что каждое понятие основано на предыдущей работе. Арифметические навыки необходимы для овладения алгебраическими понятиями, которые затем развиваются для дальнейшего использования в вычислениях и так далее. По мере того, как вы со временем выстраиваете эти концепции, математический процесс может стать автоматическим, но причина или оправдание работы могут быть давно забыты.
В этом видео мы вернемся к основам, чтобы рассмотреть коммутативные, ассоциативные и дистрибутивные свойства действительных чисел, которые учитывают математическую механику алгебры и не только.
Коммутативное свойство
Названия свойств, которые мы собираемся рассмотреть, помогают расшифровать их значения. Рассмотрим слово , коммутативное . О чем вы думаете, когда видите это слово? Когда я смотрю на это слово, я вижу слово «коммутировать». Это слово напоминает мне о «перемещении», которое свойство коммутативности позволяет вам делать при сложении или умножении алгебраических членов.{2}\) и так далее. Чтобы доказать, что перемещение или перестановка терминов допустимы, давайте рассмотрим несколько примеров использования свойства коммутативности в задачах на сложение.
О чем вы думаете, когда видите это слово? Когда я смотрю на это слово, я вижу слово «коммутировать». Это слово напоминает мне о «перемещении», которое свойство коммутативности позволяет вам делать при сложении или умножении алгебраических членов.{2}\) и так далее. Чтобы доказать, что перемещение или перестановка терминов допустимы, давайте рассмотрим несколько примеров использования свойства коммутативности в задачах на сложение.
Пример 1
Если мы сложим \(5+3\), то получим \(8\). Но если мы поменяем наши условия и сделаем это \(3 + 5\), мы все равно получим \(8\). Итак, \(5+3=3+5\).
Пример 2
Давайте немного изменим один из наших терминов для следующего примера. \(5+(-3)=2\) и \((-3)+5=2\). Итак, \(5+(-3)=(-3)+5\). Обратите внимание, что существует очень важное различие между сложением отрицательного целого числа и операцией вычитания.Важно отметить это различие, потому что свойство коммутативности не применяется к операции вычитания. Например, \(5-3\) не дает того же, что и \(3-5\). Это свойство также не относится к делению. \(100\дел 2\neq 2\дел 100\).
Это свойство также не относится к делению. \(100\дел 2\neq 2\дел 100\).
\(100\div 2=50\)\(2\div 100=\frac{1}{50}\)
Пример 3
Однако свойство коммутативности применимо к умножению. Например, \(4\умножить на 3\умножить на 5=5\умножить на 3\умножить на 4\). Давайте посчитаем, чтобы убедиться.{2}\)
\(3+10+3=10+3+3\)\(16=16\)
После добавления каждой стороны у нас останется 16 с обеих сторон, т.е. истинный. \(16=16\).
Следующее свойство, которое мы рассмотрим, это ассоциативное свойство.
Ассоциативное свойство
Опять же, название дает полезный намек на его значение. Что приходит на ум, когда вы слышите слово , ассоциативное с ? Для меня выделяется слово ассоциированное , которое могло бы также навести на мысль слово группа .Соответственно, свойство ассоциативности позволяет нам группировать термины, которые соединяются сложением или умножением различными способами. Скобки используются для группировки терминов и устанавливают порядок операций. Работа внутри скобок всегда выполняется в первую очередь. Математически это свойство выглядит так:
Скобки используются для группировки терминов и устанавливают порядок операций. Работа внутри скобок всегда выполняется в первую очередь. Математически это свойство выглядит так:
Ассоциативность сложения : \((a+b)+c=a+(b+c)\)Ассоциативность умножения : \((a\ cdot b)\cdot c=a\cdot (b\cdot c)\)
Давайте рассмотрим пример использования этого свойства в задаче на сложение.
Пример 1
Этот пример покажет, что добавление сначала двух последних терминов или добавление первых двух терминов просто не имеет значения. Давайте посмотрим на \(3+(4+5)=(3+4)+5\). Итак, сначала делаем то, что в скобках. \(4+5=9\) и \(9+3=7\).
\(3+9=7+5\)\(3+9=12\) и \(7+5=12\)
\(12=12\)
Итак \(12= 12\), потому что это обе стороны уравнения. Точно так же не имеет значения и порядок, в котором мы выполняем умножение.
Пример 2
Допустим, у нас есть \((3\cdot 4)\cdot 5=3\cdot (4\cdot 5)\).
\(12\cdot 5=3\cdot 20\)\(60=60\)
Коммутативное свойство умножения показывает, что при умножении допустимо переставлять члены. Напротив, ассоциативное свойство умножения перемещает скобки в порядке умножения.
Распределительное свойство
Наконец, последнее свойство, которое мы рассмотрим, это свойство распределения, которое выглядит следующим образом: \(a\cdot (b+c)=a\cdot b+a\cdot c\)
Нотация, опять же, диктует, что это свойство применимо только к операциям умножения и сложения.В частности, если термин умножается на выражение в круглых скобках, то умножение выполняется для каждого из терминов. Вот пример, доказывающий, что этот алгебраический ход оправдан. \(2(3+7)=2\cdot 3+2\cdot 7\)
Скобки слева говорят нам сначала добавить 3+7.
Сумма произведений в правой части уравнения дает тот же результат, что и умножение в левой.
Обзор
Хорошо, теперь, когда мы рассмотрели три свойства, давайте проверим вашу память. {2}\)
{2}\)
Думаешь, понял? Посмотрим! Ответ для числа 1 является ассоциативным свойством, потому что скобки перемещаются в порядке умножения. Ответом на вопрос номер два является распределительное свойство, потому что 3 умножается на оба члена в скобках. Это оставляет нас с ответом на вопрос номер три, являющимся коммутативным свойством, потому что мы просто переставили члены.
Как видно из нашей работы в этом видео, вы использовали коммутативные, ассоциативные и дистрибутивные свойства в течение довольно долгого времени, даже не задумываясь над тем, «почему».Вас попросят снова подумать об этих концепциях на курсах математики более высокого уровня, когда некоторые из этих свойств просто не выдерживают критики! До тех пор продолжайте уверенно использовать эти правила, чтобы управлять своей работой и мыслительными процессами.
Надеюсь, этот отзыв был вам полезен. Спасибо за просмотр и удачной учебы!
1.1: Двоичные операции — Mathematics LibreTexts
Двоичная операция
Определение:
Двоичная операция Пусть \(S\) — непустое множество, а \( \star \) называется бинарной операцией над \(S\), если \(a \star b \) определено для всех \(a ,b \в S\).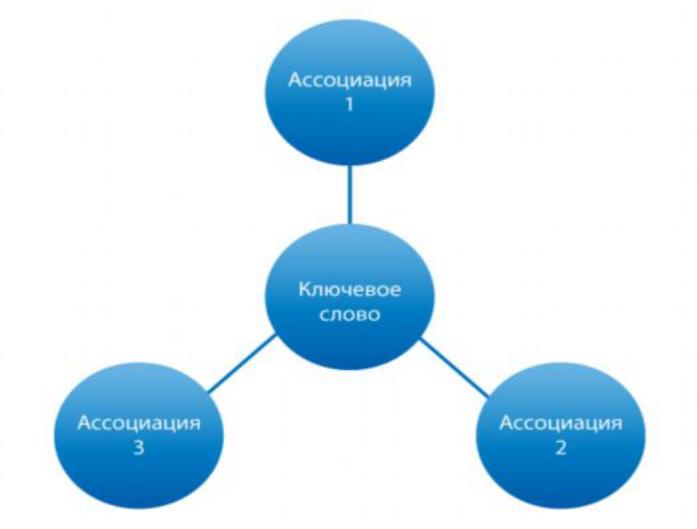 Другими словами, \(\star\) является правилом для любых двух элементов множества \(S\).
Другими словами, \(\star\) является правилом для любых двух элементов множества \(S\).
Пример \(\PageIndex{1}\): Двоичные операции
Следующие бинарные операции над \(\mathbb{Z}\):
- Арифметические операции, сложение \(+\), вычитание \(-\), умножение \( \times \) и деление \(\div \).
- Определить операцию oplus над \(\mathbb{Z}\) с помощью \(a \oplus b =ab+a+b, \forall a,b \in\mathbb{Z}\).
- Определить операцию ominus на \(\mathbb{Z}\) с помощью \(a \ominus b =ab+a-b, \forall a,b \in\mathbb{Z}\).
- Определить операцию otimes над \(\mathbb{Z}\) с помощью \(a \otimes b =(a+b)(a+b), \forall a,b \in\mathbb{Z}\).
- Определите операцию oslash на \(\mathbb{Z}\) с помощью \(a \oslash b =(a+b)(a-b), \forall a,b \in\mathbb{Z} \).
- Определить операцию min над \(\mathbb{Z}\) с помощью \(a \vee b =\min \{a,b\}, \forall a,b \in\mathbb{Z}\).
- Определить операцию max на \(\mathbb{Z}\) с помощью \(a \wedge b =\max \{a,b\}, \forall a,b \in\mathbb{Z}\).

- Определить дефект операции на \(\mathbb{Z}\) с помощью \(a \ast_3 b = a+b-3, \forall a,b \in\mathbb{Z}\).
Давайте изучим бинарные операции, прежде чем мы продолжим:
Пример \(\PageIndex{2}\):
- \(2 \oплюс 3=(2)(3)+2+3=11\).
- \(2 \otimes 3=(2+3)(2+3)=25\).
- \(2 \слеш 3=(2+3)(2-3)=-5\).
- \(2 \ominus 3=(2)(3)+2-3=5\).
- \(2 \vee 3= 2\).
- \(2 \клин 3 =3\).
Упражнение \(\PageIndex{2}\)
- \(-2 \oплюс 3\).
- \(-2 \otimes 3\).
- \(-2 \слеш 3\).
- \(-2 \минус 3\).
- \(-2 \вее 3\).
- \(-2\клин 3\).
- Ответить
-5, 1,5,-2,3
Свойства:
Свойство замыкания
Определение: Свойство замыкания
Пусть \(S\) — непустое множество. Бинарная операция \(\star\) над \(S\) называется замкнутой бинарной операцией над \(S\), если \(a \star b \in S, \forall a, b \in S\ ).
Ниже мы приведем несколько примеров закрытых бинарных операций, которые будут дополнительно изучены в классе.
Пример \(\PageIndex{3}\): Закрытые двоичные операции
Ниже приведены закрытые бинарные операции над \(\mathbb{Z}\).
- Сложение \(+\), вычитание \(-\) и умножение \( \times \).
- Определить операцию oplus над \(\mathbb{Z}\) с помощью \(a \oplus b =ab+a+b, \forall a,b \in\mathbb{Z}\).
- Определить операцию ominus на \(\mathbb{Z}\) с помощью \(a \ominus b =ab+a-b, \forall a,b \in\mathbb{Z}\).
- Определить операцию otimes над \(\mathbb{Z}\) с помощью \(a \otimes b =(a+b)(a+b), \forall a,b \in\mathbb{Z}\).
- Определите операцию oslash на \(\mathbb{Z}\) с помощью \(a \oslash b =(a+b)(a-b), \forall a,b \in\mathbb{Z} \).
- Определить операцию min над \(\mathbb{Z}\) с помощью \(a \vee b =\min \{a,b\}, \forall a,b \in\mathbb{Z}\).
- Определить операцию max на \(\mathbb{Z}\) с помощью \(a \wedge b =\max \{a,b\}, \forall a,b \in\mathbb{Z}\).

- Определить дефект операции на \(\mathbb{Z}\) с помощью \(a \ast_3 b = a+b-3, \forall a,b \in\mathbb{Z}\).
Упражнение \(\PageIndex{1}\)
Определить, закрыта ли операция ominus на \(\mathbb{Z_+}\)?
- Ответить
Операция ominus на \(\mathbb{Z_+}\) закрыта.
Пример \(\PageIndex{4}\): встречный пример
Деление (\( \div \) ) не является закрытой бинарной операцией над \(\mathbb{Z}\).
\( 2, 3 \in \mathbb{Z} \), но \( \frac{2}{3} \notin \mathbb{Z} \).
Сводка арифметических операций и соответствующих наборов:
| \(+\) | \(\раз\) | \(-\) | \(\дел\) | |
| \(\mathbb{Z_+}\) | закрытый | закрытый | не закрытый | не закрытый |
| \(\mathbb{Z}\) | закрытый | закрытый | закрытый | не закрытый |
| \(\mathbb{Q}\) | закрытый | закрытый | закрытый | закрытый (только когда \(0\) не включен) |
| \(\mathbb{R}\) | закрытый | закрытый | закрытый | закрытый (только когда \(0\) не включен) |
Ассоциативное имущество
Определение: Ассоциативное свойство
Пусть \(S\) будет подмножеством \(\mathbb{Z}\). Бинарная операция \(\star\) над \(S\) называется ассоциативной, если \( (a \star b) \star c = a \star (b \star c) , \для всех a, b, в \в S\).
Бинарная операция \(\star\) над \(S\) называется ассоциативной, если \( (a \star b) \star c = a \star (b \star c) , \для всех a, b, в \в S\).
Будем считать, что сложение (\(+\)) и умножение (\( \times \)) ассоциативны на \(\mathbb{Z_+}\). ( Вам не нужно их доказывать! ).
Ниже приведен пример доказательства, когда утверждение верно.
Пример \(\PageIndex{5}\): Ассоциативный
Определите, является ли бинарная операция oplus ассоциативной на \(\mathbb{Z}\).
Мы покажем, что бинарная операция oplus ассоциативна на \(\mathbb{Z}\).
- Доказательство:
Пусть \(a,b,c \in \mathbb{Z}\). Затем рассмотрим, \((a \oplus b) \oplus c = (ab+a+b) \oplus c = (ab+a+b)c+(ab+a+b)+c= (ab)c+ac +bc+ab+a+b+c\).
С другой стороны, \(a \oplus (b \oplus c)=a \oplus (bc+b+c)= a(bc+b+c)+a+(bc+b+c)=a(bc )+ab+ac+a+bc+b+c.\)
Поскольку умножение ассоциативно на \(\mathbb{Z}\), \((a \oplus b) \oplus c =a \oplus (b \oplus c).
 \)
\)Таким образом, бинарная операция oplus ассоциативна на \(\mathbb{Z}\). \(\Коробка\)
Ниже приведен пример того, как опровергнуть ложное утверждение.
Пример \(\PageIndex{6}\): не ассоциативный
Определить, является ли бинарная операция вычитания (\(-\)) ассоциативной на \(\mathbb{Z}\).
Ответ: Вычитание бинарной операции (\(-\)) не ассоциативно на \(\mathbb{Z}\).
- Пример счетчика :
Выберите \( a=2,b=3, c=4,\), затем \((2-3)-4=-1-4=-5 \), но \(2-(3-4)= 2-(-1)=2+1=3\).
Следовательно, бинарная операция вычитания (\(-\)) не ассоциативна на \(\mathbb{Z}\).
Коммуникативное имущество
Определение: Коммутативное свойство
Пусть \(S\) — непустое множество. Бинарная операция \(\star\) над \(S\) называется коммутативной, если \( a \star b = b \star a,\forall a, b \in S\).
Будем считать, что сложение (\(+\)) и умножение (\( \times \)) коммутативны на \(\mathbb{Z_+}\). ( Вам не нужно их доказывать! ).
Ниже приведено доказательство того, что вычитание (\(-\)) НЕ является коммутативным.
Пример \(\PageIndex{7}\): НЕ коммутативный
Определите, является ли двоичная операция вычитания \(-\) коммутативной на \(\mathbb{Z}\).
- Пример счетчика :
Выберите \(a=3\) и \(b=4\).
Затем \(a-b=3-4=-1\) и \(b-a= 4-3=1\).
Следовательно, бинарная операция вычитания \(-\) не коммутативна на \(\mathbb{Z}\).
Пример \(\PageIndex{8}\): Коммутативный
Определите, является ли бинарная операция oplus коммутативной на \(\mathbb{Z}\).
Мы покажем, что бинарная операция oplus коммутативна на \(\mathbb{Z}\).
- Доказательство:
Пусть \(a,b \in \mathbb{Z}\).

Тогда рассмотрим, \((a \oplus b) = (ab+a+b).\)
С другой стороны, \( (b \oplus a) = ba+b+a. \)
Поскольку умножение ассоциативно на \(\mathbb{Z}\), \((a \oplus b) = (b \oplus a). \)
Таким образом, бинарная операция oplus коммутативна на \(\mathbb{Z}\). \(\Коробка\)
Личность
Определение: Личность
Говорят, что непустое множество \(S\) с бинарной операцией \( \star \) имеет тождество \(e \in S\), если \( e \star a=a\star e=a , \forall a \in S.\)
Обратите внимание, что \(0\) называется аддитивным тождеством на \(( \mathbb{Z}, +)\), а \(1\) называется мультипликативным тождеством на \(( \mathbb{Z}, \times) \).
Пример \(\PageIndex{9}\): уникально ли удостоверение?
Пусть \(S\) — непустое множество, а \(\star\) — бинарная операция над \(S\). Если \(e_1\) и \(e_2\) два тождества в \((S,\star) \), то \(e_1=e_2\).
Доказательство:
Предположим, что \(e_1\) и \(e_2\) — два тождества в \((S,\star) \).
Затем \(e_1=e_1 \звезда e_2=e_2.\)
Следовательно, личность уникальна. \(\Коробка\)
Пример \(\PageIndex{10}\): Идентификация
Имеет ли \(( \mathbb{Z}, \oplus )\) идентификатор?
- Ответить
Пусть \(e\) будет тождеством на \(( \mathbb{Z}, \oplus )\).
Тогда \( e \oplus a=a\oplus e=a, \forall a \in \mathbb{Z}.\)
Таким образом, \(ea+e+a=a\) и \(ae+a+e=a\) \(\forall a \in \mathbb{Z}.\)
Так как \(ea+e+a=a\) \(\forall a \in \mathbb{Z},\) \(ea+e=0 \подразумевает e(a+1)=0\) \(\ forall a \in \mathbb{Z}.\)
Следовательно, \(e=0\).
Теперь \( 0 \oplus a=a\oplus 0=a, \forall a \in \mathbb{Z}.\)
Следовательно, \(0\) является тождеством на \(( \mathbb{Z}, \oplus )\).
Пример \(\PageIndex{11}\):
Имеет ли \(( \mathbb{Z}, \otimes)\) идентификатор?
- Ответить
Пусть \(e\) будет единицей на \(( \mathbb{Z}, \otimes)\).
 2=а,\для всех а\in\mathbb{Z}.\)
2=а,\для всех а\in\mathbb{Z}.\)Это противоречие.
Следовательно, \(( \mathbb{Z}, \otimes)\) не имеет идентичности.
Распределительная собственность
Определение: Распределительное имущество
Пусть \(S\) — непустое множество. Пусть \(\star_1\) и \(\star_2\) — две разные бинарные операции над \(S\).
Тогда \(\star_1\) называется дистрибутивным над \( \star_2\) на \(S \), если \( a \star_1 (b \star_2 c)= (a\star_1 b) \star_2 (a \ star_1 c), \для всех a,b,c,\in S \).
Обратите внимание, что умножение распределяется по сложению на \(\mathbb{Z}.\) То есть \(4(10+6)=(4)(10)+(4)(6)=40+24= 64\).
Далее, мы продолжаем до \( (a+b)(c+d) =ac+ad+bc+bd\) (FOIL).
F-первый
O-Внешний
I-Внутренний
L-последний
Это свойство очень полезно для поиска \((26)(27)\), как показано ниже:
Пример \(\PageIndex{12}\): найти \((26)(27)\)
| 20 | 6 | |
|---|---|---|
| 20 | 400 | 120 |
| 7 | 140 | 42 |
Отсюда \((26)(27) =400+120+140+42=702\).
Давай поиграем!
Пример \(\PageIndex{13}\):
Распространяется ли умножение на вычитание?
Пример \(\PageIndex{14}\):
Распределяет ли деление над сложением?
- Ответить
Пример счетчика:
Выберите a = 2, b = 3, c = 4.
Тогда a \( \div\)(b + c) = 2\(\div\)(3+4)
= 2 \(\дел\) 7.
= \(\frac{2}{7}\).
и (a \(\div\) b) + (a \(\div\) c) = \(\frac{2}{3}\) + \(\frac{2}{4}\).
= \(\frac{7}{6}\).
Поскольку \(\frac{2}{7}\) ≠ \(\frac{7}{6}\), бинарная операция \(\div\) не является дистрибутивной над +.
Пример \(\PageIndex{15}\):
Распределяет ли \( \otimes\) по \(\oplus\) на \(\mathbb{Z}\) ?
- Ответить
Пример счетчика:
Выберите a = 2, b = 3, c = 4.

Тогда 2\(\otimes \)(3\(\oplus \)4) = 2\(\otimes \)[(3)(4)+3+4]
= 2\(\ораз\)19
= (2+19)(2+19)
= 441
и (2\(\otimes \)3)\(\oplus \)(2\(\otimes \)4)=[(2+3)(2+3)]\(\oplus \)[(2 +4)(2+4)]
= 25\(\оплюс\)36
= (25)(36)+25+36
= 961.
Поскольку 441 ≠ 961, бинарная операция \( \otimes\) не является дистрибутивной над \(\oplus \) на \(\mathbb{Z}\).
Резюме
В этом разделе мы узнали следующее для непустого множества \(S\):
- Двоичная операция,
- Имущество закрытия,
- Ассоциативное имущество,
- Коммунальное имущество,
- Распределительное имущество и
- Личность.
Ассоциативное свойство
Ассоциативное свойствоАссоциативное свойство:
Набор обладает ассоциативным свойством при определенной операции, если результат операции один и тот же независимо от того, как мы группируем любые наборы из 3 или более элементов, соединенных операцией. Это определение станет более понятным, когда мы рассмотрим несколько примеров.
Это определение станет более понятным, когда мы рассмотрим несколько примеров.
Более формально, если x , y и z являются переменными, представляющими любые 3 произвольных элемента в наборе, который мы рассматриваем (назовем набор, который мы рассматриваем A), а символ # представляет нашей операции, то ассоциативное свойство для A с операцией # будет:
( x#y )# z = x #( y#z ).
Это означает, что свойство ассоциативности выполняется только для множества A и операции # if, независимо от того, какие элементы мы берем из A и подставляем вместо x , y и z , ( x# y )# z всегда будет давать нам тот же результат, что и x #( y#z ).
Помните, что круглые скобки просто говорят нам какую пару делать первой .
Обратите внимание, что при всех операциях операция может воздействовать только на одну пару элементов за раз . Таким образом, выражение x#y#z не имеет смысла, если только мы не установим правило, которое говорит нам сначала идти слева направо или сначала идти справа налево, потому что у нас нет способа узнать , которое операция, которую нужно выполнить первой : должны ли мы сначала выполнить x#y или y#z? Когда мы делаем сложение, вычитание, умножение или деление, у нас есть правило, которое говорит нам просто идти слева направо. Но это правило не обязательно для произвольных операций! Если мы работаем с какой-либо операцией, которая является , а не сложением, вычитанием, умножением или делением, то мы должны иметь круглые скобки для любого выражения с более чем двумя элементами, чтобы мы знали, какое вхождение операции нужно выполнить первым !
Таким образом, выражение x#y#z не имеет смысла, если только мы не установим правило, которое говорит нам сначала идти слева направо или сначала идти справа налево, потому что у нас нет способа узнать , которое операция, которую нужно выполнить первой : должны ли мы сначала выполнить x#y или y#z? Когда мы делаем сложение, вычитание, умножение или деление, у нас есть правило, которое говорит нам просто идти слева направо. Но это правило не обязательно для произвольных операций! Если мы работаем с какой-либо операцией, которая является , а не сложением, вычитанием, умножением или делением, то мы должны иметь круглые скобки для любого выражения с более чем двумя элементами, чтобы мы знали, какое вхождение операции нужно выполнить первым !
Давайте рассмотрим несколько примеров, чтобы лучше понять ассоциативное свойство:
Сначала рассмотрим несколько бесконечных множеств с уже знакомыми нам операциями:
а) Набор из натуральных чисел ассоциативен относительно операции сложения , потому что верно, что для любых двух натуральных чисел x, y и z (x+y)+z = x+(y +з).
b) Набор из целых чисел является , а не ассоциативным при операции деления , потому что для любых трех целых чисел x, y и z во многих случаях (x ÷ y) ÷ z ≠ x ÷ (y ÷ г)! Например:
(10 ÷ 5) ÷ 2 = 2 ÷ 2 = 1
10 ÷ (5 ÷ 2) = 10 ÷ 2,5 = 2
1 ≠ 2!
Так (10 ÷ 5) ÷ 2 ≠ 10 ÷ (5 ÷ 2)
Итак, (x ÷ y) ÷ z = x ÷ (y ÷ z) равно , а не верно для всех целых чисел x, y и z!
, чтобы увидеть еще несколько примеров!
c) Множество рациональных чисел ассоциативно относительно операции умножения , потому что верно, что для любых трех рациональных чисел x, y и z, (xy)z=x(yz).(Опять же обратите внимание, что мы не всегда записываем символ операции для умножения.
Традиционно, когда мы пишем умножение, оставляем символ умножения, так что x×y просто записывается как xy.)
d) Набор из действительных чисел является , а не ассоциативным при операции вычитания , потому что для любых трех действительных чисел x, y и z существует много случаев, когда (x – y) – z ≠ x – (у – з)! Например:
(2 – 5) – 12 = (–3) – 12 = –15
2 – (5 – 12) = 2 – (–7) = 2 + 7 = 9
–15 ≠ 9!
Так (2 – 5) – 12 ≠ 2 – (5 – 12)
Итак, (x – y) – z = x – (y – z) равно , а не верно для всех действительных чисел x, y и z!
Если все, что у нас есть, это таблица операций, может быть немного сложнее определить, обладает ли набор свойством ассоциативности при конкретной операции.Чтобы понять, как это сделать,
Давайте рассмотрим несколько простых наборов с операционными таблицами и проверим, обладают ли они свойством ассоциативности.

e) Вот таблица операций для множества {a,b,c} и операции *:
* | и | б | с |
и | и | б | с |
б | б | и | с |
с | с | с | и |
Чтобы проверить ассоциативность, мы должны проверить все возможные экземпляры уравнения (x*y)*z = x*(y*z).Это означает, что мы должны думать о каждой возможной комбинации того, чем могут быть x, y и z.
Использование приведенной выше таблицы для записи всех возможных комбинаций элементов, которые могут использоваться для x, y и z, а затем вычисление (x*y)*z и сравнение с x*(y*z) дает нам следующую таблицу.
:
Значения x, y, z
(х*у)*г
х*(у*г)
Имеет ли (x*y)*z = x*(y*z)?
х=а, у=а, г=а
(а*а)*а = а*а = а
а*(а*а) = а*а = а
а = а, Итак, (а*а)*а = а*(а*а).
х=а, у=а, г=б
(а*а)*б = а*б = б
а*(а*б) = а*б = б
b = b, поэтому (a*a)*b = a*(a*b).
х=а, у=а, г=с
(а*а)*с = а*с = с
а*(а*с) = а*а = с
с = с, Итак, (а*а)*с = а*(а*с).
х=а, у=б, г=а
(а*б)*а = б*а = б
а*(б*а) = а*б = б
b = b, поэтому (a*b)*a = a*(b*a).
х=а, у=б, г=б
(а*б)*б = б*б = а
а*(б*б) = а*а = а
а = а, Итак, (а*b)*b = а*(b*b).
х=а, у=б, г=с
(а*б)*с = б*с = с
а*(б*с) = а*с = с
c = c, Итак, (a*b)*c = a*(b*c).
х=а, у=с, г=а
(а*с)*а = с*а = с
а*(с*а) = а*с = с
с = с, Итак, (а*с)*а = а*(с*а).
х=а, у=с, г=б
(а*с)*b = с*b = с
а*(с*б) = а*с = с
c = c, Итак, (a*c)*b = a*(c*b).
х=а, у=с, г=с
(а*с)*с = с*с = а
а*(с*с) = а*а=
а = а, Итак, (а*с)*с = а*(с*с).
х=б, у=а, г=а
(б*а)*а = б*а = б
б*(а*а) = б*а = б
b = b, поэтому (b*a)*a = b*(a*a).
х=б, у=а, г=б
(б*а)*б = б*б = а
б*(а*б) = б*б = а
а = а, Итак, (b*a)*b = b*(a*b).
х=б, у=а, г=с
(б*а)*с = б*с = с
б*(а*с) = б*с = с
с = с, поэтому (b*a)*c = b*(a*c).
х=б, у=б, г=а
(б*б)*а = а*а = а
б*(б*а) = б*б = а
а = а, Итак, (b*b)*a = b*(b*a).
х=б, у=б, г=б
(б*б)*б = а*б = б
б*(б*б) = б*а = б
b = b, поэтому (b*b)*b = b*(b*b).
х=б, у=б, г=с
(б*б)*с = а*с = с
б*(б*с) = б*с = с
c = c, Итак, (b*b)*c = b*(b*c).
х=б, у=с, г=а
(b*c)*a = c*a = c
б*(с*а) = б*с = с
с = с, поэтому (b*c)*a = b*(c*a).
х=б, у=с, г=б
(b*c)*b = c*b = c
б*(с*б) = б*с = с
с = с, поэтому (b*c)*b = b*(c*b).
х=б, у=с, г=с
(б*с)*с = с*с = а
б*(с*с) = б*а = б
а ≠ б, Итак, (b*c)*c ≠ b*(c*c)!
х=с, у=а, г=а
(с*а)*а = с*а = с
с*(а*а) = с*а = с
с = с, Итак, (с*а)*а = с*(а*а).
х=с, у=а, г=б
(с*а)*b = с*b = с
с*(а*б) = с*б = с
c = c, Итак, (c*a)*b = c*(a*b).
х=с, у=а, г=с
(с*а)*с = с*с = а
с*(а*с) = с*с = а
а = а, Итак, (с*а)*с = с*(а*с).
х=с, у=б, г=а
(с*б)*а = с*а = с
с*(б*а) = с*б = с
c = c, Итак, (c*b)*a = c*(b*a).
х=с, у=б, г=б
(с*б)*б = с*б = с
с*(б*б) = с*а = с
c = c, Итак, (c*b)*b = c*(b*b).
х=с, у=б, г=с
(с*б)*с = с*с = а
с*(б*с) = с*с = а
а = а, Итак, (с*b)*с = с*(b*с).
х=с, у=с, z=а
(с*с)*а = а*а = а
с*(с*а) = с*с = а
а = а, Итак, (с*с)*а = с*(с*а).
х=с, у=с, z=b
(с*с)*b = а*b = b
с*(с*б) = с*с = а
b ≠ a, Итак, (c*c)*b ≠ c*(c*b)!
х=с, у=с, z=с
(с*с)*с = а*с = с
с*(с*с) = с*а = с
с = с, Итак, (с*с)*с = с*(с*с).
Таким образом, множество {a,b,c} при операции * является ассоциативным , а не , потому что у нас есть по крайней мере один пример , где (x*y)*z ≠ x*(y*z)! На самом деле у нас есть два примера, когда это не удается: (b*c)*c ≠ b*(c*c) и (c*c)*b ≠ c*(c*b)! Когда x равно b, y равно c и z равно c, (x*y)*z ≠ x*(y*z)! И когда x равно c, y равно c и z равно b (x*y)*z ≠ x*(y*z)!
Хотя на самом деле нет хорошего ярлыка, который можно использовать, чтобы попытаться увидеть, является ли множество под операцией, заданной таблицей операций, ассоциативным, есть несколько вещей, которые вы можете найти, которые могут сократить количество экземпляров, которые вам нужно чек:
Если набор имеет идентификатор , то нам не нужно проверять какие-либо экземпляры, включающие этот идентификатор.
Почему? Давайте посмотрим, что произойдет, если мы вычислим экземпляр, содержащий идентификатор. Для этой цели мы позволим e представлять единичный элемент нашего множества, а x и y будем представлять любые два элемента нашего множества.
Давайте посмотрим, верно ли (e* x )* y = e*( x * y ).
Сначала мы вычислим (e* x )* y . Поскольку тождество по определению не изменяет элементы, когда действует на них операцией, мы должны иметь e* x= x .Итак, (e* x )* y= x * y .
Теперь мы вычислим e*( x * y ). Опять же, поскольку тождество по определению не изменяет элементы, когда действует на них с помощью операции, мы должны иметь e*( x * y ) = x * y . Итак, (e* x )* y = e*( x * y ) верно.
Мы можем использовать аналогичные рассуждения, чтобы увидеть, что ( x *e)* y = x *(e* y ) верно и что ( x * y )*e= x *( y *e) верно.
Таким образом, выражения, содержащие тождество, всегда будут ассоциативными. Это означает, что для того, чтобы проверить, обладает ли набор ассоциативным свойством, нам нужны только выражения проверки, которые содержат только элементы, которые НЕ являются тождественными.
Это может значительно сократить количество проверяемых элементов. Чтобы убедиться в этом, давайте снова посмотрим на наш пример:
.Пример:
Вот таблица операций для набора {a,b,c} и операции *:
*
и
б
с
и
и
б
с
б
б
и
с
с
с
с
и
Обратите внимание, что этот набор имеет тождество: a, потому что всякий раз, когда a умножается на любой элемент в наборе справа или слева, он оставляет этот элемент неизменным.
Итак, чтобы проверить ассоциативность, мы должны проверить все возможные экземпляры уравнения (x*y)*z = x*(y*z), которое не включает a (поскольку a является тождеством, а мы не необходимо проверять комбинации, включающие тождество).
Значения x, y, z
(х*у)*г
х*(у*г)
Имеет ли (x*y)*z = x*(y*z)?
х=б, у=б, г=б
(б*б)*б = а*б = б
б*(б*б) = б*а = б
b = b, поэтому (b*b)*b = b*(b*b).
х=б, у=б, г=с
(б*б)*с = а*с = с
б*(б*с) = б*с = с
c = c, Итак, (b*b)*c = b*(b*c).
х=б, у=с, г=б
(b*c)*b = c*b = c
б*(с*б) = б*с = с
с = с, поэтому (b*c)*b = b*(c*b).
х=б, у=с, г=с
(б*с)*с = с*с = а
б*(с*с) = б*а = б
а ≠ б, Итак, (b*c)*c ≠ b*(c*c)!
х=с, у=б, г=б
(с*б)*б = с*б = с
с*(б*б) = с*а = с
c = c, Итак, (c*b)*b = c*(b*b).
х=с, у=б, г=с
(с*б)*с = с*с = а
с*(б*с) = с*с = а
а = а, Итак, (с*b)*с = с*(b*с).
х=с, у=с, z=b
(с*с)*b = а*b = b
с*(с*б) = с*с = а
b ≠ a, Итак, (c*c)*b ≠ c*(c*b)!
х=с, у=с, z=с
(с*с)*с = а*с = с
с*(с*с) = с*а = с
с = с, Итак, (с*с)*с = с*(с*с).
Обратите внимание, что, проверяя только экземпляры, которые не содержат идентификатор a , мы сократили количество комбинаций, которые нам нужно проверить, с 27 до 8! Это большое улучшение!
Будьте осторожны! Многие студенты делают ошибку, заключая, что набор ассоциативен, проверив лишь несколько примеров.
Ты не сможешь это сделать! Чтобы определить, является ли набор ассоциативным, ВЫ ДОЛЖНЫ ПРОВЕРИТЬ КАЖДУЮ ОДИНОЧНУЮ КОМБИНАЦИЮ ИЗ 3 ЭЛЕМЕНТОВ, если у вас нет хорошего общего аргумента, почему все комбинации будут ассоциативными, или у вас есть веская причина (например, существование элемента идентичности) для ограничения количества случаев, которые вы должны проверить. (Обратите внимание, что даже если у вас есть элемент идентификации, вы все равно должны проверить ВСЕ случаи, которые не включают элемент идентификации.)
Теперь вернитесь к доске и ответьте на вопрос групповой лекции 6: Ассоциативность!
Ассоциативность — обзор | ScienceDirect Topics
ДОКАЗАТЕЛЬСТВО
Рефлексивность отношения ≤ очевидна. Для антисимметрии наблюдайте, что если x ∈ A, Y ∈ x ≤ × ≤ y или If x ∈ D, Y ∈ A , и x ≤ y , затем y ≰ x ; в других случаях это следует из антисимметрии ≤ A . Транзитивность троек x, y, z ∈ A или x, y, z ∈ D также очевидна. Осталось рассмотреть шесть случаев, один из которых мы возьмем в качестве примера. Предположим, x = d a ≤ y ∈ A , y ≤ z = d b 2 . Тогда a ≤ A y, y ≤ A cb ≤ A 3 b.По транзитивности ≤ A , a ≤ A b . По определению ≤, d a ≤ d b по необходимости. Верхний элемент 1 и нижний элемент 0 A остаются верхним и нижним P при заказе ≤.
Транзитивность троек x, y, z ∈ A или x, y, z ∈ D также очевидна. Осталось рассмотреть шесть случаев, один из которых мы возьмем в качестве примера. Предположим, x = d a ≤ y ∈ A , y ≤ z = d b 2 . Тогда a ≤ A y, y ≤ A cb ≤ A 3 b.По транзитивности ≤ A , a ≤ A b . По определению ≤, d a ≤ d b по необходимости. Верхний элемент 1 и нижний элемент 0 A остаются верхним и нижним P при заказе ≤.
Коммутативность умножения ясна из его определения. Его ассоциативность очевидна для троек x, y, z ∈ A . С учетом коммутативности количество оставшихся случаев сокращается до трех, из которых мы снова возьмем один в качестве примера. Пусть x = d a , y ∈ A, z = d b . У нас есть четыре случая:
Пусть x = d a , y ∈ A, z = d b . У нас есть четыре случая:
- (1)
cyb < yb, cay < ay . Тогда, D A A · ( y · d b b d a d a · d y b = Cayb . Начиная с другого конца, мы получаем ( d A · y ) · d b b = d ay · d b = Cayb , по мере необходимости .
- (2)
cyb < yb, cay = ay . Заметим, что последние силы cayb = ayb . Тогда, D A A · ( y · d b b d a d a · d y b = Cayb .
 С другой стороны, ( D A · · y ) · d b b = ay · d b = ayb = CAYB , по мере необходимости.
С другой стороны, ( D A · · y ) · d b b = ay · d b = ayb = CAYB , по мере необходимости.- (3)
cyb = yb, cay < ay . Прежние силы cayb = ayb . Тогда d a · ( y · d b ) = d a · yb = 3b a; А ( d A · y ) · d b b = d = d ay · d b = CAYB = AYB , а также.
- (4)
cyb = yb, cay = ау . Тогда cayb = ayb . Далее, d a · ( y · d b ) = d a · yb = a; также ( d a · y ) · d b = ay · d b = ay3b.

Поскольку легко видеть, что 1 · x = x для всех x ∈ P , единичный элемент моноида совпадает с вершиной частичного порядка, что является другим способом сказать, что рассматриваемый моноид является целым.Таким образом, мы показали первую часть леммы 10.11.
Для части «более того» мы снова возьмем только один из восьми возможных случаев. Предположим, что x, y ∈ A с x ≤ y и z = d a ∈ D . Тогда из еще одного четырех случаев, мы подбираем все возможное, а именно, когда x · D A = AX и Y · D A = D AY .Таким образом, мы должны иметь сах = ах и сау < ау . Поскольку x ≤ y , а умножение A сохраняет порядок, мы получаем ax = сах ≤ сай < ау .



 Мероприятия.
Мероприятия. vii,
vii, Числа не обязательно совпадают с числами в определениях. Инструкции см. в Викисловаре: Макет записи § Переводы.
Числа не обязательно совпадают с числами в определениях. Инструкции см. в Викисловаре: Макет записи § Переводы. 


 \)
\)
 2=а,\для всех а\in\mathbb{Z}.\)
2=а,\для всех а\in\mathbb{Z}.\)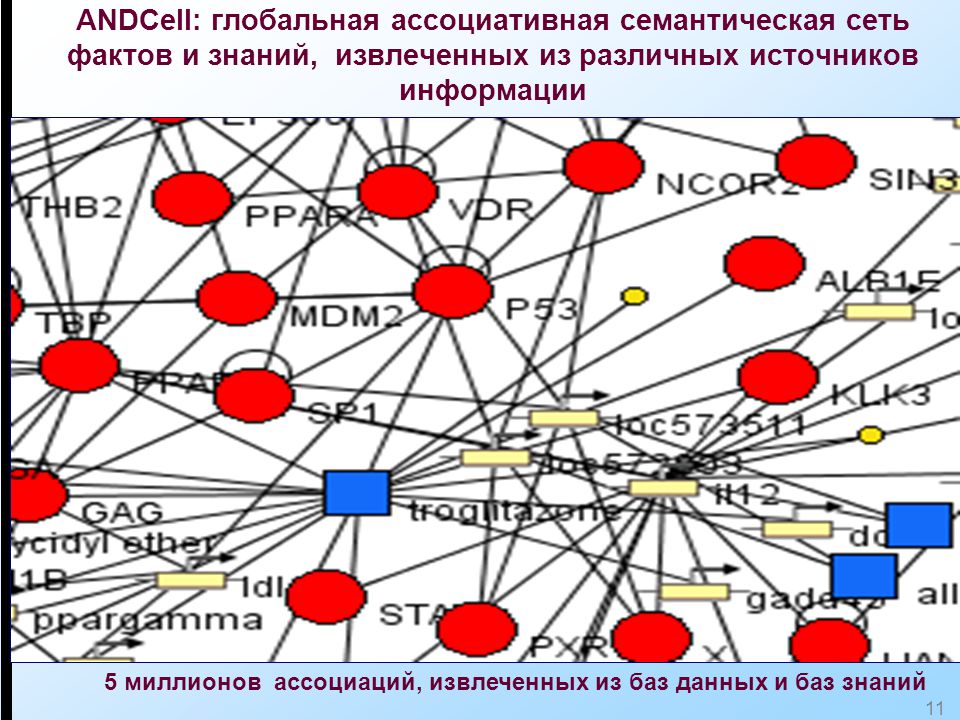

 Традиционно, когда мы пишем умножение, оставляем символ умножения, так что x×y просто записывается как xy.)
Традиционно, когда мы пишем умножение, оставляем символ умножения, так что x×y просто записывается как xy.) :
:


 Почему? Давайте посмотрим, что произойдет, если мы вычислим экземпляр, содержащий идентификатор. Для этой цели мы позволим e представлять единичный элемент нашего множества, а x и y будем представлять любые два элемента нашего множества.
Почему? Давайте посмотрим, что произойдет, если мы вычислим экземпляр, содержащий идентификатор. Для этой цели мы позволим e представлять единичный элемент нашего множества, а x и y будем представлять любые два элемента нашего множества.


 Ты не сможешь это сделать! Чтобы определить, является ли набор ассоциативным, ВЫ ДОЛЖНЫ ПРОВЕРИТЬ КАЖДУЮ ОДИНОЧНУЮ КОМБИНАЦИЮ ИЗ 3 ЭЛЕМЕНТОВ, если у вас нет хорошего общего аргумента, почему все комбинации будут ассоциативными, или у вас есть веская причина (например, существование элемента идентичности) для ограничения количества случаев, которые вы должны проверить. (Обратите внимание, что даже если у вас есть элемент идентификации, вы все равно должны проверить ВСЕ случаи, которые не включают элемент идентификации.)
Ты не сможешь это сделать! Чтобы определить, является ли набор ассоциативным, ВЫ ДОЛЖНЫ ПРОВЕРИТЬ КАЖДУЮ ОДИНОЧНУЮ КОМБИНАЦИЮ ИЗ 3 ЭЛЕМЕНТОВ, если у вас нет хорошего общего аргумента, почему все комбинации будут ассоциативными, или у вас есть веская причина (например, существование элемента идентичности) для ограничения количества случаев, которые вы должны проверить. (Обратите внимание, что даже если у вас есть элемент идентификации, вы все равно должны проверить ВСЕ случаи, которые не включают элемент идентификации.)  С другой стороны, ( D A · · y ) · d b b = ay · d b = ayb = CAYB , по мере необходимости.
С другой стороны, ( D A · · y ) · d b b = ay · d b = ayb = CAYB , по мере необходимости.