Эластичность функции – Эластичность функции
Свойства эластичности функции
Пусть функция имеет конечную или бесконечную производную на промежутке. Вспомним, что производная есть отношение дифференциалов и.
Эластичность – безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины у и х:
.
Доказательство очевидно: .
Эластичности взаимно обратных функций – взаимно обратные величины:
.
Действительно, .
Эластичность произведения двух функций и, зависящих от одного и того же аргументах, равна сумме эластичностей:
. .
Эластичность частного двух функций и, зависящих от одного и того же аргумента
.
Доказательство аналогично.
Эластичность суммы двух функций может быть найдена по формуле:
.
Доказательство. .
Эластичность элементарных функций
Вычислим эластичности некоторых элементарных функций.
1. Степенная функция . Ее эластичность
.
2. Показательная функция . Ее эластичность
.
3. Логарифмическая функция . Ее эластичность
.
4. Линейная функция . Ее эластичность
.
Функция в зависимости от величины своей эластичности может быть
совершенно эластичная ;
эластичная ;
неэластичная ;
совершенно неэластичная .
13.4 Применение эластичности в экономическом анализе Виды эластичностей в экономике
Эластичность спроса по цене , показывающая относительное изменение (выраженное в процентах) величины спроса (объема потребления) на какое-либо благо при изменении ценыр этого блага на 1%. Производная функции спроса отрицательна (функция убывает) и эластичность спроса имеет также отрицательный знак.
Различают три вида спроса в зависимости от величины :
Если , то спрос считаетсяэластичным. В этом случае повышению цены на 1% соответствует понижение спроса более чем на один процент, и наоборот, понижение цены на один процент приводит к росту покупок более чем на 1%.
Если , то спроснеэластичный. В этом случае повышение цены на 1% влечет за собой понижение спроса менее чем на 1%, и наоборот, уменьшение цены на 1% приводит к росту покупок более чем на 1%.
Если , то спроснейтрален.
Пример 13.1
.
Важно отметить, что при всех значениях р , т.е. кривая спроса , имеет постоянную эластичность, равнуюb.
Пример 13.2. В экономике цена обычно откладывается по вертикальной оси, а величина спроса по горизонтальной оси, уравнение спроса обычно записывается так, что цена р является функцией спроса , а не– функциейр. Рассмотрим уравнение спроса: . Какова эластичность спроса по цене при продаже 10 единиц продукции?
При q = 10, р = 940 – 480 +100= $560. Найдем . Приполучим. Поэтому. Таким образом, изменение цены на 1% от текущей цены $560 изменит величину спроса в обратном направлении на 2%. Мы приходим к выводу, что при цене $560 спрос эластичен.
Эластичность спроса по доходу характеризующая относительное изменение (в процентах) величины спросаq на какое-либо благо при изменении дохода потребителей этого блага на 1% .
Положительная эластичность спроса по доходу характеризует качественные товары, а отрицательная величина – некачественные товары.
Так, высокий положительный коэффициент спроса по доходу в отрасли указывает, что ее вклад в экономический рост больше, чем доля в структуре экономики, и она имеет шансы на расширение. Наоборот, если коэффициент эластичности спроса на продукцию отрасли по доходу имеет небольшое положительное или отрицательное значение, то ее может ожидать застой и перспектива сокращения производства.
Эластичность предложения по цене , показывающая относительное изменение (выраженное в процентах) величины предложениякакого-либо товара при изменении цены этого товара на 1%. Производная функции предложения положительна и эластичность предложения также положительна; приимеем неэластичное предложение, при– эластичное.
studfiles.net
Эластичность функции
где  и
и  относительные приращения функции и
аргументов соответственно. Эластичность
функции показывает приближенно, на
сколько процентов изменится функция y = f(x) при изменении аргумента x
на 1%.
относительные приращения функции и
аргументов соответственно. Эластичность
функции показывает приближенно, на
сколько процентов изменится функция y = f(x) при изменении аргумента x
на 1%.
3.15. Пусть зависимость издержек производства С от объема выпускаемой продукции Q выражается формулой Определить средние и предельные издержки при объеме продукции Q=15.
3.17. Функции спроса q и предложения s от цены p выражаются соответственно уравнениями q = 7 – p и s = p + 1.
Найти: а) равновесную цену; б) эластичность спроса и предложения для этой цены; в) изменение дохода (в процентах) при увеличении цены на 5% от равновесной.
3.18. Функции спроса q и предложения s от цены p выражаются соответственно уравнениями q = 9 – p и s = p + 1.
Найти: а) равновесную цену; б) эластичность спроса и предложения для этой цены; в) изменение дохода (в процентах) при увеличении цены на 10% от равновесной.
3.19. Функции долговременого спроса q и предложения s от цены p на мировом рынке нефти имеют соответственно вид: q = 30 – 0,9p, s = 16 + 1,2p.
1)Найти эластичность спроса в точке равновесной цены.
2)Как изменятся равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25%?
3.20.
Функция спроса q
от цены p
описывается формулой q(p)=q
где 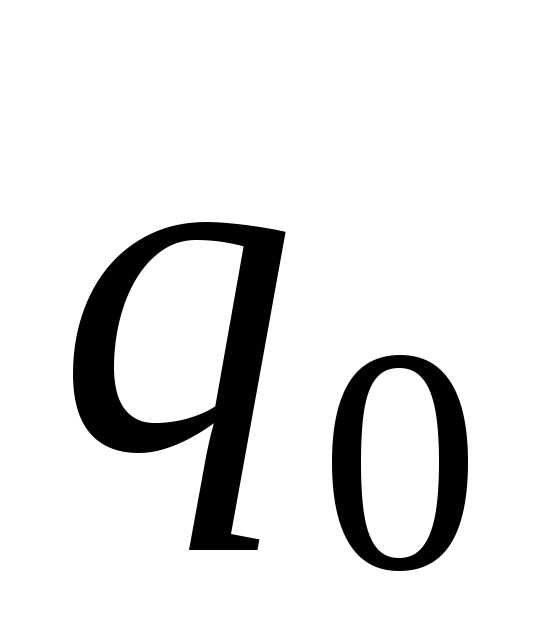 и k
– известные величины. Найти, при каких
значениях цены p
спрос будет эластичным.
и k
– известные величины. Найти, при каких
значениях цены p
спрос будет эластичным.
3.21.
Найти изменение выручки с увеличением
цены на товар при разных вариантах
эластичности спроса, если выручка V
равна произведению цены P
на величину спроса  V(P)=q(P)P.
V(P)=q(P)P.
3.22. Зависимость между себестоимостью продукции С и объемом Q ее производства выражается формулой С=50-0,4Q. Определить эластичность себестоимости при выпуске продукции, равном 30.
3.23. Найти производную n-го порядка функций :
1) ;
2)  ;
;
3) ;
4)
.

3.24. Найти пределы по правилу Лопиталя:
1)  ;
2)
;
2) ;
;
3)  ;
4)
;
4) 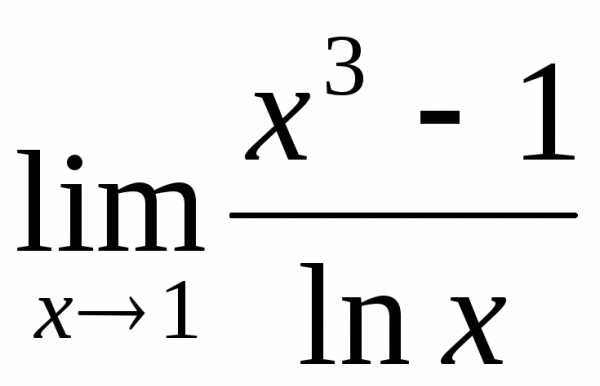 ;
;
5)  ;
6)
;
6)  ;
;
7) 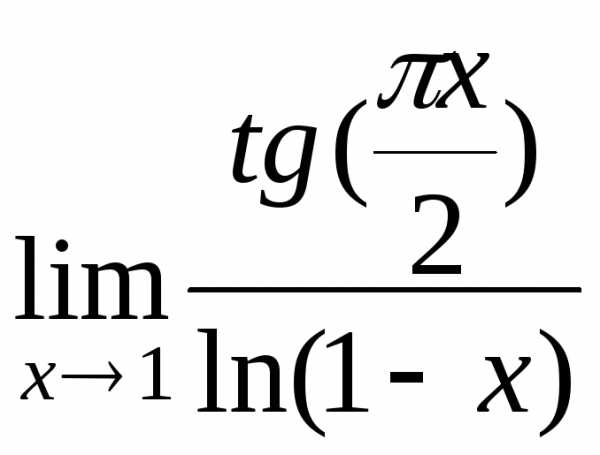
 ;
;9) 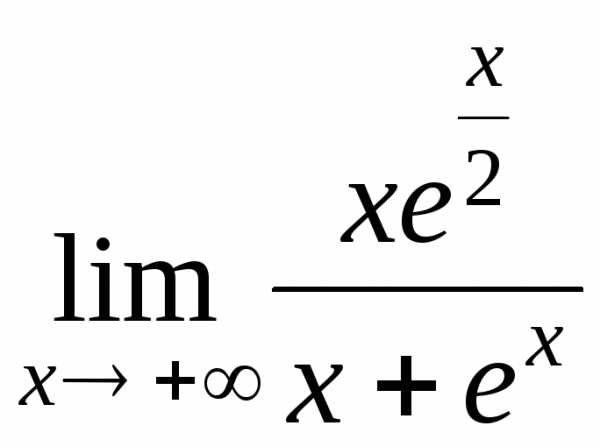 ;
10)
;
10)  .
.
3.25. Найти экстремумы функций :
1)  ;
2)
;
2) 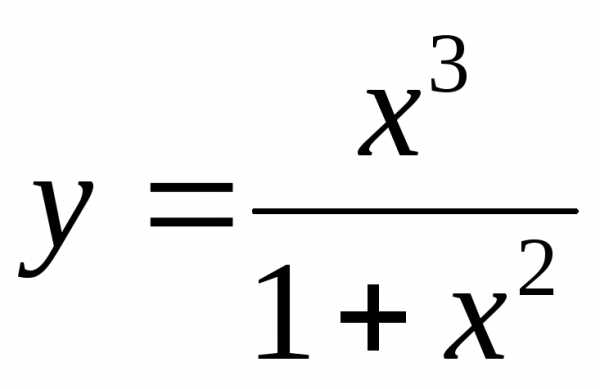 ;
3)
;
4)
;
3)
;
4)  .
.
3.26. Найти наименьшее и наибольшее значения функций:
на промежутке [-4,4];
2) 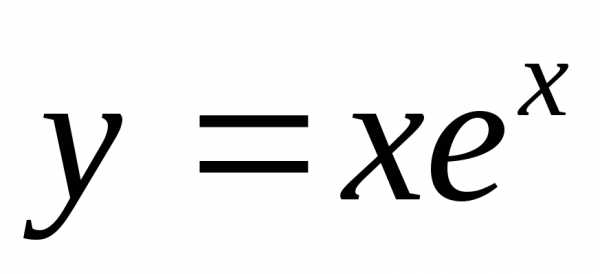 на промежутке
[-2,1];
на промежутке
[-2,1];
3) при 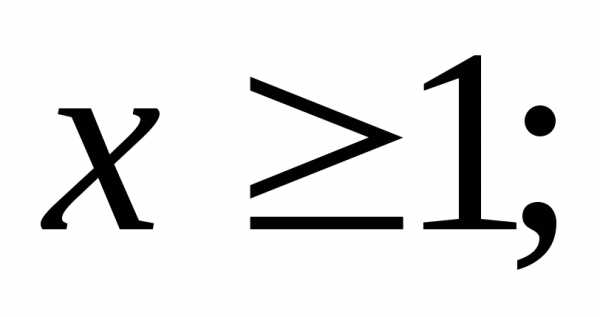
4) 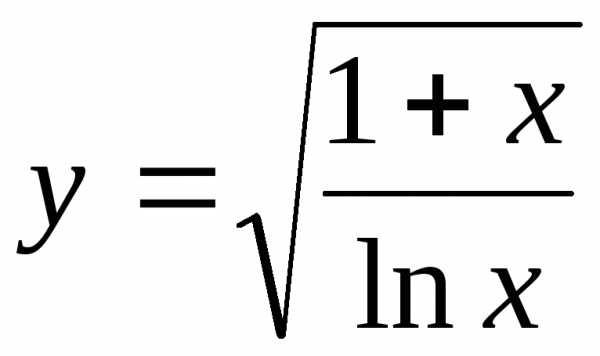 на промежутке (1, е ].
на промежутке (1, е ].
3.27. Требуется выделить прямоугольную площадку земли в 512 кв.м, огородить ее и разделить забором на три равные части параллельно одной из сторон площадки. Каковы должны быть размеры площадки, чтобы на ограждение пошло наименьшее количество материала.
3.28. При заданном периметре прямоугольного окна найдите такие его размеры, чтобы оно пропускало наибольшее количество света.
3.29. Найти максимум прибыли, если доход R и издержки C определяются формулами:
где Q- количество реализованного товара.
3.30. Зависимость объма выпуска продукции W от капитальных затрат К определяется функцией Найти интервал изменения К, на котором увеличение капитальных затрат неэффективно.
3.31. Найти точки перегиба и интервалы выпуклости графика функции:
1) ; 2) ;
3) 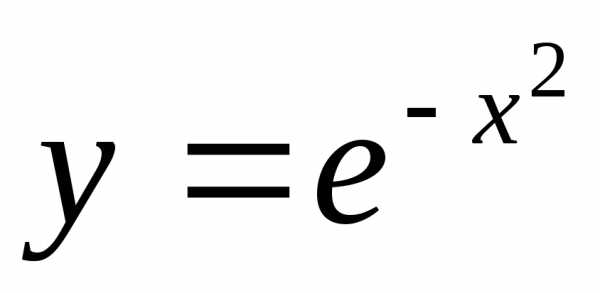 ;
4)
;
4)  ;
;
5) 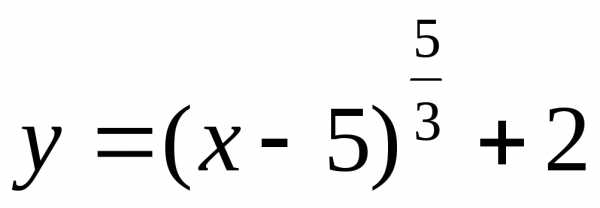 ;
6)
.
;
6)
.
3.32. Найти асимптоты графика функции:
1) 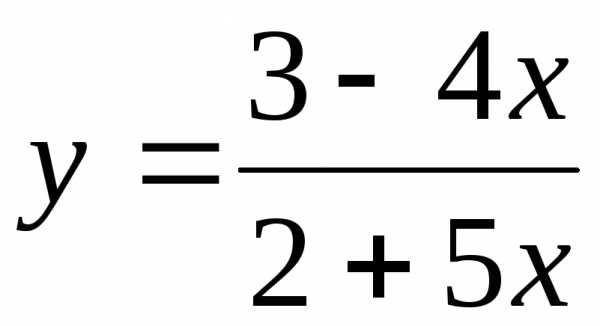 ;
2)
;
2)  ;
;
3) 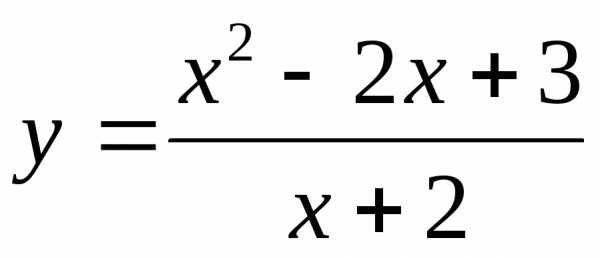 ;
4)
;
4) 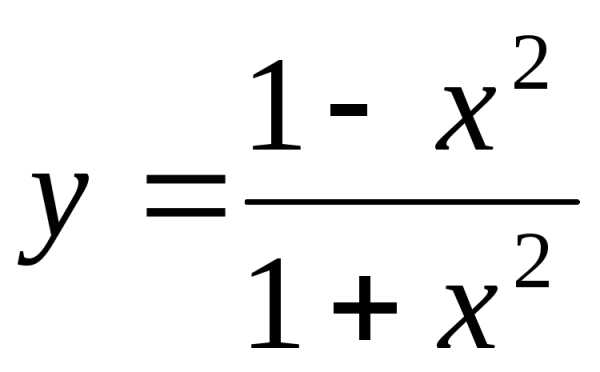 ;
;
5)  ;
6)
;
6) 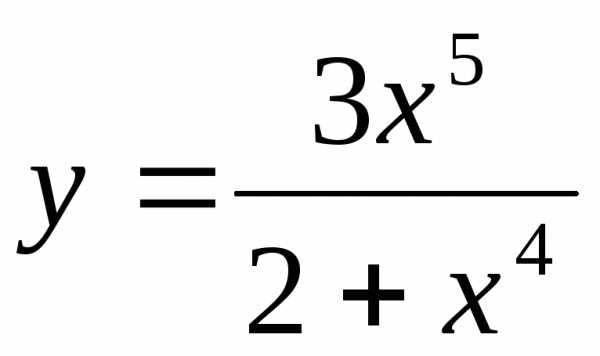 ;
;
7)  ;
8)
;
8)  .
.
studfiles.net
Эластичность функции
При описании динамики экономических явлений мы сравнивали изменения результата у(х) с величиной приложенных усилий х, ᴛ.ᴇ. изучали отношение — среднюю эффективность усилий; и переходя к пределу при х0 этого отношения, получали предельную эффективность на уровне усилий х.
В некоторых экономических задачах крайне важно проводить аналогичные сравнения не для абсолютных приращений х и у, а для относительных приращений и (безразмерных величин).
Эластичностью Ex(y) функции у принято называть предел отношения относительного приращения функции у к относительному приращению переменной х при х0, , .
Эластичность функции показывает, на сколько процентов изменится функция у = f(х) при изменении независимой переменной х на 1%.
Геометрический смысл эластичности функции По определению эластичности имеем , где — тангенс угла наклона касательной, проведенной к графику функции у=f(х) в точке М(х;у).
| В случае если f(x) – возрастает на промежутке Х, то из АВМ имеем: у = АВ, тогда , Т.о., эластичность функции f(х) в точке М равна отношению ОА к | у=f(х) у М(х;у) у В a А 0 х | В случае если f(x) убывает на промежутке Х, то из АВМ имеем АМ=у=АВ=-, | у=f(х) С у М(х;у) у А b a 0 х В |
| ВА — проекции касательной в точке М на ось ОХ. В случае если абсцисса точки B>0, то АВ<АО и >1, в случае если абсцисса точки B<0, то АВ>АО и <1. | Eсли СМ>МВ, то>1; если СМ<МВ, то <1. Замечание для убывающей функции )<0. |
В случае если >1, то тенденцию, описывающую функцией у читают эластичной, <1 – неэластичной.
Свойства эластичности функции (ЭФ)
10. ЭФ – безразмерная величина, не зависящая от единиц измерения х и у.
20. ЭФ – зависит от величины аргумента х, ᴛ.ᴇ. является функцией переменной х.
30. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций ,
40. Эластичности взаимно-обратных функций взаимно-обратны
50. ЭФ равна произведению независимой переменной х на темп роста функции , ᴛ.ᴇ. .
Читайте также
Производные высших порядков Поскольку производная функции сама является функцией, она тоже может иметь производную. Понятие производной, которое было рассмотрено выше, относится к производной первого порядка. Производной n-го порядка называется производная от… [читать подробнее].
§ 1 Экономический смысл производной Математический аппарат дифференциального исчисления широко используется в курсе современного экономического анализа. Всякая экономическая деятельность осуществляется для достижения некоторого результата у и требует приложения… [читать подробнее].
ОпределениеЭластичностью функции по переменной называется величина , показывающая, на сколько процентов примерно изменяется значение функции при увеличении аргумента на 1%. Пример 1.На сколько процентов изменится значение функции при увеличении аргумента на 1 %,… [читать подробнее].
Обозначим — эластичность функции спроса D по переменной (цене) P. Тогда: Вполне очевидно, что такая функция показывает, как изменится количество, если цена изменится на 1 единицу. Так как при возрастании цены спрос падает, эластичность функции D по Р будет функцией… [читать подробнее].
Понятие эластичности впервые было введено Аланом Маршаллом, в связи с анализом функции D. Маршалл ставил следующую задачу, как изменится спрашиваемое количество D, если соответствующая цена P на некоторые блага изменится на 1 ед. Рассмотрим представленную проблему… [читать подробнее].
referatwork.ru
Эластичность функции — это… Что такое Эластичность функции?
- Эластичность функции
Эластичность функции [function elasticity] — (иногда ее называют относительной производной) — предел соотношения между относительным приращением функции y:
(зависимой переменной) и относительным приращением независимой переменной x:
когда Δ → 0, обозначается символом Ex(y) и выражается слeдующей формулой:
Э.ф. является, таким образом, мерой реагирования одной переменной величины на изменения другой и из практических соображений ее в ряде экономико-математических моделей относят к проценту прироста независимой переменной. В этом случае эластичность y относительно x есть приближенный процентный прирост функции (повышение или понижение), соответствующий приращению независимой переменной на 1%. Различают дуговую эластичность, т. е. среднюю на каком-то отрезке кривой, и точечную эластичность (значение производной в заданной точке). Показатели эластичности применяются в аппарате производственных функций, при анализе спроса и потребления и др. См. Перекрестный коэффициент эластичности, Товары неэластичного спроса, Товары эластичного спроса, Эластичность предложения, Эластичность замещения ресурсов, Эластичность спроса от доходов, Эластичность спроса от цен.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
- Эластичность спроса от цен (по цене)
- Эластичность
Смотреть что такое «Эластичность функции» в других словарях:
эластичность функции — (иногда ее называют относительной производной) предел соотношения между относительным приращением функции y: (зависимой переменной) и относительным приращением независимой переменной x: когда ? ? 0, обозначается символом Ex(y) и выражается… … Справочник технического переводчика
Эластичность спроса от цен (по цене) — [price elasticity of demand] коэффициент, показывающий относительное изменение объема потребления (спроса) при изменении цены данного товара или цен других, связанных с ним товаров (в общем случае спрос на отдельный товар при прочих равных… … Экономико-математический словарь
эластичность спроса от цен (по цене) — Коэффициент, показывающий относительное изменение объема потребления (спроса) при изменении цены данного товара или цен других, связанных с ним товаров (в общем случае спрос на отдельный товар при прочих равных условиях зависит от уровня цен всех … Справочник технического переводчика
эластичность — [ГОСТ 28451 90] эластичность Наблюдаемая зависимость изменения одного показателя в связи с изменением другого показателя. Уровень такой зависимости характеризуется обычно коэффициентом эластичности, которой показывает размер изменения одного… … Справочник технического переводчика
Эластичность спроса от доходов (по доходу) — [income elasticity of demand] коэффициент, показывающий относительное изменение потребления (спроса) при изменении дохода (остальные факторы, от которых зависит спрос, принимаются неизменными). Исчисляется по формуле (см. Эластичность функции):… … Экономико-математический словарь
Эластичность — [elasticity] наблюдаемая зависимость изменения одного показателя в связи с изменением другого показателя. Уровень такой зависимости характеризуется обычно коэффициентом эластичности, которой показывает размер изменения одного (зависимого)… … Экономико-математический словарь
эластичность спроса от доходов (по доходу) — Коэффициент, показывающий относительное изменение потребления (спроса) при изменении дохода (остальные факторы, от которых зависит спрос, принимаются неизменными). Исчисляется по формуле (см. Эластичность функции): где E коэффициент эластичности… … Справочник технического переводчика
ЭЛАСТИЧНОСТЬ СПРОСА И ПРЕДЛОЖЕНИЯ — (англ. elasticity of supply and demand) – экономический показатель, характеризующий реакцию, соответственно, спроса и предложения на изменения цен, доходов и некоторых других факторов. Эластичность (англ. elasticity) означает меру реагирования… … Финансово-кредитный энциклопедический словарь
эластичность предложения и спроса — Эластичность мера реагирования одной переменной величины (спроса, предложения) на изменение другой (цены,…): исчисляемое в процентах изменение функции, соответствующее изменению переменной на 1 %. Спрос на товары зависит от его цены, дохода… … Справочник технического переводчика
Эластичность потребления и спроса — термин, которым в экономической литературе принято обозначать способность спроса или потребления изменяться в определённых границах под влиянием ряда экономических факторов. К. Маркс, отмечая, что на стороне спроса имеется определённая… … Большая советская энциклопедия
economic_mathematics.academic.ru
Эластичность | Экономика для школьников
Эта страница — подборка. Общая информация о подборках: http://iloveeconomics.ru/blogs/id3/1081.Общая идея всех эластичностей:
$\text{эластичность функции}\approx\frac{\text{процентное изменение функции}}{\text{процентное изменение аргумента}}$
Точечная эластичность дифференцируемой функции
Пусть f — некоторая дифференцируемая1 функция одной переменной, определённая на множестве неотрицательных чисел и принимающая неотрицательные значения.
Рассмотрим некоторую точку $x>0$, такую что $f(x)>0$.
Точечная эластичность функции f в точке x обозначается $Ef(x)$ и по определению равна следующей величине: $f'(x)\frac{x}{f(x)} $
Ту же самую величину можно записать по-другому: $$Ef(x)=\mathop{\lim }\limits_{\Delta x\to 0} \frac{\frac{\Delta f}{f(x)} }{\frac{\Delta x}{x} },$$
где $\Delta f=f(x+\Delta x)-f(x)$
(Константы x и f(x) выносятся за знак предела, и таким образом из второй формулы получаем первую).
Если в данной точке x такой предел существует, значит, при небольших $\Delta x$ мы можем записать: $Ef(x)\approx \frac{\Delta f/f}{\Delta x/x} $. То есть эластичность функции в некоторой точке x приближённо показывает отношение процентного изменения функции к процентному изменению аргумента при небольших значениях $\Delta x$ (подробнее о процентных изменениях можно почитать в главе 3 «Про размерности и проценты».
Упражнения:
Другие виды эластичности
Рассматривается функция Q(P).
Точечная эластичность функции нескольких переменных
Если функция f зависит от нескольких переменных, то нужно указывать, по какой переменной мы считаем эластичность. Например, если функция спроса на некоторый товар зависит от цены этого товара и от дохода покупателя, т.е. $Q_{d} =f(P,I)$, то мы можем посчитать две эластичности: эластичность спроса по цене и эластичность спроса по доходу. Отличие только в том, что в определении используется частная производная (что это такое — см. ниже):
Эластичность спроса по цене:$E_{P} f(P,I)=f_{P}^{‘} (P,I)\frac{P}{f(P,I)} $, где $f_{P}^{‘} (P,I)$ — (частная) производная функции f по цене.
Эластичность спроса по доходу:$E_{I} f(P,I)=f_{I}^{‘} (P,I)\frac{I}{f(P,I)} $, где $f_{I}^{‘} (P,I)$ — (частная) производная функции f по доходу.
Что такое частная производная
Пусть задана функция $f$ нескольких переменных (обозначим их число буквой n). Набор из n чисел $x_{1} ,x_{2} ,…,x_{n} $ определяет значение функции: $f(x_{1} ,x_{2} ,…,x_{n} )$. Если позволить меняться только одной переменной (например, первой), а все остальные переменные зафиксировать на некотором уровне (например, $x_{2} =8,x_{3} =0.5,…$), то фактически получится функция одной переменной. Производная этой получившейся функции — это и есть то, что называется частной производной функции $f$ по данной переменной (в нашем примере — по первой переменной). Интерпретация: если нарисовать график функции f в зависимости от этой переменной (при фиксированных значениях остальных переменных), то угловой коэффициент касательной к этому графику в некоторой точке $x_{1} $ равен частной производной функции f «в точке» $x_{1} ,x_{2} ,…,x_{n} $. Естественно, если мы поменяем значения какой-либо из фиксированных переменных (например, вместо $x_{2} =8$ поставим $x_{2} =8.5$), то весь этот график может изменить свою форму, в частности, может поменяться наклон в тех или иных точках $x_{1} $. Таким образом, частная производная функции f по первой переменной зависит не только от значения первой переменной, но и от значений остальных переменных. Это отражается и в обозначении: например, если спрос задаётся формулой $Q_{d} =f(P,I)$, то частная производная функции спроса по доходу обозначается $f_{I}^{‘} (P,I)$.
1 Дифференцируемая — значит, имеет производную или, что то же самое, имеет касательную к своему графику. Подробнее: глава 2 «Функции».
iloveeconomics.ru
Эластичность функции — Энциклопедия по экономике
Рис. 2.10 а. Эластичность функции спроса равна бесконечности спроса [c.41]В общем случае, предельной (точечной) эластичностью функции [c.98]
Эластичность функции (1) к часовому темпу равна единице, т.е. [c.21]
При исследовании чувствительности находящихся в функциональных зависимостях сопоставляемых величин используют эластичности функций. [c.87]
Эластичность функции у =f(x) показывает относительное изменение значения функции у в расчете на единицу относительного изменения аргумента х. Если эластичность переменной у по переменной х обозначить ех(у), то, используя определение эластичности, получаем [c.87]
Если f(x) считать общей (совокупной) величиной (как, например, общая или совокупная выручка), то М (f) = Ду/Дх — соответствующая ей предельная величина (например, предельная выручка, или дополнительная выручка Ду от дополнительной единицы Дх), a A (f) — средняя величина (средняя выручка, или выручка в среднем на единицу х, равная у/х, в нашем примере это — цена). Итак, эластичность функции равна отношению предельной и средней величин. [c.87]
Если же мы обратимся к графику спроса, то наша задача установления жесткости или эластичности функции спроса в данной точке будет несколько сложнее. Прежде всего надо отметить, что при поверхностном взгляде эластичность спроса часто ошибочно отождествляют с наклоном кривой спроса, что и приводит [c.97]
При изучении спроса часто используется понятие эластичности функции. Дело в том, что натуральные показатели, связанные с функцией спроса, в практическом использовании имеют два существенных недостатка, а именно они измеряются в разных единицах, их значения изменяются вместе с [c.207]
Стремящиеся к прибыли монополисты используют то же логическое обоснование, что и стремящиеся к прибыли фирмы в конкурентной отрасли. Фирма будет наращивать производство продукции до такого объема, при котором предельный доход равен предельным издержкам. При этом монополист будет устанавливать не наивысшую цену, которую он может получить, а ту, при которой он может получить большую совокупную прибыль при условии принципа сопоставления предельного дохода с предельными издержками. Таким образом, в условиях чистой монополии проблема ценообразования связана с выявлением степени эластичности функции спроса, определением средних издержек и установлением на этой основе цен, обеспечивающих фирме так называемую справедливую прибыль. [c.380]
Обозначения см. в ст. «Производственная функция», «Эластичность функции». [c.159]
См. также Эластичность функции. [c.393]
Во многих экономико-математических моделях эластичность функций относят к проценту прироста независимой переменной. Таким образом, коэффициент эластичности спроса [c.555]
Определение. Эластичностью функции у — /(ж) называется следующий предел [c.189]
Использование этой формулы позволяет вычислять эластичность функции быстрее, чем это делается по формуле (10.2). Так, найде-ная в примере 3 эластичность Ех (у] для функции у = 10 — х может быть вычислена с помощью формулы (10.3) в одну строчку [c.191]
Напомним, геометрический смысл производной f (x) — это тангенс угла наклона касательной к графику функции у = f(x] в точке С(хС УС], ус = f(x . Геометрический смысл эластичности функции f(x) в точке хс связан с разбиением данной касательной на отрезки точками А, В и С, где А(ха, 0) — точка пересечения касательной с осью Ох, -6(0, г/ ) — точка пересечения касательной с осью Оу (рис. 10.1). [c.194]
Как можно оценить эластичность функции у = f(x) по ее графику Рассмотрим вначале возрастающую функцию (эластичность при этом положительна). Выберем на графике точку М и проведем через эту точку касательную обозначим А и В — точки пересечения касательной с осями абсцисс и ординат, а С и D — проекции точки М на координатные оси. Допустим, что касательная пересекает ось ординат в отрицательной области, как это показано на рис. 2, а. [c.566]
Под частной эластичностью функции по одному из аргументов xk понимается эластичность переменной у, рассматриваемой в зависимости только от xk, при постоянных значениях остальных аргументов. Она связана с частной производной по этому аргументу соотношением [c.568]
Сумма частных эластичностей некоторой функции по всем ее аргументам получила название полной эластичности функции. Вводя обозначение [c.606]
Другое определение связано с функцией затрат длительного периода. Если средние затраты LA с ростом объема выпуска убывают, то говорят о возрастающей отдаче от масштаба, а если возрастают — об убывающей. (Поскольку в дальнейшем речь будет идти только о затратах длительного периода, букву L в обозначении затратных функций мы будем опускать). Отдачу от масштаба, соответствующую этому определению, будем называть отдачей от масштаба в смысле функции затрат (ФЗ-отдачей от масштаба). ФЗ-отдача от масштаба соответственно связана с эластичностью функции затрат. [c.640]
При анализе относительных изменений эластичность играет примерно такую же роль, что производная — при анализе абсолютных изменений. Свойства этой характеристики зависимостей изложены в статье «Эластичность функции» (сокращенно — «ЭФ»), помещенной в настоящем номере журнала, на которую мы в дальнейшем будем неоднократно ссылаться. [c.110]
Такое определение не соответствует общему определению эластичности функции. [c.111]
Советуем Вам после прочтения статьи «Эластичность функции» выполнить следующие упражнения, в которых / (х) предполагается непрерывно дифференцируемой положительной функцией при [c.179]
Как можно оценить эластичность функции y = f(x) по ее графику Рассмотрим вначале возрастающую функцию (эластичность при этом положительна). Выберем на графике точку Ми проведем через эту точку касательную [c.181]
Перед чтением настоящей статьи, возможно, полезно будет вспомнить определение и основные свойства эластичностей — они изложены в вып. 1, в Математическом приложении Эластичность функций . [c.245]
В настоящем пункте мы несколько раз будем ссылаться на Математическое приложение Эластичность функции (вып. 1), которое для краткости будем обозначать ЭФ . [c.225]
Ср. упражнение 1 к математическому приложению Эластичность функции ( ЭШ , вып. 1, стр. 183) [c.104]
Эластичность функции показывает приближенно, на сколько процентов изменится функция у = f(x) при изменении независимой переменной х на 1%. [c.46]
Обобщенная модель представляет более сложный случай, когда иид кривых IS и LMn их взаимное расположение зависят от соотношения эластичностей функций /и S по Ки /, Эта обобщенная интерпретация позволяет провести аналогию с концепцией Викселля и одновременно назвать экономику, которую рассматривает Кейнс, экономикой спада. [c.507]
Мера «относительной» чувствительности — эластичность функции (средняя (отношение процентных изменений) или предельная (к производной)) [c.47]
В различных экономических приложениях применяются (и рассматриваются в словаре) следующие функции Взвешивающие, Дифференцируемые, Гладкие, Кусочно-линейные, Кусочно-непрерывные, Линейные, Нелинейные, Непрерывные, Се-парабелъные, Экспоненты и др. См. также Вектор-функция, Гессиан, Интеграл, Мультипликативная форма представления функции, Производная, Рекурсия, Частная производная, Эластичность функции. [c.379]
ЭЛАСТИЧНОСТЬ [elasti ity] — мера реагирования одной переменной величины на изменение другой. Подробнее см. Эластичность функции. [c.424]
ЭЛАСТИЧНОСТЬ СПРОСА ОТ ДОХОДОВ (ПО ДОХОДУ) [in ome elasti ity of demand] — коэффициент, показывающий относительное изменение потребления (спроса) при изменении дохода (остальные факторы, от которых зависит спрос, принимаются неизменными). Исчисляется по формуле (см. Эластичность функции) [c.425]
ЭЛАСТИЧНОСТЬ ФУНКЦИИ [fun tion elasti ity] (иногда ее называют относительной производной) — предел отношения относительного приращения функции у (зависимой переменной) [c.426]
economy-ru.info
Вопрос 26. Понятие эластичности, геометрический смысл. Свойства эластичности.
В экономике даже самые малые приращения величин — товаров, денег и т.д. — конечны, поэтому экономический анализ удобнее вести на основе показателя, устанавливающего зависимость между относительными, процентными изменениями параметров.
Введем один из таких показателей — эластичность. Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительного изменения экономического фактора, от которого он зависит, при неизменных остальных влияющих на него факторах.
Так, если известна функциональная зависимость у=f(x), то одним из показателей реагирования одной переменной у на изменение другой х служит производная, характеризующая скорость изменения функции с изменением аргумента х. Однако в экономике этот показатель неудобен тем, что он зависит от выбора единиц измерения. Поэтому для измерения чувствительности изменения функции к изменению аргумента в экономике изучают связь не абсолютных изменений переменных х и у (Δх и Δу), а их относительных или процентных изменений, вводя понятие эластичности.
Эластичностью Ех(у) функции у = f(x) называется предел отношения относительных изменений переменных х и у. Эластичность изменения переменной у при изменении переменной х
Эластичность функции показывает приближенно, на сколько процентов изменится функция у = f(x) при изменении независимой переменной х на 1%.
Геометрически эластичность убывающей функции равна отношению расстояний по касательной от точки С(x,f(x)) до ее пересечения с осями у и х, взятому со знаком минус.
Свойства эластичности:
1. Эластичность — безразмерная величина, значение которой не зависит от того, в каких единицах измерены величины у и х.
2. Эластичности взаимно обратных функций — взаимно обратные величины:
3. Эластичность произведения двух функций и(х) и v(x), зависящих от одного и того же аргумента х, равна сумме эластичностей:
4. Эластичность частного двух функций и(х) и v(x), зависящих от одного и того же аргумента х, равна разности эластичностей
5. Эластичность суммы двух функций и(х) и v(x) может быть найдена по формуле:
Эластичности элементарных функций:
1. Эластичность степенной функции у = Xх постоянна и равна показателю степени а:
2. Эластичность показательной функции у = а* пропорциональна х: ЕХс?) = л1п(о).
3. Эластичность линейной функции
Для функций, наиболее часто встречающихся в экономико-математических исследованиях, в табл. приведены коэффициенты эластичности.
Таблица
В экономике выделяют несколько видов эластичностей:
· Эластичность спроса по цене (показывает относительное изменение величины спроса на какое то благо при изменении цены этого блага на один процент и характеризующая чувствительность потребителей к изменению цен на продукцию).
Если ценовая эластичность спроса по абсолютной величине больше единицы, то спрос называют эластичным (совершенно эластичным при бесконечно большой величине эластичности спроса). Если ценовая эластичность спроса по абсолютной величине меньше единицы, то спрос называют неэластичным (совершенно неэластичным при нулевой эластичности спроса).
И, наконец, если ценовая эластичность спроса по абсолютной величине равна единице, то говорят о спросе с единичной эластичностью.
· Эластичность спроса по доходу (характеризует в процентах изменение величины спроса на какое то благо при изменении дохода потребителя этого блага на один процент)
Положительная эластичность спроса по доходу характеризует нормальные (качественные) товары, а отрицательная величина — малоценные (некачественные) товары.
Так, высокий положительный коэффициент спроса по доходу в отрасли указывает, что ее вклад в экономический рост больше, чем доля в структуре экономики, и она имеет шансы на расширение и процветание в будущем. Наоборот, если коэффициент эластичности спроса на продукцию отрасли по доходу имеет небольшое положительное или отрицательное значение, то ее может ожидать застой и перспектива сокращения производства.
· Ценовая эластичность ресурсов (характеризует изменение в процентах величины спроса на какой-нибудь ресурс при изменении цены этого ресурса)
· Эластичность замещения одного ресурса другим.
В анализе и прогнозах ценовой политики применяется — понятие эластичность спроса по цене. Пусть D = D(P) — функция спроса от цены товара Р. Тогда эластичность спроса по цене, показывает относительное изменение (выраженное в процентах) величины спроса на какое-либо благо при изменении цены этого блага на один процент и характеризующая чувствительность потребителей к изменению цен на продукцию.
Различают три вида спроса:
а) если |Ep(D)|>l (Ep(D)< -1), то спрос считается эластичным;
б) если|Е (D) | =1 (Е (D)= -1), то спрос нейтрален;
в) если | Ep(D) | <1 (Е (D)> -1), то спрос неэластичен (совершенно неэластичен при нулевой эластичности спроса).
Рассмотрим задачу. Функция спроса q = и предложения s = p+2, где q и s – количество товара соответственно покупаемого и предлагаемого на продажу в единицу времени, p – цена единицы товара. Найти эластичность спроса и предложения по равновесной цене.
Решение:Равновесная цена определяется из равенства спроса и предложения: = p+2
Решая это уравнение, получаем решение p1=-4, p=2. Первый корень — посторонний. Следовательно, равновесная цена 2 денежных единицы.
Эластичность спроса по цене (q) = ∙ = ∙ =
При p=2 (q)= = -0,1
Эластичность предложения по цене: (s) = ∙ = ∙1 =
При p=2 (s) = = 0,5 => спрос и предложение при равновесной цене неэластичен, т.е. изменение цены не приведет к резкому изменению спроса и предложения.
infopedia.su
