Дисперсия это в эконометрике: Остаточная дисперсия формула эконометрика. Решение и анализ. Расходы на потребление
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Теория — Страница 2 — Эконометрика — это проще, чем вы думаете!
Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществляют с помощью d-критерия Дарбина-Уотсона. Этот тест считается достаточно универсальным и широко применяется в эконометрических исследованиях вследствие своей простоты, хотя и не обладает существенной эффективностью (достоверностью). Тест Дарбина-Уотсона обычно используется для установления факта наличия автокорреляционной зависимости первого порядка в ряду ошибки, то есть между соседними её значениями. Автокорреляционные зависимости второго и последующих порядков этот тест не обнаруживает.
Этот тест считается достаточно универсальным и широко применяется в эконометрических исследованиях вследствие своей простоты, хотя и не обладает существенной эффективностью (достоверностью). Тест Дарбина-Уотсона обычно используется для установления факта наличия автокорреляционной зависимости первого порядка в ряду ошибки, то есть между соседними её значениями. Автокорреляционные зависимости второго и последующих порядков этот тест не обнаруживает.
Расчётное значение d-критерия определяется по формуле:
(29)
Значение d = 0 соответствует случаю, когда между рассматриваемыми рядами остатков существует строгая положительная линейная зависимость, а значение d=4 соответствует строгой отрицательной связи. Если ряды остатков независимы, то d = 2.
Расчетное значение критерия сравнивается с нижним (d1) и верхним (d2) критическими значениями статистики Дарбина-Уотсона. При этом возможны следующие случаи:
Если , то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию.

Если , то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков.
Если то считается, что нет достаточных оснований сделать тот или иной вывод и нужно использовать дополнительный, более мощный критерий, например первый коэффициент автокорреляции:
(30)
Если расчетное значение коэффициента по модулю меньше табличного значения , то гипотеза об отсутствии автокорреляции принимается, в противном случае эта гипотеза отвергается.
Если d>2, то это свидетельствует об отрицательной автокорреляции остатков. В этом случае расчетное значение критерия необходимо преобразовать по формуле:
(31)
и сравнивать с теми же критическими значениями статистики d1 и d2.
Если имеет место автокорреляция остатков, то есть их зависимость друг от друга, то коэффициенты регрессии не смещены, но стандартные ошибки недооценены, а проверка статистической значимости коэффициентов ненадежна. Автокорреляция может появиться из-за невключения в модель значимых переменных, неверной формы функции в оценочном выражении (например, линейная модель тогда, когда она должна быть нелинейной).
Тест Дарбина-Уотсона можно применять только в случае выполнения следующих условий:
в регрессионном уравнении присутствует свободный член;
регрессоры являются нестохастическими;
в регрессионном уравнении нет лаговых значений зависимой переменной.
Кроме того, необходимо учитывать, что тест Дарбина-Уотсона проверяет только наличие автокорреляции между регрессионными остатками в последовательных наблюдениях. Однако если коррелируют показатели с лагом, большим единице (например, ), то с помощью теста Дарбина-Уотсона не удастся обнаружить никакой автокорреляции.
Следующий этап анализа модели — проверка соответствия распределения остаточной последовательности нормальному закону распределения.
P.S. Говоря о практической стороне расчёта d-критерия, должен отметить, что мои студенты иногда получали значение d=4… Вроде бы как нужно вычесть 2 (ведь значение больше 4, верно?) — и мы снова получаем d = 2, которое нужно сравнить… с каким значением? Допускаю, что из-за условности модели, которую строили студенты, и её особенностей, у них получалась «классическая» автокорреляция, однако проверить свои догадки не могу — информация про тест Дарбина-Уотсона в интернете крайне скудная…
Эконометрика ТЕСТ 2 | DamiRocK
Автокорреляция — это корреляционная зависимость уровней ряда от предыдущих значений.
***Аддитивная модель временного ряда имеет вид: Y=T+S+E
В каких пределах изменяется коэффициент детерминанта: от 0 до 1.
Величина доверительного интервала позволяет установить предположение о том, что: интервал содержит оценку параметра неизвестного.
Внутренне нелинейная регрессия — это истинно нелинейная регрессия, которая не может быть приведена к линейной регрессии преобразованием переменных и введением новых переменных.
Временной ряд — это последовательность значений признака (результативного переменного), принимаемых в течение последовательных моментов времени или периодов.
Выборочное значение Rxy не > 1, |R| < 1
Гетероскедастичность — нарушение постоянства дисперсии для всех наблюдений.
Гетероскедастичность присутствует когда: *дисперсия случайных остатков не постоянна; мы сторим неправильную версию истиной модели; две или больше независим. переменные имеют высокую корреляцию; независимая переменная исчисляется с ошибкой.
Гомоскедастичность — постоянство дисперсии для всех наблюдений, или одинаковость дисперсии каждого отклонения (остатка) для всех значений факторных переменных.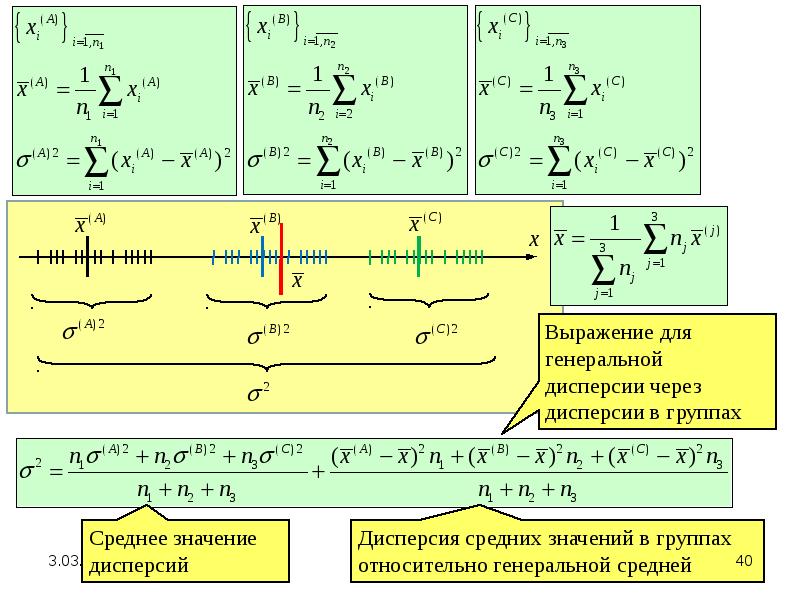
Гомоскидастичность – это когда дисперсия остатков постоянна и одинакова для всех … наблюдений.
Дисперсия — показатель вариации.
***Для определения параметров иденцифицированной модели примен.: * примен. косвенный МНК; примен. 2-х шаговый МНК; не один из сущ. методов применить нельзя.
Для определения параметров неиденцифицированной модели примен.:
Для определения параметров сверх иденцифицированной модели примен.: * примен. 2-х шаговый МНК ; не один из сущ. методов применить нельзя;; примен. косвенный МНК.
Для оценки … изменения y от x вводится: коэффициент эластичности:
Для проверки значимости отдельных параметров регрессии используется: t-тест.
Доверительная вероятность – это вероятность того, что истинное значение результативного показателя попадёт в расчётный прогнозный интервал.
Если Rxy положителен, то с ростом x увеличивается y.
***Если качественный фактор имеет 3 градации, то необх. число фиктивных переменных: ??? мой ответ был 3
Если регрессионная модель имеет показательную зависимость, то метод МНК применим после приведения к линейному виду.
Значимость уравнения регрессии — действительное наличие исследуемой зависимости, а не просто случайное совпадение факторов, имитирующее зависимость, которая фактически не существует.
Значимость уравнения регрессии в целом оценивают
Значимость частных и парных коэф. корреляции поверен. с помощью: -t-критерия Стьюдента
Интеркорреляция и связанная с ней мультиколлинеарность — это приближающаяся к полной линейной зависимости тесная связь между факторами.
Какая статистическая хар-ка выражена формулой: rxy=Ca(x;y) разделить на корень Var(x)*Var(y) : *коэф. корреляции; коэф. детерминации; t-статистика; коэф. регрессии.
корреляции; коэф. детерминации; t-статистика; коэф. регрессии.
Классический метод к оцениванию параметров регрессии основан на:
Корреляция — стохастическая зависимость, являющаяся обобщением строго детерминированной функциональной зависимости посредством включения вероятностной (случайной) компоненты.
***Коэф. автокорреляции: *характеризует тесноту линейной связи текущего и предстоящего уровней ряда; характеризует тесноту не линейной связи текущего и предстоящего уровней ряда; характеризует наличие или отсутствие тенденции.
Коэффициент детерминации изменяется в пределах: – от 0 до 1
Коэффициент детерминации — показатель тесноты стохастической связи в общем случае нелинейной регрессии
Коэффициент детерминации : – это квадрат множественного коэф. корреляции.
Коэффициент детерминации – это величина, которая характеризует связь между зависимыми и независимыми переменными.
Коэффициент детерминации R показывает долю вариаций зависимой переменной y, объяснимую влиянием факторов, включаемых в модель.
Коэффициент доверия — это коэффициент, который связывает линейной зависимостью предельную и среднюю ошибки, выясняет смысл предельной ошибки, характеризующей точность оценки, и является аргументом распределения (чаще всего, интеграла вероятностей). Именно эта вероятность и есть степень надежности оценки.
Коэффициент доверия (нормированное отклонение) — результат деления отклонения от среднего на стандартное отклонение, содержательно характеризует степень надежности (уверенности) полученной оценки.
Коэффициент корелляции Rxy используется для определения полноты связи X и Y.
Коэффициент корелляции равный 1 означает, что: -существует функциональная зависимость.
Коэффициент корелляции равный 0 означает, что: –отсутствует линейная связь.
Коэффициент корреляции рассчитывается для измерения степени линейной взаимосвязи между двумя случайными переменными.
Коэффициент корелляции меняется в пределахт: от -1 до 1
Коэффициент линейной корреляции — показатель тесноты стохастической связи между фактором и результатом в случае линейной регрессии.
Коэффициент регрессии — коэффициент при факторной переменной в модели линейной регрессии.
Коэффициент регрессии b показывает: на сколько единиц увеличивается y, если x увеличивается на 1.
Коэффициент регрессии изменяется в пределах: * применяется любое значение ; от 0 до 1; от -1 до 1;
Коэффициент эластичности измеряется в: неизмеримая величина.
Критерий Дарвина-Чотсона применяется для: – отбора факторов в модель; или – определения автокорреляции в остатках
Критерий Стьюдента — проверка значимости отдельных коэффициентов регрессии и значимости коэффициента корреляции.
Критерий Фишера показывает: статистическую значимость модели в целом.
Лаговые переменные : – это переменные, относящиеся к предыдущим моментам времени; или -это значения зависим. перемен. за предшествующий период времени.
Модель в целом статистически значима, если Fрасч > Fтабл.
***Модель сверхидентифицирована, если: *число приведён. коэф. меньше числа структурных коэф
Модель идентифицирована, если: – число параметров структурной модели равно числу параметров приведён. формы модели.
Модель неидентифицирована, если: – число приведён. коэф. больше числа структурных коэф.
***Мультиколлениарность возникает, когда: 2 или больше независимые переменные имеют высокую
корреляцию.
Мультипликативная модель временного ряда строится, если: – амплитуда сезонных колебаний возрастает или убывает.
Мультипликативная модель временного ряда имеет вид: – Y=T*S*E
Несмещённость оценки параметра регрессии, полученной по МНК, означает: – что она характеризуется наименьшей дисперсией.
От чего зависит количество точек, исключаемых из временного ряда в результате сглаживания: от применяемого метода сглаживания.
Отметьте основные виды ошибок спецификации: *отбрасывание значимой переменной; добавление незначимойпеременной; низкое значение коэф. Детерминации; выбор неправильной формы модели
Оценки коэффициентов парной регрессии является несмещённым, если: математические ожидания остатков =0.
Оценки параметров регрессии являются состоятельными, если: -увеличивается точность оценки при n, т. е. при увеличении n вероятность оценки от истинного значения параметра стремится к 0.
Оценки пароной регрессии явл. эффективными, если: * оценка обладают наименьшей дисперсией по сравнению с другими оценками; остатки равны нулю; увелич. точность оценок при увелич….исходного ряда Т, при Т((вероятность отклонения оценки от её истинного значениястремится к нулю; математическое ожидание остатков равно нулю.
точность оценок при увелич….исходного ряда Т, при Т((вероятность отклонения оценки от её истинного значениястремится к нулю; математическое ожидание остатков равно нулю.
При проверке значимости одновременно всех параметров используется: -F-тест.
При наличии гетероскедастичности следует применять: – обобщённый МНК
Применим ли МНК для нелинейной модели: -применим после приведения модели к линейному виду.
Суть коэф. детерминации r2xy состоит в следующем: – характеризует долю дисперсии результативного признака y объясняем. регресс., в общей дисперсии результативного признака.
Скорректиров. коэф. детерминации: – больше обычного коэф. детерминации
С увеличением числа объясняющих переменных скоррестированный коэффициент детерминации: – увеличивается.
Стандартный коэффициент уравнения регрессии: показывает на сколько 1 изменится y при изменении фактора xk на 1 при сохранении др.
Табличное значение критерия Стьюдента зависит от уровня доверительной вероятности и от числа включённых факторов и от длины исходного ряда.
Табличные значения Фишера (F) зависят от доверительной вероятности и от числа включённых факторов и от длины исходного ряда.
Уравнение идентифицировано, если: – D+1=H
Уравнение неидентифицировано, если: – D+1<H
Уравнение сверхидентифицировано, если: – D+1>H
Частный F-критерий: – оценивает значимость уравнения регрессии в целом
Экзогенная переменная – это зависимая переменная или результирующая y.
Экзогенная переменная – это независимая переменная или фактор-Х.
Экзогенные переменные — это переменные, которые определяются вне системы и являются независимыми
Эластичность показывает на сколько % изменится редуктивный показатель y при изменении на 1% фактора xk.
Эндогенные переменные: – это зависимые переменные от экзогенных, определяются внутри самой системы или это зависимые переменные., число кот. Равно числу уравнений в системе и кот. обознач. через y.
Эти четыре задания были в тесте, их нужно решать, у меня ответов нет (выделила зелёным цветом мой ответ, который поставила на бум):
***Дан статистический ряд наблюд. зависимости переменной Y от X
X 1.2 1.3 1.4 1.5 1.6 1.7
Y 6.59 7.10 7.57 8.08 8.59 9.08 Чему равен параметр b уравнения регрессии Y=b*x+a?
Вариан ответа: вариантов много, я выбрала 7,35
***Выберите модель с лагами:
Варианты ответов:
- yt=α+β0xt+ƒyt+ Et
- yt=α+β0Et+β1Et-1
- yt=α+β0xt+ β1Xt-1+…….
 +βkXt-k+Et
+βkXt-k+Et
***Рассчитайте текущий t для a и b , сделай выводы их достоверности при условии, что: Da=0.001 Db=0.0004 a=8 b=7 при tнабл=56
Варианты ответов:
- a – достоверно b – достоверно
- a – недостоверно b – недостоверно
- a – недостоверно b – достоверно
- a – достоверно b – недостоверно
*** Рассчитайте текущий t для a и b , сделай выводы их достоверности при условии, что: Da=0.01 Db=0.01 a=5 b=4,2 при tнабл=25
Варианты ответов:
1) a – достоверно b – достоверно
2) a – недостоверно b – недостоверно
3) a – недостоверно b – достоверно
4) a – достоверно b – недостоверно
Дополнительные понятия для помощи!!! По алфавиту.
Критерий Фишера — способ статистической проверки значимости уравнения регрессии, при котором расчетное (фактическое) значение F-отношения сравнивается с его критическим (теоретическим) значением.
Линейная регрессия — это связь (регрессия), которая представлена уравнением прямой линии и выражает простейшую линейную зависимость.
Метод инструментальных переменных — это разновидность МНК. Используется для оценки параметров моделей, описываемых несколькими уравнениями. Главное свойство — частичная замена непригодной объясняющей переменной на такую переменную, которая некоррелированна со случайным членом. Эта замещающая переменная называется инструментальной и приводит к получению состоятельных оценок параметров.
Метод наименьших квадратов (МНК) — способ приближенного нахождения (оценивания) неизвестных коэффициентов (параметров) регрессии. Этот метод основан на требовании минимизации суммы квадратов отклонений значений результата, рассчитанных по уравнению регрессии, и истинных (наблюденных) значений результата.
Множественная линейная регрессия — это множественная регрессия, представляющая линейную связь по каждому фактору.
Множественная регрессия — регрессия с двумя и более факторными переменными.
Модель идентифицируемая — модель, в которой все структурные коэффициенты однозначно определяются по коэффициентам приведенной формы модели.
Модель рекурсивных уравнений — модель, которая содержит зависимые переменные (результативные) одних уравнений в роли фактора, оказываясь в правой части других уравнений.
Несмещенная оценка — оценка, среднее которой равно самой оцениваемой величине.
Нулевая гипотеза — предположение о том, что результат не зависит от фактора (коэффициент регрессии равен нулю).
Обобщенный метод наименьших квадратов (ОМНК) — метод, который не требует постоянства дисперсии (гомоскедастичности) остатков, но предполагает пропорциональность остатков общему множителю (дисперсии). Таким образом, это взвешенный МНК.
Таким образом, это взвешенный МНК.
Объясненная дисперсия — показатель вариации результата, обусловленной регрессией.
Объясняемая (результативная) переменная — переменная, которая статистически зависит от факторной переменной, или объясняющей (регрессора).
Остаточная дисперсия — необъясненная дисперсия, которая показывает вариацию результата под влиянием всех прочих факторов, неучтенных регрессией.
Предопределенные переменные — это экзогенные переменные системы и лаговые эндогенные переменные системы.
Приведенная форма системы — форма, которая, в отличие от структурной, уже содержит одни только линейно зависящие от экзогенных переменных эндогенные переменные. Внешне ничем не отличается от системы независимых уравнений.
Расчетное значение F-отношения — значение, которое получают делением объясненной дисперсии на 1 степень свободы на остаточную дисперсию на 1 степень свободы.
Регрессия (зависимость) — это усредненная (сглаженная), т.е. свободная от случайных мелкомасштабных колебаний (флуктуаций), квазидетерминированная связь между объясняемой переменной (переменными) и объясняющей переменной (переменными). Эта связь выражается формулами, которые характеризуют функциональную зависимость и не содержат явно стохастических (случайных) переменных, которые свое влияние теперь оказывают как результирующее воздействие, принимающее вид чисто функциональной зависимости.
Регрессор (объясняющая переменная, факторная переменная) — это независимая переменная, статистически связанная с результирующей переменной. Характер этой связи и влияние изменения (вариации) регрессора на результат исследуются в эконометрике.
Система взаимосвязанных уравнений — это система одновременных или взаимозависимых уравнений. В ней одни и те же переменные выступают одновременно как зависимые в одних уравнениях и в то же время независимые в других. Это структурная форма системы уравнений. К ней неприменим МНК.
Это структурная форма системы уравнений. К ней неприменим МНК.
Система внешне не связанных между собой уравнений — система, которая характеризуется наличием одних только корреляций между остатками (ошибками) в разных уравнениях системы.
Случайный остаток (отклонение) — это чисто случайный процесс в виде мелкомасштабных колебаний, не содержащий уже детерминированной компоненты, которая имеется в регрессии.
Состоятельные оценки — оценки, которые позволяют эффективно применять доверительные интервалы, когда вероятность получения оценки на заданном расстоянии от истинного значения параметра становится близка к 1, а точность самих оценок увеличивается с ростом объема выборки.
Спецификация модели — определение существенных факторов и выявление мультиколлинеарности.
Стандартная ошибка — среднеквадратичное (стандартное) отклонение. Оно связано со средней ошибкой и коэффициентом доверия.
Степени свободы — это величины, характеризующие число независимых параметров и необходимые для нахождения по таблицам распределений их критических значений.
T-отношение (t-критерий) — отношение оценки коэффициента, полученной с помощью МНК, к величине стандартной ошибки оцениваемой величины.
Тренд — основная тенденция развития, плавная устойчивая закономерность изменения уровней ряда.
Уровень значимости — величина, показывающая, какова вероятность ошибочного вывода при проверке статистической гипотезы по статистическому критерию.
Фиктивные переменные — это переменные, которые отражают сезонные компоненты ряда для какого-либо одного периода.
Эконометрическая модель — это уравнение или система уравнений, особым образом представляющие зависимость (зависимости) между результатом и факторами. В основе эконометрической модели лежит разбиение сложной и малопонятной зависимости между результатом и факторами на сумму двух следующих компонентов: регрессию (регрессионная компонента) и случайный (флуктуационный) остаток. Другой класс эконометрических моделей образует временные ряды.
Другой класс эконометрических моделей образует временные ряды.
Эффективность оценки — это свойство оценки обладать наименьшей дисперсией из всех возможных.
Разбираем формулы среднеквадратического отклонения и дисперсии в Excel | Методы анализа
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Сморите пример расчета здесь: среднеквадратическое отклонние и дисперсия
Для этого временного ряда i=1, n=10, ,
Рассмотрим формулу среднего значения:
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. 2))/(n-1)
2))/(n-1)
=90/(10-1)=10
6. Среднеквадратическое отклонение равно = корень(10)=3,2
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Скачать файл с примером
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Как рассчитать дисперсию в Excel?
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Скачать файл с примером
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.

- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Лекции по «Эконометрике»
Лекции по эконометрике
Эконометрика – это наука, объединяющая различные статистические методы, используемые для наблюдения за ходом развития экономики, ее анализа и прогнозов, а также для выявления взаимосвязей между экономическими явлениями.
Задачи:
- Изучить экономическое явление
- Прогнозирование явлений
- Взаимосвязи явлений
Раздел I
Анализ невременных данных
Мы будем
работать с данными, которые не являются
временными, т. е. их можно переставлять
местами, не меняя смысла
е. их можно переставлять
местами, не меняя смысла
Случайная величина (с.в.) x – это числовая функция, заданная на некотором вероятностном пространстве.
Функция распределения с.в. x– это числовая функция числового аргумента, заданная равенством: F(x)=P(xC)
Характеристики случайной величины
- Математическое ожидание с.в. x.
Обозначается E(x). Показывает среднее ожидаемое значение.
Если x – дискретная с.в., то
Если x – непрерывная с.в., то , где f(x) – плотность распределения.
Т.к. при работе с данными мы не знаем вероятности, то математическое ожидание считается как , где n – количество наблюдений
Свойства математического ожидания:
- , где x и y – с.в.; a и b = const
- Если с.в. y с.в. x, то
- Если , то
Дисперсия
Обозначается D[x]=V(x). Дисперсия
– это среднее отклонение от среднего,
т. е. на сколько в среднем большинство
значений отклонится от математического
ожидания, т.е. большинство значений будет
лежать в интервале:
е. на сколько в среднем большинство
значений отклонится от математического
ожидания, т.е. большинство значений будет
лежать в интервале:
Свойства дисперсии:
- Ковариация
Обозначается Cov(x,y). Показывает однонаправленность двух случайных величин, т.е. ковариация – это мера линейной зависимости с.в.
Свойства ковариации:
Т.к. ковариация меняется от до , то использовать ее как меру линейной связи, неудобно, поэтому вводят понятие корреляции.
- Корреляция.
Обозначается Corr(x,y). Показывает силу линейной связи в интервале
Свойства корреляции:
1)
2) Если , то между x и y связи нет.
3) Если , то связь сильная положительная, т.е. рост x вызывает рост y и наоборот.
Замечание: если , т. е. линейной связи нет, то это не
значит, что нет нелинейной связи.
е. линейной связи нет, то это не
значит, что нет нелинейной связи.
Ложная корреляция.
При использовании следует помнить, что он показывает наличие только линейной связи. Ложная корреляция – в ряде случаев неправильно выбраны случайные величины, между которыми ищется корреляционная связь.
Пример: Если искать связь между длиной волос и ростом, то получится, что чем выше человек, тем короче у него волосы. Ошибка в том, что следует рассматривать эту зависимость отдельно по мужчинам и отдельно по женщинам.
Медиана
Медиана – это альтернатива определения среднего значения. Она считается по упорядоченному по возрастанию ряду из наблюдений (вариационный ряд). Показывает среднее из большинства. Обозначается med.
Пример: Имеются 10 человек. 9 человек получают 100$, 1 – 10000$. Найти средний доход человека.
Средний доход человека
Мы видим,
что среднее значение малоэффективно
и не показывает реальной ситуации.
Используем медиану.
1)
2) т.к. Т=10, то
Медиана показала реальное положение вещей.
Медиана используется, когда есть несколько сильных выбросов, т.е. несколько резко выделяющихся от других значений.
- Мода.
Мода – это число, делящее выборку пополам, т.е. 50% значений лежит выше нее, а 50% — ниже. Обозначается mod.
Пример:
Медиана показывает насколько справедливо среднее.
Оценки
Введем обозначения:
истинное значение параметра
оценка параметра
Т.к. истинное значение параметра неизвестно, то мы его находим (оцениваем) по некоторой выборке объема Т.
то число, которое скорее всего примет истинное значение.
Свойства оценок:
Мы стараемся найти и
- состоятельны, т.е. при оценка стремится к истинному значению,
т.
 е., чем больше выборка, тем точнее оценка
е., чем больше выборка, тем точнее оценка - несмещенность, т.е. математическое ожидание оценки – это истинное значение, т.е. в среднем мы получаем истинное значение
- эффективность, т.е. дисперсия оценки – минимальна
Замечание: дисперсия напрямую связана с точностью оценивания. Чем выше дисперсия, тем больше варьируемость признака, тем менее точный результат мы получаем.
Модель парной линейной регрессии
Пусть Y,X – две выборки объема Т.
Возникает вопрос. Связаны ли они между собой? Если да, то как, и как выразить эту связь количественно?
У
Необходимо подобрать
а и b
такими, чтобы линия
была как можно ближе
ко всем значениям. a
и b – неизвестные параметры.
Необходимо подобрать
a и b, минимизировав
меру расстояния от
точек, до получившейся
прямой. В качестве меры
можно взять сумму квадратов
отклонения от среднего
a
и b – неизвестные параметры.
Необходимо подобрать
a и b, минимизировав
меру расстояния от
точек, до получившейся
прямой. В качестве меры
можно взять сумму квадратов
отклонения от среднего
Т.е. мы суммируем квадраты расстояния в каждой точке между наблюдаемым значением и тем, что лежит на линии. Берется квадрат расстояний, чтобы большим расстояниям придать больший вес, а также избежать отрицательных значений.
Иногда в качестве меры отклонения берут модуль расстояния
Но вычисления с модулем гораздо сложнее. Мы будем использовать квадрат отклонений.
Для нахождения неизвестных параметров а и b, имея в распоряжении выборки Y и X объема Т, нам необходимо минимизировать следующее расстояние
Мы ищем линию, которая будет максимально близко лежать от этих точек.
Применяя метод Лагранжа в решении подобных задач, получаем что:
,
где
Мы получили
оценки неизвестных параметров a и b,
удовлетворяющие свойствам оценок, с помощью
которых можно построить уравнение регрессии
и найти качественную зависимость между
X и Y.
, ,
— вектор из двух букв a и b.
В данном случае построить регрессию, значит найти оценку вектора .
— матричная форма записи
Теорема Гаусса-Маркова
Основная теорема линейной регрессии.
Пусть есть Х и У выборки объема Т.
1)
2) — детерминированное (т.е. случайная величина)
3) а)
б) или к нормальной линейной регрессии
Оценки и получены методом наименьших квадратов, являются лучшими в классе линейных несмещенных оценок, т.к. обладают наименьшей дисперсией.
Замечание: наши оценки являются наилучшими, если мы оцениваем модель, линейную по параметру.
Пример: — линейная модель, т.к. ,
или — линейная модель по параметру
-нелинейная модель
Замечание: остатки после
построения регрессии должны иметь нормальное
распределение с параметрами математическое
ожидание=0 и дисперсия=0, т. е., оценив регрессию,
мы должны проверить остатки на нормальность.
е., оценив регрессию,
мы должны проверить остатки на нормальность.
Оценив параметры модели, мы хотим узнать, насколько точно мы оценим коэффициент. Точность оценки связана с ее дисперсией.
Поэтому найдем дисперсию и . Для простоты расчетов введем обозначения:
Тогда дисперсия оценки будет равна:
Теперь у нас есть наилучшие оценки коэффициентов регрессии a и b, однако в регрессионном уравнении есть еще один неизвестный параметр – это дисперсия ошибок .
Из этих двух формул следует, что чем больше измерений, тем точнее результат и меньше дисперсии.
Рассмотрим дисперсию ошибок более подробно.
Обозначим через — прогноз в точке
Тогда остатки моделей будут собой представлять разницу между истинными и прогнозируемыми значениями.
— случайные величины, но — остатки, — ошибки
Но
остатки в отличие
от ошибок ненаблюдаемы,
поэтому для оценки
дисперсии ошибок
проще рассмотреть
ее через остатки.
Попробуем выразить дисперсию ошибок через остатки модели.
Поскольку математическое ожидание у ошибок и остатков нулевое, то дисперсия выражается через математическое ожидание суммы:
— неизвестная дисперсия остатков
Замечание: неизвестная дисперсия остатка связана с количеством наблюдений (их должно быть как можно больше) и с ошибками (они должны быть как можно меньше). Поэтому из двух подобранных моделей мы выбираем ту, которая точнее строит прогнозы даже если она построена по выборке объемом с меньшим Т.
Ковариационная матрица
Симметричная диагональная матрица, на диагонали у которой стоят дисперсии; — выборки объема Т.
Также можно построить корреляционную
матрицу, на диагонали которой 1 –
диагональная симметричная матрица, у
которой остальные элементы –
это соответствующие
Замечание: Таким образом, используя
корреляционную матрицу для построения
регрессии, мы выбираем тот Х, коррелированность
с Y которого по модулю наибольшая, т.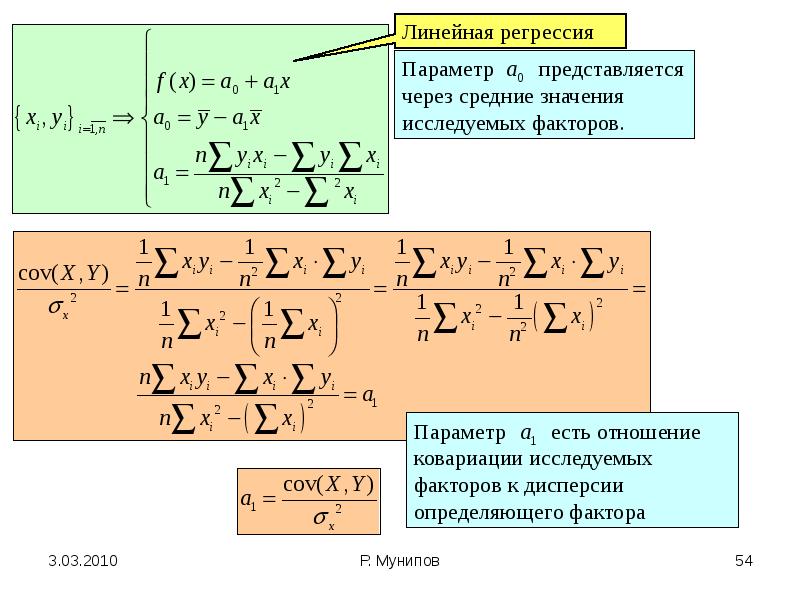 е.
мы выбираем тот параметр Х для получения
наилучших результатов, сила связи которого
с Y наибольшая, т.е. коэффициент по модулю
наибольший.
е.
мы выбираем тот параметр Х для получения
наилучших результатов, сила связи которого
с Y наибольшая, т.е. коэффициент по модулю
наибольший.
Дисперсионный анализ
Попробуем
разложить дисперсию
ESS – дисперсия, необъясненная уравнением, та, которая осталась неизвестной в остатке.
RSS – та часть дисперсии, которая объяснена регрессионным уравнением.
На основании этого вводится – коэффициент детерминации, характеризующий долю объясненной дисперсии с помощью данного регрессионного уравнения в общей дисперсии.
Этот коэффициент используется для выбора наилучшей модели из множества построенных.
Если , то мы ничего не объяснили с помощью построенной регрессии
Если , то мы учли всю изменчивость признака.
Из двух моделей выбирается та, у которой:
- все коэффициенты значимы
- максимально простая (т.е. как можно меньше параметров)
- как можно больше
- экономическая интерпретируемость коэффициентов (объясняемость)
- как можно более точный прогноз (при работе с выборкой отсекаются 5-10 значений, на которые и строится прогноз)
Модель множественной регрессии
Обобщением двумерной или
-уравнение многомерной линейной регрессии,
где
Основные гипотезы:
1)
спецификация модели — вид, линейный по параметрам
- — не зависит от t
- — независимые параметры; y – зависимый
Запишем это уравнение в матричной форме
Построить
такое уравнение регрессии означает
найти оценку параметра, т. е. оценку вектора
а.
е. оценку вектора
а.
По теореме Маркова-Гаусса если выполняются основные гипотезы 1,2,3,4, то можно применить метод наименьших квадратов, с помощью которого получится следующее уравнение:
, где — икс транспонированный
Т.к. мы находим оценки коэффициентов, а не их истинное значение, то нам хотелось бы оценить точность оценивания.
Она связана с вариацией оценки, т.е. с дисперсией: чем больше дисперсия, тем меньше точность и больше вариация. Тогда:
(**)
Используя правила перемножения матриц, получаем:
Замечание: из формулы (**) видно, что чем больше параметров, тем больше дисперсия. Поэтому мы выбираем максимально простую модель.
Оценивание качества многомерной линейной регрессии осуществляется так же, как и двумерной, но следует помнить, что растет с увеличением параметров, поэтому с помощью можно сравнивать только модели с одинаковым количеством зависимых параметров.
Спецификация модели
Под спецификацией понимают выбор
параметров регрессии. Т.к. на практике исследуется приближенная
модель, рассмотрим соотношение между
МНК-оценками параметров выбранной и истинной
модели.
Т.к. на практике исследуется приближенная
модель, рассмотрим соотношение между
МНК-оценками параметров выбранной и истинной
модели.
Рассмотрим два случая:
- Исключение. В модель не включали существенные параметры. Тогда оценивается модель,
где z — часть существенных параметров.
Как работает метод главных компонент (PCA) на простом примере / Хабр
В этой статье я бы хотел рассказать о том, как именно работает метод анализа главных компонент (PCA – principal component analysis) с точки зрения интуиции, стоящей за ее математическим аппаратом. Максимально просто, но подробно.
Математика вообще очень красивая и изящная наука, но порой ее красота скрывается за кучей слоев абстракции. Показать эту красоту лучше всего на простых примерах, которые, так сказать, можно покрутить, поиграть и пощупать, потому что в конце концов все оказывается гораздо проще, чем кажется на первый взгляд – самое главное понять и представить.
В анализе данных, как и в любом другом анализе, порой бывает нелишним создать упрощенную модель, максимально точно описывающую реальное положение дел. Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.
Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.
К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величины разные, но на самом деле они строго зависят друг от друга. В миле 1600м, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.
Но гораздо чаще бывает так, что признаки зависят друг от друга не так строго и (что важно!) не так явно. Объем двигателя в целом положительно влияет на разгон до 100 км/ч, но это верно не всегда. А еще может оказаться, что с учетом не видимых на первый взгляд факторов (типа улучшения качества топлива, использования более легких материалов и прочих современных достижений), год автомобиля не сильно, но тоже влияет на его разгон.
Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино, так сказать, и работать уже с более простой моделью. Конечно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет как раз метод PCA.
Выражаясь более строго, данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации.
Шаг 1. Подготовка данных
Здесь для простоты примера я не буду брать реальные обучающие датасеты на десятки признаков и сотни наблюдений, а сделаю свой, максимально простой игрушечный пример. 2 признака и 10 наблюдений будет вполне достаточно для описания того, что, а главное – зачем, происходит в недрах алгоритма.
Сгенерируем выборку:
x = np.arange(1,11)
y = 2 * x + np.random.randn(10)*2
X = np.vstack((x,y))
print X
OUT:
[[ 1. 2. 3. 4. 5.
6. 7. 8. 9. 10. ]
[ 2.73446908 4.35122722 7.21132988 11.24872601 9.58103444
12.09865079 13.78706794 13.85301221 15. 29003911 18.0998018 ]]
29003911 18.0998018 ]]
В данной выборке у нас имеются два признака, сильно коррелирующие друг с другом. С помощью алгоритма PCA мы сможем легко найти признак-комбинацию и, ценой части информации, выразить оба этих признака одним новым. Итак, давайте разбираться!
Для начала немного статистики. Вспомним, что для описания случайной величины используются моменты. Нужные нам – мат. ожидание и дисперсия. Можно сказать, что мат. ожидание – это «центр тяжести» величины, а дисперсия – это ее «размеры». Грубо говоря, мат. ожидание задает положение случайной величины, а дисперсия – ее размер (точнее, разброс).
Сам процесс проецирования на вектор никак не влияет на значения средних, так как для минимизации потерь информации наш вектор должен проходить через центр нашей выборки. Поэтому нет ничего страшного, если мы отцентрируем нашу выборку – линейно сдвинем ее так, чтобы средние значения признаков были равны 0. Это очень сильно упростит наши дальнейшие вычисления (хотя, стоит отметить, что можно обойтись и без центрирования).
Оператор, обратный сдвигу будет равен вектору изначальных средних значений – он понадобится для восстановления выборки в исходной размерности.
Xcentered = (X[0] - x.mean(), X[1] - y.mean())
m = (x.mean(), y.mean())
print Xcentered
print "Mean vector: ", m
OUT:
(array([-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]),
array([-8.44644233, -8.32845585, -4.93314426, -2.56723136, 1.01013247,
0.58413394, 1.86599939, 7.00558491, 4.21440647, 9.59501658]))
Mean vector: (5.5, 10.314393916)
Дисперсия же сильно зависит от порядков значений случайной величины, т.е. чувствительна к масштабированию. Поэтому если единицы измерения признаков сильно различаются своими порядками, крайне рекомендуется стандартизировать их. В нашем случае значения не сильно разнятся в порядках, так что для простоты примера мы не будем выполнять эту операцию.
Шаг 2. Ковариационная матрица
В случае с многомерной случайной величиной (случайным вектором) положение центра все так же будет являться мат. ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!
ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!
Для описания формы случайного вектора необходима ковариационная матрица.
Это матрица, у которой (i,j)-элемент является корреляцией признаков (Xi, Xj). Вспомним формулу ковариации:
В нашем случае она упрощается, так как E(Xi) = E(Xj) = 0:
Заметим, что когда Xi = Xj:
и это справедливо для любых случайных величин.
Таким образом, в нашей матрице по диагонали будут дисперсии признаков (т.к. i = j), а в остальных ячейках – ковариации соответствующих пар признаков. А в силу симметричности ковариации матрица тоже будет симметрична.
Замечание: Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.
И действительно, дисперсия одномерной случайной величины – это ковариационная матрица размера 1×1, в которой ее единственный член задан формулой Cov(X,X) = Var(X).
Итак, сформируем ковариационную матрицу Σ для нашей выборки. Для этого посчитаем дисперсии Xi и Xj, а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X). Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)
covmat = np.cov(Xcentered)
print covmat, "\n"
print "Variance of X: ", np.cov(Xcentered)[0,0]
print "Variance of Y: ", np. cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124
cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124
Шаг 3. Собственные вектора и значения (айгенпары)
О’кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X
1и X
2), а также примерную форму на плоскости. Теперь надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.
Замечание: Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.
Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна v
Тогда проекция на него будет равна v
X. Дисперсия проекции на вектор будет соответственно равна Var(v
TX). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:
Соответственно, дисперсия проекции:
Легко заметить, что дисперсия максимизируется при максимальном значении vT Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:
и
Последняя формула должна быть знакома по теме разложения матрицы на собственные вектора и значения. x является собственным вектором, а λ – собственным значением. Количество собственных векторов и значений равны размеру матрицы (и значения могут повторяться).
Кстати, в английском языке собственные значения и векторы именуются eigenvalues и eigenvectors соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.
Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором, имеющим максимальное собственное значение, равное величине этой дисперсии
.
И это справедливо также для проекций на большее количество измерений – дисперсия (ковариационная матрица) проекции на m-мерное пространство будет максимальна в направлении m айгенвекторов, имеющих максимальные собственные значения.
Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.
В библиотеке numpy реализована функция numpy.linalg.eig(X), где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.
На этом графике мы апроксимировали нашу выборку эллипсом с радиусами в 2 сигмы (т. е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.
е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.
Шаг 4. Снижение размерности (проекция)
Наибольший вектор имеет направление, схожее с линией регрессии и, спроецировав на него нашу выборку, мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.
Замечание: диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).
Часто требуется оценить объем потерянной (и сохраненной) информации. Удобнее всего представить в процентах. Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Таким образом, наш больший вектор описывает 45.994 / 46.431 * 100% = 99.06%, а меньший, соответственно, примерно 0.94%. Отбросив меньший вектор и спроецировав данные на больший, мы потеряем меньше 1% информации! Отличный результат!
Замечание: На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.
Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию v
TX (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора v
Tберем матрицу базисных векторов V
T. Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.
_, vecs = np.linalg.eig(covmat)
v = -vecs[:,1])
Xnew = dot(v,Xcentered)
print Xnew
OUT:
[ -9. 56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
dot(X,Y) — почленное произведение (так мы перемножаем векторы и матрицы в Python)
Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.
Шаг 5. Восстановление данных
С проекцией удобно работать, строить на ее основе гипотезы и разрабатывать модели. Но не всегда полученные главные компоненты будут иметь явный, понятный постороннему человеку, смысл. Иногда полезно раскодировать, к примеру, обнаруженные выбросы, чтобы посмотреть, что за наблюдения за ними стоят.
Это очень просто. У нас есть вся необходимая информация, а именно координаты базисных векторов в исходном базисе (векторы, на которые мы проецировали) и вектор средних (для отмены центровки). Возьмем, к примеру, наибольшее значение: 10.596… и раскодируем его. Для этого умножим его справа на транспонированный вектор и прибавим вектор средних, или в общем виде для всей выборки: XTvT+m
n = 9 #номер элемента случайной величины
Xrestored = dot(Xnew[n],v) + m
print 'Restored: ', Xrestored
print 'Original: ', X[:,n]
OUT:
Restored: [ 10. 13864361 19.84190935]
Original: [ 10. 19.9094105]
13864361 19.84190935]
Original: [ 10. 19.9094105]
Разница небольшая, но она есть. Ведь потерянная информация не восстанавливается. Тем не менее, если простота важнее точности, восстановленное значение отлично аппроксимирует исходное.
Вместо заключения – проверка алгоритма
Итак, мы разобрали алгоритм, показали как он работает на игрушечном примере, теперь осталось только сравнить его с PCA, реализованным в sklearn – ведь пользоваться будем именно им.
from sklearn.decomposition import PCA
pca = PCA(n_components = 1)
XPCAreduced = pca.fit_transform(transpose(X))
Параметр
n_componentsуказывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:
print 'Our reduced X: \n', Xnew
print 'Sklearn reduced X: \n', XPCAreduced
OUT:
Our reduced X:
[ -9. 56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]
56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]
Мы возвращали результат как матрицу вектор-столбцов наблюдений (это более канонический вид с точки зрения линейной алгебры), PCA в sklearn же возвращает вертикальный массив.
В принципе, это не критично, просто стоит отметить, что в линейной алгебре канонично записывать матрицы через вектор-столбцы, а в анализе данных (и прочих связанных с БД областях) наблюдения (транзакции, записи) обычно записываются строками.
Проверим и прочие параметры модели – функция имеет ряд атрибутов, позволяющих получить доступ к промежуточным переменным:
— Вектор средних: mean_
— Вектор(матрица) проекции: components_
— Дисперсии осей проекции (выборочная): explained_variance_
— Доля информации (доля от общей дисперсии): explained_variance_ratio_
Замечание: explained_variance_ показывает выборочную дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные дисперсии!
Сравним полученные нами значения со значениями библиотечной функции.
print 'Mean vector: ', pca.mean_, m
print 'Projection: ', pca.components_, v
print 'Explained variance ratio: ', pca.explained_variance_ratio_, l[1]/sum(l)
OUT:
Mean vector: [ 5.5 10.31439392] (5.5, 10.314393916)
Projection: [[ 0.43774316 0.89910006]] (0.43774316434772387, 0.89910006232167594)
Explained variance: [ 41.39455058] 45.9939450918
Explained variance ratio: [ 0.99058588] 0.990585881238
Единственное различие – в дисперсиях, но как уже упоминалось, мы использовали функцию cov(), которая использует несмещенную дисперсию, тогда как атрибут explained_variance_ возвращает выборочную. Они отличаются только тем, что первая для получения мат.ожидания делит на (n-1), а вторая – на n. Легко проверить, что 45.99 ∙ (10 — 1) / 10 = 41.39.
Все остальные значения совпадают, что означает, что наши алгоритмы эквивалентны. И напоследок замечу, что атрибуты библиотечного алгоритма имеют меньшую точность, поскольку он наверняка оптимизирован под быстродействие, либо просто для удобства округляет значения (либо у меня какие-то глюки).
Замечание: библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.
Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того, как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!
P.S.: Просьба не ругать автора за возможные неточности. Автор сам в процессе знакомства с дата-анализом и хочет помочь таким же как он в процессе освоения этой удивительной области знаний! Но конструктивная критика и разнообразный опыт всячески приветствуются!
Функция F.
 ТЕСТ
ТЕСТВозвращает результат F-теста, двустороннюю вероятность того, что разница между дисперсиями аргументов «массив1» и «массив2» несущественна.
Эта функция позволяет определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, можно определить, имеют ли эти школы различные уровни разброса результатов тестирования.
Синтаксис
F.ТЕСТ(массив1;массив2)
Аргументы функции F.ТЕСТ описаны ниже.
-
Массив1 — обязательный аргумент. Первый массив или диапазон данных.
-
Массив2 — обязательный аргумент. Второй массив или диапазон данных.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если количество точек данных в массиве «массив1» или «массив2» меньше 2 или дисперсия массива1 или массив2 0, то F.ТЕСТ возвращает значение #DIV/0! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные1 |
Данные2 |
|
|
6 |
20 |
|
|
7 |
28 |
|
|
9 |
31 |
|
|
15 |
38 |
|
|
21 |
40 |
|
|
Формула |
Описание |
Результат |
|
=F. |
F-распределение в наборах данных в ячейках A2:A6 и B2:B6. |
0,64831785 |
Регрессия как средневзвешенный эффект лечения на основе дисперсии
В книге «В основном безвредная эконометрика» Ангрист и Пишке обсуждают регрессию в контексте сопоставления. В частности, они показывают, что регрессия обеспечивает основанное на дисперсии средневзвешенное значение ковариантных конкретных различий в результатах между лечебной и контрольной группами. Сопоставление дает нам средневзвешенную разницу в результатах лечения и контроля, взвешенную эмпирическим распределением ковариант. (подробнее см. здесь). Я хотел в общих чертах обрисовать эту логику ниже.Соответствие
δATE = E [y1i | Xi, Di = 1] — E [y0i | Xi, Di = 0] = ATE
Это дает нам среднюю разницу в средних результатах для лечения и контроля (y1i, y0i ⊥ Di), т. е. в рандомизированном контролируемом эксперименте потенциальные результаты не зависят от статуса лечения
е. в рандомизированном контролируемом эксперименте потенциальные результаты не зависят от статуса лечения
Мы представляем оценку соответствия эмпирически. по:
Σ δx P (Xi, = x), где δx — это разница в средних значениях результатов между лечебной и контрольной единицами при конкретном значении X или разница в результатах для конкретной комбинации ковариат (y1, y0 ⊥ Di | xi) i.е. условная независимость предполагается — следовательно, идентификация достигается путем выбора структуры наблюдаемых.
Средние разности δx взвешиваются распределением ковариат через член P (Xi, = x).
Регрессия
Мы можем представить параметр регрессии, используя базовую формулу, которой обучают большинство студентов:
Одинарная переменная: β = cov (y, D) / v (D)
Многопараметрическая: βk = cov (y, D) *) / v (D *)
, где D * = остаток от регрессии D по всем другим ковариатам, а E (X’X) -1E (X’y) — вектор с k-м элементом cov (y, x * ) / v (x *), где x * — остаток от регрессии этого конкретного «x» по всем другим ковариатам. 2 | Xi]}.
2 | Xi]}.
Хотя алгебра громоздка и требует много обозначений, мы можем видеть, что способ, которым большинство людей знакомы с просмотром оценки регрессии cov (y, D *) / v (D *), эквивалентен термину (с использованием ожиданий) E [ σ2D (Xi) δx] / E [σ2D (Xi)], и мы можем видеть, что этот член содержит произведение условной дисперсии D и нашей ковариантной специфической разницы в обработке и контроле δx.
Следовательно, регрессия дает нам средневзвешенный эффект лечения на основе дисперсии, тогда как сопоставление обеспечивает средневзвешенный эффект лечения.
Итак, что это означает на практике? Ангрист и Писк объясняют, что регрессия придает больший вес ковариантным клеткам, где условная дисперсия статуса лечения является наибольшей или где имеется равное количество обработанных и контрольных единиц. Они заявляют, что различия мало что значат, когда вариация δx минимальна между ковариатными комбинациями.
В своем посте «Кардинальный грех сопоставления» Крис Блаттман формулирует это так:
«Для причинного вывода самое важное различие между регрессией. и сопоставление — это то, что наиболее важно для наблюдений.Регресс пытается
минимизировать квадратичные ошибки, поэтому наблюдения на полях получают много
масса. При сопоставлении упор делается на наблюдения, которые имеют схожие
X, и поэтому наблюдения на полях могут вообще не иметь веса … Сопоставление может иметь смысл, если в ваших данных есть наблюдения, которые
не имеют дела по сравнению друг с другом, и таким образом производят
Лучшая оценка »
и сопоставление — это то, что наиболее важно для наблюдений.Регресс пытается
минимизировать квадратичные ошибки, поэтому наблюдения на полях получают много
масса. При сопоставлении упор делается на наблюдения, которые имеют схожие
X, и поэтому наблюдения на полях могут вообще не иметь веса … Сопоставление может иметь смысл, если в ваших данных есть наблюдения, которые
не имеют дела по сравнению друг с другом, и таким образом производят
Лучшая оценка »
Ниже приведен очень простой надуманный пример. Предположим, наши данные выглядят так:
E [Y i | d i = 1] — E [ Y i | d i = 0] = E [Y 1i -Y 0i ] + {E [Y 0i | d i = 1] — E [Y 0i | d i = 0]}
Однако, если мы оценим различия на основе схемы точного сопоставления, мы получим гораздо меньшую оценку. 67. Если мы запустим регрессию, используя все данные, мы получим 0,75. Если мы считаем, что 3,78 смещено вверх, то и сопоставление, и регрессия значительно уменьшили его, и в зависимости от приложения разница между 0,67 и 0,75 может не иметь большого значения. Конечно, если мы запустим регрессию, включая только согласованные переменные, мы получим точно такие же результаты. (см. код R ниже). Это не сильно отличается от метода обрезки на основе оценок склонности, предложенного в Angrist и Pischke.
67. Если мы запустим регрессию, используя все данные, мы получим 0,75. Если мы считаем, что 3,78 смещено вверх, то и сопоставление, и регрессия значительно уменьшили его, и в зависимости от приложения разница между 0,67 и 0,75 может не иметь большого значения. Конечно, если мы запустим регрессию, включая только согласованные переменные, мы получим точно такие же результаты. (см. код R ниже). Это не сильно отличается от метода обрезки на основе оценок склонности, предложенного в Angrist и Pischke.
Оба метода основаны на одних и тех же предположениях для идентификации, поэтому никто не может оспаривать превосходство одного метода над другим в отношении выявления причинных эффектов.
Сопоставление имеет то преимущество, что оно непараметрическое, что устраняет проблемы с функциональной формой. Тем не менее, существует множество факторов, которые необходимо учитывать при сопоставлении (например, 1: 1, 1: много, оптимальная ширина измерителя, компромисс между дисперсией / смещением, выбор ядра и т. Д.). Хотя все эти возможности могут привести к более точным оценкам, мне интересно, не приводят ли они иногда к саду разветвляющихся тропинок.
Д.). Хотя все эти возможности могут привести к более точным оценкам, мне интересно, не приводят ли они иногда к саду разветвляющихся тропинок.
См. Также:
Более подробный набор заметок, относящихся к этой публикации, см .:
Мэтт Богард. «Регрессия и сопоставление (3) .pdf» Эконометрика, статистика, моделирование финансовых данных (2017). Доступно по адресу: http://works.bepress.com/matt_bogard/37/
Использование R MatchIt для согласования оценок склонности
Код R:
# генерировать демонстрационные данные
x <- c (4,5,6,7,8,9,10,11,12,1,2,3,
d <- c (1,1,1,1,1,1,1,1,1,0,0,0,0,0,
y <- c (6,7,8,8,9,11,12,13,14,2,3,4,
summary (lm (y ~ x + d)) # контроль регрессии для x
некоторые общие результаты малой выборки о смещении и существовании моментов
Автор
Abstract
Мы представляем несколько результатов для небольшой выборки по распределению остатков и оценок дисперсии возмущений в эконометрических моделях. Мы рассматриваем общие линейные и нелинейные модели со стохастическими регрессорами и возможными нелинейными ограничениями на параметры. Сюда входят модели авторегрессии и структурные уравнения. Для моделей, оцениваемых линейным или нелинейным методом наименьших квадратов, мы даем простые границы для ожидаемого значения (или смещения) стандартных оценок дисперсии возмущения. Границы действительны для любой корреляционной структуры между возмущениями. Мы даем простые условия, обеспечивающие существование конечных моментов для невязок и оценок дисперсии с точностью до любого заданного порядка.Когда возмущения имеют нормальное распределение, мы обнаруживаем, что все моменты существуют, и показываем, что сумма квадратов остатков ограничена случайной величиной хи-квадрат или линейной комбинацией независимых переменных хи-квадрат. Мы также представляем аналогичные результаты для ряда альтернативных методов оценки: обобщенный метод наименьших квадратов (когда коэффициенты регрессии и параметры матрицы ковариации оцениваются совместно), оценка Lp (включая минимальные абсолютные отклонения) и максимальное правдоподобие.
Мы рассматриваем общие линейные и нелинейные модели со стохастическими регрессорами и возможными нелинейными ограничениями на параметры. Сюда входят модели авторегрессии и структурные уравнения. Для моделей, оцениваемых линейным или нелинейным методом наименьших квадратов, мы даем простые границы для ожидаемого значения (или смещения) стандартных оценок дисперсии возмущения. Границы действительны для любой корреляционной структуры между возмущениями. Мы даем простые условия, обеспечивающие существование конечных моментов для невязок и оценок дисперсии с точностью до любого заданного порядка.Когда возмущения имеют нормальное распределение, мы обнаруживаем, что все моменты существуют, и показываем, что сумма квадратов остатков ограничена случайной величиной хи-квадрат или линейной комбинацией независимых переменных хи-квадрат. Мы также представляем аналогичные результаты для ряда альтернативных методов оценки: обобщенный метод наименьших квадратов (когда коэффициенты регрессии и параметры матрицы ковариации оцениваются совместно), оценка Lp (включая минимальные абсолютные отклонения) и максимальное правдоподобие.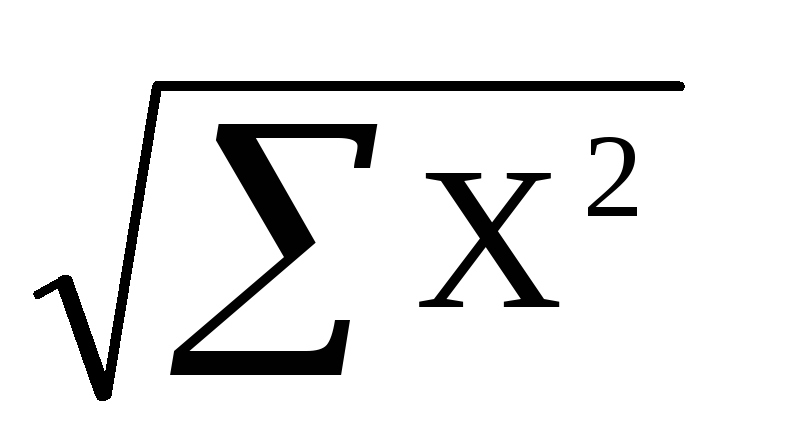 в последнем случае приводится информационное неравенство, связанное с оценкой энтропии распределения. Все доказательства просты.
в последнем случае приводится информационное неравенство, связанное с оценкой энтропии распределения. Все доказательства просты.
(Этот реферат был заимствован из другой версии этого документа.)
Предлагаемое цитирование
Загрузить полный текст от издателя
Насколько нам известно, этот элемент недоступен для скачать . Чтобы узнать, доступен ли он, есть три варианты:1. Проверьте ниже, доступна ли в Интернете другая версия этого элемента.
2. Зайдите на страницу провайдера . действительно ли он доступен.
3. Выполните поиск объекта с таким же названием, который был бы доступный.

Другие версии данной позиции:
Исправления
Все материалы на этом сайте предоставлены соответствующими издателями и авторами. Вы можете помочь исправить ошибки и упущения. При запросе исправления укажите номер этого элемента: RePEc: cor: louvco: 1985047 . См. Общую информацию о том, как исправить материал в RePEc.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, заголовка, аннотации, библиографической информации или информации для загрузки, обращайтесь:.Общие контактные данные провайдера: https://edirc.repec.org/data/coreebe.html .
Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь. Это позволяет привязать ваш профиль к этому элементу. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены.
У нас нет библиографических ссылок на этот товар. Вы можете помочь добавить их, используя эту форму .
Вы можете помочь добавить их, используя эту форму .
Если вам известно об отсутствующих элементах, цитирующих этот элемент, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылочного элемента.Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле RePEc Author Service, поскольку там могут быть некоторые цитаты, ожидающие подтверждения.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, аннотации, библиографической информации или информации для загрузки, обращайтесь: Ален ГИЛЛИС (адрес электронной почты указан ниже). Общие контактные данные провайдера: https://edirc.repec.org/data/coreebe.html .
Обратите внимание, что исправления могут отфильтроваться через пару недель. различные сервисы RePEc.
2.4 — Какова общая дисперсия ошибок?
График нашей совокупности данных показывает, что результаты вступительных испытаний в колледж для каждой субпопуляции имеют одинаковую дисперсию. Обозначим значение этой общей дисперсии как σ 2 .
Обозначим значение этой общей дисперсии как σ 2 .
То есть σ 2 количественно определяет, насколько ответы ( y ) изменяются вокруг (неизвестной) средней линии регрессии популяции \ (\ mu_Y = E (Y) = \ beta_0 + \ beta_1x \).
Почему мы должны заботиться о σ 2 ? Ответ на этот вопрос относится к наиболее частому использованию предполагаемой линии регрессии, а именно к предсказанию некоторого будущего ответа.
Предположим, у вас есть термометры двух марок (A и B), и каждая из них предлагает термометр Цельсия и термометр Фаренгейта. Вы измеряете температуру в градусах Цельсия и Фаренгейта с помощью термометров каждой марки в десять разных дней. На основе полученных данных вы получите две оценочные линии регрессии — одну для бренда A и одну для бренда B.Вы планируете использовать оценочные линии регрессии для прогнозирования температуры в градусах Фаренгейта на основе температуры в градусах Цельсия.
Будет ли эта марка термометров (A) давать более точные прогнозы на будущее…?
… или этот (B)?
Как показывают два графика, реакции по Фаренгейту для термометра марки B не отклоняются так далеко от расчетного уравнения регрессии, как для термометра марки A. Если мы используем оценочную линию бренда B для предсказания температуры по Фаренгейту, наш прогноз никогда не должен сильно отличаться от фактической наблюдаемой температуры по Фаренгейту.С другой стороны, прогнозы температуры по Фаренгейту с использованием термометра марки A могут довольно сильно отклоняться от фактической наблюдаемой температуры по Фаренгейту. Следовательно, термометр марки B должен давать более точные прогнозы на будущее, чем термометр марки A.
Следовательно, чтобы получить представление о том, насколько точными будут прогнозы на будущее, нам нужно знать, насколько ответы ( y ) изменяются вокруг (неизвестной) средней линии регрессии популяции \ (\ mu_Y = E (Y) = \ beta_0 + \ beta_1x \). Как указывалось ранее, σ 2 количественно определяет эту дисперсию в ответах. Узнаем ли мы когда-нибудь это значение σ 2 ? Нет! Поскольку σ 2 является параметром популяции, мы редко узнаем его истинное значение. Лучшее, что мы можем сделать — это оценить!
Как указывалось ранее, σ 2 количественно определяет эту дисперсию в ответах. Узнаем ли мы когда-нибудь это значение σ 2 ? Нет! Поскольку σ 2 является параметром популяции, мы редко узнаем его истинное значение. Лучшее, что мы можем сделать — это оценить!
Чтобы понять формулу для оценки σ 2 в настройке простой линейной регрессии, полезно вспомнить формулу для оценки дисперсии ответов, σ 2 , когда есть только одна популяция.2} {n-1} \]
оценивает σ 2 , дисперсию одной популяции. Оценка действительно близка к средней. Числитель суммирует, насколько далеко каждый ответ y i от оценочного среднего \ (\ bar {y} \) в квадратах, а знаменатель делит сумму на n -1, а не на n , как вы ожидаете в среднем. На самом деле нам бы хотелось, чтобы числитель суммировал в квадратах, насколько далеко каждый ответ y i от неизвестного среднего значения генеральной совокупности μ . Но нам неизвестно среднее значение численности населения μ , поэтому мы оцениваем его с помощью \ (\ bar {y} \). Это «стоит нам одной степени свободы». То есть мы должны разделить на n -1, а не на n , потому что мы оценили неизвестное среднее значение генеральной совокупности μ .
Но нам неизвестно среднее значение численности населения μ , поэтому мы оцениваем его с помощью \ (\ bar {y} \). Это «стоит нам одной степени свободы». То есть мы должны разделить на n -1, а не на n , потому что мы оценили неизвестное среднее значение генеральной совокупности μ .
Теперь давайте расширим это мышление, чтобы получить оценку дисперсии генеральной совокупности σ 2 в настройке простой линейной регрессии. Напомним, что мы предполагаем, что σ 2 одинаково для каждой из субпопуляций.В нашем примере с результатами вступительных экзаменов в колледж и средними показателями успеваемости, сколько у нас подгрупп?
На этом графике изображены четыре субпопуляции. В общем, существует столько субпопуляций, сколько существует различных значений x в популяции. Каждая субпопуляция имеет собственное среднее значение μ Y , которое зависит от x через \ (\ mu_Y = E (Y) = \ beta_0 + \ beta_1x \). 2} {n-2} \]
2} {n-2} \]
оценивает σ 2 , общую дисперсию многих субпопуляций.
Чем формула среднеквадратичной ошибки отличается от формулы дисперсии выборки? Сходства разительнее, чем различия. Числитель снова суммирует в квадратах, насколько далеко каждый ответ , и от своего расчетного среднего. Однако в настройке регрессии оценочное среднее значение равно \ (\ hat {y} _i \). И знаменатель делит сумму на n -2, а не на n -1, потому что, используя \ (\ hat {y} _i \) для оценки μ Y , мы эффективно оцениваем два параметра — пересечение популяции β 0 и наклон населения β 1 .То есть мы теряем две степени свободы.
На практике мы позволим статистическим программам, таким как R или Minitab, вычислить среднеквадратичную ошибку ( MSE ) за нас. Для выборки из 12 средних школьных баллов и результатов тестов в колледже
\ [MSE = \ frac {8. 678} {12-2} = 0.8678. \]
678} {12-2} = 0.8678. \]
Помимо отображения MSE , программное обеспечение обычно также отображает \ (S = \ sqrt {MSE} \), который оценивает σ и известен как стандартная ошибка регрессии или стандартная остаточная ошибка .Для выборки из 12 средних школьных оценок и результатов тестов колледжа \ (S = \ sqrt {0.8678} = 0.9315 \).
случайных переменных: ожидание и дисперсия
Вероятность
Анализ данных, том 1
Случайные переменные: ожидание и дисперсия$ \ def \ P {\ mathsf {\ sf P}} \ def \ E {\ mathsf {\ sf E}} \ def \ Var {\ mathsf {\ sf Var}} \ def \ Cov {\ mathsf {\ sf Cov}} \ def \ std {\ mathsf {\ sf std}} \ def \ Cor {\ mathsf {\ sf Cor}} \ def \ R {\ mathbb {R}} \ def \ c {\, | \,} \ def \ bb {\ boldsymbol} \ def \ diag {\ mathsf {\ sf diag}} $
2.{\ infty} x \, f_X (x) \, dx & X \ text {- непрерывная RV} \ end {case}, \ end {выровнять *} при условии, что сумма или интеграл существует.

Пример 2.3.1. Ожидание RV, выражающее результат правильного броска кубика является \ [\ E (X) = 1 p_X (1) + \ cdots 6 p_X (6) = \ frac {1} {6} (1+ \ cdots + 6) = 21/6 = 3,5. \] Интуитивно математическое ожидание дает долгосрочное среднее значение множества бросков костей. \ begin {align *} \ text {average} = & \ frac {1 \ cdot (\ text {# — из раз мы получим 1}) + \ cdots + 6 \ cdot (\ text {# — of-times-we-get 6})} {k} \\ & = 1 \ cdot \, \ text {частота-получения 1} + \ cdots + 6 \ cdot \, \ text {частота-получения 6} \\ & \ to \ E (X), \ end {выровнять *} как $ n \ to \ infty $, предполагая, что частота получения $ i $ в долгосрочной перспективе сходится к $ p (X = i) $.{\ infty} g (x) f_X (x) dx & X \ text {- непрерывная RV} \ end {cases}. \ label {eq: RV: expFun} \ end {align}
Доказательство. Первое равенство следует из определения, а второе равенство следует из того, что значение $ g (x) $ возникает, когда встречается $ x $, что происходит с вероятностью $ p_X (x) $ в дискретном случае или плотностью $ f_X (x) $ в непрерывный случай.
Предложение 2.3.2. Для любых констант $ a, b \ in \ mathbb {R} $ математическое ожидание $ Y = aX + b $ равно \ [\ E (aX + b) = a \ E (X) + b.\]
Доказательство. Используя предыдущее предложение, имеем \ begin {align *} \ E (aX + b) & = \ sum_x (ax + b) p_X (x) = a \ sum_x x p_X (x) + b \ sum_x p_X (x) \\ & = a \ E (x) + b \ cdot 1 \ end {выровнять *} для дискретного автофургона. В случае непрерывной ПС заменим суммирование интегралом.
В предложении выше конкретно говорится, что \ begin {align *} \ E (X + b) & = \ E (X) + b, \ text {and} \\ \ E (aX) & = a \ E (X). \ end {align *}
Дисперсия измеряет степень изменчивости RV $ X $ вокруг $ \ E (X) $.2). \] Стандартное отклонение RV $ X $ составляет $ \ std (X) = \ sqrt {\ Var (X)} $.
Поскольку дисперсия измеряет квадратичное отклонение от математического ожидания, RV с узкой pmf или pdf должна показывать низкую дисперсию, а RV с широкой pmf или pdf должна показывать большую дисперсию. 2} {2 (ba)} = \ frac {(ba) (b + a)} {2 (ba)} = \ frac {а + Ь} {2} \]
— средняя точка отрезка $ (a, b) $.2).
\ end {align} \]
2} {2 (ba)} = \ frac {(ba) (b + a)} {2 (ba)} = \ frac {а + Ь} {2} \]
— средняя точка отрезка $ (a, b) $.2).
\ end {align} \]
Поскольку \ (X \) и \ (Y \) считаются зависимыми, неквадратные члены больше не обязательно компенсируют друг друга. Вместо этого мы можем переставить следующим образом:
\ [\ begin {align} var (X + Y) & = var (X) + var (Y) + \ mathbb {E} [2XY] — 2 \ mathbb {E} [X] \ mathbb {E} [Y] \\ & = var (X) + var (Y) + 2 (\ mathbb {E} [XY] — \ mathbb {E} [X] \ mathbb {E} [Y]), \ end {align} \]
и обратите внимание, что \ (\ mathbb {E} [AB] — \ mathbb {E} [A] \ mathbb {E} [B] = Cov (A, B) \):
\ [\ begin {уравнение} … = var (X) + var (Y) + 2Cov (A, B) \; \; \; \квадратный \ end {Equation} \]
Следует отметить еще два момента. Во-первых, независимая версия доказательства — это просто частный случай зависимой версии доказательства. Когда \ (X \) и \ (Y \) независимы, ковариация между двумя случайными величинами равна нулю, и, следовательно, дисперсия суммы просто равна сумме дисперсий. Эконометрика Чем больше член дисперсии, тем больше неопределенность в статистической модели, а у больше дисперсия и ковариация наименьших квадратов оценки Чем больше сумма квадратов, тем меньше дисперсия оценок наименьших квадратов и тем точнее мы можем оценить неизвестные параметры Чем больше размер выборки N, тем меньше дисперсия и ковариация наименьших квадратов оценщиков; лучше иметь больше выборочных данных, чем меньше. Homoscedasticiteit: Voor elke X находится в различных вариантах Y gelijk, gelijkheid van. В статистике последовательность или вектор случайных величин гомоскедастичны / гомоскедичны dæst k /, если все случайные величины в последовательности или векторе имеют одинаковую конечную дисперсию. Ɪ В статистике a набор случайных величин является гетероскедастическим (или гетероскедастическим; из древнегреческий гетеро «разный» и скедасис «дисперсия»), если есть субпопуляции, которые имеют изменчивость, отличную от других. Теорема Гаусса-Маркова В статистике теорема Гаусса-Маркова, названная в честь Карла Фридриха Гаусса и Андрея Маркова, утверждает, что в модели линейной регрессии, в которой ошибки имеют нулевое математическое ожидание, некоррелированы и равны отклонений, лучшая линейная несмещенная оценка (СИНИЙ) коэффициентов дается с помощью обычной оценки наименьших квадратов (МНК). Мощность теста — это вероятность того, что тест правильно отклонит нуль, если альтернатива верна. E (ui | Xi) = 0 означает, что условное распределение ошибки с учетом объясняющей переменной имеет нулевое среднее Экспериментальные данные получены из экспериментов, предназначенных для оценки лечения или политики или для исследования причинно-следственных связей. Поперечные данные: данные по разным объектам: работникам, потребителям фирм и т. Д. За один период времени. Как данные об успеваемости в школьных округах Калифорнии. Время для одного объекта, собранные за несколько периодов времени. Дискретные случайные величины: 0,1,2,3. Непрерывные случайные величины принимают континуум из возможных результатов. Случайная величина Бернулли бинарна. Закон больших чисел гласит, что при общих условиях Y (streep) будет близко к muy с очень высокой вероятностью , когда n велико. Центральная предельная теорема гласит, что при общих условиях распределение Y (streep) хорошо аппроксимируется нормальным распределением, когда n велико. Простая случайная выборка дает n случайных наблюдений Y1, .. Yn, которые являются i.i.d. Если i.i.d. тогда Y (streep) имеет среднее значение muy и дисперсию sigma van y / n, а CLT говорит, что имеет нормальное распределение N (0,1), когда n велико, а LLN говорит, что Y (streep) сходится по вероятности муй. Стандартная ошибка регрессии — это оценка стандартного отклонения регрессии ошибка. Три допущения: (1) ошибки регрессии ui имеют нулевое среднее значение в зависимости от регрессоров Xi (2) выборочные наблюдения i.я бы. случайные выборки из совокупности (3) большие выбросы маловероятно Модели линейной регрессии находят несколько применений в реальной жизни. В эконометрике для оценки параметров модели линейной регрессии широко используется метод обыкновенных наименьших квадратов (OLS). A1. Модель линейной регрессии «линейна по параметрам». A2. Есть случайная выборка наблюдений. A3. Условное среднее значение должно быть равно нулю. A4. Нет мультиколлинеарности (или идеальной коллинеарности). А5. Сферические ошибки: гомоскедастичность и отсутствие автокорреляции A6: Необязательное предположение: Ошибочные термины должны распределяться нормально. Эти предположения чрезвычайно важны, поскольку нарушение любого из этих предположений сделало бы оценки OLS ненадежными и неверными.В частности, нарушение приведет к неправильным знакам оценок OLS, или дисперсия оценок OLS будет ненадежной, что приведет к слишком широким или слишком узким доверительным интервалам. При этом необходимо исследовать, почему оценки OLS и их допущения привлекают так много внимания. В этой статье обсуждаются свойства модели OLS. Сначала излагается знаменитая теорема Гаусса-Маркова. Теорема Гаусса-Маркова названа в честь Карла Фридриха Гаусса и Андрея Маркова. Пусть модель регрессии будет: Y = {\ beta} _ {o} + {\ beta} _ {i} {X} _ {i} + \ varepsilon Пусть {\ beta} _ {o} и {\ beta} _ {i} будут оценками OLS для {\ beta} _ {o} и {\ beta} _ {o} Согласно теореме Гаусса-Маркова, при предположениях от A 1 до A 5 модели линейной регрессии, оценки МНК {\ beta} _ {o} и {\ beta} _ {i} являются лучшими линейными объективными оценщиками (СИНИЙ) для {\ beta} _ {o} и {\ beta} _ {i}. Другими словами, оценки МНК {\ beta} _ {o} и {\ beta} _ {i} имеют минимальную дисперсию всех линейных и несмещенных оценок {\ beta} _ {o} и { \ beta} _ {i}. СИНИЙ суммирует свойства регрессии МНК. Это свойство больше связано с оценкой, чем с исходным уравнением, которое оценивается. В предположении A 1 основное внимание уделялось тому, чтобы линейная регрессия была «линейной по параметрам». Однако свойство linear оценки OLS означает, что OLS принадлежит к тому классу оценок, которые линейны по Y, зависимой переменной.Обратите внимание, что оценки МНК линейны только по отношению к зависимой переменной и не обязательно по отношению к независимым переменным. Свойство linear оценщиков OLS зависит не только от предположения A 1 , но и от всех предположений от A 1 до A 5 . Если вы посмотрите на уравнение регрессии, вы найдете член ошибки, связанный с оцениваемым уравнением регрессии. Это делает зависимую переменную также случайной.Если оценщик использует зависимую переменную, то этот оценщик также будет случайным числом. Поэтому, прежде чем описывать, что такое непредвзятость, важно упомянуть, что свойство несмещенности является свойством оценщика, а не какой-либо выборки. Беспристрастность — одно из самых желанных свойств любого оценщика. В идеале оценщик должен быть объективным оценщиком истинных значений параметра / совокупности. Рассмотрим простой пример: предположим, что существует популяция размером 1000, и вы берете 50 выборок из этой совокупности, чтобы оценить параметры совокупности.Каждый раз, когда вы берете образец, он будет иметь разные наборы из 50 наблюдений, и, следовательно, вы будете оценивать разные значения {\ beta} _ {o} и {\ beta} _ {i}. Свойство непредвзятости метода OLS говорит о том, что если вы повторно выбираете 50 выборок, то после нескольких повторных попыток вы обнаружите, что среднее значение всех {\ beta} _ {o} и {\ beta} _ {i} из выборки будут равны фактическим (или совокупным) значениям {\ beta} _ {o} и {\ beta} _ {i}. Математически, E (b o ) = β o E (b i ) = β i Здесь «E» — оператор ожидания. С точки зрения непрофессионала, если вы возьмете несколько выборок, продолжите записывать значения оценок, а затем возьмете среднее значение, вы очень близко подойдете к правильному значению генеральной совокупности. Если ваша оценка смещена, то среднее не будет равняться истинному значению параметра в генеральной совокупности. Свойство объективности OLS в эконометрике является основным минимальным требованием, которому должен удовлетворять любой оценщик. Однако этого недостаточно по той причине, что в большинстве случаев в реальных приложениях у вас не будет роскоши брать повторяющиеся образцы.Фактически, в большинстве случаев будет доступен только один образец. Во-первых, давайте посмотрим, что такое эффективные оценщики. Теперь, говоря о OLS, оценки OLS имеют наименьшую дисперсию среди всех линейных несмещенных оценок .Таким образом, это свойство регрессии OLS менее строгое, чем свойство эффективности. Просто обозначая математически, Пусть b o будет оценкой OLS, которая является линейной и несмещенной. Пусть {b} _ {o} \ ast будет любой другой оценкой {\ beta} _ {o} , , которая также является линейной и несмещенной. Затем Var \ left ({b} _ {o} \ right) Пусть {b} _ {i} будет оценкой OLS, которая является линейной и несмещенной.Пусть {b} _ {i} \ ast будет любой другой оценкой {\ beta} _ {i} , , которая также является линейной и несмещенной. Затем Var \ left ({b} _ {i} \ right) Три вышеуказанных свойства модели OLS делают оценки OLS СИНИМИ, как указано в теореме Гаусса-Маркова. Стоит уделить время некоторым другим оценочным свойствам OLS в эконометрике. Это свойство OLS говорит о том, что по мере увеличения размера выборки смещенность оценок OLS исчезает. Оценщик считается непротиворечивым, если его значение приближается к фактическому истинному значению параметра (совокупности) по мере увеличения размера выборки.Оценщик непротиворечив, если он удовлетворяет двум условиям: а. Асимптотически несмещен г. Его дисперсия сходится к 0 по мере увеличения размера выборки. Оба эти утверждения верны для оценок OLS и, следовательно, они являются согласованными оценками. Чтобы оценщик был полезным, согласованность — минимальное базовое требование. Поскольку таких оценок может быть несколько, учитывается и асимптотическая эффективность. Асимптотическая эффективность — достаточное условие, делающее МНК-оценки лучшими. OLS из-за таких желательных свойств, описанных выше, широко используются и находят несколько применений в реальной жизни. Пример: Рассмотрим банк, который хочет спрогнозировать подверженность клиента риску дефолта. регрессий OLS образуют строительные блоки эконометрики. Любой урок эконометрики начинается с предположения о регрессии OLS. Это один из любимых вопросов на собеседовании при приеме на работу и поступлении в университеты.На основе строительных блоков OLS и ослабления допущений появилось несколько различных моделей, таких как GLM (обобщенные линейные модели), общие линейные модели, гетероскедастические модели, модели многоуровневой регрессии и т. Д. Исследования в области экономики и финансов во многом определяются эконометрикой. В заключение отметим, что линейная регрессия важна и широко используется, а метод оценки МНК является наиболее распространенным. В этой статье обсуждались свойства оценок OLS, поскольку это наиболее широко используемый метод оценивания. Оценщики МНК имеют СИНИЙ цвет (т.е.они линейны, несмещены и имеют наименьшую дисперсию среди всех линейных и несмещенных оценщиков).При этом не следует забывать, что теорема Гаусса-Маркова (т.е. оценки модели OLS — СИНИЙ) выполняется только в том случае, если выполняются предположения OLS. Каждое предположение, которое делается при изучении OLS, добавляет ограничений к модели, но в то же время позволяет делать более сильные утверждения относительно OLS. n_ {1 \ leq i
n_ {1 \ leq i Econometrics summary extra — Econometrics Чем больше член дисперсии, тем больше



Свойства оценщиков OLS: полное руководство по эконометрике
Введение в свойства оценщиков OLS  Для достоверности оценок OLS при запуске моделей линейной регрессии делаются допущения.
Для достоверности оценок OLS при запуске моделей линейной регрессии делаются допущения. После этого дается подробное описание свойств модели OLS.В конце статьи кратко рассказывается о приложениях свойств OLS в эконометрике.
После этого дается подробное описание свойств модели OLS.В конце статьи кратко рассказывается о приложениях свойств OLS в эконометрике. Эти свойства OLS в эконометрике чрезвычайно важны, что делает оценки OLS одними из самых надежных и наиболее широко используемых оценок для неизвестных параметров. Эта теорема говорит, что следует использовать оценки МНК не только потому, что они несмещены, но также потому, что они имеют минимальную дисперсию среди класса всех линейных и несмещенных оценок.
Эти свойства OLS в эконометрике чрезвычайно важны, что делает оценки OLS одними из самых надежных и наиболее широко используемых оценок для неизвестных параметров. Эта теорема говорит, что следует использовать оценки МНК не только потому, что они несмещены, но также потому, что они имеют минимальную дисперсию среди класса всех линейных и несмещенных оценок. Свойство 1: Линейное

Свойство 2: Беспристрастность

Свойство 3: Лучшее: минимальное отклонение
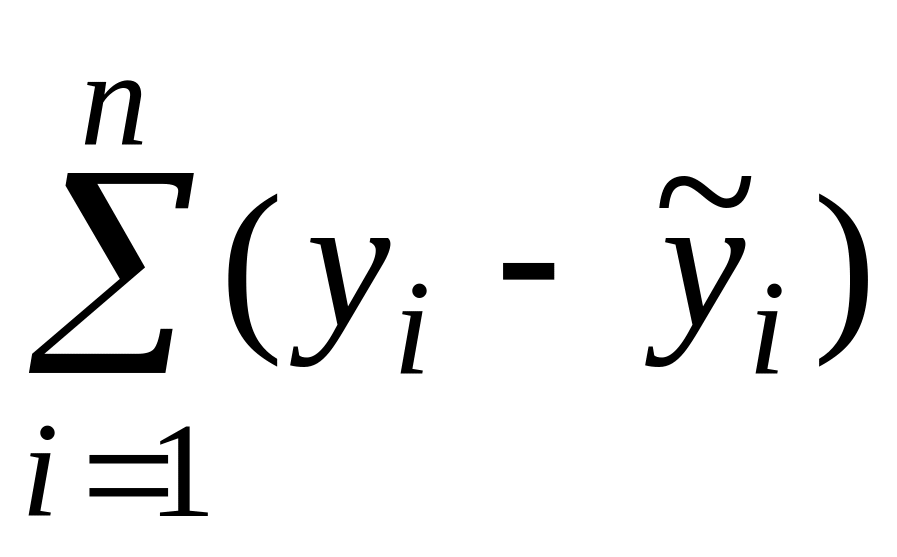 Эффективное свойство любого оценщика говорит, что оценщик представляет собой несмещенный оценщик с минимальной дисперсией . Следовательно, если вы возьмете все несмещенные оценки неизвестного параметра совокупности, оценка будет иметь наименьшую дисперсию. Оценщик с меньшей дисперсией будет иметь отдельные точки данных, близкие к среднему.В результате они с большей вероятностью дадут лучшие и точные результаты, чем другие оценщики, имеющие более высокую дисперсию. Вкратце:
Эффективное свойство любого оценщика говорит, что оценщик представляет собой несмещенный оценщик с минимальной дисперсией . Следовательно, если вы возьмете все несмещенные оценки неизвестного параметра совокупности, оценка будет иметь наименьшую дисперсию. Оценщик с меньшей дисперсией будет иметь отдельные точки данных, близкие к среднему.В результате они с большей вероятностью дадут лучшие и точные результаты, чем другие оценщики, имеющие более высокую дисперсию. Вкратце: Свойство эффективности говорит о наименьшей дисперсии среди всех несмещенных оценок, а оценки МНК имеют наименьшую дисперсию среди всех линейных и несмещенных оценок.
Свойство эффективности говорит о наименьшей дисперсии среди всех несмещенных оценок, а оценки МНК имеют наименьшую дисперсию среди всех линейных и несмещенных оценок. Свойства OLS, описанные ниже, являются асимптотическими свойствами OLS-оценок.До сих пор обсуждались свойства конечной выборки регрессии OLS. Эти свойства пытались изучить поведение оценщика МНК в предположении, что у вас может быть несколько выборок и, следовательно, несколько оценщиков одного и того же неизвестного параметра совокупности. Короче говоря, свойства заключались в том, что среднее значение этих оценок в разных выборках должно быть равно истинному параметру совокупности (несмещенность) или среднее расстояние до истинного значения параметра должно быть наименьшим (эффективным). Однако в реальной жизни у вас часто бывает только один образец.Следовательно, обсуждаются асимптотические свойства модели OLS, которая изучает, как оценки OLS ведут себя при увеличении размера выборки. Помните, что размер выборки должен быть большим.
Свойства OLS, описанные ниже, являются асимптотическими свойствами OLS-оценок.До сих пор обсуждались свойства конечной выборки регрессии OLS. Эти свойства пытались изучить поведение оценщика МНК в предположении, что у вас может быть несколько выборок и, следовательно, несколько оценщиков одного и того же неизвестного параметра совокупности. Короче говоря, свойства заключались в том, что среднее значение этих оценок в разных выборках должно быть равно истинному параметру совокупности (несмещенность) или среднее расстояние до истинного значения параметра должно быть наименьшим (эффективным). Однако в реальной жизни у вас часто бывает только один образец.Следовательно, обсуждаются асимптотические свойства модели OLS, которая изучает, как оценки OLS ведут себя при увеличении размера выборки. Помните, что размер выборки должен быть большим. Свойство 4: Асимптотическая беспристрастность
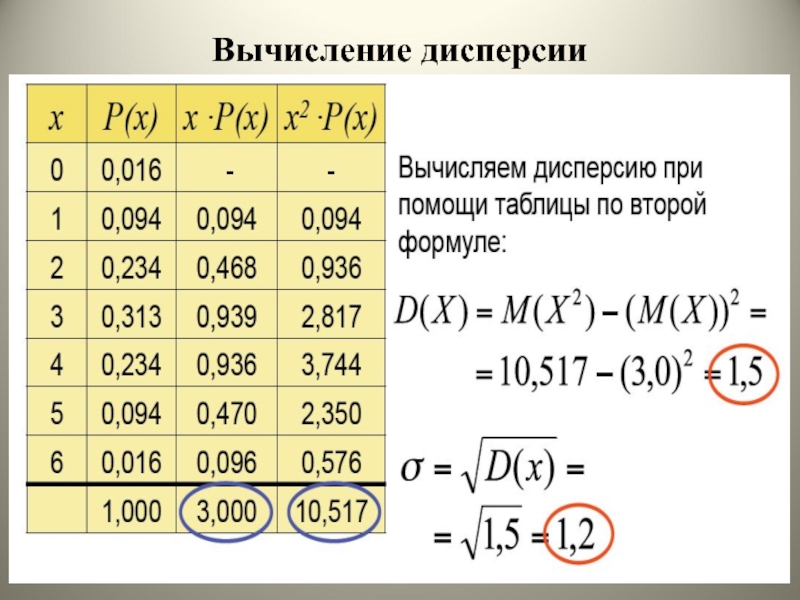
Свойство 5: Согласованность
 Банк может принять риск по умолчанию в качестве зависимой переменной и нескольких независимых переменных, таких как характеристики уровня клиента, кредитная история, тип ссуды, ипотека и т. Д.Банк может просто запустить регрессию OLS и получить оценки, чтобы увидеть, какие факторы важны при определении подверженности клиента дефолту. Оценщики OLS просты в использовании и понимании. Они также доступны в различных пакетах статистического программного обеспечения и могут широко использоваться.
Банк может принять риск по умолчанию в качестве зависимой переменной и нескольких независимых переменных, таких как характеристики уровня клиента, кредитная история, тип ссуды, ипотека и т. Д.Банк может просто запустить регрессию OLS и получить оценки, чтобы увидеть, какие факторы важны при определении подверженности клиента дефолту. Оценщики OLS просты в использовании и понимании. Они также доступны в различных пакетах статистического программного обеспечения и могут широко использоваться. OLS — это строительный блок эконометрики. Однако в реальной жизни есть проблемы, такие как обратная причинность, которые делают OLS несущественным или неуместным. Тем не менее, OLS все еще можно использовать для исследования проблем, существующих в данных поперечного сечения.Даже если метод OLS не может использоваться для регрессии, OLS используется для выявления проблем, проблем и потенциальных исправлений.
OLS — это строительный блок эконометрики. Однако в реальной жизни есть проблемы, такие как обратная причинность, которые делают OLS несущественным или неуместным. Тем не менее, OLS все еще можно использовать для исследования проблем, существующих в данных поперечного сечения.Даже если метод OLS не может использоваться для регрессии, OLS используется для выявления проблем, проблем и потенциальных исправлений.


 +βkXt-k+Et
+βkXt-k+Et
 е., чем больше выборка, тем точнее оценка
е., чем больше выборка, тем точнее оценка  29003911 18.0998018 ]]
29003911 18.0998018 ]]

 cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124
cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124

 56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
 13864361 19.84190935]
Original: [ 10. 19.9094105]
13864361 19.84190935]
Original: [ 10. 19.9094105]
 56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]
56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]

 ТЕСТ(A2:A6;B2:B6)
ТЕСТ(A2:A6;B2:B6)