Детерминация корреляция: Что такое корреляция и детерминация простыми словами? В чём их отличие?

Содержание

Линейная регрессия и корреляция (четыре) коэффициент линейной корреляции и коэффициент детерминации (вывод принципов и формул)

1. Коэффициент корреляции

Для координатных точекПрямая линия трендаЕсли вам не нужно оценивать Y по X для двух переменных, а нужно только знать, действительно ли X и Y коррелированы, и характер корреляции (положительный или отрицательный), вам следует сначала вычислить выражениеX и Y тесно связаныСтатистика его природа-коэффициент корреляции. В общем-то Указывает общий коэффициент корреляции, r представляет собой коэффициент корреляции выборки。

Предположим, двумерная совокупность, в которой и X, и Y являются случайными величинами, с N парами (X, Y). Если вы переместите координатную ось на прямоугольную координатную плоскость, отмеченную этими N (X, Y) координатными точками, переместите ось X и ось Y в с участием Выше положение каждой точки остается неизменным, а взятая координата становится (X-,Y-）。

В квадранте I (X-）>0,（Y-)> 0; в квадранте (X-）<0,（Y-）>0;

В квадранте III (X-）<0,（Y-) <0; в квадранте (X-）>0,（Y-）<0;

Когда (X, Y) обычно положительно коррелирован, в квадранте Ⅰ и Ⅲ должно быть больше точек, чем в квадранте Ⅱ и Ⅳ. Должен быть положительным

При этом, чем больше соотношение точек, попадающих в квадранты I и III, тем больше положительное значение.

Когда (X, Y) имеют отрицательную корреляцию, в квадранте II и IV больше точек, чем в квадранте I и III.Должен быть отрицательным;

При этом, чем больше соотношение точек, попадающих во II и IV квадранты, тем больше отрицательное значение;

(X, Y) не имеет корреляции в целом, поэтому точки, попадающие в Ⅰ, Ⅱ, Ⅲ и Ⅳ, распределены равномерно, а положительное и отрицательное аннулируются.=0

Приведенное выше описание,Значение можно использовать для измерения степени корреляции и характера линейной корреляции между двумя переменными. Однако степень изменения X и Y, выбранная единица измерения и размер N будут влиять наЧтобы облегчить универсальное применение, следует исключить влияние этих факторов.

Метод исключения: преобразуйте отклонение от среднего значения в соответствующую единицу стандартного отклонения, сделайте его стандартизованным отклонением, а затем разделите на N.

Коэффициент корреляции совокупности двух переменныхза:

В настоящее времяЭто не имеет ничего общего со степенью вариации, единицей измерения и размером двух переменных N. Это чистое число без единицы, и его можно использовать для сравнения корреляции и природы различных совокупностей двойных переменных. Коэффициент корреляции — это среднее произведение стандартизированных отклонений двух переменных.

Коэффициент корреляции выборки:

Приведенный выше результат может бытьРегрессионный анализ заключает:

сумма квадратов yВ регрессионном анализе он делится на две части: сумма квадратов регрессииСумма регрессии сумма квадратов. Последнее вызвано разницей в X. Если координатная точка находится ближе к линии регрессии, пара UЧем больше отношение, тем ближе линейная корреляция, которую можно определить как:

Приведенная выше формула показывает, что когда точки на диаграмме рассеяния полностью попадают на линию регрессии, Q = 0, U =，r=1;

Когда изменение y и x совершенно не связаны, U = 0, Q =，r=0;

Степень корреляции двойственных переменных определяется величиной | r |, чем ближе | r | к 1, тем ближе корреляция, и чем ближе к 0, тем больше вероятность, что она не имеет значения.

Значимость r связана со степенью свободы. Чем больше степень свободы, тем меньше влияет ошибка выборки, и r достигает значимого уровня.Чем меньше значение.

Знаменатели r и b всегда положительны, а часть числителя SP, коэффициент корреляции и коэффициент регрессии одинаковы.

2. Коэффициент детерминации (коэффициент детерминации)

Определяется как сумма квадратов, вызванных разницей в xОбщая сумма квадратовСоотношение;

Его также можно определить как сумму квадратов x, вызванных разницей yОбщая сумма квадратовСоотношение.

Разница между коэффициентом детерминации и коэффициентом корреляции:

(1) Исключить случаи r = 0 и | r | = 1,Всегда меньше | r |. Это может предотвратить преувеличенную интерпретацию степени корреляции, представленной коэффициентом корреляции.

(2) r может быть положительным или отрицательным,Он всегда положительный, а диапазон значений составляет [0,1].

В корреляционном анализе рекомендуется комбинировать эти два параметра. Положительное или отрицательное значение r указывает на характер корреляции.Размер указывает на степень корреляции.

3. Проверка гипотезы коэффициента корреляции.

（1）= 0 проверка гипотез

Проверить общий коэффициент корреляции, из которого получается коэффициент корреляции r выборки.Будь то 0, статистическое предположение:: Верный :.

Из-за ошибки выборки изЗначение r, полученное из совокупности, не обязательно равно 0. Чтобы определить, действительно ли совокупность, представленная r, линейно коррелирована, необходимо определить, что фактическое значение r исходит изОбщая вероятность. Только когда вероятность меньше 0,05, вы можете принять риск менее 5% и сделать вывод, что популяция, к которой принадлежит эта выборка, всегда линейно связана.

вВыборка из совокупности, распределение r изменяется в зависимости от размера выборки n. Когда n = 2, есть только два значения для r, -1 и 1, каждое с вероятностью 0,5; когда n = 3, распределение r имеет U-образную форму, и плотность вероятности r = 0 является наименьшей, а r стремится к1. Чем больше плотность вероятности; когда n = 4, распределение прямоугольное, а r имеет ту же плотность вероятности в диапазоне [-1,1]; только когда nРаспределение в положении «5 часов» постепенно принимает форму колокола. Поскольку диапазон значений r составляет только [-1,1], сам r не подчиняется известному теоретическому распределению. r ошибка выборки:

Для одних и тех же данных значимость линейной регрессии и значимость линейной корреляции должны быть эквивалентны.Это не совпадение, а неизбежный результат. Таким образом, при практическом применении значимость регрессии проверена, и нет необходимости проверять значимость, и наоборот.

Критическое значение r:

（2）= Проверка гипотезы C

Чтобы проверить, действительно ли фактический коэффициент корреляции r существенно отличается от заданного или теоретического коэффициента корреляции C, статистическая гипотеза выглядит так:: Верный :

, Выборочное распределение r имеет большую асимметрию и изменяется в зависимости от n иЗначение отличается, преобразуйте r в z:

（3） =Проверка гипотез

Проверить коэффициент корреляции двух выборок с участием Общий коэффициент корреляции от каждого с участием Если они равны, статистические допущения таковы:: = Верный :

Поскольку r преобразуется в z до того, как оно приближается к нормальному распределению, требуется преобразование z.

Стандартная ошибка разницы между двумя значениями z составляет:

Если нулевая гипотеза принята, с участием Объедините в один r, чтобы представить актуальную ситуацию для всех данных.

Метод слияния состоит в том, чтобы привести сумму квадратов и произведений двух выборок в. Комбинированное значение r составляет:

Это означает, что два образца имеют общий коэффициент корреляции r.

Линейный коэффициент корреляции Пирсона — statanaliz.info

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r², который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r² = 0,01 или 1%, при r = 0,5 r² = 0,25 или 25%.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;
N^-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Как посчитать коэффициент корреляции в Excel

Корреляционный анализ в Excel лучше начинать с визуализации.

На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.

Расчет доверительного интервала для коэффициента корреляции в Excel

В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:

— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.

Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

Стандартная ошибка z легко подсчитывается с помощью формулы.

Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.

Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.

Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.

Несколько важных замечаний

1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).

2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.

3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.

В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.

↓ Скачать файл с примером ↓

Поделиться в социальных сетях:

Функция КВПИРСОН

В этой статье описаны синтаксис формулы и использование RSQ в Microsoft Excel.

Описание

Возвращает квадрат коэффициента корреляции Пирсона для точек данных в аргументах «известные_значения_y» и «известные_значения_x».

Дополнительные сведения см. в статье Функция PEARSON. Значение квадрата R показывает, насколько дисперсии y связана с дисперсией x.

Синтаксис

КВПИРСОН(известные_значения_y;звестные_значения_x)

Аргументы функции КВПИРСОН описаны ниже.

Известные_значения_y Обязательный. Массив или диапазон точек данных.
Известные_значения_x Обязательный. Массив или диапазон точек данных.

Замечания

Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, приводят к возникновению ошибки.
Если аргументы известные_значения_y и известные_значения_x пусты или указанное в них количество число точек данных не совпадает, функция КВПИРСОН возвращает значение ошибки #Н/Д.
Если known_y и known_x содержат только 1 точку данных, RSQ возвращает #DIV/0! значение ошибки #ЗНАЧ!.
Коэффициент корреляции Пирсона (r) вычисляется с помощью следующего уравнения:

где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Функция КВПИРСОН возвращает значение r2, являющееся квадратом коэффициента корреляции.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Известные значения y	Известные значения x
2	6
3	5
9	11
1	7
8	5
7	4
5	4
Формула	Описание	Результат
=КВПИРСОН(A3:A9; B3:B9)	Квадрат значения корреляции Пирсона между точками данных в диапазоне A3:A9 и B3:B9.	0,05795

Python, корреляция и регрессия: часть 2 / Хабр

Предыдущий пост см. здесь.

Регрессия

Хотя, возможно, и полезно знать, что две переменные коррелируют, мы не можем использовать лишь одну эту информацию для предсказания веса олимпийских пловцов при наличии данных об их росте или наоборот. При установлении корреляции мы измерили силу и знак связи, но не наклон, т.е. угловой коэффициент. Для генерирования предсказания необходимо знать ожидаемый темп изменения одной переменной при заданном единичном изменении в другой.

Мы хотели бы вывести уравнение, связывающее конкретную величину одной переменной, так называемой независимой переменной, с ожидаемым значением другой, зависимой переменной. Например, если наше линейное уравнение предсказывает вес при заданном росте, то рост является нашей независимой переменной, а вес — зависимой.

^{Описываемые этими уравнениями линии называются}^{линиями регрессии}^{. Этот Термин был введен британским эрудитом 19-ого века сэром Фрэнсисом Гэлтоном. Он и его студент Карл Пирсон, который вывел коэффициент корреляции, в 19-ом веке разработали большое количество методов, применяемых для изучения линейных связей, которые коллективно стали известны как методы регрессионного анализа.}

Вспомним, что из корреляции не следует причинная обусловленность, причем термины «зависимый» и «независимый» не означают никакой неявной причинной обусловленности. Они представляют собой всего лишь имена для входных и выходных математических значений. Классическим примером является крайне положительная корреляция между числом отправленных на тушение пожара пожарных машин и нанесенным пожаром ущербом. Безусловно, отправка пожарных машин на тушение пожара сама по себе не наносит ущерб. Никто не будет советовать сократить число машин, отправляемых на тушение пожара, как способ уменьшения ущерба. В подобных ситуациях мы должны искать дополнительную переменную, которая была бы связана с другими переменными причинной связью и объясняла корреляцию между ними. В данном примере это может быть размер пожара. Такие скрытые причины называются спутывающими переменными, потому что они искажают нашу возможность определять связь между зависимыми переменными.

Линейные уравнения

Две переменные, которые мы можем обозначить как x и y, могут быть связаны друг с другом строго или нестрого. Самая простая связь между независимой переменной x и зависимой переменной y является прямолинейной, которая выражается следующей формулой:

Здесь значения параметров a и b определяют соответственно точную высоту и крутизну прямой. Параметр a называется пересечением с вертикальной осью или константой, а b — градиентом, наклоном линии или угловым коэффициентом. Например, в соотнесенности между температурными шкалами по Цельсию и по Фаренгейту a = 32 и b = 1. 8. Подставив в наше уравнение значения a и b, получим:

Для вычисления 10°С по Фаренгейту мы вместо x подставляем 10:

Таким образом, наше уравнение сообщает, что 10°С равно 50°F, и это действительно так. Используя Python и возможности визуализации pandas, мы можем легко написать функцию, которая переводит градусы из Цельсия в градусы Фаренгейта и выводит результат на график:

'''Функция перевода из градусов Цельсия в градусы Фаренгейта'''
celsius_to_fahrenheit = lambda x: 32 + (x * 1.8)

def ex_3_11():
    '''График линейной зависимости температурных шкал'''
    s  = pd.Series(range(-10,40))
    df = pd.DataFrame({'C':s, 'F':s.map(celsius_to_fahrenheit)})
    df.plot('C', 'F', legend=False, grid=True)
    plt.xlabel('Градусы Цельсия')
    plt.ylabel('Градусы Фаренгейта')
    plt.show()

Этот пример сгенерирует следующий ниже линейный график:

Обратите внимание, как синяя линия пересекает 0 на шкале Цельсия при величине 32 на шкале Фаренгейта. Пересечение a — это значение y, при котором значение x равно 0.

Наклон линии с неким угловым коэффициентом определяется параметром b; в этом уравнении его значение близко к 2. Как видно, диапазон шкалы Фаренгейта почти вдвое шире диапазона шкалы Цельсия. Другими словами, прямая устремляется вверх по вертикали почти вдвое быстрее, чем по горизонтали.

Остатки

К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:

Здесь, ε — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:

Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).

Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.

Обычные наименьшие квадраты

Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.

Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.

Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:

Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:

Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:

Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.

Наклон и пересечение

Мы уже рассматривали функции covariance, variance и mean, которые нужны для вычисления наклона прямой и точки пересечения для данных роста и веса пловцов. Поэтому вычисление наклона и пересечения имеют тривиальный вид:

def slope(xs, ys):
    '''Вычисление наклона линии (углового коэффициента)'''
    return xs.cov(ys) / xs.var()

def intercept(xs, ys): 
     '''Вычисление точки пересечения (с осью Y)'''
   return ys.mean() - (xs.mean() * slope(xs, ys))

def ex_3_12():
    '''Вычисление пересечения и наклона (углового коэффициента) 
       на примере данных роста и веса'''
    df = swimmer_data()
    X  = df['Рост, см']
    y  = df['Вес'].apply(np.log)
    a  = intercept(X, y)
    b  = slope(X, y) 
    print('Пересечение: %f, наклон: %f' % (a,b))

Пересечение: 1.691033, наклон: 0.014296

В результате будет получен наклон приблизительно 0.0143 и пересечение приблизительно 1. 6910.

Интерпретация

Величина пересечения — это значение зависимой переменной (логарифмический вес), когда независимая переменная (рост) равна нулю. Для получения этого значения в килограммах мы можем воспользоваться функцией np.exp, обратной для функции np.log. Наша модель дает основания предполагать, что вероятнее всего вес олимпийского пловца с нулевым ростом будет 5.42 кг. Разумеется, такое предположение лишено всякого смысла, к тому же экстраполяция за пределы границ тренировочных данных является не самым разумным решением.

Величина наклона показывает, насколько y изменяется для каждой единицы изменения в x. Модель исходит из того, что каждый дополнительный сантиметр роста прибавляет в среднем 1.014 кг. веса олимпийских пловцов. Поскольку наша модель основывается на данных о всех олимпийских пловцах, она представляет собой усредненный эффект от увеличения в росте на единицу без учета любого другого фактора, такого как возраст, пол или тип телосложения.

Визуализация

Результат линейного уравнения можно визуализировать при помощи имплементированной ранее функции regression_line и простой функции от x, которая вычисляет ŷ на основе коэффициентов a и b.

'''Функция линии регрессии'''
regression_line = lambda a, b: lambda x: a + (b * x)  # вызовы fn(a,b)(x)

def ex_3_13():
    '''Визуализация линейного уравнения
       на примере данных роста и веса'''
    df = swimmer_data()
    X  = df['Рост, см'].apply( jitter(0.5) )
    y  = df['Вес'].apply(np.log)
    a, b = intercept(X, y), slope(X, y) 
    ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=7)
    s  = pd.Series(range(150,210))
    df = pd.DataFrame( {0:s, 1:s.map(regression_line(a, b))} )  
    df.plot(0, 1, legend=False, grid=True, ax=ax)
    plt.xlabel('Рост, см.')
    plt.ylabel('Логарифмический вес')
    plt.show()

Функция regression_line возвращает функцию от x, которая вычисляет a + bx.

Указанная функция может также использоваться для вычисления каждого остатка, показывая степень, с которой наша оценка ŷ отклоняется от каждого измеренного значения y.

def residuals(a, b, xs, ys):
    '''Вычисление остатков'''
    estimate = regression_line(a, b)     # частичное применение
    return pd.Series( map(lambda x, y: y - estimate(x), xs, ys) )

constantly = lambda x: 0

def ex_3_14():
    '''Построение графика остатков на примере данных роста и веса'''
    df = swimmer_data()
    X  = df['Рост, см'].apply( jitter(0.5) )
    y  = df['Вес'].apply(np.log)
    a, b = intercept(X, y), slope(X, y) 
    y  = residuals(a, b, X, y)
    ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=12)
    s  = pd.Series(range(150,210))
    df = pd.DataFrame( {0:s, 1:s.map(constantly)} )      
    df.plot(0, 1, legend=False, grid=True, ax=ax)
    plt.xlabel('Рост, см.')
    plt.ylabel('Остатки')
    plt.show()

График остатков — это график, который показывает остатки на оси Y и независимую переменную на оси X. Если точки на графике остатков разбросаны произвольно по обе стороны от горизонтальной оси, то линейная модель хорошо подогнана к нашим данным:

За исключением нескольких выбросов на левой стороне графика, график остатков, по-видимому, показывает, что линейная модель хорошо подогнана к данным. Построение графика остатков имеет важное значение для получения подтверждения, что линейная модель применима. В линейной модели используются некоторые допущения относительно данных, которые при их нарушении делают не валидными модели, которые вы строите.

Допущения

Первостепенное допущение линейной регрессии состоит в том, что, безусловно, существует линейная зависимость между зависимой и независимой переменной. Кроме того, остатки не должны коррелировать друг с другом либо с независимой переменной. Другими словами, мы ожидаем, что ошибки будут иметь нулевое среднее и постоянную дисперсию по отношению к зависимой и независимой переменной. График остатков позволяет быстро устанавливать, является ли это действительно так.

Левая сторона нашего графика имеет более крупные значения остатков, чем правая сторона. Это соответствует большей дисперсии веса среди более низкорослых спортсменов. Когда дисперсия одной переменной изменяется относительно другой, говорят, что переменные гетероскедастичны, т.е. их дисперсия неоднородна. Этот факт представляет в регрессионном анализе проблему, потому что делает не валидным допущение в том, что модельные ошибки не коррелируют и нормально распределены, и что их дисперсии не варьируются вместе с моделируемыми эффектами.

Гетероскедастичность остатков здесь довольно мала и особо не должна повлиять на качество нашей модели. Если дисперсия на левой стороне графика была бы более выраженной, то она привела бы к неправильной оценке дисперсии методом наименьших квадратов, что в свою очередь повлияло бы на выводы, которые мы делаем, основываясь на стандартной ошибке.

Качество подгонки и R-квадрат

Хотя из графика остатков видно, что линейная модель хорошо вписывается в данные, т. е. хорошо к ним подогнана, было бы желательно количественно измерить качество этой подгонки. Коэффициент детерминации R², или R-квадрат, варьируется в интервале между 0 и 1 и обозначает объяснительную мощность линейной регрессионной модели. Он вычисляет объясненную долю изменчивости в зависимой переменной.

Обычно, чем ближе R² к 1, тем лучше линия регрессии подогнана к точкам данных и больше изменчивости в Y объясняется независимой переменной X. R² можно вычислить с помощью следующей ниже формулы:

Здесь var(ε) — это дисперсия остатков и var(Y) — дисперсия в Y. В целях понимания смысла этой формулы допустим, что вы пытаетесь угадать чей-то вес. Если вам больше ничего неизвестно об испытуемых, то наилучшей стратегией будет угадывать среднее значение весовых данных внутри популяции в целом. Таким путем средневзвешенная квадратичная ошибка вашей догадки в сравнении с истинным весом будет var(Y), т. е. дисперсией данных веса в популяции.

Но если бы я сообщил вам их рост, то в соответствии с регрессионной моделью вы бы предположили, что a + bx. В этом случае вашей средневзвешенной квадратичной ошибкой было бы или дисперсия остатков модели.

Компонент формулы var(ε)/var(Y) — это соотношение средневзвешенной квадратичной ошибки с объяснительной переменной и без нее, т. е. доля изменчивости, оставленная моделью без объяснения. Дополнение R² до единицы — это доля изменчивости, объясненная моделью.

^{Как и в случае с}^r^{, низкий}^R^{2 не означает, что две переменные не коррелированы. Просто может оказаться, что их связь не является линейной.}

Значение R² описывает качество подгонки линии регрессии к данным. Оптимально подогнанная линия — это линия, которая минимизирует значение R². По мере удаления либо приближения от своих оптимальных значений R² всегда будет расти.

Левый график показывает дисперсию модели, которая всегда угадывает среднее значение для , правый же показывает меньшие по размеру квадраты, связанные с остатками, которые остались необъясненными моделью f. С чисто геометрической точки зрения можно увидеть, как модель объяснила большинство дисперсии в y. Приведенный ниже пример вычисляет R² путем деления дисперсии остатков на дисперсию значений y:

def r_squared(a, b, xs, ys):
    '''Рассчитать коэффициент детерминации (R-квадрат)'''
    r_var = residuals(a, b, xs, ys).var() 
    y_var = ys.var()
    return 1 - (r_var / y_var)

def ex_3_15():
    '''Рассчитать коэффициент R-квадрат 
       на примере данных роста и веса'''
    df = swimmer_data()
    X  = df['Рост, см'].apply( jitter(0.5) )
    y  = df['Вес'].apply(np.log)
    a, b = intercept(X, y), slope(X, y)
    return r_squared(a, b, X, y)

0. 75268223613272323

В результате получим значение 0.753. Другими словами, более 75% дисперсии веса пловцов, выступавших на Олимпийских играх 2012 г., можно объяснить ростом.

В случае простой регрессионной модели (с одной независимой переменной), связь между коэффициентом детерминации R² и коэффициентом корреляции r является прямолинейной:

Коэффициент корреляции r может означать, что половина изменчивости в переменной Y объясняется переменной X, но фактически R² составит 0.5², т.е. 0.25.

Множественная линейная регрессия

Пока что в этой серии постов мы видели, как строится линия регрессии с одной независимой переменной. Однако, нередко желательно построить модель с несколькими независимыми переменными. Такая модель называется множественной линейной регрессией.

Каждой независимой переменной потребуется свой собственный коэффициент. Вместо того, чтобы для каждой из них пытаться подобрать букву в алфавите, зададим новую переменную β (бета), которая будет содержать все наши коэффициенты:

Такая модель эквивалентна двухфакторной линейно-регрессионной модели, где β₁ = a и β₂ = b при условии, что x₁ всегда гарантированно равен 1, вследствие чего β₁ — это всегда константная составляющая, которая представляет наше пересечение, при этом x₁ называется (постоянным) смещением уравнения регрессии, или членом смещения.

Обобщив линейное уравнение в терминах β, его легко расширить на столько коэффициентов, насколько нам нужно:

Каждое значение от x₁ до x_n соответствует независимой переменной, которая могла бы объяснить значение y. Каждое значение от β₁ до β_n соответствует коэффициенту, который устанавливает относительный вклад независимой переменной.

Простая линейная регрессия преследовала цель объяснить вес исключительно с точки зрения роста, однако объяснить вес людей помогает много других факторов: их возраст, пол, питание, тип телосложения. Мы располагаем сведениями о возрасте олимпийских пловцов, поэтому мы смогли бы построить модель, которая учитывает и эти дополнительные данные.

До настоящего момента мы предоставляли независимую переменную в виде одной последовательности значений, однако при наличии двух и более параметров нам нужно предоставлять несколько значений для каждого x. Мы можем воспользоваться функциональностью библиотеки pandas, чтобы выбрать два и более столбцов и управлять каждым как списком, но есть способ получше: матрицы.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Темой следующего поста, поста №3, будут матричные операции, нормальное уравнение и коллинеарность.

Коэффициент детерминации — Справочник химика 21

Построение и анализ многофакторной регрессионной модели позволяют судить о численном влиянии факторов на изучаемый показатель дефектности трубопровода и изменении этого показателя при варьировании значений каждого фактора. Критерием оценки адекватности модели является коэффициент детерминации который представляет собой статистическую характеристику, учитывающую как линейные, так и нелинейные виды связей и дающую возможность оценивать степень адекватности построенной модели с помощью зависимости [c.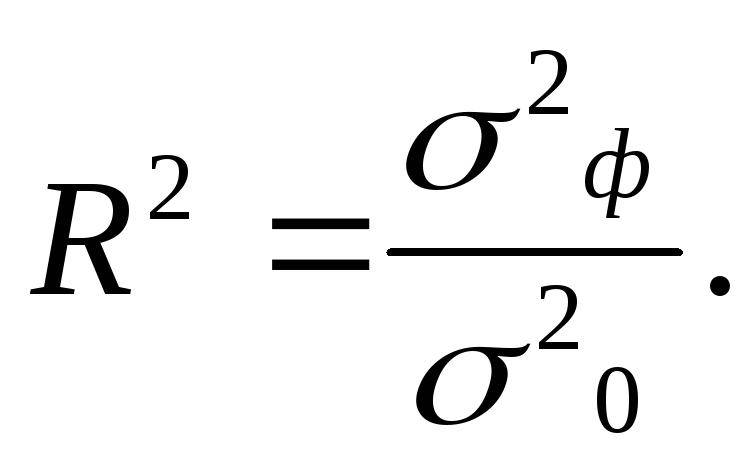 113]
Для построения статистической модели была проведена оценка вклада различных факторов на время до разрушения магистральных газопроводов. В качестве рабочего инструмента была выбрана процедура множественной регрессии, позволяющая получать модель в виде линейной комбинации воздействующих факторов. Исследования проводились с доверительной вероятностью 95 %. В качестве независимых переменных использовались величины толщин стенок труб, температур, расстояний до компрессорной станции, давлений, а также их модифицированные значения (обратная температура, обратное расстояние, отношение действующего напряжения к пределу текучести стали и др.). Расчеты проводились как с использованием константы, так и без нее. Всего было рассмотрено 48 вариантов модели. Из них была выбрана одна, имеющая наиболее высокий коэффициент детерминации. В табл. 1.6 приведены результаты расчета этой модели. Переменные имеют следующие обозначения толщина стенки трубы (мм) — Н, давление (МПа) — Р, температура (°С) — Т, величина, обратная расстоянию до компрессорной (100/км) — ЬО, время до разрушения (лет) -1.

[c.56]

Рассчитанная модель имеет достаточно высокий коэффициент детерминации. Другие рассчитанные модели имели наибольшую значимость для коэффициента, стоящего перед переменной, соответствующей толщине стенки трубы. Использование линейных моделей с константой приводит к снижению коэффициента детерминации до величин около 0,8 и уменьшению значимости коэффициентов регрессии, отвечающих температуре и давлению. Однако предпочтение было отдано модели без константы в связи с высокой вероятностью принятия нулевой гипотезы для самой константы (в пределах 0,7 — 0,8). [c.58]

Относительная теснота зависимости лучше всего измеряется коэффициентом детерминации с1 [c.26]

При числе степеней свободы 59—2 = 57 полученный коэффициент корреляции / = 0,906 значительно больше табличного [9] при уровне достоверности, превышающей 99,9%. Мерой этой связи служит коэффициент детерминации d = 0,822, указывающий, что изменения интенсивности ослабления потока Y-квантов на 82,2 /о были вызваны изменениями насыпной массы кокса. [c.28]

Коэффициент детерминации, соответственно, 0,995 0,865 0,879 0,984. Количество опытов в промышленных условиях — 19. [c.116]

Концентрация (с, мг/л) Коэффициенты уравнения полинома Коэффициент детерминации [c.11]

Другая количественная оценка удовлетворительности совпадения — это коэффициент детерминации вычисляемый по уравнению [c.167]

Исчисляемый коэффициент детерминации получился равным 0,869. Это говорит о том, что размер заработной платы водителей на 86,9% зависит от Р и АЧ -р и на 13,1% —от неучтенных в модели факторов. Средняя ошибка аппроксимации составила всего лишь 0,17%. Модель была получена на основе конкретных показателей ряда автотранспортных предприятий Владимирского транспортного управления, поэтому она может -быть использована в практической ра-боте только на этих предприятиях. Предлагаемая же. методика может быть использована в любом транспортном управлении, министерстве при планировании и анализе себестоимости автомобильных перевозок и установлении нормативов по заработной плате водителей за время работы на линии.

[c.36]

Для оценки точности зависимости рассчитываются коэффициент парной корреляции между зависимой и независимой переменными, коэффициент детерминации, фактическое значение F — критерия (отношение дисперсии зависимой переменной, связанной с действием включенного в уравнение фактора и остаточной дисперсии). [c.186]

Величина коэффициента детерминации в рассмотренном примере составляет 0,9966, что свидетельствует о высокой достоверности аппроксимации. [c.244]

Пути Коэффициенты детерминации [c.230]

Нормированные коэффициенты частной регрессии Л и В из приведенных выше уравнений называют коэффициентами путей от А к У и от В к У соответственно (рис. 14.2). Они уже не одинаковы для обоих наборов данных. Кроме того, исходя из (5) и (6), мы находим, что процентные вклады (коэффициенты детерминации) Л и В в дисперсию У также весьма различны для двух наборов данных [c.233]

Коэффициенты детерминации (по отношению к дисперсии следствия) равны [c. 235]

Судя по величинам коэффициента детерминации К зависимость содержания хлорофилла от приведенных в табл. 24 абиотических характеристик меняется в ходе сезонной сукцессии, становясь то сильнее, то слабее (табл. 25). Более низкие Ю свидетельствуют о том, что распределение водорослей в эти периоды регулируется другими факторами (это может быть содержание биогенов, пресс зоопланктона, гидродинамика). [c.57]

Коэффициент детерминации представляет собой альтернативный показатель степени зависимости между двумя переменными. Данное значение вычисляется путем возведения в квадрат коэффициента корреляции (г). [c.114]

Коэффициент детерминации часто более предпочтителен, чем коэффициент корреляции, так как его можно использовать для количественного определения [c.114]

Рассмотрим, к примеру, ситуацию, когда коэффициент корреляции между объемом выручки от реализации и расходами на рекламу составляет 0. 8. Таким образом, г — 0.8, а коэффициент детерминации = 0.82 = 0.64 (= 64%). Следовательно, это показывает, что 64% изменений в объеме реализации можно объяснить изменениями в расходах на рекламу. [c.115]

Итак, г= +1, а коэффициент детерминации / = 1. Это подразумевает, что 100% изменений в объеме реализации вызваны изменениями в расходах на рекламу. В таком случае изменения в расходах на рекламу автоматически вызывают пропорциональные изменения в объемах реализации, что для любого руководителя службы маркетинга ситуация идеальная. На практике, конечно, крайне маловероятно, что степень корреляции будет столь идеальной. Даже когда зависимость между двумя переменными значима, требуется учет множества других факторов. Так, для примеров такого рода вполне обычным значением коэффициента детерминации будет показатель в диапазоне от 0.1 до 0.3. Например, коэффициент детерминации, равный 0.2 (20%), показывает, что 20% изменений в объеме реализации вызван изменениями в расходах на рекламу.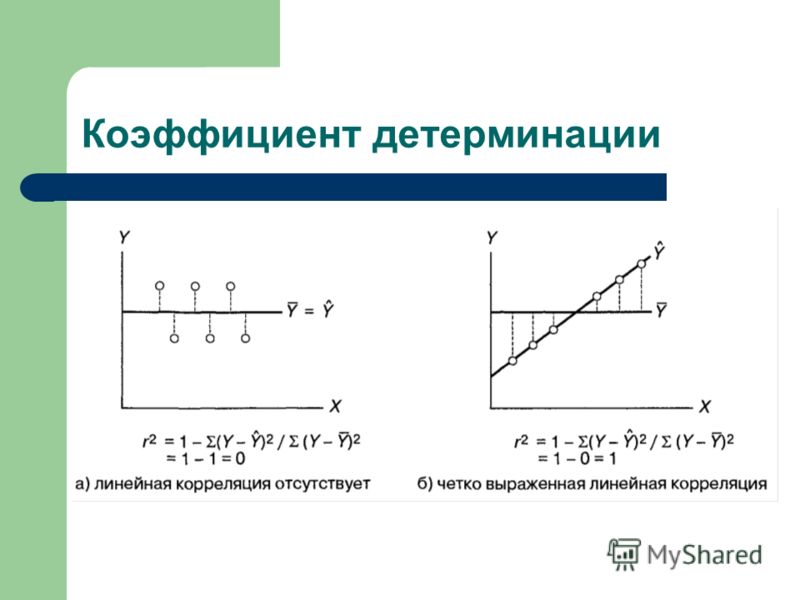 Во многих хозяйственных ситуациях 20%-ный результат служит более чем адекватным обоснованием необходимости продолжать рекламирование. [c.115]

При истолковании значений коэффициента корреляции и коэффициента детерминации следует проявлять осторожность. Существует вероятность получения очень высоких значений коэффициента корреляции при отсутствии какой-либо прямой зависимости между двумя рассматриваемыми переменными. Рассмотрим, например, следующую ситуацию, когда мы имеем для анализа собранные за 10 лет данные по стоимости экспорта из Великобритании и средней цене стиральных машин во Франции [c.115]

Данные переменные были отобраны ввиду фактического отсутствия прямой зависимости между ними. Итак, мы можем вычислить коэффициент корреляции между этими двумя переменными при х — стоимости экспорта из Великобритании и у — цене стиральных машин во Франции. Коэффициент корреляции составляет г = 0.9635. Таким образом, коэффициент детерминации = 0. 96352 = 0.928 = 92.8%. [c.115]

Такой коэффициент детерминации, видимо, указывает на то, что 92.8% изменений в цене стиральных машин во Франции вызваны колебаниями в стоимости экспорта из Великобритании. Такая зависимость называется ложной, [c.115]

Т Определение. Коэффициент детерминации, вычисляемый путем возведения в квадрат значения коэффициента корреляции, показывает объем изменения переменной (у), относимый на счет изменений в значении другой переменной (х). [c.116]

О наличии тесной взаимосвязи между этими показателями свидетельствует высокий коэффищ -ент корреляции (0,847) при уровне доверительной вероятности 99 %. Коэффициент детерминаций л =0,718 указывает, что изменение РС на 72 % вызвано изменением плотности раствора. [c.19]

Экспериментальные данные обработаны в программе Math ad Professional 2001. Показано, что коэффициенты детерминации находятся в пределах от 0,98 до 0,99, что свидетельствует о достоверности полученных результатов исследований, определяемых коэффициентом детерминации 0,75.

[c.11]

Используя уравнения регрессии, полученного при помощи программы Math ad Professional 2001 с коэффициентом детерминации 0,99, найдена зависимость i/общ (О для воды, содержащей фенол, концентрацией 20 мг/л i/общ = 0,12 г + 27,9. [c.17]

Уравнение (2) учитывает 93,8% от общей дисперсии величины у (множественный коэффициент детерминации ) = 7 = 0,938). Уравнение значимо, дисперсионное отноп1ение 2 = 90,31 значительно превосходит табличное значение Ро,о1 = 3,5. Остаточная дисперсия меньше общей дисперсии величины г/ в 16 раз (Fl = 16,2). Наибольшую значимость имеют коэффициенты при Х] и Х4. В основном коэффициенты умеренно коррелированы между собой (табл. 2). [c.9]

Для быстрой оценки неизвестных коэффициентов линейного регрессионного уравнения воспользуемся линией тренда. Для этого вьщелим на диаграмме экспериментальные точки, щелкнем правой кнопкой мыши и в открывшемся контекстном меню выберем Добавить линию тренда . На вкладке Параметры указано Показывать уравнение на диаграмме и Поместить на диаграмму величину коэффициента детерминации R4. [c.244]

Два пути из четырех прямые (У—Л—У и У—В—У) и два непрямые (У—Л—5—У и Y—B—A—Y). Числа а , и 2агЬ могут служить мерой вкладов соответствующих путей в общую дисперсию У и называются коэффициентами детерминации (в отношении дисперсии У). Исследуя рис. 14.1 описанным выше образом, мы видим, что он представляет собой диаграммы выражения (3) или (5). [c.230]

По мере увеличения ИТС все пигментные характеристики претерпевают определенные изменения (рис. 34). Для большинства из них выявлена тесная коррелящюнная связь с величинами ИТС, которая носит нелинейный характер. Высокие коэффициенты детерминации (R ) свидетельствует о закономерной изменчивости показателей по градиенту трофии (табл. 51). Близкая к функциональной зависимость (R = 0.999) отмечена не только между ИТС и Хл а, что естественным образом вытекает из расчета самого индекса, но и для суммарного количества зеленых пигментов (Хл а, Ь, с), а также каротиноидов. Содержание Хл а считается общепринятой характеристикой биомассы фитопланктона, а также трофии водоема. В то же время, известны работы (Foy, 1987), где биомассу водорослей рекомендуется оценивать по содержанию желтых пигментов. Аналогичную смысловую на- [c.117]

Дополнительные пигменты (Хл 6 и Хл с) ведут себя по-разному. Хл с так же, как и три предыдущих показателя, увеличивается пропорционально ИТС. Это согласуется с данными по составу планктонных альгоценозов, доминирующие комплексы которых в исследованных водохранилищах формируются в основном диатомовыми водорослями. Содержание Хл Ь изменяется куполообразно оно увеличивается в диапазоне ИТС 50-70 и затем снижается. Такой характер изменения влияет на тесноту связи между ИТС и Хл уменьшая коэффициент детерминации до величины, которая соответствует средней степени скор-релированности переменных (/ 2= 0.27). Это связано с индивидуальным ходом Хл Ь в отдельных водоемах, обусловленным, в свою очередь, вспышками развития зеленых водорослей (Охапкин, 1994 Корнева, Соловьева, 1996 Охапкин и др. , 1997 Komeva, Solovyova, 1998). [c.118]

Обсуждаемые зависимости получены для больших рядов, включаю1цих сезонные данные для разнотипных водоемов, расположенных в различных географических зонах. Однако и в каждом отдельном водохранилище повторяется общая картина, которую иллюстрируют графики на рис. 34. Изменения пигментных характеристик связаны с трофией вод, обусловливая от 85 до 96% объясненной вариации ИТС, о чем свидетельствуют приведенные ниже коэффициенты детерминации R [c.120]

При использовании в расчетах не осредненных данных, а всего исходного ряда (п = 2565) характер зависимости не менялся, коэффициенты детерминации R остаются значимыми, свидетельствуя о высокой степени скоррелированности переменных (табл. 54). [c.123]

Для нахождения взаимосвязи между сопротивлением сталей СР в лабораторной среде NA E и сероводородсодержащем газе ОГКМ использовали множественную нелинейную регрессию с автоматическим выбором степени аппроксимирующего полинома на РС-ХТ/АТ. Получены две линейные зависимости для сталей, имеющих высокое сопротивление СР (4.3), и остальных сталей (4.4) с высокими коэффициентами детерминации [c.327]

В главе рассмотрен анализ зависимости между двумя или более наборами значений. Графики разброса можно использовать для иллюстрации любой связи между двумя переменными. Однако результаты, полученные из таких фафиков, существенно субъективны. Для последующего и углубленного анализа зависимости необходимо использовать объективный показатель. Одним из таких показателей является линейный коэффициент корреляции, который оценивает близость соотношения двух переменных. Этот коэффициент, обозначаемый г, измеряет степень корреляции, или линейной зависимости, между двумя переменными. Значение коэффициента корреляции лежит в пределах от —1 до +1. Значения г, близкие к + 1 или —1, указывают на наличие сильной зависимости между двумя переменными. И наоборот, значения, близкие к нулю, показывают, что зависимость мала. 2), который ещё называют величиной достоверности аппроксимации. С его помощью можно определить уровень точности прогноза. Давайте узнаем, как можно произвести расчет данного показателя с помощью различных инструментов программы Excel.

Вычисление коэффициента детерминации

В зависимости от уровня коэффициента детерминации, принято разделять модели на три группы:

0,8 – 1 — модель хорошего качества;
0,5 – 0,8 — модель приемлемого качества;
0 – 0,5 — модель плохого качества.

В последнем случае качество модели говорит о невозможности её использования для прогноза.

Выбор способа вычисления указанного значения в Excel зависит от того, является ли регрессия линейной или нет. В первом случае можно использовать функцию КВПИРСОН, а во втором придется воспользоваться специальным инструментом из пакета анализа.

Способ 1: вычисление коэффициента детерминации при линейной функции

Прежде всего, выясним, как найти коэффициент детерминации при линейной функции. В этом случае данный показатель будет равняться квадрату коэффициента корреляции. Произведем его расчет с помощью встроенной функции Excel на примере конкретной таблицы, которая приведена ниже.

Выделяем ячейку, где будет произведен вывод коэффициента детерминации после его расчета, и щелкаем по пиктограмме «Вставить функцию».

Запускается Мастер функций. Перемещаемся в его категорию «Статистические» и отмечаем наименование «КВПИРСОН». Далее клацаем по кнопке «OK».

Происходит запуск окна аргументов функции КВПИРСОН. Данный оператор из статистической группы предназначен для вычисления квадрата коэффициента корреляции функции Пирсона, то есть, линейной функции. А как мы помним, при линейной функции коэффициент детерминации как раз равен квадрату коэффициента корреляции.
Синтаксис этого оператора такой:
=КВПИРСОН(известные_значения_y;известные_значения_x)
Таким образом, функция имеет два оператора, один из которых представляет собой перечень значений функции, а второй – аргументов. Операторы могут быть представлены, как непосредственно в виде значений, перечисленных через точку с запятой (;), так и в виде ссылок на диапазоны, где они расположены. Именно последний вариант и будет использован нами в данном примере.
Устанавливаем курсор в поле «Известные значения y». Выполняем зажим левой кнопки мышки и производим выделение содержимого столбца «Y» таблицы. Как видим, адрес указанного массива данных тут же отображается в окне.
Аналогичным образом заполняем поле «Известные значения x». Ставим курсор в данное поле, но на этот раз выделяем значения столбца «X».
После того, как все данные были отображены в окне аргументов КВПИРСОН, клацаем по кнопке «OK», расположенной в самом его низу.

Как видим, вслед за этим программа производит расчет коэффициента детерминации и выдает результат в ту ячейку, которая была выделена ещё перед вызовом Мастера функций. В нашем примере значение вычисляемого показателя получилось равным 1. Это значит, что представленная модель абсолютно достоверная, то есть, исключает погрешность.

Урок: Мастер функций в Microsoft Excel

Способ 2: вычисление коэффициента детерминации в нелинейных функциях

Но указанный выше вариант расчета искомого значения можно применять только к линейным функциям. Что же делать, чтобы произвести его расчет в нелинейной функции? В Экселе имеется и такая возможность. Её можно осуществить с помощью инструмента «Регрессия», который является составной частью пакета «Анализ данных».

Но прежде, чем воспользоваться указанным инструментом, следует активировать сам «Пакет анализа», который по умолчанию в Экселе отключен. Перемещаемся во вкладку «Файл», а затем переходим по пункту «Параметры».

В открывшемся окне производим перемещение в раздел «Надстройки» при помощи навигации по левому вертикальному меню. В нижней части правой области окна располагается поле «Управление». Из списка доступных там подразделов выбираем наименование «Надстройки Excel…», а затем щелкаем по кнопке «Перейти…», расположенной справа от поля.

Производится запуск окна надстроек. В центральной его части расположен список доступных надстроек. Устанавливаем флажок около позиции «Пакет анализа». Вслед за этим требуется щелкнуть по кнопке «OK» в правой части интерфейса окна.

Пакет инструментов «Анализ данных» в текущем экземпляре Excel будет активирован. Доступ к нему располагается на ленте во вкладке «Данные». Перемещаемся в указанную вкладку и клацаем по кнопке «Анализ данных» в группе настроек «Анализ».

Активируется окошко «Анализ данных» со списком профильных инструментов обработки информации. Выделяем из этого перечня пункт «Регрессия» и клацаем по кнопке «OK».

Затем открывается окно инструмента «Регрессия». Первый блок настроек – «Входные данные». Тут в двух полях нужно указать адреса диапазонов, где находятся значения аргумента и функции. Ставим курсор в поле «Входной интервал Y» и выделяем на листе содержимое колонки «Y». После того, как адрес массива отобразился в окне «Регрессия», ставим курсор в поле «Входной интервал Y» и точно таким же образом выделяем ячейки столбца «X».
Около параметров «Метка» и «Константа-ноль» флажки не ставим. Флажок можно установить около параметра «Уровень надежности» и в поле напротив указать желаемую величину соответствующего показателя (по умолчанию 95%).
В группе «Параметры вывода» нужно указать, в какой области будет отображаться результат вычисления. Существует три варианта:
- Область на текущем листе;
- Другой лист;
- Другая книга (новый файл).
Остановим свой выбор на первом варианте, чтобы исходные данные и результат размещались на одном рабочем листе. Ставим переключатель около параметра «Выходной интервал». В поле напротив данного пункта ставим курсор. Щелкаем левой кнопкой мыши по пустому элементу на листе, который призван стать левой верхней ячейкой таблицы вывода итогов расчета. Адрес данного элемента должен высветиться в поле окна «Регрессия».
Группы параметров «Остатки» и «Нормальная вероятность» игнорируем, так как для решения поставленной задачи они не важны. После этого клацаем по кнопке «OK», которая размещена в правом верхнем углу окна «Регрессия».

Программа производит расчет на основе ранее введенных данных и выводит результат в указанный диапазон. Как видим, данный инструмент выводит на лист довольно большое количество результатов по различным параметрам. Но в контексте текущего урока нас интересует показатель «R-квадрат». В данном случае он равен 0,947664, что характеризует выбранную модель, как модель хорошего качества.

Способ 3: коэффициент детерминации для линии тренда

Кроме указанных выше вариантов, коэффициент детерминации можно отобразить непосредственно для линии тренда в графике, построенном на листе Excel. Выясним, как это можно сделать на конкретном примере.

Мы имеем график, построенный на основе таблицы аргументов и значений функции, которая была использована для предыдущего примера. Произведем построение к нему линии тренда. Кликаем по любому месту области построения, на которой размещен график, левой кнопкой мыши. При этом на ленте появляется дополнительный набор вкладок – «Работа с диаграммами». Переходим во вкладку «Макет». Клацаем по кнопке «Линия тренда», которая размещена в блоке инструментов «Анализ». Появляется меню с выбором типа линии тренда. Останавливаем выбор на том типе, который соответствует конкретной задаче. Давайте для нашего примера выберем вариант «Экспоненциальное приближение».

Эксель строит прямо на плоскости построения графика линию тренда в виде дополнительной черной кривой.

Теперь нашей задачей является отобразить собственно коэффициент детерминации. Кликаем правой кнопкой мыши по линии тренда. 2)». Он размещен в самом низу окна. То есть, таким образом мы включаем отображение коэффициента детерминации на области построения. Затем не забываем нажать на кнопку «Закрыть» внизу текущего окна.

Значение достоверности аппроксимации, то есть, величина коэффициента детерминации, будет отображено на листе в области построения. В данном случае эта величина, как видим, равна 0,9242, что характеризует аппроксимацию, как модель хорошего качества.

Абсолютно точно таким образом можно устанавливать показ коэффициента детерминации для любого другого типа линии тренда. Можно менять тип линии тренда, произведя переход через кнопку на ленте или контекстное меню в окно её параметров, как было показано выше. Затем уже в самом окне в группе «Построение линии тренда» можно переключиться на другой тип. Не забываем при этом контролировать, чтобы около пункта «Поместить на диаграмму величину достоверности аппроксимации» был установлен флажок. Завершив вышеуказанные действия, щелкаем по кнопке «Закрыть» в нижнем правом углу окна.

При линейном типе линия тренда уже имеет значение достоверности аппроксимации равное 0,9477, что характеризует эту модель, как ещё более достоверную, чем рассматриваемую нами ранее линию тренда экспоненциального типа.

Таким образом, переключаясь между разными типами линии тренда и сравнивая их значения достоверности аппроксимации (коэффициент детерминации), можно найти тот вариант, модель которого наиболее точно описывает представленный график. Вариант с самым высоким показателем коэффициента детерминации будет наиболее достоверным. На его основе можно строить самый точный прогноз.
Например, для нашего случая опытным путем удалось установить, что самый высокий уровень достоверности имеет полиномиальный тип линии тренда второй степени. Коэффициент детерминации в данном случае равен 1. Это говорит о том, что указанная модель абсолютно достоверная, что означает полное исключение погрешностей.
Но, в то же время, это совсем не значит, что для другого графика тоже наиболее достоверным окажется именно этот тип линии тренда. Оптимальный выбор типа линии тренда зависит от типа функции, на основании которой был построен график. Если пользователь не обладает достаточным объемом знаний, чтобы «на глаз» прикинуть наиболее качественный вариант, то единственным выходом определения лучшего прогноза является как раз сравнение коэффициентов детерминации, как было показано на примере выше.

Читайте также:
Построение линии тренда в Excel
Аппроксимация в Excel

В Экселе существуют два основных варианта вычисления коэффициента детерминации: использование оператора КВПИРСОН и применение инструмента «Регрессия» из пакета инструментов «Анализ данных». При этом первый из этих вариантов предназначен для использования только в процессе обработки линейной функции, а другой вариант можно использовать практически во всех ситуациях. Кроме того, существует возможность отображения коэффициента детерминации для линии трендов графиков в качестве величины достоверности аппроксимации. С помощью данного показателя имеется возможность определить тип линии тренда, который располагает самым высоким уровнем достоверности для конкретной функции.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

В чем разница между коэффициентом детерминации и коэффициентом корреляции? – Гаурав Бансал

Коэффициент корреляции — это значение «R», которое указано в сводной таблице выходных данных регрессии. R квадрат также называют коэффициентом детерминации. Умножьте R на R, чтобы получить значение R-квадрата. Другими словами, Коэффициент детерминации равен квадрату Коэффициента корреляции.

R квадратный или коэфф. детерминации показывает процентное изменение у, которое объясняется всеми переменными х вместе. Чем выше, тем лучше. Оно всегда находится в диапазоне от 0 до 1. Оно никогда не может быть отрицательным, так как это значение в квадрате.

Квадрат R легко объяснить с точки зрения регрессии. Не так просто объяснить R с точки зрения регрессии.

Коэффициент корреляции — это значение R, т.е. 0,850 (или 85%). Коэффициент детерминации представляет собой значение R-квадрата, т. е. 0,723 (или 72,3%). R в квадрате — это просто квадрат R, т. е. R, умноженный на R.

Коэффициент корреляции: степень взаимосвязи между двумя переменными, скажем, x и y.Он может находиться в диапазоне от -1 до 1. 1 означает, что две переменные изменяются синхронно. Они поднимаются и опускаются вместе и имеют идеальную корреляцию. -1 означает, что две переменные находятся в полной противоположности. Один идет вверх, а другой идет вниз, совершенно отрицательным образом. Можно утверждать, что любые две переменные в этой вселенной имеют значение корреляции. Если они не коррелированы, то значение корреляции все равно может быть вычислено, которое будет равно 0. Значение корреляции всегда находится между -1 и 1 (проходя через 0, что означает отсутствие корреляции вообще — совершенно не связано).Корреляцию можно правильно объяснить для простой линейной регрессии, потому что у вас есть только одна переменная x и одна переменная y. Для множественной линейной регрессии вычисляется R, но тогда это трудно объяснить, потому что здесь задействовано несколько переменных. Вот почему R-квадрат — лучший термин. Вы можете объяснить R-квадрат как для простой линейной регрессии, так и для множественной линейной регрессии.

2.7 — Коэффициенты определения и корреляции Примеры

Давайте рассмотрим несколько примеров, чтобы попрактиковаться в интерпретации коэффициента детерминации r ² и коэффициента корреляции r .

Пример 1. Насколько сильна линейная зависимость между температурами в градусах Цельсия и температурами в градусах Фаренгейта? Вот график оценочного уравнения регрессии на основе n = 11 точек данных:

Статистическое программное обеспечение сообщает, что r ² = 100% и r = 1,000. Оба измерения говорят нам о том, что существует идеальная линейная зависимость между температурой в градусах Цельсия и температурой в градусах Фаренгейта.Мы знаем, что соотношение идеальное, а именно, что по Фаренгейту = 32 + 1,8 × по Цельсию. Поэтому неудивительно, что r ² говорит нам о том, что 100% изменения температуры в градусах Фаренгейта объясняется температурой в градусах Цельсия.

Пример 2. Насколько сильна линейная зависимость между этажностью здания и его высотой? Можно было бы подумать, что по мере увеличения количества этажей высота будет увеличиваться, но не идеально.Некоторые статистики собрали данные по набору из n = 60 зданий, зарегистрированных во Всемирном альманахе 1994 года (bldgstories.txt). Статистическое программное обеспечение сообщает r ² = 90,4% и r = 0,951 и дает следующий график:

Положительный знак r говорит нам, что связь положительна — по мере увеличения количества этажей высота увеличивается — как мы и ожидали. Поскольку r близко к 1, это говорит нам о том, что линейная зависимость очень сильная, но не идеальная.Значение r ² говорит нам о том, что 90,4% вариации высоты здания объясняются количеством этажей в здании.

Пример 3. Насколько сильна линейная зависимость между возрастом водителя и расстоянием, которое водитель может видеть? Если бы нам пришлось угадывать, мы могли бы подумать, что связь отрицательна — с возрастом расстояние уменьшается. Исследовательская фирма (Last Resource, Inc., Bellefonte, PA) собрала данные по выборке из n = 30 водителей (signdist.текст). Статистическое программное обеспечение сообщает, что r ² = 64,2% и r = -0,801, и дает следующий результат:

Отрицательный знак r говорит нам об отрицательной связи — по мере увеличения возраста вождения расстояние видимости уменьшается — как мы и ожидали. Поскольку r довольно близко к -1, это говорит нам о том, что линейная зависимость довольно сильная, но не идеальная. Значение r ² говорит нам, что 64.2% вариации дальности видимости уменьшается с учетом возраста водителя.

Пример 4. Насколько сильна линейная зависимость между ростом учащегося и его средним баллом? Данные были собраны по случайной выборке из n = 35 студентов курса статистики в Университете штата Пенсильвания (heightgpa.txt). Статистическое программное обеспечение сообщает, что r ² = 0,3% и r = -0.053 и выдал следующий результат:

Поскольку r очень близко к 0, это предполагает — надеюсь, это не удивительно — что линейной зависимости между ростом и средним баллом почти нет. Действительно, значение r ² говорит нам о том, что только 0,3% вариаций в средних баллах учащихся в выборке можно объяснить их ростом. Короче говоря, нам нужно определить еще одну более важную переменную, например, количество учебных часов, если для нас важно прогнозирование среднего балла учащегося.

10.6: Коэффициент детерминации

Цели обучения

Чтобы узнать, что такое коэффициент детерминации, как его вычислить и что он говорит нам о связи между двумя переменными $x$ и $y$.

Если точечная диаграмма набора пар $(x,y)$ не показывает ни восходящего, ни нисходящего тренда, то горизонтальная линия $\hat{y} =\overline{y}$ соответствует ей, как показано на рисунке $\PageIndex{1}$. Отсутствие какого-либо восходящего или нисходящего тренда означает, что когда элемент совокупности выбирается случайным образом, знание значения измерения $x$ для этого элемента не помогает предсказать значение измерения $y$. .

Рисунок $\PageIndex{1}$: Линия $\hat{y} =\overline{y}$ хорошо соответствует точечной диаграмме.

Если диаграмма рассеяния показывает линейный тренд вверх или вниз, полезно вычислить линию регрессии методом наименьших квадратов

\[\шляпа{у} =\шляпа{β}_1x+\шляпа{β}_0\]

и использовать его для предсказания $y$. Рисунок $\PageIndex{2}$ иллюстрирует это. На каждой панели мы нанесли данные о росте и весе из раздела 10.1. Это тот же точечный график, что и на рисунке $\PageIndex{2}$, с наложенной на него линией среднего значения $\hat{y} =\overline{y}$ на левой панели и регрессией методом наименьших квадратов. линия, наложенная на него в правой панели.Ошибки обозначены графически сегментами вертикальных линий.

Рисунок $\PageIndex{2}$: та же диаграмма рассеяния с двумя аппроксимирующими линиями

Сумма квадратов ошибок, вычисленных для линии регрессии, $SSE$, меньше суммы квадратов ошибок, вычисленных для любой другой линия. В частности, это меньше, чем сумма квадратов ошибок, вычисленных с использованием строки $\hat{y}=\overline{y}$, которая на самом деле является числом $SS_{yy}$, которое мы видели уже несколько раз.Мерой того, насколько полезно использовать уравнение регрессии для прогнозирования $y$, является то, насколько меньше $SSE$, чем $SS_{yy}$. В частности, доля суммы квадратов ошибок для линии $\hat{y} =\overline{y}$, которая устраняется путем перехода к линии регрессии методом наименьших квадратов, составляет

\[\dfrac{SS_{yy}-SSE}{SS_{yy}}=\dfrac{SS_{yy}}{SS_{yy}}-\dfrac{SSE}{SS_{yy}}=1-\ dfrac{SSE}{SS_{yy}}\]

Мы можем думать о $SSE/SS_{yy}$ как о доле изменчивости $y$, которая не может быть объяснена линейной зависимостью между $x$ и $y$, поскольку он все еще существует, даже если $x$ учитывается наилучшим образом (с использованием линии регрессии наименьших квадратов; помните, что $SSE$ является наименьшей суммой квадратов ошибок, которая может быть для любой линии) .2\).

Пример $\PageIndex{1}$

Стоимость подержанных автомобилей той марки и модели, которые обсуждались в «Примере 10.4.2» в разделе 10.4, сильно различается. Самый дорогой автомобиль в выборке из Таблицы 10.4.3 имеет стоимость $\30 500$$, что почти вдвое меньше стоимости самого дешевого автомобиля, который стоит $\20 400$$. Найдите долю изменчивости стоимости, которая объясняется линейной зависимостью между возрастом и стоимостью.

Решение :

Доля изменчивости значения $y$, которая объясняется линейной зависимостью между ним и возрастом $x$, определяется коэффициентом детерминации $r^2$. 2=(-0,819)2=0,671\]

Около $67\%$ изменчивости стоимости этого автомобиля можно объяснить его возрастом.

Пример $\PageIndex{2}$

Используйте каждую из трех формул для коэффициента детерминации, чтобы вычислить его значение на примере возраста и стоимости транспортных средств.

Решение :

В «Примере 10.4.2» в разделе 10.4 мы вычислили точные значения

\[SS_{xx}=14\\ SS_{xy}=-28,7\\ SS_{yy}=87,781\\ \hat{\beta_1}=-2.2\). Выбор того, какой из них использовать, может основываться на том, какие величины уже были рассчитаны.

Pearson Product-Moment Correlation — рекомендации по интерпретации коэффициента, обнаружению выбросов и типу необходимых переменных.

Как обнаружить выбросы?

Выброс (в корреляционном анализе) — это точка данных, которая не соответствует общей тенденции ваших данных, но может показаться непостоянной (экстремальной) величиной, а не тем, что вы ожидаете по сравнению с остальными точками данных. Вы можете обнаруживать выбросы таким же образом, как вы обнаруживаете линейную зависимость, просто нанося две переменные друг против друга на графике и визуально проверяя график на наличие заблудших (экстремальных) точек. Затем вы можете либо удалить эту конкретную точку, либо манипулировать ею, если вы можете обосновать, почему вы это сделали (существуют гораздо более надежные методы обнаружения выбросов в регрессионном анализе). В качестве альтернативы, если вы не можете обосновать удаление точек данных, вы можете вместо этого запустить непараметрический тест, такой как корреляция порядка рангов Спирмена или тау-корреляция Кендалла, которые гораздо менее чувствительны к выбросам.Это может быть вашим лучшим подходом, если вы не можете оправдать удаление выброса. На приведенной ниже диаграмме показано, как может выглядеть потенциальный выброс:

Почему так важно проверять выбросы?

Выбросы могут иметь очень большое влияние на линию наилучшего соответствия и коэффициент корреляции Пирсона, что может привести к очень разным выводам относительно ваших данных. Этот момент легче всего проиллюстрировать, изучая диаграммы рассеяния линейной зависимости с включенным выбросом и после его удаления по отношению как к линии наилучшего соответствия, так и к коэффициенту корреляции.Это показано на диаграмме ниже:

Можете ли вы установить причинно-следственную связь?

Нет, корреляция Пирсона не может определить причинно-следственную связь. Он может установить только силу линейной связи между двумя переменными. Как указывалось ранее, он даже не различает независимые и зависимые переменные.

Как сообщить о результатах корреляции продукта и момента Пирсона?

Вам необходимо указать, что вы использовали корреляцию продукта и момента Пирсона, и указать значение коэффициента корреляции, r , а также степени свободы (df).Вы должны выразить результат следующим образом:

, где степени свободы (df) — это количество точек данных минус 2 ( N — 2). Если вы не проверяли значимость корреляции, то опустите степени свободы и p -значение, чтобы вы просто сообщали: r = -0,52.

Могу ли я определить, является ли связь статистически значимой?

Да, проще всего это сделать с помощью статистической программы, такой как SPSS Statistics.Чтобы узнать, как запустить корреляцию Пирсона в SPSS Statistics, перейдите к нашему руководству: Корреляция Пирсона в SPSS Statistics. Вы должны быть осторожны, когда интерпретируете статистическую значимость корреляции. Если ваш коэффициент корреляции был определен как статистически значимый, это не означает, что у вас сильная связь. Он просто проверяет нулевую гипотезу об отсутствии связи. Отвергая нулевую гипотезу, вы принимаете альтернативную гипотезу, утверждающую, что связь существует, но без информации о силе связи или ее важности.

Что такое коэффициент детерминации?

Коэффициент детерминации r ² представляет собой квадрат коэффициента корреляции Пирсона r (т. е. r ² ). Так, например, коэффициент корреляции Пирсона, равный 0,6, даст коэффициент детерминации 0,36 (т. е. r ² = 0,6 x 0,6 = 0,36). Коэффициент детерминации по отношению к корреляции представляет собой долю дисперсии, разделяемую обеими переменными.Он дает меру количества вариаций, которые могут быть объяснены моделью (корреляция — это модель). Иногда его выражают в процентах (например, 36% вместо 0,36), когда мы обсуждаем долю дисперсии, объясняемую корреляцией. Однако не стоит писать r ² = 36% или любой другой процент. Вы должны записать это в виде пропорции (например, r ² = 0,36).

Чтобы узнать, как запустить корреляцию Пирсона в SPSS Statistics, перейдите к нашему руководству: Корреляция Пирсона в SPSS Statistics.

Библиография и Ссылки

См. список ниже:

Книга	Коэн, Дж. (1988). Статистический анализ мощности для поведенческих наук (2-е изд.). Нью-Йорк: Психология Пресс.
Книга	Коэн, Б. Х. (2013). Объяснение психологической статистики (4-е изд.). Хобокен, Нью-Джерси: John Wiley & Sons.
Журнальная статья	Эджелл, С.Е., и полдень. С. М. (1984). Влияние нарушения нормальности на t-критерий коэффициента корреляции. Психологический бюллетень , 95 (3), 576-583.
Книга	Хогг, Р. В., Маккин, Дж., и Крейг, А. Т. (2014). Введение в математическую статистику (7-е изд.). Харлоу, Эссекс: Pearson Education.
Книга	Линдеман Р.Х., Меренда П.Ф. и Голд Р.З. (1980). Введение в двумерный и многомерный анализ .Гленвью, Иллинойс: Скотт, Форесман и компания.
Книга	Наннелли, JC (1978). Психометрическая теория (2-е изд.). Нью-Йорк: Книжная компания McGraw-Hill.
Журнальная статья	Пирсон, К. (1895 г.). Вклад в математическую теорию эволюции. Психологические операции Лондонского королевского общества A , 186 , 343-414.
Журнальная статья	Пирсон, К.(1920). Заметки об истории корреляций. Биометрика , 13 , 25-45.
Книга	Шевляков Г.Л. и Оджа Х. (2016). Устойчивая корреляция: теория и приложения . Чичестер, Западный Сассекс: John Wiley & Sons.
Книга	Уилкокс, Р. (2012). Введение в надежную оценку и проверку гипотез (3-е изд.). Оксфорд: Академическая пресса.

Ссылка

на эту статью

Статистика Лаэрда (2020).Корреляция моментов произведений Пирсона. Учебники по статистике и руководства по программному обеспечению . Получено Месяц , День , Год , с https://statistics.laerd.com/statistical-guides/pearson-correlation-coefficient-statistical-guide.php

Например, если вы просматривали это руководство на 29 ^th April 2020 , вы должны использовать следующую ссылку:

Статистика Лаэрда (2020).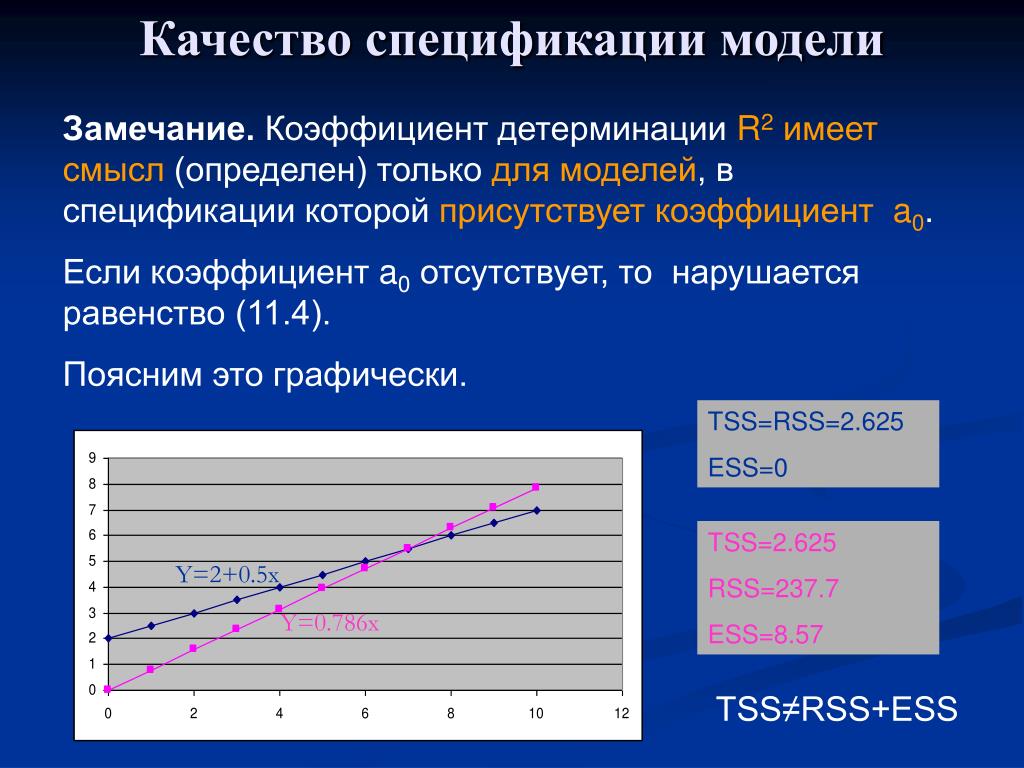 Корреляция моментов произведения Пирсона. Учебники по статистике и руководства по программному обеспечению .Получено 29 апреля 2020 г. с https://statistics.laerd.com/statistical-guides/pearson-correlation-coefficient-statistical-guide.php

Корреляция и простая линейная регрессия – Биометрия природных ресурсов

Во многих исследованиях мы измеряем более одной переменной для каждого человека. Например, мы измеряем осадки и рост растений, или количество молодняка в месте гнездования, или эрозию почвы и объем воды. Мы собираем пары данных и вместо того, чтобы исследовать каждую переменную отдельно (одномерные данные), мы хотим найти способы описания двумерных данных , в которых измеряются две переменные для каждого субъекта в нашей выборке.Имея такие данные, мы начинаем с определения того, существует ли связь между этими двумя переменными. Когда значения одной переменной изменяются, видим ли мы соответствующие изменения в другой переменной?

Мы можем описать взаимосвязь между этими двумя переменными графически и численно.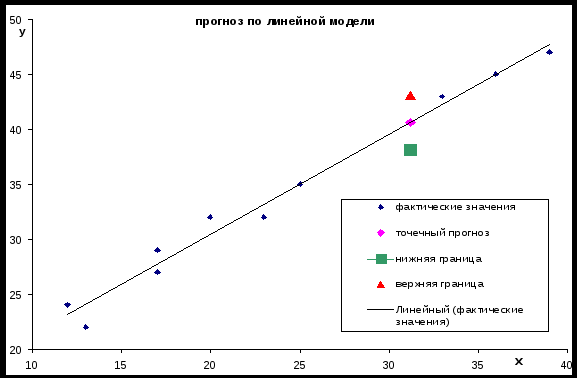 Начнем с рассмотрения концепции корреляции.

Корреляция определяется как статистическая связь между двумя переменными.

Корреляция существует между двумя переменными, когда одна из них каким-то образом связана с другой.Диаграмма рассеяния — лучшее место для начала. Диаграмма рассеяния (или диаграмма рассеивания) представляет собой график парных (x, y) выборочных данных с горизонтальной осью x и вертикальной осью y. Каждая отдельная пара (x, y) отображается как одна точка.

Рисунок 1. Диаграмма рассеяния обхвата груди в зависимости от длины.

В этом примере мы отображаем обхват груди медведя (y) в зависимости от длины медведя (x). Изучая диаграмму рассеяния, мы должны изучить общую картину нанесенных точек. В этом примере мы видим, что значение обхвата груди имеет тенденцию к увеличению по мере увеличения значения длины.Мы можем видеть восходящий наклон и прямолинейный узор в точках графика.

Диаграмма рассеяния может идентифицировать несколько различных типов взаимосвязей между двумя переменными.

Отношение имеет отсутствие корреляции когда точки на диаграмме рассеяния не показывают никакой закономерности.
Связь является нелинейной , когда точки на диаграмме рассеяния следуют шаблону, но не прямой линии.
Связь является линейной , когда точки на диаграмме рассеяния следуют несколько прямолинейному образцу.Именно эту связь мы и рассмотрим.

Линейные зависимости могут быть как положительными, так и отрицательными. Положительные отношения имеют точки, которые наклонены вверх вправо. По мере увеличения значений x значения y увеличиваются. По мере уменьшения значений x значения y уменьшаются. Например, при изучении растений высота обычно увеличивается по мере увеличения диаметра.

Рисунок 2. Диаграмма рассеяния высоты в зависимости от диаметра.

Отрицательные связи имеют точки, уменьшающиеся вниз вправо.По мере увеличения значений x значения y уменьшаются. По мере уменьшения значений x значения y увеличиваются. Например, по мере увеличения скорости ветра температура охлаждения ветром снижается.

Рис. 3. Диаграмма рассеяния зависимости температуры от скорости ветра.

Нелинейные отношения имеют явный паттерн, но не линейный. Например, с возрастом рост увеличивается до определенной точки, а затем выравнивается после достижения максимального роста.

Рисунок 4. Диаграмма рассеяния роста в зависимости от возраста.

Когда две переменные не связаны между собой, между ними нет прямой или нелинейной связи. Когда одна переменная изменяется, это не влияет на другую переменную.

Рисунок 5. Диаграмма рассеяния роста по сравнению с площадью.

Коэффициент линейной корреляции

Поскольку визуальные осмотры в значительной степени субъективны, нам нужна более точная и объективная мера для определения корреляции между двумя переменными. Для количественной оценки силы и направления связи между двумя переменными мы используем коэффициент линейной корреляции:

, где x̄ и sx — выборочное среднее и стандартное отклонение выборки x , а х и sy — среднее значение и стандартное отклонение y . Размер выборки составляет n .

Альтернативный расчет коэффициента корреляции:

где

Коэффициент линейной корреляции также называют коэффициентом корреляции момента продукта Пирсона в честь Карла Пирсона, который первоначально разработал его. Эта статистика численно описывает, насколько сильна прямолинейная или линейная связь между двумя переменными и направлением, положительным или отрицательным.

Свойства «r»:

Всегда между -1 и +1.
Это безразмерная мера, поэтому «r» будет одним и тем же значением, независимо от того, измеряете ли вы две переменные в фунтах и дюймах или в граммах и сантиметрах.
Положительные значения «r» связаны с положительными отношениями.
Отрицательные значения «r» связаны с отрицательными отношениями.

Примеры положительной корреляции

Рисунок 6. Примеры положительной корреляции.

Примеры отрицательной корреляции

Рисунок 7.

Примеры отрицательной корреляции.

Корреляция не причинно-следственная связь!!! Тот факт, что две переменные коррелированы, не означает, что одна переменная вызывает изменение другой переменной.

Изучите следующие две диаграммы рассеяния. Оба этих набора данных имеют r = 0,01, но они очень разные. На графике 1 показана небольшая линейная зависимость между переменными x и y . График 2 показывает сильную нелинейную зависимость.Коэффициент линейной корреляции Пирсона измеряет только силу и направление линейной зависимости. Игнорирование диаграммы рассеяния может привести к серьезной ошибке при описании связи между двумя переменными.

Рисунок 8. Сравнение диаграмм рассеяния.

Когда вы исследуете взаимосвязь между двумя переменными, всегда начинайте с диаграммы рассеяния. Этот график позволяет искать закономерности (как линейные, так и нелинейные). Следующим шагом является количественное описание силы и направления линейной зависимости с использованием «r». Как только вы установили, что существует линейная зависимость, вы можете сделать следующий шаг в построении модели.

Простая линейная регрессия

После того, как мы определили две коррелирующие переменные, мы хотели бы смоделировать эту взаимосвязь. Мы хотим использовать одну переменную в качестве предиктора или объясняющей переменной для объяснения другой переменной, ответа или зависимой переменной . Для этого нам нужна хорошая связь между нашими двумя переменными.Затем модель можно использовать для прогнозирования изменений в нашей переменной отклика. Сильная связь между предикторной переменной и переменной отклика приводит к хорошей модели.

Рисунок 9. Диаграмма рассеяния с регрессионной моделью.

Простая модель линейной регрессии — это математическое уравнение, которое позволяет нам предсказать ответ для заданного значения предиктора.

Наша модель примет вид х = b 0 + b1x , где b 0 — точка пересечения с осью y, b 1 — наклон, x — переменная-предиктор и × an. оценка среднего значения переменной ответа для любого значения переменной-предиктора.

Пересечение по оси y представляет собой прогнозируемое значение для ответа ( y ), когда x = 0. Наклон описывает изменение y для каждого единичного изменения x . Давайте посмотрим на этот пример, чтобы прояснить интерпретацию наклона и точки пересечения.

Пример 1

Гидролог создает модель для прогнозирования объемного расхода ручья на мостовом переходе с предикторной переменной дневного количества осадков в дюймах.

х = 1.6 + 29 х . Пересечение у 1,6 можно интерпретировать следующим образом: в день без осадков будет 1,6 галлона. воды/мин. течет в ручье на этом мостовом переходе. Наклон говорит нам о том, что если в тот день шел дождь на один дюйм, поток в ручье увеличился бы еще на 29 галлонов/мин. Если бы в тот день выпало 2 дюйма дождя, поток увеличился бы еще на 58 галлонов/мин.

Пример 2

Каким был бы средний расход реки, если бы в тот день выпало 0,45 дюйма дождя?

х = 1.6 + 29 x = 1,6 + 29(0,45) = 14,65 галлона/мин.

Линия регрессии методом наименьших квадратов (сокращенные уравнения)

Уравнение имеет вид ŷ = b 0 + b1 x

где — наклон, а b0 = × — b1 x̄ — точка пересечения по оси Y линии регрессии.

Альтернативное расчетное уравнение для уклона:

Эта простая модель лучше всего подходит для наших выборочных данных.Линия регрессии не проходит через каждую точку; вместо этого он уравновешивает разницу между всеми точками данных и прямолинейной моделью. Разница между наблюдаемым значением данных и предсказанным значением (значение на прямой линии) является ошибкой или остатком . Критерий для определения линии, которая лучше всего описывает связь между двумя переменными, основан на остатках.

Остаток = Наблюдаемый – Прогнозируемый

Например, если вы хотите предсказать обхват груди черного медведя по его весу, вы можете использовать следующую модель.

Обхват груди = 13,2 +0,43 вес

Расчетный обхват груди медведя весом 120 фунтов составляет 64,8 дюйма.

Обхват груди = 13,2 + 0,43 (120) = 64,8 дюйма

Но измеренный обхват груди медведя (наблюдаемое значение) для медведя весом 120 фунтов на самом деле составлял 62,1 дюйма.

Остаток будет 62,1 – 64,8 = -2,7 дюйма

Отрицательная невязка указывает на завышение модели. Положительный остаток указывает на то, что модель недооценивает.В данном случае модель завышала обхват груди медведя, который на самом деле весил 120 фунтов.

Рисунок 10. Диаграмма рассеяния с моделью регрессии, иллюстрирующая остаточное значение.

Эта случайная ошибка (остаток) учитывает все непредсказуемые и неизвестные факторы, не включенные в модель. Обычная линия регрессии методом наименьших квадратов минимизирует сумму квадратов ошибок между наблюдаемыми и прогнозируемыми значениями, чтобы создать линию наилучшего соответствия. Различия между наблюдаемыми и прогнозируемыми значениями возводятся в квадрат, чтобы иметь дело с положительными и отрицательными различиями.

Коэффициент детерминации

После того, как мы подобрали нашу линию регрессии (вычислим b 0 и b 1), мы обычно хотим знать, насколько хорошо модель соответствует нашим данным. Чтобы определить это, нам нужно вернуться к идее дисперсионного анализа. В ANOVA мы разделили вариацию, используя суммы квадратов, чтобы мы могли определить эффект лечения, противоположный случайной вариации, которая имела место в наших данных. Идея та же, что и для регрессии. Мы хотим разделить общую изменчивость на две части: вариацию из-за регрессии и вариацию из-за случайной ошибки.И мы снова будем вычислять суммы квадратов, чтобы помочь нам в этом.

Предположим, что общая изменчивость в измерениях выборки относительно среднего значения выборки обозначена как , называемая суммами квадратов общей изменчивости относительно среднего (SST) . Квадратная разница между прогнозируемым значением и средним значением выборки обозначается , называемая суммами квадратов из-за регрессии (SSR) . SSR представляет изменчивость, объясненную линией регрессии. Наконец, изменчивость, которая не может быть объяснена линией регрессии, называется суммами квадратов из-за ошибки (SSE) и обозначается .SSE на самом деле является квадратом остатка.

Рисунок 11. Иллюстрация взаимосвязи между средним значением y и прогнозируемым и наблюдаемым значением конкретного y.

Сумма квадратов и средняя сумма квадратов (точно так же, как ANOVA) обычно представлены в таблице регрессионного анализа дисперсии. Отношение средних сумм квадратов регрессии (MSR) и средних сумм квадратов ошибок (MSE) образуют статистику F-теста, используемую для проверки регрессионной модели.

Соотношение между этими суммами квадратов определяется как

Общая вариация = объясненная вариация + необъяснимая вариация

Чем больше объясненная вариация, тем лучше модель предсказывает.Чем больше необъяснимая вариация, тем хуже прогнозирует модель. Количественной мерой объяснительной способности модели является R2, Коэффициент детерминации:

Коэффициент детерминации измеряет процентное изменение переменной отклика ( y ), которое объясняется моделью.

Диапазон значений от 0 до 1.
Значение R2, близкое к нулю, указывает на модель с очень небольшой объяснительной силой.
Значение R2, близкое к единице, указывает на модель с большей объяснительной силой.

Коэффициент детерминации и коэффициент линейной корреляции связаны математически.

Р ² = р ²

Однако они имеют два совершенно разных значения: r — это мера силы и направления линейной зависимости между двумя переменными; R 2 описывает процентное изменение « y », которое объясняется моделью.

Графики невязки и нормальной вероятности

Даже если вы определили с помощью диаграммы рассеяния, коэффициента корреляции и R2, что x полезно для прогнозирования значения y , результаты регрессионного анализа действительны только тогда, когда данные удовлетворяют необходимым регрессионным предположениям.

Переменная отклика (y) является случайной величиной, в то время как предикторная переменная (x) считается неслучайной или фиксированной и измеряется без ошибок.
Соотношение между y и x должно быть линейным, заданным моделью.
Ошибка случайного члена значения ε независимы, имеют среднее значение 0 и общую дисперсию σ2, не зависят от x и нормально распределены.

Мы можем использовать остаточный график для проверки постоянной дисперсии, а также для того, чтобы убедиться, что линейная модель действительно адекватна.График остатка — это диаграмма рассеяния остатка (= наблюдаемые — прогнозируемые значения) по сравнению с прогнозируемым или подобранным (как используется на графике остатка) значением. Центральная горизонтальная ось устанавливается на ноль. Одним из свойств остатков является то, что они в сумме равны нулю и имеют нулевое среднее значение. Остаточный график должен быть свободен от каких-либо шаблонов, а остатки должны выглядеть как случайный разброс точек около нуля.

Остаточный график без каких-либо закономерностей указывает на то, что предположения модели удовлетворяются для этих данных.

Рисунок 12. Остаточный график.

Остаточный график, имеющий форму «веера», указывает на гетерогенную дисперсию (непостоянную дисперсию). Остатки имеют тенденцию разветвляться или разветвляться по мере увеличения или уменьшения дисперсии ошибки.

Рисунок 13. Остаточный график, указывающий на непостоянную дисперсию.

Остаточный график, который имеет тенденцию к «скаканию», указывает на то, что линейная модель не подходит. Модель может нуждаться в терминах более высокого порядка x или может потребоваться нелинейная модель для лучшего описания отношения между y и x .Можно также рассмотреть преобразования x или y .

Рис. 14. Остаточный график, указывающий на необходимость модели более высокого порядка.

График нормальной вероятности позволяет нам проверить нормальное распределение ошибок. Он отображает остатки в зависимости от ожидаемого значения остатка, как если бы он был получен из нормального распределения. Напомним, что когда остатки распределены нормально, они будут следовать прямолинейному образцу с наклоном вверх.

Этот график не является необычным и не указывает на ненормальность остатков.

Рисунок 15. График нормальной вероятности.

Следующий график ясно иллюстрирует ненормальное распределение остатков.

Рисунок 16. График нормальной вероятности, иллюстрирующий ненормальное распределение.

Наиболее серьезные нарушения нормальности обычно проявляются в хвостах распределения, потому что именно здесь нормальное распределение больше всего отличается от других типов распределений с аналогичным средним значением и разбросом. Кривизна на одном или обоих концах графика нормальной вероятности указывает на ненормальность.

Модель населения

Наша регрессионная модель основана на выборке из n двумерных наблюдений, взятых из большей совокупности измерений.

Мы используем средние значения и стандартные отклонения наших выборочных данных для вычисления наклона ( b 1) и точки пересечения с координатой Y ( b 0), чтобы создать обычную линию регрессии методом наименьших квадратов. Но мы хотим описать соотношение между х и х в популяции, а не только в наших выборочных данных.Мы хотим построить модель населения . Теперь мы будем думать о линии наименьших квадратов, вычисленной по выборке, как об оценке истинной линии регрессии для совокупности.

Модель популяции
, где μy — средний ответ популяции, β0 — пересечение оси y, а β1 — наклон для модели популяции.

В нашей популяции может быть много разных ответов на значение x . В простой линейной регрессии модель предполагает, что для каждого значения x наблюдаемые значения переменной отклика y нормально распределены со средним значением, зависящим от x .Мы используем µy для представления этих средних. Мы также предполагаем, что все эти средние значения лежат на прямой при построении графика относительно x (линия средних).

Рисунок 17. Статистическая модель линейной регрессии; средний ответ является прямолинейной функцией переменной-предиктора.

Затем выборочные данные соответствуют статистической модели:

Данные = подходит + остаток

, где ошибки (εi) независимы и нормально распределены N (0, σ). Линейная регрессия также предполагает равную дисперсию х (σ одинакова для всех значений х ).Мы используем ε (греческий эпсилон) для обозначения остаточной части статистической модели. Ответ y представляет собой сумму его среднего значения и случайного отклонения ε от среднего значения. Отклонения ε представляют собой «шум» в данных. Другими словами, шум — это изменение y из-за других причин, которые не позволяют наблюдаемым ( x, y ) сформировать идеально прямую линию.

Выборочные данные, используемые для регрессии, представляют собой наблюдаемые значения y и x .Ответ y на данное x является случайной величиной, и регрессионная модель описывает среднее значение и стандартное отклонение этой случайной величины y . Точка пересечения β0, наклон β1 и стандартное отклонение σ от до являются неизвестными параметрами регрессионной модели и должны быть оценены по выборочным данным.

Значение х из линии регрессии наименьших квадратов на самом деле является предсказанием среднего значения y (мкГ) для заданного значения x .
Линия регрессии наименьших квадратов ( ), полученная из выборочных данных, является наилучшей оценкой истинной линии регрессии населения
().

ŷ — несмещенная оценка среднего отклика μy
b 0 — несмещенная оценка точки пересечения β0
b 1 — несмещенная оценка наклона β1

Оценка параметра

Когда у нас есть оценки β0 и β1 (из наших выборочных данных b 0 и b 1), линейная зависимость определяет оценки μy для всех значений x в нашей совокупности, а не только для наблюдаемых значений х .Теперь мы хотим использовать линию наименьших квадратов в качестве основы для вывода о совокупности, из которой была взята наша выборка.

Предположения модели

говорят нам, что b 0 и b 1 нормально распределены со средними значениями β0 и β1 со стандартными отклонениями, которые можно оценить по данным. Процедуры вывода о линии регрессии совокупности будут аналогичны процедурам, описанным в предыдущей главе для средних значений. Как всегда, важно проверять данные на наличие выбросов и важных наблюдений.

Чтобы сделать это, нам нужно оценить σ, стандартную ошибку регрессии. Это стандартное отклонение ошибок модели. Он измеряет изменение y относительно линии регрессии населения. Мы будем использовать остатки для вычисления этого значения. Помните, что предсказанное значение y ( p̂ ) для конкретных x является точкой на линии регрессии. Это несмещенная оценка среднего отклика (мкГ) для этих x . Остаток:

остаток = наблюдаемый – прогнозируемый

e i = y i – · =

Невязка e i соответствует отклонению модели εi, где Σ e i = 0 со средним значением 0.Стандартная ошибка регрессии s представляет собой несмещенную оценку σ.

Величина s представляет собой оценку стандартной ошибки регрессии (σ), а s 2 часто называют среднеквадратической ошибкой (MSE). Небольшое значение s предполагает, что наблюдаемые значения y близки к истинной линии регрессии, и линия должна давать точные оценки и прогнозы.

Доверительные интервалы и тесты значимости для параметров модели

В предыдущей главе мы построили доверительные интервалы и провели тесты значимости для параметра совокупности μ (среднее значение совокупности).Мы полагались на статистику выборки, такую как среднее значение и стандартное отклонение для точечных оценок, пределы погрешности и статистику испытаний. Вывод для параметров совокупности β0 (наклон) и β1 (у-пересечение) очень похож.

Вывод для наклона и пересечения основан на нормальном распределении с использованием оценок b 0 и b 1. Стандартные отклонения этих оценок кратны σ, стандартной ошибке генеральной регрессии. Помните, мы оцениваем σ как s (изменчивость данных о линии регрессии).Поскольку мы используем s , мы полагаемся на t-распределение Стьюдента с ( n – 2) степенями свободы.

Стандартная ошибка оценки β0

Стандартная ошибка оценки β1

Мы можем построить доверительные интервалы для наклона регрессии и точки пересечения во многом так же, как мы делали это при оценке среднего значения генеральной совокупности.

A доверительный интервал для β0 : b 0 ± t α/2 SEb0

A доверительный интервал для β1 : b 1 ± t α/2 SEb1

, где SEb0 и SEb1 — стандартные ошибки точки пересечения с осью y и наклона соответственно.

Мы также можем проверить гипотезу H0: β1 = 0. Когда мы заменяем β1 = 0 в модели, член x выпадает, и мы остаемся с μy = β0. Это говорит нам о том, что среднее значение y НЕ зависит от x . Другими словами, между x и y нет прямой зависимости, а регрессия y на x не имеет значения для предсказания y .

Проверка гипотезы для β1

H0: β1 =0

h2: β1 ≠ 0

Статистика теста: t = b1 / SEb1

Мы также можем использовать F-статистику (MSR/MSE) в таблице регрессионного дисперсионного анализа*

*Напомним, что t2 = F

Итак, давайте соберем все это вместе на примере.

Пример 3

Индекс биотической целостности (ИБИ) является мерой качества воды в ручьях. Как управляющий природными ресурсами в этом регионе, вы должны отслеживать, отслеживать и прогнозировать изменения качества воды. Вы хотите создать простую модель линейной регрессии, которая позволит вам прогнозировать изменения IBI в лесной местности. В следующей таблице приведены выборочные данные по прибрежному лесному региону, а также данные по IBI и площади лесов в квадратных километрах. Пусть площадь леса будет переменной-предиктором (x), а IBI будет переменной отклика (y).

Таблица 1. Наблюдаемые данные о биотической целостности и площади лесов.

Начнем с расчета описательной статистики и диаграммы рассеяния IBI в зависимости от площади лесов.

х = 47,42; сх 27,37; х = 58,80; су = 21,38; г = 0,735

Рисунок 18. Диаграмма рассеяния IBI в зависимости от площади лесов.

Между двумя переменными существует положительная линейная зависимость. Коэффициент линейной корреляции r = 0,735. Это указывает на сильную, положительную, линейную связь.Другими словами, площадь лесов является хорошим предиктором IBI. Теперь давайте создадим простую модель линейной регрессии, используя площадь леса, чтобы предсказать IBI (отклик).

Сначала мы вычислим b 0 и b 1, используя уравнения сокращения.

==0,574

= 31,581

Уравнение регрессии .

Теперь воспользуемся программой Minitab для расчета регрессионной модели. Результат появится ниже.

Регрессионный анализ: IBI в сравнении с площадью леса

Уравнение регрессии: IBI = 31.6 + 0,574 Площадь леса

Предиктор	Коэф.	SE Коэф.	Т	Р
Константа	31.583	4,177	7,56	0,000
Лесной массив	0.57396	0,07648	7,50	0,000
S = 14,6505	Р-кв = 54,0%	R-Sq(adj) = 53,0%

Дисперсионный анализ
Источник	ДФ	нержавеющая сталь	МС	Ф	Р
Регрессия	1	12089	12089	56.32	0,000
Остаточная ошибка	48	10303	215
Всего	49	22392

Оценки для β0 и β1 равны 31.6 и 0,574 соответственно. Мы можем интерпретировать точку пересечения y как означающую, что при нулевой площади лесов IBI будет равен 31,6. На каждый дополнительный квадратный километр лесной площади IBI будет увеличиваться на 0,574 единицы.

Коэффициент детерминации R2 составляет 54,0%. Это означает, что 54% вариации IBI объясняется этой моделью. Приблизительно 46 % вариаций IBI связаны с другими факторами или случайными вариациями. Мы хотели бы, чтобы R2 был как можно выше (максимальное значение 100%).

Графики невязки и нормальной вероятности не указывают на какие-либо проблемы.

Рисунок 19. График невязки и нормальной вероятности.

Оценка σ , стандартной ошибки регрессии, равна с = 14,6505. Это мера вариации наблюдаемых значений относительно линии регрессии населения. Нам бы хотелось, чтобы это значение было как можно меньше. MSE равно 215. Помните, что = s . Стандартные ошибки для коэффициентов составляют 4,177 для точки пересечения с осью y и 0.07648 для склона.

Мы знаем, что значения b 0 = 31,6 и b 1 = 0,574 являются выборочными оценками истинных, но неизвестных параметров совокупности β0 и β1. Мы можем построить 95% доверительные интервалы, чтобы лучше оценить эти параметры. Критическое значение (tα/2) получается из распределения Стьюдента с (n – 2) степенями свободы. Размер нашей выборки равен 50, поэтому у нас будет 48 степеней свободы. Ближайшее табличное значение — 2,009.

95% доверительные интервалы для β0 и β1

б 0 ± tα/2 SEb0 = 31.6 ± 2,009(4,177) = (23,21, 39,99)

б 1 ± tα/2 SEb1 = 0,574 ± 2,009(0,07648) = (0,4204, 0,7277)

Следующим шагом является проверка того, что наклон значительно отличается от нуля, используя уровень значимости 5%.

t = b1 / SEb1 = 0,574/0,07648 = 7,50523

У нас есть 48 степеней свободы, и ближайшее критическое значение из t-распределения Стьюдента равно 2,009. Статистика теста больше критического значения, поэтому мы отвергаем нулевую гипотезу.Наклон значительно отличается от нуля. Мы обнаружили статистически значимую связь между площадью лесов и IBI.

Выходные данные Minitab также содержат статистику теста и значение p для этого теста.

Уравнение регрессии: IBI = 31,6 + 0,574 Площадь леса
Предиктор	Коэф.	SE Коэф.	Т	Р
Константа	31.583	4,177	7,56	0,000
Лесной массив	0,57396	0,07648	7,50	0,000
С = 14,6505	Р-Кв = 54,0%	R-Sq(adj) = 53,0%

Дисперсионный анализ
Источник	ДФ	нержавеющая сталь	МС	Ф	Р
Регрессия	1	12089	12089	56.32	0,000
Остаточная ошибка	48	10303	215
Всего	49	22392

Статистика t-теста равна 7,50 с соответствующим p-значением 0,000. Значение p меньше уровня значимости (5%), поэтому мы отвергаем нулевую гипотезу.Наклон значительно отличается от нуля. Тот же результат можно получить из статистики F-теста 56,32 (7,5052 = 56,32). Значение p такое же (0,000), как и заключение.

Доверительный интервал для

мкс г

Теперь, когда мы создали регрессионную модель, построенную на значительной взаимосвязи между переменной-предиктором и переменной-ответом, мы готовы использовать модель для

оценка среднего значения y для заданного значения x
предсказание конкретного значения y для заданного значения x

Рассмотрим первый вариант.Выборочные данные n пар, взятые из совокупности, использовались для вычисления коэффициентов регрессии b 0 и b 1 для нашей модели и дают нам среднее значение y для конкретного значения . x через нашу модель населения

. Для каждого конкретного значения x существует среднее значение y ( μ y ), которое попадает в уравнение прямой (линия средних). Помните, что может быть много различных наблюдаемых значений y для конкретного x , и предполагается, что эти значения имеют нормальное распределение со средним значением, равным σ2, и дисперсией σ2.Поскольку вычисленные значения b 0 и b 1 варьируются от выборки к выборке, каждая новая выборка может давать слегка отличающееся уравнение регрессии. Каждая новая модель может использоваться для оценки значения y для значения x . Как далеко наша оценка будет от истинного среднего значения населения для этого значения x ? Это зависит, как всегда, от изменчивости нашей оценки, измеряемой стандартной ошибкой.

Можно показать, что оценочное значение y , когда x = x 0 (некоторое заданное значение x ), является несмещенной оценкой среднего значения генеральной совокупности, и что p̂ нормально распределяется с стандартная ошибка

Мы можем построить доверительный интервал, чтобы лучше оценить этот параметр (μy), следуя той же процедуре, которая была показана ранее в этой главе.

, где критическое значение tα/2 взято из t-таблицы Стьюдента с ( n – 2) степенями свободы.

Статистическое программное обеспечение, такое как Minitab, рассчитает для вас доверительные интервалы. Используя данные из предыдущего примера, мы воспользуемся программой Minitab для вычисления 95%-го доверительного интервала для среднего отклика для средней площади лесов площадью 32 км.

Прогнозируемые значения для новых наблюдений
Новые наблюдательные приспособления	SE Подходит для	95%	ДИ
1	49.9496	2.38400	(45.1562,54.7429)

Если вы отобрали много областей со средней площадью 32 км. лесной площади, ваша оценка среднего IBI будет от 45,1562 до 54,7429.

Вы можете повторить этот процесс много раз для нескольких различных значений x и построить доверительные интервалы для среднего отклика.

х	95% ДИ
20	(37.13, 48,88)
40	(50.22, 58.86)
60	(61.43, 70.61)
80	(70.98, 84.02)
100	(79.88, 98.07)

Рисунок 20. 95% доверительные интервалы для среднего ответа.

Обратите внимание, как изменяется ширина 95% доверительного интервала для разных значений x .Так как ширина доверительного интервала уже для центральных значений x , следует, что µy оценивается более точно для значений x в этой области. По мере продвижения к крайним пределам данных ширина интервалов увеличивается, указывая на то, что было бы неразумно экстраполировать за пределы данных, использованных для создания этой модели.

Интервалы предсказания

Что делать, если вы хотите предсказать конкретное значение y , когда x = x 0? Или, возможно, вы хотите предсказать следующее измерение для заданного значения x ? Эта задача отличается от построения доверительного интервала для µy.Вместо построения доверительного интервала для оценки параметра совокупности нам нужно построить интервал прогнозирования. Выбор для прогнозирования определенного значения y приводит к некоторой дополнительной ошибке в прогнозе из-за отклонения y от линии средних значений. Изучите рисунок ниже. Вы можете видеть, что ошибка в прогнозе состоит из двух компонентов:

Ошибка при использовании подобранной линии для оценки линии средних
Ошибка, вызванная отклонением y от линии средних, измеренных по σ2

Рис. 21.Иллюстрируя два компонента ошибки прогноза.

Дисперсия разницы между y и является суммой этих двух дисперсий и формирует основу для стандартной ошибки используемой для прогнозирования. Результирующая форма интервала прогнозирования выглядит следующим образом:

, где x 0 — заданное значение переменной-предиктора, n — количество наблюдений, а tα/2 — критическое значение с ( n – 2) степенями свободы.

Программное обеспечение, такое как Minitab, может вычислять интервалы прогнозирования.Используя данные из предыдущего примера, мы воспользуемся программой Minitab для вычисления 95-процентного интервала прогнозирования для IBI определенного лесного массива площадью 32 км.

Прогнозируемые значения для новых наблюдений
Новые наблюдения	Подходит для	SE Подходит для	95% ИП
1	49.9496	2.38400	(20.1053, 79.7939)

Вы можете повторить этот процесс много раз для нескольких различных значений x и построить интервалы прогнозирования для среднего отклика.

х	95% ИП
20	(13.01, 73.11)
40	(24.77, 84.31)
60	(36.21, 95.83)
80	(47,33, 107,67)
100	(58,15, 119,81)

Обратите внимание, что полосы интервала прогнозирования шире, чем соответствующие полосы доверительного интервала, что отражает тот факт, что мы прогнозируем значение случайной величины, а не оцениваем параметр генеральной совокупности.Мы ожидаем, что прогнозы для отдельного значения будут более изменчивыми, чем оценки среднего значения.

Рисунок 22. Сравнение доверительных интервалов и интервалов прогнозирования.

Преобразования для линеаризации отношений данных

Во многих случаях отношение между x и y нелинейно. Чтобы упростить базовую модель, мы можем преобразовать или преобразовать либо x , либо y , либо и то, и другое, чтобы получить более линейную зависимость.Есть много общих преобразований, таких как логарифмические и обратные. Включение членов более высокого порядка в x также может помочь линеаризовать отношение между x и y . Ниже показаны некоторые распространенные формы диаграмм рассеяния и возможные варианты преобразования. Тем не менее, выбор преобразования часто является скорее результатом проб и ошибок, чем установленными правилами.

Рисунок 23. Примеры возможных преобразований для переменных x и y.

Пример 4

Леснику необходимо создать простую модель линейной регрессии для прогнозирования объема дерева с использованием диаметра на уровне груди (dbh) для деревьев сахарного клена. Он собирает dbh и объем для 236 деревьев сахарного клена и строит зависимость объема от dbh. Ниже приведены диаграмма рассеяния, коэффициент корреляции и результаты регрессии от Minitab.

Рисунок 24. Диаграмма рассеяния объема в зависимости от dbh.

Коэффициент линейной корреляции Пирсона равен 0,894, что указывает на сильную положительную линейную зависимость.Однако диаграмма рассеяния показывает отчетливую нелинейную зависимость.

Регрессионный анализ: объем в сравнении с dbh

Уравнение регрессии: объем = – 51,1 + 7,15 дбч
Предиктор	Коэф.	SE Коэф.	Т	Р
Константа	-51.097	3,271	-15,62	0,000
дбч	7.1500	0,2342	30,53	0,000
С = 19,5820	Р-Кв = 79,9%		R-Sq(adj) = 79,8%

Дисперсионный анализ
Источник	ДФ	нержавеющая сталь	МС	Ф	Р
Регрессия	1	357397	357397	932.04	0,000
Остаточная ошибка	234	89728	383
Всего	235	447125

R2 составляет 79,9%, что указывает на довольно сильную модель, а наклон значительно отличается от нуля.Однако и остаточный график, и остаточный график нормальной вероятности указывают на серьезные проблемы с этой моделью. Преобразование может помочь создать более линейную зависимость между объемом и децибелами.

Рис. 25. Графики невязки и нормальной вероятности.

Объем был преобразован в натуральный логарифм объема и построен в зависимости от dbh (см. диаграмму рассеяния ниже). К сожалению, это мало помогло улучшить линейность этой зависимости. Затем лесничий произвел натуральное логарифмическое преобразование dbh.Диаграмма рассеяния натурального логарифма объема по сравнению с натуральным логарифмом dbh указывает на более линейную зависимость между этими двумя переменными. Коэффициент линейной корреляции равен 0,954.

Рисунок 26. Диаграммы рассеяния натурального логарифма объема в зависимости от dbh и натурального логарифма объема в зависимости от натурального логарифма dbh.

Ниже приведены результаты регрессионного анализа Minitab.

Регрессионный анализ: lnVOL и lnDBH

Уравнение регрессии: lnVOL = – 2.86 + 2,44 лнДБХ
Предиктор	Коэф.	SE Коэф.	Т	Р
Константа	-2,8571	0,1253	-22,80	0,000
лнДБХ	2.44383	0.05007	48,80	0,000
С = 0,327327	Р-Кв = 91,1%	R-Sq(adj) = 91,0%

Дисперсионный анализ
Источник	ДФ	нержавеющая сталь	МС	Ф	Р
Регрессия	1	255.19	255,19	2381,78	0,000
Остаточная ошибка	234	25.07	0,11
Всего	235	280,26

Рис. 27. Графики невязки и нормальной вероятности.

Модель, использующая преобразованные значения объема и dbh, имеет более линейную зависимость и более положительный коэффициент корреляции. Наклон значительно отличается от нуля, а R2 увеличился с 79,9% до 91,1%. Остаточный график показывает более случайный характер, а график нормальной вероятности показывает некоторое улучшение.

Существует много возможных комбинаций преобразования для линеаризации данных. Каждая ситуация уникальна, и пользователю может потребоваться попробовать несколько вариантов, прежде чем выбрать наилучшее преобразование для x или y , или обоих.

Программные решения

Минитаб

Выходные данные Minitab показаны выше в упр. 4.

Excel

Рис. 28. Графики невязки и нормальной вероятности.

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка браузера для приема файлов cookie

Существует множество причин, по которым файл cookie не может быть установлен правильно.Ниже приведены наиболее распространенные причины:

В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.

Коэффициент детерминации – определение, интерпретация, расчет

Что такое коэффициент детерминации?

Коэффициент детерминации (R² или r-квадрат) — это статистическая мера в регрессионной модели, определяющая долю дисперсии зависимой переменной, которая может быть объяснена независимой переменной. Независимая переменная. Независимая переменная — это ввод, предположение или фактор который изменяется, чтобы оценить его влияние на зависимую переменную (результат).. Другими словами, коэффициент детерминации говорит о том, насколько хорошо данные соответствуют модели (степень соответствия).

Хотя коэффициент детерминации дает некоторые полезные сведения о регрессионной модели, при оценке статистической модели не следует полагаться исключительно на показатель. Он не раскрывает информацию о причинно-следственной связи между независимыми и зависимыми переменными. Зависимая переменная. Зависимая переменная — это переменная, значение которой будет изменяться в зависимости от значения другой переменной, называемой независимой переменной., и это не свидетельствует о правильности регрессионной модели. Поэтому пользователь всегда должен делать выводы о модели, анализируя коэффициент детерминации вместе с другими переменными в статистической модели.

Коэффициент детерминации может принимать любые значения от 0 до 1. Кроме того, статистический показатель часто выражается в процентах.

Интерпретация коэффициента детерминации (R²)

Наиболее распространенная интерпретация коэффициента детерминации заключается в том, насколько хорошо регрессионная модель соответствует наблюдаемым данным.Например, коэффициент детерминации 60 % показывает, что 60 % данных соответствуют регрессионной модели. Как правило, более высокий коэффициент указывает на лучшее соответствие модели.

Однако не всегда высокое значение r-квадрата хорошо для регрессионной модели. Качество коэффициента зависит от нескольких факторов, включая единицы измерения переменных, характер переменных, используемых в модели, и применяемое преобразование данных. Таким образом, иногда высокий коэффициент может указывать на проблемы с регрессионной моделью.

Не существует универсального правила, определяющего, как включать коэффициент детерминации в оценку модели. Контекст, в котором основан прогноз или эксперимент, чрезвычайно важен, и в разных сценариях выводы статистической метрики могут различаться.

Расчет коэффициента

Математически Коэффициент определения можно найти с помощью следующей формулы:

, где:

SS _Revere — сумма квадратов из-за регрессии (

SS _total – Общая сумма квадратов

смыслы прямые.

Общая сумма квадратов измеряет вариацию наблюдаемых данных (данные, используемые в регрессионном моделировании). Сумма квадратов из-за регрессии измеряет, насколько хорошо модель регрессии представляет данные, которые использовались для моделирования.

Дополнительные ресурсы

Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI: .Кроме того, концепции статистики могут помочь инвесторам контролировать

Биномиальное распределениеБиномиальное распределениеБиномиальное распределение — это обычное распределение вероятностей, которое моделирует вероятность получения одного из двух результатов при заданном числе параметров

Центральная предельная теоремаЦентральная предельная теоремаЦентральная предельная теорема утверждает, что случайной величины предполагает близкое к нормальному или нормальное распределение, если размер выборки большой

Регрессионный анализРегрессионный анализРегрессионный анализ представляет собой набор статистических методов, используемых для оценки отношений между зависимой переменной и одной или несколькими независимыми переменными.

РубрикаРазное

Детерминация корреляция: Что такое корреляция и детерминация простыми словами? В чём их отличие?

Линейная регрессия и корреляция (четыре) коэффициент линейной корреляции и коэффициент детерминации (вывод принципов и формул)

1. Коэффициент корреляции

2. Коэффициент детерминации (коэффициент детерминации)

3. Проверка гипотезы коэффициента корреляции.

（1）= 0 проверка гипотез

（2）= Проверка гипотезы C

（3） =Проверка гипотез

Линейный коэффициент корреляции Пирсона — statanaliz.info

Выборочный коэффициент корреляции

Как посчитать коэффициент корреляции в Excel

Расчет доверительного интервала для коэффициента корреляции в Excel

Несколько важных замечаний

Функция КВПИРСОН

Описание

Синтаксис

Замечания

Пример

Python, корреляция и регрессия: часть 2 / Хабр

Регрессия

Линейные уравнения

Остатки

Обычные наименьшие квадраты

Наклон и пересечение

Интерпретация

Визуализация

Допущения

Качество подгонки и R-квадрат

Множественная линейная регрессия

Коэффициент детерминации — Справочник химика 21

Вычисление коэффициента детерминации

Способ 1: вычисление коэффициента детерминации при линейной функции

Способ 2: вычисление коэффициента детерминации в нелинейных функциях

Способ 3: коэффициент детерминации для линии тренда

Помогла ли вам эта статья?

В чем разница между коэффициентом детерминации и коэффициентом корреляции? – Гаурав Бансал

2.7 — Коэффициенты определения и корреляции Примеры

10.6: Коэффициент детерминации

Pearson Product-Moment Correlation — рекомендации по интерпретации коэффициента, обнаружению выбросов и типу необходимых переменных.

Как обнаружить выбросы?

Почему так важно проверять выбросы?

Можете ли вы установить причинно-следственную связь?

Как сообщить о результатах корреляции продукта и момента Пирсона?

Могу ли я определить, является ли связь статистически значимой?

Что такое коэффициент детерминации?

Ссылка

Корреляция и простая линейная регрессия – Биометрия природных ресурсов

Коэффициент линейной корреляции

Примеры положительной корреляции

Примеры отрицательной корреляции

Простая линейная регрессия

Пример 1

Пример 2

Коэффициент детерминации

Графики невязки и нормальной вероятности

Модель населения

Оценка параметра

Доверительные интервалы и тесты значимости для параметров модели

Пример 3

Регрессионный анализ: IBI в сравнении с площадью леса

Доверительный интервал для

Интервалы предсказания

Преобразования для линеаризации отношений данных

Пример 4

Регрессионный анализ: объем в сравнении с dbh

Регрессионный анализ: lnVOL и lnDBH

Программные решения

Минитаб

Excel

Произошла ошибка при настройке пользовательского файла cookie

Настройка браузера для приема файлов cookie

Почему этому сайту требуются файлы cookie?

Что сохраняется в файле cookie?

Коэффициент детерминации – определение, интерпретация, расчет

Что такое коэффициент детерминации?

Интерпретация коэффициента детерминации (R²)

Расчет коэффициента

Дополнительные ресурсы

Добавить комментарий Отменить ответ