Действия с корнями и степенями формулы: Правила действий со степенями и корнями, примеры.

Содержание

Корни и степени, возведение в степень, извлечение корня

Формулы преобразования степени числа. Свойства степени

(ab)ⁿ=aⁿbⁿ
Степень произведения двух чисел равна произведению каждого из сомножителей в этой степени

( a / b )ⁿ = aⁿ / bⁿ
Степень частного равна частному этих чисел, каждое из которых возведено в данную степень

aⁿ a^m = a^n+m
Произведение двух одинаковых чисел в разную степень равно этому числу в степени, равной сумме этих степеней

aⁿ / a^m = a^n-m если n > m
Частное двух одинаковых чисел в разной степени равно этому числу в степени разности числителя и знаменателя, при условии, что степень числа в числителе больше степени в знаменателе.

(aⁿ )^m=a^nm
Число в степени, возводимое в степень равно числу в степени, равной их произведению

Формулы преобразования корня числа. Свойства корня

ⁿ√0 = 0
Корень произвольной степени из нуля равен нулю

ⁿ√1 = 1
Корень произвольной степени из единицы равен единице

Корень числа произвольной степени, возведенный в эту же степень, равен этому числу.

Корень произвольной степени от произведения равен произведению корней этой же степени каждого из множителей

Корень произвольной степени частного двух чисел равен частному корней этой степени этих же чисел

Содержание главы:
Задача про бросание гранаты | Описание курса | Дробь в степени числа.

Нахождение дробной степени числа

Корень и его свойства. Подробная теория с примерами (ЕГЭ — 2021)

Как умножать корни? На этот вопрос помогает ответить самое простое и базовое свойство: $ \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}$

Начнем с простенького:

$ \sqrt{5}\cdot \sqrt{2}=\sqrt{10}$

$ \sqrt{2}\cdot \sqrt{3}=\sqrt{6}$

Корни из получившихся чисел ровно не извлекаются? Не беда – вот вам такие примеры:

$ \sqrt{2}\cdot \sqrt{8}=\sqrt{16}=4$

$ \sqrt{12,5}\cdot \sqrt{2}=\sqrt{25}=5$

А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:

$ \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{10}=\sqrt{100}=10$

С этим вроде все ясно. Едем дальше. А если перед нами такое выражение:

$ 3\sqrt{5}$

Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из $ 9$!

$ 3\sqrt{5}=\sqrt{9}\cdot \sqrt{5}=\sqrt{45}$.

Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:

$ 3\sqrt{10}-\sqrt{45}\cdot \sqrt{2}=\sqrt{90}-\sqrt{90}=0$.

Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно!

Только надо помнить, что вносить под знак корня четной степени мы можем только положительные числа.

Посмотрим, где это еще может пригодиться. Например, в задаче требуют сравнить два числа:

Что больше: $ 3\sqrt{7}\ или\ 2\sqrt{17}$?

Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня? Тогда вперед:

$ 3\sqrt{7}=\sqrt{9\cdot 7}=\sqrt{63}$

$ 2\sqrt{17}=\sqrt{4\cdot 17}=\sqrt{68}$

Ну и, зная, что чем больше число под знаком корня, тем больше сам корень! Т.е. если $ 68>63$, значит, $ 68>63$.

Отсюда твердо делаем вывод, что $ 3\sqrt{7}<2\sqrt{17}$. И никто не убедит нас в обратном!

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

$ \sqrt{98}=\sqrt{49\cdot 2}=\sqrt{49}\cdot \sqrt{2}=7\sqrt{2}$

Можно было пойти по иному пути и разложить на другие множители:

$ \sqrt{98}=\sqrt{7\cdot 14}$

Что дальше? А дальше раскладываем на множители до самого конца:

$ \sqrt{98}=\sqrt{7\cdot 14}=\sqrt{7\cdot 7\cdot 2}=\sqrt{{{7}^{2}}\cdot 2}=7\sqrt{2}$

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

$ \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}$

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

$ \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}=\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}$

Разве это конец? Не останавливаемся на полпути!

$ \begin{array}{l}\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 12\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}=\\=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 2\cdot 2\cdot 3\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}\end{array}$

На простые множители разложили. Что дальше?

А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

$ \begin{array}{l}\sqrt{5\cdot 3\cdot 3\cdot 2\cdot 2\cdot 3\cdot 5\cdot 2\cdot 3\cdot 2}=\sqrt{5\cdot 5\cdot 3\cdot 3\cdot 3\cdot 3\cdot 2\cdot 2\cdot 2\cdot 2}=\\=\sqrt{25}\cdot \sqrt{81}\cdot \sqrt{16}=5\cdot 9\cdot 4=180\end{array}$

Вот и все, не так все и страшно, правда?

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

$ \sqrt{15}\cdot \sqrt{54}\cdot \sqrt{10}=?$

Получилось $ 90$? Молодец, все верно!

А теперь попробуй вот такой пример решить:

$ \sqrt{4225}=?$

А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам. Ну что, начнем раскладывать $ 4225$ на множители?

Сразу заметим, что поделить число на $ 5$ (вспоминаем признаки делимости):

$ \sqrt{4225}=\sqrt{845\cdot 5}=\sqrt{169\cdot 5\cdot 5}=\sqrt{13\cdot 13\cdot 5\cdot 5}=5\cdot 13=65$

А теперь попробуй сам (опять же, без калькулятора!):

$ \sqrt{2304}=?$

Ну что, получилось $ 48$? Молодец, все верно!

Корень n-й степени и его свойства

Корень n-й степени и его свойства

Что такое корень n-й степени? Как извлечь корень?

В восьмом классе вы уже успели познакомиться с квадратным корнем. Решали типовые примеры с корнями, применяя те или иные свойства корней. Также решали квадратные уравнения, где без извлечения квадратного корня — никак. Но квадратный корень — это лишь частный случай более широкого понятия — корня n-й степени.

Помимо квадратного, бывает, например, кубический корень, корень четвёртой, пятой и более высоких степеней. И для успешной работы с такими корнями неплохо бы всё-таки для начала быть на «ты» с корнями квадратными.) Поэтому у кого проблемы с ними — настоятельно рекомендую повторить.

Извлечение корня — это одна из операций, обратных возведению в степень.) Почему «одна из»? Потому, что, извлекая корень, мы ищем основание по известным степени и показателю. А есть ещё одна обратная операция — нахождение показателя по известным степени и основанию. Такая операция называется нахождением

логарифма. Она более сложная, чем извлечение корня и изучается в старших классах.)

Итак, знакомимся!

Во-первых, обозначение. Квадратный корень, как мы уже знаем, обозначается вот так: . Называется этот значок очень красиво и научно — радикал. А как обозначают корни других степеней? Очень просто: над «хвостиком» радикала дополнительно пишут показатель той степени, корень которой ищется. Если ищется кубический корень, то пишут тройку: . Если корень четвёртой степени, то, соответственно, . И так далее.) В общем виде корень n-й степени обозначается вот так:

, где .

Число a, как и в квадратных корнях, называется подкоренным выражением, а вот число n для нас здесь новое. И называется показателем корня.

Как извлекать корни любых степеней? Так же, как и квадратные — сообразить, какое число в n-й степени даёт нам число a.)

Как, например, извлечь кубический корень из 8? То есть ? А какое число в кубе даст нам 8? Двойка, естественно.) Вот и пишут:

Или . Какое число в четвёртой степени даёт 81? Тройка.) Значит,

А корень десятой степени из 1? Ну, ежу понятно, что единица в любой степени (в том числе и в десятой) равна единице. ) То есть:

и вообще .

С нулём та же история: ноль в любой натуральной степени равен нулю. Стало быть, .

Как видим, по сравнению с квадратными корнями, здесь уже посложнее соображать, какое число в той или иной степени даёт нам подкоренное число a. Сложнее подбирать ответ и проверять его на правильность возведением в степень n. Ситуация существенно облегчается, если знать в лицо степени популярных чисел. Поэтому сейчас — тренируемся. 🙂 Распознаём степени!)

Ответы (в беспорядке):

Да-да! Ответов побольше, чем заданий.) Потому, что, к примеру, 2⁸, 4⁴ и 16²– это всё одно и то же число 256.

Потренировались? Тогда считаем примерчики:

Ответы (тоже в беспорядке): 6; 2; 3; 2; 3; 5.

Получилось? Великолепно! Движемся дальше.)

Ограничения в корнях. Арифметический корень n-й степени.

В корнях n-й степени, как и в квадратных, тоже есть свои ограничения и свои фишки. По своей сути, они ничем не отличаются от таковых ограничений для квадратных корней.

Например, попробуем посчитать вот такой корень:

Не подбирается ведь, да? Что 3, что -3 в четвёртой степени будет +81. 🙂 И с любым корнем чётной степени из отрицательного числа будет та же песня. А это значит, что извлекать корни чётной степени из отрицательных чисел нельзя. Это запретное действие в математике. Такое же запретное, как и деление на ноль. Поэтому такие выражения, как , и тому подобные — не имеют смысла.

Зато корни

нечётной степени из отрицательных чисел — пожалуйста!

Например, ; , и так далее.)

А из положительных чисел можно со спокойной душой извлекать любые корни, любых степеней:

В общем, понятно, думаю. ) И, кстати, корень совершенно не обязан извлекаться ровно. Это просто примеры такие, чисто для понимания.) Бывает, что в процессе решения (например, уравнений) выплывают и довольно скверные корни. Что-нибудь типа . Из восьмёрки кубический корень извлекается отлично, а тут под корнем семёрка. Что делать? Ничего страшного. Всё точно так же. – это число, которое при возведении в куб даст нам 7. Только число это очень некрасивое и лохматое. Вот оно:

Причём, это число никогда не кончается и не имеет периода: цифры следуют совершенно беспорядочно. Иррациональное оно… В таких случаях ответ так и оставляют в виде корня.) А вот если корень извлекается чисто (к примеру, ), то, естественно, надо корень посчитать и записать:

Идём дальше.

Снова берём наше подопытное число 81 и извлекаем из него корень четвёртой степени:

Потому, что три в четвёртой будет 81. Ну, хорошо! Но ведь и минус три в четвёртой тоже будет 81!

Получается неоднозначность:

И, чтобы её устранить, так же, как и в квадратных корнях, ввели специальный термин: арифметический корень n-й степени из числа a – это такое неотрицательное число, n-я степень которого равна a.

А ответ с плюсом-минусом называется по-другому — алгебраический корень n-й степени. У любой чётной степени алгебраическим корнем будет два противоположных числа. В школе же работают только с арифметическими корнями. Поэтому отрицательные числа в арифметических корнях попросту отбрасываются. Например, пишут: . Сам плюс, конечно же, не пишут: его

подразумевают.

Всё, казалось бы, просто, но… А как же быть с корнями нечётной степени из отрицательных чисел? Ведь там-то всегда при извлечении получается отрицательное число! Так как любое отрицательное число в нечётной степени также даёт отрицательное число. А арифметический корень работает только с неотрицательными числами! На то он и арифметический.)

В таких корнях делают вот что: выносят минус из-под корня и ставят перед корнем. Вот так:

В таких случаях говорят, что выражен через арифметический (т.е. уже неотрицательный) корень .

Но есть один пунктик, который может вносить путаницу, — это решение простеньких уравнений со степенями. Например, вот такое уравнение:

Пишем ответ: . На самом деле, этот ответ — всего-навсего сокращённая запись двух ответов:

Непонятка здесь заключается в том, что чуть выше я уже написал, что в школе рассматриваются только неотрицательные (т.е. арифметические) корни. А тут один из ответов с минусом… Как быть? Да никак! Знаки здесь — это результат решения уравнения. А сам корень — величина всё равно неотрицательная! Смотрите сами:

Ну как, теперь понятнее? Со скобочками?)

С нечётной степенью всё гораздо проще — там всегда получается один корень. С плюсом или с минусом. Например:

Итак, если мы просто извлекаем корень (чётной степени) из числа, то мы всегда получаем один неотрицательный результат. Потому что это — арифметический корень. А вот, если мы решаем уравнение с чётной степенью, то мы получаем два противоположных корня, поскольку это — решение уравнения.

С корнями нечётных степеней (кубическими, пятой степени и т.д.) проблем никаких. Извлекаем себе и не паримся со знаками. Плюс под корнем — значит, и результат извлечения с плюсом. Минус — значит, минус.)

А теперь настал черёд познакомиться со свойствами корней. Некоторые уже будут нам знакомы по квадратным корням, но добавится и несколько новых. Поехали!

Свойства корней. Корень из произведения.

Это свойство уже знакомо нам из квадратных корней. Для корней других степеней всё аналогично:

То есть, корень из произведения равен произведению корней из каждого множителя отдельно.

Если показатель n чётный, то оба подкоренных числа a и b должны быть, естественно, неотрицательными, иначе формула смысла не имеет. В случае нечётного показателя ограничений никаких нет: выносим минусы из-под корней вперёд и дальше работаем с арифметическими корнями.)

Как и в квадратных корнях, здесь эта формула одинаково полезна как слева направо, так и справа налево. Применение формулы слева направо позволяет извлекать корни из произведения. Например:

Эта формула, кстати говоря, справедлива не только для двух, а для любого числа множителей. Например:

Также по этой формуле можно извлекать корни из больших чисел: для этого число под корнем раскладывается на множители поменьше, а дальше извлекаются корни отдельно из каждого множителя.

Например, такое задание:

Число достаточно большое. Извлекается ли из него корень ровно — тоже ~~без калькулятора~~ непонятно. Хорошо бы его разложить на множители. На что точно делится число 3375? На 5, похоже: последняя цифра — пятёрка.) Делим:

Ой, снова на 5 делится! 675:5 = 135. И 135 опять на пятёрку делится. Да когда ж это кончится!)

135:5 = 27. С числом 27 всё уже ясно — это тройка в кубе. Значит,

Тогда:

Извлекли корень по кусочкам, ну и ладно.)

Или такой пример:

Снова раскладываем на множители по признакам делимости. Каким? На 4, т.к. последняя парочка цифр 40 — делится на 4. И на 10, т.к. последняя цифра — ноль. Значит, можно поделить одним махом сразу на 40:

Про число 216 мы уже знаем, что это шестёрка в кубе. Стало быть,

А 40, в свою очередь, можно разложить как . Тогда

И тогда окончательно получим:

Чисто извлечь корень не вышло, ну и ничего страшного. Всё равно мы упростили выражение: мы же знаем, что под корнем (хоть квадратным, хоть кубическим — любым) принято оставлять самое маленькое число из возможных. ) В этом примере мы проделали одну весьма полезную операцию, тоже уже знакомую нам из квадратных корней. Узнаёте? Да! Мы вынесли множители из-под корня. В данном примере мы вынесли двойку и шестёрку, т.е. число 12.

Как вынести множитель за знак корня?

Вынести множитель (или множители) за знак корня очень просто. Раскладываем подкоренное выражение на множители и извлекаем то, что извлекается.) А что не извлекается — так и оставляем под корнем. Смотрите:

Раскладываем число 9072 на множители. Так как у нас корень четвёртой степени, в первую очередь пробуем разложить на множители, являющиеся четвёртыми степенями натуральных чисел — 16, 81 и т.д.

Попробуем поделить 9072 на 16:

Поделилось!

А вот 567, похоже, делится на 81:

Значит, .

Тогда

Свойства корней. Умножение корней.

Рассмотрим теперь обратное применение формулы — справа налево:

На первый взгляд, ничего нового, но внешность обманчива.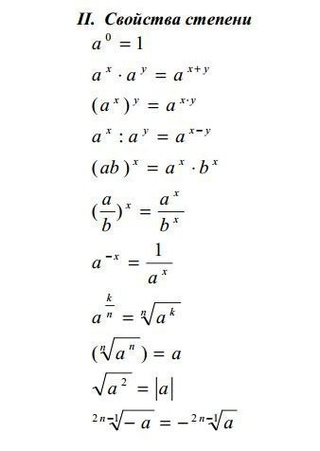 ) Обратное применение формулы значительно расширяет наши возможности. Например:

Хм, ну и что тут такого? Умножили и всё. Здесь и впрямь ничего особенного. Обычное умножение корней. А вот такой пример!

Отдельно из множителей корни чисто не извлекаются. Зато из результата — отлично. )

Опять же формула справедлива для любого числа множителей. Например, надо посчитать вот такое выражение:

Здесь главное — внимание. В примере присутствуют разные корни — кубические и четвёртой степени. И ни один из них точно не извлекается…

А формула произведения корней применима только к корням с одинаковыми показателями. Поэтому сгруппируем в отдельную кучку кубические корни и в отдельную — четвёртой степени. А там, глядишь, всё и срастётся.))

И калькулятора не понадобилось.)

Как внести множитель под знак корня?

Следующая полезная вещь — внесение числа под корень. Например:

Можно ли убрать тройку внутрь корня? Элементарно! Если тройку превратить в корень, то сработает формула произведения корней. Итак, превращаем тройку в корень. Раз у нас корень четвёртой степени, то и превращать будем тоже в корень четвёртой степени.) Вот так:

Тогда

Корень, между прочим, можно сделать из любого неотрицательного числа. Причём той степени, какой хотим (всё от конкретного примера зависит). Это будет корень из n-й степени этого самого числа:

А теперь — внимание! Источник очень грубых ошибок! Я не зря здесь сказал про неотрицательные числа. Арифметический корень работает только с такими. Если у нас в задании где-то затесалось отрицательное число, то либо минус так и оставляем, перед корнем (если он снаружи), либо избавляемся от минуса под корнем, если он внутри. Напоминаю, если под корнем чётной степени получается отрицательное число, то выражение не имеет смысла.

Например, такое задание. Внести множитель под знак корня:

Если мы сейчас внесём под корень минус два, то жестоко ошибёмся:

В чём здесь ошибка? А в том, что четвёртая степень, в силу своей чётности, благополучно «съела» этот минус, в результате чего заведомо отрицательное число превратилось в положительное . А верное решение выглядит так:

В корнях нечётных степеней минус хоть и не «съедается», но его тоже лучше оставлять снаружи:

Здесь корень нечётной степени — кубический, и мы имеем полное право минус тоже загнать под корень. Но предпочтительнее в таких примерах минус также оставлять снаружи и писать ответ выраженным через арифметический (неотрицательный) корень , поскольку корень хоть и имеет право на жизнь, но арифметическим не является.

Итак, с внесением числа под корень тоже всё ясно, я надеюсь.) Переходим к следующему свойству.

Свойства корней. Корень из дроби. Деление корней.

Это свойство также полностью повторяет таковое для квадратных корней. Только теперь мы его распространяем на корни любой степени:

Корень из дроби равен корню из числителя, делённому на корень из знаменателя.

Если n чётно, то число a должно быть неотрицательным, а число b – строго положительным (на ноль делить нельзя). В случае нечётного показателя единственным ограничением будет .

Это свойство позволяет легко и быстро извлекать корни из дробей:

Идея понятна, думаю. Вместо работы с дробью целиком мы переходим к работе отдельно с числителем и отдельно со знаменателем.) Если дробь десятичная или, о ужас, смешанное число, то предварительно переходим к обыкновенным дробям:

А теперь посмотрим, как эта формула работает справа налево. Здесь тоже выявляются очень полезные возможности. Например, такой примерчик:

Из числителя и знаменателя корни ровно не извлекаются, зато из всей дроби — прекрасно.) Можно решить этот пример и по-другому — вынести в числителе множитель из-под корня с последующим сокращением:

Как вам будет угодно. Ответ всегда получится один — правильный. Если ошибок не наляпать по дороге.)

Итак, с умножением/делением корней разобрались. Поднимаемся на следующую ступеньку и рассматриваем третье свойство — корень в степени и корень из степени.

Корень в степени. Корень из степени.

Как возвести корень в степень? Например, пусть у нас есть число . Можно это число возвести в степень? В куб, например? Конечно! Помножить корень сам на себя три раза, и — по формуле произведения корней:

Здесь корень и степень как бы взаимоуничтожились или скомпенсировались. Действительно, если мы число, которое при возведении в куб даст нам тройку, возведём в этот самый куб, то что получим? Тройку и получим, разумеется! И так будет для любого неотрицательного числа. В общем виде:

Если показатели степени и корня разные, то тоже никаких проблем. Если знать свойства степеней.)

Если показатель степени меньше показателя корня, то просто загоняем степень под корень:

В общем виде будет:

Идея понятна: возводим в степень подкоренное выражение, а дальше упрощаем, вынося множители из-под корня, если это возможно. Если n чётно, то a должно быть неотрицательным. Почему — понятно, думаю.) А если n нечётно, то никаких ограничений на a уже нету:

Разберёмся теперь с корнем из степени. То есть, в степень будет возводиться уже не сам корень, а подкоренное выражение. Здесь тоже ничего сложного, но простора для ошибок значительно больше. Почему? Потому, что в игру вступают отрицательные числа, которые могут вносить путаницу в знаках. Пока начнём с корней нечётных степеней — они гораздо проще.

Пусть у нас есть число 2. Можно его возвести в куб? Конечно!

А теперь — обратно извлечём из восьмёрки кубический корень:

С двойки начали, к двойке же и вернулись.) Ничего удивительного: возведение в куб скомпенсировалось обратной операцией — извлечением кубического корня.

Другой пример:

Здесь тоже всё путём. Степень и корень друг друга скомпенсировали. В общем виде для корней нечётных степеней можно записать такую формулку:

Эта формула справедлива для любого действительного числа a. Хоть положительного, хоть отрицательного.

То есть, нечётная степень и корень этой же степени всегда друг друга компенсируют и получается подкоренное выражение. 🙂

А вот с чётной степенью этот фокус может уже не пройти. Смотрите сами:

Здесь пока ничего особенного. Четвёртая степень и корень четвёртой же степени тоже друг друга уравновесили и получилась просто двойка, т.е. подкоренное выражение. И для любого неотрицательного числа будет то же самое. А теперь всего лишь заменим в этом корне два на минус два. То есть, посчитаем вот такой корень:

Минус у двойки благополучно «сгорел» из-за четвёртой степени. И в результате извлечения корня (арифметического!) мы получили положительное число. Было минус два, стало плюс два.) А вот если бы мы просто бездумно «сократили» степень и корень (одинаковые же!), то получили бы

Что является грубейшей ошибкой, да.

Поэтому для чётного показателя формула корня из степени выглядит вот так:

Здесь добавился нелюбимый многими знак модуля, но в нём страшного ничего нет: благодаря ему, формула также работает для любого действительного числа a. И модуль просто отсекает минусы:

И так далее.) Эта формула — аналог формулы корня квадратного из квадрата:

Только в корнях n-й степени появилось дополнительное разграничение на чётные и нечётные степени. Чётные степени, как мы видим, более капризные, да.)

А теперь рассмотрим новое полезное и весьма интересное свойство, уже характерное именно для корней n-й степени: если показатель корня и показатель степени подкоренного выражения умножить (разделить) на одно и то же натуральное число, то значение корня не изменится.

Чем-то напоминает основное свойство дроби, не правда ли? В дробях мы тоже числитель и знаменатель можем умножать (делить) на одно и то же число (кроме нуля). На самом деле, это свойство корней — тоже следствие основного свойства дроби. Когда мы познакомимся со степенью с рациональным показателем, то всё станет ясно. Что, как и откуда. )

Прямое применение этой формулы позволяет нам упрощать уже совершенно любые корни из любых степеней. В том числе, если показатели степени подкоренного выражения и самого корня разные. Например, надо упростить вот такое выражение:

Поступаем просто. Выделяем для начала под корнем четвёртую степень из десятой и — вперёд! Как? По свойствам степеней, разумеется! Выносим множитель из-под корня или работаем по формуле корня из степени.

А вот упростим, используя как раз это свойство. Для этого четвёрку под корнем представим как :

И теперь — самое интересное — сокращаем мысленно показатель под корнем (двойку) с показателем корня (четвёркой)! И получаем:

Вся цепочка преобразований выглядит так:

Или такой пример:

Это было прямое применение формулы. А вот обратное применение ещё сильнее повышает наш математический уровень. Сомневаетесь? Напрасно! Дело в том, что обратное применение этой формулы справа налево позволяет нам сравнивать различные корни. Очень мощная штука!

Как сравнивать корни?

Допустим, надо (без калькулятора!) сравнить два числа:

Корень квадратный из пяти — это двойка с хвостиком. Корень кубический из десяти — это тоже двойка с хвостиком. А вот какой из двух хвостиков длиннее, а какой короче — вопрос. С ходу так и не скажешь. Пока показатели корней — разные.) А вот, если их как-то преобразовать к одинаковым, то всё, глядишь, и наладится! Для этого ищем наименьшее общее кратное показателей корней. В данном случае показатели корней равны 2 и 3, т.е. оба корня будем приводить к шестёрке. Как? По вышеупомянутому свойству:

Берём . Как корень из квадратного превратить в корень шестой степени, но так, чтобы суть выражения не изменилась? Чтобы получить шестёрку в показателе корня, надо исходный показатель корня 2 домножить на 3. Это нам надо. Но тогда и пятёрку под корнем придётся дополнительно возвести в степень 3 (т. е. в куб): это уже математике надо. Значит,

С числом всё аналогично. Только десятку под корнем будем дополнительно возводить в квадрат:

Теперь дело за малым — сравнить два числа и .

Ясно, что , а значит, и и, стало быть,

Если перед корнями тусуются какие-то множители, то убираем их внутрь корней и — по накатанной колее. Например, такое задание:

Сравнить и .

Первым делом вносим множители под корни:

А теперь — приводим оба корня к одному показателю. К четвёрке.)

Ну, число уже и так приведено и уже готово для сравнения. А вот преобразуем:

Вот теперь всё и прояснилось: , поэтому .

А это значит, что

Этот принцип сравнения одинаковых корней по подкоренным выражениям, строго говоря, основывается на монотонном возрастании функции . То есть, большему числу соответствует и больший корень. И наоборот.) В разделе по функциям и графикам мы этому факту уделим отдельное внимание, а здесь мы просто им пользуемся. Себе во благо. 🙂

Что ж, осталось последнее усилие. Собираем волю в кулак и знакомимся с последним (и тоже новым для нас) свойством корней — корень под корнем.

Как извлечь корень из корня?

Это свойство на самом деле очень простое и по своей сути очень похоже на возведение степени в степень. Так как является обратным к этой операции.) Вот как оно выглядит:

Чтобы извлечь корень из корня, надо перемножить показатели корней.

Это свойство позволяет несколько вложенных корней заменить одним корнем. Например:

Или такой пример:

Причём вложений может быть сколько угодно — формула всё равно сработает:

Как видим, никаких хитростей. Просто перемножаем показатели и считаем (если считается).

Вот, собственно, всё что я пока хотел рассказать.)) Следующим этапом нашей работы с корнями будет преобразование иррациональных выражений. Но это — в следующий раз.

А теперь, как всегда, делаем задания.

Задание 1

Вычислить:

Задание 2

Вычислить:

Задание 3

Найти значение выражения:

Задание 4

Вынести множитель из-под знака корня:

Внести множитель под знака корня:

Задание 5

Решите уравнение:

Задание 6

Вычислите:

Ответы в беспорядке: 1,2; ; 2; ; 3; 6; ; 20; ; 72; 2,1; 5; 0,4; -2; ; 12; 6; 14; 4; 20/3; ; -8; ; ; 20; 42.

Всё решилось? Одной левой? Великолепно! Корни — не ваш камень преткновения.) Не всё получилось? Не беда! Не ошибается тот, кто ничего не делает.)

Действия со степенями с примерами решения

Содержание:

Поговорим о действиях со степенями
Пример 1:
Отрицательные степени
Пример 2:
Пример 3:

Поговорим о действиях со степенями

Пусть — натуральные числа. Тогда То есть — это указание умножить число само на себя раз. Пример. Обсуждение. А что такое ? Это Типовая ошибка. Пожалуйста, не путайте умножение и сложение. Еще раз повторим:

Для действий со степенями существуют ровно три базовые формулы, а все остальные формулы выводятся из них. Дальше мы узнаем, что бывают различные степени, в том числе отрицательные и дробные (т. е. ). Базовые формулы верны для любых степеней. По для натуральных степеней их легко проверить и вывести. Итак, давайте перейдем к формулам.

Обсуждение.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

В какой степени? Сколько раз мы умножали 2 само на себя? Обратите внимание, какую операцию мы произвели со степенями. Л теперь продолжите формулу:

Обсуждение. Продолжим формулу.

Какую операцию мы произвели со степенями?

А теперь продолжите формулу:

Замечание Мы увидели, что То есть

Возможно вам будут полезны данные страницы:

Пример 1:

На игре формул строится алгоритм быстрого возведения в степень. Свойства степени с натуральным показателем.

Эти свойства верны и для степени с целым и рациональным показателями. Действия со степенями.

Упростите выражения:

Отрицательные степени

Натуральные степени имели интуитивно понятный смысл. Дальше мы будем говорить о степенях, которые вводятся определениями. То есть мы сами договариваемся о том, какой смысл они имеют.

В этом случаи мы используем обозначение

Мы договоримся:

Пример 2:

Теперь осталось обсудить отрицательные и дробные степени. Можно понимать так: отрицательная степень — это «лифт», перемещающий все, кроме минуса, в другую часть дроби: сверху-вниз, снизу вверх. Минус при вынесении его из отрицательной степени никогда не меняет знак самого выражения!

Проще говоря: посмотрите на формулу. В левой части имеется минус в степени, а в правой части минуса нет. Разберем решение некоторых типовых задач из ЕГЭ. Будем разбирать по шагам. Будем использовать таблицу степеней.

Пример 3:

Пример. Как я это узнала? Знаю, что и сдвиг равен трем знакам. Можете проверить умножением. Пример. и сдвиг равен четырем знакам.

Алгебра. Ч. I-II. Киселев А.П.2

ОГЛАВЛЕНИЕ. Ч.II.

Уроки алгебры 3
Предисловие 6
Глава 1 ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ СО СТЕПЕНЯМИ И КОРНЯМИ
I. Возведение в степень 7
1. Действие возведения в степень (7). 2. Степень отрицательного числа (7). 3. Возведение в степень одночленов (7).
II. Возведение в квадрат многочлена 8
4. Вывод формулы (8). 5. Замечание о знаках (9).
III. Понятие об иррациональных числах 10
6. Соизмеримые и несоизмеримые отрезки (10). 7. Понятие об измерении (10). 8. Иррациональные числа и их приближённые значения (11). 9. Равенство и неравенство между иррациональными числами. Вещественные числа (12). 10. Определение действий над иррациональными числами (13). 11. Извлечение корня. Определение (14). 12. Приближённые корни любой степени (15).
IV. Преобразование иррациональных выражений 16
13. Рациональные и иррациональные алгебраические выражения (16). 14. Основное свойство радикала (17). 15. Извлечение арифметического корня из произведения, из степени и из дроби (18). 16. Простейшие преобразования радикалов (19). 17. Подобные радикалы (20). 18. Действия над иррациональными одночленами (21).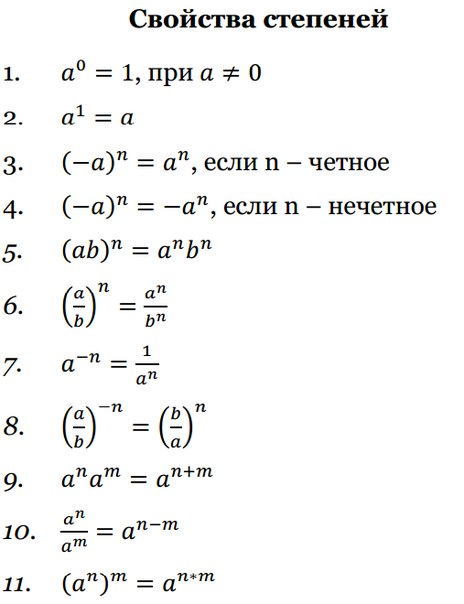 19. Действия над иррациональными многочленами (24). 20.Освобождение знаменателя дроби от радикалов (24).
V. Иррациональные уравнения 26
21. Задача (26). 22. Посторонние решения (27). 23. Освобождение уравнения от двух квадратных радикалов (28).

Глава 2 ФУНКЦИИ И ИХ ГРАФИКИ
I. Функциональная зависимость 29
24. Постоянные и переменные величины (29). 25. Аргумент и функция (30). 26. Три способа выражения функциональной зависимости (31). 27. Метод координат (32). 28. Определение положения точки на плоскости (34).
II. Прямая и обратная пропорциональность 35
29. Прямая пропорциональная зависимость (35). 30. Общее определение пропорциональной зависимости (36). 31. Обратная пропорциональная зависимость (36). 32. Общее определение обратной пропорциональной зависимости (37). 33. График прямой пропорциональной зависимости (38). 34. Изменение положения прямой при изменении коэффициента пропорциональности (39). 35. График обратной пропорциональности (40).
III. Линейная функция 42
36. Двучлен первой степени. Задача (42). 37. График двучлена первой степени (43). 38. Изменение двучлена у = кх + + Ъ с изменением х (45). 39. Замечания (45). 40. Построение прямой у = кх + Ъ по двум точкам (46).

Глава 3 КВАДРАТИЧНАЯ ФУНКЦИЯ
I. Дополнительные сведения о квадратных уравнениях 48
41. Формула корней квадратного уравнения (48). 42. Дискриминант (48). 43. Свойства корней квадратного уравнения (теорема Виета) (49). 44. Трёхчлен второй степени (51). 45. Разложение трёхчлена второй степени (51).
II. График квадратичной функции 53
46. График функции у = х2 (53). 47. График функции у = ах2 (55). 48. График функции у = ах2 + Ь (56). 49. График трёхчлена второй степени (56). 50. Графический способ решения квадратного уравнения (59). 51. Биквадратное уравнение (61). 52. Уравнения, левая часть которых разлагается на множители, а правая есть нуль (62). 53. Двучленное уравнение (63). 54. Ре¬шение двучленных уравнений третьей степени (63). 55. Различные значения корня (64). 56. Трёхчленное уравнение (65).
III. Системы уравнений второй степени 66
57. Степень уравнения с несколькими неизвестными (66). 58. Общий вид полного уравнения второй степени с двумя неизвестными (66). 59. Системы двух уравнений, из которых одно первой степени, а другое — второй (66). 60. Искусственные приёмы (67). 61. Система двух уравнений, из которых каждое второй степени (69). 62. Графический способ решения систем уравнений второй степени (70).

Глава 4 НЕРАВЕНСТВА
I. Неравенства первой степени 73
63. Предварительное замечание (73). 64. Основные свойства неравенств (73). 65. Вопросы относительно неравенств (74). 66. Равносильные неравенства (74). 67. Теорема 1 (75). 68. Теорема 2 (75). 69. Теорема 3 (77). 70. Доказательство неравенства (78). 71. Решение неравенства первой степени с одним неизвестным (78). 72. Два неравенства первой степени с одним неизвестным (79).

Глава 5 ПРОГРЕССИИ
I. Арифметическая прогрессия 80
73. Задача (80). 74. Определение (80). 75. Формула любого члена арифметической прогрессии (81). 76. Формула суммы членов арифметической прогрессии (82). 11. Замечание (84). 78. Формула суммы квадратов чисел натурального ряда (84).
II. Геометрическая прогрессия 86
79. Задача (86). 80. Определение (87). 81. Сравнение геометрической прогрессии с арифметической прогрессией (87). 82. Формула любого члена геометрической прогрессии (88). 83. Формула суммы членов геометрической прогрессии (89). 84. Пример на геометрическую прогрессию (90).
III. Бесконечные прогрессии 91
85. Некоторые свойства бесконечных прогрессий (91). 86. Понятие о пределе (93). 87. Формула суммы бесконечно убывающей геометрической прогрессии (94). 88. Применение геометрической прогрессии к десятичным периодическим дробям (95).

Глава 6 ОБОБЩЕНИЕ ПОНЯТИЯ О ПОКАЗАТЕЛЯХ
I. Целые показатели 98
89. Свойства целых положительных показателей (98). 90. Нулевой показатель (99). 91. Отрицательные целые показатели (99). 92. Действия над степенями с отрицательными показателями (100).
II. Дробные показатели 101
93. В каком смысле употребляются дробные показатели (101). 94. Основное свойство дробного показателя (102). 95. Действия над степенями с дробными показателями (102). 96. Примеры на действия с дробными и отрицательными показателями (103).
III. Понятие об иррациональном показателе 104
97. Смысл степени с иррациональным показателем (104).
IV. Показательная функция 105
98. Определение (105). 99. Свойства показательной функции (106). 100. График показательной функции (108).

Глава 7 ЛОГАРИФМЫ
I. Общие свойства логарифмов 111
101. Два действия, обратных возведению в степень (111). 102. Определение (112). 103. Логарифмическая функция и её график (113). 104. Основные свойства логарифмов (114). 105. Практическое значение логарифмических таблиц (116). 106. Логарифмы произведения, частного, степени и корня (117). 107. Логарифмирование алгебраического выражения (119). 108. Замечания (120).
II. Свойства десятичных логарифмов 121
109. Свойства десятичных логарифмов (121). 110. Следствия (124).
III. Устройство и употребление таблиц 125
111. Система логарифмов (125). 112. Преобразование отрицательного логарифма (125). 113. Описание четырёхзначных таблиц и пользование ими (126). 114. Интерполирование (128). 115. Таблицы антилогарифмов (129). 116. Замечание об интерполировании (130). 117. Действия над логарифмами с отрицательными характеристиками (130). 118. Замена вычитаемых логарифмов слагаемыми (131). 119. Примеры вычислений с помощью логарифмов (132). 120. Употребление пятизначных таблиц (135).
IV. Показательные и логарифмические уравнения 135
121. Примеры уравнений (135). 122. Формула сложных процентов (136).

Глава 8 ИССЛЕДОВАНИЕ УРАВНЕНИЙ

I. Исследование уравнений первой степени с одним неизвестным 139
123. Что значит исследовать уравнение (139). 124. Общий вид уравнения первой степени с одним неизвестным (139). 125. Положительное решение (139). 126. Отрицательное решение (140). 127. Нулевое решение (141). 128. Случай, когда уравнение не имеет корня (141). 129. Как надо понимать равенство — = ±оо (142). 130. Неограниченный рост корня (142). 131. Неопределённое решение (143). 132. Графическое истолкование решения уравнения ах = Ъ (143). II. Исследование системы двух уравнений первой степени с двумя неизвестными 145 133. Общие формулы (145). 134. Исследование (145).
III. Исследование квадратного уравнения 147
135. Исследование формул (147). 136. Задача о двух источниках света (148).

Глава 9 МНИМЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
137. Мнимые числа (151). 138. Комплексные числа (151). 139. Действия над комплексными числами (152). 140. Геометрическое изображение комплексного числа (155). 140а. Тригонометрическая форма комплексного числа (156). 1406. Действия с комплексными числами, выраженными в тригонометрической форме (160).

Глава 10 НЕКОТОРЫЕ СВЕДЕНИЯ ОБ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЯХ
I. Делимость многочлена 169
141. Делимость многочлена, целого относительно ж, на разность х — а. (169). 142. Делимость двучлена жт =р ат на х =р =р а (171). 143. Частные, получаемые при делении жт =р ат на х =р а (171). 144. Общий вид алгебраического уравнения (172). 145. Некоторые свойства алгебраического уравнения (172).

Глава 11 НЕОПРЕДЕЛЁННЫЕ УРАВНЕНИЯ
146. Вводные замечания (175). 147. Признак невозможности решения уравнения в целых числах (175). 148. Признак невозможности решения уравнения в положительных числах (176). 149. Общая формула корней неопределённого уравнения (176). 150. Способ подстановки (178). 151. Частный вид неопределённого уравнения (179). 152. Общее решение неопределённого уравнения (179). 153. Упрощение решения уравнения (182). 154. Положительные решения (185).

Глава 12 СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА
I. Соединения 189
155. Определение (189). 156. Размещения (189). 157. Задачи (191). 158. Перестановки (191). 159. Задачи (192). 160. Сочетания (192). 161. Другой вид формулы числа сочетаний (193). 162. Свойство сочетаний (193).
II. Бином Ньютона 194
163. Произведение биномов, отличающихся только вторыми членами (194). 164. Формула бинома Ньютона (196). 165. Свойства формулы бинома Ньютона (197). 166. Применение формулы бинома к многочлену (199).

ДОПОЛНЕНИЯ
I. Непрерывные дроби 201
167. Определение непрерывной дроби (201). 168. Обращение непрерывной дроби в обыкновенную (201). 169. Обращение обыкновенной дроби в непрерывную (202). 170. Подходящие дроби (203). 171. Закон составления подходящих дробей (204). 172. Теорема 1 (206). 173. Теорема 2 (207). 174. Теорема 3 (209). 175. Приближённые значения данной арифметической дроби (210). 176. Извлечение квадратного корня (210). 177. Нахождение решения неопределённого уравнения (211). 178. Вычисление логарифма (213).
II. О пределах 214
179. Определения (214). 180. Некоторые свойства бесконечно малых величия (215). 181. Свойства пределов (216).
III. Исследование квадратного трёхчлена. Неравенства второй степени 221
182. Задача (221). 183. Квадратный трёхчлен, имеющий вещественные различные корни (222). 184. Квадратный трёхчлен, имеющий равные корни (228). 185. Квадратный трёхчлен, имеющий мнимые корни (230). 186. Общий вывод (232). 187. Неравенства второй степени (234).
Ответы к упражнениям 241

< Предыдущая		Следующая >

Свойства корней и степеней / Блог / Справочник :: Бингоскул

Формулы корней n-ой степени и их свойства

Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение:
(\sqrt[n] { a } )^k =\sqrt[n] { a^k }
Чтобы извлечь корень из корня, достаточно перемножить показатели корней:
\sqrt[n] { \sqrt[k] { a } } =\sqrt[n*k] { a }
Значение корня не изменится, если одновременно его показатель увеличить в k раз и подкоренное значение возвести в степень k:
\sqrt[n] { a^m } = \sqrt[n*k] { a^ { m*k } }
Корень из произведения равен произведению корней:
\sqrt[n] { a*b } = \sqrt[n] { a } * \sqrt[n] { b }
Корень из дроби — это корень из числителя и корень из знаменателя:
\sqrt[n] { \frac { a } { b } } = \frac { \sqrt[n] { a } } { \sqrt[n] { b } }
Корень из n-ой степени в степени n
(\sqrt[n] { a } )^n =a
Корень из квадрата:
(\sqrt { a^2 } ) = |a|

Формулы степеней и их свойства

Возведение в нулевую степень:
a^0 = 1
Произведение степеней:
a^m * a^n = a^ { m+n }
Деление степеней:
a^m : a^n = a^ { m — n }
Возведение степени в степень:
(a^m)^n = a^ { m*n }
При возведении в степень произведения каждый из множителей возводится в степень и результаты перемножают:
(a*b)^m = a^m * b^m
При возведении в степень частного возводят в эту степень и делимое, и делитель, результаты делят:
(\frac { a } { b } )^m = \frac { a^m } { b^m }
Степень с отрицательным рациональным показателем:
a^ { -n } = \frac { 1 } { a^n }
Обыкновенная дробь с отрицательным показателем заменяется на обратную ей дробь с положительным показателем:
(\frac { a } { b } )^ { -m } =(\frac { b } { a } )^ { m }
Степень с рациональным показателем:
a^ { \frac { 1 } { n } } = \sqrt[n] { a }
a^ { \frac { m } { n } } = \sqrt[n] { a^m }

Смотри также: Основные формулы по математике

Решай с разбором:

Сложение корней с разными степенями.

Сложение и вычитание корней, примеры. Что такое квадратный корень

Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .

Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.

Шаг 2. Вынесение множителя числа из-под корня

Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .

Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .

В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .

Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .

Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.

Шаг 3. Сокращение знаменателя

Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .

Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .

Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .

Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .

Пример сложного сокращения знаменателя

Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.

Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .

Получаем:

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе

Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.

Пример вычисления приблизительного значения

Необходимо вычислить приблизительное значение данного выражения √7 + √5 .

В итоге получаем:

√7 + √5 ≈ 2,65 + 2,24 = 4,89 .

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.

Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.

В наше время современных электронных вычислительных машин вычисление корня из числа не представляется сложной задачей. Например, √2704=52, это вам подсчитает любой калькулятор. К счастью, калькулятор есть не только в Windows, но и в обычном, даже самом простеньком, телефоне. Правда если вдруг (с малой долей вероятности, вычисление которой, между прочим, включает в себя сложение корней) вы окажитесь без доступных средств, то, увы, придется рассчитывать только на свои мозги.

Тренировка ума никогда не помещает. Особенно для тех, кто не так часто работает с цифрами, а уж тем более с корнями. Сложение и вычитание корней — хорошая разминка для скучающего ума. А еще я покажу поэтапно сложение корней. Примеры выражений могут быть следующие.

Уравнение, которое нужно упростить:

√2+3√48-4×√27+√128

Это иррациональное выражение. Для того чтобы его упростить нужно привести все подкоренные выражения к общему виду. Делаем поэтапно:

Первое число упростить уже нельзя.2×2)

Переписываем выражение с упрощенными слагаемыми:

√2+12×√3-12×√3+8×√2

Теперь складываем числа одним и тем же подкоренным выражением. Нельзя складывать или вычитать выражения с разными подкоренными выражениями. Сложение корней требует соблюдение этого правила.

Ответ получаем следующий:

√2+12√3-12√3+8√2=9√2

√2=1×√2 — надеюсь, то, что в алгебре принято опускать подобные элементы, не станет для вас новостью.

Выражения могут быть представлены не только квадратным корнем, но так же и с кубическим или корнем n-ной степени.

Сложение и вычитание корней с разными показателями степени, но с равнозначным подкоренным выражением, происходит следующим образом:

Если мы имеем выражение вида √a+∛b+∜b, то мы можем упростить это выражение так:

∛b+∜b=12×√b4 +12×√b3

12√b4 +12×√b3=12×√b4 + b3

Мы привели два подобных члена к общему показателю корня. Здесь использовалось свойство корней, которое гласит: если число степени подкоренного выражения и число показателя корня умножить на одно и то же число, то его вычисление останется неизменным.

На заметку: показатели степени складываются только при умножении.

Рассмотрим пример, когда в выражении присутствуют дроби.

5√8-4×√(1/4)+√72-4×√2

Будем решать по этапам:

5√8=5*2√2 — мы выносим из-под корня извлекаемую часть.

4√(1/4)=-4 √1/(√4)= — 4 *1/2= — 2

Если в тело корня представлено дробью, то часто этой дроби не измениться, если извлечь квадратный корень из делимого и делителя. В итоге мы получили описанное выше равенство.

√72-4√2=√(36×2)- 4√2=2√2

10√2+2√2-2=12√2-2

Вот и получился ответ.

Главное помнить, что из отрицательных чисел не извлекается корень с четным показателем степени. Если четной степени подкоренное выражение является отрицательным, то выражение является нерешаемым.

Сложение корней возможно только при совпадении подкоренных выражений, так как они являются подобными слагаемыми. То же самое относиться и к разности.

Сложение корней с разными числовыми показателями степени производиться посредством приведения к общей корневой степени обоих слагаемых. Это закон действует так же как приведение к общему знаменателю при сложении или вычитании дробей.

Если в подкоренном выражении имеется число, возведенное в степень, то это выражение можно упростить при условии, что между показателем корня и степени существует общий знаменатель.

В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.

Шаги

Часть 1 из 2: Определение корней

Обозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.

Корень обозначают знаком.
Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: (27)
Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5 (2)
Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.

Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.

Нельзя складывать корни с разными подкоренными выражениями, например, (2) + (3) (5). Но вы можете сложить числа, стоящие под одним корнем, например, (2 + 3) = (5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).

Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, (64) + (64) (эта сумма не равна (64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2 из 2: Упрощение и сложение корней

Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)

Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2 (3) + 2 (50) + (32) + 6 (3) + (81)
Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2 (50) + (32) + 2 (3) + 6 (3) + (81)

Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.

В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10 (2) + 4 (2) + 2 (3) + 6 (3) + (81)

Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10 (2) + 4 (2) + 2 (3)+ 6 (3) + 3 (3)

Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.

10 (2) + 4 (2) = 14 (2).

2 (3)+ 6 (3) = 8 (3).

Окончательное упрощенное выражение: 14 (2) + 8 (3) + 3 (3)

Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.

Внимание, только СЕГОДНЯ!

Все интересное

Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…

Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*&ordf-&radic-y нужно внести x под корень. Инструкция 1Определите степень…

Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…

Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…

Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …

Корень в математике может иметь два значения: это арифметическое действие и каждое из решений уравнения, алгебраического, параметрического, дифференциального или любого другого. Инструкция 1Корень n-ной степени из числа a — это такое число, что…

При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…

Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…

Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением.n = a. Корни нечетной степени существуют для отрицательных и положительных чисел, а корни четной степени — только для положительных.…

Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.

Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)

Вы ведь тоже ещё не вкурили?

Урок получился довольно большим, поэтому я разделил его на две части:

Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.

Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.

Основное правило умножения

Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:

Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}. \\ \end{align}\]

Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .

Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.

Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.

Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:

\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]

И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.

Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.{2n}}}=\left| a \right|. \\ \end{align}\]

Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:

Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?

При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)

Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.

Умножение корней с разными показателями

Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?

Да конечно можно. Всё делается вот по этой формуле:

Правило умножения корней.{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!
Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.
4. Силы, корни и радикалы
На этой странице
Связанный раздел
Не пропустите главу «Экспоненты и радикалы», где мы более подробно рассмотрим эти темы.
На этой странице мы продолжим рассмотрение того, как работают числа, прежде чем применять процедуры к алгебре. Все работает так же, за исключением того, что в алгебре мы используем буквы для обозначения чисел.
Индексы
Индексы (или степени , или степени ) очень полезны в математике.Индексы — это удобный способ записи умножения, в котором много повторяющихся членов.
Пример индекса
Для примера 5 ³, мы говорим, что:
5 — это базовый и
3 — это индекс (или степени , или степени ).
5 ³ означает «умножить 5 на себя 3 раза».
[Или, точнее, «многократно умножить 5 на себя так, чтобы в умножении было три 5», или даже лучше, «три пятерки, умноженные вместе».См. Обсуждение этого вопроса в разделе «Камни преткновения в математике». -1 = 1 / 5`
Эти легко испортить, и они могут лишить вас сна без надобности, когда вы позже будете заниматься алгеброй.-1 = 1 / a`

Умножение чисел с одинаковым основанием

Нам часто нужно умножить что-то вроде следующего:

4 ³ × 4 ⁵

Мы замечаем, что числа имеют одинаковое основание (то есть 4), и мы думаем об этом так:

4 ³ × 4 ⁵ `= \ underbrace {(4 xx 4 xx 4)} _ {3″ из них «} xx \ underbrace {(4 xx 4 xx 4 xx 4 xx 4)} _ {5 «из них»} `

Мы получаем 3 четверки из первой сетки и 5 четверок из второй, так что в сумме у нас будет 3 + 5 = 8 четверок, умноженных вместе.

4 ³ × 4 ⁵ = 4 ^{3 + 5} = 4 ⁸ (Если кому-то интересно, окончательный ответ 65 536 .:-)

В общем, можно сказать для любого числа a и индексов m и n :

a ^м × a ⁿ = a ^{( m + n )}

Деление чисел с одинаковым основанием

В качестве примера разделим 3 ⁶ на 3 ²:

. 2}` = {(3xx3xx3xx3xx3xx3)} / (3xx3) `= 3 × 3 × 3 × 3 = 3 ⁴ = 81

Мы вычли 2 тройки наверху и 2 тройки внизу дроби, оставив 4 тройки наверху (и цифру 1 на Нижний).(m-n) `

Повышение выражения индекса до индекса

В качестве примера возведем число 4 ² в степень 3:

(4 ²) ³ = 4 ² × 4 ² × 4 ²

Из приведенного выше примера умножения мы видим, что это даст нам 4 ⁶. Мы могли бы это сделать как:

(4 ²) ³ = 4 ^{2 × 3} = 4 ⁶

В общем у нас для любой базы a и индексов m и n :

( a ^м ) ⁿ = a ^mn

Повышение производительности продукта

Пример числа:

(5 × 2) ³ = 5 ³ × 2 ³

В этом случае с числами лучше сначала произвести умножение в скобках, а затем возвести наш ответ в степень 3. n, (ane0)`

ПРИМЕЧАНИЕ 1: Эти правила применяются, когда a и b являются положительными и m и n являются целыми числами .7`

, потому что это , в отличие от терминов (буквенная часть возведена в другую степень). (Мы можем разложить это на множители, но не можем каким-либо образом расширить или добавить термины.)

Чтобы узнать, как все это используется в алгебре, перейдите по ссылке:

Корни и радикалы

Мы используем радикальный знак : `sqrt (\ \)`

Означает «квадратный корень». Квадратный корень на самом деле является дробным индексом и эквивалентен возведению числа в мощность 1/2.(1/2) = sqrt (25) = 5`

Так же можно

Кубический корень: `root (3) x` (что эквивалентно возведению в степень 1/3) и
Корень четвертой степени: `root (4) x` (степень 1/4) и так далее.

См. Больше в разделе «Дробные экспоненты».

Ключевые моменты, на которые следует обратить внимание:

Связанный раздел

Как упоминалось выше, если вам нужна дополнительная информация по этой теме, перейдите в: Показатели и Радикалы.

Если a ≥ 0 и b ≥ 0, имеем:

`sqrt (axxb) = sqrt (a) xxsqrt (b)`

Однако это работает только для умножения.2) = а`

Это смущает многих студентов. Но это просто означает:

Начните с числа
Квадрат
Найдите квадратный корень из результата
Закончите с номером, с которого вы начали

Например, начать с 3.

Квадрат, получится 9.

Извлеките квадратный корень и получите 3, то есть с того места, где вы начали.

Почему это важно? Часто нам нужно «отменить» квадрат при решении уравнения, поэтому мы находим квадратный корень из обоих стороны.Приятно знать, что ты делаешь.

Классные занятия: Roots — Texas Instruments

Категория	Описание	Разрешить
Аналитические и рабочие файлы cookie	Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте).
Рекламные и маркетинговые файлы cookie	Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах.Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы.
Функциональные куки	Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи для обеспечения расширенной функциональности, в том числе более персонализированного и актуального опыта на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.
Файлы cookie социальных сетей	Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей.
Строго необходимо	Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на TI.com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie).	Всегда на связи

4 простых способа умножения экспонент [+ действия]

Что общего у землетрясений, фондового рынка, информатики и ядерной физики?

Все они включают экспонент умножения .

Показатели являются неотъемлемой частью алгебры, полиномиальных уравнений и курсов математики более высокого уровня, но многим студентам сложно понять, как с ними работать. Вы ознакомились с правилами экспонента со своим классом, и теперь пора применить их.

Давайте рассмотрим: правила экспоненты

Прежде чем вы начнете учить своих учеников умножению экспоненты, вы можете провести с ними быстрый обзор основ работы показателей.

Показатели (также называемые степенью ) регулируются правилами, как и все остальное в математическом классе.Вот краткое резюме:

Показатель степени — это способ выражения повторного умножения . Например, 35 представляет собой три, умноженные на себя пять раз:

35 = 3 × 3 × 3 × 3 × 3 = 243

35 = 243

Первое число называется основанием . Это число, которое умножается.

Второе, меньшее число — это показатель степени . Он представляет собой количество раз, когда основание умножается само на себя.

Существует семь правил экспоненты :

Правило произведения степеней : сложение степеней при умножении подобных оснований
Правило отношения степеней : вычитание степеней при делении подобных оснований
Правило силы полномочий : Умножение степеней вместе при увеличении степени на другой показатель
Степень произведения rul e: Распределение мощности на каждую основу при возведении нескольких переменных в степень
Степень правила частного : Распределение мощности на все значения в частное
Правило нулевой степени : Любое основание, возведенное в степень нуля, становится единицей
Правило отрицательной экспоненты : Чтобы изменить отрицательную экспоненту на положительную, переверните ее на обратную

Понятно? Тогда давай продолжим.

Как умножить экспоненты 4 способами

Помните, что все эти стратегии — просто ярлыки, помогающие упростить более сложные уравнения. Чтобы найти фактическое значение показателя степени, учащиеся должны сначала понять, что это означает: повторное умножение .

Познакомьте студентов с основами, такими как выражение показателей в виде произведений, прежде чем переходить к умножению показателей.

Когда они освоятся с концепцией, пора начинать.

1. Умножение степеней с одним и тем же основанием

При умножении степеней используйте первое правило: складывайте степени при умножении одинаковых оснований.

52 × 56 =?

Основания уравнения остаются неизменными, а значения показателей складываются.

52 × 56 = 58

Но почему это работает? Давайте посмотрим немного внимательнее:

Сложение экспонент — это всего лишь быстрый путь к ответу. Когда мы складываем экспоненты, мы увеличиваем количество раз, когда основание умножается само на себя.

Это правило остается неизменным, независимо от сложности вопроса. Вот более сложный пример с переменными:

(2𝒙8) (3𝒙5) =?

Сначала умножьте числа (2 и 3) вместе, поскольку они представляют собой коэффициенты , а не основание. (Коэффициент — это число, умноженное на переменную, например 𝒙.)

Затем сложите показатели степени.

(2𝒙8) (3𝒙5) = 6𝒙13

2. Умножение степеней с разными основаниями

Можно умножать экспоненты с разными основаниями, но есть одна важная загвоздка: экспоненты должны быть одинаковыми.

Вот как это сделать:

54 × 24 =?

Сначала перемножьте основания вместе. Затем добавьте показатель степени. Вместо того, чтобы складывать два показателя вместе, оставьте то же самое.

54 × 24 = 104

Вот почему это работает:

Это из-за правила четвертой степени: распределяет мощность на каждую базу при возведении нескольких переменных в степень . Это уравнение также можно записать как (5 × 2) 4, что означает, что показатель степени распределяется между 5 и 2.

Теперь давайте попробуем умножить переменные на показатели.

(3y3) (4y3) =?

Помните, что правило выполняется до тех пор, пока , поскольку показатели степени и переменные равны (потому что переменные 𝒙 и y нельзя комбинировать).

(3y3) (4y3) = 12y3

3. Умножение показателей степени с разными основаниями и показателями

Что происходит, когда вы хотите умножить разные показатели степени с разными основаниями?

Короткий ответ: вы не можете. В отличие от приведенных выше примеров, здесь нет ярлыка.

Например:

Поскольку 24 и 32 не имеют ничего общего, чтобы их можно было объединить, ответ не может быть упрощен до одного показателя степени и должен быть выражен как обычное число.

4. Умножение отрицательных показателей

Это может показаться сложным, но умножение показателей степени на отрицательные числа в точности совпадает с умножением показателей степени на неотрицательные числа.

Начните с изучения свойств отрицательных чисел. В частности, просмотрите, как их складывать и умножать.Ваши ученики должны чувствовать себя комфортно, работая с отрицательными числами, прежде чем они перейдут к отрицательным показателям.

Тогда запомните правило седьмого показателя степени: , чтобы изменить отрицательный показатель степени на положительный, переверните его на обратное значение .

То же основание, разные степени:

4-3 × 42 =?

Помните — складывайте экспоненты с одинаковыми основаниями.

4-3 × 42 = 4-1

Чтобы решить эту экспоненту, переверните отрицательную экспоненту в обратную.

4-1 = ¼ = 0.25

Другое основание, но одинаковые показатели:

2-5 × 3-5 =?

Как и выше, умножьте основания и оставьте экспоненты прежними.

2-5 × 3-5 = 6-5

Чтобы решить, переверните отрицательный показатель степени в обратную величину.

6-5 = ⅙5

Если показатели степени не имеют ничего общего, решите уравнение напрямую:

2-3 × 32

Сначала преобразуйте отрицательные показатели степени в обратные, затем вычислите.

При умножении показателей степени напомните учащимся:

Сложить показатели , если основания одинаковые
Умножить основания , если показатели одинаковые
Если ничего не одинаковое , просто решите это

Упражнения для тренировки умножения на экспоненты

1.Prodigy

Повышение беглости математики — важная часть уверенности учащихся в курсах математики в средней школе и колледже. Студенты могут практиковать умножение показателей и другие математические концепции с Prodigy, в то время как вы задаете индивидуальные внутриигровые вопросы, основанные на содержании урока.

Ваш класс будет исследовать мир, наполненный увлекательными заданиями, экзотическими домашними животными и изучением математики. Вы сможете выбрать, на какие вопросы они будут отвечать, и в режиме реального времени получать данные о том, что они усвоили, над чем работают и где им может потребоваться дополнительная помощь.

Обладая 1400 навыками, вы сможете создать материалов, соответствующих учебной программе, по любой теме, которую вы изучаете, включая умножение показателей.

2. Exponent War

Education.com

Классическая карточная игра, но с невероятно интересным поворотом!

Студенты работают в командах по два человека и соревнуются друг с другом. Раздайте каждой команде колоду карт (с вынутыми дамами, валетами и королями) и попросите каждого игрока вытащить две карты.Первая карта — это база, а вторая карта — экспонента.

Каждой паре предстоит соревноваться, чтобы решить свое уравнение и найти продукт. Побеждает команда с наибольшим ответом. Установите таймер для класса и посмотрите, кто наберет больше очков.

Пока ученики играют, пройдитесь по классу и убедитесь, что они не пропустили ни одной ступеньки. Если вы видите много ошибок или затруднений у учащихся, примите это как знак того, что вам, возможно, придется пересмотреть.

3. Показательная охота за мусорщиками

Дайте вашим ученикам возможность искать сокровища и исследовать класс с помощью показательной охоты за мусорщиками.

Разделите ваш класс на группы по три или четыре человека. В зависимости от количества групп, сделайте несколько разных наборов карточек. Начинайте каждый набор с карточки, на которой есть проблема. Напишите ответ на проблему на следующей карточке, а другую задачу на обратной стороне. Продолжайте, пока не получите три или четыре набора задач (или больше).

Начиная с первой карточки, каждая группа должна решить задачу и найти правильный ответ где-нибудь еще в классе .Найдя правильную карточку с ответами, они могут перевернуть ее и решить следующую задачу. Раздайте учащимся записки для решения и позвольте им начать поиск ответов. Какая бы команда ни финишировала первой, становится победителем!

4. Exponent Jeopardy

Каждый ученик любит классическую игру Jeopardy. Используя настраиваемый шаблон, замените мелочи вопросами, которые дают студентам возможность попрактиковаться в умножении показателей, и разделите класс на две команды.

Вот несколько советов, которые помогут обеспечить бесперебойную работу игры:

Если у вас большой класс, подумайте о том, чтобы разделить класс на несколько игр, чтобы у каждого ученика была возможность участвовать.
Чтобы объединить математические и компьютерные навыки, Предложите учащимся сделать игру самостоятельно.Дайте им шаблон (или пусть более продвинутые ученики начнут с нуля) и попросите их сделать небольшую игру.
Используйте его в качестве конечного упражнения перед тестом и комбинируйте более важные вопросы с более сложными ответами

5. Рабочие листы для умножения показателей

Рабочие листы — это проверенный метод развития математики свободное владение определенным набором навыков. Они также могут быть индикатором понимания учащимся, когда используются как часть стратегии формирующего оценивания.Вот некоторые из наших фаворитов:

Если вы ищете рабочий лист, который охватывает больше, чем просто умножение экспонент, ознакомьтесь с нашей таблицей правил экспонент (с ключом ответа).

Для чего-то более уникального, попробуйте это упражнение с умножением полиномов. Как и в обычном рабочем листе, в нем есть вопросы, на которые студенты должны ответить, но он также содержит «банк ответов» для студентов. Вырежьте сопутствующие полоски и перемешайте их. Попросите учащихся сопоставить ответы с правильным разделом на своем листе после решения уравнения и демонстрации своей работы.

Степень умножения: давайте рассмотрим

Если ваши ученики помнят только три вещи, убедитесь, что это следующие концепции:

Сложите степени вместе при умножении как основание
Умножьте основания при умножении как экспонентах
произведение многократного умножения

Если они помнят эти три правила, у них будет прочный фундамент, построенный еще до первого урока алгебры в старшей школе.

Как всегда, делайте это медленно и убедитесь, что учащиеся понимают основы, прежде чем все усложняется. Это может показаться сложной идеей для преподавания, но придерживайтесь шагов и продвигайтесь в логическом порядке, чтобы увидеть, как знания ваших учеников растут.

Создайте или войдите в свою учетную запись учителя на Prodigy — бесплатной игровой платформе для обучения математике, которую легко использовать как преподавателям, так и ученикам. Он соответствует учебным планам англоязычных стран, его любят более миллиона учителей и 50 миллионов студентов.

Зарегистрируйтесь сейчас

Капиллярное действие — Химия LibreTexts

Капиллярное действие можно определить как подъем жидкости через тонкую трубку, цилиндр или проницаемое вещество за счет адгезионных и когезионных сил, взаимодействующих между жидкостью и поверхностью. Когда межмолекулярное связывание самой жидкости существенно хуже поверхности вещества, с которым она взаимодействует, возникает капиллярность . Также диаметр контейнера, а также силы тяжести будут определять количество поднимаемой жидкости.Хотя вода обладает этим уникальным свойством, жидкость, подобная ртути, не будет обладать такими же свойствами из-за того, что она имеет более высокую силу сцепления, чем силу сцепления.

Силы в капиллярном действии

Три основные переменные, которые определяют, обладает ли жидкость капиллярным действием:

Сила сцепления : это межмолекулярная связь вещества, при котором его взаимное притяжение заставляет их сохранять определенную форму жидкости.
Поверхностное натяжение : Это происходит в результате схожих молекул, сил сцепления, которые объединяются вместе, образуя непроницаемую поверхность на водной поверхности. Поверхностное натяжение измеряется в Ньютон / метр.
Сила сцепления : Когда возникают силы притяжения между непохожими молекулами, это называется силами сцепления.

Капиллярное действие возникает только тогда, когда силы адгезии в жидкости превышают силы сцепления, которые неизменно становятся поверхностным натяжением.

Рисунок \ (\ PageIndex {1} \): можно увидеть, что в воде сила адгезионных сил больше, чем сила когезионных сил. Это приводит к вогнутому образованию воды в капиллярной трубке; это известно как капиллярное притяжение. В качестве альтернативы для ртути силы сцепления сильнее, чем силы сцепления, что позволяет мениску отклоняться от стенок капиллярной трубки. Это известно как капиллярное отталкивание. Commons.wikimedia.org/wiki/Fi… (PSF) (bjl) .svg

Хороший способ запомнить разницу между адгезионными и когезионными силами состоит в том, что с ad hesive force вы добавляете другой набор молекул, молекул поверхности, для жидкости к связь с. При силе взрыва co молекулы жидкости только co будут действовать со своим собственным видом. Снижение поверхностного натяжения также увеличивает капиллярное действие. Это связано с тем, что уменьшение поверхностного натяжения означает, что межмолекулярные силы уменьшаются, тем самым уменьшая силы сцепления.В результате капиллярное действие будет еще больше.

Рисунок \ (\ PageIndex {2} \): Масштабируемая иллюстрация капиллярного действия для капилляров с большим и малым отверстием, а также для положительных и отрицательных углов смачивания. (Общественное достояние; Эдуард Конечный через Википедию).

Приложения

Практическое использование капиллярного действия очевидно во всех формах нашей повседневной жизни. Это позволяет эффективно и эффективно выполнять наши задачи. Некоторые применения этого уникального свойства включают:

Основные свойства используются для поглощения воды с помощью бумажных полотенец.Благодаря своим когезионным и адгезионным свойствам жидкость впитывается в бумажное полотенце. Жидкость с определенной скоростью течет в бумажное полотенце.
Метод, называемый тонкослойной хроматографией, использует капиллярное действие, при котором слой жидкости используется для отделения смесей от веществ.
Капиллярное действие естественным образом помогает нам выкачивать слезную жидкость в глаза. Этот процесс очищает глаз и удаляет всю пыль и частицы, которые находятся вокруг протоков глаза.
Для выработки энергии: Капиллярное действие можно использовать в качестве источника возобновляемой энергии.Позволяя воде подниматься по капиллярам, испаряться, когда достигает вершины, конденсату и опускаться обратно вниз, вращая турбину на своем пути для создания энергии, капиллярное действие может производить электричество! Хотя эта идея все еще находится в разработке, она показывает потенциал, который имеет капиллярное действие, и насколько это важно.

Рисунок \ (\ PageIndex {3} \): Капиллярное действие проявляется в природе повсюду вокруг нас. Эти свойства позволяют воде проникать через ксилему растения.Вода начинается с корней и поднимается вверх к самым высоким ветвям растения. commons.wikimedia.org/wiki/File:GemeineFichte.jpg

При измерении уровня жидкости в пробирке или бюретке для получения точных показаний обязательно измерять уровень жидкости на линии мениска. Можно измерить высоту (обозначенную буквой h) пробирки, бюретки или другого столба с жидкостью, используя формулу:

\ [h = \ dfrac {2 \ gamma \ cos \ theta} {\ rho \; g \; r} \]

В этой формуле

γ представляет собой поверхностное натяжение в среде жидкость-воздух,
θ — угол контакта или степень контакта,
ρ — плотность жидкости в репрезентативном столбе,
g — ускорение под действием силы тяжести и
r — радиус трубки, в которой находится жидкость.{-5}} {r} \]
Однако для выполнения этой формулы должны выполняться следующие условия.
- γ = 0,0728 Н / м (при температуре воды 20 ° C)
- θ = 20 °
- ρis 1000 кг / м ³
- г = 9,8 м / с ²
Формула для определения объема жидкости, переносимой в среде:
Когда определенные пористые объекты сталкиваются с жидкой средой, они начинают поглощать жидкость со скоростью, которая фактически уменьшается с течением времени.Эта формула записывается как:
\ [V = S * A \ sqrt {t} \]
В этой конкретной формуле
- A — влажная зона (поперечное сечение),
- S — сорбционная способность (способность среды абсорбировать с использованием процесса капиллярного действия),
- V — объем жидкости, поглощенной во времени, т .
Вопросы
1. Назовите один способ усилить капиллярное действие и один способ его уменьшить.
2. Если сцепление больше, чем адгезия, будет ли мениск выпуклым или вогнутым?
3. Какой была бы высота жидкости в столбе на Земле с поверхностным натяжением жидкость-воздух 0f 0,0973 Н / м, углом контакта 30 градусов, плотностью 1200 кг / м ³? Учтите, что радиус трубки составляет 0,2 метра.
4. Какой была бы высота воды в стеклянной трубке радиусом 0,6 мм?
Решения
1. Увеличьте капиллярное действие: увеличьте температуру, уменьшите диаметр капиллярной трубки, выполните любое количество действий для уменьшения поверхностного натяжения и т. Д.! Уменьшение капиллярного действия: шаги, противоположные шагам, которые вы предпримете для увеличения, также увеличивают плотность жидкости, с которой вы работаете.
2. Мениск приведет к выпуклому образованию.
3. Используя приведенную выше формулу, высота жидкости будет 7,165 * 10 ^-5 м в высоту.
4. Используя приведенную выше формулу, высота воды в стеклянной трубке будет 0,014 м.
Список литературы
1. Петруччи, Ральф и Уильям Харвуд. Ф. Джеффри Херринг. Джеффри Мадура. Общая химия: принципы и современные приложения. 9 изд. Река Аппер Сэдл, Нью-Джерси: Пирсон, 2007.
2. Циклический гравитационный генератор энергии капиллярного действия для тепличной жидкости, Р. Смит, 9.11.2005 14:38,
3. Капиллярное действие, Википедия
4. Капиллярное действие, от USGS Water Science for Schools. USGS Georgia Water Science Center — Домашняя страница . Интернет. 4 июня 2011 г.
Авторы и авторство
- Ахилл Пейрис, Бекки Штейн
Как возвести число в степень в Excel с помощью формулы и оператора
Часто пользователям нужно возвести число в степень.Как это сделать правильно с помощью «Excel»?
В этой статье мы постараемся разобраться в популярных вопросах пользователей и дадим инструкции, как правильно пользоваться системой. MS Office Excel позволяет выполнять ряд математических функций: от самых простых до самых сложных. Эта универсальная программа рассчитана на все случаи жизни.
Взаимодействие с другими людьми
Как в excel возвести в степень?
Прежде чем искать нужную функцию, обратите внимание на математические законы:
1. «1» останется «1» в любой степени.».
Мы построили 8 в «квадрат» (то есть во второй степени) и получили результат вычисления в ячейку «A2».
Вариант 2. Использование функции
В Microsoft Office Excel есть удобная функция «МОЩНОСТЬ», которую вы можете активировать для простых и сложных математических вычислений.
Функция выглядит так:
= МОЩНОСТЬ (Число, Степень)
ВНИМАНИЕ!
1. Цифры в этой формуле указываются без пробелов и других знаков.
2. Первая цифра — это значение «число». Это основа (то есть фигура, которую мы строим). Microsoft Office Excel позволяет вводить любое действительное число.
3. Вторая цифра — значение «градус». Это индикатор, в котором мы строим первую фигуру.
4. Значения обоих параметров могут быть меньше нуля (со знаком «-»).
Взаимодействие с другими людьми
Формула возведения в степень в Excel
Примеры использования функции = МОЩНОСТЬ ().
Использование мастера функций:
1. Запустите мастер функций с помощью комбинации горячих клавиш SHIFT + F3 или щелкните кнопку в начале строки формулы «fx» (вставка функции). Из выпадающего списка «Или выберите категорию:» выберите «Math & Trig», а в нижнем поле «Select a function:» укажите нужную нам функцию «POWER» и нажмите OK. Или выберите: «ФОРМУЛЫ» — «Библиотека функций» — «Math & Trig» — «POWER».
2. В открывшемся диалоговом окне заполните поля аргументами.Например, нам нужно возвести «2» в степень до «3». Затем в первом поле введите «2», а во втором — «3».
3. Нажимаем кнопку «ОК» и попадаем в ячейку, в которую была введена формула, нужное нам значение. В этой ситуации в «кубе» стоит «2», т.е. 2 * 2 * 2 = 8. Программа все рассчитала правильно и выдала вам результат.
Если вам кажется, что лишние клики — сомнительное удовольствие, предлагаем вариант попроще.
Ввод функции вручную:
1. В строке формулы ставим знак «=» и начинаем вводить название функции.Обычно достаточно написать «= po…» — и система сама угадает, что предложит вам полезный вариант.
2. Как только вы увидели такую подсказку, просто нажмите клавишу «Tab». Или вы можете продолжить писать, вручную вводя каждую букву. Затем в скобках укажите необходимые параметры: два числа, разделенных точкой с запятой.
3. После этого нажимаем «Enter» — и в ячейке появляется вычисленное значение 8.
Последовательность действий простая, а результат пользователь получает достаточно быстро.В аргументах вместо чисел можно указать ссылки на ячейки.
Степень квадратного корня в Excel
Для извлечения корня по формулам Microsoft Excel мы используем немного другой, но очень удобный способ вызова функций:
1. Перейти на вкладку «ФОРМУЛЫ». В разделе «Библиотека функций» на панели инструментов щелкните инструмент «Math & Trig». И из выпадающего списка выберите опцию «SQRT».
2. Введите аргумент функции по запросу системы.В нашем случае нужно было найти корень из «25», поэтому вводим его в строку. После ввода номера просто нажмите кнопку «ОК». В ячейке отобразится цифра, полученная в результате математического расчета корня.
ВНИМАНИЕ! Если нам нужно знать корень степени в Excel, мы не используем функцию = КОРЕНЬ (). Напомним теорию из математики:
«Корнем n-й степени числа a является число b, n-я степень которого равна a», то есть:
ⁿ √a = b; b ⁿ = a
«Корень n-й степени из числа a будет равен увеличению степени того же числа a на 1 / n», то есть:
ⁿ √a = a ^{1 / n}
Отсюда следует, что для вычисления математической формулы корня в n-й степени например:
⁵ √32 = 2
В Excel вы должны написать по этой формуле: = 32 ^ (1/5), то есть: = a ^ (1 / n) — где a — число; N-степень:
Или через эту функцию: = МОЩНОСТЬ (32,1 / 5)
В аргументах формулы и функции вы можете указать ссылки на ячейки вместо чисел.
Как в Excel записать число в степень?
Для вас часто важно, чтобы число в градусе правильно отображалось при печати и красиво смотрелось в таблице. Как в Excel написать число в градусе? Здесь вам нужно использовать вкладку «Формат ячеек». В нашем примере мы записали «3» в ячейку «А1», которая должна быть представлена с точностью до -2.
Последовательность действий следующая:
1. Щелкните правой кнопкой мыши ячейку с номером и выберите вкладку «Формат ячеек» во всплывающем меню.Если не получилось — найдите вкладку «Формат ячеек» в верхней панели или нажмите CTRL + 1.
2. В появившемся меню выберите вкладку «Число» и установите формат для ячейки «Текст». Щелкните ОК.
3. В ячейке A1 введите «-2» рядом с «3» и выберите его.
4. Опять вызываем формат ячеек (например, нажав горячие клавиши CTRL + 1) и теперь только нам доступна вкладка «Шрифт», где мы ставим галочку напротив «Надстрочный индекс». И жмем ОК.
5. Результат должен иметь следующее значение:
Использовать функции Excel просто и удобно.С ними вы сэкономите время на выполнении математических расчетов и поиске необходимых формул.
Калькулятор корней многочлена
Считается, что у этого многочлена есть два корня, оба равные 3. Каждый изучает «теорему о множителях», обычно во втором курсе алгебры, как способ найти все корни, являющиеся рациональными числами. Также можно научиться находить корни всех квадратичных многочленов, используя при необходимости квадратные корни (полученные из дискриминанта).
Для неприводимых многочленов вида a x n + b корни могут быть вычислены как произведение действительного числа на комплексный корень из 1, поэтому используется метод, использованный в предыдущем абзаце. Для a x 2n + b x n + c возможны два случая.
Наш онлайн-калькулятор интегралов дает вам мгновенные математические решения для поиска интегралов и первообразных с простыми для понимания пошаговыми пояснениями.
Алгебра -> Полиномы-и-рациональные-выражения-> РЕШЕНИЕ: Найдите полиномиальное уравнение с действительными коэффициентами, которое имеет заданные корни 5 и -3i x ^ 3- ___ x ^ 2 + _____ x = 0 Вход в алгебру: многочлены, рациональные выражения и уравнения Раздел
Калькулятор полиномов — это бесплатный онлайн-инструмент, который отображает сложение, вычитание, умножение и деление двух полиномов.Онлайн-калькулятор полиномов BYJU ускоряет вычисления и отображает результирующий полином за доли секунды для различных операций, таких как сложение, вычитание, умножение, деление, производная и интегрирование.
Нахождение действительных корней полиномиальных уравнений Шаг 4 Разложите многочлен на множители. Синтетическая замена 2 приводит к остатку 0, поэтому 2 является корнем, а многочлен в факторизованной форме равен (x — 2) (x2 + 5x + 6). Пример 3 (продолжение) (x — 2) (x2 + 5x + 6) = 0 Установите уравнение равным 0.(x — 2) (x + 2) (x + 3) = 0 Разложите на множители x2 + 5x + 6.
два многочлена с рациональными коэффициентами, каждый меньшей степени. Основная теорема алгебры используется для доказательства первого из этих утверждений. Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые полные корни будут встречаться парами, известными как
Хемплинг, Скотт: 9780989327701: Amazon.com: Книги
Об авторе
Скотт Хемплинг преподавал закон и политику в области коммунального хозяйства целому поколению регулирующих органов и практиков.Как поверенный, он помогал клиентам из всех секторов промышленности — регулирующим органам, коммунальным предприятиям, потребительским организациям, независимым конкурентам и экологическим организациям. В качестве свидетеля-эксперта он неоднократно давал показания перед комиссиями штата, комитетами Конгресса США и законодательными собраниями Арканзаса, Калифорнии, Мэриленда, Миннесоты, Невады, Северной Каролины, Южной Каролины, Вермонта и Вирджинии. Как преподаватель и ведущий семинаров, он выступал в Соединенных Штатах, а также в Канаде, Центральной Америке, Германии, Индии, Италии, Ямайке, Мексике и Нигерии.Его статьи публиковались в The Electricity Journal, Public Utilities Fortnightly, ElectricityPolicy.com и других профессиональных изданиях, охватывающих такие темы, как слияния и поглощения, введение конкуренции на ранее монополистических рынках, корпоративная реструктуризация, повышение рейтинга, инвестиции в коммунальные услуги в некоммунальные предприятия, передача планирование, возобновляемые источники энергии и вопросы юрисдикции штата и федерации. С 2006 по 2011 год он был исполнительным директором Национального института нормативных исследований.Хемплинг — адъюнкт-профессор Юридического центра Джорджтаунского университета, где он преподает курсы по коммунальному праву и нормативным судебным спорам. Первый том его юридического трактата «Регулирование деятельности коммунальных предприятий: закон структуры рынка, ценообразования и юрисдикции» будет опубликован Американской ассоциацией адвокатов осенью 2013 года. Это первый том двухтомного трактата, второй из который будет касаться права корпоративной структуры, слияний и поглощений. Хемплинг получил B.А. с отличием по (1) экономике и политическим наукам и (2) музыке от Йельского университета, где он был награжден континентальной стипендией зерновых и исследовательским грантом Паттерсона. Он получил докторскую степень с отличием от Юридического центра Джорджтаунского университета, где был удостоен награды американской юриспруденции в области конституционного права. Более подробная информация доступна на сайте www.

РубрикаРазное

Действия с корнями и степенями формулы: Правила действий со степенями и корнями, примеры.

Корни и степени, возведение в степень, извлечение корня

Формулы преобразования степени числа. Свойства степени

Формулы преобразования корня числа. Свойства корня

Корень и его свойства. Подробная теория с примерами (ЕГЭ — 2021)

Корень n-й степени и его свойства

Действия со степенями с примерами решения

Отрицательные степени

Алгебра. Ч. I-II. Киселев А.П.2

Свойства корней и степеней / Блог / Справочник :: Бингоскул

Сложение корней с разными степенями.

Шаг 1. Извлечение квадратных корней

Шаг 2. Вынесение множителя числа из-под корня

Шаг 3. Сокращение знаменателя

Пример сложного сокращения знаменателя

Шаг 4. Вычисление приблизительного значения на калькуляторе

Пример вычисления приблизительного значения

Шаги

Основное правило умножения

Умножение корней с разными показателями

Инструкция

4. Силы, корни и радикалы

На этой странице

Связанный раздел

Индексы

Пример индекса

Умножение чисел с одинаковым основанием

Деление чисел с одинаковым основанием

Повышение выражения индекса до индекса

Повышение производительности продукта

Корни и радикалы

Ключевые моменты, на которые следует обратить внимание:

Связанный раздел

Классные занятия: Roots — Texas Instruments

4 простых способа умножения экспонент [+ действия]

Давайте рассмотрим: правила экспоненты

Как умножить экспоненты 4 способами

1. Умножение степеней с одним и тем же основанием

2. Умножение степеней с разными основаниями

3. Умножение показателей степени с разными основаниями и показателями

4. Умножение отрицательных показателей

То же основание, разные степени:

Другое основание, но одинаковые показатели:

Если показатели степени не имеют ничего общего, решите уравнение напрямую:

Упражнения для тренировки умножения на экспоненты

1.Prodigy

2. Exponent War

3. Показательная охота за мусорщиками

4. Exponent Jeopardy

5. Рабочие листы для умножения показателей

Степень умножения: давайте рассмотрим

Капиллярное действие — Химия LibreTexts

Силы в капиллярном действии

Приложения

Формула для определения объема жидкости, переносимой в среде:

Вопросы

Список литературы

Авторы и авторство

Как возвести число в степень в Excel с помощью формулы и оператора

Как в excel возвести в степень?

Вариант 2. Использование функции

Формула возведения в степень в Excel

Степень квадратного корня в Excel

Как в Excel записать число в степень?

Калькулятор корней многочлена

Хемплинг, Скотт: 9780989327701: Amazon.com: Книги

Об авторе

Добавить комментарий Отменить ответ