Cos равен 0: Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
Таблица косинусов (полная, градусы и значения)
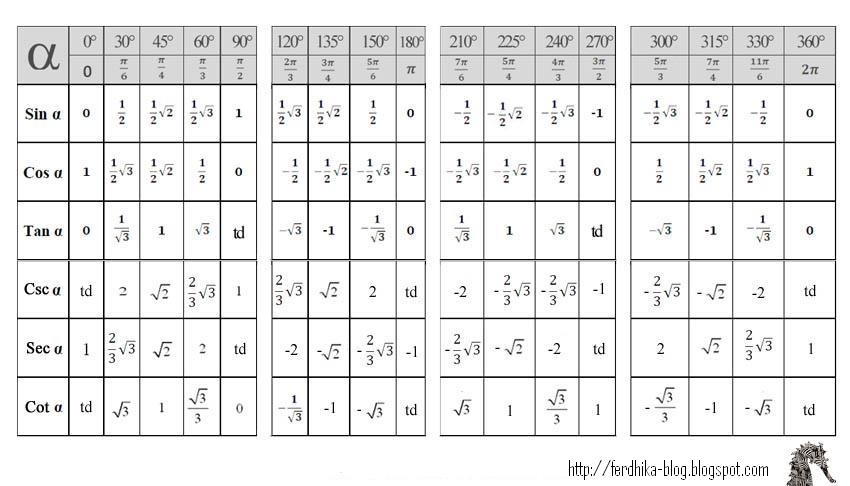
В данной таблице представлены значения косинусов от 0° до 360°. Таблица косинусов нужна, чтобы узнать, чему равен косинус угла. Нужно только найти его в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-kosinusov — uchim.org
Таблица косинусов для 0°-180°
|
|
|
Таблица косинусов для 181°-360°
|
|
|
Как легко запомнить таблицу косинусов (видео)
Существуют также следующие таблицы тригонометрических функций: таблица синусов, таблица тангенсов и таблица котангенсов.
Всё для учебы » Математика в школе » Таблица косинусов (полная, градусы и значения)
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-kosinusov
Таблица косинусов
К содержанию
Таблица косинусов 0° — 180°.
|
|
|
Таблица косинусов 180° — 360°.
|
|
|
Другие заметки по алгебре и геометрии
Полезная информация?
Cos 0- значение, объяснение и часто задаваемые вопросы
Cos 0 равен 1 (Cos 0 = 1). Другими словами, значение Cos 0 равно 1. Теперь вопрос в том, как было получено значение Cos 0. Значение может быть определено с помощью квадрантов единичного круга. Этот процесс обсуждается в следующем разделе.
Другими словами, значение Cos 0 равно 1. Теперь вопрос в том, как было получено значение Cos 0. Значение может быть определено с помощью квадрантов единичного круга. Этот процесс обсуждается в следующем разделе.
Как вы уже знаете, тригонометрические функции относятся к угловым функциям, которые относятся к углам треугольника. Для изучения периодических явлений световых и звуковых волн использовались тригонометрические функции. Эти функции также имеют решающее значение для изучения гармонических колебаний и изменений средней температуры.
Формула для нахождения Cos
Функция косинуса угла подчиняется определенной формуле. Согласно этой формуле значение функции косинуса угла равно длине прилежащей стороны, деленной на длину стороны гипотенузы. Формула написана ниже.
Cos X = \[\frac{\text{Смежная сторона}}{\text{Сторона гипотенузы}}\]
Эта формула говорит о функции косинуса (cos) и о том, как определить ее значение. Возьмем пример прямоугольного треугольника, один из острых углов которого равен х. Тогда формула косинуса cos x = (прилежащая сторона) / (гипотенуза), где сторона, примыкающая к углу x, соответствует названию, а сторона гипотенузы самая длинная (та, что противоположна прямому углу в треугольнике ). Помимо этой общей формулы, существуют и другие специальные формулы, но этой также достаточно, чтобы учащиеся хорошо поняли, как рассчитывается значение cos.
Возьмем пример прямоугольного треугольника, один из острых углов которого равен х. Тогда формула косинуса cos x = (прилежащая сторона) / (гипотенуза), где сторона, примыкающая к углу x, соответствует названию, а сторона гипотенузы самая длинная (та, что противоположна прямому углу в треугольнике ). Помимо этой общей формулы, существуют и другие специальные формулы, но этой также достаточно, чтобы учащиеся хорошо поняли, как рассчитывается значение cos.
Почему важны тригонометрические функции?
В математике они необходимы для некоторых вещей, таких как комплексный анализ и анализ Фурье. С другой стороны, они будут универсальными в качестве решений, примеров, приемов и многих упражнений во всех областях математики, включая дифференциальные уравнения, геометрию, топологию, гильбертовы пространства и т. д.
Если говорить о физике и инженерии, то эти функции должны встречается повсюду. Всякий раз, когда что-то циклично, всякий раз, когда что-то повторяется во времени, вы можете ожидать, что в его описании будут указаны sin и cos. Сюда также входят звуковые волны, электромагнитные волны (включая свет), любые типы волн, поведение частиц и так далее.
Сюда также входят звуковые волны, электромагнитные волны (включая свет), любые типы волн, поведение частиц и так далее.
Помимо использования в фундаментальной теории и теоретическом моделировании, эти функции предназначены для построения блоков и мотивации во вторичных целях, таких как помощь учащимся в расширении их знаний и помощь в развитии. Их не только легко запомнить, но и очень весело решать и играть с учениками.
Как найти значение Cos 0?
Существует три основных тригнометрических соотношения: функция синуса, функция косинуса и функция тангенса. С помощью функций sin, cos и tan можно вычислить углы треугольника.
Чтобы понять функцию косинуса острого угла, вам нужно нарисовать прямоугольный треугольник на листе бумаги. Треугольник, очевидно, имеет три стороны, и эти стороны можно определить следующим образом: Выберите угол треугольника, и противоположная сторона выбранного угла будет называться «противоположная сторона». Сторона треугольника, расположенная напротив прямого угла, называется стороной гипотенузы. Примечательно, что это самая длинная сторона прямоугольного треугольника. Наконец, «прилежащая сторона» относится к оставшейся стороне треугольника. Определение значения Cos 0 с помощью единичного круга Используя единичный круг, можно получить значение «Cos 0». Процесс начинается с принятия единичной окружности, центр которой совпадает с началом осей координат.
Сторона треугольника, расположенная напротив прямого угла, называется стороной гипотенузы. Примечательно, что это самая длинная сторона прямоугольного треугольника. Наконец, «прилежащая сторона» относится к оставшейся стороне треугольника. Определение значения Cos 0 с помощью единичного круга Используя единичный круг, можно получить значение «Cos 0». Процесс начинается с принятия единичной окружности, центр которой совпадает с началом осей координат.
Почему значение Cos всегда меньше или равно 1?
Самый простой способ понять причину состоит в том, что измерение длины сторон прямоугольного треугольника всегда меньше, чем измерение длины угла гипотенузы. Итак, отношение любой стороны и гипотенузы также всегда меньше значения 1.
Что такое Cos 0?
Значение косинуса прямоугольного треугольника с углом 0° известно как косинус угла 0°. Косинус угла 0° — это величина, обозначающая остаток длины прилежащей стороны от длины гипотенузы, если угол прямоугольного треугольника равен 0°.
В шестидесятеричной системе косинус угла, равный нулю градусов, математически выражается как косинус 0°, а точное значение косинуса угла 0° = 1 . Таким образом, математически это записывается в следующей форме в тригонометрии, т.е. cos 0 ° = 1
. Мы также можем выразить косинус угла ноль градусов в двух других формах тригонометрической математики, т.е. круговая система и сотенная система.
Cos 0 в круговой системе
В круговой системе косинус нуля градусов математически представляется как косинус нуля радиан. Это записывается в следующем виде в круговой системе cos (0) =1. Отмечается, что в методе единичного круга один полный оборот образует угол 2π радиан в самом центре единичного круга, поскольку все углы треугольника являются столь необходимыми кратными π/2, и это часто известно как квадрантные углы в академических кругах. Следовательно, координаты точек треугольника становятся (1, 0), (0, 1), (–1, 0) и (0, –1) соответственно. Поэтому, используя квадрантные углы, мы можем легко получить значения Cos.
99) =1. В этой системе один из прямых углов делится на 100 одинаковых частей, которые известны как градации. Она также известна как французская система измерения. Каждая ступень делится на 100 одинаковых частей, называемых минутами, а каждая минута делится на 100 одинаковых частей, называемых секундами. Таким образом, 1 прямой угол равен 100 градусам (1009), 1 градус равен 100 минутам (100′), а 1 минута равна 100 секундам (100 дюймов).
Поэтому, используя квадрантные углы, мы можем легко получить значения Cos.
99) =1. В этой системе один из прямых углов делится на 100 одинаковых частей, которые известны как градации. Она также известна как французская система измерения. Каждая ступень делится на 100 одинаковых частей, называемых минутами, а каждая минута делится на 100 одинаковых частей, называемых секундами. Таким образом, 1 прямой угол равен 100 градусам (1009), 1 градус равен 100 минутам (100′), а 1 минута равна 100 секундам (100 дюймов).
Базовое понимание определения Cos 0 как 1
Значение Cos 0 градусов:
Чтобы лучше понять функцию косинуса острого угла, начните с рассмотрения прямоугольного треугольника с интересующего вас угла и сторон треугольника. Все стороны (три) треугольника определяются следующим образом:
Противоположная сторона известна как сторона, противоположная интересующему углу.

Сторона гипотенузы находится напротив прямого угла и является самой длинной стороной в треугольнике.
Оставшаяся сторона называется смежной стороной, и именно здесь она образует сторону угла интереса вместе с прямым углом.
Как помнить об этих ценностях?
Такая сложная задача по запоминанию множества значений или просто случайных чисел тригонометрических функций поначалу кажется полноценным наказанием, не имеющим академической цели или пользы. Кто-то использует таблицу для запоминания значений, кто-то круговую единицу делает до в 0 градусов, угол изучается по Единичной окружности в координатах (1,0). Эти координаты есть не что иное, как тригонометрические величины. Координата x — это значение, относящееся к cos, а координата y — это значение, относящееся к sin.
Но лучше всего понять, как действует формула. Это было то, что вы не будете грабить числа и забывать позже, а также иметь полное представление о значении Cos 0, почему оно равно 1 и многом другом.
Это было то, что вы не будете грабить числа и забывать позже, а также иметь полное представление о значении Cos 0, почему оно равно 1 и многом другом.
Чему равен cos(0)?
В математике функция косинуса (cos) — это функция, которая связывает внутренний угол треугольника с длиной его стороны. Функция косинуса, а также функция синуса и тангенса являются тремя основными тригонометрическими функциями. В прямоугольном треугольнике косинус угла равен отношению стороны, прилежащей к углу, к длине гипотенузы прямоугольного треугольника. Математически это:
cos(A) = смежный/гипотенуза
Функция косинуса принимает угловые измерения в качестве входных данных и возвращает отношение в качестве выходных данных. Когда угол A=0°, функция косинуса принимает значение:
cos(0) = 1
Косинус угла, равного нулю градусов, равен 1. Чтобы понять, почему, рассмотрим, что происходит с прямоугольным треугольником. поскольку один из его углов стремится к 0. Когда угол приближается к 0, противоположная сторона становится все меньше и меньше. По мере того, как этот угол становится меньше, длины гипотенузы и стороны, прилегающей к углу, становятся все меньше и меньше. Как только измерение угла достигнет 0, гипотенуза и прилежащая сторона будут идеально лежать друг на друге, попадая в отношение 1 к 1. Таким образом, косинус 0 равен 1,
Когда угол приближается к 0, противоположная сторона становится все меньше и меньше. По мере того, как этот угол становится меньше, длины гипотенузы и стороны, прилегающей к углу, становятся все меньше и меньше. Как только измерение угла достигнет 0, гипотенуза и прилежащая сторона будут идеально лежать друг на друге, попадая в отношение 1 к 1. Таким образом, косинус 0 равен 1,
Основы триггерных функций
Три триггерные функции представляют общее соответствие между внутренними углами треугольника и длинами его сторон. Тот факт, что между сторонами и углами прямоугольного треугольника существует повторяющаяся взаимосвязь, является следствием того факта, что в подобных треугольниках сохраняются отношения между их сторонами. Прямоугольный треугольник 3-4-5 имеет те же пропорции, что и треугольник 6-8-10; последний просто кратен первому. Таким образом, любые соотношения между длинами сторон двух треугольников будут абсолютно одинаковыми.
Рассмотрим простой прямоугольный треугольник. угол. Гипотенуза всегда является самой длинной стороной в треугольнике.
угол. Гипотенуза всегда является самой длинной стороной в треугольнике.
Противоположная сторона — это сторона, расположенная прямо напротив интересующего угла.
Сторона , примыкающая к , находится непосредственно рядом с углом, который не является гипотенузой.
Следуя этим обозначениям, мы можем определить три основные триггерные функции следующим образом:
sin(A) = противоположное/гипотенуза
cos(A) = смежное/гипотенуза
tan(A) = противоположное /adjacent
Поскольку подобные треугольники имеют одинаковые пропорции, значения этих функций не зависят от размера прямоугольного треугольника, а только от того, равен ли угол оценки (A). Хорошая мнемоника для запоминания определений триггерных функций — это аббревиатура SOH-CAH-TOA (произносится как «со-ках-тоа») 9.0003
Давайте пронумеруем эти абстрактные формулы. Скажем, у нас есть прямоугольный треугольник с длинами сторон 3 и 4 и гипотенузой длины 5:
Кредит: Автор
Мы можем вычислить значения триггерных функций относительно угла A следующим образом:
sin(A) = противоположный/гипотенуза = 4/5 = 0,8
cos(A) = смежный/гипотенуза = 3/5 = 0,6
tan(A) = противоположный/прилегающий = 4/3 = 1,3
Обратите внимание, что синус и косинус функции эквивалентны с учетом разных углов. Установив угол B в качестве угла интереса, мы можем вычислить триггерные функции следующим образом:0003
Установив угол B в качестве угла интереса, мы можем вычислить триггерные функции следующим образом:0003
sin(B) = 3/5 = cos(A) = 0,6
cos(B) = 4/5 = sin(A) = 0,8
Это приводит нас к общему правилу, что для любого прямоугольного треугольника, где углы A и B не являются прямыми углами:
sin (A) = cos(B) и sin(B) = cos(A)
В дополнение к 3 основным триггерным функциям есть 3 обратные триггерные функции. Обратные функции являются обратными основными функциями и называются секансом, косекансом и котангенсом. Их можно определить как:
сек(А) = 1/sin(А) = гипотенуза/противоположная
cosec(A) = 1/cos(A) = гипотенуза/смежный
cotan(A) = 1/tan(A) = смежный/противоположный измерение, и вас попросят вычислить синус этого угла только из этого значения. К сожалению, простого алгоритма для этого нет. Вычисление значений sin вручную под заданным углом требует много времени и сложных вычислений. Вместо этого большинство калькуляторов используют справочные таблицы, таблицы со списком измерений углов и соответствующих значений греха. Эти таблицы были рассчитаны с предельной точностью. Однако существует интересный способ концептуализации угловых измерений, который делает вычисление некоторых значений триггерных функций интуитивно понятным и простым.
Эти таблицы были рассчитаны с предельной точностью. Однако существует интересный способ концептуализации угловых измерений, который делает вычисление некоторых значений триггерных функций интуитивно понятным и простым.
Триггерные функции и единичный круг
Внутреннее действие триггерных функций можно понять по отношению к структуре единичного круга на координатной плоскости. Единичная окружность — это окружность с радиусом, равным единице, с центром в начале координат плоскости (0,0). Перетаскивание радиуса вокруг исходной точки вычерчивает круг, длина окружности которого составляет ровно 2π единиц. По теореме Пифагора эта окружность есть множество всех точек (x, y) таких, что x 2 +y 2 =1
Углы можно измерить с помощью длины дуги на окружности, которую описывает угол. Эти единицы называются радианами. Поскольку длина окружности единичного круга равна ровно 2π, угол в радианах, равный 2π, соответствует 360 °. Аналогично, π/2 радиана соответствует 90°, π радианам — 180°, π/3 радиана — 60° и т. д.
д.
Единица окружности и преобразование между радианами и градусами. Предоставлено: Gustav B через WikiCommons CC BY-SA 3.0
Любую точку на единичной окружности можно представить как конечную точку линии, идущей от центральной точки с углом θ с центром в начале координат. Значения x и y этой точки соответствуют сторонам прямоугольного треугольника. Это понимание приводит к некоторым интересным свойствам триггерных функций. Поскольку по определению единичный круг имеет радиус 1, sin(θ) = y и cos(θ) = x. По теореме Пифагора и определению единичной окружности верно, что cos 2 (θ) + sin 2 (θ) = 1.
Что произойдет с прямоугольным треугольником, если мы изменим угол луча от начала координат? Изменение угла, на который линия выходит из начала координат, приводит к соответствующему изменению других сторон треугольника. Когда мы уменьшаем угол, сторона, противоположная углу, также становится меньше. а соседняя сторона становится больше. Когда мы увеличиваем угол, противоположная сторона становится больше, а соседняя сторона уменьшается. Поэтому, изменяя угол, мы можем визуализировать, как изменяется отношение сторон треугольника.
Поэтому, изменяя угол, мы можем визуализировать, как изменяется отношение сторон треугольника.
Анимация, показывающая, как стороны треугольника меняются в ответ на изменение угла. Предоставлено: WikiCommons CC0 1.0
Обратите внимание сразу на несколько вещей. Что происходит, когда угол равен 0? Каковы отношения сторон друг к другу? Когда угол приближается к 0, синус угла (противоположный/гипотенуза) становится все меньше и меньше. Когда угол достигает 0, длина противоположной стороны достигает 0, поэтому полное отношение между противолежащей стороной и гипотенузой равно 0. Итак, мы знаем, что sin(0) = 0.
А если увеличить угол? По мере того, как мы увеличиваем угол, длина противоположной стороны увеличивается, пока мы не достигнем π/2 рад (90°), после чего длина противоположной стороны и гипотенузы станет одинаковой. Если стороны имеют одинаковую длину, то их отношение равно 1, поэтому мы знаем, что sin(π/2) = 1.
Рассмотрим функцию косинуса. Что происходит со значением косинуса при уменьшении угла? По мере приближения к 0 отношение между прилежащей стороной и гипотенузой становится больше, пока прилежащая сторона и гипотенуза не станут равными, когда угол равен 0. Итак, мы знаем, что cos(0) = 1. Аналогично, по мере того, как угол приближается к π/2, прилежащая сторона становится все меньше и меньше по отношению к гипотенузе, пока не станет равной 0; таким образом, cos(π/2) = 0
Что происходит со значением косинуса при уменьшении угла? По мере приближения к 0 отношение между прилежащей стороной и гипотенузой становится больше, пока прилежащая сторона и гипотенуза не станут равными, когда угол равен 0. Итак, мы знаем, что cos(0) = 1. Аналогично, по мере того, как угол приближается к π/2, прилежащая сторона становится все меньше и меньше по отношению к гипотенузе, пока не станет равной 0; таким образом, cos(π/2) = 0
А как насчет функции тангенса? Когда угол равен 0, отношение противоположной стороны к соседней стороне также равно 0, поэтому мы можем определить, что tan(0) = 0. По мере увеличения угла противоположная сторона становится больше, а соседняя сторона уменьшается. пока не достигнет точки, где две стороны имеют одинаковую длину. Прямоугольный треугольник может иметь две равные стороны только тогда, когда оба непрямых угла равны 45°. Это означает, что под углом 45° длины двух сторон равны, поэтому их отношение равно 1.

 9613
9613 7547
7547 4226
4226 0175
0175 4226
4226 7431
7431 9511
9511 9976
9976 8829
8829 6157
6157 2588
2588 1564
1564 5446
5446 8387
8387 9877
9877 9272
9272 6947
6947 3746
3746
 4226
4226 7193
7193 9336
9336 9336
9336 7193
7193 4226
4226 0349
0349 3746
3746 682
682 9205
9205