Что такое множество состоящее из одного элемента: а) пустого множества; б) множества, состоящего из одного элемента
МНОЖЕСТВ ТЕОРИЯ | Энциклопедия Кругосвет
Содержание статьи- Терминология.
- Булева алгебра.
- Сравнение множеств.
- Парадоксы.
- Аксиома выбора.
МНОЖЕСТВ ТЕОРИЯ. Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в математике, например в математическом анализе, геометрии и теории вероятностей.
Терминология.
Если каждый элемент множества B является элементом множества A, то множество B называется подмножеством множества A. Например, если множество A состоит из чисел 1, 2 и 3, то у него существует 8 подмножеств (три из них содержат по 1 элементу, три – содержат по 2 элемента, одно подмножество, по определению, есть само множество A и восьмое подмножество – это пустое множество, не содержащее ни одного элемента). Запись x О A означает, что x – элемент множества A, а B М A – что B является подмножеством множества A. Если универсальное множество, из которого мы берем элементы всех множеств, обозначить через I, то элементы, принадлежащие I, но не входящие в A, образуют множество, называемое дополнением множества A и обозначаемое C(A) или Aў. Множество, не содержащее ни одного элемента, называется пустым множеством.
Запись x О A означает, что x – элемент множества A, а B М A – что B является подмножеством множества A. Если универсальное множество, из которого мы берем элементы всех множеств, обозначить через I, то элементы, принадлежащие I, но не входящие в A, образуют множество, называемое дополнением множества A и обозначаемое C(A) или Aў. Множество, не содержащее ни одного элемента, называется пустым множеством.
Над множествами можно производить операции, напоминающие операции, производимые в арифметике над числами. Объединением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A и B (элемент, принадлежащий множествам A и B одновременно засчитывается при включении в AB только один раз). Пересечением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих как A, так и B.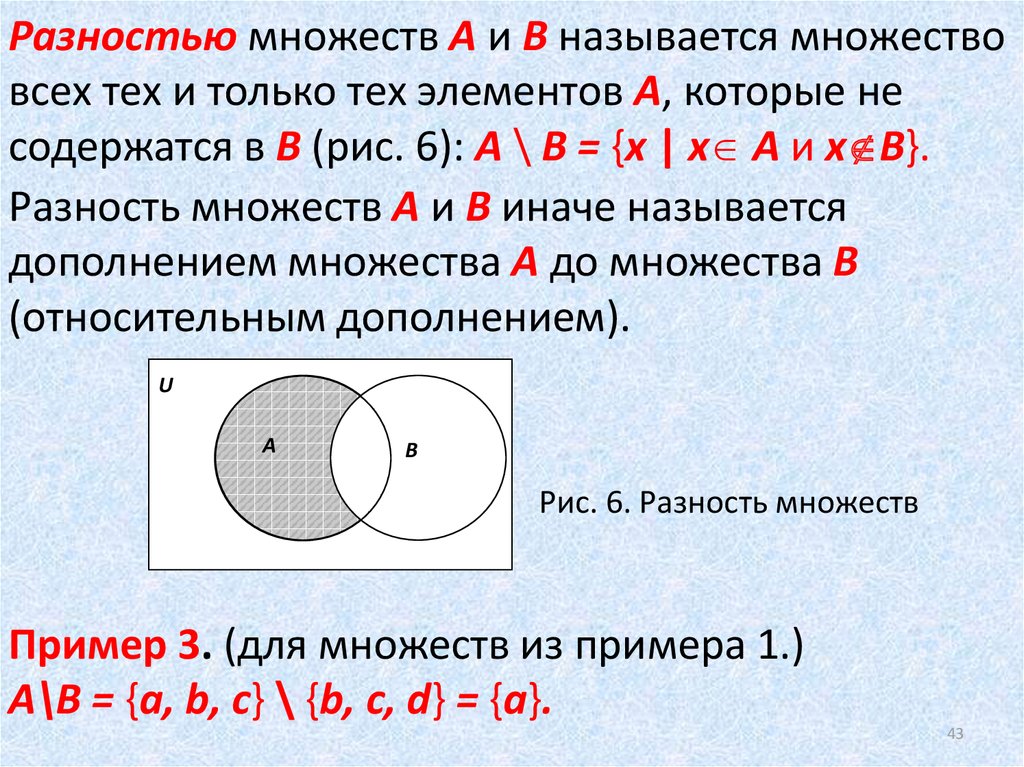 Предположим, например, что множество I состоит из всех букв русского алфавита, A – из всех согласных, а множество B – из букв, встречающихся в слове «энциклопедия». Тогда объединение AB состоит из всех букв алфавита, кроме а, ё, у, ъ, ь, ы, ю, пересечение AB – из букв д, к, л, н, п, ц, а дополнение C(A) – из всех гласных. Раздел теории множеств, который занимается исследованием операций над множествами, называется алгеброй множеств. Пустое множество играет в алгебре множеств роль нуля, и поэтому его часто обозначают символом О; например, AO = A, AO = O.
Предположим, например, что множество I состоит из всех букв русского алфавита, A – из всех согласных, а множество B – из букв, встречающихся в слове «энциклопедия». Тогда объединение AB состоит из всех букв алфавита, кроме а, ё, у, ъ, ь, ы, ю, пересечение AB – из букв д, к, л, н, п, ц, а дополнение C(A) – из всех гласных. Раздел теории множеств, который занимается исследованием операций над множествами, называется алгеброй множеств. Пустое множество играет в алгебре множеств роль нуля, и поэтому его часто обозначают символом О; например, AO = A, AO = O.
Булева алгебра.
Алгебра множеств является подразделом булевых алгебр, впервые возникших в трудах Дж.Буля (1815–1864). В аксиомах булевой алгебры отражена аналогия между понятиями «множества», «событие» и «высказывания». Логические высказывания можно записать с помощью множеств и проанализировать с помощью булевой алгебры.
Логические высказывания можно записать с помощью множеств и проанализировать с помощью булевой алгебры.
Даже не вдаваясь в детальное изучение законов булевой алгебры, мы можем получить представление о том, как она используется на примере одной из логических задач Льюиса Кэрролла. Пусть у нас имеется некоторый набор утверждений:
-2831. Не бывает котенка, который любит рыбу и которого нельзя научить всяким забавным штукам;
2. Не бывает котенка без хвоста, который будет играть с гориллой;
3. Котята с усами всегда любят рыбу;
4. Не бывает котенка с зелеными глазами, которого можно научить забавным штукам;
5. Не бывает котят с хвостами, но без усов.
Какое заключение можно вывести из этих утверждений?
Рассмотрим следующие множества (универсальное множество I включает в себя всех котят): A – котята, любящие рыбу; B – котята, обучаемые забавным штукам; D – котята с хвостами; E – котята, которые будут играть с гориллой; F – котята с зелеными глазами и G – котята с усами. Первое утверждение гласит, что множество котят, которые любят рыбу, и дополнение множества котят, обучаемых забавным штукам, не имеют общих элементов. Символически это записывается как
Первое утверждение гласит, что множество котят, которые любят рыбу, и дополнение множества котят, обучаемых забавным штукам, не имеют общих элементов. Символически это записывается как
-2831. AC(B) = O.
Аналогичным образом остальные утверждения можно записать так:
-2832. C(D)E = O;
3. G М A;
4. BF = O;
5. D М G.
Принимая во внимание теоретико-множественный смысл символов (или воспользовавшись законами булевой алгебры), мы можем переписать утверждения 1, 2 и 4 в виде
1. A М B;
2. E М D;
4. B М C(F).
Таким образом, мы переформулировали исходные утверждения в следующие:
-2831. Котят, которые любят рыбу, можно обучить забавным штукам;
2. У котят, которые будут играть с гориллой, есть хвосты;
4. У котят, которых можно обучить забавным штукам, глаза не зеленые;
Теперь можно расположить символические записи утверждений в таком порядке, чтобы последний символ предыдущего утверждения совпадал с первым символом следующего (этому условию удовлетворяет расположение утверждений в порядке 2, 5, 3, 1, 4). Возникает цепочка включений E М D М G М A М B М C(F), из которой можно сделать вывод, что E М C(F) или «Не бывает котенка с зелеными глазами, который будет играть с гориллой». Такое заключение едва ли очевидно, если рассматривать пять исходных утверждений в их словесной формулировке.
Возникает цепочка включений E М D М G М A М B М C(F), из которой можно сделать вывод, что E М C(F) или «Не бывает котенка с зелеными глазами, который будет играть с гориллой». Такое заключение едва ли очевидно, если рассматривать пять исходных утверждений в их словесной формулировке.
Сравнение множеств.
Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие. Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа.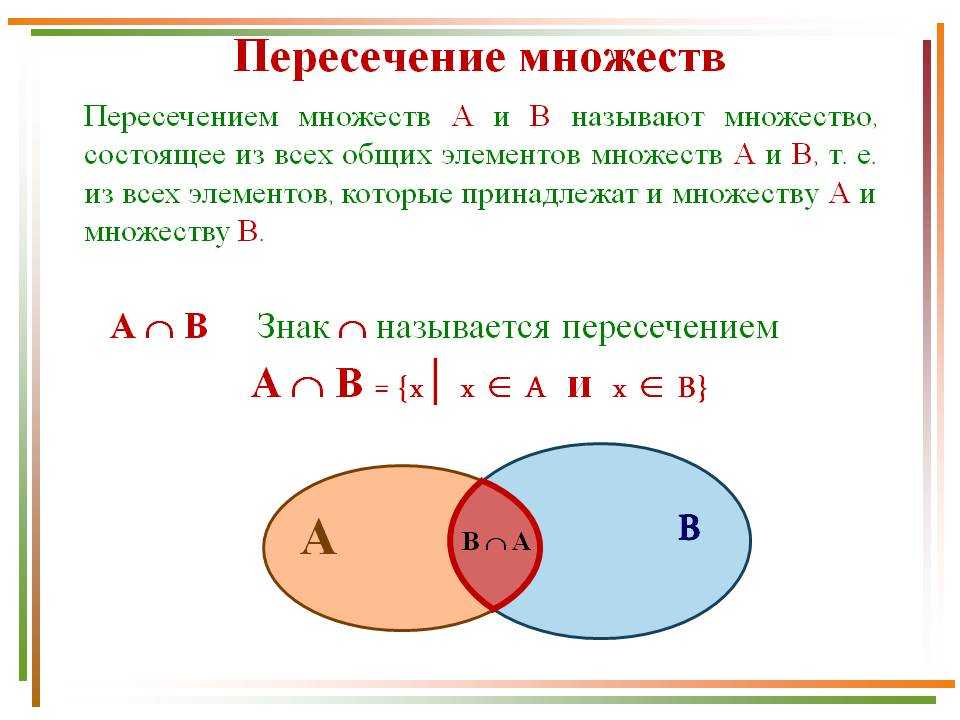 Мы могли бы утверждать: «Столиц штатов ровно столько, сколько штатов». Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел.
Мы могли бы утверждать: «Столиц штатов ровно столько, сколько штатов». Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел. Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б.Рассел (1872–1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством.
Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б.Рассел (1872–1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством. Иногда это свойство принимают за определение бесконечного.
Иногда это свойство принимают за определение бесконечного.
Если можно установить взаимно однозначное соответствие между некоторым множеством и множеством положительных целых чисел, то говорят, что такое множество счетно. Для обозначения количества элементов в счетном множестве часто используют символ А0 (алеф-нуль). Так называемые «трансфинитные» числа, например А0, могут не подчиняться обычным законам арифметики. Например, так как существует А0 четных чисел, А0 нечетных и А0 целых чисел, то приходится признать, что А0 + А0 = А0. Идея сравнения множеств путем установления взаимно однозначного соответствия между ними используется в различных разделах математики. Число всех действительных чисел, как показал основатель научной теории множеств Г.Кантор (1845–1918), больше, чем А0 чисел. Следовательно, если можно показать, что множество действительных чисел, обладающих некоторым особым свойством, является всего лишь счетным множеством, то заведомо должны существовать действительные числа, этим свойством не обладающие. Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными.
Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными.
Поразительная и далеко не очевидная теорема, высказанная в качестве гипотезы Кантором и доказанная Э.Шрёдером и Ф.Бернштейном около 1896, утверждает, что если можно установить взаимно однозначное соответствие между множеством A и подмножеством множества B, и между множеством B и подмножеством множества A, то существует взаимно однозначное соответствие между всем множеством A и всем множеством B.
Парадоксы.
Мы уже упоминали о том, что в теории множеств встречаются такие утверждения, как парадокс Тристрама Шенди, которые выглядят противоречащими здравому смыслу. Эти парадоксы возникают просто потому, что теория множеств, подобно многим математическим и физическим теориям, облекает свои идеи в обычные слова, вкладывая в них особый смысл. Однако существуют и парадоксы, возникающие из-за внутренних логических трудностей самой теории множеств. Обильным источником парадоксов такого типа служит широко распространенная практика задания множества путем указания некоторого свойства его элементов, например, «множество, состоящее из английских слов, содержащих менее 19 букв».
Обильным источником парадоксов такого типа служит широко распространенная практика задания множества путем указания некоторого свойства его элементов, например, «множество, состоящее из английских слов, содержащих менее 19 букв».
Некритическое использование такого рода определений может привести к трудностям. Например, некоторые статьи в этой энциклопедии содержат ссылки на себя, другие таких ссылок не содержат. Мы могли бы включить в нашу энциклопедию дополнительную статью, состоящую только из перечня статей, не содержащих ссылок на себя. Принадлежала бы такая статья множеству статей, не содержащих ссылок на себя, или не принадлежала бы? Любой ответ противоречил бы отличительному свойству, которым по их определению наделены элементы множества. Это – одна из форм так называемого парадокса Рассела, названного в честь своего автора Бертрана Рассела. «Множество всех множеств» – еще одно понятие, также приводящее к парадоксу. Существование парадоксов показывает, с какой осторожностью следует пользоваться терминологией теории множеств. Тем не менее теория множеств настолько полезна, что большинство математиков не хотели бы отказываться от нее. Было затрачено много усилий, чтобы развить методы, позволяющие исключить возникновение парадоксов в теории множеств. В приложениях теории множеств к другим разделам математики универсальное множество I обычно само является некоторым определенным множеством и парадоксальные ситуации здесь не возникают.
Тем не менее теория множеств настолько полезна, что большинство математиков не хотели бы отказываться от нее. Было затрачено много усилий, чтобы развить методы, позволяющие исключить возникновение парадоксов в теории множеств. В приложениях теории множеств к другим разделам математики универсальное множество I обычно само является некоторым определенным множеством и парадоксальные ситуации здесь не возникают.
Аксиома выбора.
Неожиданные трудности в теории множеств могут возникнуть, казалось бы, в самых простых случаях. Если, например, задано семейство непересекающихся множеств, ни одно из которых не пусто, то интуитивно кажется очевидным, что мы можем построить новое множество, содержащее ровно по одному элементу из каждого множества, входящего в это семейство. Но если наше семейство содержит бесконечно много множеств, то для построения нового множества может потребоваться бесконечное число произвольных выборов, а законность такого процесса при тщательном анализе становится отнюдь не очевидной. Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э.Цермело (1871–1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гёдель (1906–1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора. См. также АБСТРАКТНЫЕ ПРОСТРАНСТВА; ФУНКЦИЯ.
Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э.Цермело (1871–1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гёдель (1906–1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора. См. также АБСТРАКТНЫЕ ПРОСТРАНСТВА; ФУНКЦИЯ.
|
Множество — это произвольная совокупность определённых и различимых объектов, мысленно объединённых в единое целое. Эти объекты называются элементами, или членами множества. Множество представляет собой одну из базисных категорий философского (см. Философия) и научного (см. Наука) дискурсов, рассматриваемая, как правило, совместно с категорией единого, а также одно из главных логико-математических понятий, развитое на основании этих категорий. Введение в рассмотрение множества тех или иных предметов является одной из основных познавательных операций; при этом понятие множества становится отчётливым лишь в предположении, что элементы данного множества можно рассматривать как отдельные предметы. Кроме того, обычно предполагается возможность сравнивать — различать и отождествлять — любые два элемента множества. Основным принципом образования множества служит возможность рассматривать, в связи с каждым свойством, множество предметов, обладающих этим свойством. В соответствии с этим, в связи с каждым понятием можно рассматривать множество предметов, обладающих тем свойством, которое выражается этим понятием; соответствующее ему множество может состоять из любого (конечного) числа предметов; оно может также быть бесконечным; оно может быть и пустым, то есть вовсе не содержать элементов — так, в частности, бывает тогда, когда рассматриваемое понятие логически противоречиво (например, множество всех круглых квадратов пусто, так как никакой квадрат не может быть круглым).  Понятие множества подробно рассматривалась уже в античной философии. Платон вводит понятие множества, исходя из противопоставления единого и иного. Единое, по определению, не подразумевает ничего, кроме себя, то есть не допускает никакого отношения и может быть мыслимо лишь само по себе. Иное же всегда есть иное по отношению к чему-то (также иному по отношению к нему). Следовательно, иное подразумевает множество. Однако множество невозможно мыслить, исключив представление о едином, поскольку в противном случае каждая его часть (элемент) не может быть рассмотрена как единство, а будет дробиться до бесконечности. Этот аргумент был впоследствии развит Проклом, который всякое множество рассматривал как причастное единому в двух отношениях: во-первых, как ограниченное целое, а во-вторых, как составленное из единичностей. Мысль о причастности множества единому он истолковал так, что всякое множество произведено от единого-в-себе, а единство является одновременно производящей мощью, которая уменьшается вместе с количественным ростом множества, поскольку последний означает уменьшение причастности единому. Философия Нового времени не уделила понятию множества такого серьёзного внимания, как античная. И. Кант ввёл эту категорию в свою таблицу чистых понятий рассудка как одну из трёх категорий количества (две другие — единство и цельность), но, рассматривая схемы количества, говорил уже не о множестве, а об экстенсивной величине. Последняя должна быть рассмотрена как цельность, формируемая последовательным прибавлением друг к другу множества частей. Дальнейший философский интерес к понятию множества обусловлен развитием теории множеств в математике. Именно с этой теорией был в значительной мере связан кризис оснований математики, потребовавший значительной переоценки не только содержания математического знания, но и его философских оснований. В качестве математической теории «учение о множествах» было создано Г. Кантором, который, впрочем, рассматривал его не как одну из математических дисциплин, а как фундамент для всей математики. Из понятия множества предполагалось вывести все основные математические понятия, прежде всего понятие числа. В основе канторовского представления о множестве лежит аристотелевское определение Ещё одно введённое Кантором понятие, которое порождает трудности, — это понятие непрерывного множества. Важным результатом Кантора является теорема о том, что мощность любого множества всегда меньше мощности множества всех его подмножеств. В частности, множество всех подмножеств множества натуральных чисел превосходит последнее по мощности, то есть является несчётным. Канторовский проект создания теории множеств как основания математики был позднее осуществлён Э. Цермело, который создал аксиоматическую теорию множеств. |
Множества,их элементы,поджмножества
Определение 1
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Предметы или объекты, образующие данное множество, называются его элементами. Например, число $6$ будет являться элементом множества натуральных чисел, а число $0,9$ не будет являться элементом множества натуральных чисел.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Определение 2
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Определение 3
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
В математике часть множества называют — подмножество. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества.
Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества.
Обозначение множеств, подмножеств и их элементов
Чаще всего множества обозначаются латинскими буквами- $A, B, C , D, X, Y, Z, W$ и Т.Д.
Элементы множеств обозначаются строчными буквами $a,b,c,d,x,y,z$ и Т.Д.
Записать принадлежность некоторого элемента к некоторому множеству, например то, что некоторой элемент $a$ будет входить в множество $A$ математически можно так: $a\in A$.Прочитать данную запись можно так: a принадлежит множеству $A$.
Если же некоторый элемент, например, $b$ не принадлежит множеству $B$, то это записывается так: $b\notin B$.Читают эту запись так: $b$ не принадлежит множеству $B$
Например, если обозначить множество целых чисел за $A$, что тогда можно записать: $3\in A$, $7,5\notin B$
Пустое множество в математике обозначают так: $ᴓ$
Для обозначения того, что множество $B$ является подмножеством множества $A$, используют обозначение: Знак $\subset $ обозначает включение одного множества в другое множество.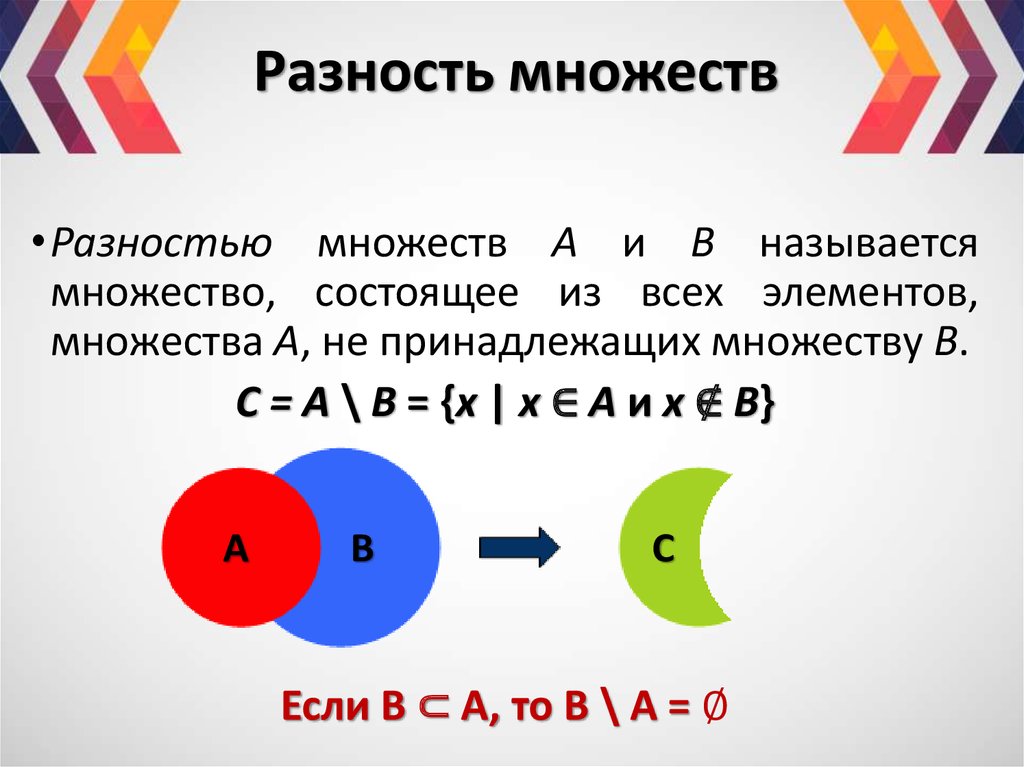
Пример 1
Определить какие элементы из перечисленных $12,38,54,79,934$ будут входить в множество $A$- чисел кратных $3$.
Решение: По условию множество $A$ содержит в себе элементы, каждый из которых должен быть кратным, т.е. делится без остатка на $3.$ Значит для того чтобы определить будут ли заданные числа являться элементами множества $A$ нам надо проверить какие из них будут делится на $3$ без остатка, какие нет.
Вспомним признак делимости на $3$: Если сумма цифр, входящих в состав числа делится на $3$, то число делится на $3$ без остатка.
$12$ делится на $3$, т.к. сумма цифр числа $12$ равна $3$
число $38$ на $3$ без остатка делится не будет, т.к. сумма цифр $3+8=11$ не делится на $3$ без остатка
аналогично т.к. суммы цифр числа $54$ равна $9$ доказываем, что на $3$ оно делится, в число $74$ на $3$ делится не будет, т.к. сумма цифр равна $11.$
Найдем сумму цифр числа $934: 9+3+4=16$, число $16$ не кратно $3$ ,значит и число $934$ на $3$ без остатка делится не будет
Теперь сделаем вывод, какие числа будут являться элементами множества $A$:
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ {\rm :\ }54\in A. \]
\]
Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
Конечные множества с небольшим количеством элементов обычно записывают в фигурных скобках $\left\{a,b,c\right\}$
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Второй способ задания множеств применим как для конечных. так и для бесконечных множеств. Он заключается в том, что указывается свойство, которым обладает каждый элемент данного множества — множество задают описанием, т.е. указав его характеристическое свойство, т. е свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.
Пример 2
Например, с помощью описания можно задать такие множество натуральных чисел от $1$ до $9$ включительно. Характеристическим свойством, т. е. свойством, которым обладают все элементы этого множества для данных элементов будет являться то, что все они являются натуральными числами и каждое из них не меньше $1$ и не больше $9$. Перечислением указанное множество можно задать следующим образом:
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Пример 3
Например, рассмотрим множества
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
$B=\left\{9,8,7,6,5,4,3,2,1\right\}$
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Пример 4
Например, рассмотрим два множества:
$A=\left\{1\ ,2,3,4,5\right\}$
$B=\left\{9,7,5,3,\right\}$
Общей частью этих множеств будет множество $C=\left\{3,5,\right\}$
Математически это можно обозначить так: $А\cap B=\left\{3,5\right\}$
Пересечением множеств $A$ и $B$ называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество $A$ и в множество $B$.
Объединение множеств
Из двух множеств $A$ и $B$ можно образовать новое множество, объединяя все элементы множества $A$ и все элементы множества $B$
Математически это можно обозначить так:$\ А\ \cup B$
Объединением множеств $A$ и $B$ называется новое множество$\ А\ \cup B$, состоящее из тех и только из тех элементов, которые входят хотя бы в одно из множеств $A$ или $B$.
Разность множеств
Разностью двух множеств $A$ и $B$ называют такое множество, в которое входят все элементы из множества $A$, не принадлежащие множеству $B$.
Мат. логика, основания математики, теория алгоритмов
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| tandser |
| ||
05/03/06 |
| ||
| |||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| незваный гость |
| |||
17/10/05 |
| |||
| ||||
| tandser |
| ||
05/03/06 |
| ||
| |||
| RIP |
| |||
11/01/06 |
| |||
| ||||
| radical |
| ||
20/10/06 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Модераторы Математики, Супермодераторы
Элементы теории множеств. Множества и операции над ними
Понятие множества является одним из основных математических понятий. Это неопределяемое понятие, его можно только описать или пояснить на примерах. Так, можно говорить о множестве букв в латинском алфавите, множество всех книг в данной библиотеке, множестве студентов в данной группе, множестве всех точек данной линии. Чтобы задать множество, достаточно перечислить элементы или указать характеристические свойства элементов, т.е. такое свойство, которым обладают все элементы данного множества и только они.
Это неопределяемое понятие, его можно только описать или пояснить на примерах. Так, можно говорить о множестве букв в латинском алфавите, множество всех книг в данной библиотеке, множестве студентов в данной группе, множестве всех точек данной линии. Чтобы задать множество, достаточно перечислить элементы или указать характеристические свойства элементов, т.е. такое свойство, которым обладают все элементы данного множества и только они.
Определение 1.1.Предметы (объекты), составляющие некоторое множество, называются его элементами.
Множество принято обозначать прописными латинскими буквами, а элементы множества – строчными буквами. То, что x является элементом множества A, записывается так: x A (x принадлежит A). Запись вида x A (x A) означает, что x не принадлежит A, т.е. не является элементом множества A.
Элементы множества принято записывать в фигурных скобках. Например, если A – множество, состоящее из первых трех букв латинского алфавита, то его записывают так: A={a,b,c}.
Например, если A – множество, состоящее из первых трех букв латинского алфавита, то его записывают так: A={a,b,c}.
Множество может содержать бесконечно много элементов (множество точек прямой, множество натуральных чисел), конечное число элементов (множество школьников в классе), либо вообще не содержать ни одного элемента (множество студентов пустой аудитории).
Определение 1.2.Множество, не содержащее ни одного элемента, называется пустым множеством, обозначается Ø.
Определение 1.3.Множество A называется подмноже-ством множества B, если каждый элемент множества A принадлежит и множеству B. Это обозначается A B (A – подмножество B).
Пустое множество считают подмножеством любого множества. Если множество A не является подмножеством множества B, то пишут A B.
Определение 1.4. Два множества A и B называют равными, если являются подмножествами друг друга. Обозначают A = B. Это означает, что если x A, то x B и наоборот, т.е. если и , то .
Два множества A и B называют равными, если являются подмножествами друг друга. Обозначают A = B. Это означает, что если x A, то x B и наоборот, т.е. если и , то .
Определение 1.5.Пересечение множеств A и B называют множество M, элементы которого являются одновременно элементами обоих множеств A и B. Обозначают M= A B. Т.е. x A B, то x A и x B.
Записывают A B={ x | x A и x B }. (Вместо союза и – ставятся знаки , &).
Определение 1.6.Если A B= Ø, то говорят, что множества A и B не пересекаются.
Аналогично можно определить пересечение 3-х, 4-х и любого конечного числа множеств.
Определение 1.7.Объединением множеств A и B называют множество M, элементы которого принадлежат хотя бы одному из данных множеств. Обозначают M=A B. Т.о. A B={ x | x A или x B }. (Вместо союза или – ставится знак ).
Обозначают M=A B. Т.о. A B={ x | x A или x B }. (Вместо союза или – ставится знак ).
Аналогично определяется и множество A1 A2 … An. Оно состоит из элементов, каждый из которых принадлежит хотя бы одному из множеств A1, A2,…, An(а может быть, и нескольким сразу).
Пример 1.8. 1) если A={1;2;3;4;5} и B={1;3;5;7;9}, то A B={1;3;5} и A B={1;2;3;4;5;7;9}.
2) если A={2;4} и B={3;7}, то A B= Ø и A B={2;3;4;7}.
3) если A={летние месяцы} и B={месяцы, в которых 30 дней}, то A B={июнь} и A B={апрель; июнь; июль; август; сентябрь; ноябрь}.
Определение 1.9.Натуральными называются числа 1,2,3,4,…, используемые для счета предметов.
Множество натуральных чисел обозначается N, N={1;2;3;4;…;n;…}. Оно является бесконечным, имеет наименьший элемент 1 и не имеет наибольшего элемента.
Пример 1.10. A – множество натуральных делителей числа 40. Перечислить элементы этого множества. Верно ли, что 5 A, 10 A, -8 A, 4 A, 0 A, 0 A.
A = {1,2,4,5,8,10,20,40}. (В,В,Н,Н,Н,В)
Пример 1.11.Перечислите элементы множеств, заданных характеристическими свойствами:
а) А={x | (x-1)(2x-1)(3+x)=0}, получаем A = {1; ;-3}
б) B={x | -1,1< x < 5 x N}, имеем B = {1;2;3;4}.
Пример 1.12.Дано множество чисел K = {21;54;153;171;234}. Составить подмножество чисел из K, которые а) делятся на 7; б) делятся на 9; в) не делятся на 5; г) делятся на 4.
а) A = {21}, б) B = {54;153;171;234}, в) C = K, г) D= Ø
Пример 1. 13.Множество C состоит из 11 элементов, множество D – из 8. Сколько элементов содержит C D , если C D содержит 15 элементов?
13.Множество C состоит из 11 элементов, множество D – из 8. Сколько элементов содержит C D , если C D содержит 15 элементов?
Поскольку A+B –A B=A B, тогда 11+8–15=4
Определение 1.14.Разность множеств A и B называется множество M, элементы которого принадлежат множеству A и не принадлежат множеству B.
Обозначают M=A \ B.
Таким образом, A \ B={x | x A и x B}.
Пример 1.15. Если A = {1;2;3;4;5} и B = {1;5}, то A\B={2;3;4}.
Дата добавления: 2016-06-15; просмотров: 10455; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Урок 10. некоторые сведения из теории множеств — Информатика — 10 класс
Информатика, 10 класс. Урок № 10.
Тема — Некоторые сведения из теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором, создателем теории множеств.
Оно было введено в математику немецким ученым Георгом Кантором, создателем теории множеств.
Георг Кантор
(1845—1918)
Немецкий математик, создатель теории множеств
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое. Под множеством мы можем понимать: учеников класса, фрукты, деревянные предметы, числа и т. д.
Например:
Множество учеников класса | |
Множество деревянных предметов | |
Множество чисел | |
Множество фруктов |
Множества принято обозначать прописными буквами латинского алфавита (A,B,C,D и т. д.).
Множество можно задать перечислением всех его элементов, заключенных в фигурные скобки:
A={Маша, Ваня, Петя….} | B={Банан, яблоко, виноград…. |
C={миска, подставка под карандаши, разделочная доска….} | D={1,2,3,4,5….} |
Из некоторых элементов одного множества можно составить новое. Тогда такое множество Е принято называть подмножеством D:
D={1,2,3,4,5,6,7,8…}
E={2,4,6,8…}
Для наглядности множества можно изображать в виде окружности, так называемых кругов Эйлера, где элементы, входящие в множество, изображают внутри круга, а остальные вне:
Пересечением множеств называется множество их общих элементов.
Например:
Пусть множество A будет состоять из элементов 1,3,6,9,12,15, а множество B из элементов 2,4,6,8,10,12. Тогда в пересечение этих множеств будет входить 2,6,12:
A={1,3,6,9,12,15} B={2,4,6,8,10,12} A⋂B={2,6,12} |
Множество может не содержать элементы, тогда оно будет называться пустым.
Если множества не имеют общих элементов, то их пересечение — пустое множество:
С⋂D=ø |
Объединением двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов:
A={1,3,6,9}
B={2,4,6,8}
A⋃B={1,2,3,4,6,8,9}
Разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В:
A={1,3,6,9}
B={2,4,6,8}
A\B={1,3,9}
Если множество А является подмножеством B, то дополнением называется разность множества А и В:
A={2,4,6}
B={1,2,3,4,5,6}
Мощностью множества называется число его элементов: A={1,2,3,4,5,6}
|A|=5
Таким образом, мощность непересекающихся множеств будет являться суммой мощностей каждого множества:
A={1,3,5,7}
B={2,4,6,8}
|A⋃B|=8
Для вычисления мощности пересекающихся множеств можно использовать принцип включений и исключений:
|A⋃B|= |A|+|B|–| A⋂B|
A={1,2,3,4,5,6}
B={2,4,6,8}
|A⋃B|=6+4–3=7
Для вычисления мощности пересечения трех множеств принцип включений и исключений выглядит так:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|-|B⋂C|+|A⋂B⋂C|
Задание №1.
В классе 17 пловцов, 8 борцов и 13 футболистов. Известно, что в классе 25 детей, а ребят занимающихся футболом и плаваньем — 10, борьбой и плаваньем — 3, борьбой и футболом — 2 и только один ребенок занимается всеми тремя видами спорта. Сколько детей в классе не занимаются спортом?
Дано:
|A|=17, |B|=8, |C|=13
|A⋂B|=3, |A⋂C|=10, |B⋂C|=2
|A⋂B⋂C|=1
по формуле включения:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|–|B⋂C|+|A⋂B⋂C|=17+8+13–3–10–2+1=24
Таким образом, в классе 24 ребенка занимаются хотя бы одним видом спорта, ответ 1
Задание №2.
- Множество общих элементов двух множеств
- Совокупность объектов произвольной природы, которая рассматривается как единое целое
- Число элементов множества
- Множество элементов, не входящих в подмножество
- Множество, состоящее из всех элементов двух (или более) множеств и не содержащее никаких других элементов
Проверьте свои ответы:
- Пересечение
- Множество
- Мощность
- Дополнение
- Объединение
Задание №3
Закрасьте область цветом:
- Зеленым — R\(P\Q)
- Красным — (P⋂R)\Q
- Желтым — (P∪Q)\R
Ваше решение должно быть таким:
элементарная теория множеств.
 Почему набор из одного элемента не равен элементу?
Почему набор из одного элемента не равен элементу?Я думаю, вы сбиваетесь с толку, потому что пытаетесь использовать понятия из «теории множеств» 1 непосредственно в реальных вещах. Математика не работает в реальном мире — она работает в мире аксиом, утверждений и доказательств.
Отступление в формальную логику
Теория есть не что иное, как:
- набор символов: операторы, функциональные символы, переменные и т. д., и
- аксиомы: утверждения, сделанные с использованием этих операторов, функциональных символов и переменных в сочетании с символами, определяемыми используемой логикой, часто логикой первого порядка, также известной как логика предикатов (как в случае с теорией множеств).
Это все чисто теоретических и символических объектов. Они не имеют смысла (по крайней мере, внутреннего смысла). Итак, для теории множеств у нас есть оператор $\in$, постоянный символ $\emptyset$ и бесконечное множество 2 переменных. 3
3
Аксиомы — это утверждения, подобные аксиоме экстенсиональности в теории множеств: $$\forall x \forall y [ \forall z ( z \in x \iff z \in y) \подразумевает x = y].$$ Символы $\forall$, $\iff$, $\implies$ и $=$ определяются логикой первого порядка. Мы можем построить другие операторы чисто символически из грамматики операторов, функциональных символов и переменных. Эти утверждения также не имеют внутреннего смысла.
Из утверждения мы можем попытаться доказать или опровергнуть утверждение, строя различные доказательства, используя логическую систему в сочетании с аксиомами. Само доказательство (опять же) чисто символическое. Если мы можем доказать утверждение, мы говорим, что оно «истинно», а если мы можем опровергнуть его, мы говорим, что оно «ложно».
Я постоянно упоминаю, что все эти объекты являются чисто символическими, потому что важно понимать, что теория сама по себе бесполезна, по крайней мере, для целей описания множеств. Во вселенной теории множеств нет даже ничего , называемого множеством — только операторы, утверждения, аксиомы и значения истинности. Она называется «теорией множеств» только потому, что мы имеем в виду ее конкретное применение.
Она называется «теорией множеств» только потому, что мы имеем в виду ее конкретное применение.
Назад к реальности
Итак, если теории чисто символичны и бессмысленны, что хорошего в теории множеств или даже в формальной математике? Ответ заключается в том, что мы выбираем другие системы, называемые моделями, и сопоставляем теорию с моделью. Мы обеспечиваем отображение символических объектов на объекты в модели и показываем, что аксиомы «истинны» 4 для модели. Мы говорим, что модель является интерпретацией теории, и тогда мы знаем, что для любого формального утверждения в нашей теории есть соответствующее утверждение о модели с тем же значением истинности. (Здесь я машу рукой.)
Так почему же $x \neq \{x\}$?
Потому что, в конце концов, если мы хотим применить теорию теории множеств к нашей модели множеств, нам нужно выбрать модель множеств, которая интерпретирует теорию теории множеств — а в теории множеств утверждение $\exists x \exists y (x = y \land x \in y)$ может быть опровергнуто, следовательно, ложно, и, следовательно, соответствующее утверждение должно быть ложным в нашей модели. Итак, мы знаем, что ваша модель, в которой армия одного солдата равна самому солдату, — это , а не модель теории множеств.
Итак, мы знаем, что ваша модель, в которой армия одного солдата равна самому солдату, — это , а не модель теории множеств.
Так почему же создатели теории множеств решили, что их теория работает именно так? Как я уже сказал, у теории нет внутреннего смысла, поэтому ее создатели имели возможность выбирать из бесчисленной бесконечной вселенной теорий — так что это был реальный выбор. Я думаю, вероятно, потому, что они сочли свою теорию хорошим компромиссом:
- интуитивно понятный: наличие моделей, понятных большинству математиков,
- полезно: иметь модели, которые понадобятся математикам в их работе,
- мощный: наличие аксиом, которые могут фиксировать истинностное значение самых разных утверждений, и
- сговорчивый: наличие аксиом, которые фактически позволяют доказать большинство полезных утверждений. 5
Как уже говорили другие, можно определить других теорий, которые охватывают свойство, которое вы упомянули, но, по-видимому, у них есть компромиссы в этих областях. Мы решили построить большую часть нашей математики на основе современной формулировки теории множеств, так что это было Достаточно хорошо™ .
Мы решили построить большую часть нашей математики на основе современной формулировки теории множеств, так что это было Достаточно хорошо™ .
1 Я взял эту фразу в устрашающие кавычки, потому что на протяжении веков существовало множество формулировок теорий множеств. Наиболее популярной сегодня является теория множеств Цермело-Френкеля, и именно ее имеет в виду большинство людей, говоря «теория множеств».
2 Это, конечно, , немного , вызывающий вопрос, потому что мы определяем теорию множеств , используя множеств, но есть различие. Набор переменных не часть вселенной множеств, описываемых теорией. Это чисто часть формализации теории.
3 Обратите внимание, что оператор скобок $\{\cdot\}$, также известный как нотация построения множеств, не является частью этой теории. Он определяется исключительно с точки зрения $\in$ и $=$.
4 Больше пугающих кавычек, потому что, как видите, это рекурсивное определение. Нам потребуется использовать некоторую формальную логическую систему, чтобы доказать это соответствие. Есть причина, по которой Уайтхед и Рассел Principia Mathematica только завершает доказательство того, что $1 + 1 = 2$ во втором томе .
Нам потребуется использовать некоторую формальную логическую систему, чтобы доказать это соответствие. Есть причина, по которой Уайтхед и Рассел Principia Mathematica только завершает доказательство того, что $1 + 1 = 2$ во втором томе .
5 Теорема Гёделя о неполноте показывает, что любая «достаточно мощная» теория в логике первого порядка либо неполна (имеет утверждения, которые нельзя доказать или опровергнуть), либо непоследовательна (имеет утверждения, которые могут быть и доказаны и опровергнуты ). Таким образом, цель теории состоит в том, чтобы сделать многие полезные утверждения доказуемыми и избежать противоречий. Это часть «ремесла» формальной логики.
Элементарная теория множеств. Элемент нотации Singleton (множество с одним элементом)
Задавать вопрос
спросил
Изменено 2 года, 2 месяца назад
Просмотрено 2к раз
$\begingroup$
Мне было интересно, какие обозначения используются для обозначения элемента синглтона (или единичного множества, или множества с кардинальностью 1).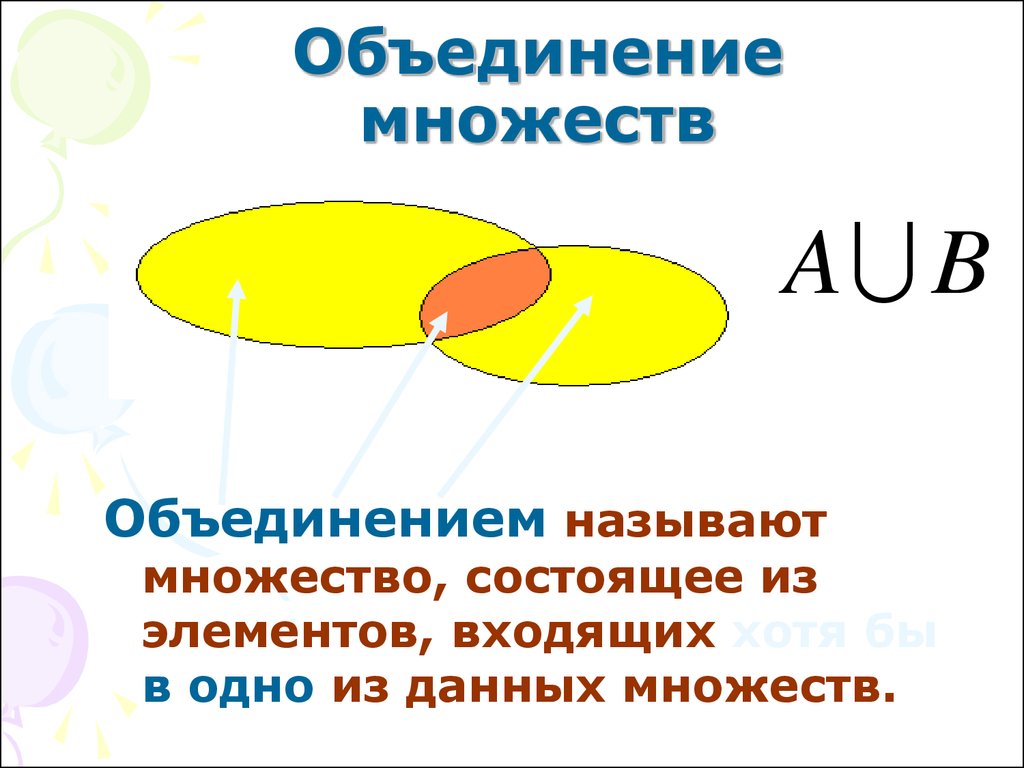 Это было бы обратным построению множества:
Это было бы обратным построению множества:
$$X = \{y\} \tag{1}$$ $$у = \текст{? } X \text{ ?} \tag{2}$$
Я не видел таких примеров, но думаю, что использование таких обозначений, как $X_1$ или $X_0$, вводит в заблуждение. Общий случай $X$ может быть даже несчетным, хотя он, очевидно, счетен, когда $|X|=1$. Например, если $M$ представляет собой набор наборов действительных чисел:
$$\forall X \in M \,:\,|X|=1 \Rightarrow P(X_0) \tag{3}$$
Это кажется возможным, но так как все $X$ не t исчисляемо выглядит обманчиво.
Я нашел этот пост, в котором использовалась нотация $$y = \iota X \tag{4}$$
Лингвистически похоже на английский артикль «the». Я бы, вероятно, прочитал вышесказанное как «y равно X».
Я не знаю, насколько широко используется или признается это обозначение. Есть ли другие обозначения, возможно, более распространенные?
нотация теории элементарных множеств
$\endgroup$
6
$\begingroup$
Как сказал Асаф, в контекстах (например, ZFC), где все является набором, вы можете использовать $\bigcup X$. К сожалению, я ожидаю, что только сторонники теории множеств поймут, что вы делаете, без дополнительных объяснений. Я использовал обозначение $\text{TheUnique}(X)$, но это было в статье, близкой к информатике, где подобные многобуквенные символы довольно распространены.
К сожалению, я ожидаю, что только сторонники теории множеств поймут, что вы делаете, без дополнительных объяснений. Я использовал обозначение $\text{TheUnique}(X)$, но это было в статье, близкой к информатике, где подобные многобуквенные символы довольно распространены.
$\endgroup$
5
$\begingroup$
Если вы хотите строго придерживаться теоретико-множественного контекста, тогда $y=\bigcup\{y\}=\bigcup X$. Но это может работать не очень хорошо вне теоретико-множественного контекста.
В случае, когда $X$ является подмножеством упорядоченного множества, тогда также $y=\min X=\max X$. Там, вероятно, нет хорошего и общего обозначения для этого. Но я, честно говоря, не понимаю, зачем он нам нужен.
$\endgroup$
2
$\begingroup$
Я бродил по улице в поисках этого ответа, и, судя по моим дальнейшим поискам, это лучшее, что у меня есть. Количественная оценка уникальности — довольно краткий способ показать, что это унитарный набор.
Количественная оценка уникальности — довольно краткий способ показать, что это унитарный набор.
Левую сторону, возможно, нужно обернуть экзистенциальной квантификацией. Пожалуйста, отредактируйте по мере необходимости; Я всего лишь инженер, а не математик.
$$ x = ValueOf(X) \Longleftrightarrow \exists! х : х \in X $$
$\endgroup$
3
$\begingroup$
Это, вероятно, огромное излишество, но вы можете использовать тау Бурбаки, который выбирает произвольный элемент в наборе или произвольный элемент, удовлетворяющий некоторому предикату. Если набор пуст или предикат никогда не бывает истинным, он возвращает что-то произвольное. Этот оператор также иногда записывается как $\varepsilon$. Вы можете немного расширить его, чтобы работать с множествами напрямую, а не с правильно построенными формулами или в дополнение к ним.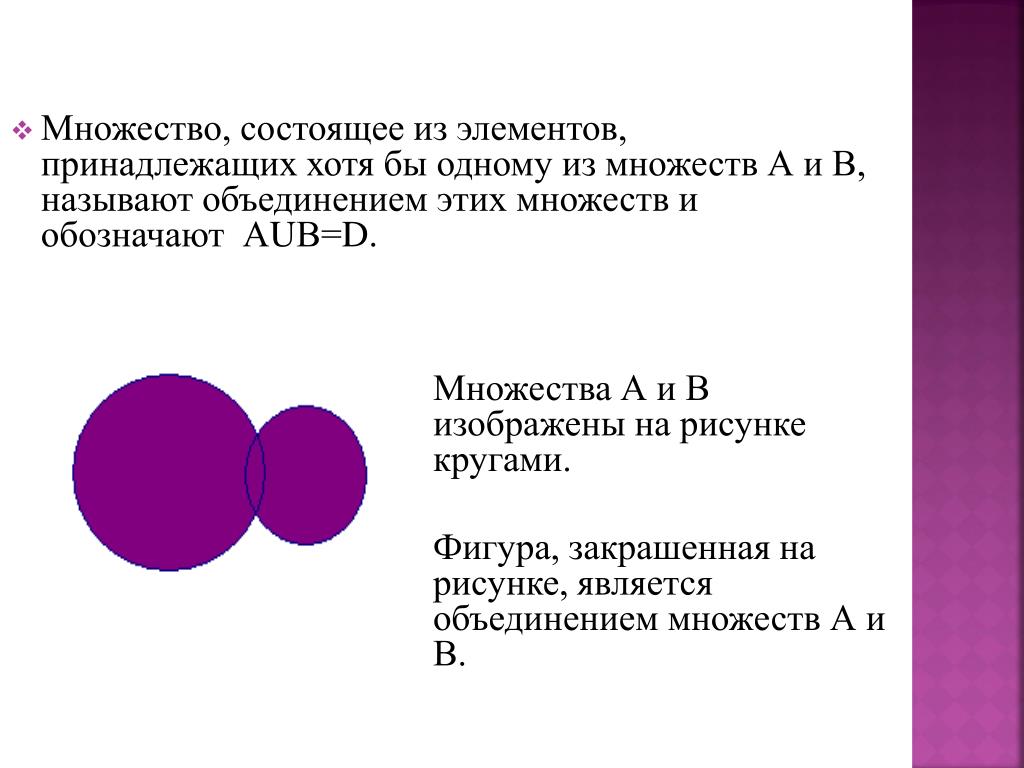
$$ \tau(X) \in X \;\;\; \text{тогда и только тогда, когда $X$ непусто} $$ $$ \tau(X) \not\in X \;\;\; \text{тогда и только тогда, когда $X$ пуст} $$
Использование этой штуки требует аксиомы глобального выбора, которая может быть проблемой, а может и не быть.
Кроме того, ничто не мешает вам создать собственную нотацию, а затем явно назвать ее нестандартной и определить ее, если нет широко используемой нотации.
$$\mathop{\text{el}}(X) = \text{единственный $x$ в $X$ равен $X$ является одноэлементным}$$
$$\mathop{\text{el}}(X) \;\;\;\text{не определено, если $X$ не является одноэлементным} $$
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
21-110: Наборы
21-110: Наборы Понятие множества — одна из самых фундаментальных идей математики. По сути, набор — это просто набор объектов. Область математики
которая изучает множества, названная теорией множеств , была основана немецким
математик Георг
Кантор во второй половине XIX в. Сегодня концепция наборов
пронизывает почти всю современную математику; почти любой другой математический
концепция (включая кажущуюся фундаментальной концепцию чисел!) была
определяются прямо или косвенно в терминах множеств.
По сути, набор — это просто набор объектов. Область математики
которая изучает множества, названная теорией множеств , была основана немецким
математик Георг
Кантор во второй половине XIX в. Сегодня концепция наборов
пронизывает почти всю современную математику; почти любой другой математический
концепция (включая кажущуюся фундаментальной концепцию чисел!) была
определяются прямо или косвенно в терминах множеств.
Основные определения и обозначения
Набор представляет собой набор объектов, рассматриваемых как математический
объект сам по себе. (Полезная метафора для набора — картонная
коробка — коробка может содержать предметы, и мы можем думать о том,
объекты в коробке по отдельности или думать о коробке и ее содержимом
вместе как единый объект.) Объекты в наборе называются элемент (или элемент ) набора; говорят элементы
до принадлежат набору (или быть в наборе ), а набор
Говорят, что содержит элемента. Обычно элементы множества
другие математические объекты, такие как числа, переменные или геометрические
точки.
Обычно элементы множества
другие математические объекты, такие как числа, переменные или геометрические
точки.
Письменные наборы
Набор часто записывается путем перечисления его элементов между фигурными фигурные скобки { }. Например, набор, содержащий числа 1, 2, и 3 будет записано как {1, 2, 3}.
Когда элементы набора следуют очевидному шаблону, но их слишком много
из них для явного перечисления, обычно перечисляются первые несколько элементов (чтобы
установить шаблон) и последний элемент (чтобы указать, где шаблон
останавливается) с многоточием (…) между ними, чтобы указать, что
элементы в середине были опущены. Например, чтобы записать множество положительных
целые числа от 1 до 100, мы можем написать
{1, 2, 3, …, 100}. Если ни один элемент не написан после
многоточие, предполагается, что шаблон будет продолжаться вечно; так набор написан
{1, 2, 3, …} содержит все положительные целые числа.
Иногда элементы множества продолжаются бесконечно в обоих случаях. «направления» — например, множество всех целых чисел (оба
положительный и отрицательный) можно записать как
{…, –3, –2, –1, 0, 1, 2, 3, …}.
«направления» — например, множество всех целых чисел (оба
положительный и отрицательный) можно записать как
{…, –3, –2, –1, 0, 1, 2, 3, …}.
Множество также можно описать на естественном языке с помощью английских фраз. За
Например, «множество всех положительных целых чисел» описывает конкретное
установлен. Важно, чтобы описание было точным, чтобы не было сомнений.
о том, является ли тот или иной объект элементом множества. Обычный
Примером неточного описания является такая фраза, как «числа
от 1 до 10». В этой фразе есть несколько неясностей. Являются ли
числа 1 и 10 сами являются элементами множества или они исключены? Находятся включены все действительных чисел от 1 до 10 или только целые числа?
Наконец, фраза, вероятно, должна быть более ясной в отношении того факта, что эти
числа следует рассматривать как набор, а не по отдельности. Более точный
описанием этого набора может быть «множество положительных целых чисел, не превышающих
чем 10” (если в наборе есть числа 1 и 10 и только
включены целые числа) или «множество действительных чисел между 1
и 10, исключая» (если в наборе есть числа с дробной
части, но не сами цифры 1 и 10).
Символ ∈ используется для обозначения «является элементом», просто поскольку символ = используется для обозначения «равно». Например, чтобы сказать что число 2 является элементом множества {1, 2, 3}, мы можем напишите 2 ∈ {1, 2, 3}. Чтобы выразить обратное, «не является элементом», мы ставим косую черту через символ и напишите ∉. Например, мы можем написать 4 ∉ {1, 2, 3}.
Часто полезно присваивать имена наборам. Эти имена обычно выбирают
быть одиночными буквами, аналогично использованию букв для представления чисел в
алгебра. Очень распространенным соглашением является использование заглавных букв в именах
наборы и строчные буквы для представления элементов наборов. Таким образом, для
например, если мы присвоим букву А к комплекту
{1, 2, 3}, написав A = {1, 2, 3}, мы
тогда можно сказать, что 2 ∈ A . Мы также можем написать a ∈ A , под которым мы подразумеваем, что a – число (возможно, неизвестное), являющееся элементом
установить A — другими словами, значение a должно
быть либо 1, 2, либо 3.
Равенство множеств
Говорят, что два набора равны , если каждый элемент первого набора является элементом второго множества, и наоборот. Например, если A = {1, 2, 3} и B = {2, 3, 1}, то множества A и B равны. Каждый элемент A также является элемент B , и каждый элемент B также является элемент A . Мы выражаем равенство множеств знаком равенства, поэтому в этом случае мы пишем A = B . Когда два набора равны, они считаются одним и тем же набором. Важно помнить, что равенство между множествами — это другое понятие, чем равенство между числами.
Одним из следствий этого определения равенства является то, что порядок, в котором
перечисление элементов множества не имеет значения. Мы заботимся только о том, какие
объекты являются элементами множества, а не порядком их появления. Так, например,
выражения {1, 2, 3} и {2, 3, 1} описывают
тот же набор.
Другим последствием является то, что количество раз, когда элемент перечисляется, не имеющий отношения. Набор {1, 2, 1, 3, 3, 3} равен набор {1, 2, 3}, поскольку каждый элемент первого набора является элементом второго, и наоборот. (Неважно, что числа 1 и 3 перечислены несколько раз в первом наборе.)
[Иногда нам нужно использовать набор объектов, в котором порядок равен важный. Такая коллекция называется последовательностью или заказанный список . Примером может служить использование упорядоченных пар форма ( x , y ) для представления точек в двумерная плоскость; точка (2, 5) отличается от точка (5, 2). Точно так же нам иногда нужна коллекция объектов в что имеет смысл, чтобы элемент появлялся более одного раза. Такой сборник называется мультисет . Когда мы ссылаемся на набор , однако следует понимать, что порядок и повторение элементов не имеет значения.]
Наборы, содержащие другие наборы
Элементами набора может быть что угодно — даже другие наборы. Например,
предположим, что у нас есть два набора: A = {1, 2, 3} и B = {2, 3, 4, 5}. Думайте о A как о
коробка с цифрами 1, 2 и 3 и B в качестве
коробка с цифрами 2, 3, 4 и 5. Ничто не мешает
нам поставить коробку A и ящик B вместе в большой коробке C . Точно так же мы можем сделать
набор C , содержащий набор A и
установите B в качестве элементов. Мы можем записать набор C как
{ A , B } или, если хотите, мы можем сказать
Например,
предположим, что у нас есть два набора: A = {1, 2, 3} и B = {2, 3, 4, 5}. Думайте о A как о
коробка с цифрами 1, 2 и 3 и B в качестве
коробка с цифрами 2, 3, 4 и 5. Ничто не мешает
нам поставить коробку A и ящик B вместе в большой коробке C . Точно так же мы можем сделать
набор C , содержащий набор A и
установите B в качестве элементов. Мы можем записать набор C как
{ A , B } или, если хотите, мы можем сказать
C = { {1, 2, 3}, {2, 3, 4, 5} }.
Набор, содержащий другие наборы, подобен коробке, содержащей другие коробки. В этом
случай, набор C имеет два элемента , которые являются двумя
наборы A и B . Эти элементы
set C сами являются наборами; набор A состоит из трех
элементов, а набор B состоит из четырех элементов.
Следовательно, верно, что A ∈ C , потому что A является элементом C . Точно так же верно что B ∈ C . Конечно, это тоже верно что, скажем, 1 ∈ A , потому что число 1 является элемент набора А .
Однако верно , а не , что 1 ∈ C , потому что 1 не является элементом множества C . только два элемента из C являются наборы A и B , и ни один из этих двух элементов не является числом 1. (Набор A содержит номер 1, но А сам по себе не является номер 1.)
Возвращаясь к метафоре коробки, мы должны думать об элементах множества (a
коробка) как объекты, которые прямо внутри коробки.
номер 1 не находится непосредственно внутри коробки C ; вместо этого это
спрятан внутри коробки A . Таким образом, 1 не является элементом
set C , но 1 – это элемент
набор А .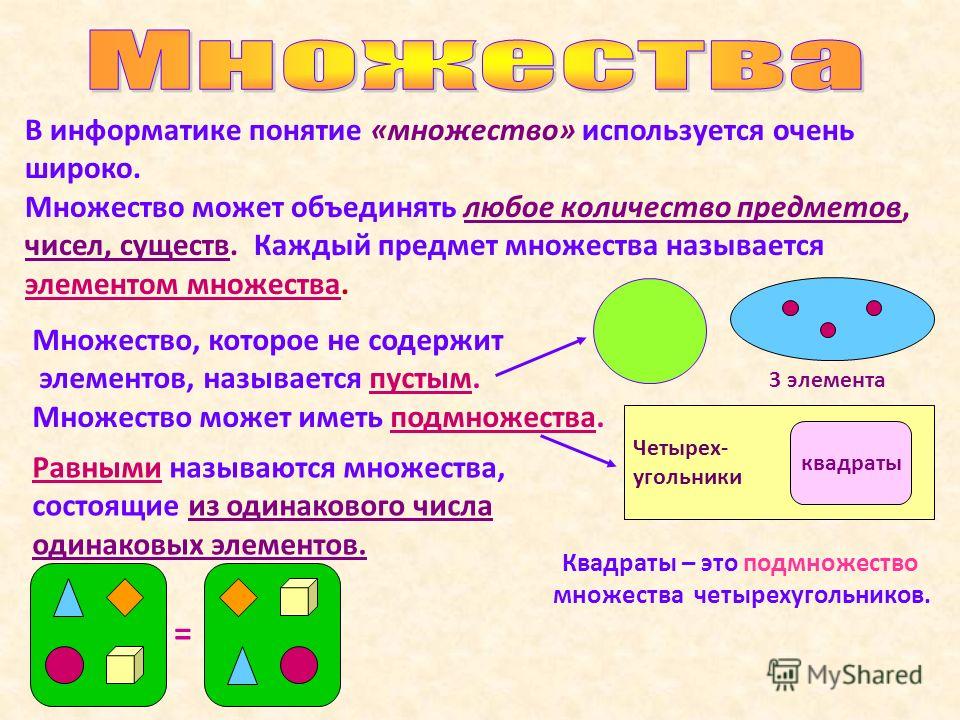
Аналогично, хотя верно, что 2 ∈ A и также верно, что 2 ∈ B , , а не верно, что 2 ∈ C , потому что число 2 напрямую не внутри коробки C .
Теперь рассмотрим набор
D = {1, 2, 3, 2, 3, 4, 5},
, который совпадает с набором {1, 2, 3, 4, 5}, поскольку
порядок и повторение элементов значения не имеют. Набор D отличается от набора C — эти наборы не
равный. Чтобы убедиться в этом, достаточно найти один элемент в одном множестве, который
не является элементом другого множества. Ну, например, число 1 – это
элемент D , но (как объяснялось выше) не является элементом
из С ; поэтому наборы не равны. Думая о C и D в виде коробок, мы видим, почему они не совпадают:
набор C — это блок, содержащий два блока (которые сами по себе бывают
содержать несколько чисел), тогда как набор D представляет собой коробку,
непосредственно содержит пять чисел (и никаких ящиков).
В качестве другого примера рассмотрим два набора E = {1} и F = {{1}}. Эти множества не равны. В наборе E есть один элемент, номер 1; в установить F также имеет один элемент, но единственный элемент из F — это другой набор, а не число. Таким образом, тогда как set E – это поле, содержащее число 1, set F – это поле, содержащее поле, содержащее число 1. (Другими словами, набор F представляет собой коробку содержащий E — вы видите это?) Оба они отличается от самого числа 1. Так что это правда, что 1 ∈ E , а на самом деле E ∈ F (поскольку единственный элемент из F это набор E ), но это не верно что 1 ∈ F .
Множества, содержащие другие множества, распространены в некоторых областях математики, но мы не будет видеть их очень часто в этом курсе. (Математики, работающие в эти области часто называют множество, содержащее другие множества, «набором наборы» или «семейство наборов», чтобы избежать неловкой фразы «набор наборов»)
Мощность
Мощность множества — это количество элементов,
содержит. (Иногда мощность множества называют просто
«размер» набора, потому что размер
более короткое слово; но «мощность» — технически правильный термин.)
(Иногда мощность множества называют просто
«размер» набора, потому что размер
более короткое слово; но «мощность» — технически правильный термин.)
Обычно пишут | А | означать мощность набор А . Например, если A = {1, 4, 8}, тогда | А | = 3, потому что A состоит из трех элементов. Это та же запись, что и для абсолютного значения числа, но контекст поясняет, что имеется в виду: если набор окружают вертикальные полосы, они относятся к мощности множества.
Мощность множества может быть бесконечной. Например, мощность набор положительных целых чисел {1, 2, 3, …} равен бесконечный.
Пустой набор
Мы думали о наборах как о коробках. Какой набор соответствует
идея пустой коробки? Ясно, что это должно быть множество, не содержащее ни одного элемента
все. Мы называем такое множество пустым множеством . Так как любые два пустых множества
содержат точно такие же элементы (точнее, вообще не содержат элементов), мы
считать любые два пустых множества равными и, следовательно, одним и тем же множеством. Так что мы обычно
обратитесь к пустому набору , потому что на самом деле он только один.
Так что мы обычно
обратитесь к пустому набору , потому что на самом деле он только один.
Существует два распространенных способа записи пустого множества. Первый способ, как вы можно ожидать, { }. Другое обозначение — круг или ноль с прорежьте его, что выглядит как ∅. Оба { } и ∅ – символы пустого набора.
Обратите внимание, что между ∅ и {∅} есть разница. во-первых, это пустой набор, который представляет собой пустой ящик. Второй — коробка , содержащее , является пустой коробкой, поэтому вторая коробка не пуста — у нее есть коробка в нем! Не пишите {∅}, когда имеете в виду пустой набор, потому что {∅} относится к набору, содержащему пустой набор, который не является как и само пустое множество.
Кардинальность пустого множества равна 0, что логично, поскольку
пустое множество не содержит элементов. Заявление x ∈ ∅ всегда ложно, несмотря ни на что x есть, потому что нет такой вещи как пустой элемент
установлен.
Подмножества
Выше мы определили два набора A и B равными, если каждый элемент A является элементом B , и наоборот наоборот Если убрать из этого определения «наоборот», то получим определение подмножества.
Мы говорим, что множество A является подмножеством установить B , если каждый элемент A также является элементом
из B . Мы используем символ ⊆ для обозначения «является подмножеством
из»; например, A ⊆ B означает
« A является частью B ». Мы также можем
поверните этот символ в другую сторону и запишите множества в другом порядке, чтобы получить В ⊇ А ; это значит то же самое, что А ⊆ В . Чтобы написать, что А это
не является подмножеством B , мы рисуем косую черту через символ подмножества: А ⊈ В . Интуитивно, подмножество B является «частью» B .
Интуитивно, подмножество B является «частью» B .
Например, рассмотрим наборы C = {1, 2} и D = {1, 2, 3, 4}. Набор C является подмножеством D , потому что каждый элемент C является также элемент D . Итак, мы можем написать C ⊆ D . У данного набора есть много подмножеств; за например, другое подмножество D — это {1, 3, 4}.
Чтобы запомнить, в каком направлении писать символ ⊆, подумайте о мощностей множеств и символа неравенства ≤. Если А является подмножеством B , то B должно содержать не менее много элементов, как A (просто потому, что B содержит все элементы A ), поэтому мощность из B должно быть больше или равно количеству элементов из А . Другими словами,
А ⊆ В подразумевает, что
| А | ≤ | Б |.
Обратите внимание, что символы выше «указывают» в одном направлении.
Существует очень важное различие между символами ∈ и ⊆. Символ ∈ используется для обозначения элемента . набора, тогда как символ ⊆ используется для обозначения подмножества . Например, рассмотрим набор
Д = {1, 2, 3, 4}.
Набор {2, 4} является подмножеством D , потому что каждый
элемент {2, 4} также является элементом D , поэтому он
правильно писать {2, 4} ⊆ D . Но
set {2, 4} – это , а не элемент набора D ,
потому что четыре элемента множества D — это все числа
( D не имеет наборов в качестве элементов), поэтому некорректно
напишите {2, 4} ∈ D . С другой стороны,
номер 2 является элементом D , поэтому правильно писать
2 ∈ D ; но число 2 равно не подмножество
из D (поскольку число 2 – это число, а не набор), поэтому
неправильно писать 2 ⊆ D . Если мы хотим обратиться к
подмножество D , содержащее только число 2, мы должны
напишите {2}, то есть набор, содержащий 2 (обратите внимание, что набор {2}
отличается от числа 2). Набор {2} является подмножеством
из D , то есть {2} ⊆ D ; но это не элемент D , потому что D не
имеют какие-либо множества в качестве элементов, поэтому некорректно писать
{2} ∈ Д .
Если мы хотим обратиться к
подмножество D , содержащее только число 2, мы должны
напишите {2}, то есть набор, содержащий 2 (обратите внимание, что набор {2}
отличается от числа 2). Набор {2} является подмножеством
из D , то есть {2} ⊆ D ; но это не элемент D , потому что D не
имеют какие-либо множества в качестве элементов, поэтому некорректно писать
{2} ∈ Д .
Когда A является подмножеством B ,
набор B иногда называют надмножеством из А . Мы также можем сказать
« B содержит A как подмножество», но
следует быть очень осторожным со словом «содержит», потому что, как
отмечено в предыдущем абзаце, есть большая разница между высказыванием
« B содержит A в качестве элемента»
(что означает A ∈ B ) и сказать B «содержит» A в качестве подмножества» (значение А ⊆ В ). попробую использовать слово
содержит только для ссылки на элементы, а не на подмножества.
попробую использовать слово
содержит только для ссылки на элементы, а не на подмножества.
Внимательное прочтение определения подмножества показывает, что каждое множество является
подмножество самого себя. Например, используя приведенный выше набор D ,
очевидно верно, что «каждый элемент D также является
элемент D », поэтому по определению D является
подмножество D . Мы часто хотим исключить этот случай, поэтому мы определяем правильное подмножество набора B быть подмножеством B , который не является самим B . Мы пишем A ⊂ B означает, что A является
правильное подмножество B . [Это использование символов ⊆
и ⊂ означает «является подмножеством (или равным)» и «является
правильное подмножество», соответственно, соответствует использованию неравенства
символы ≤ и < означают «меньше или равно» и
«строго меньше» соответственно. ]
]
Пустое множество считается подмножеством любого множества (включая его самого). Это может показаться довольно странным соглашением. Пожалуй, лучшее оправдание это происходит от того, что мы переворачиваем определение подмножества с ног на голову и задаемся вопросом, что оно средства для набора A не быть подмножеством из B . Из определения это должно означать, что существует некоторое элемент в A , который не является элементом B . Так что значит сказать, что пустое множество не является подмножеством из B ? Это означало бы, что в пустом множестве есть какой-то элемент это не элемент B — но это не может быть правдой, потому что в пустом наборе нет элементов! Итак, с этого момента точки зрения, имеет смысл сказать, что пустое множество является подмножеством каждый набор.
[Следует отметить, что использование символов ⊆ и ⊂
описанное выше не является универсальным. Некоторые авторы используют символ ⊂ для
означает «является подмножеством» (для которого мы используем
символ ⊆) и ввести новый символ ⊊, символ подмножества
с перечеркнутой полосой «равно», что означает «является правильным
подмножество» (для которого мы используем символ ⊂). ]
]
Наборы цифр
Есть несколько наборов чисел, которые настолько часто используются, что их специальные символы. Двойные прописные буквы, иногда называемые жирным шрифтом на доске. часто используются буквы (в частности, буквы ℝ, ℤ, ℕ и ℚ). В качестве альтернативы буквы могут быть просто набраны в полужирный. [Из-за возможности того, что необычные символы, такие как классная доска, жирным шрифтом, может отображаться не во всех веб-браузерах, я буду использовать простое полужирное начертание буквы здесь.]
Множество всех действительных чисел, как положительных, так и отрицательных (и нулей), равно называется R (от «настоящего»). Множество действительных чисел включает все числа, обычно встречающиеся в алгебре, тригонометрии или исчислении курс. (Он не содержит комплексных чисел, таких как как √−1.)
Набор целых чисел (положительных, отрицательных и нулевых) называется Z (от немецкого слова Zahlen, означающего
«числа»). Другими словами, Z = {…, –3, –2, –1, 0, 1, 2, 3, …}.
Набор натуральных чисел называется N (для
«естественный»). Множество натуральных чисел содержит все положительные
целые числа и никаких отрицательных целых чисел. К сожалению, нет единого мнения о
следует ли считать ноль натуральным числом. Некоторые авторы включают 0
в комплекте N , а других нет. Причина этого отсутствия
согласованность заключается в том, что иногда полезно включать ноль, а иногда нет,
в зависимости от ситуации. Таким образом, математики используют любое определение, которое подходит
их лучше всего в то время, но они знают о различиях в использовании, поэтому
они всегда очень тщательно указывают, какое именно определение они используют
в каждом конкретном случае, чтобы избежать какой-либо путаницы или двусмысленности, и как только они
выбрав определение, они придерживаются его. Для этого класса давайте договоримся
что 0 равно не натуральное число, если не указано иное. В
другими словами, если не указано иное, мы будем использовать символ N для
представляют набор {1, 2, 3, …}. Если мы хотим обратиться к
набор {0, 1, 2, 3, …}, когда мы используем это
определение N , мы всегда можем написать N ∪ {0}
(о значении символа ∪ мы поговорим чуть позже).
В качестве альтернативы, термины положительное целое число и неотрицательное число
целых всегда однозначны: ноль не положителен, но он
неотрицательный. Следовательно, другой способ обратиться к множеству
{1, 2, 3, …} — это «множество положительных
целые числа», а {0, 1, 2, 3, …} – это
множество неотрицательных целых чисел».
Если мы хотим обратиться к
набор {0, 1, 2, 3, …}, когда мы используем это
определение N , мы всегда можем написать N ∪ {0}
(о значении символа ∪ мы поговорим чуть позже).
В качестве альтернативы, термины положительное целое число и неотрицательное число
целых всегда однозначны: ноль не положителен, но он
неотрицательный. Следовательно, другой способ обратиться к множеству
{1, 2, 3, …} — это «множество положительных
целые числа», а {0, 1, 2, 3, …} – это
множество неотрицательных целых чисел».
Наконец, множество рациональных чисел называется Q (от слова
«частное»). Рациональное число — это число, которое может быть
записывается точно как дробь или частное двух целых чисел. Например,
число 2/3 является рациональным числом, как и число –7/2. Все
целые числа являются рациональными числами, потому что любое целое число можно записать в виде дроби
со знаменателем 1; например, целое 5 можно записать
как 5/1. Другие примеры рациональных чисел включают числа, которые могут быть
записывается как завершающая десятичная дробь (например, число 8,13 может быть
записывается как 813/100) или как повторяющаяся десятичная дробь (например,
число 0,333… можно записать как 1/3). Не все действительные числа
однако рациональны. Примеры вещественных чисел, которые нельзя записать точно
как дробь двух целых чисел включает
√2
и № ; десятичные расширения этих чисел продолжаются вечно
и никогда не повторять. В этом курсе у нас не будет особой необходимости различать
рациональные числа из действительных чисел, поэтому мы редко (если вообще когда-либо) будем использовать
символ Q .
Не все действительные числа
однако рациональны. Примеры вещественных чисел, которые нельзя записать точно
как дробь двух целых чисел включает
√2
и № ; десятичные расширения этих чисел продолжаются вечно
и никогда не повторять. В этом курсе у нас не будет особой необходимости различать
рациональные числа из действительных чисел, поэтому мы редко (если вообще когда-либо) будем использовать
символ Q .
Обратите внимание, что эти четыре набора чисел являются (правильными) подмножествами друг друга: N ⊂ Z ⊂ Q ⊂ R .
Обозначение конструктора наборов
Перечислить все элементы набора можно, если набор не слишком
большой. Для больших наборов мы можем пропустить некоторые элементы, написав
многоточие (…), как мы видели, но это возможно только тогда, когда
элементы следуют шаблону, который хорошо виден в первых нескольких элементах.
Это не всегда так. Например, множество всех простых чисел между
100 и 500 можно было бы записать как
{101, 103, 107, …, 499}, но это не очень
полезно написать, потому что очень трудно угадать правильный
закономерность только из этих цифр (и это выражение не исключает
неправильные шаблоны, такие как «набор всех нечетных чисел между 100
и 500, кроме кратных 5″).
В подобных ситуациях часто лучше описать набор, указав условие для членства. (Наше английское описание набора выше делает именно это; фактически он говорит, что условие для числа Элемент набора состоит в том, что число должно быть простым и лежать в пределах 100. и 500.) Когда мы хотим таким образом описать множество, мы можем использовать нотация построителя набора .
Когда мы используем нотацию построителя наборов, мы должны сначала установить универсальный набор (иногда называемый доменом дискурса или вселенная дискурса ), которая представляет собой множество всех возможных объектов
на рассмотрении. Например, можно сказать, что универсальное множество
это R , множество всех действительных чисел; или, возможно, Z ,
набор целых чисел. Другая возможность состоит в том, чтобы использовать ранее определенный набор в качестве
универсальный набор. Если мы определили А = {1, 2, 3},
например, мы можем использовать A в качестве универсального набора.
После того, как мы выбрали универсальный набор, мы можем «построить» набор, выбор всех элементов универсального множества, удовлетворяющих заданному условие. Например, если универсальный набор равен R , мы можем определить установить B , скажем, как набор всех элементов R , которые больше 17. (Таким образом, B содержит числа 18 и 29,4, например, но не содержит 11,26 или -30.) Это установить B можно записать, используя нотацию конструктора наборов, как
.B = { x ∈ R | x > 17 }.
В системе построения наборов вертикальная черта | следует читать как «такой, что» или «удовлетворяющий условию, что». Итак Вышеприведенное выражение можно прочитать как « B — это набор, который содержит все элементы x универсального набора R удовлетворяющие условию 90 253 x 90 254 > 17».
Обратите внимание, что универсальный набор указан слева от вертикальной
bar, и дается имя для представления произвольного элемента универсального множества
с помощью символа ∈. Справа от полосы находится условие
которым элемент должен удовлетворять, чтобы быть членом множества, которое мы
строительство. Имя произвольного элемента ( x в примере
выше) может быть любым; приведенный выше пример означает то же самое, что и, скажем,
Справа от полосы находится условие
которым элемент должен удовлетворять, чтобы быть членом множества, которое мы
строительство. Имя произвольного элемента ( x в примере
выше) может быть любым; приведенный выше пример означает то же самое, что и, скажем,
B = { z ∈ R | z > 17 },
или даже
B = { ♣ ∈ R | ♣ > 17 },
, хотя ♣ не очень распространенное имя переменной (и оно, вероятно, вызовет некоторое недоумение, поэтому его, вероятно, следует избегать).
Почему важен универсальный набор? Ответ состоит в том, что множество, описанное с помощью Нотация создателя множества всегда будет подмножеством универсального множества. Рассмотрим набор
C = { x ∈ N | x > 17 },
, который определяется точно так же, как набор B выше.
за исключением того, что универсальный набор был изменен на N . Наборы B и C имеют много общего; Например,
число 20 является элементом как B , так и C .
Однако, поскольку C состоит из элементов N .
а не элементы R , набор C содержит только
(положительные) целые числа и не содержит чисел с дробной частью. Так,
например, число 23,456 является элементом B , но не элемент C .
Наборы B и C имеют много общего; Например,
число 20 является элементом как B , так и C .
Однако, поскольку C состоит из элементов N .
а не элементы R , набор C содержит только
(положительные) целые числа и не содержит чисел с дробной частью. Так,
например, число 23,456 является элементом B , но не элемент C .
В качестве другого примера нотации конструктора наборов рассмотрим набор
.D = { n ∈ N | n ≤ 10 }.
Что это значит? Читая слева направо по одному символу за раз, мы читай « D – это набор, содержащий все элемент N в универсальном наборе N удовлетворяющий при условии, что n ≤ 10». Здесь универсальный набор есть множество N натуральных чисел (которое, как мы договорились, не include 0), поэтому мы видим, что
D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Обратите внимание, что набор, описанный с помощью нотации конструктора наборов, может быть пустым, если нет элементы универсального множества удовлетворяют указанному условию! Например, набор
E = { n ∈ N | n < 0 }
— пустое множество, потому что натуральных чисел меньше нуля не существует. А несколько более тонкий пример набора, который оказывается пустым, это
F = { n ∈ N | 8 < n < 9 },
, которое пусто, потому что нет натурального числа n , которое удовлетворяет неравенству 8 < n < 9. (Напомним, что 8 < n < 9 — сокращение для «8 < n и n < 9». Ни одно натуральное число не удовлетворяет этому условию, потому что каждое натуральное число либо меньше или равно 8, либо больше или равно 9.)
Вариации нотации конструктора наборов
Условие в нотации построителя набора не нужно записывать в
математические символы. Обычно условие записывается как
английская фраза. Например, мы можем определить S как набор
совершенные квадраты, написав
Обычно условие записывается как
английская фраза. Например, мы можем определить S как набор
совершенные квадраты, написав
S = { t ∈ Z | t является полным квадратом}.
(Здесь в качестве универсального набора мы использовали Z вместо N , даже хотя никакое отрицательное целое число не является полным квадратом, потому что ноль равен а идеальный квадрат, и мы хотели включить его в набор S . Этот пример, в котором было бы удобно, чтобы 0 был в N . Ну ладно.)
Если универсальный набор указан явно в словах до или после использование нотации построителя наборов, он часто опускается в нотации построителя наборов сам. Например, при определении нескольких наборов мы можем сказать:
Пусть
К = { x | x ≠ 0 }, L = { x | −6 ≤ x < 1 }, M = { x | x ≥ 50 и x идеально}, , где универсальный набор — это набор действительных чисел.
В этом случае, поскольку универсальный набор указан как набор реальных чисел, мы должны читать определение множества K как » K это множество, содержащее все действительные номер x , удовлетворяющий условию, что 90 253 x 90 254 ≠ 0». Другими словами, K – это набор всех действительных чисел, кроме 0. Можете ли вы понять определения L и M ?
Иногда вместо вертикальной черты используется двоеточие (:). нотация построителя множества. Это особенно распространено, когда состояние включает в себя выражение абсолютного значения, потому что вертикальные полосы, используемые в абсолютном значении обозначение можно легко спутать с вертикальной чертой, используемой в конструкторе наборов. обозначение.
Набор операций
Есть несколько операций, которые можно выполнить над множествами, чтобы получить
новые комплекты из старых. Эти операции столь же фундаментальны для теории множеств, как и
сложение и умножение относятся к арифметике.
Соединения и пересечения
Рассмотрим наборы
| A | = | {1, 2, 3, 5, 8, 13}, | ||||||
| B | = | {2, 4, 4, 8, 8, 8, 8, 8, 8, 8, | = | {2, 4, 4, 4, 8, 8, 8, | = | {2, 4, 4, 4, 8, | = | . |
Одна полезная вещь, которую можно сделать с этими наборами, — «поместить их вместе» — другими словами, создать новый набор, содержащий все элемент A , а также каждый элемент B . Такой набор называется соединением из A и B , и записывается A ∪ B . В этом примере мы есть
A ∪ B = {1, 2, 3, 4, 5, 6, 8, 13}.
Обратите внимание, что числа 2 и 8 содержатся в обоих А и B , но каждый из них указан только один раз.
in A ∪ B , потому что количество раз
элемент, указанный в наборе, не имеет значения.
Какими бы ни были наборы A и B , всегда правда что А ⊆ ( А ∪ В ) и B ⊆ ( A ∪ B ). Делать понимаешь почему?
Еще одна полезная операция — выбрать элементы, которые A и B имеют общие черты. Это называется пересечение A и B , и написано А ∩ В . В нашем текущем примере у нас есть
А ∩ В = {2, 8}.
Какими бы ни были наборы A и B , всегда правда что ( A ∩ B ) ⊆ A и ( A ∩ B ) ⊆ B . Делать понимаешь почему?
Если наборов A и B не имеют общих элементов, они называются непересекающимися . В этом случае пересечение A ∩ B пусто установлен.
Предположим, что одно из двух множеств, с которыми мы работаем, является пустым множеством. Независимо от того
что такое набор A , всегда верно, что А ∪ ∅ = А и A ∩ ∅ = ∅. Вы понимаете, почему?
Независимо от того
что такое набор A , всегда верно, что А ∪ ∅ = А и A ∩ ∅ = ∅. Вы понимаете, почему?
Дополнения
Еще одна полезная вещь, которую можно сделать с набором, — рассмотреть все, что есть. а не в комплекте. Для того, чтобы иметь точное значение для «все», нам нужно указать универсальный набор (как мы сделали, когда используя нотацию конструктора наборов). Совокупность всех элементов универсального множества, не являются элементами множества называется дополнением A , и написано А . (Еще один распространенный обозначение дополнения A А в .)
Например, предположим, что универсальный набор равен Н . Пусть P быть набором простых чисел; то есть
P = { n ∈ N | n простое } = {2, 3, 5, 7, 11, 13, 17, …}.
Затем P , дополнение P , это набор составных чисел (и число 1, который не является ни простым, ни составным):
P = {1, 4, 6, 8, 9, 10, 12, …}.
Установить разницу
Иногда нам нужно обратиться ко всем элементам в некоторых установить A , которые являются , а не элементами какого-либо другого набор B . Эта операция называется установка разности (иногда называется относительным дополнением ) и записывается А \ В . (Некоторые авторы используют стандартный знак минус и напишите A − B , но операция множества разница сильно отличается от обычной идеи вычитания, поэтому обратная косая черта более распространена.)
Например, если у нас есть наборы
| A | = | {3, 4, 5, 10, 14, 17}, |
| B | = | {4, 5, 17}, |
then установленная разница A \ B равна
А \ В = {3, 10, 14},
, потому что это элементы A , которые не являются элементами
из B .
Нет необходимости, чтобы один набор был подмножеством другого. Например, рассмотреть наборы
| C | = | {1, 3, 6, 10, 15}, | ||||
| D | = | {1, 4, 6, 10, 2044, | = | {1, 4, 6, 4, 10444, | = | {1, 4, 6, 4, 4, 10444. |
Ни один из этих наборов не является подмножеством другого. Операция установки разницы однако по-прежнему имеет смысл. У нас есть
C \ D = {3, 15},
, потому что это элементы C , которые не являются элементами из D ; и
D \ C = {4, 5, 20},
, потому что это элементы D , которые не являются элементами C .
Обратите внимание, что если универсальный набор называется U , то мы можем выразить дополнение множества A как разность множеств:
А = U \ А .
Давайте подумаем, как ведет себя пустой набор с разницей в наборе операция. Независимо от того, какой набор A это всегда верно, что А \ ∅ = А и ∅ \ A = ∅. Вы понимаете, почему?
Скобки
Когда мы выполняем две или более операции над множествами, нам часто нужно включать круглые скобки, чтобы сделать порядок вычислений однозначным. Например, предположим у нас есть наборы
| A | = | {1, 2, 3}, |
| B | = | {2, 3, 4}, |
| C | = | {3, 4, 5}. |
Рассмотрим выражение ( A ∪ B ) ∩ C . Мы сначала оцените A ∪ B , потому что это в скобки. Мы видим, что А ∪ В = {1, 2, 3, 4}, так
( A ∪ B ) ∩ C = {1, 2, 3, 4} ∩ C = {3, 4}.
С другой стороны, предположим, что у нас есть выражение А ∪ ( B ∩ C ), который точно так же, за исключением размещения скобок. Мы тут сначала оцените B ∩ C , что {3, 4}, поэтому мы получаем
A ∪ ( B ∩ C ) = A ∪ {3, 4} = {1, 2, 3, 4}.
Этот пример показывает, что размещение скобок важно. Скобки свободны — если вы не уверены, нужны ли вам круглые скобки в выражении, поместите их на всякий случай.
Диаграммы Венна
диаграммы Венна, введенные английским математиком Джоном Венном в 1881 году очень полезны для понимания отношений между наборы.
На диаграмме Венна наборы представлены перекрывающимися формами.
самая внешняя форма, которая обычно представляет собой прямоугольник, представляет собой универсальный
установлен. Внутри этого прямоугольника находятся другие формы (часто круги), представляющие
различные наборы. Эти формы могут перекрываться, указывая на возможность того, что две или
несколько наборов могут иметь некоторые общие элементы.
Эти формы могут перекрываться, указывая на возможность того, что две или
несколько наборов могут иметь некоторые общие элементы.
Ниже показан наиболее распространенный способ построения диаграммы Венна для двух наборов. A и B . Здесь универсальный набор по телефону U .
Например, предположим, что универсальный набор равен
.U = {1, 2, 3, …, 12}
и мы определяем наборы
| A | = | {1, 2, 3, 7, 9, 11}, | ||||||||||
| B | = | {3, 4, 7, 7, | = | {3, 4, 7, 7, | = | {3, 4, 7, 7, | = | {3, 4, 7, | = | {3, 4, 7, | = |
На приведенной ниже диаграмме Венна показаны целые числа от 1 до 12 в
соответствующие места. Например, число 1 находится внутри круга.
помечен A , но вне круга с пометкой B ,
потому что 1 является элементом A , но не B . число 7 находится внутри обоих кругов, потому что оно является элементом обоих A и B . Число 5 находится внутри прямоугольника,
потому что это элемент универсального множества, но он вне обоих кругов,
потому что это ни в A или B .
число 7 находится внутри обоих кругов, потому что оно является элементом обоих A и B . Число 5 находится внутри прямоугольника,
потому что это элемент универсального множества, но он вне обоих кругов,
потому что это ни в A или B .
Из этой диаграммы легко увидеть, например, что A ∩ B = {3, 7, 11}.
Диаграмма Венна особенно полезна, когда мы думаем об абстрактных или неизвестные наборы, а не конкретные примеры, такие как наборы выше. В этом случай, когда мы не можем явно выписать элементы множеств; вместо этого мы представляем различные области самой диаграммы как метафоры для различных наборов, которые мы работают с. Полезно заштриховать или раскрасить части диаграммы, чтобы выделить определенные области.
Заштрихованные области на диаграммах ниже показывают области, соответствующие указанные наборы.
| А | Б |
| А ∪ В | А ∩ В |
| А | Б |
| А \ В | Б \ А |
Одним из способов использования диаграмм Венна является проверка того, что два выражения действительно описывают
тот же набор. Например, рассмотрим два выражения
Например, рассмотрим два выражения
( A ∪ B ) \ ( A ∩ B ) а также ( A \ B ) ∪ ( B \ A ).
Нарисуем диаграммы Венна для этих наборов. Мы начнем с выражение слева. Диаграммы Венна для А ∪ В и A ∩ B показаны ниже.
| А ∪ В | А ∩ В |
Теперь заштрихованная область на диаграмме Венна для ( A ∪ B ) \ ( A ∩ B ) должны включать области, заштрихованные на диаграмме Венна для A ∪ B , но , а не , заштриховано Венном схема для A ∩ Б . Итак, диаграмма Венна для ( A ∪ B ) \ ( A ∩ B ) выглядит так:
| ( A ∪ B ) \ ( A ∩ B ) |
Теперь рассмотрим другое выражение:
( A \ B ) ∪ ( B \ A ). Диаграммы Венна для A \ B и B \ A показаны ниже.
Диаграммы Венна для A \ B и B \ A показаны ниже.
| А \ В | В \ А |
Теперь заштрихованная область на диаграмме Венна для ( A \ B ) ∪ ( B \ A ) должна включать заштрихованную область на диаграмме Венна для A \ B , а также заштрихованная область в Венне схема для B \ A . Итак, диаграмма Венна для ( А \ В ) ∪ ( В \ А ) выглядит так:
| ( A \ B ) ∪ ( B \ A ) |
Обратите внимание, что это точно такая же диаграмма Венна, которую мы получили для
( A ∪ B ) \ ( A ∩ B ).
Это показывает, что эти два выражения представляют собой разные способы именования одного и того же
установлен. Другими словами, для любых двух наборов A и B будет
правда что
Другими словами, для любых двух наборов A и B будет
правда что
( A ∪ B ) \ ( A ∩ B ) = ( A \ B ) ∪ ( 5 3 A 2 0 ).
(Этот набор иногда называют симметричной разностью A и B , письменный А ∆ В .)
вопросов
Вот несколько вопросов о наборах, чтобы проверить ваше понимание.
- Запишите множество положительных четных целых чисел не менее чем в трех различных способы.
- В каждом из следующих утверждений решите, является ли
пусто _ можно правильно заполнить
символ ∈, символ ⊆, оба или ни один из них.
- 2 _ {2, {2}, {5}}
- 5 _ {2, {2}, {5}}
- {2} _ {2, {2}, {5}}
- {5} _ {2, {2}, {5}}
- {{2}} _ {2, {2}, {5}}
- {{5}} _ {2, {2}, {5}}
- {{2}, {5}} _ {2, {2}, {5}}
- Укажите элемент каждого из следующих наборов: З \ Н , Q \ Z , и R \ Q .

- Пусть A и B будут множествами, и пусть U обозначают
универсальный набор. Определите, являются ли следующие утверждения обязательно правда. Если да, объясните почему. Если нет, приведите контрпример.
- Если | У | = 14 и | А | = 8, тогда | А | = 6,
- Наборы A и A не пересекаются.
- Если | А | = 7 и | Б | = 3, тогда | А \ В | = 4,
- Составьте диаграмму Венна для трех наборов A , B , и C . Заштрихуйте область, соответствующую ( A ∪ B ) ∩ C .
- Предположим, что A и B являются наборами с
| А | = 5, | Б | = 10 и
| A ∩ B | = 3. Что такое
| А ∪ В |? (Подсказка: нарисуйте диаграмму Венна.
 )
)
Назад на стр. 21-110
Последнее обновление: 19 марта 2010 г. Брайан КеллНабор Python (с примерами)
В этом руководстве вы узнаете все о наборах Python; как они создаются, добавляются или удаляются из них элементы, и все операции, выполняемые над множествами в Python.
Набор — это неупорядоченный набор элементов. Каждый элемент набора уникален (без дубликатов) и должен быть неизменным (не может быть изменен).
Однако сам набор может изменяться. Мы можем добавлять или удалять элементы из него.
Наборы также можно использовать для выполнения математических операций над наборами, таких как объединение, пересечение, симметричная разность и т. д. через запятую или с помощью встроенной функции set() .
Может иметь любое количество элементов, и они могут быть разных типов (целые числа, числа с плавающей запятой, кортежи, строки и т. д.). Но множество не может иметь в качестве своих элементов изменяемые элементы, такие как списки, наборы или словари.
# Различные типы наборов в Python
# набор целых чисел
мой_набор = {1, 2, 3}
печать (мой_набор)
# набор смешанных типов данных
my_set = {1.0, "Привет", (1, 2, 3)}
print(my_set) Вывод
{1, 2, 3}
{1.0, (1, 2, 3), "Привет"} Попробуйте также следующие примеры.
# набор не может иметь дубликатов
# Вывод: {1, 2, 3, 4}
my_set = {1, 2, 3, 4, 3, 2}
печать (мой_набор)
# мы можем сделать множество из списка
# Вывод: {1, 2, 3}
my_set = установить ([1, 2, 3, 2])
печать (мой_набор)
# в наборе не может быть изменяемых элементов
# здесь [3, 4] — изменяемый список
# это вызовет ошибку.
my_set = {1, 2, [3, 4]} Выход
{1, 2, 3, 4}
{1, 2, 3}
Traceback (последний последний вызов):
Файл "", строка 15, в
my_set = {1, 2, [3, 4]}
TypeError: unhashable type: 'list' Создать пустой набор немного сложно.
Пустые фигурные скобки {} создаст пустой словарь в Python. Чтобы создать набор без каких-либо элементов, мы используем функцию
Чтобы создать набор без каких-либо элементов, мы используем функцию set() без каких-либо аргументов.
# Различать набор и словарь при создании пустого набора
# инициализируем {}
а = {}
# проверить тип данных a
печать (тип (а))
# инициализируем с помощью set()
а = установить ()
# проверить тип данных a
печать (тип (а)) Выход
<класс 'дикт'>
Изменение набора в Python
Наборы изменяемы. Однако, поскольку они неупорядочены, индексация не имеет смысла.
Мы не можем получить доступ к элементу набора или изменить его с помощью индексации или нарезки. Установить тип данных не поддерживает его.
Мы можем добавить один элемент, используя метод add() , и несколько элементов, используя метод update() . 9Метод 1991 update() может принимать кортежи, списки, строки или другие наборы в качестве аргумента. Во всех случаях дубликаты избегаются.
# инициализировать my_set
мой_набор = {1, 3}
печать (мой_набор)
# мой_набор[0]
# если вы раскомментируете строку выше
# вы получите сообщение об ошибке
# TypeError: объект 'set' не поддерживает индексацию
# добавить элемент
# Вывод: {1, 2, 3}
my_set.add(2)
печать (мой_набор)
# добавить несколько элементов
# Вывод: {1, 2, 3, 4}
my_set.update([2, 3, 4])
печать (мой_набор)
# добавить список и установить
# Вывод: {1, 2, 3, 4, 5, 6, 8}
my_set.update([4, 5], {1, 6, 8})
печать (мой_набор) Выход
{1, 3}
{1, 2, 3}
{1, 2, 3, 4}
{1, 2, 3, 4, 5, 6, 8} Удаление элементов из набора
Конкретный элемент можно удалить из набора с помощью методов discard() и remove() .
Единственная разница между ними состоит в том, что функция discard() оставляет набор без изменений, если элемент отсутствует в наборе. С другой стороны, функция remove() вызовет ошибку в таком состоянии (если элемент отсутствует в наборе).
Следующий пример проиллюстрирует это.
# Разница между discard() и remove()
# инициализировать my_set
my_set = {1, 3, 4, 5, 6}
печать (мой_набор)
# отбросить элемент
# Вывод: {1, 3, 5, 6}
my_set.discard(4)
печать (мой_набор)
# удалить элемент
# Вывод: {1, 3, 5}
my_set.remove(6)
печать (мой_набор)
# отбросить элемент
# отсутствует в my_set
# Вывод: {1, 3, 5}
my_set.discard(2)
печать (мой_набор)
# удалить элемент
# отсутствует в my_set
# вы получите сообщение об ошибке.
# Вывод: KeyError
my_set.remove(2) Выход
{1, 3, 4, 5, 6}
{1, 3, 5, 6}
{1, 3, 5}
{1, 3, 5}
Traceback (последний последний вызов):
Файл "", строка 28, в
KeyError: 2 Точно так же мы можем удалить и вернуть элемент, используя метод pop() .
Поскольку набор является неупорядоченным типом данных, невозможно определить, какой элемент будет извлечен. Это совершенно произвольно.
Мы также можем удалить все предметы из набора, используя 9Метод 1991 clear() .
# инициализировать my_set
# Вывод: набор уникальных элементов
my_set = установить ("HelloWorld")
печать (мой_набор)
# извлекаем элемент
# Вывод: случайный элемент
печать (my_set.pop())
# извлечь другой элемент
my_set.pop()
печать (мой_набор)
# очистить my_set
# Вывод: установить()
my_set.clear()
print(my_set) Вывод
{'H', 'l', 'r', 'W', 'o', 'd', 'e'}
ЧАС
{'г', 'В', 'о', 'д', 'е'}
set() Python Set Operations
Наборы можно использовать для выполнения математических операций над множествами, таких как объединение, пересечение, разность и симметричная разность. Мы можем сделать это с помощью операторов или методов.
Рассмотрим следующие два набора для следующих операций.
>>> А = {1, 2, 3, 4, 5}
>>> B = {4, 5, 6, 7, 8} Set Union
Set Union в PythonUnion of A и B представляет собой набор всех элементов из обоих наборов.
Объединение выполняется с помощью | оператор. То же самое можно сделать с помощью метода
То же самое можно сделать с помощью метода union() .
# Установить метод объединения
# инициализируем А и Б
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8}
# использовать | оператор
# Вывод: {1, 2, 3, 4, 5, 6, 7, 8}
напечатать (А | В) Выход
{1, 2, 3, 4, 5, 6, 7, 8} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию объединения
>>> А.союз(Б)
{1, 2, 3, 4, 5, 6, 7, 8}
# используем функцию объединения на B
>>> Б.союз(А)
{1, 2, 3, 4, 5, 6, 7, 8} Пересечение множества
Пересечение множества в PythonПересечение A и B — это набор элементов, общих для обоих наборов.
Пересечение выполняется с помощью 9Оператор 1991 и годов. То же самое можно сделать, используя метод пересечения() .
# Пересечение множеств
# инициализируем А и Б
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8}
# использование и оператор
# Вывод: {4, 5}
печать(A и B) Вывод
{4, 5} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию пересечения на A
>>> А.пересечение(Б)
{4, 5}
# используем функцию пересечения на B
>>> Б.пересечение(А)
{4, 5} Set Difference
Set Difference в PythonОтличие набора B от набора A ( A — B ) это набор элементов, которые есть только в
3 5 4 Bно не в . Точно так же B — A является набором элементов в B , но не в A .
Различие выполняется с помощью оператора - . То же самое можно сделать с помощью метода Differenti() .
# Разница двух наборов
# инициализируем А и Б
А = {1, 2, 3, 4, 5}
В = {4, 5, 6, 7, 8}
# use - оператор на A
# Вывод: {1, 2, 3}
печать(A - B) Вывод
{1, 2, 3} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию разницы на A
>>> А.разница(Б)
{1, 2, 3}
# use - оператор на B
>>> Б - А
{8, 6, 7}
# используем функцию разности на B
>>> Б. разница(А)
{8, 6, 7}
разница(А)
{8, 6, 7} 9Б)
Выход
{1, 2, 3, 6, 7, 8} Попробуйте выполнить следующие примеры в оболочке Python.
# использовать функцию symmetric_difference на A
>>> А.симметричная_разница(Б)
{1, 2, 3, 6, 7, 8}
# использовать функцию symmetric_difference на B
>>> Б. симметричная_разница (А)
{1, 2, 3, 6, 7, 8} Другие методы установки Python
Существует много методов установки, некоторые из которых мы уже использовали выше. Вот список всех методов, которые доступны с установленными объектами:
| Метод | Описание |
|---|---|
| добавить() | Добавляет элемент в набор |
| очистить() | Удаляет все элементы из набора |
| копировать() | Возвращает копию набора |
| разница() | Возвращает разницу двух или более наборов в виде нового набора |
| разность_обновление() | Удаляет все элементы другого набора из этого набора |
| сброс() | Удаляет элемент из набора, если он является членом. (Ничего не делать, если элемента нет в наборе) (Ничего не делать, если элемента нет в наборе) |
| пересечение() | Возвращает пересечение двух наборов как новый набор |
| cross_update() | Обновляет набор пересечением себя и другого |
| isdisjoint() | Возвращает Истинно , если два набора имеют нулевое пересечение |
| issubset() | Возвращает True , если другой набор содержит этот набор |
| issuperset () | Возвращает True , если этот набор содержит другой набор |
| поп() | Удаляет и возвращает произвольный элемент набора. Вызывает KeyError , если набор пуст |
| удалить() | Удаляет элемент из набора. Если элемент не является членом, вызывает ошибку KeyError | .
| симметричная_разность() | Возвращает симметричную разность двух наборов в виде нового набора |
| симметричная_разница_обновление() | Обновляет набор с симметричной разностью себя и другого |
| объединение() | Возвращает объединение наборов в новый набор |
| обновление() | Обновляет набор объединением себя и других |
Другие операции с множествами
Проверка принадлежности множества
Мы можем проверить, существует ли элемент в множестве или нет, используя ключевое слово в .
# в ключевом слове в наборе
# инициализировать my_set
my_set = установить ("яблоко")
# проверяем, присутствует ли 'a'
# Вывод: Истина
print('a' в my_set)
# проверить, присутствует ли 'p'
# Вывод: Ложь
print('p' нет в my_set) Выход
Правда False
Перебор набора
Мы можем перебирать каждый элемент набора с помощью цикла for .
>>> для письма в наборе ("яблоко"):
... печать (письмо)
...
а
п
е
l Встроенные функции с набором
Встроенные функции, такие как all() , any() , enumerate() , len() , max() , min ( ) , sorted() , sum() и т. д. обычно используются с наборами для выполнения различных задач.
| Функция | Описание |
|---|---|
| все() | Возвращает True , если все элементы набора истинны (или если набор пуст). |
| любой() | Возвращает True , если любой элемент набора истинен. Если набор пуст, возвращает False . |
| перечислить() | Возвращает перечисляемый объект. Он содержит индекс и значение для всех элементов набора в виде пары. |
| лен() | Возвращает длину (количество элементов) в наборе. |
| макс() | Возвращает самый большой элемент в наборе. |
| мин() | Возвращает наименьший элемент в наборе. |
| отсортировано() | Возвращает новый отсортированный список из элементов набора (сам набор не сортируется). |
| сумма() | Возвращает сумму всех элементов набора. |
Python Frozenset
Frozenset — это новый класс, обладающий характеристиками набора, но его элементы нельзя изменить после назначения. В то время как кортежи — это неизменяемые списки, замороженные наборы — неизменные наборы.
Изменяемые наборы нельзя хэшировать, поэтому их нельзя использовать в качестве ключей словаря. С другой стороны, наборы заморозки можно хешировать и использовать в качестве ключей к словарю.
Frozensets можно создавать с помощью функции Frozenset().
Этот тип данных поддерживает такие методы, как: союз() . Будучи неизменным, он не имеет методов, которые добавляют или удаляют элементы.
# Фрозенсеты # инициализируем А и Б A = замороженный набор ([1, 2, 3, 4]) B = замороженный набор ([3, 4, 5, 6])
Попробуйте эти примеры в оболочке Python.
>>> A.isdisjoint(B)
ЛОЖЬ
>>> А.разница(Б)
замороженный набор ({1, 2})
>>> А | Б
замороженный набор ({1, 2, 3, 4, 5, 6})
>>> А.добавить(3)
...
AttributeError: у объекта «замороженный набор» нет атрибута «добавить» Как создать набор Python только с одним элементом?
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 54к раз
Если у меня есть строка и я хочу создать набор, который изначально содержит только эту строку, есть ли более питонический подход, чем следующий?
мой набор = набор() мойSet.добавить(мояСтрока)
Следующее дает мне набор букв в myString :
mySet = set(myString)
набор python python-3.x
В версиях 2.7 и 3.x можно использовать:
mySet = {'abc'}
2
Например, простой способ:
mySet = set([myString])
Для Python2.7+:
set_display ::= "{" (expression_list | понимание) "}"
Пример:
>>> myString = 'foobar'
>>> с = {моя строка}
>>> с
установить(['foobar'])
>>> s = {'спам'}
>>> с
установить(['спам'])
Обратите внимание, что пустое {} не является набором , это dict .
Справка по набору : Набор классов
(объект) | set() -> новый пустой объект набора | set(iterable) -> новый заданный объект
Как видите, set() ожидает итерацию, и строки тоже итерируемы, поэтому он преобразует строковые символы в набор.
Поместите строку в некоторую итерацию и передайте ее set() :
>>> set(('foo',)) #кортеж
установить (['foo'])
>>> установить(['foo']) #список
установить (['foo'])
set(obj) будет перебирать obj и добавлять в набор все уникальные элементы. Поскольку строки также являются итерируемыми, если вы передадите строку в set() , вы получите уникальные буквы в своем наборе. Вы можете сначала поместить свой объект в список:
set(["mystring"])
Однако это не элегантно, ИМО. Вы знаете, даже для создания пустого словаря мы предпочитаем {} вместо dict() . То же самое. Я буду использовать следующий синтаксис:
myset = {"mystring"}
Обратите внимание, что для кортежей после них нужна запятая:
mytuple = ("mystring",)
Если набор также вряд ли изменится, рассмотрите возможность использования замороженного набора :
mySet = замороженный набор ([myString])
использовать mySet = {mystring}
Python 3.г.6.9 (по умолчанию, 24 сентября 2019 г., 14:35:19) Введите «авторское право», «кредиты» или «лицензия» для получения дополнительной информации. IPython 7.8.0 — улучшенный интерактивный Python. Тип '?' за помощью. В [1]: def s(i): ...: г = установить () ...: р.добавить(я) ...: вернуть г ...: В [2]: %timeit s(1234) 218 нс ± 5,99 нс на петлю (среднее значение ± стандартное отклонение для 7 запусков, 1000000 циклов в каждом) В [3]: %timeit установлено ([1234]) 201 нс ± 3 нс на петлю (среднее значение ± стандартное отклонение для 7 циклов, 10000000 циклов в каждом) В [4]: %timeit {1234} 51,7 нс ± 1,7 нс на петлю (среднее значение ± стандартное отклонение для 7 прогонов, 10000000 циклов в каждом)
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Теория множеств > Базовая теория множеств (Стэнфордская философская энциклопедия)
характеризуется своими элементами. Таким образом, два множества равны тогда и только тогда, когда
если они имеют точно такие же элементы. Основное отношение в множестве
Теория есть теория элементальности или членства. Мы пишем \(a\in A\) в
указать, что объект \(a\) является элемент или
элемент множества \(A\). Мы также говорим, что \(a\) принадлежит
до \(А\). Таким образом, множество \(А\) равно множеству \(В\) тогда и только тогда, когда для
каждое \(а\), \(а\в А\) тогда и только тогда, когда \(а\в В\). В частности, есть
только один набор без каких-либо элементов. Это множество называется, естественно,
пустой набор и представлен символом
\({\varничего}\).
Таким образом, два множества равны тогда и только тогда, когда
если они имеют точно такие же элементы. Основное отношение в множестве
Теория есть теория элементальности или членства. Мы пишем \(a\in A\) в
указать, что объект \(a\) является элемент или
элемент множества \(A\). Мы также говорим, что \(a\) принадлежит
до \(А\). Таким образом, множество \(А\) равно множеству \(В\) тогда и только тогда, когда для
каждое \(а\), \(а\в А\) тогда и только тогда, когда \(а\в В\). В частности, есть
только один набор без каких-либо элементов. Это множество называется, естественно,
пустой набор и представлен символом
\({\varничего}\).
Мы говорим, что \(A\) является подмножеством множества \(B\), записанным \(A\subseteq B\), если каждый элемент \(A\) является элементом \(B\). Таким образом, \(A=B\), если и только если \(A\subseteq B\) и \(B\subseteq A\). Заметь \({\varnothing}\subseteq A\), для каждого набора \(A\).
Имея наборы \(A\) и \(B\), можно выполнить некоторые основные операции с из них получаются следующие множества:
Множество \(A\cup B\), называемое объединением \(A\) и \(B\), чьи элементами являются элементы \(A\) и элементы \(B\).

Множество \(A\cap B\), называемое пересечением точек \(A\) и \(B\), элементами которого являются элементы, общие для \(A\) и \(B\).
Множество \(A-B\), называемое разность \(A\) и \(B\), чье элементами являются те элементы \(A\), которые не являются членами \(В\).
Проверка того, что эти операции удовлетворяют следующим свойства:
Ассоциативность:
Коммутативность:
Распределение:
Идемпотентность:
\(А \стакан А=А\)
\(А \крышка А=А\)
\(A \cup {\varnothing}=A\)
\(A\cap {\varnothing}={\varnothing}\)
\(А — А={\varничего}\)
Если \(A\subseteq B\), то
Имея объект \(a\), мы можем сформировать множество, в котором \(a\) является единственным
элемент. Это множество обозначается через \(\{ a \}\). В более общем плане, учитывая
\(a,b,c,\ldots\), мы можем сформировать множество, имеющее \(a,b,c,\ldots\) в качестве
элементы, которые мы обозначаем через \(\{ a,b,c, \ldots\}\). Конечно можем
на самом деле запишите все элементы множества, когда их не слишком много.
многие из них. В случае бесконечных множеств это явно не так.
возможный.
Это множество обозначается через \(\{ a \}\). В более общем плане, учитывая
\(a,b,c,\ldots\), мы можем сформировать множество, имеющее \(a,b,c,\ldots\) в качестве
элементы, которые мы обозначаем через \(\{ a,b,c, \ldots\}\). Конечно можем
на самом деле запишите все элементы множества, когда их не слишком много.
многие из них. В случае бесконечных множеств это явно не так.
возможный.
Если \(a=b\), то \(\{ a,b\}=\{ a\}\). Кроме того, для любых \(a\) и \(b\) пара \(\{ a,b\}\) совпадает с парой \(\{ b,a\}\). Итак, если мы хотим принять во внимание порядок, в котором два элемента пары Учитывая, нам нужно найти другой способ представления пары. Таким образом, мы определить упорядоченную пару \((a,b)\) как множество \(\{ \{ a\},\{ а, б\}\}\). Легко проверить, что две упорядоченные пары \((a,b)\) и \((c,d)\) равны тогда и только тогда, когда \(a=c\) и \(b=d\). Заказ сейчас важно, ибо если \(a\ne b\), то \((a,b)\ne (b,a)\).
Декартово произведение \(A\times B\) двух множеств, \(A\) и
\(B\), определяется как множество всех упорядоченных пар \((a,b)\) таких, что
\(а\в А\) и \(б\в В\). n\).
n\).
Бинарное отношение \(R\) на множестве \(A\) называется рефлексивным , если \((a,a)\in R\) для каждого \(a\in A\). Он называется симметричным , если \((b,a)\in R\) всякий раз, когда \((a,b)\in R\). И это называется транзитивным , если \((a,c)\in R\) всякий раз, когда \((a,b)\in R\) и \((b,c)\в R\). Отношение, которое является рефлексивным, симметричным и транзитивным называется отношением эквивалентности . Отношение тождества на любое множество \(A\) является парадигматическим примером эквивалентности связь. Другим примером является отношение на множестве всех конечных множества натуральных чисел, состоящие из всех пар \((a,b)\) таких, что \(a\) и \(b\) имеют одинаковое количество элементов.
Если \(R\) является отношением эквивалентности на множестве \(A\) и \((a,b)\in R\),
тогда мы говорим, что \(a\) и \(b\) являются \(R\)-эквивалентными . За
каждый \(a\in A\), классов эквивалентности \(a\), обычно обозначаемый
через \([a]_R\), это множество всех элементов \(A\), которые являются \(R\)-эквивалентными
к \(а\). Множество всех классов \(R\)-эквивалентности называется
фактор-множество и обозначается \(A/R\). Можно легко
проверьте, что \(A/R\) является разделом раздела \(A\), то есть ни один элемент
из \(A/R\) пусто, любые два элемента из \(A/R\) не пересекаются, и каждый
\(a\in A\) принадлежит (ровно) одному элементу \(A/R\), а именно классу
\([а]_Р\).
Множество всех классов \(R\)-эквивалентности называется
фактор-множество и обозначается \(A/R\). Можно легко
проверьте, что \(A/R\) является разделом раздела \(A\), то есть ни один элемент
из \(A/R\) пусто, любые два элемента из \(A/R\) не пересекаются, и каждый
\(a\in A\) принадлежит (ровно) одному элементу \(A/R\), а именно классу
\([а]_Р\).
Если \(R\) является бинарным отношением, то вместо него обычно пишут \(aRb\) из \((a,b)\in R\).
Бинарное отношение \(R\) на множестве \(A\) называется антисимметричным если \(a=b\), когда \(aRb\) и \(bRa\). Отношение \(R\) на множестве \(A\), т.е.
рефлексивной, антисимметричной и транзитивной, называется
(возвратный) частичный заказ . Если удалить из \(R\) все пары
\((a,a)\), для каждого \(a\in A\), мы получаем строгих частичных
заказ. Отношение \(\subseteq\) на любом множестве множеств является примером
частичный заказ. Частичный порядок на заданном множестве \(A\) обычно
представленный символом \(\leq\), и соответствующий строгий частичный
упорядочение по \(<\). Частичный порядок \(\leq\) на множестве \(A\) с
дополнительное свойство, состоящее в том, что либо \(a\leq b\), либо \(b\leq a\) для всех
элементы \(a\) и \(b\) из \(A\), называется 92\) также является линейным порядком на
\(В\). Если \(\leq\) — линейный порядок на множестве \(A\), то говорят, что \(a\in
A\) является \(\leq\)-наименьшим элементом \(A\), если нет \(b\in A\) различных
из \(a\) такое, что \(b\leq a\). Число \(0\) является наименьшим элементом
\(\mathbb{N}\), но \(\mathbb{Z}\) не имеет наименьшего элемента.
Частичный порядок \(\leq\) на множестве \(A\) с
дополнительное свойство, состоящее в том, что либо \(a\leq b\), либо \(b\leq a\) для всех
элементы \(a\) и \(b\) из \(A\), называется 92\) также является линейным порядком на
\(В\). Если \(\leq\) — линейный порядок на множестве \(A\), то говорят, что \(a\in
A\) является \(\leq\)-наименьшим элементом \(A\), если нет \(b\in A\) различных
из \(a\) такое, что \(b\leq a\). Число \(0\) является наименьшим элементом
\(\mathbb{N}\), но \(\mathbb{Z}\) не имеет наименьшего элемента.
Линейный порядок \(\leq\) на множестве \(A\) является хорошим порядком, если каждое непустое подмножество \(A\) имеет \(\leq\)-наименьший элемент. Эквивалентно, если нет бесконечного строго убывающего последовательность \[\ldots < a_2< a_1< a_0\] элементов \(A\). Таким образом, обычный порядок \(\mathbb{N}\) является правильным порядком. Но обычное порядок на \(\mathbb{Z}\) не такой, потому что в нем нет наименьшего элемента.
2. Функции
A (\(1\)-арные) функция на множестве \(A\) является бинарным отношением \(F\)
на \(A\) такие, что для каждого \(a\in A\) существует ровно одна пара
\((а,б)\в F\). Элемент \(b\) называется значением из \(F\) на
\(a\) и обозначается через \(F(a)\). А множество \(A\) называется
домен из \(F\). Обозначение \(F:A\to B\) указывает, что \(F\)
есть функция с областью определения \(A\) и значениями в множестве \(B\). Для \(n\geq
2\), \(n\)-арная функция 9п\к Б\),
для некоторого \(B\).
Элемент \(b\) называется значением из \(F\) на
\(a\) и обозначается через \(F(a)\). А множество \(A\) называется
домен из \(F\). Обозначение \(F:A\to B\) указывает, что \(F\)
есть функция с областью определения \(A\) и значениями в множестве \(B\). Для \(n\geq
2\), \(n\)-арная функция 9п\к Б\),
для некоторого \(B\).
Функция \(F:A\to B\) является однозначной , если для всех элементов
\(a\) и \(b\) из \(A\), если \(a\ne b\), то \(F(a)\ne F(b)\). А также
есть на , если для любого \(b\in B\) существует некоторое \(a\in A\) такое
что \(F(a)=b\). Наконец, \(F\) является биективным , если оно является взаимно однозначным.
и на. Таким образом, биекция \(F:A\to B\) устанавливает взаимно-однозначное
соответствие между элементами \(A\) и элементами \(B\), а \(A\)
является биективным с \(B\), если существует такой
биекция. тождественная функция на множестве \(A\), обозначаемая
\(Id:A\to A\) и состоит из всех пар \((a,a)\), где \(a\in
A\) тривиально является биекцией.
Учитывая функции \(F:A\to B\) и \(G:B\to C\), композиция \(F\) и \(G\) , записанные \(G\circ F\), есть функция \(G\circ F:A\to C\), элементами которого являются все пары \((a,G(F(a)))\), где \(a\in A\). Если \(F\) и \(G\) биекции, то и \(G\circ F\).
3. Наборы и формулы
Формальная язык теории множеств является языком первого порядка язык, единственным нелогическим символом которого является символ бинарного отношения \(\в\).
Для любой формулы \(\varphi(x,y_1,\ldots ,y_n)\) языка теории множеств и множеств \(A,B_1,\ldots ,B_n\), можно сформировать множество всех те элементы \(A\), которые удовлетворяют формуле \(\varphi(x,B_1,\ldots ,В_п)\). Это множество обозначается \(\{ a\in A: \varphi(a,B_1,\ldots ,В_п)\}\). Ниже приведены некоторые примеры
\({\varnothing}=\{ a\in A: a\ne a\}\)
\(А=\{а\в А: а=а\}\)
\(A-B=\{ a\in A: a\not \in B\}\).
\(A\cap B=\{ a\in A: a\in B\}\).

И если \(B\) и \(C\) являются подмножествами \(A\), то
Учитывая подмножество \(C\subseteq A\times B\), проекция \(C\) (по первой координате) есть множество
\(\{ a\in A: \существует b\in B ((a,b)\in C)\}\).
Однако это не тот случай, когда при любой формуле \(\varphi(x,y_1,\ldots,y_n)\) и множеств \(B_1,\ldots,B_n\), можно сформировать множество всех тех множеств, которые удовлетворяют формуле \(\varphi(x,B_1,\ldots,B_n)\). Пусть \(\varphi(x)\) будет формулой \(х\не \в х\). Если бы \(A\) было множеством всех множеств, удовлетворяющих формулы, то \(А\в А\) тогда и только тогда, когда \(А\не \в А\). Противоречие! Это противоречие известно как Парадокс Рассела , после Бертран Рассел, открывший его в 1901 г. (см. парадокс Рассела).
4. Порядковые номера
Первым порядковым номером является \({\varnothing}\). Учитывая порядковый номер
\(\alpha\), следующий больший порядковый номер, называемый
(немедленно) преемник \(\alpha\), это набор \(\alpha \cup \{
\альфа\}\). Таким образом, преемником \(\alpha\) является просто набор \(\alpha\)
вместе с еще одним элементом, а именно \(\alpha\)
сам. конечных порядковых чисел получены
начиная с \({\varnothing}\) и многократно беря преемника.
Таким образом, преемником \(\alpha\) является просто набор \(\alpha\)
вместе с еще одним элементом, а именно \(\alpha\)
сам. конечных порядковых чисел получены
начиная с \({\varnothing}\) и многократно беря преемника.
В теории множеств натуральных чисел определяются как конечные ординалы. Таким образом,
\(0= {\varnothing}\)
\(1= {\varnothing}\cup \{ {\varnothing}\}=\{ {\varnothing}\}\)
\(2= \{ {\varnothing}\} \cup \{\{{\varnothing}\}\}=\{ {\varnothing}, \{ {\varnothing}\}\}\)
\(3= \{ {\varnothing}, \{ {\varnothing}\}\}\cup \{ \{ {\varnothing}, \{ {\varnothing}\}\}\} =\{ {\varnothing}, \{ {\varnothing}\}, \{ {\varnothing}, \{ {\varnothing}\}\}\}\)
\(\вточки\)
Обратите внимание, что \(1=\{ 0\}\), \(2=\{ 0,1\}\), \(3=\{ 0,1,2\}\) и в
вообще имеем \(n=\{ 0,1,2,\ldots ,n-1\}\). Итак, каждое натуральное число
\(n\) — это просто набор своих предшественников.
Множество \(A\) является конечным , если существует однозначное соответствие между некоторым натуральным числом \(n\) и элементами \(A\), т. е. биекция \(F:n\to A\), и в этом случае мы говорим, что \(A\) имеет \(n\) элементов. Набор бесконечен , если он не конечен.
Множество всех конечных ординалов обозначается греческой буквой омега
(\(\омега\)). Таким образом, \(\omega\) — это просто набор \(\mathbb{N}\) натуральных
числа. \(\omega\) также является порядковым номером, первым бесконечным
порядковый. Обратите внимание, что \(\omega\) не является преемником какого-либо порядкового номера, и
поэтому он называется предельным порядковым номером . Когда у нас есть \(\omega\), мы можем
продолжайте генерировать больше порядковых номеров, взяв его преемника \(\omega \cup
\{ \omega \}\), затем его преемник \((\omega \cup \{\omega\}) \cup
\{\omega \cup \{\omega \}\}\) и так далее. Все порядковые числительные больше
чем \(0\) производятся таким образом, а именно, либо путем взятия
преемник последнего произведенного порядкового номера, или, если такого последнего нет
порядковый номер, взяв набор всех произведенных до сих пор ординалов, как в
случай \(\omega\), который дает новый предельный порядковый номер. Обратите внимание, однако,
что нельзя взять набор из все порядковые номера, для этого
множество было бы новым предельным ординалом, что невозможно, так как мы
уже все были.
Обратите внимание, однако,
что нельзя взять набор из все порядковые номера, для этого
множество было бы новым предельным ординалом, что невозможно, так как мы
уже все были.
Как и в случае с конечными ординалами, каждый бесконечный ординал — это просто набор его предшественники. Одним из следствий этого является то, что отношение \(\in\) является строгим порядком на любом множестве ординалов. Таким образом, для любых ординалов \(\alpha\) и \(\beta\) мы определяем \(\alpha <\beta\) тогда и только тогда, когда \(\альфа\в\бета\). Тогда соответствующий рефлексивный порядок равен определяется как \(\alpha \leq \beta\) тогда и только тогда, когда \(\alpha <\beta\) или \(\альфа=\бета\). Заметим теперь, что \(\alpha \subseteq \beta\), если и только если \(\alpha \leq \beta\).
5. Счетные и несчетные множества
Если \(A\) конечное множество, то существует биекция \(F:n\to A\) между
натуральные числа \(n\) и \(A\). Любая такая биекция дает
a , считая элементов \(A\), а именно \(F(0)\) есть
первый элемент \(A\), \(F(1)\) — второй и так далее. Каждое бесконечное подмножество счетного множества также счетно: для
предположим, что \(F:\omega \to A\) является биекцией, а \(B\subseteq A\) является
бесконечный. Тогда множество \(\{ n\in \omega: F(n)\in B\}\) является бесконечным
подмножество \(\omega\), следовательно, счетно, и поэтому существует биекция
\(G:\omega \to \{n\in \omega : F(n)\in B\}\). Тогда состав
функция \(F\circ G:\omega \to B\) является биекцией. Объединение счетного множества и конечного множества также
исчисляемый. Более того, объединение двух счетных множеств тоже счетно: поскольку
мы уже показали, что объединение счетного множества и конечного
множество также счетно, достаточно убедиться, что объединение двух
непересекающиеся счетные множества также счетны. Итак, предположим, что \(A\) и \(B\) равны
счетные множества и \(F:\omega \to A\) и \(G:\omega \to B\)
биекций, то функция \(H:\omega \to A\cup B\), состоящая из всех
пар \((2n,F(n))\), плюс все пары \((2n+1, G(n))\) — биекция. Так как любое рациональное число задается парой целых чисел, т.е.
частное \(\frac{m}{n}\), где \(m,n\in \mathbb{Z}\) и \(n\ne 0\),
множество \(\mathbb{Q}\) рациональных чисел также счетно. Однако Георг Кантор обнаружил, что множество \(\mathbb{R}\) вещественных
числа не исчисляются. Предположим, что, стремясь к противоречию,
что \(F:\omega \to \mathbb{R}\) является биекцией. Пусть \(a_0=F(0)\). Выбирать
наименьшее \(k\) такое, что \(a_0 Существование несчетных множеств следует из гораздо более общего
факт, также обнаруженный Кантором. А именно, для любого множества \(A\) множество
все его подмножества, называемые степенным набором из \(A\), и обозначаемые
\(\mathcal{P}(A)\), не является биективным с \(A\): предположим, что \(F:A\to
\mathcal{P}(A)\) является биекцией. Существуют также неисчисляемые порядковые номера. множество всех конечных и
исчисляемые ординалы также являются порядковыми номерами, называемыми \(\omega_1\), и
первый неисчисляемый порядковый номер. Точно так же множество всех ординалов, которые
биективный с некоторым порядковым номером, меньшим или равным \(\omega_1\), также
порядковое число, называемое \(\omega_2\), и не биецируется с \(\omega_1\),
и так далее. мощность или размер конечного множества \(A\) есть
единственное натуральное число \(n\), такое что существует биекция \(F:n\to
А\). В случае бесконечных множеств их мощность определяется не
натуральным числом, а бесконечным порядковым номером. Однако, в отличие от
конечные множества, бесконечное множество \(A\) биективно со многими различными
порядковые номера. В частности, мощность порядкового числа \(\alpha\) равна
наименьший порядковый номер \(\каппа\), который биецируется с ним. Заметь
\(\kappa\) не биективен ни с каким меньшим порядковым номером, иначе
будет \(\альфа\). Порядковые числа, которые не биективны с
любые меньшие порядковые числа называются количественными числами . Таким образом, все
натуральные числа являются количественными, как и \(\omega\), \(\omega_1\),
\(\omega_2\) и так далее. В общем, для любого кардинала \(\каппа\)
множество всех ординалов, которые биективны с некоторым ординалом \(\leq
\каппа\) тоже кардинал; это наименьший кардинал больше, чем
\(\каппа\). Бесконечные кардиналы представлены буквой алеф
(\(\алеф\)) еврейского алфавита. Таким образом, наименьший бесконечный
кардинал — \(\omega =\aleph_0\), следующий — \(\omega_1=\aleph_1\),
который является первым несчетным кардиналом, затем следует
\(\omega_2=\aleph_2\) и т. д. Мощность любого множества \(A\), обозначаемого \(|A|\), является единственным
кардинальное число, биективное с \(A\). Мы уже видели, что
\(|\mathbb{R}|\) несчетно, следовательно, больше, чем \(\aleph_0\), но
неизвестно, какое это кардинальное число. Гипотеза о том, что
\(|\mathbb{R}|=\aleph_1\), сформулированная Кантором в 1878 г., является
знаменитый Гипотеза континуума . Таким образом, все
конечные множества счетны. Бесконечное множество \(A\) есть
называется счетным , если существует биекция \(F:\omega \to A\)
между множеством натуральных чисел и \(A\). Набор \(\mathbb{N}\) из
натуральные числа (тривиально) счетны. Если \(A\) бесконечное подмножество
\(\omega\), то \(A\) также счетно: ибо пусть \(F:\omega \to A\) будет
такой, что \(F(n)\) является наименьшим элементом \(A\), не входящим в множество
\(\{ F(m)\in A: m
Таким образом, все
конечные множества счетны. Бесконечное множество \(A\) есть
называется счетным , если существует биекция \(F:\omega \to A\)
между множеством натуральных чисел и \(A\). Набор \(\mathbb{N}\) из
натуральные числа (тривиально) счетны. Если \(A\) бесконечное подмножество
\(\omega\), то \(A\) также счетно: ибо пусть \(F:\omega \to A\) будет
такой, что \(F(n)\) является наименьшим элементом \(A\), не входящим в множество
\(\{ F(m)\in A: m Для заданных множеств \(A\) и \(B\), которые без потери
общности, мы можем предположить, что они не пересекаются, и при заданных биекциях
\(F:\omega \to A\) и \(G:n\to B\), для некоторого \(n<\omega\) пусть \(H:\omega
\to A\cup B\) — биекция, заданная формулой: \(H(m)=G(m)\), для каждого
\(m
Для заданных множеств \(A\) и \(B\), которые без потери
общности, мы можем предположить, что они не пересекаются, и при заданных биекциях
\(F:\omega \to A\) и \(G:n\to B\), для некоторого \(n<\omega\) пусть \(H:\omega
\to A\cup B\) — биекция, заданная формулой: \(H(m)=G(m)\), для каждого
\(m
 Тогда подмножество \(\{ a\in A: a\not \in
F(a)\}\) множества \(A\) есть значение \(F(a)\) некоторого \(a\in A\). Но тогда \(a\in
F(a)\) тогда и только тогда, когда \(a\not \in F(a)\). Следовательно, если \(А\) — любое бесконечное
множество, то \(\mathcal{P}(A)\) несчетно.
Тогда подмножество \(\{ a\in A: a\not \in
F(a)\}\) множества \(A\) есть значение \(F(a)\) некоторого \(a\in A\). Но тогда \(a\in
F(a)\) тогда и только тогда, когда \(a\not \in F(a)\). Следовательно, если \(А\) — любое бесконечное
множество, то \(\mathcal{P}(A)\) несчетно. 5.1 Кардиналы
 Например, множество \(\mathbb{N}\) биективно с
\(\omega\), но и с его преемником \(\omega \cup \{\omega\}\): by
присваивая \(0\) \(\omega\) и \(n+1\) \(n\), для всех \(n\in \omega\), мы
получить биекцию между \(\omega \cup \{\omega \}\) и \(\omega\). Но
поскольку ординалы хорошо упорядочены, мы можем определить мощность
бесконечное множество как наименьший ординал, биективный с ним.
Например, множество \(\mathbb{N}\) биективно с
\(\omega\), но и с его преемником \(\omega \cup \{\omega\}\): by
присваивая \(0\) \(\omega\) и \(n+1\) \(n\), для всех \(n\in \omega\), мы
получить биекцию между \(\omega \cup \{\omega \}\) и \(\omega\). Но
поскольку ординалы хорошо упорядочены, мы можем определить мощность
бесконечное множество как наименьший ординал, биективный с ним.
Дополнительная литература


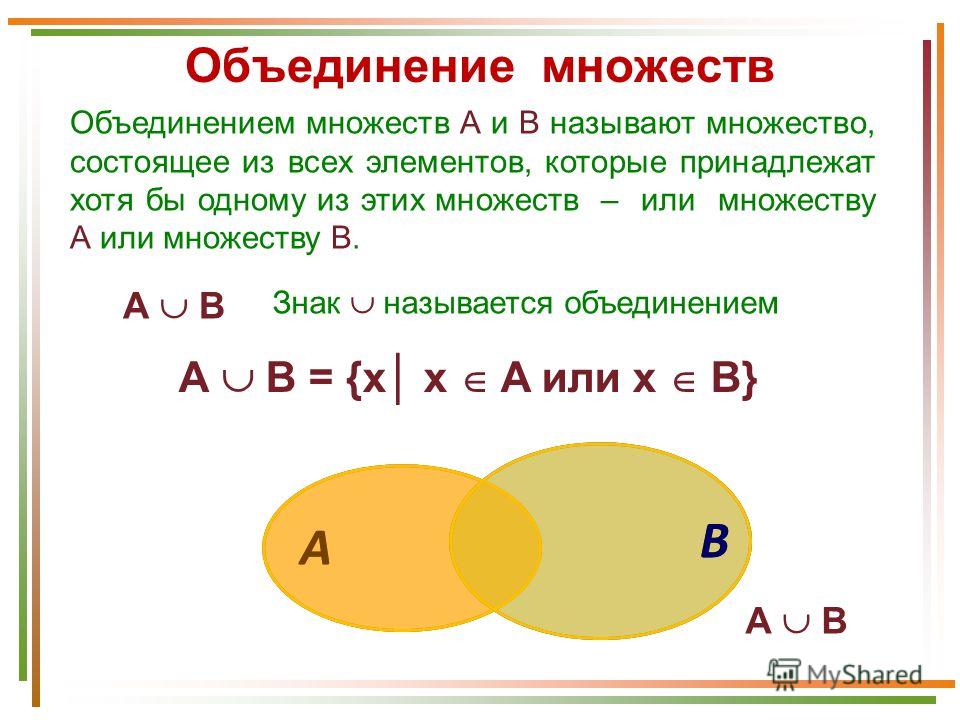



 Само множество также рассматривается как сущность и может объединяться в совокупность с другими множествами. Причём часто используемый Кантором приём формирования множеств состоит в выделении всех предметов, обладающих данным свойством. Этот приём вызвал в дальнейшем серьёзные подозрения из-за того, что не указывает никакой конструктивной процедуры, а потому вводит в рассмотрение объекты, имеющие сомнительный онтологический статус. Для Кантора ясное указание свойства было достаточным основанием признать существующим и предмет, которому это свойство приписывается. Иными словами, свойство конституирует сущность, о которой сказывается. Но поскольку свойство отождествлено с множеством, всякое множество является конституирующим для своих элементов. Существование объекта всегда обусловлено его включением в множество. Поэтому Кантор строит бесконечную иерархию всё более мощных множеств, последовательно включаемых одно в другое. Это явно противоречит идеям Прокла, который в наращивании множественности видел угасание производящей мощи и нарастание неопределённости (беспредельность).
Само множество также рассматривается как сущность и может объединяться в совокупность с другими множествами. Причём часто используемый Кантором приём формирования множеств состоит в выделении всех предметов, обладающих данным свойством. Этот приём вызвал в дальнейшем серьёзные подозрения из-за того, что не указывает никакой конструктивной процедуры, а потому вводит в рассмотрение объекты, имеющие сомнительный онтологический статус. Для Кантора ясное указание свойства было достаточным основанием признать существующим и предмет, которому это свойство приписывается. Иными словами, свойство конституирует сущность, о которой сказывается. Но поскольку свойство отождествлено с множеством, всякое множество является конституирующим для своих элементов. Существование объекта всегда обусловлено его включением в множество. Поэтому Кантор строит бесконечную иерархию всё более мощных множеств, последовательно включаемых одно в другое. Это явно противоречит идеям Прокла, который в наращивании множественности видел угасание производящей мощи и нарастание неопределённости (беспредельность).
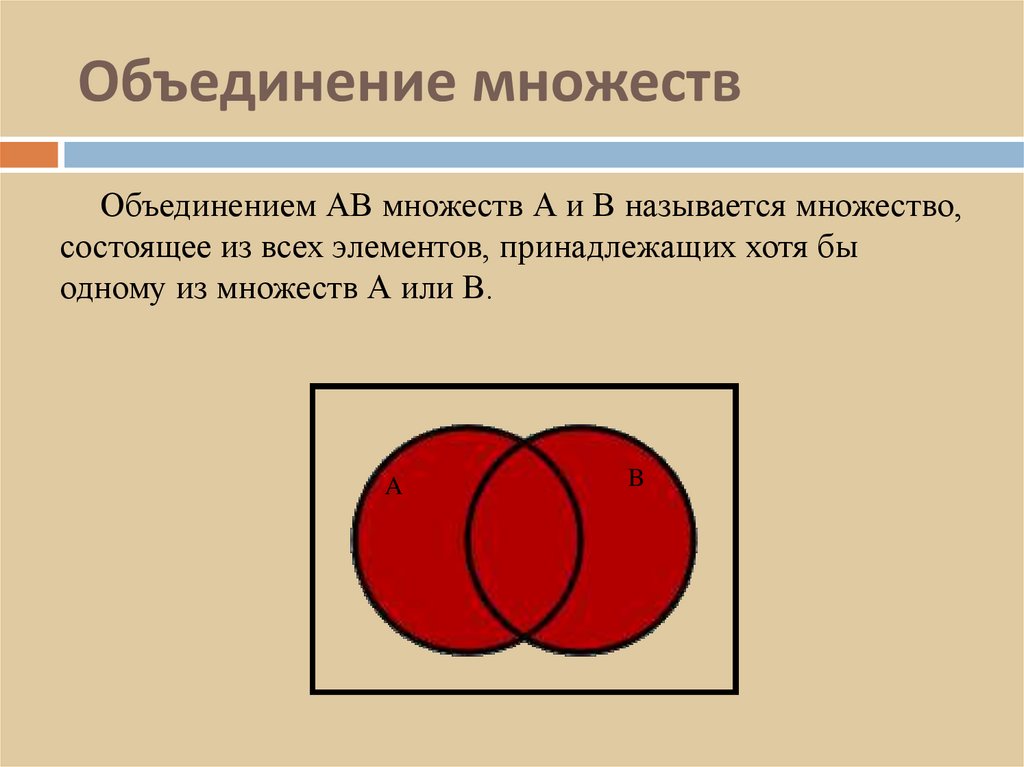 Кантор доказал также существование взаимно-однозначного соответствия между этим несчётным множеством и множеством всех точек произвольного отрезка прямой или множеством всех действительных чисел, лежащих в заданном интервале. Такие множества Кантор назвал непрерывными, а их множество — континуумом. Хотя эти множества довольно прочно вошли во многие учебники, их использование нельзя считать полностью логически оправданным. Уже Аристотель считал рассмотрение непрерывной конфигурации как множества грубой ошибкой. К этому можно добавить, что если признать, например, отрезок прямой состоящим из бесконечного числа отличимых друг от друга элементов, то невозможно представить никакого способа
Кантор доказал также существование взаимно-однозначного соответствия между этим несчётным множеством и множеством всех точек произвольного отрезка прямой или множеством всех действительных чисел, лежащих в заданном интервале. Такие множества Кантор назвал непрерывными, а их множество — континуумом. Хотя эти множества довольно прочно вошли во многие учебники, их использование нельзя считать полностью логически оправданным. Уже Аристотель считал рассмотрение непрерывной конфигурации как множества грубой ошибкой. К этому можно добавить, что если признать, например, отрезок прямой состоящим из бесконечного числа отличимых друг от друга элементов, то невозможно представить никакого способа  В рамках этой теории действительно оказалось возможным дать определения основных понятий математики, исходя из понятия множества. Однако за подходом Цермело можно увидеть совершенно иные, нежели у Кантора, философские основания. Термины «множество» и «элемент множества» вводятся как неопределяемые, точнее, они определяются системой отношений, фиксированных в аксиомах. Последнее может значить, что они должны быть рассмотрены не как сущности, обладающие свойствами, а как неопределённые сами но себе объекты, обозначающие лишь места в заданной теорией абстрактной структуре.
В рамках этой теории действительно оказалось возможным дать определения основных понятий математики, исходя из понятия множества. Однако за подходом Цермело можно увидеть совершенно иные, нежели у Кантора, философские основания. Термины «множество» и «элемент множества» вводятся как неопределяемые, точнее, они определяются системой отношений, фиксированных в аксиомах. Последнее может значить, что они должны быть рассмотрены не как сущности, обладающие свойствами, а как неопределённые сами но себе объекты, обозначающие лишь места в заданной теорией абстрактной структуре. 01.2007, 21:52
01.2007, 21:52  Что является истинной — их равенсто или все же их неравенство.
Что является истинной — их равенсто или все же их неравенство.

 Но если обратиться к определению пустого множества, начинаешь сомневаться. Пустое множество -это множество, не содержащее элементов. Множество пустых множеств — это множество множества, не содержащего элементов, т. е. по сути дела, если нарисовать диаграмму Венна-Эйлера, выходит что B и C — по крайней мере, так считает большинство, кому я задавал эту задачу, равны.
Но если обратиться к определению пустого множества, начинаешь сомневаться. Пустое множество -это множество, не содержащее элементов. Множество пустых множеств — это множество множества, не содержащего элементов, т. е. по сути дела, если нарисовать диаграмму Венна-Эйлера, выходит что B и C — по крайней мере, так считает большинство, кому я задавал эту задачу, равны.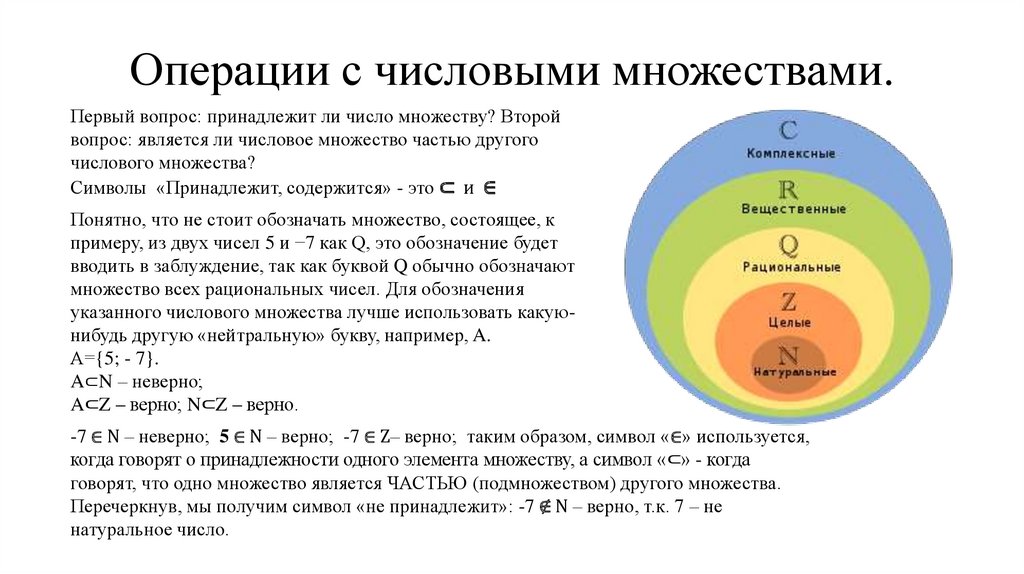 Поскольку пустое множество существует (и даже единственно), то множество никак не может быть пустым (ведь хотя бы один элемент в нем содержится).
Поскольку пустое множество существует (и даже единственно), то множество никак не может быть пустым (ведь хотя бы один элемент в нем содержится). 
 }
}