Число в квадрате умножить на число в квадрате: Простой способ возведения числа в квадрат.

Быстрое возведение чисел от 1 до 100 в квадрат / Хабр

Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни

Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.

Правило 1 (отсекает 10 чисел)

Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.

70 * 70 = 4900.

В таблице отмечены красным.

Правило 2 (отсекает 10 чисел)

Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.

75 * 75 = 7 * 8 = 56 … 25 = 5625.

В таблице отмечены зеленым. 2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.

Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.

Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

Возведение в степень в Python, квадрат числа на примерах

В этом руководстве разберем процесс возведения в степень в Python.

В математике возведение в степень — это операция, при которой число умножается само на себя несколько раз. Python предоставляет встроенные операторы и функции для выполнения возведения в степень. ) — это оператор возведения числа в степень, ведь именно он обозначает эту операцию в математике. Однако в большинстве языков программирования этот знак выступает в качестве побитового

xor.

В Python оператор возведения в степень обозначается двумя символами звездочки ** между основанием и числом степени.

Функциональность этого оператора дополняет возможности оператора умножения *: разница лишь в том, что второй оператор указывает на то, сколько раз первые операнд будет умножен сам на себя.

print(5**6)

Чтобы умножить число 5 само на себя 6 раз, используется ** между основанием 5 и операндом степени 6. Вывод:

15625

Проверим оператор с другими значениями.

Инициализируем целое число, отрицательное целое, ноль, два числа с плавающей точкой float, одно больше нуля, а второе — меньше. Степеням же присвоим случайные значения. 8 = 0.00390625

pow() или math.power() для возведения в степень

Также возводить в степень в Python можно с помощью функции pow() или модуля math, в котором есть своя реализация этого же модуля.

В обе функции нужно передать два аргумента: основание и саму степень. Попробуем вызвать обе функции и посмотрим на результат.

import math

print(pow(-8, 7))
print(math.pow(-8, 7))

print(pow(2, 1.5))
print(math.pow(2, 1.5))

print(pow(4, 3))
print(math.pow(4,3))

print(pow(2.0, 5))
print(math.pow(2.0, 5))

Вывод:

-2097152
-2097152.0
2.8284271247461903
2.8284271247461903
64
64.0
32.0
32.0

Отличие лишь в том, что math.pow() всегда возвращает значение числа с плавающей точкой, даже если передать целые числа. А вот pow() вернет число с плавающей точкой, если таким же был хотя бы один из аргументов.

numpy.np() для возведения в степень

В модуле numpy есть своя функция power() для возведения в степень. Она принимает те же аргументы, что и pow(), где первый — это основание, а второй — значение степени.

Выведем те же результаты.

print(np.power(-8, 7))
print(np.power(2, 1.5))
print(np.power(4, 3))
print(np.power(2.0, 5))

-2097152
2.8284271247461903
64
32.0

Как получить квадрат числа в Python?
Для возведения числа в квадрат, нужно указать 2 в качестве степени. Встроенной функции для получения квадрата в Python нет.

Например, квадрат числа 6 — 6**2 —> 36.

Сравнение времени работы разных решений

Теперь сравним, сколько занимает выполнение каждой из трех функций и оператора **. Для этого используем модуль timeit.

Основанием будет 2, а значением степени — 9999999.

import numpy as np
import math
import time

start = time.process_time()
val = 2**9999999
print('** за', time.process_time() - start, 'ms')

start = time.process_time()
val = pow(2, 9999999)
print('pow() за', time.process_time() - start, 'ms')

start = time.process_time()
val = np.power(2, 9999999)
print('np.power() за', time.process_time() - start, 'ms')

start = time.process_time()
val = math.pow(2, 9999999)
print('math.pow() за', time.process_time() - start, 'ms')
  

** за 0.078125 ms
pow() за 0.0625 ms
np.power() за 0.0 ms
Traceback (most recent call last):
  File "C:\Programs\Python\Python38\test.py", line 18, in <module>
    val = math.pow(2, 9999999)
OverflowError: math range error

В первую очередь можно обратить внимание на то, что math.pow() вернула ошибку OverflowError. Это значит, что функция не поддерживает крупные значения степени.

Различия между остальными достаточно простые, но можно увидеть, что np.power() — самая быстрая.

Приёмы быстрых вычислений

На олимпиаде Кенгуру и на Внешнем независимом тестировании запрещено пользоваться калькуляторами. Поэтому очень важно научиться тратить на вычисления как можно меньше времени, чтобы использовать его на обдумывание задач.

Умножение двузначного числа на 11

Чтобы двузначное число умножить на 11, сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.

Примеры:
45х11
Складываем 4+5=9. Поэтому результатом будет 495.

76х11
Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.

Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b

Умножение и деление на 5 и 25

Чтобы число умножить число на 5, его нужно разделить на 2 и умножить на 10. Чтобы число разделить на 5, его нужно умножить на 2 и разделить на 10.

Аналогично, умножение/деление на 25 заменяется делением/умножением на 4 и умножением/делением на 100

Примеры:
36х5
Делим 36 на 2, получаем 18. Умножаем 18 на 10 и получаем 180.

3/5
Умножаем 3 на 2 и получаем 6. Делим 6 на 10 и получаем 0,6

45/25
Умножаем 45 на 4, получаем 180. Делим 180 на 100, получаем 1,8

84х25
Делим 84 на 4, получаем 21. Умножаем 21 на 100 и получаем 2100.

Математическое обоснование:
Поскольку 5=10/2, умножение/деление на 2 можно свести к более простым умножениям/делениям на 2 и 10.

Возведение в квадрат числа, оканчивающегося на 5

Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.

Примеры:
65²
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.

115²
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.

Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)² = 100n²+100n+25 = 100n(n+1)+25, откуда и следует данное правило.

Возведение в квадрат числа, близкого к круглому

Целесообразно воспользоваться формулами квадрата суммы или разности.

Примеры:
19² = (20-1)² = 400–40+1=361

42² = (40+2)² = 1600+160+4 = 1764

Математическое обоснование:
Формула квадрата суммы: (a+b)² = a²+2ab+b²
Формула квадрата разности: (a-b)² = a²–2ab+b²

Вычитание из степени десятки

Для вычитания числа из степени десятки, нужно последнюю его цифру заменить дополнением до десяти, а остальные (включая первые виртуальные нули) – дополнениями до девяти.

Примеры:
1000-725 = (9-7)(9-2)(10-5) = 275
100000 – 1237 = 100000 – 01237 = (9-0)(9-1)(9-2)(9-3)(10-7) = 98763

Математическое обоснование:
Правило следует из алгоритма вычитания столбиком.

Прибавление числа, близкого к степени десятки

Вместо прибавления числа, состоящего из девяток и оканчивающегося на 9 (8, 7, 6 и т. д.), прибавьте следующую большую степень десятки и вычтите 1 (2, 3, 4 и.т.д)

Примеры:
125+999 = 1125-1 = 1124
6528+996 =7258-4=7254

Математическое обоснование:
Для k-значного числа 99…9 = 100..00 – 1

Упрощённые признаки делимости на 4 и 8

Обычно для проверки делимости на 4 применяется следующий признак: Если двуциферное окончание числа делится на 4, то и само число делится на 4.

Однако, использовав обобщённый признак делимости, заметим, что число 10 даёт остаток 2 при делении на 4. Поэтому переформулируем правило так: Если сумма последней цифры с удвоенной предпоследней делится на 4, то и само число делится на 4.

Аналогично для делимости на 8. Вместо проверки на делимость трёхциферного окончания, можно выполнять проверку суммы последней, удвоенной предпоследней и учетверённой третьей с конца цифры.

Примеры:
Число 1324
4+2*2=8 – делится на 4.
4+2*2+3*4=20 – не делится на 8

Число 6328
8+2*2=12 – делится на 4.
8+2*2+3*4=24 – делится на 8

Математическое обоснование:
Обобщённый признак делимости подробно рассмотрен в отдельной статье.

Как возвести число в квадрат в Excel. Квадрат числа в Эксель через формулу и функцию

При постоянных расчетах в таблицах Excel пользователь рано или поздно столкнется с необходимостью возведения определенных чисел в квадрат. Подобная процедура очень часто выполняется при решении различных задач – начиная простой математикой и заканчивая сложными инженерными расчетами. Однако, даже несмотря на значительное применение этой функции, программа Excel не имеет отдельной формулы, по которой можно возводить числа из ячеек в квадрат. Чтобы сделать это, нужно научиться пользоваться общей формулой, которая предназначена для возведения отдельных цифр или сложных цифровых значений в различные степени. » на необходимую.

Второй способ, который считается более сложным в плане возведения определенного числа в квадрат, – через функцию СТЕПЕНЬ. Она нужна для того, чтобы возводить различные числовые значения в ячейках таблицы Excel в требуемые степени. Внешний вид всей математической формулы привязанной к данному оператору: =СТЕПЕНЬ(требуемое число;степень). Расшифровка:

1. Степень – вторичный аргумент функции. Он обозначает определенную степень для дальнейших расчетов результата из начальной цифры или числового значения. Если необходимо вывести квадрат числа, на этом месте нужно прописать цифру 2.
2. Число – первый аргумент функции. Представляет собой требуемое числовое значение, к которому будет применяться математическая процедура возведения в квадрат. Его можно прописать координатой ячейки с числом или конкретной цифрой.

Порядок действий по возведению числа во вторую степень через функцию СТЕПЕНЬ:

1. Выбрать ту клетку таблицы, в которой будет выводиться результат после проведения расчетов.
2. Нажать на символ добавления функции – «fx».
3. Перед пользователем должно появиться окно «Мастер функций». Здесь необходимо открыть уже действующую категорию, из открывшегося списка выбрать «Математические».

Выбор категории функций для дальнейшего возведения числа в степень

4. Из предложенного перечня операторов нужно выбрать «СТЕПЕНЬ». Подтвердить выбор нажатием кнопки «ОК».
5. Далее необходимо настроить два аргумента функции. В свободном поле «Число» нужно вписать ту цифру или значение, которое будет возводиться в степень. В свободном поле «Степень» необходимо указать требуемую степень (если это возведение в квадрат – 2).
6. Последнее действие – завершение расчета нажатием кнопки «ОК». Если все сделано правильно, в выбранной заранее ячейке появится готовое значение.

Способ возведения числа в степень с использованием координат ячейки:

1. В отдельную клетку вписать то число, которое будет возводиться в квадрат.
2. Далее в другую ячейку вставить функцию через «Мастер функций». Выбрать из списка «Математические», нажать на функцию «СТЕПЕНЬ».
3. В открывшемся окне, где должны указываться аргументы функции, необходимо вписать другие значения, в отличие от первого способа. В свободном поле «Число» необходимо указать координаты ячейки, в которой находится числовой значение, возводимое в степень. Во второе свободное поле вводится цифра 2.

Введение координат ячейки с числом в «Мастер функций»

4. Останется нажать кнопку «ОК» и получить готовый результат в отмеченной ячейке.

Нельзя забывать о том, что функция СТЕПЕНЬ является общей, подходит для возведения чисел в различные степени.

По официальной статистике, среди остальных математических действий пользователи, работающие в таблицах Excel, возводят различные числовые значения в квадрат гораздо чаще, чем выполняют другие процедуры из данной группы. Однако из-за того, что отдельной функции для данного действия в программе нет, можно использовать отдельную формулу, в которую подставляется требуемое число, или же воспользоваться отдельным оператором СТЕПЕНЬ, который доступен на выбор в «Мастере функций».

Оцените качество статьи. Нам важно ваше мнение:

Выжить без калькулятора: 17 секретов быстросчёта

Компьютеры сделали жизнь легче, а нас тупее. Таблицу умножения ещё помним, но сложить числа в уме стало задачей запредельной. Тянемся к калькулятору, вычисляя проценты, и не можем сравнить выгодность перловой крупы в пакетиках: восемь по 40 граммов или пять по 50. Отрешённо достаём смартфон в магазине. Выживайте в офисном плену, удивляя коллег несложными арифметическими фишками.

В сексе и подсчётах пальцы важный инструмент. На руках их десять, как лунных месяцев женской беременности, что подметили римляне, создавая десятичное исчисление. Славяне не брали в учёт большой палец, приспособив по три фаланги на четырёх пальцах, поэтому считали двенадцатерично – дюжинами.

Потомственные арабские торговцы умеют показывать цены руками: левой – числа от 0 до 99, правой – сотни. В Африке сохранились базары, где продавцы и покупатели торгуются руками под картонкой, спрятав пальцы от посторонних взглядов – даже супруг не знает, о какой скидке договорилась жена на шафранный рис. 4=16, поэтому максимальное число, которое может показать программист одной рукой – 31, двумя – 1’023.

Выживайте в офисном плену, удивляя коллег несложными фишками:

1. Сложение двух чисел быстрее выполнить, округлив их до десятков, а потом из общей суммы вычесть значения округления:

56+25=(56+4)+(25+5)=90-(4+5)=81

2. Трёхзначные числа складывают слева направо – сотни+десятки+единицы:

564+982=500+900+60+80+4+2=1’546

3. При вычитании двух чисел одно увеличьте на несколько единиц, второе – уменьшите на столько же – результат не изменится:

90-56=(90-6)-(56-6)=34

4. Умножение на 1,5 – добавляем к исходному числу его половину:

62*1,5=62+31=93

5. Умножение на 4 выполняется как пара последовательных умножения на два:

16х4=32х2=64

6. Умножить на 5 – разделите число на 2 и допишите справа ноль:

84*5=84/2*10=420

7. Умножение на 8 – вы уже догадались

8. Умножить на 9 однозначное число помогают пальцы рук – загибаем это число, теперь десятки – количество пальцев до загнутого, единицы – после:

9*5 – загибаем пятый палец, до него пальцев – 4, после – 5, значит 9*5=45

9. Умножить любое число на 9 – приписать 0 и отнять исходное:

82*9=820-82=738

10. Умножить на 11 двухзначное число – результатом будет трёхзначное: первая цифра исходного, сумма обеих цифр, вторая цифра начального числа:

36*11=300, затем 3+6, затем 6 = 396

11. Умножение и деление на 25 легче делать, вспомнив, что 100= 25*4; на 20 – 100=20*5.

12. Деление на 5 выполняется умножением на два и переносом запятой на один символ вперёд

420/5=840/10=84

13. Возведение в квадрат числа от 11 до 19 проводится суммированием трёх слагаемых: число, умноженное на 10, последняя цифра, умноженная на 10 и последняя цифра в квадрате:

16²=160+60+36=256

14. Возведение в квадрат двузначного числа, оканчивающегося на 5 – цифру десятков умножить на цифру, большую на единицу, и к произведению приписать справа число 25:

95²=9*10 и 25 = 90 и 25 = 9’025

15. Возведение в квадрат двузначного числа, начинающегося на 5 – прибавить к 25 вторую цифру числа и приписать справа квадрат второй цифры (получится однозначное число – припишите перед ним 0):

59²=25+9 и 9² = 34 и 81 = 3’481

16. Если запомнить результаты возведения в квадрат чисел от 21 до 25 (441, 484, 529, 576, 625), можно научится возводить в квадрат двузначное число N, по формуле Рачинского:

N²=(N-25)*100+(50-N)²

73²=48*100+23²= 4’800+ 529 = 5’329

17. Вычисляя процент, например 30% от 80, разделите оба значения на 10 и перемножьте:

3*8=24

Всем дано поровну, только считаем по-разному.  Вам, например, любимый нужен для ровного счета или для полного счастья? Считаете себя умными, но вы же знаете, как у нас считают: слёзы – единственная вода, за которую не приходит счёт, а на нём у многих суммы с восьмью нулями, жаль, что других цифр там нет.

Читайте также:

Быстрое возведение чисел от 1 до 100 в квадрат

Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни

Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.

Правило 1 (отсекает 10 чисел)

Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900.
В таблице отмечены красным.

Правило 2 (отсекает 10 чисел)

Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”. 2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.

Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.

Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

Автор: LysoSutriN

Источник

Степени и возведение в степень, вторая, третья, четвёртая степени

Когда число умножается само на себя, произведение называется степенью.

Так      2.2 = 4, квадрат или вторая степень 2-х
     2. 2.2 = 8, куб или третья степень.
     2.2.2.2 = 16, четвёртая степень.

Также,      10.10 = 100, вторая степень 10.
     10.10.10 = 1000, третья степень.
    10.10.10.10 = 10000 четвёртая степень.

И      a.a = aa, вторая степень a
     a.a.a = aaa, третья степень a
     a.a.a.a = aaaa, четвёртая степень a

Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.

Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель. Это число или буква называется показателем степени или степенью числа. Так, а² равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a³ означает aaa, то есть здесь a повторяется три раза как множитель.

Показатель первой степени есть 1, но он обычно не записывается. Так, a¹ записывается как a.

Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a.      Но a⁴ = a.a.a.a

Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a^x, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень. Так, b^m и dⁿ возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b^m = b³; но если m = 5, тогда b^m=b⁵.

Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)³ есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a³ + 3a²b + 3a²d + 3ab² + 6abd + 3ad² + b³ + d³.

Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.

Так, в ряде      aaaaa, aaaa, aaa, aa, a;
или        a⁵, a⁴, a³, a², a¹;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.

Tак a.a = a², второй член. И a³.a = a⁴
     a².a = a³, третий член. a⁴.a = a⁵.

Если мы начнем слева делить на a,
мы получим a⁵:a = a⁴      и a³:a = a².
a⁴:a = a³       a²:a = a¹

Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.

Так, a:a = a/a = 1. (1/a):a = 1/aa
     1:a = 1/a      (1/aa):a = 1/aaa.

Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.

Или a⁵, a⁴, a³, a², a, 1, 1/a, 1/a², 1/a³.

Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.

Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a³) = a³.

Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
(a + b)³, (a + b)², (a + b), 1, 1/(a + b), 1/(a + b)², 1/(a + b)³.

Для удобства используется еще одна форма записи обратных степеней.

Согласно этой форме, 1/a или 1/a¹ = a^-1. И 1/aaa или 1/a³ = a^-3.
1/aa или 1/a² = a^-2. 1/aaaa или 1/a⁴ = a^-4.

А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a⁰.

Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать      a⁴, a³, a², a¹, a⁰, a^-1, a^-2, a^-3, a^-4.
Или      a⁺⁴, a⁺³, a⁺², a⁺¹, a⁰, a^-1, a^-2, a^-3, a^-4.

А ряд только отдельно взятых степеней будет иметь вид:
     +4,+3,+2,+1,0,-1,-2,-3,-4.

Корень степени может выражен более чем одной буквой.

Так, aa.aa или (aa)² есть второй степенью aa.
И aa.aa.aa или (aa)³ есть третьей степенью aa.

Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.

Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:

Умножайте величину саму на себя столько раз, сколько указано в степени числа.

Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.

Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.

Четвертая степень a есть a⁴ или aaaa. (Art. 195.)
Шестая степень y есть y⁶ или yyyyyy.
N-ая степень x есть xⁿ или xxx….. n раз повторенное.

Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.

Tак (ay)² =a²y²; (ay)² = ay.ay.
Но ay.ay = ayay = aayy = a²y².
Так, (bmx)³ = bmx.bmx.bmx = bbbmmmxxx = b³m³x³.

Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.

Пример 1. Четвертая степень dhy есть (dhy)⁴, или d⁴h⁴y⁴.

Пример 2. Третья степень 4b, есть (4b)³, или 4³b³, или 64b³.

Пример 3. N-ая степень 6ad есть (6ad)ⁿ или 6ⁿaⁿdⁿ.

Пример 4. Третья степень 3m.2y есть (3m.2y)³, или 27m³.8y³.

Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,

(a + b)¹ = a + b, первая степень.
(a + b)¹ = a² + 2ab + b², вторая степень (a + b).
(a + b)³ = a³ + 3a²b + 3ab² + b³, третья степень.
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴, четвертая степень.

Квадрат a — b, есть a² — 2ab + b².

3 + 3a² + 3a + 1.

Квадрат a + b + h есть a² + 2ab + 2ah + b² + 2bh + h²

Упражнение 1. Найдите куб a + 2d + 3

Упражнение 2. Найдите четвертую степень b + 2.

Упражнение 3. Найдите пятую степень x + 1.

Упражнение 4. Найдите шестую степень 1 — b.

Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.

Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a² + 2ah + h²      также, (a — h)(a — h) = a² — 2ah + h².

Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.

Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.

Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.

Пример 1. Квадрат 2a + b, есть 4a² + 4ab + b².

Пример 2. Квадрат ab + cd, есть a²b² + 2abcd + c²d².

Пример 3. Квадрат 3d — h, есть 9d₂ + 6dh + h².

Пример 4. Квадрат a — 1 есть a² — 2a + 1.

Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.

Во многих случаях является эффективным записывать степени без умножения.

Так, квадрат a + b, есть (a + b)².
N-ая степень bc + 8 + x есть (bc + 8 + x)ⁿ

В таких случаях, скобки охватывают все члены под степенью.

Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.

Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]² или (a + b)².(c + d)².

Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.

Куб a.(b + d), есть [a.(b + d)]³, или a³.(b + d)³.

Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.

Вторая степень (- a) есть +a²
Третья степень (-a) есть -a³
Четвёртая степень (-a) есть +a⁴
Пятая степень (-a) есть -a⁵

Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a²
И -a.-a = +a²

Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.

Третья степень a² есть a^2.3 = a⁶.

Для a² = aa; куб aa есть aa.aa.aa = aaaaaa = a⁶; что есть шестой степенью a, но третьей степенью a².

Четвертая степень a³b² есть a^3.4b^2.4 = a¹²b⁸

Третья степень 4a²x есть 64a⁶x³.

Пятая степень (a + b)² есть (a + b)¹⁰.

N-ая степень a³ есть a³ⁿ

N-ая степень (x — y)^m есть (x — y)^mn

(a³.b³)² = a⁶.b⁶

(a³b²h⁴)³ = a⁹b⁶h¹²

Правило одинаково применяется к отрицательным степеням.

Пример 1. Третья степень a^-2 есть a^-3.3=a^-6.

Для a^-2 = 1/aa, и третья степень этого
(1/aa). (1/aa).(1/aa) = 1/aaaaaa = 1/a⁶ = a^-6

Четвертая степень a²b^-3 есть a⁸b^-12 или a⁸/b¹².

Квадрат b³x^-1, есть b⁶x^-2.

N-ая cтепень ax^-m есть x^-mn или 1/x.

Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.

Пример 1. Квадрат -a³ есть +a⁶. Квадрат -a³ есть -a³.-a³, которое, согласно правилам знаков при умножении, есть +a⁶.

2. Но куб -a³ есть -a⁹. Для -a³.-a³.-a³ = -a⁹.

3. N-ая степень -a³ есть a³ⁿ.

Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.

Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.

Квадрат a/b есть a²/b². Согласно правилу умножению дробей,
     (a/b)(a/b) = aa/bb = a²b²

Вторая, третья и n-ая степени 1/a есть 1/a², 1/a³ и 1/aⁿ.

Примеры двочленов, в которых один из членов является дробью.

1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)² = x² + 2.x.(1/2) + 1/2² = x² + x + 1/4
(x — 1/2)² = x² — 2.x.(1/2) + 1/2² = x² — x + 1/4

2. Квадрат a + 2/3 есть a² + 4a/3 + 4/9.

3. Квадрат x + b/2 = x² + bx + b²/4.

4 Квадрат x — b/m есть x² — 2bx/m + b²/m².

Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.

Так, в дроби ax^-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax_-2/y = (a/y).x^-2 = (a/y).(1/x² = a/yx².

В дроби a/by³ мы можем переместить у из знаменателя в числитель.
Тогда a/by₂ = (a/b).(1/y³) = (a/b).y^-3 = ay^-3/b.

Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.

Так, ax³/b = a/bx^-3. Для x³ обратным есть x_-3, что есть x³ = 1/x^-3.

Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.

Так, a/b = 1/ba^-1, or ab^-1.

Квадратное число — элементарная математика

Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на само себя, полученное произведение называется квадратным числом, или точным квадратом, или просто «квадратом». ” Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — квадратные числа.

Более формально: квадратное число — это число в форме n × n или n ² , где n — любое целое число.

Математический фон

Объекты, расположенные в квадратном массиве

Название «квадратное число» происходит от того факта, что это конкретное количество объектов может быть расположено так, чтобы заполнить идеальный квадрат.

Дети могут поэкспериментировать с монетами (или квадратными плитками), чтобы увидеть, какие из них можно расположить в виде идеально квадратного массива.

Банка по четыре пенни:

Банка по девяти пенни:

И шестнадцать пенсов тоже можно:

Но семь пенсов или двенадцать пенсов не могут быть устроены таким образом. Числа (объектов), которые могут быть организованы в квадратный массив, называются «квадратными числами».

Квадратные массивы должны быть заполнены, если мы хотим считать число квадратным.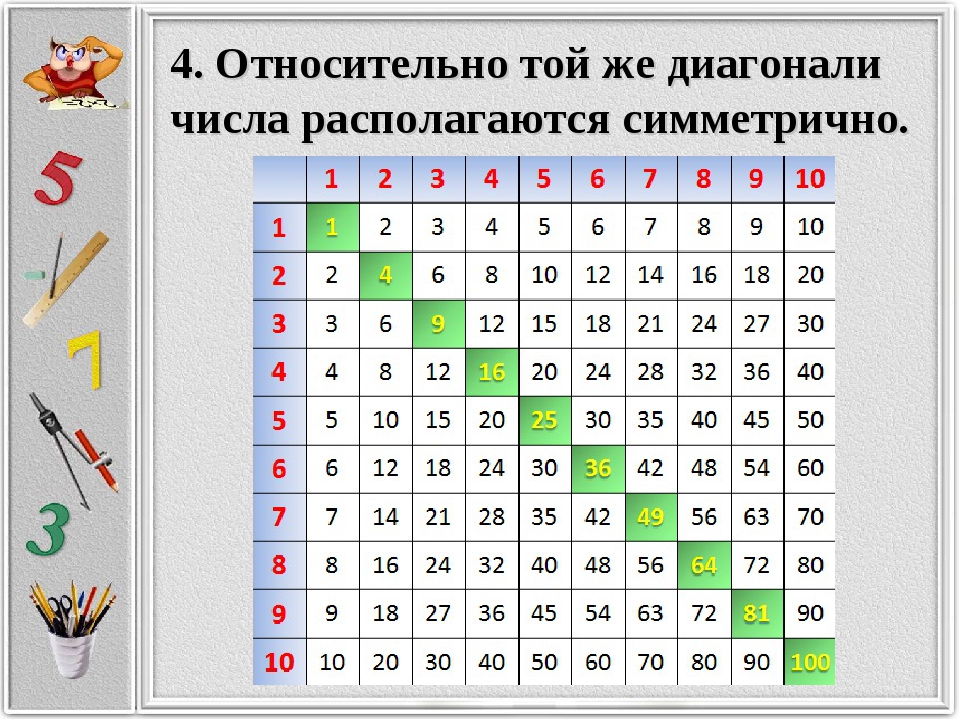 Здесь 12 пенни расположены в квадрате, но не в полном квадратном массиве, поэтому 12 не является квадратным числом.

Число 12 не квадратное.

Детям может понравиться изучать, какое количество монеток можно расположить на таком открытом квадрате. Их не называют «квадратными числами», но они построены по интересной схеме.

Квадраты из квадратных плиток тоже интересно делать. Число квадратных плиток, которые помещаются в квадратный массив, является «квадратным числом».

Вот две платы, 3 × 3 и 5 × 5 .Сколько красных плиток в каждой? Чернить? Желтый?
Есть какие-нибудь из этих квадратных чисел?
Что делать, если таким же образом выложить доску 4 × 4 или 6 × 6 ?
Можете ли вы предсказать количество плиток на доске 7 × 7 или 10 × 10 ?

Квадратные числа в таблице умножения

Квадратные числа появляются по диагонали стандартной таблицы умножения.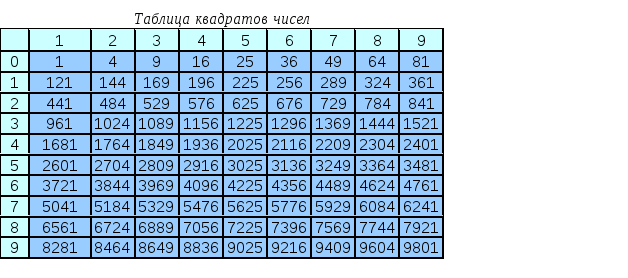

Соединения с треугольными числами

Если вы посчитаете зеленые треугольники в каждом из этих рисунков, вы увидите последовательность чисел: 1, 3, 6, 10, 15, 21,…, последовательность, называемую (достаточно подходящим образом) треугольными числами.

Если вы посчитаете белые треугольники, которые находятся в «пробелах» между зелеными, последовательность чисел начинается с 0 (потому что у первого рисунка нет пробелов), а затем продолжается: 1, 3, 6, 10, 15,… , снова треугольные числа!

Замечательно, что если вы посчитаете все крошечные треугольники в каждом рисунке — и зеленые, и белые, — цифры будут квадратными числами!

Связь между квадратными и треугольными числами с другой стороны

Постройте ступенчатую систему из стержней Кюизенера, скажем, W, R, G.Затем постройте следующую ступеньку: W, R, G, P.

.

Каждая из них «треугольная» (если не учитывать ступенчатую грань). Соедините два последовательных треугольника вместе, и получится квадрат:. Этот квадрат такого же размера, как 16 белых стержней, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).

Вот еще один пример:. Когда они сложены вместе, они образуют квадрат, площадь которого равна 64, опять же, квадрат длины (в белых стержнях) самого длинного стержня.(Коричневый стержень имеет длину 8 белых стержней, а 64 равно 8 умноженным на 8, или «8 в квадрате».)

Ступеньки из квадратов номеров

Ступеньки, которые поднимаются и снова спускаются, как эта, также содержат квадратное количество плиток. Когда плитки отмечены шахматной доской, как здесь, дополнительное предложение, описывающее количество красных плиток (10), количество черных плиток (6) и общее количество плиток (16), снова показывает связь между треугольные числа и квадратные числа: 10 + 6 = 16.

Приглашение учеников 2-го (или даже 1-го) класса построить модели ступенек и написать числовые предложения, описывающие эти модели, — хороший способ дать им возможность попрактиковаться в описательных числовых предложениях, а также подружиться с квадратными числами.

Вот два примера. Цвет используется здесь, чтобы помочь вам увидеть, что описывается. Детям нравится цвет, но он им не нужен, и они часто могут увидеть творческие способы описания рисунков ступенек, которые они построили с помощью одноцветных плиток.Или они могут раскрасить миллиметровую бумагу размером 1 дюйм, чтобы записать свой образец ступенек и показать, как они преобразовали его в числовое предложение.

Ромбовидную форму, сделанную из пенсов, также можно описать числовым предложением 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25.

От одного квадратного числа к другому: два изображения со стержнями Cuisenaire

(1) Начните с W. Добавьте две последовательные штанги, W + R; затем еще два, R + G; тогда G + P; тогда….

1;

прибавить 1 + 2;

прибавить 2 + 3;

прибавить 3 + 4;

прибавить 4 + 5;

добавить 5 + 6;

добавить 6 + 7

(2) Начните с W. Для каждого нового квадрата добавьте два стержня, которые соответствуют сторонам предыдущего квадрата, и новую букву W, чтобы заполнить угол.

предварительное вычисление алгебры — Если возведение числа в квадрат означает умножение этого числа на себя, то не следует ли извлечение квадратного корня из числа означать деление числа на само себя?

Поскольку этот вопрос напрямую зависит от некоторых фундаментальных математических идей, в данном ответе делается попытка объяснить эти идеи аналогичным фундаментальным способом.

Возведение числа в квадрат можно рассматривать как процедуру.Конкретная процедура возведения числа в квадрат может использовать шаблон вроде следующего:

$$ \ Box \ longrightarrow \ Box \ times \ Box \ longrightarrow \ Box $$

Мы помещаем «входное» значение, например, $ 2 $, в крайнее левое поле, например:

$$ 2 \ longrightarrow \ Box \ times \ Box \ longrightarrow \ Box $$

Затем мы делаем копии самого левого блока и помещаем их в два коробки посередине:

$$ 2 \ longrightarrow 2 \ times 2 \ longrightarrow \ Box $$

Обратите внимание, что эти два поля должны содержать по одно и то же число. Наконец, выполняем указанное умножение и записываем результат в последнем поле справа:

$$ 2 \ longrightarrow 2 \ times 2 \ longrightarrow 4 $$

Чтобы извлечь квадратный корень, мы хотим перевернуть процедуру, то есть работайте в обратном направлении. Итак, берем «входное» число, например, 9 $, и положите в коробку справа:

$$ \ Box \ longrightarrow \ Box \ times \ Box \ longrightarrow 9 $$

Теперь нам нужно решить, что поместить в два поля посередине.Мы знаем, что нам нужно, чтобы содержимое двух ящиков было одинаковым, и мы знаем, что что при умножении результат должен быть 9 долларов. Предположим, мы предполагаем, что число в каждой коробке должно быть 3 доллара. Тогда имеем:

$$ \ Box \ longrightarrow 3 \ times3 \ longrightarrow 9 $$

Мы можем подтвердить, что $ 3 \ times3 $ действительно дает результат $ 9 $, поэтому все пока хорошо. Теперь нам просто нужно определить, какое число было в крайнее левое поле. Мы знаем, что средние поля были заполнены копированием этого поля, поэтому он должен был содержать еще и 3 доллара. Итак, у нас

$$ 3 \ longrightarrow 3 \ times3 \ longrightarrow 9 $$

И поэтому квадратный корень из 9 долларов равен 3 долларам, а не 9/9 долларам. (Ну, и тот факт, что мы отказываемся положить -3 доллара в две коробки в в середине, потому что жизнь лучше, когда мы последовательно следуем правилу который гласит, что «квадратный корень» никогда не должен быть отрицательным числом.)

Мы можем позже научиться находить квадратные корни способом, который не так полагаются на удачное предположение. Но это вопрос алгоритм для вычисления квадратного корня, а не определение квадратного корня.

квадратных чисел (ключевой этап 2)

Урок

Квадратное число — это число, полученное в результате умножения числа на само себя.

Например,

• 1 — квадратное число. Это 1 × 1.

• 4 — квадратное число. Это 2 × 2.

• 9 — квадратное число. Это 3 × 3.

Примечание: 2 × 2 можно записать 2 ² («2 в квадрате»).

Оксфордский словарь английского языка определяет квадратное число как «произведение числа, умноженного на само себя».

Квадратные числа

Квадратные числа:

В числовом квадрате квадратные числа ниже заштрихованы:

Это просто квадратные числа до 100. Квадратных чисел бесконечно много, они продолжаются бесконечно.

Как найти квадратные числа

Найти квадратные числа легко.Просто умножьте число на само себя.

Первые 10 квадратных чисел находятся путем умножения 1 на себя, а затем 2 на себя, как показано ниже.

Квадратные числа в алгебре

В алгебре вместо цифр используются буквы.

Так же, как мы можем возвести число в квадрат …

… мы можем квадратное письмо:

Примечание: Мы бы сказали x ² как «x в квадрате», точно так же, как мы сказали бы 2 ² как «2 в квадрате».

Вот несколько примеров квадратных букв в алгебре:

• Квадратные уравнения имеют член x ² :

• Теорема Пифагора связывает квадрат длин сторон прямоугольного треугольника друг с другом.

  На изображении ниже показана формула теоремы Пифагора и длины сторон a , b и c прямоугольного треугольника:

• Площадь круга связана с квадратом его радиуса.

  На изображении ниже показана формула для площади круга и радиуса круга, r :

Помогите нам улучшить математику Monster

• Вы не согласны с чем-то на этой странице?
• Вы заметили опечатку?

Сообщите нам, используя эту форму

См. Также

Как размножаться Что такое алгебра? Нахождение площади круга Что такое целое число? Что такое квадратный корень?

Как умножить квадратный корень

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Квадраты и квадратные корни — разница и примеры

Что такое квадрат числа?

В математике квадрат числа — это результат умножения числа на само себя. Слово квадрат обычно эквивалентно возведению числа в степень 2 и обозначается надстрочным индексом 2.

Например, квадрат 4 записывается как 4 ² , что дает 16 в качестве ответа. В данном случае 16 — это квадрат числа 4.

Ниже приведен список квадратов первых двенадцати чисел:

1 x 1 = 1 7 x 7 = 49
2 x 2 = 4 8 x 8 = 64
3 x 3 = 9 9 x 9 = 81
4 x 4 = 16 10 x 10 = 100
5 x 5 = 25 11 x 11 = 121
6 x 6 = 36 12 x 12 = 144

Возведение в квадрат отрицательных чисел

Квадрат отрицательного числа является положительным числом.Например, -3 x -3 станет 9, однако — 3 x 3 = -9, это потому, что -3 — это число, отличное от 3.

Что такое квадратный корень числа?

Квадратный корень — это операция, обратная возведению числа в квадрат. Другими словами, квадратный корень — это операция, которая отменяет показатель степени 2. Квадратный корень из числа x таков, что число y является квадратом x, упрощенно записывается как y ² = x.

Например, 5 и — 5 являются квадратными корнями из 25, потому что:

5 x 5 = 25 и -5 x -5 = 25.

Квадратный корень числа x обозначается знаком корня √x или x ^1/2 . Например, квадратный корень из 16 представлен как √16 = 4. Число, квадратный корень которого вычисляется, называется подкоренным выражением. В этом выражении √16 = 4, число 16 — подкоренное выражение.

Свойства

• Полное квадратное число имеет точный квадратный корень.
• Четное совершенное число имеет четный квадратный корень.
• Нечетное совершенное число имеет нечетный квадратный корень.
• Квадратный корень отрицательного числа не определен.
• Квадратные корни имеют только числа, оканчивающиеся четным числом нулей.

Нахождение квадратного корня чисел

• Повторное вычитание :
  Этот метод включает в себя успешное и многократное вычитание нечетных чисел, таких как 1, 3, 5 и 7, из числа до достижения нуля. Квадрат числа равен числу или частоте вычитания числа.Предположим, нам нужно вычислить квадрат совершенного числа, такого как 16, количество выполненных вычитаний равно 4, поэтому квадратный корень из 16 равен 4.
• Простое факторизация :
  В этом методе точное квадратное число равно факторизованные последовательными делениями. Простые множители группируются в пары, и вычисляется произведение каждого числа. Следовательно, произведение представляет собой квадратный корень из числа. Чтобы найти квадрат совершенного числа, такого как: 144, выполняется как:

1. 144 = 2 × 2 × 2 × 2 × 3 × 3.
2. Соедините простые множители.
3. Выбор одного числа из каждой пары.
4. 2 × 2 × 3 = 12.
5. Таким образом, √144 = 12.

• Метод деления:
  Метод деления — подходящий метод вычисления квадрата большого числа.
  
  Это следующие шаги:

1. Полоса помещается над каждой парой цифр, начиная с правой стороны.
2. Разделите число на левом конце на число, квадрат которого меньше или эквивалентен числам под левым концом.
3. Возьмите это число в качестве делителя и частного. Аналогичным образом возьмите крайнее левое число в качестве делимого.
4. Разделите, чтобы получить результат.
5. Потяните вниз следующее число с полосой справа от остатка.
6. Умножьте делитель на 2.
7. Справа от этого нового делителя найдите подходящий делимый. Этот процесс повторяется до тех пор, пока мы не получим в качестве остатка ноль. Следовательно, квадрат числа равен частному.

Практические вопросы

1.Запишите значение

(a) √81

(b) √1

(c) √121

(d) √0

2. Найдите квадратные числа из следующего списка чисел: 2 6 11 14 16 18 24 25.

3. Запишите значение (a) 3² (b) 6 в квадрате c) 8² (d) 9 в квадрате (e) 12²

4. Я думаю о двух числах. Оба числа представляют собой квадратные числа больше 1. Если сумма этих чисел равна 100. Какие два числа?

5. Перечислите все квадратные числа от 0 до 100.

Ответы на практические вопросы

1. (a) √81 = 9, (b) √1 = 1 (c) √121 = 11 (d) √0 = 0

2 . Квадратные числа: 16 и 25

3. (a) 3² = 9 (b) 6 в квадрате = 36 c) 8 = 64² (d) 9 в квадрате = 81 (e) 12² = 144

4. 36 и 64 — квадратные числа

5. 1, 4, 9, 16, 25, 36, 49, 64 и 81

Предыдущий урок | Главная страница | Следующий урок

Калькулятор в квадрате (степень двойки) — Калькулятор капитана

Калькулятор в квадрате чисел (степень двойки)

Обратите внимание: для работы этого калькулятора требуется JavaScript.

Определение — Что такое квадрат числа?

Квадрат числа — это когда число умножается само на себя.
Например, 2 ² = 2 x 2 = 4, 4 ² = 4 x 4 = 16, 172 ² = 172 x 172 = 29 584.

Напишите число в квадрате с маленькой двойкой, поднятой вверху справа от числа. Это называется показателем. 10 ² — это «10 в квадрате», а маленькая цифра «2» означает, что число возведено в квадрат.

Формула

— Как вычислить квадратные числа

Квадрат числа находится путем умножения этого числа на само себя.

число ² = число x число

Пример

5 ² = 5 • 5 = 25

10 ² = 10 • 10 = 100

24 ² = 24 • 24 = 576

Как набрать квадрат числа

• В Microsoft Word и других продуктах Office выделите цифру «2», затем щелкните правой кнопкой мыши и выберите «Шрифт», чтобы открыть меню шрифтов.2.

Таблица чисел в квадрате

Обратите внимание: для работы этого калькулятора требуется JavaScript.

Часто задаваемые вопросы

Что такое «квадрат» в математике?

Число в квадрате умножается само на себя. 3 ² равно 3 • 3 = 9. 7 ² равно 7 • 7 = 49.
Возведенное 2 следующее число означает, что оно возведено в квадрат.

В чем разница между «возведением в квадрат», «показателем 2» и «степенью двойки»?

Все они означают одно и то же.
Мы находим, что «квадрат» звучит более естественно.Термины «экспонента» и «степень» обычно используются для показателей степени больше 3, имеющих дробные или десятичные дроби.

Источники и другие ресурсы

Другие калькуляторы экспонент

Ментальная математика — БУДЬТЕ ИЛИ B2: КВАДРАТ ДВУХЗНАЧНЫХ ЧИСЕЛ

Я рад представить новую функцию CompAct. Начиная с этого выпуска, мы будем включать отрывки из книги «Секреты ментальной математики: руководство по математическим вычислениям и удивительным математическим трюкам» Артура Бенджамина и Майкла Шермера.Random House, Inc. любезно предоставила нам разрешение воспроизводить отрывки из этой книги каждый квартал в CompAct. Большая часть знаний, которые можно почерпнуть из этой книги, зависит от накопления определенных навыков в предыдущих главах; однако я постараюсь включить отдельные разделы. Приведенный ниже выбор включает упрощенный метод вычисления квадрата двузначного числа на основе некоторой базовой алгебры.

—Пол Рамирес, соредактор

Возведение чисел в квадрат (умножение числа на само) — одно из самых простых, но самых впечатляющих умений в уме.Я до сих пор помню, где был, когда узнал, как это делать. Мне было 13 лет, я ехал в автобусе навестить отца на работе в центре Кливленда. Я часто совершал это путешествие, поэтому мои мысли начали блуждать. Не знаю почему, но я начал думать о числах, которые в сумме дают 20, и мне стало интересно, насколько большим может быть произведение двух таких чисел?

Я начал с середины с 10 × 10 (или 10 ² ), произведение которого равно 100. Затем я умножил 9 × 11 = 99, 8 × 12 = 96, 7 × 13 = 91, 6 × 14. = 84, 5 × 15 = 75, 4 × 16 = 64 и т. Д.Я заметил, что продукты становились все меньше, и их разница от 100 составляла 1, 4, 9, 16, 25, 36,… — или 1 ² , 2 ² , 3 ² , 4 ² , 5 ² , 6 ² ,… (см. Таблицу ниже).

Числа, которые добавляют к 20		Расстояние от 10	Их продукт	Отличия товара от 100
10	10	0	100	0
9	11	1	99	1
8	12	2	96	4
7	13	3	91	9
6	14	4	84	16
5	15	5	75	25
4	16	6	64	36
3	17	7	51	49
2	18	8	36	64
1	19	9	19	81

Этот узор меня поразил.Затем я попробовал числа, которые складываются с 26, и получил аналогичные результаты. Сначала я вычислил 13 ² = 169, затем вычислил 12 × 14 = 168, 11 × 15 = 165, 10 × 16 = 160, 9 × 17 = 153 и так далее. Как и раньше, расстояния, на которые эти продукты находились от 169, составляли 1 ² , 2 ² , 3 ² , 4 ² и так далее (см. Таблицу ниже).

На самом деле существует простое алгебраическое объяснение этого явления (см. Почему эти уловки работают). В то время я недостаточно хорошо знал свою алгебру, чтобы доказать, что эта закономерность всегда будет иметь место, но я экспериментировал с достаточным количеством примеров, чтобы убедиться в этом.

Затем я понял, что этот шаблон может помочь мне легче возводить числа в квадрат. Предположим, я хочу возвести в квадрат число 13. Вместо умножения 13 × 13,

Числа, которые добавляют к 26		Расстояние от 13	Их продукт	Отличия товара от 169
13	13	0	169	0
12	14	1	168	1
11	15	2	165	4
10	16	3	160	9
9	17	4	153	16
8	18	5	144	25

Почему бы не получить приблизительный ответ, используя два числа, которые легче умножить, но которые также можно добавить к 26? Я выбрал 10 × 16 = 160.Чтобы получить окончательный ответ, я просто добавил 32 = 9 (поскольку 10 и 16 — это каждые 3 от 13). Таким образом, 132 = 160 + 9 = 169. Отлично!

Схема этого метода выглядит следующим образом:

Теперь посмотрим, как это работает для другого квадрата:

Чтобы возвести в квадрат 41, вычтите 1, чтобы получить 40, и добавьте 1, чтобы получить 42. Затем умножьте 40 × 42. Не паникуйте! Это просто замаскированная задача умножения 2 на 1 (в частности, 4 × 42). Поскольку 4 × 42 = 168, 40 × 42 = 1680. Почти готово! Все, что вам нужно сложить, — это квадрат 1 (число, на которое вы пошли вверх и вниз от 41), что даст вам 1680 + 1 = 1681.

Можно ли возвести в квадрат двузначное число так просто? Да, с помощью этого метода и небольшой практики это возможно. И это работает независимо от того, округляете ли вы сначала в меньшую или большую сторону. Например, давайте рассмотрим 77 ² , вычислив его как округлением в большую, так и в меньшую сторону:

или

В этом случае преимущество округления в большую сторону состоит в том, что вы практически закончили, как только вы завершили задачу умножения, потому что легко добавить 9 к числу, оканчивающемуся на 0!

На самом деле, для всех двузначных квадратов я всегда округляю в большую или меньшую сторону до ближайшего кратного 10.Итак, если число, которое нужно возвести в квадрат, оканчивается на 6, 7, 8 или 9, округляйте в большую сторону, а если число, которое нужно возвести в квадрат, заканчивается на 1, 2, 3 или 4, округляйте в меньшую сторону. (Если число заканчивается на 5, вы делаете и то, и другое!) С помощью этой стратегии вы добавите только числа 1, 4, 9, 16 или 25 к вашему первому вычислению.

Давайте попробуем другую задачу. Вычислите в уме 56 ² , прежде чем смотреть, как мы это сделали, ниже:

Возвести в квадрат числа, оканчивающиеся на 5, еще проще. Поскольку вы всегда будете округлять в большую и меньшую сторону на 5, оба числа для умножения будут кратны 10.Следовательно, умножение и сложение особенно просты. Мы отработали 85 ² и 35 ² , ниже:

Как вы видели в главе 0, когда вы возводите в квадрат число, оканчивающееся на 5, округление вверх и вниз позволяет сразу же выпалить первую часть ответа, а затем закончить ее числом 25. Например, если вы хотите вычислить 75 ² , округляя до 80 и до 70, вы получите «Пятьдесят шестьсот… двадцать пять!»

Для чисел, оканчивающихся на 5, у вас не должно возникнуть проблем с тем, чтобы победить кого-нибудь с помощью калькулятора, а немного потренировавшись с другими квадратами, скоро вы сможете обыграть калькулятор с любым двузначным квадратным числом.Не стоит опасаться даже большого числа людей. Вы можете попросить кого-нибудь дать вам действительно большое двузначное число, что-то около 90-х, и это будет звучать так, как если бы вы выбрали для вычисления невозможную задачу. Но на самом деле это еще проще, потому что они позволяют округлить до 100.

Допустим, ваша аудитория дает вам 96 ² . Попробуйте сами, а потом проверьте, как мы это сделали.

Разве не все было просто? Вы должны были округлить в большую сторону от 4 до 100 и от 4 до 92, а затем умножить 100 × 92, чтобы получить 9200.На этом этапе вы можете сказать вслух: «Девяносто двести», а затем закончить словами «Шестнадцать» и наслаждаться аплодисментами!

Почему эти уловки работают

Этот раздел предназначен для учителей, студентов, любителей математики и всех, кому интересно, почему наши методы работают. Кому-то теория может показаться такой же интересной, как и ее применение. К счастью, вам не нужно понимать, почему работают наши методы, чтобы понимать, как их применять. У всех фокусов есть рациональное объяснение, и математические фокусы ничем не отличаются.Именно здесь математик раскрывает свои самые сокровенные секреты!

В этой главе, посвященной задачам умножения, закон распределения — это то, что позволяет нам разбивать задачи на их составные части. Распределительный закон гласит, что для любых чисел a, b и c:

(b + c) × a = (b × a) + (c × a)

То есть внешний термин a распределяется или применяется отдельно к каждому из внутренних терминов b и c. Например, в нашей первой мысленной задаче умножения 42 × 7 мы пришли к ответу, рассматривая 42 как 40 + 2, а затем распределив 7 следующим образом:

42 × 7 = (40 + 2) × 7 = (40 × 7) + (2 × 7) = 280 + 14 = 294

Вы можете задаться вопросом, почему вообще действует закон о распределении.Чтобы понять это интуитивно, представьте, что у вас есть 7 сумок, каждая из которых содержит 42 монеты, 40 из которых золотые и 2 серебряные. Сколько всего у вас монет? Есть два способа прийти к ответу. Во-первых, по самому определению умножения есть монеты 42 × 7. С другой стороны, есть золотые монеты 40 × 7 и серебряные монеты 2 × 7. Следовательно, всего у нас есть (40 × 7) + (2 × 7) монет. Ответив на наш вопрос двумя способами, мы получаем 42 × 7 = (40 × 7) + (2 × 7). Обратите внимание, что числа 7, 40 и 2 можно заменить любыми числами (a, b или c), и применима та же логика.Вот почему действует закон распределения!

Используя аналогичные рассуждения для золотых, серебряных и медных монет, мы можем получить:

(b + c + d) × a = (b × a) + (c × a) + (d × a)

Следовательно, чтобы решить задачу 326 × 7, мы разбиваем 326 на 300 + 20 + 6, а затем распределяем 7 следующим образом: 326 × 7 = (300 + 20 + 6) × 7 = (300 × 7) + (20 × 7) + (6 × 7), которые мы затем складываем, чтобы получить наш ответ. Что касается возведения в квадрат, следующая алгебра оправдывает мой метод. Для любых чисел A и d

A2 = (A + d) × (A — d) + d ²

Здесь A — возведенное в квадрат число; d может быть любым числом, но я выбрал расстояние от A до ближайшего числа, кратного 10.