Часть элементов некоторого множества – Кроссворд Классификация объектов (6 класс)
Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
Определение. Наибольшим элементом непустого
подмножества  линейно упорядоченного множества
линейно упорядоченного множества называется элемент
называется элемент такой, что.
такой, что.
Определение. Наименьшим элементом непустого
подмножества  линейно упорядоченного множества
линейно упорядоченного множества называется элемент
называется элемент такой, что.
такой, что.
Теорема 7. Любое непустое
подмножество 
Доказательство.
Возможны случаи:
— наименьший элемент подмножества;
. Рассмотрим множество .
 ,
т.к.
,
т.к.
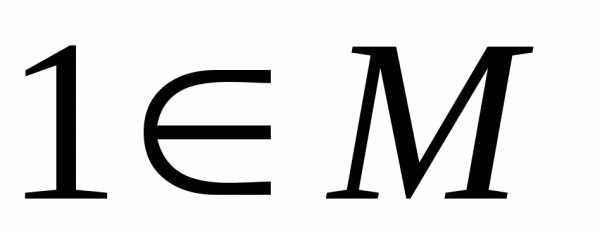 .
.
Такой элемент
.
.
Такой элемент обязательно найдется, т.к. в противном
случае
обязательно найдется, т.к. в противном
случае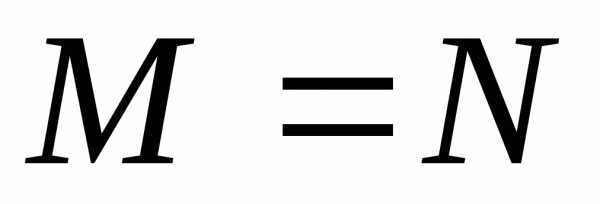
 наименьший в
наименьший в ..
Предположим, что.
Тогда
..
Предположим, что.
Тогда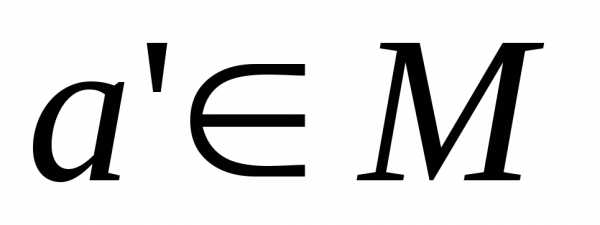 .
Последнее противоречит условию
.
Последнее противоречит условию 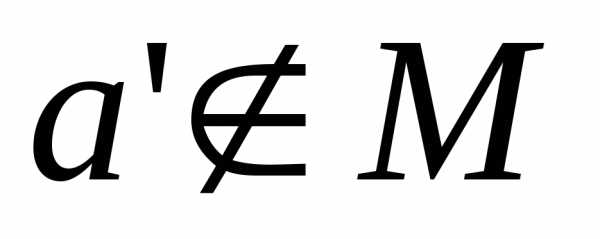 ,
следовательно, предположение неверно.
Тогдатакой, что.
Таким образом,
,
следовательно, предположение неверно.
Тогдатакой, что.
Таким образом, 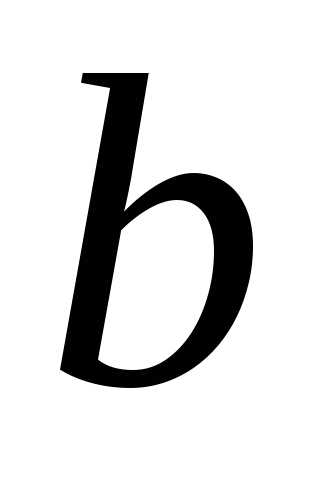 — наименьший в
— наименьший в .
.что и требовалось доказать.
Теорема 8. Любое непустое
ограниченное сверху подмножество  множества натуральных чисел имеет
наибольший элемент.
множества натуральных чисел имеет
наибольший элемент.
Доказательство.
Пусть  ограничено сверху элементом
ограничено сверху элементом ,
т.е..
Рассмотрим множество.
,
т.е..
Рассмотрим множество.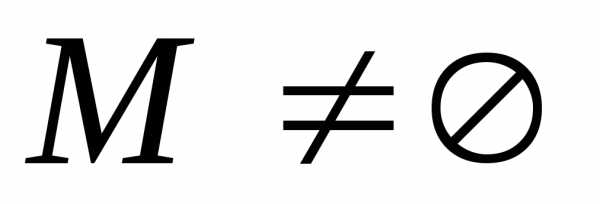 ,
т.к.
,
т.к.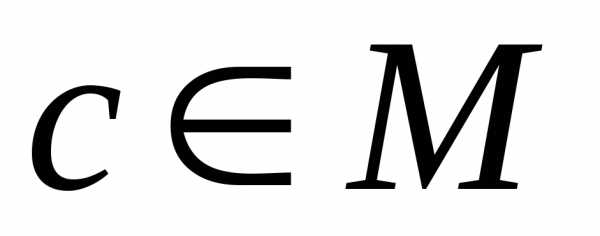 .
Тогда, по теореме 3,
.
Тогда, по теореме 3,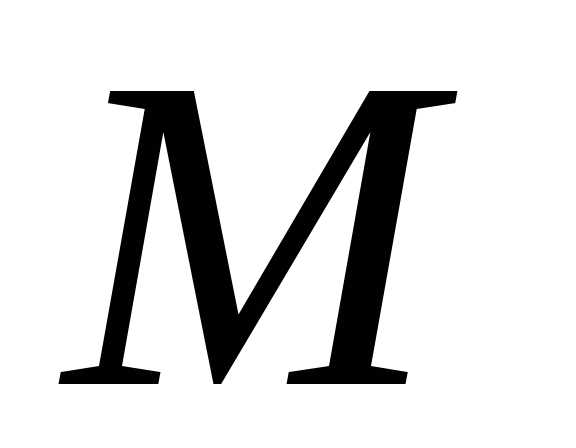
 ,
причем
,
причем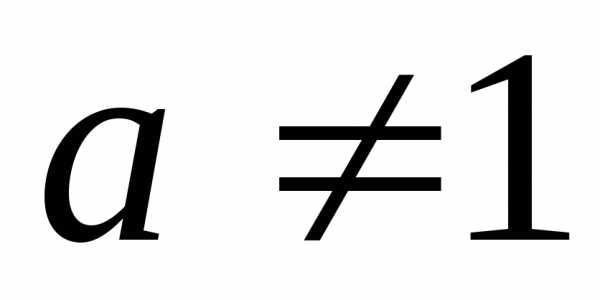 ,
т. к. в противном случае
,
т. к. в противном случае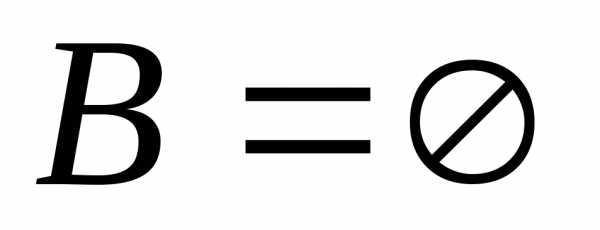 .
По следствию 4) из аксиом Пеано,.
Предположим, что,
следовательно,
.
По следствию 4) из аксиом Пеано,.
Предположим, что,
следовательно,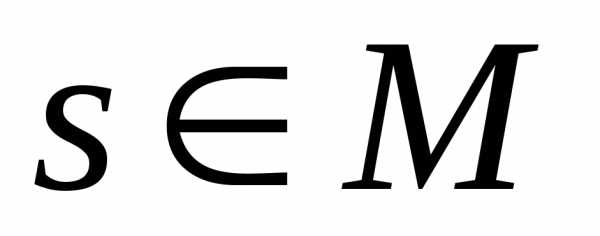 .
Последнее противоречит тому, что
.
Последнее противоречит тому, что 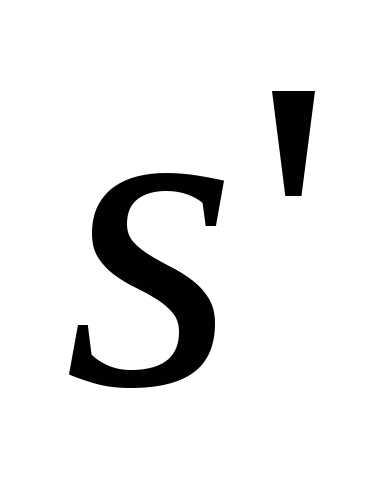 — наименьший в
— наименьший в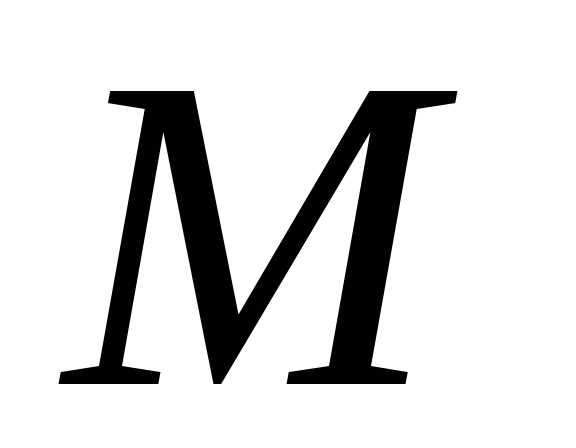
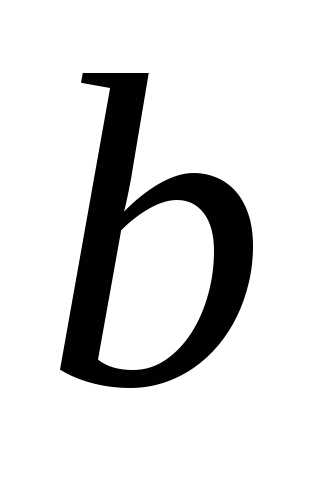 — наибольший в
— наибольший в .
.что и требовалось доказать.
Іі и ііі формы метода математической индукции для натуральных чисел.
Теорема 9 (ІІ
форма): Если утверждение 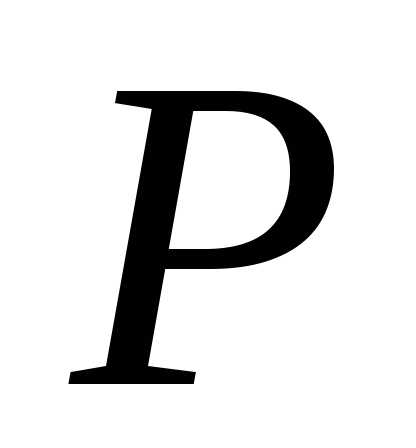 о натуральных числах верно для 1 и для
произвольного натурального числа
о натуральных числах верно для 1 и для
произвольного натурального числа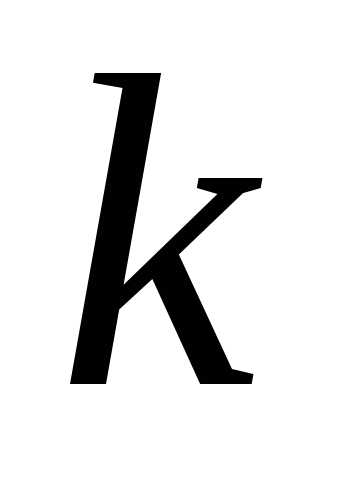 ,
большего 1, из верности утверждения
,
большего 1, из верности утверждения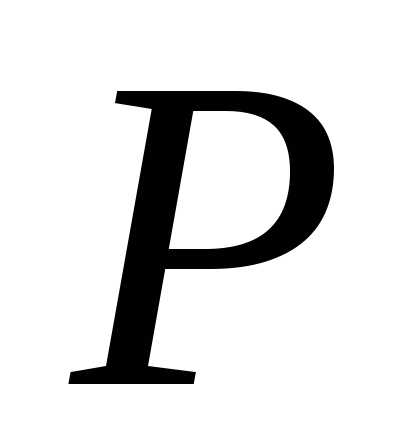
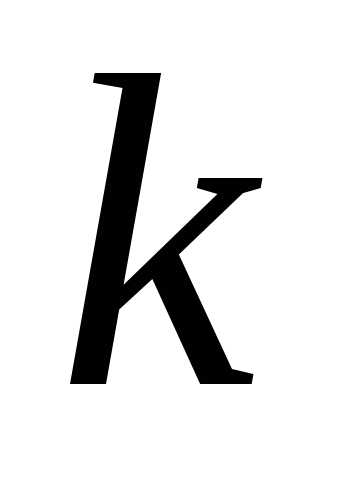 ,
следует верность утверждения для числа
,
следует верность утверждения для числа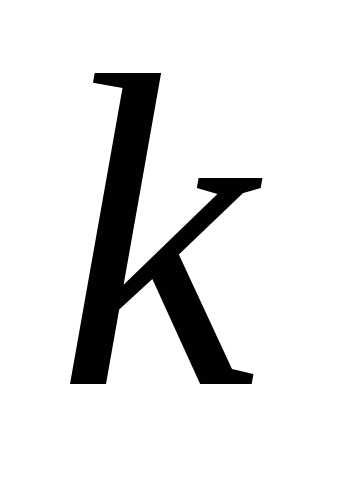 ,
то утверждение верно для каждого
натурального числа.
,
то утверждение верно для каждого
натурального числа.Доказательство.
Предположим, что
.
Рассмотрим множество.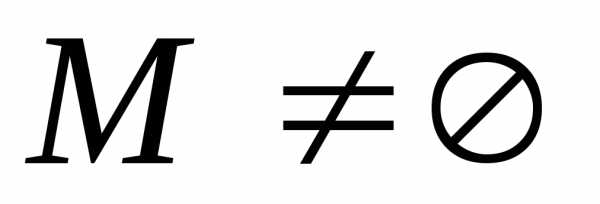 ,
т.к.
,
т.к.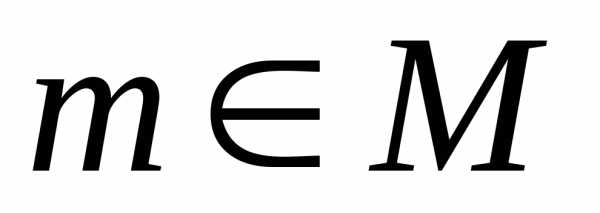 .
Тогда, по теореме 3,
.
Тогда, по теореме 3,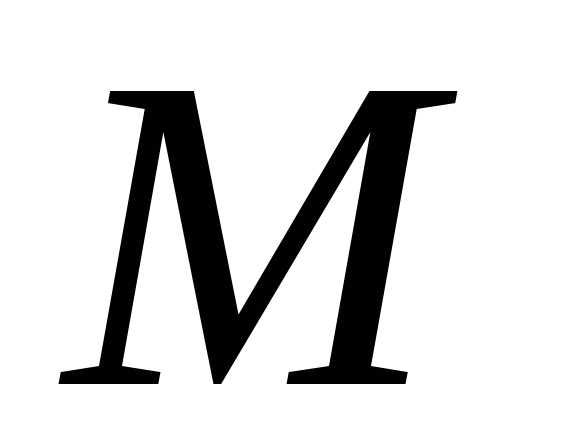 имеет наименьший элемент
имеет наименьший элемент
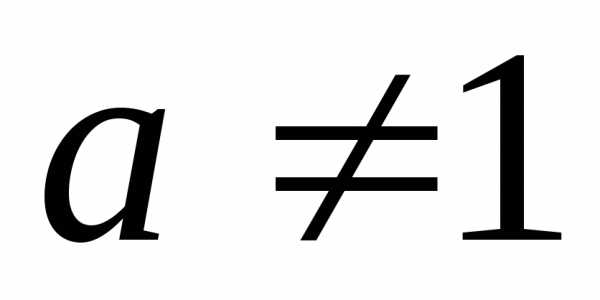 ,
,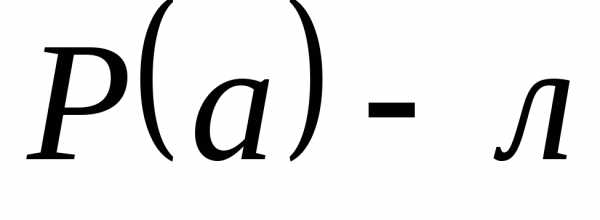 .
По следствию 4) из аксиом Пеано,,
причем.
.
По следствию 4) из аксиом Пеано,,
причем.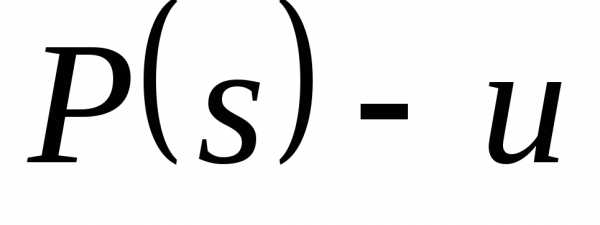 ,
т.к. в противном случае,
,
т.к. в противном случае, не будет наименьшим в
не будет наименьшим в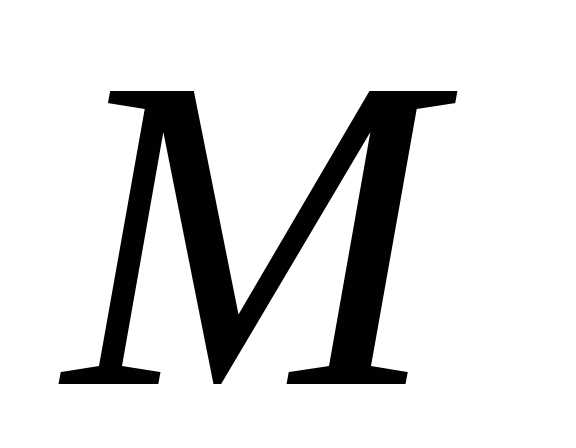 .
Тогда, согласно индуктивному предположению,
.
Тогда, согласно индуктивному предположению,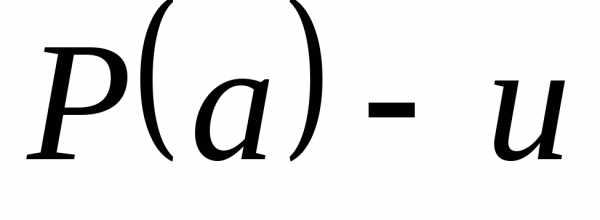 ,
но это противоречит условию
,
но это противоречит условию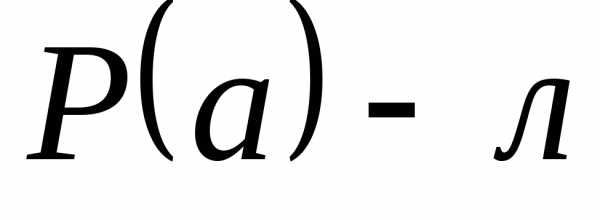
что и требовалось доказать.
Теорема 10 (ІІІ
форма): Если утверждение 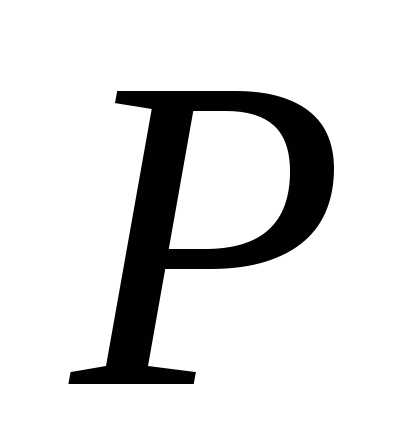 о натуральных числах верно для всех
чисел некоторого непустого неограниченного
сверху подмножества множества натуральных
чисел и из верности утверждения
о натуральных числах верно для всех
чисел некоторого непустого неограниченного
сверху подмножества множества натуральных
чисел и из верности утверждения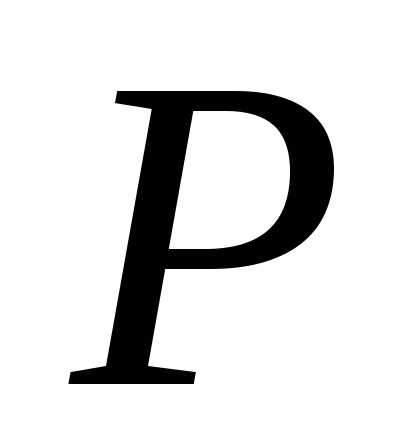 для произвольного натурального числа
для произвольного натурального числа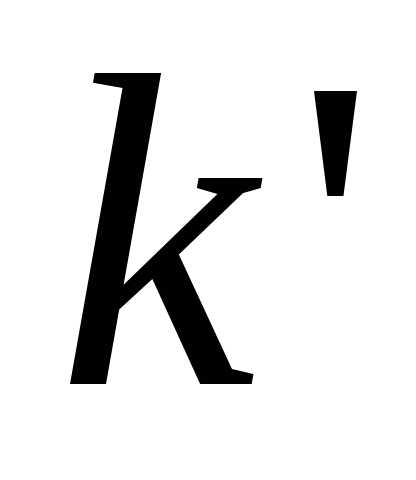
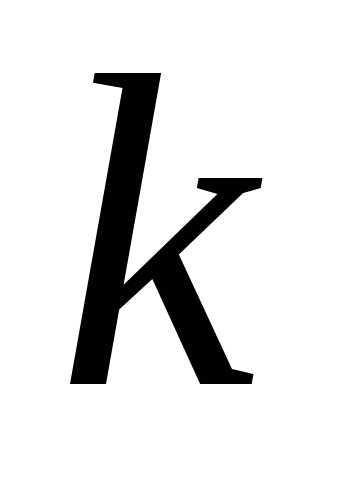 ,
то утверждение верно для каждого
натурального числа.
,
то утверждение верно для каждого
натурального числа.Доказательство.
Предположим, что
.
Рассмотрим множество.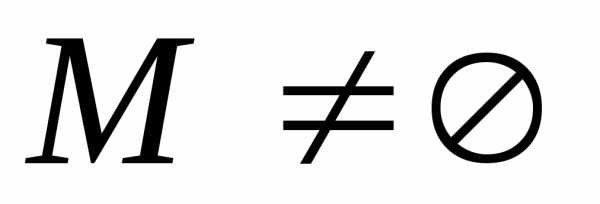 ,
т.к.
,
т.к.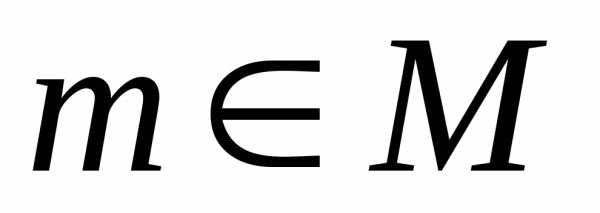 .
Также
.
Также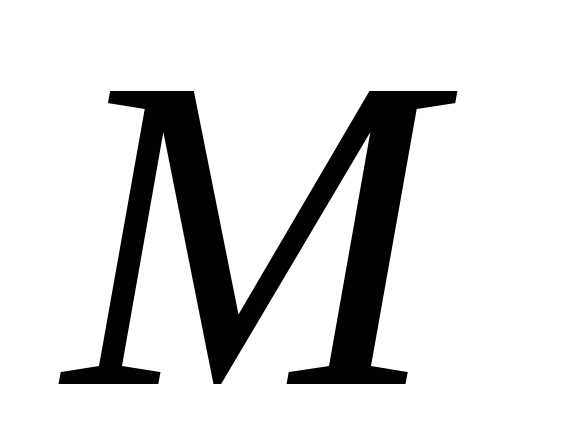 ограничено сверху любым элементом из
ограничено сверху любым элементом из .
Тогда, по теореме 4,
.
Тогда, по теореме 4,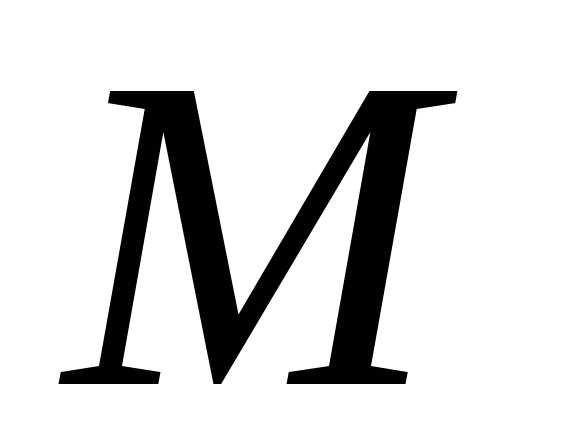
 ,
причем
,
причем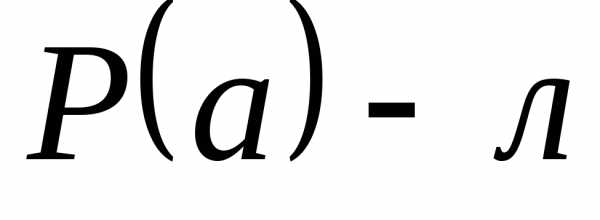 .
Рассмотрим элемент
.
Рассмотрим элемент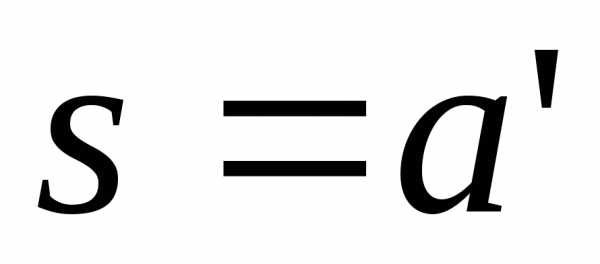 .
.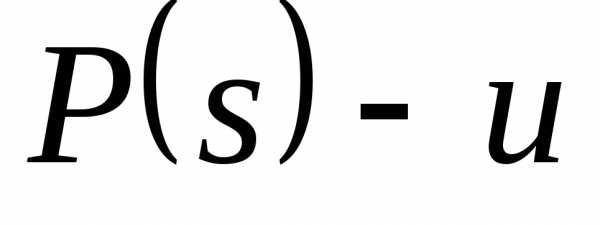 ,
т.к. в противном случае,
,
т.к. в противном случае, не будет наибольшим в
не будет наибольшим в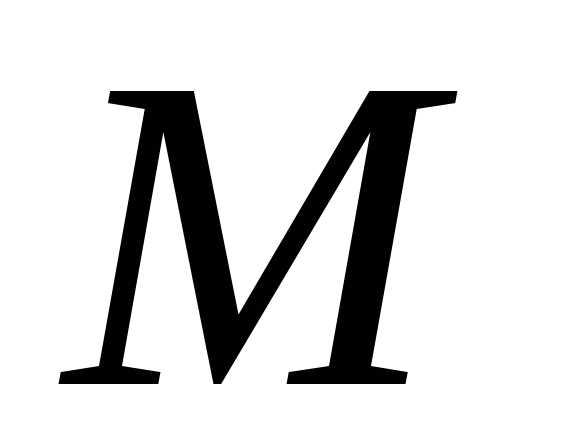 .
Согласно индуктивному предположению,
.
Согласно индуктивному предположению,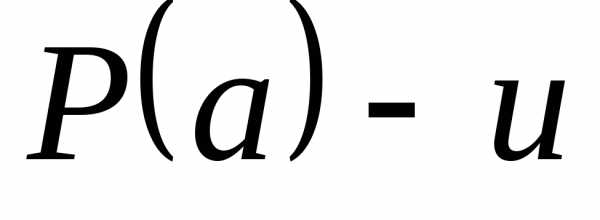
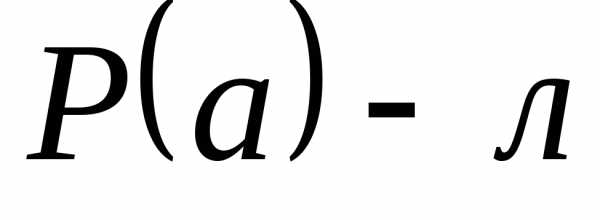 .
Таким образом, предположение неверно,
и.
.
Таким образом, предположение неверно,
и.что и требовалось доказать.
Архимедовская расположенность полукольца натуральных чисел.
Теорема 11. Полукольцо натуральных чисел является архимедовски расположенным, т.е. выполняются следующее условие (аксиома Архимеда): для любых натуральных чисел a,b a<nb для некоторого натурального n.
Доказательство.
.
что и требовалось доказать.
Теорема 12.
Доказательство.
Для доказательства
этого утверждения достаточно показать,
что натуральные числа 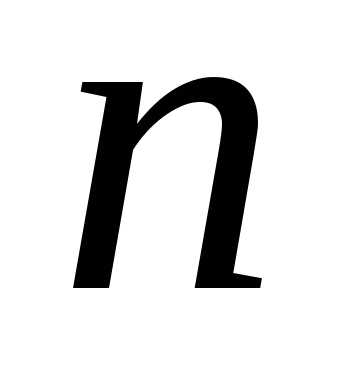 и
и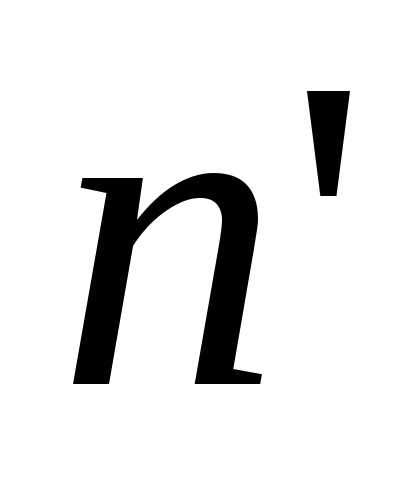 являются соседними. Предположим обратное:
пусть
являются соседними. Предположим обратное:
пусть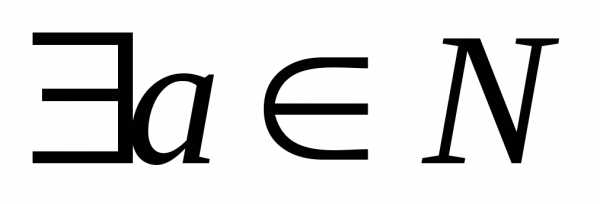 такое, что.
Тогда.
Последнее противоречит условию
такое, что.
Тогда.
Последнее противоречит условию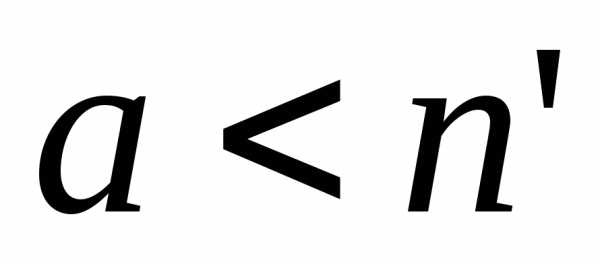 .
Следовательно, предположение неверно.
.
Следовательно, предположение неверно.
что и требовалось доказать.
studfiles.net
Множества,их элементы,поджмножества
Определение 1
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Предметы или объекты, образующие данное множество, называются его элементами. Например, число $6$ будет являться элементом множества натуральных чисел, а число $0,9$ не будет являться элементом множества натуральных чисел.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Определение 2
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Определение 3
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
В математике часть множества называют — подмножество. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества.
Обозначение множеств, подмножеств и их элементов
Чаще всего множества обозначаются латинскими буквами- $A, B, C , D, X, Y, Z, W$ и Т.Д.
Элементы множеств обозначаются строчными буквами $a,b,c,d,x,y,z$ и Т.Д.
Записать принадлежность некоторого элемента к некоторому множеству, например то, что некоторой элемент $a$ будет входить в множество $A$ математически можно так: $a\in A$.Прочитать данную запись можно так: a принадлежит множеству $A$.
Если же некоторый элемент, например, $b$ не принадлежит множеству $B$, то это записывается так: $b\notin B$.Читают эту запись так: $b$ не принадлежит множеству $B$
Например, если обозначить множество целых чисел за $A$, что тогда можно записать: $3\in A$, $7,5\notin B$
Пустое множество в математике обозначают так: $ᴓ$
Для обозначения того, что множество $B$ является подмножеством множества $A$, используют обозначение: Знак $\subset $ обозначает включение одного множества в другое множество.
Пример 1
Определить какие элементы из перечисленных $12,38,54,79,934$ будут входить в множество $A$- чисел кратных $3$.
Решение: По условию множество $A$ содержит в себе элементы, каждый из которых должен быть кратным, т.е. делится без остатка на $3.$ Значит для того чтобы определить будут ли заданные числа являться элементами множества $A$ нам надо проверить какие из них будут делится на $3$ без остатка, какие нет.
Вспомним признак делимости на $3$: Если сумма цифр, входящих в состав числа делится на $3$, то число делится на $3$ без остатка.
$12$ делится на $3$, т.к. сумма цифр числа $12$ равна $3$
число $38$ на $3$ без остатка делится не будет, т.к. сумма цифр $3+8=11$ не делится на $3$ без остатка
аналогично т.к. суммы цифр числа $54$ равна $9$ доказываем, что на $3$ оно делится, в число $74$ на $3$ делится не будет, т.к. сумма цифр равна $11.$
Найдем сумму цифр числа $934: 9+3+4=16$, число $16$ не кратно $3$ ,значит и число $934$ на $3$ без остатка делится не будет
Теперь сделаем вывод, какие числа будут являться элементами множества $A$:
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ {\rm :\ }54\in A.\]Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
Конечные множества с небольшим количеством элементов обычно записывают в фигурных скобках $\left\{a,b,c\right\}$
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Второй способ задания множеств применим как для конечных. так и для бесконечных множеств. Он заключается в том, что указывается свойство, которым обладает каждый элемент данного множества — множество задают описанием, т.е. указав его характеристическое свойство, т. е свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.
Пример 2
Например, с помощью описания можно задать такие множество натуральных чисел от $1$ до $9$ включительно. Характеристическим свойством, т. е. свойством, которым обладают все элементы этого множества для данных элементов будет являться то, что все они являются натуральными числами и каждое из них не меньше $1$ и не больше $9$. Перечислением указанное множество можно задать следующим образом:
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Пример 3
Например, рассмотрим множества
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
$B=\left\{9,8,7,6,5,4,3,2,1\right\}$
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Пример 4
Например, рассмотрим два множества:
$A=\left\{1\ ,2,3,4,5\right\}$
$B=\left\{9,7,5,3,\right\}$
Общей частью этих множеств будет множество $C=\left\{3,5,\right\}$
Математически это можно обозначить так: $А\cap B=\left\{3,5\right\}$
Пересечением множеств $A$ и $B$ называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество $A$ и в множество $B$.
Объединение множеств
Из двух множеств $A$ и $B$ можно образовать новое множество, объединяя все элементы множества $A$ и все элементы множества $B$
Математически это можно обозначить так:$\ А\ \cup B$
Объединением множеств $A$ и $B$ называется новое множество$\ А\ \cup B$, состоящее из тех и только из тех элементов, которые входят хотя бы в одно из множеств $A$ или $B$.
Разность множеств
Разностью двух множеств $A$ и $B$ называют такое множество, в которое входят все элементы из множества $A$, не принадлежащие множеству $B$.
spravochnick.ru
Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 5
.
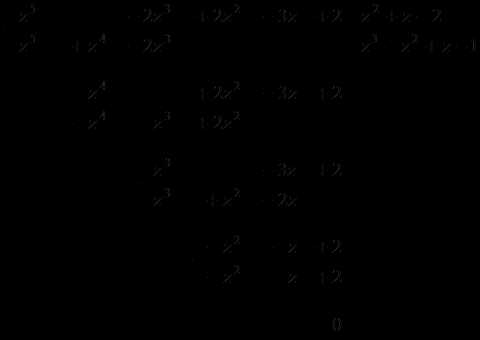
Таким образом, .
Делителями свободного члена являются . Проверка показывает, что является корнем уравнения ( не является).
Окончательно получаем:
.
Таким образом, исходное алгебраическое уравнение имеет один двукратный корень и три простых корня .
6. Элементы комбинаторики
Определение 1: Упорядоченным подмножеством множества называют некоторую часть элементов из множества , расположенных в определенном порядке. Упорядоченные подмножества с одинаковым составом элементов, но различающиеся их порядком следования, считают различными (в отличие от обычных подмножеств).
Пример 1: Упорядоченными подмножествами множества являются: — пустое множество, — множества из одного элемента, — упорядоченные множества из двух элементов, — упорядоченные множества из трех элементов.
Определение 2: Пусть имеется множество , состоящее из элементов. Размещением из элементов по элементов называют любое упорядоченное подмножество множества , состоящее из элементов.
Определение 3: Числом размещений из по называют число различных упорядоченных — элементных подмножеств множества , состоящего из элементов.
(24)
Действительно, в качестве первого элемента можно взять любой из элементов множества , в качестве второго элемента – любой из оставшихся элементов, и т.д., наконец, в качестве последнего (- го) элемента – один из оставшихся элементов.
Пример 2: Найти число размещений .
Перебрав все упорядоченные двухэлементные подмножества множества , состоящего из трех элементов (пример 1), находим: . С другой стороны,
Определение 4: Перестановкой называют размещение из элементов по ().
Число различных перестановок определяется формулой:
(25)
Определение 5: Четностью (знаком) перестановки называют число где — число парных перестановок (только два некоторых элемента меняются местами), которые переводят тождественную перестановку в перестановку (или наоборот). После каждой парной перестановки четность перестановки меняется.
Пример 3: Определить четность перестановки .
Укажем последовательность парных перестановок, которая переводит исходную перестановку в тождественную: . Число парных перестановок (число стрелок) , следовательно, перестановка нечетная ().
Определение 6: Сочетанием из элементов по элементов называют любое обычное (неупорядоченное) — элементное подмножество множества , состоящего из элементов.
Определение 7: Числом сочетаний из по называют число различных (неупорядоченных) — элементных подмножеств множества , состоящего из элементов.
(26)
Действительно, поскольку каждому сочетанию из элементов соответствует различных перестановок этих элементов, мы имеем .
Кроме того, .
Пример 4: Найти число сочетаний .
Перебрав все двухэлементные подмножества множества , состоящего из трех элементов (пример 1: ), находим: . С другой стороны,
Используя понятие числа сочетаний можно легко получить формулу разложения для любой натуральной степени бинома (двучлена) . Действительно, при перемножении
слагаемое может быть получено следующими способами: в произвольных скобках из возможных мы выбираем в качестве множителя , в остальных – мы выбираем . Таким образом, число раз, которое встречается слагаемое в разложении бинома равно числу способов выбора некоторых скобок из возможных, то есть . В итоге, формула разложения для натуральной степени бинома
(формула Ньютона) имеет вид:
(27)
Коэффициенты разложения носят название также биномиальных коэффициентов.
Частными случаями формулы (27) являются хорошо известные формулы:
Пример 5: Получить формулу разложения для .
7. Понятие функции
Определение 1: Функцией называют правило, по которому каждому элементу некоторого числового множества ставится в соответствие один (однозначная функция) или несколько (многозначная функция) элементов числового множества .
vunivere.ru
1. Метод математической индукции
В математике при доказательстве утверждений часто используется метод математической индукции. Индукция бывает полной и неполной.
Неполная математическая индукция возможно только в том случае, если осуществим полный перебор. Иначе применяют принцип полной математической индукции.
Суть этого принципа состоит в следующем: если некоторое предложение A(n), где n – натуральное число, истинно для n = 1 (или при другом значении n, при котором имеет смысл это утверждение) и из предположения его справедливости для некоторого натурального значения n = k следует справедливость утверждения для следующего натурального значения n = k + 1, то утверждение справедливо для всех натуральных значений n.
Не знаю, писать ли пример?
2. Понятие множества, подмножества, пустого множества. Диаграммы Венна. Число подмножеств конечного множества.
Под множеством понимается некоторая, вполне определенная совокупность объектов или элементов. Множество— любое собрание определенных и различных между собой объектов, мыслимое как единое целое.
Множество А есть подмножество множества, если каждый элемент А есть элемент В\ т.е. если (xпринадлежит А), то (х принадлежит В). В частности, каждое множество есть подмножество самого себя. Таким образом, A не принадлежит В, если существует элемент А, не принадлежащий В.
Пустое множество, обозначаемое перечеркнутый 0 или {}, есть множество, которое не содержит элементов. Универсальное множество U есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.
Диаграмма Венна.
Диаграммы Венна —инструмент, позволяющий изображать множества и иллюстрировать операции над ними. Множества в диаграммах Венна изображаются внутренними частями кругов, их пересечениями, объединениями и
т.д. Прямоугольник изображает универсальное множество. На рис. 2.1 приведена диаграмма Венна для множества А которое изображено внутренней частью круга. Внешняя часть круга, находящаяся внутри прямоугольника, изображает А1.
На рис. 2.2 приведена диаграмма Венна для двух множеств, скажем, A и В каждое множество изображено кругом, и круги пересекаются.
Как показывает диаграмма, внутренняя часть прямоугольника разделена на четыре части. Множеству А и В соответствует закрашенная часть диаграммы на рис. 2.3. Закрашенная область на рис. 2.4 представляет А или В.
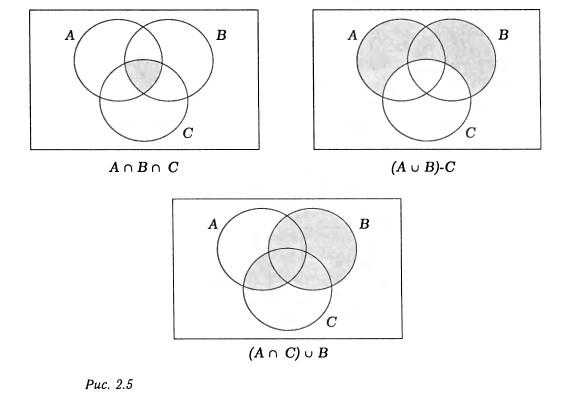
Закрашенные области на рис. 2.5 изображают множества АиВ, (АилиВилиС),
(АиВиС), (АилиВ) —С и (АиС)илиВ. (тут символы были заменены на буквенное обозначение) Множество А-В представлено закрашенной областью на рис. 2.6. Диаграмма Венна для трех множеств, например, А, В и С, показана на рис. 2.7. Эта диаграмма состоит из восьми частей.
Используя диаграммы Венна, можно показать
равенство двух множеств. 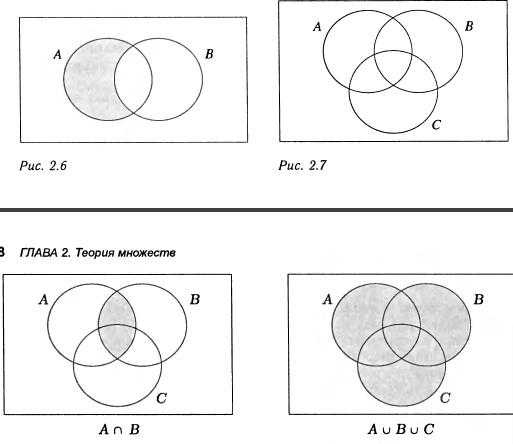
Число подмножеств конечного множества  _____________________________________________________________________________________
_____________________________________________________________________________________
3. Операции объединения, пересечения множеств, определения и свойства коммутативности и ассоциативности. Взаимная дистрибутивность операций пересечения и объединения.
Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. Объединение множеств А и В обозначается Аи В. Сформулированное выше определение можно записать так: А и В = {х : х принадлежит А или х принадлежит В}.
_____________
Если для любых элементов aиbмножестваMсправедливо равенствоab=ba, то операцию называют коммутативной.
Свойство коммутативности: A&B=B&A
A U B=B UA
______________
Если для любых элементов a,b,cмножестваMсправедливо равенствоa(bc)=(ab)c, то операцию называют ассоциативной.
Свойство ассоциативности: A& (B&C) = (A&B) &C
A U (B U C) = (A U B) U C
_______________
Взаимная дистрибутивность операций пересечения и объединения.
Теорема(закон дистрибутивности)

studfiles.net

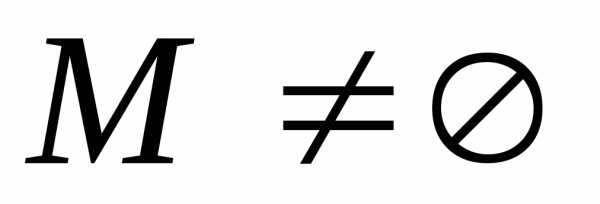 ,
т.к.
,
т.к.