Арифметическую прогрессию: Арифметическая прогрессия – Определение, Примеры, Формулы 9 класс
Арифметическая прогрессия – Определение, Примеры, Формулы 9 класс
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
- Словесно — когда правило последовательности объясняется словами:
«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23…»
- Аналитически — когда указана формула ее n-го члена: yn = f(n).
Последовательность yn = C называют постоянной или стационарной.
- Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

- Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4…
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
- Последовательность {yn} называют возрастающей, если каждый ее член кроме первого больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < …
- Последовательность {yn} называют убывающей, если каждый ее член кроме первого меньше предыдущего:
Возрастающие и убывающие последовательности называют монотонными последовательностями.
- Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: yn = yn+T.
 Число T — длина периода.
Число T — длина периода.
Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1,
N-ый член последовательности можно задать формулой. Например:
Например:
- Формула an = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
- Формула an = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6…
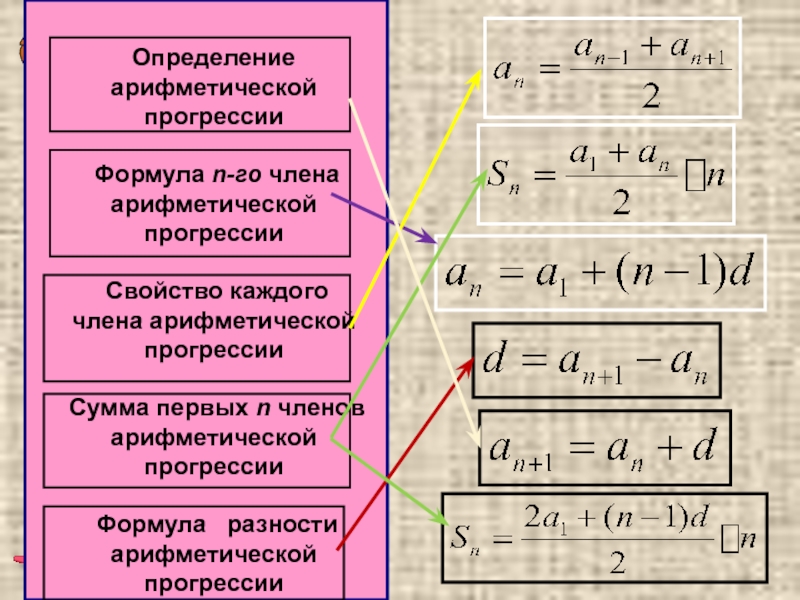
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.
| Арифметическая прогрессия — это числовая последовательность a1, a2,…, an,… для которой для каждого натурального n выполняется равенство: an+1= an + d, где d — это разность арифметической прогрессии. |
Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.
Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:
Если известны первый член a1 и n-ый член прогрессии, разность можно найти так:
Арифметическая прогрессия бывает трех видов:
- Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.
Пример: последовательность чисел 11, 14, 17, 20, 23… — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.
- Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.
Пример: последовательность чисел 50, 48, 46, 44, 42… — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.
- Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.
Пример: последовательность чисел 23, 23, 23, 23, 23… — это стационарная арифметическая прогрессия, так как ее разность d = 0.

Экзамены — это почти всегда стресс. Подготовка к ЕГЭ по математике онлайн в школе Skysmart поможет снять волнение перед экзаменом и придаст уверенности в своих знаниях.
Свойство арифметической прогрессии
Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.
Формула n-го члена арифметической прогрессии
Из определения арифметической прогрессии следует, что равенство истинно:
Поэтому:
и т.д.
Значит,
Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.
Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.
Формулу an = a1 + d * (n — 1) называют формулой n-го члена арифметической прогрессии.
Формулы арифметической прогрессии
В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:
- Рекуррентной формулой:
- Формулой n-го члена: an = a1+ d · (n — 1).
- Формулой вида an = kn + b, где k и b — числа, n — число членов последовательности.
Сумма первых n членов арифметической прогрессии (аn) обозначается Sn:
Формулы нахождения суммы n членов арифметической прогрессии:
Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:
Рассмотрим пример арифметической прогрессии.
Дано: арифметическая прогрессия (an), где a1 = 0 и d = 2.
Найти: первые пять членов прогрессии и десятый член прогрессии.
Решение арифметической прогрессии:
- Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:
a2 = a1 + d = 0 + 2 = 2;
a3 = a2 + d = 2 + 2 = 4;
a4 = a3 + d = 4 + 2 = 6;
a5 = a4 + d = 6 + 2 = 8.

- Используем общую формулу an = a1 + d * (n — 1).
По условиям задачи n = 10, подставляем в формулу:
a10 = a1 + 2 * (10 — 1) = 0 + 2⋅9 = 18.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность (bn), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.
Если последовательность (bn) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:
| bn+1 = bn * q, где q — знаменатель геометрической прогрессии |
Если в геометрической прогрессии (bn) известен первый член b1 и знаменатель q, то можно найти любой член прогрессии:
- b2 = b1 * q;
- b3 = b2 * q = b1 * q * q = b1 * q²;
- b4 = b1 * q³;
- и т.
 д.
д.
Общий член геометрической прогрессии bn можно вычислить при помощи формулы:
bn = b1 * qn−1, где n — порядковый номер члена прогрессии, b1 — первый член прогрессии, q — знаменатель.
Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.
Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.
Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.
формула n-го члена прогрессии 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 10.
Определение арифметической прогрессии: формула n-го члена прогрессии.
Сегодня познакомимся с последовательностью, которая получается по определенному закону (правилу).
Рассмотрим последовательность натуральных чисел, которые при делении на 5 дают в остатке 2.
Каждый ее член, начиная со второго, получается прибавлением к предыдущему члену числа 5. Эта последовательность является примером арифметической прогрессии.
Итак, арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Другими словами, последовательность an – арифметическая прогрессия, если для любого натурального n выполняется условие an+1=an+d, где d – некоторое число.
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна d, то есть при любом натуральном n верно равенство:an+1-an=d. Это число d называют разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию достаточно указать ее первый член и разность.
a1=1 и d=2, то получим арифметическую прогрессию: 1,3,5,7,…
a1=-5 и d=3, то получим арифметическую прогрессию: -5,-2,1,4,7,…
a1=-3 и d=-2, то получим арифметическую прогрессию: -3,-5,-7,…
a1=4 и d=0, то получим арифметическую прогрессию: 4,4,4,4,…
Итак, зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т. д. Но если надо будет найти сотый, или двухсотый члены, то этот способ не очень удобен.
д. Но если надо будет найти сотый, или двухсотый члены, то этот способ не очень удобен.
Давай попробуем вывести формулу для нахождения любого члена арифметической прогрессии. Итак, по определению арифметической прогрессии:
a2=a1+d
a3=a2+d=a1+d+d=a1+2d
a4=a3+d=a1+2d+d=a1+3d
a5=a4+d=a1+3d+d=a1+4d
Что же мы видим? Что любой член арифметической прогрессии можно найти по формуле: an=a1+dn-1 – это и есть формула n — го члена арифметической прогрессии.
Рассмотрим примеры.
1) Последовательность an – арифметическая прогрессия, в которой a1=2,3 и d=0,36. Найти 101-й член этой прогрессии.
Воспользуемся формулой: an=a1+dn-1
a101=2,3+0,36100-1=2,3+0,36∙100=2,3+36=38,3
Ответ: 38,3
2) Выясним являются ли числа -31,5 и 16 членами арифметической прогрессии (an): 27, 4; 24,3; 21,2; …
В данной арифметической прогрессии
a1=27,4
d=a2-a1=24,3-27,4=-3,1
Запишем формулу n-го члена арифметической прогрессии:
an=a1+dn-1
an=27,4-3,1n-1, то есть
an=27,4-3,1n+3,1
an=30,5-3,1n
Числа -31,5 и 16 будут членами арифметической прогрессии, если существует такое натуральное число n, при котором значение выражения 30,5 — 3,1n = -31,5 (1)
30,5 — 3,1n = 16 (2)
Решим эти уравнения. Из (1) находим, что n = 20, из (2) n=42131.
Из (1) находим, что n = 20, из (2) n=42131.
А, значит, число -31,5 является двадцатым членом арифметической прогрессии. Число 16 не является членом арифметической прогрессии.
Отсюда понятно, что любую арифметическую прогрессию можно задать формулой an = kn + b, где k и b некоторые числа.
Верно и обратное, если последовательность (an), заданная формулой an = kn + b, где k и b некоторые числа, является арифметической прогрессией.
Рассмотрим еще один пример.
Найти 25-й член и n-й член арифметической прогрессии: -2; -0,5; 1; 2,5; 4;…
Итак, a1 = -2; d = 2,5 — 1 = 1,5.
Воспользуемся формулой n-го члена арифметической прогрессии:
an=a1+dn-1
a25=-2+1,525-1=-2+1,5∙24=34
an=-2+1,5n-1=-2+1,5n-1,5=1,5n-3,5.
Отметим важное свойство арифметической прогрессии.
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то есть своих соседей.
Например, дана арифметическая прогрессия: an: … ; 11; x; 27;…
x=11+272=19
Итак, в арифметической прогрессии
an=an-1+an+12.
Итак, сегодня мы познакомились с арифметической прогрессией, ее свойством, а так же вывели формулу n-го члена арифметической прогрессии. А в следующий раз мы выведем формулу нахождения суммы первых n-членов арифметической прогрессии.
Арифметическая прогрессия — это… Что такое Арифметическая прогрессия?
У этого термина существуют и другие значения, см. Прогрессия.Арифмети́ческая прогре́ссия — числовая последовательность вида
- ,
то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага или разности прогрессии):
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
Арифметическая прогрессия является монотонной последовательностью. При она является возрастающей, а при — убывающей. Если , то последовательность будет стационарной. Эти утверждения следуют из соотношения для членов арифметической прогрессии.
При она является возрастающей, а при — убывающей. Если , то последовательность будет стационарной. Эти утверждения следуют из соотношения для членов арифметической прогрессии.
Свойства
Общий член арифметической прогрессии
Член арифметической прогрессии с номером может быть найден по формуле
- , где — первый член прогрессии, — ее разность.
Доказательство
Характеристическое свойство арифметической прогрессии
Последовательность есть арифметическая прогрессия для ее элементов выполняется условие .
Доказательство
Необходимость:
Поскольку — арифметическая прогрессия, то для выполняются соотношения:
.
Сложив эти равенства и разделив обе части на 2, получим .
Достаточность:
Имеем, что для каждого элемента последовательности, начиная со второго, выполняется . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду . Поскольку соотношения верны при всех , с помощью математической индукции покажем, что .
Поскольку соотношения верны при всех , с помощью математической индукции покажем, что .
База индукции :
— утверждение истинно.
Переход индукции:
Пусть наше утверждение верно при , то есть . Докажем истинность утверждения при :
Но по предположению индукции следует, что . Получаем, что .
Итак, утверждение верно и при . Это значит, что .
Обозначим эти разности через . Итак, , а отсюда имеем для . Поскольку для членов последовательности выполняется соотношение , то это есть арифметическая прогрессия.
Сумма первых членов арифметической прогрессии
Сумма первых членов арифметической прогрессии может быть найдена по формулам
- , где — первый член прогрессии, — член с номером , — количество суммируемых членов.
- , где — первый член прогрессии, — разность прогрессии, — количество суммируемых членов.
Доказательство
Сходимость арифметической прогрессии
Арифметическая прогрессия расходится при и сходится при . Причем
Причем
Доказательство
Записав выражение для общего члена и исследуя предел , получаем искомый результат.
Связь между арифметической и геометрической прогрессиями
Пусть — арифметическая прогрессия с разностью и число . Тогда последовательность вида есть геометрическая прогрессия со знаменателем .
Доказательство
Проверим характеристическое свойство для образованной геометрической прогрессии:
Воспользуемся выражением для общего члена арифметической прогрессии:
Итак, поскольку характеристическое свойство выполняется, то — геометрическая прогрессия. Ее знаменатель можно найти, например, из соотношения .
Арифметические прогрессии высших порядков
Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:
- 0, 1, 4, 9, 16, 25, 36…,
разности которых образуют простую арифметическую прогрессию с разностью 2:
- 1, 3, 5, 7, 9, 11…
Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.
В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.
Примеры
- .
См. также
Ссылки
Арифметическая прогрессия на примерах
Арифметической прогрессией называют последовательность чисел (членов прогрессии )
в которой каждый последующий член отличается от предыдущего на сталое слагаемое, которое еще называют шагом или разницей прогрессии.
Таким образом, задавая шаг прогрессии и ее первый член можно найти любой ее элемент по формуле
1) Каждый член арифметической прогрессии, начиная со второго номера является средним арифметическим от предыдущего и следующего члена прогрессии
Обратное утверждение также верно. Если среднее арифметическое соседних нечетных (четных) членов прогрессии равно члену, который стоит между ними, то данная последовательность чисел является арифметической прогрессией . По этим утверждением очень просто проверить любую последовательность.
Также по свойству арифметической прогрессии, приведенную выше формулу можно обобщить до следующей
В этом легко убедиться, если расписать слагаемые справа от знака равенства
Ее часто применяют на практике для упрощения вычислений в задачах.
2) Сумма n первых членов арифметической прогрессии вычисляется по формуле
Запомните хорошо формулу суммы арифметической прогрессии, она незаменима при вычислениях и довольно часто встречается в простых жизненных ситуациях.
3) Если нужно найти не всю сумму, а часть последовательности начиная с k-го ее члена, то в Вам пригодится следующая формула суммы
4) Практический интерес представляет отыскание суммы n членов арифметической прогрессии начиная с k-го номера . Для этого используйте формулу
На этом теоретический материал заканчивается и переходим к решению распространенных на практике задач.
Пример 1. Найти сороковой член арифметической прогрессии 4;7;…
Решение:
Согласно условию имеем
Определим шаг прогрессии
По известной формуле находим сороковой член прогрессии
Пример2. Арифметическая прогрессия задана третьим и седьмым ее членом . Найти первый член прогрессии и сумму десяти.
Арифметическая прогрессия задана третьим и седьмым ее членом . Найти первый член прогрессии и сумму десяти.
Решение:
Распишем заданные элементы прогрессии по формулам
От второго уравнения вычтем первое, в результате найдем шаг прогрессии
Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии
Вычисляем сумму первых десяти членов прогрессии
Не применяя сложных вычислений ми нашли все искомые величины.
Пример 3. Арифметическую прогрессию задано знаменателем и одним из ее членов . Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых.
Решение:
Запишем формулу сотого элемента прогрессии
и найдем первый
На основе первого находим 50 член прогрессии
Находим сумму части прогрессии
и сумму первых 100
Сумма прогрессии равна 250.
Пример 4.
Найти число членов арифметической прогрессии, если:
а3-а1=8, а2+а4=14, Sn=111.
Решение:
Запишем уравнения через первый член и шаг прогрессии и определим их
Полученные значения подставляем в формулу суммы для определения количества членов в сумме
Выполняем упрощения
и решаем квадратное уравнение
Из найденных двух значений условии задачи подходит только число 8 . Таким образом сумма первых восьми членов прогрессии составляет 111.
Пример 5.
Решить уравнение
1+3+5+…+х=307.
Решение: Данное уравнение является суммой арифметической прогрессии. Выпишем первый ее член и найдем разницу прогрессии
Найденные величины подставим в формулу суммы прогрессии для отыскания числа слагаемых
Как и в предыдущем задании, выполним упрощения и решим квадратное уравнение
Выбираем более логичное из двух значений . Имеем, что сумма 18 членов прогрессии с заданными величинами а1=1, d=2 равна Sn=307.
На этом знакомство с арифметической прогрессией только начинается. В книгах вы найдете много подобных задач, методика решений которых не была рассмотрена . Приведенного материала должно хватить Вам с головой, чтобы разобраться и решить задачи самостоятельно. Если же нет то обращайтесь и мы Вам поможем с вычислениями.
В книгах вы найдете много подобных задач, методика решений которых не была рассмотрена . Приведенного материала должно хватить Вам с головой, чтобы разобраться и решить задачи самостоятельно. Если же нет то обращайтесь и мы Вам поможем с вычислениями.
Похожие материалы:
Задачи на арифметическую прогрессию
15 задач.arifmeticheskaya_progressiya.docx
1. Найдите ближайший к нулю положительный член арифметической прогрессии 49,5; 47,7;….
2. Турист, поднимаясь в гору, за первый час достиг высоты 580 м, а за каждый следующий час поднимался на высоту на 40 м меньше, чем в предыдущий. За сколько часов он достигнет высоты 2500 м, поднимаясь от подножия горы?
3. Найдите сумму всех натуральных чисел, не превосходящих 170, которые делятся на 6.
4. Три положительных числа образуют арифметическую прогрессию с разностью d, а квадраты этих чисел, взятые в том же порядке, образуют геометрическую прогрессию. Найдите все возможные значения d.
5. Сумма трёх чисел, образующих арифметическую прогрессию, равна 15. Если к этим числам прибавить соответственно 1, 1 и 4, то они образуют геометрическую прогрессию. Найдите эти числа.
Сумма трёх чисел, образующих арифметическую прогрессию, равна 15. Если к этим числам прибавить соответственно 1, 1 и 4, то они образуют геометрическую прогрессию. Найдите эти числа.
6. Три положительных числа образуют возрастающую арифметическую прогрессию. Если второе из них уменьшить на 1, а первое и третье оставить без изменения, то получится геометрическая прогрессия, первый член которой совпадает со знаменателем. Найдите разность данной арифметической прогрессии.
7. Дана возрастающая арифметическая прогрессия. Первый, второй и пятый ее члены образуют геометрическую прогрессию. Найдите, во сколько раз четвертый член данной арифметической прогрессии больше первого?
8. Существует ли арифметическая прогрессия, в которой a₃= 7; a₆=13; a₈= 17.
9. Три числа образуют арифметическую прогрессию, их сумма равна 24. Если первое число оставить без изменения, из второго числа вычесть 2, а к третьему прибавить 4, то получим геометрическую прогрессию. Найдите эти числа, если известно, что первое из них больше трех.
10. Могут ли числа √3, 2, √8 быть членами ( необязательно последовательными) арифметической прогрессии?
11. Является ли число 4 членом арифметической прогрессии, первые два члена которой соответственно равны -8 и -5?
12.Гусеница проползла за первую минуту 39 см, а за каждую следующую минуту на 2 см меньше, чем за предыдущую. Через сколько минут она проползет 4 м?
13. Арифметическая прогрессия задана формулой aₙ= 3n+2. Найдите сумму членов этой прогрессии с нечетными номерами, меньшими 50.
14. Предприятие поставило себе цель выпускать каждый год на 15 единиц продукции больше, чем в предыдущий. Сколько единиц продукции произведет предприятие за 13 лет, начинай с 8-го года, если в первый год было произведено 50 единиц продукции?
15. Восьмой член арифметической прогрессии в 3 раза больше шестого. Найдите сумму первых девяти членов этой прогрессии?
Ответы
1) 0,9
2) 5 ч
3) 2436
4) 0
5) {11, 5, -1} и {2,5,8}
6) 3
7) 7
8) Да
9) 18; 8; -2
10) Нет
11) Да
12) 20
13) 1925
14) 3185
15) 0
Как создать арифметическую прогрессию? — MS Excel
Кроме простого автозаполнения ячеек данными при необходимости можно создать и арифметическую прогрессию. Excel 2007 может автоматически продолжать заполнение прогрессии числами, комбинациями чисел и текста, датами и временем, основываясь на установленном образце.
Excel 2007 может автоматически продолжать заполнение прогрессии числами, комбинациями чисел и текста, датами и временем, основываясь на установленном образце.
1 способ:
- В окне открытого листа введите начальные значения создаваемого ряда прогрессии в первую ячейку и вторую ячейку диапазона.
Например: 1, 2; 07:00, 08:00; пн, вт; янв, фев. - Выделите эти ячейки и наведите курсор на правый нижний угол выделенной зоны.
- Курсором в виде тонкого черного креста при нажатой левой кнопке мыши протащите маркер заполнения по столбцу (вверх или вниз) либо по строке (вправо или влево).
Получится результат – 4,5; 09:00, 10:00; ср, чт; мар, апр.
Чтобы использовать принцип автозаполнения ячеек, а не создание арифметической прогрессии, при использовании маркера заполнения нажмите и держите клавишу Ctrl.
2 способ:
- В окне открытого листа в первую ячейку диапазона введите начальное значение создаваемого ряда прогрессии.

- Наведите курсор мыши на правый нижний угол ячейки и, когда курсор станет тонким черным крестом, при нажатой ПРАВОЙ кнопке мыши протащите маркер заполнения вверх или вниз по столбцу либо вправо, либо влево по строке.
- В конце нужного диапазона отпустите правую кнопку мыши.
- В контекстном меню выберите пункт «Заполнить».
3 способ:
- В окне открытого листа введите начальные значения создаваемого ряда прогрессии в первую ячейку и вторую ячейку диапазона.
- Выделите эти ячейки и наведите курсор на правый нижний угол выделенной зоны.
- Курсором в виде тонкого черного креста при нажатой ПРАВОЙ кнопке мыши протащите маркер заполнения по столбцу (вверх или вниз) или по строке (вправо или влево) и отпустите кнопку мыши.
- В контекстном меню выберите в списке пункт «Линейное приближение» (рис. 2.108).
Рис. 2.108. Контекстное меню прогрессии
4 способ:
- В окне открытого листа введите начальное значение создаваемого ряда прогрессии в первую ячейку диапазона.

- Выделите диапазон ячеек и перейдите к вкладке «Главная».
- В группе «Редактирование» раскройте меню кнопки «Заполнить» и в списке команд выберите пункт «Прогрессия» (рис. 2.109).
- В окне «Прогрессия» (рис. 2.110) в группе «Тип» активируйте пункт «Арифметическая».
- В графе «Шаг» введите число развития прогрессии, то есть значение, на которое будут увеличиваться все числа, а в графе «Предельное значение» при необходимости задайте максимально возможное число прогрессии.
- Закройте окно кнопкой «ОК»
Рис. 2.109. Вкладка «Главная». Меню кнопки «Заполнить». Пункт «Прогрессия
Рис. 2.110. Окно «Прогрессия»
Задачи для ОГЭ. Арифметическая прогрессия
Задачи для ОГЭ с ответами и решениями
Арифметическая прогрессия
перейти к содержанию задачника
- Дана арифметическая прогрессия , разность которой равна , . Найдите .
- Дана арифметическая прогрессия , разность которой равна , .
 Найдите .
Найдите . - Дана арифметическая прогрессия , разность которой равна , . Найдите сумму первых семи ее членов.
- Дана арифметическая прогрессия , разность которой равна , . Найдите сумму первых 15 ее членов.
- Арифметическая прогрессия задана условием . Найдите .
- Арифметическая прогрессия задана условиями , . Найдите .
- Арифметическая прогрессия задана условиями , . Найдите .
- Дана арифметическая прогрессия 11; 18; 25; … . Какое число стоит в этой последовательности на 6-м месте?
- Дана арифметическая прогрессия 7; 12; 17; … . Какое число стоит в этой последовательности на 7-м месте?
- Дана арифметическая прогрессия 10; 5; 0; … . Какое число стоит в этой последовательности на 61-м месте?
- Арифметическая прогрессия задана условиями , . Найдите сумму первых 17 ее членов.
- Дана арифметическая прогрессия 35; 32; 29; … . Найдите первый отрицательный член этой прогрессии.
- В первом ряду кинозала 40 мест, а в каждом следующем на 2 больше, чем в предыдущем.
 Сколько мест в ряду с номером ?
Сколько мест в ряду с номером ? - В первом ряду кинозала 30 мест, а в каждом следующем на 1 больше, чем в предыдущем. Сколько мест в ряду с номером ?
- Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
- Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадратов больше, чем в предыдущей. Сколько квадратов в 12-й строке?
- В арифметической прогрессии , . Найдите разность арифметической прогрессии.
- В арифметической прогрессии , . Найдите разность арифметической прогрессии.
- Дана арифметическая прогрессия . Найдите сумму первых десяти ее членов.
- Арифметическая прогрессия задана условием . Найдите сумму первых шести членов прогрессии.
- Арифметическая прогрессия задана условием . Найдите сумму первых пяти членов прогрессии.
- Арифметическая прогрессия задана условием .
 Найдите сумму первых десяти членов прогрессии.
Найдите сумму первых десяти членов прогрессии.
перейти к содержанию задачника
Ответы
- -39,5
- 20,6
- 105,7
- 453
- 73,9
- -7
- -9
- 46
- 37
- -290
- -2329
- -1
- 122
- 48
- -0,6
- 10
- 75
- -40,5
- 275
- -59,5
Метки ОГЭ. Смотреть запись.
арифметических прогрессий | Блестящая вики по математике и науке
Важная терминология
- Начальный член: В арифметической прогрессии первое число в ряду называется «начальным членом».
- Общее различие: Значение, на которое увеличиваются или уменьшаются следующие друг за другом члены, называется «общей разницей».
Рекурсивная формула
Мы можем описать арифметическую последовательность с помощью рекурсивной формулы, которая определяет, как каждый член соотносится с предыдущим. Поскольку в арифметической последовательности каждый член задается предыдущим термином с добавленной общей разницей, мы можем написать рекурсивное описание следующим образом:
Поскольку в арифметической последовательности каждый член задается предыдущим термином с добавленной общей разницей, мы можем написать рекурсивное описание следующим образом:
Срок = Предыдущий срок + Общая разница. \ text {Срок} = \ text {Предыдущий термин} + \ text {Общая разница.} Срок = Предыдущий термин + Общая разница.
Короче, с общей разницей ddd, имеем:
an = an − 1 + d.a_n = a_ {n-1} + d.an = an − 1 + d.
Явная формула
Хотя приведенная выше рекурсивная формула позволяет нам описать отношения между членами последовательности, часто бывает полезно иметь возможность написать явное описание терминов в последовательности, которое позволило бы нам найти любой термин.
Если мы знаем начальный термин, следующие термины связаны с ним путем повторного добавления общей разницы. Таким образом, явная формула
Срок = Начальный срок + Общая разница × Количество шагов от начального срока. \ text {Срок} = \ text {Начальный термин} + \ text {Общая разница} \ times \ text {Число шагов от начального срока}. Срок = Начальный срок + Общая разница × Количество шагов от начального срока.
Срок = Начальный срок + Общая разница × Количество шагов от начального срока.
Мы можем записать это с общей разницей ddd как:
an = a1 + d (n — 1).a_n = a_1 + d (n-1) .an = a1 + d (n-1).
Какая последовательность описывается выражением an = 2 + 4 (n − 1) a_n = 2 + 4 (n-1) an = 2 + 4 (n − 1)?
Показать ответ
Последовательность 2,6,10,14,… 2, 6, 10, 14, \ dots2,6,10,14,….
Из явной формулы видно, что начальный член равен 2, а общая разница равна 4.
Какова явная формула арифметической прогрессии 3,6,9,12,… 3, 6, 9, 12, \ dots3,6,9,12,…?
Показать ответ
Используя приведенную выше форму, у нас есть начальный член, a1 = 3a_1 = 3a1 = 3, и общая разница, ddd, равная 3.Таким образом, an = 3 + 3 (n − 1) a_n = 3 + 3 (n-1) an = 3 + 3 (n − 1).
Обратите внимание, что мы можем упростить это выражение до an = 3 + 3n − 3 = 3na_n = 3 + 3n-3 = 3nan = 3 + 3n − 3 = 3n.
{\ text {th}} 15-м экзамене.
Если все его оценки соответствуют арифметической прогрессии с положительной общей разницей, на каком экзамене он получил нулевые оценки?
Арифметическая прогрессия — обзор
3.2 Арифметическая прогрессия
Арифметическая прогрессия — это последовательность, которая начинается с числа a и затем увеличивается с фиксированным шагом d : a , a + d , a + 2 d ,….Пусть s n обозначает сумму первых n членов, так что
sn = a + a + d + a + 2d +… + a + n − 1d.
Мы хотим найти простое выражение для s n .
Мы можем сделать это, записав s n в их естественном порядке, а затем с членами в обратном порядке.
sn = a + a + d + (a + 2d) +… + (a + (n − 1) d), sn = (a + n − 1d) + (a + (n − 2) d) + (a + ( п — 3) г) +… + а.
Затем, добавляя соответствующие члены,
2sn = 2a + n − 1d) + 2a + n − 1d +… + (2a + n − 1d⏟nterms = n (2a + n − 1d).∴sn = na + 12nn − 1d.
Мы доказали следующий небольшой результат. (Вежливое название небольшого результата, обычно шаг к чему-то более интересному, — это лемма.)
Лемма 3.1 Сумма первых n членов арифметической прогрессии a , a + d , a + 2 d ,… is na + 12nn − 1d. ℕ
Только что доказанный результат и другие ему подобные часто становятся намного яснее, если мы используем обозначение Σ для суммирования.Общий член приведенной выше арифметической прогрессии: a + ( k — 1) d , это k -й член, так что a + ( a + d ) +… + ( a + ( n — 1) d ) — это сумма членов, когда k = 1, k = 2,… и k = n , все сложенные вместе, и запишем это как
∑k = 1na + k − 1d.
В более общем смысле, если f — это некоторая формула, включающая k , ∑ n k = 1 f ( k ) обозначает f (1) + f (2 ) +…. + f ( k ), сумма значений, полученных при последовательной замене k на 1, 2,…, n или любые другие значения, обозначенные знаком Σ. Таким образом, ∑ 5 k = 3 f ( k ) = f (3) + f (4) + f (5). Обратите внимание, что k здесь является «фиктивной» переменной и что ∑ n k = 1 f ( k ) не зависит от k ; мы могли бы заменить k на любой другой символ, который нам подходит, кроме символа, который уже имеет другое значение в этом выражении.∑ n n = 1 n не годится, так как символ n имеет два значения.
Другой распространенный простой тип последовательности — это геометрическая прогрессия , которая представляет собой последовательность вида a , ar , ar 2 , ar 3 ,… r будучи называется обыкновенным соотношением . Снова есть формула для суммы первых n членов.Пусть s n = a + ar +… + ar n −1 , сумма первых n членов. Тогда
sn = a + ar +… + arn − 1rsn = ar +… + arn − 1 + arnso1 − rsn = a − arn = a (1 − rn).
Следовательно, при условии r ≠ 1 (чтобы избежать деления на ноль)
sn = a1 − rn1 − r.
(Обратите внимание на форму этого: первый член прогрессии умножает все выражение, а степень r в числителе — это количество членов.Если r > 1, обычно лучше записать sn = arn − 1r − 1, чтобы знаменатель был положительным.
В случае, когда r = 1, формула не имеет смысла, но в этом случае все суммированные члены равны, поэтому ответ прост.) Мы доказали:
Лемма 3.2 Если r ≠ 1 и n — натуральное число
a + ar +… + arn − 1 = ∑k = 1nark − 1 = a1 − rn1 − r.ℕ
Этот результат имеет чрезвычайно полезное следствие (которое мы называем следствием). Предположим, мы хотим разложить на множители x n — y n .Тогда (при условии x ≠ 0) xn − yn = xn1 − ynxn = xn1 − yxn. Здесь мы должны заметить, что мы можем использовать формулу из леммы 3.2 с r = y / x и a = 1. Тогда
1 + yx +… + yn − 1xn − 1 = 1 − yxn1 − yxprovidedyx ≠ 1.
Таким образом, 1 − yxn = 1 − yx1 + yx +… + yn − 1xn − 1 и умножение на x n дает
(*) xn − yn = x − yxn − 1 + xn − 2y +… + xyn − 2 + yn − 1.
Мы доказали это для всех действительных чисел, удовлетворяющих двум условиям: x ≠ 0 и x ≠ y .
В двух исключенных случаях, x = 0 и x = y , результат тривиален для проверки, поэтому мы независимо замечаем, что результат верен для них, и ограничение можно снять. Основное достоинство (*) состоит в том, что x n — y n имеет множитель x — y , хотя выражение для второго множителя также полезно.
Эти два примера — арифметическая и геометрическая прогрессии — полезны, но они создают немного вводящее в заблуждение впечатление, поскольку легко доказать формулы напрямую, как только вы заметите уловку.Более широко применяемый способ доказательства истинности формулы для всех натуральных чисел — использование математической индукции. Обратите внимание, что мы хотим доказать, что результат верен для всех натуральных чисел, поэтому мы не можем сделать это, проверяя каждое значение по очереди.
Сумма первых n членов арифметической последовательности
Предположим, что последовательность номеров арифметика (то есть он увеличивается или уменьшается на постоянную величину с каждым членом), и вы хотите найти сумму первых п условия.
Обозначим эту частичную сумму через S п . потом
S п знак равно п ( а 1 + а п ) 2 ,
где п это количество терминов, а 1 это первый член и а п это последний срок.Сумма первых п члены арифметической последовательности называются арифметический ряд .
Пример 1:
Найдите сумму первых 20 члены арифметического ряда, если а 1 знак равно 5 и а 20 знак равно 62 .
S 20 знак равно 20 ( 5 + 62 ) 2 S 20 знак равно 670
Пример 2:
Найдите сумму первых 40 термины арифметики последовательность 2 , 5 , 8 , 11 , ⋯ .
Сначала найдите 40 th срок:
а 40 знак равно а 1 + ( п — 1 ) d знак равно 2 + 39 ( 3 ) знак равно 119
Затем найдите сумму:
S п знак равно п ( а 1 + а п ) 2 S 40 знак равно 40 ( 2 + 119 ) 2 знак равно 2420
Пример 3:
Найдите сумму:
∑ k знак равно 1 50 ( 3 k + 2 )
Первая находка а 1 и а 50 :
а 1 знак равно 3 ( 1 ) + 2 знак равно 5 а 50 знак равно 3 ( 50 ) + 2 знак равно 152
Затем найдите сумму:
S k знак равно k ( а 1 + а k ) 2 S 50 знак равно 50 ( 5 + 152 ) 2 знак равно 3925
Смотрите также: сигма-обозначение ряда и n-й член арифметической последовательности
Искусство решения задач
В алгебре арифметическая последовательность , иногда называемая арифметической прогрессией , представляет собой последовательность чисел, такую, что разница между любыми двумя последовательными членами постоянна.
Эта константа называется общей разностью последовательности.
Например, это арифметическая последовательность с общей разницей и арифметическая последовательность с общей разницей; тем не менее, и не являются арифметическими последовательностями, поскольку разница между последовательными терминами варьируется.
Более формально последовательность представляет собой арифметическую прогрессию тогда и только тогда, когда. Аналогичное определение справедливо для бесконечных арифметических последовательностей. Чаще всего он встречается в трехчленной форме: а именно, что константы, и находятся в арифметической прогрессии тогда и только тогда, когда.
Недвижимость
Поскольку каждый член представляет собой общее расстояние от предыдущего члена, каждый член арифметической последовательности может быть выражен как сумма первого члена и кратного общей разности. Позвольте быть первым членом, быть th членом и быть общей разницей любой арифметической последовательности; тогда, .
Общая лемма состоит в том, что для данного члена и члена арифметической последовательности общая разность равна.
Доказательство : Пусть последовательность имеет первый член и общую разницу.Затем, используя результат выше, по желанию.
Другая распространенная лемма состоит в том, что последовательность находится в арифметической прогрессии тогда и только тогда, когда является средним арифметическим для любых следующих друг за другом членов. В символах,. Это в основном используется для выполнения замен, хотя иногда служит определением арифметических последовательностей.
Сумма
Арифметический ряд — это сумма всех членов арифметической последовательности. Все бесконечные арифметические ряды расходятся. Что касается конечных серий, для вычисления их значения используются две основные формулы.
Во-первых, если арифметический ряд имеет первый член, последний член и общее количество членов, то его значение равно.
Доказательство : Пусть серия будет равна, и пусть будет ее общая разница.
Тогда мы можем написать двумя способами: Добавление этих двух уравнений отменяет все термины, включающие; и так, как положено.
Во-вторых, если арифметический ряд имеет первый член, общую разницу и члены, он имеет значение.
Доказательство : последний член имеет значение.Тогда по приведенной выше формуле ряд имеет значение. Это завершает доказательство.
Проблемы
Вот некоторые проблемы с решениями, использующими арифметические последовательности и ряды.
Вводные задачи
Промежуточные проблемы
- 2003 AIME I, проблема 2
- Найдите корни многочлена, учитывая, что корни образуют арифметическую прогрессию.
См. Также
Класс 10 Арифметическая прогрессия — основы, задачи и примеры решения
Арифметическая прогрессия
Если мы наблюдаем, то мы можем заметить, что есть некоторая закономерность в некоторых вещах, например, 2,4,6,8 — все четные числа, а разница такая же, как два.
Это означает, что добавляя 2 к каждому четному числу, мы получаем новое четное число. То же самое происходит и с нечетными числами. Таких закономерностей много. Итак, давайте узнаем больше о теме и шаблонах.
Как следует из названия, арифметика означает сложение или вычитание, а прогрессия означает ряд.
Последовательность чисел, при которой разница между последовательными членами постоянна, тогда последовательность называется арифметической прогрессией.
Например, 3,7,11,15,19,23.Здесь каждый член отличается от предыдущего на 4, и, поскольку разница постоянна, это арифметическая прогрессия.
- Постоянная разница фактически известна как общая разность и обозначается d.
- Первый член AP обозначается a.
Следовательно, общая форма арифметической прогрессии — это a, a + d, a + 2d, a + 3d, a + 4d ………… .n раз.
- Здесь мы можем заметить, что общее различие между каждым термином — d.
Общая разница:
Общая разница может быть положительной, отрицательной или даже нулевой.
- Если разница положительная, точка доступа называется увеличивающейся. Например 2, 12, 22, 32, 42, 52.
- Если разница отрицательная, то AP называется уменьшающейся AP. Например, 12, 10, 8, 6, 4.
- Если разница равна нулю, она называется постоянной AP. Например 5, 5, 5, 5, 5, 5, 5, 5.
Если мы обозначим первый член 1, второй член 2 и так далее, то член n th будет n .Тогда сформированная таким образом AP будет иметь вид 1 , 2 , 3 , …………… ..a n .
Итак, a 2 -a 1 = a 3 -a 2 = a 4 -a 3 ……… .. = a n -a n-1 = d.
N th Срок действия AP
Не всегда возможно определить все термины AP, если он содержит много терминов.
Например, если нам нужно определить 1000 th член AP с четными номерами, то это не так просто, а также требует времени.
Следовательно, мы обобщаем результат, чтобы найти член n th AP
Пусть 1 , 2 , 3 , …………… ..a n , будет AP из n элементов, и здесь 1 — это первый член, а d — общая разница. .
a 2 = a + d = a + (2-1) d
a 3 = a + 2d = a + (3-1) d
a 4 = a + 3d = a + (4-1) d
Аналогично
Общее условие a n = a + (n-1) d
И последний член AP l = a + (n-1) d , если есть n член
Example1 : — Найдите 10 -й член AP 2,12, 22, 32….
Решение : — Здесь первый член a = 2, а общая разница d равна
12-2 = 10 = г.
Используя формулу и положив n = 10, получаем
a 10 = 2+ (10-1) 10 = 2 + 90 = 92.
Пример 2 : — Какой член AP 15,10, 5, 0… будет -40?
Решение : — Здесь a = 15 и d = -5.
А здесь как мы знаем, что n = -40.
Подставляя значения в формулу, получаем
-40 = 15 + (п-1) (- 5)
-55 = (п-1) (- 5)
Следовательно (n-1) = 11 и, следовательно, n = 12.
Таким образом, 12 -й член будет -40.
Сумма N условий AP
Рассмотрим AP с первым членом a и общей разностью d
a, a + d, a + 2d, a + 3d, a + 4d ……………………… a + (n-1) d.
Пусть S обозначает сумму первых n членов и, следовательно,
- Здесь важно помнить, что n = S n -S n-1.
Это означает, что член n -го AP равен разности его суммы n -го члена и суммы (n-1) -го члена .
Пример 3 : — Найти сумму 10 членов AP -3, 1, 5, 9,13 .
.?
Решение : — Здесь a = -3 и d = 4
Следовательно, подставив значения в формулу, мы получим
Следовательно, сумма первых 10 членов равна 150.
Проблемы Word
Пример 4 : — Раман начал работать в компании с годовой зарплатой 5000 рупий в год и получал ежегодную надбавку в размере 200 рупий в год.Через сколько лет его зарплата будет 8000 рупий?
Решение : — Здесь последовательность будет 5000, 5200, 5400, 5800, 6000 ……… .8000
Здесь первый член a = 5000 и d = 200, a n = 8000
Используя формулу и подставляя в нее значения, получаем
8000 = 5000 + (п-1) 200
3000 = (n-1) 200 и, следовательно, (n-1) = 15
Следовательно, n = 16, что означает, что через 16 лет годовая зарплата Рамана будет 8000 рупий в год.
Пример 5 : — Подрядная компания должна заплатить штраф, если работы задерживаются.
100 рупий за первый день, 150 рупий за второй, 200 рупий за третий и так далее. Узнайте, сколько денег должен заплатить подрядчик, если работа задерживается на 30 дней.
Решение : — Формируется последовательность 100, 150, 200, 250…
Здесь a = 100, d = 50 и n = 30
Следовательно, подставив значения в формулу, мы получим
S n = 15 [200 + 1450]
S n = 15 x 1650 = 24750.
Следовательно, подрядчик должен заплатить 24 750 рупий в качестве штрафа за задержку работ на 30 дней.
Практические вопросы
Q1) Запишите первые четыре члена AP, если
- a = 3 и d = 5 ii) a = 12 и d = -2
- a = 4 и d = -2 iv) a = 10 и d = 10
Q2) Найдите 1 , 2 , 4 и d следующих AP
- 10, 5, 0, -5, -10… .. б) -20, -12, -4, 4… ..
Q3) Найдите член n th следующего AP
- 5, 11, 17, 23, 29 …….
- 10, 15, 20, 25 ……….
Q4) Определите AP, первый член которого равен 8 и 3 -й член , член равен 24.
Q5) Сколько двузначных чисел делятся на 5?
Q6) Найдите сумму первых 200 четных чисел.
Резюме
- Последовательность, имеющая общее отличие, известна как AP.
- Общий термин: a n = a + (n-1) d
- Общая разность d может быть положительной, отрицательной или нулевой.
- Сложение, вычитание, умножение или деление двух AP также приводит к AP.
Арифметическая прогрессия и решение арифметической прогрессии (AP)
В природе многие вещи следуют этому образцу, например, отверстие в виде сот, Лепестки цветка розы. Подобно этому Арифметическая прогрессия — это тип числового шаблона. В этом номере расположены по шаблону.
Последовательность: это набор чисел, расположенных в определенном порядке.Последовательность:
a 1 , a 2 , a 3 , a 4 , a 5 … .a nНапример, последовательность нечетных чисел
1, 3, 5, 7 …… ..Серия: Серия — это несколько терминов в последовательности. Если в последовательности n членов, то сумма n членов обозначается S n .
S n = a 1 + a 2 + a 3 +… + a n
Общий n-й член серии AP:
a 1 , a 2 , a 3 , a 4 ,….., а н
a, a + d, a + d + d, a + d + d + d, …… ..
а1 = а = а (1-1) d
a2 = a + d = a (2-1) d
a3 = a + 2d = a (3-1) d
a n = a + (n-1) d
Итак, формула для вычисления n-го члена равна
.a n = Первый член + (номер члена — 1) общая разница
Q1: найти 13 член серии AP
2, 4, 6, 8, 10 …………
Решение:
Первый член a = 2 Общая разница (d) = 4-2 = 2 = 6-4
Итак, примените формулу I.
е. а п = а + (п-1) г
a 13 = 2+ (13-1) 2
а 13 = 26
Q2: Если 11
-й член равен 47, а первый член равен 7. В чем разница между ними?Решение:
a = 7 a 11 = 47 n = 11 d =?
а 11 = а + (п-1) д
47 = 7 + (11-1) д
47-7 = 10 дней
40 = 10 дней
д = 4
Общая разница (d) = 4.
Сумма первых n членов ряда AP:
Предположим, что это AP серий 1, 2, 3, 4, ……, 49, 50
Таким образом, сумма этих членов составляет S 50 = 1 + 2 + 3 + 4 +….+ 49 + 50 …… (1)
Запишите в обратном порядке получим
S 50 = 50 + 49 + …… + 4 + 2 + 3 + 1 …… (2)
Теперь сложите уравнение 1 и 2
2 S 50 = 51 + 51 + …… + 51 + 51 + 51 + 51 (50 раз)
2S 50 = 50X51
S 50 = 50X51 / 2
Теперь о n условиях AP
Первые n членов серии AP
a, a + d, a + 2d, ……….
а + (п-2) г, а + (п-1) г
, поэтому S n = a + (a + d) + (a + 2d) + ……. + [A + (n-2) d] + [a + (n-1) d]
Запишите в обратном порядке
S n = [a + (n-1) d] + [a + (n-2) d] + …… + (a + d) + a
Теперь добавьте их
2S n = [2a + (n-1) d] + [2a + (n-1) d] + ……… [2a + (n-1) d] + [2a + (n-1) d] …… (n терминов)
2S n = n [2a + (n-1) d]
Sn = n / 2 [2a + (n-1) d]
S n = n / 2 {a + a n }; где a n = a + (n-1) d = l (последний член)
Так S n = n / 2 {a + l)
Q3: Найдите сумму первых 10 членов
11,17, 23, 29,35, …………
Решение:
Из уравнения a = 11 d = 6 n = 10
Итак, мы можем использовать формулу S n = n / 2 (2a + (n-1) d)
S n = 10/2 (2X 11+ (10-1) 6)
S n = 5 (22 + 9X6)
S n = 5 (22 + 54)
S n = 5 (76)
S n = 380
Q4: Найдите сумму этой последовательности….
.
10,15,20,25,30, ………… .., 100
Решение:
Из уравнения a = 10; л = 100 г = 5
L = а + (n-1) d
100 = 10+ (п-1) 5
90 = (п-1) 5
90 = 5н-5
90 + 5 = 5n
95/5 = n
п = 19
Теперь мы можем использовать s n = n / 2 (a + l)
S n = 19/2 (10 + 100)
S n = 19X110 / 2
S n = 1045
Чтобы получить больше блогов Arithmetic Progression и Math, зарегистрируйтесь сегодня бесплатно.
Для получения помощи в решении задач по математике и домашних заданий по математике Позвоните нам по телефону +1 855 688 8867
РешенияNCERT для математики класса 10 Глава 5 Развитие арифметики Ex 5.1
Получите бесплатно Решения NCERT для математики класса 10 Глава 5 Ex 5.1 PDF. Арифметические успехи Математика класса 10 Решения NCERT чрезвычайно полезны при выполнении домашних заданий.
Упражнение 5.1 Математика для класса 10 Решения NCERT были подготовлены опытными учителями LearnCBSE.in. Подробные ответы на все вопросы в главе 5 Maths Class 10 Arithmetic Progressions Exercise 5.1 предоставлено в учебнике NCERT.
Темы и подтемы в классе 10 по математике Глава 5 Арифметические прогрессии:
Название раздела Название темы 5 Арифметические прогрессии 5,1 Введение 5,2 Арифметические прогрессии 5,3 Новый срок действия AP 5.4 Сумма первых N членов AP 5,5 Сводка Решения NCERT для математики класса 10 Глава 5 Арифметическая прогрессия Пример 5.1
РешенияNCERT для математики класса 10 Глава 5 Развитие арифметики Ex 5.
1 являются частью решений NCERT для математики класса 10. Здесь мы привели NCERT Solutions for Class 10 Maths Глава 5 Арифметические прогрессии Упражнение 5.1
Доска CBSE Учебное пособие NCERT Класс Класс 10 Субъект Математика Глава 5 Название отдела Арифметические прогрессии Упражнение Пр. 5.1 Количество решенных вопросов 4 Категория Решения NCERT Мы также ответили на 106 вопросов из главы 9 — Арифметические достижения в учебнике по математике для 10 класса Р.
Д. Шарма.
Страница №: 99
Пр. 5.1. Класс 10. Математика. Вопрос 1.
В какой из следующих ситуаций список задействованных чисел составляет арифметическую прогрессию и почему?
(i) Стоимость проезда на такси после каждого км, когда стоимость проезда составляет 15 фунтов стерлингов за первый км и 8 фунтов стерлингов за каждый дополнительный км.
(ii) Количество воздуха, присутствующего в цилиндре, когда вакуумный насос удаляет \ (\ frac {1} {4} \) воздуха, остающегося в цилиндре за раз.
(iii) Стоимость рытья колодца после каждого метра копания, когда она стоит 150 фунтов стерлингов за первый метр и увеличивается на 50 фунтов стерлингов за каждый последующий метр.
(iv) Сумма денег на счете каждый год, когда 10000 фунтов стерлингов депонируются под сложные проценты под 8% годовых.
Решение:
youtube.com/embed/videoseries?list=PLXX3lyEZ5Op4WGaV4WfPZv8BJC6J2_r1L» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Пр. 5.1 Класс 10 Математика Вопрос 2.
Запишите первые четыре члена AP, когда первый член a и общая разность d даны следующим образом:
(i) a = 10, d = 10
(ii) a = -2 , d = 0
(iii) a = 4, d = -3
(iv) a = -1, d = \ (\ frac {1} {2} \)
(v) a = -1,25, d = -0,25
Раствор:
Вы также можете бесплатно загрузить PDF-файл Ex 5.1 Class 10 Arithmetic Progressions NCERT Solutions или сохранить изображения решений и распечатать их, чтобы они были всегда под рукой при подготовке к экзамену.
Скачать Решения NCERT для математики 10 класса, глава 5, арифметические прогрессии PDF
Пр. 5.1, класс 10, математика, вопрос 3.
Для следующих AP запишите первый член и общую разницу:
(i) 3, 1, -1, -3, ……
(ii) -5, -1, 3, 7, ……
(iii) \ (\ frac {1} {3} \), \ (\ frac {5} {3} \), \ (\ frac {9} {3} \), \ (\ frac {13} {3} \), …… ..
(iv) 0,6, 1,7, 2,8, 3,9, …….
Решение:Ex 5.1 Class 10 Maths Вопрос 4.
Какие из перечисленных точек доступа? Если они образуют AP, найдите общую разницу d и напишите еще три члена.
(i) 2, 4, 8, 16, …….
(ii) 2, \ (\ frac {5} {2} \), 3, \ (\ frac {7} {2} \), …….
(iii) -1,2, -3,2, -5,2, -7,2, ……
(iv) -10, -6, -2,2,… ..
(v) 3, 3 + \ (\ sqrt {2 } \), 3 + 2 \ (\ sqrt {2} \), 3 + 3 \ (\ sqrt {2} \),… ..
(vi) 0,2, 0,22, 0,222, 0,2222, ……
(vii ) 0, -4, -8, -12,… ..
(viii) \ (\ frac {-1} {2} \), \ (\ frac {-1} {2} \), \ (\ гидроразрыв {-1} {2} \), \ (\ frac {-1} {2} \), …….
(ix) 1, 3, 9, 27, …….
(x) a, 2a, 3a, 4a, …….
(xi) a, a2, a3, a4, …….
(xii) \ (\ sqrt {2} \), \ (\ sqrt {8} \), \ (\ sqrt {18} \), \ (\ sqrt {32} \),… ..
(xiii ) \ (\ Sqrt {3} \), \ (\ sqrt {6} \), \ (\ sqrt {9} \), \ (\ sqrt {12} \),… ..
(xiv) 12, 32, 52, 72, ……
(xv) 12, 52, 72, 73, ……
Решение:
Математика 10 класса Арифметические прогрессии Интеллектуальные карты
Арифметическая прогрессия (AP)
Рассмотрим
(i) 1, 2, 3, 4, ……
(ii) 3, 3, 3, 3,… ..
(i) и (ii) — это последовательность чисел, каждое число в этих последовательностях называется термином.Арифметическая прогрессия (AP) — это последовательность чисел, в которой каждый член получается добавлением фиксированного числа «d» к предыдущему члену, за исключением первого члена.
Фиксированное число называется общей разницей. Он может быть положительным, отрицательным или нулевым.
Любая арифметическая прогрессия может быть представлена как:
a, a + d, a + 2d, a + 3d,… ..
где «a» — первый член, а «d» — общая разница. Арифметические прогрессии, у которых нет последнего члена, называются бесконечными арифметическими прогрессиями.например:
6, 9, 12, 15, …….Формула общей разности (d)
Последовательность чисел a 1 , a 2 , a 3 …. является AP, если разница a 2 — 1 , 3 — 2 , 4 — 3 …. дает то же значение, т.е. если k + 1 — k, одинаково для разных значений k.
Разница ( k + 1 — k ) называется общей разницей (d).Здесь k + 1 и k являются (k + 1) -м и k-м членами соответственно.
∴ d = a 2 — a 1 = a 3 — a 2 = a 4 — a 3n
th Срок (или общий срок) арифметической прогрессииВ AP, с первым членом ‘a’ и общей разницей d, член n th (или общий термин) задается как,
a n = a + (n — 1) d
. AP может быть конечным или бесконечным в зависимости от того, является ли количество членов конечным или бесконечным.
Если в AP есть m терминов, тогда m является последним термином и иногда обозначается как «l».Сумма ПЕРВОГО ‘n’ условий A.P.
(i) Сумма первых n членов AP определяется как
, где a — первый член, а d — общая разность
(ii) Если l — последний член конечной AP, скажем, n th , тогда сумма всех членов AP равна,
Обратите внимание, что сумма первых n натуральных чисел равнаСреднее арифметическое между двумя числами
Если a, b, c находятся в AP.
.Тогда b называется средним арифметическим значений a и c и определяется выражением
МАТЕМАТИКИ КЛАССА 10 ГЛАВА 5 УПРАЖНЕНИЕ 5.1 РЕШЕНИЯ AP НА HINDI
Дополнительные ресурсы для CBSE Class 10
Справочник по формулам для математики и естествознания 10-го класса
Мы надеемся, что NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1, поможет вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 10, глава 5, арифметические вычисления, упражнение 5.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
.


 Число T — длина периода.
Число T — длина периода.

 д.
д.

 Найдите .
Найдите . Сколько мест в ряду с номером ?
Сколько мест в ряду с номером ? Найдите сумму первых десяти членов прогрессии.
Найдите сумму первых десяти членов прогрессии. {\ text {th}} 15-м экзамене.
{\ text {th}} 15-м экзамене.


 В случае, когда r = 1, формула не имеет смысла, но в этом случае все суммированные члены равны, поэтому ответ прост.) Мы доказали:
В случае, когда r = 1, формула не имеет смысла, но в этом случае все суммированные члены равны, поэтому ответ прост.) Мы доказали: В двух исключенных случаях, x = 0 и x = y , результат тривиален для проверки, поэтому мы независимо замечаем, что результат верен для них, и ограничение можно снять. Основное достоинство (*) состоит в том, что x n — y n имеет множитель x — y , хотя выражение для второго множителя также полезно.
В двух исключенных случаях, x = 0 и x = y , результат тривиален для проверки, поэтому мы независимо замечаем, что результат верен для них, и ограничение можно снять. Основное достоинство (*) состоит в том, что x n — y n имеет множитель x — y , хотя выражение для второго множителя также полезно.

 Эта константа называется общей разностью последовательности.
Эта константа называется общей разностью последовательности.
 Тогда мы можем написать двумя способами: Добавление этих двух уравнений отменяет все термины, включающие; и так, как положено.
Тогда мы можем написать двумя способами: Добавление этих двух уравнений отменяет все термины, включающие; и так, как положено. Это означает, что добавляя 2 к каждому четному числу, мы получаем новое четное число. То же самое происходит и с нечетными числами. Таких закономерностей много. Итак, давайте узнаем больше о теме и шаблонах.
Это означает, что добавляя 2 к каждому четному числу, мы получаем новое четное число. То же самое происходит и с нечетными числами. Таких закономерностей много. Итак, давайте узнаем больше о теме и шаблонах.
 Например, если нам нужно определить 1000 th член AP с четными номерами, то это не так просто, а также требует времени.
Например, если нам нужно определить 1000 th член AP с четными номерами, то это не так просто, а также требует времени.
 .?
.? 100 рупий за первый день, 150 рупий за второй, 200 рупий за третий и так далее. Узнайте, сколько денег должен заплатить подрядчик, если работа задерживается на 30 дней.
100 рупий за первый день, 150 рупий за второй, 200 рупий за третий и так далее. Узнайте, сколько денег должен заплатить подрядчик, если работа задерживается на 30 дней.
 Последовательность:
Последовательность:  е. а п = а + (п-1) г
е. а п = а + (п-1) г а + (п-2) г, а + (п-1) г
а + (п-2) г, а + (п-1) г .
. Упражнение 5.1 Математика для класса 10 Решения NCERT были подготовлены опытными учителями LearnCBSE.in. Подробные ответы на все вопросы в главе 5 Maths Class 10 Arithmetic Progressions Exercise 5.1 предоставлено в учебнике NCERT.
Упражнение 5.1 Математика для класса 10 Решения NCERT были подготовлены опытными учителями LearnCBSE.in. Подробные ответы на все вопросы в главе 5 Maths Class 10 Arithmetic Progressions Exercise 5.1 предоставлено в учебнике NCERT. 1 являются частью решений NCERT для математики класса 10. Здесь мы привели NCERT Solutions for Class 10 Maths Глава 5 Арифметические прогрессии Упражнение 5.1
1 являются частью решений NCERT для математики класса 10. Здесь мы привели NCERT Solutions for Class 10 Maths Глава 5 Арифметические прогрессии Упражнение 5.1 Д. Шарма.
Д. Шарма. .
.  .
.  Разница ( k + 1 — k ) называется общей разницей (d).Здесь k + 1 и k являются (k + 1) -м и k-м членами соответственно.
Разница ( k + 1 — k ) называется общей разницей (d).Здесь k + 1 и k являются (k + 1) -м и k-м членами соответственно. 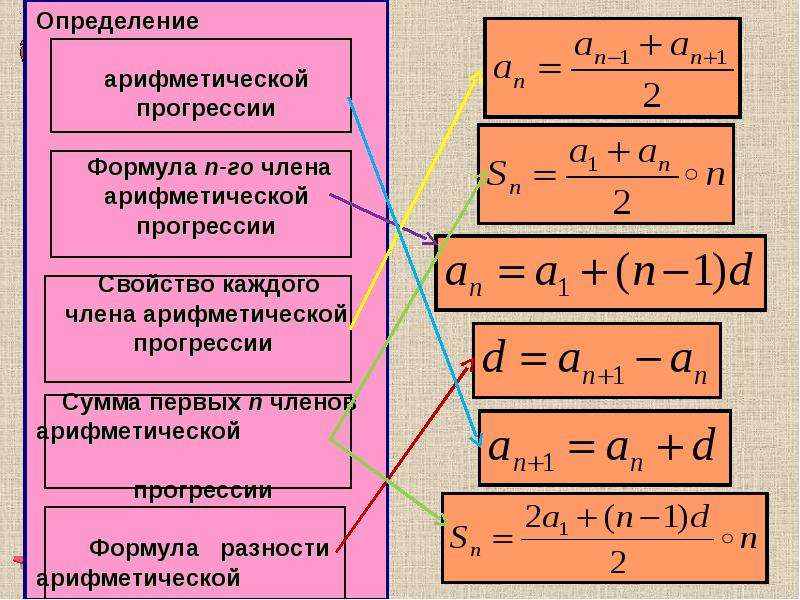 Тогда b называется средним арифметическим значений a и c и определяется выражением
Тогда b называется средним арифметическим значений a и c и определяется выражением 