Абсолютный ряд динамики пример: понятие и классификация. Показатели уровней ряда динамики. Примеры решения задач

Примеры решения задач — Статистика

Условие задачи

Определить вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные абсолютные приросты, темпы роста, темпы прироста, средний уровень ряда, средний темп роста, средний темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По расчетам сделать выводы. Графически изобразить полученный ряд динамики.

Годы	Объем производства, млн.р.
2011	12
2012	10
2013	11
2014	10
2015	9

Решение задачи

Данный ряд динамики – интервальный, так как значение показателя заданы за определенный интервал времени.

 

Определяем цепные и базисные показатели ряда динамики

Абсолютные приросты цепные:	Абсолютные приросты базисные:
Темпы роста цепные:	Темпы роста базисные:
Темпы прироста цепные:	Темпы прироста базисные:

Показатели динамики объема производства 2011-2015 гг

Годы	Объем производства, млн. р.	Абсолютные приросты, млн.р.		Темпы роста, %		Темпы прироста, %
		цепные	базисные	цепные	базисные	цепные	базисные
2011	12	——	——	100.0	100.0	——	——
2012	10	-2	-2	83. 3	83.3	-16.7	-16.7
2013	11	1	-1	110.0	91.7	10.0	-8.3
2014	10	-1	-2	90.9	83.3	-9.1	-16.7
2015	9	-1	-3	90. 0	75.0	-10.0	-25.0

Определяем средние показатели ряда динамики

Средний уровень исследуемого динамического ряда найдем по формуле средней арифметической:

Среднегодовой абсолютный прирост:

Среднегодовой темп роста:

Среднегодовой темп прироста:

Строим график

График динамики объема производства 2011-2015 гг

Таким образом на протяжении всего исследуемого периода за исключением 2013 года объем производства продукции на предприятиях снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном выражении.

Задачи по рядам динамики

Теория по решению задач.

Рядом динамики называется ряд статистических чисел, которые характеризуют изменение величины общественного явление во времени.

Моментный ряд динамики – это ряд динами, уровни которого характеризуют размеры общественно-экономических явлений по состоянию на определенный момент.

В моментных рядах динамики средние уровни вычисляются двумя способами:

1)  если ряд динамики имеет равные промежутки времени между двумя составными датами:

, где

— средний уровень ряда динамики;

у – абсолютные уровни ряда динами;

n – число абсолютных уровней ряда динамики.

2)  если ряд динамики имеет неодинаковые промежутки времени между двумя составными датами:

, где

t – периоды времени между датами.

Периодический (интервальный) ряд – это ряд динамики, уровни которого характеризуют размеры общественно-экономических явлений за определенные периоды времени (неделя, месяц, полугодие и т.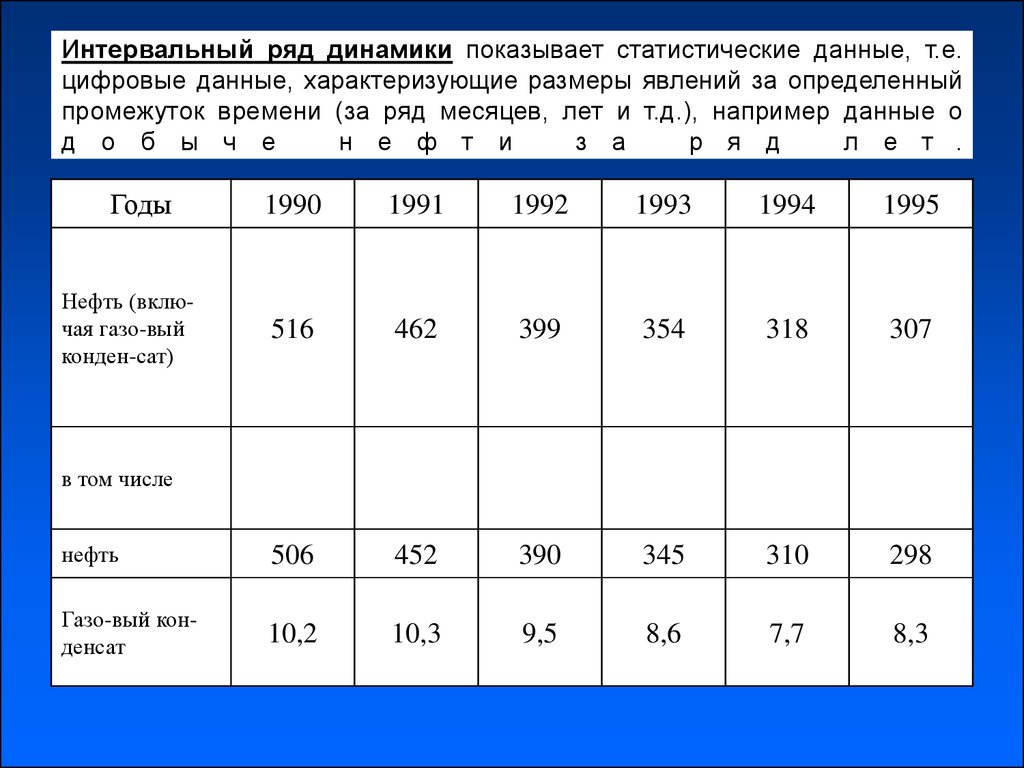 д.).

Средние уровни в периодических рядах исчисляются как простая средняя арифметическая:

Один из важнейших вопросов, возникающих при изучении рядов динамики – это выявление тенденции развития экономического явления в динамике. Для этой цели применяются разнообразные статистические методы, в частности:

—  метод укрупнения периодов:

у1=у1+у2+у3

у2=у4+у5+у6

у3=у7+у8+у9 и т. д.

—  метод скользящей средней:

и т. д.

—  метод аналитического выравнивания:

, где

t – время

n – число членов ряда

у – исходные уровни ряда динамики

а0 и а1 – параметры уравнения, которые необходимо определять.

Основные показатели рядов динамики:

1.  Абсолютный прирост (∆у):

а) базисный ∆уб=уn-уо

б) цепной ∆уц=уn-уn-1

∆уб – абсолютный прирост базисный;

∆уц – абсолютный прирост цепной;

уn — уровень сравниваемый;

у0 – уровень периода, принятого за базу сравнение;

уn-1 – уровень, предшествующий сравниваемому периоду.

2.  Средний абсолютный прирост ():

n – число показателей в периоде.

3.  Абсолютное значение одного процента прироста (А):

∆Т – темп прироста

4.  Темп роста (Т):

—  базисный

—  цепной

5.  Темп прироста (∆Т):

—  базисный:

—  цепной:

6.  Средний темп роста ()

у1, у2, уn –коэффициенты цепного темпа роста

n – число коэффициентов

уо и уn – начальный и конечный абсолютные показатели ряда динамики.

7.  средний темп прироста (

Задача по товарообороту

Имеется следующая информация о реализации продуктов сельскохозяйственного производства магазинами города:

Среднегодовая реализация, (тыс. грн.):

Таблица № 1

Квартал	1998г.	1999г.	2000г.
1	340	515	435
2	280	330	420
3	420	438	380
4	510	240	377

Для выявления основной тенденции развития товарооборота произведите сглаживание уровней ряда динамики:

1.  Методом укрепления периодов по трем кварталам.

2.  Методом скользящей средней.

Ход решения задачи:

1.  Метод укрупнения периодов:

у1=у1+у2+у3 у1=340+280+420=1040

у2=у4+у5+у6 у2=510+515 +320=1355

у3=у7+у8+у9 у3=438+240+435=1113

у4=у10+у11+у12 у4=420+380+377=1177

Таким образом, укрупненный ряд динамики имеет следующий вид:

1040; 1355; 1113; 1177.

2.  Метод скользящей средней:

Т. о. выровненный ряд динамики примет следующий вид:

346,7; 403,3; 481,7; 451,7; 427,7; 336; 371; 365; 411,7; 292,3.

Задача по приростам

Имеется следующая информация о выпуске продукции заводом за 1996-2001 г. г. (тыс. грн.).

Таблица № 2

Годы	1996г.	1997г.	1998г.	1999г.	2000г.	2001г.
Валовая продукция	30,2	33,4	28,6	29,4	35,8	31,7

Определите:

1)  абсолютные приросты;

2)  темп роста и прироста;

3)  абсолютное значение 1 % прироста;

4)  средний абсолютный прирост;

5)  среднегодовой темп роста и прироста.

Ход решения задачи:

1.  Абсолютные приросты:

∆уб=уn-уо ∆уц=уn-уn-1

97г.: 33,4-30,2=3,2 33,4-30,2=3,2

98г.: 28,6-30,2=-1,6 28,6-33.ю4=-4,8

99г.: 29,4-30,2=-0,8 29,4-28,6=0,8

00г.: 35,8-30,2=5.6 35,8-29,4=6,4

01г.: 31,7-30,2=1,56 31,7-35,8=-4,1

2.  Темпы роста и прироста:

а) темпы роста:

б) темпы прироста:

или вторым способом:

∆Тб=Тб-1 (или 100 %)

∆Тц=Тц-1 (или 100 %)

97г.: 1,106-1=0,106 (10,6%) 1,106-1=0,106 (10,6%)

98г.: 0,947-1=-0,053 (-5,3%) 0,856-1=-0,144 (-14,4%)

99г.: 0,973-1=-0,027 (-2,7%) 1,028-1=0,028 (2,8%)

00г.: 1,185-1=0,185 (18,5%) 1,218-1=0,218 (21,8%)

01г.: 1,05-1=0,05 (5%) 0,885-1=-0,115 (-11,5%)

3.  Определяем абсолютное значение 1 % прироста

97г.: 0,01х30,2=0,302

98г. : 0,01х33,4=0,334

99г.: 0,01х28.6=0,286

00г.: 0,01х29,4=0,294

01г.: 0,01х35,8=0,358

4.  Определим средний абсолютный прирост:

или вторым способом:

5.  Определим среднегодовой темп роста и прироста:

а) среднегодовой темп роста

вторым способом

б) среднегодовой темп прироста:

Абсолютное время, относительное время и фазы — aas-timeseries v0.1b5.dev1+g7fe352c

Типы осей времени

До сих пор все рассмотренные нами примеры включали временные ряды с абсолютным временем на оси x. Однако также можно отображать относительное время или даже фазы. Чтобы взглянуть на это, мы будем использовать набор данных, состоящий из лучевых скоростей как функции времени:

из astropy.timeseries импортировать TimeSeries
 

ts = TimeSeries.read('https://aperiosoftware. github.io/timeseries.js/examples/data/phase.csv', format='ascii.csv')
 

Длина временного ряда = 26

time	relative	phase	flux	error	flux_lo	flux_hi
object	int64	float64	float64	float64	float64	float64
2016-03-22T12:30:28.000	0	0,0	0,98	0,15	0.97	1.0
2016-03-22T12:30:38.000	10	0.1	1.02	0.15	1.0	1.03
2016-03-22T12:30:48.000	20	0.2	1.01	0.15	1.0	1.02
2016-03-22T12:30:58.000	30	0.3	0.87	0.15	0. 85	0.89
2016-03-22T12:31:08.000	40	0.4	0.75	0.15	0.72	0.76
2016-03-22T12:31:18.000	50	0.5	0.7	0.15	0.69	0.71
2016-03-22T12:31:28.000	60	0.6	0.71	0.15	0.7	0.72
2016-03- 22T12:31:38.000	70	0.7	0.82	0.15	0.805	0.835
2016-03-22T12:31:48.000	80	0.8	0.97	0.15	0.96	0.985
2016-03-22T12:31:58.000	90	0.9	1.02	0.15	1.01	1.04
…	…	…	. ..	…	…	…
2016-03-22T12:33:08.000	160	0.6	0.69	0.15	0.65	0.75
2016-03-22T12:33:18.000	170	0.7	0.73	0.15	0.68	0.78
2016-03-22T12:33:28.000	180	0.8	0.86	0,15	0,8	0.91
2016-03-22T12:33:38.000	190	0.9	1.0	0.15	0.98	1.02
2016-03-22T12:33:48.000	200	1.0	0.99	0.15	0.97	1.02
2016-03-22T12:33:58.000	210	0.1	1.01	0.15	1.0	1.02
2016-03-22T12:34:00.000	212	0. 12	1.007	0.15	1.0	1.024
2016-03-22T12:34:05.000	217	0.17	1.011	0.15	0.995	1.025
2016-03-22T12:34:16.000	228	0.28	0.94	0.15	0.89	1.01
2016-03-22T12 :34:20.000	232	0,32	0,84	0,15	0,78	0,9

. -вычисленная фаза для заданного периода и эпохи. Вы также можете, например, вычислить их на лету и добавить к существующему объекту TimeSeries.

Прежде чем мы продолжим, нам нужно обновить объект TimeSeries, чтобы включить информацию о единицах измерения для столбца относительного времени — мы можем сделать это, используя:

из единиц импорта astropy как u
относительный = ts['относительный']
ts.remove_column («относительный»)
ts['относительный'] = относительный * u. s
 

Теперь мы можем создать фигуру, которая показывает относительное время вместо абсолютного времени, указав time_mode при создании фигуры:

из импорта aas_timeseries InteractiveTimeSeriesFigure
fig = InteractiveTimeSeriesFigure(title='Кривая радиальной скорости', time_mode='relative')
fig.add_markers(time_series=ts, time_column='relative', column='flux', color='orange', size=50)
fig.ylabel='Радиальная скорость (км/с)'
fig.preview_interactive()
 

Точно так же мы можем создать фигуру, показывающую скорость как функцию фазы, используя:

fig = InteractiveTimeSeriesFigure(title='Кривая радиальной скорости', time_mode='фаза')
fig.add_markers (time_series = ts, time_column = «фаза», столбец = «поток», цвет = «оранжевый», размер = 50)
fig.ylabel='Радиальная скорость (км/с)'
fig.preview_interactive()
 

time_mode также может передаваться при создании представлений, поэтому мы можем сделать фигуру, показывающую абсолютное время по умолчанию, и иметь представление с относительным временем и фазовыми осями:

fig = InteractiveTimeSeriesFigure(title='Кривая радиальной скорости', time_mode='absolute')
fig. ylabel='Радиальная скорость (км/с)'
fig.add_markers(time_series=ts, time_column='time', column='flux', color='orange', size=50)
view1 = fig.add_view(title='По фазе', empty=True, time_mode='фаза')
view1.add_markers (time_series = ts, time_column = «фаза», столбец = «поток», цвет = «оранжевый», размер = 50)
view2 = fig.add_view(title='По относительному времени', empty=True, time_mode='относительно')
view2.add_markers (time_series = ts, time_column = «относительный», столбец = «поток», цвет = «оранжевый», размер = 50)
fig.preview_interactive()
 

Форматирование осей времени

Для каждого из различных типов осей времени можно настроить формат осей с помощью настройки time_format . Для фигуры/представления с абсолютным временем time_format может быть установлено в 'jd' , 'mjd' , 'unix' , 'iso' или '06'

:0 :

fig = InteractiveTimeSeriesFigure(title='Кривая радиальной скорости', time_mode='absolute') fig.

add_markers(time_series=ts, time_column='time', column='flux', color='orange', size=50) fig.time_format = 'jd' fig.preview_interactive()

Для рисунков/видов с относительным временем time_format может быть установлен на «секунды» , «часы» , «дни» или «годы» :

fig = InteractiveTimeSeriesFigure(title=’Кривая радиальной скорости’, time_mode=’relative’) fig.add_markers(time_series=ts, time_column=’relative’, column=’flux’, color=’orange’, size=50) fig.time_format = ‘часы’ fig.preview_interactive()

И, наконец, для фаз можно установить значение 9039.5 «единица» , "радиан" или "градус" :

fig = InteractiveTimeSeriesFigure(title='Кривая радиальной скорости', time_mode='фаза')
fig.add_markers (time_series = ts, time_column = «фаза», столбец = «поток», цвет = «оранжевый», размер = 50)
fig.time_format = 'радианы'
fig.preview_interactive()
 

Анализ временных рядов: основы

ЧТО ТАКОЕ ВРЕМЕННОЙ РЯД?

Временной ряд представляет собой совокупность наблюдений за четко определенными элементами данных, полученных посредством повторных измерений во времени. Например, измерение стоимости розничных продаж в каждом месяце года будет включать временной ряд. Это связано с тем, что доход от продаж четко определен и последовательно измеряется через равные промежутки времени. Данные, собранные нерегулярно или только один раз, не являются временными рядами.

Наблюдаемый временной ряд можно разложить на три компонента: тренд (долгосрочное направление), сезонный (систематические, связанные с календарем движения) и нерегулярный (бессистемные, краткосрочные колебания).

ЧТО ТАКОЕ СЕРИИ STOCK И Flow?

Временные ряды можно разделить на два разных типа: запасы и потоки.

Серия акций представляет собой измерение определенных атрибутов в определенный момент времени и может рассматриваться как «инвентаризация». Например, Ежемесячное обследование рабочей силы представляет собой критерий запаса, поскольку он определяет, было ли лицо занято в учетную неделю.

Потоковые ряды — это ряды, которые являются мерой активности за определенный период. Например, обзоры деятельности Розничная торговля . Производство также является показателем потока, потому что определенное количество продукции производится каждый день, а затем эти суммы суммируются, чтобы получить общую стоимость производства за данный отчетный период.

Основное различие между рядами акций и потоков заключается в том, что ряды потоков могут содержать эффекты, связанные с календарем (эффекты торговых дней). Оба типа рядов по-прежнему могут быть скорректированы с учетом сезонных колебаний с использованием одного и того же процесса сезонной корректировки.

ЧТО ТАКОЕ СЕЗОННЫЕ ЭФФЕКТЫ?

Сезонный эффект – это систематический и календарный эффект. Некоторые примеры включают резкое увеличение количества воды в большинстве розничных серий, которое происходит примерно в декабре в связи с периодом Рождества, или увеличение потребления воды летом из-за более теплой погоды. Другие сезонные эффекты включают эффекты рабочих дней (количество рабочих или торговых дней в данном месяце различается из года в год, что влияет на уровень активности в этом месяце) и перенос праздников (время праздников, таких как Пасха, варьируется, поэтому последствия праздника будут ощущаться в разные периоды каждый год).

ЧТО ТАКОЕ СЕЗОННАЯ РЕГУЛИРОВКА И ЗАЧЕМ ОНА НУЖНА?

Сезонная корректировка — это процесс оценки и последующего удаления из временного ряда влияний, которые носят систематический и календарный характер. Наблюдаемые данные нуждаются в сезонной корректировке, поскольку сезонные эффекты могут скрывать как истинное основное движение ряда, так и некоторые несезонные характеристики, которые могут представлять интерес для аналитиков.

ПОЧЕМУ МЫ НЕ МОЖЕМ ПРОСТО СРАВНИТЬ ИСХОДНЫЕ ДАННЫЕ ЗА ОДИН ПЕРИОД КАЖДОГО ГОДА?

Сравнение исходных данных за один и тот же период каждого года не устраняет полностью все сезонные эффекты. Некоторые праздники, такие как Пасха и Китайский Новый год, каждый год приходятся на разные периоды, поэтому они будут искажать наблюдения. Кроме того, ежегодные значения будут искажены любыми изменениями сезонных моделей, которые происходят с течением времени. Например, рассмотрим сравнение двух последовательных мартовских месяцев, т. е. сравните уровень исходного ряда, наблюдаемого в марте для 2000 и 2001 годов. Это сравнение игнорирует эффект движущегося праздника Пасхи. Пасха в большинстве случаев приходится на апрель, но если Пасха приходится на март, уровень активности в этом месяце для некоторых серий может сильно различаться. Это искажает первоначальные оценки. Сравнение этих двух месяцев не будет отражать основную структуру данных. Сравнение также игнорирует эффекты торгового дня. Если два последовательных месяца марта имеют разный состав торговых дней, это может отражать разные уровни активности в первоначальных условиях, даже если базовый уровень активности не изменился. Аналогичным образом можно игнорировать любые изменения сезонных моделей. В исходных оценках также присутствует влияние нерегулярной составляющей. Если величина нерегулярного компонента ряда велика по сравнению с величиной компонента тренда, основное направление ряда может быть искажено.

Однако основным недостатком сравнения годовых исходных данных является отсутствие точности и временные задержки при определении поворотных моментов в ряду. Точки разворота возникают, когда меняется направление базового уровня ряда, например, когда постоянно уменьшающийся ряд начинает неуклонно расти. Если мы сравним данные исходного ряда с разницей в год, мы можем пропустить поворотные моменты, происходящие в течение года. Например, если март 2001 г. имеет более высокую первоначальную оценку, чем март 2000 г., то, сравнивая эти значения по годам, мы можем сделать вывод, что уровень активности в течение года увеличился. Однако этот ряд мог увеличиваться до сентября 2000 г., а затем начал неуклонно уменьшаться.

КОГДА СЕЗОННАЯ РЕГУЛИРОВКА НЕПОДХОДИТ?

Когда во временном ряду преобладают трендовые или нерегулярные компоненты, почти невозможно идентифицировать и удалить те небольшие сезонные факторы, которые присутствуют. Следовательно, сезонная корректировка несезонного ряда нецелесообразна и часто приводит к введению искусственного сезонного элемента.

ЧТО ТАКОЕ СЕЗОННОСТЬ?

Сезонный компонент состоит из эффектов, которые достаточно стабильны в отношении времени, направления и величины. Он возникает из-за систематических, связанных с календарем влияний, таких как:

• Природные условия
  колебания погоды, характерные для сезона
  (нехарактерные погодные условия, такие как снег летом, считаются нерегулярными факторами)
• Деловые и административные процедуры
  начало и конец учебного семестра
• Социальное и культурное поведение
  Рождество

Он также включает связанные с календарем систематические эффекты, которые не являются стабильными в годовом исчислении или вызваны изменениями в календаре от года к году, например:

• Эффекты торгового дня
  количество появлений каждого дня недели в данном месяце будет отличаться от года к году
  — В марте 2000 г. было 4 выходных дня, а в марте 2002 г. — 5 выходных
• Эффекты переноса праздников
  праздников, которые происходят каждый год, но точное время которых смещается
  — Пасха, Китайский Новый год

КАК МЫ ОПРЕДЕЛЯЕМ СЕЗОННОСТЬ?

Сезонность во временном ряду можно идентифицировать по регулярно расположенным пикам и впадинам, которые имеют постоянное направление и примерно одинаковую величину каждый год относительно тренда. Следующая диаграмма изображает строго сезонный ряд. В Новом Южном Уэльсе наблюдается очевидный сезонный рост розничных продаж в декабре из-за рождественских покупок. В этом примере величина сезонной составляющей увеличивается со временем, как и тренд.

Рисунок 1. Ежемесячные розничные продажи в розничных универмагах Нового Южного Уэльса (NSW)

ЧТО ТАКОЕ НЕРЕГУЛЯРНОЕ?

Нерегулярный компонент (иногда также известный как остаток) — это то, что остается после оценки и удаления сезонных и трендовых компонентов временного ряда. Это происходит из-за краткосрочных колебаний ряда, которые не являются ни систематическими, ни предсказуемыми. В крайне нерегулярных рядах эти колебания могут преобладать над движениями, что будет маскировать тенденцию и сезонность. Следующий график представляет собой очень нерегулярный временной ряд:

Рисунок 2: Ежемесячная стоимость разрешений на строительство, Австралийская столичная территория (ACT)

КАКОВА ТЕНДЕНЦИЯ?

Тенденция ABS определяется как «долгосрочное» движение во временном ряду без связанных с календарем и нерегулярных эффектов и является отражением основного уровня. Это результат таких факторов, как рост населения, инфляция цен и общие экономические изменения. На следующем графике показан ряд, в котором наблюдается очевидный восходящий тренд с течением времени:

Рисунок 3: Квартальный валовой внутренний продукт

КАКИЕ ОСНОВНЫЕ МОДЕЛИ ИСПОЛЬЗУЮТСЯ ДЛЯ ДЕКОМПОЗИЦИИ НАБЛЮДАЕМОГО ВРЕМЕННОГО РЯДА?

Модели декомпозиции обычно являются аддитивными или мультипликативными, но могут также принимать другие формы, например псевдоаддитивные.

Аддитивная декомпозиция

В некоторых временных рядах амплитуда как сезонных, так и нерегулярных колебаний не изменяется при повышении или понижении уровня тренда. В таких случаях целесообразна аддитивная модель.

В аддитивной модели наблюдаемый временной ряд (O _t ) считается суммой трех независимых компонентов: сезонного S _t , тренда T _t и нерегулярного
I _t .

То есть

Каждый из трех компонентов имеет те же единицы измерения, что и исходная серия. Сезонно скорректированный ряд получается путем оценки и удаления сезонных эффектов из исходного временного ряда. Расчетный сезонный компонент обозначается Скорректированные с учетом сезонных колебаний оценки могут быть выражены как:

В символах

На следующем рисунке показан типичный аддитивный ряд. Базовый уровень ряда колеблется, но величина сезонных всплесков остается приблизительно стабильной.

Рисунок 4: Государственное управление и другие текущие трансферты другим секторам

Мультипликативное разложение

Во многих временных рядах амплитуда как сезонных, так и нерегулярных колебаний увеличивается по мере повышения уровня тренда. В этой ситуации обычно подходит мультипликативная модель.

В мультипликативной модели исходный временной ряд выражается как произведение трендовой, сезонной и нерегулярной составляющих.

или

Затем данные с учетом сезонных колебаний становятся:

или

В этой модели тренд имеет те же единицы измерения, что и исходный ряд, но сезонные и нерегулярные компоненты представляют собой безразмерные факторы, распределенные вокруг 1.

Большинство рядов, проанализированных ABS, демонстрируют характеристики мультипликативной модели. По мере изменения основного уровня ряда меняется и величина сезонных колебаний.

Рис. 5. Ежемесячные объявления о вакансиях в Новом Южном Уэльсе, Канаде

Псевдоаддитивная декомпозиция

Мультипликативная модель не может использоваться, когда исходный временной ряд содержит очень маленькие значения или нулевые значения. Это потому, что нельзя разделить число на ноль. В этих случаях используется псевдоаддитивная модель, сочетающая в себе элементы как аддитивной, так и мультипликативной моделей. Эта модель предполагает, что сезонные и нерегулярные вариации зависят от уровня тренда, но не зависят друг от друга.

Исходные данные могут быть выражены в следующей форме:

Псевдоаддитивная модель продолжает соглашение мультипликативной модели о том, что как сезонный фактор S _t , так и нерегулярный фактор I _t сосредоточены вокруг единицы. Следовательно, нам нужно вычесть единицу из S _t и I _t , чтобы гарантировать, что члены T _t x (S _t — 1) и T _t x (I _t — 1) расположены по центру. около нуля. Эти члены можно интерпретировать как аддитивные сезонные и аддитивные нерегулярные компоненты соответственно, и поскольку они сосредоточены вокруг нуля исходных данных O _t будет сосредоточено вокруг значений тренда T _t .

Сезонно скорректированная оценка определяется как:

где и — оценки тренда и сезонного компонента. В псевдоаддитивной модели тренд имеет те же единицы измерения, что и исходный ряд, но сезонные и нерегулярные компоненты являются безразмерными факторами, распределенными около 1.

Пример ряда, для которого требуется псевдоаддитивная модель декомпозиции, показан ниже. Эта модель используется, поскольку зерновые культуры производятся только в определенные месяцы, а производство сельскохозяйственных культур практически равно нулю в течение одного квартала каждого года.

Рисунок 6: Квартальная валовая стоимость производства зерновых культур

Пример: разложение Шискина

Разложение Шискина дает графики исходного ряда, сезонно скорректированные ряды, трендовые ряды, остаточные факторы (нерегулярные ряды) и межмесячные (сезонные) и внутримесячные (рабочие дни) факторы, которые объединяются для формирования комбинированных поправочных коэффициентов. Остаточные (нерегулярные) факторы находятся путем деления сезонно скорректированного ряда на трендовый ряд. На рис. 7 показано разложение Шискина для ряда австралийских розничных продаж.

Рисунок 7: Разложение Шискина для общего розничного оборота Австралии, май 1990 г. – май 2000 г.

Чтобы выбрать подходящую модель декомпозиции, аналитик временных рядов исследует график исходного ряда и пробует ряд моделей, выбирая ту, которая дает наиболее стабильный сезонный компонент. Если величина сезонной составляющей относительно постоянна независимо от изменений тренда, то подходит аддитивная модель. Если она меняется в зависимости от изменения тренда, наиболее вероятным кандидатом является мультипликативная модель. Однако если ряд содержит значения, близкие или равные нулю, а величина сезонной составляющей оказывается зависимой от уровня тренда, то наиболее подходящей является псевдоаддитивная модель.

ЧТО ТАКОЕ СЕЗОННАЯ И НЕРЕГУЛЯРНАЯ (SI) КАРТА?

После оценки компонента тренда его можно удалить из исходных данных, оставив объединенные сезонные и нерегулярные компоненты или SI.