А в пятой степени а: УПРОСТИТЕ ВЫРАЖЕНИЕ; А в третьей степени умножить на А в четвёртой степени умножить на А в шестой степени
Степени и возведение в степень, вторая, третья, четвёртая степени
Когда число умножается само на себя, произведение называется степенью.
Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.
Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.
И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a
Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.
Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель
 Это число или буква называется показателем степени или степенью числа. Так, а2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a3 означает aaa, то есть здесь a повторяется три раза как множитель.
Это число или буква называется показателем степени или степенью числа. Так, а2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a3 означает aaa, то есть здесь a повторяется три раза как множитель.Показатель первой степени есть 1, но он обычно не записывается. Так, a1 записывается как a.
Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении ax, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень
Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении ax, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень
Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)3 есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a3 + 3a2b + 3a2d + 3ab2 + 6abd + 3ad2 + b3 + d3.

Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a5, a4, a3, a2, a1;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.
Tак a.a = a2, второй член. И a3.a = a4
a2.a = a3, третий член. a4.a = a5.
Если мы начнем слева делить на a,
мы получим a5:a = a4 и a3:a = a2.
a4:a = a3 a2:a = a1
Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.
Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.
Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.
Или a5, a4, a3, a2, a, 1, 1/a, 1/a
Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.
Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a3) = a3.
Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
(a + b)3, (a + b)2, (a + b), 1, 1/(a + b), 1/(a + b)2, 1/(a + b)3.
Для удобства используется еще одна форма записи обратных степеней.
Согласно этой форме, 1/a или 1/a1 = a-1. И 1/aaa или 1/a3 = a-3.
1/aa или 1/a2 = a-2. 1/aaaa или 1/a4 = a-4.
А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a0.
Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a4, a3, a2, a1, a0, a-1, a-2
Или a+4, a+3, a+2, a+1, a0, a-1, a-2, a-3, a-4.
А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.
Корень степени может выражен более чем одной буквой.
Так, aa.aa или (aa)2 есть второй степенью aa.
И aa.aa.aa или (aa)3 есть третьей степенью aa.
Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.
Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:
Умножайте величину саму на себя столько раз, сколько указано в степени числа.
Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.
Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.
Четвертая степень a есть a4 или aaaa. (Art. 195.)
Шестая степень y есть y6 или yyyyyy.
N-ая степень x есть xn или xxx….. n раз повторенное.
Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.
Tак (ay)2 =a2y2; (ay)2 = ay.ay.
Но ay.ay = ayay = aayy = a2y2.
Так, (bmx)3 = bmx.bmx.bmx = bbbmmmxxx = b3m3x3.
Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.
Пример 1. Четвертая степень dhy есть (dhy)4, или d4h4y4.
Пример 2. Третья степень 4b, есть (4b)3, или 43b3, или 64b3.
Пример 3. N-ая степень 6ad есть (6ad)n или 6nandn.
Пример 4. Третья степень 3m.2y есть (3m.2y)3, или 27m3.8y3.
Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,
(a + b)1 = a + b, первая степень.(a + b)1 = a2 + 2ab + b2, вторая степень (a + b).
(a + b)3 = a3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4, четвертая степень.
Квадрат a — b, есть a2 — 2ab + b2.
3 + 3a2 + 3a + 1.
Квадрат a + b + h есть a2 + 2ab + 2ah + b2 + 2bh + h2
Упражнение 1. Найдите куб a + 2d + 3
Упражнение 2. Найдите четвертую степень b + 2.
Упражнение 3. Найдите пятую степень x + 1.
Упражнение 4. Найдите шестую степень 1 — b.
Квадраты суммы
Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a2 + 2ah + h2 также, (a — h)(a — h) = a2 — 2ah + h2.
Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.
Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.
Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.
Пример 1. Квадрат 2a + b, есть 4a2 + 4ab + b2.
Пример 2. Квадрат ab + cd, есть a2b2 + 2abcd + c2d2.
Пример 3. Квадрат 3d — h, есть 9d2 + 6dh + h2.
Пример 4. Квадрат a — 1 есть a2 — 2a + 1.
Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.
Во многих случаях является эффективным записывать степени без умножения.
Так, квадрат a + b, есть (a + b)2.
N-ая степень bc + 8 + x есть (bc + 8 + x)n
В таких случаях, скобки охватывают все члены под степенью.
Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.
Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]2 или (a + b)2.(c + d)2.
Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.
Куб a.(b + d), есть [a.(b + d)]3, или a3.(b + d)3.
Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.
Вторая степень (- a) есть +a2
Третья степень (-a) есть -a3
Четвёртая степень (-a) есть +a4
Пятая степень (-a) есть -a5
Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a2
И -a.-a = +a2
Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.
Третья степень a2 есть a2.3 = a6.Для a2 = aa; куб aa есть aa.aa.aa = aaaaaa = a6; что есть шестой степенью a, но третьей степенью a2.
Четвертая степень a3b2 есть a3.4b2.4 = a12b8
Третья степень 4a2x есть 64a6x3.
Пятая степень (a + b)2 есть (a + b)10.
N-ая степень a3 есть a3n
N-ая степень (x — y)m есть (x — y)mn
(a3.b3)2 = a6.b6
(a3b2h4)3 = a9b6h12
Правило одинаково применяется к отрицательным степеням.
Пример 1. Третья степень a-2 есть a-3.3=a-6.
Для a-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a6 = a-6
Четвертая степень a2b-3 есть a8b-12 или a8/b12.
Квадрат b3x-1, есть b6x-2.
N-ая cтепень ax-m есть x-mn или 1/x.
Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.
Пример 1. Квадрат -a3 есть +a6. Квадрат -a3 есть -a3.-a3, которое, согласно правилам знаков при умножении, есть +a6.
2. Но куб -a3 есть -a9. Для -a3.-a3.-a3 = -a9.
3. N-ая степень -a3 есть a3n.
Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.
Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.
Квадрат a/b есть a2/b2. Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a2b2
Вторая, третья и n-ая степени 1/a есть 1/a2, 1/a3 и 1/an.
Примеры двочленов, в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)2 = x2 + 2.x.(1/2) + 1/22 = x2 + x + 1/4
(x — 1/2)2 = x2 — 2.x.(1/2) + 1/22 = x2 — x + 1/4
2. Квадрат a + 2/3 есть a2 + 4a/3 + 4/9.
3. Квадрат x + b/2 = x2 + bx + b2/4.
4 Квадрат x — b/m есть x2 — 2bx/m + b2/m2.
Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.
Так, в дроби ax-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax-2/y = (a/y).x-2 = (a/y).(1/x2 = a/yx2.
В дроби a/by3 мы можем переместить у из знаменателя в числитель.
Тогда a/by2 = (a/b).(1/y3) = (a/b).y-3 = ay-3/b.
Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.
Так, ax3/b = a/bx-3. Для x3 обратным есть x-3, что есть x3 = 1/x-3.
Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.
Так, a/b = 1/ba-1, or ab-1.
Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности, геометрии и математике! Также на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1 | 21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024 | 31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049 | 41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576 | 51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625 |
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176 | 71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249 | 81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824 | 91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401 | 101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000 |
Остались вопросы?
Здесь вы найдете ответы. x=3
log2(3)=x
x=3
log2(3)=x
90 в 10 степени
90 в 10 =34867844009999998976.00000
12 в степени 1/3
Сложная формула но в кратце ответ — 6
Слишком сложно?
Таблица степеней не по зубам? Тебе ответит эксперт через 10 минут!
УК РФ Статья 264. Нарушение правил дорожного движения и эксплуатации транспортных средств / КонсультантПлюс
УК РФ Статья 264. Нарушение правил дорожного движения и эксплуатации транспортных средств
(в ред. Федерального закона от 13.02.2009 N 20-ФЗ)
1. Нарушение лицом, управляющим автомобилем, трамваем либо другим механическим транспортным средством, правил дорожного движения или эксплуатации транспортных средств, повлекшее по неосторожности причинение тяжкого вреда здоровью человека, —
наказывается ограничением свободы на срок до трех лет, либо принудительными работами на срок до двух лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет или без такового, либо арестом на срок до шести месяцев, либо лишением свободы на срок до двух лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет или без такового.
2. Деяние, предусмотренное частью первой настоящей статьи, повлекшее по неосторожности причинение тяжкого вреда здоровью человека, если оно:
а) совершено лицом, находящимся в состоянии опьянения;
б) сопряжено с оставлением места его совершения, —
наказывается принудительными работами на срок до пяти лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет либо лишением свободы на срок от трех до семи лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет.
(в ред. Федерального закона от 17.06.2019 N 146-ФЗ)
(часть 2 в ред. Федерального закона от 23.04.2019 N 65-ФЗ)
3. Деяние, предусмотренное частью первой настоящей статьи, повлекшее по неосторожности смерть человека, —
наказывается принудительными работами на срок до четырех лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет либо лишением свободы на срок до пяти лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет.
(в ред. Федеральных законов от 07.12.2011 N 420-ФЗ, от 31.12.2014 N 528-ФЗ)
4. Деяние, предусмотренное частью первой настоящей статьи, повлекшее по неосторожности смерть человека, если оно:
а) совершено лицом, находящимся в состоянии опьянения;
б) сопряжено с оставлением места его совершения, —
наказывается лишением свободы на срок от пяти до двенадцати лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет.
(в ред. Федерального закона от 17.06.2019 N 146-ФЗ)
(часть 4 в ред. Федерального закона от 23.04.2019 N 65-ФЗ)
5. Деяние, предусмотренное частью первой настоящей статьи, повлекшее по неосторожности смерть двух или более лиц, —
наказывается принудительными работами на срок до пяти лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет либо лишением свободы на срок до семи лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет.
(в ред. Федеральных законов от 07.12.2011 N 420-ФЗ, от 31.12.2014 N 528-ФЗ)
6. Деяние, предусмотренное частью первой настоящей статьи, повлекшее по неосторожности смерть двух или более лиц, если оно:
а) совершено лицом, находящимся в состоянии опьянения;
б) сопряжено с оставлением места его совершения, —
наказывается лишением свободы на срок от восьми до пятнадцати лет с лишением права занимать определенные должности или заниматься определенной деятельностью на срок до трех лет.
(в ред. Федерального закона от 17.06.2019 N 146-ФЗ)
(часть 6 в ред. Федерального закона от 23.04.2019 N 65-ФЗ)
Примечание. Утратило силу с 1 июля 2015 года. — Федеральный закон от 31.12.2014 N 528-ФЗ.
Примечания. 1. Под другими механическими транспортными средствами в настоящей статье и статье 264.1 настоящего Кодекса понимаются трактора, самоходные дорожно-строительные и иные самоходные машины, а также транспортные средства, на управление которыми в соответствии с законодательством Российской Федерации о безопасности дорожного движения предоставляется специальное право.
2. Для целей настоящей статьи и статей 263 и 264.1 настоящего Кодекса лицом, находящимся в состоянии опьянения, признается лицо, управляющее транспортным средством, в случае установления факта употребления этим лицом вызывающих алкогольное опьянение веществ, который определяется наличием абсолютного этилового спирта в концентрации, превышающей возможную суммарную погрешность измерений, установленную законодательством Российской Федерации об административных правонарушениях, или в случае наличия в организме этого лица наркотических средств, психотропных веществ или их аналогов либо новых потенциально опасных психоактивных веществ, а также лицо, управляющее транспортным средством, не выполнившее законного требования уполномоченного должностного лица о прохождении медицинского освидетельствования на состояние опьянения в порядке и на основаниях, предусмотренных законодательством Российской Федерации.
(в ред. Федеральных законов от 03.07.2016 N 328-ФЗ, от 17.06.2019 N 146-ФЗ)
(примечания введены Федеральным законом от 31. 12.2014 N 528-ФЗ)
12.2014 N 528-ФЗ)
Берут ли в армию с плоскостопием 1, 2 и 3 степени? (Не всегда)
Почему я уверен, что с ним можно не служить, если эта степень считается призывной?
В начале статьи я написал, что 20% призывников имеют перспективы по освобождению от армии, если у них есть заключение о плоскостопии 2 степени. Но как такое возможно? Ведь в Расписании болезней, а именно в 68 статье, четко написано, что только при продольном плоскостопии 3 степени можно претендовать на военный билет. Других оснований для освобождения просто не существует.
Я полностью согласен, что с плоскостопием второй степени берут в армию, и такая форма заболевания абсолютно не подходит для получения военного билета. За исключением одного случая: степень плоскостопия была выставлена некорректно или уже не актуальна. Вот примеры из нашей практики, когда можно и нужно работать с призывником, у которого есть заключение о 2-ой степени:
Заключение о плоскостопии 2 степени было выставлено давно, и свежих результатов нет
Самая распространенная практика: призывники и родители регулярно приезжают к нам с амбулаторными картами, в которых несколько лет назад была указана вторая степень. Однако во время анализа документов и разговора мы узнаем, что молодой человек не проходил лечение и даже не носил ортопедические стельки.
Однако во время анализа документов и разговора мы узнаем, что молодой человек не проходил лечение и даже не носил ортопедические стельки.
Плоскостопие без соответствующего лечения в большинстве случаев — прогрессирующее заболевание. Поэтому если у призывника пять лет назад было плоскостопие 2 степени с углом 150 градусов, то сейчас может быть уже 3 степень с углом 157 градусов. То есть та форма плоскостопия, с которой не берут в армию. Поэтому когда мы видим старые данные в документах, то сначала обязательно смотрим стопы. После этого мы рекомендуем, где и как (это крайне важно) лучше обновить данные, чтобы проверить состояние здоровья в данный момент. И часто в таких случаях у клиента, который думал о том, что у него вторая степень, оказывается плоскостопие третьей степени.
Вывод: со временем плоскостопие может перейти на третью степень, поэтому так важно перепроверять заболевание.
В заключении о плоскостопии 2 степени занижены градусы
Да, и такое периодически бывает. Не нам судить, было ли это сделано умышленно специалистом или это вопрос к качеству оборудования или компетенции врача, который расчертил снимок.
Не нам судить, было ли это сделано умышленно специалистом или это вопрос к качеству оборудования или компетенции врача, который расчертил снимок.
Каждый раз, когда нам звонят молодые люди и говорят, что у них плоскостопие 2-ой степени, мы просим их показать заключения и снимки. Дело в том, что при самой процедуре рентгена стоп крайне важны детали. И мы должны их узнать, чтобы сделать выводы о том, насколько данные верны. Например, нам нужно понимать:
- Как именно вы вставали на рентген?
- Где был центр тяжести?
- Где находились поручни?
- В какое время суток вы делали снимок?
Все это крайне важно. Также у нас зачастую есть вопросы к оборудованию, на котором делали снимок. Порой мы видим снимки из частных центров или районных поликлиник в настолько плохом качестве, что на них можно интерпретировать любые градусы. Все подобные снимки мы сами перепроверяем, а также крайне внимательно проводим визуальный осмотр стоп.
Вывод: снимки и заключения зачастую зависит от множества деталей, начиная с времени проведения обследования и заканчивая качеством самого рентген-оборудования. Поэтому важно их перепроверять.
В заключении указаны верные градусы, но неправильная степень
Ещё один пример непредумышленной ошибки, с которым мы встречались: бывает так, что на консультацию к нам приходили молодые люди, уверенные в том, что у них плоскостопие второй степени. Но смотришь на их стопы, а они визуально с третьей степенью. Слушаешь жалобы, а в них — серьёзный болевой синдром даже при незначительной ходьбе. Проверяешь снимки и заключения, а в них написано «плоскостопие 2 степени с углом в 159 градусов». И понимаешь, что врач просто ошибся цифрой и вместо тройки написал двойку. Так что и в этом случае мы на консультации действуем по принципу «доверяй, но проверяй».
Вывод: врачи — тоже люди и могут допускать опечатки. Так бывает. Поэтому нужно внимательнее читать заключения и разбираться, почему врач написал именно так, а не иначе.
***
Подведу итоги: заключение о плоскостопии второй степени может быть ошибочным и не всегда является приговором. Примерно в 20% случаев у призывников, которые к нам приезжают или звонят, мы видим ошибки в снимках, заключении или самой процедуре рентгена. Все эти детали крайне важны.В таких мы перепроверяем данные и получаем четкое представление о том, что у призывника есть отличные перспективы получить военный билет и мы способны ему в этом помочь.
Новогодние огни зажглись на главной ёлке Большого Подольска 25 декабря
Шумным, веселым и задорным был городской праздник «Новогодний серпантин» в сквере Поколений в субботу, 25 декабря. В течение вечера на главной новогодней площадке царила атмосфера чуда и волшебства, приправленная ароматом мандаринов и свежей выпечки, привлекали внимание гостей световые иллюминации и богатое убранство пушистой красавицы-ели.
В гостях у сказки
Организаторы праздника подготовили увлекательную программу. Со сцены звучали песни и поздравления, а лучшие творческие коллективы учреждений культуры Подольска дарили зрителям красивые хореографические номера под бурные аплодисменты. Дети и взрослые в сопровождении ростовых кукол водили хороводы, отгадывали загадки, пели песни и читали новогодние стихи.
Со сцены звучали песни и поздравления, а лучшие творческие коллективы учреждений культуры Подольска дарили зрителям красивые хореографические номера под бурные аплодисменты. Дети и взрослые в сопровождении ростовых кукол водили хороводы, отгадывали загадки, пели песни и читали новогодние стихи.
Поздравил жителей и гостей Большого Подольска с наступающим Новым годом первый заместитель главы администрации Виктор Чуб. В ходе праздничной программы он вручил Благодарность Президента Российской Федерации Владимира Путина художнику-живописцу Подольского городского отделения «Союз художников России» Владимиру Сиухову и ценные подарки победителям муниципального конкурса на лучшую новогоднюю игрушку-поделку.
Активно принимала участие в конкурсах с призами третьеклассница Лилия с друзьями.
— Встретив здесь своих друзей я обрадовалась, мы сразу же побежали к ёлке петь новогодние песни и водить хоровод, — сказала она. — Веточки у неё пушистые и красивые. Я очень жду приезда Деда Мороза со Снегурочкой, думаю, на наш праздник они очень спешат. Хочется поскорее рассказать стихотворение и получить свой новогодний подарок.
— Веточки у неё пушистые и красивые. Я очень жду приезда Деда Мороза со Снегурочкой, думаю, на наш праздник они очень спешат. Хочется поскорее рассказать стихотворение и получить свой новогодний подарок.
Играли в снежки, фотографировались на фоне главного новогоднего атрибута — нарядной ёлки, с любопытством рассматривали световые иллюминации Екатерина Судакова с двумя младшими сестрами Викторией и Анастасией. Они признались, что всю неделю готовились к городскому празднику и ждали его с нетерпением: придумывали поделки для новогодних выставок, разучивали песни.
— Новый год – это время чудес и хорошего настроения, — сказала Екатерина. — В каждом доме сейчас радостная подготовка к празднику. Вот и мы с сестрами не остались в стороне — установили дома ель, нарядили её, испекли вкусные пироги, а еще я связала нам яркие новогодние шапочки и теплые варежки. И теперь не страшны нам ни мороз, ни холода! Потрясающий праздник организовали, всюду слышен звонкий детский смех!
Посетили сказочный вечер в сквере, порадовали детей сладкими подарками и любимые герои новогоднего праздника — Дед Мороз со своей внучкой Снегурочкой. Держа в одной руке мешок с подарками, а в другой — ледяной посох, добрый волшебник искренне поздравил всех с наступающим Новым годом, после чего поприветствовал будущего хозяина года — Водяного Тигра, который пожелал мальчишкам и девчонкам крепкого здоровья, успехов в новом году и веселых каникул. После чего наступил самый долгожданный и волнующий момент праздника — зажжение огней на 22-метровой ели и красочное огненное шоу с фейерверком. Под дружные возгласы взрослых и детей «Раз, два, три, елочка, гори!» на зеленой красавице вспыхнули разноцветные огоньки.
Держа в одной руке мешок с подарками, а в другой — ледяной посох, добрый волшебник искренне поздравил всех с наступающим Новым годом, после чего поприветствовал будущего хозяина года — Водяного Тигра, который пожелал мальчишкам и девчонкам крепкого здоровья, успехов в новом году и веселых каникул. После чего наступил самый долгожданный и волнующий момент праздника — зажжение огней на 22-метровой ели и красочное огненное шоу с фейерверком. Под дружные возгласы взрослых и детей «Раз, два, три, елочка, гори!» на зеленой красавице вспыхнули разноцветные огоньки.
Ледовая сказка под открытым небом
Одним из главных событий и сюрпризов городского праздника «Новогодний серпантин» стало открытие II Фестиваля-конкурса ледяных скульптур «Сказки планеты Земля». Гостей встречали изысканные образы героев сказок народов мира — Кот в сапогах из произведения Шарля Перро, композиция «Добрыня Никитич и Змей Горыныч» из русской народной сказки, фигура Мухи-Цокотухи из сказки Корнея Чуковского, композиция из чувашского фольклорного произведения «Девушка на Луне» и другие. Особое внимание горожан привлекла скульптура Екатерины II, пописывающей Указ о преобразовании села Подол в город в связи с созданием в составе Московской губернии Подольского уезда.
Особое внимание горожан привлекла скульптура Екатерины II, пописывающей Указ о преобразовании села Подол в город в связи с созданием в составе Московской губернии Подольского уезда.
— Я и представить не могу, сколько времени и сил уходит на создание таких скульптур, — сказала Марина Тибитова. — В каждой из них отчетливо виден талант мастера. Это волшебная сказка! Понравилась скульптура Екатерины Великой. Фигура сделана очень искусно, всё продумано вплоть до мельчайших деталей, не говоря уже про портретное сходство. Здорово, что все произведения искусства подсвечены разноцветными светодиодами, ими можно любоваться и в вечернее время. Такие мероприятия заряжают энергией, дарят всем радость!
Над созданием хрупких ледяных шедевров трудились лучшие скульпторы России, приехавшие в Подольск из разных уголков страны. В течение нескольких дней мастера с помощью подручных инструментов вырезали из бесформенных ледяных глыб оригинальные трехметровые композиции. Как рассказал художник-скульптор из Екатеринбурга Максим Беспалов, волшебство его ледяной фигуры заключается в игре света, потому что именно от структуры льда зависит её сказочное сияние.
Как рассказал художник-скульптор из Екатеринбурга Максим Беспалов, волшебство его ледяной фигуры заключается в игре света, потому что именно от структуры льда зависит её сказочное сияние.
— Моя скульптура называется «Серебряное копытце», она создана по сказке русского писателя Павла Петровича Бажова, — сказал Максим Беспалов. — В эту работу вложено много труда. Ледяной скульптурой я занимаюсь с 2003 года, уже достаточно давно. В летнее время создаю композиции из песка, а также скульптуры с помощью 3D-печати. На создание ледяного шедевра было заявлено 15 блоков, я их все использовал. Вес одного блока примерно 100 кг. В Подольске я впервые, в восторге от города. Очень понравилась дворянская усадьба в Дубровицах.
По итогам фестиваля участников наградили почетными дипломами и памятными подарками. Оценивало работы профессиональное жюри во главе с академиком Российской академии художеств, Заслуженным художником Российской Федерации, Заслуженным работником культуры Московской области Александром Рожниковым. Он рассказал, что особое внимание при оценке ледяных скульптур было обращено на технику и мастерство обработки льда, учитывались композиционное решение и оригинальность.
Он рассказал, что особое внимание при оценке ледяных скульптур было обращено на технику и мастерство обработки льда, учитывались композиционное решение и оригинальность.
— В этом году фестиваль выдался еще ярче, еще масштабнее, — сказал Александр Рожников. — Ребята — молодцы, каждая композиция оригинальна. Низкий поклон подольчанам за сохранение культуры, главе муниципалитета Николаю Пестову — за организацию такого красивого фестиваля. Центральная часть города преобразилась — красивая ёлка, яркая сцена, веселые представления. Я счастлив, что меня во второй раз пригласили выступить в качестве председателя жюри. Пусть люди радуются, что в России есть такие мастера, такой прекрасный город Подольск!
Лауреатами третьей степени стали скульптор из Минска Вадим Бандарец с композицией «Муха-Цокотуха», а также Николай Торхов из Рязани, его ледяная фигура – «Снежная королева». Лауреаты второй степени – Александр Жидков из Пензенской области, композиция «Добрыня Никитич и Змей Горыныч», Иван Савенков из Москвы, его работа – «Сказка о золотом петушке», а также Архип Скрябин из Якутска с композицией «Сказка о рыбаке». Дипломы лауреата первой степени завоевали скульптор из Пензы Сергей Кныш с ледовой композицией «Василиса Прекрасная» и Андрей Молоков из города Чебоксары, его фигура – «Девушка на Луне». Приз зрительских симпатий достался Максиму Беспалову из Екатеринбурга с композицией «Серебряное копытце». Кубок главы Городского округа Подольск завоевал мастер из Сергиево-Посадского городского округа Николай Жданов с композицией «Сказка о царе Салтане», а Кубок скульпторов – Евгений Гоманов из Ростова-на-Дону, его работа «Ворон Кутх». Гран-при фестиваля-конкурса у Александра Скареднова из Тюмени, его работа – «Кот в сапогах».
Дипломы лауреата первой степени завоевали скульптор из Пензы Сергей Кныш с ледовой композицией «Василиса Прекрасная» и Андрей Молоков из города Чебоксары, его фигура – «Девушка на Луне». Приз зрительских симпатий достался Максиму Беспалову из Екатеринбурга с композицией «Серебряное копытце». Кубок главы Городского округа Подольск завоевал мастер из Сергиево-Посадского городского округа Николай Жданов с композицией «Сказка о царе Салтане», а Кубок скульпторов – Евгений Гоманов из Ростова-на-Дону, его работа «Ворон Кутх». Гран-при фестиваля-конкурса у Александра Скареднова из Тюмени, его работа – «Кот в сапогах».
Завершилась программа традиционным красочным фейерверком. В Большом Подольске продолжается череда новогодних праздников и развлечений в рамках проекта «Зима в Подмосковье».
Пресс-служба администрации Городского округа Подольск
Фото Андрея Сигиды
Липецкая область – на 39 месте по привлекательности труда для пенсионеров
Липецкая область в России оказалась на 39 месте по привлекательности труда для пенсионеров. Среди регионов Черноземья она в этом ранжировании заняла последнюю позицию. Исследование провели эксперты РИА Новости.
Среди регионов Черноземья она в этом ранжировании заняла последнюю позицию. Исследование провели эксперты РИА Новости.
Для оценки ситуации на рынке труда в регионах России для пожилых людей эксперты РИА Новости рассчитали индекс привлекательности рынка труда для пенсионеров – в нем учли фактическую занятость пенсионеров, их возможности по поиску работы, абсолютный и относительный уровень зарплаты, а также здоровье и долголетие пожилых людей. Для расчетов использовали девять показателей – кроме уровней занятости и оплаты труда эксперты учли долю безработицы, простоту поиска работы, соотношение зарплат россиян старшего возраста и всех работающих в регионе, комфортность работы и жизни в регионе, продолжительность жизни после выхода на пенсию. Анализ проводился для мужчин 60-72 лет и женщин 55-72 лет.
Анализ проводился для мужчин 60-72 лет и женщин 55-72 лет.
Наиболее благоприятные условия на рынке труда для пенсионеров оказались в Москве и Санкт-Петербурге. Их итоговые баллы составили 70 и 69,2 балла. В этих городах граждане, достигшие пенсионного возраста, зачастую продолжают работать и получать достойную зарплату. Кроме того, им легче найти новую работу после увольнения. В первую десятку также вошли Ленинградская область (60) Воронежская область (59,7), Нижегородская область (58), Ростовская область (55,2), Калининградская область (52,4), Краснодарский край (50,7) и Рязанская область (48). На другом конце рейтинга расположились в основном национальные республики, что говорит о невысокой привлекательности рынка труда для пенсионеров в них – аутсайдерами стали республика Алтай, Чечня, Тува, Бурятия, Северная Осетия—Алания с индексом от 12,4 до 22,5.
Липецкая область оказалась в рейтинге на 39 месте, кроме того, она не смогла обойти ни один из регионов Центрального Черноземья: так, Воронежская область по привлекательности рынка труда для пенсионеров обосновалась на четвертом месте, Курская область – на 13, Тамбовская область – на 23, Белгородская – на 28.
Симптомы и способы лечения цистита
Циститы в холодное время года — явление нередкое, переохлаждение — один из главных провокаторов этой болезни. А сейчас впереди ещё и череда корпоративов и семейных праздников, на которые многим захочется нарядиться, а красивая одежда далеко не всегда тёплая, к сожалению. Поэтому сегодня в нашей рубрике «Что у вас болит?» говорим о цистите: выяснили у врачей, откуда он берётся и лечится ли подручными средствами по бабушкиным рецептам.
Откуда берётся цистит?
Цистит — это вызываемое бактериями острое инфекционное заболевание мочевого пузыря. Провоцирующих факторов много: это и повреждение слизистой оболочки мочевого пузыря, и варикозное расширение вен, и гормональный дисбаланс. Также провоцировать болезнь могут сахарный диабет, ИППП, гиподинамия, ожирение, мочекаменная болезнь, аномальное строение мочевыводящих путей и длительное использование мочевого катетера. И вроде бы мочевой пузырь есть у всех, но подвержены циститу чаще женщины — в силу особенностей строения мочеполовой системы.
— Мужчины болеют крайне редко, за 15 лет практики я могу случаи по пальцам пересчитать, как правило, это осложнения другого заболевания, например уретрита или простатита, а также следствие аденомы простаты. У женщин из-за того, что уретра короткая, восходящим путём инфекция попадает в мочевой пузырь и вызывает цистит, — говорит врач-уролог «Новой больницы» Андрей Меркулов. — У мужчин это, как правило, сильное переохлаждение, связанное с зимней рыбалкой, например.
У женщин факторов риска больше. Есть такой вариант цистита, как посткоитальный, то есть связанный с половым контактом. Он может возникать в том числе при начале половой жизни, поэтому его ещё называют «циститом медового месяца».
— В плане возраста наиболее подвержены циститам женщины после 50–55 лет и сексуально активные женщины в репродуктивном возрасте. Особенно когда речь идёт о незащищённых или бесконтрольные половых связях. Речь не идёт только о половой инфекции, это может быть попадание в мочевыводящие пути даже своих же бактерий. У меня была пациентка, у неё вернулся муж из командировки, и после секса с ним возник цистит.
У меня была пациентка, у неё вернулся муж из командировки, и после секса с ним возник цистит.
До этого проблем не было, 5 лет они женаты. Выяснилось, что, пока он был в командировке, женщина удалила зуб и стоматолог-хирург назначил ей сильный антибиотик. Он вызвал нарушение нормальной микрофлоры кишечника и дисбиоз влагалища, поскольку пациентке при ее стройном телосложении не были назначены пробиотик и противогрибковый препарат в профилактических целях. Из-за близкого расположения уретры к влагалищу произошло попадание инфекции в мочевой пузырь, — объясняет врач.
В большинстве случаев циститы вызывает кишечная флора, но может оказаться, что бактерия попала из дыхательных путей, носоглотки. Кишечная палочка Escherichia coli становится причиной примерно 85% циститов — у неё есть микрофибры, и она успешно закрепляется в мочевыводящих путях, даёт колонии. В 10–20% виновником оказывается стафилококк Staphylococcus spp.
Ещё реже — бактерии Klеbsiеlla pnеumoniaе и Protеus mirabilis.
— Когда девушка идёт к гинекологу и сдаёт мазок на собственный бактериальный фон, там может присутствовать та же кишечная бактерия, но в концентрации 10 во второй-третьей степени это никто не будет лечить. Так же и в мочевыводящих путях: в норме бактерии у нас у всех попадают в мочу, но если она не превысит эту концентрацию, организм её свободно убивает.
А если ей удалось закрепиться и концентрация превысила 10 в четвёртой степени — это воспалительный процесс. Я всегда пациенткам говорю: если у вас неблагоприятный бактериальный фон во влагалище (кандидозы, дисбиозы, бактовагинозы), вопрос попадания инфекции в мочевыводящие пути по короткой уретре — это вопрос времени. Поэтому мы часто работаем в связке с гинекологом, — объясняет уролог.
Как лечат цистит?
Способ только один — антибиотик. Бактерии в моче быть не положено — она от природы стерильна, там нет бактерий. Антибиотик убивает в моче бактерию — пациент здоров.
— Всё остальное: травы, спазмолитики, обезболивающие — это всё симптоматическая терапия. Патогенетическая, самая основная — антибиотик, — объясняет Андрей Меркулов. — Как правило, уролог у нас в стране стоит на четвёртом месте в лечении цистита. На первом у нас мамы, бабушки, подруги, сестры, на втором — фармацевты в аптеке, на третьем — терапевты и гинекологи, потом только уролог, хотя это основной специалист по лечению цистита.
Патогенетическая, самая основная — антибиотик, — объясняет Андрей Меркулов. — Как правило, уролог у нас в стране стоит на четвёртом месте в лечении цистита. На первом у нас мамы, бабушки, подруги, сестры, на втором — фармацевты в аптеке, на третьем — терапевты и гинекологи, потом только уролог, хотя это основной специалист по лечению цистита.
Нередко к урологу попадают, когда процесс уже запущен или не поддаётся лечению подручными средствами. А лечить цистит нужно сразу же. Попадание бактерии в мочевыводящие пути чревато восходящей инфекцией в почку: если не лечить цистит, он может осложниться пиелонефритом.
— У одной пациентки может быть вялотекущая симптоматика в течение длительного времени, у другой — за пару дней инфекция поражает почку, — говорит доктор. — Острый цистит чаще всего лечится 3–5 дней, а пиелонефрит не менее 10 и даже 14. Если цистит возникает регулярно и лечится неправильно, то может перерасти в хроническую форму, тогда уже недостаточно медикаментозного лечения в виде таблеток, необходимо проводить дополнительное обследование и проводить комплексную терапию в виде инстилляций (вливания — прим. ред.) в мочевой пузырь лекарственных препаратов, чтобы заживить травмированные стенки мочевого пузыря.
ред.) в мочевой пузырь лекарственных препаратов, чтобы заживить травмированные стенки мочевого пузыря.
Нельзя при цистите принимать алкоголь и агрессивную пищу — острое, перченое, солёное. Пациенткам рекомендуется половой покой. Если болит низ живота, в отличие от других болезней, можно использовать тепло: приложить грелку или лечь в горячую ванну — это расслабляет спазмированный мочевой пузырь.
Однако тепло разрешается только при условии, что цистит ничем не осложнён и воспаление не начало подниматься выше. Если к обычным симптомам цистита добавляются слабость, озноб, повышение температуры и боли в пояснице, греться нельзя ни в коем случае. Снимать спазмы также можно с помощью дротаверина, однако это не должно быть основным лечением — дротаверин только снимет болевой симптом.
Что ещё почитать о здоровье?
— развенчиваем с врачами мифы о половых инфекциях: как часто сдавать анализы и когда пора к врачу;
— задаём гинекологу «стыдные» вопросы, которые пациентки боятся задать сами;
— разбираемся, что такое ПМС на самом деле и можно ли его вылечить.
Степени и экспоненты
Степень — это произведение числа на себя.
Обычно степень представлена с помощью базового числа и показателя степени. Базовое число сообщает , какое число умножается. Показатель , — небольшое число, написанное выше и справа от основного числа, сообщает , сколько раз умножается базовое число.
Например,? 6 в 5-й степени? можно записать как? 6 5 .? Здесь базовое число 6, а показатель степени 5. Это означает, что 6 умножается на себя 5 раз: 6 x 6 x 6 x 6 x 6
6 x 6 x 6 x 6 x 6 = 7,776 или 6 5 = 7,776
| базовый номер | 2-я степень | 3-я степень | 4-я степень | 5-я степень |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1,024 |
| 5 | 25 | 125 | 625 | 3,125 |
| 6 | 36 | 216 | 1,296 | 7,776 |
| 7 | 49 | 343 | 2,401 | 16,807 |
| 8 | 64 | 512 | 4,096 | 32,768 |
| 9 | 81 | 729 | 6,561 | 59,049 |
| 10 | 100 | 1,000 | 10,000 900 | 100,000 |
| 11 | 121 | 1,331 | 14,641 | 161,051 |
| 12 | 144 | 1,728 | 20,736 | 248832 |
Факториалы Таблица умножения чисел и формул в 5 степени?
Корни и степени алгебраических выражений
При решении алгебраических выражений обязательно знать, когда корни и степени могут или не могут быть распределены по всему уравнению. Узнайте о правилах экспонент, корней и степеней для эффективного решения алгебраических выражений на экзамене SAT.
Узнайте о правилах экспонент, корней и степеней для эффективного решения алгебраических выражений на экзамене SAT.
Элементы анализа влияния на бизнес
Анализ воздействия на бизнес (BIA) определяет важные бизнес-операции и собирает информацию для планирования непредвиденных событий, которые могут остановить эти операции.Определите процессы сбора данных, анализа, приоритезации подразделения и важность получения одобрения.
Экспоненты и корни: определение и примеры
Экспоненты и корни используются, чтобы сделать числа намного больше или намного меньше.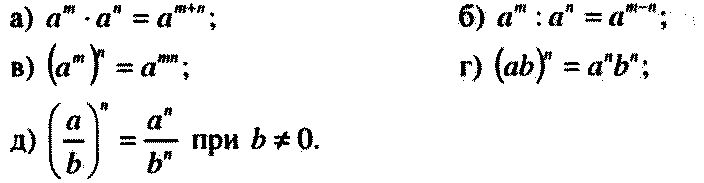 В этом уроке мы узнаем, как работать с экспонентами и корнями. Мы попрактикуемся в решении множества задач с обоими, включая примеры с отрицательными числами.
В этом уроке мы узнаем, как работать с экспонентами и корнями. Мы попрактикуемся в решении множества задач с обоими, включая примеры с отрицательными числами.
Решение рациональных уравнений с буквальными коэффициентами
Буквальные коэффициенты — это представители известных или неизвестных переменных, которые используются для представления числа.Изучите определение буквальных коэффициентов и изучите метод нахождения общего знаменателя и решения рационального уравнения.
Что такое переменная в алгебре?
В алгебре переменная — это любая буква или символ, представляющий число с неизвестным значением. Изучите части алгебраической задачи, которые являются переменными, константами и коэффициентами, поймите, почему используются переменные, и проанализируйте практические задачи.
Изучите части алгебраической задачи, которые являются переменными, константами и коэффициентами, поймите, почему используются переменные, и проанализируйте практические задачи.
Площадь треугольников и прямоугольников
Площадь двухмерной фигуры представляет собой пространство, охватываемое ее периметром, но расчеты площади меняются в зависимости от фигуры.Узнайте, как вычислять и решать площади прямоугольных, наклонных и наклонных треугольников.
Как разложить квадратные уравнения на множители: FOIL in Reverse
Метод FOIL можно использовать в обратном порядке для определения стандартных кратных из заданного уравнения. Узнайте, как разложение квадратных уравнений на множители с помощью FOIL в обратном порядке применяется к умножению биномов и разложению уравнений для упрощения квадратных уравнений.
Узнайте, как разложение квадратных уравнений на множители с помощью FOIL в обратном порядке применяется к умножению биномов и разложению уравнений для упрощения квадратных уравнений.
Как найти неизвестное в пропорции
В какой-то мере поиск неизвестного может быть проблемой.На этом уроке вы узнаете, как найти эти неизвестные в пропорциях, а затем посмотрите, что такое пропорция, вычислите пропорции и проверьте результаты этих вычислений.
Упрощение квадратного корня из частных
Узнайте, как упростить извлечение квадратного корня. См. Примеры, включая квадратный корень из дроби, квадратный корень из переменных и квадратные корни в знаменателе.
См. Примеры, включая квадратный корень из дроби, квадратный корень из переменных и квадратные корни в знаменателе.
Как записывать наборы с использованием нотации Set Builder
В математике обозначение набора определяет критерии и свойства набора с помощью символов.Узнайте, что такое нотация множеств, изучите нотацию множеств с числами и узнайте, как писать множества, используя нотацию построителя множеств.
Практика упрощения алгебраических выражений
Алгебраические выражения упрощаются с помощью двух полезных концепций: объединения одинаковых терминов и свойства распределения. Узнайте, как использовать объединение подобных терминов и свойство распределения для упрощения алгебраических выражений, и поймите решения практических задач.
Узнайте, как использовать объединение подобных терминов и свойство распределения для упрощения алгебраических выражений, и поймите решения практических задач.
Обратная функция — это функция, которая отменяет предыдущую функцию и выражается со степенью отрицательной.Изучите обратные функции, подтвердите обратные, найдите обратные и узнайте о тесте горизонтальной линии.
Умножение бинома на одночлен
Одночлены (одночлены) можно умножить на двучлены (двучлены), используя свойство распределенности. Узнайте, как свойство распределения позволяет умножать члены в круглых скобках и за их пределами, решая примеры уравнений.
Узнайте, как свойство распределения позволяет умножать члены в круглых скобках и за их пределами, решая примеры уравнений.
Четвертая и пятая степени.
Иллюзия разделения мировой власти Хотя глупость — очень разрозненная сущность, в конце концов, она всегда остается абсолютной и высшей силой человеческого рода.
Карл Уильям Браун
Разделение властей — это модель управления государством.Модель впервые была разработана в Древней Греции и Риме. Согласно этой модели, государство разделено на ветви, каждая из которых имеет отдельные и независимые полномочия и зоны ответственности, так что полномочия одной ветви не противоречат полномочиям, связанным с другими ветвями. Обычно ветви делятся на законодательную, исполнительную и судебную.
Аристотель впервые упомянул идею «смешанного правительства» или гибридного правительства в своей работе «Политика», где он опирался на многие конституционные формы городов-государств Древней Греции. В Римской республике римский сенат, консулы и ассамблеи показали пример смешанного правительства согласно Полибию.
В Римской республике римский сенат, консулы и ассамблеи показали пример смешанного правительства согласно Полибию.
Термин «трехсторонняя система» принадлежит французскому политическому философу эпохи Просвещения барону де Монтескье. Монтескье описал разделение политической власти между законодательной, исполнительной и судебной властями. Подход Монтескье заключался в том, чтобы представить и защитить форму правления, которая не была чрезмерно централизована во всех своих полномочиях в пользу одного монарха или подобного правителя.Он основал эту модель на Конституции Римской республики и британской конституционной системе. Монтескье придерживался мнения, что Римская республика разделяла власть, так что никто не мог узурпировать полную власть. В британской конституционной системе Монтескье видел разделение властей между монархом, парламентом и судами. Монтескье действительно указал, что «независимость судебной власти должна быть реальной, а не просто очевидной». «Судебная власть обычно рассматривалась как самая важная из властей, независимая и неконтролируемая», а также считалась опасной.
Политические СМИ — это средства коммуникации, принадлежащие, управляемые, управляемые или иным образом находящиеся под влиянием политических субъектов, предназначенные для распространения взглядов на связанную сущность. Подобный термин, нормативные СМИ, подчеркивает технические и социальные характеристики самих СМИ при принятии решений. Гарольд Иннис, а затем Маршалл Маклюэн, оба канадских теоретика СМИ, оказали влияние на разработку этой теории. В то время как в официальной газете, журнале, телеканале легко распознать политическое средство массовой информации, которое прямо заявляет о своей принадлежности к какой-либо группе, серьезные опасения могут быть связаны с передачей сообщений политическим интересам и беспристрастностью СМИ, которые не декларируют свои партийные союзы.
Это влияние не всегда заметно и заставляет людей принимать идеи, выдвигаемые теми, кто хочет контролировать коммуникацию на благо общества, или заставляет тех, кто поддерживает свободу общения и расширение прав и возможностей меньшинств, выступать против них. Некоторые считают, что большие общества действительно нуждаются в канализации коммуникации. В этом смысле политические СМИ часто предназначены для формирования или, по крайней мере, влияния на общественное мнение, наименее общий знаменатель для всех членов общества.
Некоторые считают, что большие общества действительно нуждаются в канализации коммуникации. В этом смысле политические СМИ часто предназначены для формирования или, по крайней мере, влияния на общественное мнение, наименее общий знаменатель для всех членов общества.
Это улица с односторонним движением, которую иногда используют не по назначению.Греки могли извлечь уроки из Египта фараонов, что некоторые риски могут возникнуть, когда медиум и руководители находятся в личном союзе, концентрируя слишком много власти в одних руках. Это, однако, подразумевает признание концепции СМИ как власти, которая широко, но не всегда разделяется. Противники действительно утверждают, что простой факт создания сообщения сам по себе не приводит к прямым результатам в общественном мнении, если только это не рассматривается как просто пассивная масса перед непреодолимой коммуникацией …
Современные демократические теории и их реализации, особенно после теорий Монтескье, основываются на разделении властей: исполнительная (правительство и полиция), законодательная (парламент) и судебная (суд) ветви власти разделены. Обычно в последнее время, особенно на журналистском жаргоне, СМИ, тем не менее, определяются как мнимая четвертая власть, и отличие от других часто выражается в том, что способность (в конечном итоге) влиять на общественное мнение с помощью СМИ не сильно контролируется. , потому что медиа такие «эфирные», и их будет сложно взвесить.
Обычно в последнее время, особенно на журналистском жаргоне, СМИ, тем не менее, определяются как мнимая четвертая власть, и отличие от других часто выражается в том, что способность (в конечном итоге) влиять на общественное мнение с помощью СМИ не сильно контролируется. , потому что медиа такие «эфирные», и их будет сложно взвесить.
Другие вместо этого предполагают, что это не будет разницей, поскольку контроль над официальными полномочиями чрезвычайно трудно проверить на практике.Действительно, зачастую бывает нелегко выяснить, кто действительно контролирует среду и какую потенциальную эффективность она может иметь для достижения этих целей. Затем утверждается, что когда одна из трех «канонических» властей Монтескье получает дополнительную власть в СМИ, это было бы чрезвычайно опасно для выживания демократии, и возможный конфликт интересов оспаривается.
Наконец, что не менее важно, у нас есть пятая власть, термин, очевидно созданный Игнасио Рамонетом, который намеревается продолжить серию из трех классических ветвей разделения властей барона де Монтескье и четвертой власти, средств массовой информации. Термин «пятая власть» может использоваться для обозначения экономических систем, Интернета или церкви.
Термин «пятая власть» может использоваться для обозначения экономических систем, Интернета или церкви.
Если под пятой степенью имеется в виду экономическая система, это относится к власти, которую правительство оказывает в экономической сфере через государственные компании и механизм экономического вмешательства, который по своей сути является финансовым. Исторически отношения между властью и экономикой определялись в узких рамках, прежде всего как меркантилизм Нового времени. Однако, поскольку U.С. крах фондового рынка 1929 г., возникли четыре современные позиции: капитализм защищает минимальное или вспомогательное государство, ограниченное законодательством, которое способствует эффективному функционированию свободного рынка. Эта система, впервые предложенная Адамом Смитом, получила распространение в духе глобализации, преобладавшей после падения Берлинской стены.
Социализм защищает общую собственность рабочих и контроль над средствами производства и собственностью в целом, а также за построение плановой экономики.
Фашизм отстаивает центральный авторитарный стиль экономического вмешательства, который обычно определяется как корпоративизм.
Социал-демократия выступает за государственное регулирование частного предпринимательства и контроль над частной конкуренцией, справедливую торговлю, прогрессивное налогообложение и государственное финансирование программ, субсидируемых государством. В этой системе стратегические секторы, такие как транспорт, энергетика и военный сектор, могут контролироваться государственным сектором.
Вторым кандидатом в «пятую власть» является Интернет, который представляет собой новый вид социального средства массовой информации, которое не может быть включено в более узкую, одностороннюю сферу СМИ четвертой власти.Если рассматривать ее как пятую ветвь власти, то она единственная, которая контролируется самим обществом без регулирования со стороны государства.
Согласно Ramonet, пользователи Интернета вместе образуют мощный двигатель дебатов и демократических действий. С глобализацией 21 век может, наконец, принести общение и информацию всем людям. «Человек года» 2006 года журнала Time (ВЫ в зеркале экрана ПК) несет то же самое сообщение.
С глобализацией 21 век может, наконец, принести общение и информацию всем людям. «Человек года» 2006 года журнала Time (ВЫ в зеркале экрана ПК) несет то же самое сообщение.
Интернет — это одновременно массовая и личная среда, гибкая и масштабируемая.Интернет обеспечивает способ коммуникации, который невозможно было предвидеть в обществах прошлого. Как писал Маклюэн: «В этот электрический век мы видим, что мы все больше и больше переводим себя в форму информации, продвигаясь к технологическому расширению сознания» (Маклюэн , 86) ». Программное обеспечение потенциально может позволить цементировать структуры, которые противостоят демократии и конкуренции идей, а также структуры, которые могут получить достаточно полный контроль над частными коммуникациями и изолировать возможные голоса несогласных.
В настоящее время Сеть не может быть полностью идентифицирована как политическая среда из-за отсутствия центральной власти и общей политической коммуникации. На местном уровне правительства в действительности могли бы использовать цензуру, первые эксперименты которой были восприняты с относительно небольшим скандалом.
Еще одним сильным кандидатом на титул «Пятой державы» является церковь из-за концепции отделения церкви от государства. Эта концепция была принята в ряде стран в разной степени в зависимости от применимых правовых структур и преобладающих взглядов на надлежащую роль религии в обществе.Эта концепция отделения власти Церкви от трех других властей государства намного старше, чем концепции власти Экономики или власти Интернета.
Уловка пятого корня | Найдите 5-й корень в своей голове
У Numberphile есть хорошее видео, посвященное уловке с корнем пятой степени: кто-то возводит двузначное число в пятую степень, читает его вслух, и вы сразу же сообщаете им, какое это было число.
Вот вкратце трюк.Для любого числа n , n 5 оканчивается той же последней цифрой, что и n . Вы можете доказать это грубой силой или теоремой Эйлера. Поэтому, когда кто-то говорит вам n 5 , вы сразу узнаете последнюю цифру. Теперь вам нужно найти первую цифру, и вы можете сделать это, приблизительно изучив степени (10k) 5 для i = 1, 2, 3,…, 9. Затем вы можете определить первую цифру с помощью диапазон.
Вы можете доказать это грубой силой или теоремой Эйлера. Поэтому, когда кто-то говорит вам n 5 , вы сразу узнаете последнюю цифру. Теперь вам нужно найти первую цифру, и вы можете сделать это, приблизительно изучив степени (10k) 5 для i = 1, 2, 3,…, 9. Затем вы можете определить первую цифру с помощью диапазон.
Вот где видео немного расплывчато.В нем говорится, что вам не нужно очень точно знать степень 10 k . Это правда, но насколько точно и вам нужно знать диапазоны?
Если двузначное число кратно 10, вы узнаете нули в конце, а последняя ненулевая цифра будет первой цифрой n . Например, если n 5 = 777 600 000, то вы знаете, что n кратно 10, а поскольку последняя ненулевая цифра равна 6, n = 60.5 | | — + ————— + ————— | | 1 | 59 049 | 161,051 | | 2 | 2,476,099 | 4,084,101 | | 3 | 20,511,149 | 28 629 151 | | 4 | 90,224,199 | 115,856,201 | | 5 | 282 475 249 | 345 025 251 | | 6 | 714,924,299 | 844,596,301 | | 7 | 1,564,031,349 | 1 804 229 351 | | 8 | 3,077,056,399 | 3 486 784 401 | | 9 | 5,584,059,449 | 6,240,321,451 | | — + ————— + ————— |
Таким образом, любая пятая степень меньше миллиона имеет однозначный корень пятой степени. Любое число от 1 до 3 миллионов имеет первую цифру 1. И т. Д.
Любое число от 1 до 3 миллионов имеет первую цифру 1. И т. Д.
Если хотите, можете выбрать следующие границы.
| --- + ---------------- | | k | верхняя граница | | --- + ---------------- | | 1 | 1,000,000 | | 2 | 3,000,000 | | 3 | 25,000,000 | | 4 | 100,000,000 | | 5 | 300,000,000 | | 6 | 800,000,000 | | 7 | 1,700,000,000 | | 8 | 3,200,000,000 | | 9 | 6,000,000,000 | | --- + ---------------- |
В видеоролике Numberphile говорится, что вам нужно попросить кого-нибудь произнести номер вслух, словами.Итак, как только вы слышите «шесть миллиардов…», вы знаете, что первая цифра n — 9. Если вы слышите «пять миллиардов» или «четыре миллиарда», вы знаете, что первая цифра — 8. Если вы слышите «три миллиарда». », Тогда вы должны обратить внимание на следующее число, чтобы решить, будет ли первая цифра 7 или 8. Когда вы услышите несколько первых слогов числа, вы можете перестать обращать внимание, пока не услышите последний или два слога.
020: Пятая держава (4 или 6 членов)
III. Сумма / суммы пятых степеней
Сумма / суммы пятых степеней
5.1 Четыре члена
5.2 Шесть членов
5,3 Семь терминов
5,4 Восемь членов
5,5 Десять членов
5,6 Двенадцать членов
5.1 Четыре члена
Хотя предполагается, что x 1 k + x 2 k = y 1 k + y 2 k не имеет нетривиальных рациональных решений для k> 4, — это солнц как корни квадратичных систем для k = 5.
А. Дебовес
(a√2 + b) 5 + (-b + c√-2) 5 = (a√2-b) 5 + (b + c√-2) 5
, где a 2 + b 2 = c 2 .
Пьезы
(√p + √q) 5 + (√p-√q) 5 = (√r + √s) 5 + (√r-√s) 5
{p, q, r, s} = {5vw 2 , -1 + uw 2 , 5v, — (u + 10v) + w 3 }, где w = u 2 + 10uv + 5в 2 .
Тогда можно установить v = 5t 2 так, чтобы {p, r} были квадратами. Другой вопрос, можно ли сделать из {q, s} нетривиальных квадратов. В более общем смысле, приведенное выше уравнение для k = 5,6,7,8 имеет полиномиальное soln, и первые два могут быть приведены к общей форме. Для k = 5 это уменьшается до,
√p (p 2 + 10pq + 5q 2 ) = √r (r 2 + 10rs + 5s 2 )
, тогда {p, q, r, s} = {5 (bc-ad) v 2 , u 3 — (10bc + w) v 2 , 5 (bc-ad) u 2 , -v 3 + (10ad + w) u 2 }
, где {u, v, w} = {a 2 + 10ab + 5b 2 , c 2 + 10cd + 5d 2 , ac + 5bd}
с четырьмя свободными переменными {a, b, c, d}.Для k = 6,
(√p + √q) 6 + (√p-√q) 6 = (√r + √s) 6 + (√r-√s) 6
или после расширения,
(p + q) (p 2 + 14pq + q 2 ) = (r + s) (r 2 + 14rs + s 2 )
, тогда {p, q, r, s} = {-u 2 + vw, u 2 -vx, v 2 -ux, -v 2 + uw}
, где {u, v, w, x} = {a 2 + 14ab + b 2 , c 2 + 14cd + d 2 , ac + bc + 13ad + bd, ac + 13bc + ad + bd}
Форма: (p + cq) (p 2 + apq + bq 2 ) k = (r + cs) (r 2 + ars + bs 2 ) k
Это обобщает две вышеупомянутые формы, и, как уже обсуждалось в разделе Третьи силы , требуется лишь небольшое преобразование, чтобы принять c = 0 без потери общности. Этот автор нашел soln с c = 0 as,
Этот автор нашел soln с c = 0 as,
{p, q, r, s} = {bvw k , -1 + uw k , bv, — (u + av) + w k + 1 }, где w = u 2 + auv + bv 2
для произвольных u, v . Примечание: это можно доказать для k = 1,2. Используя компьютерную алгебру, легко увидеть, что это верно и для других малых k> 2. Но у меня нет доказательств, что это так для всех натуральных k.
5.2 Шесть членов: x 1 5 + x 2 5 + x 3 5 = x 4 5 + x 5 5 + x 6 5
(Для базы данных solns <более 5000> в радиусе поиска 17700 см. Результаты Дункана Мура здесь.)По работам Эйлера,
a k + b k = c k + d k
для k = 3 или 4 и последующие работы других авторов, следующим шагом было открытие полинома от солнц до,
a k + b k + c k = d k + e k + f k
для k = 5 или 6, с первым для k = 5 Састри и Чоула в 1934 году, а затем для k = 6 Рао, Брудно и т. Д.Ли,
Д.Ли,
a k + b k + c k + d k = e k + f k + g k + h k
для k = 7 или 8, как окажется, будет иметь полиномиальные solns, еще предстоит увидеть, поскольку теперь известны конкретные sols в целых числах для обоих, с более чем сорока для k = 7, так как Экл нашел первое в 1996 году и только один пока что для k = 8, найденный Куосой в 2006 году.
(Обновление: 20.06.09) Особые случаи :
a) x 1 5 + x 2 5 + x 3 5 + x 4 5 + x 5 5 = 0
Это противоречит гипотезе Эйлера о сумме степеней, и для пятой степени пока известно только три :
(1967) [27, 84, 110, 133, -144] = 0 (по Л.Ландер, Т. Паркин)
(1996) [5027, 6237, 14068, -220, -14132] = 0 (Р. Шер, Э. Зайдл)
Шер, Э. Зайдл)
(2004) [55, 3183, 28969, 85282, -85359] = 0 (по Дж. Фраю)
Можно ли это свести к решению эллиптической кривой, как для версии четвертой степени x 1 4 + x 2 4 + x 3 4 = x 4 4 все еще остается быть увиденным.
b) x 1 5 + x 2 5 + x 3 5 + x 4 5 + x 5 5 = 1
Точно так же, как три третьих степени целых чисел со знаком могут суммироваться до 1 (известный пример которого включает номер такси 1729 = 1 3 + 12 3 = 9 3 + 10 3 ), пять пятых степеней также могут это сделать.Пока найдено только восемь. Наименьшее из них было предоставлено Лендером, Паркином и Селфриджем, а три других были позже предоставлены Сейджи Томитой, которые были независимо обнаружены Дунканом Муром, который также дал еще четыре:
[1, 89, 118] = [38, 47, 123]
[1, 127, 430] = [16, 310, 412]
[1, 328, 709] = [5, 388, 705]
[1, 588, 772] = [59, 511, 791]
[1, 561, 1151] = [401, 616, 1146]
[1, 1073, 2297] = [379, 686, 2306]
[1, 4167, 4283] = [1039, 2601, 4811]
[1, 4823, 6377] = [1089, 3501, 6611]
Примечание 1 : Мур провел поиск в радиусе 17700, и это единственные солнечные лучи, которые имеют единичный член. Тем не менее, это также включает термин с нулями , найденный Бобом Шером и Эдом Зайдлом в 1997 году,
Тем не менее, это также включает термин с нулями , найденный Бобом Шером и Эдом Зайдлом в 1997 году,
[0, 220, 14132] = [5027, 6237, 14068]
, хотя другой такой формы неизвестен. Предположительно, чем больше радиус, тем больше шансов найти еще одного.
Примечание 2 : сумма и разности 5 шестых степеней могут в сумме равняться единице, и в радиусе 17800 Мур нашел пять,
[1, 132, 133] = [71, 92, 147]
[1, 173, 294] = [75, 154, 295]
[1, 55, 330] = [159, 268, 311]
[1, 500, 515] = [197, 409, 556]
[1, 1123, 1143] = [573, 815, 1255]
Можно предположить, что если радиус достаточно велик, то может быть и член нуль .(Хотя, как ни странно, солнцев с единичным членом в диапазоне 2000-17000 больше нет.)
Примечание 3 : семь 7-й степени также могут суммировать до 1, хотя пока известны только две, и могут ли они также суммировать до нуля, как для 5-й степени, вероятно, но пример все еще неизвестен. Глянь сюда.) Томита дал полную таблицу [x 1 , x 2 , x 3 ] = [x 4 , x 5 , x 6 ] для положительных результатов x i <1000, и Мур составил таблицу побольше с суммой почти 18 000 5 .Когда все члены являются целыми числами с одним равным единице, неизвестно, может ли существовать параметризация, в отличие от третьих степеней, где существует бесконечное семейство, которое, как показала недавняя работа этого автора, включает уравнение Пелла. Soln еще не известен для 1+ x 2 5 + x 3 5 + x 4 5 + x 5 5 = z 5 с положительным x i , как видно из базы данных Джеймса Уолдби с z <10,000.(Для семь 5 th степеней, равных единице, — это формулы , также зависящие от уравнений Пелла, которые будут приведены позже.
Глянь сюда.) Томита дал полную таблицу [x 1 , x 2 , x 3 ] = [x 4 , x 5 , x 6 ] для положительных результатов x i <1000, и Мур составил таблицу побольше с суммой почти 18 000 5 .Когда все члены являются целыми числами с одним равным единице, неизвестно, может ли существовать параметризация, в отличие от третьих степеней, где существует бесконечное семейство, которое, как показала недавняя работа этого автора, включает уравнение Пелла. Soln еще не известен для 1+ x 2 5 + x 3 5 + x 4 5 + x 5 5 = z 5 с положительным x i , как видно из базы данных Джеймса Уолдби с z <10,000.(Для семь 5 th степеней, равных единице, — это формулы , также зависящие от уравнений Пелла, которые будут приведены позже. )
)c) x 1 5 + x 2 5 + x 3 5 + x 4 5 + x 5 5 = y 1 5 + y 2 5 + y 3 5 + y 4 5 + y 5 5 = z 5
Наименьшее число, у которого третья степень выражается как сумма трех положительных третьих степеней в двух путях , равно 41 как,
[2, 17, 40] = [6, 32, 33] = [41]
Для четвертых степеней как четырех четвертых степеней двумя способами, Ярек Вроблевски нашел, что это 31127 (см. Базу данных Вроблевского здесь),
[2260, 4870, 17386, 30335] = [2495, 11998, 16430, 30320] = [31127]
Первая пятая степень , выражаемая как сумма пяти положительных пятых степеней двумя способами, была найдена Уолдби как 744,
.
[14, 95, 545, 586, 644] = [100, 210, 414, 629, 651] = [744]
( Примечание : Между прочим, число 744 занимает видное место в j-функции j (τ) , поскольку это постоянный член его расширения в ряд,
j ( τ ) = 1 / q + 744 + 196884q + 214q 2 +…
, который объясняет, почему постоянная Рамануджана (и другие) превышает куб почти на эту величину, e π√163 ≈ 640320 3 + 744, хотя это свойство 744 5 , вероятно, не связано.)
d) a 5 + 2b 5 + 2c 5 = d 5
Есть солнце к 4 + 2b 4 + 2c 4 = d 4 , наименьшее из которых похоже на пифагорейское: [2, 2, 3, 4, 4] = [5] . Есть также один для пятой степени, пока единственный, представленный в базе данных Уолдби как: [526, 526, 1349, 1349, 1355] = [1685]
e) x 1 k + x 2 k + x 3 k = x 4 k + x 5 k + x 6 k
Наименьшее soln оказывается хорошим для как k = 1,5: [24, 28, 67] = [3, 54, 62].
Для шестой степени наименьшая подходит для и k = 2,6: [3, 19, 22] = [10, 15, 23].
Фактически, из 198 солнц в базе данных Томиты для [5.3.3], цитированной выше, которая является полной для членов <1000, почти 2/3 (66%) подходят для k = 1,5. Было бы интересно проверить процентное соотношение [6.3.3] с членами ниже границы, которая подходит для k = 2,6. Почему они внезапно стали хорошими для и двух степеней — это пища для размышлений, но может быть просто из-за увеличения числа членов и симметричного характера уравнения.Для более высоких степеней также с минимальным количеством членов есть solns, действительные для трех степеней , например,
[344, 902, 1112, 1555] = [479, 662, 1237, 1535], для k = 1,3,7
и другие, найденные А. Дж. Чоудри всякий раз, когда некоторая кубика с несколькими переменными имеет рациональный корень. А также,
[51, 253, 412, 600, 624] = [100, 187, 429, 603, 621], для k = 1,3,9
, найденный Вроблевски, и пока единственный. Есть только один известный [8.4.4], найденный Куосой, но я уверен, что один в конечном итоге окажется подходящим для k = 2,8 или, если он подписан, даже подходящим для k = 1,2,8, как некоторые к = 1,2,6. ( Конечная нота )
Есть только один известный [8.4.4], найденный Куосой, но я уверен, что один в конечном итоге окажется подходящим для k = 2,8 или, если он подписан, даже подходящим для k = 1,2,8, как некоторые к = 1,2,6. ( Конечная нота )
(Обновление, 03.11.09): f) x 1 k + x 2 k + x 3 k = x 4 k + x 5 k + x 6 k , с x 1 + x 2 + x 3 = x 4 + x 5 + x 6 = 0
Внизу этой веб-страницы я спросил, есть ли в этой системе для k = 1,5 нетривиальные солнечные лучи по сравнению с аналогичной версией для 7-й степени с восемью членами и побочным условием x 1 + x 2 + x 3 + x 4 = x 5 + x 6 + x 7 + x 8 = 0 разрешимо, подходит для k = 1,3,7 и сводится Чоудри к нахождению рациональный корень многомерной кубики. Вроблевски проверил свою базу данных за 2002 год и нашел четыре, а именно:
Вроблевски проверил свою базу данных за 2002 год и нашел четыре, а именно:
[105, 1153, -1258] = [455, 582, -1037]
[31, 47242, -47273] = [5681, 9717, -15398]
[3914, 51858, — 55772] = [19264, 25403, -44667]
[12292, 59070, -71362] = [27745, 37983, -65728]
Система, по сути, также сводится к нахождению нетривиального рационального корня кубики. Используйте форму L 1 ,
(a + bp + q) k + (b-bp + q) k + (c + ap + q) k = (a + cp + q) k + (b + ap + q) к + (c-cp + q) к
, что уже верно для k = 1, общая форма будет доказана позже.Пусть p = q / a + 1, и это будет равняться x 1 + x 2 = x 5 . Расширение для k = 5 и после удаления тривиальных факторов приведет к кубической в q с коэффициентами в {a, b, c}. ( Конец обновления )
(Обновление от 26. 06.09): В ответ на электронное письмо Томита любезно создал полную [6.3.3] таблицу с терминами <1000. Действительно, из 59 солнцев почти 3/4 (75 %) были хорошими для k = 2,6, больше, чем для k = 1,5.Для [7.4.4] в базе данных Вроблевски (что составляет , а не — полный список ниже определенной границы), и исключая 18 солнц из кубики Чоудри с учетом k = 1,3,7, остается 40 и почти 1/4 для k = 1,7. Если можно будет предоставить полный список с терминами <10 000, я считаю, что процент будет больше. А вот , почему у есть такая тенденция к всесезонности, неизвестно. ( Конечная нота ) (Обновление от 17.07.09): просматривая Интернет, я снова наткнулся на страницу Тома Вомака.Я прочитал его диссертацию много лет назад и, перечитав ее, понял, что он заметил ту же точку зрения о изобилии k = 2,6 (и Питера Монтгомери, а также других до него). Фактически, Womack выполнил поиск и обнаружил, что из 207 солнц с общей суммой <5717 6 почти 90% были для k = 2,6 (только 22 были только для k = 6), много более высокий процент, чем тот, который дает меньший набор soln Tomita.
06.09): В ответ на электронное письмо Томита любезно создал полную [6.3.3] таблицу с терминами <1000. Действительно, из 59 солнцев почти 3/4 (75 %) были хорошими для k = 2,6, больше, чем для k = 1,5.Для [7.4.4] в базе данных Вроблевски (что составляет , а не — полный список ниже определенной границы), и исключая 18 солнц из кубики Чоудри с учетом k = 1,3,7, остается 40 и почти 1/4 для k = 1,7. Если можно будет предоставить полный список с терминами <10 000, я считаю, что процент будет больше. А вот , почему у есть такая тенденция к всесезонности, неизвестно. ( Конечная нота ) (Обновление от 17.07.09): просматривая Интернет, я снова наткнулся на страницу Тома Вомака.Я прочитал его диссертацию много лет назад и, перечитав ее, понял, что он заметил ту же точку зрения о изобилии k = 2,6 (и Питера Монтгомери, а также других до него). Фактически, Womack выполнил поиск и обнаружил, что из 207 солнц с общей суммой <5717 6 почти 90% были для k = 2,6 (только 22 были только для k = 6), много более высокий процент, чем тот, который дает меньший набор soln Tomita. Насколько высокий будет этот процент для полного списка с общей суммой , которая на больше? И что это означает для восьми положительных членов, действительных для k = 1,7 или k = 2,8? (Учитывая, что единственный известный пока для k = 8 не является всесезонным.) ( Конечная нота .) (Обновление 10/7/09): Дункан Мур, который проделал большую работу с номерами такси и такси , имеет большую базу данных, которая включает [5.3.3] и [6.3.3]. Ниже определенной границы для 5-й степени он нашел почти 5400 солнц, около 59% из которых являются всесезонными для k = 1,5. Для 6-й степени было 405, с 92% всесезонного для k = 2,6, увеличение из базы данных Womack. Приближаются ли эти проценты асимптотически к определенному значению, неизвестно.( Конец обновления .)
Насколько высокий будет этот процент для полного списка с общей суммой , которая на больше? И что это означает для восьми положительных членов, действительных для k = 1,7 или k = 2,8? (Учитывая, что единственный известный пока для k = 8 не является всесезонным.) ( Конечная нота .) (Обновление 10/7/09): Дункан Мур, который проделал большую работу с номерами такси и такси , имеет большую базу данных, которая включает [5.3.3] и [6.3.3]. Ниже определенной границы для 5-й степени он нашел почти 5400 солнц, около 59% из которых являются всесезонными для k = 1,5. Для 6-й степени было 405, с 92% всесезонного для k = 2,6, увеличение из базы данных Womack. Приближаются ли эти проценты асимптотически к определенному значению, неизвестно.( Конец обновления .)Были найдены различные тождества для 5-й степени после преобразования в симметричную форму, где { x i , y i } не обязательно положительные, которые принадлежат четырем классам:
1. x 1 5 + x 2 5 + x 3 5 = y 1 5 + y 2 5 + y 3 5 , X 1 + x 2 = y 1 + y 2 ,
x 1 5 + x 2 5 + x 3 5 = y 1 5 + y 2 5 + y 3 5 , X 1 + x 2 = y 1 + y 2 ,
2.x 1 5 + x 2 5 + x 3 5 = y 1 5 + y 2 5 + y 3 5 , (Moessner’s , с неизвестными линейными отношениями между x i , y i )
3. x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k , К = 1,5
4.x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k , x 1 -x 2 = y 1 -y 2 , k = 1,5
Если вам известно о еще , пожалуйста, пришлите его, чтобы его можно было добавить в коллекцию. Первые два класса имеют красивую идентичность.
Первые два класса имеют красивую идентичность.
Састри, Чоула (1934)
(u 5 + 25v 5 ) 5 + (u 5 -25v 5 ) 5 + (10u 3 v 2 ) 5 = (u 5 ) + 75v 5 ) 5 + (u 5 -75v 5 ) 5 + (-50uv 4 ) 5
Если {u, v} выбраны так, что Abs [u / v] = x находится в диапазоне 25 1/5 (u 5 + av 5 ) 5 + (u 5 -av 5 ) 5 — (u 5 + bv 5 ) 5 — (u 5 -bv 5 ) 5 = 20 (a 2 -b 2 ) (u 3 v 2 ) 5 + 10 (a 4 -b 4 ) ( УФ 4 ) 5 Если рациональное {a, b} может быть найдено таким, что, 20 (a 2 -b 2 ) = mp 5 (ур. 10 (a 4 -b 4 ) = nq 5 (уравнение 2) , то это дает тождество для (5,4, m + n). Для m = n = 1 Састри и Чоула нашли {a, b} = {75, 25} и {p, q} = {10, 50}. Q: Существуют ли другие, а не просто числа, кратные этим двум в пятой степени, или другие малые m, n? (Обновление, 18.11.09): Дэйв Русин показал, что система может быть приведена к определенной гиперэллиптической кривой , то есть имеет только конечное число рациональных солнц, и, вероятно, известное солнце является единственным нетривиальным.Он дал преобразование, {a, b, p, q} = {m 2 y / (5n), m 3 n, -2mx, 20m 2 x}, где m = (4x 5 -5) / (5н 2 ) и уравнение 1, уравнение 2 верны, если, -4 2 x 10 + 5 2 = y 2 , рациональное решение которого, по-видимому, равно только {x, y} = {1,3}. (Обновление от 15.12.09): Тони Риццо указал, что если {a, b} = {75r 3 , 25r 3 }, то {m, n} = {r, r 2 } . Для r = 2 это дает тождество (5,4,6), (u 5 + 600v 5 ) 5 + (u 5 -600v 5 ) 5 — (u 5 + 200v 5 ) 5 — (u 5 -200v 5 ) 5 = 2 (2u 3 v 2 ) 5 + 4 (4uv 4 ) 5 Если {u, v} выбраны так, что Abs [u / v] = x находится в пределах диапазона 200 1/5 Обновление, 23. Месснер (1951) т 6 (a + 20t) 5 + t 3 (b-20t 2 -20t 4 ) 5 + (c + 20t 5 ) 5 = t 6 (a-20t) 5 + t 3 (b + 20t 2 + 20t 4 ) 5 + (c-20t 5 ) 5 , где {a, b, c} = {t 6 + 8t 4 + 12t 2 -1, t 6 + 8t 4 -8t 2 -1, t 6 — 12 4 -8т 2 -1}. Поскольку t произвольно, можно установить t = v 5 , чтобы иметь равные суммы пятой степени. Обратите внимание на красивую симметрию терминов и на то, что коэффициенты после отрицания являются палиндромными. Конечно, это не единичный результат. Кто-нибудь еще знает такую же простую идентичность, а также линейные отношения между x i , y i , если таковые имеются, для этого? ( Конец обновления . (Обновление, 22.02.10): Герардин дал красивую идентичность в 4-й степени с маленькими коэффициентами {1,2,3}, (a + 3a 2 -2a 3 + a 5 + a 7 ) 4 + (1 + a 2 -2a 4 -3a 5 + a 6 ) 4 = (a-3a 2 -2a 3 + a 5 + a 7 ) 4 + (1 + a 2 -2a 4 + 3a 5 + a 6 ) 4 и Чоудри дали версию 5-й степени, (aa 3 -2a 5 + a 9 ) 5 + (1 + a 2 -2a 6 + 2a 7 + a 8 ) 5 + (2a 3 + 2a 4 -2a 7 ) 5 = (a + 3a 3 -2a 5 + a 9 ) 5 + (1 + a 2 -2a 6 -2a 7 + a 8 ) 5 + (-2a 3 + 2a 4 + 2a 7 ) 5 , что на самом деле хорошо для k = 1,5. x 1 k + x 2 k + x 3 k + x 4 k = y 1 k + y 2 k + y 3 k + y 4 k (ур.1) где, {x 1 , x 2 , x 3 , x 4 } = {a + b + c, a-b-c, -a + b-c, -a-b + c} {y 1 , y 2 , y 3 , y 4 } = {d + e + f, -d + e-f, -d-e + f, d-e-f} Раскрывая одну сторону уравнения, получаем ∑ x i 1 = 0 ∑ x i 5 = 80abc (a 2 + b 2 + c 2 ) и аналогично для y i . Метод 1: a + b-c = -d + e + f; ab = de; c (a 2 + b 2 + c 2 ) = f (d 2 + e 2 + f 2 ) Метод 2: a + b-c = -d + e + f; c = f; ab (a 2 + b 2 + c 2 ) = de (d 2 + e 2 + f 2 ) , тогда ∑ x i k = ∑ y i k , для k = 1,5. Чоудри показал, что с заданной начальной точкой, даже с тривиальной, с помощью подходящих подстановок и решения системы линейных уравнений можно найти бесконечное количество нетривиальных солнц. Фактически, непосредственно решая метод 1, можно получить уравнение четвертой степени, которое имеет рациональный корень, если некоторый многочлен четвертой степени превращается в квадрат, следовательно, его можно рассматривать как эллиптическую кривую. Источник : «О равных суммах пятых степеней», Indian Jour. Чистая и прикладная математика, ноябрь 1997 г. Обновление, 24.11.09): Чоудри (1999) рассмотрел общую формулу ax 5 + by 5 + cz 5 = au 5 + bv 5 + cw 5 (ур.1) для случая a + b + c = 0. Исключая ситуацию, когда abc (a-b) (a-c) (b-c) = 0, он отдал soln на, ax 5 + по 5 + cz 5 = t 2 (au 5 + bv 5 + cw 5 ) as, {x, y, z} = {(p 1 t 2 -p 1 t + q 1 ) r 1 , (p 2 t 2 -p 2 t + q 2 ) r 2 , (p 3 t 2 -p 3 t + q 3 ) r 3 } {u, v, w} = {(q 1 t 2 -p 1 t + p 1 ) r 1 , (q 2 t 2 -p 2 t + p 2 ) r 2 , (q 3 t 2 -p 3 t + p 3 ) r 3 } где. {p 1 , p 2 , p 3 } = {17a 2 + 14ab + 14b 2 , 14a 2 + 14ab + 17b 2 , 17a 2 + 20ab + 17b 2 } {q 1 , q 2 , q 3 } = {2a 2 -ab-b 2 , -a 2 -ab + 2b 2 , 2a 2 + 5ab + 2b 2 } {r 1 , r 2 , r 3 } = {a + 2b, -2a-b, a-b} задана константа {a, b}, для произвольных t .Затем можно установить t = v 5 , чтобы удовлетворить уравнению 1. Например, для {a, b, c} = {1,2, -3} после транспонирования членов мы получаем soln на, x 5 + 2y 5 + 3z 5 = u 5 + 2v 5 + 3w 5 {x, y, z} = {101t 10 -101t 5 -4, 4t 12 -88t 7 + 88t 2 , 25t 10 -25t 5 +4} {u, v, w} = {-4t 12 -101t 7 +101, 88t 10 -88t 5 +4, 4t 12 -25t 7 + 25t 2 } ( Конец обновления . (Обновление, 03.02.10): Choudhry (-8m 6 + 2mn 5 ) k + (8m 5 n + n 6 ) k + 2 (8m 6 ) k = (8m 6 + 2mn 5 ) k + (8m 5 nn 6 ) k + 2 (n 6 ) k , для k = 1,5 Положительное значение может быть получено, если n> m и в диапазоне 2 2/5 < n / m <2 3/5 , или прибл.1,32 < н / м <1,51. С переносом терминов в одну сторону, (-8 м 6 + 2 мес 5 ) к + (8 м 5 n + n 6 ) к — (8 м 6 + 2 мес 5 ) к — (8 м 5 nn 6 ) k + 2 (8m 6 ) k = 2 (n 6 ) k Для n = 1 тождество доказывает, что целое число 2 является суммой / разностью шести целых пятых степеней бесконечным множеством способов. Примечание : В каком-то смысле это версия 5-й степени, (-6x 3 + y 3 ) 3 + (6x 3 + y 3 ) 3 — (6x 2 y) 3 = 2 (y 3 ) 3 , где для y = 1 доказывает, что 2 бесконечно является суммой / разностью трех целых 3-х степеней. Q : Кто-нибудь может дать подобную идентичность, выражающую 2 как целые 7-е степени? ( Конец обновления .) Теорема (Lander): «Дано рациональное решение для 1 k + a 2 k + a 3 k = b 1 k + b 2 k + b 3 k для оба k = 1,5, назовите эту систему S 5 , тогда она может сгенерировать последующие. » В книге « Геометрические аспекты диофантовых уравнений, включающих равные суммы одинаковых степеней » Лендер начал с формы (u + x) k + z k + (v + y) k = (v + x) k + y k + (u + z) k , (назовите это L 0 ) — общее решение для k = 1. В любом случае, L 0 при расширении для k = 5 имеет красивую симметричную форму, (xz) u 4 +2 (x 2 -z 2 ) u 3 +2 (x 3 -z 3 ) u 2 + (x 4 -z 4 ) u = (xy) v 4 +2 (x 2 -y 2 ) v 3 +2 (x 3 -y 3 ) v 2 + (x 4 -лет 4 ) v , где все пятые степени равны нулю, и, как таковая, представляет собой поверхность четвертой степени. 1. Использование точки P 1 (x 1 , y 1 , z 1 ) Определите {u, v, x, y, z} = {-a 3 + b 3 , a 2 -b 2 , x 0 + (x 1 -x 0 ) t, y 0 + (y 1 -y 0 ) t, z 0 + (z 1 -z 0 ) t}, где, x 1 = y 1 = z 1 = (x 0 d 1 + y 0 d 2 + z 0 d 3 ) / (d 1 + д 2 + д 3 ) {d 1 , d 2 , d 3 } = {a 1 4 -b 1 4 , a 2 4 -b 2 4 , А 3 4 -b 3 4 } {x 0 , y 0 , z 0 } = {a 1 + a 3 -b 3 , b 2 , a 3 } Однако еще осталось найти т. 2. Использование точки P 2 (x 2 , y 2 , z 2 ) Определите {u, v, x, y, z} = {-a 3 + b 3 , a 2 -b 2 , x 0 + (x 2 -x 0 ) t, y 0 + (y 2 -y 0 ) t, z 0 + (z 2 -z 0 ) t}, где, {x 2 , y 2 , z 2 } = {x 1 -d 0 , x 1 -d 0 + u, x 1 -d 0 + v} x 1 = (x 0 d 1 + y 0 d 2 + z 0 d 3 ) / (d 1 + d 2 + d 3 ) d 0 = (d 2 u + d 3 v) / (d 1 + d 2 + d 3 ) и {d 1 , d 2 , d 3 }, {x 0 , y 0 , z 0 } определяются так же, как в первом пункте. {a 1 , a 2 , a 3 , b 1 , b 2 , b 3 } = {p, -p, q, q, r, -r} {a 1 , a 2 , a 3 , b 1 , b 2 , b 3 } = {p, -p, q, r, q, -r} для первой и второй точек соответственно, и это даст полиномы 9-й степени. Теорема (Пьезас): «Полное решение для S 5 , или x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k , для k = 1,5 необходимо решить только квадратное уравнение с дискриминантом D , который является полиномом четвертой степени от одной переменной. Доказательство : Можно показать, что результат Лендера можно кратко закодировать в форме L 1 , (a + bp + q) k + (b-bp + q) k + (c + ap + q) k = (a + cp + q) k + (b + ap + q) к + (c-cp + q) к , с которыми мы сталкивались раньше. Это уже верно для k = 1. Это подмножество Lander L 0 , (u + x) k + z k + (v + y) k = (v + x) k + y k + (u + z) k за исключением случая uv (u-v) = 0.Чтобы увидеть это, просто приравняйте первые пять членов L 1 к L 0 , и всегда можно найти рациональные {a, b, c, p, q}, используя, {a, b, c, p, q} = {(1 + t) (st + yz) / (2t), — (1 + t) (st-y + z) / (2t), (1+ t) (y + tu-tx + ty-z) / (2t), t / (1 + t), (st-y + z + 2tz) / (2t)}, где {s, t} = {u + xy, — (uv) / u} , следовательно, случаи со знаминателем (1 + t) t = uv (u-v) = 0 должны быть исключены, иначе происходит деление на ноль. n 1 k + (n 2 + n 3 ) k = (n 1 + n 2 ) k + n 3 k , который после расширения, как легко видеть, имеет тривиальные солнечные лучи для k <6, отличных от k = 1, поэтому не представляет интереса.С учетом этого, расширяя L 1 при k = 5, это сокращается до полинома от p , который представляет собой всего лишь квадратичную форму , (Poly1) p 2 + (Poly2) p + (Poly3) = 0 (ур.1) без учета тривиального множителя p (p-1). Poly i находятся в {a, b, c, q}, а как полиномы в q имеют степень 1,1,3 соответственно. D: = (Poly2) 2 -4 (Poly1) (Poly3) степени 1 + 3 и, следовательно, квартика в q , таким образом доказывая теорему. Найти полиномиальное soln можно двумя способами: 1-й метод : Поскольку Poly1 линейен в q , все, что нам нужно сделать, это установить Poly1 = 0 и решить для q с уравнением 2 (b + c) (b 2 + c 2 ) q = (a 4 -c 4 ) — (a + b) (b + c) (b 2 + в 2 ) и (ур.1) сводится к линейному уравнению (Poly2) p + (Poly3) = 0, где p легко решается. В соответствии с результатом Лендера, это дает девятые полиномы градусов от одной из переменных {a, b, c}. Между прочим, суммы слагаемых x 1 + x 2 , y 1 + y 3 имеют простой вид, (a + bp + q) + (b-bp + q) = (a 4 -c 4 ) / ((b + c) (b 2 + c 2 )) (a + cp + q) + (c-cp + q) = (a 4 -b 4 ) / ((b + c) (b 2 + c 2 )) для {p, q}, как определено выше. (a + bp + q) — (b-bp + q) = (a + cp + q) — (b + ap + q) , что верно, если c = a + 2b . Используя это ограничение, полиномы уменьшаются до седьмого град.Поскольку уравнение однородно, его можно положить b = 1 без ограничения общности, и мы имеем тождество, (at + p + q) k + (t-p + q) k + (ct + ap + q) k = (at + cp + q) k + (t + ap + q) к + (ct-cp + q) к , k = 1,5, с = а + 2 t = 4a (a-2) (a + 3) (a 2 + 4a + 5) 2 p = (a 2 +1) (a 2 + 8a + 11) (a 3 + 15a 2 + 33a + 31) q = -2a (a + 1) (a-2) (a 2 + 4a + 5) (a 3 + 15a 2 + 33a + 31) , где общий множитель (a + 1) членов должен быть удален. (Обновление 13.07.09) 2-й метод : Мы непосредственно находим q , так что дискриминант D представляет собой квадрат. Чтобы найти тривиальное решение, нужно разложить L 1 для k = 5,7 и исключить p между ними. Разложив полученный на множители, можно найти линейную зависимость между {a, b, c, q}, задаваемую формулой, 2 (b + c) q = a 2 -b 2 -c 2 -ab-ac-bc Используя этот q , D становится простым квадратом, D: = (a 2 -b 2 ) 2 (a 2 -c 2 ) 2 (b-c) 2 / (b + c) 2 Это тривиальное решение, но, как было показано в первом методе, что D является квартикой в q , из этой начальной точки можно затем найти бесконечное число из нетривиальных единиц. Пьезы Полный критерий для решения системы x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k для k = 1,5 уже было дано выше, с подмножеством, также удовлетворяющим x 1 -x 2 = y 1 -y 2 .Мы также можем изучить другие методы ради упражнения. Это подмножество может быть полностью определено любой из двух хороших форм. Пусть, (a + d) k + (b + d) k + (c-2d) k = (ad) k + (bd) k + (c + 2d) k уже верно для k = 1, и если развернуть для k = 5, сводится к простому уравнению, (a 4 + b 4 -2c 4 ) + 2 (a 2 + b 2 -8c 2 ) d 2 — 6d 4 = 0 Один из способов решить это — рассматривать его как квадратичный по d 2 и сделать его дискриминант (многочлен четвертой степени) квадратом, хотя это нелегко сделать для этой конкретной квартики. (p + r) k + (pr) k + (2q + s) k = (q + r) k + (qr) k + (2p + s) k , который для удобства после масштабирования можно принять с = 1 без потери общности. Если расширить это до k = 5, получим только квадратичную величину по r 2 . Решение для r 2 , r 2 = -p 2 -pq-q 2 ± y, , где y — квадратный корень из дискриминанта, y 2 = 4q 4 + (8 + 5p) q 3 +2 (4 + 4p + 3p 2 ) q 2 + (4 + 8p + 8p 2 + 5p 3 ) q + (1 + 2p + 2p 2 ) 2 (ур.1) Это проще сделать квадратом, представляющим собой многочлен с квадратом в начале и постоянным членом, и показывает, как использование соответствующей формы может упростить задачу. (p + r) k + (pr) k + (2q + 1) k = (q + r) k + (qr) k + (2p + 1) k , К = 1,5 имеет солнце, q = — (80p + 40) / (57p + 80), r = z / (57p + 80), 40 2 + 10160p + 22999p 2 + 14478p 3 + 3249p 4 = z 2 q = 3 (13p 2 + 10p + 8) / (9p-16), r = z / (9p-16), 8 2 + 656p + 1999p 2 + 2922p 3 + 1629p 4 = г 2 q = (13p 2 + 14p + 8) / (3p + 16), r = z / (3p + 16), 24 2 + 1232p + 1183p 2 + 542p 3 + 181p 4 = г 2 , где нужно решить эллиптическую кривую за p . u 1 p 4 + u 2 p 3 + u 3 p 2 + u 4 p + u 5 = (v 1 p 2 + v 2 п + в 3 ) 2 Поскольку u i выражаются в терминах {a, b}, то неизвестными являются {a, b, v 1 , v 2 , v 3 }. Добавив еще одно ограничение, можно также найти простую форму для S 5 . Например, (v + 8) k + (u-8) k + (-u + 2v + 7) k = (-u + 2v + 8) k + (v-8) k + (u + 7) к Это уже верно для k = 1. Расширение для k = 5 дает только квадратичную в v и легко решается.Для рационального v нужно сделать его дискриминант, полином четвертой степени от и , в виде квадрата, y 2 = -43281 + 40110u-4597u 2 + 390u 3 -31u 4 x 1 -x 2 = y 1 -y 2 x 2 -nx 3 = -ny 1 + y 3 x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k для k = 1,5 и n = 15.За исключением случая n = 1, который является тривиальным, я еще не проверил, для каких других n эта система решима. (обновление 7/12/09): еще один, подчиняющийся системе M 1 , но с n = 2 — это (1-2q + 2r) к + (-3-2q) к + (1 + 2q) к = (2 + q + r) к + (-2 + qr) к + (-1-4q + 2r) к Опять же, это уже верно для k = 1 и при разложении на k = 5 дает квадратичную величину в r . y 2 = — (384 + 1112q + 1297q 2 + 738q 3 + 171q 4 ) с небольшой рациональной точкой при q = -16/15. Q: Любое другое простое решение для системы M 1 для некоторого целого n ? ( Конечная нота .) Примечание 1 : Между прочим, учитывая единичную квартику формы, y 2 = x 4 + (Poly1) x 3 + (Poly2) x 2 + (Poly3) x + (Poly4) превратить в квадрат, а Poly_i — полиномы от переменной p степени 1,2,3,4 соответственно (например, ур.1 выше), каково максимально возможное количество линейных солнц вида x = (ap + b) или x = (ap + b) / (cp + d)? Примечание 2 : Полный критерий x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + x 3 k , k = 1,5, где x 1 -x 2 = y 1 -y 2 также был дан Бремнером, хотя я еще не видел этой работы. Примечание 3 : Можно доказать, что k = 1,2,5 дает только тривиальные рациональные результаты. Полное решение для k = 1,2 принадлежит Л. Диксону (Форма 4 в Суммах трех квадратов ) (ad + e) k + (bc + e) k + (ac + bd + e) k = (ac + e) k + (bd + e) k + (ad + bc + e) к и разложение на k = 5 дает просто квадратичный полином от e с дискриминантом D , D = -2 (a 2 -ab + b 2 ) (c 2 -cd + d 2 ) , который должен быть квадратным.Но пусть {a, b, c, d} = {u + v, 2v, x + y, 2y}, и это станет, D = -2 (u 2 + 3v 2 ) (x 2 + 3y 2 ) , и очевидно, что нет реальных значений, таких что D становится положительным действительным квадратом. Примечание 4 : Является ли a 5 + b 5 + c 5 = d 5 + e 5 + f 5 где a + b + c = d + e + f = 0 разрешимо? (Аналогичное уравнение для седьмых степеней действительно имеет соль.) Это может быть полностью параметризовано как, p 5 + q 5 + (- p-q) 5 = r 5 + s 5 + (- r-s) 5 , который в раскрытом виде равен pq (p + q) (p 2 + pq + q 2 ) = rs (r + s) (r 2 + rs + s 2 ) , хотя кажется неизвестным, разрешимо ли это нетривиально. Из Википедии, бесплатной энциклопедии. В арифметике и алгебре пятая степень числа n является результатом умножения пяти экземпляров числа n вместе: n5 = n × n × n × n × n. Пятая степень также образуется путем умножения числа на его четвертую степень или квадрата числа на его куб. 2 в степени 5 = 25 = 32.Чтобы придерживаться 2 в степени 5 в качестве примера, вставьте 2 для основания и введите 5 в качестве индекса, также известного как экспонента или степень. 2 в 5-й степени — это возведение в степень, которое относится к категории степеней 2. Показатели — это числа, которые говорят вам, сколько раз использовать это число при умножении. Если число считается «5-й степенью», это означает, что показатель степени для этого числа равен 5, и вы должны умножить это число само на себя пять раз. 0,00001 «Пятая степень 3» означает просто число, которое вы получите, если умножите 3 вместе пять раз. Итак, это — 3 × 3 × 3 × 3 × 3 — что равняется 243. Это также можно записать 35, где маленькая 5 означает «в пятой степени». 1024 10 в шестой степени означает, что шесть десятков будут умножены вместе, например: 10 x 10 x 10 x 10 x 10 x 10. 3 в степени 5 = 35 = 243. Чтобы использовать, например, 3 в степени 5, вставьте 3 для основания и введите 5 в качестве индекса, также известного как экспонента или степень. Десятка в шестой степени равна одному миллиону или 1 000 000, то есть единице, за которой следуют шесть нулей. Показатель числа 3, 5, также называемый индексом или степенью, обозначает, сколько раз нужно умножить основание (3). 3 в степени 5 = 35 = 243. Экспоненты — это сокращение для многократного умножения одного и того же самого на себя.Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5) (5) (5) = 5 3 . «Показатель», равный 3 в этом примере, означает, сколько раз умножается значение. То, что умножается (в этом примере 5), называется «базой». Этот процесс использования экспонент называется «возведением в степень», где показатель — это «степень». Выражение «5 3 » произносится как «пять в третьей степени» или «пять в третьей степени». Есть две специально названные степени: «до второй степени» обычно произносится как «в квадрате», а «до третьей степени» обычно произносится как «в кубе».Итак, «5 3 » обычно произносится как «пять кубов». Когда мы имеем дело с числами, мы обычно просто упрощаем; мы лучше будем иметь дело с «27», чем с «3 3 ». Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x 6 », чем с « xxxxxx ». У экспонентов есть несколько правил, которые мы можем использовать для упрощения выражений. Чтобы упростить это, я могу думать в терминах того, что означают эти показатели. ( x 3 ) ( x 4 ) = ( xxx ) ( xxxx ) Теперь я могу убрать скобки и сложить все множители: ( xxx ) ( xxxx ) = xxxxxxx Это семь копий переменной.«Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как: xxxxxxx = x 7 Собираем все вместе, шаги следующие: ( x 3 ) ( x 4 ) = ( xxx ) ( xxxx ) = xxxxxxx = х 7 Тогда упрощенная форма ( x 3 ) ( x 4 ) будет: Обратите внимание, что x 7 также равно x (3 + 4) . Всякий раз, когда вы умножаете два члена с одинаковым основанием, вы можете складывать экспоненты: ( x м ) ( x n ) = x (m + n) Однако мы НЕ можем упростить ( x 4 ) ( y 3 ), потому что основания разные: ( x 4 ) ( y 3 ) = xxxxyyy = ( x 4 ) ( y 3 ).Ничего не сочетается. Теперь, когда я знаю правило (а именно, что я могу добавлять силы к одной и той же базе), я могу начать с перемещения баз, чтобы расположить все одинаковые базы рядом друг с другом: ( a 5 b 3 ) ( a b 7 ) = ( a 5 ) ( a ) ( b 3 ) ( б 7 ) Теперь я хочу добавить мощности на a и b . Все, что не имеет силы, в техническом смысле «возведено в степень 1». Все, что находится в степени 1, является самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как: ( a 5 ) ( a ) ( b 3 ) ( b 7 ) = ( a 5 ) ( a 1 ) ( b 3 ) ( б 7 ) Теперь могу комбинировать: ( a 5 ) ( a 1 ) ( b 3 ) ( b 7 ) = a 5 + 1 b 3 + 7 = a 6 b 10 Если сложить все вместе, моя ручная работа будет выглядеть так: ( a 5 b 3 ) ( a b 7 ) = ( a 5 a 1 ) ( b 3 b 7 ) = В следующем примере есть две силы, одна из которых в некотором смысле находится «внутри» другой. Чтобы сделать упрощение, я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, заключенного в круглые скобки. В этом случае база четвертой степени равна x 2 . Умножение четырех копий этой базы дает мне: Каждый фактор в приведенном выше расширении — это «умножение двух копий» переменной.Это расширяется как: ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 ) = ( xx ) ( xx ) ( xx ) ( xx ) Убрав круглые скобки, получим: ( xx ) ( xx ) ( xx ) ( xx ) = xxxxxxxx Это строка из восьми копий переменной. xxxxxxxx = x 8 Собираем все вместе: ( x 2 ) 4 = ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 ) = ( xx ) ( xx ) ( xx ) ( xx ) = xxxxxxxx = х 8 Обратите внимание, что ( x 2 ) 4 = x 8 , и что 2 × 4 = 8.Это демонстрирует правило второй степени: Всякий раз, когда у вас есть выражение в степени, которое возведено в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень: Если в скобках указан продукт, а в скобках — мощность, то питание идет на каждый элемент внутри. ( xy 2 ) 3 = ( xy 2 ) ( xy 2 ) ( xy 2 ) = ( xxx ) ( y 2 y 2 y 2 ) = ( xxx ) ( yyyyyy ) = x 3 y 6 = ( x ) 3 ( y 2 ) 3 Другой пример: Предупреждение: это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяются» по сложению. Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильный. Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x — 2) 2 , не пытайтесь делать это в уме.Вместо этого запишите это; «в квадрате» означает «умножение двух копий», поэтому: ( x — 2) 2 = ( x — 2) ( x — 2) = x ( x — 2) — 2 ( x — 2) = xx — 2 x — 2 x + 4 = x 2 — 4 x + 4. Ошибка в виде ошибочной попытки «распределить» экспоненту чаще всего совершается, когда ученик пытается делать все в своей голове, вместо того, чтобы показать свою работу.Делайте все аккуратно, и вы вряд ли совершите эту ошибку. Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. ( a 2 ) 4 ( b 3 ) 4 ( c 1 ) 4 = ( a 2 × 4 ) ( b 3 × 4 ) ( c 1 × 4 ) = a 8 b 12 c 4 Партнер Есть еще одно правило, которое может или не может быть выполнено в вашем классе на данном этапе: Все, что находится в нулевой степени, равно «1» (пока «что-нибудь» не является нулем само по себе). Это правило объясняется на следующей странице. Кого волнует эта фигня в квадратных скобках? Я точно не знаю, потому что нулевая мощность снаружи означает, что значение всего этого равно 1.Ха! [(3 x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0 = 1 Между прочим, как только ваш класс охватывает «до нуля», вы должны ожидать упражнений, подобных приведенному выше, на следующем тесте. Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с помощью экспонент. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите здесь множество отработанных примеров.) Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию. URL: https://www.purplemath.com/modules/exponent.htm 1)
1) Трудно не заметить, что это, по сути, наименьшая тройка Пифагора , -4 2 +5 2 = 3 2 , и интересно, что она появляется в контексте 5-й степени.( Конец обновления .)
Трудно не заметить, что это, по сути, наименьшая тройка Пифагора , -4 2 +5 2 = 3 2 , и интересно, что она появляется в контексте 5-й степени.( Конец обновления .) 11.09):
11.09): )
) (Различия между LHS и RHS выделены синим цветом.) Хотя существуют тождества для k = 6, , ни один из не известен с такими маленькими коэффициентами. ( Кто-нибудь может найти? ) Другие личности 5-го градуса можно найти с помощью ff. два метода Чоудри. Дано,
(Различия между LHS и RHS выделены синим цветом.) Хотя существуют тождества для k = 6, , ни один из не известен с такими маленькими коэффициентами. ( Кто-нибудь может найти? ) Другие личности 5-го градуса можно найти с помощью ff. два метода Чоудри. Дано, Уравнение 1 можно сократить до 6 членов, если x 4 = y 4 . Таким образом, если,
Уравнение 1 можно сократить до 6 членов, если x 4 = y 4 . Таким образом, если, Примечание : Чоудри также использовал уравнение 1 и его замены для решения k = 1,3,7.
Примечание : Чоудри также использовал уравнение 1 и его замены для решения k = 1,3,7.
 )
) Источник: Диофантово уравнение x 1 5 + x 2 5 + 2x 3 5 = y 1 5 + y 2 5 + 2y 3 5 , Ганита, Т. 48, No. 2, 1997, 115-116.
Источник: Диофантово уравнение x 1 5 + x 2 5 + 2x 3 5 = y 1 5 + y 2 5 + 2y 3 5 , Ганита, Т. 48, No. 2, 1997, 115-116. Есть ли 6-я град — неизвестно. Мы уже видели, что при начальном soln на 1 k + a 2 k = b 1 k + b 2 k для k = 2, 3 или 4, можно использовать это, чтобы найти больше солнц.Оказывается, есть версия quintic , хотя и с небольшим условием,
Есть ли 6-я град — неизвестно. Мы уже видели, что при начальном soln на 1 k + a 2 k = b 1 k + b 2 k для k = 2, 3 или 4, можно использовать это, чтобы найти больше солнц.Оказывается, есть версия quintic , хотя и с небольшим условием,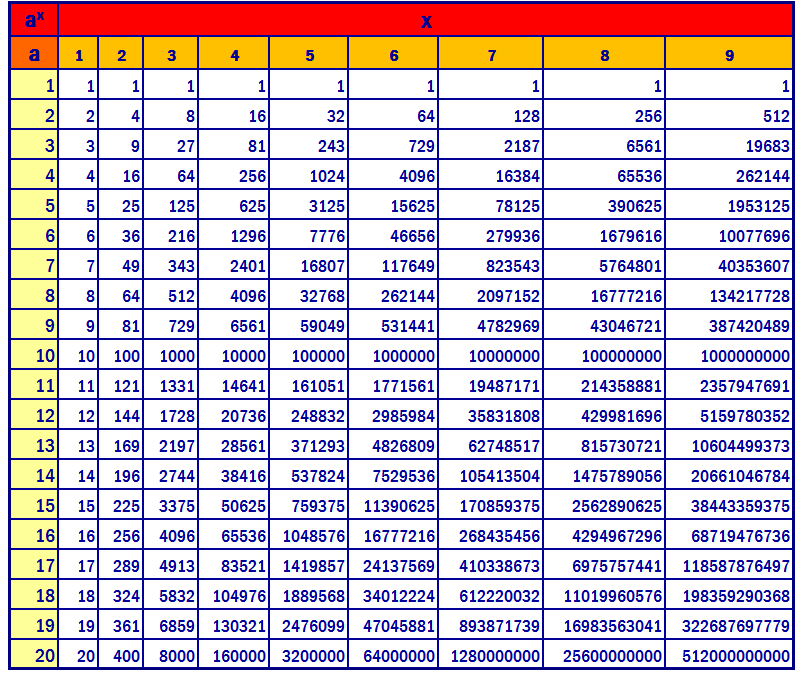 Это также может быть верно для k = 5 при использовании соответствующих значений. ( Примечание : Между прочим, следует отметить, что уравнение, x 1 k + x 2 k +… + x k + 1 k = 0 одновременно, действительное для трех нечетных мощности k = 1,3, n имеет тривиальные solns только тогда, когда n = 5. Используя форму выше и функцию Mathematica Resultant [] для исключения одной переменной при k = 3 и 5, можно увидеть, что там являются лишь тривиальными солнцами.Напротив, — это нетривиальных солнц, когда k = 1,3,7, найденное Чоудри, и k = 1,3,9, найденное Вроблевски. Будет ли k = 1,3,11, еще предстоит выяснить.)
Это также может быть верно для k = 5 при использовании соответствующих значений. ( Примечание : Между прочим, следует отметить, что уравнение, x 1 k + x 2 k +… + x k + 1 k = 0 одновременно, действительное для трех нечетных мощности k = 1,3, n имеет тривиальные solns только тогда, когда n = 5. Используя форму выше и функцию Mathematica Resultant [] для исключения одной переменной при k = 3 и 5, можно увидеть, что там являются лишь тривиальными солнцами.Напротив, — это нетривиальных солнц, когда k = 1,3,7, найденное Чоудри, и k = 1,3,9, найденное Вроблевски. Будет ли k = 1,3,11, еще предстоит выяснить.) После умного геометрического анализа Лендер дал метод вывода полиномиальных выражений для всех переменных. Если исходный soln {a i , b i } на L 0 , это приводит к новому, обычно намного большему, двумя способами. Первая,
После умного геометрического анализа Лендер дал метод вывода полиномиальных выражений для всех переменных. Если исходный soln {a i , b i } на L 0 , это приводит к новому, обычно намного большему, двумя способами. Первая, .Когда все эти выражения подставляются в L 0 , если {a i , b i } является soln, тогда уравнение является квартикой с четырьмя корнями {0,0,1, t}, поэтому это просто linear eqn в t , которое затем легко решается. Можно также использовать второй подход,
.Когда все эти выражения подставляются в L 0 , если {a i , b i } является soln, тогда уравнение является квартикой с четырьмя корнями {0,0,1, t}, поэтому это просто linear eqn в t , которое затем легко решается. Можно также использовать второй подход,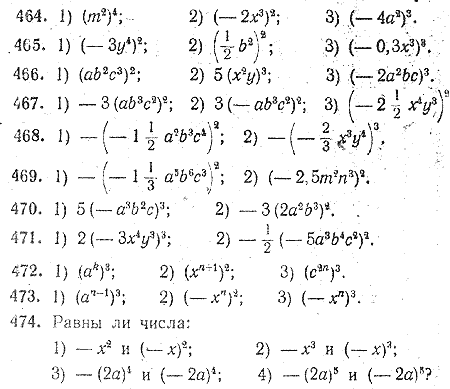 Используя их, уравнение 0 снова сводится к линейному уравнению в t . Также можно найти полиномиальное soln, используя тривиальное начальное. Пусть,
Используя их, уравнение 0 снова сводится к линейному уравнению в t . Также можно найти полиномиальное soln, используя тривиальное начальное. Пусть, Таким образом, образуя D , квадрат можно рассматривать как эллиптическую кривую.«
Таким образом, образуя D , квадрат можно рассматривать как эллиптическую кривую.« Используя эти выражения, можно заметить, что шестые члены L 1 и L 0 также равны.Тот факт, что L 1 менее общий, чем L 0 , не имеет значения, поскольку для исключительного случая L 0 сводится к четырехчленной форме,
Используя эти выражения, можно заметить, что шестые члены L 1 и L 0 также равны.Тот факт, что L 1 менее общий, чем L 0 , не имеет значения, поскольку для исключительного случая L 0 сводится к четырехчленной форме, (К сожалению, их утомительно явно записывать.) Дискриминант D равен,
(К сожалению, их утомительно явно записывать.) Дискриминант D равен, Этот автор обнаружил, что степень многочленов может быть уменьшена до , если предположить определенные линейные отношения между членами. Известно, что система для k = 1,5 может иметь побочное условие x 1 -x 2 = y 1 -y 2 . Пусть,
Этот автор обнаружил, что степень многочленов может быть уменьшена до , если предположить определенные линейные отношения между членами. Известно, что система для k = 1,5 может иметь побочное условие x 1 -x 2 = y 1 -y 2 . Пусть, (А. Месснер также нашел седьмой градус солнца в 1951 году, но я не знаю, является ли это таким же, поскольку Лендер указал источник как итальянский журнал.) В качестве альтернативы, если используется c = a-2b, они уменьшаются до восьмой deg, хотя мне не удалось найти линейной зависимости между терминами. Вопрос: Итак, есть 5-й, 7-й, 8-й и 9-й градусы солнца. Что-нибудь для 6-го градуса? (Примечание: как уже обсуждалось, форма L 1 также может использоваться для соответствующих более высоких степеней k. Позже она будет использована, чтобы доказать, что система k = 1,2,6 также может быть сокращена, опять же, просто решить квадратичный.)
(А. Месснер также нашел седьмой градус солнца в 1951 году, но я не знаю, является ли это таким же, поскольку Лендер указал источник как итальянский журнал.) В качестве альтернативы, если используется c = a-2b, они уменьшаются до восьмой deg, хотя мне не удалось найти линейной зависимости между терминами. Вопрос: Итак, есть 5-й, 7-й, 8-й и 9-й градусы солнца. Что-нибудь для 6-го градуса? (Примечание: как уже обсуждалось, форма L 1 также может использоваться для соответствующих более высоких степеней k. Позже она будет использована, чтобы доказать, что система k = 1,2,6 также может быть сокращена, опять же, просто решить квадратичный.) Для простоты можно установить c = a + 2b, и следующая точка дает слагаемые для x i , y i как полиномы 13-й степени после удаления общих множителей.
Для простоты можно установить c = a + 2b, и следующая точка дает слагаемые для x i , y i как полиномы 13-й степени после удаления общих множителей. Однако мы можем использовать альтернативную форму:
Однако мы можем использовать альтернативную форму: Эта квартика также довольно особенная, поскольку ее солнц достаточно много, чтобы их можно было линейно параметризовать по трем путям, а именно {q 1 , q 2 , q 3 } = {- (80p + 40) / (57p + 80), — (p + 2), — (3p + 2) / 3}, хотя последние два тривиальны по сравнению с исходным уравнением.Однако всегда можно получить нетривиальные точки. Затем будут даны три параметрических солнца, каждое из которых включает отдельную эллиптическую кривую. Таким образом,
Эта квартика также довольно особенная, поскольку ее солнц достаточно много, чтобы их можно было линейно параметризовать по трем путям, а именно {q 1 , q 2 , q 3 } = {- (80p + 40) / (57p + 80), — (p + 2), — (3p + 2) / 3}, хотя последние два тривиальны по сравнению с исходным уравнением.Однако всегда можно получить нетривиальные точки. Затем будут даны три параметрических солнца, каждое из которых включает отдельную эллиптическую кривую. Таким образом, Первый q был найден методом Ферма. Существуют тривиальные p, такие как {-1/2, -80/57, 0}, но они могут приводить к нетривиальным, например p = -15/38 и т. Д. Следующие два q были найдены с использованием метода Ферма на два тривиальных линейных солнца. Они не дают полностью всех значений, которые делают дискриминант квадратом, но можно показать, что три q как линейные многочлены — это , только имеют форму q = (ap + b) или q = (ap + b) / ( cp + d) для некоторых рациональных {a, b, c, d}. Чтобы показать это, учитывая ур.1, подставьте q = (ap + b) в уравнение и предположите, что полученный многочлен является квадратом,
Первый q был найден методом Ферма. Существуют тривиальные p, такие как {-1/2, -80/57, 0}, но они могут приводить к нетривиальным, например p = -15/38 и т. Д. Следующие два q были найдены с использованием метода Ферма на два тривиальных линейных солнца. Они не дают полностью всех значений, которые делают дискриминант квадратом, но можно показать, что три q как линейные многочлены — это , только имеют форму q = (ap + b) или q = (ap + b) / ( cp + d) для некоторых рациональных {a, b, c, d}. Чтобы показать это, учитывая ур.1, подставьте q = (ap + b) в уравнение и предположите, что полученный многочлен является квадратом, Расширяя вышеуказанное и собирая мощности p , мы получаем систему из пяти уравнений с пятью неизвестными, а окончательное уравнение в этом случае имеет два рациональных решения.Аналогичный подход для q = (ap + b) / (cp + d) даст одно рациональное решение.
Расширяя вышеуказанное и собирая мощности p , мы получаем систему из пяти уравнений с пятью неизвестными, а окончательное уравнение в этом случае имеет два рациональных решения.Аналогичный подход для q = (ap + b) / (cp + d) даст одно рациональное решение. Из этой начальной точки можно затем вычислить бесконечное количество рациональных точек. Фактически, это полное решение системы, назовите его M 1 ,
Из этой начальной точки можно затем вычислить бесконечное количество рациональных точек. Фактически, это полное решение системы, назовите его M 1 , Его дискриминант — квартика от q , а если его построить в квадрат, то это будет
Его дискриминант — квартика от q , а если его построить в квадрат, то это будет Я обновлю этот раздел, чтобы сравнить методы, когда прочитаю его.
Я обновлю этот раздел, чтобы сравнить методы, когда прочитаю его. К такому же выводу пришел Чоудри в своей статье Система одновременных уравнений x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k , k = 1,2,5 не имеет нетривиальных солнц в целых числах , The Mathematics Student, Vol 70, 2001.(Однако неизвестно, имеет ли случай k = 2,5 солнышко или нет, хотя с помощью базы данных Мура легко доказать, что их нет в радиусе 17000.)
К такому же выводу пришел Чоудри в своей статье Система одновременных уравнений x 1 k + x 2 k + x 3 k = y 1 k + y 2 k + y 3 k , k = 1,2,5 не имеет нетривиальных солнц в целых числах , The Mathematics Student, Vol 70, 2001.(Однако неизвестно, имеет ли случай k = 2,5 солнышко или нет, хотя с помощью базы данных Мура легко доказать, что их нет в радиусе 17000.) 5. См. Обновление 11/03/09 выше.)
5. См. Обновление 11/03/09 выше.) Что значит 5-я степень? — AnswersToAll
При чем здесь 5-я степень?
Как сделать 2 в 5-й степени?
Что означает двойка в пятой степени?

Что означает 10 в степени 5?
10-5 = 0,00001. (Стотысячная) 107 = 10 000 000. Что такое 3 в 5-й степени?
Что такое 2 в 10-й степени?
Ответ: Значение 2 возведено в 10-ю степень i.э., 210 это 1024. Что означает 10 до 6?
Как решить 3 в 5-й степени?
Как выглядит 10 в 6-й степени?
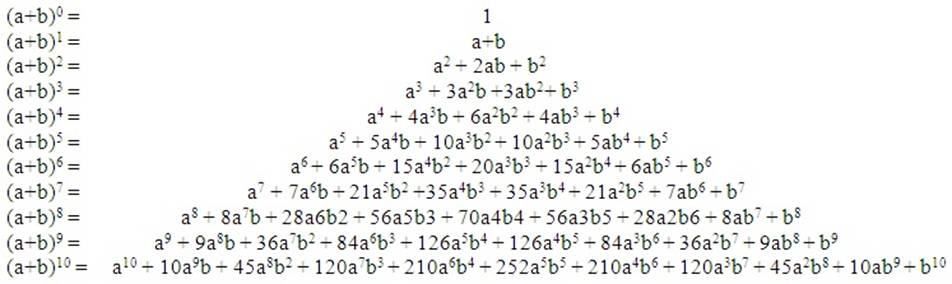
Что такое 3 в 5-й степени?
экспонентов: основные правила | Purplemath
Purplemath
MathHelp.
 com
com «До третьей» означает «умножение трех копий», а «до четвертой» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме. Сначала я расширяюсь:
«До третьей» означает «умножение трех копий», а «до четвертой» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме. Сначала я расширяюсь: Это демонстрирует первое основное правило экспоненты:
Это демонстрирует первое основное правило экспоненты: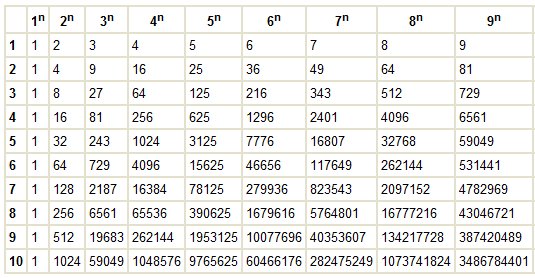 Однако у второго и , похоже, нет мощности. Что мне добавить для этого срока?
Однако у второго и , похоже, нет мощности. Что мне добавить для этого срока?
 «Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
«Умножение восьми копий» означает «в восьмой степени», поэтому это означает: Например:
Например: На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25.
На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25. (Мне нужно помнить, что у c внутри скобок это «в степени 1».)
(Мне нужно помнить, что у c внутри скобок это «в степени 1».) Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:
Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд: Упростить [(3
x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0  Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
