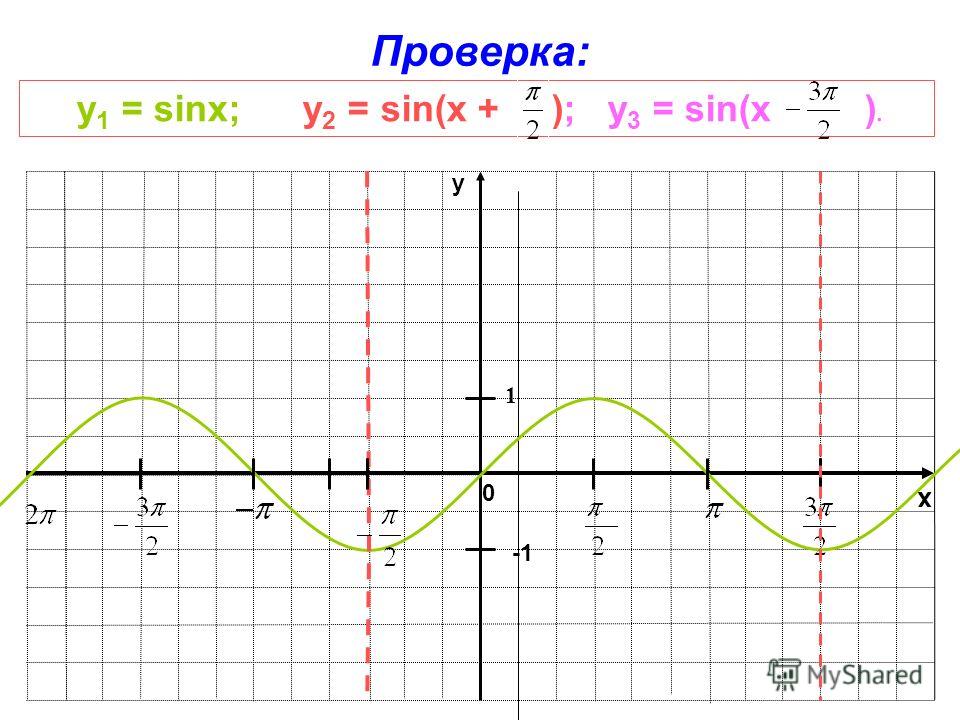
2 синус х 1: Решите уравнение (2*sin(x)-1)*(sqrt(-cos(x))+1)=0 ((2 умножить на синус от (х) минус 1) умножить на (квадратный корень из (минус косинус от (х)) плюс 1) равно 0)
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. |
|
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. |
|
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) ) |
|
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) ) |
|
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) ) |
|
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град.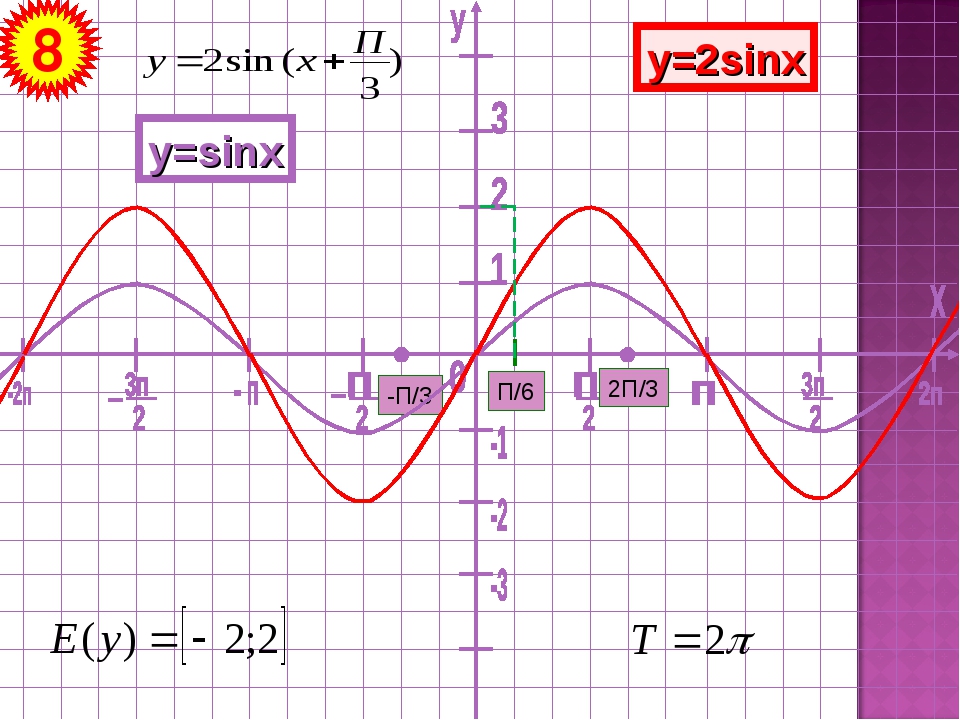 ) ) |
|
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | ||
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. 4) 4) |
|
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти точное значение | sin(300) | |
| 59 | Найти точное значение | cos(30) | |
| 60 | Найти точное значение | cos(60) | |
| 61 | Найти точное значение | cos(0) | |
| 62 | Найти точное значение | arctan( квадратный корень 3) | |
| 63 | Найти точное значение | cos(135) | |
| 64 | Найти точное значение | cos((5pi)/3) | |
| 65 | Найти точное значение | cos(210) | |
| 66 | Найти точное значение | sec(60 град. ) ) |
|
| 67 | Найти точное значение | sin(300 град. ) | |
| 68 | Преобразовать из градусов в радианы | 135 | |
| 69 | Преобразовать из градусов в радианы | 150 | |
| 70 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 72 | Преобразовать из градусов в радианы | 89 град. | |
| 73 | Преобразовать из градусов в радианы | 60 | |
| 74 | Найти точное значение | sin(135 град. 8) 8) |
|
| 80 | Найти точное значение | sin(225) | |
| 81 | Найти точное значение | sin(240) | |
| 82 | Найти точное значение | cos(150 град. ) | |
| 83 | Найти точное значение | tan(45) | |
| 84 | Вычислить | sin(30 град. ) | |
| 85 | Найти точное значение | sec(0) | |
| 86 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 87 | Найти точное значение | cos((5pi)/6) | |
| 88 | Найти точное значение | csc(30) | |
| 89 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 90 | Найти точное значение | tan((5pi)/3) | |
| 91 | Найти точное значение | tan(0) | |
| 92 | Вычислить | sin(60 град.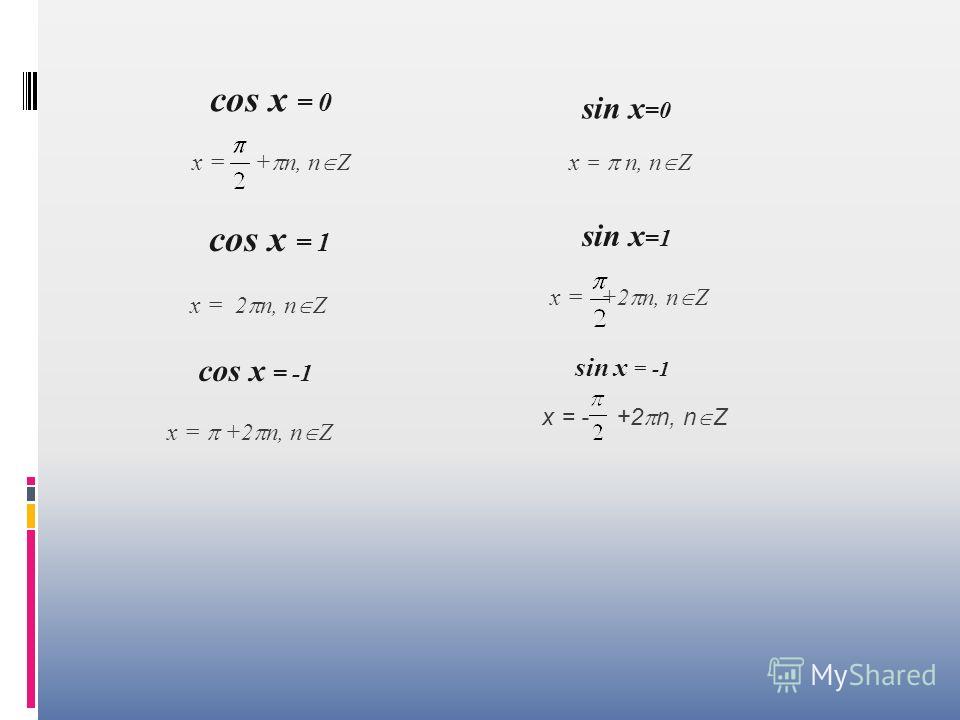 ) ) |
|
| 93 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 94 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 95 | Вычислить | arcsin(-1) | |
| 96 | Найти точное значение | sin((7pi)/4) | |
| 97 | Найти точное значение | arcsin(-1/2) | |
| 98 | Найти точное значение | sin((4pi)/3) | |
| 99 | Найти точное значение | csc(45) | |
| 100 | Найти точное значение | cos((4pi)/3) |
Пример №80 из задания 13 (профильный уровень) ЕГЭ 11 класс
а) Решите уравнение `cosx+sqrt((2-sqrt(2))/2 *(sinx+1))=0`.
 2))/4=(-2+sqrt(2)+sqrt(2)+2)/4=(sqrt(2))/2`.
2))/4=(-2+sqrt(2)+sqrt(2)+2)/4=(sqrt(2))/2`.Первый корень:
`sinx=-1`;
`x=-pi/2+2pin, n in Z`;
Второй корень:
`sinx=(sqrt(2))/2`;
`x=pi/4+2pin, n in Z`;
`x=(3pi)/4+2pin, n in Z`.
С учетом ОДЗ остаются следующие корни (см. тригонометрическую окружность ниже):
`x=-pi/2+2pin, n in Z` и `x=(3pi)/4+2pin, n in Z`.
б) С помощью числовой окружности отберем корни, принадлежащие промежутку `[-(11pi)/2; -4pi]`.
Получились следующие корни: `-(21pi)/4; -(9pi)/2`.
Решение №2 (скан):
$IMAGE3$Ответ: а) `-pi/2+2pin; (3pi)/4+2pin, n in Z`;
б) `-(21pi)/4; -(9pi)/2`.
Простейшие тригонометрические уравнения с косинусом и синусом. Часть 1
Ключ к решению простейших тригонометрических уравнений – в отличном знании тригонометрического круга. Если вы знаете значения стандартных точек и их синусы и косинусы, то проблем с уравнениями не будет. А если пробелы все-таки есть, то восполнить их можно в статье «Как запомнить тригонометрический круг?»

Эта статья состоит из двух частей:
Решение простейших уравнений с косинусом
Решение простейших уравнений с синусом
Алгоритм решения простейших уравнений с косинусом
Любой алгоритм проще всего понять на конкретных примерах, поэтому сразу с них и начнем.
Пример №1. Решить уравнение \(\cosx=\frac{1}{2}\).
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси косинусов значение, которому косинус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению для каждой из полученных точек на круге. Для уравнений с косинусом значения в верхней и нижней точках всегда будут отличаться только знаком.
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn,n∈Z\) (подробнее о формуле в этом видео
Возможно, у вас возник вопрос, почему мы в ответ добавляем \(+2πn\), \(n∈Z\). Дело в том, что у каждой точки на тригонометрическом круге есть множество значений, и каждое значение будет решением уравнения, а значит все они обязательно должны быть в ответе.
Но проблема в том, что значений этих бесконечно много, и просто в строчку их не запишешь. Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
Пример №2. Решить уравнение \(\cosx=-\frac{\sqrt{3}}{2}\).
С 1-3 шагом всё понятно, а вот над 4 шагом надо подумать.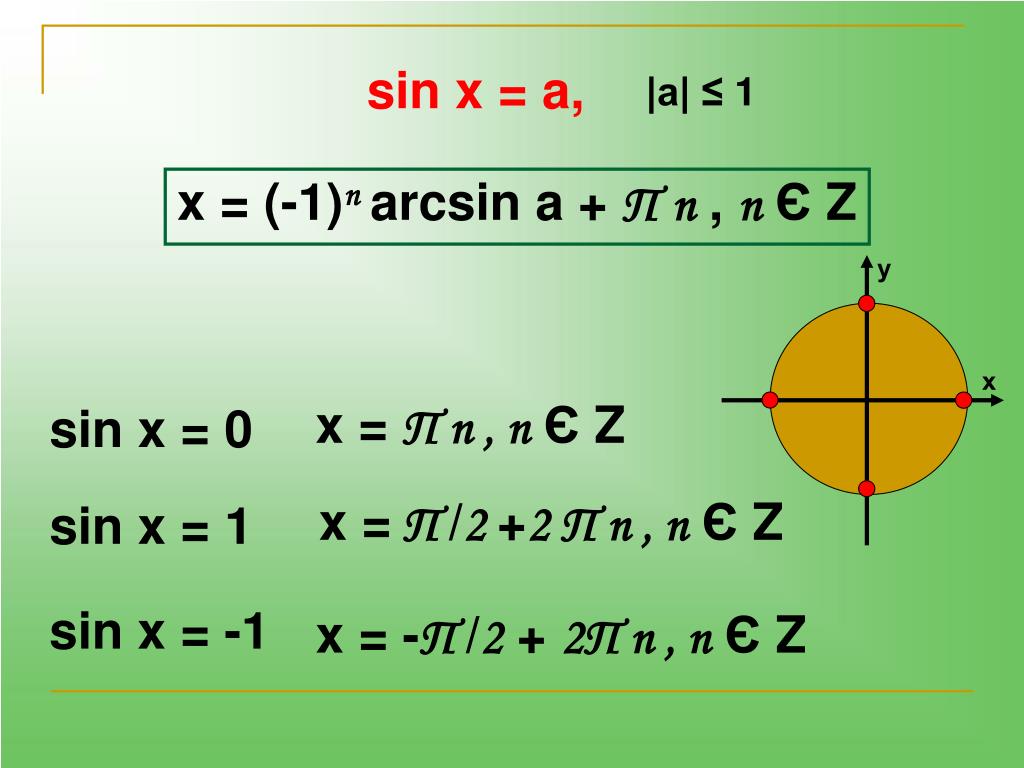 Как найти значения полученных точек? Можно заметить, что дуга между точкой со значением \(π\) и найденной точкой равняется π/6 (см. картинку ниже). И чтоб из точки π прийти к верхней найденной точке надо пройти в отрицательную сторону расстояние \(\frac{π}{6}\), то есть значение верхней точки равно \(π-\frac{π}{6}=\frac{5π}{6}\). Значит значение нижней \(-\frac{5π}{6}\).
Как найти значения полученных точек? Можно заметить, что дуга между точкой со значением \(π\) и найденной точкой равняется π/6 (см. картинку ниже). И чтоб из точки π прийти к верхней найденной точке надо пройти в отрицательную сторону расстояние \(\frac{π}{6}\), то есть значение верхней точки равно \(π-\frac{π}{6}=\frac{5π}{6}\). Значит значение нижней \(-\frac{5π}{6}\).
Пример №3. Решить уравнение \(\cosx=1\).
Видно, что в этом случае у косинуса только одна точка на круге будет решением, и эта точка совпадает с нулём на окружности. Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
Пример №4. Решить уравнение \(\cosx=-\frac{7}{6}\).
Значения косинуса (как и синуса) для любого аргумента всегда лежат между \(-1\) и \(1\) включительно, поэтому равняться \(-\frac{7}{6}\) косинус никак не может. Значит такое уравнение не имеет решений.
Значит такое уравнение не имеет решений.
Вот так решаются простейшие тригонометрические уравнения вида \(\cosx=a\). Для наглядности мы все рассказанное выше объединили на одной инфографике — взглянув на нее вы сразу вспомните суть. Пользуйтесь на здоровье.
Алгоритм решения простейших уравнений с синусом
Пример №5. Решить уравнение \(\sinx=\frac{\sqrt{3}}{2}\).
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси синусов, значение, которому синус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Для уравнений с синусом значение второй точки можно найти, если вычесть из π значение первой точки.
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример №6. Решить уравнение \(\sinx=-\frac{\sqrt{2}}{2}\).
Так как суть, думаю, вам уже ясна, дальнейшие объяснения мы опускаем.
Пример №7. Решить уравнение \(\sinx=0\).
В уравнениях с \(0\), главное не перепутать к какой оси надо проводить перпендикуляр. Ось синусов – вертикальная, соответственно перпендикуляр будет горизонтален.
Пример №8. Решить уравнение \(\sinx=\frac{\sqrt{5}}{2}\).
Вот в принципе и всё. Как обычно, в конце – инфографика для наглядности.
Смотрите также:
Синус
Косинус
Решение уравнений \(tg\;x=a\) и \(ctg\;x=a\)
Тригонометрические уравнения
§ 19. РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Простейшими тригонометрическими уравнениями называют уравнения
cos x = a, sin x = a, tg x = a, ctg x = a.
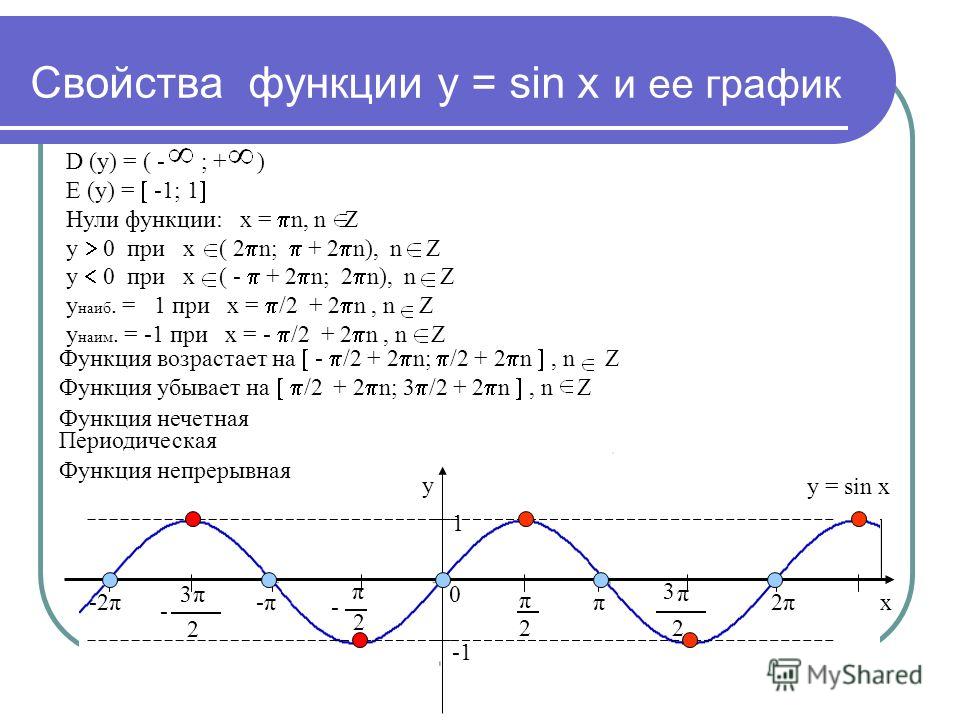
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
19.1. Уравнение cos x = a
Таблица 1
Объяснение и обоснование
- Корни уравнения cos x = a.
При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a < -1 не пересекает график функции y = cos x).
Пусть | a | ≤ 1. Тогда прямая y = a пересекает график функции y = cos x (рис. из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).
Косинус – четная функция, поэтому на промежутке [-π; 0] уравнение cos x = a также имеет только один корень – число, противоположное x1, то есть x2 = — arccos a.
Таким образом, на промежутке [-π; π] (длиной 2π) уравнение cos x = a при |a| ≤ 1 имеет только корни x = ±arccos a.
Функция y = cos x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных на 2πn (n ∈ Z). Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1:
x = ±arccos a + 2πn, n ∈ Z (1)
- Частые случаи решения уравнения cos x = a.
Полезно помнить специальные записи корней уравнения cos x = a при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность.
Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка А или точка В (рис. из пункта 2 табл. 1). Тогда
Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка С, следовательно, x = 2πk, k ∈ Z.
Также cos x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, x = п + 2πk, k ∈ Z
Примеры решения задач
19. 2. Уравнение sin x = a
2. Уравнение sin x = a
Таблица 2
Объяснение и обоснование
1.Корни уравнения sin x = a.
При |a| > 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a < -1 не пересекает график функции y = sin x).
Рисунок 1
Пусть |a| ≤ 1. Тогда прямая y = a пересекает график функции y = sin x (рис. 1). На промежутке функция y = sin x возрастает от -1 до 1. Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень, который по определению арксинуса равен: x1 = arcsin a (и для этого корня sin x = a).
На промежутке функция y = sin x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень x2 = π — arcsin a (рис. 1). Для проверки правильности записи значения второго корня x2 заметим, что x2 = π — x1, тогда sin x2 = sin (π- x1) = sin x1 = a. То есть x2 – корень уравнения sin x = a.
Таким образом на промежутке (длиной 2π) уравнение sin x = a при |a| ≤ 1 имеет только корни x1 = arcsin a, x2 = π — arcsin a.
Функция y = sin x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных 2πk (k ∈ Z). Получаем следующие формулы корней уравнения sin x = a при |a| ≤ 1:
x=arcsin a + 2πk, k ∈ Z. (1)
x= π — arcsin a + 2πk, k ∈ Z. (2)
Все значения корней уравнения sin x = a при |a| ≤ 1, которые дают формулы (1) и (2), можно записать с помощью одной формулы
x=(-1)n arcsin a + 2πn, n ∈ Z (3)
Действительно, из формулы (3) при четном n = 2k получаем x = arcsin a + 2πk – формулу (1), а при нечетном n = 2k +1 – формулу x= — arcsin a + π(2k+1)= π — arcsin a + 2πk, то есть формулу (2).
2.Частые случаи решения уравнения sin x = a.
Рисунок 2
Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).
Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда
Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,
Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,
Примеры решения задач
Замечание. Ответ к задаче 1 часто записывают в виде:
Ответ к задаче 1 часто записывают в виде:
19.3. Уравнения tg x = a и ctg x = a
Объяснение и обоснование
1.Корни уравнений tg x = a и ctg x = a
Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.
Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:
При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).
Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:
При a = 0
таким образом, уравнение ctg x = 0 имеет корни
Примеры решения задач
Вопросы для контроля
- Какие уравнения называют простейшими тригонометрическими?
- Запишите формулы решения простейших тригонометрических уравнений.
 В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам? - Выведите формулы решения простейших тригонометрических уравнений.
- Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.
Упражнения
Решите уравнение (1-11)
Найдите корни уравнения на заданном промежутке (12-13)
Все формулы по тригонометрии
Все формулы по тригонометрии
Основные тригонометрические тождества
sin2x + cos2x = 1
tgx ctgx = 1
tg2x + 1 | = | 1 |
cos2x |
ctg2x + 1 | = | 1 |
sin2x |
Формулы двойного аргумента
sin2x = 2sinx cosx
sin2x | = | 2tgx | = | 2ctgx | = | 2 |
1 + tg2x | 1 + ctg2x | tgx + ctgx |
cos2x = cos2 — sin2x = 2cos2x — 1 = 1 — 2sin2x
cos2x | = | 1 — tg2x | = | ctg2x — 1 | = | ctgx — tgx |
1 + tg2x | ctg2x + 1 | ctgx + tgx |
tg2x | = | 2tgx | = | 2ctgx | = | 2 |
1 — tg2x | ctg2x — 1 | ctgx — tgx |
ctg2x | = | ctg2x — 1 | = | ctgx — tgx |
2ctgx | 2 |
Формулы тройного аргумента
sin3x = 3sinx — 4sin3x cos3x = 4cos3x — 3cosx
tg3x | = | 3tgx — tg3x |
1 — 3tg2x |
ctg3x | = | ctg3x — 3ctgx |
3ctg2x — 1 |
Формулы половинного аргумента
sin2 | x | = | 1 — cosx |
2 | 2 |
cos2 | x | = | 1 + cosx |
2 | 2 |
tg2 | x | = | 1 — cosx |
2 | 1 + cosx |
ctg2 | x | = | 1 + cosx |
2 | 1 — cosx |
tg | x | = | 1 — cosx | = | sinx |
2 | sinx | 1 + cosx |
ctg | x | = | 1 + cosx | = | sinx |
2 | sinx | 1 — cosx |
Формулы квадратов тригонометрических функций
sin2x | = | 1 — cos2x |
2 |
cos2x | = | 1 + cos2x |
2 |
tg2x | = | 1 — cos2x |
1 + cos2x |
ctg2x | = | 1 + cos2x |
1 — cos2x |
sin2 | x | = | 1 — cosx |
2 | 2 |
cos2 | x | = | 1 + cosx |
2 | 2 |
tg2 | x | = | 1 — cosx |
2 | 1 + cosx |
ctg2 | x | = | 1 + cosx |
2 | 1 — cosx |
Формулы кубов тригонометрических функций
sin3x | = | 3sinx — sin3x |
4 |
cos3x | = | 3cosx + cos3x |
4 |
tg3x | = | 3sinx — sin3x |
3cosx + cos3x |
ctg3x | = | 3cosx + cos3x |
3sinx — sin3x |
Формулы тригонометрических функций в четвертой степени
sin4x | = | 3 — 4cos2x + cos4x |
8 |
cos4x | = | 3 + 4cos2x + cos4x |
8 |
Формулы сложения аргументов
sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ
tg(α + β) | = | tgα + tgβ |
1 — tgα tgβ |
ctg(α + β) | = | ctgα ctgβ — 1 |
ctgα + ctgβ |
sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ
tg(α — β) | = | tgα — tgβ |
1 + tgα tgβ |
ctg(α — β) | = | ctgα ctgβ + 1 |
ctgα — ctgβ |
Формулы суммы тригонометрических функций
sinα + sinβ | = 2sin | α + β | ∙ cos | α — β |
2 | 2 |
cosα + cosβ | = 2cos | α + β | ∙ cos | α — β |
2 | 2 |
(sinα + cosα)2 = 1 + sin2α
tgα + tgβ | = | sin(α + β) |
cosα cosβ |
ctgα + ctgβ | = | sin(α + β) |
sinα sinβ |
Формулы разности тригонометрических функций
sinα — sinβ | = 2sin | α — β | ∙ cos | α + β |
2 | 2 |
cosα — cosβ | = -2sin | α + β | ∙ sin | α — β |
2 | 2 |
(sinα — cosα)2 = 1 — sin2α
tgα — tgβ | = | sin(α — β) |
cosα cosβ |
ctgα — ctgβ | = – | sin(α — β) |
sinα sinβ |
Формулы произведения тригонометрических функций
sinα ∙ sinβ | = | cos(α — β) — cos(α + β) |
2 |
sinα ∙ cosβ | = | sin(α — β) + sin(α + β) |
2 |
cosα ∙ cosβ | = | cos(α — β) + cos(α + β) |
2 |
tgα ∙ tgβ | = | cos(α — β) — cos(α + β) | = | tgα + tgβ |
cos(α — β) + cos(α + β) | ctgα + ctgβ |
ctgα ∙ ctgβ | = | cos(α — β) + cos(α + β) | = | ctgα + ctgβ |
cos(α — β) — cos(α + β) | tgα + tgβ |
tgα ∙ ctgβ | = | sin(α — β) + sin(α + β) |
sin(α + β) — sin(α — β) |
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 | ||
| (2) | Основное тождество через тангенс и косинус | 1 + tg2(α) = 1/cos2(α) | ||
| (3) | Основное тождество через котангенс и синус | 1 + ctg2(α) = 1/sin2(α) | ||
| (4) | Соотношение между тангенсом и котангенсом | tg(α)ctg(α) = 1 | ||
| (5) | Синус двойного угла | sin(2α) = 2sin(α)cos(α) | ||
| (6) | Косинус двойного угла | cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α) | ||
| (7) | Тангенс двойного угла |
| ||
| (8) | Котангенс двойного угла |
| ||
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) | ||
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) | ||
| (11) | Косинус суммы/разности | cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) | ||
| (12) | Синус суммы/разности | sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) | ||
| (13) | Тангенс суммы/разности | tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β)) | ||
| (14) | Котангенс суммы/разности | ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β)) | ||
| (15) | Произведение синусов | sin(α)sin(β) = ½(cos(α–β) – cos(α+β)) | ||
| (16) | Произведение косинусов | cos(α)cos(β) = ½(cos(α+β) + cos(α–β)) | ||
| (17) | Произведение синуса на косинус | sin(α)cos(β) = ½(sin(α+β) + sin(α–β)) | ||
| (18) | Сумма/разность синусов | sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) | ||
| (19) | Сумма косинусов | cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β)) | ||
| (20) | Разность косинусов | cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β)) | ||
| (21) | Сумма/разность тангенсов | tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β) | ||
| (22) | Формула понижения степени синуса | sin2(α) = ½(1 – cos(2α)) | ||
| (23) | Формула понижения степени косинуса | cos2(α) = ½(1 + cos(2α)) | ||
| (24) | Сумма/разность синуса и косинуса | sin(α) ± cos(α) = &sqrt;2sin(α±π/4) | ||
| (25) | Сумма/разность синуса и косинуса с коэффициентами | Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²))) | ||
| (26) | Основное соотношение арксинуса и арккосинуса | arcsin(x) + arccos(x) = π/2 | ||
| (27) | Основное соотношение арктангенса и арккотангенса | arctg(x) + arcctg(x) = π/2 |
Т.к. D> 0, то уравнение имеет два корня.
w1 = (-b + sqrt (D)) / (2 * a)
w2 = (-b - sqrt (D)) / (2 * a)
или
$$ w_ {1} = \ frac {1} {2} $$
$$ w_ {2} = — \ frac {1} {3} $$
делаем обратную замену
$$ \ sin {\ left (x \ right)} = w $$
Дано уравнение
$$ \ sin {\ left (x \ right)} = w $$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$ x = 2 \ pi n + \ operatorname {asin} {\ left (w \ right)} $$
$$ x = 2 \ pi n — \ operatorname {asin} {\ left (w \ right)} + \ pi $$
Или
$$ x = 2 \ pi n + \ operatorname {asin} {\ left (w \ right)} $$
$$ x = 2 \ pi n — \ operatorname {asin} {\ left (w \ right)} + \ pi $$
, где n — любое целое число
подставляем w:
$$ x_ {1} = 2 \ pi n + \ operatorname {asin} {\ left (w_ {1} \ right)} $$
$$ x_ {1} = 2 \ pi n + \ operatorname {asin} {\ left (\ frac {1} {2} \ right)} $$
$$ x_ {1} = 2 \ pi n + \ frac {\ pi} {6} $ $
$$ x_ {2} = 2 \ pi n + \ operatorname {asin} {\ left (w_ {2} \ right)} $$
$$ x_ {2} = 2 \ pi n + \ operatorname {asin } {\ l eft (- \ frac {1} {3} \ right)} $$
$$ x_ {2} = 2 \ pi n — \ operatorname {asin} {\ left (\ frac {1} {3} \ right) } $$
$$ x_ {3} = 2 \ pi n — \ operatorname {asin} {\ left (w_ {1} \ right)} + \ pi $$
$$ x_ {3} = 2 \ pi n — \ operatorname {asin} {\ left (\ frac {1} {2} \ right)} + \ pi $$
$$ x_ {3} = 2 \ pi n + \ frac {5 \ pi} {6} $$
$$ x_ {4} = 2 \ pi n — \ operatorname {asin} {\ left (w_ {2} \ right)} + \ pi $$
$$ x_ {4} = 2 \ pi n — \ operatorname {asin} {\ left (- \ frac {1} {3} \ right)} + \ pi $$
$$ x_ {4} = 2 \ pi n + \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} + \ pi $$
$$ x_ {1} = \ frac {\ pi} {6} $$
$$ x_ {2} = \ frac {5 \ pi} {6} $$
$$ x_ {3} = \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} + \ pi $$
$$ x_ {4} = — \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} $$
$$ x_ {1} = \ frac {\ pi} {6} $$
$$ x_ {2} = \ frac {5 \ pi} {6} $$
$$ x_ {3} = \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} + \ pi $$
$$ x_ {4 } = — \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} $$
Данные корни
$$ x_ {4} = — \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} $$
$$ x_ {1} = \ frac {\ pi} {6} $$
$ $ x_ {2} = \ frac {5 \ pi} {6} $$
$$ x_ {3} = \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} + \ pi $$
являются точками смены знака неравенства в решениях.
 {2} {\ left (x \ right)} — \ sin {\ left (x \ right)} — 1 \ leq 0 $$
{2} {\ left (x \ right)} — \ sin {\ left (x \ right)} — 1 \ leq 0 $$2 6 * sin (-asin (1/3) - 1/10) - sin (-asin (1/3) - 1/10) - 12 -1 + 6 * sin (1/10 + asin (1/3)) + sin (1/10 + asin (1/3))
но2 -1 + 6 * sin (1/10 + asin (1/3)) + sin (1/10 + asin (1/3))> = 0
Тогда
$$ x \ leq - \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} $$
не выполняется
значит одно из решений нашего неравенства будет при:
$$ x \ geq - \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} \ wedge x \ leq \ frac {\ pi} {6} $$_____ _____ / \ / \ ------- • ------- • ------- • ------- • ------- x4 x1 x2 x3
Другие решения неравенства будем получать переход на следующий полюс
и т.д.
Ответ:
$$ x \ geq - \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} \ wedge x \ leq \ frac {\ pi} {6} $$
$$ x \ geq \ frac {5 \ pi} {6} \ wedge x \ leq \ operatorname {asin} {\ left (\ frac {1} {3} \ right)} + \ pi $$
| 1 | Найти точное значение | грех (30) | |
| 2 | Найти точное значение | грех (45) | |
| 3 | Найти точное значение | грех (60) | |
| 4 | Найти точное значение | sin (30 град. ) ) | |
| 5 | Найти точное значение | sin (60 град.) | |
| 6 | Найти точное значение | загар (30 град.) | |
| 7 | Найти точное значение | арксин (-1) | |
| 8 | Найти точное значение | грех (пи / 6) | |
| 9 | Найти точное значение | cos (пи / 4) | |
| 10 | Найти точное значение | sin (45 град.) | |
| 11 | Найти точное значение | грех (пи / 3) | |
| 12 | Найти точное значение | арктан (-1) | |
| 13 | Найти точное значение | cos (45 град.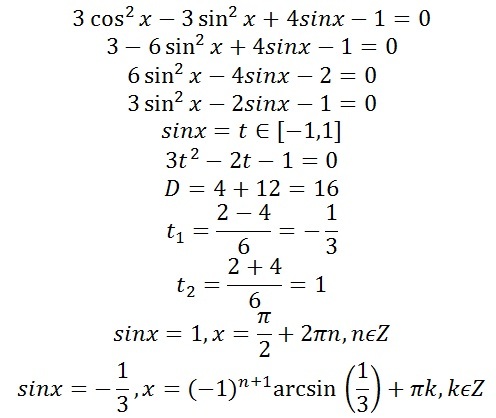 ) ) | |
| 14 | Найти точное значение | cos (30 град.) | |
| 15 | Найти точное значение | коричневый (60) | |
| 16 | Найти точное значение | мск (45 град.) | |
| 17 | Найти точное значение | загар (60 град.) | |
| 18 | Найти точное значение | сек (30 град.) | |
| 19 | Преобразовать из радианов в градусы | (3pi) / 4 | |
| 20 | График | у = грех (х) | |
| 21 | Преобразовать из радианов в градусы | пи / 6 | |
| 22 | Найти точное значение | cos (60 град. ) ) | |
| 23 | Найти точное значение | cos (150) | |
| 24 | Найти точное значение | желто-коричневый (45) | |
| 25 | Найти точное значение | грех (30) | |
| 26 | Найти точное значение | грех (60) | |
| 27 | Найти точное значение | cos (пи / 2) | |
| 28 | Найти точное значение | тан (45 град.) | |
| 29 | График | у = грех (х) | |
| 30 | Найти точное значение | arctan (- квадратный корень 3) | |
| 31 | Найти точное значение | мкр (60 град. ) ) | |
| 32 | Найти точное значение | сек (45 град.) | |
| 33 | Найти точное значение | мкр (30 град.) | |
| 34 | Найти точное значение | грех (0) | |
| 35 | Найти точное значение | грех (120) | |
| 36 | Найти точное значение | cos (90) | |
| 37 | Преобразовать из радианов в градусы | пи / 3 | |
| 38 | Найти точное значение | грех (45) | |
| 39 | Найти точное значение | желто-коричневый (30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | коричневый (60) | |
| 42 | Упростить | квадратный корень x ^ 2 | |
| 43 | Найти точное значение | cos (45) | |
| 44 | Упростить | грех (тета) ^ 2 + соз (тета) ^ 2 | |
| 45 | Преобразовать из радианов в градусы | пи / 6 | |
| 46 | Найти точное значение | детская кроватка (30 град. 4) 4) | |
| 56 | Найти точное значение | sin ((3pi) / 4) | |
| 57 | Найти точное значение | загар (пи / 2) | |
| 58 | Найти точное значение | грех (300) | |
| 59 | Найти точное значение | cos (30) | |
| 60 | Найти точное значение | cos (60) | |
| 61 | Найти точное значение | cos (0) | |
| 62 | Найти точное значение | arctan (квадратный корень 3) | |
| 63 | Найти точное значение | cos (135) | |
| 64 | Найти точное значение | cos ((5pi) / 3) | |
| 65 | Найти точное значение | cos (210) | |
| 66 | Найти точное значение | сек (60 град. ) ) | |
| 67 | Найти точное значение | sin (300 град.) | |
| 68 | Преобразовать из градусов в радианы | 135 | |
| 69 | Преобразовать из градусов в радианы | 150 | |
| 70 | Преобразовать из радианов в градусы | (5pi) / 6 | |
| 71 | Преобразовать из радианов в градусы | (5pi) / 3 | |
| 72 | Преобразовать из градусов в радианы | 89 град. | |
| 73 | Преобразовать из градусов в радианы | 60 | |
| 74 | Найти точное значение | sin (135 град. 8) 8) | |
| 80 | Найти точное значение | грех (225) | |
| 81 | Найти точное значение | грех (240) | |
| 82 | Найти точное значение | cos (150 град.) | |
| 83 | Найти точное значение | желто-коричневый (45) | |
| 84 | Вычислить | sin (30 град.) | |
| 85 | Найти точное значение | сек (0) | |
| 86 | Упростить | arcsin (- (квадратный корень 2) / 2) | |
| 87 | Найти точное значение | cos ((5pi) / 6) | |
| 88 | Найти точное значение | csc (30) | |
| 89 | Найти точное значение | arcsin ((квадратный корень 2) / 2) | |
| 90 | Найти точное значение | коричневый ((5pi) / 3) | |
| 91 | Найти точное значение | коричневый (0) | |
| 92 | Вычислить | sin (60 град. ) ) | |
| 93 | Найти точное значение | arctan (- (квадратный корень 3) / 3) | |
| 94 | Преобразовать из радианов в градусы | (3pi) / 4 | |
| 95 | Вычислить | арксин (-1) | |
| 96 | Найти точное значение | sin ((7pi) / 4) | |
| 97 | Найти точное значение | арксин (-1/2) | |
| 98 | Найти точное значение | sin ((4pi) / 3) | |
| 99 | Найти точное значение | csc (45) | |
| 100 | Найти точное значение | cos ((4pi) / 3) |
Пример №80 из задания 13 (профильный уровень) ЕГЭ 11 класс
а) Решите уравнение `cosx + sqrt ((2-sqrt (2)) / 2 * (sinx + 1)) = 0`.
 2-4 * 2 * (- sqrt (2)) = 4-4sqrt (2) + 2 + 8sqrt (2) = » 6 + 4кв (2) `.2)) / 4 = (- 2 + sqrt (2) + sqrt (2) +2) / 4 = (sqrt (2)) / 2`.
2-4 * 2 * (- sqrt (2)) = 4-4sqrt (2) + 2 + 8sqrt (2) = » 6 + 4кв (2) `.2)) / 4 = (- 2 + sqrt (2) + sqrt (2) +2) / 4 = (sqrt (2)) / 2`.Первый корень:
`sinx = -1`;
`x = -pi / 2 + 2pin, n в Z`;
Второй корень:
`sinx = (sqrt (2)) / 2`;
`x = pi / 4 + 2pin, n in Z`;
`x = (3pi) / 4 + 2pin, n в Z`.
С учетом ОДЗ остаются следующие корни (см. Тригонометрическую окружность ниже):
`x = -pi / 2 + 2pin, n в Z` и` x = (3pi) / 4 + 2pin, n в Z`.
б) С помощью числовой окружности отберем корни, между промежутками `[- (11pi) / 2; -4pi] `.
Получились следующие корни: `- (21pi) / 4; — (9pi) / 2`.
Решение №2 (скан):
$ IMAGE3 $Ответ: а) `-pi / 2 + 2pin; (3pi) / 4 + 2pin, n в Z`;
б) `- (21pi) / 4; — (9pi) / 2`.
Sin 180 градусов
Напомним, что $ \ pi $ радианы равны 180 $ градусам. Итак, если у нас есть угол, равный $ \ theta $ градусов, то эквивалентный радианный угол равен $ \ dfrac {\ theta} {180} \ pi $. Отсюда следует, что $$ \ sin_d (\ theta) = \ sin_r \ left (\ dfrac {\ theta} {180} \ pi \ right) \ text {.} $$ Следовательно, чтобы преобразовать радианы обратно в градусы, разделите 180 на Пи и умножьте полученное значение на число радианов. Вы получите действительное число, которое в целой части представляет собой количество градусов. Чтобы получить минуты, вам нужно умножить дробь на 60 и получить целое число.
Отсюда следует, что $$ \ sin_d (\ theta) = \ sin_r \ left (\ dfrac {\ theta} {180} \ pi \ right) \ text {.} $$ Следовательно, чтобы преобразовать радианы обратно в градусы, разделите 180 на Пи и умножьте полученное значение на число радианов. Вы получите действительное число, которое в целой части представляет собой количество градусов. Чтобы получить минуты, вам нужно умножить дробь на 60 и получить целое число.
Я использую программу Vision Builder AI 2010. У меня проблема, из-за которой изображение меняет ориентацию во время проверки. Кто-нибудь слышал об этой проблеме или, возможно, имел некоторое представление о том, почему изображение поворачивается на 180 с теми же шагами проверки.Я просто использую шаг получения изображения a … Умножает x на π / 180 °. Этот оператор преобразует xиз радиан в градусы. Когда x является вектором, матрицей или комплексным числом, оператор градусов применяется к каждому из элементов x. Удерживая нажатой клавишу Alt, нажмите 0176 с помощью цифровой клавиатуры.
e = Epeak x sin θ Мгновенное напряжение равно пиковому напряжению, умноженному на синус угла якоря генератора. Значение синуса получается из тригонометрических таблиц. В следующей таблице отражены несколько углов и их значение синуса.-1 (1/2) на вашем вычислении, и вы обнаружите, что это 30 градусов. Это только одно значение, вам нужно найти другое значение для x. Теперь, оглядываясь на то, что я сказал ранее, sin положителен в 1-м и 2-м квадранте. Нам нужно найти значение x во 2-м квадранте. как нам это сделать? Таблица синусов для 0 ° -180 °. Из графика sin мы видим, что sinø = 0, когда ø = 0 градусов, 180 градусов и 360 градусов. Обратите внимание, что график tan имеет асимптоты (линии, к которым график приближается, но никогда не пересекает).Это красные линии (на самом деле они не являются частью графика). Также обратите внимание, что графики sin, cos и tan являются периодическими. 18 ноября 2020 г. · Каждый прямоугольный треугольник имеет один угол 90 градусов (например, угол квадрата или прямоугольника) и два угла, каждый из которых находится в диапазоне от 0 до 90 градусов (как мы поговорим о будущем, сумма всех трех углов составляет 180 градусов).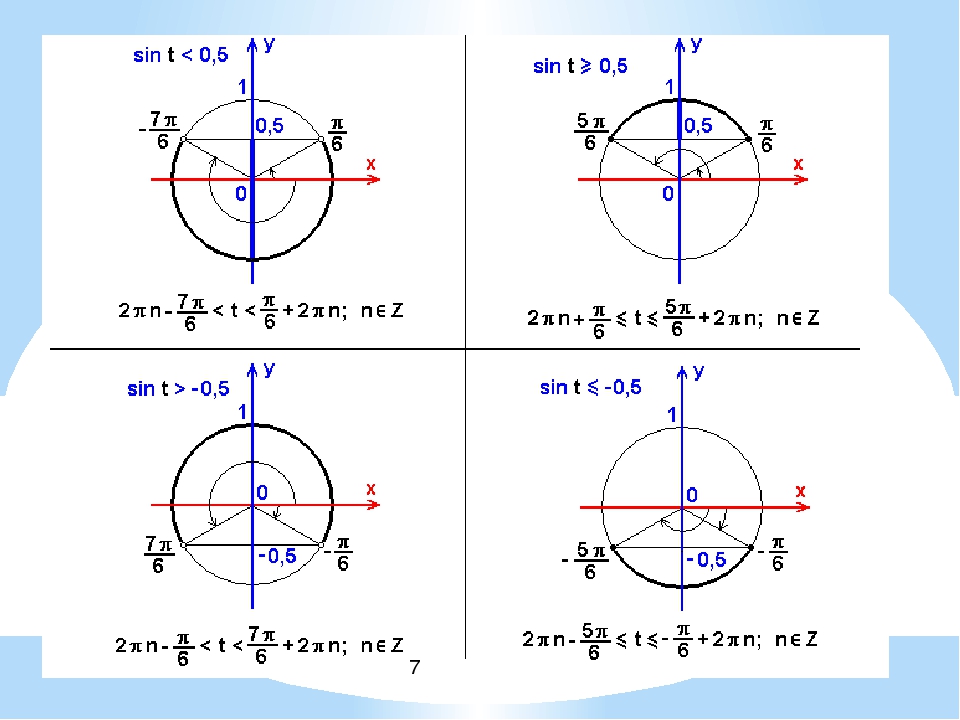 Для нашего обсуждения синуса, косинуса и тангенса (которые, не волнуйтесь, являются … Возвращает синус указанного угла.В следующем примере Sin используется для оценки определенных тригонометрических идентичностей для выбранных углов. // Пример для тригонометрических методов Math.Sin (double) // и Math.Cos (double). using пространство имен System; // Вычислить тригонометрические тождества с заданным …
Для нашего обсуждения синуса, косинуса и тангенса (которые, не волнуйтесь, являются … Возвращает синус указанного угла.В следующем примере Sin используется для оценки определенных тригонометрических идентичностей для выбранных углов. // Пример для тригонометрических методов Math.Sin (double) // и Math.Cos (double). using пространство имен System; // Вычислить тригонометрические тождества с заданным …
Ответы: соотношение 1 из 40 и 1,4321 градуса. Предположим, мы вводим уклон, рассчитанный путем подъема по длине склона. Введите 2.44992 и, прочитав вторую строку вывода, мы увидим, что это дает соотношение 1 к 40 и 1.Угол 4321 градус. График в верхней части страницы показывает небольшой диапазон углов от нуля до 20 градусов. 26 октября 2017 г. · Наконец, самолет сбавил скорость, но не раньше, чем он развернулся почти на 180 градусов и остановился в конце взлетно-посадочной полосы. Связанные: 5 кнопок, которые вы надеетесь, что ваш пилот никогда не должен нажимать.
29 мая 2014 г.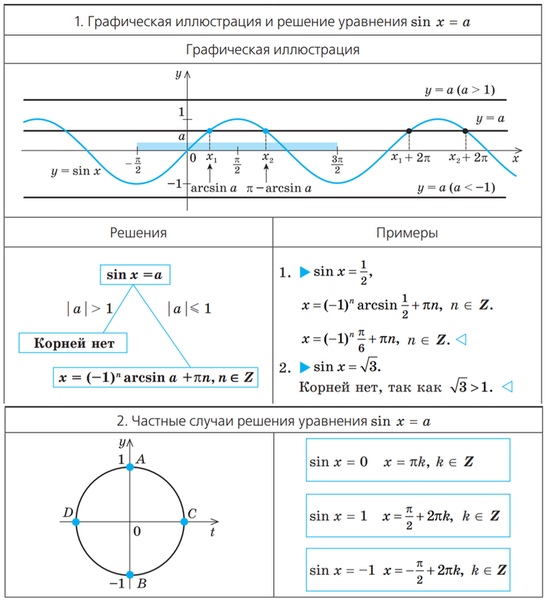

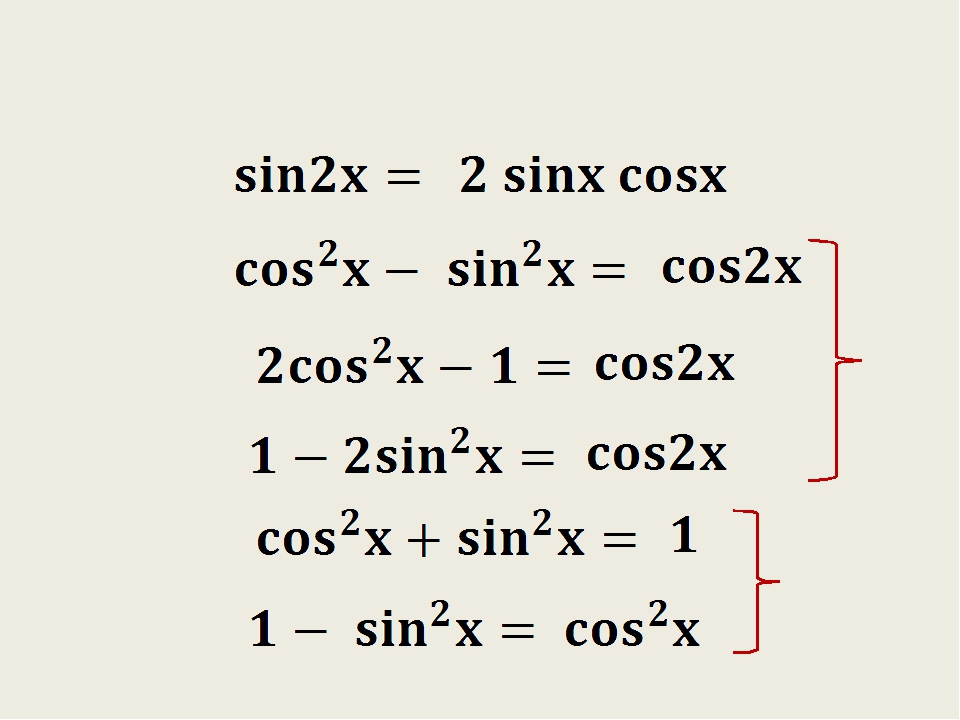 РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам? Математика (при поддержке «Ветвистого древа») 2009—2016
Математика (при поддержке «Ветвистого древа») 2009—2016