Гистограмма частот гистограмма относительных частот: Полигон и гистограмма примеры построения Теория вероятностей…
Построение полигона, гистограммы, кумуляты, огивы
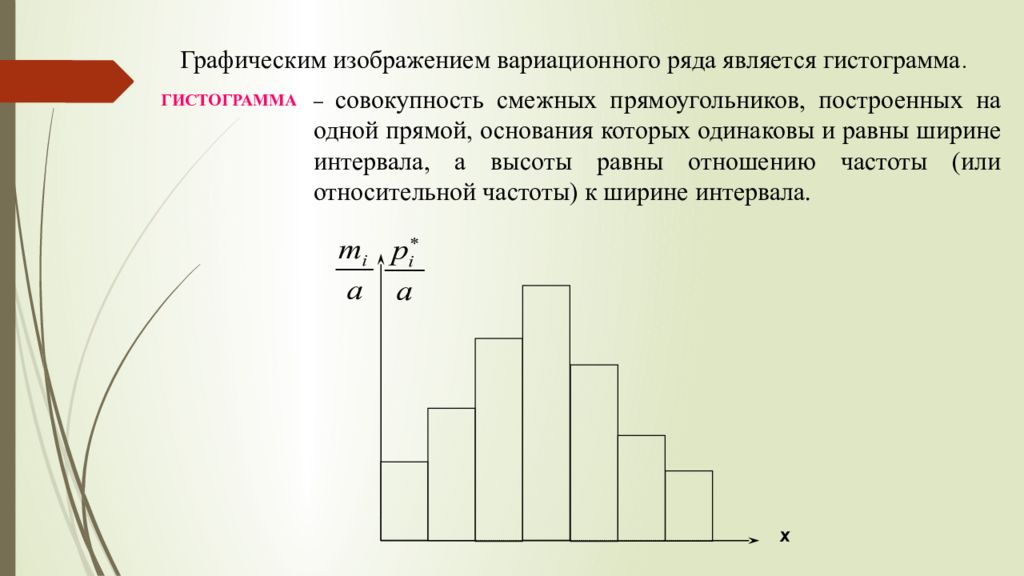
Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты (в случае равных интервалов) должны быть пропорциональны частотам. При построении гистограммы с неравными интервалами по оси ординат наносят не частоты, а плотность частоты . Это необходимо сделать для устранения влияния величины интервала на распределение и иметь возможность сравнивать частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
Пример 2
Построить гистограмму частот и относительных частот (частостей)
Если вам сейчас не требуется платная помощь, но может потребоваться в дальнейшем, то, чтобы не потерять контакт, вступайте в группу ВК.
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму частот (случай неравных интервалов).
| 2-4 | 4-8 | 8-13 | 13-15 | 15-17 | 17-20 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Вычислим плотности частоты:
| Интервалы, | Длина интервала, | Плотность частоты, | |
| 2 – 4 | 15 | 2 |
7. 500
|
| 4 – 8 | 35 | 4 | 8.750 |
| 8 – 13 | 64 | 5 | 12.800 |
| 13 – 15 | 55 | 2 | 27.500 |
| 15 – 17 | 21 | 10.500 | |
| 17 – 20 | 10 | 3 |
3. 333
|
| Итого | 200 | — | — |
Гистограмма частот
- К оглавлению решебника по
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путём последовательного суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву.
Пример 4
Построить кумулятивную кривую:
| 2 | 5 | 8 | 11 | 14 | 17 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Вычислим накопленные частоты:
| Накопленные частоты, | ||
| 15 | 15 | |
| 7 | 35 | 50 |
| 8 | 64 | 114 |
| 15 | 55 | 169 |
| 16 | 21 | |
| 17 | 10 | 200 |
| Итого | 200 | — |
Кумулятивная кривая
- К оглавлению решебника по
Полигон и гистограмма | matematicus.
ru
ruГистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле:
xi-xi-1
Высоты гистограммы определяется по формуле:
Формула размаха выборки R:
R=xmax−xmin
Количество интервалов в выборке определяется по формуле:
k≈1+log2n≈1+3,221·lgn
Длина l интервала гистограммы, формула:
l=R/n
Формула эмпирической плотности распределения выборки имеет вид:
хi — значения частот;
ni— частоты;
wi — относительные частоты;
n — объём выборки;
В водоёме проведены измерения температуры воды в течение 20 дней.
Статистика отчета измерений:
11, 15, 18, 14, 12, 13, 11, 14, 18, 19, 18, 14, 15, 16, 14, 18, 21, 17, 13, 16
Построить гистограмму относительных, абсолютных и накопленных частот выборки, вычислить эмпирическую плотность распределения частот.
Решение.
По условию задачи объем выборки равен 20.
Отсортируем и упорядочим вариационный ряд, начиная от самого минимального значения, получим:
11, 11, 12, 13, 13, 14, 14, 14, 14, 15, 15, 16, 16, 17, 18, 18, 18, 18, 19, 21
Найдем размах выборки
R=21-11=10
Количество интервалов в выборке равно:
k≈log220+1≈5,32
Округляя до целого числа, имеем
k=5
Определим длину каждого интервала
l=10/5=2
Получаем таблицу интервалов
| Номер интервала | Абсолютная частота, ni | Частотный интервал |
1. | 3 | [11;13) |
| 2. | 6 | [13;15) |
| 3. | 4 | [15;17) |
| 4. | 5 | [17;19) |
| 5. | 2 | [19;21) |
Таблица относительных частот и эмпирическая плотность распределения частоты
| Частотный интервал | Относительная частота, wi=ni/n | Эмпирическая плотность распределения частоты ni/Δ |
| [11;13) | 0.15 | 1.5 |
| [13;15) | 0.3 | 3 |
| [15;17) | 0.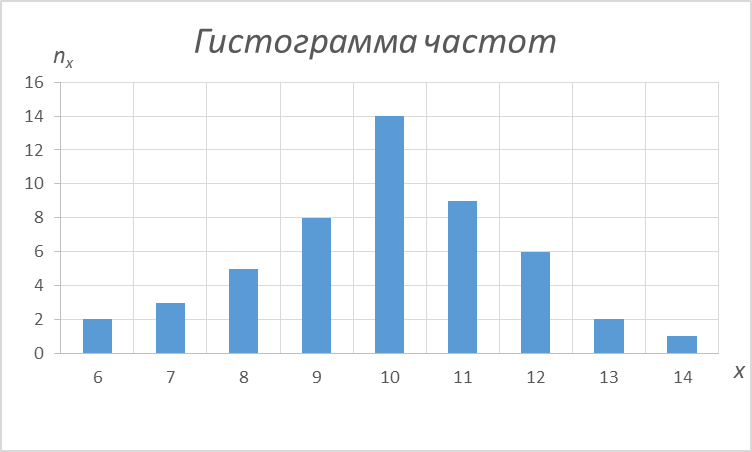 2 | 2 |
| [17;19) | 0.25 | 0.25 |
| [19;21) | 0.1 | 0.1 |
График гистограммы абсолютных частот
График гистограммы относительных частот
График гистограммы накопленных частот
Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni и соединяют точки.
Пример графика полигона частот хi, ni
Пример графика полигона относительных частот хi, wi
Полигон и гистограмма — Студопедия
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Определение.
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1), (x2, n2), (xk, nk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.
Определение. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1, w1), (x2, w2), (xk, wk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат wi. Точки (xi, wi) соединяют отрезками прямых и получают полигон относительных частот.
На рисунке изображен полигон относительных частот следующего распределения:
| x | 1,5 | 3,5 | 5,5 | 7,5 |
| w | 0,1 | 0,2 | 0,4 | 0,3 |
Рис.
6. Полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-ый интервал.
Определение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты).
Рис. 7. Гистограмма частот.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии .
Площадь i-го частичного прямоугольника равна = — сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
На рисунке 2 изображена гистограмма частот распределения объема n =100, приведенного в таблице 1.
| Частичный интервал, длиною h=5 | Сумма частот вариант частичного интервала | Плотность частоты |
| 5 – 10 | 0,8 | |
| 10 – 15 | 1,2 | |
| 15 – 20 | 3,2 | |
| 20 – 25 | 7,2 | |
| 25 – 30 | 4,8 | |
| 30 – 35 | 2,0 | |
| 34 – 40 | 0,8 |
Определение. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны отношению (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-го частичного прямоугольника равна = — относительной частоте вариант, попавших в i-й интервал.
Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Примеры.
1. В результате выборки получена следующая таблица распределения частот.
Построить полигоны частот и относительных частот распределения.
Для начала построим полигон частот.
Рис. 8. Полигон частот.
Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.
n = 3 + 10 + 7 = 20.
.
Получаем
| 0,15 | 0,50 | 0,35 |
Построим полигон относительных частот.
Рис. 9. Полигон относительных частот.
2. Построить гистограммы частот и относительных частот распределения.
Найдем плотность частоты :
| Частичный интервал, длиною h = 3 | Сумма частот вариант частичного интервала | Плотность частоты |
| 2 – 5 | ||
| 5 – 8 | 3,3 | |
| 8 – 11 | 8,3 | |
| 11 – 14 |
Построим гистограмму частот.
Рис. 10. Гистограмма частот.
Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.
.
Теперь найдем относительные частоты :
Получим:
| Частичный интервал | Сумма относительных частот | Плотность частоты |
| 2 – 5 | 0,18 | 0,06 |
| 5 – 8 | 0,2 | 0,07 |
| 8 – 11 | 0,5 | 0,16 |
| 11 – 14 | 0,12 | 0,04 |
Плотности частот нужно вычислить.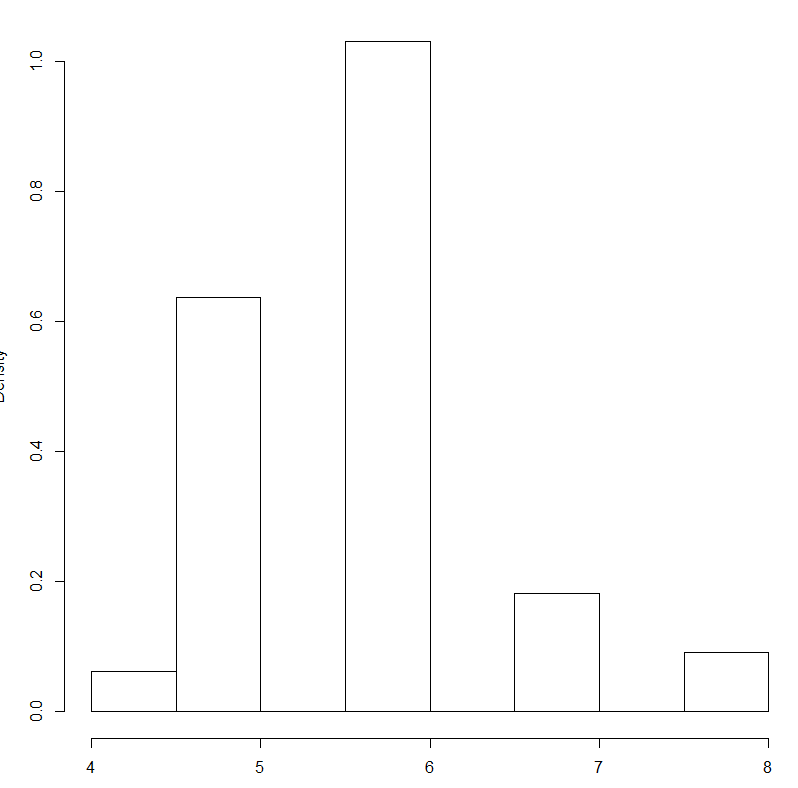
При этом h = 3.
Построим гистограмму относительных частот.
Рис.11. Гистограмма относительных частот.
3.2.2 Полигон и гистограмма
Пусть результаты выборки количественного признака X из генеральной совокупности представлены вариационным рядом. Кумулята, будучи функцией распределения выборки, служит ее интегральной вероятностной характеристикой. Для изучения локальных свойств нужна функция, аналогичная ряду распределения или плотности вероятности. Графиками таких вариационных рядов служат полигон и гистограмма.
Точечный вариационный ряд наглядно можно представить с помощью полигона частот, а интервальный – с помощью гистограммы.
Полигоном частот
называется ломаная, звенья которой
соединяют отрезками точки с координатами
(x1, n1), (x2, n2), .
.. , (xk, nk)
для полигона абсолютных частот и точки
с координатами (x1,
), (x2,
), … , (xk,
)
для полигона относительных частот.
Для
их построения, исходя из условия задачи,
необходимо составить точечный (либо
интервальный) вариационный ряд абсолютных
или относительных частот. Если задан
интервальный вариационный ряд, то для
построения полигона частот необходимо
найти середины интервалов 1,
2,
… , k – точки x1, x2, … , xk.
Затем, в декартовой системе координат
надо отложить на оси абсцисс все возможные
значения вариант x1, x2, … , xk,
а на оси ординат соответствующие им
абсолютные частоты n1, n2,
… , nk (или относительные частоты
,,…,).
Для построения полигона абсолютных
(относительных) частот необходимо
соединить отрезками полученные точки
с координатами (x1,n1), (x2,n2), … , (xn,nk)
(или, соответственно, (x1,
), (x2,
), … , (xk,
)).
Гистограммой абсолютных (относительных) частот называется ступенчатая фигура, состоящая из прямоугольников, основания которых есть частичные интервалы длиною h, высотами которых служат значения, пропорциональные частоте интервала ni (или ). Отношенияназываютплотности частоты, а отношения плотности относительной частоты.
Для
построения гистограммы необходимо
найти размах выборки – ее границы, т.е.
и,
длину интервалов,
а такжеk – число интервалов.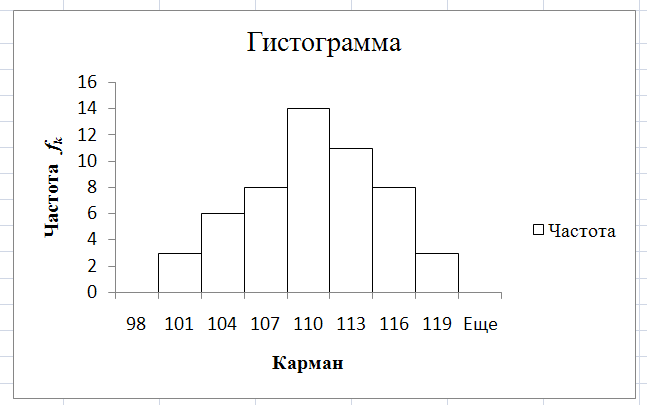
При удачном подборе интервалов гистограмма и полигон дают представление о графике функции плотности вероятности распределения генеральной совокупности, что используется для формулировки предположения о виде исследуемого теоретического закона распределения (п.3.6.6).
Заметим, что, если за единицу высоты принять 1/h, площадь каждого i-го прямоугольника равна произведению основания на высоту: т.е. частотеi-го интервала (или сумме частот вариант, входящих в этот интервал). Тогда площадь всей гистограммы частот равна сумме всех частот , т.е. объему выборки, причем площадь каждого столбца гистограммы пропорциональна частоте попадания наблюдений в данный интервал группировки. Если в качестве высот прямоугольников выбрать отношения, то площадь фигуры под гистограммой относительных частот равна единице, т.к..
Т.о., площадь гистограммы частот равна сумме всехчастот, т.е..
Задача
2.
Представить
графическое распределение размеров
зарплаты сотрудников фирмы за неделю
(в долларах), если они получили следующую
зарплату:
152.74; 176.66; 162.48; 167.72; 181.09; 155.00; 196.17; 169.60; 172.88; 182.47; 181.69; 186.91; 190.10; 176.14; 192.70; 178.59; 167.27; 175.14; 160.00; 177.46; 165.18; 167.77; 178.46; 165.00; 185.20; 157.02; 172.14; 192.22; 179.40; 191.03; 188.68; 169.51; 200.15; 178.47; 176.33; 179.05; 180.95; 174.28; 175.00; 178.45; 150.10; 176.86; 187.71; 168.33; 195.00; 172.37; 179.04; 182.05; 186.19; 190.05; 196.27; 209.28; 203.16; 168.52; 200.00; 196.30.
xmax=209.28, xmin=150.10.
Решение.
Построим интервальный вариационный ряд с интервалом h=10:
Интервалы зарплаты | 150-160 | 160-170 | 170-180 | 180-190 | 190-200 | 200-210 |
ni | 4 | 11 | 18 | 10 | 9 | 4 |
Для построения точечного вариационного ряда найдем середины интервалов:
xi | 155 | 165 | 175 | 185 | 195 | 205 |
ni | 4 | 11 | 18 | 10 | 9 | 4 |
Составим графики
распределения зарплаты (Рис.
2а,б)
Интервальному вариационному ряду соответствует гистограмма (Рис. 2(а). Точечному вариационному ряду соответствует полигон (Рис. 2(б).
Рис. 2 (а, б)
Задача 3. Даны результаты изменения напряжения (в вольтах) в электросети. Составить вариационный ряд и начертить график распределения напряжения, если значения напряжения следующие:
227, 229, 215, 230, 232, 223, 220, 222, 228, 219,
222, 221, 227, 226, 226, 229, 217, 215, 218, 220,
216, 220, 220, 221, 225, 224, 212, 217, 219, 220.
Решение.
Составим вариационный ряд, по которому построим гистограмму (Рис.3). Имеем
xmax=232, xmin=212. Применим формулу Стерджесса и подсчитаем число интервалов:
Тогда вариационный ряд абсолютных частот примет вид:
xi
212-217
217-222
222-227
227-232
ni
7
12
7
5
Соответствующая
гистограмма абсолютных частот представлена
на рисунке 3(а), а относительных частот
— на рисунке 3(б).
Рис.3 (а) Рис. 3(б)
Задача 4. Контролер на рынке выявлял отклонение весов в граммах от стандарта на основе выборки. Закон распределения выборки задан вариационным рядом абсолютных частот:
xi
-2
0
3
5
8
ni
5
1
7
3
4
Составить
закон распределения относительных
частот и построить их графики.
Решение:
Найдем объем выборки: .
Найдем относительные частоты по формуле :.
Составим вариационный ряд относительных частот:
-2 | 0 | 3 | 5 | 8 | |
0.25 | 0.05 | 0.35 | 0.15 | 0.20 |
4. Полигон для вариационного ряда распределения абсолютных частот представлен на рисунке 4а. Полигон вариационного ряда относительных частот представлен на рисунке 4б:
Величина
интервала группировки значительно
влияет на вид гистограммы: чем больше
величина h,
тем менее различимы особенности
распределений.
1.4 Гистограмма и полигон частот
Пусть – выборка объема, содержащаяразличных вариант, из генеральной совокупности случайной величиныс неизвестной плотностью вероятностей. Приближением (оценкой) неизвестной плотности вероятностей могут служитьгистограммаилиполигон относительных частот. Гистограмма и полигон относительных частот служат для геометрического изображения группированного вариационного ряда.
Гистограмма относительных частот
представляется в виде примыкающих друг
к другу прямоугольников с основаниями
,
равными ширине интервалов группировок,
и высотами(рис. 1). Для гистограммы относительных
частот площадь ступенчатой фигуры
соответствует сумме вероятностей и
равна.
Площадь любого прямоугольника гистограммы
равна вероятности попадания значений
рассматриваемой случайной величины в
интервал, соответствующий основанию
прямоугольника.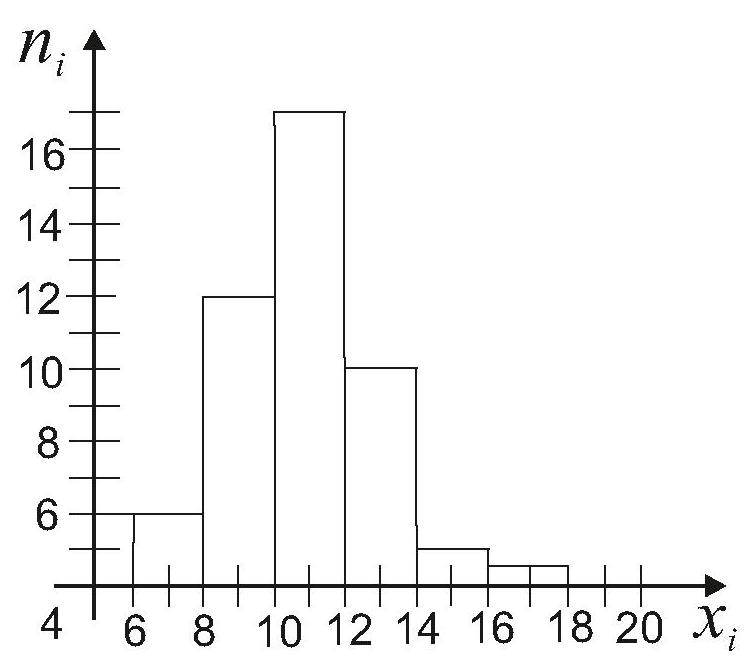
Рис. 1 — Гистограмма и полигон относительных частот
Полигоном относительных частотназывается ломаная, соединяющая точки,, …,(рис. 1), где– середины интервалов группировки;– высоты прямоугольников гистограммы.
При увеличении объема выборки и уменьшении длин интервалов гистограмма и полигон относительных частот приближаются к графику неизвестной функции – плотности вероятности генеральной совокупности.
По виду гистограммы или полигона частот можно выдвинуть гипотезу о виде распределения генеральной совокупности. Например, если гистограмма имеет вид, представленный на рис. 2а, то можно предположить, что генеральная совокупность имеет нормальный закон распределения с плотностью вероятностей ; рис. 2б – равномерное распределения с плотностью вероятностей; рис. 2в – показательное распределение с плотностью вероятностей.
2а 2б 2в
Рис.
2Виды гистограмм
ПРИМЕР 3
Требуется построить гистограмму и полигон относительных частот для известного группированного вариационного ряда. На их основе выдвинуть нулевую гипотезу о виде распределения генеральной совокупности. В данном случае это нормальное распределение. На одном чертеже с гистограммой построить график теоретической плотности вероятностей. Сделать вывод об их визуальном совпадении.
Для удобства заполним таблицу. В таблицу занесены середины интервалов , в четвертый – относительные частоты интервалов, в пятый – высоты прямоугольников гистограммы относительных частот.
Таблица 6
Индекс | Интервал | Середина интервала | Относит. частота | Высота прямоуг. | |
1 | -5,5 | 0,0404 | 0,0404 | ||
2 | -4,5 | 0,1212 | 0,1212 | ||
3 | -3,5 | 0,1616 | 0,1616 | ||
4 | -2,5 | 0,2121 | 0,2121 | ||
5 | -1,5 | 0,2323 | 0,2323 | ||
6 | -0,5 | 0,1212 | 0,1212 | ||
7 | 0,5 | 0,1010 | 0,1010 | ||
8 | 1,5 | 0,0101 | 0,0101 | ||
Сумма | 1 | 1 | |||
По данным таблицы построим гистограмму.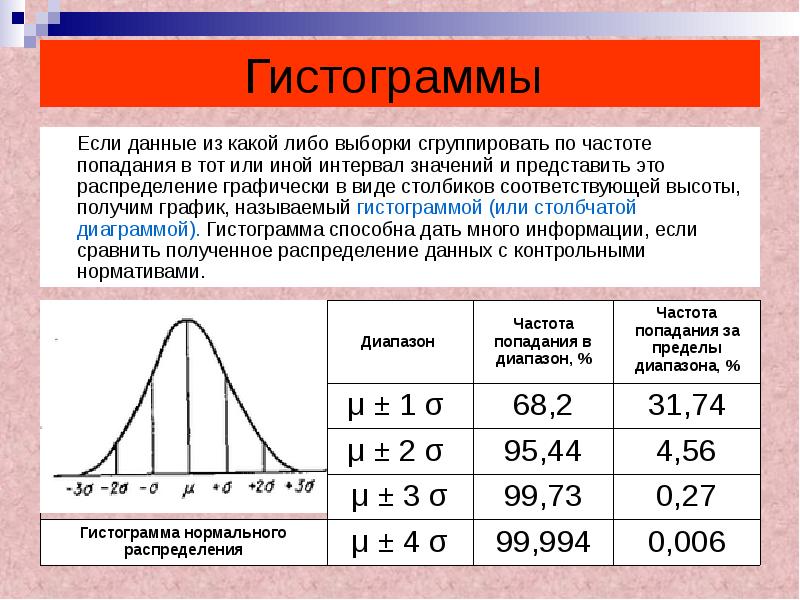
Для этого в прямоугольной системе
координат на оси абсцисс откладываем
значения границ интервалов разбиения
и на каждом из интервалов с номером
строим прямоугольник с высотой.
Для такой гистограммы площадь ступенчатой фигуры соответствует сумме вероятностей и равна . Площадь каждого прямоугольника гистограммы равна вероятности попадания случайной величины в интервал, соответствующий основанию прямоугольника
Рис.3. Гистограмма относительных частот и кривая теоритической плотности вероятностей
Полигон относительных частот – ломаная, соединяющая точки ,
Гистограмма и полигон относительных частот, являющиеся статистическими оценками плотности вероятностей генеральной совокупности, схожи с кривой плотности вероятностей нормального закона. На основании этого выдвигаем нулевую гипотезу : Генеральная совокупность, из которой взята выборка, распределена по нормальному закону с параметрами,, то есть теоретическая плотность вероятностей имеет вид:
Рис.
4 Полигон относительных частот
Вычислим значения теоретической плотности вероятностей в точках – середины интервалов по таблице П 2 Приложения. Результаты вычислений занесем в таблицу. Заметим, что.
Таблица 7
1 | -5,5000 | -2,0083 | 0,0531 | 0,0324 | |
2 | -4,5000 | -1,3980 | 0,1501 | 0,0916 | |
3 | -3,5000 | -0,7878 | 0,2925 | 0,1785 | |
4 | -2,5000 | -0,1776 | 0,3927 | 0,2396 | |
5 | -1,5000 | 0,4326 | 0,3633 | 0,2217 | |
6 | -0,5000 | 1,0429 | 0,2316 | 0,1413 | |
7 | 0,5000 | 1,6531 | 0,1017 | 0,0621 | |
8 | 1,5000 | 2,2633 | 0,0308 | 0,0188 | |
0,0000 | 0,3989 | 0,2434 | |||
Из рисунка 3 видно, что график теоретической
плотности вероятностей и гистограмма
достаточно хорошо совпадают.
Как вы используете hist для построения относительных частот в R?
Как вы используете hist() для построения относительных частот в R?
Если я сделаю следующее, то получу график плотности, но мне нужен график относительной частоты:
a <- c(0,0,0,1,1,2)
hist(a, freq=FALSE)
Я хочу видеть гистограмму со следующими относительными частотами:
.5 0 до 1,
.33 от 1 до 2,
и .166 за 2 к 3.
r histogramПоделиться Источник Will 01 ноября 2010 в 21:30
5 ответов
14
вы можете попробовать использовать функцию histogram() в решетке
a <- c(0,0,0,1,1,2)
library(lattice)
histogram(a)
значение по умолчанию-процент.
Поделиться Greg 01 ноября 2010 в 21:49
7
Я добавил новую функцию в пакет HistogramTools на CRAN, PlotRelativeFrequency() , которая берет объект гистограммы и генерирует график относительной частоты гистограммы.
Это доступно теперь из R-Forge и будет в HistogramTools 0.3 для следующего выпуска CRAN .
В принципе, вам просто нужно сделать две модификации гистограмм по умолчанию в R. Во-первых, вам нужно разделить каждый отсчет на сумму всех отсчетов, и вам нужно заменить метку оси y, чтобы отметить, что теперь она строит относительные частоты.
x<-runif(100)
h<-hist(x, plot=F)
h$counts <- h$counts / sum(h$counts)
plot(h, freq=TRUE, ylab="Relative Frequency")
Или просто…
install.packages("HistogramTools", repos="http://R-Forge.R-project.org")
library(HistogramTools)
PlotRelativeFrequency(hist(x, plot=F))
Поделиться MurrayStokely 10 октября 2013 в 17:54
6
hist(a, breaks=c(0, 1, 2, 3), freq=FALSE, right=FALSE)
Поделиться caracal 01 ноября 2010 в 22:04
- hist с одним значением в Matlab
Когда вы используете функцию hist, как это: [h x] = hist(data, 1000) работает просто отлично, пока данные длиннее, чем один length(data) > 1 .
Но если это = 1 , то он будет делать это: Где данные распространяются от -500 до 500. Есть ли способ остановить это? - R density() функция
Извините, если этот вопрос тривиален, но я не вижу решения: я часто использую функцию density() , всегда без проблем, но теперь я работаю с некоторым набором данных-давайте назовем его tab-с (многими) относительно небольшими значениями, и вдруг density(tab) дает что — то вроде абсолютных…
Но если это = 1 , то он будет делать это: Где данные распространяются от -500 до 500. Есть ли способ остановить это?
2
Не совсем традиционная гистограмма…
h<-hist(yourdata)
plot(h$mids,100*h$counts/sum(h$counts),type="h")
Поделиться Alessandro Jacopson 19 июня 2011 в 10:07
1
histo<-hist(yourvariable)
barplot(histo$counts/n,col="white",space=0)->bp # n=length(yourvariable)
axis(1,at=c(bp),labels=histo$mids)
title(ylab="Relative Frequency",xlab="Your Variable Name")
Поделиться king2rook1 06 августа 2013 в 16:23
Похожие вопросы:
какое программное обеспечение вы используете для построения диаграмм для презентации и отчета?
Какое программное обеспечение вы используете для построения диаграмм для презентации и отчета? Предположим, вы хотите нарисовать диаграмму, иллюстрирующую рукопожатие TCP.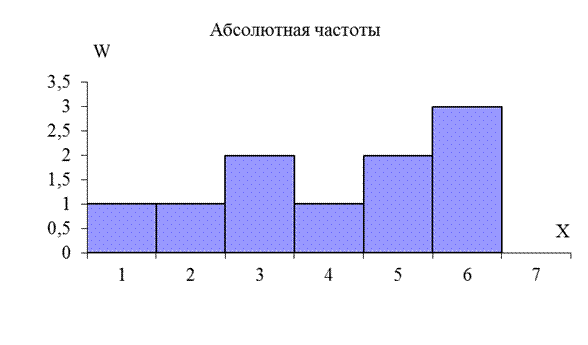
Я использую visio, но…
Какой фреймворк вы используете для построения своих приложений?
Существует целый ряд фреймворков, которые обеспечивают каркас для построения приложений , таких как CSLA , XAF , SCSF ,… Используете ли вы его сами или строите с нуля?
Как вы используете Team Foundation Build для построения нескольких сред?
Когда вы используете Team Foundation Build для построения проекта для нескольких сред, выполняете ли вы одну сборку для всех сред или сохраняете отдельный сценарий сборки для каждой среды? Подумайте…
Какой инструмент вы используете для построения программы Erlang?
Какой инструмент вы используете для построения программы Erlang: Emake, makiefile или другой?
Используйте функцию hist() в R, чтобы получить проценты в отличие от необработанных частот
Как можно построить процентные соотношения в отличие от необработанных частот, используя функцию hist() в R?
hist с одним значением в Matlab
Когда вы используете функцию hist, как это: [h x] = hist(data, 1000) работает просто отлично, пока данные длиннее, чем один length(data) > 1 .
Но если это = 1 , то он будет делать это: Где данные…
R density() функция
Извините, если этот вопрос тривиален, но я не вижу решения: я часто использую функцию density() , всегда без проблем, но теперь я работаю с некоторым набором данных-давайте назовем его tab-с…
Вычисление абсолютных, относительных и кумулятивных частот в R
У меня есть две переменные, X и Y: x <- c(1.18,1.42,0.69,0.88,1.69,1.09,1.53,1.02,1.19,1.32) y <- c(1.72,1.42,1.69,0.79,1.79,0.77,1.44,1.29,1.96,0.99) Я хотел бы создать таблицу абсолютных,…
участок без границы (например, hist) в r
Если вы вызовете функцию hist на r, то заметите, что поле, обычно окружающее область построения, не появляется, вместо этого внизу и слева появляются только линейки, указывающие масштаб построения….
Как преобразовать список списков в словарь относительных частот?
У меня есть список списков, которые я хотел бы преобразовать в словарь относительных частот.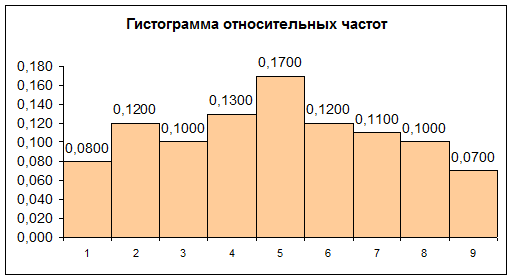
Список списков: [[‘SBS1’, ‘SBS5’, ‘SBS7a’, ‘SBS7b’, ‘SBS7c’, ‘SBS7d’], [‘SBS1’, ‘SBS5’, ‘SBS7a’, ‘SBS7b’,…
Гистограмма — относительная частота — Большая Энциклопедия Нефти и Газа, статья, страница 1
Гистограмма — относительная частота
Cтраница 1
Гистограмма относительных частот может быть получена из гистограммы частот сжатием вдоль оси ординат в п раз или увеличением масштаба на оси ординат в п раз. [1]
Гистограмма относительных частот — это фигура, состоящая из т прямоугольников, опирающихся на интервалы группировки. [2]
Па рис. 50 изображена гистограмма относительных частот данного статистического распределения и график плот-пост t распределения. [3]
На рис. 56 изображена гистограмма относительных частот данного статистического распределения и график плотности распределения.
[4]
На рис. 52 изображена гистограмма относительных частот данного статистического распределения и график плотности распределения. [5]
На рис. 52 изображена гистограмма относительных частот данного статистического распределения к график плотности распределения. [6]
На рис. 56 изображена гистограмма относительных частот данного статистического распределения и график плотности распределения. [7]
Легко видеть, что площадь гистограммы относительных частот равна единице. [8]
Ег сли по вертикальной оси откладывать относительную частоту m / / n, получим так называемую гистограмму относительных частот. Отметим, что число наблюдений ( вариант), попадающих в определенный интервал, равно площади соответствующего прямоугольника на гистограмме частот.
На гистограмме же относительных частот площадь каждого прямоугольника равна относительной частоте m / / n попадания варианты х — в соответствующий интервал. Графики этих гистограмм приведены на рис. 19.2, а и 19.2 6 соответственно.
[9]
Требуется: составить таблицу статистического распределения, разбив промежуток ] 0 25 на пять участков, имеющих одинаковые длины; построить гистограмму относительных частот. [10]
Требуется: составить таблицу статистического распределения, разбив промежуток ( 0 25) на пять участков, имеющих одинаковые длины; построить гистограмму относительных частот. [11]
Требуется: составить таблицу статистического распределения, разбив промежуток ] 0 25 [ на пять разрядов, имеющих одинаковые длины; построить гистограмму относительных частот. [12]
Требуется: составить таблицу статистического распределения, разбив промежуток ( 0 25) на пять участков, имеющих одинаковые длины; построить гистограмму относительных частот.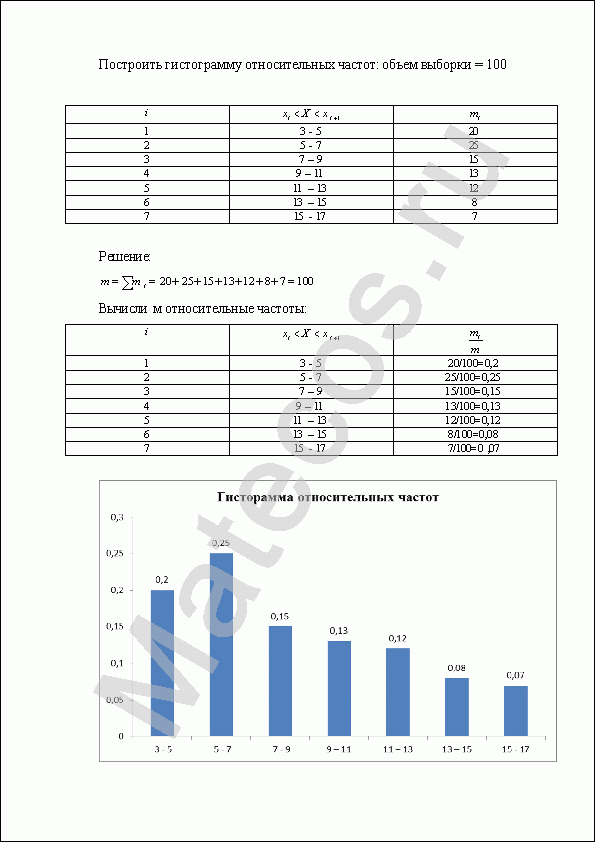
[13]
Из теоремы Бернулли следует, что если объем выборки п стремится к бесконечности, а длины интервалов группировки — к нулю, то гистограмма относительных частот для значений непрерывной случайной величины стремится к графику плотности вероятностей этой случайной величины. [14]
На гистограмме статистические закономерности распределения признака просматриваются достаточно отчетливо. Площадь гистограммы относительных частот равна единице. [15]
Страницы: 1
Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
участок частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам.
При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияние величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения гистограммы относительных частот (гистограммы частостей) высоты в равных интегралов должны быть пропорциональны относительной частота , а в неравных интервалов высота плотности плотности относительной частоты .
Пример 2
Построить гистограмму частот и относительных частот (частостей)
Если вам сейчас не требуется платная помощь, но может потребоваться в дальнейшем, чтобы не потерять контакт, вступайте в группу ВК.
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму частот (неравных интервалов).
| 2-4 | 4-8 | 8-13 | 13-15 | 15-17 | 17-20 | |
| 15 | 35 год | 64 | 55 | 21 год | 10 |
Вычислим плотности частоты:
| Интервалы, | Длина интервала, | Плотность частоты, | |
| 2–4 | 15 | 2 | 7. 500 |
| 4–8 | 35 год | 4 | 8,750 |
| 8–13 | 64 | 5 | 12,800 |
| 13–15 | 55 | 2 | 27.500 |
| 15–17 | 21 год | 2 | 10 500 |
| 17–20 | 10 | 3 | 3,333 |
| Итого | 200 | — | — |
Гистограмма частот
- К оглавлению решебника по
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные контрольные точки путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и представляют ломаную линию, т.е. кумуляту.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
Пример 4
Построить кумулятивную кривую:
| 2 | 5 | 8 | 11 | 14 | 17 | |
| 15 | 35 год | 64 | 55 | 21 год | 10 |
Вычислим накопленные частоты:
| Накопленные частоты, | ||
| 2 | 15 | 15 |
| 7 | 35 год | 50 |
| 8 | 64 | 114 |
| 15 | 55 | 169 |
| 16 | 21 год | 190 |
| 17 | 10 | 200 |
| Итого | 200 | — |
Кумулятивная кривая
- К оглавлению решебника по
3. 2.2 Полигон и гистограмма
2.2 Полигон и гистограмма Пусть результаты выборки количественного признака X из генеральной совокупности представленной вариационным рядом. Кумулята, будучи функцию распределения выборки, служат ее интегральной вероятностной характеристикой. Для изучения локальных характеристика нужна функция, аналогичная ряду распределения или плотности вероятности. Графиками таких вариационных рядов трава полигон и гистограмма .
Точечный вариационный ряд наглядно можно представить с помощью полигона частот, а интервальный — с с помощью гистограммы.
Полигоном частот
называется ломаная, звенья которой
соединяют отрезками точки с координатами
( x 1 , n 1 ), ( x 2 , n 2 ), … , ( x k , к к )
для полигона абсолютных частот и точки
с координатами ( x 1 ,
), ( x 2 ,
), .
.. , ( x k ,
)
для полигона относительных частот.
Для
их построения, исходя из условий задачи,
необходимо составить точечный (либо
интервальный) вариационный абсолютных рядных
или относительных частот. Если задан
интервальный вариационный ряд, то для
построения полигона частот необходимо
найти середины интервалов 1 ,
2 ,
…, к — точка x 1 , х 2 , … , x к .Затем в декартовой системе координат
надо отложить на оси абсцисс все возможные
значения вариант x 1 , х 2 , … , х к ,
а на оси ординат соответствующие им
абсолютные частоты n 1 , n 2 ,
…, к к (или относительные частоты
,,…,).
Для построения полигона абсолютных
(относительных) частот необходимо
соединить отрезками полученные точки
с координатами ( x 1 , n 1 ), ( x 2 , n 2 ), .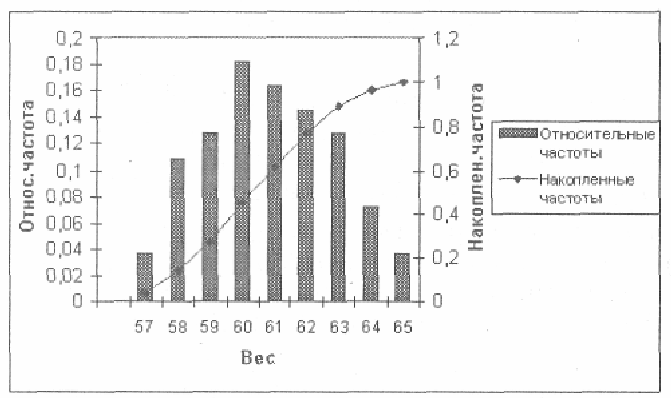
.. , ( x n , n k )
(или, соответственно, ( x 1 ,
), ( x 2 ,
), … , ( x k ,
)).
Гистограмма абсолютных (относительных) частот называется ступенчатая фигура, состоящая из прямоугольников, основания которых есть частичные интервалы длиною ч , высотами наблюдения места, пропорциональные частоты интервала n i (или ).Отношенияназывают плотности частоты, а отношения плотности относительной частоты.
Для построения гистограммы необходимо найти размах выборки — ее границы, т.е. и, длина интервалов, а также к — число интервалов.
При
удачный подборе интервалов гистограмма
и полигон дают представление на графике
функции плотности вероятности
распределения генеральной совокупности,
что используется для формулировки
предположения о виде исследуемого
теоретического закона распределения
(п.
3.6.6).
Заметим, что, если за единицу высоты принять 1/ ч , площадь каждого из -го прямоугольника равна произведению основания на высоту: т.е. частота и -го интервала (или сумме частот вариант, входящий в этот интервал). Тогда площадь всей гистограммы частоты равной сумме всех частот , т.е. объему выборки, причем площадь каждого столбца гистограммы пропорциональна случай попадания наблюдений в данный интервал группировки. Если в качестве высот прямоугольников выбрать отношения, то площадь фигуры под гистограммой относительных частот равной единице, т.к ..
Т.о., площадь гистограммы частот равна сумме всехчастот, т.е ..
Задача 2. Представить графическое распределение размеров зарплаты сотрудников фирмы за неделю (в долларах), если они получили первую зарплату:
152,74;
176,66; 162,48; 167,72; 181.09; 155,00; 196,17; 169.60; 172,88;
182,47; 181,69; 186,91; 190,10; 176,14; 192,70; 178,59; 167,27;
175,14; 160,00; 177,46; 165,18; 167,77; 178,46; 165,00; 185,20;
157.
02; 172,14; 192,22; 179,40; 191.03; 188,68; 169,51; 200,15;
178,47; 176,33; 179,05; 180,95; 174,28; 175,00; 178,45; 150,10;
176,86; 187,71; 168,33; 195,00; 172,37; 179,04; 182,05; 186,19;
190,05; 196,27; 209,28; 203,16; 168,52; 200,00; 196.30.
x макс. = 209,28, x мин. = 150,10.
Решение.
Построим интервальный вариационный ряд с интервалом ч = 10:
Интервалы зарплаты | 150-160 | 160-170 | 170-180 | 180-190 | 190-200 | 200-210 |
n i | 4 | 11 | 18 | 10 | 9 | 4 |
Для построения точечного вариационного ряда найдем середины интервалов:
x i | 155 | 165 | 175 | 185 | 195 | 205 |
n i | 4 | 11 | 18 | 10 | 9 | 4 |
Составим графики
распределения зарплаты (Рис.
2а, б)
Интервальному вариационному ряду соответствует гистограмма (Рис. 2 (а). Точечному вариационному ряду соответствует полигон (Рис. 2 (б).
Рис. 2 (а, б)
Задача 3. Даны результаты изменения напряжения (в вольтах) в электросети. Составить вариационный ряд и начертить график распределения напряжения, если значения следующие напряжения:
227, 229, 215, 230, 232, 223, 220, 222, 228, 219,
222, 221, 227, 226, 226, 229, 217, 215, 218, 220,
216, 220, 220, 221, 225, 224, 212, 217, 219, 220.
Решение.
Составим вариационный ряд по которому построим гистограмму (Рис.3). Имеем
x макс. = 232, x мин. = 212. Применим формулу Стерджесса и подсчитаем число интервалов:
Тогда вариационный абсолютных частот примет вид:
x i
212-217
217-222
222-227
227-232
n i
7
12
7
5
Соответствующая
гистограмма абсолютных номинальных представлен
на рисунке 3 (а), а относительных частот
— на рисунке 3 (б).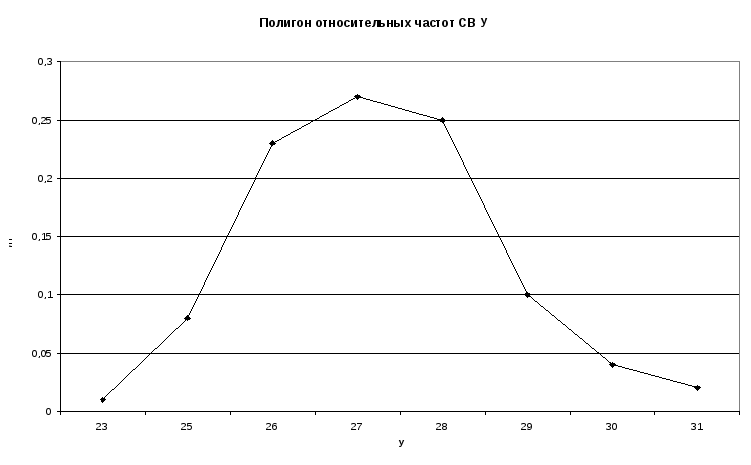
Рис.3 (а) Рис. 3 (б)
Задача 4. Контролер на рынке выявлял отклонение весов в граммах от стандарта на основе выборки. Закон распределения выборки задан вариационным рядом абсолютных частот:
x i
-2
0
3
5
8
n i
5
1
7
3
4
Составить
закон распределения относительных
графики и построить их графики.
Решение:
Найдем объем выборки: .
Найдем относительные частоты по формуле :.
Составим вариационный ряд относительных частот:
-2 | 0 | 3 | 5 | 8 | |
0.25 | 0,05 | 0,35 | 0,15 | 0,20 |
4. Полигон для вариационного ряда распределения абсолютных представлен на рисунке 4а. Полигон вариационного ряда относительных частот представлен на рисунке 4б:
Величина
интервала группировки значительно
влияет на вид гистограммы: чем больше
величина ч ,
тем менее различимы особенности
распределений.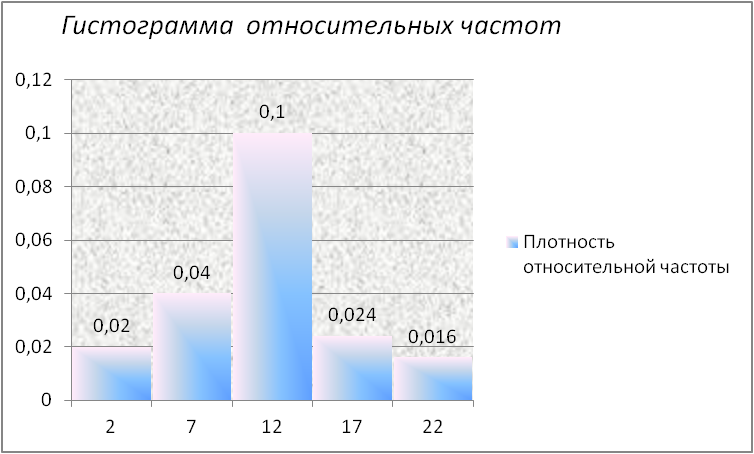
Полигон и гистограмма — Студопедия
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Определение. Полигоном часто называют ломаную, отрезками которой соединяют точки (x 1 , n 1 ), (x 2 , n 2 ), (x k , n k ).
Для построения полигона частот на абсцисс откладывают варианты x и , а на оси ординат — соответствующие им частоты n и .Точки (x i , n i ) соединяют отрезками прямых и цифровых полигон частот.
Определение. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x 1 , w 1 ), (x 2 , w 2 ), (x k , w k ).
Для построения полигона частот на абсцисс откладывают варианты x и , а на оси ординат w и .
Точки (x i , w i ) соединяют относительными отрезками прямых и геометрических частот.
На рисунке изображен полигон относительных частот следующего распределения:
| x | 1,5 | 3,5 | 5,5 | 7,5 |
| w | 0,1 | 0,2 | 0,4 | 0,3 |
Рис. 6. Полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на частичных интервалов длинной h и находят для каждого частичного интервала и — количество частот вариант, попавших в i-ый интервал.
Определение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями среды частичные интервалы длиною h, а высоты равны относительно (плотность частоты).
Рис.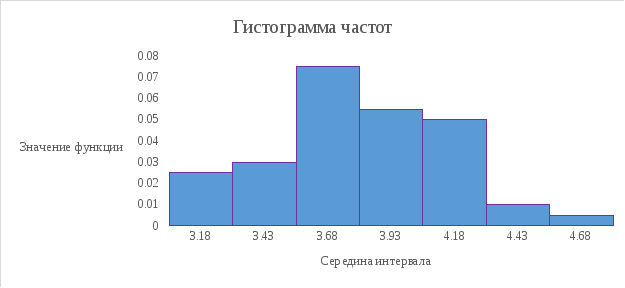
7. Гистограмма частот.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии.
Площадь i-го частичного прямоугольника равна = — сумме частот вариант i-го интервала; Следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
На рисунке 2 изображена гистограмма частот распределения размера n = 100, приведенного в таблице 1.
| Частичный интервал, длиною h = 5 | Сумма частот вариант частичного интервала | Плотность частоты |
| 5–10 | 0,8 | |
| 10–15 | 1,2 | |
| 15-20 | 3,2 | |
| 20-25 | 7,2 | |
| 25–30 | 4,8 | |
| 30-35 | 2,0 | |
| 34-40 | 0,8 |
Определение.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых занимают частичные интервалы длинною h, а высоты равны относительно (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии. Площадь i-го частичного прямоугольника равна = — относительной частоты вариант, попавших в i-й интервал.Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Примеры.
1. В результате выборки получена следующая таблица распределения частот.
Построить полигоны частот и относительных частот распределения.
Для начала построим полигон частот.
Рис.
8. Полигон частот.
Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.
п = 3 + 10 + 7 = 20.
.
Получаем
| 0,15 | 0,50 | 0,35 |
Построим полигон относительных частот.
Рис. 9. Полигон относительных частот.
2. Построить гистограммы частот и относительных распределений.
Найдем плотность частоты:
| Частичный интервал, длиною h = 3 | Сумма частот вариант частичного интервала | Плотность частоты |
| 2–5 | ||
| 5–8 | 3,3 | |
| 8–11 | 8,3 | |
| 11–14 |
Построим гистограмму частот.
Рис. 10. Гистограмма частот.
Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.
.
Теперь найдем относительные частоты:
Получим:
| Частичный интервал | Сумма относительных частот | Плотность частоты |
| 2–5 | 0,18 | 0,06 |
| 5–8 | 0,2 | 0,07 |
| 8–11 | 0,5 | 0,16 |
| 11–14 | 0,12 | 0,04 |
Плотности частот нужно вычислить.При этом h = 3.
Построим гистограмму относительных частот.
Рис.11. Гистограмма относительных частот.
Гистограмма частот в Excel 2016
Excel 2016 обзавелся новыми типами графиков. Причем, это не какие-нибудь дизайнерские новшества, самые настоящие статистические диаграммы.
Так, «ящик с усами» использовать для анализа выборки. Диаграмма Парето пригодится при анализе вклада отдельных элементов в общую общую.В этой рассмотрим еще одну новую диаграмму из Excel 2016 — гистограмму частот .
На первый взгляд и в более ранних версиях Excel можно изобразить частоты с помощью диаграмм. Можно, но для этого необходимо числовые данные сгруппировать. То есть для каждой категории (интервала, группы, года и т.д.) нужно посчитать частоту. Теперь появилась возможность изобразить данные в один клик без предварительных расчетов и группировок.
Строится такая диаграмма в один клик.Выделяем ряд данных и нажимаем кнопку гистограммы частот.
Собственно, все. Тут же представлена соответствующая диаграмма.
Возникает вопрос: как Excel делит данные на интервалы? Справка Excel говорит, что с помощью формулы.
Количество интервалов получается достаточным для того, чтобы визуально прикинуть, каков характер распределения анализируемых данных.
Интервалы легко перестроить под свои потребности. Можно, например, задать нижнюю и верхнюю границу, за пределами которых будут объединены в один интервал.
При выборе варианта выхода за нижнюю и верхнюю границы, судя по той же справке, их значения рассчитываются, как расстояние ± 3σ от средней арифметической.
Однако рассчитываемые автоматически легко значения изменить в настройках.
Это был пример, когда данные разбиваются на интервалы. Такой вариант группировки установлен по умолчанию (см. Окно параметров настройки оси выше).
Распределение частот можно получить и по имеющейся категориим (должен быть указан соответствующий столбец).Выбираем в настройках «По категориям» и получаем новые частоты.
Проведем эксперимент. С помощью функций СЛУЧМЕЖДУ смоделируем равномерно распределенную выборку в пределах, скажем, от 0 до 200. Пусть выборка состоит из 100 значений. Теперь изобразим гистограмму частот.
Как видно, частоты примерно одинаковы.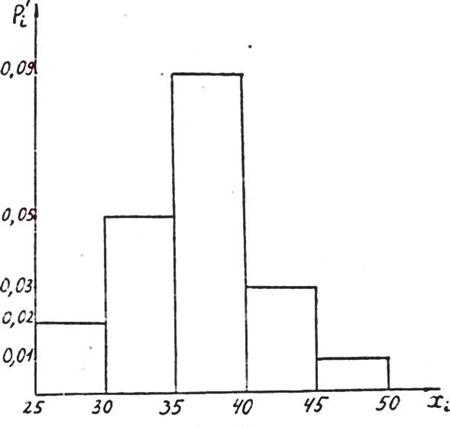
А теперь смоделируем нормальную выборку, со средней 100 и стандартным отклонением 30.
Отчетлива видна характерная конфигурация нормального распределения.
Поделиться в социальных сетях:
Гистограмма распределения частот — Энциклопедия по экономике
Вследствие воздействия на производственный процесс случайных факторов вероятность возникновения отклонений от установленного номинального значения параметров ЕПК воздействия. Для того, чтобы определить качество производственного процесса, нужно провести достаточное наблюдение и построить гистограмму распределения отклонений по их абсолютному количеству.
На рис. 8.2 сплошными линиями показаны примеры гистограмм для двух характерных отклонений. Первый случай. Кроме номинальных значений ЕПК устанавливаются допустимые отклонения (допуски). Пример — требования к установке сборных конструкций.
[c.153] При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах.Это необходимо для устранения возможности определения размера интервала и сравнения частоты. [c.32]
Для достоверной оценки и разброса показателей механической торговой системы количество сделок на периоде тестирования не должно быть немного меньше минимального значения. Считая, что результат отдельной сделки (например, размер прибыли) является случайной величиной, оценим минимальный объем выборки для определения этого распределения величины.Для определения положения распределения необходимо построить гистограмму эмпирических частот и провести сравнение эмпирических и теоретических частот по критерию хи-квадрат.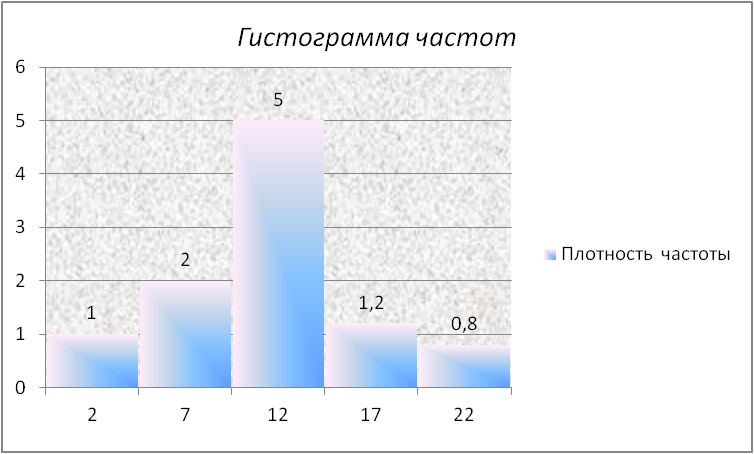
[c.180]
Первичные данные о доходах были трансформированы в ряд распределения, который имеет интервалы шириной 1%, начиная с —8% и заканчивая + 12%. Эти данные будут использованы для составления графиков распределения частот, распределения относительных частот, распределения кумулятивных частот и гистограмм. Данные для построения рядов распределения частот приведены в табл.2.4. [c.72]
Наряду с частотами подсчитываются относительные частоты, накопленные частоты и накопленные относительные частоты. Полученные результаты также записывают в виде таблицы, первая последовательность содержит соответствующие им частоты (абсолютные, накопленные и накопленные относительные частоты). Как и для «точечной» выборки, для выборки, сгруппированной по интервалам по значениям накопленных частот, может быть построена выборочная функция распределения.Для наглядного представления выборки часто используют ее графическое отображение — гистограмму частот и гистограмму относительных частот. Любая из этих гистограмм представляет собой кусочно-постоянную функцию, при-
[c.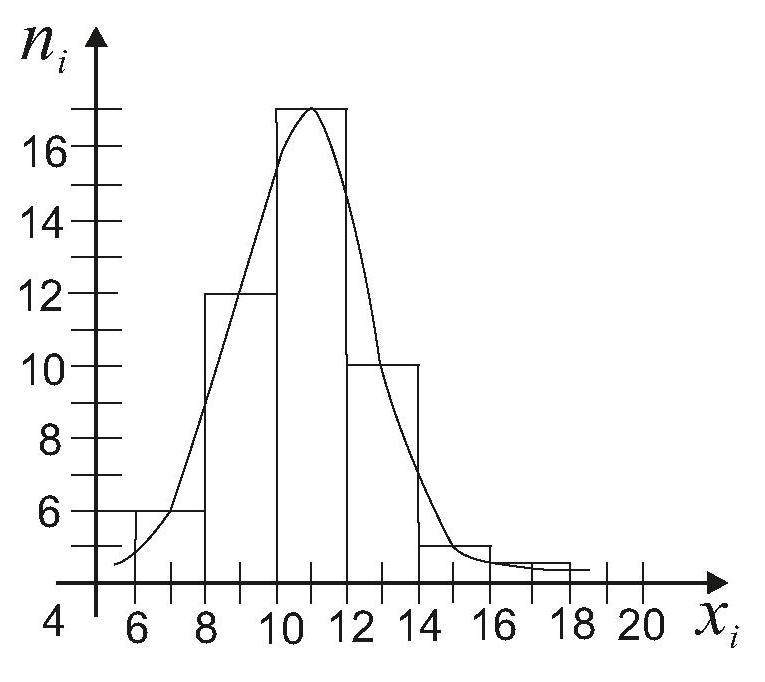
257]
Для графического изображения функциональной связи можно воспользоваться системой координат (рис. 12, а). По оси абсцисс откладываются величины показателя — фонд заработной платы, а по оси ординат — относительные частоты. Очевидно, что каждому значению ординаты соответствуют два значения на оси абсцисс (начала и конца интервала).Поэтому на графике, называемом гистограммой, отмечается не точка, линия, соединяющая две точки, и сам график представляет собой сочетание прямоугольников. От гистограммы легко перейти к полигону, соединив между собой средние точки прямо- [c.80]
Распределение частот. Пок гистограммы распределения вероятности всех чисел. [c.837]
Гистограмма — это классическое графическое отображение распределения относительных отметок различных событий в виде колонок (столбиков), которые соответствуют значениям параметров (измеряемых величин) процесса.Такой подход позволяет получить гистограмму ширины рассеивания и основных моментов распределения (положение, форму).
Т. е. появляется возможность сделать закономерности наглядными. Как и карта управления качеством, гистограмма процессов, это в основном для обеспечения качества производственных предприятий. Пример гистограммы долей качественной продукции в различных партиях товара приведен на рис. 10.4.
[c.47]
Метод, основанный на вычислении средней арифметической, или просто средней, обычно считается наиболее приемлемым.Он очевиден просто сложите значения и поделите сумму на их количество. Все просто, в том числе отработка данных таблиц частот. Однако, несмотря на всю эту простоту, часто этот метод наименее адекватен. Рассмотрим распределение заработной платы на рис. 1.17. Данная диаграмма иллюстрирует типичное распределение доходов работников крупной организации. Это положительно асимметричное распределение, с областью больших отклонений в правой части диаграммы. Доходы основной массы представленной в левой части диаграммы.Только несколько моделей имеют доходы, представленные у верхней границы диаграммы.
Вот эти-то несколько работников и искажают значение средней, и усредненное значение, полученное путем расчета арифметической средней, максимально приемлемо репрезентативное значение. Значение моды соответствует максимальному значению частот, представленных в распределении. При такой форме распределения это значение находится в области значений параметров заработной платы.Значение медианы, как центральное значение, выступает в роли компромиссного решения часто наилучшим показателем. На рис. 1.17 значения средней, моды и медианы. Эти три показателя будут находиться в соответствии с другом, только если распределение данных симметрично. Если число отрицательно асимметрично, последовательность значений меняется на обратную. Так, средняя будет наименьшим значением, а мода — наибольшим. На рис. 1.18 представления три типа распределения с помощью показанных трех средних.Рисунки просто отображают форму каждого распределения. Так, проведенные кривые очерчивают контуры гистограммы. Например, на рис.
1.18 (i) отображающая форма, представляющая такое же распределение, что мы видим и на рис. 1.17.
[c.30]
В определенных непересекающихся интервалы и показатели частоты попадания в них фактических значений времени пролеживания предметов труда. В. табл. 9 приведен интервальный вариационный ряд времени пролеживания на складе детали пакет ротора изделия IV.Предварительные предположения о виде определяемого закона распределения получены на основе анализа гистограммы, которая построена по данному интервальному ряду (рис. 14). Аналогичные исследования интервальных вариационных рядов и гистограмм были выполнены для всех рассматриваемых выборочных единиц, характеризующих изменения времени пролеживания на межцеховом складе деталей и сборочных единиц в переходящих заделах. [c.75]
Проверка статистических гипотез о виде распределения случайных величин.При построении математической модели исследуемых процессов часто возникают задачи сопоставления полученного материала с известными теоретическими распределениями.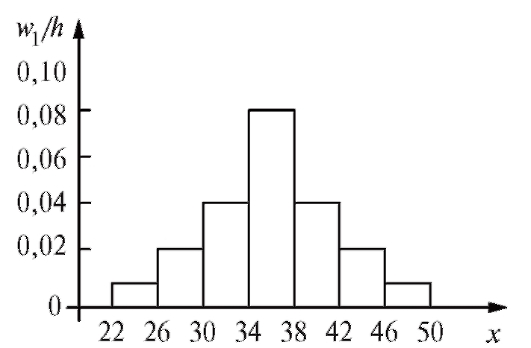
Если сопоставить вероятность попадания в интервалы, на разбита выборка, с помощью частотами, полученными из наблюдений, или провести графическое сравнение полигонов и гистограмм с некоторой теоретической функцией распределения, то можно получить представление о степени близости теоретического и эмпирического распределения.[c.72]
Ниже на рис. 6.3.10 и 6.3.11 представлены гистограмма и полигон распределения относительных частот. [c.314]
Гистограмма должна быть построена так, чтобы каждая «столбика» представляла собой относительную частоту распределения, а общая их площадь составляла 100% распределения. Горизонтальная ось показывает изменения в доходах на 0,01%. Однако два интервала — «более — 0,04 и до 0,02» и «более + 0,02 и до + 0,04» — уменьшить изменения на 0,02%. [c.74]
Что касается гистограмм, в которых непрерывные данные относительной характеристики, то при большом числе данных соответственное сужение интервалов в распределении влечет за собой необходимое приближение гистограммы к гладкой кривой.
Если же число данных будет беспредельно большое, то гистограмма превратится в безукоризненную кривую. В этом случае кривая распределения может рассматриваться как распределение генер альной совокупности.
[c.56]
Для того, чтобы изобразить ряд вариантов распределения графически (фиг. 1), по оси X показывают, а по оси К — соответствующие им частоты. Такой график называется гистограммой. [c.424]
Графическое изображение ряда распределения может быть получено также с помощью полигона.По вертикальной оси этого графика откладывают те же величины, что и при построении гистограммы. По горизонтальной оси откладывают средние точки групп. Таким образом, линейный график, по одной оси которого отложены частоты групп, а по другой — их средние точки, называют полигоном. [c.219]
В отличие от гистограммы столбиковая диаграмма представляет данные по годам, а не группы ряда распределения по горизонтальной оси проставляются годы, а не границы групп ряда по вертикальной оси могут быть отложены как результат измерения, так и частота.
Прямоугольники не соприкасаются друг с другом и могут иметь любую подходящую, но одинаковую ширину.
[c.219]
Гистограммы. Это один из вариантов столбчатой диаграммы, отображающей зависимость частоты появления показателей качества услуги, продукта или процесса в интервале значений. Гистограмма позволяет выявить закон распределения исследуемой величины. [c.263]
При непрерывной вариации используют, как известно, интервальные вариационные ряды, графическим изображением служат гистограмма.Для построения гистограммы по оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов. Эти интервалы основания прямоугольников, равны либо пропорциональны частотам, либо частостям распределения в соответствующих интервалах. [c.57]
Как известно плотность распределения — это число единиц совокупности, приходящееся на единицу ширины интервала. При равных интервалах плотность распределения прямо пропорциональна частотам или частостям, которые используются для построения прямоугольников.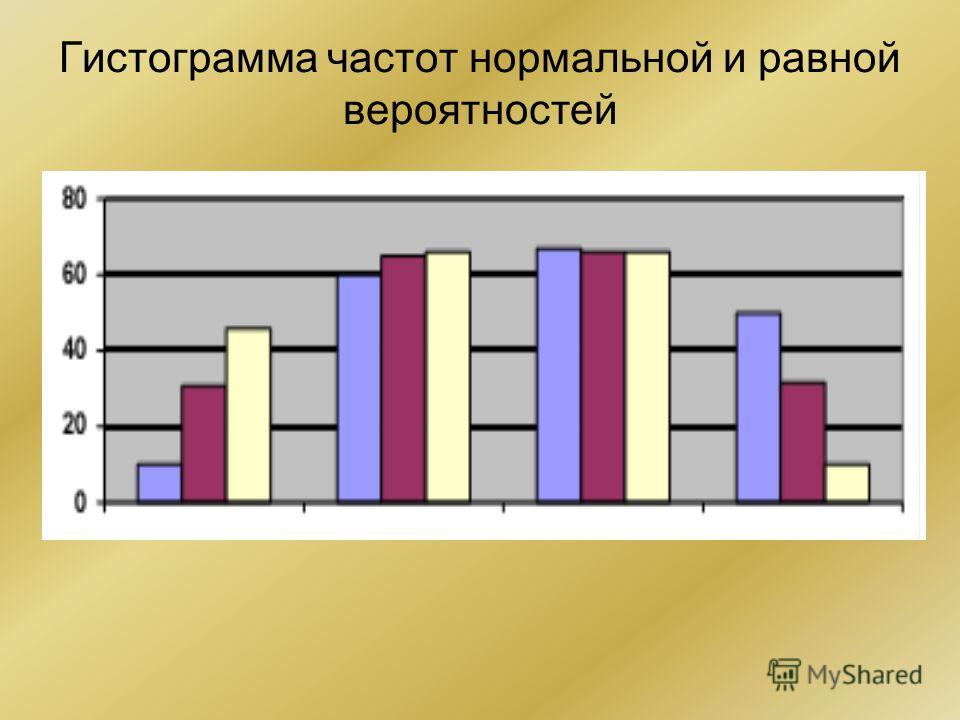
При неравных интервалах гистограмма строится только по плотности распределения.
[c.57]
Обычно не возможными данных высказать разумную догадку (гипотезу) относительно распределения случайной альтернативы, пока не будет собрано и проанализировано достаточное количество экспериментальных. Собранные данные обычно суммируют в виде распределения относительных частот (гистограммы), пример которой приведен на рис.7.3. [c.90]
Если из процесса извлекаются малые выборки фиксированного объема и строится гистограмма распределения дефектных изделий, обнаруживаемых в каждой выборке, наблюдается однохвостовое распределение, где большинство выборок содержит нулевой брак, следующая за ней категория — только одно дефектное изделие, следующее -—Два дефектных изделий.Если размер распределения значительно, гистограмма распределения распределения частот числа дефектных изделий в каждой выборке будет несимметричной, но все же будет два хвоста, а вершина распределения — вблизи среднего числа дефектных изделий в выборке.
Это распределение частот не описывается нормальным распределением.
[c.129]
Как указывалось (раздел 7.9), гистограмма распределения частот может быть описана распределением Пуассона.Можно использовать Пуассонову диаграммную бумагу для построения карт, соответствующих уровня вероятности, соответствующего предела корректировки и предупреждения для любой вероятности, а не только для уровней За и 2сг, которые обычно используются. Можно также использовать таблицы для любых пределов корректировки и предупреждения при заданных вероятностях. [c.132]
Распределение частотного признака. Гистограмма и кумулята. Функции распределения вероятностей и плотности распределения вероятности.Типы распределения. Средние величины. Средние степенные квадратические, арифметические, геометрические, гармонические. Мажорантность средних степенных. Средние хронологические. Средние относительные величины. Мода, медиана, квантили. Моменты. Дисперсия, показатель асимметрии, эксцесс, куртозис. [c.49]
Вариационный ряд определить долю неответивших респондентов табл.
15.2 один респондент из 30 не ответил на вопрос), а также долю ошибочных ответов. Значения, равные 0 или 8, соответствуют ошибочным ответам.Следует определить количество случаев с такими значениями и соответственно откорректировать результат. Кроме того, можно установить наличие выбросов, т.е. случаях с экстремальными значениями. При анализе распределения доходов относительно размера домохозяйства (семьи) следует считать несколько семей, состоящих не меньше чем девяти человек. Распределение частот также определяет форму эмпирического распределения переменных. Частотные данные можно использовать для построения или вертикальных столбчатых диаграмм, на которых по оси значений значения, а по оси 7 — абсолютные (частоты) или относительные (частости) значения.На рис. представлена гистограмма для данных табл. 15.2. По гистограмме можно проверить, соответствует ли наблюдаемое распределение предполагаемому маркетологом распределению.
[c.557]
Существенная помощь в анализе вариационного ряда и его свойств оказывает графическое изображение.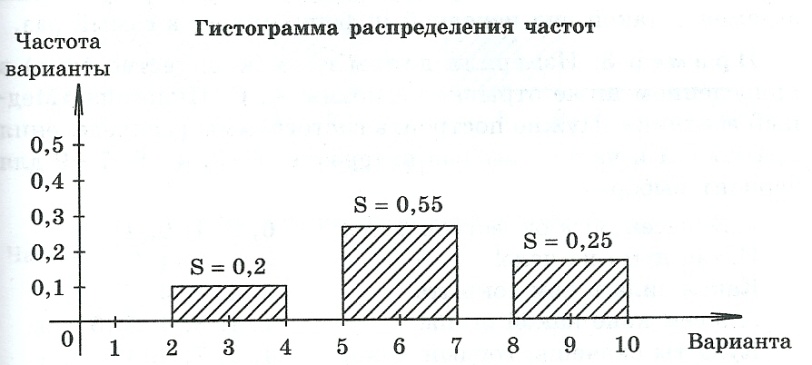
Интервальный изображается столбиковой диаграммой, в которой представлены основания столбиков, расположенные на оси абсцисс, — это интервалы значений переменных признака, а высота столбиков — частоты, соответствующие масштабу по оси ординат.Графическое изображение распределения хозяйств области по урожайности зерновых культур приведено на рис. 5.l.iДиаграмма этого рода часто называется гистограммой (от греческого слова гистос — ткань, строение).
[c.98]
Полигон ⚠️ относительных частот: определение, как найти, примеры
Что такое полигон относительных частот
Схематическое изображение статистического ряда распределения может быть представлена полигоном и гистограммой частот.Такжеют понятия полигон относительных частот и гистограмма относительных частот
Определение Полигон относительных частот — это ломаная, состоящая из отрезков, соединяющих точки с координатами (x i , ω i ).
Построение полигона частот
Алгоритм составления полигона относительных частот: на оси OX отмечают варианты x i , на оси OY откладывают значения ω i . Затем точки с координатами (x i , ω i ) соединяют прямыми отрезками.Ломаная, образованная в результате, является полигоном относительных частот.
Пример
Полигон частот для распределения:
x и : 1,5; 3,5; 5,5; 7,5.
ω и : 0,1; 0,2; 0,4; 0,3.
Гистограмма относительных частот, описание
ОпределениеГистограмма относительных частот — это фигура ступенчатого вида, в установленных пределах. Основанием этих прямоугольников являются частичные интервалы длиною h, а высотами используется плотность относительной частоты — величина определяемая с помощью отношения ω i / h.
Строить гистограмму следует, соблюдая следующий порядок.
На оси абсцисс указывают частичные интервалы. Над ними на расстоянии, равном плотности относительной частоты (ω и / h), отмечают отрезки, параллельные оси OX.
Пример
Интервалы, x i : 2–5, 5–8, 8–11, 11–14, 14–17, 17–20.
Частота вариант, n и : 15, 35, 64, 55, 21, 10 (всего 200).
Относительные частоты, ω и : 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (всего 1000).
Гистограмма данного распределения имеет вид:
Площадь прямоугольников гистограммы
Площадь одного прямоугольника, входящего в форму гистограммы относительных частот, равную относительную частоту вариант и вычисляется по формуле:
\ (h \ frac {\ omega_i} h = \ omega_i \)
Для вычисления площади всей гистограммы необходимо сложить площади всех прямоугольников, составляющих ступенчатую фигуру. Следовательно, искомая величина будет равна единице.
Примеры решения задач
Задача 1
Постройте полигон относительных частот для следующего вариационного ряда:
x i : 2, 7, 8, 15, 16, 17.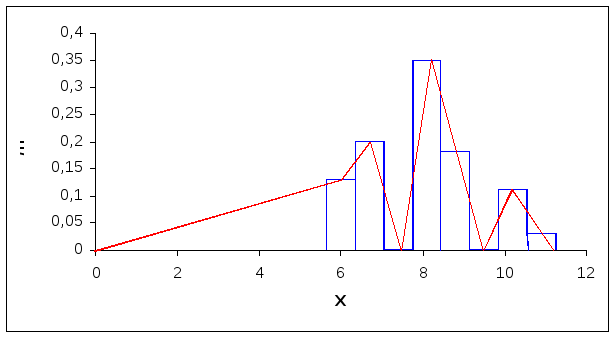
n i : 15, 35, 64, 55, 21, 10.
Решение
Для начала вычислить относительные частоты:
x i : 2, 7, 8, 15, 16, 17.
n i : 15, 35, 64, 55, 21, 10 (итого 200).
ω i : 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (итого 1000).
Построим искомую ломаную:
Задача 2
Построить гистограмму относительных частот распределения, имея следующие данные:
Частичный интервал при длине h, равной 3: 2–5, 5–8, 8–11, 11–14.
n i : 9, 10, 25, 6.
Решение
Сначала определим относительные частоты. Для этого установим объем выборочной совокупности n:
n = Σn i = 50.
Затем найдем ω i :
ω 1 = 9/50 = 0,18
ω 2 = 10/50 = 0,2
ω 3 = 25/50 = 0,5
ω 4 = 6/50 = 0,12
Далее вычислим ω и / ч, то есть плотность частоты:
0,18 / 3 = 0,06
0,2 / 3 = 0,07
0,5 / 3 = 0,16
0,12 / 3 = 0,04
Образуются следующие данные:
Частичный интервал: 2–5, 5–8, 8–11, 11–14.
Сумма относительных частот: 0,18; 0,2; 0,5; 0,12.
Плотность частоты: 0,06; 0,07; 0,16; 0,04.
Как вы используете историю для построения относительных частот в R?
Как вы используете hist () для построения относительных частот в R?
Если я сделаю следующее, то получу график плотности, но мне нужен график относительной частоты:
а <- с (0,0,0,1,1,2)
hist (a, freq = ЛОЖЬ)
Я хочу видеть гистограмму со относительными частотами:
.От 5 0 до 1,
.33 от 1 до 2,
и .166 за 2 к 3.
р гистограммаПоделиться Источник Уилл 01 ноября 2010 в 21:30
5 ответов
14
вы можете попробовать использовать функцию гистограмма () в решетке
а <- с (0,0,0,1,1,2)
библиотека (решетка)
гистограмма (а)
значение по умолчанию-процент.
Поделиться Грег 01 ноября 2010 в 21:49
7
Я который добавил функцию в пакет HistogramTools на CRAN, PlotRelativeFrequency () , берет объект гистограммы и генерирует график относительной частоты гистограммы. Это доступно теперь из R-Forge и будет в HistogramTools 0.3 для следующего выпуска CRAN.
В принципе, вам просто нужно сделать модификации гистограмм по умолчанию в R.Во-первых, вам нужно разделить каждый отсчет на сумму всех отсчетов, и вам нужно заменить метку оси y, чтобы отметить, что теперь она строит относительные частоты.
x <-runif (100)
h <-hist (x, график = F)
h $ counts <- h $ counts / sum (h $ counts)
plot (h, freq = TRUE, ylab = "Относительная частота")
Или просто ...
install.packages ("HistogramTools", repos = "http://R-Forge.R-project. org")
библиотека (HistogramTools)
PlotRelativeFrequency (hist (x, plot = F))
org")
библиотека (HistogramTools)
PlotRelativeFrequency (hist (x, plot = F))
Поделиться МюррейСтокли 10 октября 2013 в 17:54
6
hist (a, breaks = c (0, 1, 2, 3), freq = FALSE, right = FALSE)
Поделиться каракал 01 ноября 2010 в 22:04
- история с одним размером в Matlab
Когда вы используете функцию hist, как это: [h x] = hist (data, 1000) работает просто отлично, пока данные длиннее, чем один length (data)> 1.Но если это = 1, то он будет делать это: Где данные распространяются от -500 до 500. Есть ли способ остановить это?
- R density () функция
Я часто использую небольшую функцию плотности (), всегда без проблем, но теперь я работаю с некоторым набором данных-давайте назовем его tab-с (широко) относительноими значениями, и вдруг плотность (tab) дает что - то вроде абсолютных .
..
..
2
Не совсем традиционная гистограмма...
h <-hist (ваши данные)
сюжет (h $ mids, 100 * h $ counts / sum (h $ counts), type = "h")
Поделиться Алессандро Якопсон 19 июня 2011 в 10:07
1
histo <-hist (ваша переменная)
barplot (histo $ counts / n, col = "white", space = 0) -> bp # n = length (ваша переменная)
ось (1, at = c (bp), labels = histo $ mids)
title (ylab = "Относительная частота", xlab = "Имя вашей переменной")
Поделиться king2rook1 06 августа 2013 в 16:23
Похожие вопросы:
какое программное обеспечение вы используете для построения диаграмм для презентации и отчета?
Какое программное обеспечение вы используете для построения диаграмм для презентации и отчета? Предположим, вы хотите нарисовать диаграмму, иллюстрирующую рукопожатие TCP.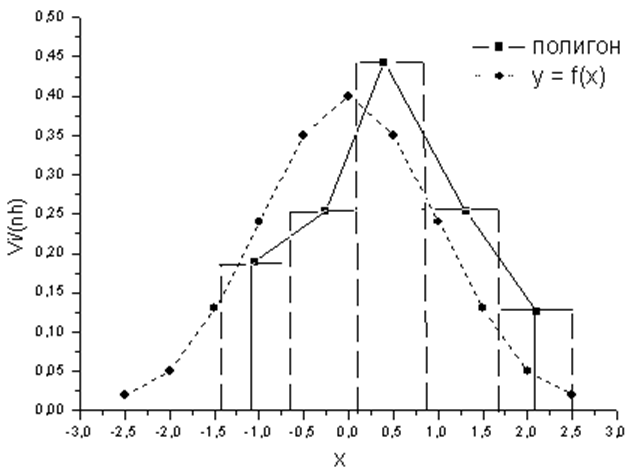
Я использую visio, но ...
Какой фреймворк вы используете для построения своих приложений?
Существует целый ряд фреймворков, которые обеспечивают ряд каркас для построения приложений, таких как CSLA, XAF, SCSF, ... Используете ли вы его сами или строите с нуля?
Как вы используете Team Foundation Build для построения нескольких сред?
Когда вы используете Team Foundation Build для построения проекта для нескольких сред, выполняются ли вы одну сборку для всех сред или сохраняете отдельный сценарий сборки для каждой среды? Подумайте...
Какой инструмент вы используете для построения программы Erlang?
Какой инструмент вы используете для построения программы Erlang: Emake, makiefile или другой?
Используйте функцию hist () в R, чтобы получить проценты в отличие от необработанных частот
Как можно построить процентные соотношения в отличие от необработанных частот, используя функцию hist () в R?
гист с одним значением в Matlab
Когда вы используете функцию hist, как это: [h x] = hist (data, 1000) работает просто отлично, пока данные длиннее, чем один length (data)> 1.