Формула производных функций: Формулы производных функции

формулы, значение, как писать функции

Производная функции – одно из фундаментальных понятий в математике, без понимания которого становится невозможным решение большинства математических и физических задач. Что же это такое?

Производная функции — краткое описание, суть

Если совсем просто, то:

Производная – это скорость изменения функции в данной точке.

Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:

 

Она понимается в двух смыслах: геометрическом и физическом.

Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

 

Физический смысл: производная пути по времени равна скорости прямолинейного движения. Таким образом, значение скорости в определённый момент времени t₀

определяется по формуле:

 

Вычисление производной называется дифференцированием. Обратный процесс – интегрированием.

Основные правила нахождения производных

Дифференцирование строится на следующих правилах.

Правило №1: производная от произведения числа на функцию равна

(c * f (x))’ = c * f’ (x),

где с – любое число.

Правило №2: производная от суммы функций равна

(f (x) + g (x))’ = f ‘ (x) + g’ (x).

Правило №3: производная от разности функций равна

(f (x) – g (x))’ = f ‘ (x) – g’ (x).

Правило №4: производная от произведения двух функций равна

(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x).

Правило №5: производная от дроби равна

 

Существует и так называемая сложная функция (композиция функции) вида f (g(x)). В данном случае f (x) считается внешней функцией, g (x) – внутренней.

Правило дифференцирования сложной функции

Производная сложной функции вычисляется по формуле:

[ f (g (x))]’ = f ‘ (g (x)) g’ (x).

Пример нахождения

Задача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.

Решение: так как (x¹⁰)’=10x⁹,

то ((x+2) ¹⁰)’=(u¹⁰)’=10u⁹⋅u’=10(x+2) ⁹⋅1=10(x+2) ⁹.

Ответ: 10(x+2) ⁹.

Логарифмическая производная

Логарифмическая производная — это производная от натурального логарифма функции.

Вычисляется по формуле:

 

Часто применяется для упрощения дифференцирования некоторых функций.

Пример поиска производной

Пусть y = y(x).

Для удобства прологарифмируем данную функцию:

ln y = ln y(x).

Теперь вычислим производную по правилу дифференцирования сложной функции:

 

Из этого следует, что

 

Тогда ответ:

 

Производная обратной функции

Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равная обратной величине производной данной функции.

Общая формула:

 

Формулы и пример решения

Производные обратных тригонометрических функций:

 

Задача: продифференцировать y=x²-7lnx.

Решение: находим по формуле

 

отсюда

 

Производная функции, заданной параметрически

Пусть функция задана параметрическим уравнением:

 

Тогда производная равна:

 

Формулировка, решение примеров

Задача: продифференцировать функцию.

 

Решение: (при записи производной всегда необходимо писать t в нижнем индексе)

 

Подставляем в формулу:

 

Ответ:

 

В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.

Производная неявной функции

Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.

Теоретическое обоснование

Для нахождения производной неявной функции нужно:

1. Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
2. Решить полученное уравнение относительно производной у’ (х).

Решение в примерах

Задача: решить функцию , заданную неявно:

 

Решение:

1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства

 

Получим

 

Считая, что у – это функция от х, находим производную как от сложной функции:

 

Тогда

 

Для заданной функции имеем:

 

2) Решаем полученное уравнение относительно у’:

 

Ответ:

 

Полная таблица производных

Приводим табличную форму, которая существенно облегчает вычисления:

 

Формул из этого списка достаточно для дифференцирования любой элементарной функции.

Решение элементарных производных, примеры

Задача№1: найти производную функции

 

Решение: данная функция является сложной, поэтому

 

Ответ:

 

Задача №2: найти производную функции 

 

Решение:

 

Ответ:

 

Изучение производных и интегралов занимает большое количество времени. ФениксХэлп может помочь вам в решении контрольных и самостоятельных работ по этой теме и многим другим.

Производная произведения двух дифференцируемых функций определяется формулой. Формулы производных. Защита персональной информации

С правочные материалы по теме «производная». Базовый школьный уровень.
Теоретические сведения для учеников, преподавателей и репетиторов по математике. В помощь к проведению занятий.

Определение: производной функции в точке называется предел отношения приращения функции к приращению переменной, то есть

Таблица производных основных математических функций:

Правила вычисления производных

Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)

Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).

Производная от произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).

Комментарий репетитора по математике: когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!

Производная от частного двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.

Производная от произведения числа на функцию . Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.

Производная сложной функции:

Для вычисления производной сложной функции необходимо найти производную внешней функции и умножить ее на производную внутренней функции.

Ваши комментарии и отзывы к странице с производными:
Александр С.
Очень нужна была таблица. В интернете одна из самых. За пояснения и правила тоже огромное спасибо. Хотя бы по одному примеру ещё к ним и вообще было бы отлично было. Еще раз огромное спасибо.

Колпаков А.Н, репетитор по математике: хорошо, постараюсь в ближайшее время дополнить страницу примерами.

Виртуальный математический справочник.

Колпаков Александр Николаевич, репетитор по математике.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.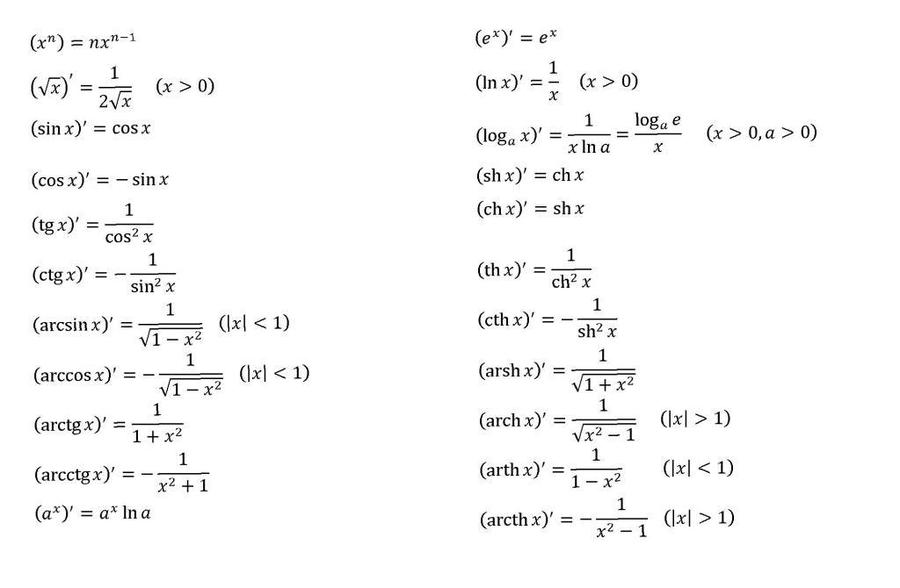

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса».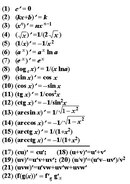 Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Что такое производная функция — это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.

в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как?у.
Найдем тангенс угла в треугольнике MPN используя для этого точки М и N.

tg? = NP/MP = ?у/?x.

При?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол? будет?. Следовательно, tg ? максимальное значение для tg ?.

tg ? = lim от?x-0 tg ? = lim от?x-0 ?у/?x

Таблица производных

Если проговаривать формулировку каждой формулы производных . Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
2) Х со штрихом равняется единице.
3) Если есть постоянный множитель, просто выносим ео за производную.
4) Чтобы найти производную степень, нужно показатель данной степени умножить на степень с таким же основанием, у которого показатель на 1 меньше.
5) Поиск корня равен одному, деленному 2 этих корня.
6) Производная одного, деленного на Х равняется одному разделенному на Х возведенный в квадрат, со знаком минус.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
10) П котангенс равняется одному со знаком минус, деленная на синус в квадрате.

В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.

1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
3) Производная в делении равняется умножению первого значения на второе, отнимая от себя умножение второго значения на первое. Дробь деления на второе значение в квадрате.
4) Формулировка является частным случаем третьей формулы.

В этом уроке мы продолжаем изучать производные функций и переходим к более сложной теме, а именно, к производным произведения и частного. Если вы смотрели предыдущий урок, то наверняка поняли, что мы рассматривали лишь самые простые конструкции, а именно, производную степенной функции, суммы и разности. В частности, мы узнали, что производная суммы равна их сумме, а производная разности равна, соответственно, их разности. К сожалению, в случае с производными частного и произведения формулы будут гораздо сложнее. Начнем мы именно с формулы производной произведения функций.

Производные тригонометрических функций

Для начала позволю себе небольшое лирическое отступление. Дело в том, что помимо стандартной степенной функции — $y={{x}^{n}}$, в этом уроке будут встречаться и другие функции, а именно, $y=\sin x$, а также $y=\cos x$ и прочая тригонометрия — $y=tgx$ и, разумеется, $y=ctgx$. {\prime }}=1\cdot \left(\sqrt{x}-1 \right)+x\frac{1}{3\sqrt{x}}= \\& =\sqrt{x}-1+\sqrt{x}\cdot \frac{1}{3}=\frac{4}{3}\sqrt{x}-1 \\\end{align}\]

Ответ найден.

Зачем раскладывать производные на множители?

Только что мы использовали несколько очень важных математических фактов, которые сами по себе не имеют отношения к производным, однако без их знания все дальнейшее изучение этой темы просто не имеет смысла.

Во-первых, решая самую первую задачу и, уже избавившись от всех знаков производных, мы зачем-то начали раскладывать это выражение на множители.

Во-вторых, решая следующую задачу, мы несколько раз переходили от корня к степени с рациональным показателем и обратно, при этом используя формулу 8-9-го класса, которую стоило бы повторить отдельно.

По поводу разложения на множители ― зачем вообще нужны все эти дополнительные усилия и преобразования? На самом деле, если в задаче просто сказано «найти производную функции», то эти дополнительные действия не требуются. Однако в реальных задачах, которые ждут вас на всевозможных экзаменах и зачетах, просто найти производную зачастую недостаточно. Дело в том, что производная является лишь инструментом, с помощью которой можно узнать, например, возрастание или убывание функции, а для этого требуется решать уравнение, раскладывать его на множители. И вот здесь этот прием будет очень уместен. Да и вообще, с функцией, разложенной на множители, гораздо удобней и приятней работать в дальнейшем, если требуются какие-то преобразования. Поэтому правило № 1: если производную можно разложить на множители, именно так и стоит поступать. И сразу правило № 2 (по сути, это материал 8-9-го класса): если в задаче встречается корень n -ной степени, причем, корень явно больше двух, то этот корень можно заменить обычной степенью с рациональным показателем, причем в показателе появится дробь, где n ― та самая степень ― окажется в знаменателе этой дроби.

Разумеется, если под корнем присутствует какая-то степень (в нашем случае это степень k ), то она никуда не девается, а просто оказывается в числителе этой самой степени. {2}}}\]

Мы нашли ответ. Как и предполагалось, объем вычисления оказался существенно меньше, чем для первой функции.

В чем разница между обозначениями?

У внимательных учеников наверняка уже возник вопрос: почему в одних случаях мы обозначаем функцию как $f\left(x \right)$, а в других случаях пишем просто $y$? На самом деле, с точки зрения математики нет абсолютно никакой разницы ― вы вправе использовать как первое обозначение, так и второе, при этом никаких штрафных санкций на экзаменах и зачетах не последует. Для тех, кому все-таки интересно, поясню, почему авторы учебников и задач в одних случаях пишут $f\left(x \right)$, а в других (гораздо более частых) ― просто $y$. Дело в том, что записывая функцию в виде\, мы неявно намекаем тому, кто будет читать наши выкладки, что речь идет именно об алгебраической интерпретации функциональной зависимости. Т. е., есть некая переменная $x$, мы рассматриваем зависимость от этой переменной и обозначаем ее $f\left(x \right)$. При этом, увидев вот такое обозначение, тот, кто будет читать ваши выкладки, например, проверяющий, будет подсознательно ожидать, что в дальнейшем его ждут лишь алгебраические преобразования ― никаких графиков и никакой геометрии.

С другой стороны, используя обозначения вида\, т. е., обозначая переменную одной единственной буквой, мы сразу даем понять, что в дальнейшем нас интересует именно геометрическая интерпретация функции, т. е., нас интересует, в первую очередь, ее график. Соответственно, столкнувшись с записью вида\, читатель вправе ожидать графических выкладок, т. е., графиков, построений и т. д., но, ни в коем случае, не аналитических преобразований.

Еще хотел бы обратить ваше внимание на одну особенность оформления задач, которые мы сегодня рассматриваем. Многие ученики считают, что я привожу слишком подробные выкладки, и многие из них можно было бы пропустить или просто решить в уме. Однако именно такая подробная запись позволит вам избавится от обидных ошибок и значительно увеличит процент правильно решенных задач, например, в случае самостоятельной подготовки к контрольным или экзаменам. Поэтому если вы еще неуверенны в своих силах, если вы только начинаете изучать данную тему, не спешите ― подробно расписывайте каждый шаг, выписывайте каждый множитель, каждый штрих, и очень скоро вы научитесь решать такие примеры лучше, чем многие школьные учителя. {2}}x} \\\end{align}\]

Теперь, если мы сравним полученный результат с тем, что мы получили ранее, при вычислении по другому пути, то мы убедимся, что получили одно и то же выражение. Таким образом, каким бы путем мы не шли при вычислении производной, если все посчитано верно, то ответ будет одним и тем же.

Важные нюансы при решении задач

В заключении хотел бы рассказать вам еще одну тонкость, связанную с вычислением производной частного. То, что я вам сейчас расскажу, не было в изначальном сценарии видеоурока. Однако за пару часов до съемок я занимался с одним из своих учеников, и мы как раз разбирали тему производных частного. И, как выяснилось, этот момент многие ученики не понимают. Итак, допустим, нам нужно посчитать снять штрих следующей функции:

В принципе, ничего сверхъестественного на первый взгляд в ней нет. Однако в процессе вычисления мы можем допустить много глупых и обидных ошибок, которые я бы хотел сейчас разобрать.

Итак, считаем эту производную. {\prime }}$ можно рассматривать и как производную частного, и как производную степенной функции. При этом если все вычисления выполнены верно, то ответ всегда получится одним и тем же. Во-вторых, при вычислении производных, содержащих и переменную, и константу, принципиально важным является то, где находится переменная ― в числителе или в знаменателе. В первом случае, когда переменная находится в числителе, мы получаем простую линейную функцию, которая элементарно считается. А в случае, если переменная стоит в знаменателе, то мы получаем более сложное выражение с сопутствующими выкладками, приведенными ранее.

На этом урок можно считать законченным, поэтому если вам что-то непонятно по производным частного или произведения, да и вообще, если у вас есть любые вопросы по этой теме, не стесняйтесь ― заходите на мой сайт, пишите, звоните, и я обязательно постараюсь вам помочь.

Сами по себе производные ― тема отнюдь не сложная, но очень объемная, и то, что мы сейчас изучаем, будет использоваться в будущем при решении более сложных задач. 2}\] \(\bullet\) Производная сложной функции: \[\big(h(f(x))\big)’=h’_f(f)\cdot f’_x(x)\]

 

Факт 3.
\(\bullet\) Если \(y=f(x)\) – некоторая функция, то касательная к ней в точке с абсциссой \(x_0\) имеет вид: \[y=f(x_0)+f'(x_0)\cdot (x-x_0)\] \(\bullet\) Следовательно, \(k=f'(x_0)=\mathrm{tg}\,\alpha\) – тангенс угла наклона касательной к положительному направлению оси \(Ox\), он же угловой коэффициент касательной, если ее уравнение записать как \(y=kx+b\).

 

Факт 4.
\(\bullet\) Если \(f'(x)>0\) на \((a;b)\), то \(f(x)\) возрастает на \((a;b)\).
\(\bullet\) Если \(f'(x)<0\) на \((a;b)\), то \(f(x)\) убывает на \((a;b)\).
\(\bullet\) Если \(f'(x_0)=0\) и в точке \(x_0\) производная меняет свой знак, то \(x_0\) — функции \(f(x)\):
— если производная меняет знак с “\(-\)” на “\(+\)” (считая слева направо), то \(x_0\) — ;
— если производная меняет знак с “\(+\)” на “\(-\)” (считая слева направо), то \(x_0\) — . b f(x)\,dx=F(b)-F(a)\] \(\bullet\) Тогда \(F(b)-F(a)\) равно площади закрашенной фигуры \(ABCD\), называемой криволинейной трапецией:

 

Исчисление I — Формулы дифференцирования

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-3: Формулы дифференциации

В первом разделе этой главы мы увидели определение производной и вычислили пару производных, используя это определение. Как мы видели в этих примерах, вычисление пределов требовало большого объема работы, а функции, с которыми мы работали, были не очень сложными.

Для более сложных функций использование определения производной было бы почти невыполнимой задачей. К счастью для нас, нам не придется слишком часто использовать это определение. Нам придется использовать его время от времени, однако у нас есть большой набор формул и свойств, которые мы можем использовать, чтобы значительно упростить нашу жизнь и позволят нам избежать использования определения, когда это возможно.\prime} = f’\left( x \right) \pm g’\left( x \right)\hspace{0.25in} \mbox{OR} \hspace{0.25in}\frac{d}{{dx} }\left( {f\left( x \right) \pm g\left( x \right)} \right) = \frac{{df}}{{dx}} \pm \frac{{dg}}{ {дх}}\)

Другими словами, чтобы дифференцировать сумму или разность, все, что нам нужно сделать, это дифференцировать отдельные термины, а затем сложить их вместе с соответствующими знаками. Обратите внимание, что это свойство не ограничивается двумя функциями.

Доказательство этого свойства см. в разделе «Доказательство различных производных формул» в главе «Дополнительно».\prime} = cf’\left( x \right)\hspace{0.25in} \mbox{OR} \hspace{0.25in}\frac{d}{{dx}}\left( {cf\left( x \ right)} \right) = c\frac{{df}}{{dx}}\), \(c\) — любое число

Другими словами, мы можем «вынести» мультипликативную константу из производной, если нам нужно. Доказательство этого свойства см. в разделе «Доказательство различных производных формул» главы «Дополнительно».

Обратите внимание, что мы не включили здесь формулы для производных произведений или частных двух функций.Производная произведения или частное двух функций не есть произведение или частное производных отдельных частей. Мы рассмотрим их в следующем разделе.

Далее, давайте кратко рассмотрим пару основных «вычислительных» формул, которые позволят нам фактически вычислить некоторые производные.

Формулы

1. Если \(f\влево( x \вправо) = c\), то \(\displaystyle f’\влево( x \вправо) = 0\hspace{0,25 дюйма} \mbox{ИЛИ} \hspace{0. {n — 1}}\), \(n\) — любое число.

   Эту формулу иногда называют степенным правилом . Все, что мы здесь делаем, это ставим исходный показатель степени вперед, умножаем и затем вычитаем единицу из исходного показателя степени.

   Также обратите внимание, что для использования этой формулы \(n\) должно быть числом, оно не может быть переменной. Также обратите внимание, что основание, \(x\), должно быть переменной, а не числом. В некоторых последующих разделах будет заманчиво злоупотреблять степенным правилом, когда мы запускаем некоторые функции, где показатель степени не является числом и/или основание не является переменной.

   Доказательство этой формулы см. в разделе «Доказательство различных производных формул» в главе «Дополнительно». На самом деле в этом разделе есть три разных доказательства. Первые два ограничивают формулу тем, что \(n\) является целым числом, потому что на данный момент это все, что мы можем сделать на данный момент. { — \, \, \ frac {7} {5}}} \конец{выравнивание*}\]

   Убедитесь, что вы можете работать с дробными показателями.{\ кв. 2 — 1}} \]

   Ответ немного запутан, и мы не будем уменьшать показатели до десятичных дробей. Тем не менее, эта проблема не так уж сложна, она просто выглядит так на первый взгляд.

   Существует общее правило, касающееся деривативов этого класса, и вам необходимо выработать привычку его использовать. Когда вы видите радикалы, вы всегда должны сначала преобразовать радикал в дробную экспоненту, а затем максимально упростить экспоненту. Соблюдение этого правила избавит вас от многих проблем в будущем.2}} \right)\) Показать решение

   В этой функции мы не можем просто дифференцировать первое слагаемое, дифференцировать второе слагаемое, а затем снова умножать их. Это просто не сработает. Мы подробно обсудим это в следующем разделе, поэтому, если вы не уверены, что верите в это, подождите немного, и мы скоро рассмотрим это, а также покажем вам пример того, почему это не сработает. 3}}} + 4\) увеличивается, уменьшается или не изменяется в \(х = — 2\)? Показать решение

   Мы знаем, что скорость изменения функции определяется производной функции, поэтому все, что нам нужно сделать, это переписать функцию (чтобы иметь дело со вторым членом), а затем взять производную.4}}}\]

   Обратите внимание, что мы переписали последний член производной обратно в виде дроби. Это не то, что мы делали до сих пор, и это делается здесь только для того, чтобы помочь с оценкой на следующем этапе. Часто проще проводить оценку с положительными показателями.

   Итак, вычислив производную, мы получим

   \[f’\left( { — 2} \right) = 6\left( 4 \right) — \frac{{900}}{{16}} = — \frac{{129}}{4} = — 32.25\]

   Итак, при \(x = — 2\) производная отрицательна, поэтому функция убывает при \(x = — 2\).

   Пример 4 Найдите уравнение касательной к \(f\left( x \right) = 4x — 8\sqrt x \) в точке \(x = 16\). 2} — 7t + 10} \right) = 6\left( {t — 2 } \вправо)\влево( {т — 5} \вправо)\]

   Причина факторинга дериватива станет очевидной в ближайшее время.

   Теперь нам нужно определить, где производная положительная, а где отрицательная. Есть несколько способов сделать это. Мы предпочитаем следующий метод.

   Поскольку многочлены непрерывны, мы знаем из теоремы о промежуточном значении, что если многочлен когда-либо меняет знак, то он должен сначала пройти через нуль. Итак, если бы мы знали, где производная равна нулю, мы знали бы единственные точки, в которых производная могла бы изменить знак .

   Из факторизованной формы производной видно, что производная будет равна нулю при \(t = 2\) и \(t = 5\). Нанесем эти точки на числовую прямую.

   Теперь мы можем видеть, что эти две точки делят числовую прямую на три отдельных участка. В каждой из этих областей мы знаем , что производная будет того же знака. Напомним, что производная может менять знак только в двух точках, которые используются для деления числовой строки на области.

   Следовательно, все, что нам нужно сделать, это проверить производную в контрольной точке в каждой области, и производная в этой области будет иметь тот же знак, что и контрольная точка. Вот числовая строка с показанными тестовыми точками и результатами.

   Здесь указаны интервалы, в которых производная положительна и отрицательна.

   \[\begin{array}{rl}{{\mbox{positive : }}}&{ — \infty

   Мы включили здесь отрицательные \(t\), потому что могли бы, даже если они не имеют особого смысла для этого проблема.Зная это, мы также можем ответить на вопрос. Объект движется вправо и влево со следующими интервалами.

   \[\begin{array}{rl}{{\mbox{перемещение вправо: }}}&{ — \infty

   Убедитесь, что вы можете выполнять работу, которую мы только что сделали в этом примере. В течение следующих двух глав вас будут много раз просить определить, где функции положительны и/или отрицательны. Если вам нужен обзор или вы хотите попрактиковаться в подобных задачах, вам следует обратиться к разделу «Решение неравенств» в обзоре алгебры/триггеров.

   Формулы для первой производной функции

   y является функцией y = y(x)
   C = константа, производная (y’) константы равна 0

   у = С => у’ = 0
   

   Пример: у = 5, у’ = 0

   Если y является функцией типа y = x ⁿ формула производной:

   y = x ⁿ => y’ = nx ^n-1

   Пример: y = x ³ y’ = 3x ^3-1 = 3x ²
   y = x ^-3 y’ = -3x ^-4

   Из верхней формулы мы можем сказать для производной y’ функции y = x = x ¹ , что:

   если у = х, то у’=1

   у = f ₁ (х) + f ₂ (х) + f ₃ (х) …=>
   y’ = f’ ₁ (x) + f’ ₂ (x) + f’ ₃ (x) . ..

   Эта формула представляет собой производную функции, являющейся суммой функций.
   Пример: если у нас есть две функции f(x) = x ² + x + 1 и g(x) = x ⁵ + 7 и y = f(x) + g(x), тогда y’ = f'(x) + g'(x) =>
   y’ = (x ² + x + 1)’ + (x ⁵ + 7)’ = 2x ¹ + 1 + 0 + 5x ⁴ + 0 = 5x ⁴ + 2x + 1
   

   Если функция кратна двум функциям, производная определяется как:

   у = f (х).g(x) => y’ = f'(x)g(x) + f(x)g'(x)

   Если f(x) = C(C — константа) и y = f(x)g(x)
   y = Cg(x) y’=C’.g(x) + C.g'(x) = 0 + С.д'(х) = С.д'(х)

   y = Cf(x) => y’ = Cf'(x)

   В разделе задачи есть примеры следующих формул.

   г =

   г’ =

   f'(x)g(x) — f(x)g'(x) g 2 (x)

   у = ln х => у’ = ¹ / _х

   у = е ^х => у’ = е ^х

   у = грех х => у’ = потому что х

   y = cos x => y’ = -sin x

   y = tan x => y’ = ¹ / _{cos ² x}

   y = кроватка x => y’ = — ¹ / _{sin ² x}

   Когда функция является функцией функции: u = u(x)

   у = f (и) => у’ = f’ (и). ты

   Пример: пусть y = sin(x ² )
   Здесь u = x ² , f(u) = sin(u), производные f'(u) = cos(u), u’ = 2x
   y’ = (sin(u))’⋅u’ = cos(x ² )⋅2x = 2⋅x⋅cos(x ² )

   Задачи на производные

   1) f(x) = 10x + 4y. Чему равна первая производная f'(x) = ?
   Решение: Мы можем использовать формулу для производной функции, которая является суммой функции
   f(x) = f ₁ (x) + f ₂ (x), f ₁ (x) = 10x, f ₂ (x) = 4y для функции f ₂ (x) = 4y, y является константой, поскольку аргумент f ₂ (x) равен x поэтому f’ ₂ (x) = (4y)’ = 0.Следовательно, производная функция f(x): f'(x) = 10 + 0 = 10.

   ---

   2) Вычислите производную f(x) =

   Решение: У нас есть две функции h(x) = x ¹⁰ и g(x) = 4,15 + cos x
   , функция f(x) равна h(x), деленной на g(x). h'(x) = 10x ⁹ g'(x) = 0 — sin x = -sin x

   f'(x) =

   h'(x).g(x) — h(x).g'(x) (g(x)) 2

   f'(х) =

   10x 9 (4.15 + cos x) — x 10 (-sin x) (4.15 + cosx) 2

   =

   x 10 sin x + 10(60 + cos x)x 9 (60 + cosx) 2 3 3) f(x) = ln(sinx). чему равна производная функции f(x)? Решение: Чтобы решить задачу, мы должны использовать последнюю формулу. Как мы видим, f(x) является функцией функции функции f(x) = h(g(x)), где h = ln и g = sin x Калькулятор производных Подробнее о производных на математическом форуме Регистрация на форуме Производная формула функции. Стандартное обозначение, производное от некоторых… | Фикри Мульяна Сетиаван | Упрощенная математика Исчисление для всех Стандартное обозначение, производная некоторых общих функций и цепное правило дифференцирования Как я объяснял в предыдущей статье, основная тема производных/дифференциалов заключается в том, насколько быстро происходит изменение. И — как вы знаете —  скорость изменения представлена ​​градиентом функции на графике . То есть чем больше градиент функции, тем быстрее изменяется значение функции. В предыдущей статье мы видели, что градиент функции в точке может быть выражен как f’(x). f’(x) также показывает скорость изменения функции f(x). f’(x) — это то, что мы назвали производной/дифференцированием f(x). Прежде чем перейти к следующему обсуждению, следует знать, что существует специальное обозначение, которым можно заменить приведенную выше формулу для производной. ∆x обозначается как dx, а f(x+∆x)-f(x) обозначается как df(x) или dy. буква d в ​​dx и dy представляет изменение значения , заменяя символ ∆x.использование этого обозначения с буквой d также приводит к записи limit x->0 больше не требуется, потому что буква d в ​​самом dx представляет собой очень небольшое отличие от x. Итак, мы можем сказать, что f’(x)=dy/dx. Это обозначение означает « разделить очень маленькое значение y на очень маленькое значение x ». Это обозначение f’(x) = dy/dx — это то, что мы будем часто использовать в дифференциале позже. Есть несколько производных общих функций, о которых следует помнить.Икс. 4. Производная f(x) = ln x Из приведенного выше расчета мы знаем, что производная ln x равна 1/x. С помощью приведенной выше формулы нам очень легко вычислить производную функции. Например, легко вычислить производную x². А как насчет производной от (x+3)²? Это легко, нам просто нужно расширить его, вычислив (x+3)(x+3) как обычно. А как насчет производной от (x+3)⁵⁶? Вы все еще хотите расширить его? Нет, вы потратите слишком много времени. К счастью, у нас есть цепное правило, чтобы решить эту проблему. Вот утверждение, которое я процитировал с сайта khanacademy.org : Цепное правило гласит, что производная от f(g(x)) равна f’(g(x))⋅g’(x). Другими словами, это помогает нам различать *составные функции*. Например, sin(x²) является составной функцией, поскольку ее можно построить как f(g(x)) для f(x)=sin(x) и g(x)=x². Итак, цепное правило можно использовать для получения составной функции. Если вы забыли, составная функция — это просто функция, в которой есть другая функция.Общая форма — f (g (x)), где функция g (x) становится областью определения функции f (x). Примером может служить функция (x+3)⁵⁶ ранее. Функция g(x) здесь равна g(x)=x+3 и f(x) =x⁵⁶. Тогда как использовать цепное правило для производных составных функций? Это просто. Предположим, что функция, которую вы хотите вывести, это f(g(x)). Чтобы вычислить производную, вы должны вывести функцию f(g(x)) по g(x), а затем умножить на производную функции g(x) по x. Для функции f(g(h(x))) метод тот же.Выведите функцию f(g(h(x))) относительно g(h(x)), затем умножьте результат на производную от g(h(x)) по h(x). Затем результат умножается на производную от h(x) по x. Это правило применяется, потому что в основном, потому что производная (dy/dx) — это просто дробь, поэтому мы можем разбить ее на более мелкие дроби, например: Какова производная от (x+3)⁵⁶? Какова производная следующей функции f(x)? Как вычислять производные — видео и расшифровка урока Вычисление производных Возможно, вы помните нечто, называемое разностным коэффициентом, из курса алгебры или предварительного исчисления.Коэффициент разности функции f ( x ) представляет собой формулу, которая дает наклон линии через любые две точки с x -координатами x и x + h на функции: ( f ( x + h ) — f ( x )) / h Это ключ к вычислению производных. Производные вычисляются путем нахождения предела разностного отношения функции, когда ч приближается к 0, как вы можете видеть ниже. В принципе, мы можем вычислить производную f ( x ), используя предельное определение производных со следующими шагами: Найти f ( x + h). Вставьте f ( x + h ), f ( x ) и h в предельное определение производной. Упростить частное разности. Возьмите предел, поскольку h приближается к 0, упрощенного разностного частного. Пример Итак, рассмотрим нашу гоночную функцию f(x) = -7×2 + 280x. Сначала мы находим F ( x + H ): F ( x + h ) = -7 ( x + h ) 2 + 280 ( x + h ) = -7 ( x 2 + 2 h + h 2) + 280 x + 280 h = -7 x 2 — 7 h — 7 h — 7 ч. 2 + 280 x + 280 h Теперь мы подключаемся к определению предела, упрощаем и находим предел, как вы можете видеть здесь. Хорошо. Теперь, когда вы это сделали, мы видим, что производная f ( x ) равна: f ‘ ( x ) = -14 x + 280 Мы можем использовать эту формулу рассчитать скорость победителя в любой момент гонки. Например, рассмотрим ее скорость через 10 секунд. Подставляем x = 10 в формулу производной: f ‘ ( x ) = -14(10) + 280 = 140 Получаем, что производная f = x 90 составляет 140, так что через 10 секунд гонки она ехала со скоростью 140 миль в час! Вау, это так быстро! Другой пример Итак, еще один пример использования этого определения предела для вычисления производной.Рассмотрим функцию g ( x ) = 1 / x , где x ≠ 0. Чтобы найти производную, используя предельное определение производных, сначала найдем g ( x + h ): г ( x + ч ) = 1 / ( x + ч ) Теперь мы подставляем g ( x + h ), g ( x ) и h в определение предела и находим предел, как вы можете видеть ниже. Мы видим, что производное г ( x ) = 1/ x — г ‘( x ‘ ( x ) = -1 / x 2. Формулы для производных Мы всегда можем использовать предельное определение производных для вычисления производных. Однако у нас также есть несколько хороших формул для производных различных типов общих функций. Эти формулы являются прямым следствием предельного определения функции. Имея их под рукой, можно значительно упростить задачу, поэтому не стесняйтесь просматривать таблицу ниже: Давайте еще раз рассмотрим наш пример с гоночным автомобилем. Из таблицы видно, что производная суммы функций есть сумма производных. Следовательно, производная нашей функции гоночного автомобиля f ( x ) = -7 x 2 + 280 x равна сумме производных -7 x 2 и 280 x . Чтобы найти эти производные, мы видим, что изображение дает формулу для производной функции вида x n как nax ( n — 1). Следовательно, производная от -7 x 2 равна (2)(-7) x 2-1 = -14 x , а производная от 280 x равна (1)(280) x 0 = 280. Все вместе имеем, что производная от f ( x ) равна: f ‘ ( x ) = -14 x + 280 5 9 получаем, что получаем тот же результат, что и при использовании предельного определения производных. Резюме урока Производная функции, f ( x ), представляет собой скорость изменения значения функции относительно x . Мы можем вычислить производные, используя предельное определение производной, которое, как вы можете видеть здесь, делается путем нахождения предела разностного отношения функции, когда h приближается к 0: Это предельное определение можно использовать не только для вычисления производных, но и для нахождения формул для производных обычных функций, что в целом может значительно упростить вычисление производных. Чем больше мы работаем с производными, тем лучше мы знакомимся с такими сокращениями, как эти формулы, поэтому, вероятно, стоит продолжать практиковаться! Производная Производная Определение производной Дана производная функции f ( x ) в точке и обозначается Некоторые основные производные В таблице ниже u , v и w являются функциями переменной х . a , b , c и n являются константами (с некоторыми ограничениями всякий раз, когда они применяются). обозначают натуральный логарифм функция и e естественная база для . Напомним, что . Цепная линейка Последняя формула известна как формула цепного правила. Это может быть переписано как Другая аналогичная формула дается Производная обратной функции Обратной функцией y ( x ) является функция x ( y ), мы имеем Производная тригонометрических функций и их обратные Напомним определения тригонометрических функций Производная экспоненциальной и логарифмической функций Вспомним определение логарифмической функции с основанием a > 0. (с участием ): Производная гиперболических функций и их обратные Напомним определения тригонометрических функций Производные высшего порядка Пусть х = f ( х ).У нас есть: В некоторых книгах также используются следующие обозначения для высших производных. использовал: Высшая производная формула продукта: формула Лейбница Где биномиальные коэффициенты. Например, у нас есть [Дифференциальные уравнения] [Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Комплексные переменные] [Матричная алгебра] Домашняя страница S.O.S MATHematics Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем С.ОПЕРАЦИОННЫЕ СИСТЕМЫ. Математика CyberBoard. Copyright 1999-2022 MathMedics, LLC. Все права защищены. Свяжитесь с нами Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США пользователей онлайн за последний час Производная по первому принципу | Блестящая математика и естественные науки вики Рассмотрим функцию f:[a,b]→R,f : [a,b] \rightarrow \mathbb{R}, f:[a,b]→R, где a,b∈R a, b \in \mathbb{R} а,b∈R. Как правило, производная определяется только для значений в интервале (a,b) (a,b) (a,b).Пусть c∈(a,b) c \in (a,b) c∈(a,b) число, при котором измеряется скорость изменения. Сначала рассмотрим интервал (c,c+ϵ), (c, c+ \epsilon ),(c,c+ϵ), где ϵ \epsilon ϵ — число, сколь угодно близкое к нулю. Пусть 0<δ<ϵ 0 < \delta < \epsilon 0<δ<ϵ . Скорость изменения (m)(m)(m) определяется выражением f(x2)−f(x1)x2−x1 \frac{f(x_2) — f(x_1)}{x_2 — x_1} x2​−x1 ​f(x2​)−f(x1​)​. Таким образом, для заданного значения δ \delta δ скорость изменения от c cc до c+δ c + \delta c+δ может быть определена как м=f(c+δ)−f(c)(c+δ)−c.-} \frac{ f(c + h) — f(c) }{h}.m−​=h→0−lim​hf(c+h)−f(c)​. Говорят, что функция fff является производной в ccc, если m+=m− m_+ = m_- m+=m−​. Равное значение называется производной от fff при ccc. Предел lim⁡h→0f(c+h)−f(c)h \lim_{h \to 0} \frac{ f(c + h) — f(c) }{h} limh→0​hf (c+h)−f(c)​, если она существует (согласно вышеприведенным условиям), является производной от fff в ccc, и метод нахождения производной по такому пределу называется производной по первому принципу . Часто предел также выражается как ddxf(x)=lim⁡x→cf(x)−f(c)x−c\frac{\text{d}}{\text{d}x} f(x ) = \lim_{x \to c} \frac{ f(x) — f(c) }{xc} dxd​f(x)=limx→c​x−cf(x)−f(c)​. 6. Производные произведения и частные М. Борна ПРАВИЛО ПРОДУКТА Если u и v являются двумя функциями x , то производная произведения uv определяется как… `(d(uv))/(dx)=u(dv)/(dx)+v(du)/dx` На словах это можно запомнить как: «Производная произведения двух функций равна первому произведению второй производной плюс второму умножению производной первой.» Откуда взялась эта формула? Как и все встречающиеся нам формулы дифференцирования, она основана на производных от первых принципов. Пример 1 Если у нас есть продукт, подобный у = (2 х 2 + 6 x )(2 x 3 + 5 x 2 ) мы можем найти производную без умножения выражение справа. 2)` (в главе Дифференциация трансцендентных функций.) Почленно умножить это выражение невозможно, поэтому нужен метод дифференцирования произведений таких функций. Примечание Мы можем записать правило произведения разными способами: `(d(uv))/(dx)=uv’+vu’` ИЛИ `(d(fg))/(dx)` `=f(x)d/(dx)g(x)+g(x)d/(dx)f(x)`… и т. д. ЧАСТНОЕ ПРАВИЛО ( частное — это всего лишь дробь.2)` Нужна помощь в решении другой задачи исчисления? Попробуйте решение проблем. Отказ от ответственности: IntMath.com не гарантирует точность результатов. Решатель задач предоставлен Mathway. . РубрикаРазное Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт